Continuous and Intermittent Drying of Osmotically Pretreated Melon Pieces: Analysis of Energy Savings and Preservation of Bioactive Compounds
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Materials and Procedures
2.1.1. Materials Preparation
2.1.2. Pre-Treatment
2.1.3. Drying
2.2. Drying Described by Empirical Models: Energy Savings
2.3. Drying Described by a Diffusion Model: Moisture Distribution
2.4. Three-Dimensional Analytical Solution of the Diffusion Equation: Local Value and Mean Value
2.5. Optimizer for Determining the Parameters of Equation (23)
2.6. Characterization of Bioactive Compounds
3. Results
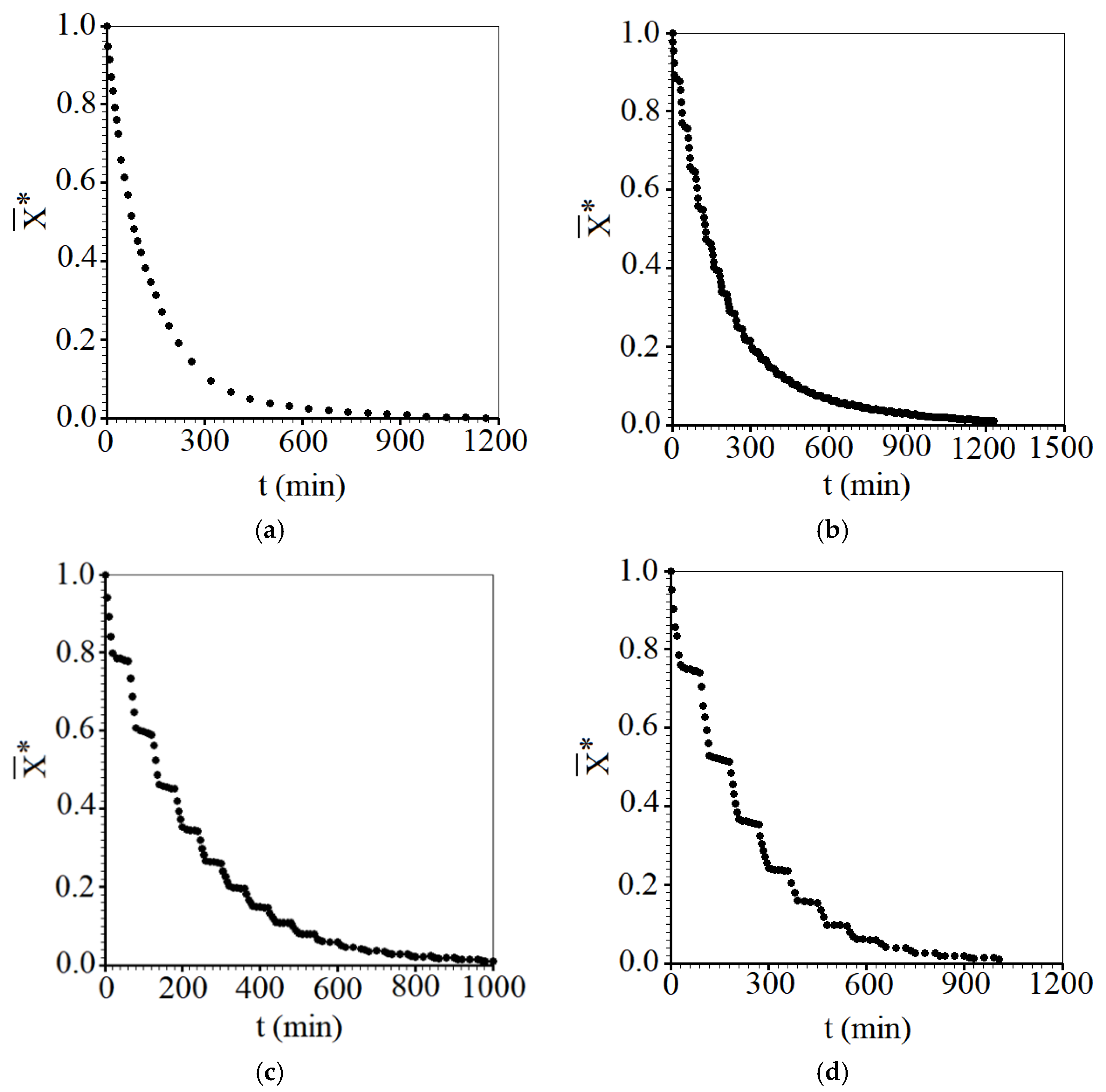
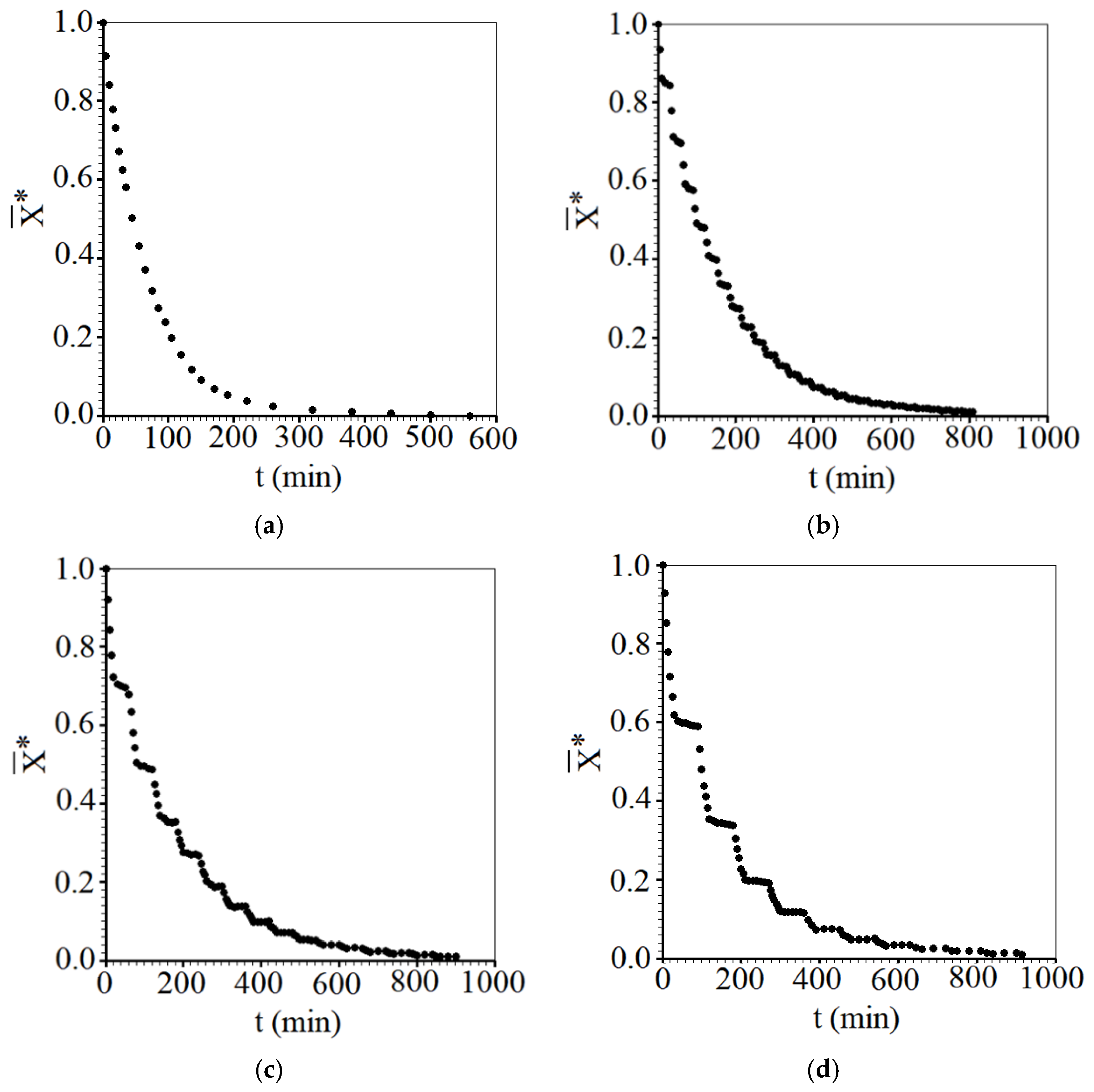
3.1. Experimental Results of Convective Drying
3.2. Drying Described by Empirical Models
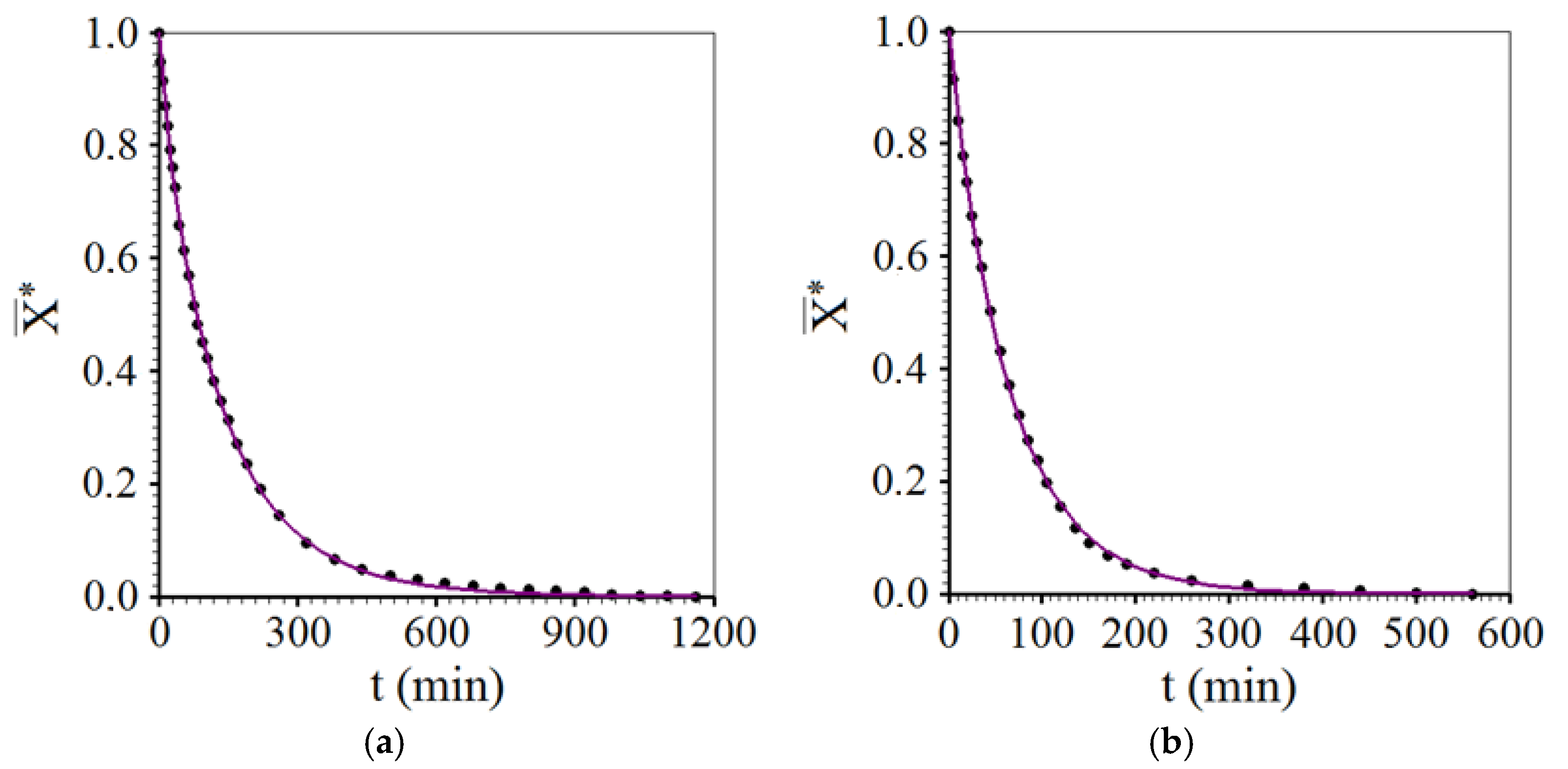
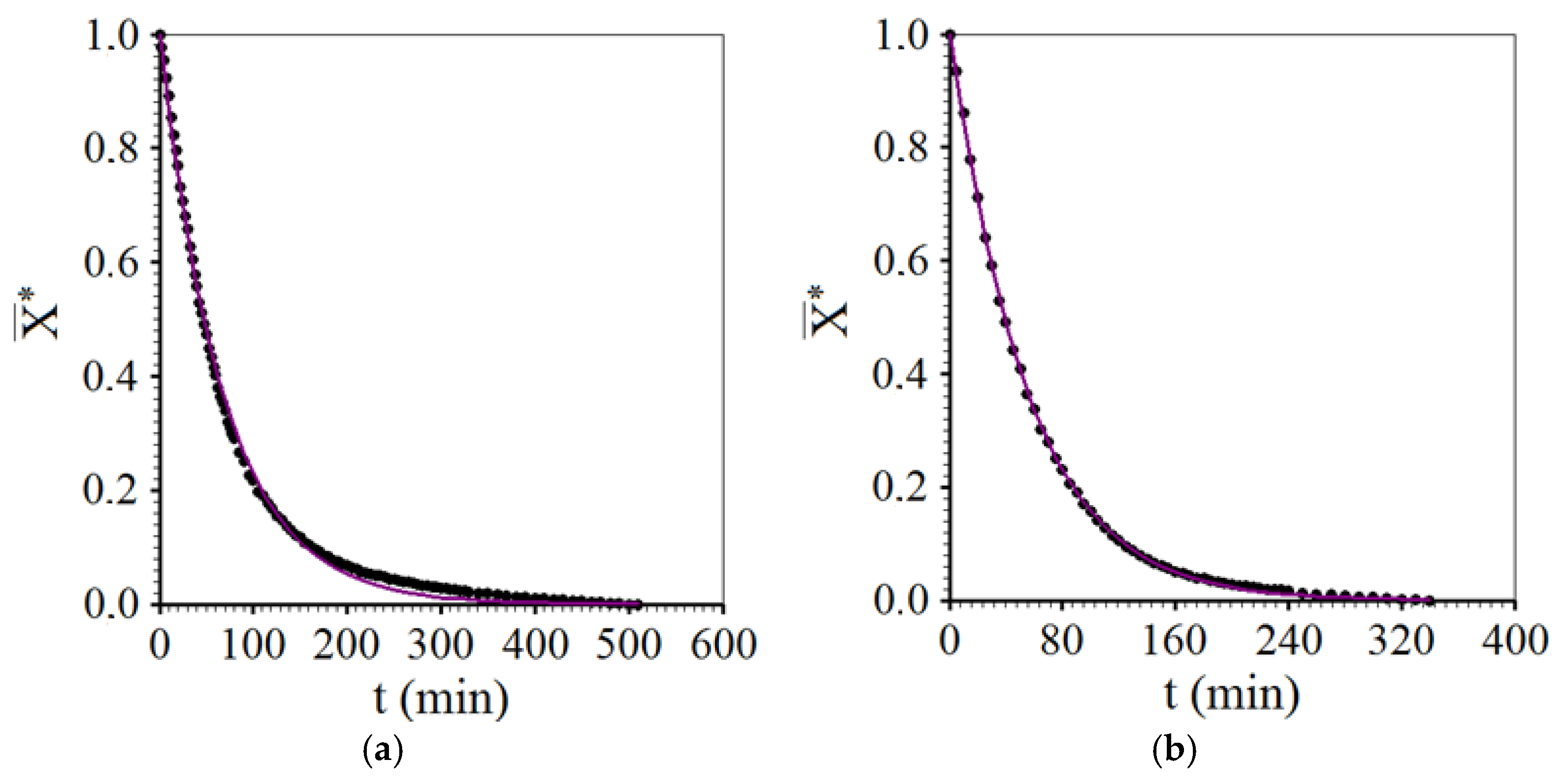
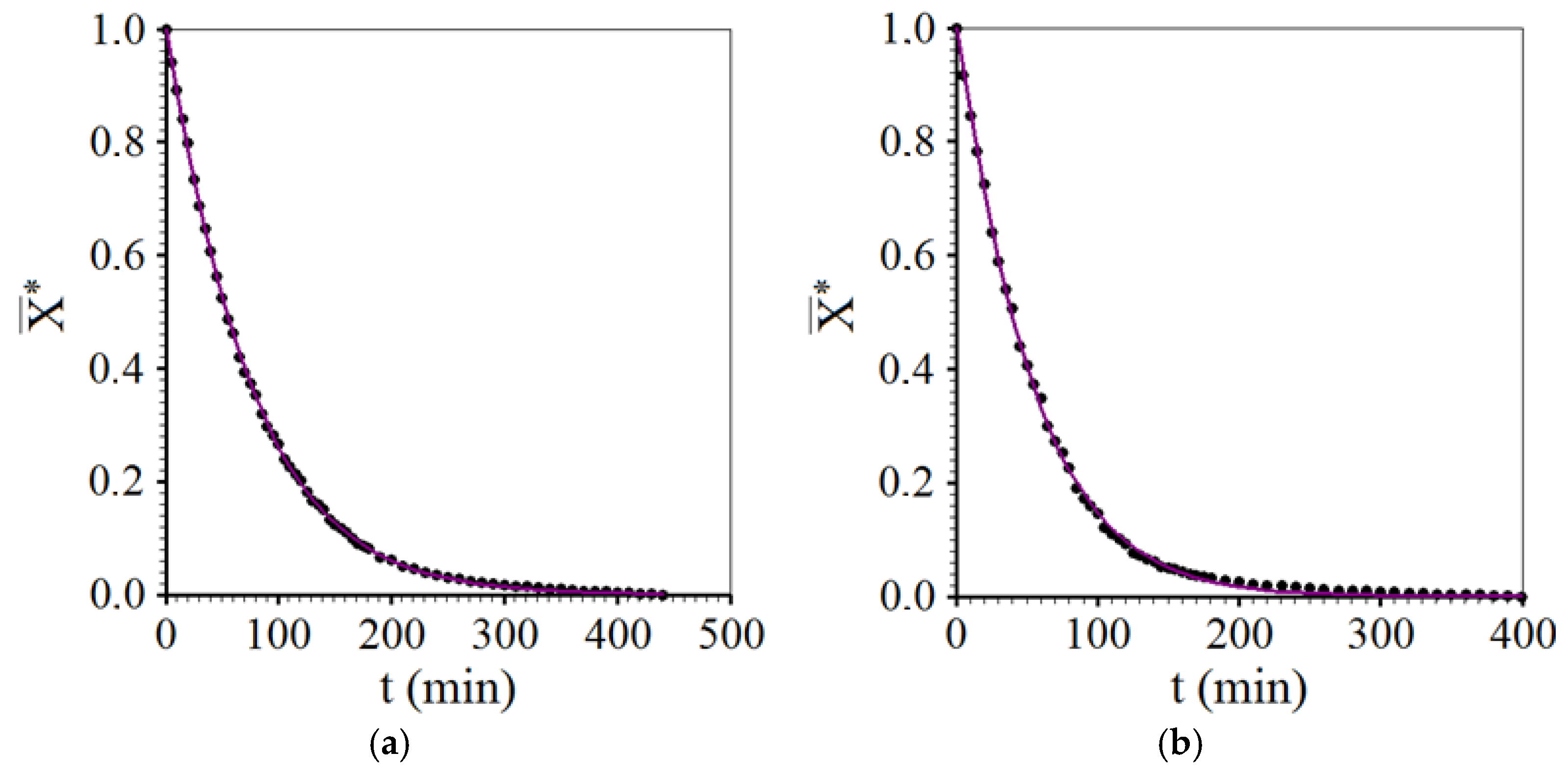
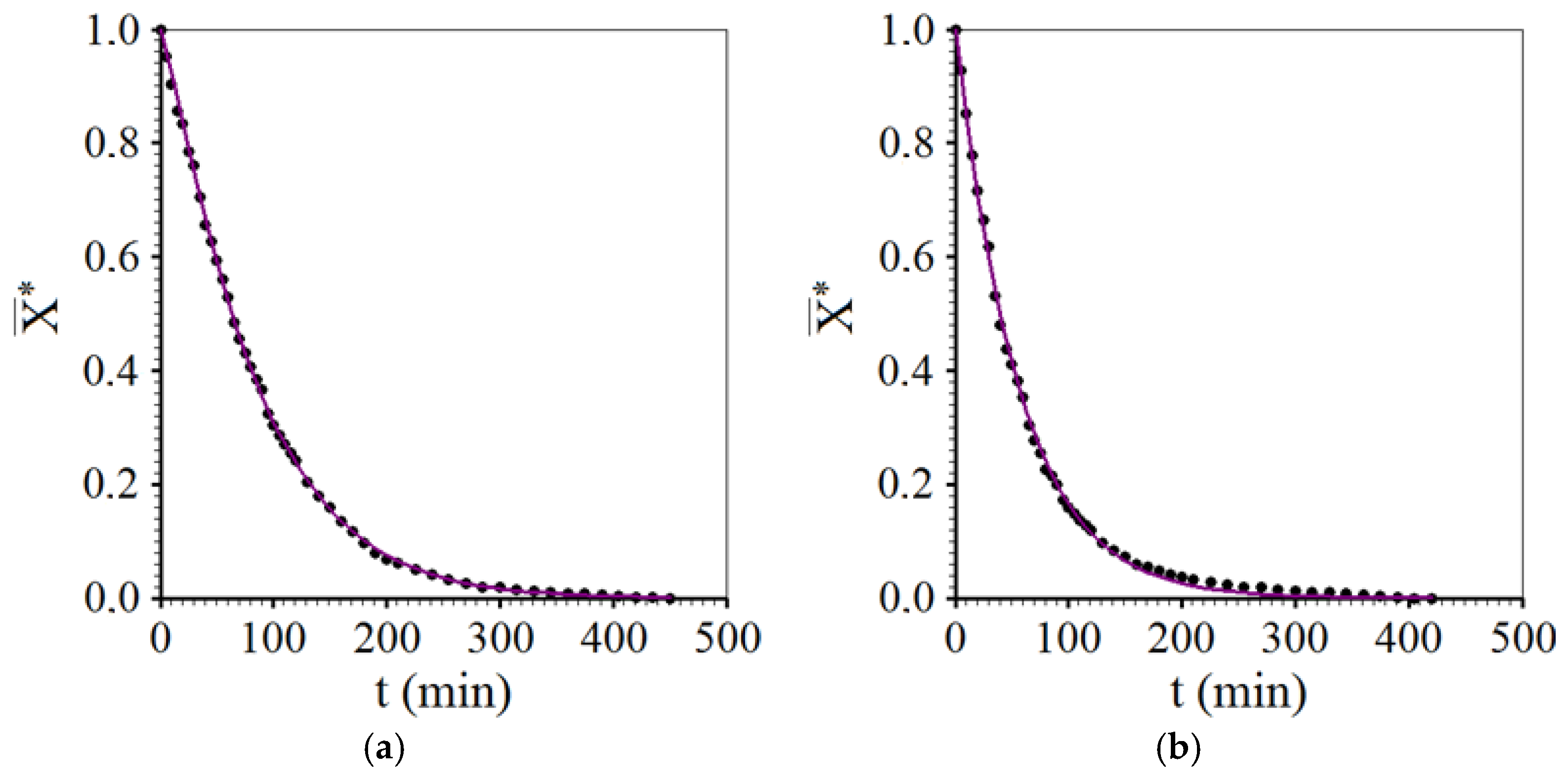
3.3. Drying Described by Diffusion Model
3.4. Bioactive Characterization of Dried Melon
4. Conclusions
- (1)
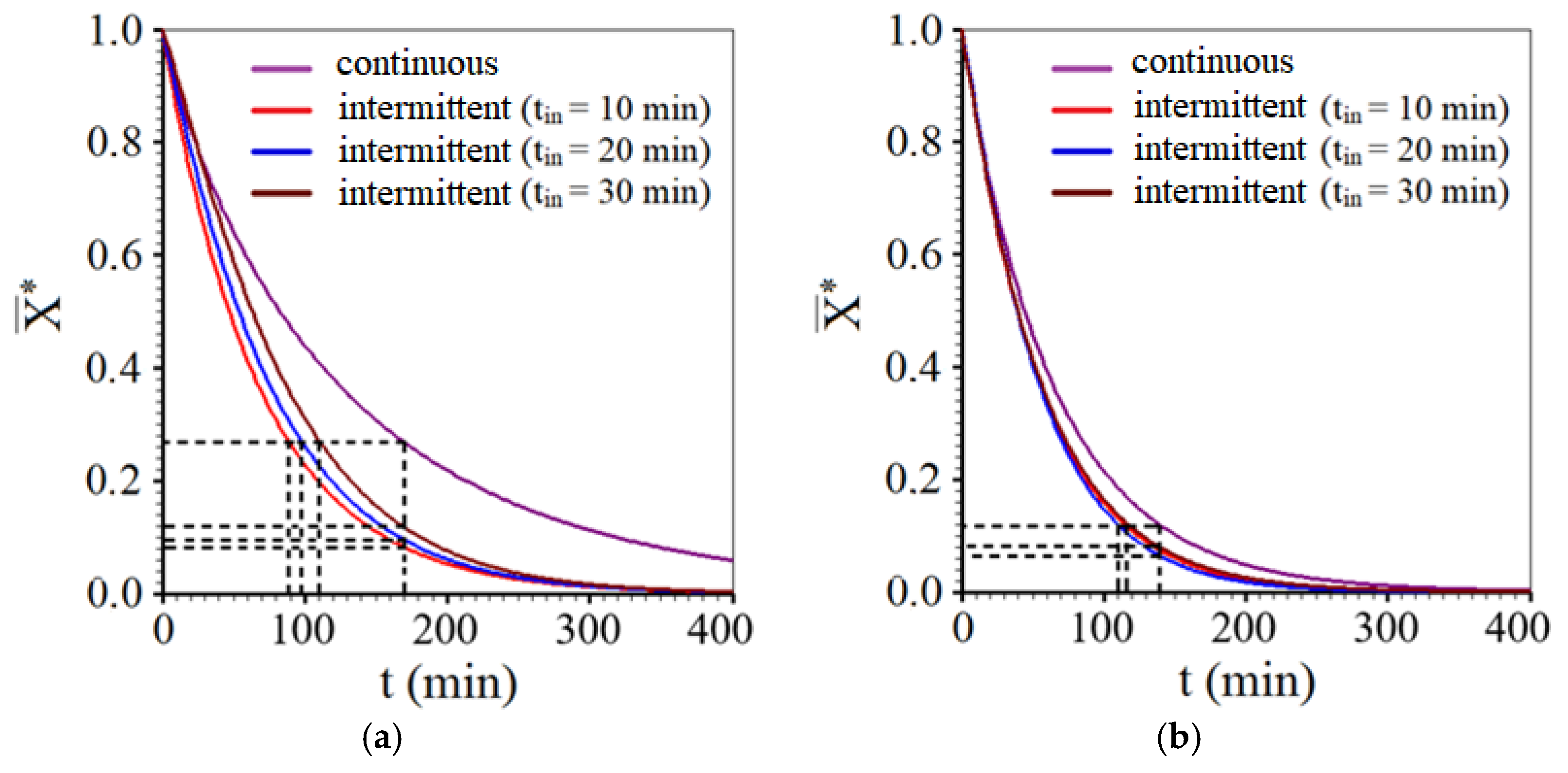
- Considering all the drying experiments, the greatest savings in effective operating time were obtained for the intermittent drying experiment with tin = 10 min, at 50 °C, resulting in a reduction of 47.1% compared to the time taken by continuous drying at the same temperature.
- (2)
- It was found that not only the intermittency is important for the reduction in the effective time, but also the tempering period, which considerably affected the drying kinetics, especially at the temperature of 50 °C. On the other hand, for the temperature of 70 °C, the tempering periods influenced the intermittent drying kinetics a little less. Even so, intermittent kinetics promoted an average reduction of approximately 21.4% in effective operating time compared to the time of continuous drying.
- (3)
- The three-dimensional diffusion model with third-kind boundary condition adequately described all the drying processes of melon pieces. In addition, the model clearly indicated the effect of intermittency compared to continuous drying: large increase in the effective mass diffusivity. This effect was responsible for increasing the drying rate and, consequently, reducing the energy consumption of the oven running at constant power.
- (4)
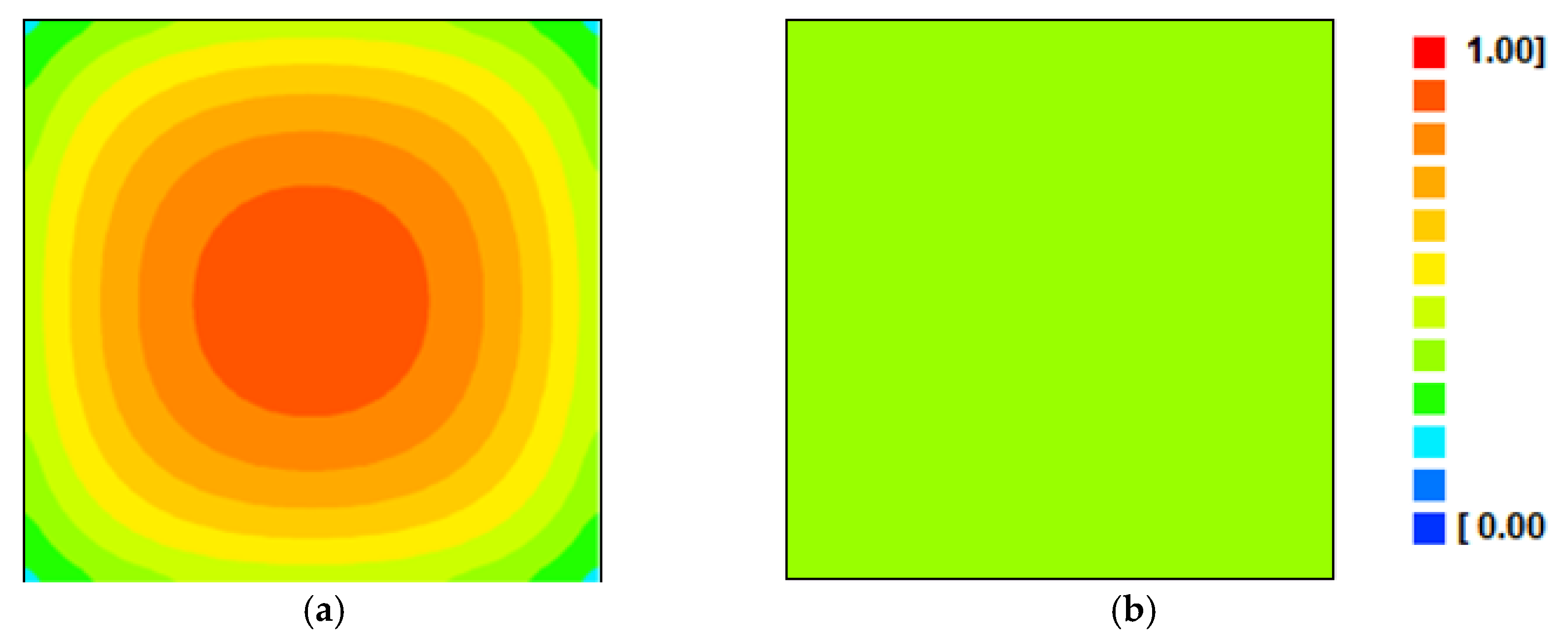
- Another effect of intermittency, compared to continuous drying, noticeable with the use of the diffusion model, consisted of the strong decrease in the Biot number for mass, as a consequence of the increase in effective diffusivity, indicating a more homogeneous distribution of moisture inside the product over time.
- (5)
- It was found that the type of drying influenced the bioactive properties of the final product. In general, there was a greater preservation of bioactive compounds in intermittent drying than in continuous drying. Regarding temperature, drying processes at 50 °C were, in general, the ones that most preserved these compounds.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kist, B.B. Anuário Brasileiro de Horti&Fruti 2022; Editora Gazeta Santa Cruz: Santa Cruz do Sul, Brazil, 2022; 96p. [Google Scholar]
- FAO. Food and Agriculture Organization of the United Nations. 2017. Available online: https://brasil.un.org/pt-br/78207-fao-30-de-toda-comida-produzida-no-mundo-vai-parar-no-lixo (accessed on 9 June 2024).
- Martins, F.P.; Neto, J.C.B.; Silva, A.J.O.; Siqueira, A.M.O. Drying: A Review. J. Eng. Exact Sci. 2020, 6, 4. [Google Scholar] [CrossRef]
- Silva, W.P.; Aires, J.E.F.; Castro, D.S.; Silva, C.M.D.P.S.; Gomes, J.P. Numerical description of guava osmotic dehydration including shrinkage and variable effective mass diffusivity. LWT-Food Sci. Technol. 2024, 59, 859–866. [Google Scholar] [CrossRef]
- Silva, W.P.; Silva, C.M.D.P.S.; Aires, J.E.F.; Silva Junior, A.F. Osmotic dehydration and convective drying of coconut slices: Experimental determination and description using one-dimensional diffusion model. J. Saudi Soc. Agric. Sci. 2014, 13, 162–168. [Google Scholar] [CrossRef]
- Salehi, F. Recent advances in the ultrasound-assisted osmotic dehydration of agricultural products: A review. Food Biosci. 2023, 51, 102307. [Google Scholar] [CrossRef]
- Kumar, C.; Karim, M.A.; Joardder, M.U.H. Intermittent drying of food products: A critical review. J. Food Eng. 2014, 121, 48–57. [Google Scholar] [CrossRef]
- Pham, N.D.; Khan, M.I.H.; Joardder, M.U.H.; Rahman, M.M.; Mahiuddin, M.D.; Abesinghe, A.M.N.; Karim, M.A. Quality of plant-based food materials and its prediction during intermittent drying. Crit. Rev. Food Sci. Nutr. 2019, 59, 1197–1211. [Google Scholar] [CrossRef] [PubMed]
- Van Engeland, C.; Spreutels, L.; Legros, R.; Haut, B. Comprehensive analysis of intermittent drying. A theoretical approach. Food Bioprod. Process. 2022, 13, 86–101. [Google Scholar] [CrossRef]
- Golmohammadi, M.; Foroughi-Dahr, M.; Rajabi-Hamaneh, M.I.; Shojamoradi, A.; Hashemi, S. Study on Drying Kinetics of Paddy Rice: Intermittent Drying. Iran. J. Chem. Chem. Eng. 2016, 35, 105–117. [Google Scholar]
- Diamante, L.M.; Ihns, R.; Savage, G.P.; Vanhanen, L. A new mathematical model for thin layer drying of fruits. Int. J. Food Sci. Technol. 2010, 45, 1956–1962. [Google Scholar] [CrossRef]
- Kaleta, A.; Górnicki, K. Evaluation of drying models of apple (var. McIntosh) dried in a convective dryer. Int. J. Food Sci. Technol. 2010, 45, 891–898. [Google Scholar] [CrossRef]
- Mercali, G.D.; Tessaro, I.C.; Norena, C.P.Z.; Marczak, L.D.F. Mass transfer kinetics during osmotic dehydration of bananas (Musa sapientum, Shum.). Int. J. Food Sci. Technol. 2010, 45, 2281–2289. [Google Scholar] [CrossRef]
- Silva, C.M.D.P.S.; Silva, W.P.; Farias, V.S.O.; Gomes, J.P. Effective diffusivity and convective mass transfer coefficient during the drying of bananas. Eng. Agrícola 2012, 32, 342–353. [Google Scholar] [CrossRef]
- Silva, W.P.; Silva, C.M.D.P.S. LAB Fit Curve Fitting Software, 2009, 7.2.46. Available online: www.labfit.net (accessed on 3 April 2024).
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Hemisphere Publishing Corporation: New York, NY, USA, 1980; Volume 1, p. 193. [Google Scholar]
- Beck, J.V.; Cole, K.D.; Haji-Sheikh, A.; Litkouhi, B. Heat Conduction Using Green’s Functions; Chapter Ten: Galerkin-Based Green’s Functions and Solutions; Hemisphere Publishing Corporation: New York, NY, USA, 1992; Volume 1, pp. 293–335. [Google Scholar]
- Maliska, C.R. Transferência de Calor e Mecânica dos Fluidos Computacional; LTC Editora S.A.: Rio de Janeiro, Brazil, 2004; p. 453. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2001; p. 912. [Google Scholar]
- Luikov, A.V. Analytical Heat Diffusion Theory; Academic Press, Inc. Ltd.: London, UK, 1992. [Google Scholar]
- Crank, J. The Mathematics of Diffusion; Clarendon Press: Oxford, UK, 1992; p. 414. [Google Scholar]
- Silva, W.P.; Precker, W.J.; Silva, C.M.D.P.S.; Gomes, J.P. Determination of effective diffusivity and convective mass transfer coefficient for cylindrical solids via analytical solution and inverse method: Application to the drying of rough rice. J. Food Eng. 2010, 98, 302–308. [Google Scholar] [CrossRef]
- Bevington, P.R.; Robinson, D.K. Data Reduction and Error Analysis for the Physical Sciences, 2nd ed.; WCB-McGraw-Hill: Boston, MA, USA, 1992. [Google Scholar]
- Taylor, J.R. An Introduction to Error Analysis, 2nd ed.; University Science Books: Sausalito, CA, USA, 1997. [Google Scholar]
- Silva, W.P.; Precker, W.J.; Silva, C.M.D.P.S.; Silva, D.D.P.S. Determination of the effective via minimization of the objective function by scanning: Application to drying of cowpea. J. Food Eng. 2009, 95, 298–304. [Google Scholar] [CrossRef]
- AOAC. Official Methods of Analysis, 43rd ed.; Association Official Analytical Chemistry: Washington, DC, USA, 1997; 1018p. [Google Scholar]
- Benassi, M.T.; Antunes, A.J. A comparison of metaphosphoric and oxalic acids as extractant solutions for the determination of vitamin C in selected vegetables. Arq. Biol. Tecnol. 1998, 31, 507–513. [Google Scholar]
- Lichtenthaler, H.K. Chlorophylls and carotenoids: Pigments of photosynthetic biomembranes. Methods Enzymol. 1987, 148, 350–382. [Google Scholar] [CrossRef]
- Francis, F.J. Analysis of anthocyanins. In Anthocyanins as Food Colors; Markakis, P., Ed.; Academic Press: New York, NY, USA, 1982; pp. 181–207. [Google Scholar]
- Silva, F.A.S.; Azevedo, C.A.V. The Assistat Software Version 7.7 and its use in the analysis of experimental data. Afr. J. Agric. Res. 2016, 11, 3733–3740. [Google Scholar]
- Silva, W.P.; Silva, C.M.D.P.S.; Gama, F.J.A.; Gomes, J.P. Mathematical models to describe thin-layer drying and to determine drying rate of whole bananas. J. Saudi Soc. Agric. Sci. 2014, 13, 67–74. [Google Scholar] [CrossRef]
- Mendonça, A.P.; Sampaio, P.T.B.; Almeida, F.A.C.; Ferreira, R.F.; Novais, J.M. Determinação das curvas de secagem das sementes de andiroba em secador solar. Rev. Bras. Eng. Agrícola Ambient. 2015, 19, 382–387. [Google Scholar] [CrossRef][Green Version]
- Santos, N.C.; Barros, S.L.; Monteiro, S.S.; Silva, S.N.; Ribeiro, V.H.A.; Silva, V.M.A.; Gomes, J.P.; Santiago, A.M.; Luiz, M.R.; Vieira, D.M.; et al. Kinetics of drying and physical-chemical quality of peach cv. Hubimel. J. Agric. Sci. 2019, 11, 223–232. [Google Scholar] [CrossRef]
- Lima, L.S.L.; SILVA, W.P.; Pereira, J.C.A.; Gomes, J.P.; Silva, C.M.D.P.S.; Júnior, A.F.S. Description of continuous and intermittent drying of sapodilla with elimination of tempering period: Saving in drying time. Sylwan 2020, 164, 444–459. [Google Scholar]
- Pereira, J.C.A.; Silva, W.P.; Gomes, J.P.; Queiroz, A.J.M.; Figueirêdo, R.M.F.; Melo, B.A.; Santiago, A.M.; Lima, A.G.B.; Macedo, A.D.B. Continuous and intermittent drying of rough rice: Effects on process effective time and effective mass diffusivity. Agriculture 2020, 10, 282. [Google Scholar] [CrossRef]
- Zhu, Z.; Yang, Z.; Wang, F. Experimental research on intermittent heat pump drying with constant and time-variant intermittency ratio. Dry. Technol. 2016, 34, 1630–1640. [Google Scholar] [CrossRef]
- Silva, R.C.; Silva, W.P.; Gomes, J.P.; Queiroz, A.J.M.; Figueirêdo, R.M.F.; Lima, A.G.B.; Rocha, A.P.T.; Silva, L.D.; Ferreira, J.P.L.; Santos, D.C.; et al. A New Empirical Model for Predicting Intermittent and Continuous Drying of “Neve” Melon (Cucumis melo sp.) Seeds. Agriculture 2022, 12, 328. [Google Scholar] [CrossRef]
- Filippin, A.P.; Filho, L.M.; Fadel, V.; Mauro, M.A. Thermal intermittent drying of apples and its effects on energy consumption. Dry. Technol. 2018, 36, 1662–1677. [Google Scholar] [CrossRef]
- Silva, W.P.; Galvão, I.B.; Silva, C.M.D.P.S.; Aires, J.E.F.; Figuêiredo, R.M.F. Empirical model for describing continuous and intermittent drying kinetics of apple pieces. Heat Mass Transf. 2019, 56, 1263–1274. [Google Scholar] [CrossRef]
- Silva, W.P.; Rodrigues, A.F.; Silva, C.M.D.P.S.; Castro, D.S.; Gomes, J.P. Comparison between continuous and intermittent drying of whole bananas using empirical and diffusion models to describe the processes. J. Food Eng. 2015, 166, 230–236. [Google Scholar] [CrossRef]
- Silva, W.P.; Silva, C.M.D.P.S. Convective Adsorption-Desorption Software. 2009. Available online: https://www.labfit.net/Convective.htm (accessed on 3 April 2024).
- Rodrigues, A.F.; Silva, W.P.; Gomes, J.P.; Silva, C.M.D.P.S.; Ramos, I.C.C. Estudo da Secagem de Bananas Através do Modelo de Difusão Usando Soluções Analíticas. In Proceedings of the Convibra 2015—Agronmy Congress, Virtual, 20–24 September 2015. [Google Scholar]
- Aires, K.L.C.A.F.; Silva, W.P.; Aires, J.E.F.; Silva Júnior, A.F.; Silva, C.M.D.P. Convective drying of osmotically dehydrated apples described by three-dimensional numerical solution of the diffusion equation with analysis of water effective diffusivity spatial distribution. Dry. Technol. 2019, 37, 2034–2046. [Google Scholar]
- Pinheiro, R.M.M.; Silva, W.P.; Miranda, D.S.A.; Silva, C.M.D.P.S.; Pessoa, T. Osmotic dehydration of cubic pieces of melon: Description through a three-dimensional diffusion model considering the resistance to mass flows on the surface. Heat Mass Transf. 2020, 57, 405–415. [Google Scholar] [CrossRef]
- Ferreira, J.P.L.; Castro, D.S.; Moreira, I.S.; Silva, W.P.; Figueirêdo, R.M.F.; Queiroz, A.J.M. Convective drying kinetics of osmotically pretreated papaya cubes. Rev. Bras. Eng. Agrícola Ambient. 2020, 24, 200–208. [Google Scholar] [CrossRef]
- Lima, L.S.L.; Silva, W.P.; Pereira, J.C.A.; Silva, C.M.D.P.S. Study of Continuous and Intermittent Drying of Pear Through Mathematical and Diffusion Models. J. Agric. Stud. 2022, 10, 1. [Google Scholar] [CrossRef]
- Pinheiro, M.N.C.; Castro, L.M.M.N. Conductive hydro-drying of cayenne chili paste: Effects of intermittency, temperature and salt concentration on product quality and energy efficiency. Food Sci. Technol. 2023, 9, 7. [Google Scholar] [CrossRef]
- Silva, W.P.; Rodrigues, A.F.; Silva, C.M.D.P.S.; Gomes, J.P. Numerical approach to describe continuous and intermittent drying including the tempering period: Kinetics and spatial distribution of moisture. Dry. Technol. 2017, 35, 72–280. [Google Scholar] [CrossRef]
- Silva, W.P.; Precker, J.W.; Silva, C.M.D.P.S.; Silva, D.D.P.S.; Silva, C.D.P.S. Measurement of Specific Heat and Newton’s Law of Cooling: A Refinement in the Analysis of the Experimental Data. Rev. Bras. Ensino Física 2003, 25, 4. [Google Scholar] [CrossRef]
- Nanadegani, F.S.; Sunden, B. Prediction of mass transfer coefficient of the continuous phase in a structured packed extraction column in the presence of SiO2 nanoparticles. Front. Heat Mass Transf. 2020, 14, 21. [Google Scholar] [CrossRef]
- Demiray, E.; Tulek, Y.; Yilmaz, Y. Degradation kinetics of lycopene, b-carotene and ascorbic acid in tomatoes during hot air drying. LWT-Food Sci. Technol. 2013, 50, 172–176. [Google Scholar] [CrossRef]
- Silva, W.P.; Nunes, J.S.; Gomes, J.P.; Silva, C.M.D.P.S. Obtaining anthocyanin from jambolan fruit: Kinetics, extraction rate, and prediction of process time for different agitation frequencies. Food Sci. Nutr. 2018, 6, 1664–1669. [Google Scholar] [CrossRef]
- Aboul-Enein, H.Y.; Berczynski, D.X.; Kruk, I. Phenolic compounds: The role of redox regulation in neurodegenerative disease and cancer. Mini Rev. Med. Chem. 2013, 13, 385–398. [Google Scholar] [CrossRef] [PubMed]
- Amadeu, L.T.S.; Figueirêdo, R.M.F.; Queiroz, A.J.M.; Reis, C.G.; Lima, T.L.B.; Costa, P.S. Resíduos de frutas na elaboração de geleia de melão Pele de Sapo. Rev. Verde 2020, 15, 153–159. [Google Scholar] [CrossRef]
- Castro, D.S.; Oliveira, T.K.B.; Lemos, D.M.; Rocha, A.P.T.; Almeida, R.D. Efeito da temperatura sobre a composição físico-química e compostos bioativos de farinha de taro obtida em leito de jorro. Braz. J. Food Technol. 2017, 20, e2016060. [Google Scholar] [CrossRef][Green Version]
- Silva, G.D.; Barros, Z.M.P.; Medeiros, R.A.B.; Carvalho, C.B.O.; Brandão, S.C.R.; Azoubel, P.M. Pretreatments for melon drying implementing ultrasound and vacuum. LWT 2016, 74, 114–119. [Google Scholar] [CrossRef]
- Cunha, R.M.C.; Brandão, S.C.R.; Medeiros, R.A.B.; Júnior, E.V.S.; Silva, J.H.F.; Azoubel, P.M. Effect of ethanol pretreatment on melon convective drying. Food Chem. 2020, 333, 127502. [Google Scholar] [CrossRef] [PubMed]
- Saleh, R.M.; Kulig, B.; Emiliozzi, A.; Hensel, O.; Sturm, B. Impact of critical control-point based intermittent drying on drying kinetics and quality of carrot (Daucus carota var. laguna). Therm. Sci. Eng. Prog. 2020, 20, 100682. [Google Scholar] [CrossRef]


| Experiment | Drying | tin (min) | tout (min) | Temperature (°C) |
|---|---|---|---|---|
| E1 | Continuous | - | - | 50 |
| E2 | Intermittent | 10 | 20 | 50 |
| E3 | Intermittent | 20 | 40 | 50 |
| E4 | Intermittent | 30 | 60 | 50 |
| E5 | Continuous | - | - | 70 |
| E6 | Intermittent | 10 | 20 | 70 |
| E7 | Intermittent | 20 | 40 | 70 |
| E8 | Intermittent | 30 | 60 | 70 |
| Model | Expression | Reference | Equation |
|---|---|---|---|
| Henderson and Pabis | [11] | (3) | |
| Lewis | [12] | (4) | |
| Page | [11] | (5) | |
| Peleg | [13] | (6) | |
| Silva et al. ii | [14] | (7) | |
| Wang and Singh | [12] | (8) |
| Model | Reference | T (°C) | Parameters | R2 | χ2 | |
|---|---|---|---|---|---|---|
| a × 10−1 | b × 10−3 | |||||
| Henderson and Pabis | [11] | 50 | 9.705 ± 0.064 | 7.81 ± 0.12 | 0.9986 | 7.235 × 10−3 |
| 70 | 9.890 ± 0.031 | 15.289 ± 0.095 | 0.9997 | 7.885 × 10−4 | ||
| Lewis | [12] | 50 | 0.082 ± 0.001 | - | 0.9987 | 1.140 × 10−2 |
| 70 | 0.155 ± 0.001 | - | 0.9997 | 1.181 × 10−3 | ||
| Page | [11] | 50 | 0.135 ± 0.004 | 892.1 ± 6.3 | 0.9997 | 1.386 × 10−3 |
| 70 | 0.169 ± 0.005 | 979.7 ± 7.2 | 0.9997 | 9.066 × 10−4 | ||
| Peleg | [13] | 50 | 867 ± 22 | 891.4 ± 7.4 | 0.9960 | 1.759 × 10−2 |
| 70 | 469 ± 22 | 857 ± 16 | 0.9886 | 3.300 × 10−2 | ||
| Silva et al.ii | [14] | 50 | 0.067 ± 0.001 | 14.5 ± 1.4 | 0.9994 | 3.070 × 10−3 |
| 70 | 0.148 ± 0.002 | 5.2 ± 1.4 | 0.9997 | 7.470 × 10−4 | ||
| Wang and Singh | [12] | 50 | −0.034 ± 0.002 | 0.002 ± 0.002 | 0.8834 | 1.148 × 100 |
| 70 | −0.073 ± 0.004 | 0.011 ± 0.001 | 0.8901 | 6.620 × 10−1 | ||
| Intermittent | T (°C) | Parameters | R2 | χ2 | |
|---|---|---|---|---|---|
| a × 10−1 | b × 10−3 | ||||
| tin = 10 min | 50 | 0.148 ± 0.006 | 1000 ± 10 | 0.9979 | 2.019 × 10−2 |
| 70 | 0.154 ± 0.003 | 1039.2 ± 4.9 | 0.9997 | 1.329 × 10−3 | |
| tin = 20 min | 50 | 0.099 ± 0.001 | 1066 ± 3.5 | 0.9998 | 7.974 × 10−4 |
| 70 | 0.131 ± 0.004 | 1083.0 ± 7.6 | 0.9995 | 1.991 × 10−3 | |
| tin = 30 min | 50 | 0.060 ± 0.002 | 1146.15 ± 6.5 | 0.9997 | 1.668 × 10−3 |
| 70 | 0.159 ± 0.007 | 1027 ± 10 | 0.9991 | 3.849 × 10−3 | |
| T (°C) | Drying | D (m2 min−1) | h (m min−1) | Bix | R2 | χ2 |
|---|---|---|---|---|---|---|
| 50 | Continuous | 4.007 × 10−8 | 2.243 × 10−5 | 2.25 | 0.9996 | 1.830 × 10−3 |
| Inter. (tin = 10 min) | 4.818 × 10−5 | 2.563 × 10−5 | 2.25 × 10−3 | 0.9986 | 1.718 × 10−2 | |
| Inter. (tin = 20 min) | 3.540 × 10−5 | 2.318 × 10−5 | 2.75 × 10−3 | 0.9996 | 2.119 × 10−3 | |
| Inter. (tin = 30 min) | 4.115 × 10−5 | 1.928 × 10−5 | 1.75 × 10−3 | 0.9978 | 1.130 × 10−2 | |
| 70 | Continuous | 2.460 × 10−7 | 3.082 × 10−5 | 0.535 | 0.9997 | 7.662 × 10−4 |
| Inter. (tin = 10 min) | 5.952 × 10−5 | 3.271 × 10−5 | 2.50 × 10−3 | 0.9998 | 6.316 × 10−4 | |
| Inter. (tin = 20 min) | 5.706 × 10−5 | 3.353 × 10−5 | 2.50 × 10−3 | 0.9987 | 5.259 × 10−3 | |
| Inter. (tin = 30 min) | 5.742 × 10−5 | 3.076 × 10−5 | 2.25 × 10−3 | 0.9992 | 3.295 × 10−3 |
| Parameters | Experiments | ||
|---|---|---|---|
| 50 °C | 70 °C | ||
| Ascorbic acid (mg/100 g) | Continuous | 13.89 aA ± 0.75 | 10.0 bB ± 1.0 |
| Inter. tin = 10 min | 14.57 aA ± 0.41 | 12.2 bA ± 1.6 | |
| Inter. tin = 20 min | 14.91 aA ± 0.85 | 12.22 bA ± 0.49 | |
| Inter. tin = 30 min | 14.8 aA ± 1.7 | 12.1 bA ± 1.2 | |
| Flavonoids (mg/100 g) | Continuous | 8.37 aB ± 0.01 | 3.98 bC ± 0.02 |
| Inter. tin = 10 min | 15.32 aA ± 0.03 | 11.65 bA ± 0.04 | |
| Inter. tin = 20 min | 8.38 aB ± 0.02 | 3.95 bC ± 0.02 | |
| Inter. tin = 30 min | 9.39 aB ± 0.07 | 6.80 bB ± 0.04 | |
| Anthocyanins (mg/100 g) | Continuous | 1.23 aB ± 0.02 | 0.50 bC ± 0.01 |
| Inter. tin = 10 min | 2.83 aA ± 0.03 | 2.43 aA ± 0.08 | |
| Inter. tin = 20 min | 1.70 aAB ± 0.02 | 0.47 bC ± 0.01 | |
| Inter. tin = 30 min | 1.38 aAB ±0.02 | 1.12 aB ± 0.01 | |
| Carotenoids (μg/100 g) | Continuous | 126.76 bD ± 0.83 | 166.11 aD ± 0.21 |
| Inter. tin = 10 min | 143.32 bC ± 0.42 | 180.01 aA ± 0.88 | |
| Inter. tin = 20 min | 307.18 aA ± 0.49 | 266.13 bB ± 0.19 | |
| Inter. tin = 30 min | 200.48 aB ± 0.89 | 206.98 aC ± 2.40 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pereira, J.C.A.; Silva, W.P.d.; Gomes, J.P.; Queiroz, A.J.d.M.; Figueirêdo, R.M.F.d.; Paiva, Y.F.; Santos, F.S.d.; Melo, B.A.d.; Silva Júnior, A.F.d.; Souto, L.M.d.; et al. Continuous and Intermittent Drying of Osmotically Pretreated Melon Pieces: Analysis of Energy Savings and Preservation of Bioactive Compounds. Agriculture 2025, 15, 480. https://doi.org/10.3390/agriculture15050480
Pereira JCA, Silva WPd, Gomes JP, Queiroz AJdM, Figueirêdo RMFd, Paiva YF, Santos FSd, Melo BAd, Silva Júnior AFd, Souto LMd, et al. Continuous and Intermittent Drying of Osmotically Pretreated Melon Pieces: Analysis of Energy Savings and Preservation of Bioactive Compounds. Agriculture. 2025; 15(5):480. https://doi.org/10.3390/agriculture15050480
Chicago/Turabian StylePereira, Joan Carlos Alves, Wilton Pereira da Silva, Josivanda Palmeira Gomes, Alexandre José de Melo Queiroz, Rossana Maria Feitosa de Figueirêdo, Yaroslávia Ferreira Paiva, Francislaine Suelia dos Santos, Bruno Adelino de Melo, Aluizio Freire da Silva Júnior, Leidjane Matos de Souto, and et al. 2025. "Continuous and Intermittent Drying of Osmotically Pretreated Melon Pieces: Analysis of Energy Savings and Preservation of Bioactive Compounds" Agriculture 15, no. 5: 480. https://doi.org/10.3390/agriculture15050480
APA StylePereira, J. C. A., Silva, W. P. d., Gomes, J. P., Queiroz, A. J. d. M., Figueirêdo, R. M. F. d., Paiva, Y. F., Santos, F. S. d., Melo, B. A. d., Silva Júnior, A. F. d., Souto, L. M. d., Santos, D. d. C., Farias, J. Q., & Lima, A. G. B. d. (2025). Continuous and Intermittent Drying of Osmotically Pretreated Melon Pieces: Analysis of Energy Savings and Preservation of Bioactive Compounds. Agriculture, 15(5), 480. https://doi.org/10.3390/agriculture15050480








