Relationship of Genetic Connectedness Among Flocks with Effective Population Size in Dairy-Oriented Pag Sheep
Abstract
1. Introduction
2. Materials and Methods
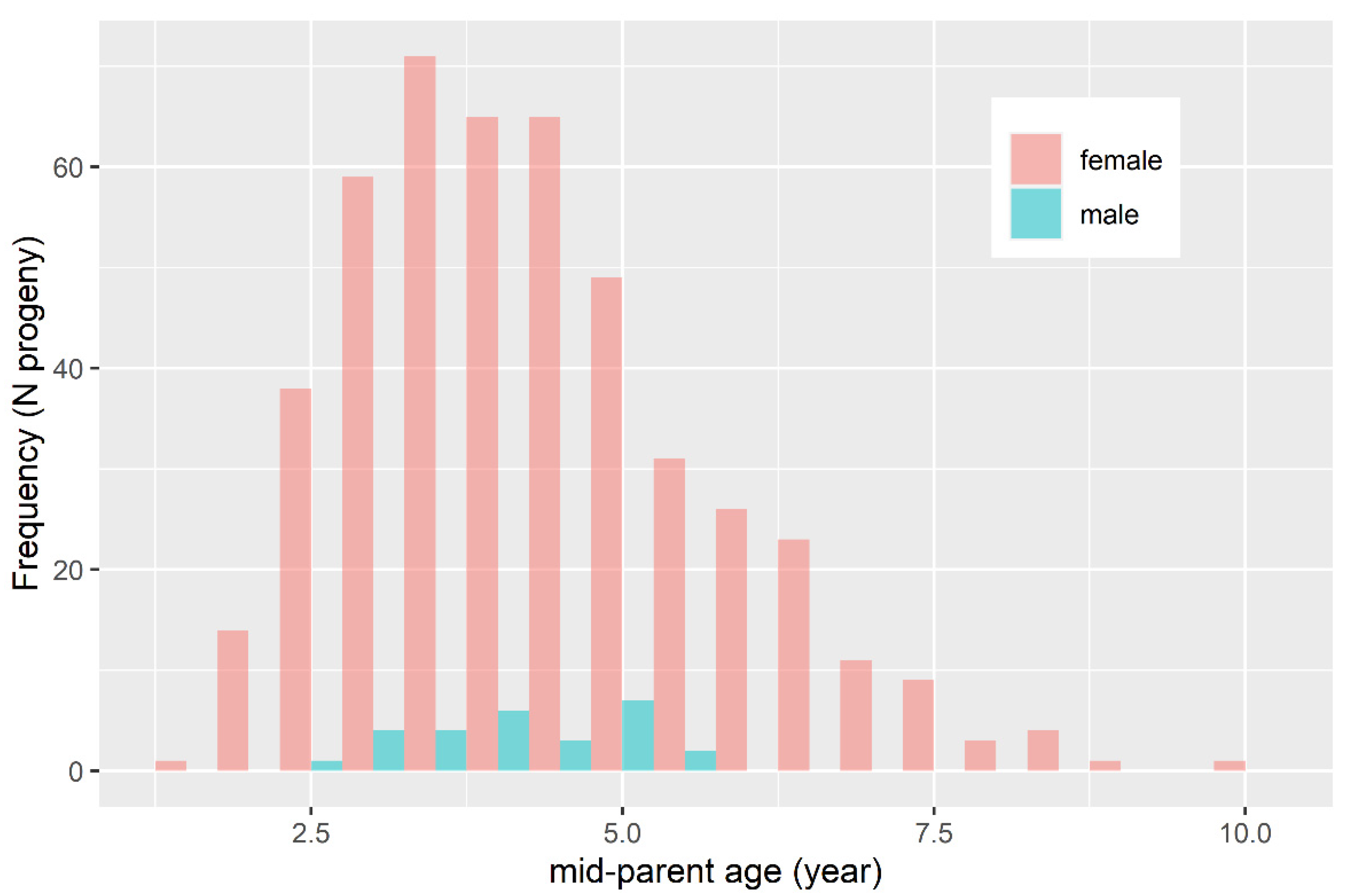
2.1. Data
2.2. Statistical Analysis
2.2.1. Pedigree Quality
2.2.2. Effective Population Size (Rates)
2.2.3. Connectedness Analysis
3. Results
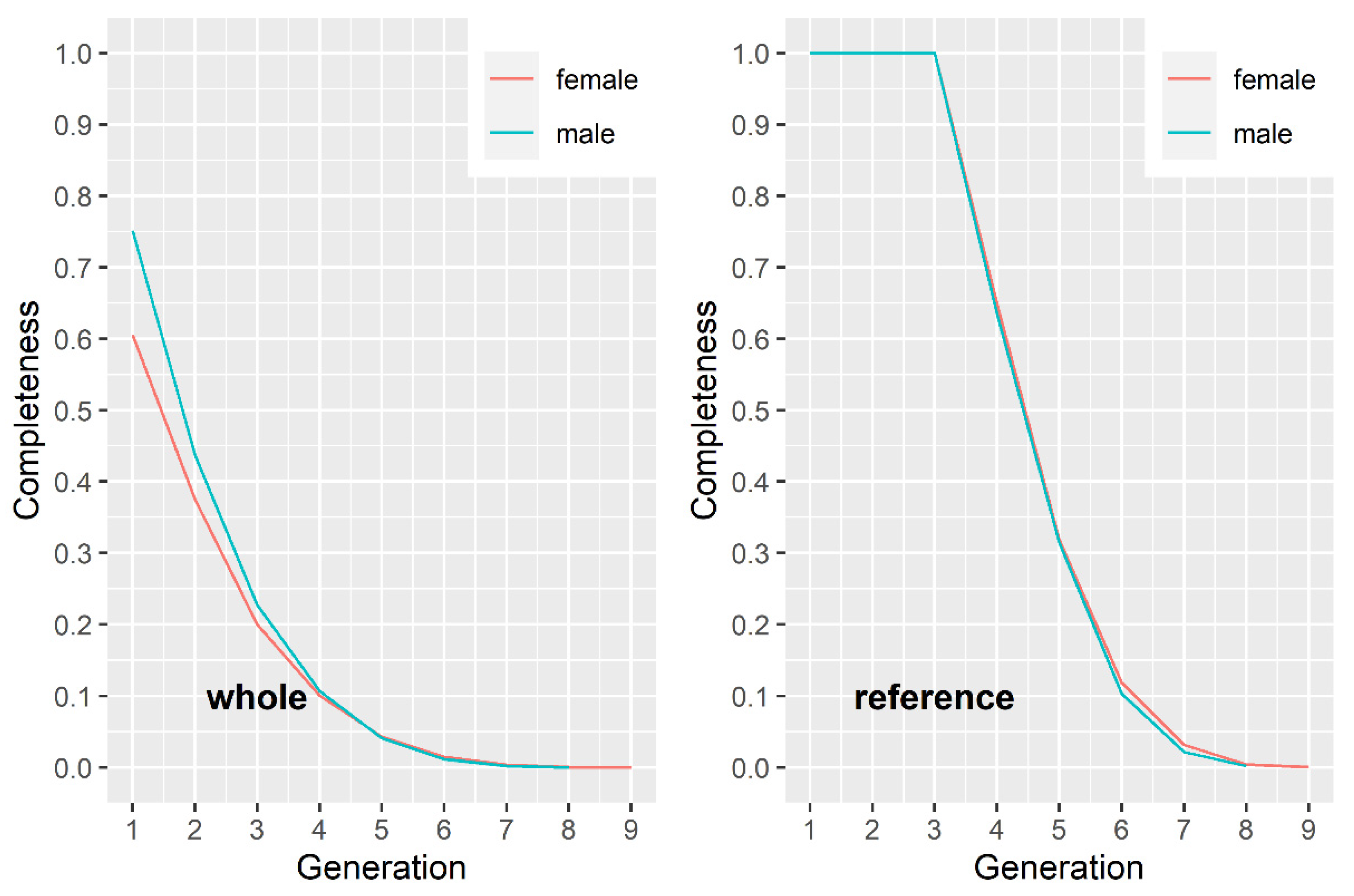
3.1. Quality Control of the Pedigree and Formation of the Reference Population
3.2. Effective Population Size
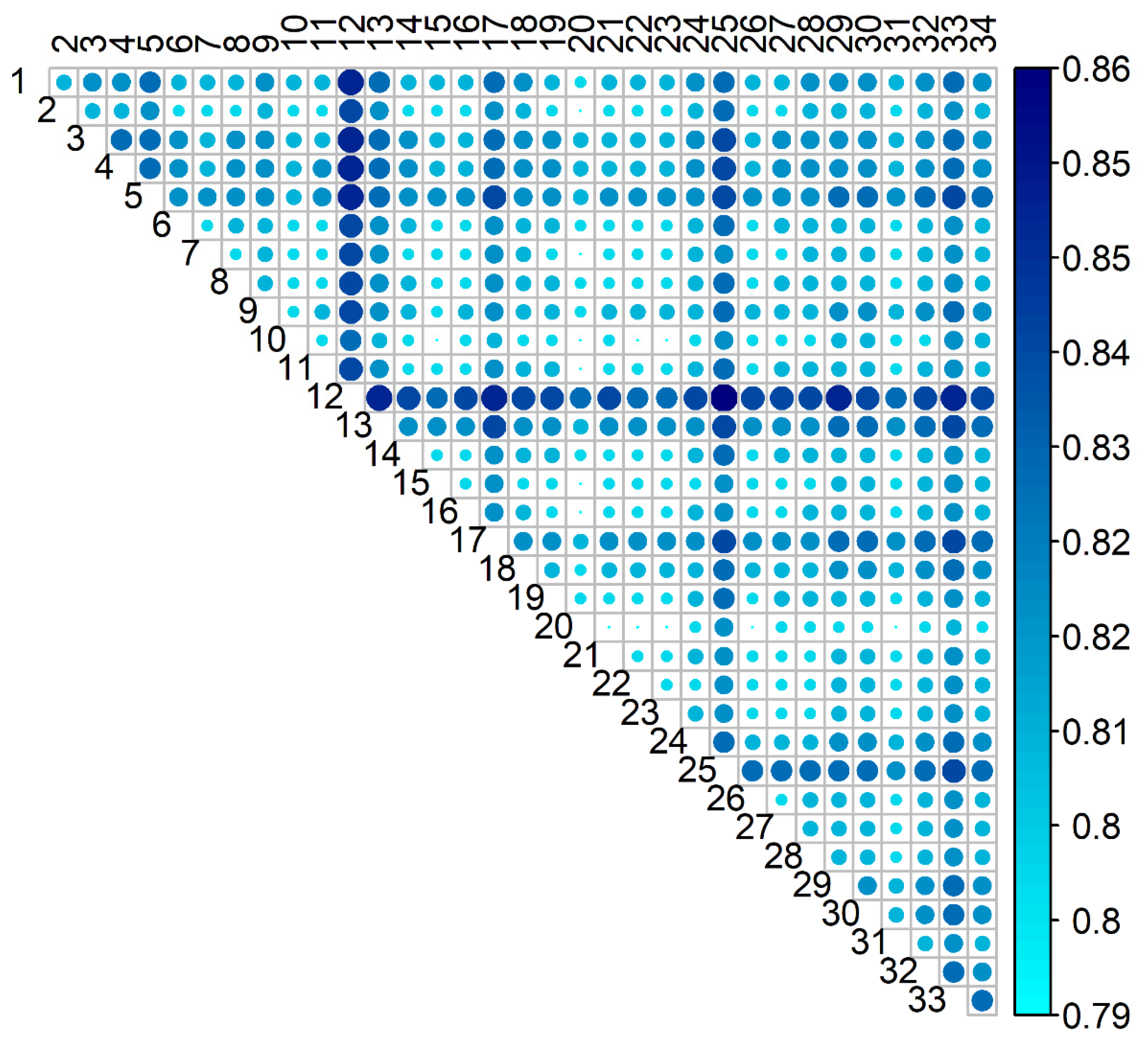
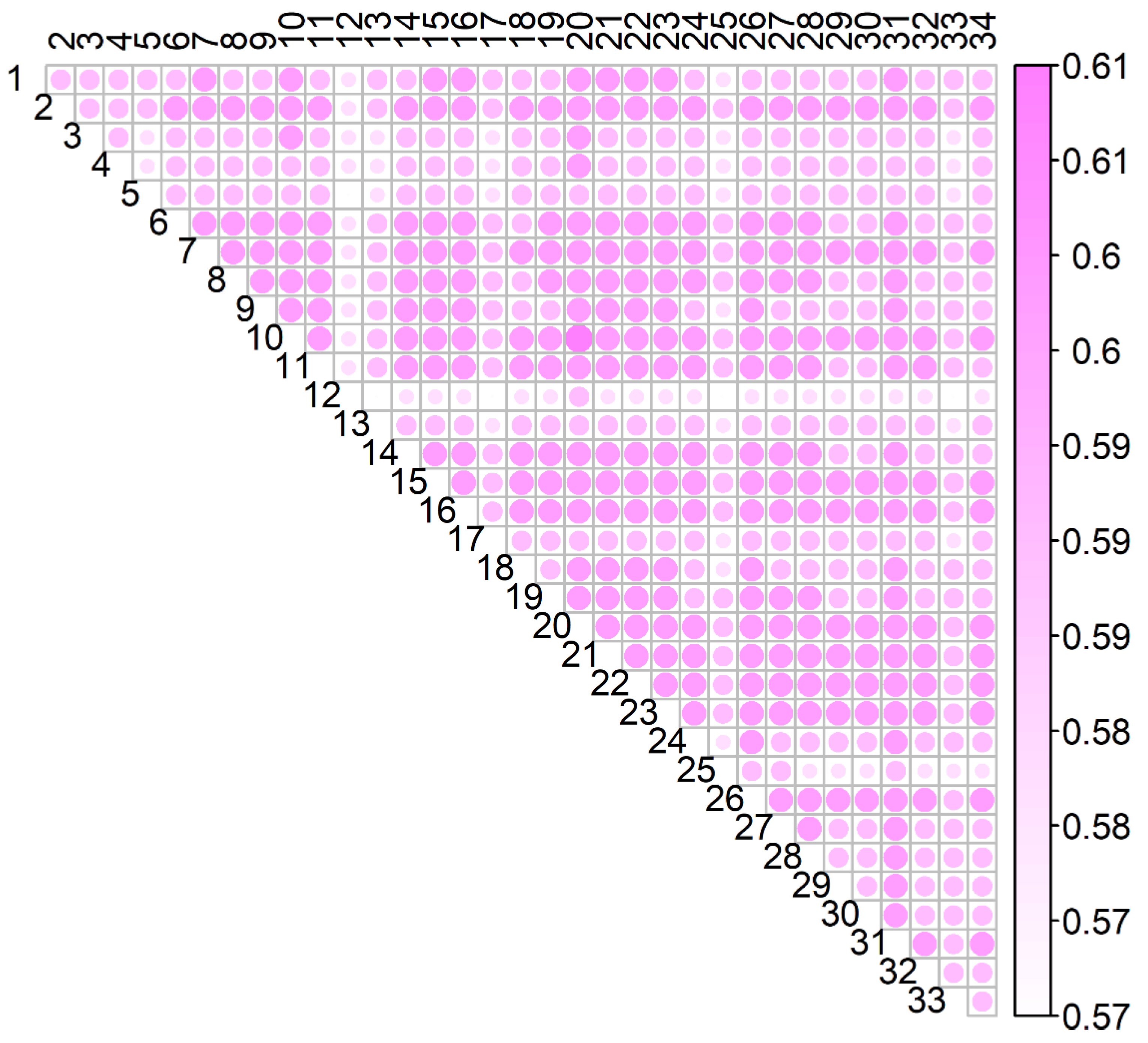
3.3. Connectedness
3.3.1. Prediction Error Variance of Differences in EBVs Between Animals Belonging to Different Flocks (PEVD)
3.3.2. Coefficient of Determination of the Difference Between Predicted Breeding Values (CD)
3.4. Relationship Between Connectedness Rate and Effective Population Size Rate
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wellmann, R. OptiSel: Optimum Contribution Selection and Population Genetics; Version 2.0.5; ACM Digital Library: New York, NY, USA, 2021. [Google Scholar]
- Woolliams, J.A.; Berg, P.; Dagnachew, B.S.; Meuwissen, T.H.E. Genetic Contributions and Their Optimization. J. Anim. Breed. Genet. 2015, 132, 89–99. [Google Scholar] [CrossRef] [PubMed]
- CAAF—Croatian Agency for Agriculture and Food. Annual Report for Year 2023; CAAF: Osijek, Croatia, 2024. [Google Scholar]
- Pavić, V.; Mioč, B.; Barać, Z.; Vnučec, I.; Sušić, V.; Antunac, N.; Samaržija, D. Vanjština paške ovce. Stočarstvo 2005, 59, 83–90. [Google Scholar]
- Antunac, N.; Hudik, S.; Mikulec, N.; Maletić, M.; Horvat, I.; Radeljević, B.; Havranek, J. Proizvodnja i kemijski sastav istarske i paške skute. Mljekarstvo 2011, 61, 226–233. [Google Scholar]
- Barać, Z.; Mioč, B.; Špehar, M. Utjecaj stadija i redoslijeda laktacije, sezone janjenja i stada na udjele mliječne masti i bjelančevina u mlijeku paške ovce. Mljekarstvo 2013, 63, 81–90. [Google Scholar]
- Mioč, B.; Držaić, V.; Vnučec, I.; Barać, Z.; Prpić, Z.; Pavić, V. Utjecaj spola na klaoničke pokazatelje paške janjadi. Stočarstvo 2012, 66, 95–106. [Google Scholar]
- Vnučec, I.; Držaić, V.; Mioč, B.; Prpić, Z.; Antunović, Z.; Kegalj, A. Effect of Sex on Meat Chemical Composition and Fatty Acid Composition in Suckling Pag Sheep Lambs. Vet. Arhiv 2016, 86, 217–227. [Google Scholar]
- ICAR—International Committee for Animal Recording. Section 16. In Guidelines for Performance Recording in Dairy Sheep and Dairy Goats; ICAR: Utrecht, The Netherlands, 2018. [Google Scholar]
- CAAF (Croatian Agency for Agriculture and Food). Annual Report for Year 2019; Croatian Agency for Agriculture and Food: Osijek, Croatia, 2020. [Google Scholar]
- Špehar, M.; Mulc, D.; Barać, Z.; Mioč, B.; Kasap, A. Estimation of Genetic Parameters for Dairy Traits in Pag Sheep with Single and Multi-Trait Test–Day Models. Small Rumin. Res. 2019, 183, 106029. [Google Scholar] [CrossRef]
- Usai, M.G.; Salaris, S.; Casu, S.; Sechi, T.; Miari, S.; Carta, P.; Carta, A. Feasibility of Genomic Predictions of Sarda Breed Rams Using a Female Reference Population. In Proceedings of the 11th World Congress on Genetics Applied to Livestock Production, Auckland, New Zealand, 7 February 2018. [Google Scholar]
- Cesarani, A.; Gaspa, G.; Correddu, F.; Cellesi, M.; Dimauro, C.; Macciotta, N.P.P. Genomic Selection of Milk Fatty Acid Composition in Sarda Dairy Sheep: Effect of Different Phenotypes and Relationship Matrices on Heritability and Breeding Value Accuracy. J. Dairy Sci. 2019, 102, 3189–3203. [Google Scholar] [CrossRef] [PubMed]
- Baloche, G.; Legarra, A.; Sallé, G.; Larroque, H.; Astruc, J.-M.; Robert-Granié, C.; Barillet, F. Assessment of Accuracy of Genomic Prediction for French Lacaune Dairy Sheep. J. Dairy Sci. 2014, 97, 1107–1116. [Google Scholar] [CrossRef]
- Legarra, A.; Baloche, G.; Barillet, F.; Astruc, J.M.; Soulas, C.; Aguerre, X.; Arrese, F.; Mintegi, L.; Lasarte, M.; Maeztu, F.; et al. Within- and across-Breed Genomic Predictions and Genomic Relationships for Western Pyrenees Dairy Sheep Breeds Latxa, Manech, and Basco-Béarnaise. J. Dairy Sci. 2014, 97, 3200–3212. [Google Scholar] [CrossRef] [PubMed]
- Legarra, A.; Aguilar, I.; Misztal, I. A Relationship Matrix Including Full Pedigree and Genomic Information. J. Dairy Sci. 2009, 92, 4656–4663. [Google Scholar] [CrossRef] [PubMed]
- Foulley, J.L.; Schaeffer, L.R.; Song, H.; Wilton, J.W. Progeny Group Size In An Organized Progeny Test Program of Ai Beef Bulls Using Reference Sires. Can. J. Anim. Sci. 1983, 63, 17–26. [Google Scholar] [CrossRef]
- Foulley, J.L.; Bouix, J.; Goffinet, B.; Elsen, J.M. Connectedness in Genetic Evaluation. In Advances in Statistical Methods for Genetic Improvement of Livestock; Advanced Series in Agricultural Sciences; Springer: Berlin/Heidelberg, Germany, 1990; Volume 18. [Google Scholar]
- Foulley, J.L.; Hanocq, E.; Boichard, D. A Criterion for Measuring the Degree of Connectedness in Linear Models of Genetic Evaluation. Genet. Sel. Evol. 1992, 24, 315–330. [Google Scholar] [CrossRef]
- Laloë, D. Precision and Information in Linear Models of Genetic Evaluation. Genet. Sel. Evol. 1993, 25, 557–576. [Google Scholar] [CrossRef]
- Eikje, L.S.; Ådnøy, T.; Klemetsdal, G. The Norwegian Sheep Breeding Scheme: Description, Genetic and Phenotypic Change. Animal 2008, 2, 167–176. [Google Scholar] [CrossRef] [PubMed]
- Simm, G.; Lewis, R.M.; Collins, J.E.; Nieuwhof, G.J. Use of Sire Referencing Schemes to Select for Improved Carcass Composition in Sheep. J. Anim. Sci. 2001, 79, E255. [Google Scholar] [CrossRef]
- Kennedy, B.W.; Trus, D. Considerations on Genetic Connectedness between Management Units under an Animal-Model. J. Anim. Sci. 1993, 71, 2341–2352. [Google Scholar] [CrossRef] [PubMed]
- Lewis, R.M.; Crump, R.E.; Simm, R.E.; Thompson, R. Assessing Connectedness in Across-Flock Genetic Evaluations. Proc. Br. Soc. Anim. Sci. 1999, 1999, 121. [Google Scholar] [CrossRef]
- Yu, H.; Spangler, M.L.; Lewis, R.M.; Morota, G. Genomic Relatedness Strengthens Genetic Connectedness Across Management Units. G3 2017, 7, 3543–3556. [Google Scholar] [CrossRef]
- Yu, H.; Spangler, M.L.; Lewis, R.M.; Morota, G. Do Stronger Measures of Genomic Connectedness Enhance Prediction Accuracies across Management Units? J. Anim. Sci. 2018, 28, 4490–4500. [Google Scholar] [CrossRef]
- Yu, H.; Morota, G. GCA: An R Package for Genetic Connectedness Analysis Using Pedigree and Genomic Data. BMC Genom. 2021, 22, 119. [Google Scholar] [CrossRef] [PubMed]
- Wright, S. Evolution in Mendelian Populations. Genetics 1931, 16, 97–159. [Google Scholar] [CrossRef]
- Leroy, G.; Gicquel, E.; Boettcher, P.; Besbes, B.; Furre, S.; Fernandez, J.; Danchin-Burge, C.; Alnahhas, N.; Baumung, R. Coancestry Rate’s Estimate of Effective Population Size for Genetic Variability Monitoring. Conserv. Genet. Resour. 2020, 12, 275–283. [Google Scholar] [CrossRef]
- Leroy, G.; Mary-Huard, T.; Verrier, E.; Danvy, S.; Charvolin, E.; Danchin-Burge, C. Methods to Estimate Effective Population Size Using Pedigree Data: Examples in Dog, Sheep, Cattle and Horse. Genet. Sel. Evol. 2013, 45, 1. [Google Scholar] [CrossRef] [PubMed]
- Granado-Tajada, I.; Rodríguez-Ramilo, S.T.; Legarra, A.; Ugarte, E. Inbreeding, Effective Population Size, and Coancestry in the Latxa Dairy Sheep Breed. J. Dairy Sci. 2020, 103, 5215–5226. [Google Scholar] [CrossRef] [PubMed]
- Deniskova, T.; Dotsev, A.; Lushihina, E.; Shakhin, A.; Kunz, E.; Medugorac, I.; Reyer, H.; Wimmers, K.; Khayatzadeh, N.; Sölkner, J.; et al. Population Structure and Genetic Diversity of Sheep Breeds in the Kyrgyzstan. Front. Genet. 2019, 10, 1311. [Google Scholar] [CrossRef]
- Falconer, D.S.; Mackay, T.F.C. Introduction to Quantitative Genetics, 4th ed.; Longman: Essex, UK, 1996. [Google Scholar]
- Gutiérrez, J.P.; Cervantes, I.; Molina, A.; Valera, M.; Goyache, F. Individual Increase in Inbreeding Allows Estimating Effective Sizes from Pedigrees. Genet. Sel. Evol. 2008, 40, 359. [Google Scholar] [CrossRef] [PubMed]
- Cervantes, I.; Goyache, F.; Molina, A.; Valera, M.; Gutiérrez, J.P. Estimation of Effective Population Size from the Rate of Coancestry in Pedigreed Populations: Effective Population Size from Rate of Coancestry. J. Anim. Breed. Genet. 2011, 128, 56–63. [Google Scholar] [CrossRef] [PubMed]
- Maignel, L.; Boichard, D.; Boichard, E. Genetic Variability of French Dairy Breeds Estimated from Pedigree Information. In Proceedings of the Open Session of the Interbull Annual Meeting, Veldhoven, The Netherlands, 23–24 June 1996; pp. 49–54. [Google Scholar]
- MacCluer, J.W.; Boyce, A.J.; Dyke, B.; Weitkamp, L.R.; Pfenning, D.W.; Parsons, C.J. Inbreeding and Pedigree Structure in Standardbred Horses. J. Hered. 1983, 74, 394–399. [Google Scholar] [CrossRef]
- Rodríguez-Ramilo, S.T.; Elsen, J.M.; Legarra, A. Inbreeding and Effective Population Size in French Dairy Sheep: Comparison between Genomic and Pedigree Estimates. J. Dairy Sci. 2019, 102, 4227–4237. [Google Scholar] [CrossRef] [PubMed]
- Hashemi, M.; Ghavi Hossein-Zadeh, N. Population Genetic Structure Analysis of Shall Sheep Using Pedigree Information and Effect of Inbreeding on Growth Traits. Ital. J. Anim. Sci. 2020, 19, 1195–1203. [Google Scholar] [CrossRef]
- Rafter, P.; McHugh, N.; Pabiou, T.; Berry, D.P. Inbreeding Trends and Genetic Diversity in Purebred Sheep Populations. Animal 2022, 16, 100604. [Google Scholar] [CrossRef] [PubMed]
- Kárpáti, E.; Gulyás, L.; Posta, J.; Sáfár, L.; Gáspárdy, A. The First In-Deep Pedigree Analysis of Repatriated Gyimes Racka Sheep for a Sustainable Preservation of Its Genetic Resource. Chem. Eng. Trans. 2023, 107, 343–348. [Google Scholar] [CrossRef]
- Kasap, A.; Ramljak, J.; Špehar, M. Estimation of Population-Specific Genetic Parameters Important for Long-Term Optimum Contribution Selection—Case Study on a Dairy Istrian Sheep Breed. Animals 2021, 11, 2356. [Google Scholar] [CrossRef]
- Kuehn, L.A.; Lewis, R.M.; Notter, D.R. Connectedness in Targhee and Suffolk Flocks Participating in the United States National Sheep Improvement Program1. J. Anim. Sci. 2009, 87, 507–515. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kominakis, A.P. Effect of Unfavourable Population Structure on Estimates of Heritability, Systematic Effects and Breeding Values. Arch. Anim. Breed. 2008, 51, 601–610. [Google Scholar] [CrossRef]
| Population | Statistics | NEG | NFG | NMG | PCI |
|---|---|---|---|---|---|
| Whole population | max | 5.74 | 4.00 | 9.00 | 1.00 |
| median | 1 | 1.00 | 2.00 | 0.25 | |
| mean | 1.36 | 0.89 | 2.26 | 0.29 | |
| Reference population | max | 5.74 | 4.00 | 9.00 | 0.97 |
| median | 4.09 | 3.00 | 6.00 | 0.79 | |
| mean | 4.12 | 3.05 | 6.39 | 0.79 |
| GI (Years) | ||||
|---|---|---|---|---|
| 8 (2008–2011) | 1833 | 0.0096 | 52 | 0.03 |
| 7 (2009–2012) | 1703 | 0.0083 | 60 | 0.04 |
| 6 (2010–2013) | 1721 | 0.0069 | 73 | 0.04 |
| 5 (2011–2014) | 1700 | 0.0066 | 76 | 0.04 |
| 4 (2012–2015) | 1719 | 0.0058 | 86 | 0.05 |
| 3 (2013–2016) | 1740 | 0.0050 | 100 | 0.06 |
| 2 (2014–2017) | 1715 | 0.0043 | 117 | 0.07 |
| 1 (2015–2018) | 1457 | 0.0039 | 127 | 0.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Špehar, M.; Ramljak, J.; Držaić, V.; Mioč, B.; Barać, Z.; Kasap, A. Relationship of Genetic Connectedness Among Flocks with Effective Population Size in Dairy-Oriented Pag Sheep. Agriculture 2025, 15, 474. https://doi.org/10.3390/agriculture15050474
Špehar M, Ramljak J, Držaić V, Mioč B, Barać Z, Kasap A. Relationship of Genetic Connectedness Among Flocks with Effective Population Size in Dairy-Oriented Pag Sheep. Agriculture. 2025; 15(5):474. https://doi.org/10.3390/agriculture15050474
Chicago/Turabian StyleŠpehar, Marija, Jelena Ramljak, Valentino Držaić, Boro Mioč, Zdravko Barać, and Ante Kasap. 2025. "Relationship of Genetic Connectedness Among Flocks with Effective Population Size in Dairy-Oriented Pag Sheep" Agriculture 15, no. 5: 474. https://doi.org/10.3390/agriculture15050474
APA StyleŠpehar, M., Ramljak, J., Držaić, V., Mioč, B., Barać, Z., & Kasap, A. (2025). Relationship of Genetic Connectedness Among Flocks with Effective Population Size in Dairy-Oriented Pag Sheep. Agriculture, 15(5), 474. https://doi.org/10.3390/agriculture15050474










