A Gated Ridge Regression-Based Multimodal Spectral Fusion Approach for Predicting Soil Organic Matter

Abstract

The fusion of Raman and visible–near-infrared (VIS–NIR) spectroscopy provides a promising pathway for rapid and non-destructive soil analysis. However, conventional fusion strategies often fail to properly balance modality discrepancies and complementary information. To address this limitation, this study develops an adaptive Gated Ridge Regression fusion model (Fusion_GatedRidge) for predicting soil organic matter (SOM). A total of 246 soil samples collected from a dryland agricultural region in Shanxi Province were analyzed using laboratory Raman and VIS–NIR spectroscopy. After standard preprocessing, three baseline fusion frameworks—EarlyFusion_Ridge, AE_LatentFusion, and WeightedLate_Fusion—were implemented for comparison with the proposed gated fusion method. Under fivefold cross-validation, Fusion_GatedRidge achieved the best performance, with an R² of 0.83, RMSE of 2.01 g·kg⁻¹, and RPD of 2.39. Compared with single-modality models, R² increased by up to 18.6% and RMSE decreased by up to 23.0%. The gating mechanism dynamically adjusted the contributions of Raman and VIS–NIR features, leading to more stable predictions with residuals largely within −2 to 2 g·kg⁻¹. Overall, the proposed model demonstrates that adaptive modality weighting enhances the exploitation of complementary spectral information and significantly improves SOM prediction accuracy. These findings offer a concise and effective multimodal fusion framework for laboratory-based soil nutrient assessment.

1. Introduction

With the rapid development of precision agriculture, field management is increasingly moving toward high spatiotemporal resolution and data-driven decision-making, creating a strong demand for rapid, accurate, and non-destructive measurement of key soil attributes such as soil organic matter (SOM) [1,2]. Compared with traditional wet chemistry, proximal sensing techniques such as visible–near-infrared (VIS–NIR), mid-infrared, and Raman spectroscopy offer fast acquisition, low cost, and minimal sample preparation. These advantages have made them widely used for efficient prediction and monitoring of soil physicochemical properties [3,4,5]. In recent years, the integration of spectroscopic sensors into field-based, vehicle-mounted, or high-throughput systems has further reduced the time between soil sampling and management decisions, supporting rapid diagnosis and precise fertilization in modern agriculture [1,6].

However, each single spectral modality presents inherent limitations when applied to complex soil matrices. VIS–NIR spectra are strongly affected by particle size, moisture, and scattering, leading to weak absorption features, high noise, and overlapping bands [7]. Raman spectroscopy, while directly reflecting molecular vibrations and functional group information, is often influenced by fluorescence background, baseline drift, and sample heterogeneity—issues that are particularly pronounced in soils containing diverse minerals, organic matter, and impurities [8,9]. Because these two modalities reflect complementary physical–chemical mechanisms—VIS–NIR capturing broad absorption and scattering patterns and Raman encoding molecular structural fingerprints—multimodal fusion is considered a promising pathway to improve prediction accuracy and robustness [10,11,12].

Multisource spectral fusion has been successfully applied in soil contamination assessment, mineral identification, and fertilizer quality analysis. For instance, pXRF–VIS–NIR fusion significantly improved regional-scale cadmium estimation [13], while XRF–NIR fusion demonstrated strong robustness for monitoring heavy metals in complex urban–industrial transition zones. In fertilizer evaluation, LIBS–NIR fusion has been shown to outperform single-modality models for quantifying key nutrient indicators. In mineralogical and geochemical analysis, integrated Raman–VIS–NIR spectra have also demonstrated the general value of cross-modal complementarity [14].

Despite the promise of spectral fusion, several methodological challenges remain in soil applications. First, substantial differences in feature dimensionality, numerical scale, and noise properties between Raman and VIS–NIR cause early concatenation (Early Fusion) to suffer from redundancy, scale mismatch, and instability [15,16,17]. Second, most fusion methods rely on manually assigned or fixed modality weights, lacking the ability to adaptively adjust contributions based on sample characteristics [18,19,20]. Third, although deep learning and attention-based fusion methods (e.g., Transformer, Outer-Product Attention) can learn weighting functions, they require large datasets, incur high computational cost, and exhibit limited interpretability—conditions unsuitable for typical soil datasets with modest sample sizes [21,22]. Fourth, existing approaches often treat feature extraction, weighting, and prediction as separate processes, lacking a unified, lightweight, and interpretable fusion framework [23,24].

These limitations constitute an explicit research gap that this study aims to address. To avoid confusion about application scenarios, the scope of this study is clarified here:

We used a dataset of 246 soil samples collected from a single, uniformly managed field, and both Raman and VIS–NIR spectra were acquired under controlled laboratory conditions. Thus, the objective of this study is to investigate methodological improvements in multimodal fusion—rather than cross-regional generalization—under a controlled environment that ensures fair modality comparison and reliable evaluation of fusion strategies.

In response to the above challenges, we propose a Gated Ridge Regression fusion framework (Fusion_GatedRidge), which forms an integrated architecture of feature extraction → adaptive gating fusion → regularized prediction. Specifically:

(1) Autoencoders extract compact latent features from Raman and VIS–NIR spectra, reducing noise and redundancy; (2) a learnable gating mechanism adaptively adjusts modality contributions based on sample-specific characteristics, enabling numerically stable and flexible fusion; and (3) ridge regression is used for final prediction, and its linear structure—combined with gating weights—allows quantitative interpretation of modality contributions. Compared with EarlyFusion_Ridge, AE_LatentFusion, and WeightedLate_Fusion, the proposed model offers improved interpretability, adaptive weighting capability, scale stability, and small-sample applicability.

2. Materials and Methods

2.1. Research Subjects and Data Collection

Soil sampling for this study was conducted in a typical dryland agricultural region of Jinzhong City, Shanxi Province, which represents the characteristic agro-ecological conditions of the central Loess Plateau. The sampling area is located within 112°34′13″–113°7′51″ E and 37°23′41″–37°53′04″ N, featuring a temperate continental arid climate with an annual mean temperature of approximately 9.8 °C, annual precipitation around 450 mm, about 2662 h of sunshine per year, and a frost-free period of roughly 158 days. The dominant soil type in the region is cinnamon soil, and major crops include maize, millet, sorghum, soybean, potato and fruit tree.

Soil sampling was conducted in mid-October 2022, following crop harvest. Based on the principles of “equal quantity, random distribution, and five-point composite sampling,” soil samples were collected from the center of each sampling unit at depths of 0–20 cm and 20–40 cm, yielding a total of 246 representative samples. All samples were air-dried, ground, and passed through a 2 mm sieve, after which they were divided into two portions: one for the determination of soil organic matter (SOM) content, and the other for VIS–NIR and Raman spectral measurements. SOM was quantified using the potassium dichromate oxidation method with external heating [25,26].

VIS–NIR spectra were collected in November 2022 using a Starter Kit hyperspectral imaging system (Headwall Photonics Inc., Bolton, Massachusetts, USA) under controlled indoor conditions to ensure measurement consistency. Before data acquisition, white reference calibration and dark current correction were performed to convert raw radiance to calibrated reflectance and remove background electronic noise. During scanning, illumination was stabilized using a fixed halogen light source, and the laboratory temperature and humidity were maintained within a narrow range to minimize environmental interference. The hyperspectral system covered 379.66–1704.28 nm across 1029 spectral bands, with spectral resolutions of 0.727 nm in the visible region and 4.715 nm in the near-infrared region. Samples were placed at a fixed working distance of 20 mm, and the scanning speed (15.55 mm∙s⁻¹) and exposure time (0.9 ms) were kept constant throughout the measurement process. The effective spectral range of 425–1650 nm was retained for analysis to avoid low-SNR edge regions.

Raman spectra were acquired using an Acuuman SR-510 portable research-grade Raman spectrometer (Ocean Insight, Orlando, FL, USA). The instrument operated with a 785 nm laser, covering 66.07–3107.65 cm⁻¹ with a spectral resolution of 1.99 cm⁻¹. Each sample was measured three times, and the average spectrum was used to minimize random errors. To eliminate low signal-to-noise regions, only the 403.84–3000.61 cm⁻¹ range was retained for modeling.

By maintaining consistent sample preparation and acquisition parameters, the comparability and complementarity between Raman and VIS–NIR spectra were ensured, providing a robust foundation for multimodal spectral fusion modeling.

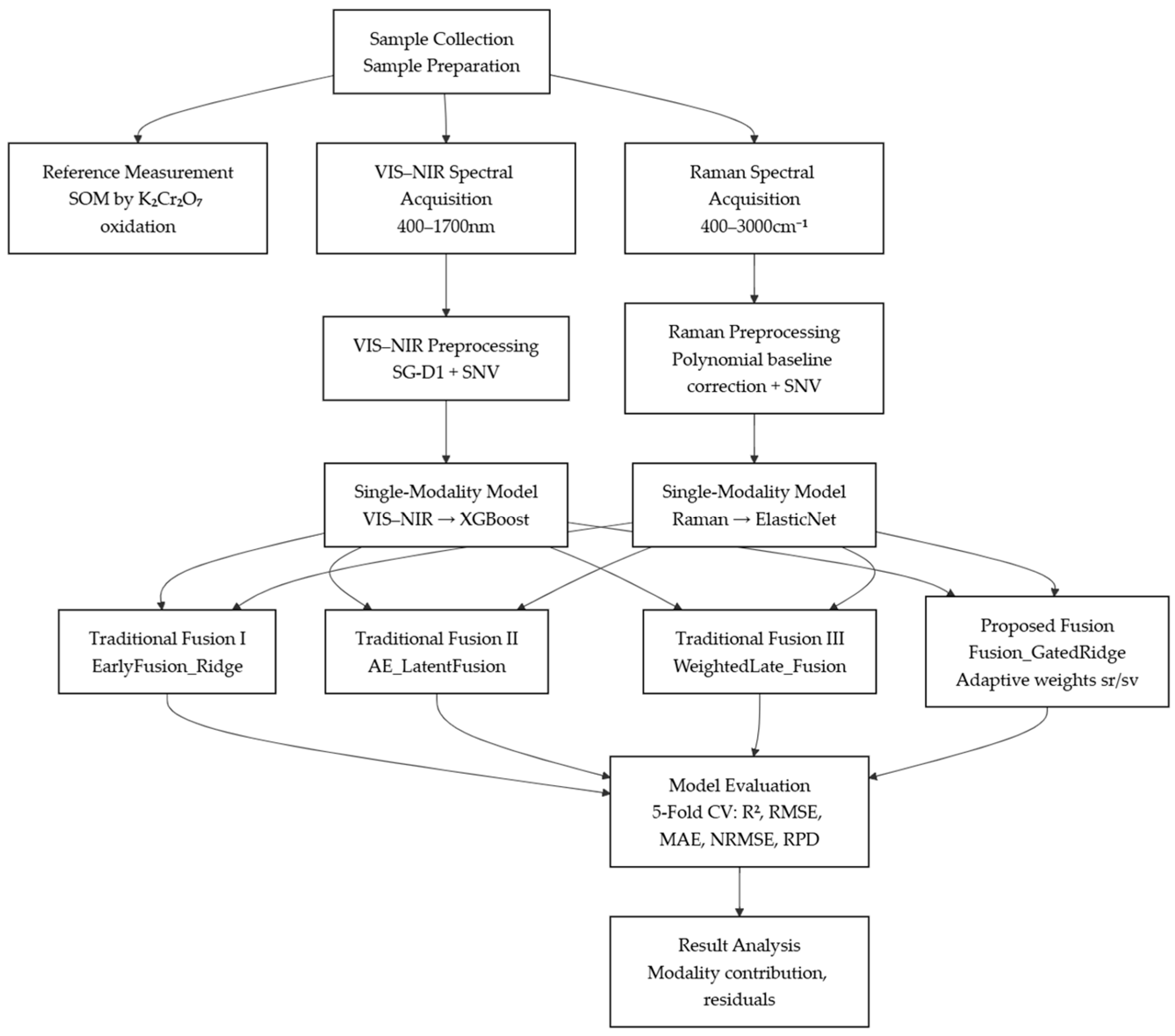
Model training employed a single five-fold cross-validation (5-fold CV) [27,28]. The dataset was randomly divided into five mutually exclusive subsets. In each iteration, four folds were used for model training and the remaining fold served as the validation set, until all folds had been used once. The final performance was obtained by aggregating the results from the five validation folds, providing an unbiased estimate of model generalization. The technical workflow for soil nutrient prediction is shown in Figure 1.

2.2. Spectral Preprocessing Methods

2.2.1. Baseline Correction

During Raman spectral acquisition, fluorescence background, light scattering, and instrumental noise often generate a slowly varying baseline drift that can obscure characteristic Raman peaks and reduce calibration accuracy [8,28]. To mitigate this interference, a low-order polynomial baseline correction method was applied.

In this approach, the measured Raman spectrum is treated as the sum of the true Raman signal and a smoothly varying background. The baseline is estimated by fitting a low-order polynomial to the slowly varying component of the spectrum using least-squares optimization [29,30]. The fitted baseline is then subtracted from the original spectrum to obtain the corrected signal.

This procedure effectively removes low-frequency background variations caused by fluorescence and instrumental drift, thereby improving peak visibility and enhancing the reliability of subsequent spectral analysis and modeling.

2.2.2. Standard Normal Variate, SNV

Variations in particle size, density, and illumination among different soil samples can cause overall shifts or scaling in the spectral signals, thereby reducing the comparability of samples during model calibration. The Standard Normal Variate (SNV) transformation is a sample-wise normalization preprocessing method designed to eliminate intensity differences caused by scattering effects.

By centering each spectrum on its own mean and scaling by its standard deviation, SNV effectively removes multiplicative and additive effects, thus improving the consistency and comparability of spectral features across samples.

For each sample spectrum vector $x=\left[x_1,x_2,\dots ,x_n\right]$, the SNV transformation is mathematically expressed as [31]:

$$x_i^{\prime }={\displaystyle \frac{x_i-\mu }{\sigma }}$$

(1)

where $\mu ={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{x}_i$ is the mean of the spectrum, and $\sigma =\sqrt{{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{(x_i-\overline{x})}^2}$ is the standard deviation; After SNV processing, each spectrum is standardized to have a mean of 0 and a variance of 1, which effectively reduces the effects of light scattering and instrument drift, thereby enhancing the stability and robustness of subsequent regression modeling.

2.2.3. Savitzky–Golay First Derivative

To further suppress noise and enhance fine spectral structures in the VIS–NIR data, this study applied the Savitzky–Golay (SG) smoothing filter and subsequently computed the first derivative of each spectrum (SG-D1). The SG filter performs local polynomial fitting within a moving window and is widely recognized for its ability to smooth spectral signals while preserving peak shapes and subtle absorption details [32]. In this study, an 11-point window and a second-order polynomial were used, providing an effective balance between noise reduction and feature retention.

To further highlight weak absorption bands and reduce baseline variations, the first derivative of the SG-smoothed spectra was calculated (SG-D1) [33]. This derivative operation enhances diagnostically relevant spectral features associated with soil organic matter (SOM), thereby improving the sensitivity and robustness of subsequent regression modeling.

Importantly, both SG smoothing and SG-D1 rely solely on each individual sample’s local window and do not use any global dataset statistics. As such, the preprocessing procedure does not introduce information leakage during cross-validation, ensuring methodological rigor and reproducibility [34,35].

2.3. Single-Modality Regression Models

Before performing multi-source spectral data fusion modeling, this study first established single-modality regression models to evaluate the independent representation and prediction capabilities of different spectral modalities (Raman and VIS–NIR). Building single-modality models helps to clarify each spectrum’s standalone predictive ability and provides a reference input for multi-modal fusion, allowing for a clearer assessment of the feature contributions and complementarity between modalities. For Raman spectra, which are characterized by high dimensionality, collinearity, and noise, an ElasticNet regression model was employed to achieve robust prediction through a combination of L1 and L2 regularization.

For visible–near-infrared (VIS–NIR) spectra, which exhibit strong nonlinearity and complex absorption structures, the Extreme Gradient Boosting (XGBoost) algorithm was utilized to capture nonlinear feature interactions and enhance model accuracy.

2.3.1. ElasticNet Regression

ElasticNet regression combines the strengths of Lasso (L1) and Ridge (L2) regularization to achieve both variable selection and stable coefficient shrinkage [36,37]. By jointly penalizing coefficient magnitude and sparsity, ElasticNet effectively handles multicollinearity commonly found in high-dimensional spectral data.

The two hyperparameters controlling the balance between L1/L2 regularization and the overall penalty strength are automatically optimized through cross-validation. This enables ElasticNet to select informative Raman features while suppressing noise and redundant wavelengths, improving both predictive accuracy and physical interpretability.

2.3.2. XGBoost Regression

XGBoost is a gradient-boosted decision tree algorithm that builds an ensemble of regression trees in a stage-wise manner, where each new tree fits the residuals or gradients from the previous stage [38,39]. Through second-order gradient approximation and explicit model regularization, XGBoost achieves high predictive accuracy while preventing overfitting.

Several strategies—including learning-rate shrinkage, row/column subsampling, and L1/L2 regularization—further enhance the model’s robustness. For spectral regression tasks, XGBoost can naturally capture nonlinear relationships and interactions among wavelengths and is particularly effective for continuous, noisy spectral datasets.

2.4. Traditional Multimodal Fusion

2.4.1. EarlyFusion_Ridge

EarlyFusion_Ridge regression is a typical early fusion strategy. In this approach, Raman and VIS–NIR spectral features—after baseline correction, SG-D1, and SNV preprocessing—are directly concatenated, allowing both modalities to be represented within a unified high-dimensional feature space. A Ridge regression model with L2 regularization is then applied to the concatenated features to predict the target variable [40,41].

Ridge regression incorporates a penalty on the squared magnitude of the coefficients, which effectively alleviates multicollinearity commonly present in high-dimensional spectral data, prevents overfitting to noisy variables, and improves numerical stability [42,43]. During training, to ensure that features from different modalities contribute on a comparable scale, standardization (zero mean and unit variance) is performed within each training fold, and the same transformation is applied to the corresponding validation fold, thereby preventing information leakage.

2.4.2. AE_LatentFusion

AE_LatentFusion aims to learn compact, noise-reduced feature representations for each modality (Raman and VIS–NIR) before fusion. Instead of directly combining high-dimensional spectra, a separate autoencoder is trained for each modality to compress its spectral vector into a lower-dimensional latent representation. This process reduces noise, removes redundant information, and balances the dimensionality gap between modalities.

After training, the encoder parts of the autoencoders generate latent feature matrices for Raman and VIS–NIR data. These latent features—now more compact and modality-aligned—are concatenated to form a unified feature matrix. A regression model (e.g., Ridge or ElasticNet) is then trained on the fused latent features to predict the target variable [44,45].

By combining modality-specific compression with shared modeling in the latent space, this approach captures both unique and complementary information from the two spectral sources. As a result, it enhances prediction robustness, reduces the influence of noise and irrelevant features, and provides a more interpretable representation of how each modality contributes to the final prediction.

2.4.3. WeightedLate_Fusion

The WeightedLate_Fusion performs multimodal fusion at the decision level. Instead of combining features from different spectra, it first trains separate regression models for each modality independently—for example, ElasticNet for Raman spectra and XGBoost for VIS–NIR spectra. Each model outputs its own prediction sequence based solely on its corresponding modality.

After these modality-specific predictions are obtained, they are integrated through a weighted combination. The idea is that each modality contributes to the final prediction in proportion to its predictive reliability. In practice, the weights can be determined through validation performance (such as each model’s R² on a held-out set) or set empirically according to domain knowledge.

Because this method directly fuses predictions rather than raw features, it avoids issues such as dimensional mismatch or differences in noise structure between spectra. It also allows each modality to use the algorithm best suited to its characteristics. As a result, weighted averaging provides a simple yet flexible late-fusion framework that often improves overall robustness and generalization, especially when the strengths of Raman and VIS–NIR models differ across samples [46,47].

2.5. A Modality-Gated Ridge Regression Fusion Model

2.5.1. Method Overview

To overcome the limitations of conventional early, latent, and late fusion strategies—such as linear constraints, unaligned latent spaces, and fixed modality weights—this study proposes a Modality-Gated Ridge Fusion (Fusion_GatedRidge) approach. Building upon latent representations extracted via multimodal autoencoders, the method introduces learnable gating weights to adaptively modulate the contribution of each modality, while employing ridge regression to model the output variable. The core idea is that, during fusion, the contributions of Raman and VIS–NIR modalities to the prediction are not assumed to be constant. Instead, gating parameters $s_r$, $s_v$ dynamically scale each modality’s latent features, allowing the model to adaptively adjust the relative importance of modalities for each sample. Ridge regression is then applied in this gated feature space to jointly optimize the model parameters, achieving both robust performance and interpretable fusion representation.

2.5.2. Model Architecture and Principle

(1)

Data Input and Alignment

From the preprocessing stage, the Raman spectral matrix $X^{\left(r\right)}\in {\mathbb{R}}^{n\times k_r}$, the VIS–NIR spectral matrix $X^{\left(v\right)}\in {\mathbb{R}}^{n\times k_v}$, and the target vector $y\in {\mathbb{R}}^n$ are obtained. Both spectral datasets are aligned according to sample indices before being used as model inputs.

(2)

Latent Feature Extraction

Following the AE_LatentFusion strategy, independent autoencoders are constructed for Raman and VIS–NIR modalities:

$$\underset{{\theta }_m,{\varphi }_m}{\min }{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{‖x_i^{\left(m\right)}-g_{{\varphi }_m}\left(f_{{\theta }_m}\right(x_i^{\left(m\right)}\left)\right)‖}^2 m\in \left\{r,v\right\}$$

(2)

The encoder outputs latent feature representations as:

$$Z^{\left(r\right)}=f_{{\theta }_r}\left(X^{\left(r\right)}\right) Z^{\left(v\right)}=f_{{\theta }_v}\left(X^{\left(v\right)}\right)$$

(3)

where $Z^{\left(r\right)}\in {\mathbb{R}}^{n\times k_r}$, $Z^{\left(v\right)}\in {\mathbb{R}}^{n\times k_v}$.

(3)

Modality-Gating Mechanism

The modality-gating mechanism introduces two adjustable weighting coefficients $s_r$ and $s_v$ to balance the contributions of Raman and VIS–NIR modalities. These coefficients act as a scaling gate layer in the latent feature space, dynamically modulating the relative importance of each modality before fusion. For a given pair ($s_r$, $s_v$), the latent representations are reweighted and concatenated as:

$$Z=\left[{s_{r}Z}^{\left(r\right)}\parallel s_v{Z}^{\left(v\right)}\right]$$

(4)

Rather than relying on manually assigned weights, the optimal gating coefficients ($s_r^{*}$, $s_v^{*}$) are determined in a fully data-driven manner. A grid-search or cross-validation procedure is performed over predefined candidate sets $G_r$ and $G_v$. For each weight combination, a Ridge regression model is trained on the training subset and evaluated on the validation subset. The optimal coefficients are selected by maximizing the validation R²:

$$(s_r^{*},s_v^{*})=arg \underset{s_r\in G_r,s_v\in G_v}{\max }{\mathrm{R}}_{val}^2(s_r,s_v)$$

(5)

In this optimization formulation, $s_r$ and ${ s}_v$ represent the gating coefficients assigned to the Raman and VIS–NIR modalities, respectively, which control their relative contributions in the fused latent representation. The sets $G_r$ and $G_v$ denote the predefined candidate grids from which the gating coefficients are selected. For each possible combination $(s_r,s_v)$, a Ridge regression model is trained and evaluated on the validation set, yielding a validation coefficient of determination denoted as ${\mathrm{R}}_{val}^2(s_r,s_v)$. The operator argmax identifies the specific pair of coefficients that maximizes this validation performance. Thus, the resulting $(s_r^{*},s_v^{*})$ corresponds to the optimal gating weights that achieve the best predictive accuracy on the validation set, ensuring an adaptively balanced contribution between the two modalities.

(4)

Ridge Regression–Based Fusion Prediction

The gated latent features $Z$ are then fed into a ridge regression model defined as:

$$\underset{\beta ,b}{\min }{\displaystyle \frac{1}{n}}{‖y-(Z\beta +b1)‖}_2^2+{\lambda }_1{‖\beta ‖}_1+{\lambda }_2{‖\beta ‖}_2^2$$

(6)

where $\lambda >0$ is the ridge regularization term used to prevent overfitting and control coefficient magnitudes.

The optimal model parameters (${\beta }^{*}$, $b^{*}$) are obtained via cross-validation, and the final prediction is given by:

$$\widehat{y}=Z{\beta }^{*}+b^{*}$$

(7)

2.5.3. Modality Contribution Analysis

The coefficients $\beta$ of the fused ridge regression model quantitatively represent the relative contribution of each modality.

If the concatenated feature matrix is defined as $Z=\left[Z^{\left(r\right)}{|Z}^{\left(v\right)}\right]$, then the relative contributions of Raman and VIS–NIR modalities are computed as:

$$C_r={\displaystyle \frac{{\sum }_{j=1}^{k_r}\left|{\beta }_j\right|}{{\sum }_{j=1}^{k_r+k_v}\left|{\beta }_j\right|}} C_v={\displaystyle \frac{{\sum }_{j=k_r+1}^{k_r+k_v}\left|{\beta }_j\right|}{{\sum }_{j=1}^{k_r+k_v}\left|{\beta }_j\right|}}$$

(8)

where ${\beta }_j$ is the $j$-th coefficient in the ridge regression model, $k_r$ and $k_v$ denote the dimensions of the Raman and VIS–NIR latent features, respectively, and $C_r+C_v=1$.

This formulation enables the model not only to perform accurate prediction but also to interpret the relative contribution and information share between modalities, enhancing the transparency and explainability of multimodal fusion learning.

2.6. Evaluation Metrics

To ensure the generalization performance and robustness of the model, this study employed five-fold cross-validation (5-fold CV) to train and evaluate all regression models.

The specific procedure is as follows: The dataset was randomly divided into five approximately equal subsets (Fold1–Fold5). In each iteration, one subset was used as the validation set, while the remaining four subsets served as the training set. This process was repeated five times so that each sample was used exactly once for validation.

The five validation results were then averaged across five key performance metrics—Coefficient of Determination (R²), Root Mean Square Error (RMSE), Mean Absolute Error (MAE), Normalized Root Mean Square Error (NRMSE), and Ratio of Performance to Deviation (RPD)—to obtain the overall model evaluation results.

The basic principles for computing these performance metrics in each fold are expressed as follows [48,49]:

$${\mathrm{R}}^2=1-{\displaystyle \frac{{\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2}{{\sum }_{i=1}^n{(y_i-\overline{y})}^2}}$$

(9)

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2}$$

(10)

$$\mathrm{M}\mathrm{A}\mathrm{E}={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n\left|(y_i-{\widehat{y}}_i)\right|$$

(11)

$$\mathrm{N}\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}={\displaystyle \frac{\sqrt{\frac{1}{n}{\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2}}{y_{max}{-y}_{min}}}$$

(12)

$$\mathrm{R}\mathrm{P}\mathrm{D}={\displaystyle \frac{\sqrt{\frac{1}{n-1}{\sum }_{i=1}^n{(y_i-\overline{y})}^2}}{\sqrt{\frac{1}{n}{\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2}}}$$

(13)

In the equations, $y_i$ represents the observed (actual) value, ${\widehat{y}}_i$ denotes the predicted value, and $\overline{y}$ is the mean of the observed values. The variable $n$ indicates the total number of samples, while $y_{max}$ and $y_{min}$ refer to the maximum and minimum actual values, respectively. R² quantifies the proportion of variance explained by the model, whereas RMSE and MAE describe absolute prediction errors. NRMSE is a dimensionless metric obtained by normalizing RMSE, enabling error comparison across datasets with different scales. RPD evaluates the relationship between the model error and the natural variability of the dataset, providing an additional measure of predictive performance.

2.7. Paired Nonparametric Significance Testing of Fusion Model Performance

To assess whether the performance improvement achieved by the proposed Fusion_GatedRidge multimodal fusion method is statistically significant across cross-validation folds, paired statistical tests were conducted on the per-fold evaluation metrics (R² and RMSE). Because all folds are derived from the same data partitioning and therefore constitute repeated measurements rather than independent samples, the resulting paired structure violates the assumption of independence required by parametric tests. Accordingly, a nonparametric paired test—the Wilcoxon signed-rank test—was employed to evaluate model differences.

The Wilcoxon signed-rank test is used to compare the performance differences of two methods measured on the same set of samples (here, the validation folds). Its procedure includes the following steps [50,51]:

(1)

Compute the per-fold performance differences

$$d_i=M_{GatedRidge,i}-M_{Baseline,i}$$

(14)

where $M_{GatedRidge,i}$ denotes the performance metric (R² or RMSE) of the proposed Fusion_GatedRidgee model on fold i, and $M_{Baseline,i}$ represents the corresponding metric of a baseline fusion method evaluated on the same fold. The baseline group includes three commonly used multimodal fusion strategies: EarlyFusion_Ridge, AE_LatentFusion and WeightedLate_Fusion. The paired difference $d_i$ reflects the performance improvement of Fusion_GatedRidge relative to the baseline method on each fold:

If $d_i>0$: Fusion_GatedRidge outperforms the baseline (higher R² or lower RMSE).

If $d_i<0$: Fusion_GatedRidge performs worse than the baseline on that fold.

If $d_i=0$: Both models achieve identical performance on that fold.

(2)

Remove zero differences, rank the remaining differences by their absolute values, and assign ranks.

(3)

Apply signs: multiply each rank by the sign (positive or negative) of its corresponding difference to obtain signed ranks.

(4)

Calculate the sum of positive and negative ranks ($T^{+}$ and $T^{-}$):

$$T^{+}=\sum (positive ranks)$$

(15)

$$T^{-}=\sum (negative ranks)$$

(16)

(5)

Compute the Wilcoxon test statistic W based on the rank sums and obtain the one-sided p-value for statistical inference.

(6)

Combining the rank-sum statistic W, the standardized effect size can be computed [52,53,54].

$$r={\displaystyle \frac{Z}{\sqrt{n}}}$$

(17)

where n denotes the number of folds (n = 5). The effect size r is interpreted as follows: 0.1 small effect, 0.3 medium effect, 0.5 large effect, 0.8 very large effect.

3. Results

3.1. Characteristics of Sample Data

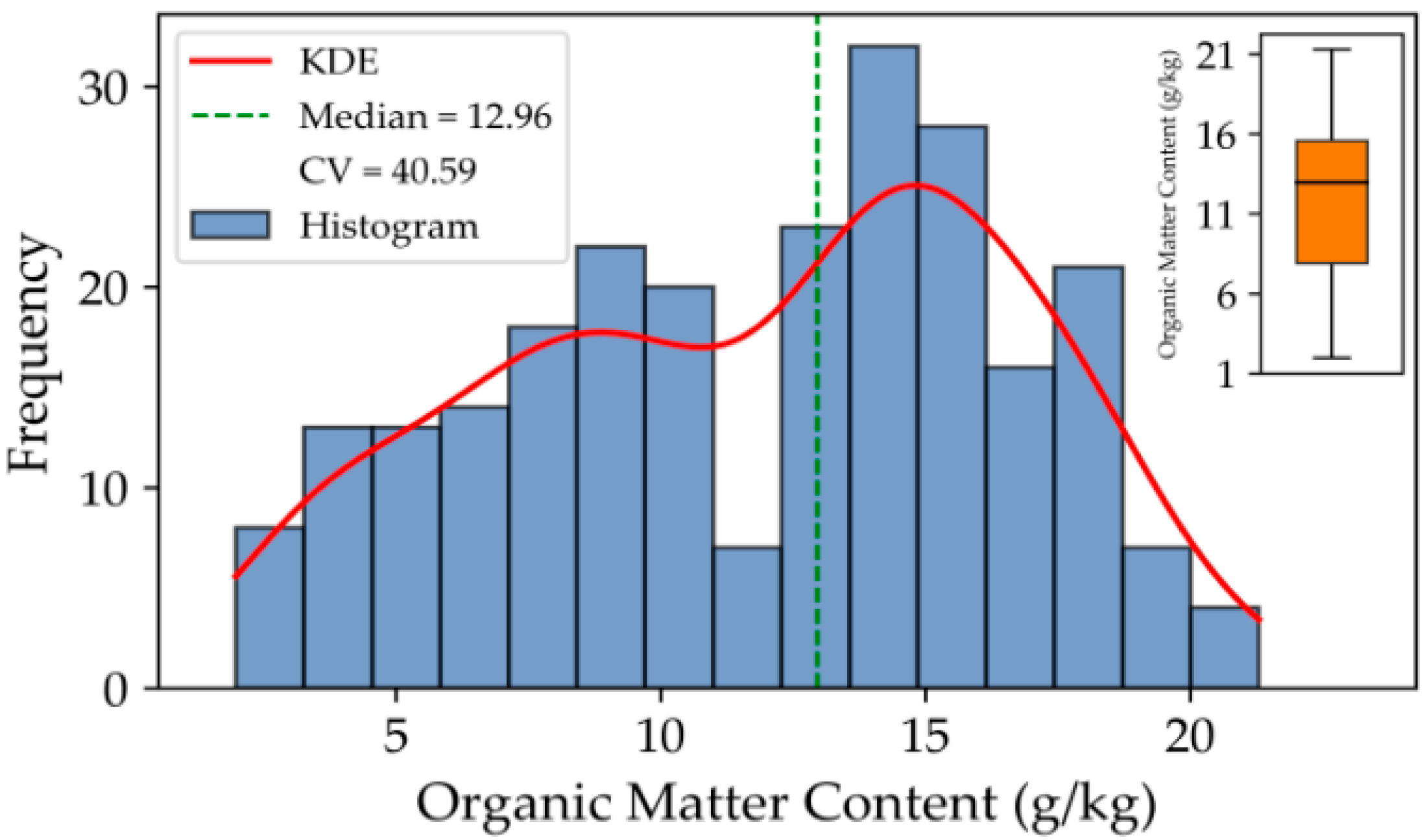
Figure 2 illustrates the frequency distribution and kernel density curve of soil organic matter (SOM) content across all samples. Overall, the SOM content exhibits a right-skewed unimodal distribution, indicating that most soil samples have moderate to low SOM levels, with only a few samples showing higher values. The SOM content ranges from 1.97 to 21.30 g·kg⁻¹, reflecting a wide distribution that covers both low- and high-content soils. The median value is 12.96 g·kg⁻¹, and the coefficient of variation (CV) is 40.59%, suggesting a moderate degree of dispersion and highlighting the noticeable variability of SOM among different sampling sites.

From the histogram and kernel density estimation (KDE) curve, the overall distribution appears smooth without significant multimodal characteristics, suggesting that the sampling was well-balanced and adequately represents the overall variation trend of SOM across the study area. The boxplot analysis further shows that most samples fall within the 8–16 g·kg⁻¹ range, while a few high-value samples may correspond to plots with stronger fertilization intensity or more favorable organic matter accumulation conditions.

These results confirm that the dataset effectively captures the main distribution characteristics and spatial variability of soil organic matter in the study region, providing a reliable foundation for subsequent spectral modeling and nutrient spatial distribution analyses.

3.2. Characteristic Analysis of Spectra

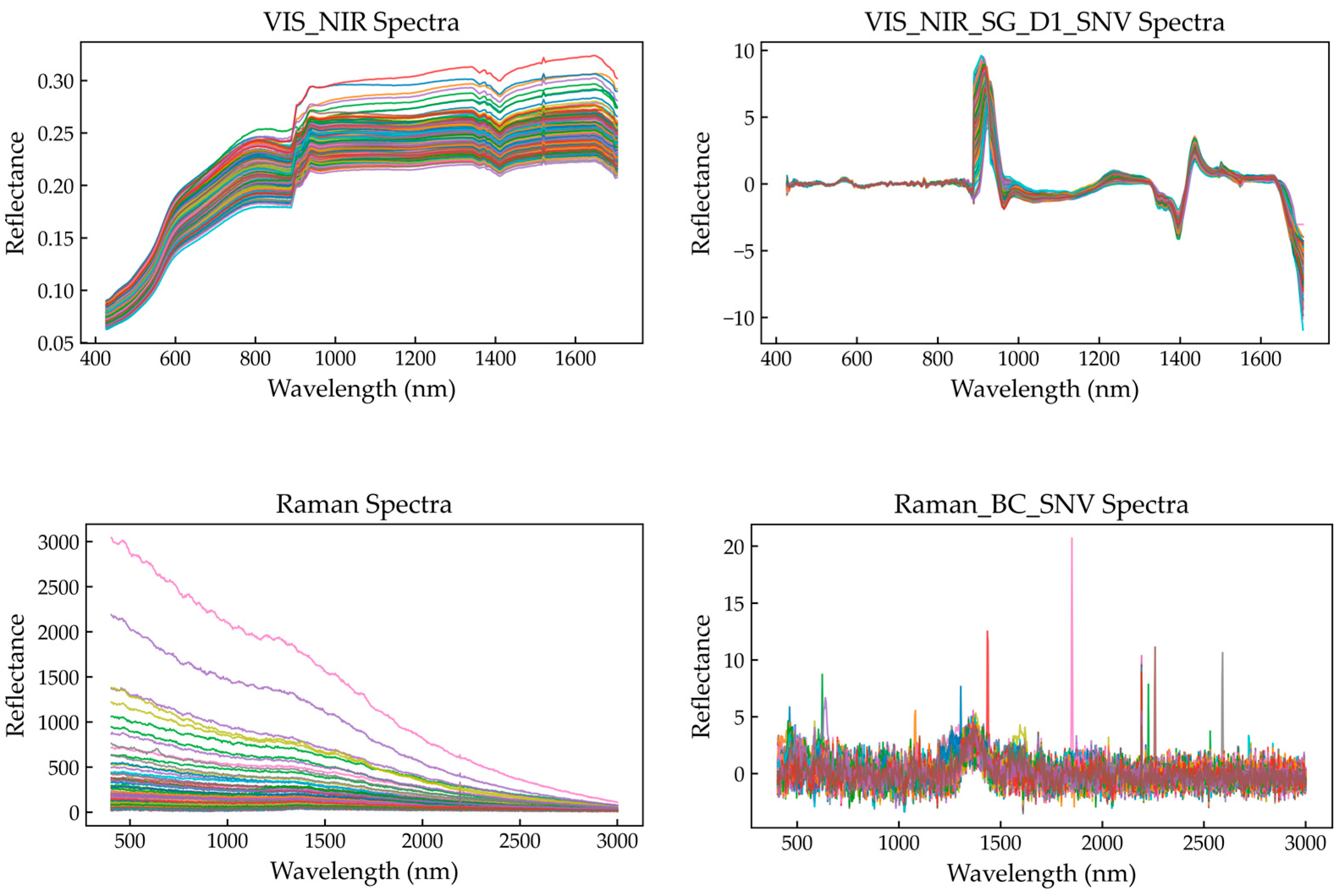
To ensure the comparability and stability of the spectral data, both the visible–near-infrared (VIS–NIR) and Raman spectra were subjected to targeted preprocessing. Figure 3 compares the original and preprocessed spectra, with the left panels showing the unprocessed curves and the right panels displaying the corresponding results after preprocessing. The comparison clearly demonstrates that preprocessing effectively corrected baseline drift and amplitude inconsistencies, leading to more uniform spectral patterns among samples.

For the VIS–NIR spectra, the original reflectance curves (Figure 3, upper left) show an overall upward trend across 400–1700 nm with local fluctuations, exhibiting evident baseline drift and multiplicative scattering effects. After applying the Savitzky–Golay (SG) filter for smoothing and computing the first derivative (SG–D1), followed by Standard Normal Variate (SNV) transformation, baseline trends were substantially reduced while local absorption features were enhanced. The processed spectra (Figure 3, upper right) oscillate around zero with clearer variation patterns, and absorption peaks at 970, 1200, and 1450 nm become more pronounced. The waveform shapes and amplitudes among samples also appear more consistent. These transformations ensure that spectral variation primarily reflects chemical composition differences rather than physical scattering effects, facilitating the extraction of meaningful chemical information during model training.

For the Raman spectra, the original spectra (Figure 3, lower left) show strong fluorescence background interference, with a pronounced exponential baseline decay that obscures several diagnostic Raman peaks. After polynomial baseline correction to remove fluorescence interference and subsequent SNV normalization (Figure 3, lower right), baseline variations among samples were largely eliminated, with signals centered around zero. The corrected spectra retain distinct Raman peaks at 1000, 1450, and 1600 cm⁻¹, corresponding primarily to vibrations of functional groups such as C–H and C=C within organic matter. Similarly to the derivative-enhanced VIS–NIR spectra, the baseline-corrected Raman spectra exhibit enhanced peak definition and standardized scaling, providing mutually comparable and complementary inputs for the subsequent multimodal fusion modeling.

3.3. Single-Modality Modeling Results

To analyze the performance of individual spectral modalities in predicting soil organic matter (SOM) content, single-modality regression models were constructed based on visible–near-infrared (VIS–NIR) and Raman spectra, respectively.

The VIS–NIR model employed an XGBoost regressor (Single_VIS_NIR_XGB), while the Raman model used ElasticNet regression (Single_Raman_EN).

Both models were evaluated using five-fold cross-validation, and the average performance metrics were adopted as the overall evaluation results, as shown in

Table 1. Performance comparison of single-modality models (mean ± standard deviation).

Model	R2	RMSE	MAE	NRMSE	RPD
Single_VIS_NIR_XGB	0.74 ± 0.03	2.42 ± 0.13	1.87 ± 0.6	0.13 ± 0.01	1.98 ± 0.11
Single_Raman_EN	0.70 ± 0.10	2.61 ± 0.31	2.03 ± 0.28	0.14 ± 0.02	1.84 ± 0.27

.

As shown in Table 1, the VIS–NIR model outperformed the Raman model overall. The VIS–NIR model achieved an R² of 0.74, RMSE of 2.42 g·kg⁻¹, and RPD of 1.98, indicating a moderate level of quantitative prediction capability. In contrast, the Raman model yielded an R² of 0.70, RMSE of 2.61 g·kg⁻¹, and RPD of 1.84, suggesting slightly lower predictive accuracy and higher error levels.

In terms of error metrics, both models achieved NRMSE values of 0.13 and 0.14, respectively, reflecting good relative stability after normalization. Since both models produced RPD > 1.8, they can be considered effective for providing meaningful predictive information, though they do not yet reach the threshold for precise quantitative prediction (RPD > 2.0).These findings highlight the potential of multimodal fusion—by combining the complementary strengths of Raman and VIS–NIR spectra, it is possible to further enhance model robustness and predictive accuracy.

3.4. Multimodal Fusion Results

Table 2. Performance comparison of traditional multimodal fusion models (mean ± standard deviation).

Model	R2	RMSE	MAE	NRMSE	RPD
EarlyFusion_Ridge	0.72 ± 0.09	2.52 ± 0.30	2.02 ± 0.18	0.13 ± 0.01	1.90 ± 0.28
AE_LatentFusion	0.71 ± 0.06	2.59 ± 0.23	2.10 ± 0.18	0.13 ± 0.01	1.86 ± 0.20
WeightedLate_Fusion	0.61 ± 0.03	3.00 ± 0.23	2.44 ± 0.21	0.16 ± 0.01	1.60 ± 0.06
Fusion_GatedRidge	0.83 ± 0.05	2.01 ± 0.21	1.56 ± 0.19	0.10 ± 0.01	2.39 ± 0.28

summarizes the five-fold cross-validation performance of the four multimodal fusion strategies. Among the traditional approaches, EarlyFusion_Ridge achieved the strongest results (R² = 0.72, RMSE = 2.52 g·kg⁻¹, RPD = 1.90), indicating that direct feature concatenation can provide a basic level of cross-modal complementarity. AE_LatentFusion showed comparable but slightly reduced performance (R² = 0.71), suggesting that although autoencoders effectively reduce redundancy, unconstrained latent features may not fully capture Raman–VIS–NIR interactions. WeightedLate_Fusion performed the weakest (R² = 0.61, RMSE = 3.00 g·kg⁻¹), likely due to its reliance on fixed weights, which limits responsiveness to sample-level variability.

In contrast, the proposed Fusion_GatedRidge model substantially outperformed all traditional fusion strategies across every evaluation metric. Its R² increased to 0.83 and RMSE decreased to 2.01 g·kg⁻¹, while RPD rose to 2.39, exceeding the commonly accepted threshold (RPD > 2.0) for reliable predictions. These gains confirm that the adaptive gating mechanism effectively balances Raman and VIS–NIR contributions at the latent feature level, reducing noise accumulation and enhancing cross-modal interaction modeling. The contribution analysis based on Equation (8) further showed stable and interpretable modality weights across folds, reinforcing the robustness of the fusion process.

Compared with single-modality models, Fusion_GatedRidge improved R² by 12–19% and reduced RMSE by 17–23%, demonstrating that complementary chemical (Raman) and physical–optical (VIS–NIR) information can be synergistically exploited only when adaptive weighting is employed. Overall, the results highlight that while traditional fusion methods provide moderate improvement over single modalities, significant performance enhancement is achieved only through the adaptive gating and regularized prediction framework introduced in this study.

3.5. Results of the Paired Nonparametric Significance Testing

The performance advantage of the proposed Fusion_GatedRidge model across folds is statistically significant (

Table 3. Paired Wilcoxon test and effect size r for Fusion_GatedRidge against baseline fusion models.

Metric	Base	TargetCol	T_Pos	T_Neg	p_One_Sided	Effect_Size_r
R2	AE_LatentFusion	Fusion_GatedRidge	15	0	0.03125	0.83
R2	EarlyFusion_Ridge	Fusion_GatedRidge	15	0	0.03125	0.83
R2	WeightedLate_Fusion	Fusion_GatedRidge	15	0	0.03125	0.83
RMSE	AE_LatentFusion	Fusion_GatedRidge	0	15	1	−0.83
RMSE	EarlyFusion_Ridge	Fusion_GatedRidge	0	15	1	−0.83
RMSE	WeightedLate_Fusion	Fusion_GatedRidge	0	15	1	−0.83

). Following the paired-difference computation defined in Equation (14), Fusion_GatedRidge achieved higher R² values than all three baseline models in every fold (T⁺ = 15, T⁻ = 0). Based on the Wilcoxon signed-rank procedure described in Equations (15) and (16), the one-sided p-value was 0.031, and the effect size, calculated using Equation (17), was r = 0.83, indicating a very large effect.

For RMSE, the paired differences computed via Equation (14) showed that Fusion_GatedRidge achieved lower errors in all folds (T⁺ =15, T⁻ = 0). Under the “smaller-is-better” direction, the Wilcoxon statistic derived from Equations (15) and (16) yielded a one-sided p-value of 0.031, and the corresponding effect size |r| = 0.83 (via Equation (17)) also represents a very large effect.

Together, these statistical findings demonstrate that the superiority of Fusion_GatedRidge over traditional fusion methods is not only numerically evident but also statistically validated, underscoring its substantial practical relevance.

3.6. Optimal Gating Parameters and Modal Contributions

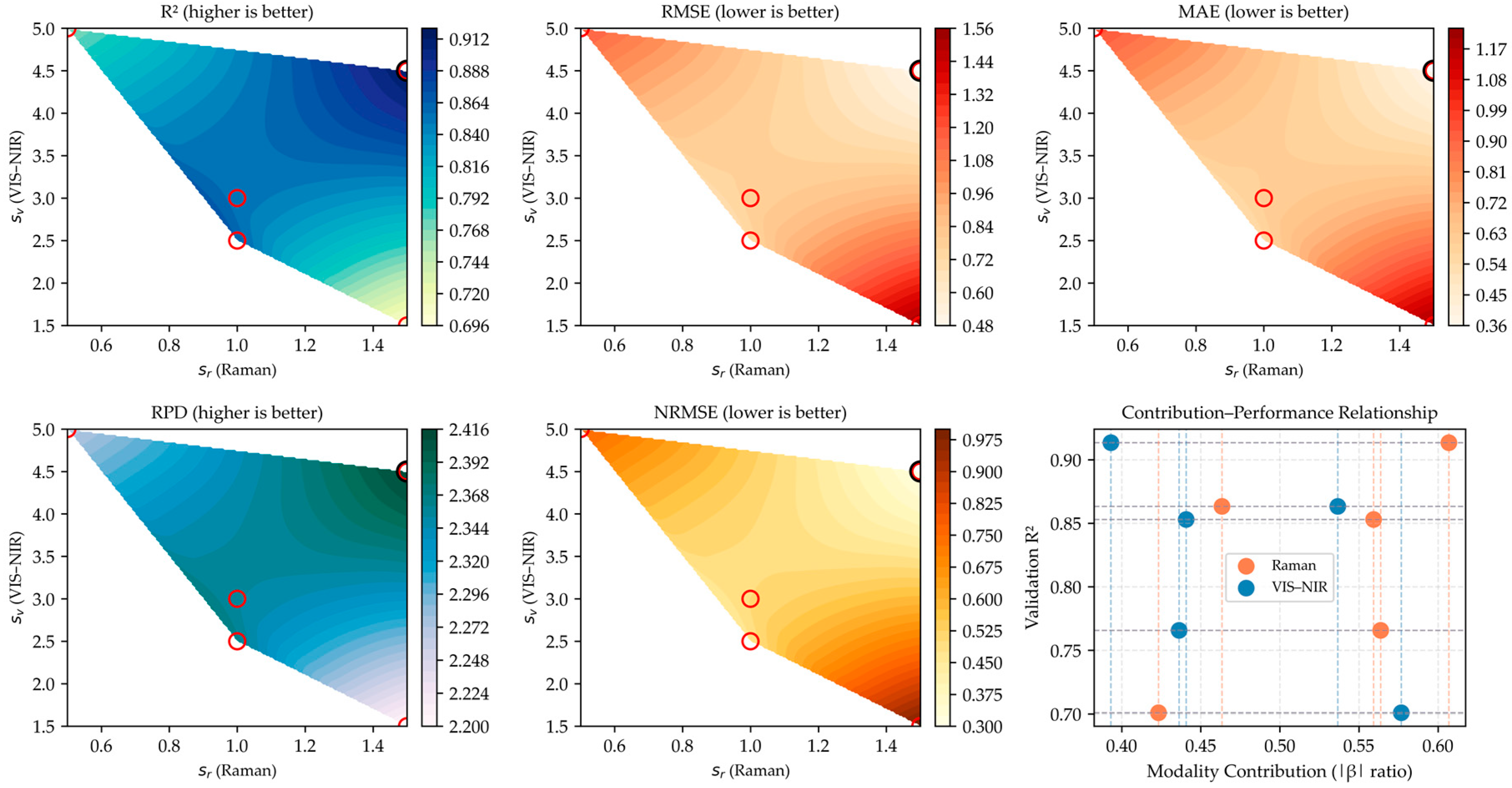
Figure 4 illustrates the performance response surface of the gated fusion model under different combinations of Raman weights ($s_r$) and VIS–NIR weights ($s_v$). The response surface is generated from one validation fold and is used solely to visualize how the model’s performance varies with different modality weightings. Although the absolute values do not represent the final cross-validated performance, the overall trend consistently shows that combinations around $s_r$ ≈ 1.5 and $s_v$ ≈ 4.5 yield relatively better validation results. This indicates that assigning higher weight to VIS–NIR features while moderately scaling Raman features is beneficial, supporting the effectiveness of the adaptive gating mechanism.

From the response surface distribution, regions of high R² and RPD closely overlap with areas of low RMSE, MAE, and NRMSE, confirming that the gating mechanism effectively facilitates complementarity between the two spectral modalities.

As the weights of Raman and VIS–NIR increase moderately, the explanatory power of the model improves; however, when one modality becomes dominant, prediction performance deteriorates.

This trend suggests that excessive dependence on a single modality can lead to amplified noise or redundant information. The smooth distribution of NRMSE further indicates that the gated fusion model maintains robustness and generalization stability across cross-validation folds. The bottom-right panel of Figure 4 shows the relationship between the modal contribution ratios ($\left|\mathrm{\beta }\right|$) of Raman and VIS–NIR spectra and the model’s R² values.

Overall, the modality-gated fusion approach demonstrated significant advantages in leveraging the complementarity of Raman and VIS–NIR spectra. By adaptively allocating modality weights, the model achieved a dynamic balance between structural vibration information (Raman) and reflectance-based spectral information (VIS–NIR).

3.7. Error Analysis

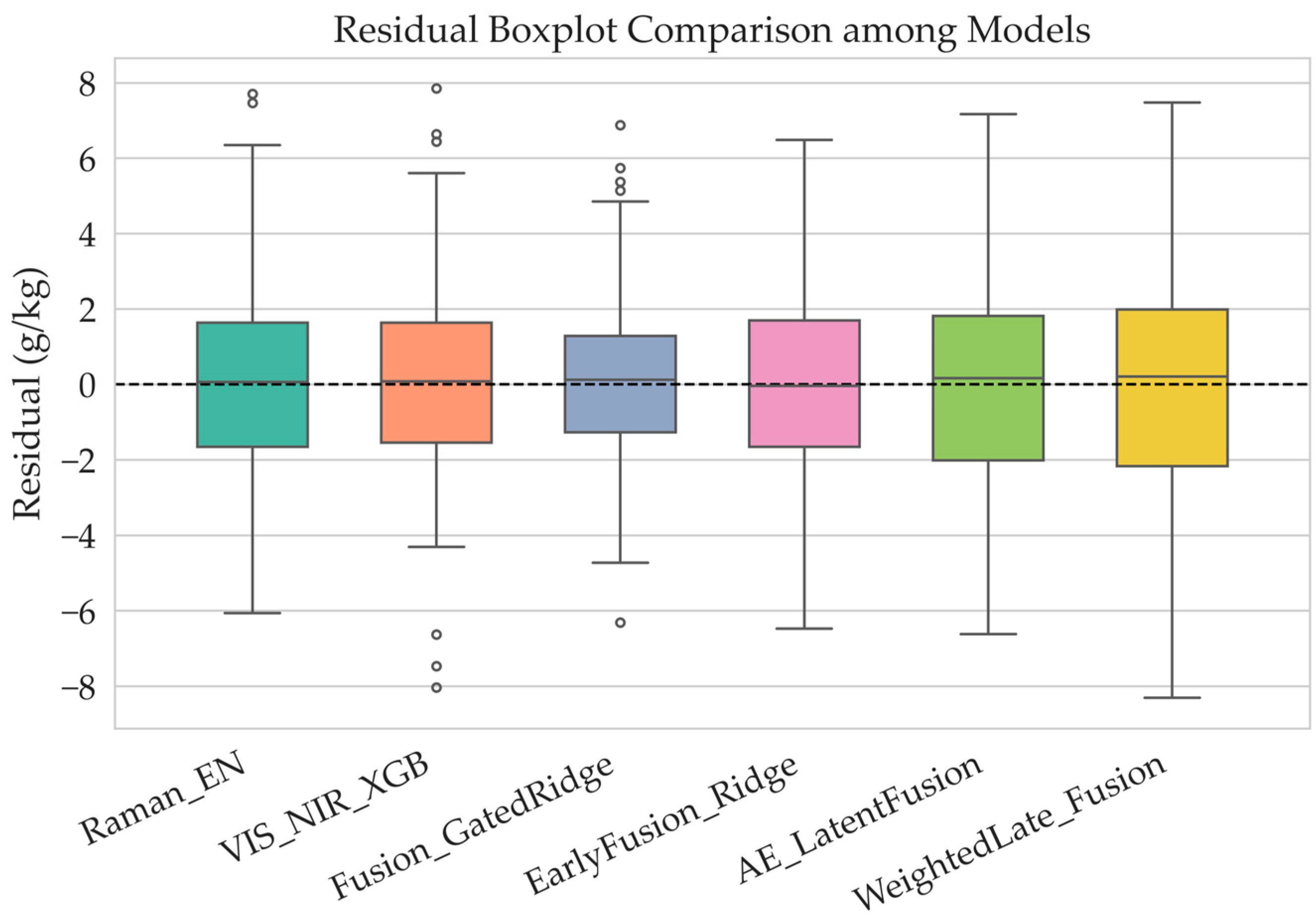
Figure 5 is Residual Boxplot Comparison among Models illustrates the residual distribution characteristics of six models—Raman_EN, VIS_NIR_XGB, Fusion_GatedRidge, EarlyFusion_Ridge, AE_LatentFusion, and WeightedLate_Fusion—in predicting soil organic matter (SOM). Overall, the median residuals of all models are close to zero, indicating that no significant systematic bias occurred during prediction and that the overall model fitting trend is reasonable. Most residuals are concentrated within the −2 to 2 g·kg⁻¹ range, accounting for over 80% of all samples, suggesting that all models achieved relatively high prediction accuracy, with only a few samples showing large deviations. For single-modality models (Raman_EN and VIS_NIR_XGB), the residuals exhibit a slightly wider spread, as indicated by the larger interquartile range. This implies higher variability in predictions. Notably, the Raman_EN model occasionally displays larger negative residuals in low-SOM samples, indicating limited generalization ability in the low-value range.

In contrast, the fusion models (EarlyFusion_Ridge, AE_LatentFusion, WeightedLate_Fusion) show more compact residual distributions with narrower boxes and fewer outliers, reflecting their advantage in suppressing random errors and improving prediction stability.

Among them, the Fusion_GatedRidge and AE_LatentFusion models demonstrate the most concentrated residuals, almost entirely within the −2 to 2 g·kg⁻¹ range, indicating the smallest variability and the highest robustness.

Overall, fusion models show markedly better residual compactness and stability compared to single-modality models, with Fusion_GatedRidge and AE_LatentFusion achieving the most consistent and least-biased results.This outcome confirms that multisource spectral fusion effectively reduces model uncertainty and enhances SOM prediction accuracy and consistency.

The Fusion_GatedRidge Regression model, in particular, introduces learnable gating parameters ($s_r$, $s_v$) that dynamically adjust the fusion ratio between Raman and VIS–NIR spectra based on sample characteristics. When $s_r$ ≈ 1.0 and $s_v$ ≈ 3.0, the model achieves optimal performance with an R² of 0.83, and residuals predominantly distributed between −2 and 2 g·kg⁻¹, indicating high prediction accuracy, stability, and generalization ability.

In summary, the gated fusion model effectively integrates the molecular-structure-sensitive features of Raman spectroscopy with the optical reflectance characteristics of VIS–NIR spectroscopy, achieving synergistic modeling of chemical and physical information. This provides a new, adaptive fusion approach for non-destructive nutrient detection in complex soil samples, ensuring high precision, interpretability, and robustness.

4. Discussion

In this study, three traditional fusion strategies (EarlyFusion_Ridge, AE_LatentFusion, and WeightedLate_Fusion) were compared with the newly proposed Fusion_GatedRidge to evaluate multimodal spectral integration for SOM estimation. The results show that Fusion_GatedRidgeconsistently achieved the best performance, with R² = 0.83 and residuals mostly within −2 to 2 g·kg⁻¹, indicating small and well-centered prediction errors. Compared with single-modality models (VIS–NIR: R² ≈ 0.74; Raman: R² ≈ 0.70), the fused model achieved a substantial improvement in accuracy and robustness. These outcomes align with previous findings such as Zhang et al. [13], who reported R² = 0.95 for VIS–NIR + XRF fusion, confirming the considerable potential of multisource spectral integration in complex soil systems.

EarlyFusion_Ridge offers a straightforward feature concatenation scheme, but previous studies have shown that low-level fusion is prone to issues such as scale mismatch and increased sensitivity to modality-specific noise [40]. AE_LatentFusion using autoencoders reduced redundancy and extracted compact feature representations, while WeightedLate_Fusion demonstrated moderate flexibility but remained dependent on manually assigned weights. In contrast, the Fusion_GatedRidge model introduced learnable weighting parameters ($s_r$, $s_v$), enabling adaptive balancing of Raman and VIS–NIR contributions at the sample level. This adaptive gating helped maintain stable R² values (0.76–0.91) across fivefold CV, confirming the robustness of the learned fusion. Similar conclusions were drawn in Atrey et al. [55] and Xu et al. [56], where feature-level fusion outperformed simple concatenation by more effectively leveraging intermodal complementarity.

From a mechanistic perspective, Raman spectroscopy captures chemical bond vibrations (e.g., C–H, C=O), providing molecular-level information, whereas VIS–NIR primarily reflects optical and physical properties such as moisture, color, and scattering [2,5]. Their combination therefore enables simultaneous characterization of chemical and physical attributes, which improves the model’s sensitivity to SOM variation. Bai et al. [10] demonstrated that outer-product fusion (OPA) can extract cross-modal interactions in NIR + Raman data. However, advanced fusion methods such as OPA, Transformer-based multimodal attention, or deep cross-modal architectures generally require large training datasets, have high computational cost due to quadratic attention or high-order tensor operations, and suffer from limited interpretability—issues incompatible with soil spectroscopy, where datasets are typically small, noisy, and require transparent modeling [7,14,19,20]. The Fusion_GatedRidge model achieves part of the benefit of adaptive weighting while avoiding the computational burden and interpretability limitations of these deep multimodal methods, making it more suitable for soil spectral applications.

Generalization analysis further demonstrated that the Fusion_GatedRidge model maintained consistent predictive behavior, with stable R² values across folds and symmetrically distributed residuals. Prior studies such as Song et al. [28], Heil and Schmidhalter [48], and Gholizadeh et al. [57] similarly highlighted that multimodal fusion improves reliability across varying soil backgrounds. Our results reinforce these findings and show that adaptive weighting can further enhance robustness in moderate-sized soil spectral datasets.

Nevertheless, several limitations remain. This study was conducted on dried laboratory soil samples, and additional validation under varying field moisture and environmental conditions is required. The feature selection pipeline relied primarily on RFE and autoencoder-derived representations; future work may incorporate CARS, SPA, or GA for more robust wavelength screening. Furthermore, the present analysis focused solely on SOM, whereas extending multimodal fusion to TN and TP would provide a more comprehensive assessment of soil nutrient status. Recent advances in multimodal fusion offer additional pathways for improvement. Li et al. [23] showed that outer-product fusion can outperform simple concatenation in VIS–NIR + MIR applications, underscoring the benefits of explicitly modeling mid-level cross-modal interactions. In parallel, Li et al. [45] demonstrated that two-branch CNN fusion of image and spectral features can further enhance prediction accuracy. These studies collectively suggest that future work could explore lightweight Transformer modules or multimodal attention mechanisms—tailored to small-sample soil spectral scenarios—to improve predictive accuracy and generalization while maintaining interpretability.

5. Conclusions

This study developed a multimodal spectral fusion framework based on Fusion_GatedRidge Regression, which effectively integrates Raman and VIS–NIR spectral information to enhance the prediction accuracy of soil organic matter (SOM) content.

The proposed model achieved an R² of 0.83 and an RMSE of 2.01 g·kg⁻¹, markedly outperforming both single-modality (Raman or VIS–NIR) and traditional fusion models.

Through adaptive adjustment of modality weights ($s_r$ and $s_v$), the gating mechanism dynamically balanced feature contributions, thereby improving model robustness and interpretability. Residuals were concentrated within the −2 to 2 g·kg⁻¹ range, indicating a strong overall model fit across most samples. Compared with existing static fusion models, the proposed gated fusion strategy achieved higher adaptability and predictive accuracy without increasing model complexity. The dynamic modality weighting effectively mitigated spectral noise and sample heterogeneity, demonstrating the complementary advantages of multisource spectral integration. However, this study primarily relied on laboratory air-dried soil samples, and the model’s applicability to in situ moist soils and different soil textures requires further validation.

Future research should integrate advanced feature selection algorithms (e.g., CARS, SPA, GA) and deep fusion architectures (such as Multimodal Attention Networks, MMAE) to enhance cross-regional generalization. Moreover, expanding the prediction targets to include total nitrogen (TN) and total phosphorus (TP) could provide a more comprehensive framework for precision agriculture soil nutrient monitoring, offering a scalable and generalizable analytical pathway.