Nominal Evaluation of Automatic Multi-Sections Control Potential in Comparison to a Simpler One- or Two-Sections Alternative with Predictive Spray Switching
Abstract
1. Introduction
2. Materials and Methods
2.1. Complexity of the Spraying Process
2.2. Four Hierarchical Planning Levels
2.3. Area Coverage Path Planning Level
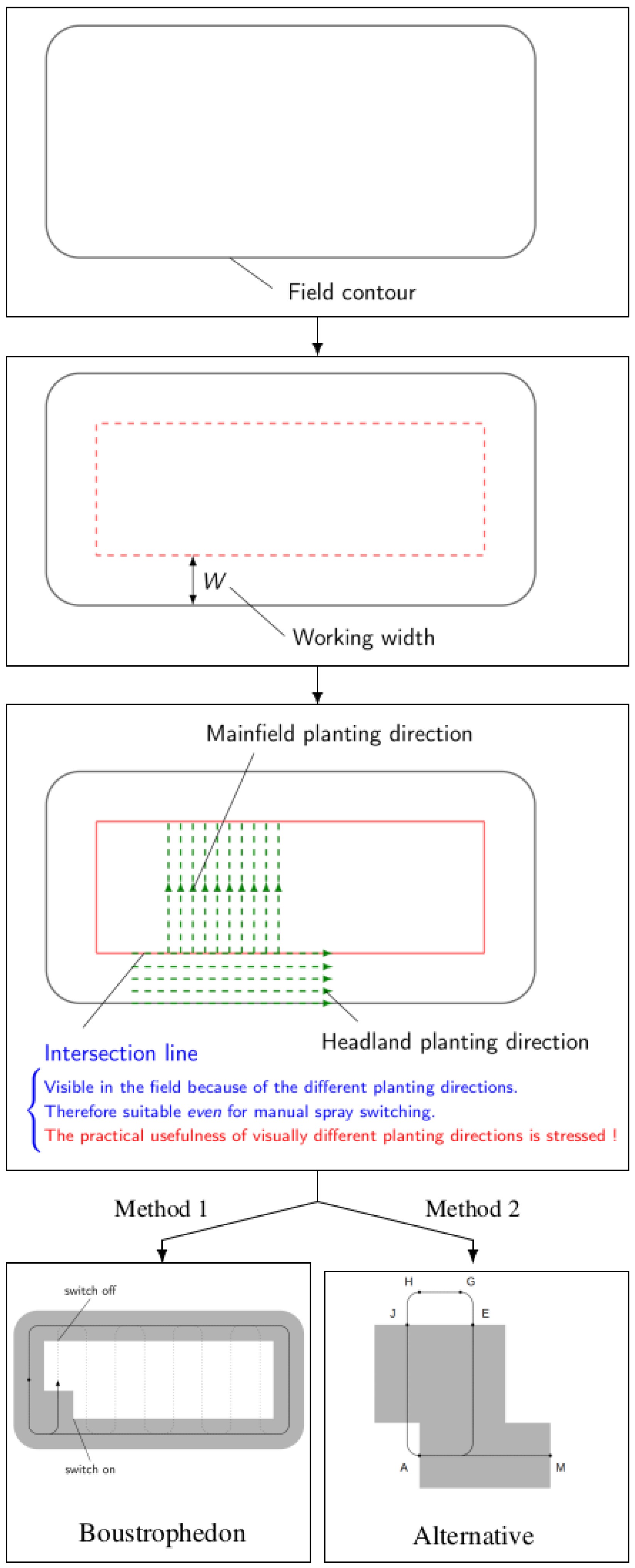
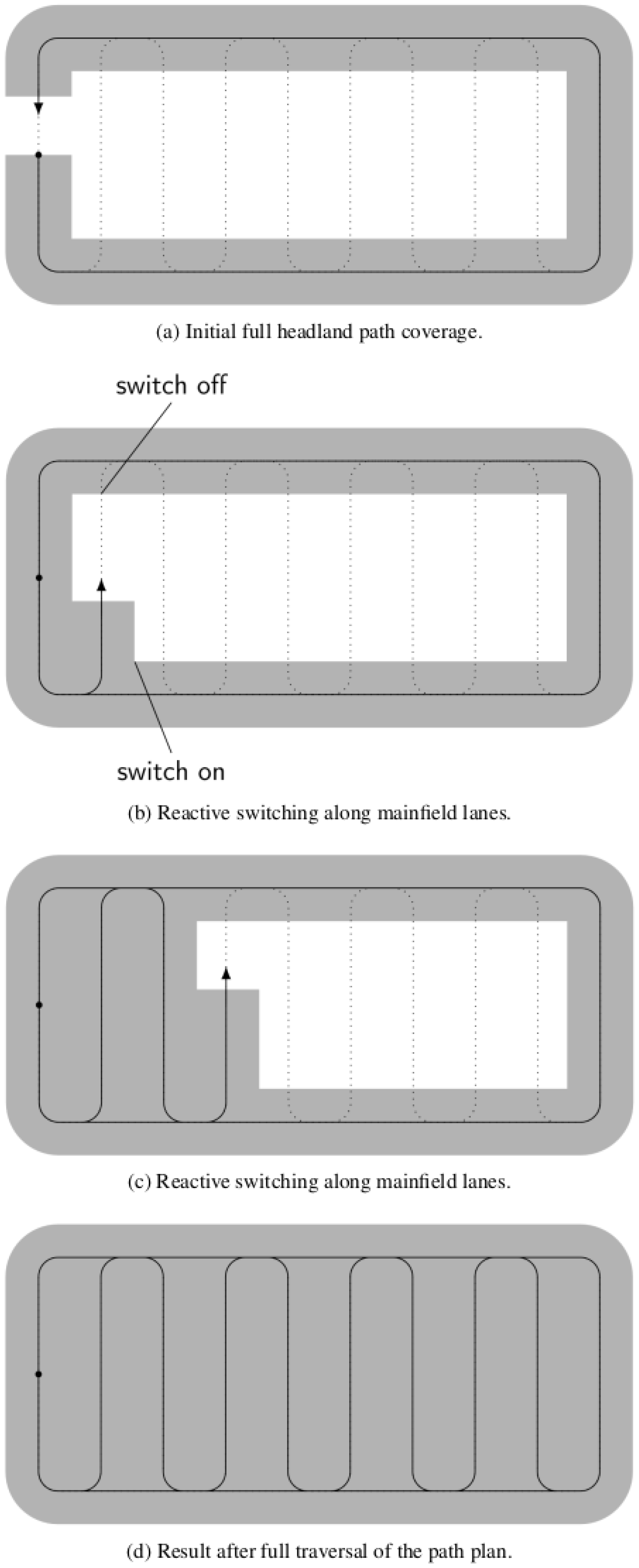
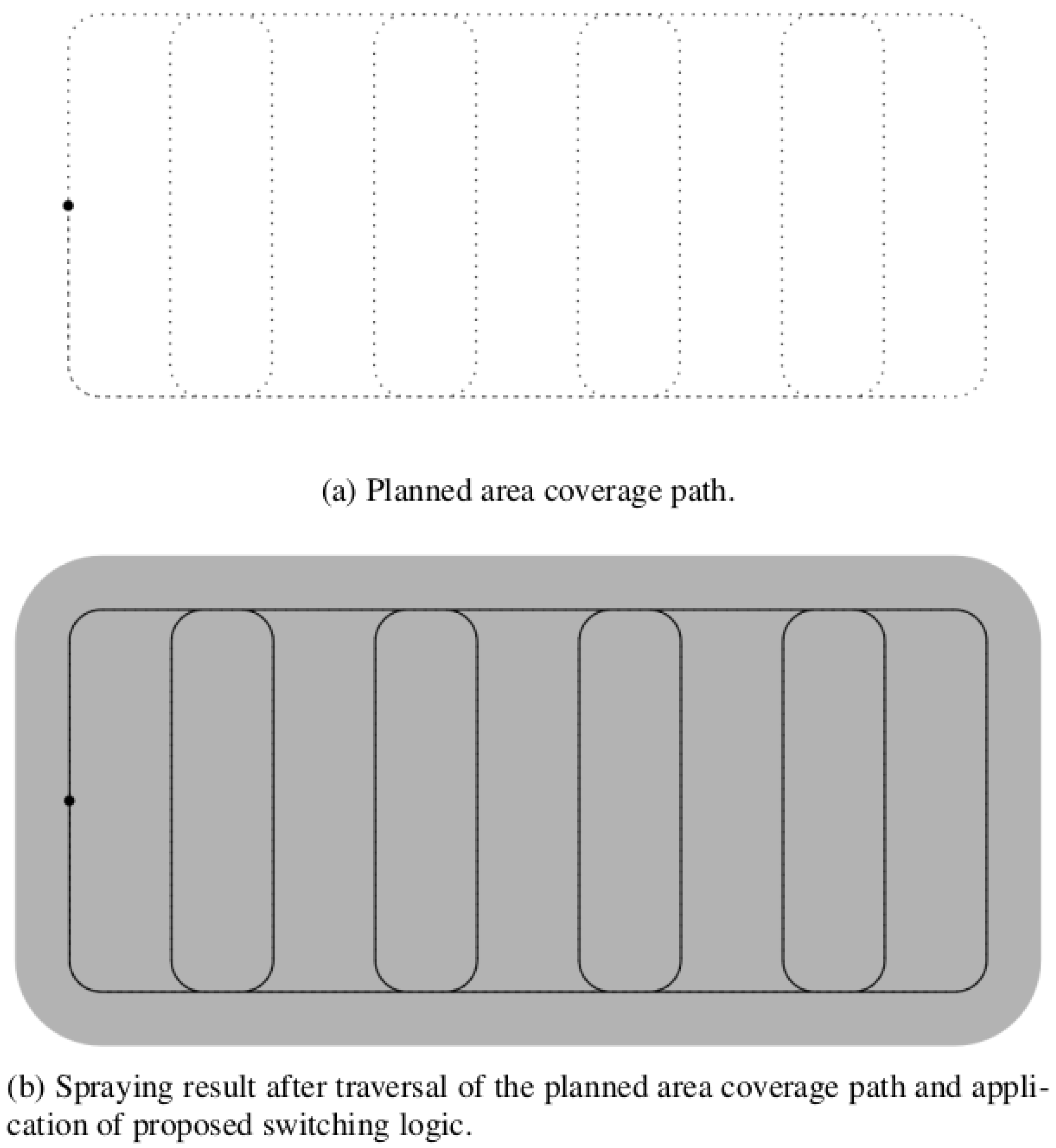
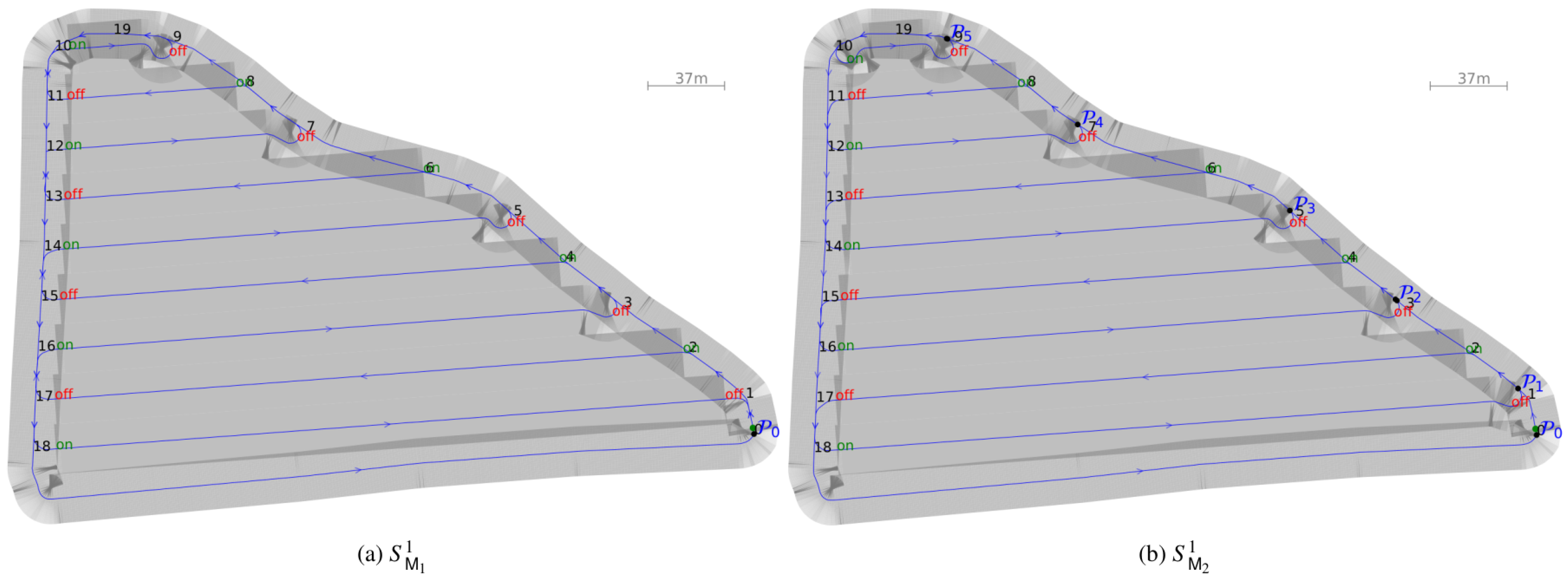
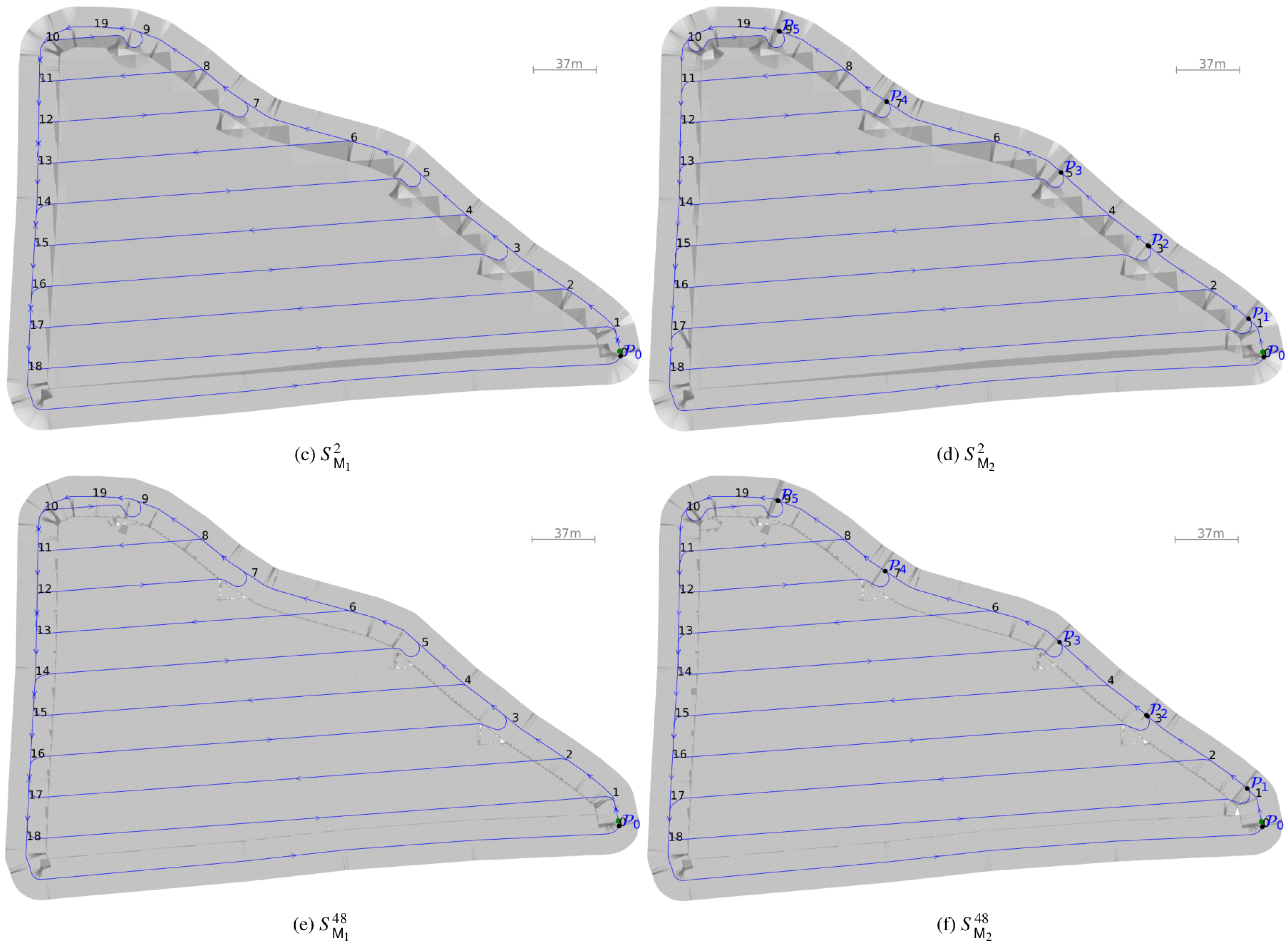
- Boustrophedon: Boustrophedon paths, whose name is derived from Ancient Greek for “like the ox turns”, represents the standard pattern for area coverage applications and agricultural real-world praxis. It is characterized by a full headland coverage before mainfield lanes are traversed in a meandering pattern. See Figure 8a,c.
- Alternative: The method from [9] is used for area coverage path planning. It differs from the Boustrophedon method by optimizing the sequence of lanes and turns to minimize total path length, often employing less conventional but more efficient field patterns for non-convex and obstructed areas. For convexly shaped field areas, the method can be reduced to a recurring path pattern that is discussed in detail in [37] and shown in Figure 8b,d. Headland path edges and headland-to-mainfield lane transitions can be smoothed [38,39].
2.4. Block Switching Level
- Boustrophedon: The associated switching logic on top of this area coverage path planning method is illustrated in Figure 9.
2.5. Sections Switching Level
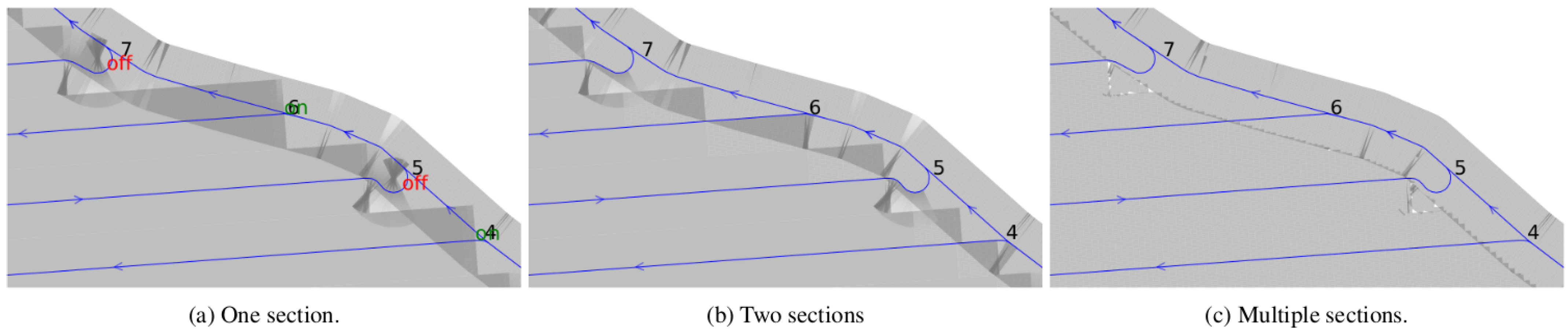
2.6. Strategy 1: Automatic Section Control
2.7. Strategy 2: GPS-Free, Maximal 2 Sections, and Visual Cues
3. Results
3.1. Comparison of 6 Experimental Setups
3.2. 10 Nominal Real-World Field Examples
4. Discussion
4.1. Key Findings
- The pathlength savings potential for the optimization-based method in comparison to the Boustrophedon-based method was between −3.9% and −12.3% (see Table 2). yielded better results throughout all experiments. Since path planning precedes spraying according to the hierarchical structure of Figure 6, it can be designed independently from the spraying technique.
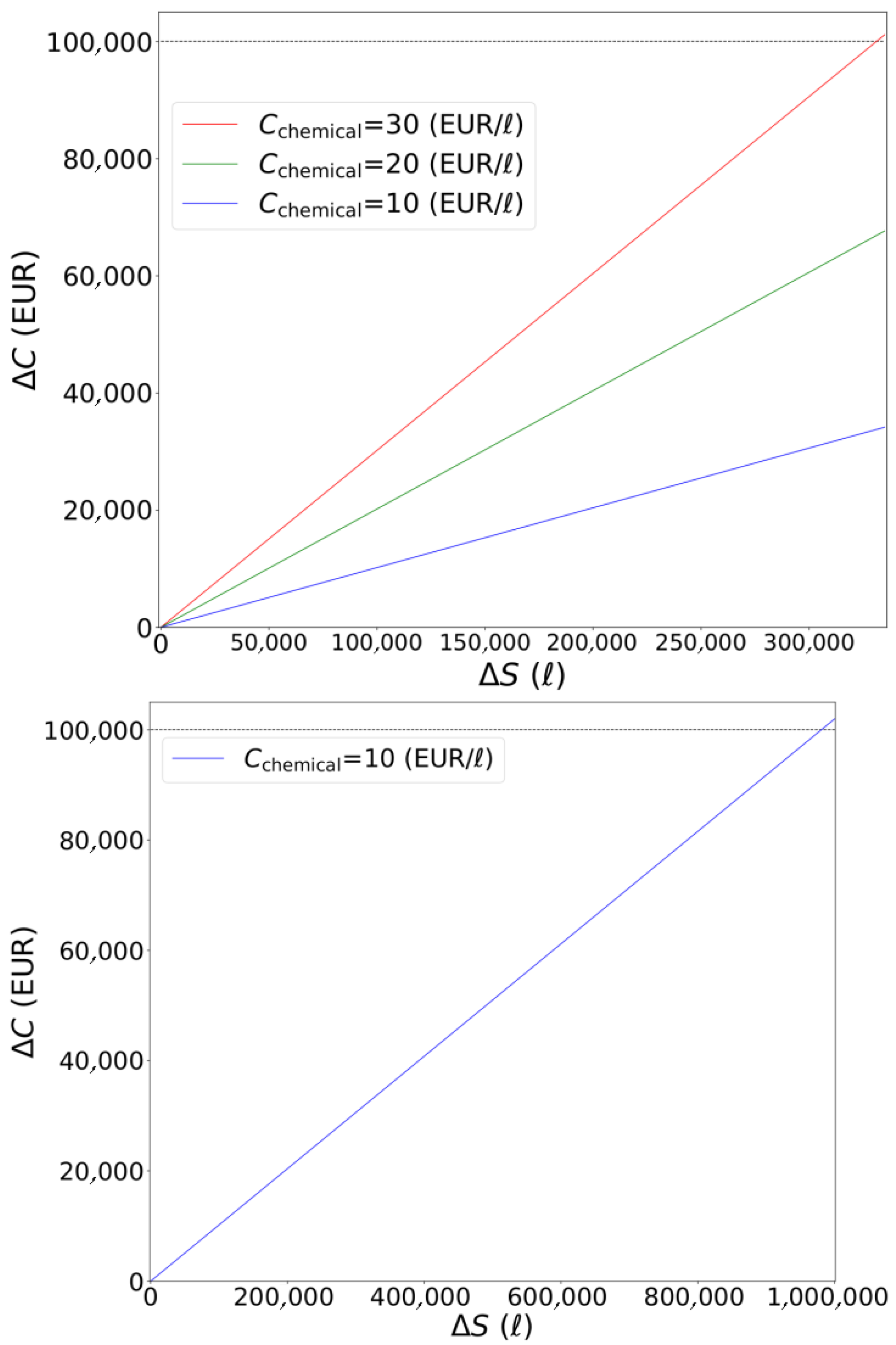
- Regarding spray volume results in Table 3 two main comments can be made. First, the multi-sections method with 48 sections over a 24 m wide boom bar approached the reference spray volume . For field 1, the difference was 2.1%. For a higher number of sections this percentage is expected to further decrease. In contrast, for the 1- and 2-sections case, the percentage difference was higher. For example, for and the differences with respect to were 21% and 26.9%, respectively. Second, while these and similar increases in spray volumes for other fields in Table 3 seemed high, an important note with respect to spray composition is made. For cereal crop production the water ratio in a spray mixture is typically very high. For example, for a 100ℓ spray volume typically around 99ℓ are water and only 1ℓ are chemical (fungicides, herbicides, etc). This is from an economic point of view very important, since economic input material costs for water and chemical greatly differ. Hence, the aforementioned 21% increase for does not imply a 21% increase in input material costs. Instead, denoting chemical and water cost measured in monetary cost per litre (EUR/ℓ) by and and assuming a water ratio of 99%, the new cost is calculated as . If the actual increase in input material costs is much lower than the aforementioned 21%. Implications are discussed in detail in the next Section 4.2.
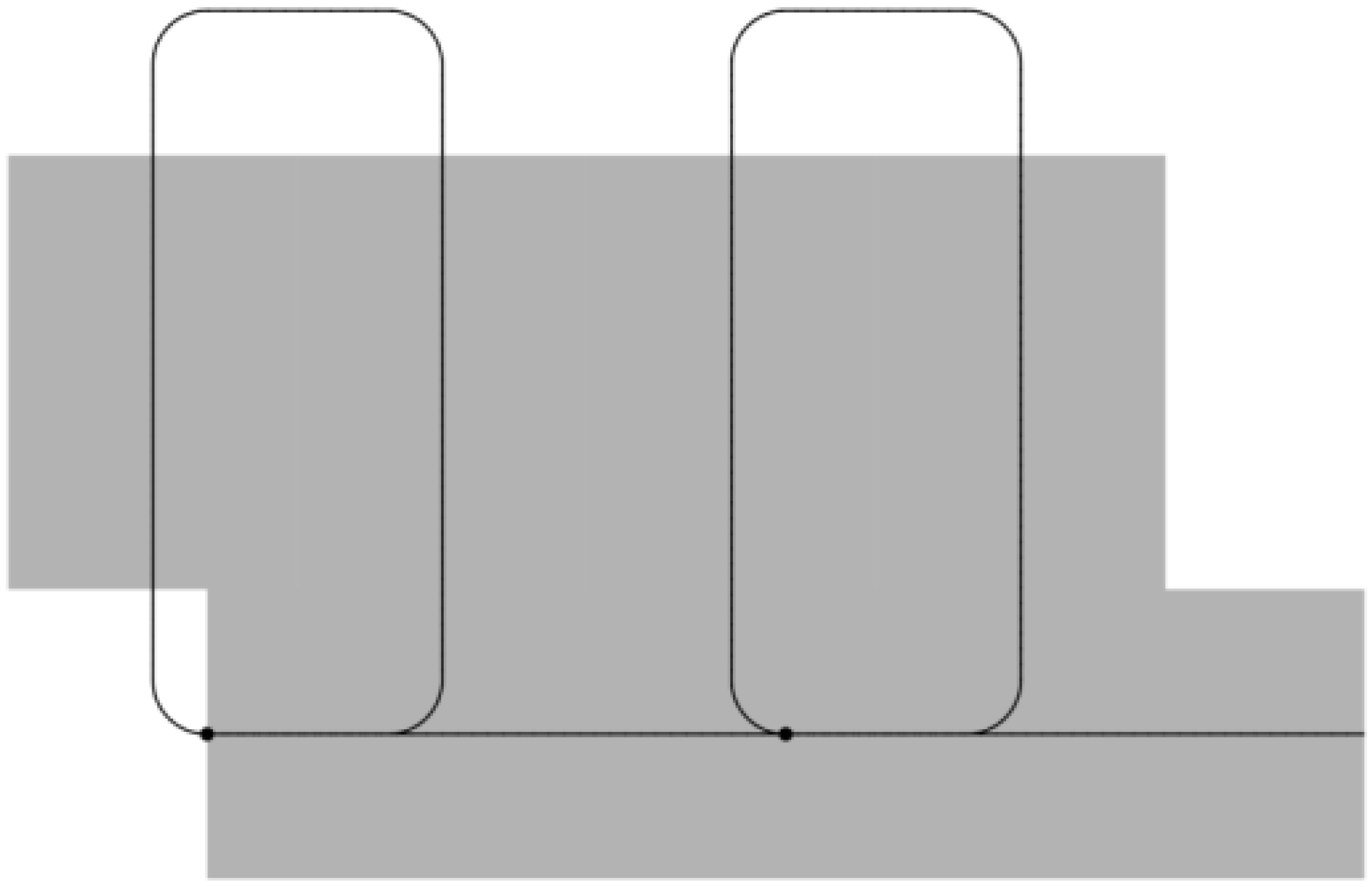
- Both the 1- and 2-sections setup can be implemented robustly, and crucially and in contrast to the ASC-setup, without the need for any localization sensors. This can be achieved by planting crops in a different direction along the headland and mainfield areas, before using the intersection line between those two areas as visual reference line at which spray switching commands can be triggered. This approach is also appropriate for manual operation. See Figure 7 for illustration.
4.2. Economic Cost Discusstion
4.3. Limitations
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ASC | Automatic Section Control. |
| Field size, (ha). | |
| Total farm size, (ha). | |
| Cost for pesticides, (EUR/ℓ). | |
| Cost for water for spray mixture, (EUR/ℓ). | |
| Purchase price difference for ASC, (EUR). | |
| L | Pathlength for machinery, (m). |
| Number of field runs per crop cycle, (-). | |
| Number of years until profitability for ASC, (-). | |
| Spray volume reference for a given field, (ℓ). | |
| S | Spray volume required for a given field, (ℓ). |
| W | Machinery working width, (m). |
| Inter-nozzle spacing along the boom bar, (m). |
References
- Portman, R.W. Calibrating Single Nozzle and Boom Sprayers; Washington State University: Pullman, WA, USA, 1979. [Google Scholar]
- Smith, D.; Oakley, D.; Williams, E.; Kirkpatrick, A. Broadcast spray deposits from fan nozzles. Appl. Eng. Agric. 2000, 16, 109–113. [Google Scholar] [CrossRef]
- Sharda, A. Boom Dynamics During Control System Response on Agricultural Sprayers. Ph.D. Thesis, Auburn University, Auburn, AL, USA, 2011. [Google Scholar]
- Vijayakumar, V.; Ampatzidis, Y.; Schueller, J.K.; Burks, T. Smart spraying technologies for precision weed management: A review. Smart Agric. Technol. 2023, 6, 100337. [Google Scholar] [CrossRef]
- Hafeez, A.; Husain, M.A.; Singh, S.; Chauhan, A.; Khan, M.T.; Kumar, N.; Chauhan, A.; Soni, S. Implementation of drone technology for farm monitoring & pesticide spraying: A review. Inf. Process. Agric. 2023, 10, 192–203. [Google Scholar] [CrossRef]
- Plessen, M. Path planning for spot spraying with uavs combining tsp and area coverages. Smart Agric. Technol. 2025, 11, 100965. [Google Scholar] [CrossRef]
- Hassen, N.S.; Sidik, N.A.C.; Sheriff, J.M. Effect of nozzle type, angle and pressure on spray volumetric distribution of broadcasting and banding application. J. Mech. Eng. Res. 2013, 5, 76–81. [Google Scholar] [CrossRef]
- Galceran, E.; Carreras, M. A survey on coverage path planning for robotics. Robot. Auton. Syst. 2013, 61, 1258–1276. [Google Scholar] [CrossRef]
- Plessen, M.G. Optimal in-field routing for full and partial field coverage with arbitrary non-convex fields and multiple obstacle areas. Biosyst. Eng. 2019, 186, 234–245. [Google Scholar] [CrossRef]
- Utamima, A.; Djunaidy, A. Agricultural routing planning: A narrative review of literature. Procedia Comput. Sci. 2022, 197, 693–700. [Google Scholar] [CrossRef]
- Pour Arab, D.; Spisser, M.; Essert, C. Complete coverage path planning for wheeled agricultural robots. J. Field Robot. 2023, 40, 1460–1503. [Google Scholar] [CrossRef]
- Höffmann, M.; Patel, S.; Büskens, C. Optimal guidance track generation for precision agriculture: A review of coverage path planning techniques. J. Field Robot. 2024, 41, 823–844. [Google Scholar] [CrossRef]
- Luck, J.; Pitla, S.; Shearer, S.; Mueller, T.; Dillon, C.; Fulton, J.; Higgins, S. Potential for pesticide and nutrient savings via map-based automatic boom section control of spray nozzles. Comput. Electron. Agric. 2010, 70, 19–26. [Google Scholar] [CrossRef]
- Han, S.; Hendrickson, L.L.; Ni, B.; Zhang, Q. Modification and testing of a commercial sprayer with PWM solenoids for precision spraying. Appl. Eng. Agric. 2001, 17, 591. [Google Scholar] [CrossRef]
- Johnson, M.; Swetnam, L. Sprayer Nozzles: Selection and Calibration; University of Kentucky: Lexington, KY, USA, 1996. [Google Scholar]
- Holterman, H.; Van De Zande, J.; Porskamp, H.; Huijsmans, J. Modelling spray drift from boom sprayers. Comput. Electron. Agric. 1997, 19, 1–22. [Google Scholar] [CrossRef]
- Wolf, T. Best management practices for herbicide application technology. Prairie Soils Crops J. 2009, 2, 24–30. [Google Scholar]
- Balsari, P.; Gil, E.; Marucco, P.; van de Zande, J.C.; Nuyttens, D.; Herbst, A.; Gallart, M. Field-crop-sprayer potential drift measured using test bench: Effects of boom height and nozzle type. Biosyst. Eng. 2017, 154, 3–13. [Google Scholar] [CrossRef]
- Mangus, D.L.; Sharda, A.; Engelhardt, A.; Flippo, D.; Strasser, R.; Luck, J.D.; Griffin, T. Analyzing the nozzle spray fan pattern of an agricultural sprayer using pulse width modulation technology to generate an on-ground coverage map. Trans. ASABE 2017, 60, 315–325. [Google Scholar] [CrossRef]
- Grisso, R.D.; Askew, S.D.; McCall, D.S. Nozzles: Selection and Sizing; Virginia Cooperative Extension: Danville, VA, USA, 2019. [Google Scholar]
- Cui, L.; Xue, X.; Ding, S.; Le, F. Development of a DSP-based electronic control system for the active spray boom suspension. Comput. Electron. Agric. 2019, 166, 105024. [Google Scholar] [CrossRef]
- Burgers, T.A.; Gaard, J.D.; Hyronimus, B.J. Comparison of three commercial automatic boom height systems for agricultural sprayers. Appl. Eng. Agric. 2021, 37, 287–298. [Google Scholar] [CrossRef]
- Vong, C.N.; Larbi, P.A. Development and prototype testing of an agricultural nozzle clog detection device. Trans. ASABE 2021, 64, 49–61. [Google Scholar] [CrossRef]
- Fabula, J.; Sharda, A.; Luck, J.D.; Brokesh, E. Nozzle pressure uniformity and expected droplet size of a pulse width modulation (PWM) spray technology. Comput. Electron. Agric. 2021, 190, 106388. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, T.; Song, C.; Yu, X.; Shan, C.; Gu, H.; Lan, Y. Evaluation of spray drift of plant protection drone nozzles based on wind tunnel test. Agriculture 2023, 13, 628. [Google Scholar] [CrossRef]
- Wang, S.; Li, X.; Nuyttens, D.; Zhang, L.; Liu, Y.; Li, X. Evaluationof compact air-induction flat fan nozzles for herbicide applications: Spray drift and biological efficacy. Front. Plant Sci. 2023, 14, 1018626. [Google Scholar] [CrossRef] [PubMed]
- Hussain, I.; Han, X.; Zhang, Z.; Mao, X.; Guo, J. Enhancing precision agriculture with advanced variable-rate spraying and autonomous vehicles: A comprehensive review. Comput. Electron. Agric. 2025, 238, 110812. [Google Scholar] [CrossRef]
- Carreño Ruiz, M.; Bloise, N.; Guglieri, G.; D’Ambrosio, D. Numerical analysis and wind tunnel validation of droplet distribution in the wake of an unmanned aerial spraying system in forward flight. Drones 2022, 6, 329. [Google Scholar] [CrossRef]
- Luck, J.D.; Sharda, A.; Pitla, S.K.; Fulton, J.P.; Shearer, S.A. Generating ‘As-Applied’ Pesticide Distribution Maps from a Self-Propelled Agricultural Sprayer Based on Nozzle Pressure Data. In 2010 Pittsburgh, Pennsylvania, June 20–June 23, 2010; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2010; p. 1. [Google Scholar]
- Plessen, M. Predictive Spray Switching for an Efficient Path Planning Pattern for Area Coverage. AgriEngineering 2025, 7, 235. [Google Scholar] [CrossRef]
- Sequeira, E.G. Structured vs. Unstructured Scan Path in Static Visual Search Performance. Master’s Thesis, Kansas State University, Manhattan, KS, USA, 1979. [Google Scholar]
- Tao, J.M.; Luh, J. Coordination of two redundant robots. In Proceedings of the 1989 IEEE International Conference on Robotics and Automation, Scottsdale, AZ, USA, 14–19 May 1989; IEEE Computer Society: Piscataway, NJ, USA, 1989; pp. 425–426. [Google Scholar]
- ISO 11783-10:2015; Tractors and Machinery for Agriculture and Forestry—Serial Control and Communications Data Network—Part 10: Task Controller and Management Information System Data Interchange. ISO 11783-10:2015: Geneva, Switzerland, 2015.
- Tan, C.S.; Mohd-Mokhtar, R.; Arshad, M.R. A comprehensive review of coverage path planning in robotics using classical and heuristic algorithms. IEEE Access 2021, 9, 119310–119342. [Google Scholar] [CrossRef]
- Jayalakshmi, K.; Nair, V.G.; Sathish, D. A Comprehensive Survey on Coverage Path Planning for Mobile Robots in Dynamic Environments. IEEE Access 2025, 13, 60158–60185. [Google Scholar] [CrossRef]
- Plessen, M.G. Freeform path fitting for the minimisation of the number of transitions between headland path and interior lanes within agricultural fields. Artif. Intell. Agric. 2021, 5, 233–239. [Google Scholar] [CrossRef]
- Plessen, M.M.G. Partial field coverage based on two path planning patterns. Biosyst. Eng. 2018, 171, 16–29. [Google Scholar] [CrossRef]
- Plessen, M. Smoothing of headland path edges and headland-to-mainfield lane transitions based on a spatial domain transformation and linear programming. Biosyst. Eng. 2025, 257, 104229. [Google Scholar] [CrossRef]
- He, Z.; Bao, Y.; Yu, Q.; Lu, P.; He, Y.; Liu, Y. Dynamic path planning method for headland turning of unmanned agricultural vehicles. Comput. Electron. Agric. 2023, 206, 107699. [Google Scholar] [CrossRef]
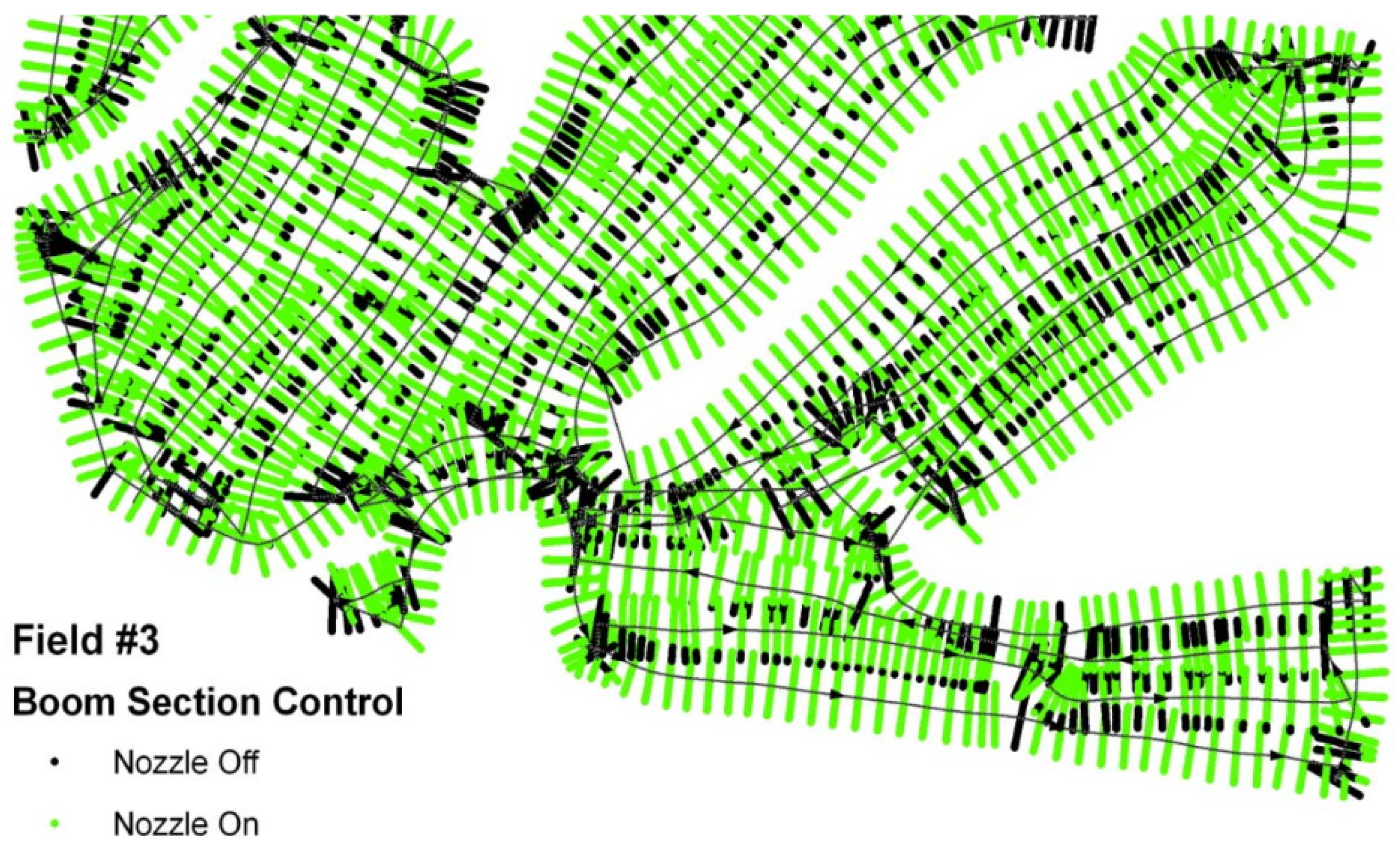
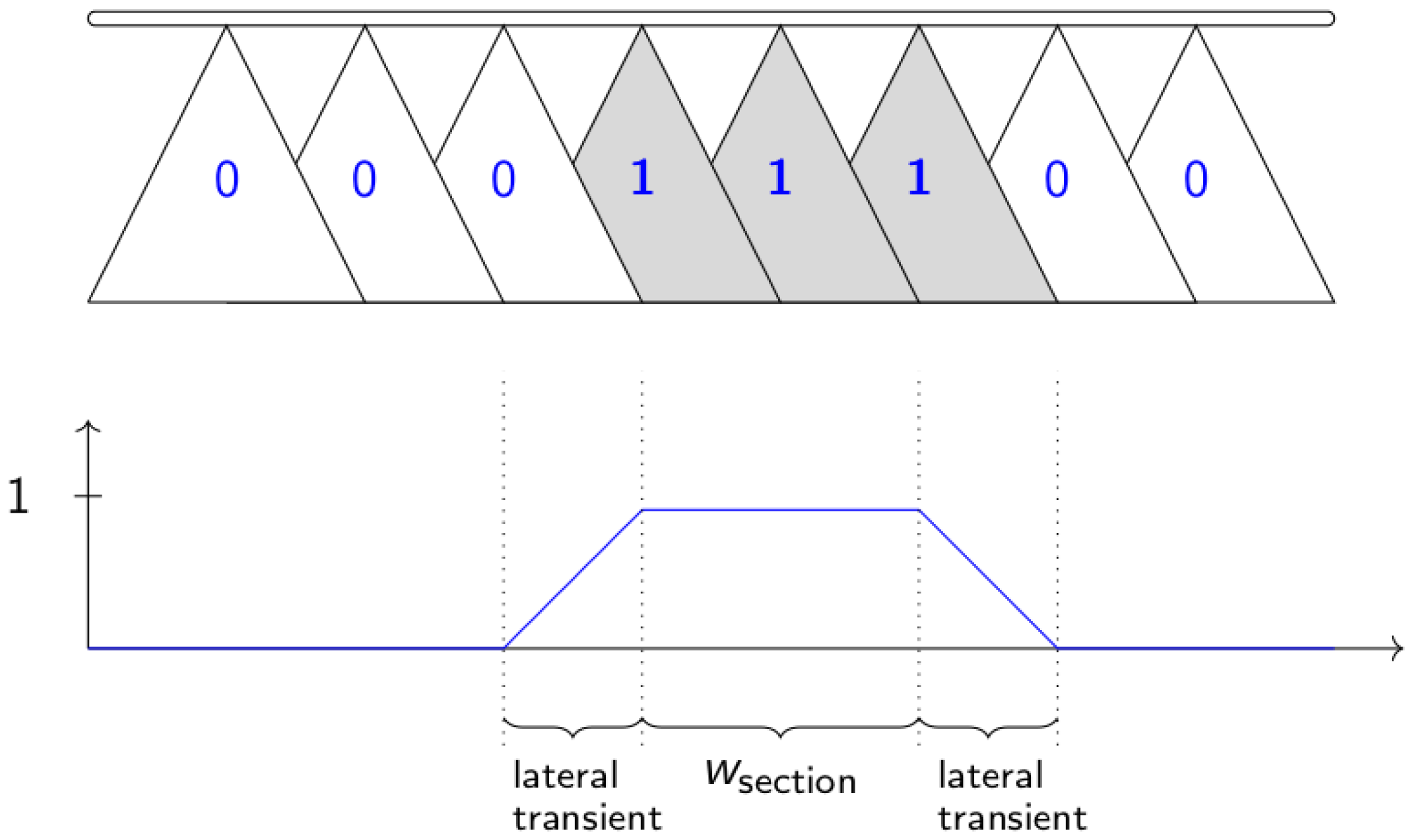
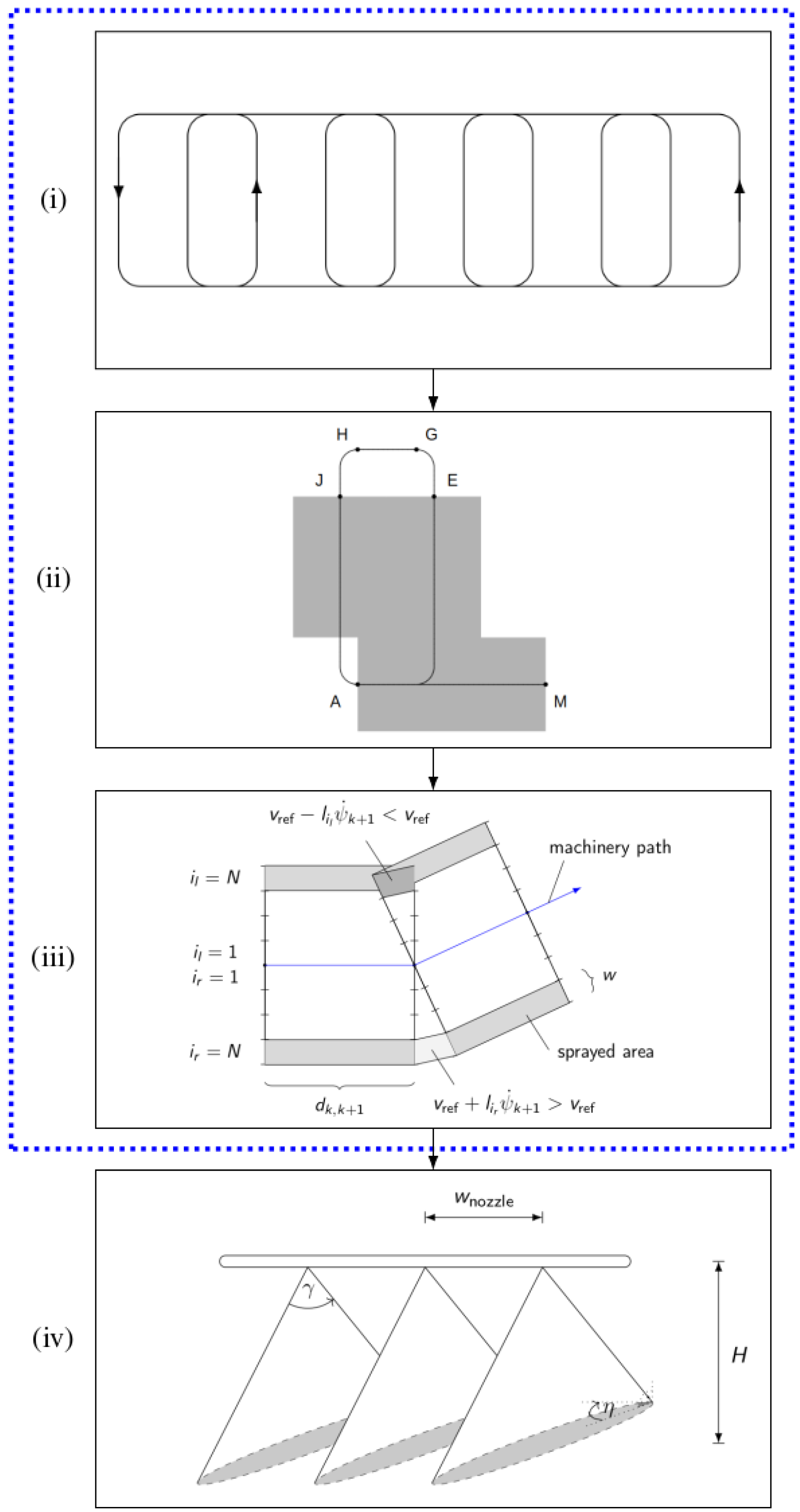





| Nr. | Factors Affecting Spraying Results | References |
|---|---|---|
| 1 | Machinery traveling speed changes | [17] |
| 2 | Varying traveling speeds of different | [20] |
| boom sections along the boom bar | ||
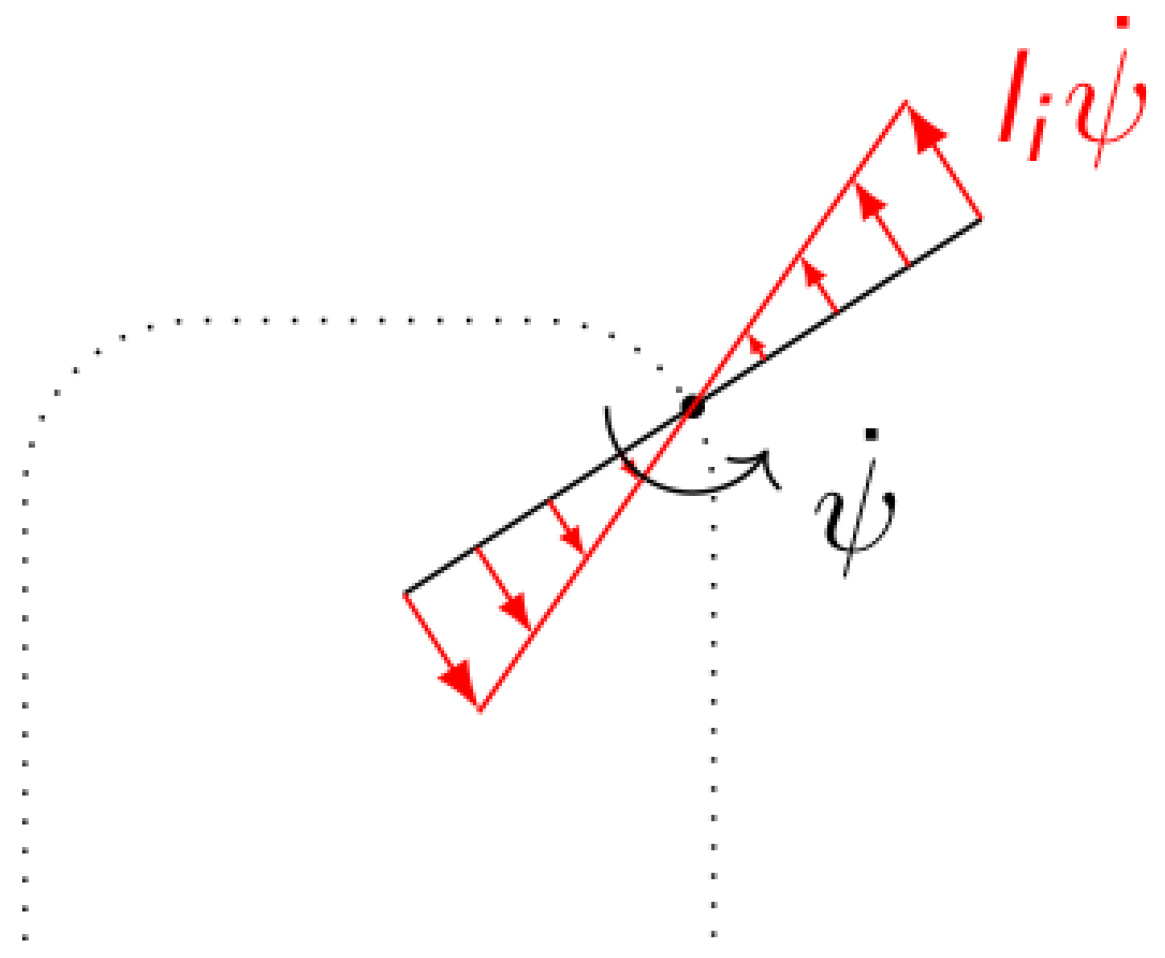
| during turn maneuvers, see Figure 3 | ||
| 3 | Oscillations and inertia of mechanical | [20,21] |
| boom structure during turn maneuvers | ||
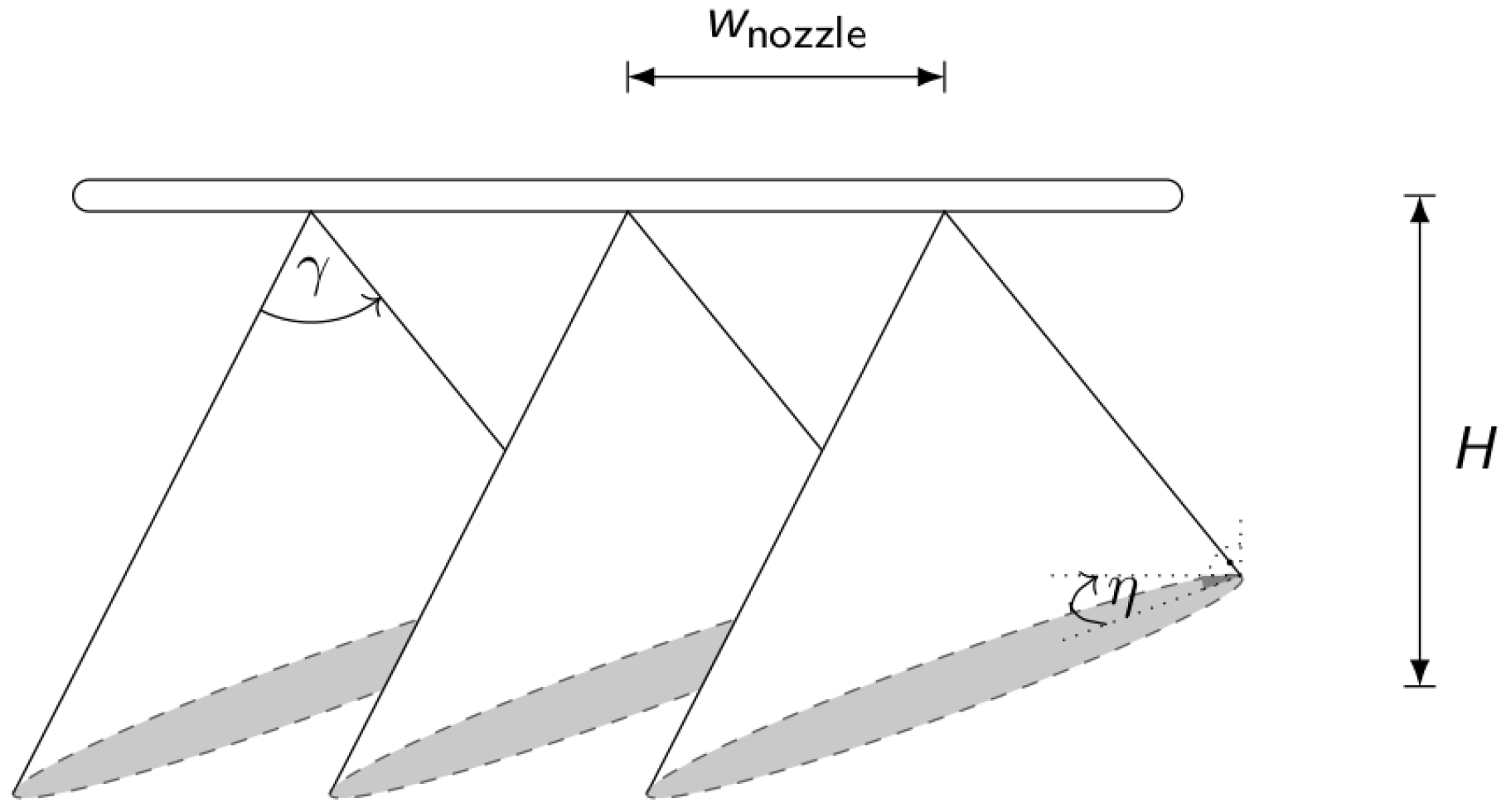
| 4 | Boom height and vertical boom bar | [18,21,22] |
| oscillations, H in Figure 4 | ||
| 5 | Nozzle type selection | [7,15,18] |
| 6 | Nozzle spray overlap of adjacent nozzles | [19] |
| 7 | Nozzle spacing, in Figure 4 | [7,20] |
| 8 | Nozzle clogging | [20,23] |
| 9 | Water volume and spray composition | [20] |
| 10 | Spray pressure or nozzle flow rate | [7,17,24] |
| 11 | Spray droplet size | [7,17,19] |
| 12 | Spray fan angle, in Figure 4 | [7,19] |
| 13 | Angled nozzles along the vertical axis | [20] |
| (‘z-axis’) such that adjacent spray | ||
| patterns do not intersect, in Figure 4 | ||
| 14 | Non-perpendicular spray angles towards | [20] |
| field ground for 3D topography | ||
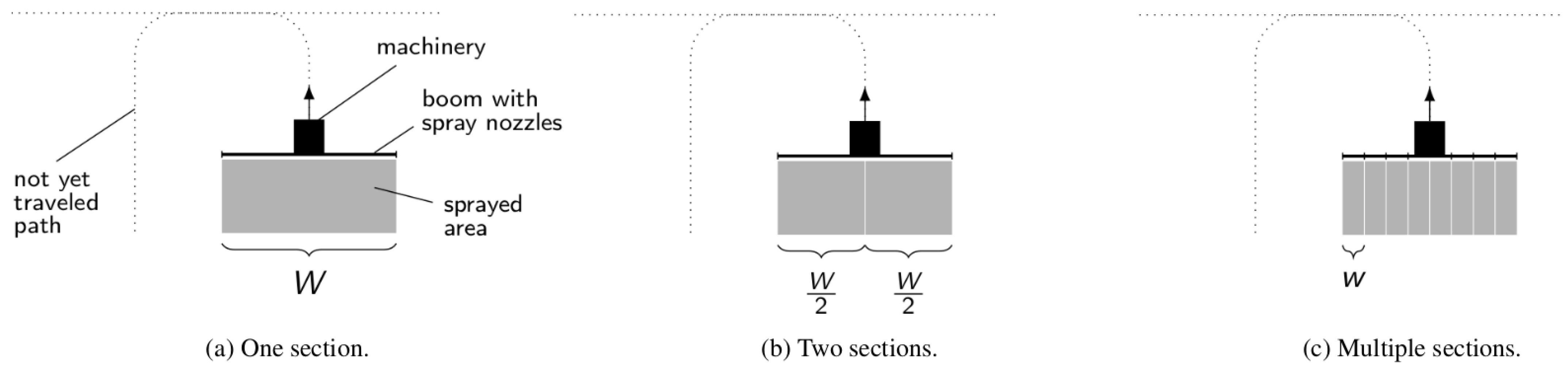
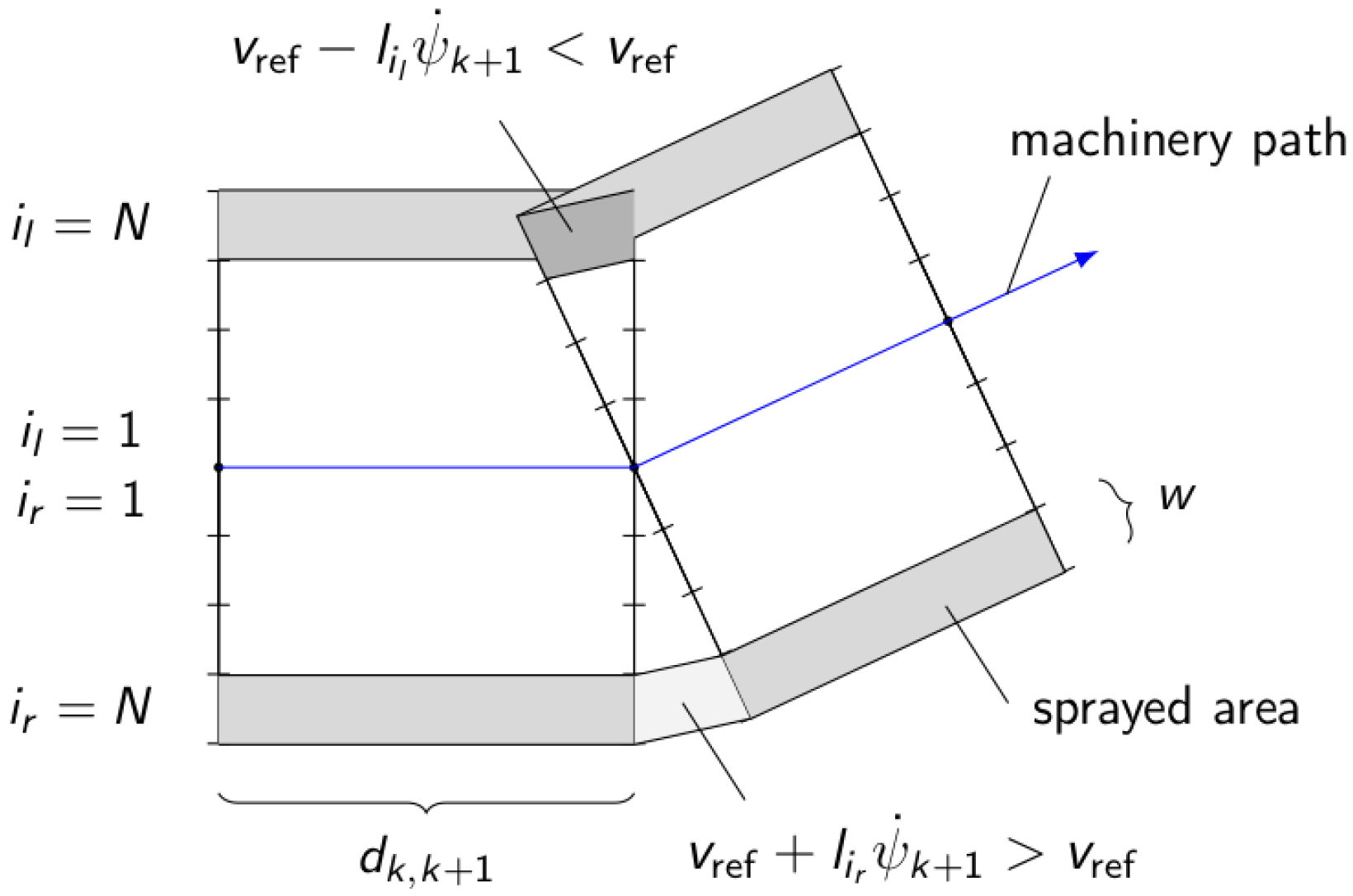
| 15 | Section width selection, | [20] |
| in Figure 5 | ||
| 16 | Cross wind and spray drift | [16,17,25,26] |
| 17 | Occupancy grid hyperparameters | [33] |
| 18 | For ASC requirement of at least 1 | [13,27] |
| accurate localization sensor | ||
| (e.g., RTK-GPS) | ||
| 19 | Pulse-Width-Modulation (PWM) for | [14,24] |
| individual nozzle flow rate control | ||
| 20 | Reactive spraying (i.e., with delays) unless | [30] |
| spraying is directly coupled to automated | ||
| vehicle steering and velocity control |
| Ex. | (m) | (%) | |||
|---|---|---|---|---|---|
| 1 | 6.0 ha | 3394 m | 3166 m | −228 m | −6.7% |
| 2 | 14.6 ha | 8002 m | 7368 m | −634 m | −7.9% |
| 3 | 10.1 ha | 5995 m | 5488 m | −507 m | −8.5% |
| 4 | 11.8 ha | 6428 m | 5954 m | −474 m | −7.4% |
| 5 | 13.5 ha | 7231 m | 6784 m | −447 m | −6.2% |
| 6 | 38.5 ha | 19413 m | 18447 m | −966 m | −5.0% |
| 7 | 6.5 ha | 3512 m | 3346 m | −166 m | −4.7% |
| 8 | 13.6 ha | 7713 m | 7087 m | −625 m | −8.1% |
| 9 | 4.5 ha | 2834 m | 2485 m | −349 m | −12.3% |
| 10 | 7.2 ha | 3890 m | 3739 m | −151 m | −3.9% |
| Ex. | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 6.0 ha | 282.8ℓ | 358.9ℓ | 342.3ℓ | 288.7ℓ | 372.7ℓ | 352.8ℓ | 289.7ℓ |
| 76.1ℓ | 59.5ℓ | 5.9ℓ | 89.9ℓ | 70.0ℓ | 6.9ℓ | |||
| 26.9% | 21.0% | 2.1% | 31.8% | 24.7% | 2.4% | |||
| 2 | 14.6 ha | 682.1ℓ | 881.2ℓ | 849.3ℓ | 695.7ℓ | 901.6ℓ | 856.0ℓ | 697.2ℓ |
| 119.1ℓ | 167.2ℓ | 13.6ℓ | 219.5ℓ | 173.9ℓ | 15.1ℓ | |||
| 29.2% | 24.5% | 2.0% | 32.2% | 25.5% | 2.2% | |||
| 3 | 10.1 ha | 473.8ℓ | 676.3ℓ | 646.8ℓ | 487.2ℓ | 681.2ℓ | 645.8ℓ | 488.9ℓ |
| 202.5ℓ | 173.0ℓ | 13.4ℓ | 207.4ℓ | 172.0ℓ | 15.1ℓ | |||
| 42.7% | 36.5% | 2.8% | 43.8% | 36.3% | 3.2% | |||
| 4 | 11.8 ha | 552.6ℓ | 702.9ℓ | 656.6ℓ | 560.6ℓ | 721.3ℓ | 665.5ℓ | 561.7ℓ |
| 150.3ℓ | 104.0ℓ | 8.0ℓ | 168.7ℓ | 112.9ℓ | 9.1ℓ | |||
| 27.2% | 18.8% | 1.4% | 30.5% | 20.4% | 1.6% | |||
| 5 | 13.5 ha | 629.7ℓ | 780.2ℓ | 758.9ℓ | 638.7ℓ | 756.3ℓ | 733.1ℓ | 640.5ℓ |
| 150.5ℓ | 129.2ℓ | 9ℓ | 126.6ℓ | 103.4ℓ | 10.8ℓ | |||
| 23.9% | 20.5% | 1.4% | 20.1% | 16.4% | 1.7% | |||
| 6 | 38.5 ha | 1799.7ℓ | 2621.3ℓ | 2592.1ℓ | 1859.1ℓ | 2627.2ℓ | 2593.2ℓ | 1860.9ℓ |
| 821.6ℓ | 792.4ℓ | 59.4ℓ | 827.5ℓ | 793.5ℓ | 61.2ℓ | |||
| 45.6% | 44.0% | 3.3% | 45.9% | 44.1% | 3.4% | |||
| 7 | 6.5 ha | 304.6ℓ | 489.6ℓ | 486.8ℓ | 314.6ℓ | 495.9ℓ | 490.1ℓ | 315.1ℓ |
| 185.0ℓ | 182.2ℓ | 10.0ℓ | 191.3ℓ | 185.5ℓ | 10.5ℓ | |||
| 60.7% | 59.8% | 3.2% | 62.8% | 60.9% | 3.4% | |||
| 8 | 13.6 ha | 636.4ℓ | 980.9ℓ | 938.5ℓ | 668.8ℓ | 1086.4ℓ | 972.4ℓ | 665.5ℓ |
| 344.5ℓ | 302.1ℓ | 32.4ℓ | 450.0ℓ | 336.0ℓ | 29.1ℓ | |||
| 54.1% | 47.5% | 5.1% | 70.7% | 52.8% | 4.6% | |||
| 9 | 4.5 ha | 211.1ℓ | 397.9ℓ | 371.8ℓ | 225.3ℓ | 479.1ℓ | 450.6ℓ | 225.8ℓ |
| 186.8ℓ | 160.7ℓ | 14.2ℓ | 268.0ℓ | 239.5ℓ | 14.7ℓ | |||
| 88.5% | 76.1% | 6.7% | 126.9% | 113.4% | 6.9% | |||
| 10 | 7.2 ha | 336.3ℓ | 434.2ℓ | 410.8ℓ | 342.7ℓ | 436.5ℓ | 413.0ℓ | 343.3ℓ |
| 97.9ℓ | 74.5ℓ | 6.4ℓ | 100.2ℓ | 76.7ℓ | 7.0ℓ | |||
| 29.1% | 22.1% | 1.9% | 29.8% | 22.8% | 2.1% |
| Ex. | |||||
|---|---|---|---|---|---|
| (ha) | (ℓ/ha) | (ℓ/ha) | (ℓ/ha) | (ℓ/ha) | |
| 1 | 6.0 | 11.7 | 8.9 | 13.8 | 10.5 |
| 2 | 14.6 | 12.7 | 10.5 | 14.0 | 10.9 |
| 3 | 10.1 | 18.7 | 15.8 | 19.0 | 13.5 |
| 4 | 11.8 | 12.0 | 8.1 | 13.5 | 8.8 |
| 5 | 13.5 | 10.5 | 8.9 | 8.6 | 6.9 |
| 6 | 38.5 | 19.8 | 19.0 | 19.9 | 19.0 |
| 7 | 6.5 | 26.9 | 26.5 | 27.8 | 26.9 |
| 8 | 13.6 | 22.9 | 19.8 | 30.9 | 22.6 |
| 9 | 4.5 | 38.4 | 32.6 | 56.3 | 50.0 |
| 10 | 7.2 | 12.7 | 9.4 | 12.9 | 9.7 |
| Avg. | 12.6 | 18.6 | 16.7 | 22.5 | 18.7 |
| Parameter | Value | Unit |
|---|---|---|
| 0.002 | EUR/ℓ | |
| EUR/ℓ | ||
| ha | ||
| 8 | - |
| For = 18.6 ℓ/ha | For = 22.5 ℓ/ha | ||||
| 100,000 EUR | 100,000 EUR | ||||
| 30 | 74.2 | 219.7 | 30 | 61.3 | 181.6 |
| 100 | 22.3 | 65.9 | 100 | 18.4 | 54.5 |
| 300 | 7.4 | 22.0 | 300 | 6.1 | 18.2 |
| 600 | 3.7 | 11.0 | 600 | 3.1 | 9.1 |
| 1000 | 2.2 | 6.6 | 1000 | 1.8 | 5.4 |
| 200,000 EUR | 200,000 EUR | ||||
| 30 | 148.4 | 439.3 | 30 | 122.6 | 363.2 |
| 100 | 44.5 | 131.8 | 100 | 36.8 | 109.0 |
| 300 | 14.8 | 43.9 | 300 | 12.3 | 36.3 |
| 600 | 7.4 | 22.0 | 600 | 6.1 | 18.2 |
| 1000 | 4.5 | 13.2 | 1000 | 3.7 | 10.9 |
| For = 16.7 ℓ/ha | For = 18.7 ℓ/ha | ||||
| 100,000 EUR | 100,000 EUR | ||||
| 30 | 82.6 | 244.7 | 30 | 73.8 | 218.5 |
| 100 | 24.8 | 73.4 | 100 | 22.1 | 65.5 |
| 300 | 8.3 | 24.5 | 300 | 7.4 | 21.8 |
| 600 | 4.1 | 12.2 | 600 | 3.7 | 10.9 |
| 1000 | 2.5 | 7.3 | 1000 | 2.2 | 6.5 |
| 200,000 EUR | 200,000 EUR | ||||
| 30 | 165.2 | 489.3 | 30 | 147.6 | 437.0 |
| 100 | 49.6 | 146.8 | 100 | 44.3 | 131.1 |
| 300 | 16.5 | 48.9 | 300 | 14.8 | 43.7 |
| 600 | 8.3 | 24.5 | 600 | 7.4 | 21.8 |
| 1000 | 5.0 | 14.7 | 1000 | 4.4 | 13.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plessen, M. Nominal Evaluation of Automatic Multi-Sections Control Potential in Comparison to a Simpler One- or Two-Sections Alternative with Predictive Spray Switching. Agriculture 2025, 15, 2304. https://doi.org/10.3390/agriculture15212304
Plessen M. Nominal Evaluation of Automatic Multi-Sections Control Potential in Comparison to a Simpler One- or Two-Sections Alternative with Predictive Spray Switching. Agriculture. 2025; 15(21):2304. https://doi.org/10.3390/agriculture15212304
Chicago/Turabian StylePlessen, Mogens. 2025. "Nominal Evaluation of Automatic Multi-Sections Control Potential in Comparison to a Simpler One- or Two-Sections Alternative with Predictive Spray Switching" Agriculture 15, no. 21: 2304. https://doi.org/10.3390/agriculture15212304
APA StylePlessen, M. (2025). Nominal Evaluation of Automatic Multi-Sections Control Potential in Comparison to a Simpler One- or Two-Sections Alternative with Predictive Spray Switching. Agriculture, 15(21), 2304. https://doi.org/10.3390/agriculture15212304






