Figure 1.
Division of analysis zones within the map of Ecuador.
Figure 1.
Division of analysis zones within the map of Ecuador.
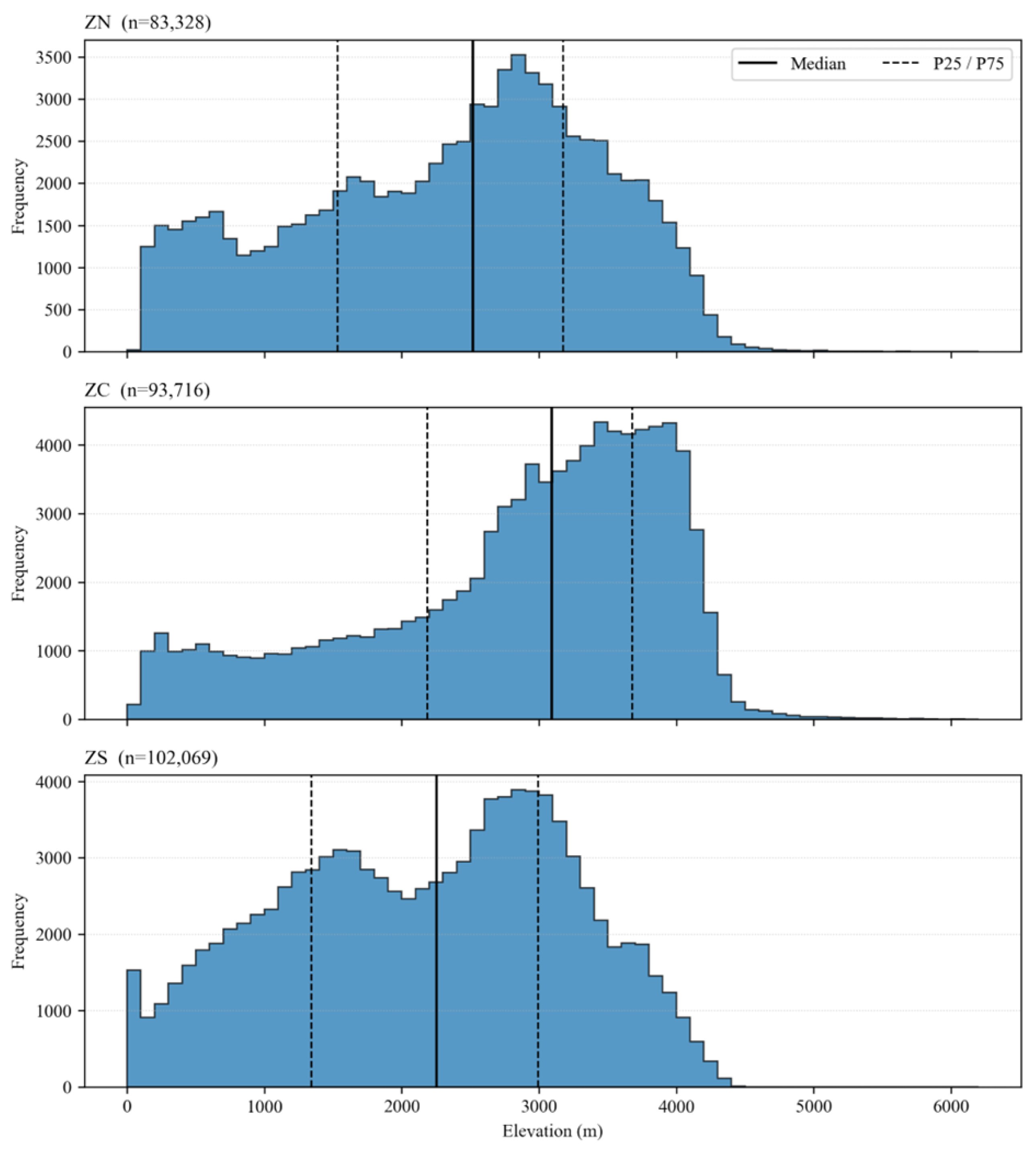
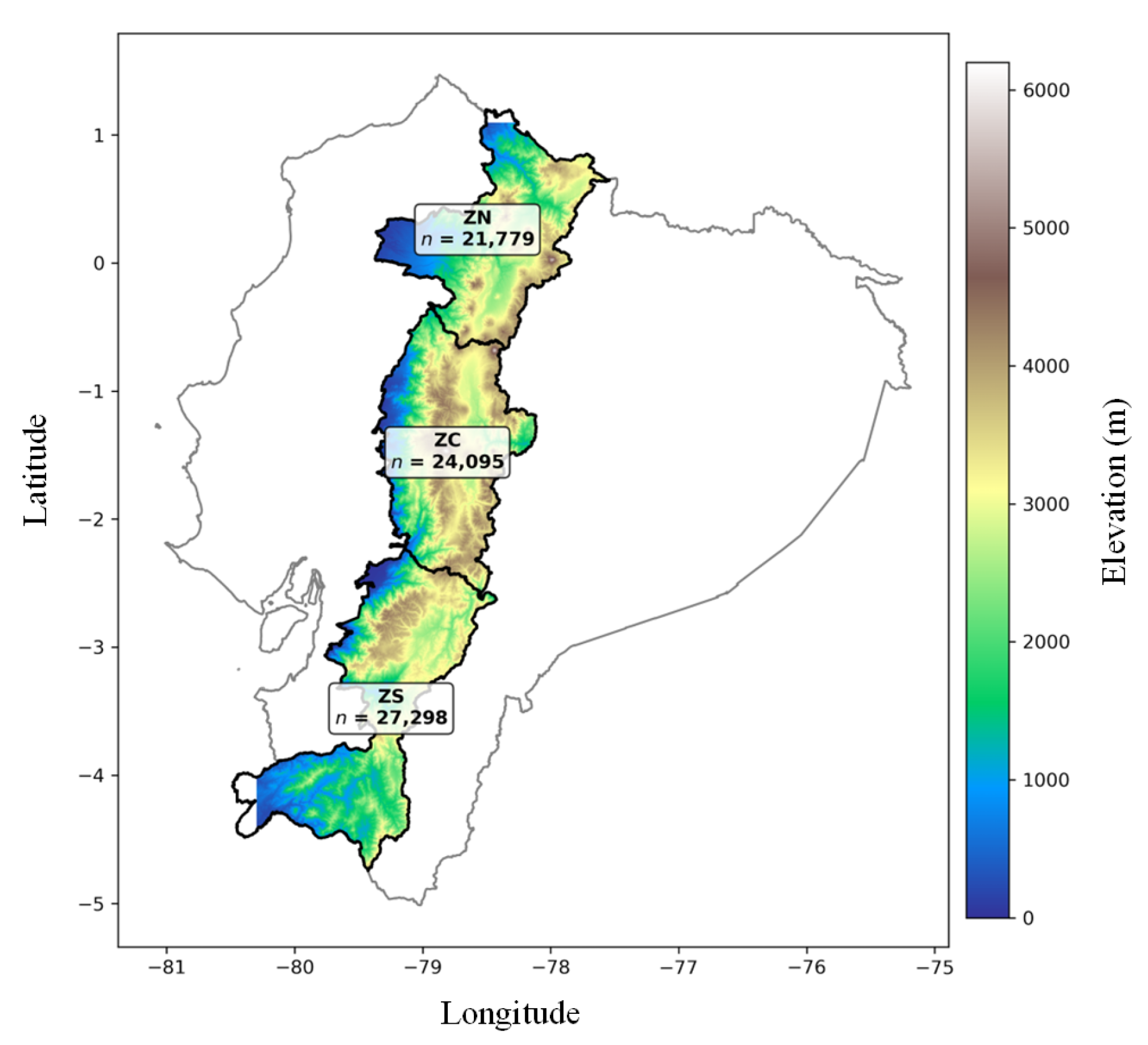
Figure 2.
Northern (ZN), Central (ZC), and Southern (ZS) regions of the Ecuadorian highlands over a SRTM15+ DEM clipped to the Sierra. Gray line shows the continental boundary; black outlines show zone limits. Labels report the number of 1 km grid cells (n) intersecting each zone (ZN = 21,779; ZC = 24,095; ZS = 27,298). Color bar indicates elevation (m).
Figure 2.
Northern (ZN), Central (ZC), and Southern (ZS) regions of the Ecuadorian highlands over a SRTM15+ DEM clipped to the Sierra. Gray line shows the continental boundary; black outlines show zone limits. Labels report the number of 1 km grid cells (n) intersecting each zone (ZN = 21,779; ZC = 24,095; ZS = 27,298). Color bar indicates elevation (m).
Figure 3.
Station vs. POWER/MERRA-2 comparisons at a monthly scale (2015–2022). Panels show observed values at station coordinates versus colocated POWER/MERRA-2 estimates; the dashed line is the 1:1 reference. Colors differentiate zones (ZN, ZC, ZS). (a) Tmax (monthly). (b) Tmin (monthly). (c) Precipitation (mm/month).
Figure 3.
Station vs. POWER/MERRA-2 comparisons at a monthly scale (2015–2022). Panels show observed values at station coordinates versus colocated POWER/MERRA-2 estimates; the dashed line is the 1:1 reference. Colors differentiate zones (ZN, ZC, ZS). (a) Tmax (monthly). (b) Tmin (monthly). (c) Precipitation (mm/month).
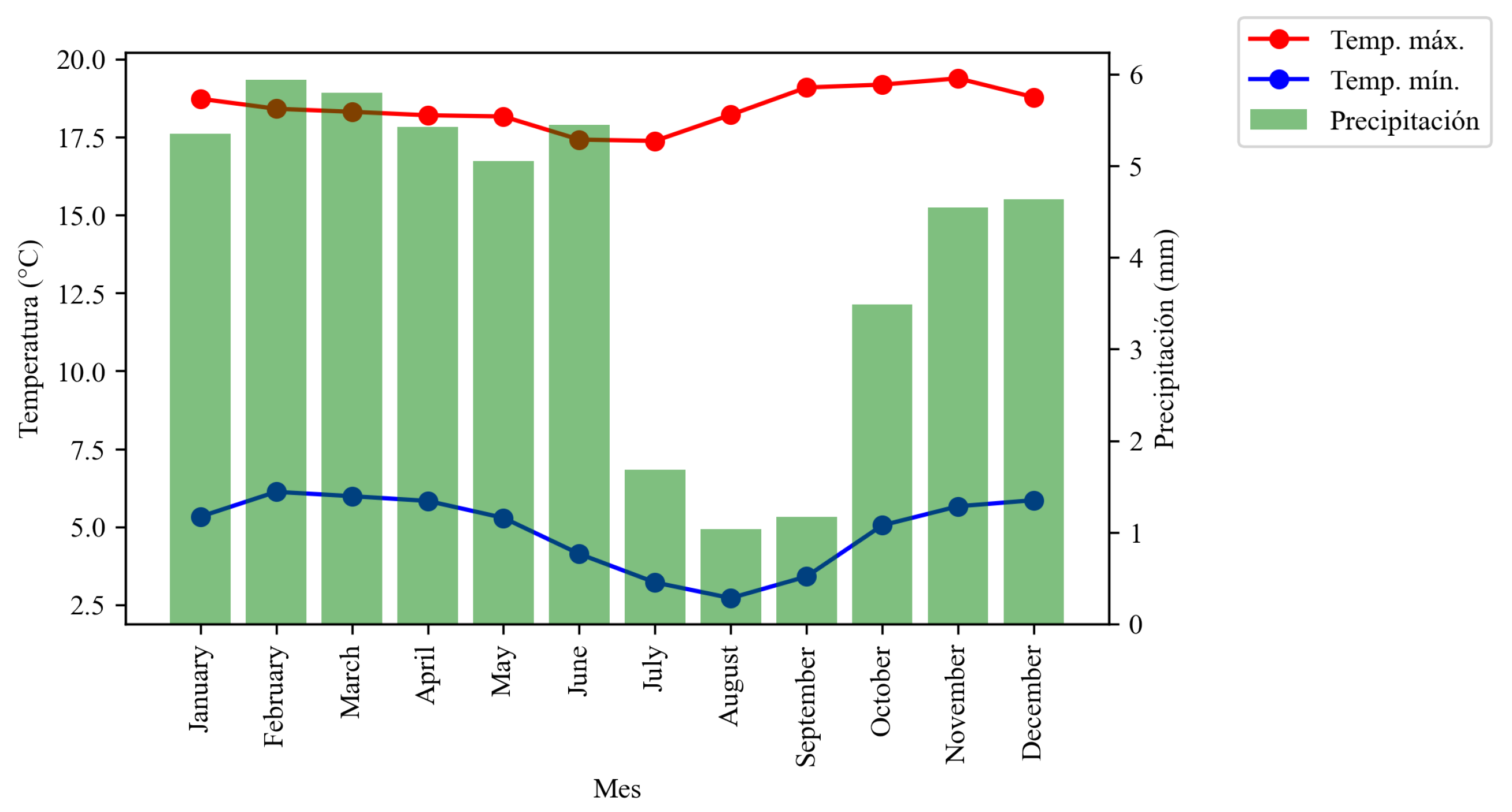
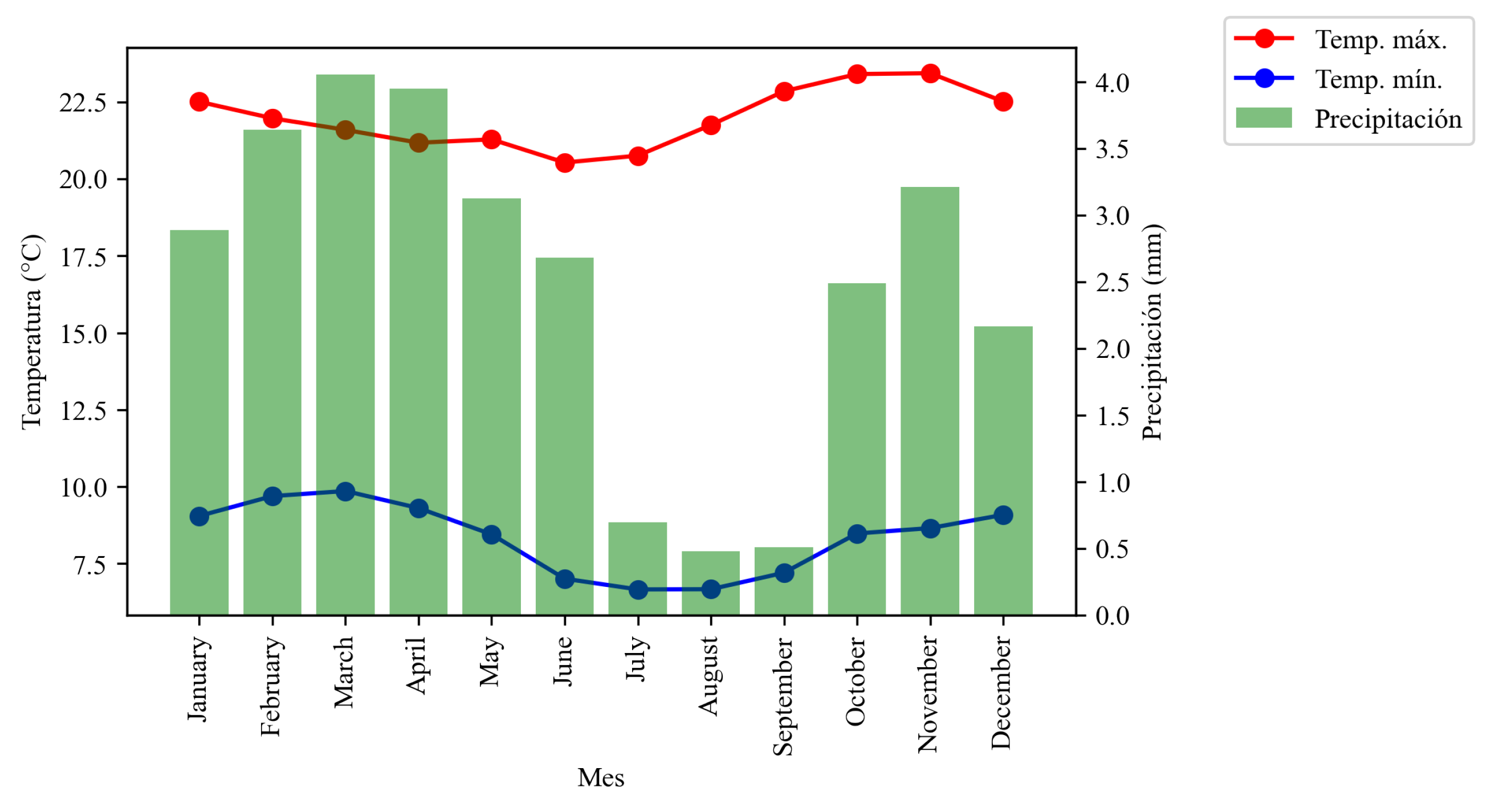
Figure 4.
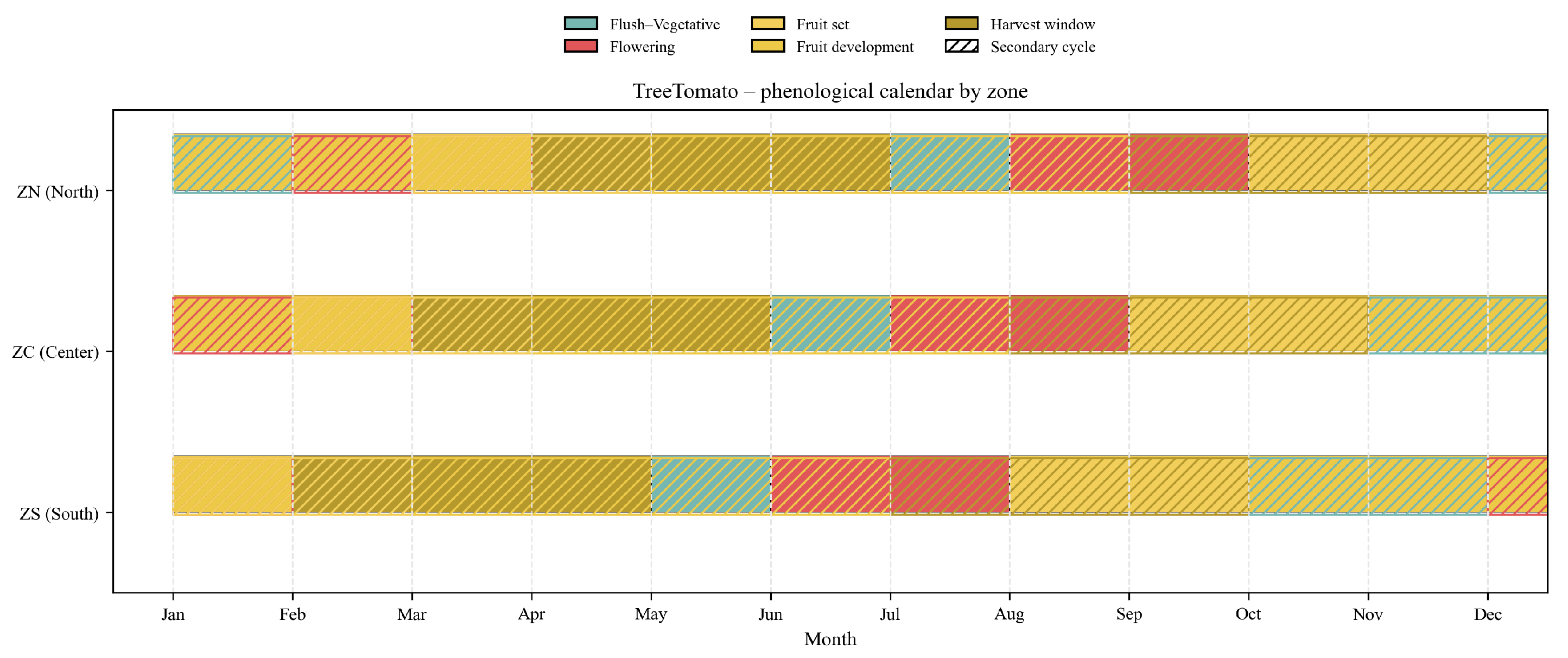
Graph showing temperatures and precipitation in the northern part of the country.
Figure 4.
Graph showing temperatures and precipitation in the northern part of the country.
Figure 5.
Graph showing temperatures and precipitation in the central region of the country.
Figure 5.
Graph showing temperatures and precipitation in the central region of the country.
Figure 6.
Graph showing temperatures and precipitation in the southern part of the country.
Figure 6.
Graph showing temperatures and precipitation in the southern part of the country.
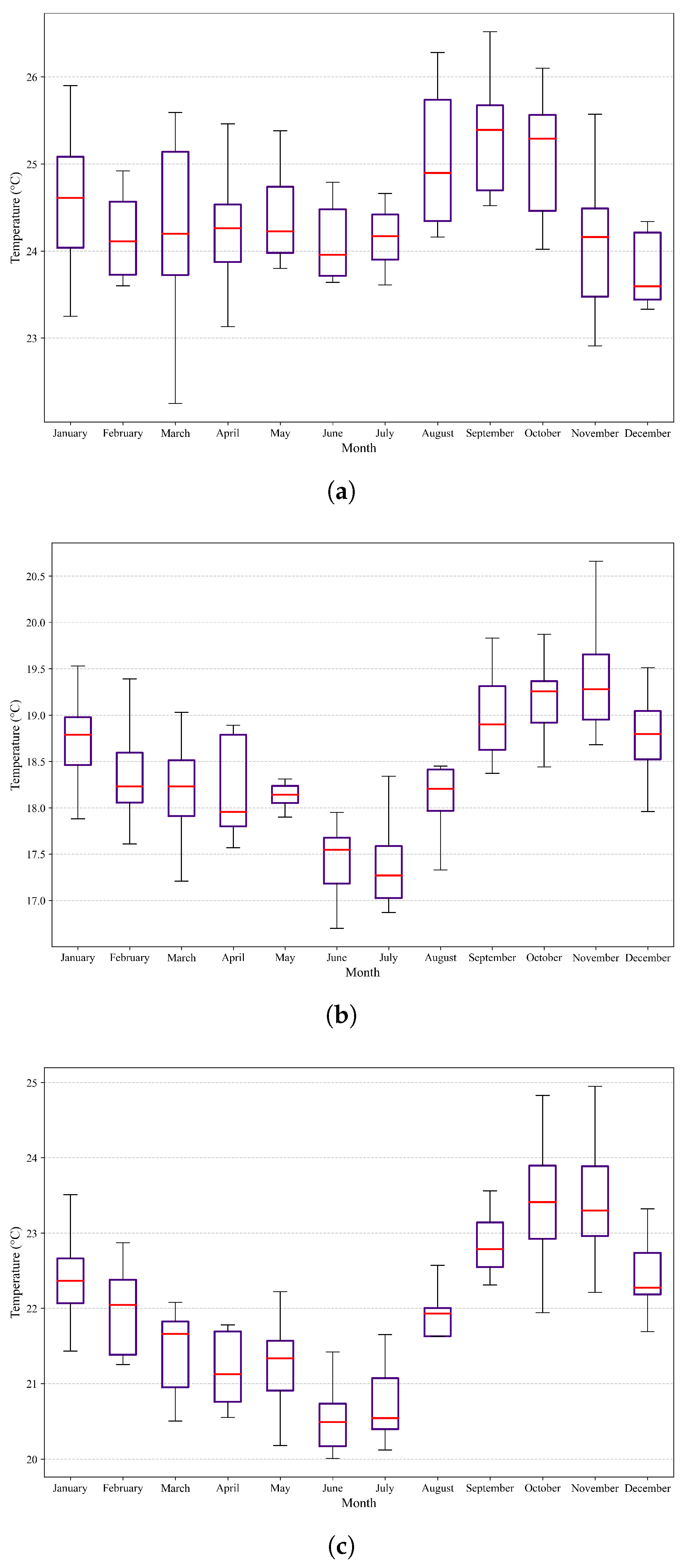
Figure 7.
Box plots and whiskers of variations in maximum temperatures in the three study areas. (a) Variation in maximum temperature in the northern region. (b) Variation in maximum temperature in the central zone. (c) Variation in maximum temperature in the southern region.
Figure 7.
Box plots and whiskers of variations in maximum temperatures in the three study areas. (a) Variation in maximum temperature in the northern region. (b) Variation in maximum temperature in the central zone. (c) Variation in maximum temperature in the southern region.
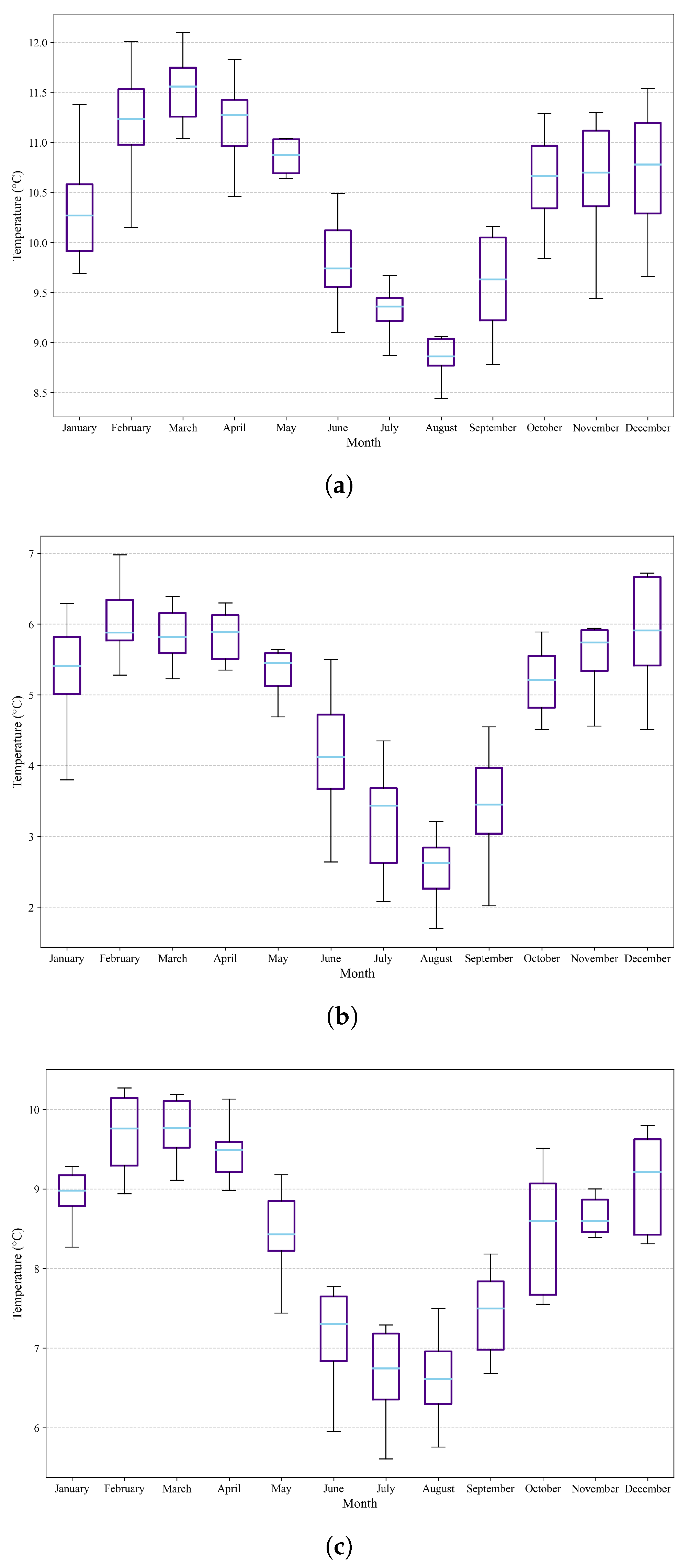
Figure 8.
Box plots and whiskers showing variations in minimum temperatures in the three study areas. (a) Variation in minimum temperature in the northern region. (b) Variation in minimum temperature in the central zone. (c) Variation in minimum temperature in the southern region.
Figure 8.
Box plots and whiskers showing variations in minimum temperatures in the three study areas. (a) Variation in minimum temperature in the northern region. (b) Variation in minimum temperature in the central zone. (c) Variation in minimum temperature in the southern region.
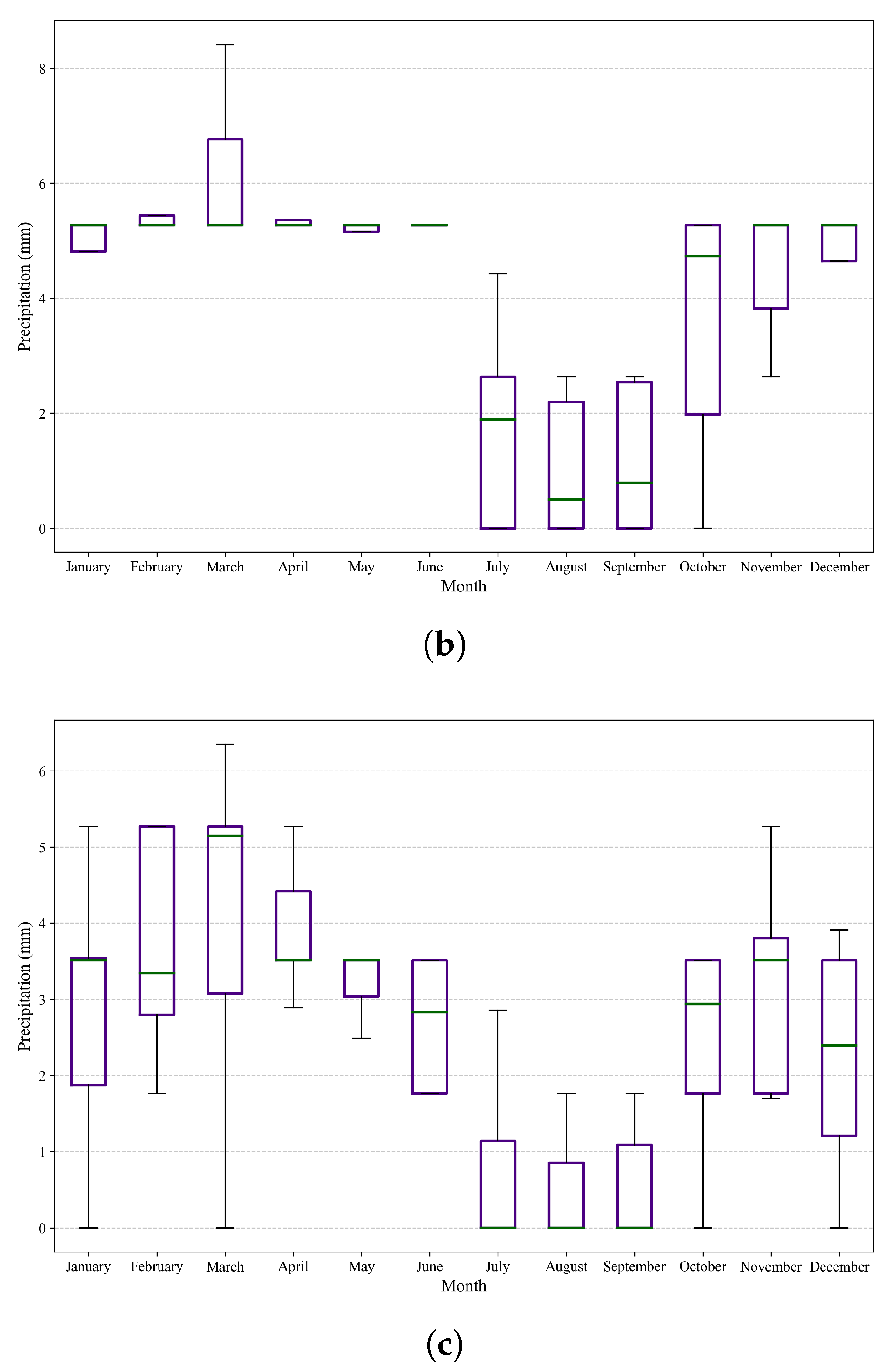
Figure 9.
Box plots and whiskers showing variations in precipitation in the three study areas. (a) Variation in precipitation in the northern region. (b) Variation in precipitation in the central region. (c) Variation in precipitation in the southern region.
Figure 9.
Box plots and whiskers showing variations in precipitation in the three study areas. (a) Variation in precipitation in the northern region. (b) Variation in precipitation in the central region. (c) Variation in precipitation in the southern region.
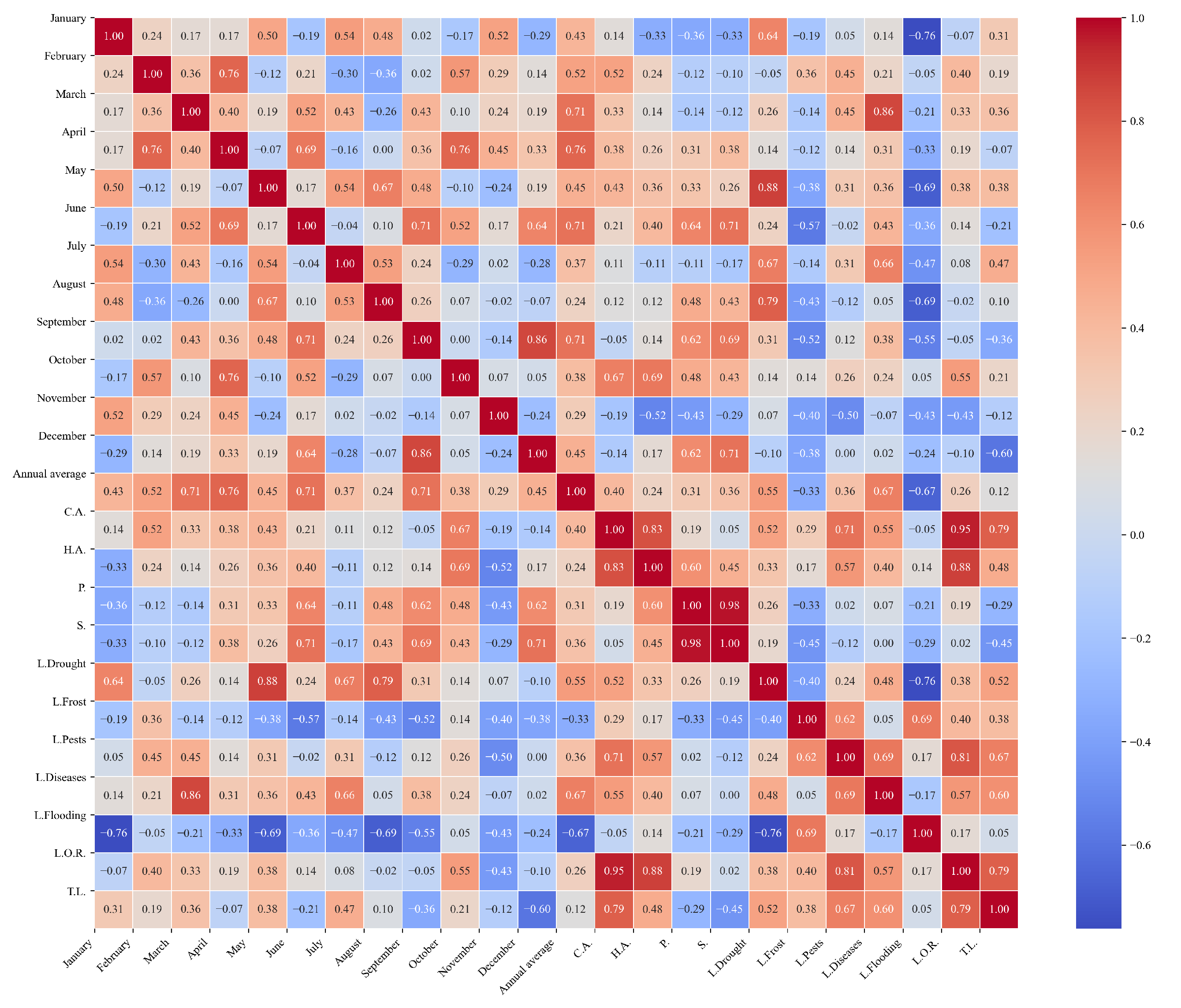
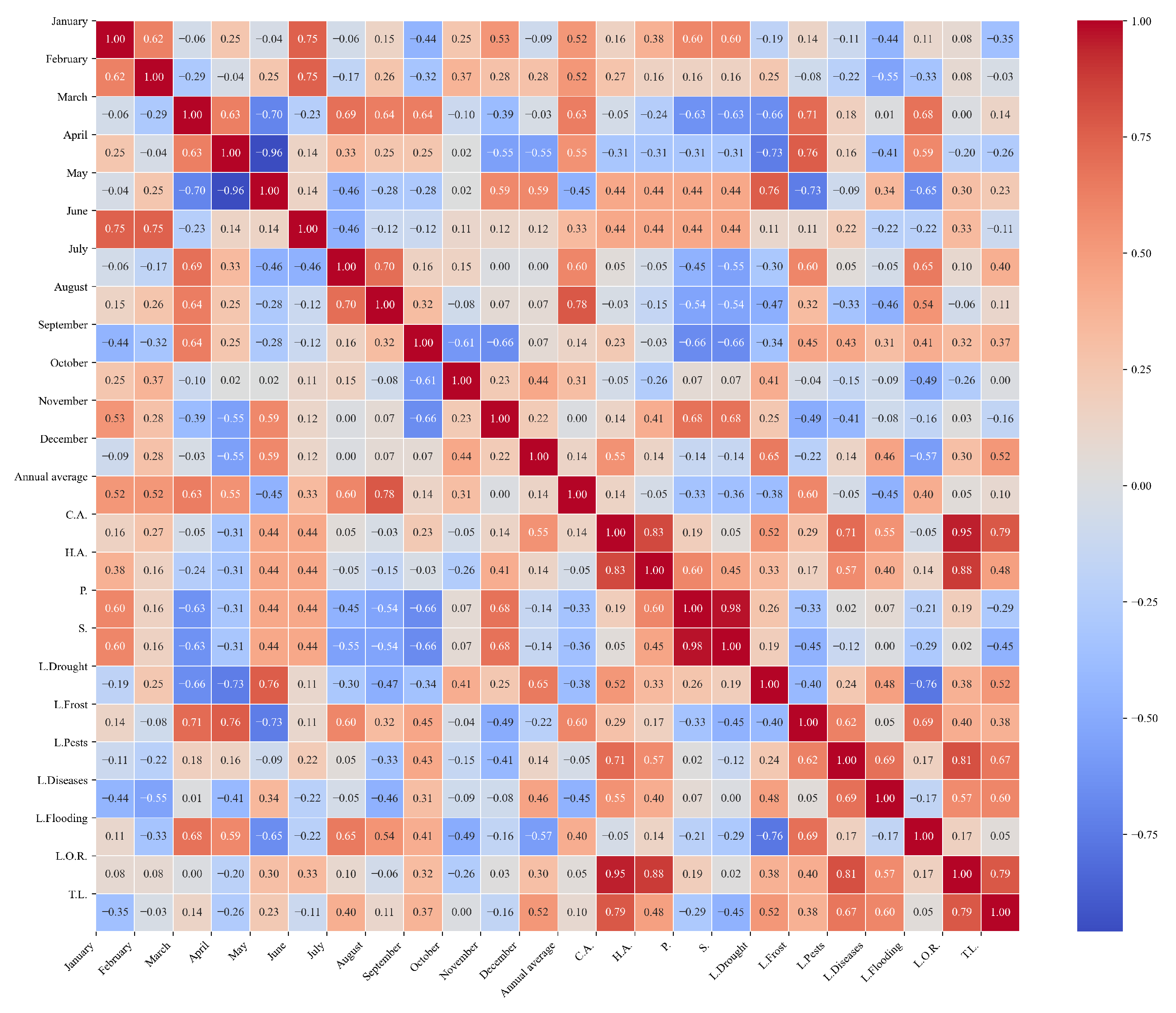
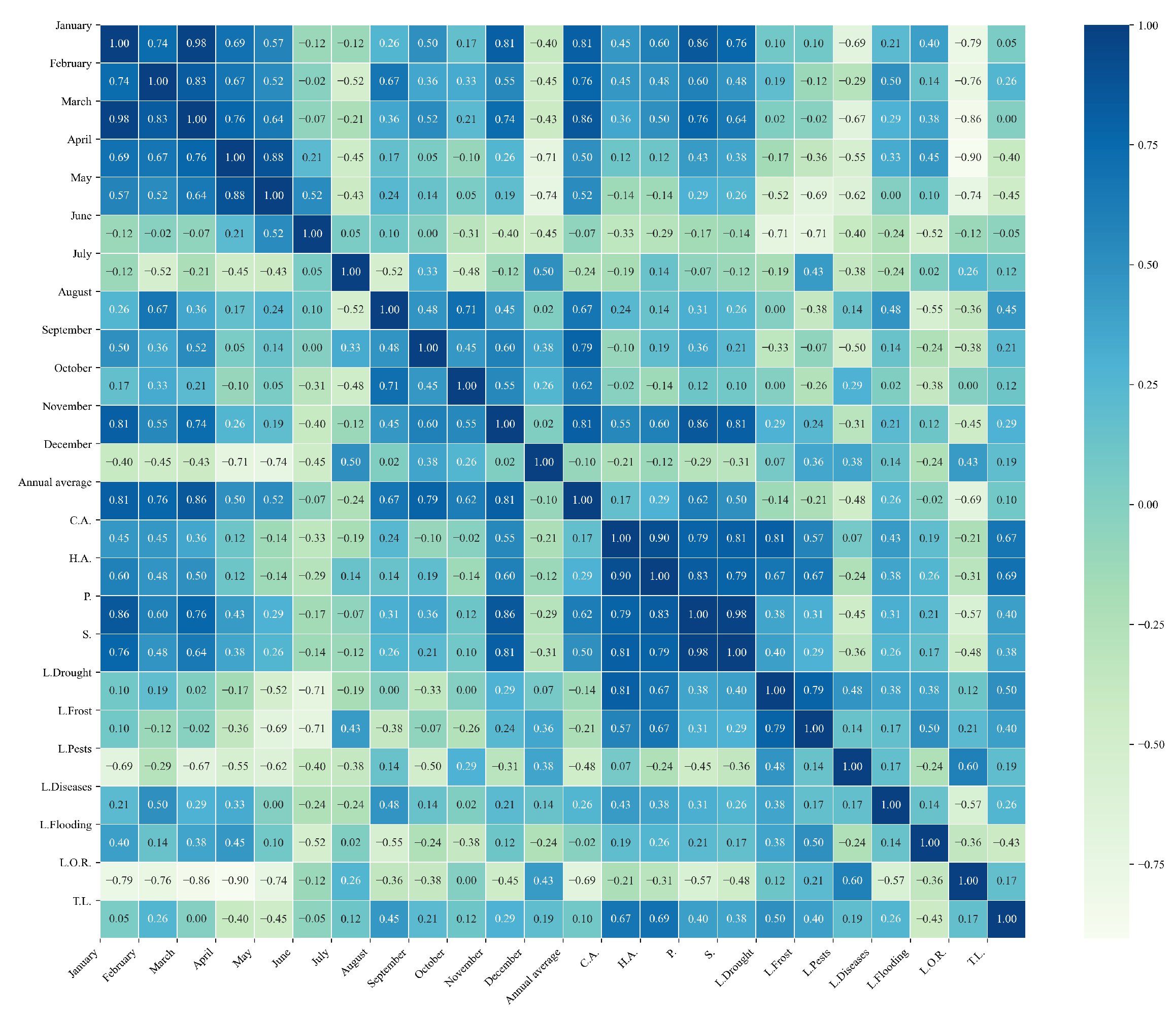
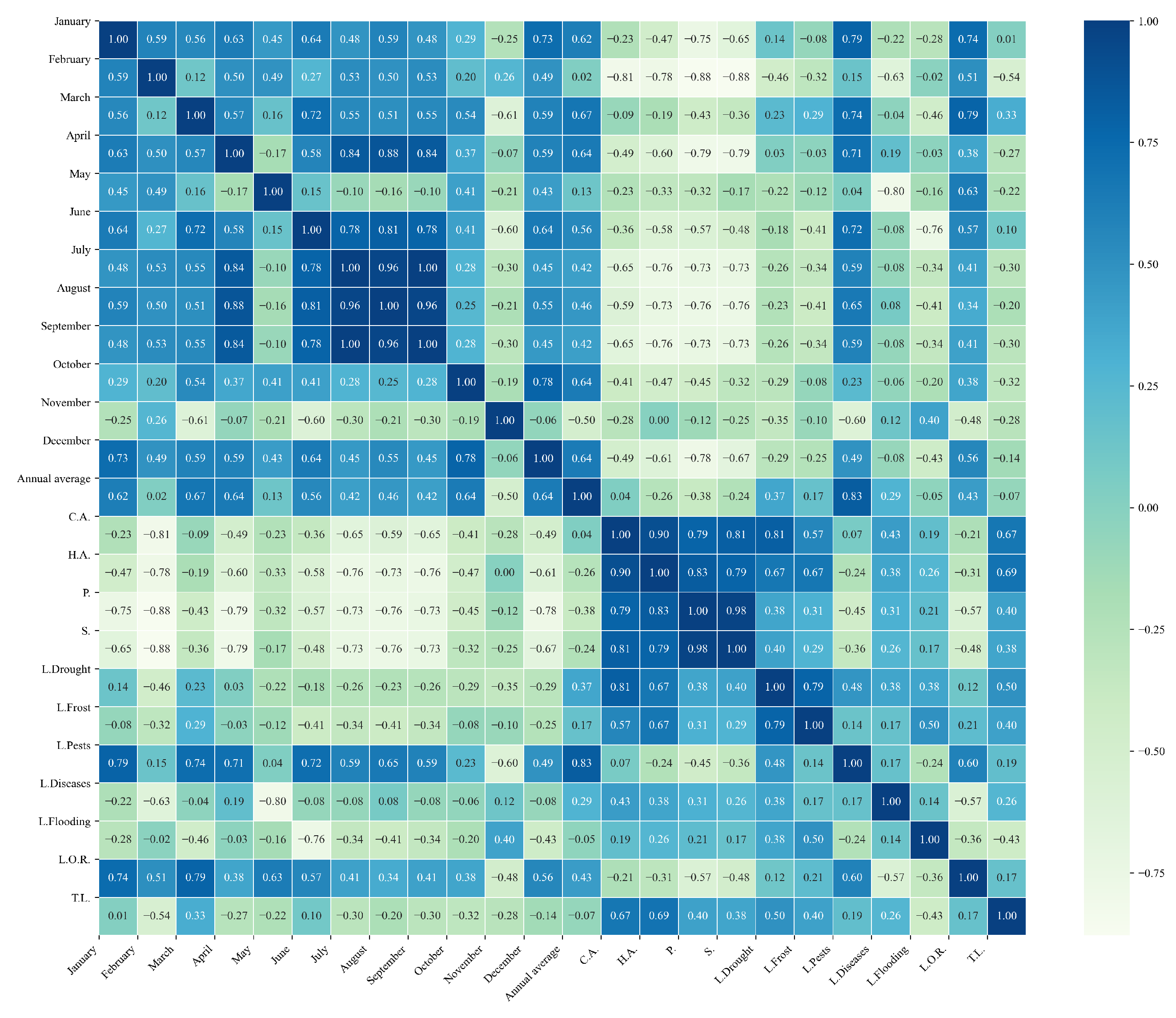
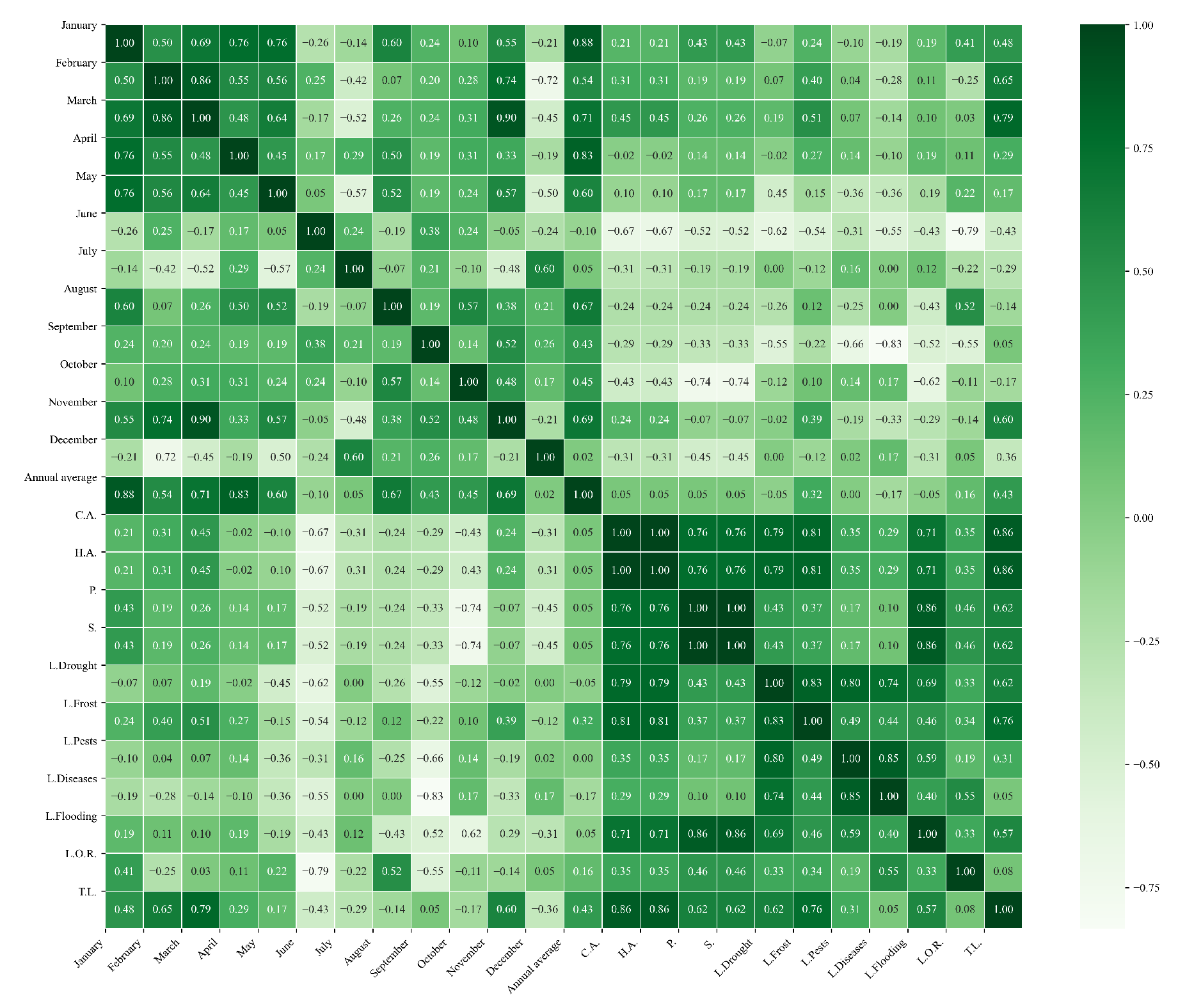
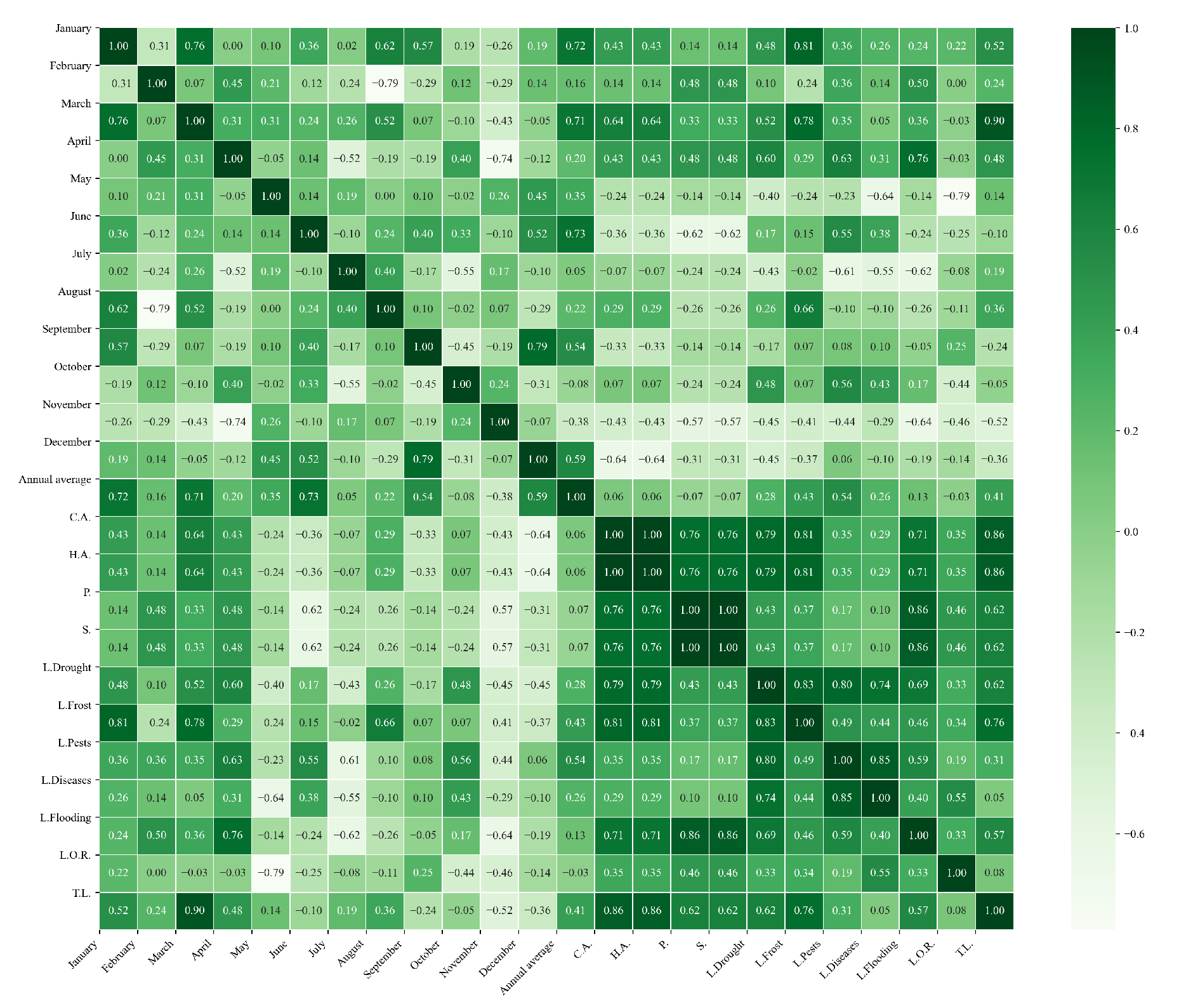
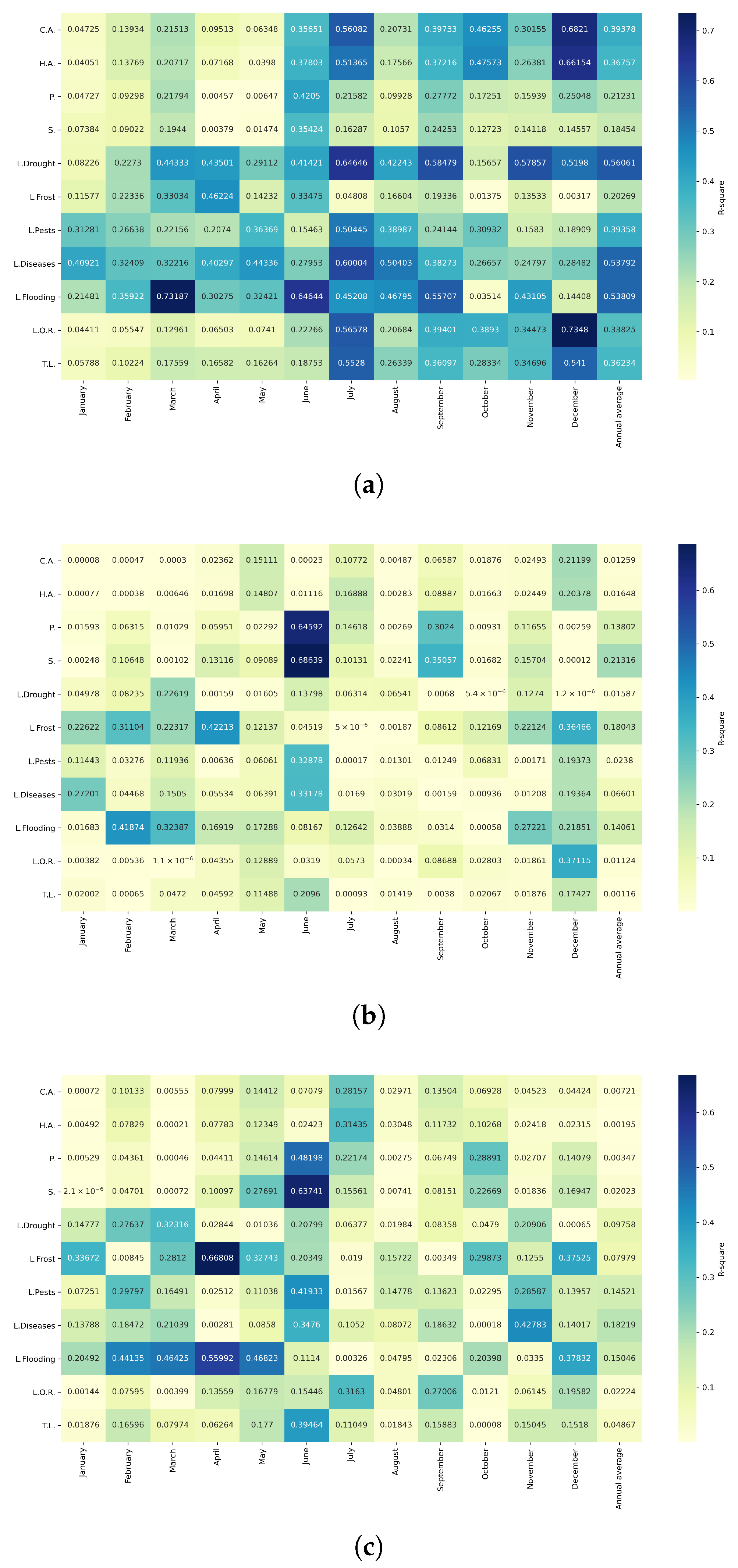
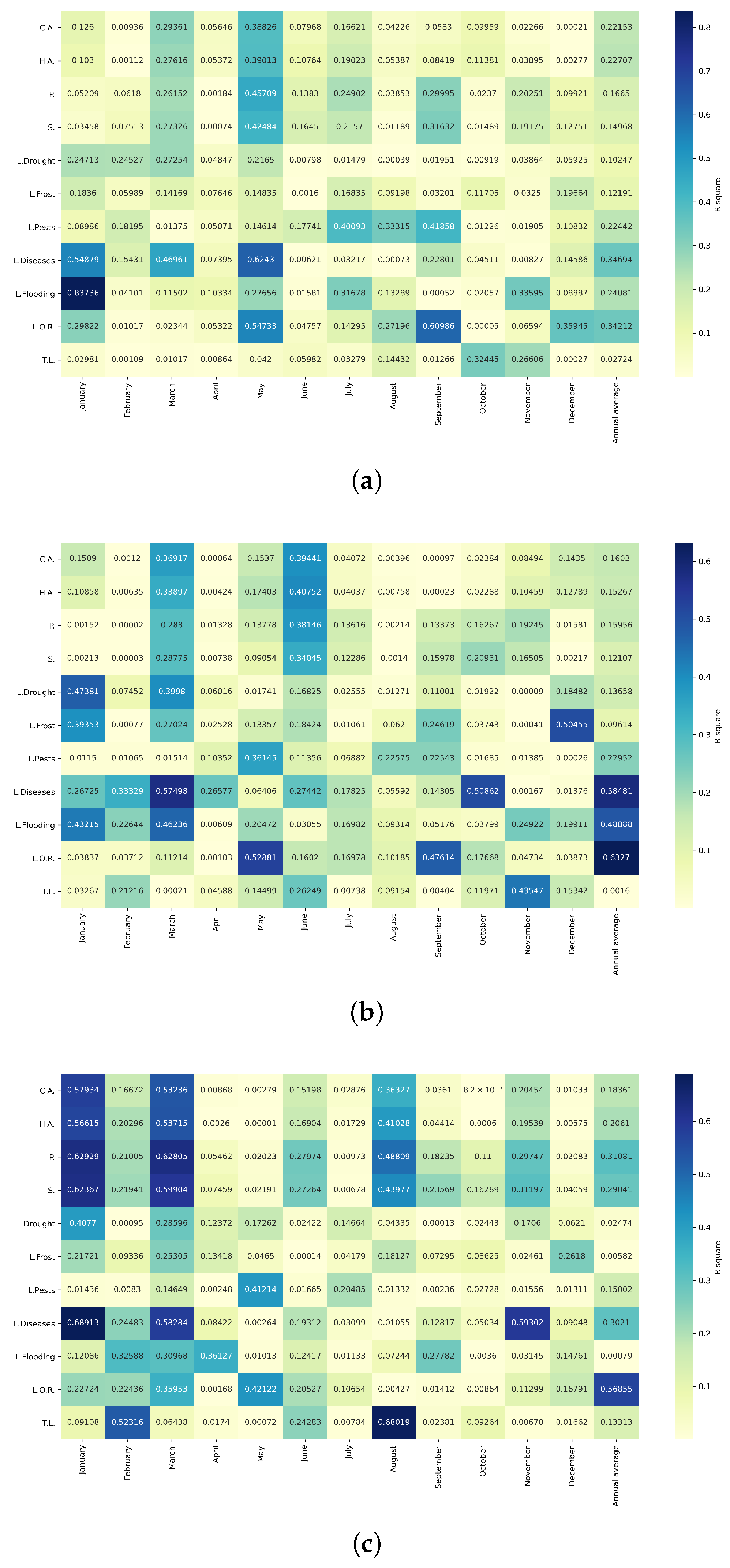
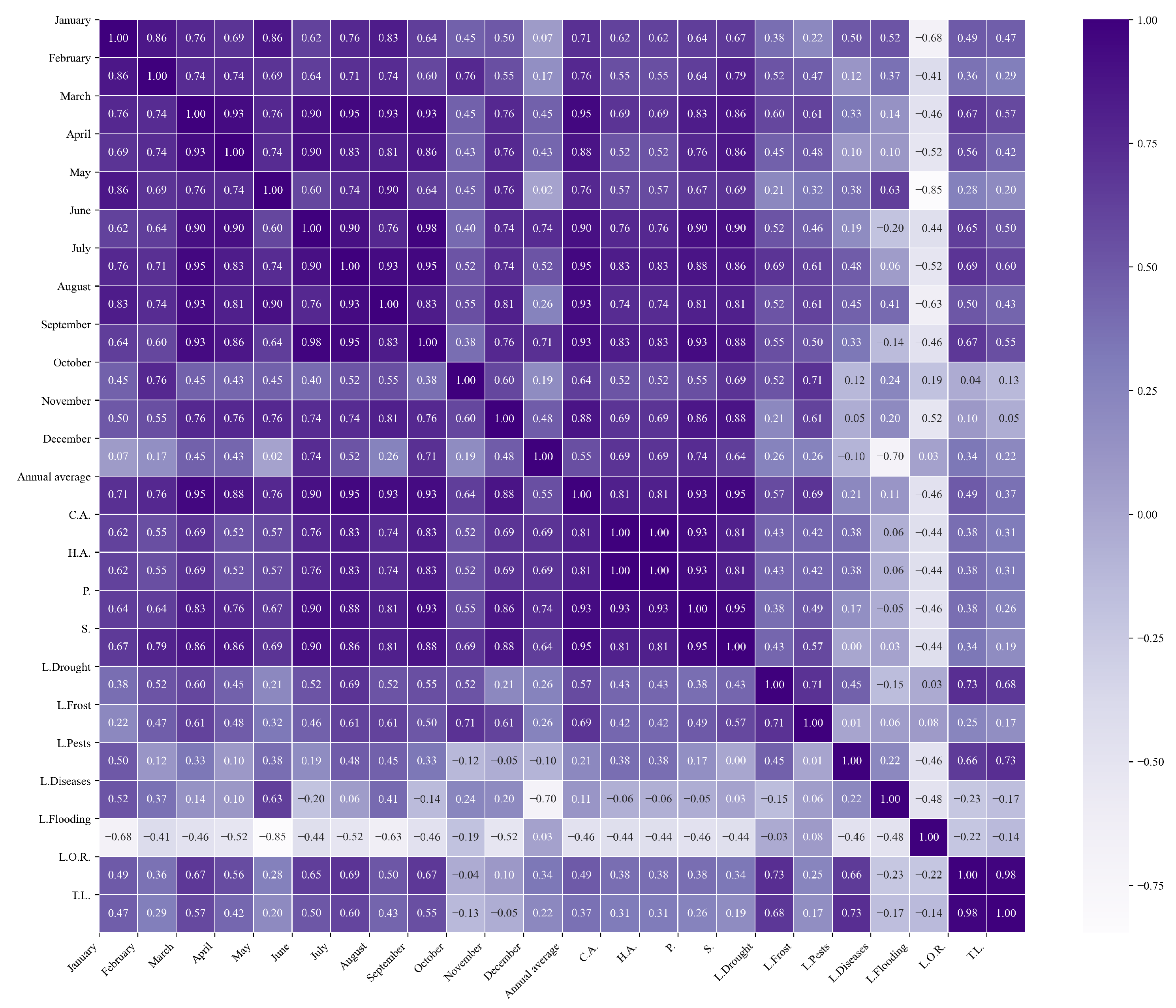
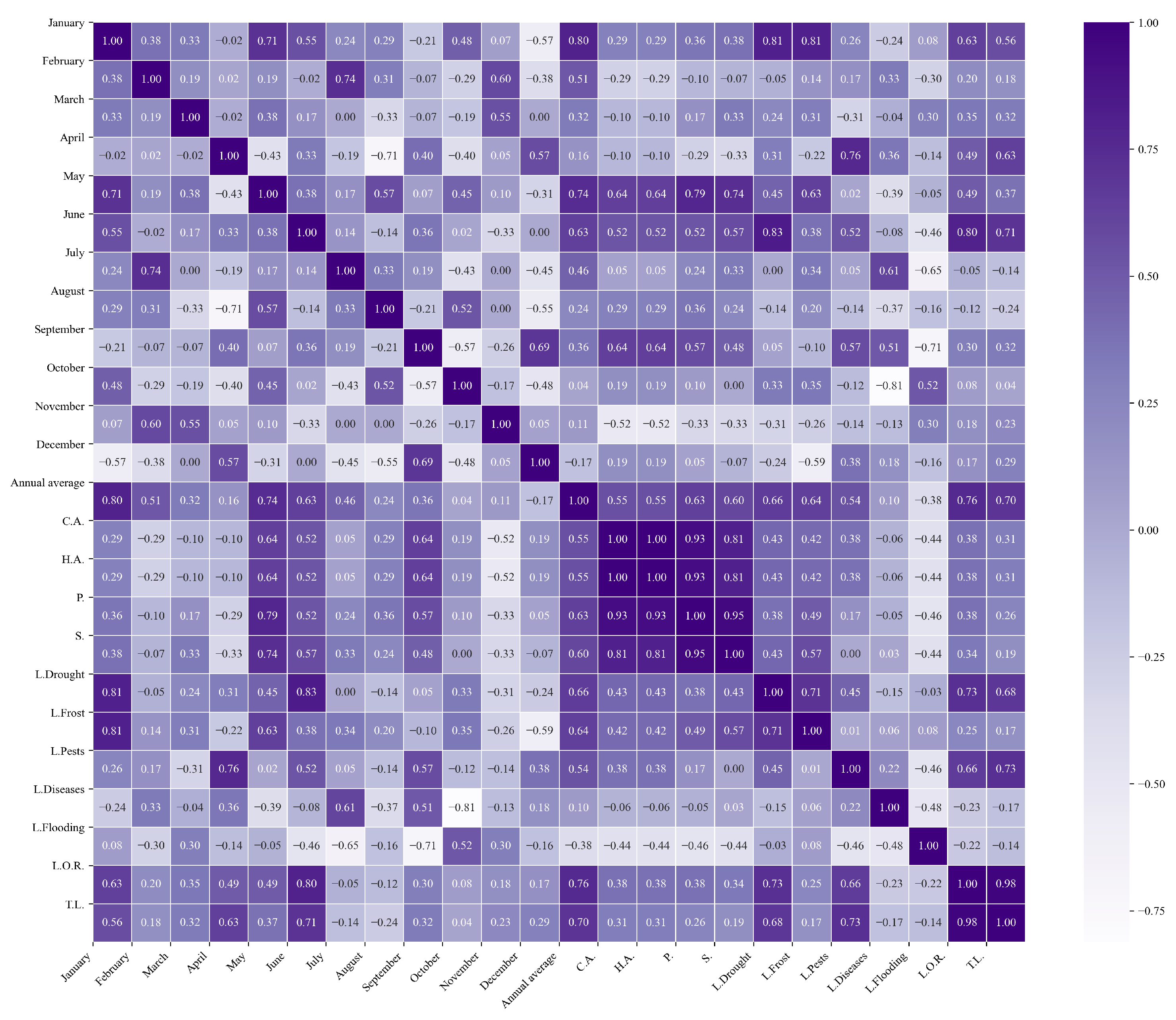
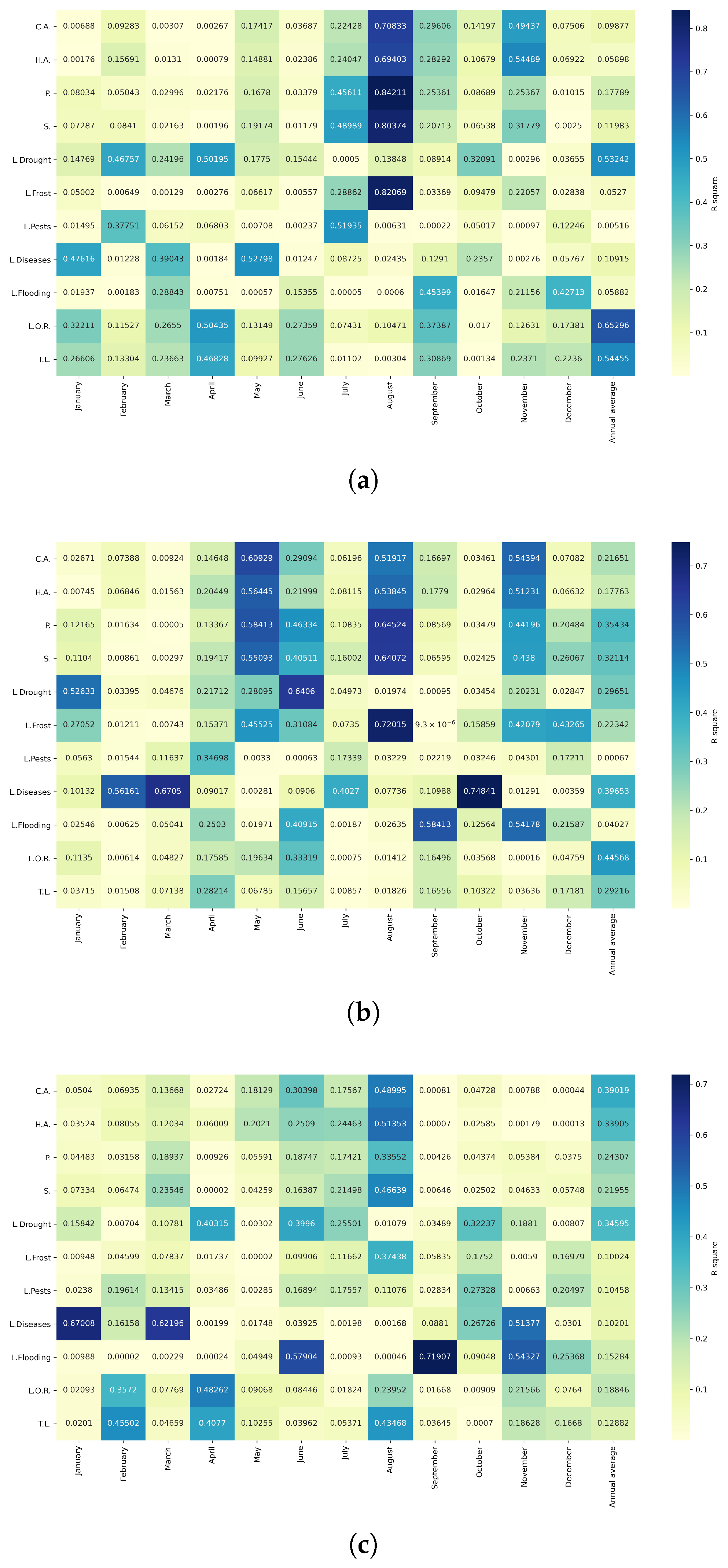
Figure 10.
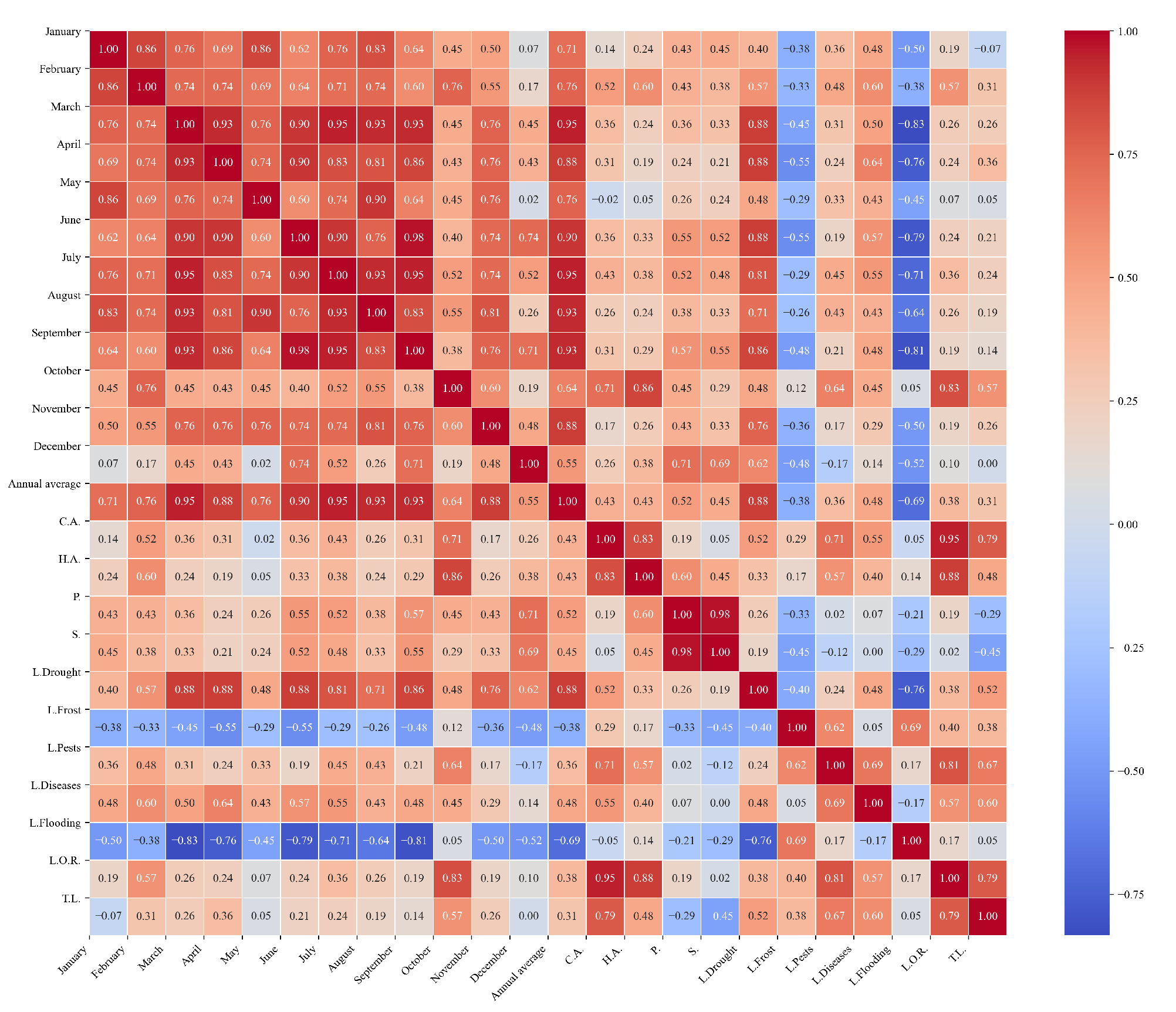
Heatmap of correlations between monthly maximum temperatures and agricultural variables for quinoa cultivation in the northern zone of Ecuador.
Figure 10.
Heatmap of correlations between monthly maximum temperatures and agricultural variables for quinoa cultivation in the northern zone of Ecuador.
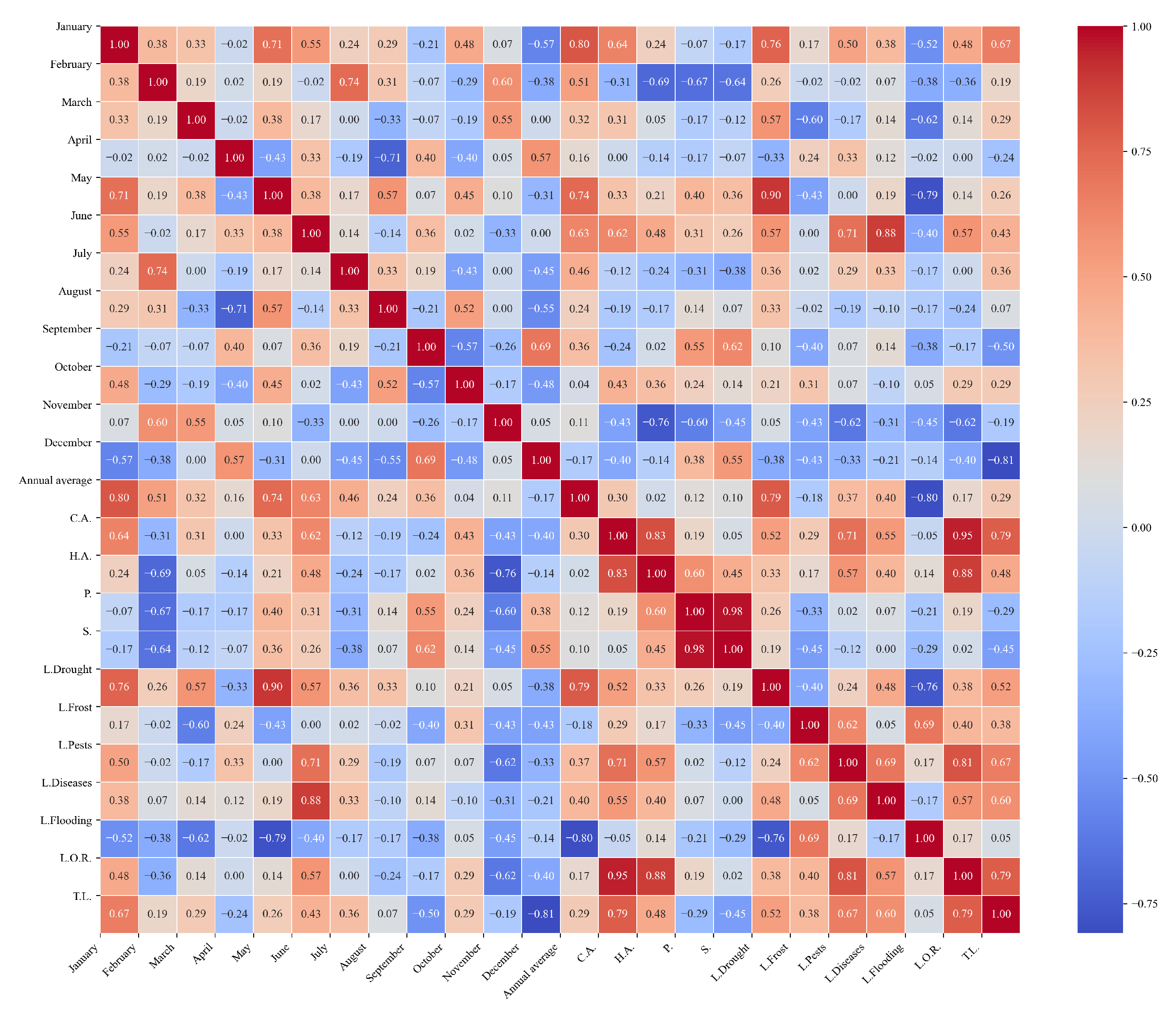
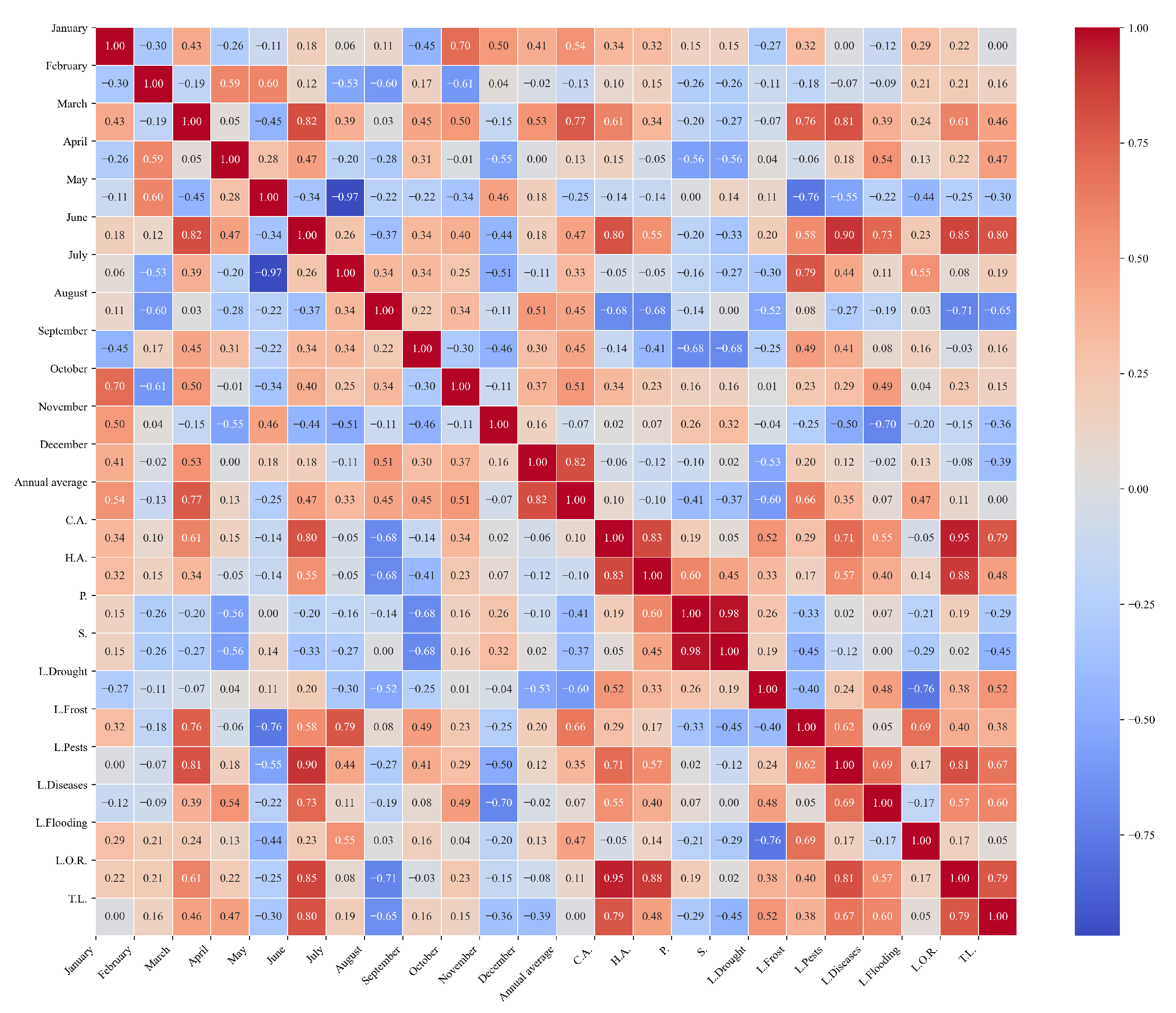
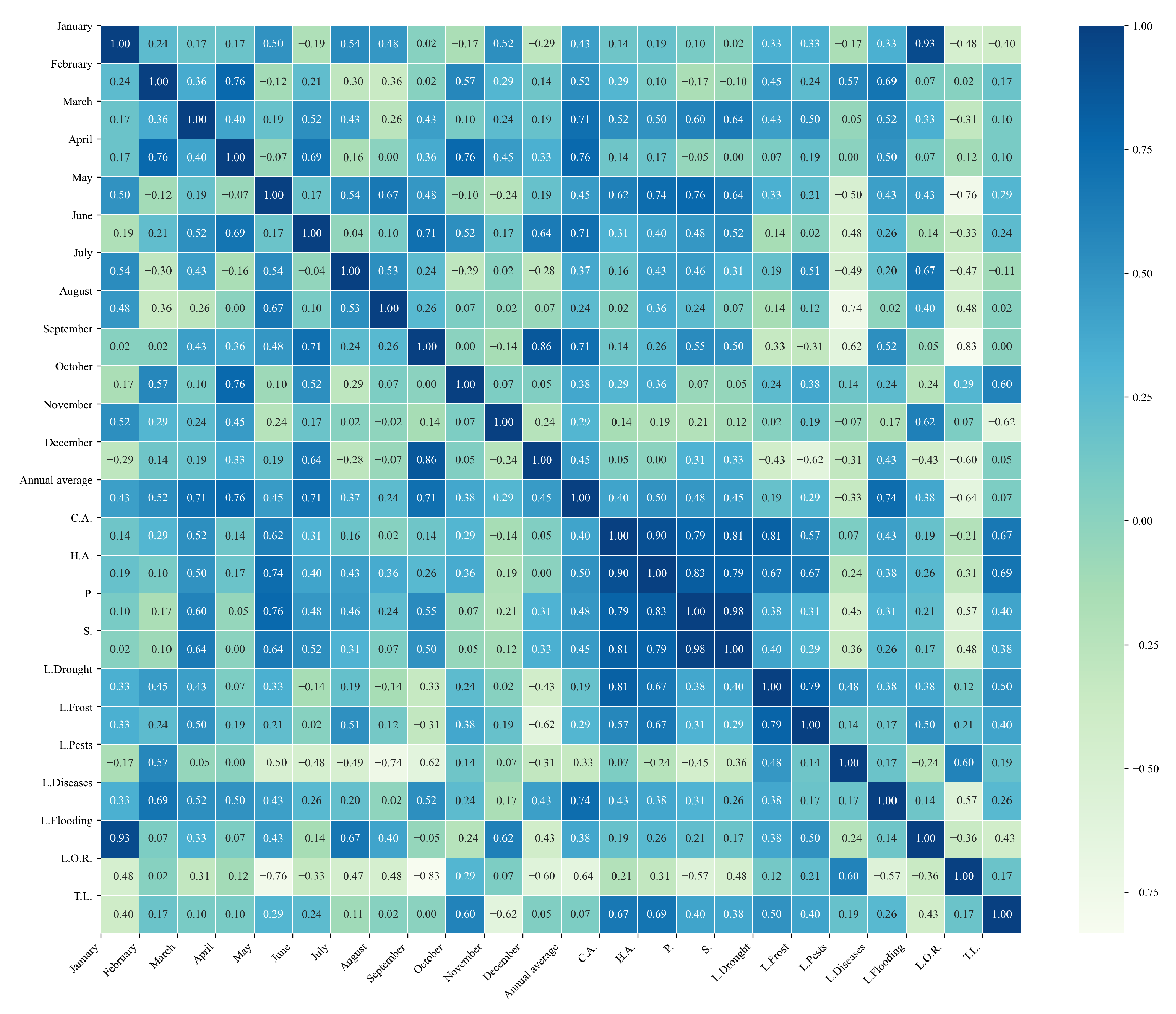
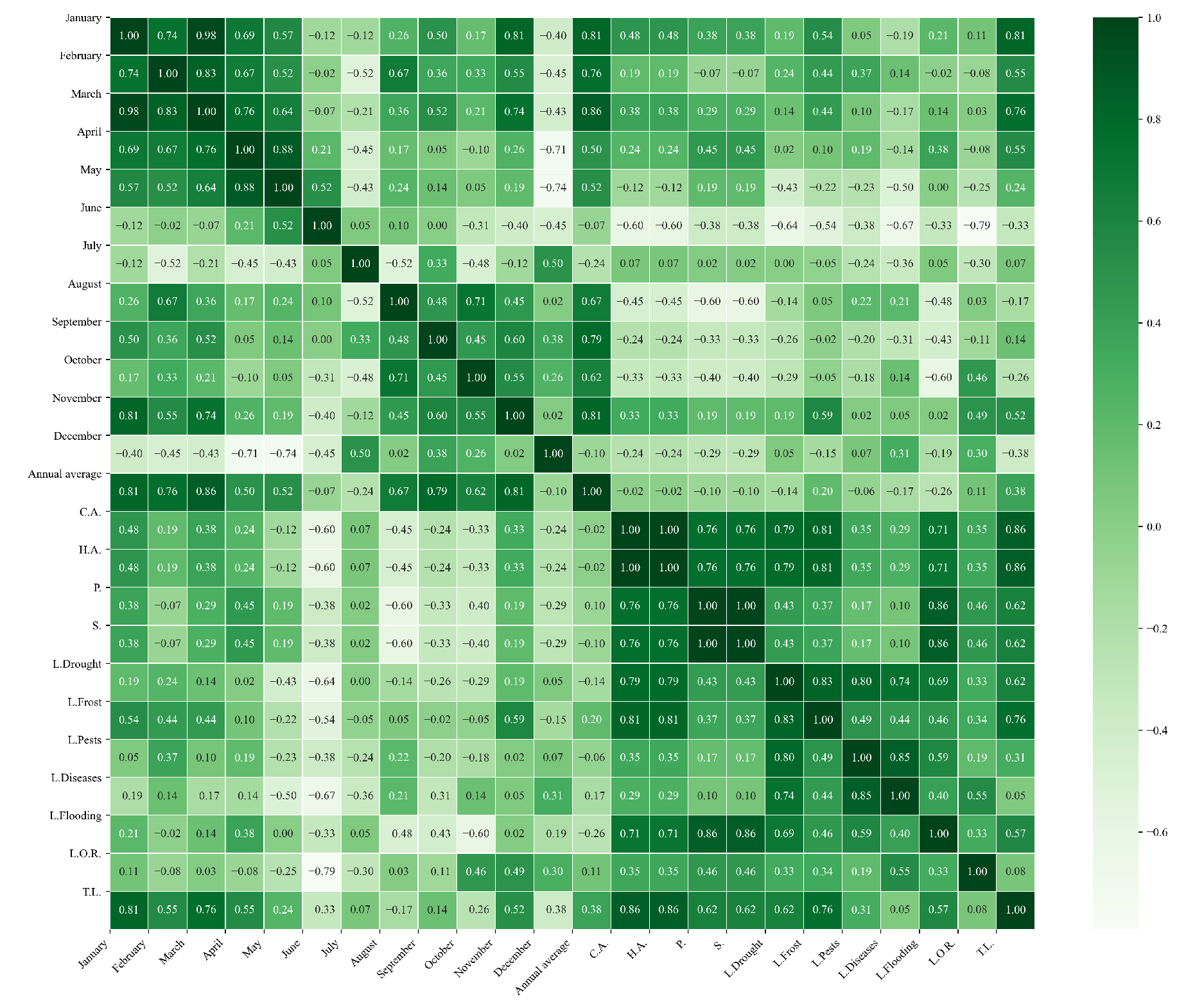
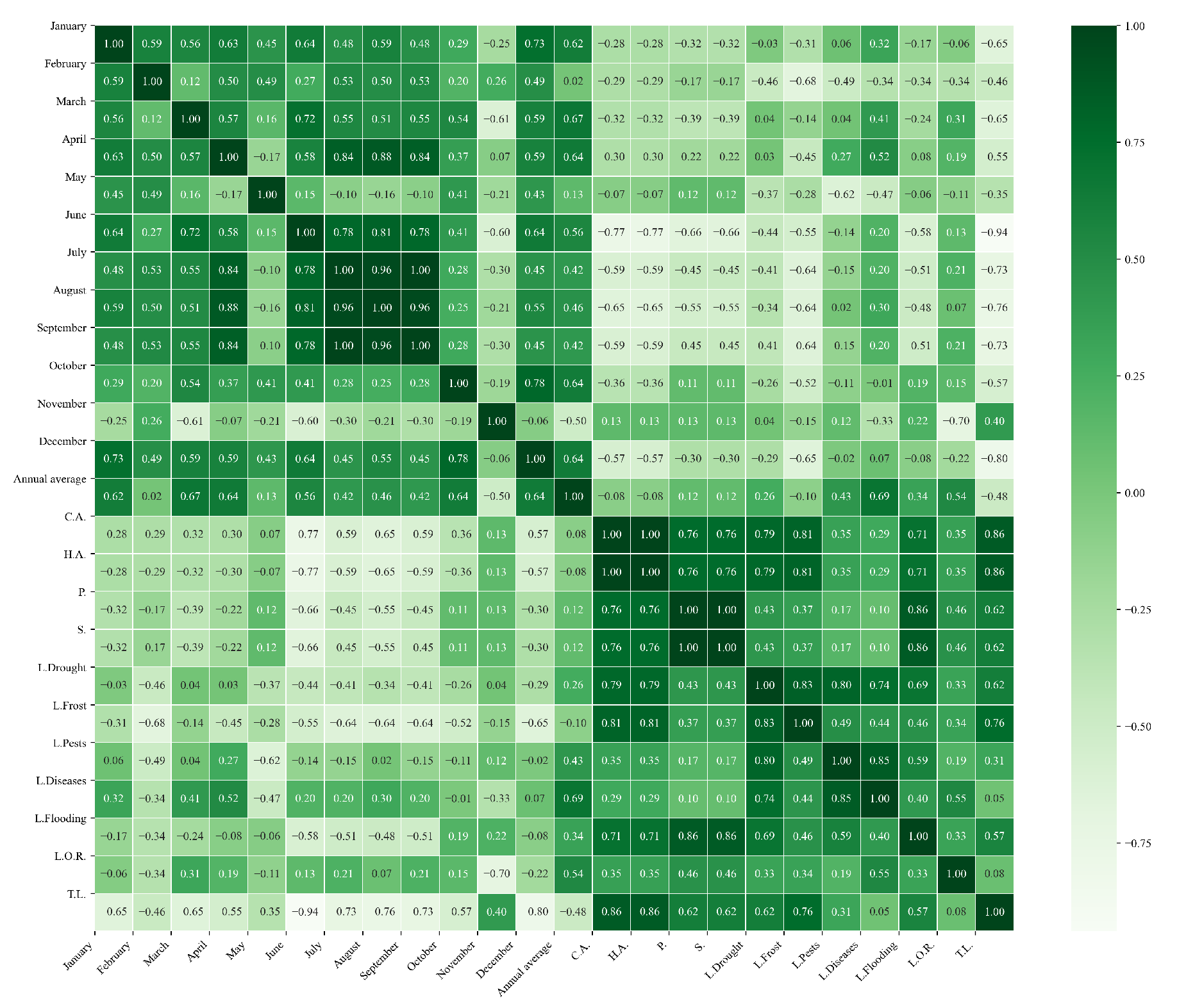
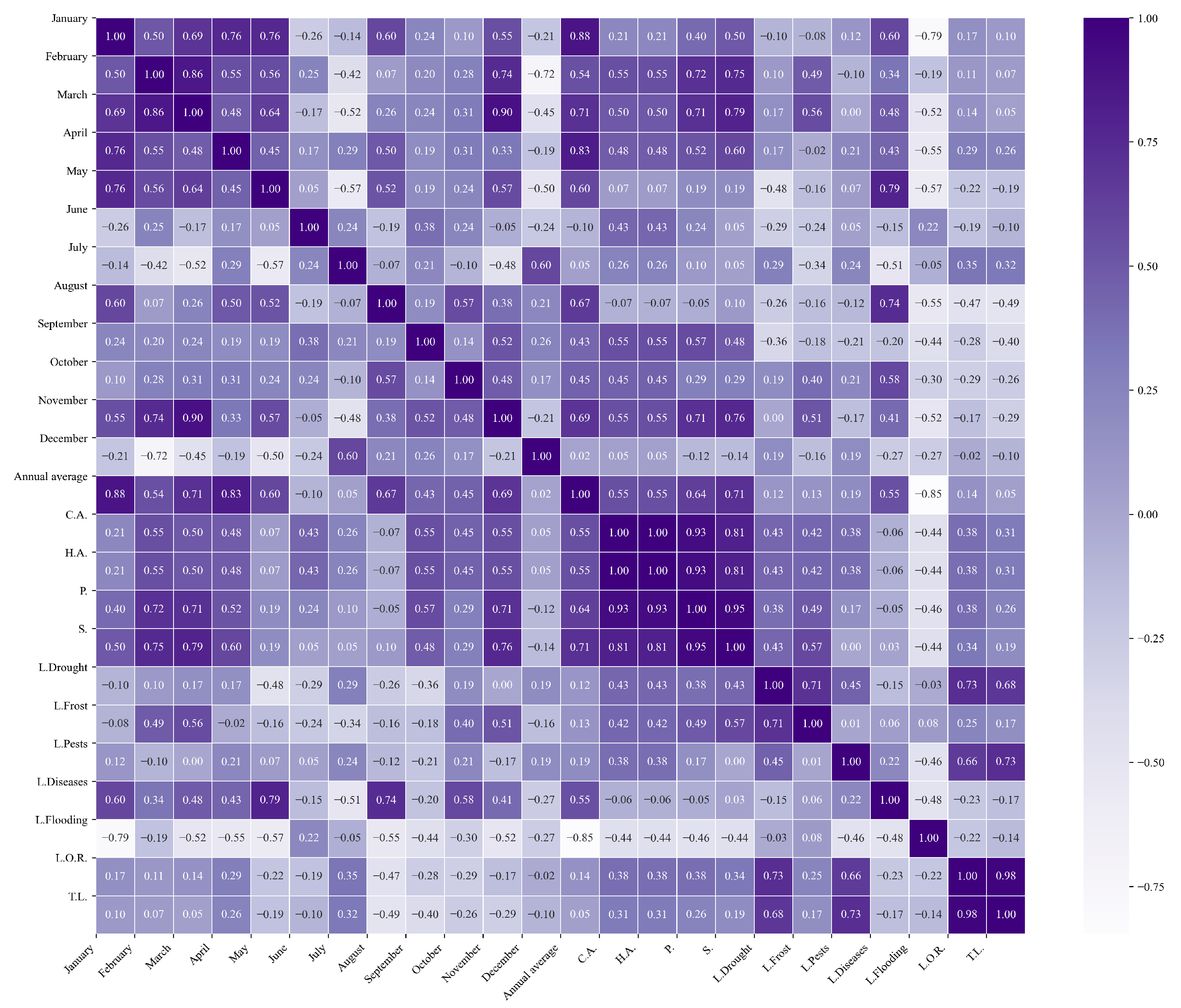
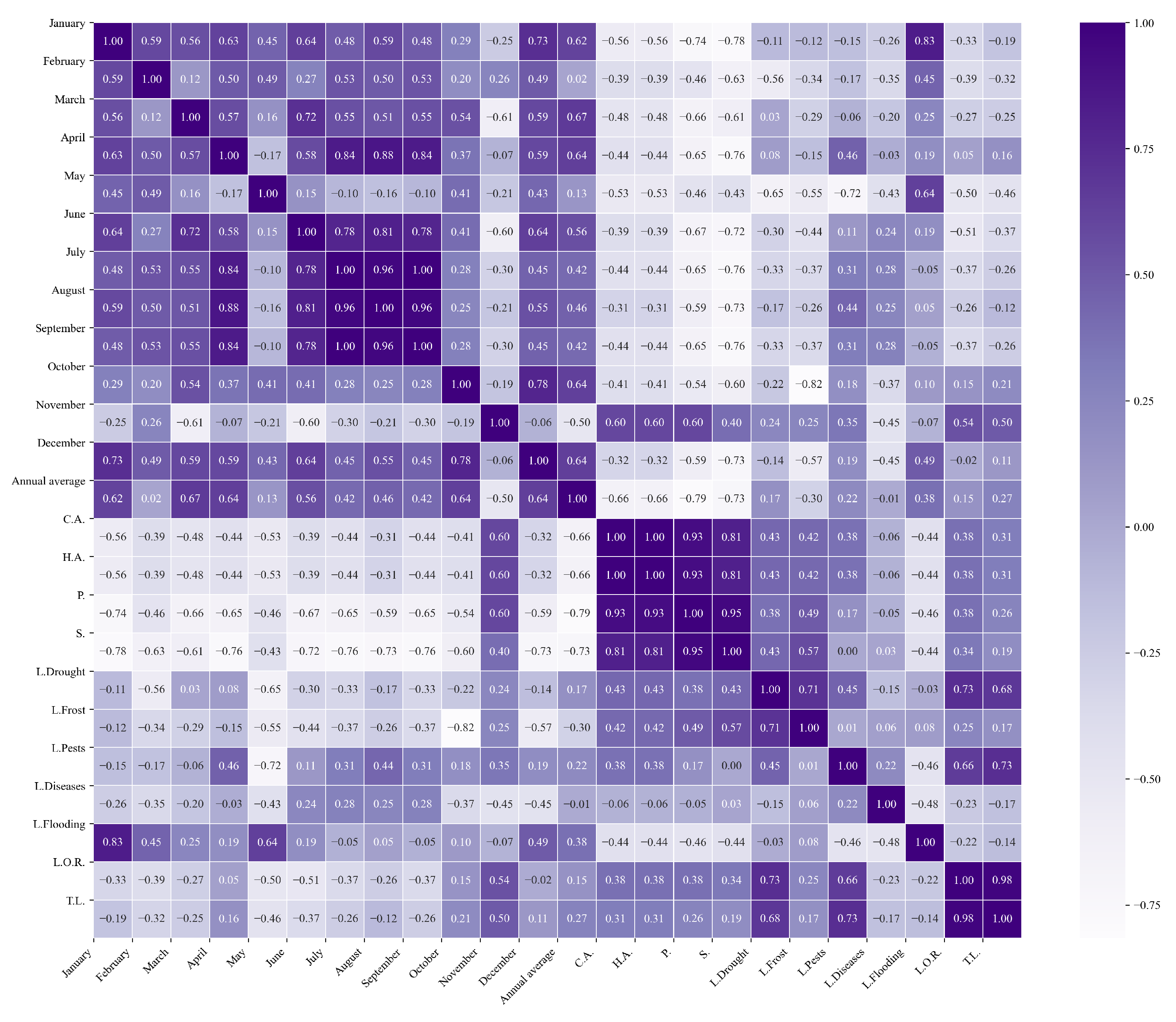
Figure 11.
Heatmap of correlations between monthly maximum temperatures and agricultural variables for quinoa cultivation in the central zone of Ecuador.
Figure 11.
Heatmap of correlations between monthly maximum temperatures and agricultural variables for quinoa cultivation in the central zone of Ecuador.
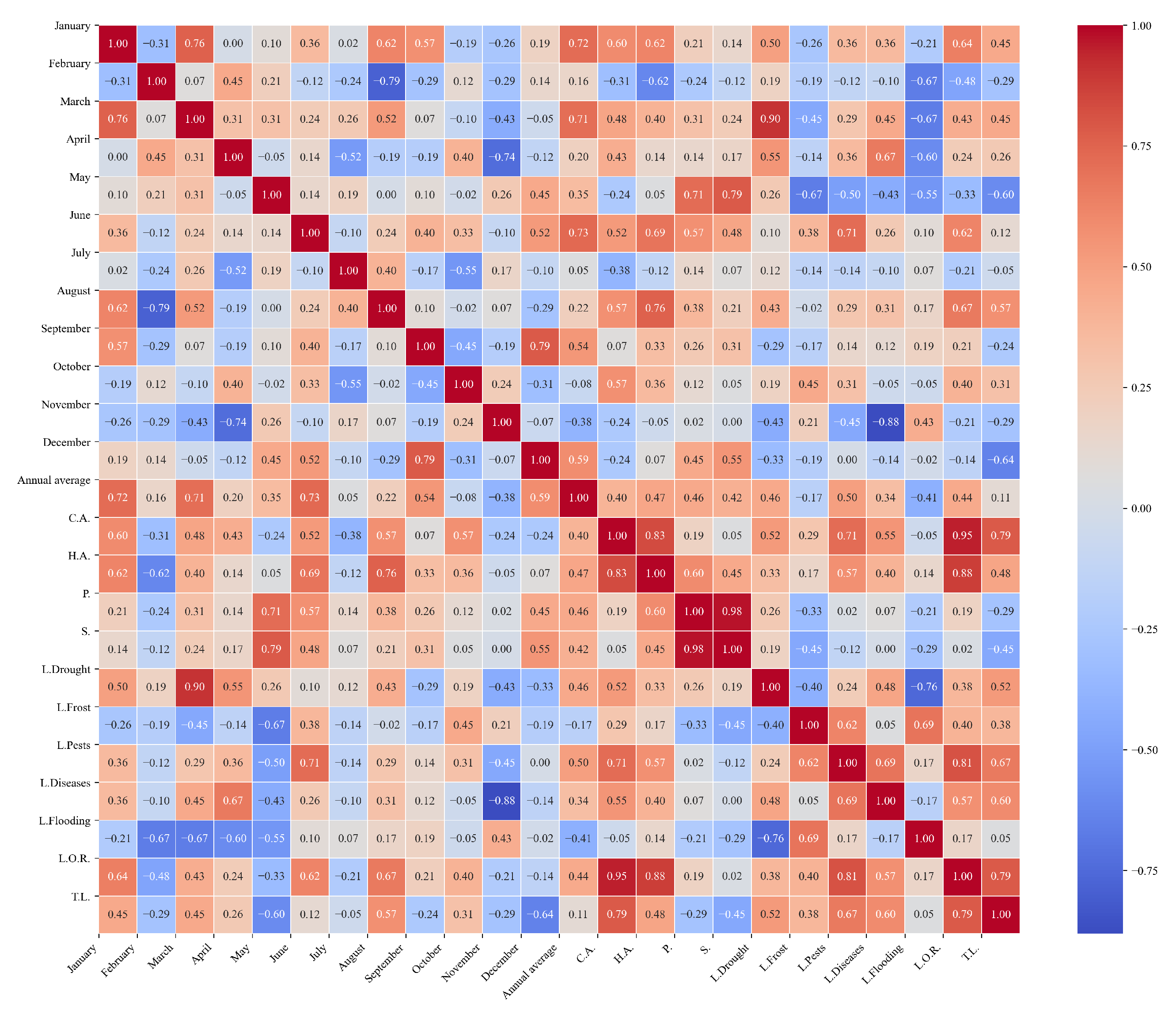
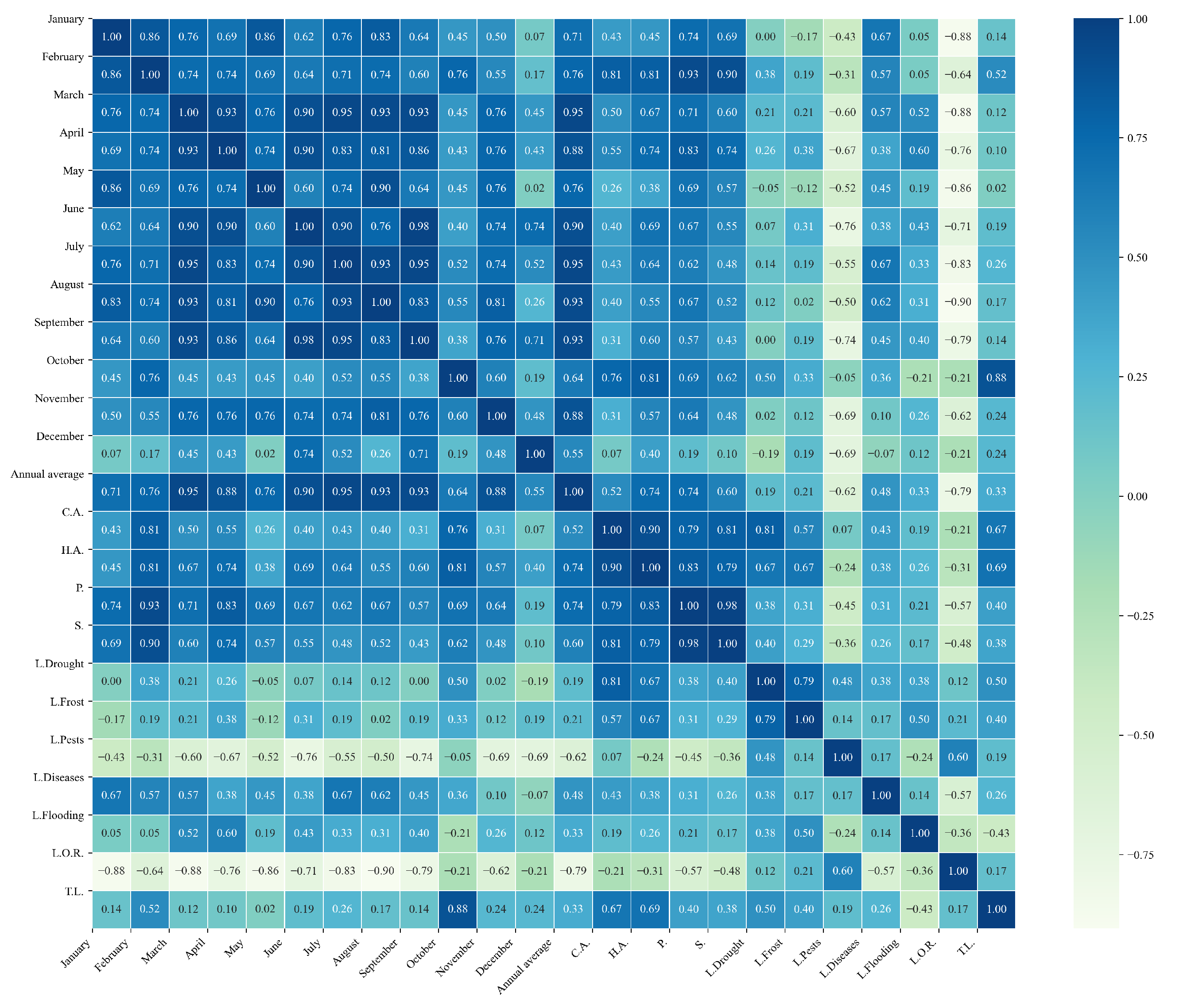
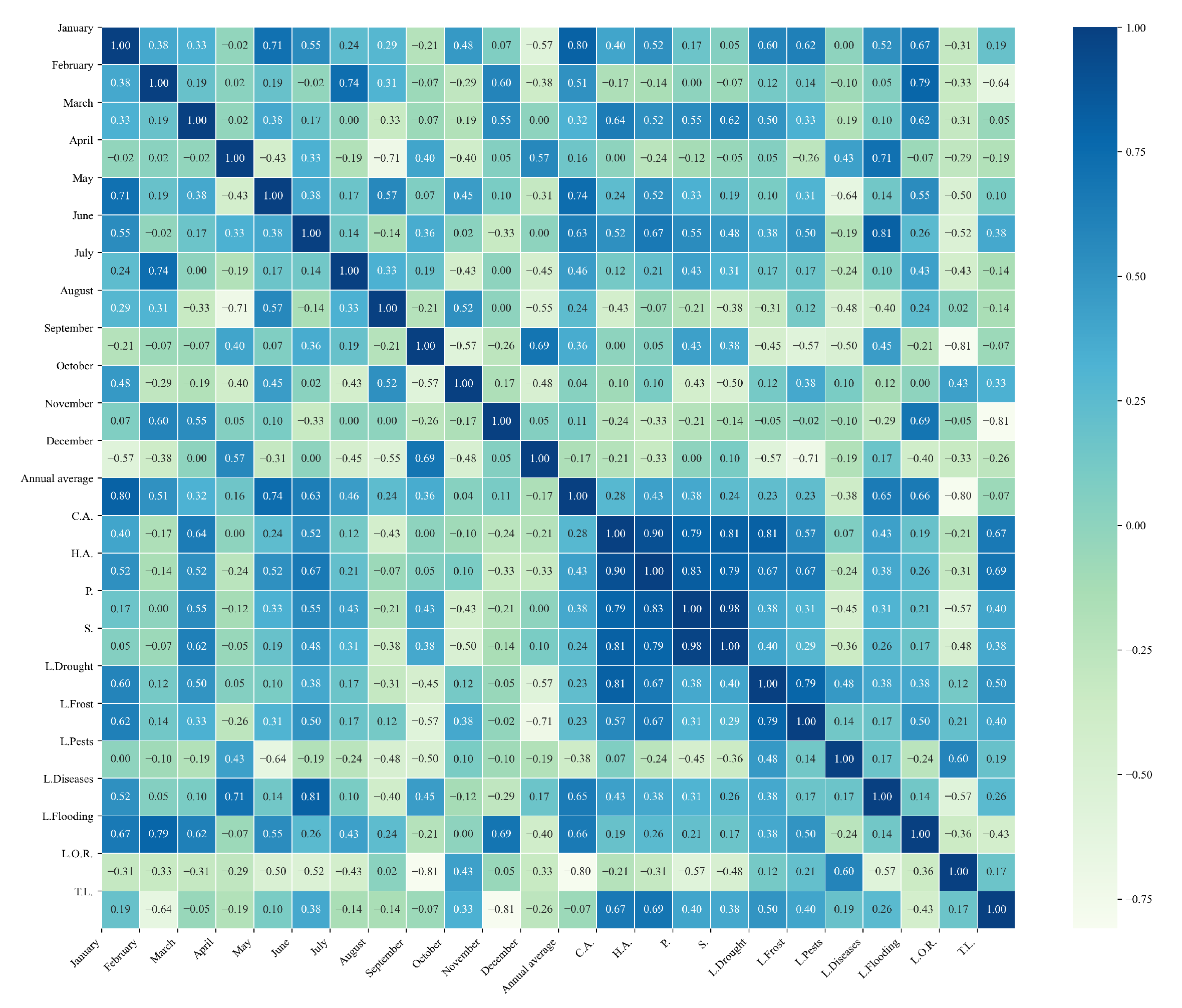
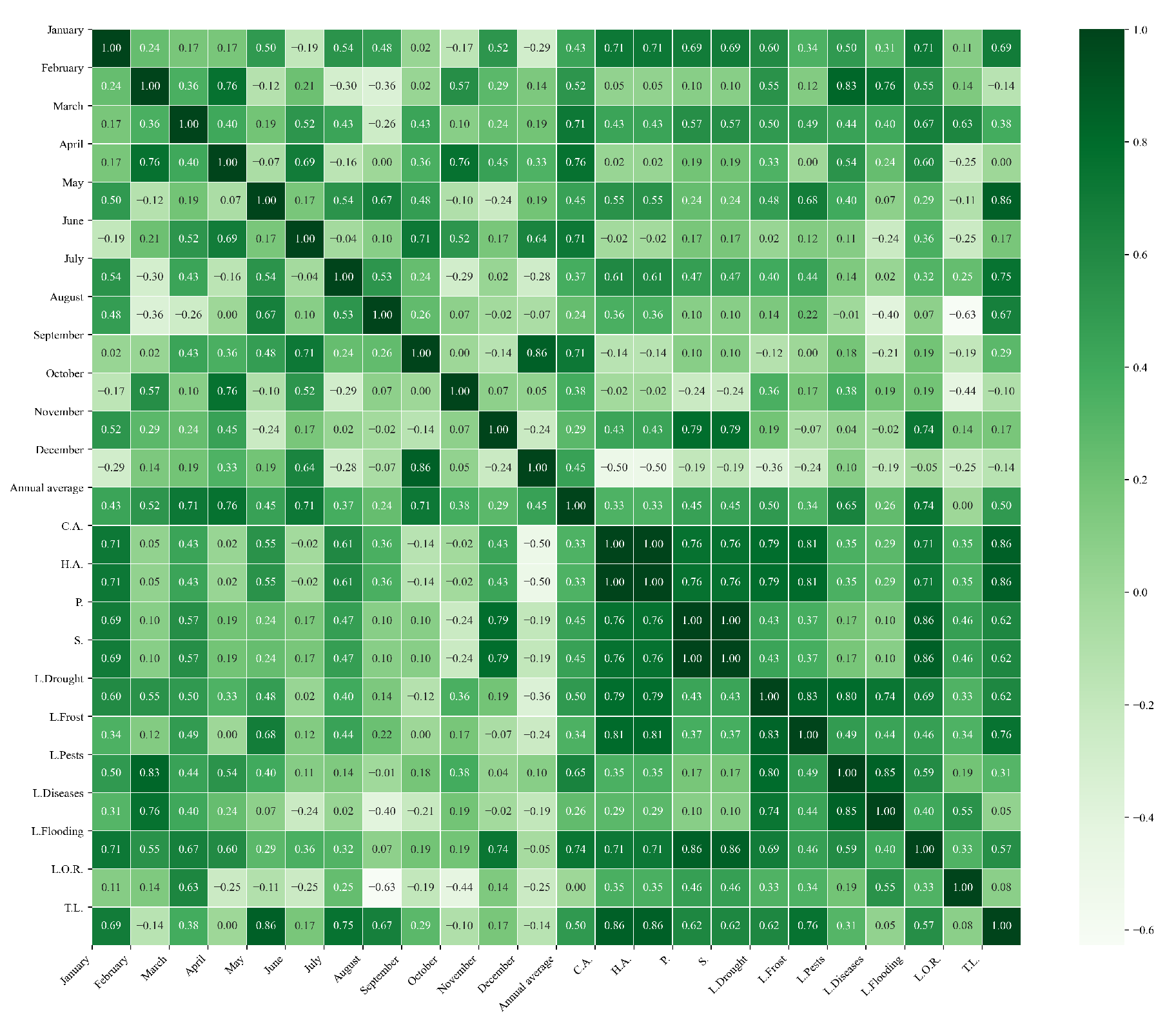
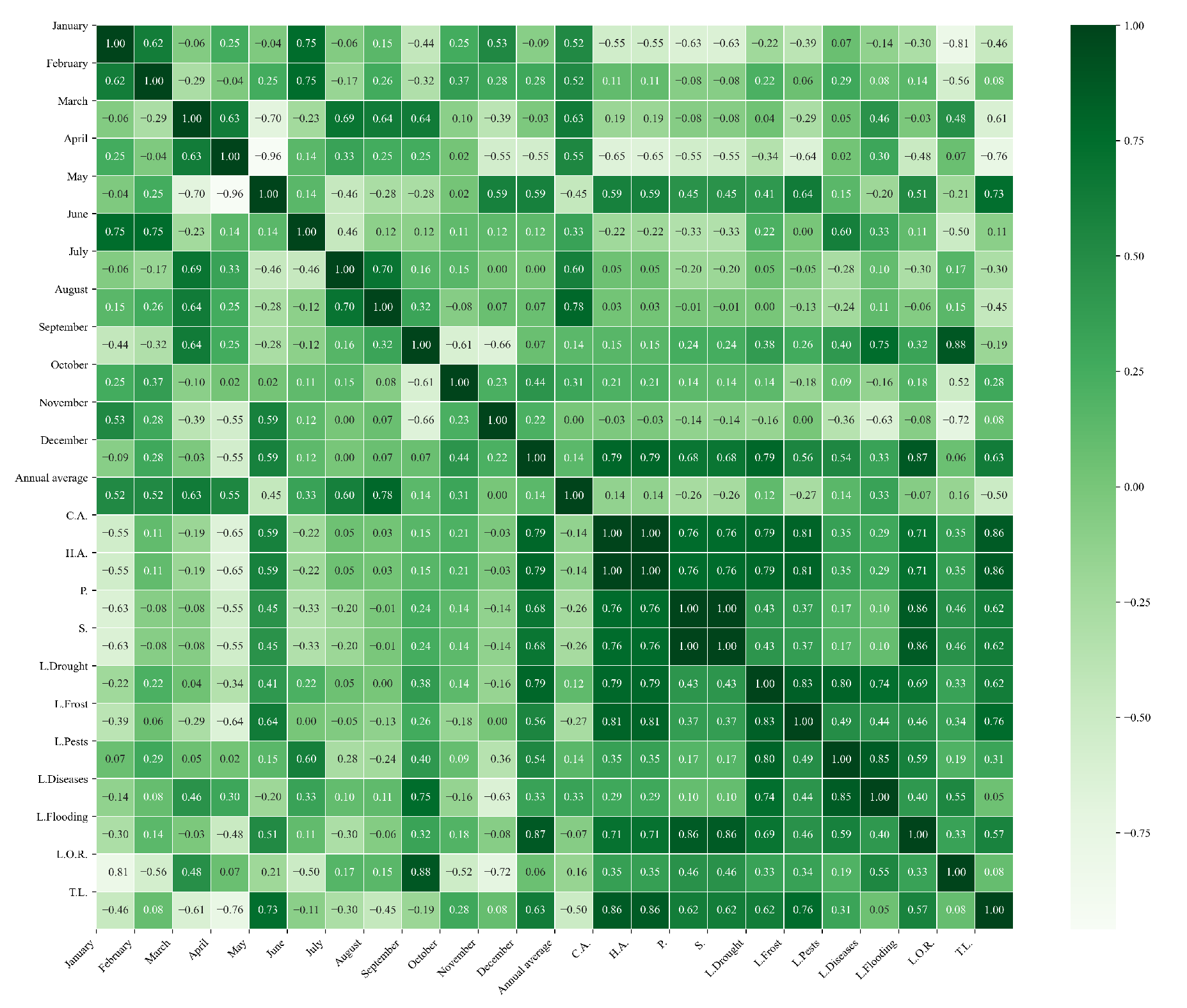
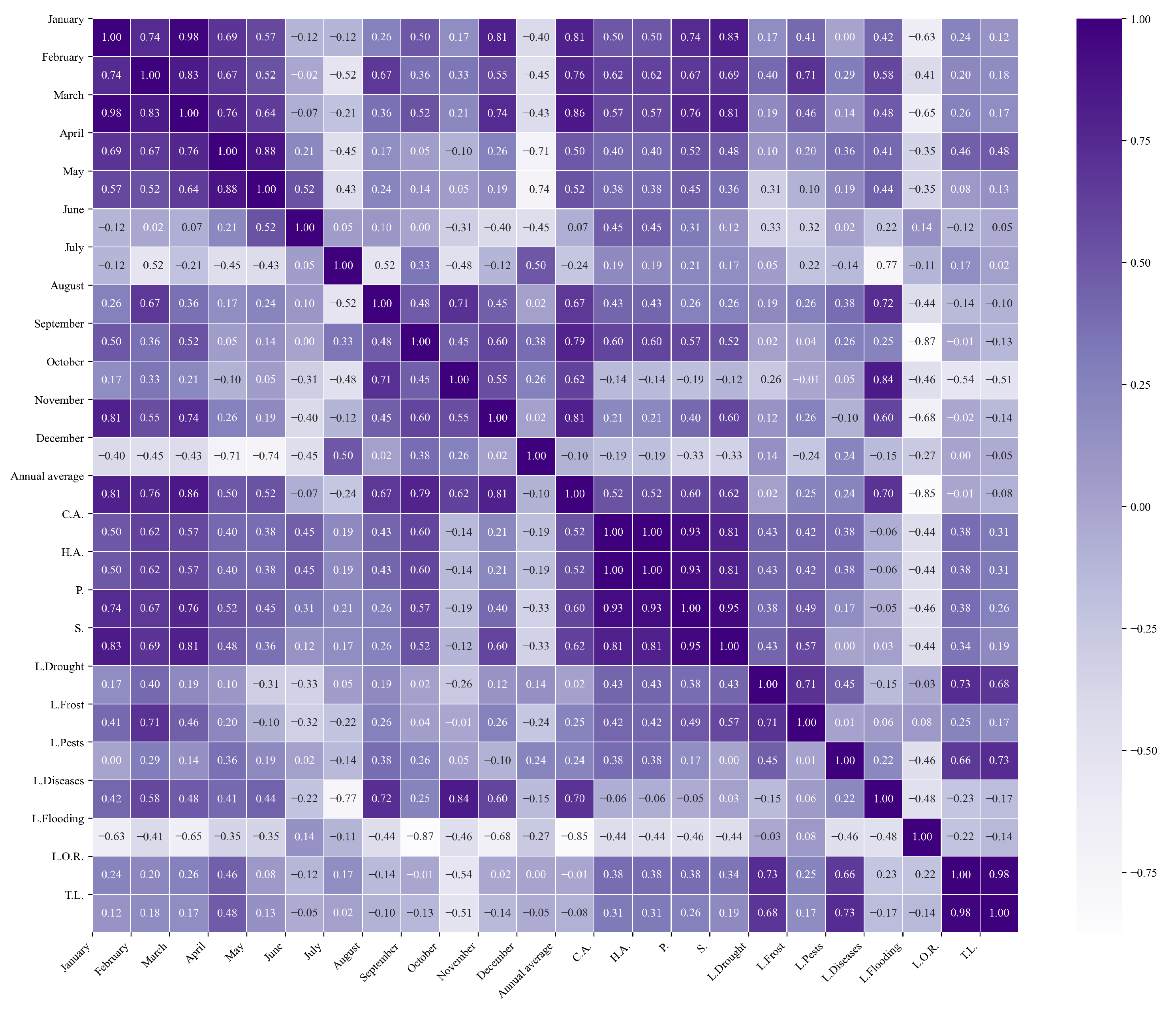
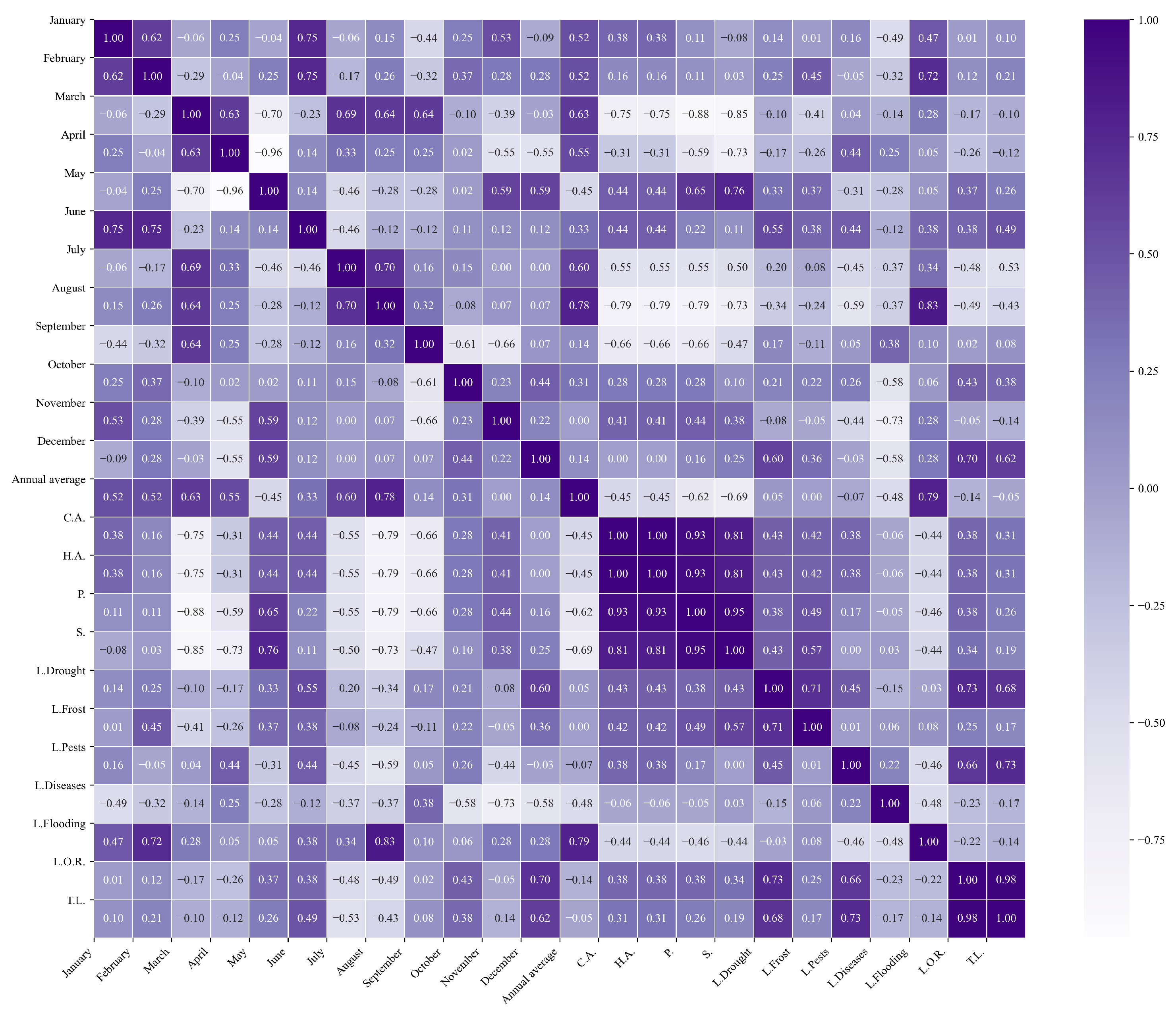
Figure 12.
Heatmap of correlations between monthly maximum temperatures and agricultural variables for quinoa cultivation in the southern zone of Ecuador.
Figure 12.
Heatmap of correlations between monthly maximum temperatures and agricultural variables for quinoa cultivation in the southern zone of Ecuador.
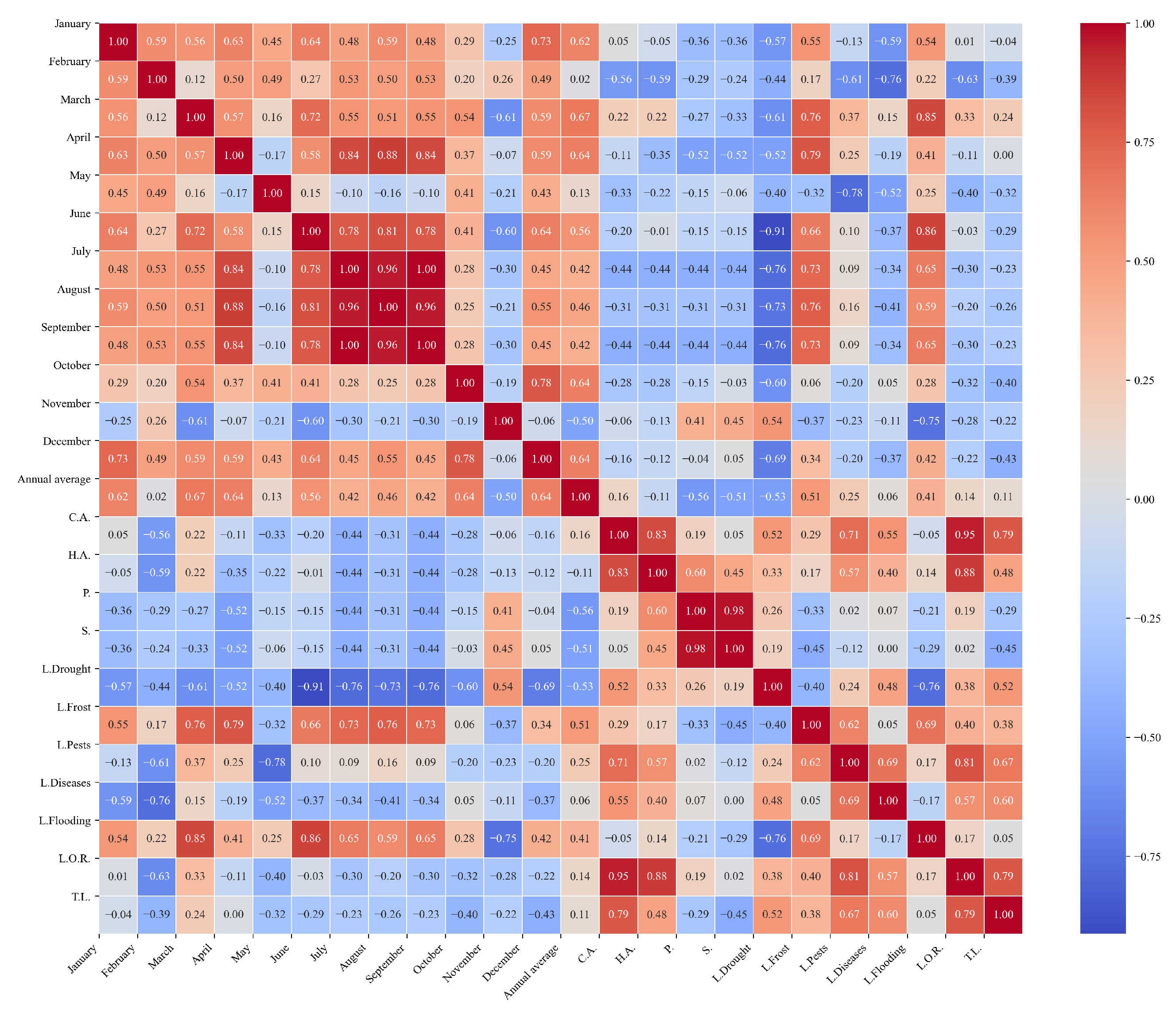
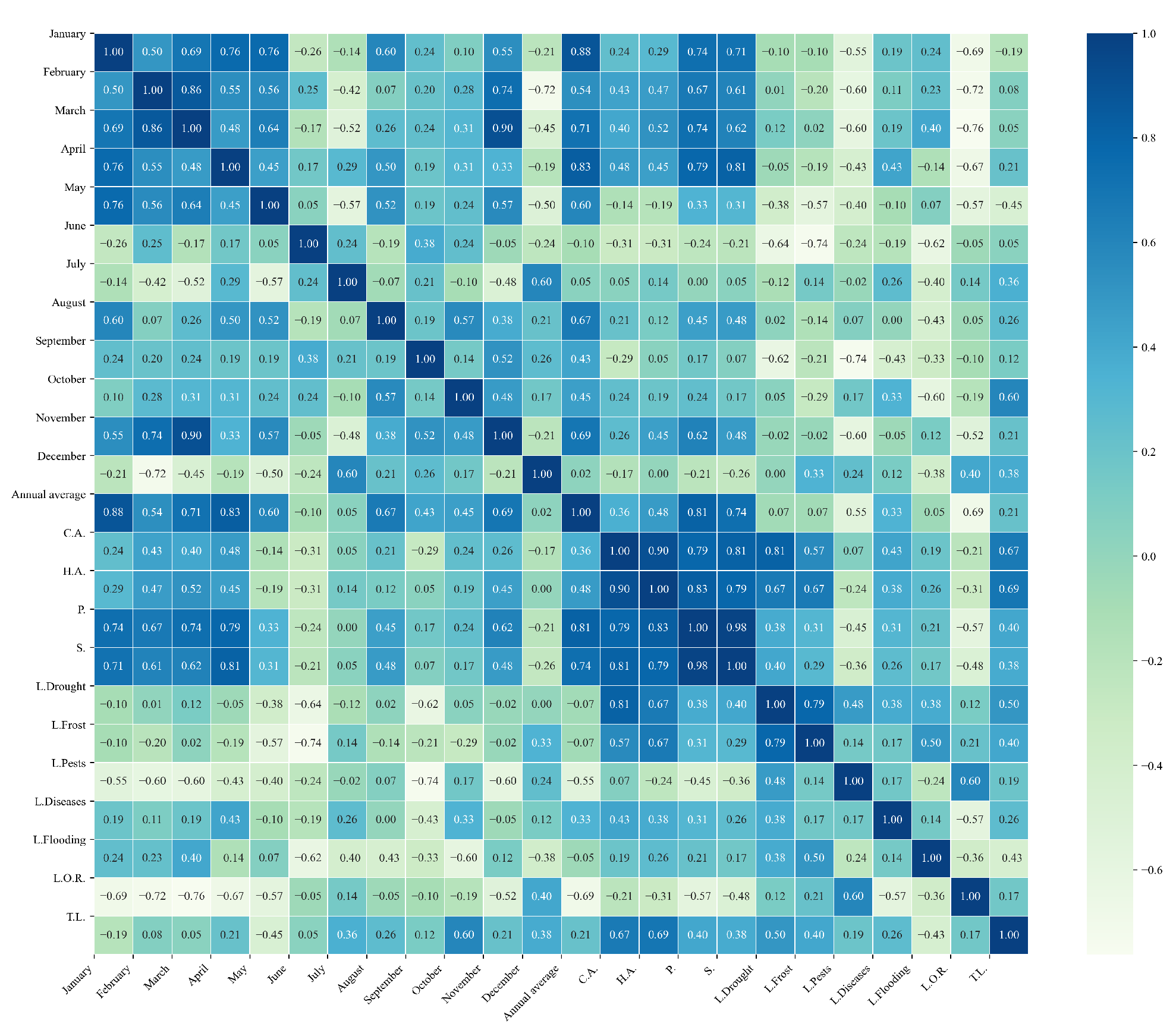
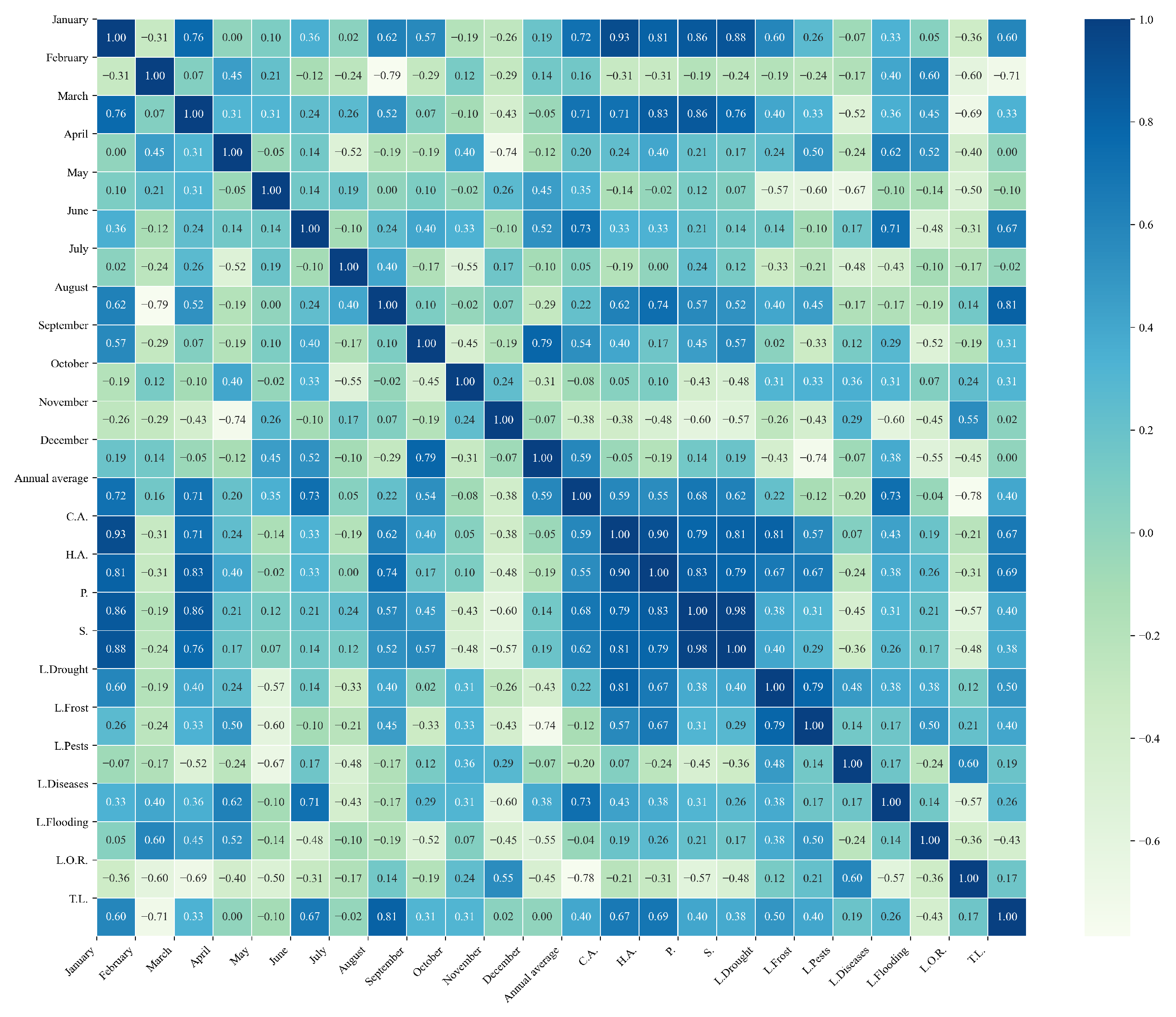
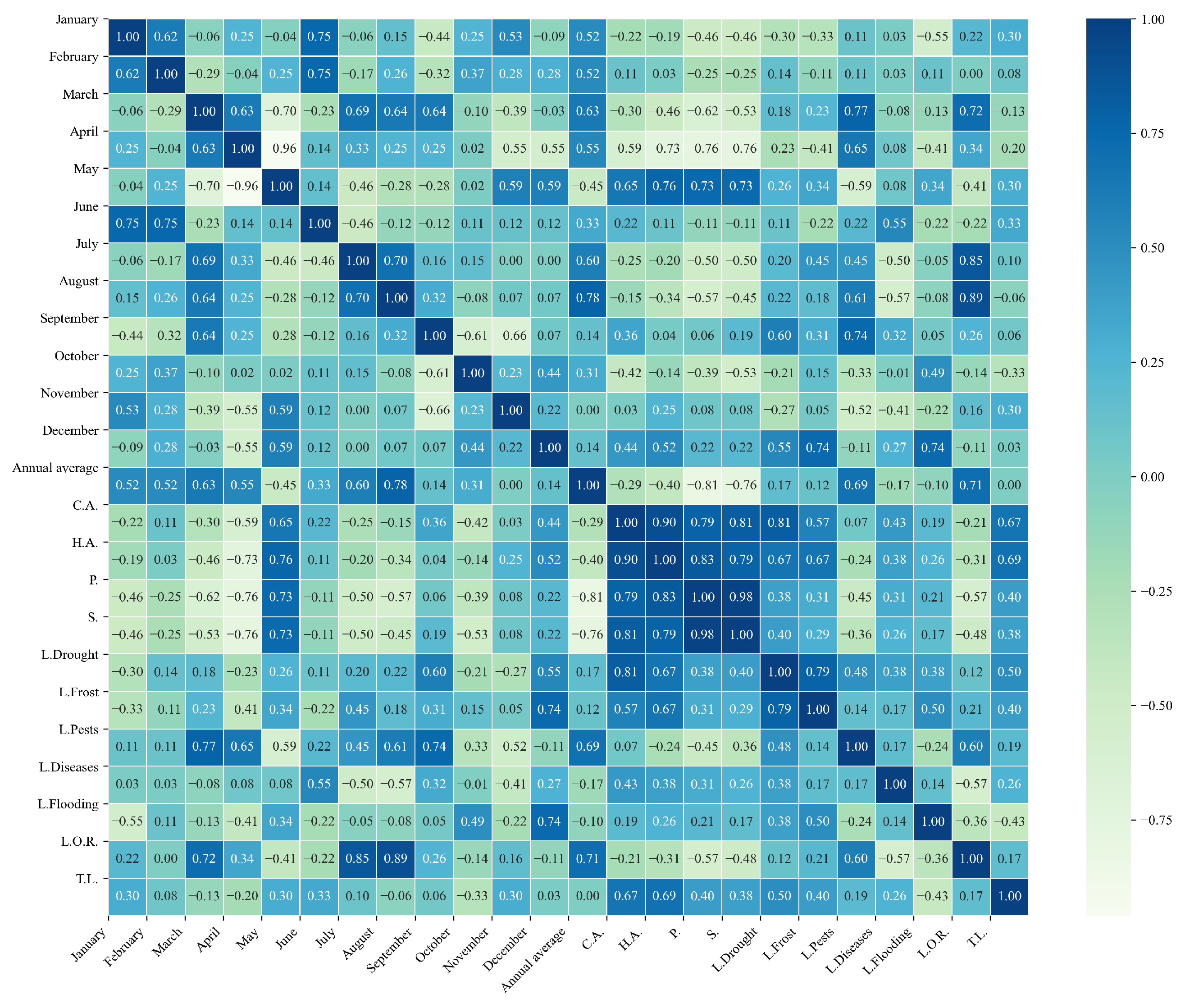
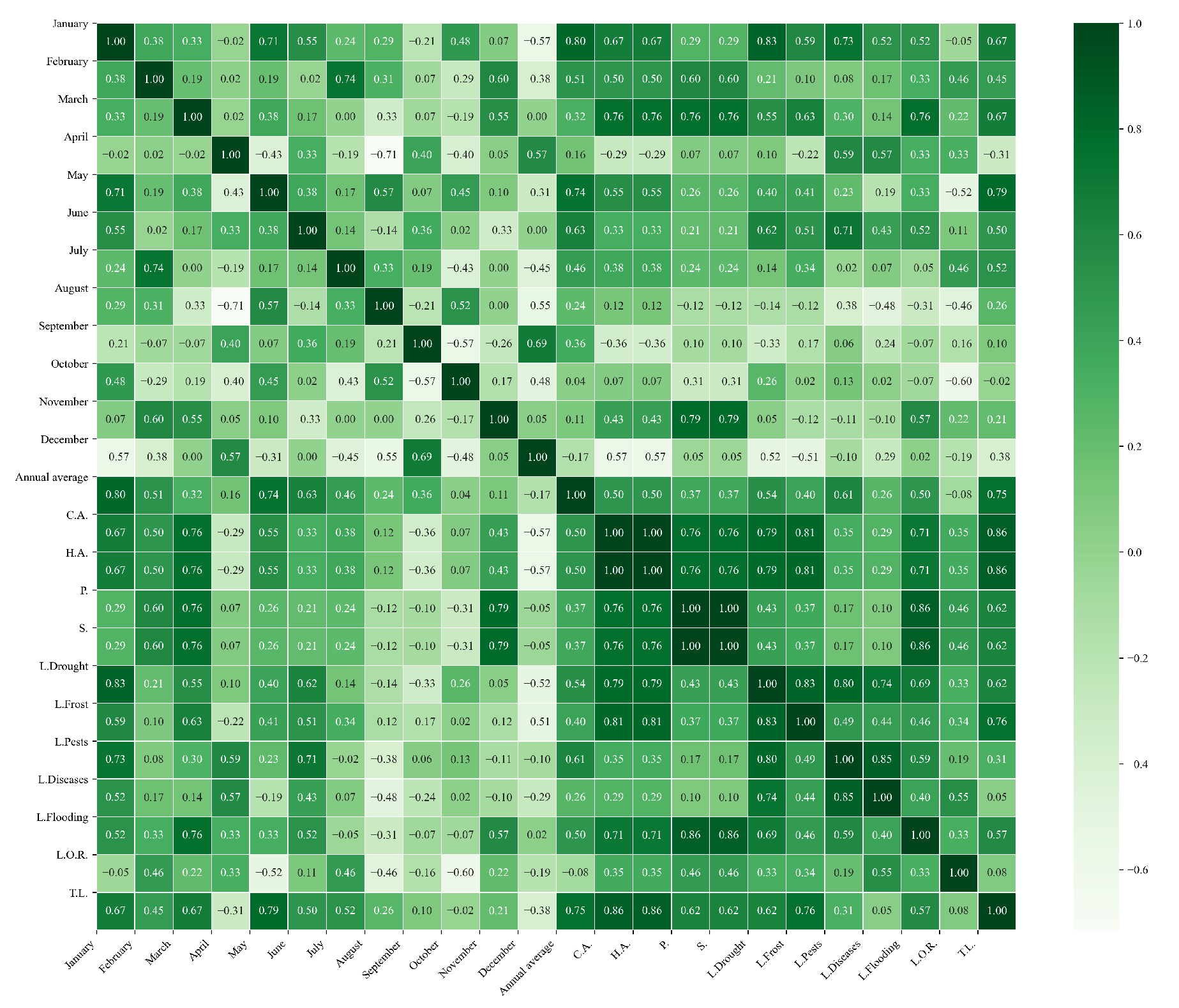
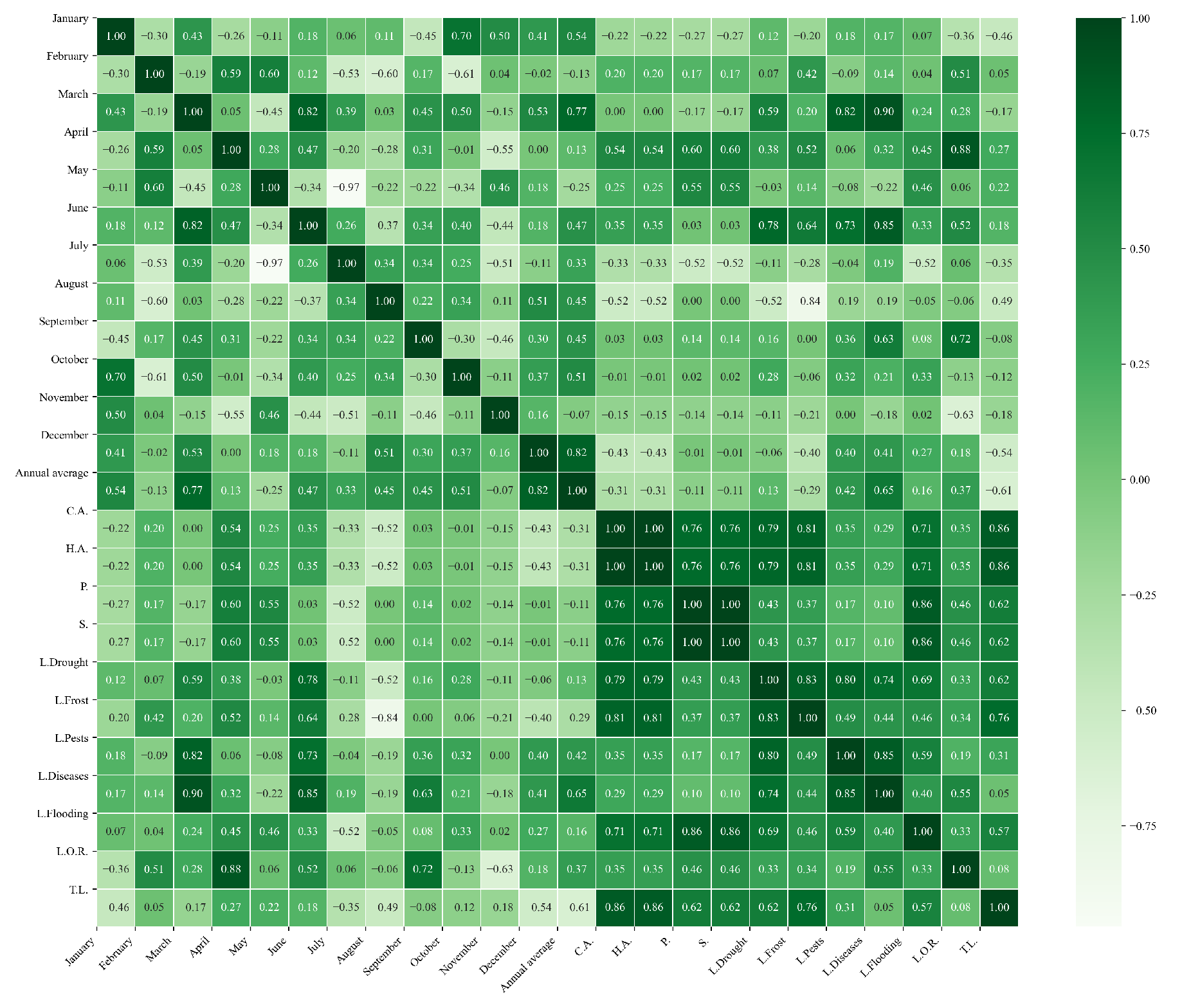
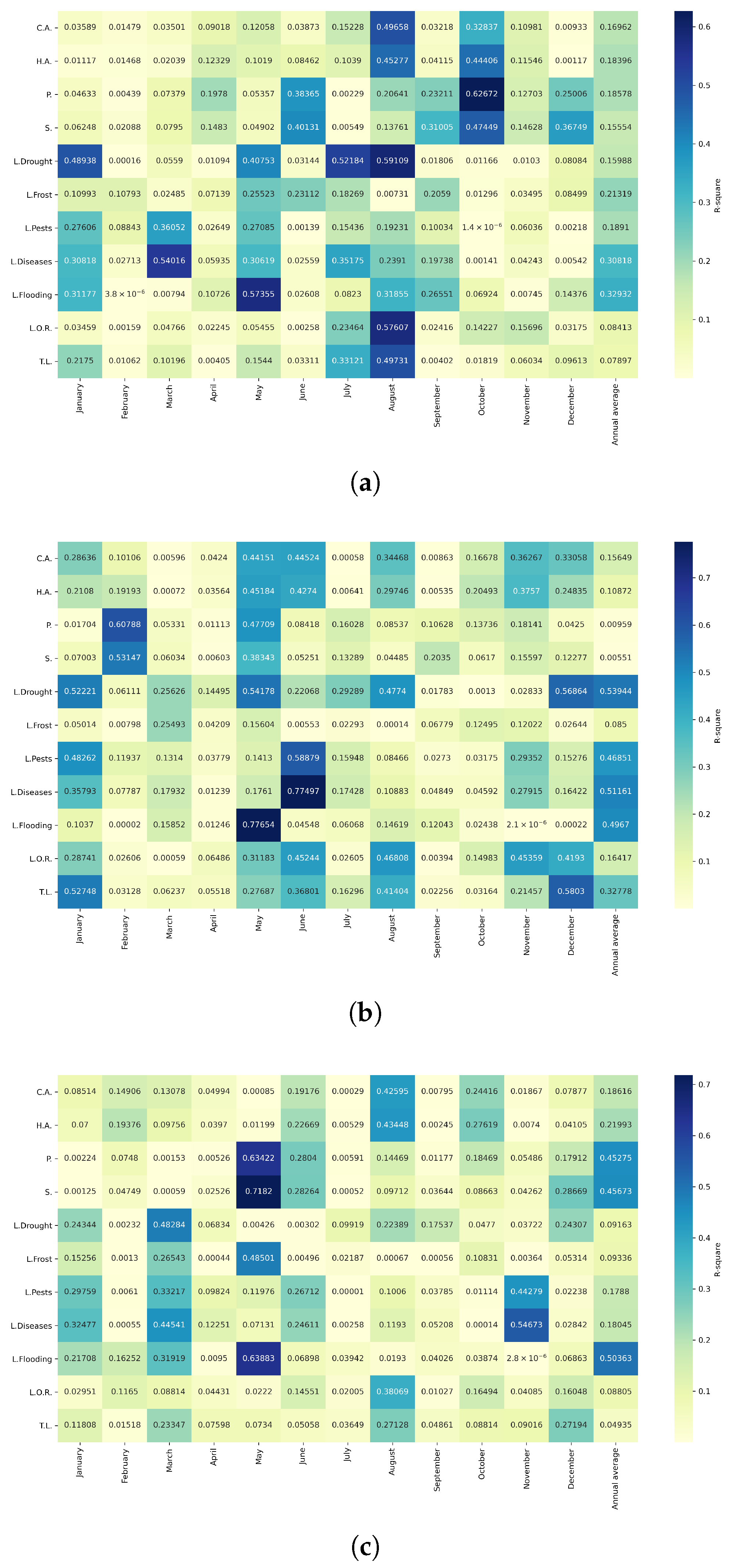
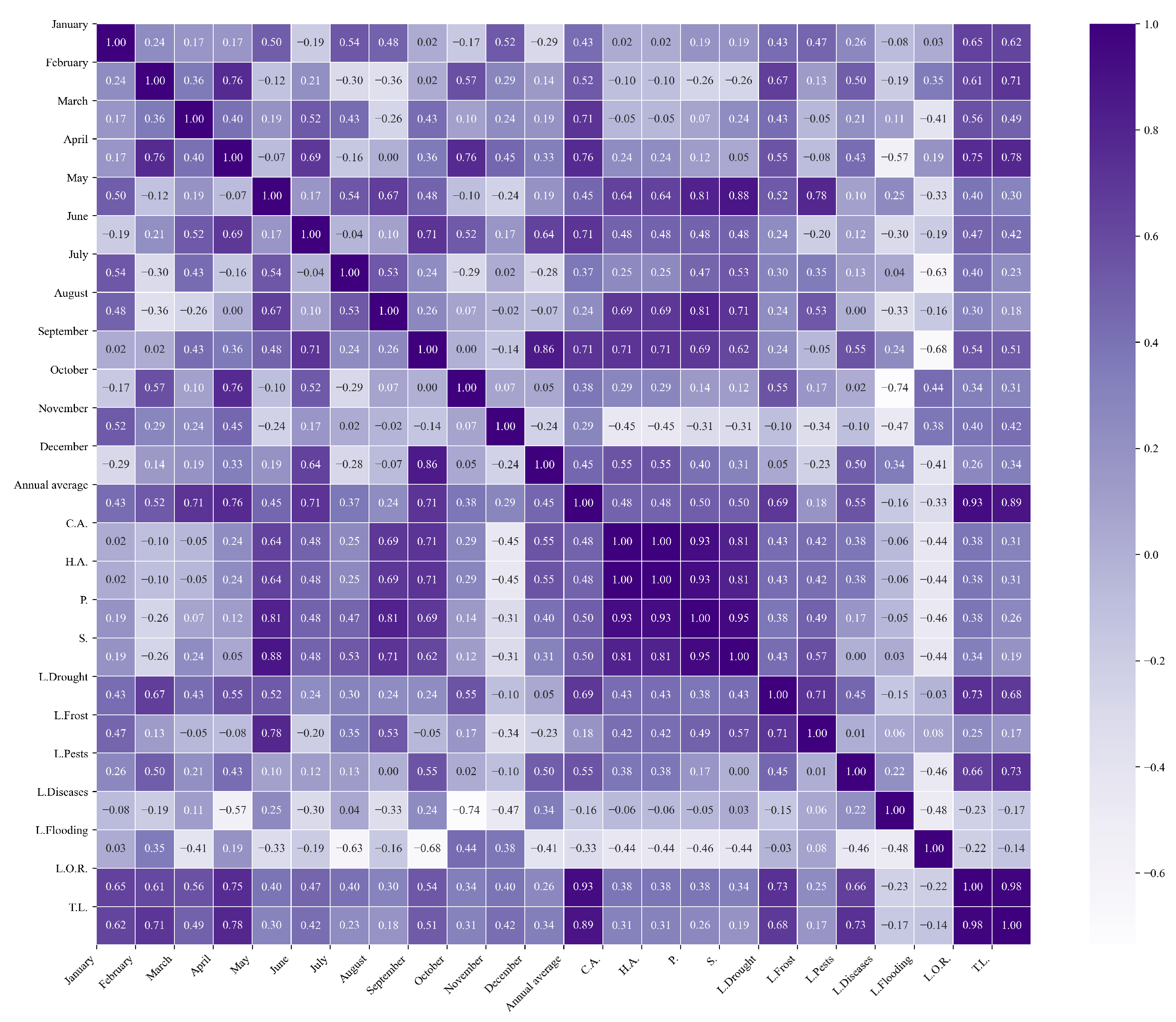
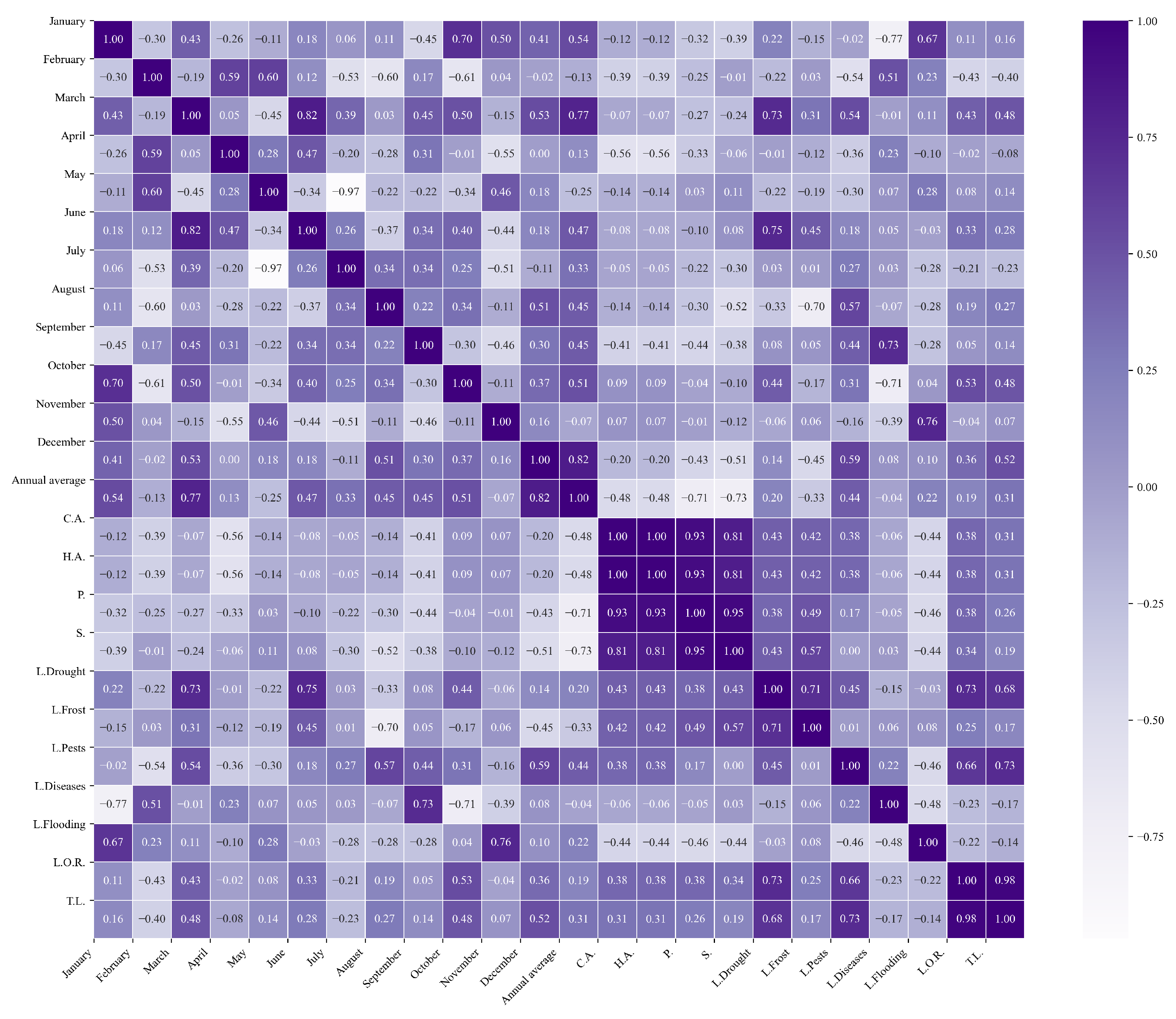
Figure 13.
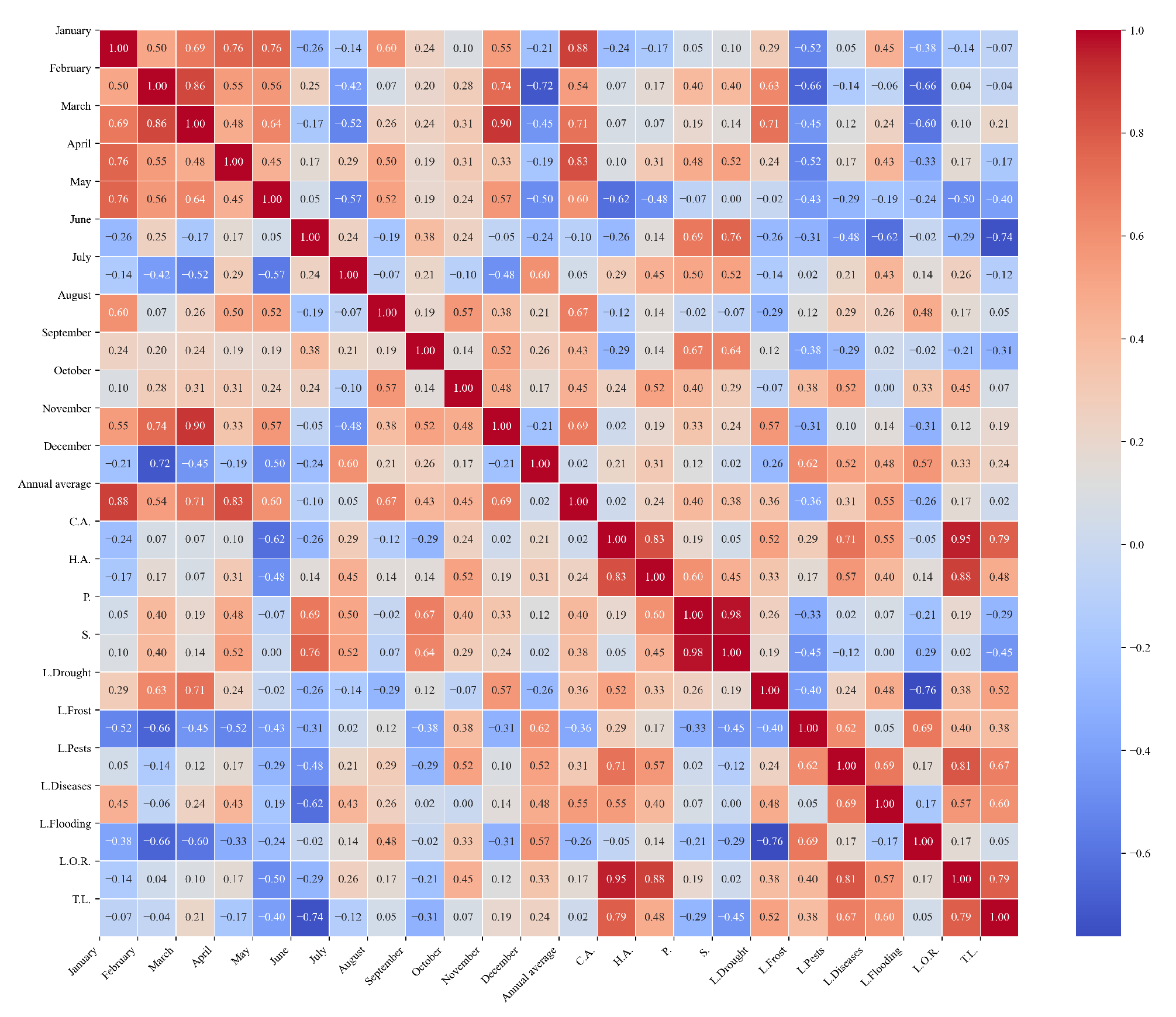
Heatmap of correlations between monthly minimum temperatures and agricultural variables for quinoa cultivation in the northern zone of Ecuador.
Figure 13.
Heatmap of correlations between monthly minimum temperatures and agricultural variables for quinoa cultivation in the northern zone of Ecuador.
Figure 14.
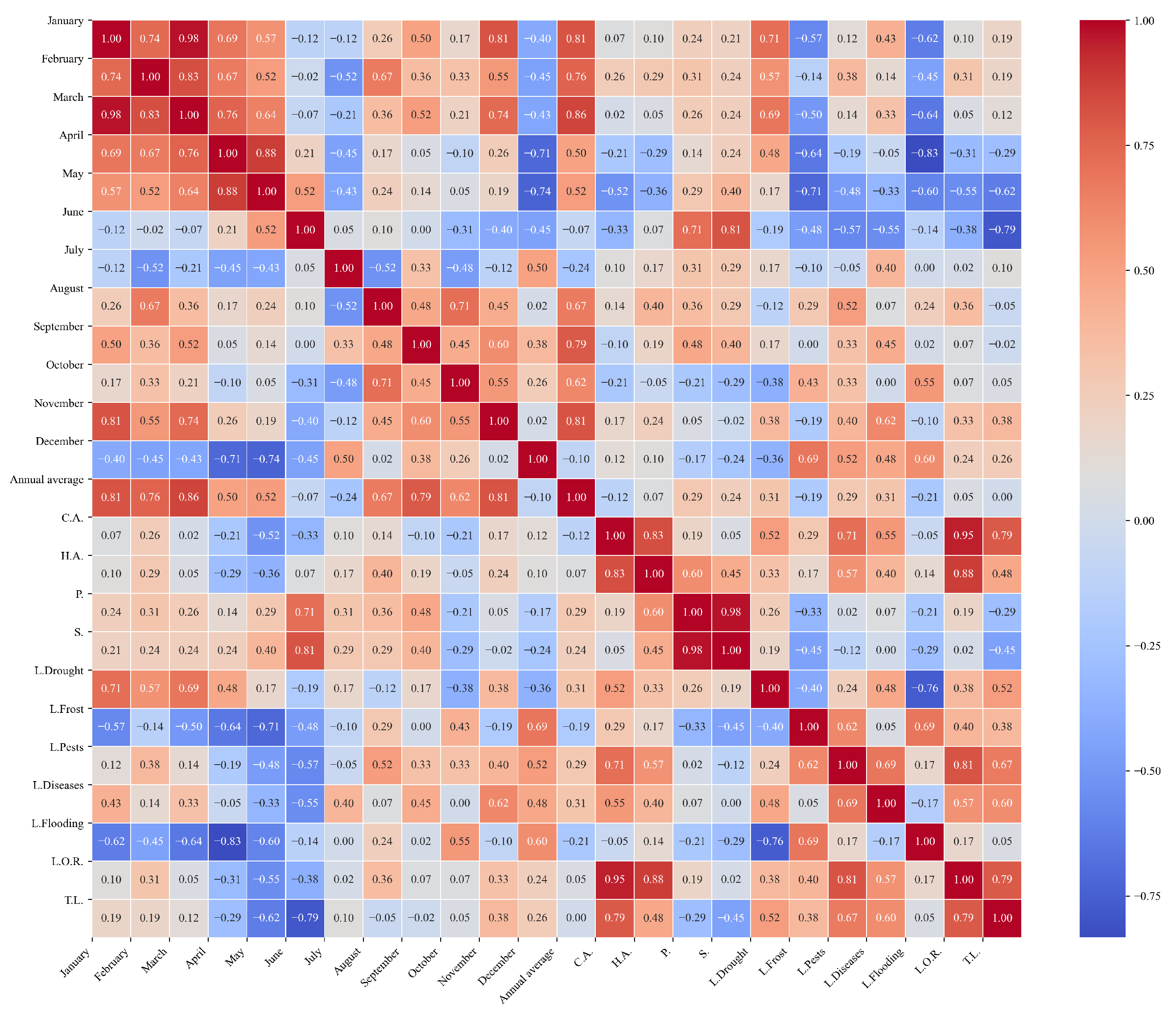
Heatmap of correlations between monthly minimum temperatures and agricultural variables for quinoa cultivation in the central zone of Ecuador.
Figure 14.
Heatmap of correlations between monthly minimum temperatures and agricultural variables for quinoa cultivation in the central zone of Ecuador.
Figure 15.
Heatmap of correlations between monthly minimum temperatures and agricultural variables for quinoa cultivation in the southern zone of Ecuador.
Figure 15.
Heatmap of correlations between monthly minimum temperatures and agricultural variables for quinoa cultivation in the southern zone of Ecuador.
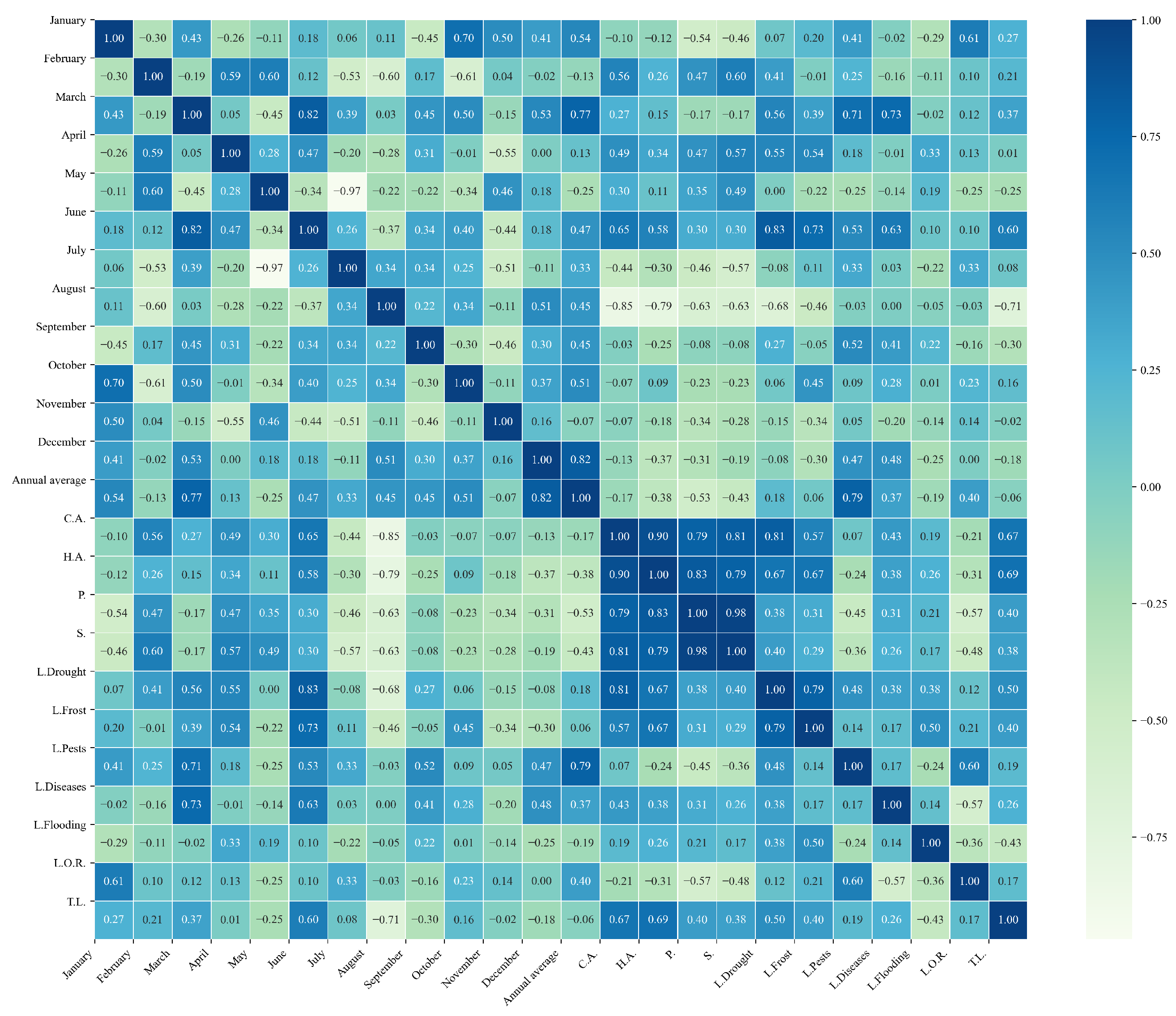
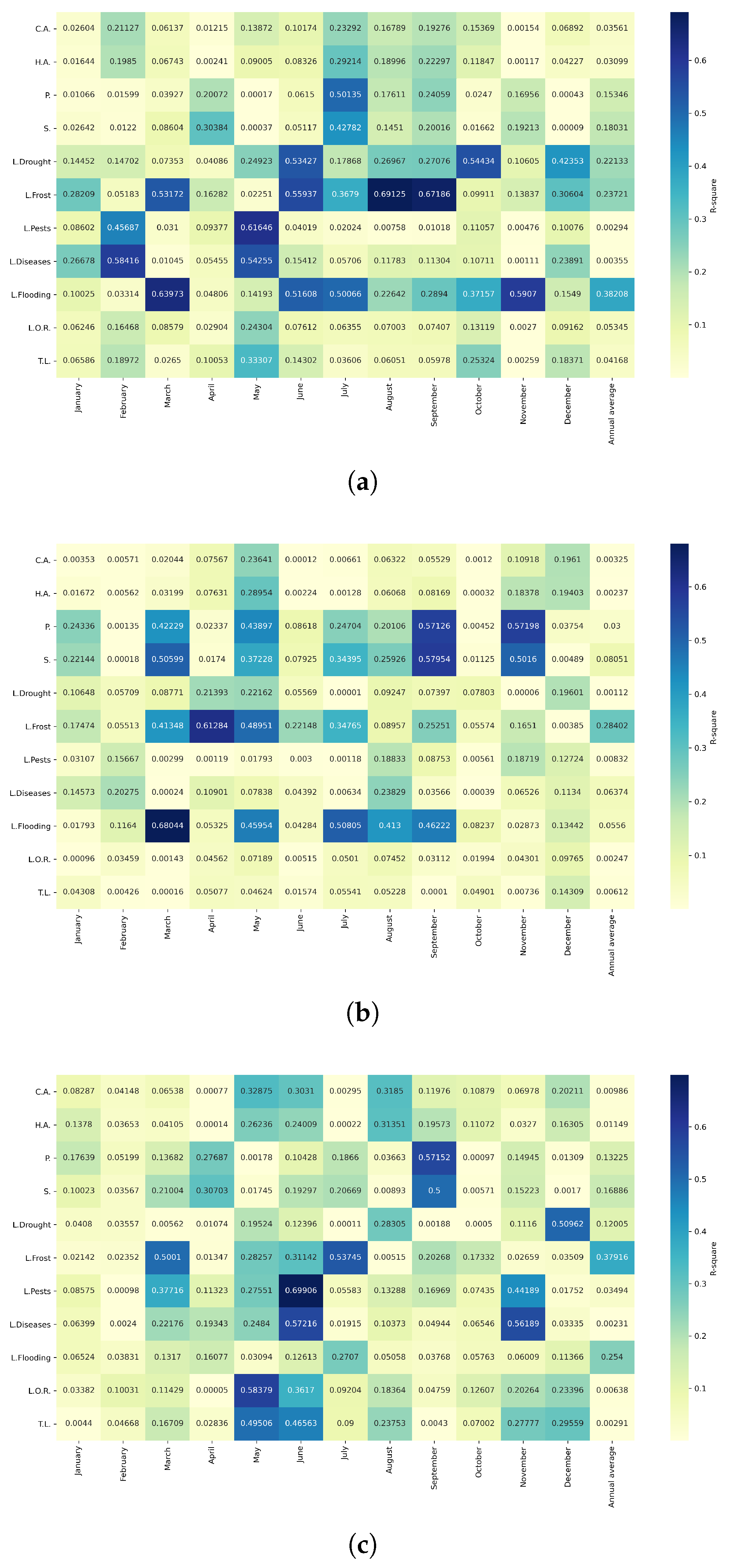
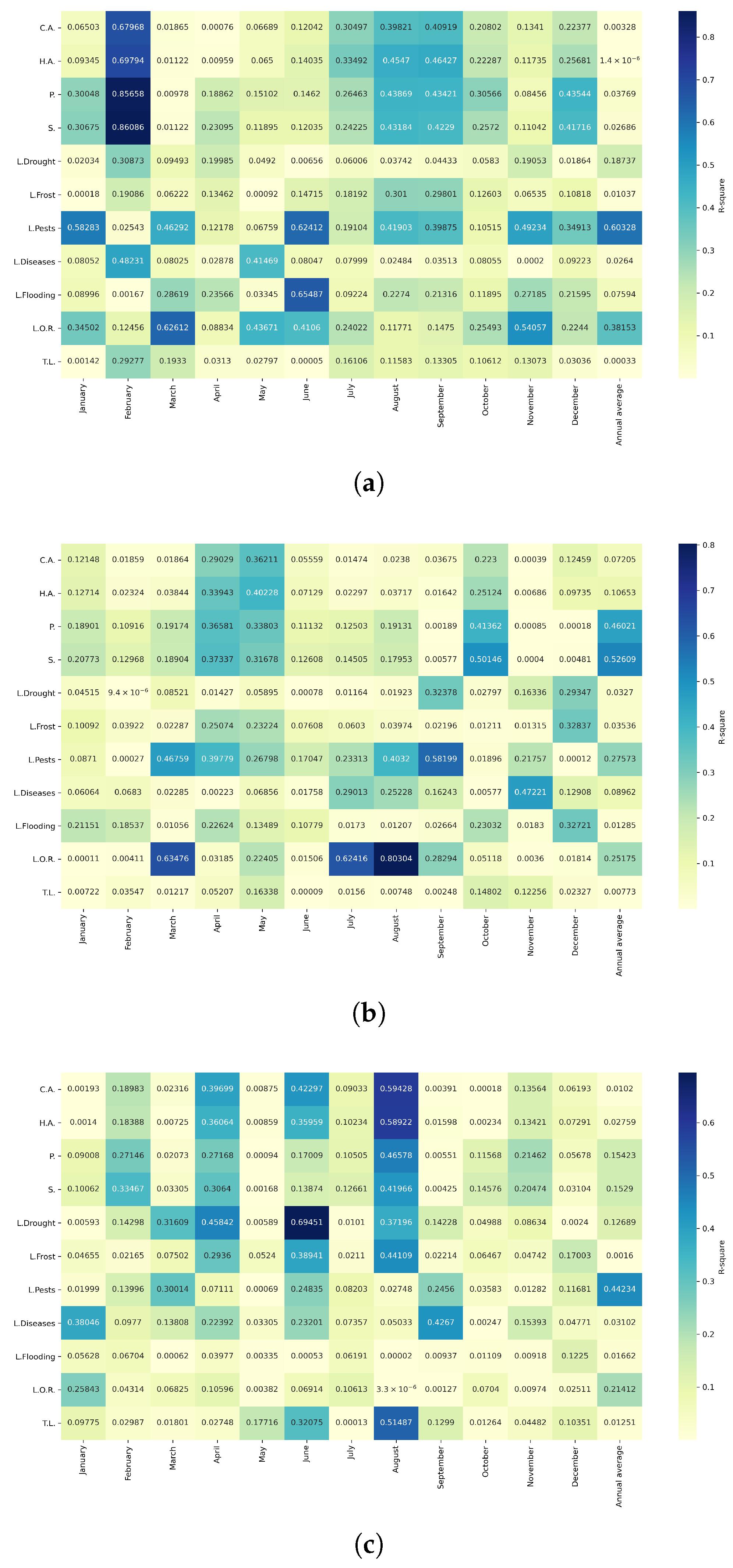
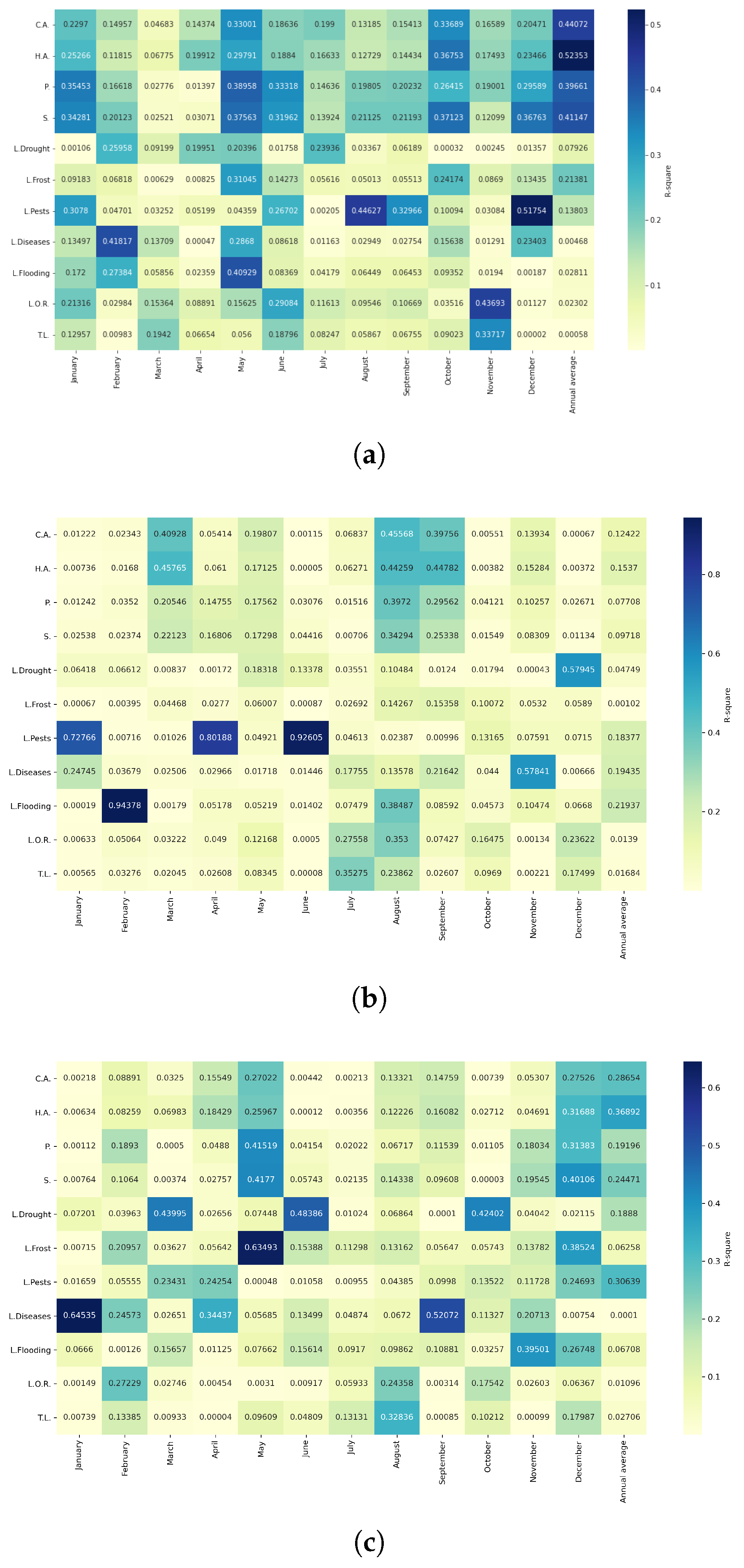
Figure 16.
Heatmap of correlations between monthly average precipitation and agricultural variables for quinoa cultivation in the northern zone of Ecuador.
Figure 16.
Heatmap of correlations between monthly average precipitation and agricultural variables for quinoa cultivation in the northern zone of Ecuador.
Figure 17.
Heatmap of correlations between monthly average precipitation and agricultural variables for quinoa cultivation in the central zone of Ecuador.
Figure 17.
Heatmap of correlations between monthly average precipitation and agricultural variables for quinoa cultivation in the central zone of Ecuador.
Figure 18.
Heatmap of correlations between monthly average precipitation and agricultural variables for quinoa cultivation in the southern zone of Ecuador.
Figure 18.
Heatmap of correlations between monthly average precipitation and agricultural variables for quinoa cultivation in the southern zone of Ecuador.
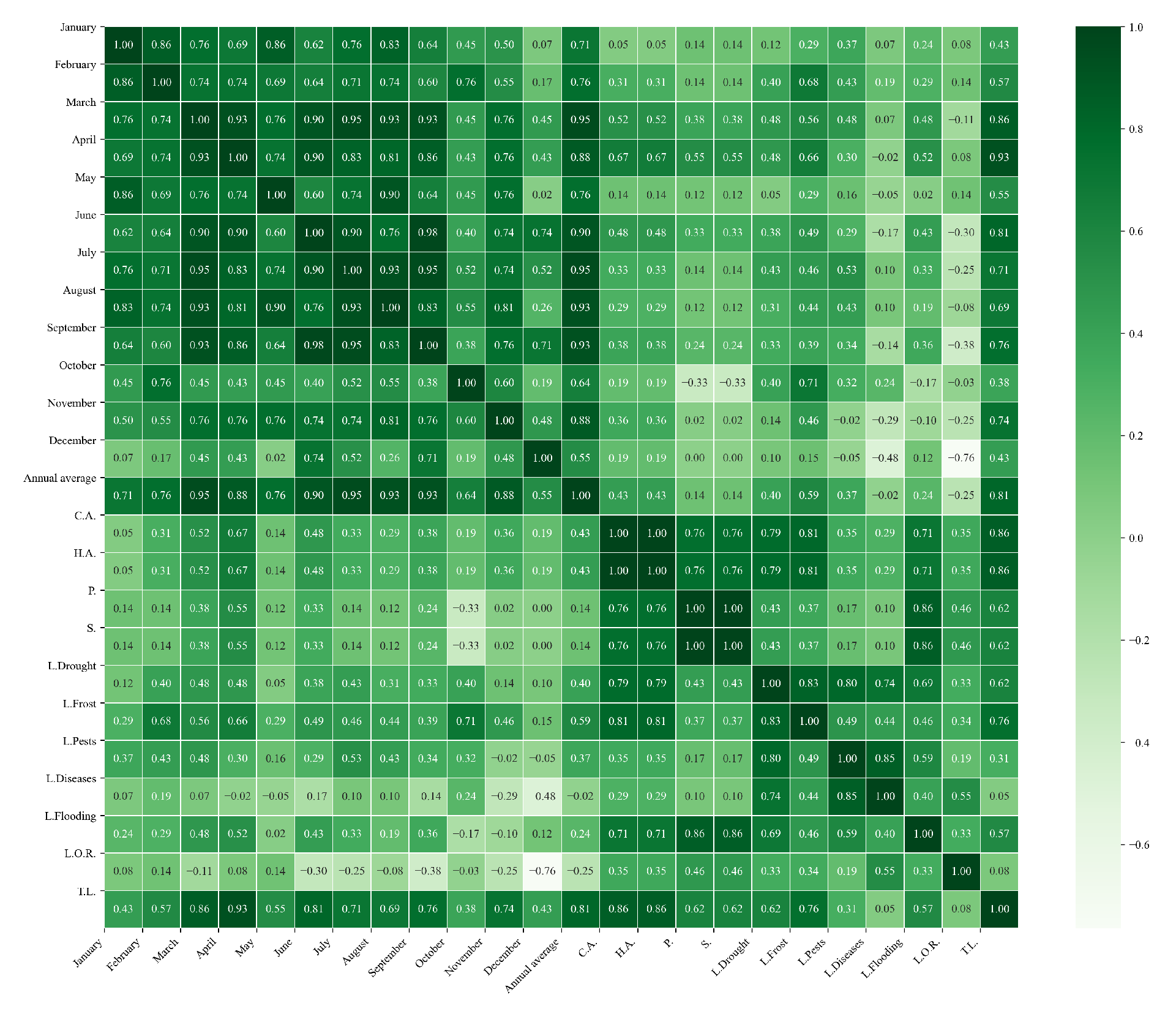
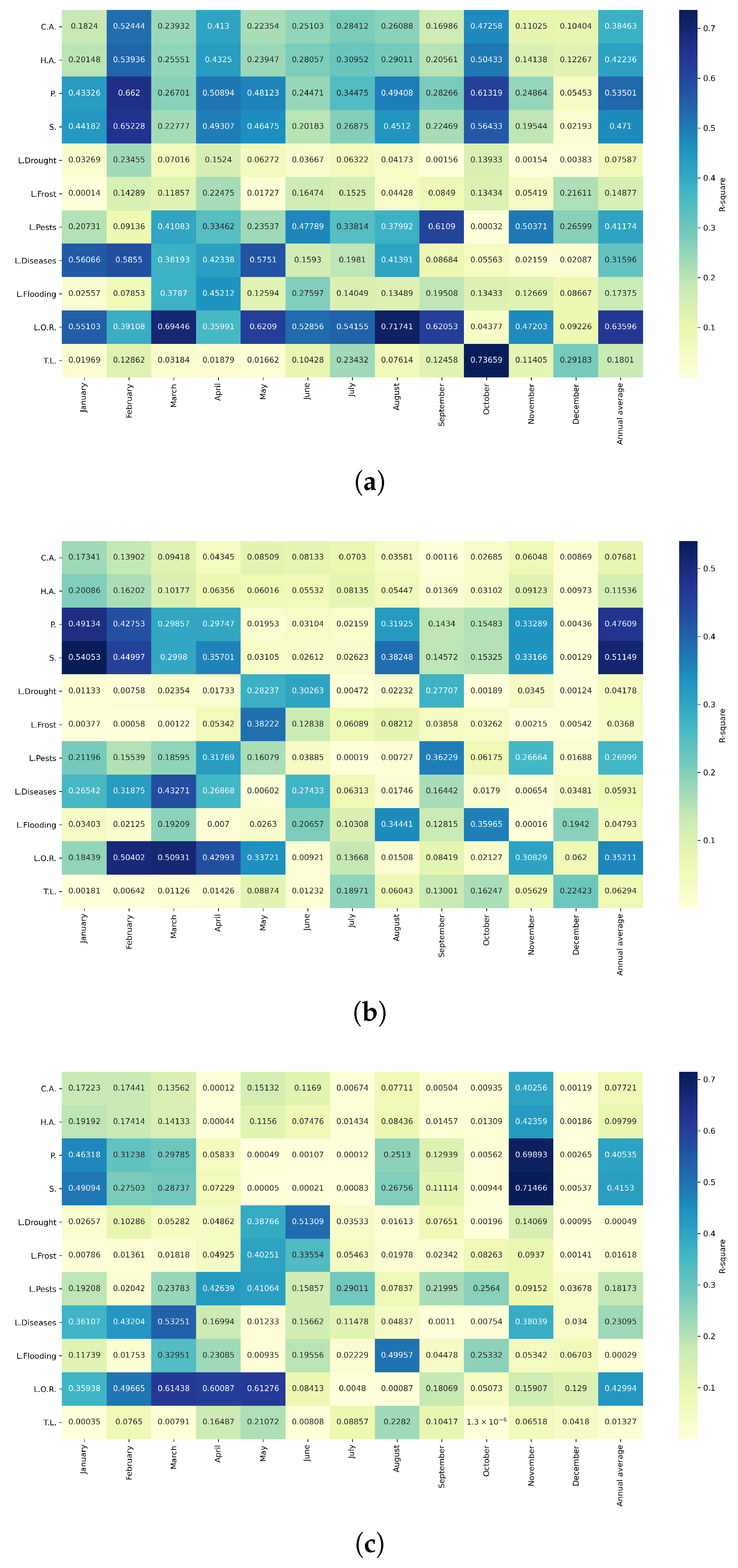
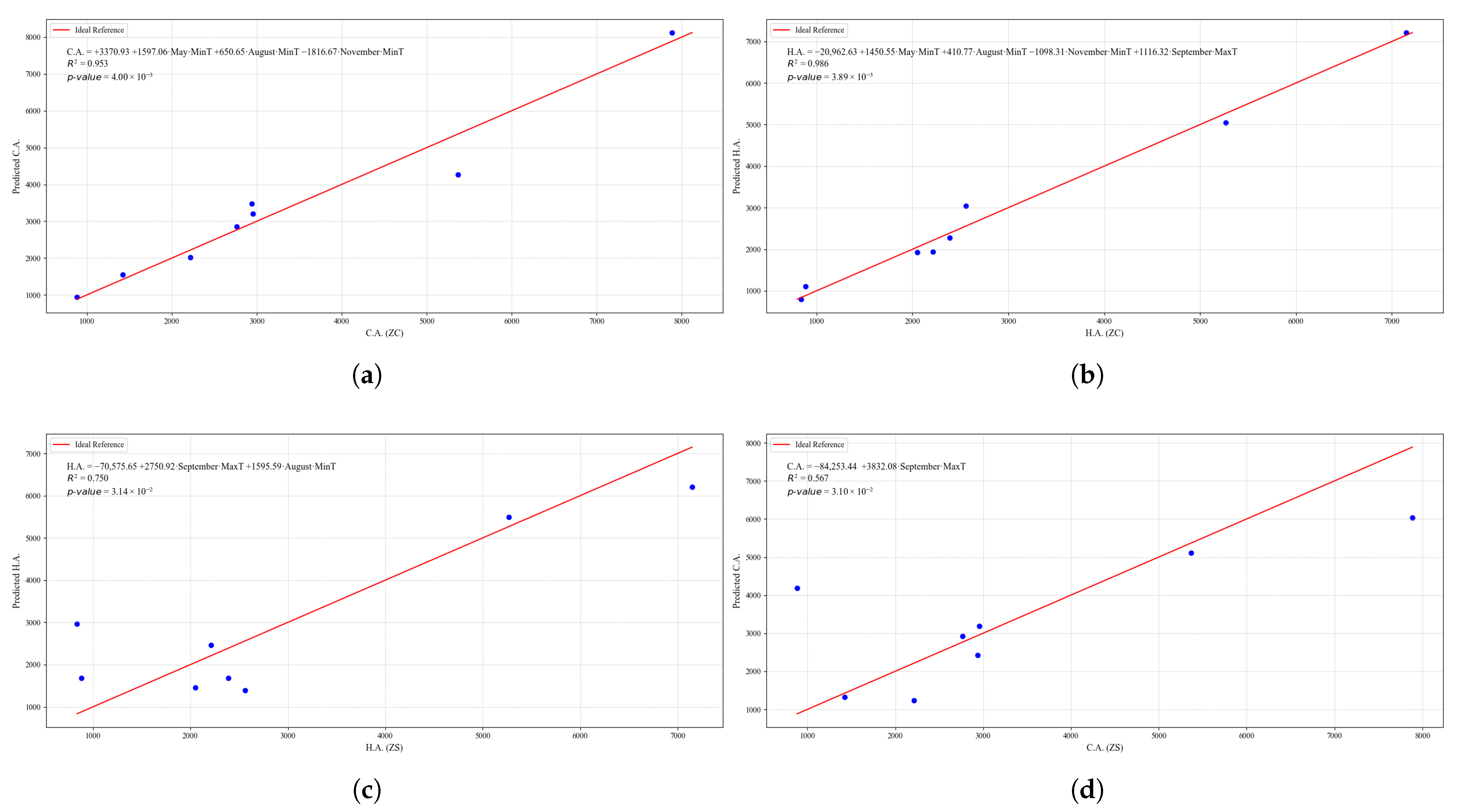
Figure 19.
Heatmaps of simple linear regressions between quinoa cultivation variables and maximum temperatures in the three study zones. (a) Heatmap of values between dependent variables of quinoa cultivation and monthly maximum temperature values in the northern zone. (b) Heatmap of values between dependent variables of quinoa cultivation and monthly maximum temperature values in the central zone. (c) Heatmap of values between dependent variables of quinoa cultivation and monthly maximum temperature values in the southern zone.
Figure 19.
Heatmaps of simple linear regressions between quinoa cultivation variables and maximum temperatures in the three study zones. (a) Heatmap of values between dependent variables of quinoa cultivation and monthly maximum temperature values in the northern zone. (b) Heatmap of values between dependent variables of quinoa cultivation and monthly maximum temperature values in the central zone. (c) Heatmap of values between dependent variables of quinoa cultivation and monthly maximum temperature values in the southern zone.
Figure 20.
Heatmaps of simple linear regressions between quinoa cultivation variables and minimum temperatures in the three study zones. (a) Heatmap of values between dependent variables of quinoa cultivation and monthly minimum temperature values in the northern zone. (b) Heatmap of values between dependent variables of quinoa cultivation and monthly minimum temperature values in the central zone. (c) Heatmap of values between dependent variables of quinoa cultivation and monthly minimum temperature values in the southern zone.
Figure 20.
Heatmaps of simple linear regressions between quinoa cultivation variables and minimum temperatures in the three study zones. (a) Heatmap of values between dependent variables of quinoa cultivation and monthly minimum temperature values in the northern zone. (b) Heatmap of values between dependent variables of quinoa cultivation and monthly minimum temperature values in the central zone. (c) Heatmap of values between dependent variables of quinoa cultivation and monthly minimum temperature values in the southern zone.
Figure 21.
Heatmaps of simple linear regressions between quinoa cultivation variables and average monthly precipitation in the three study zones. (a) Heatmap of values between quinoa cultivation dependent variables and average monthly precipitation in the northern zone. (b) Heatmap of values between quinoa cultivation dependent variables and average monthly precipitation in the central zone. (c) Heatmap of values between quinoa cultivation dependent variables and average monthly precipitation in the southern zone.
Figure 21.
Heatmaps of simple linear regressions between quinoa cultivation variables and average monthly precipitation in the three study zones. (a) Heatmap of values between quinoa cultivation dependent variables and average monthly precipitation in the northern zone. (b) Heatmap of values between quinoa cultivation dependent variables and average monthly precipitation in the central zone. (c) Heatmap of values between quinoa cultivation dependent variables and average monthly precipitation in the southern zone.
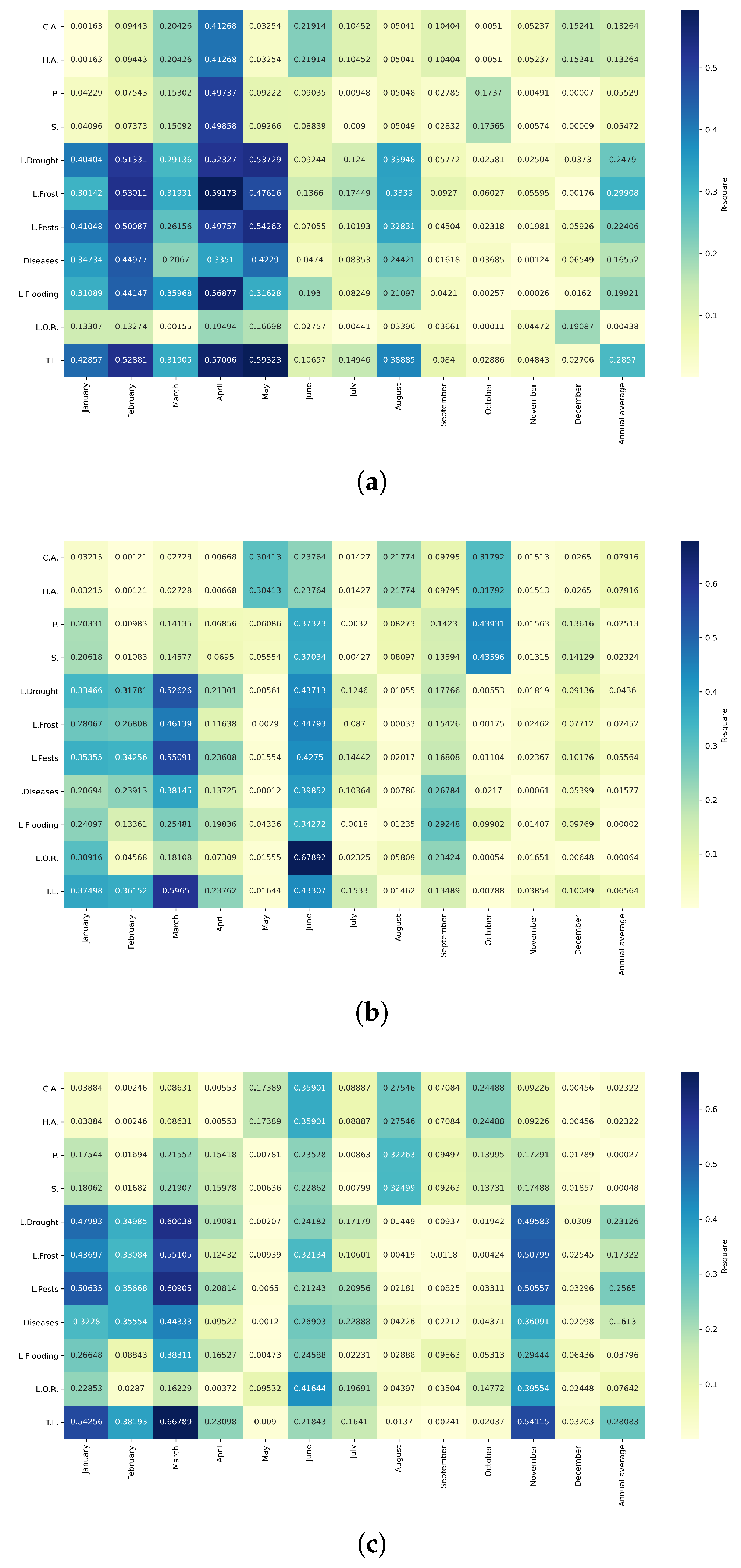
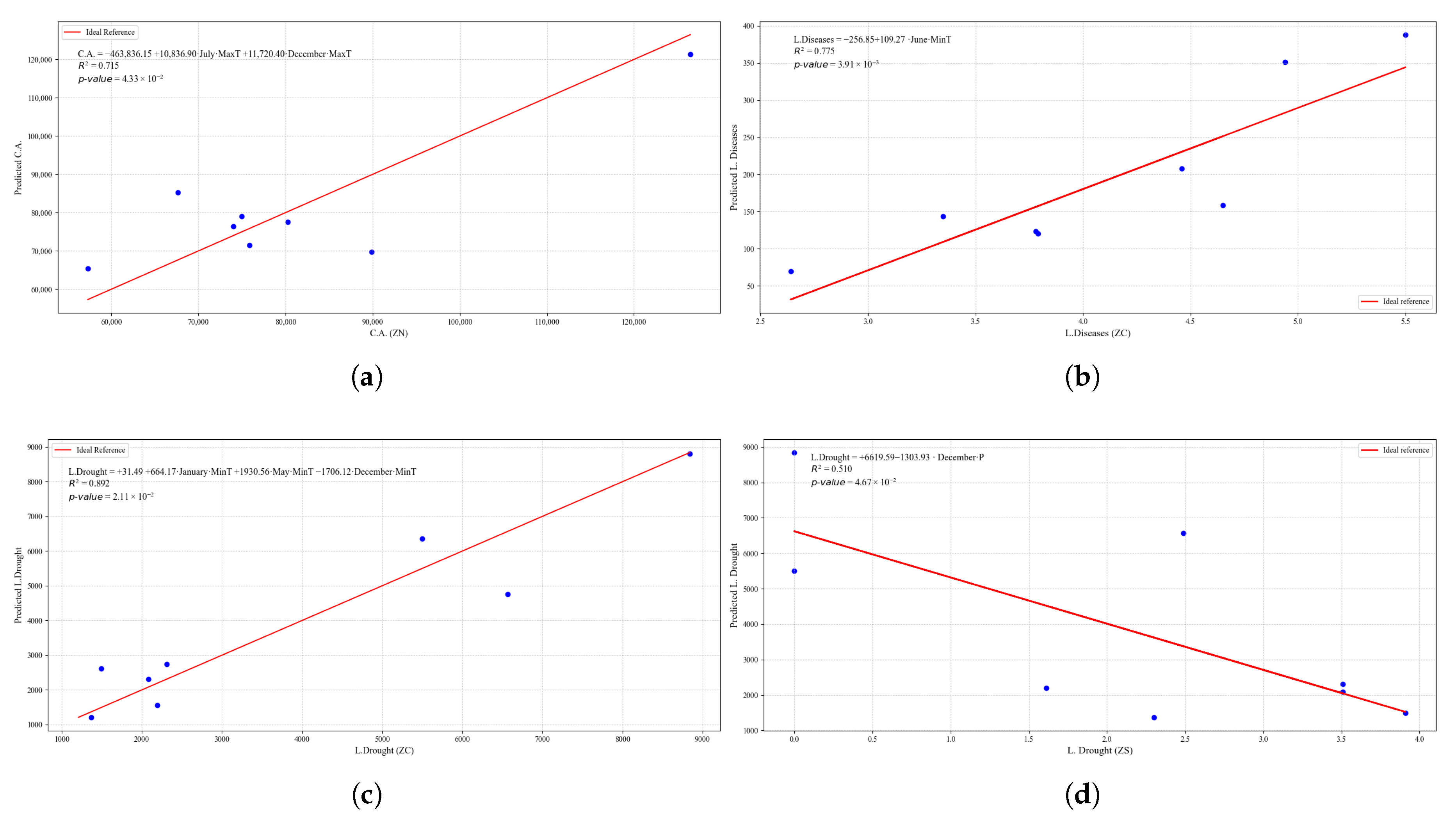
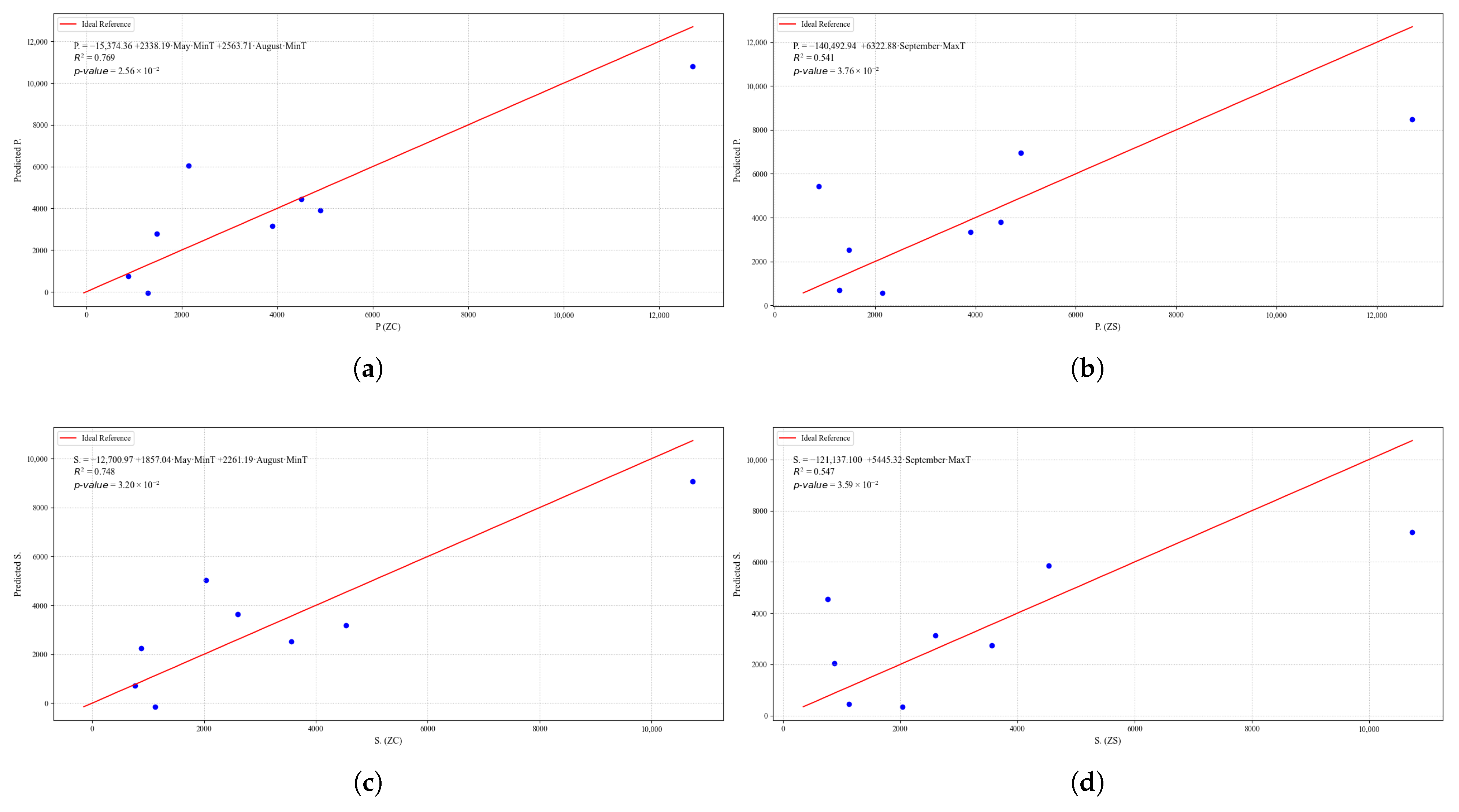
Figure 22.
Simple linear regression models between quinoa crop variables and average climatic variables in the three study zones, selected for their relevance and statistical significance. (a) Linear regression model of the C.A. variable in the central zone. (b) Linear regression model of the H.A. variable in the central zone. (c) Linear regression model of the H.A. variable in the southern zone. (d) Linear regression model of the C.A. variable in the southern zone.
Figure 22.
Simple linear regression models between quinoa crop variables and average climatic variables in the three study zones, selected for their relevance and statistical significance. (a) Linear regression model of the C.A. variable in the central zone. (b) Linear regression model of the H.A. variable in the central zone. (c) Linear regression model of the H.A. variable in the southern zone. (d) Linear regression model of the C.A. variable in the southern zone.
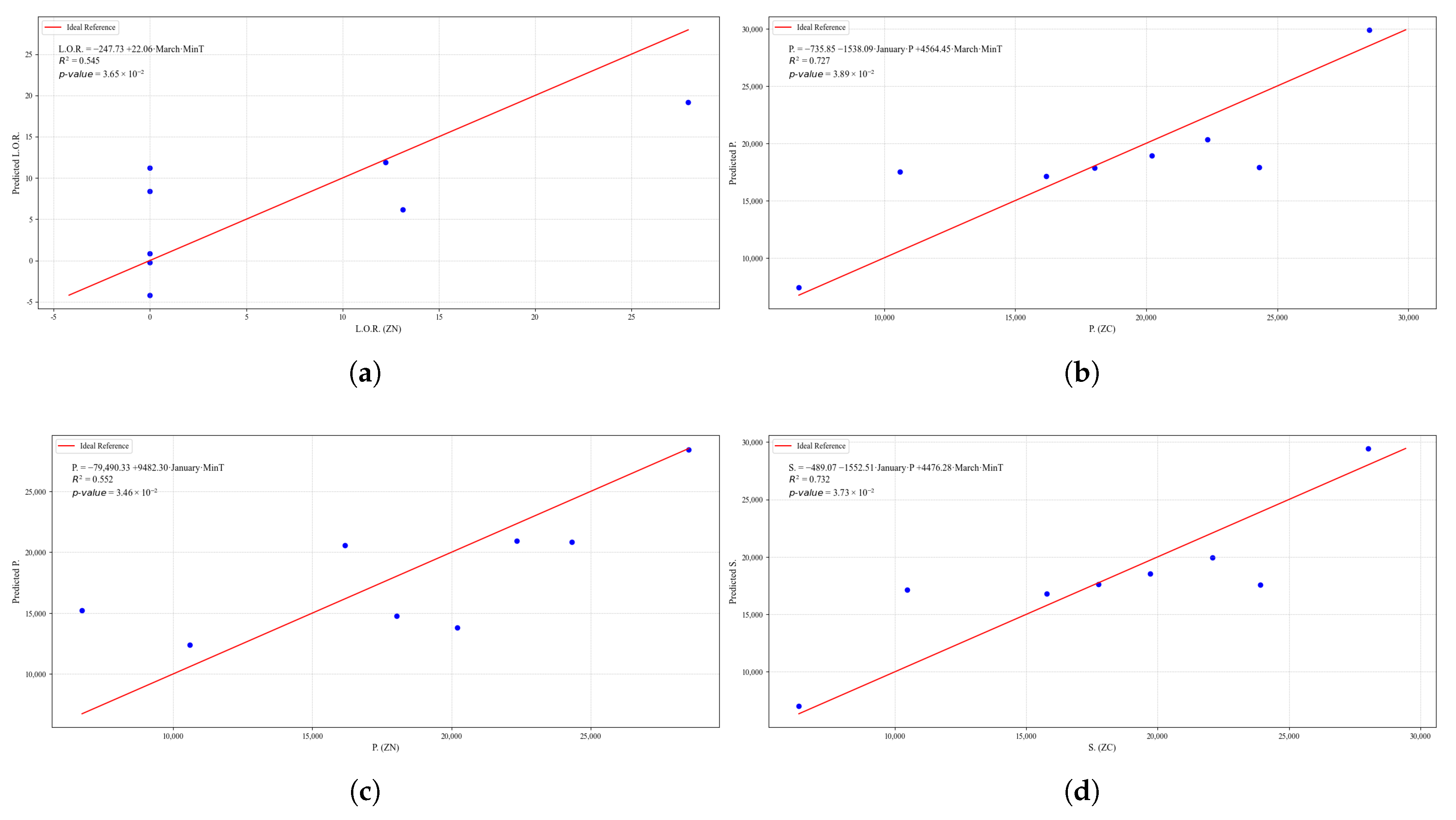
Figure 23.
Simple linear regression models between quinoa crop variables and average climatic variables in the three study zones, selected for their relevance and statistical significance. (a) Linear regression model of the tP. variable in the central zone. (b) Linear regression model of the P. variable in the southern zone. (c) Linear regression model of the S. variable in the central zone. (d) Linear regression model of the S. variable in the southern zone.
Figure 23.
Simple linear regression models between quinoa crop variables and average climatic variables in the three study zones, selected for their relevance and statistical significance. (a) Linear regression model of the tP. variable in the central zone. (b) Linear regression model of the P. variable in the southern zone. (c) Linear regression model of the S. variable in the central zone. (d) Linear regression model of the S. variable in the southern zone.
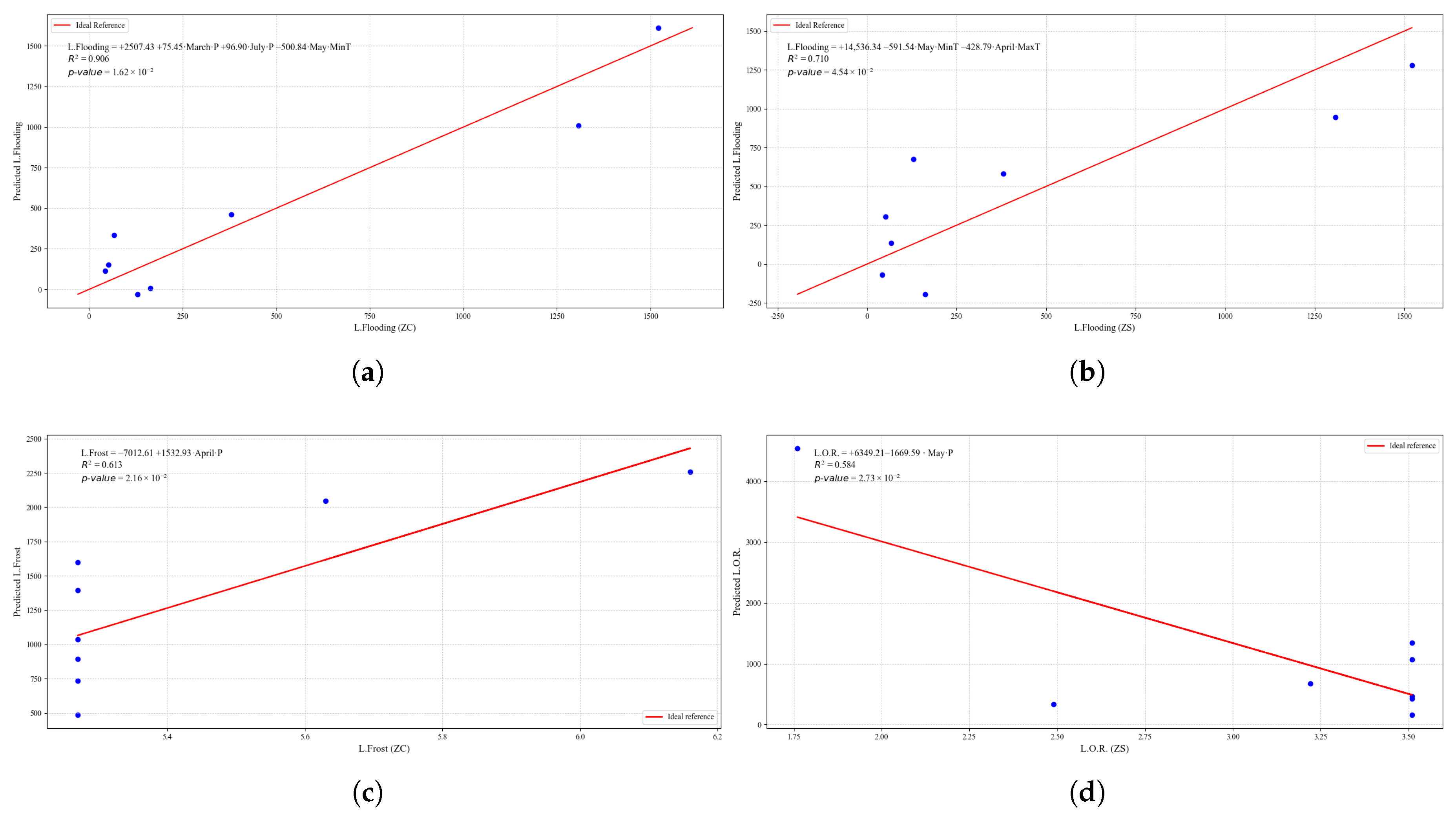
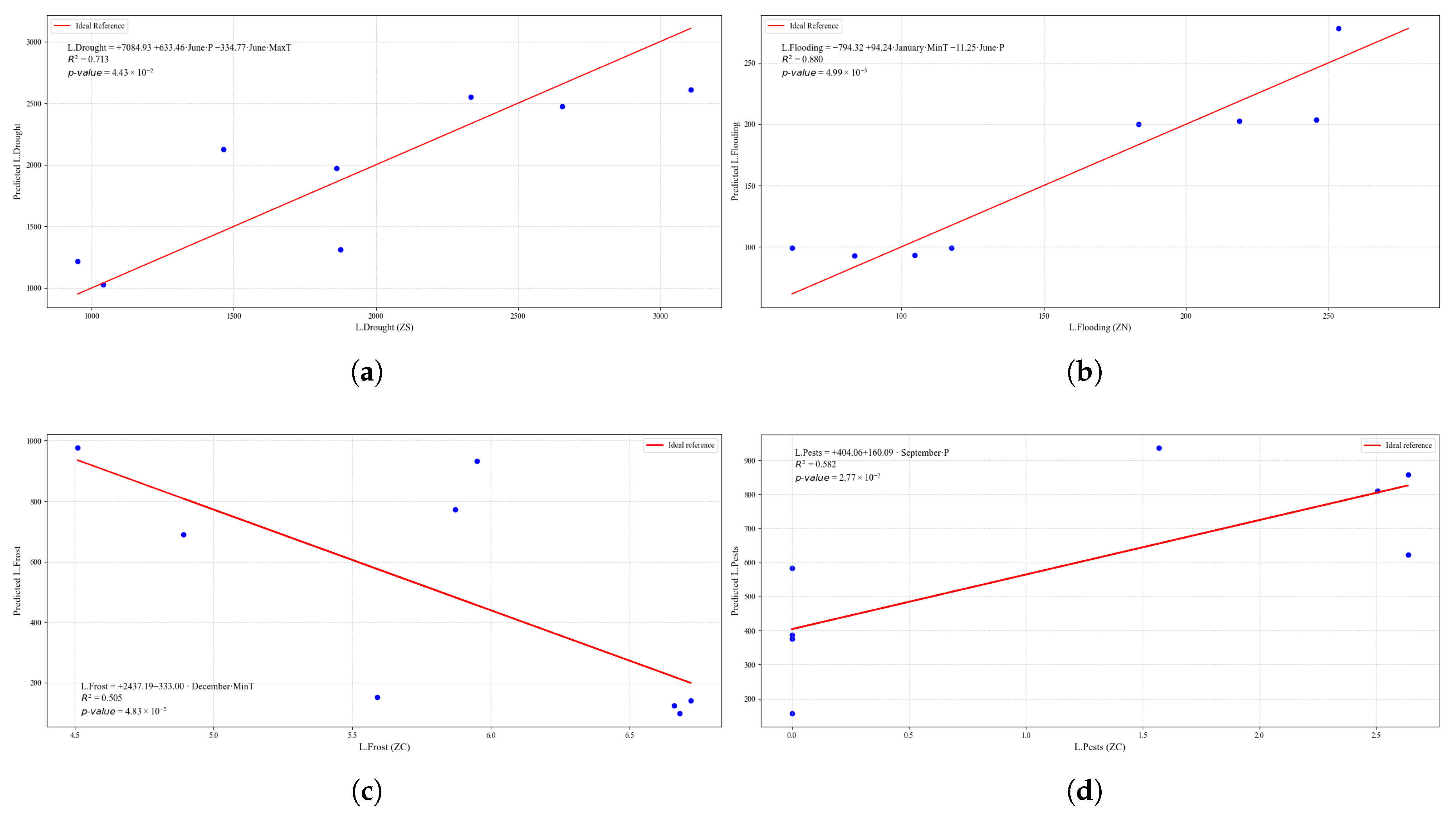
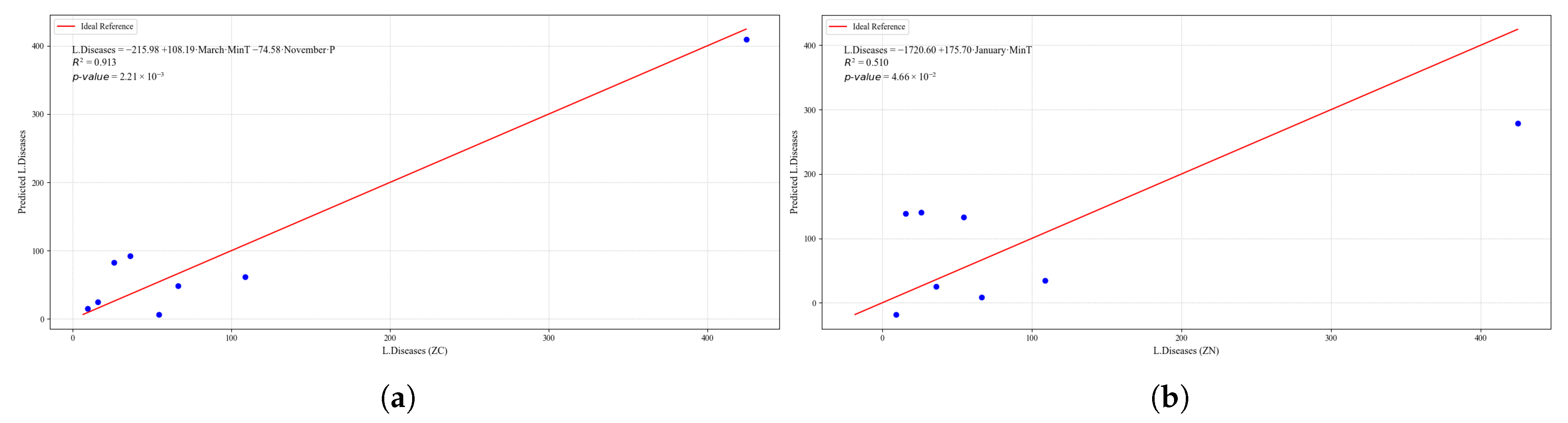
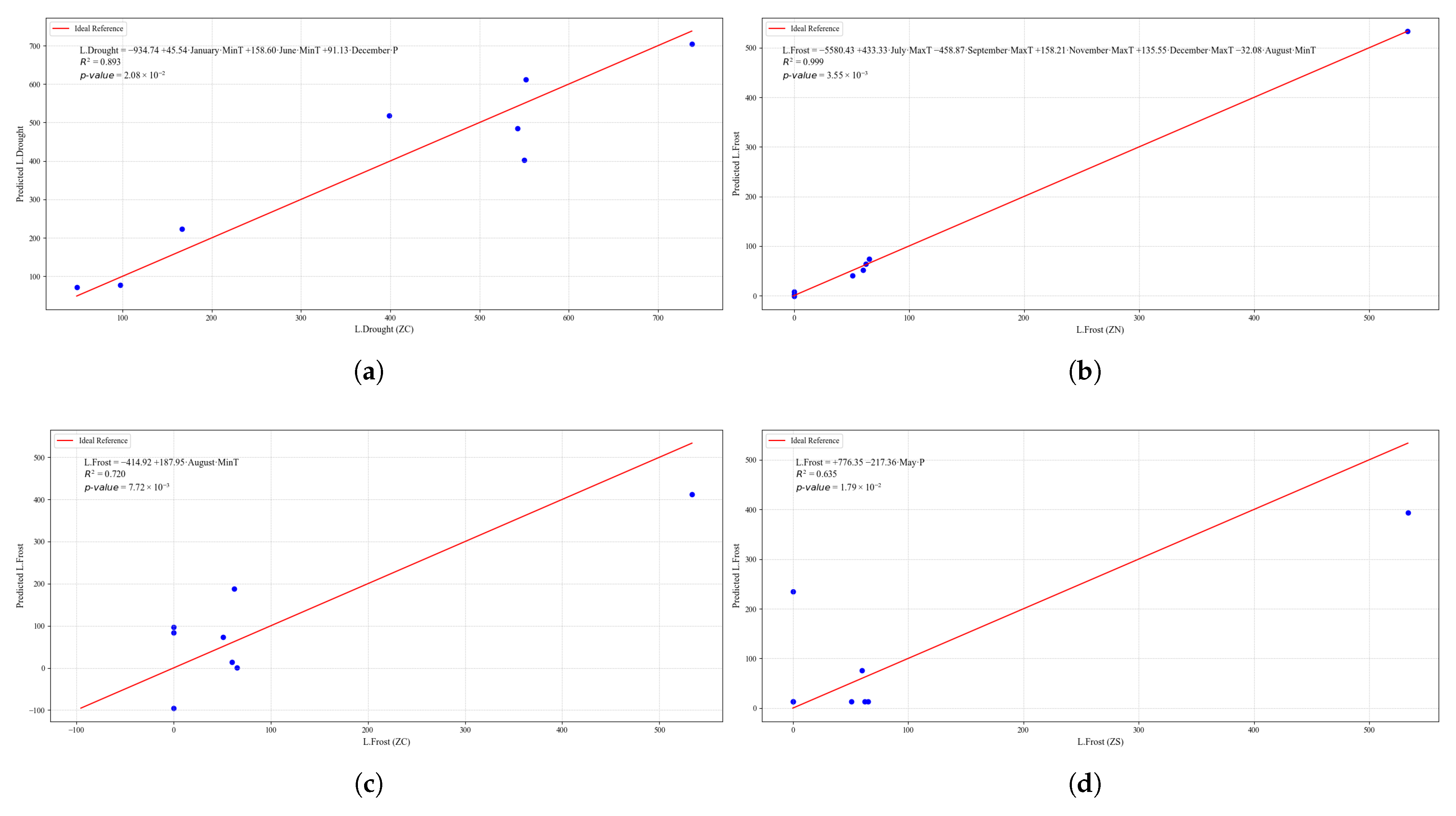
Figure 24.
Simple linear regression models between quinoa crop variables and average climatic variables in the three study zones, selected for their relevance and statistical significance. (a) Linear regression model of the L.Drought variable in the central zone. (b) Linear regression model of the L.Frost variable in the northern zone. (c) Linear regression model of the L.Frost variable in the central zone. (d) Linear regression model of the L.Frost variable in the southern zone.
Figure 24.
Simple linear regression models between quinoa crop variables and average climatic variables in the three study zones, selected for their relevance and statistical significance. (a) Linear regression model of the L.Drought variable in the central zone. (b) Linear regression model of the L.Frost variable in the northern zone. (c) Linear regression model of the L.Frost variable in the central zone. (d) Linear regression model of the L.Frost variable in the southern zone.
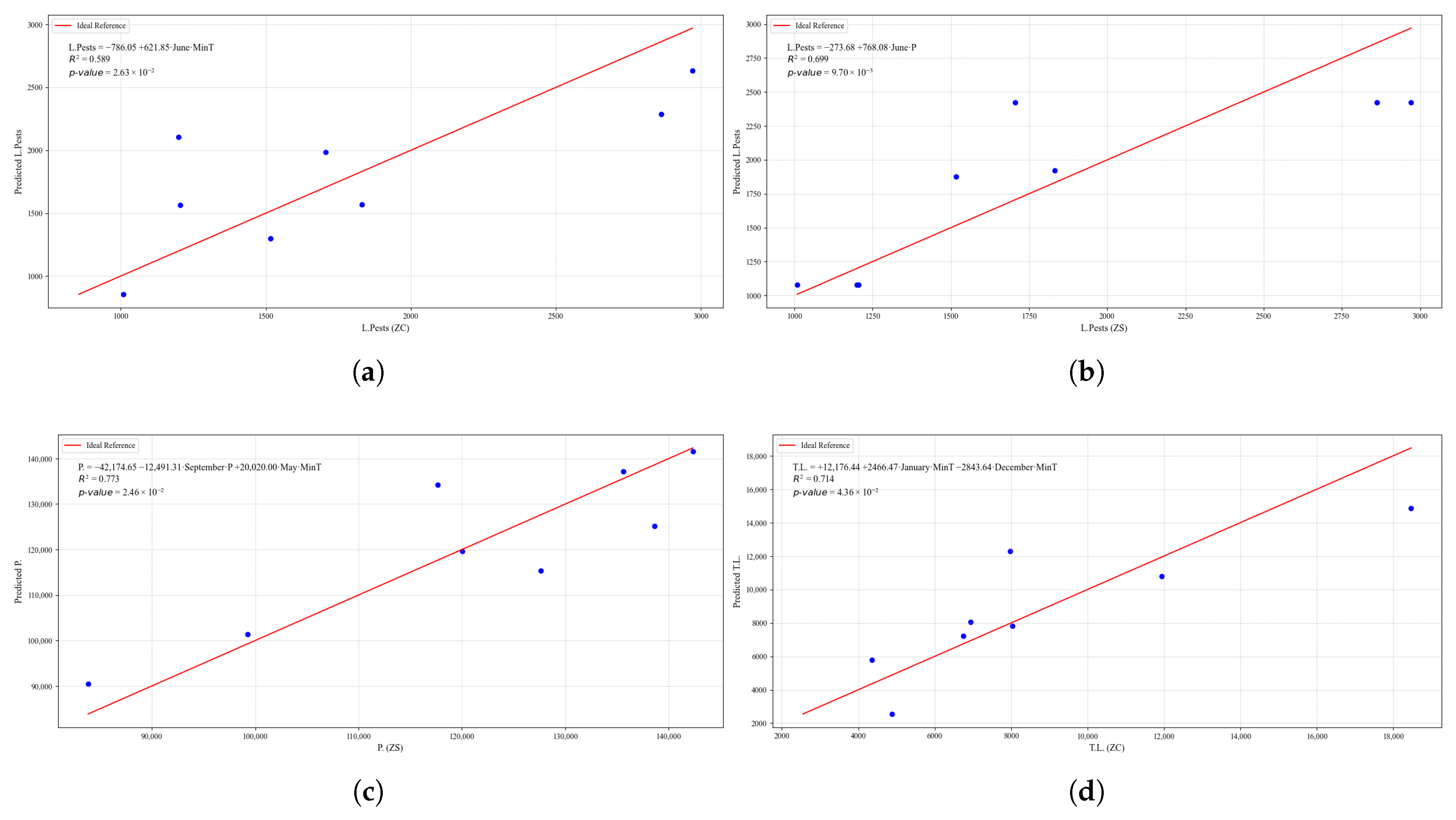
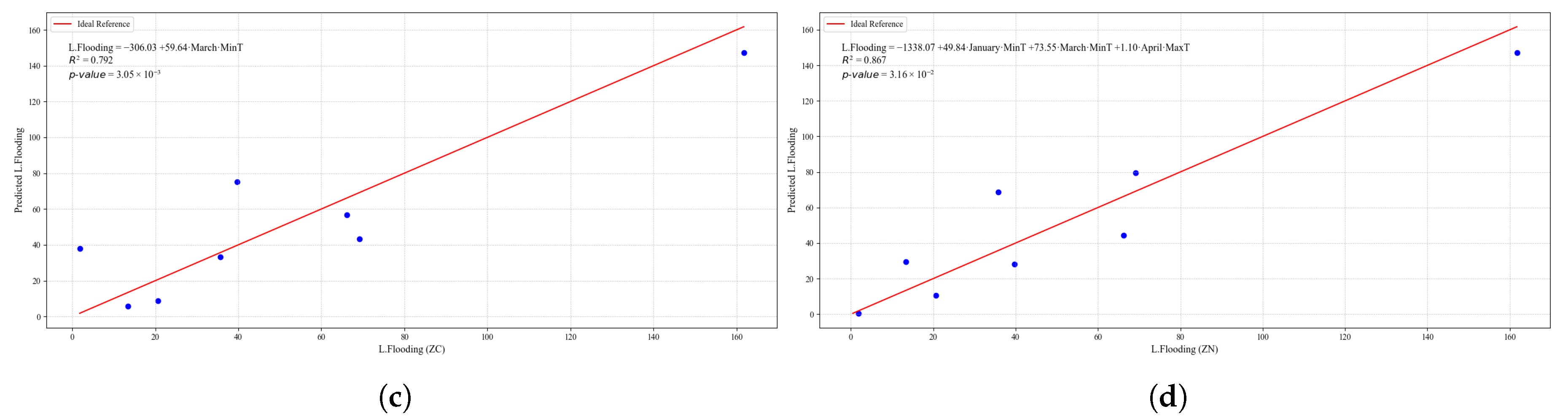
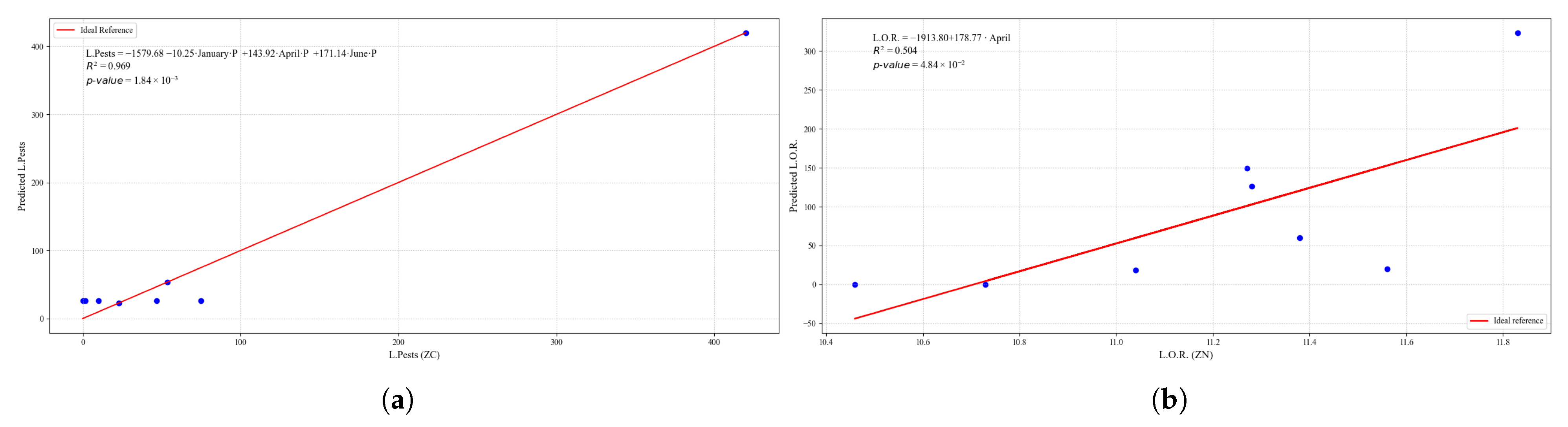
Figure 25.
Simple linear regression models between quinoa crop variables and average climatic variables in the three study zones, selected for their relevance and statistical significance. (a) Linear regression model of the L.Pests variable in the central zone. (b) Linear regression model of the L.O.R. variable in the northern zone.
Figure 25.
Simple linear regression models between quinoa crop variables and average climatic variables in the three study zones, selected for their relevance and statistical significance. (a) Linear regression model of the L.Pests variable in the central zone. (b) Linear regression model of the L.O.R. variable in the northern zone.
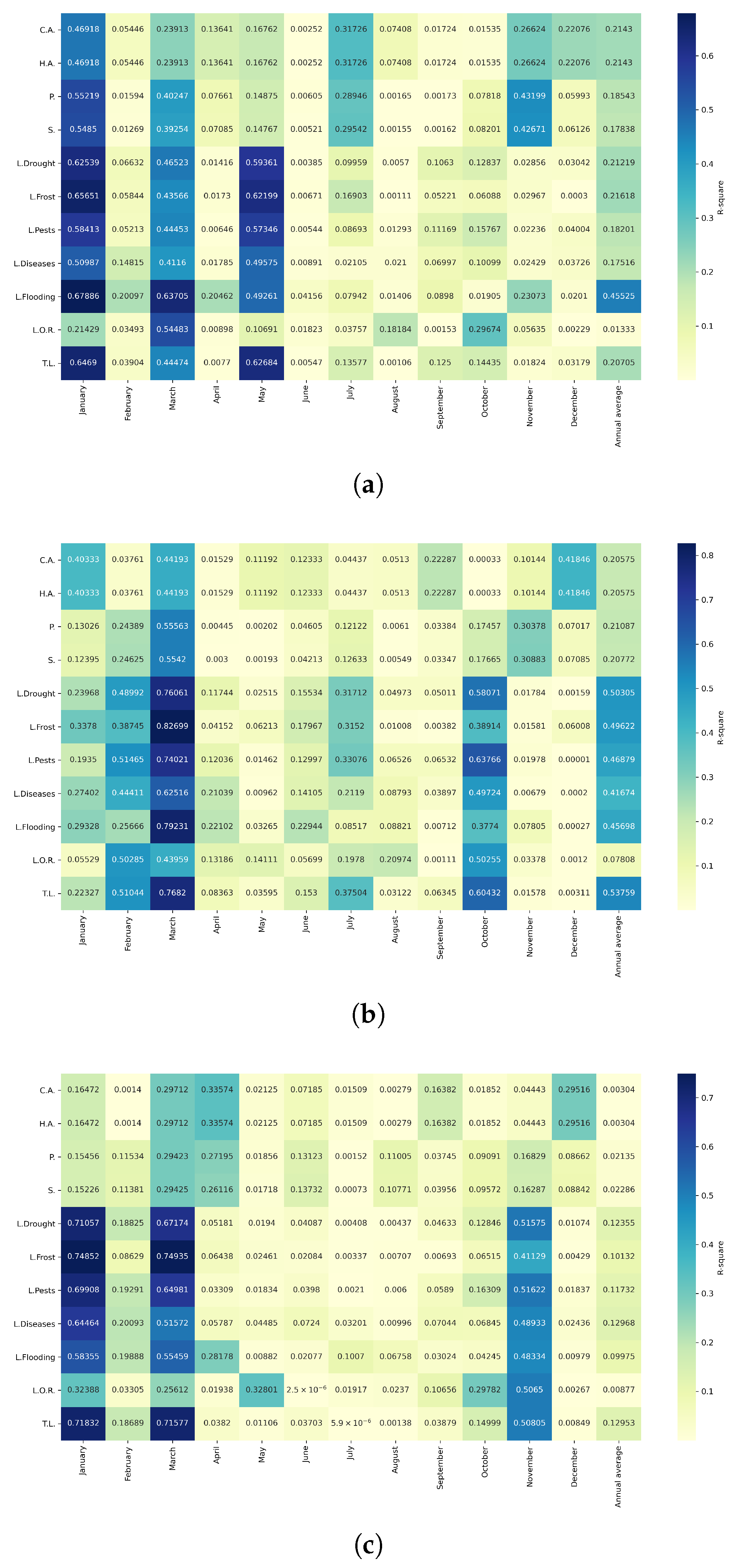
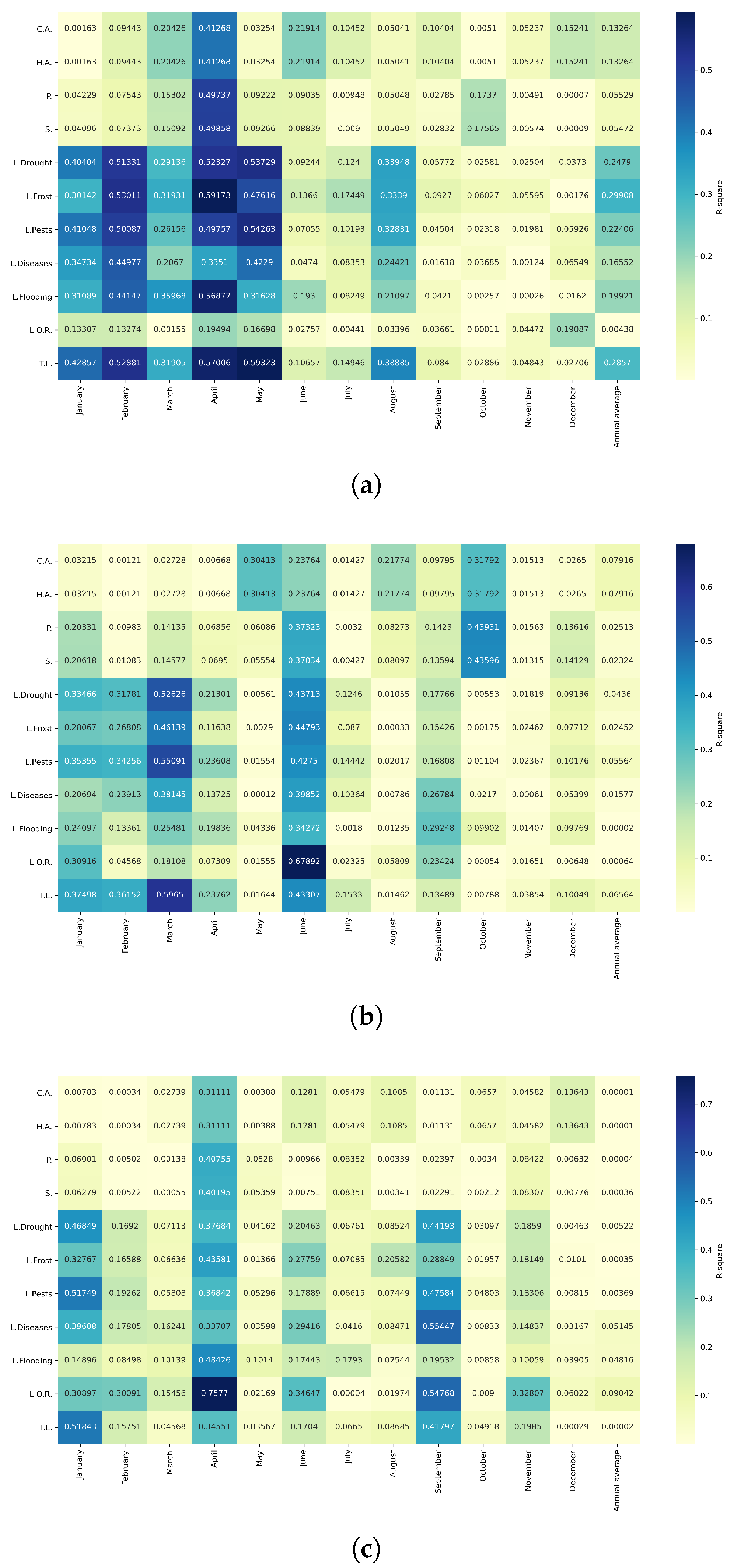
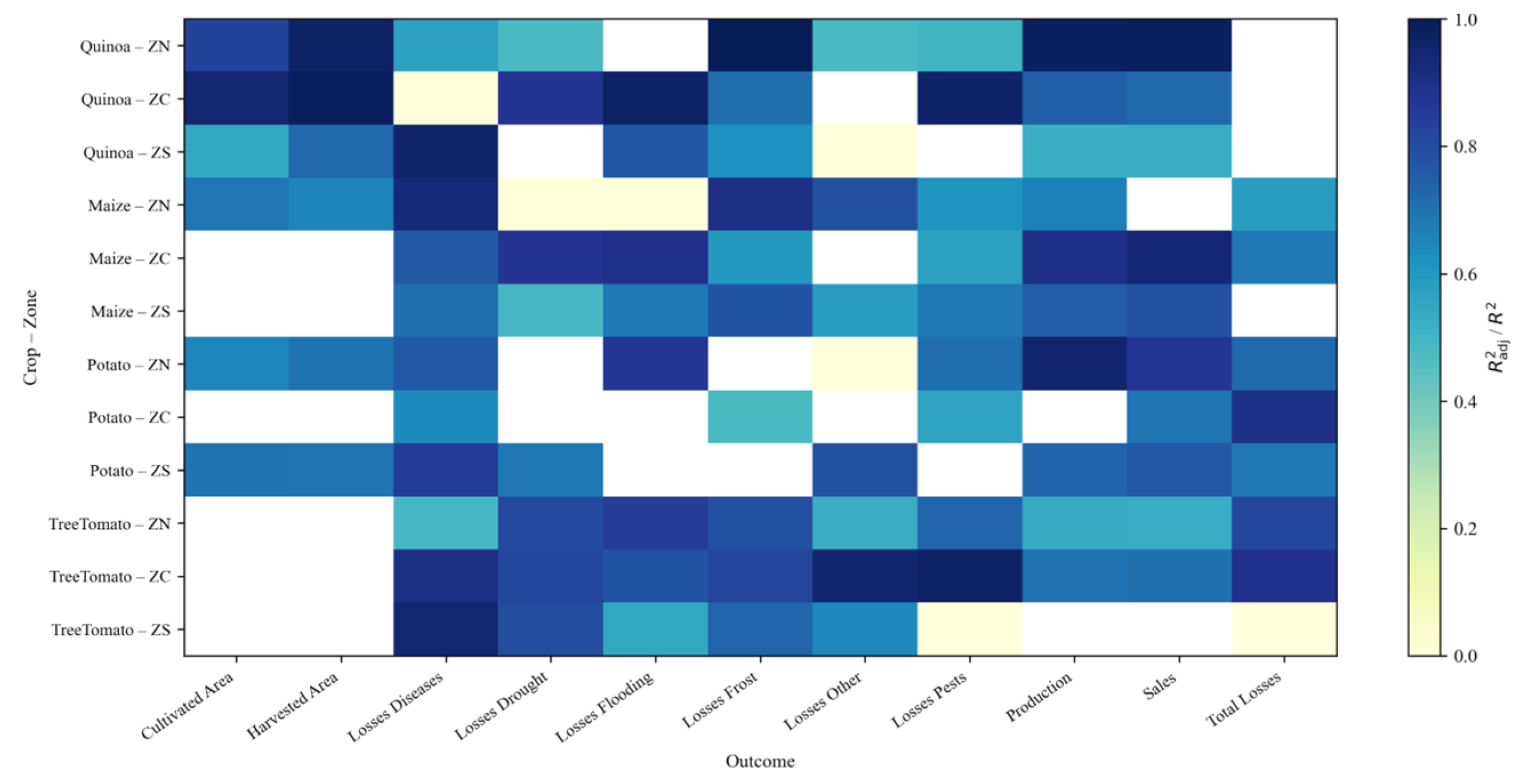
Figure 26.
Model performance () by crop–zone (rows) and outcome (columns). Cells show the fit of the best specification per crop–zone–outcome, prioritizing . Empty (white) cells indicate no retained model.
Figure 26.
Model performance () by crop–zone (rows) and outcome (columns). Cells show the fit of the best specification per crop–zone–outcome, prioritizing . Empty (white) cells indicate no retained model.
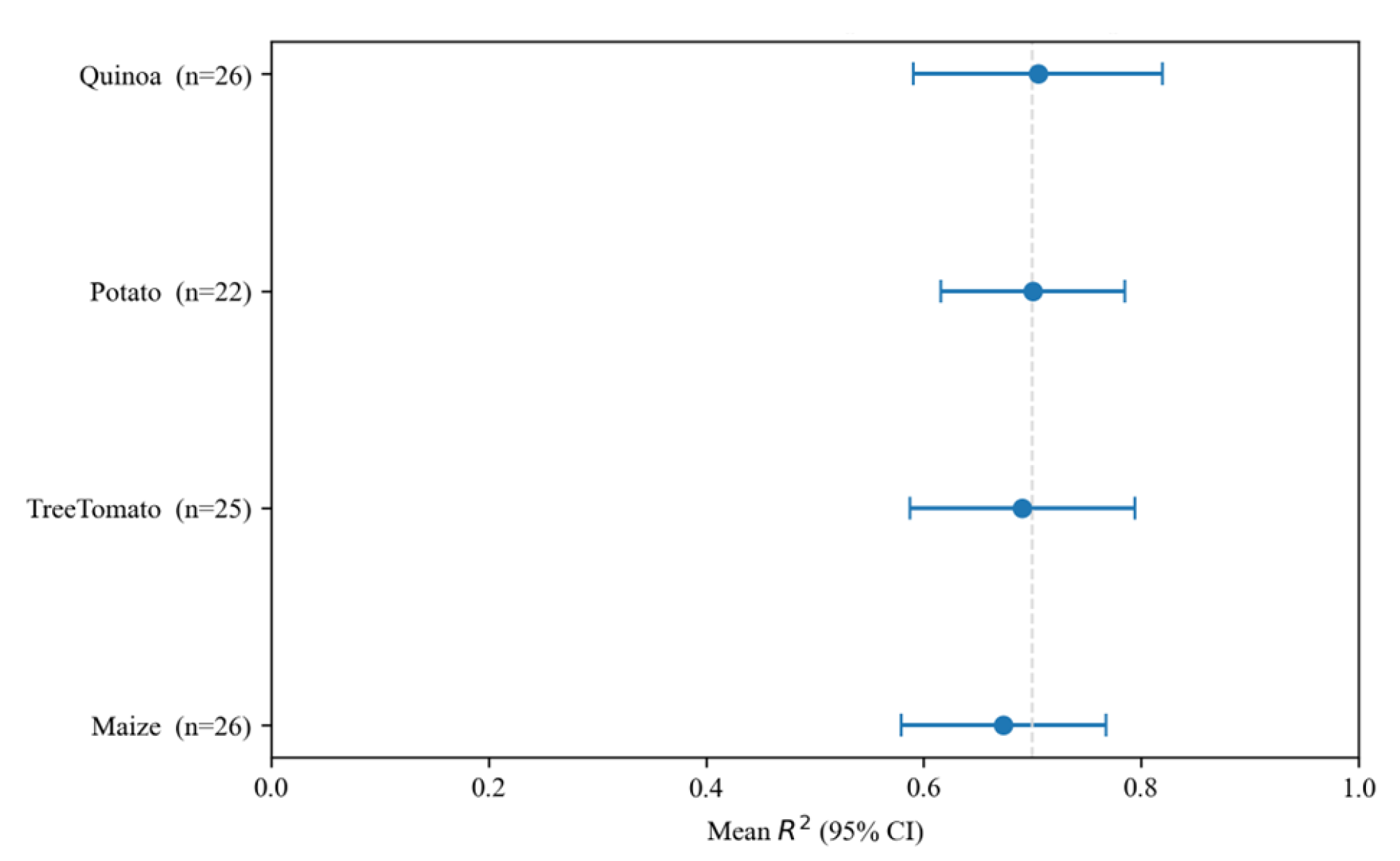
Figure 27.
Meta-summary by crop: mean and 95% CI across zones and outcomes (sample size n in labels). The dashed vertical line marks as a reference for strong models.
Figure 27.
Meta-summary by crop: mean and 95% CI across zones and outcomes (sample size n in labels). The dashed vertical line marks as a reference for strong models.
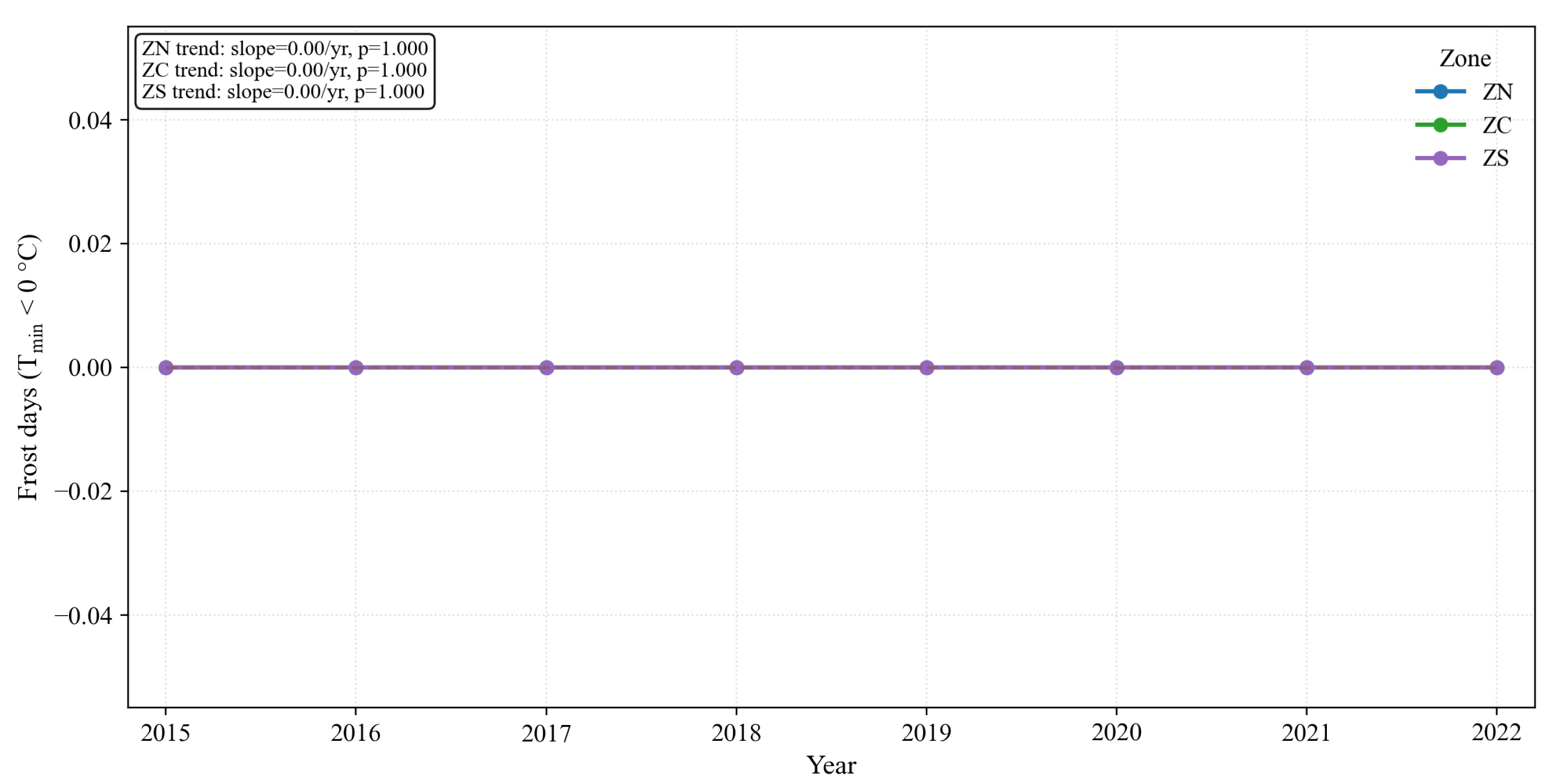
Figure 28.
Annual frost days (Tmin < 0 °C) by zone (2015–2022) with linear trends. POWER/MERRA-2 detects virtually zero frost days across zones, consistent with under-detection of local frosts at 0.5° resolution over complex terrain.
Figure 28.
Annual frost days (Tmin < 0 °C) by zone (2015–2022) with linear trends. POWER/MERRA-2 detects virtually zero frost days across zones, consistent with under-detection of local frosts at 0.5° resolution over complex terrain.
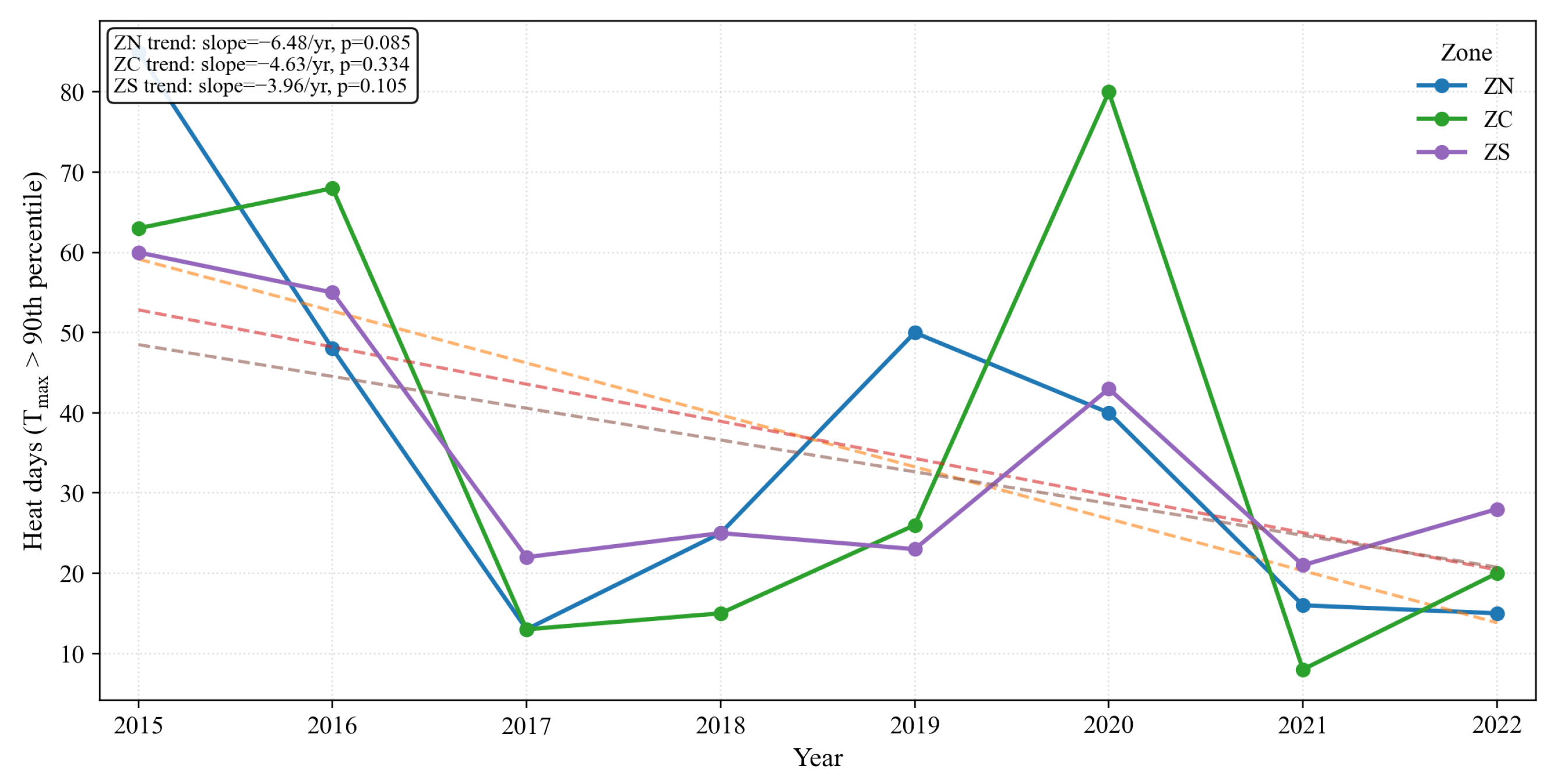
Figure 29.
Annual heat-day frequency (days with above the point-specific 90th percentile; TX90) by zone (2015–2022) with linear trends. All zones show interannual variability and no recent intensification of short-duration heat stress.
Figure 29.
Annual heat-day frequency (days with above the point-specific 90th percentile; TX90) by zone (2015–2022) with linear trends. All zones show interannual variability and no recent intensification of short-duration heat stress.
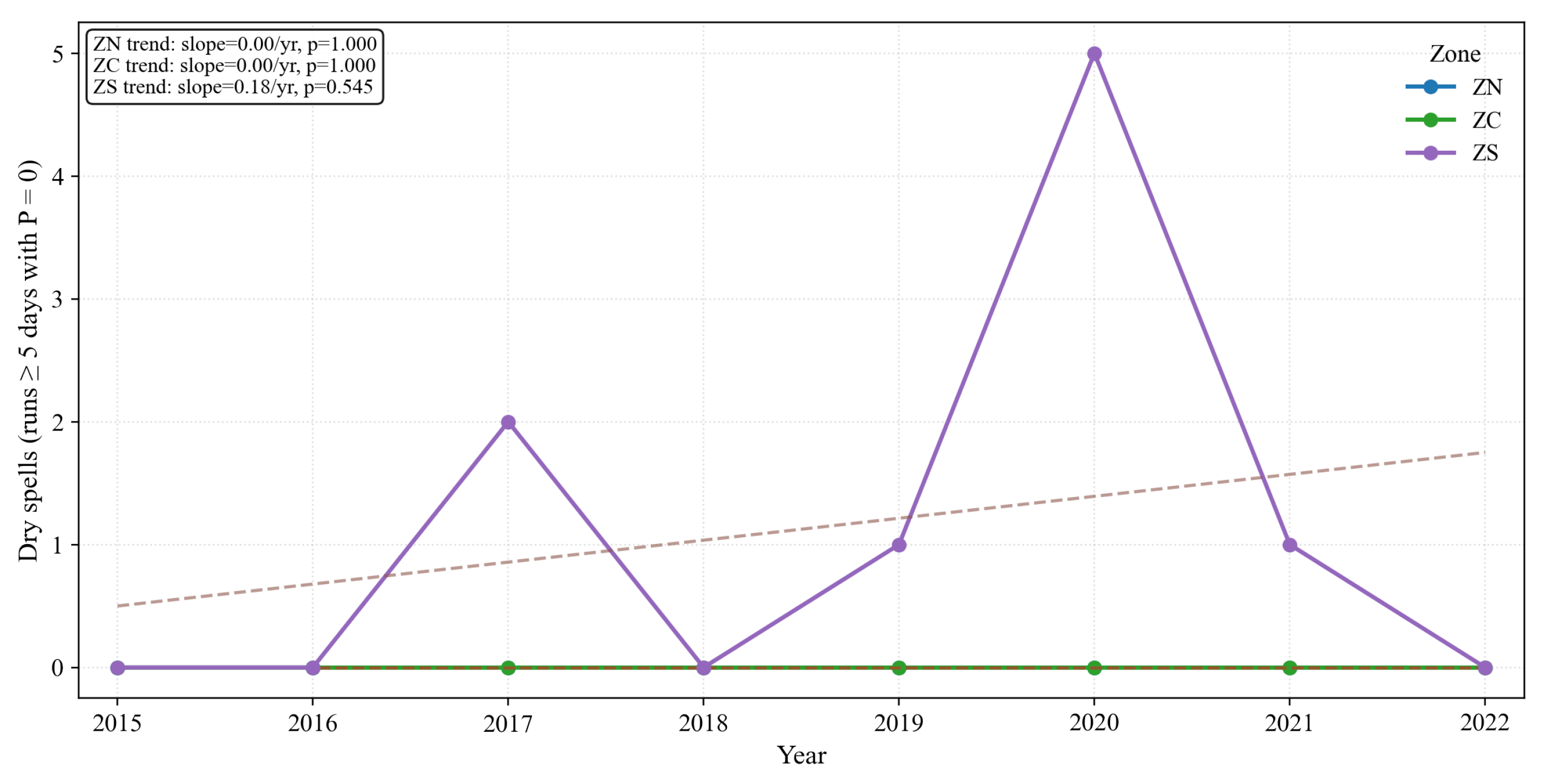
Figure 30.
Annual count of dry spells (runs ≥5 consecutive days with ) by zone (2015–2022) with linear trends. The south concentrates the largest counts and shows a small, non-significant upward tendency; the center exhibits weaker changes; the north remains near zero.
Figure 30.
Annual count of dry spells (runs ≥5 consecutive days with ) by zone (2015–2022) with linear trends. The south concentrates the largest counts and shows a small, non-significant upward tendency; the center exhibits weaker changes; the north remains near zero.
Figure 31.
Maximum consecutive dry days (CDDmax) per year by zone (2015–2022) with linear trends. Longer dry sequences occur in the south (up to ∼8 days), with a weak positive tendency; north and center remain shorter and comparatively flat.
Figure 31.
Maximum consecutive dry days (CDDmax) per year by zone (2015–2022) with linear trends. Longer dry sequences occur in the south (up to ∼8 days), with a weak positive tendency; north and center remain shorter and comparatively flat.
Table 1.
Cultivated area, harvested area, production, sales, and losses due to different causes for soft corn during the period of 2015–2022 in Ecuador.
Table 1.
Cultivated area, harvested area, production, sales, and losses due to different causes for soft corn during the period of 2015–2022 in Ecuador.
| Year | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 |
|---|
| Cultivated area (ha) | 126,461 | 80,249 | 89,890 | 74,961 | 67,620 | 74,017 | 75,877 | 57,309 |
| Harvested area (ha) | 107,993 | 68,313 | 81,851 | 66,989 | 63,258 | 69,131 | 69,123 | 50,376 |
| Production (t) | 138,647 | 99,257 | 120,028 | 117,641 | 135,599 | 142,336 | 127,631 | 83,852 |
| Sales (t) | 102,459 | 75,649 | 89,042 | 88,351 | 108,177 | 115,311 | 98,571 | 64,300 |
| Total losses | 18,468 | 11,936 | 8039 | 7972 | 4361 | 4887 | 6754 | 6932 |
| Losses due to drought | 8841 | 6568 | 2081 | 5501 | 2311 | 2195 | 1493 | 1369 |
| Losses due to frost | 1597 | 1035 | 1394 | 894 | 487 | 733 | 2257 | 2046 |
| Losses due to pests | 2970 | 2862 | 1705 | 1010 | 1200 | 1205 | 1832 | 1517 |
| Losses due to diseases | 388 | 351 | 208 | 70 | 159 | 123 | 120 | 144 |
| Losses due to flooding | 129 | 51 | 1308 | 66 | 43 | 163 | 380 | 1522 |
| Losses due to other reasons | 4543 | 1068 | 1343 | 431 | 162 | 468 | 672 | 335 |
Table 2.
Cultivated area, harvested area, production, sales, and losses due to different causes for soft potato during the period of 2015–2022 in Ecuador.
Table 2.
Cultivated area, harvested area, production, sales, and losses due to different causes for soft potato during the period of 2015–2022 in Ecuador.
| Year | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 |
|---|
| Cultivated area (ha) | 32,036 | 32,741 | 32,187 | 23,974 | 20,626 | 25,923 | 20,950 | 19,390 |
| Harvested area (ha) | 29,703 | 29,634 | 29,532 | 22,099 | 19,675 | 24,882 | 19,088 | 17,926 |
| Production (t) | 397,520 | 422,589 | 377,243 | 269,200 | 275,345 | 408,313 | 244,748 | 251,433 |
| Sales (t) | 341,849 | 378,853 | 343,764 | 239,609 | 253,706 | 374,009 | 219,550 | 232,513 |
| Total losses | 2333 | 3107 | 2655 | 1875 | 951 | 1041 | 1861 | 1464 |
| Losses due to drought | 977 | 773 | 932 | 690 | 141 | 98 | 124 | 151 |
| Losses due to frost | 387 | 621 | 858 | 582 | 156 | 375 | 936 | 810 |
| Losses due to pests | 441 | 1344 | 333 | 190 | 420 | 306 | 537 | 199 |
| Losses due to diseases | 183 | 253 | 104 | 245 | 218 | 61 | 83 | 117 |
| Losses due to flooding | 39 | 10 | 185 | 94 | 13 | 28 | 72 | 154 |
| Losses due to other reasons | 304 | 104 | 240 | 71 | — | 170 | 108 | 31 |
Table 3.
Cultivated area, harvested area, production, sales, and losses due to different causes for soft tree tomato during the period of 2015–2022 in Ecuador.
Table 3.
Cultivated area, harvested area, production, sales, and losses due to different causes for soft tree tomato during the period of 2015–2022 in Ecuador.
| Year | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 |
|---|
| Cultivated area (ha) | 1982 | 2075 | 1952 | 2026 | 1685 | 1044 | 1009 | 1364 |
| Harvested area (ha) | 1982 | 2075 | 1952 | 2026 | 1685 | 1044 | 1009 | 1364 |
| Production (t) | 16,175 | 28,512 | 20,212 | 22,343 | 24,316 | 10,605 | 6742 | 18,031 |
| Sales (t) | 15,779 | 28,018 | 19,715 | 22,081 | 23,904 | 10,472 | 6350 | 17,750 |
| Total losses | 241 | 2360 | 187 | 149 | 135 | 41 | 137 | 66 |
| Losses due to drought | 30 | 118 | 22 | 22 | — | — | — | — |
| Losses due to frost | 6 | 428 | 6 | 1 | 1 | — | 7 | — |
| Losses due to pests | 54 | 425 | 66 | 26 | 16 | 9 | 109 | 36 |
| Losses due to diseases | 36 | 162 | 66 | 40 | 69 | 2 | 21 | 13 |
| Losses due to flooding | — | 28 | 12 | — | — | — | — | 13 |
| Losses due to other reasons | 116 | 1200 | 15 | 61 | 48 | 30 | 1 | 4 |
Table 4.
Cultivated area, harvested area, production, sales, and losses due to different causes for soft quinoa during the period of 2015–2022 in Ecuador.
Table 4.
Cultivated area, harvested area, production, sales, and losses due to different causes for soft quinoa during the period of 2015–2022 in Ecuador.
| Year | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 |
|---|
| Cultivated area (ha) | 7886 | 2765 | 1424 | 2215 | 2957 | 5365 | 2940 | 885 |
| Harvested area (ha) | 7148 | 2214 | 882 | 2048 | 2559 | 5267 | 2390 | 837 |
| Production (t) | 12,707 | 3903 | 1286 | 2146 | 4505 | 4903 | 1482 | 884 |
| Sales (t) | 10,739 | 3559 | 1128 | 2039 | 2603 | 4538 | 875 | 765 |
| Total losses | 738 | 552 | 542 | 167 | 399 | 98 | 550 | 49 |
| Losses due to drought | 534 | 65 | — | 63 | — | 51 | 60 | — |
| Losses due to frost | 47 | 54 | 2 | — | 75 | 10 | 420 | 23 |
| Losses due to pests | — | 282 | — | — | — | 37 | 9 | 26 |
| Losses due to diseases | — | — | 14 | — | — | — | — | — |
| Losses due to flooding | 126 | 1 | 507 | 86 | — | — | 60 | — |
| Losses due to other reasons | 31 | 150 | 20 | 19 | 323 | — | — | — |
Table 5.
Climatic datasets and variables used (NASA POWER/MERRA-2). All variables are temporally averaged, two-dimensional monthly means.
Table 5.
Climatic datasets and variables used (NASA POWER/MERRA-2). All variables are temporally averaged, two-dimensional monthly means.
| Variable | POWER/MERRA-2 | Source | Temporal Support | Notes/IDs/Citations |
|---|
| Precipitation (bias-corrected) | M2TMNXLFO | NASA POWER (GMAO MERRA-2) | Monthly mean | Bias-corrected precipitation; dataset ID M2TMNXLFO [37]. |
| Maximum air temperature (2 m) | M2TMNXSLV | NASA POWER (GMAO MERRA-2) | Monthly mean | Single-level product; dataset ID M2TMNXSLV [38]. |
| Minimum air temperature (2 m) | M2TMNXSLV | NASA POWER (GMAO MERRA-2) | Monthly mean | Single-level product; dataset ID M2TMNXSLV [38]. |
Table 6.
Study area regionalization of the Ecuadorian highlands (N–C–S).
Table 6.
Study area regionalization of the Ecuadorian highlands (N–C–S).
| Region | Provinces |
|---|
| North (ZN) | Carchi, Imbabura, Pichincha. |
| Center (ZC) | Cotopaxi, Tungurahua, Chimborazo, Bolívar. |
| South (ZS) | Cañar, Azuay, Loja. |
Table 7.
Sampling lattice and number of grid cells (“sampling points”) per region.
Table 7.
Sampling lattice and number of grid cells (“sampling points”) per region.
| Grid (Product) | ZN | ZC | ZS | Definition/Note |
|---|
| MERRA-2 native (0.5° × 0.625°) | 11 | 12 | 17 | Sampling points are the centroids of all valid grid cells intersecting each region mask (all_touched=true); counts correspond to the spatial lattice used to extract monthly values (2015–2022). |
| POWER regridded (0.5° × 0.5°) | 15 | 16 | 18 | Same definition; shown for completeness given the 0.5° POWER grid commonly used in applications. |
Table 8.
Validation of POWER/MERRA-2 against in situ stations (monthly, 2015–2022). Median skill by region. RMSE/bias in °C for temperature and mm/month for precipitation.
Table 8.
Validation of POWER/MERRA-2 against in situ stations (monthly, 2015–2022). Median skill by region. RMSE/bias in °C for temperature and mm/month for precipitation.
| Variable | Region | n Stations | r (Median) | RMSE | Bias | KGE |
|---|
| Tmax | ZN | 2 | 0.56 | 1.65 | 1.19 | 0.40 |
| Tmax | ZC | 1 | 0.63 | 1.65 | −1.21 | 0.37 |
| Tmax | ZS | 2 | 0.39 | 2.19 | 1.32 | 0.27 |
| Tmin | ZN | 2 | 0.54 | 2.41 | 2.16 | 0.43 |
| Tmin | ZC | 1 | 0.55 | 1.30 | −0.45 | 0.43 |
| Tmin | ZS | 2 | 0.29 | 1.57 | 0.74 | 0.23 |
| Precip | ZN | 2 | 0.48 | 73.89 | 40.11 | 0.16 |
| Precip | ZC | 1 | 0.23 | 125.61 | 71.05 | −0.57 |
| Precip | ZS | 2 | 0.41 | 77.75 | 33.06 | −0.28 |
Table 9.
Maximum temperature, minimum temperature, and precipitation values for the northern region.
Table 9.
Maximum temperature, minimum temperature, and precipitation values for the northern region.
| Variable | Year | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | Mean |
|---|
| Maximum temperature (°C) | 2015 | 24.92 | 24.45 | 25.17 | 24.57 | 24.73 | 24.79 | 25.28 | 26.05 | 26.52 | 26.10 | 25.57 | 26.56 | 25.39 |
| 2016 | 25.90 | 26.10 | 25.59 | 25.46 | 25.38 | 24.42 | 24.66 | 26.28 | 25.67 | 25.40 | 24.40 | 23.39 | 25.22 |
| 2017 | 24.10 | 24.21 | 23.50 | 24.01 | 23.80 | 23.74 | 23.75 | 24.16 | 24.54 | 25.36 | 22.91 | 23.57 | 23.97 |
| 2018 | 23.25 | 23.60 | 24.17 | 24.19 | 23.91 | 23.95 | 23.95 | 24.40 | 25.18 | 24.49 | 24.24 | 24.17 | 24.12 |
| 2019 | 25.07 | 24.01 | 25.13 | 24.52 | 24.43 | 24.65 | 24.34 | 25.29 | 25.68 | 24.02 | 24.08 | 24.34 | 24.63 |
| 2020 | 25.12 | 24.92 | 24.23 | 24.33 | 24.76 | 23.96 | 24.31 | 25.63 | 25.60 | 26.05 | 24.76 | 23.62 | 24.77 |
| 2021 | 24.30 | 23.77 | 23.80 | 23.13 | 24.00 | 23.64 | 24.03 | 24.50 | 24.75 | 25.22 | 23.25 | 23.46 | 23.99 |
| 2022 | 23.85 | 22.22 | 22.25 | 23.47 | 24.02 | 22.54 | 23.61 | 24.18 | 24.52 | 24.37 | 23.55 | 23.33 | 23.49 |
| Minimum temperature (°C) | 2015 | 10.55 | 11.07 | 11.61 | 11.28 | 11.04 | 9.78 | 10.00 | 9.87 | 9.82 | 11.04 | 9.89 | 10.39 | 10.53 |
| 2016 | 11.38 | 11.50 | 12.10 | 11.27 | 11.68 | 9.70 | 9.67 | 8.83 | 10.02 | 9.84 | 10.86 | 11.03 | 10.66 |
| 2017 | 9.84 | 11.63 | 11.77 | 11.56 | 10.64 | 10.37 | 8.87 | 8.44 | 9.27 | 11.29 | 11.06 | 10.53 | 10.44 |
| 2018 | 10.59 | 11.06 | 10.98 | 11.04 | 10.89 | 9.23 | 9.35 | 9.06 | 8.78 | 10.61 | 11.29 | 9.66 | 10.21 |
| 2019 | 10.58 | 11.40 | 11.74 | 11.83 | 10.86 | 10.49 | 9.37 | 9.03 | 10.16 | 10.72 | 11.30 | 11.33 | 10.73 |
| 2020 | 9.69 | 10.15 | 11.27 | 10.73 | 11.03 | 10.04 | 9.33 | 8.89 | 10.14 | 10.51 | 9.44 | 11.54 | 10.23 |
| 2021 | 9.99 | 12.01 | 11.22 | 11.38 | 10.71 | 9.66 | 8.22 | 8.79 | 9.44 | 10.94 | 10.52 | 11.15 | 10.34 |
| 2022 | 9.94 | 10.73 | 11.51 | 10.46 | 10.16 | 9.10 | 9.37 | 8.70 | 9.08 | 9.24 | 10.54 | 9.99 | 9.90 |
| Precipitation (mm/day) | 2015 | 14.36 | 13.38 | 13.55 | 13.30 | 13.69 | 15.01 | 15.29 | 16.18 | 16.71 | 15.06 | 15.68 | 16.16 | 14.86 |
| 2016 | 14.53 | 14.60 | 13.49 | 14.19 | 13.70 | 14.73 | 14.99 | 17.44 | 15.65 | 15.56 | 13.53 | 12.36 | 14.56 |
| 2017 | 14.26 | 12.58 | 11.73 | 12.45 | 13.16 | 13.36 | 14.89 | 15.72 | 15.27 | 14.07 | 11.86 | 13.04 | 13.53 |
| 2018 | 12.66 | 12.54 | 13.18 | 13.16 | 13.02 | 14.71 | 14.59 | 15.34 | 16.39 | 13.88 | 12.94 | 14.51 | 13.91 |
| 2019 | 14.49 | 12.61 | 13.38 | 12.69 | 13.56 | 14.17 | 14.98 | 16.26 | 15.52 | 13.30 | 12.79 | 13.01 | 13.90 |
| 2020 | 15.43 | 14.76 | 12.97 | 13.61 | 13.73 | 13.92 | 14.98 | 16.73 | 15.46 | 15.54 | 15.32 | 12.08 | 14.54 |
| 2021 | 14.31 | 11.76 | 12.59 | 11.75 | 13.29 | 13.98 | 15.80 | 15.71 | 15.31 | 14.28 | 12.73 | 12.31 | 13.65 |
| 2022 | 13.91 | 11.48 | 10.73 | 13.01 | 13.86 | 13.44 | 14.25 | 15.48 | 15.44 | 15.12 | 13.00 | 13.34 | 13.59 |
Table 10.
Maximum temperature, minimum temperature, and precipitation values for the central region.
Table 10.
Maximum temperature, minimum temperature, and precipitation values for the central region.
| Variable | Year | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | Mean |
|---|
| Maximum temperature (°C) | 2015 | 22.35 | 21.45 | 21.40 | 21.11 | 21.07 | 20.67 | 21.63 | 22.16 | 23.65 | 23.34 | 23.15 | 23.26 | 22.10 |
| 2016 | 22.94 | 22.03 | 22.32 | 21.61 | 21.47 | 20.60 | 20.89 | 22.79 | 22.53 | 22.89 | 23.20 | 22.03 | 22.11 |
| 2017 | 22.10 | 20.63 | 20.08 | 20.74 | 20.32 | 20.50 | 21.43 | 21.90 | 22.23 | 22.95 | 22.01 | 22.29 | 21.43 |
| 2018 | 21.39 | 21.53 | 21.15 | 20.92 | 21.09 | 21.18 | 20.82 | 21.52 | 22.81 | 22.23 | 22.68 | 21.65 | 21.58 |
| 2019 | 22.11 | 21.08 | 20.96 | 21.46 | 21.13 | 20.86 | 21.49 | 22.05 | 23.09 | 22.17 | 22.50 | 22.29 | 21.76 |
| 2020 | 23.15 | 22.18 | 21.77 | 21.45 | 22.30 | 21.41 | 21.15 | 22.99 | 23.46 | 23.65 | 23.63 | 21.72 | 22.40 |
| 2021 | 20.54 | 20.71 | 20.52 | 20.55 | 21.14 | 20.75 | 20.86 | 21.69 | 22.33 | 22.96 | 21.91 | 22.08 | 21.34 |
| 2022 | 22.25 | 20.36 | 20.61 | 20.66 | 21.00 | 20.11 | 20.80 | 22.13 | 22.80 | 23.39 | 22.40 | 22.30 | 21.57 |
| Minimum temperature (°C) | 2015 | 17.79 | 17.42 | 18.06 | 18.19 | 17.90 | 17.08 | 16.46 | 16.98 | 17.30 | 18.28 | 17.30 | 18.08 | 17.57 |
| 2016 | 19.08 | 18.91 | 18.31 | 17.76 | 17.48 | 16.30 | 17.23 | 16.40 | 17.07 | 16.37 | 16.22 | 17.72 | 17.40 |
| 2017 | 17.23 | 17.94 | 17.99 | 17.68 | 16.82 | 16.66 | 15.56 | 15.79 | 16.05 | 17.41 | 16.15 | 17.55 | 16.90 |
| 2018 | 17.38 | 17.94 | 17.77 | 17.23 | 17.33 | 15.65 | 16.25 | 16.62 | 16.48 | 16.51 | 17.42 | 17.30 | 16.99 |
| 2019 | 18.15 | 17.94 | 18.55 | 17.99 | 17.63 | 16.62 | 16.09 | 15.76 | 16.65 | 17.33 | 17.26 | 17.53 | 17.29 |
| 2020 | 16.76 | 18.31 | 18.18 | 17.88 | 17.26 | 16.98 | 16.06 | 15.09 | 16.64 | 16.94 | 16.43 | 17.52 | 17.00 |
| 2021 | 17.63 | 18.35 | 17.33 | 17.75 | 16.59 | 15.55 | 14.06 | 16.15 | 16.20 | 17.05 | 16.40 | 16.61 | 16.64 |
| 2022 | 16.30 | 17.38 | 17.74 | 16.87 | 16.27 | 15.17 | 15.86 | 15.78 | 15.68 | 16.44 | 16.21 | 16.15 | 16.32 |
| Precipitation (mm/day) | 2015 | 15.54 | 13.48 | 12.73 | 11.97 | 12.00 | 13.87 | 16.67 | 17.27 | 17.66 | 17.09 | 15.83 | 16.41 | 15.04 |
| 2016 | 13.66 | 11.30 | 11.61 | 11.98 | 13.20 | 15.98 | 15.41 | 19.16 | 17.36 | 16.90 | 16.56 | 14.46 | 14.80 |
| 2017 | 14.98 | 10.84 | 10.55 | 11.36 | 11.80 | 12.32 | 14.91 | 16.77 | 16.98 | 17.23 | 15.34 | 14.45 | 13.96 |
| 2018 | 13.32 | 13.05 | 11.98 | 13.01 | 12.74 | 16.42 | 16.52 | 17.40 | 18.37 | 15.62 | 14.66 | 14.48 | 14.80 |
| 2019 | 13.55 | 11.20 | 10.45 | 10.62 | 11.84 | 14.01 | 16.34 | 18.63 | 18.42 | 15.55 | 15.14 | 15.47 | 14.27 |
| 2020 | 16.96 | 12.01 | 11.05 | 11.55 | 14.70 | 14.83 | 16.65 | 19.20 | 16.48 | 17.39 | 15.72 | 13.34 | 14.99 |
| 2021 | 10.92 | 9.90 | 11.06 | 10.80 | 12.87 | 13.99 | 17.59 | 16.45 | 17.64 | 16.11 | 14.46 | 14.34 | 13.84 |
| 2022 | 15.51 | 10.55 | 9.34 | 12.36 | 13.09 | 14.50 | 15.93 | 17.27 | 18.45 | 18.10 | 15.96 | 15.53 | 14.72 |
Table 11.
Maximum temperature, minimum temperature, and precipitation values for the southern region.
Table 11.
Maximum temperature, minimum temperature, and precipitation values for the southern region.
| Variable | Year | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | Mean |
|---|
| Maximum temperature (°C) | 2015 | 24.01 | 23.46 | 23.37 | 22.15 | 22.32 | 22.27 | 23.51 | 24.06 | 25.67 | 24.85 | 25.12 | 25.45 | 23.85 |
| 2016 | 25.61 | 24.56 | 24.31 | 23.20 | 23.36 | 21.93 | 22.44 | 24.20 | 24.61 | 25.09 | 25.61 | 23.56 | 24.04 |
| 2017 | 23.41 | 22.32 | 21.80 | 22.00 | 21.38 | 21.93 | 22.57 | 23.40 | 24.39 | 24.61 | 24.32 | 24.13 | 23.02 |
| 2018 | 23.79 | 23.16 | 23.35 | 22.81 | 23.17 | 22.85 | 22.77 | 23.13 | 24.39 | 24.42 | 24.10 | 23.20 | 23.43 |
| 2019 | 24.29 | 22.98 | 23.00 | 23.06 | 23.46 | 22.83 | 23.51 | 23.42 | 24.62 | 23.56 | 24.20 | 23.76 | 23.56 |
| 2020 | 24.47 | 24.04 | 23.24 | 22.98 | 23.70 | 23.27 | 22.38 | 24.36 | 24.85 | 25.41 | 25.46 | 23.37 | 23.96 |
| 2021 | 22.98 | 23.39 | 21.81 | 22.29 | 22.86 | 22.42 | 22.44 | 23.57 | 24.34 | 25.37 | 23.40 | 23.76 | 23.22 |
| 2022 | 23.36 | 22.38 | 22.02 | 22.20 | 22.38 | 21.77 | 22.39 | 23.38 | 24.68 | 25.61 | 24.66 | 24.67 | 23.29 |
| Minimum temperature (°C) | 2015 | 10.28 | 10.34 | 10.96 | 10.60 | 9.58 | 9.10 | 8.44 | 8.77 | 8.05 | 10.32 | 9.57 | 9.40 | 9.62 |
| 2016 | 11.07 | 11.19 | 11.85 | 10.69 | 9.17 | 8.82 | 8.16 | 7.49 | 8.81 | 8.32 | 8.52 | 9.90 | 9.50 |
| 2017 | 10.11 | 9.64 | 10.64 | 10.51 | 9.18 | 8.10 | 6.83 | 7.69 | 8.60 | 9.61 | 8.86 | 10.13 | 9.16 |
| 2018 | 9.80 | 10.40 | 10.50 | 10.31 | 9.73 | 6.59 | 7.73 | 8.07 | 6.13 | 9.72 | 10.85 | 9.51 | 9.11 |
| 2019 | 10.12 | 11.58 | 10.71 | 11.07 | 10.01 | 8.22 | 7.82 | 7.47 | 8.76 | 9.75 | 9.24 | 10.58 | 9.61 |
| 2020 | 10.17 | 10.30 | 10.65 | 8.77 | 10.30 | 8.42 | 8.46 | 8.40 | 9.28 | 8.89 | 9.14 | 10.79 | 9.47 |
| 2021 | 9.82 | 10.69 | 10.21 | 10.36 | 9.44 | 8.72 | 7.27 | 7.86 | 8.33 | 10.24 | 9.69 | 10.34 | 9.41 |
| 2022 | 9.20 | 10.44 | 10.29 | 9.82 | 8.52 | 6.63 | 8.17 | 7.06 | 8.20 | 8.95 | 9.59 | 9.22 | 8.84 |
| Precipitation (mm/day) | 2015 | 12.68 | 12.73 | 11.62 | 12.38 | 13.30 | 14.67 | 15.51 | 15.29 | 17.61 | 14.53 | 15.55 | 16.04 | 14.33 |
| 2016 | 13.59 | 12.22 | 12.14 | 14.14 | 13.20 | 14.41 | 17.24 | 16.71 | 15.80 | 16.77 | 17.09 | 13.66 | 14.75 |
| 2017 | 11.98 | 10.52 | 10.92 | 11.47 | 12.91 | 14.98 | 15.44 | 15.71 | 15.79 | 15.00 | 15.46 | 14.01 | 13.68 |
| 2018 | 12.52 | 13.31 | 12.43 | 13.75 | 16.22 | 16.02 | 15.36 | 15.07 | 18.26 | 14.70 | 13.25 | 13.69 | 14.55 |
| 2019 | 11.13 | 11.81 | 11.86 | 13.41 | 15.06 | 15.48 | 16.09 | 15.95 | 15.86 | 13.81 | 14.96 | 13.18 | 14.05 |
| 2020 | 13.89 | 12.66 | 13.58 | 12.95 | 14.85 | 14.31 | 16.60 | 15.96 | 15.57 | 16.52 | 16.31 | 12.58 | 14.65 |
| 2021 | 12.60 | 10.73 | 11.80 | 13.59 | 13.85 | 15.85 | 14.72 | 15.72 | 16.01 | 15.14 | 13.71 | 13.42 | 13.93 |
| 2022 | 10.65 | 10.09 | 12.58 | 13.55 | 15.04 | 14.73 | 16.57 | 16.32 | 16.49 | 16.66 | 15.07 | 15.45 | 14.43 |
Table 12.
Proposed early-warning thresholds by crop, based on percentile ranges of critical climatic variables. Thresholds are general by crop and phenological stage, with suggested management actions.
Table 12.
Proposed early-warning thresholds by crop, based on percentile ranges of critical climatic variables. Thresholds are general by crop and phenological stage, with suggested management actions.
| Crop | Critical Phenology | Sensitive Variable | Yellow (≈P75) | Orange (≈P90) | Red (≈P95) | Main Risk | Recommended Action |
|---|
| Quinoa | Flowering–grain filling | Precipitation (excess)/Tmin (low) | ≥P75 rain/≤P25 Tmin | ≥P90 rain/≤P10 Tmin | ≥P95 rain/Tmin extremes | Flooding, pests, frost | Drainage, row covers, adjust planting dates |
| Corn | Sowing–flowering | Precipitation (deficit/excess)/Tmax (high) | ≤P25 (drought)/≥P75 (rain) | ≤P10/≥P90 | ≤P5/≥P95 | Drought, flooding, heat stress | Irrigation, drainage, staggered planting dates |
| Potato | Tuber initiation–bulking | Tmin (frost)/Precipitation (excess) | Tmin ≤ P25/P75 rain | Tmin ≤ P10/P90 rain | Tmin ≤ P5/P95 rain | Frost, fungal diseases | Anti-frost covers, fungicide application |
| Tree tomato | Flowering–fruiting | Precipitation (high)/Tmin (low) | ≥P75 rain | ≥P90 rain | ≥P95 rain | Fungal diseases, flower abortion | Preventive fungicide, pruning, ventilation |
Table 13.
Normality tests for production variables of the four key highland crops. Shapiro–Wilk test (p-value), Anderson–Darling statistic.
Table 13.
Normality tests for production variables of the four key highland crops. Shapiro–Wilk test (p-value), Anderson–Darling statistic.
| Crop | Variable | Result | Shapiro–Wilk (p) | Anderson–Darling | Notes |
|---|
| Corn | L.Flooding | Non-normal | 0.0033 | 1.0882 | Deviates in both tests |
| L.O.R. | Non-normal | 0.00088 | 1.1922 | Deviates in both tests |
| L.Drought | Marginal normality | 0.0522 | N/A | Close to threshold |
| T.L. | Marginal normality | 0.0590 | N/A | Close to threshold |
| C.A. | Marginal normality | 0.0667 | N/A | Close to threshold |
| Potato | L.Frost | Non-normal | 0.0289 | 0.7350 | Deviates in both tests |
| L.Diseases | Non-normal | 0.0035 | 0.9779 | Deviates in both tests |
| P. | Marginal normality | 0.0545 | N/A | Near 5% threshold |
| Tomato | L.Drought | Non-normal | <0.00001 | 1.9850 | Strong deviation |
| L.Frost | Non-normal | 0.00079 | 1.1826 | Deviates in both tests |
| L.Pests | Non-normal | 0.0000017 | 2.3017 | Strong deviation |
| L.Diseases | Non-normal | 0.00032 | 1.3429 | Deviates in both tests |
| L.O.R. | Non-normal | 0.00379 | 1.0514 | Deviates in both tests |
| T.L. | Non-normal | 0.0000101 | 1.9479 | Deviates in both tests |
| L.Flooding | Marginal normality | 0.0722 | N/A | Close to threshold |
| Quinoa | P. | Non-normal | 0.0129 | 0.7792 | — |
| S. | Non-normal | 0.0135 | 0.7631 | — |
| L.Frost | Non-normal | 0.0000558 | 1.6378 | Strong deviation |
| L.Pests | Non-normal | 0.00013 | 1.4794 | Strong deviation |
| L.Diseases | Non-normal | 0.0000251 | 1.7634 | Strong deviation |
| L.Flooding | Non-normal | 0.0000115 | 1.9325 | Strong deviation |
| L.O.R. | Non-normal | 0.0347 | 0.6522 | — |
| T.L. | Non-normal | 0.00429 | 0.9853 | — |
Table 14.
Normality tests for maximum temperature. Shapiro–Wilk test (p-value), Anderson–Darling statistic.
Table 14.
Normality tests for maximum temperature. Shapiro–Wilk test (p-value), Anderson–Darling statistic.
| Zone | Variable | Result | SW p | AD |
|---|
| North | December | Non-normal | 0.00220 | 1.0447 |
| All others | Normal | >0.05 | <0.709 |
| Central | February | Marginal normality | 0.0991 | – |
| April | Marginal normality | 0.0602 | – |
| All others | Normal | >0.05 | <0.709 |
| South | April | Marginal normality | 0.0776 | – |
| South | All others | Normal | >0.05 | <0.709 |
Table 15.
Normality tests for minimum temperature. Shapiro–Wilk test (p-value), Anderson–Darling statistic.
Table 15.
Normality tests for minimum temperature. Shapiro–Wilk test (p-value), Anderson–Darling statistic.
| Zone | Variable | Result | SW p | AD |
|---|
| North | All variables | Normal | >0.05 | <0.709 |
| Central | All variables | Normal | >0.05 | <0.709 |
| South | June | Non-normal | 0.0354 | 0.7165 |
| Annual mean | Marginal | 0.0543 | – |
| Others | Normal | >0.05 | <0.709 |
Table 16.
Normality tests for precipitation. Shapiro–Wilk test (p-value), Anderson–Darling statistic.
Table 16.
Normality tests for precipitation. Shapiro–Wilk test (p-value), Anderson–Darling statistic.
| Zone | Month/Variable | Result | SW p | AD |
|---|
| North | Jan, Mar, Apr, Jun, Jul, Aug, Sep, Oct | Non-normal | <0.05 | Up to 2.1909 |
| Feb, May, Nov, Dec | Normal | >0.05 | <0.709 |
| Central | Jan, Feb, Apr, May, Jun, Aug, Sep, Oct, Nov, Dec | Non-normal | <0.05 | Up to 1.7882 |
| Mar, Jul, Annual mean | Normal | >0.05 | <0.709 |
| South | Apr, May, Jun, Jul, Aug, Sep, Oct | Non-normal | <0.05 | Up to 1.2214 |
| Jan, Feb, Mar, Nov, Dec, annual mean | Normal | >0.05 | <0.709 |
Table 17.
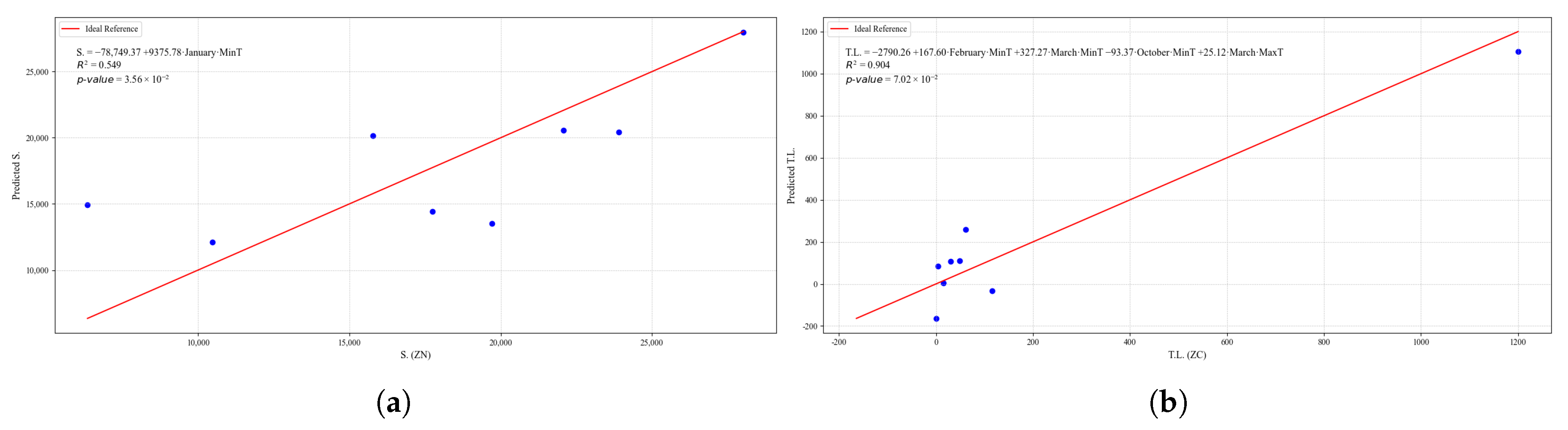
Summary of multiple linear regression models for different dependent variables. The table presents the equations used, along with the corresponding and p-values, indicating the strength and statistical significance of each model. The results allow for the evaluation of the relationship between climatic variables and quinoa crop characteristics.
Table 17.
Summary of multiple linear regression models for different dependent variables. The table presents the equations used, along with the corresponding and p-values, indicating the strength and statistical significance of each model. The results allow for the evaluation of the relationship between climatic variables and quinoa crop characteristics.
| Variable | Equations | | p-Value | | AICc | LOYO MSE | VIFmax |
|---|
| C.A. | [(‘July’, ‘MaxTempZN’), (‘August’, ‘MaxTempZN, MinTempZN’), (‘September’, ‘MaxTempZN’), (‘November’, ‘MaxTempZN’), (‘December’, ‘MaxTempZN’)] | 0.872 | 0.614 | 0.83 | 149.84 | | 123.54 |
| [(‘May’, ‘MinTempZC’), (‘August’, ‘MinTempZC’), (‘November’, ‘MinTempZC’)] | 0.953 | 0.0040 | 0.946 | 130.9 | | 1.67 |
| [(‘September’, ‘MaxTempZS’)] | 0.567 | 0.0310 | 0.547 | 143.21 | | 1 |
| H.A. | [(‘July’, ‘MaxTempZN’), (‘August’, ‘MinTempZN’), (‘September’, ‘MaxTempZN’), (‘November’, ‘MaxTempZN, MinTempZN’), (‘December’, ‘MaxTempZN’)] | 0.977 | 0.279 | 0.969 | 135.46 | | 41.43 |
| [(‘May’, ‘MinTempZC’), (‘August’, ‘MinTempZC’), (‘September’, ‘MaxTempZC’), (‘November’, ‘MinTempZC’)] | 0.986 | 0.00389 | 0.984 | 123.59 | | 1.91 |
| [(‘August’, ‘MinTempZS’), (‘September’, ‘MaxTempZS’)] | 0.749 | 0.0314 | 0.726 | 140.82 | | 1.34 |
| P. | [(‘July’, ‘MaxTempZN’), (‘August’, ‘MaxTempZN, MinTempZN’), (‘September’, ‘MaxTempZN’), (‘November’, ‘MaxTempZN’), (‘December’, ‘MaxTempZN’)] | 0.982 | 0.243 | 0.977 | 142.21 | | 123.43 |
| [(‘May’, ‘MinTempZC’), (‘August’, ‘MinTempZC’)] | 0.769 | 0.0256 | 0.747 | 149.19 | | 1.56 |
| [(‘September’, ‘MaxTempZS’)] | 0.541 | 0.0376 | 0.520 | 152.07 | | 1 |
| S. | [(‘July’, ‘MaxTempZN’), (‘August’, ‘MaxTempZN, MinTempZN’), (‘September’, ‘MaxTempZN’), (‘November’, ‘MaxTempZN’), (‘December’, ‘MaxTempZN’)] | 0.991 | 0.176 | 0.988 | 134.52 | | 123.54 |
| [(‘May’, ‘MinTempZC’), (‘August’, ‘MinTempZC’)] | 0.747 | 0.0320 | 0.723 | 147.42 | | 1.56 |
| [(‘September’, ‘MaxTempZS’)] | 0.547 | 0.0359 | 0.527 | 149.47 | | 1 |
| T.L. | — | — | — | — | — | — | — |
| — | — | — | — | — | — | — |
| — | — | — | — | — | — | — |
| L.Drought | [(‘April’, ‘MinTempZN’)] | 0.501 | 0.917 | 0.479 | 109.15 | | 1 |
| [(‘January’, ‘MinTempZC’), (‘June’, ‘MinTempZC’), (‘December’, ‘PrecipitationZC’)] | 0.892 | 0.0208 | 0.877 | 102.41 | | 2.95 |
| — | — | — | — | — | — | — |
| L.Frost | [(‘July’, ‘MaxTempZN’), (‘August’, ‘MinTempZN’), (‘September’, ‘MaxTempZN’), (‘November’, ‘MaxTempZN’), (‘December’, ‘MaxTempZN’)] | 0.998 | 0.00355 | 0.998 | 69.13 | 664.52 | 27.21 |
| [(‘August’, ‘MinTempZC’)] | 0.720 | 0.00772 | 0.707 | 99.02 | | 1 |
| [(‘May’, ‘PrecipitationZS’)] | 0.634 | 0.0179 | 0.618 | 101.15 | | 1 |
| L.Pests | [(‘July’, ‘MinTempZN’), (‘December’, ‘PrecipitationZN’)] | 0.542 | 0.142 | 0.499 | 101.70 | | 5.97 |
| [(’January’, ’PrecipitationZC’), (’April’, ’PrecipitationZC’), (’June’, ’PrecipitationZC’)] | 0.968 | 0.00184 | 0.964 | 83.19 | | 8.47 |
| — | — | — | — | — | — | — |
| L.Diseases | [(‘May’, ‘MaxTempZN, MinTempZN’)] | 0.608 | 0.907 | 0.571 | 94.52 | | 3.23 |
| [(‘January’, ‘MaxTempZC, MinTempZC, PrecipitationZC’), (‘February’, ‘MinTempZC’), (‘March’, ‘MinTempZC, PrecipitationZC’), (‘October’, ‘MinTempZC’), (‘November’, ‘PrecipitationZC’)] | 1.000 | 0 | 0 | 0 | 0 | 0 |
| [(‘March’, ‘MaxTempZS, MinTempZS’), (‘September’, ‘PrecipitationZS’), (‘November’, ’MaxTempZS, MinTempZS’)] | 0.990 | 0.316 | 0.96 | 84.01 | | 8.73 |
| L.Flooding | — | — | — | — | — | — | — |
| [(‘February’, ‘PrecipitationZC’), (‘September’, ‘MinTempZC’), (‘November’, ‘MinTempZC’)] | 0.973 | 0.128 | 0.97 | 56.94 | 524.2 | 2.51 |
| [(‘June’, ‘MinTempZS’), (‘September’, ‘MinTempZS’), (‘November’, ‘MinTempZS’)] | 0.798 | 0.750 | 0.768 | 73.31 | | 2.95 |
| L.O.R. | [(‘April’, ‘MinTempZN’)] | 0.504 | 0.0484 | 0.482 | 95.96 | | 1 |
| — | — | — | — | — | — | — |
| [(‘May’, ‘PrecipitationZS’)] | 0.003 | 0.896 | -0.042 | 101.56 | | 1 |