Systematic Calibration and Validation of Discrete Element Model Parameters for Cotton Root Systems
Abstract
1. Introduction
2. Materials and Methods
2.1. Determination of Basic Physical Properties of Cotton Root Systems
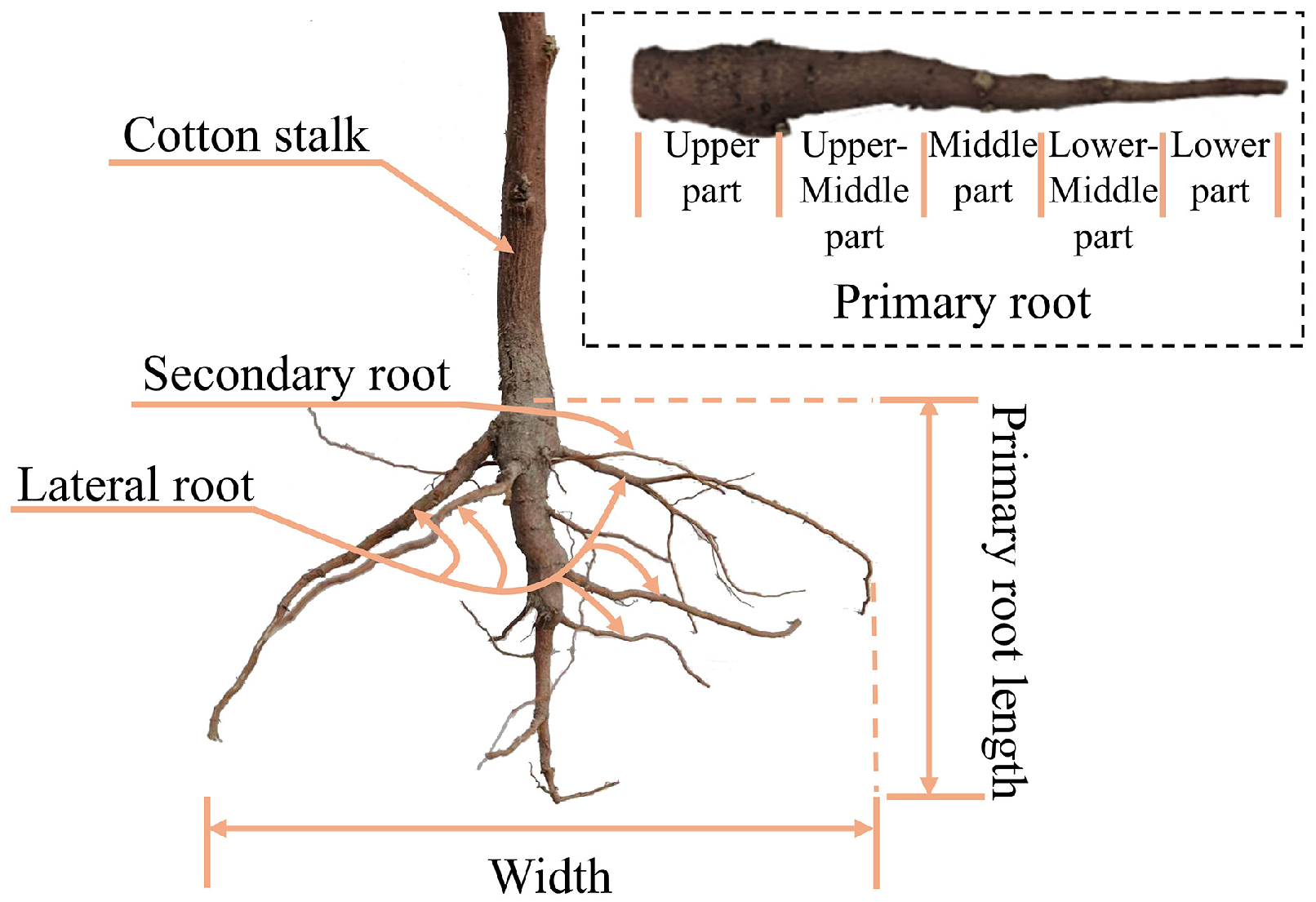
2.1.1. Morphological Parameters
2.1.2. Intrinsic and Contact Parameters
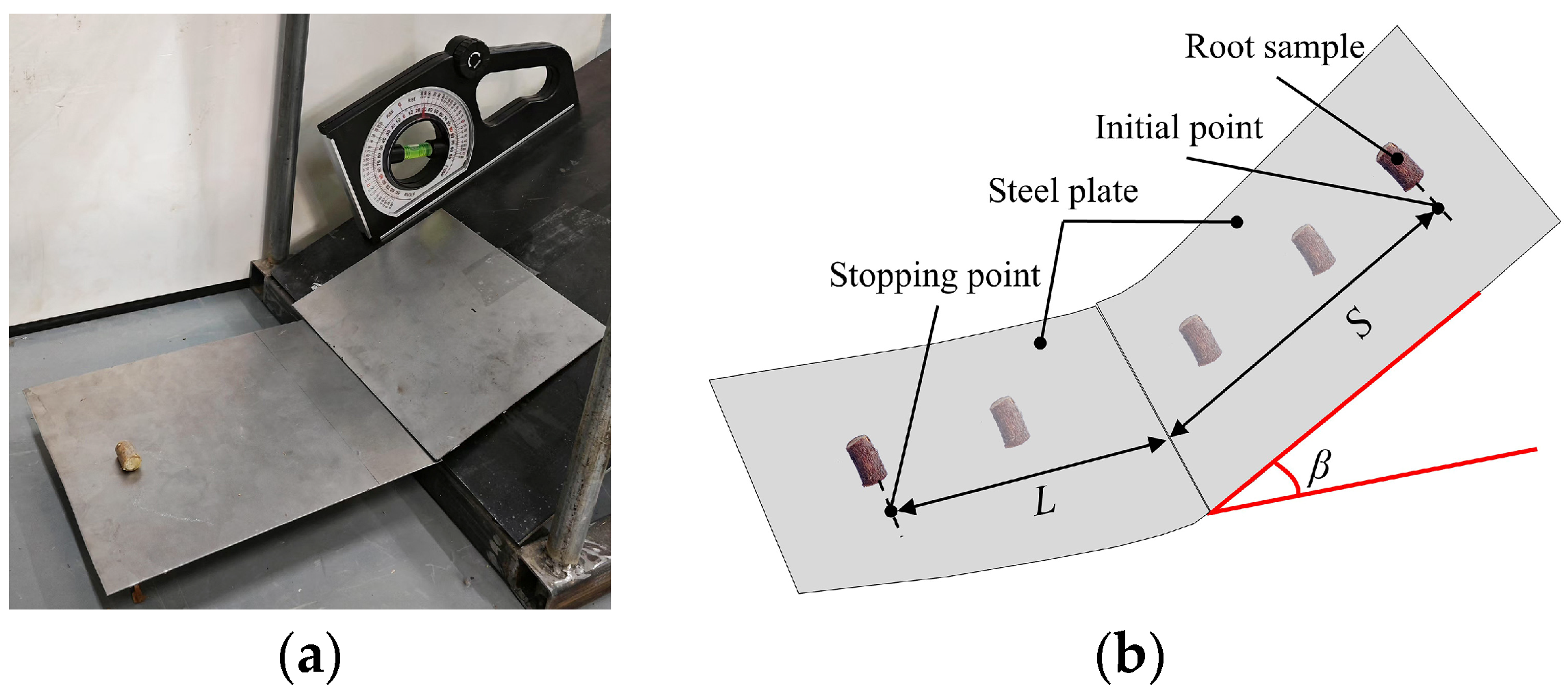
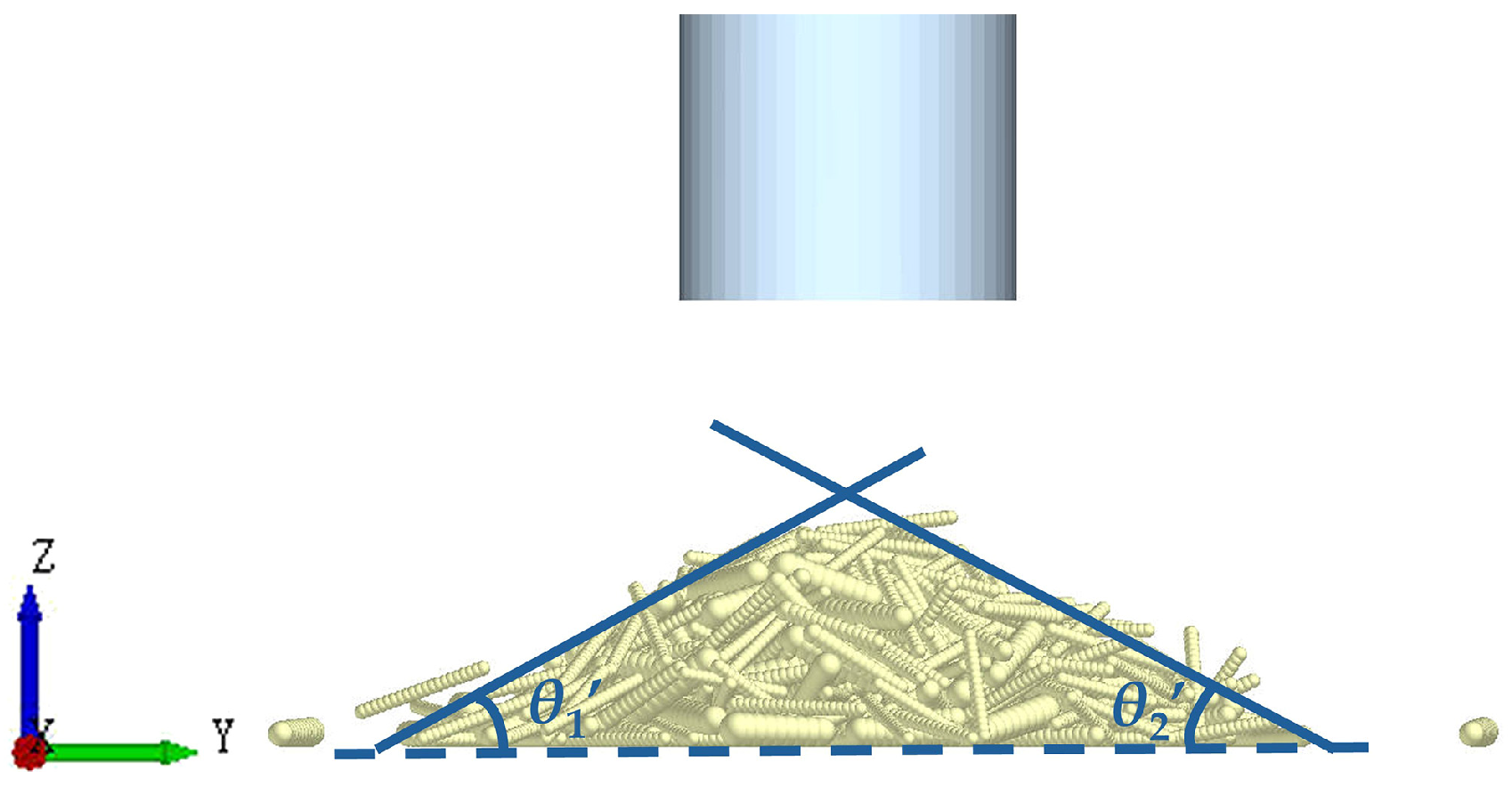
2.2. Physical Test of the Cotton Roots Stacking Angle
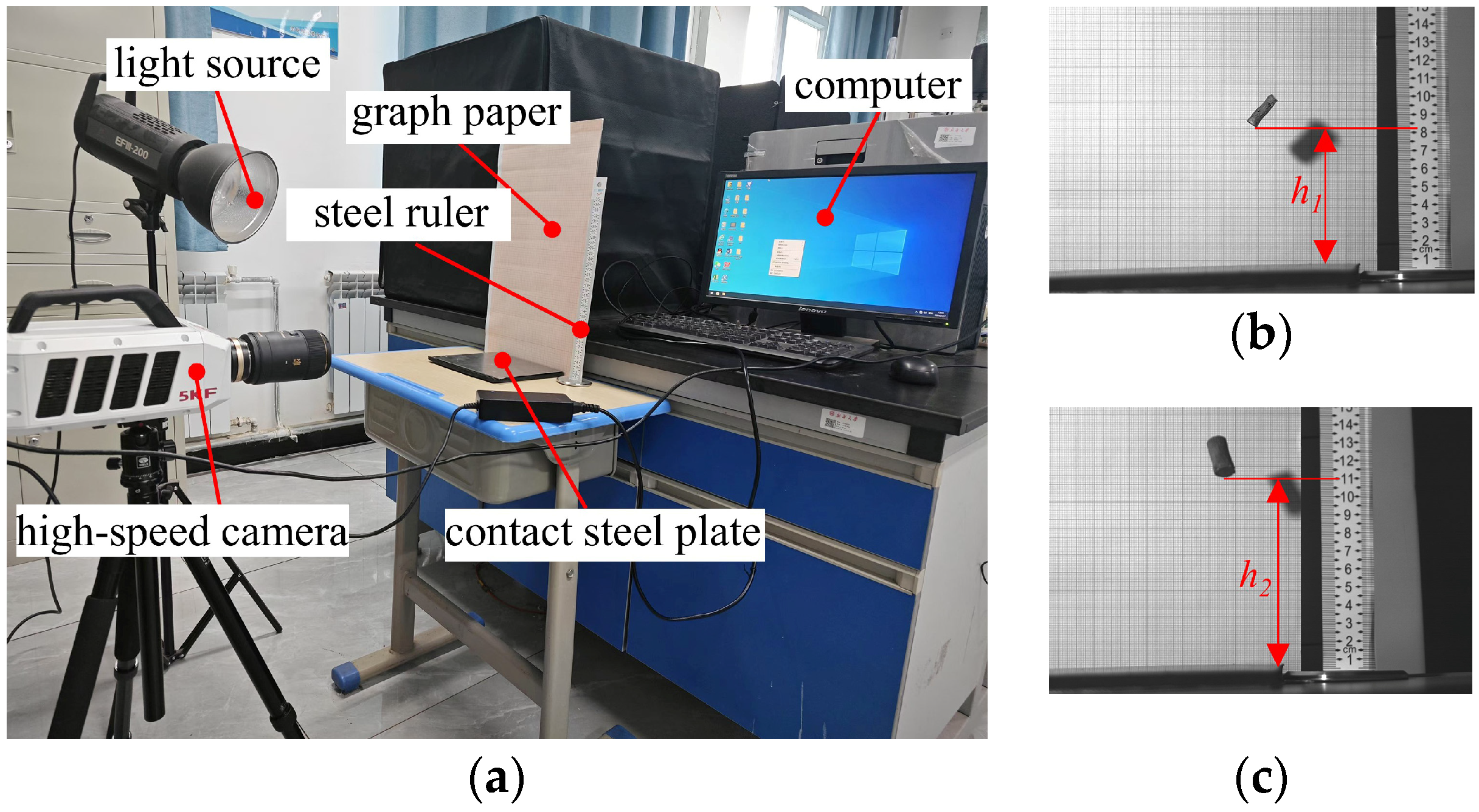
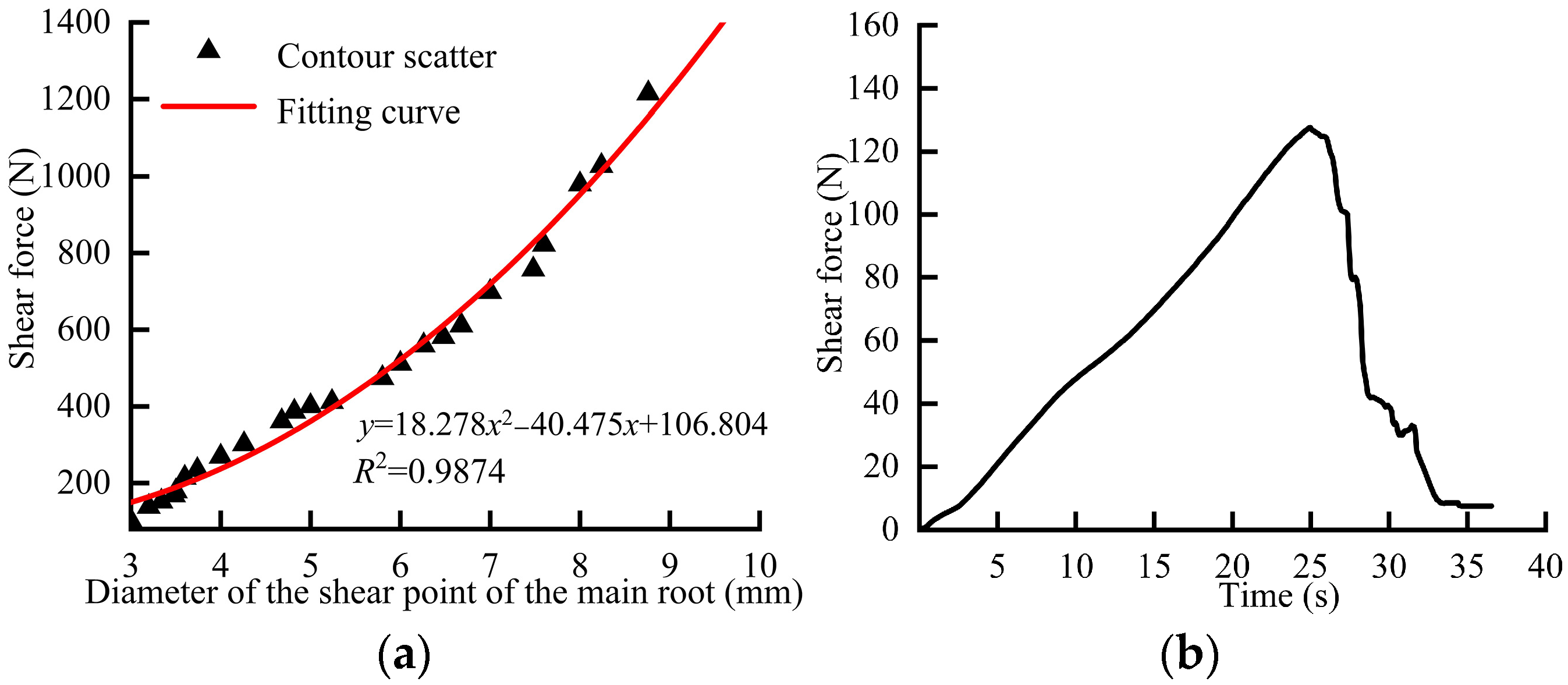
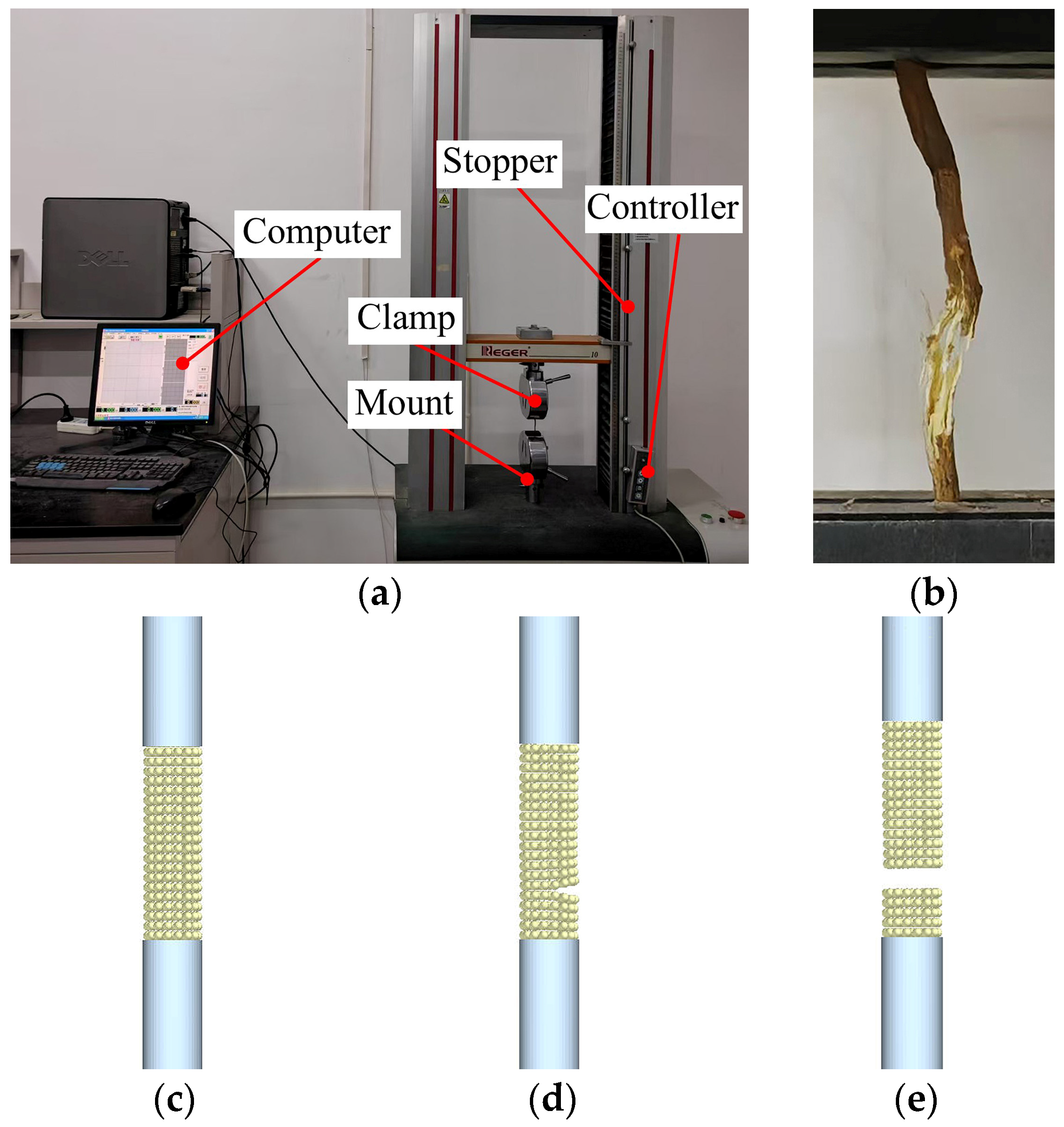
2.3. Measurement of Cotton Roots Shear Mechanical Properties
2.4. Establishment of the Discrete Element Simulation Model
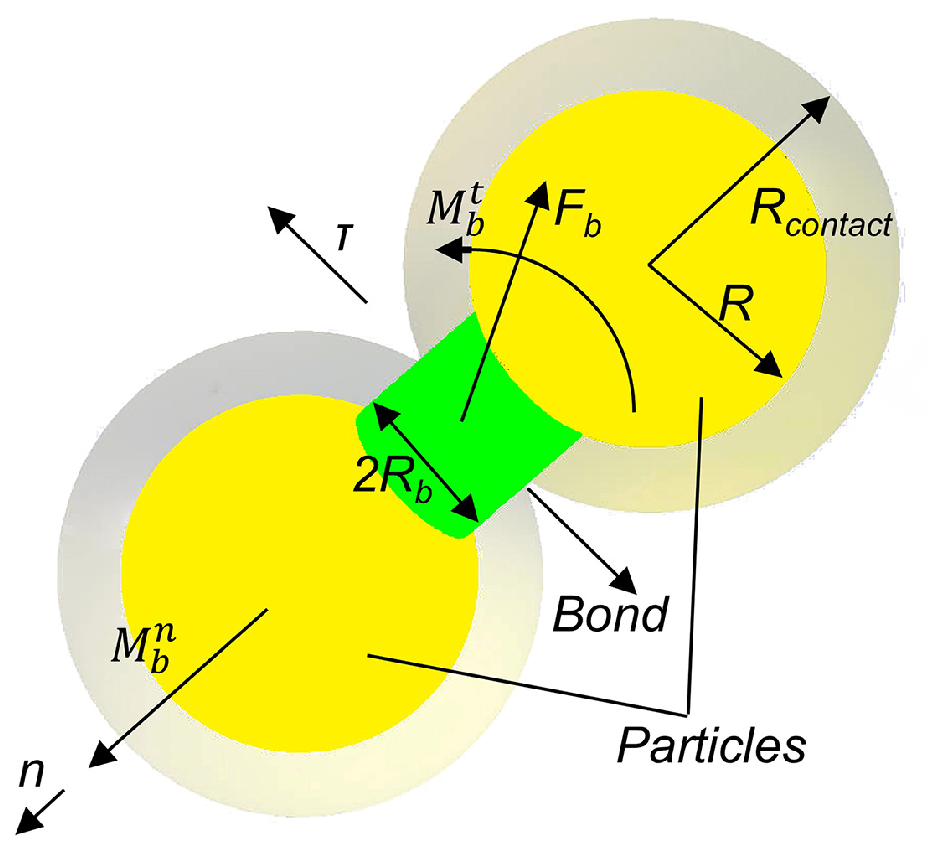
2.4.1. Selection of the Discrete Element Contact Model
2.4.2. Root System Modeling Based on the 3D Scanning
2.4.3. Establishment of the Simulation Model for the Stacking Angle Test
2.4.4. Establishment of the Cotton Roots Shear Simulation Model
2.5. Parameter Calibration Method
2.5.1. Plackett–Burman Test
2.5.2. Steepest Ascent Test
2.5.3. Box–Behnken Test
2.5.4. CCD Test
3. Results and Discussion
3.1. Calibration of the Contact Parameters
3.1.1. Plackett–Burman Test Analysis
3.1.2. Steepest Ascent Test Analysis
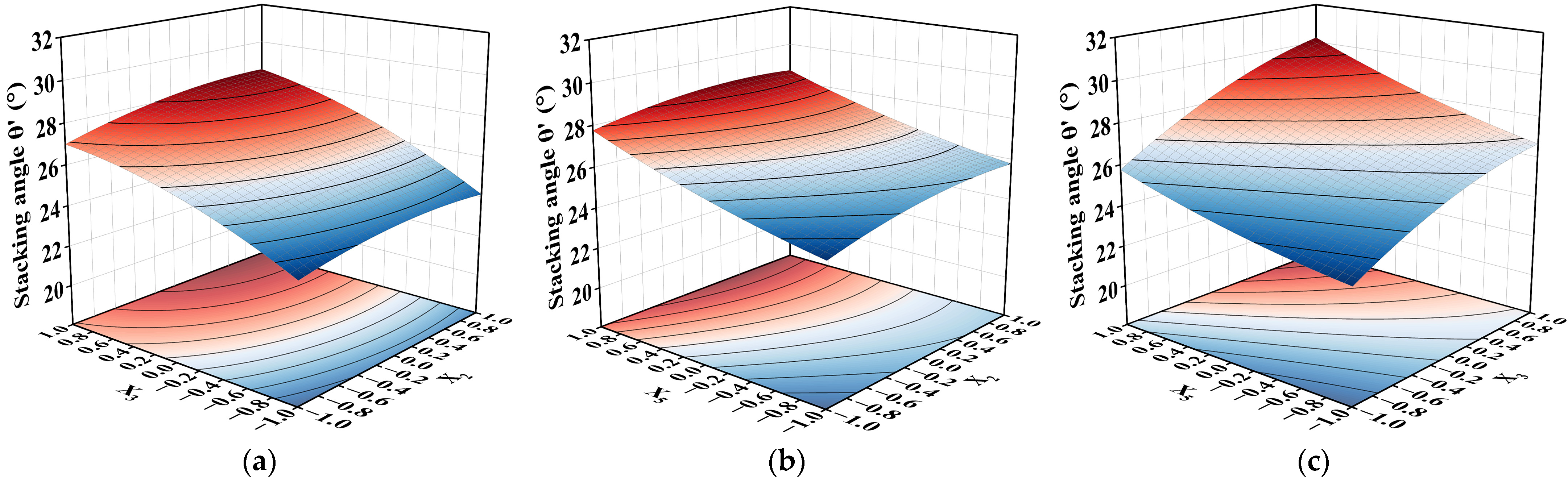
3.1.3. Box–Behnken Test Analysis
3.1.4. Contact Parameters Optimization and Simulation Test Verification
3.2. Calibration of the Bonding Parameters
3.2.1. CCD Test Analysis
3.2.2. Bonding Parameters Optimization and Simulation Test Verification
3.3. Field Trial Validation
4. Conclusions
- (1)
- This study, based on systematic real-time measurements of cotton root systems during harvest, successfully gathered critical data, including profile structure parameters, friction characteristic parameters, stacking angles, and mechanical characteristic parameters of the root systems. The detailed dimensions of the root system were obtained through physical measurements, revealing static friction coefficients between cotton roots and steel in the range of 0.563 to 0.616, rolling friction coefficients between 0.05 and 0.085, and restitution coefficients ranging from 0.429 to 0.612. Moreover, the average stacking angle, determined via stacking angle tests, was found to be 26.61°. The peak shearing force of the main root with varying axial diameters, measured through shear tests, ranged from 102.174 N to 1215.233 N, while the average peak shear force of lateral roots was recorded at 146.077 N. The average maximum tensile breaking force identified in lateral root tensile tests was 36.287 N. Using these foundational physical parameters, the cotton root bonding model was constructed by integrating the root structure derived from the 3D laser scans and utilizing the particle fast-filling function within EDEM software.
- (2)
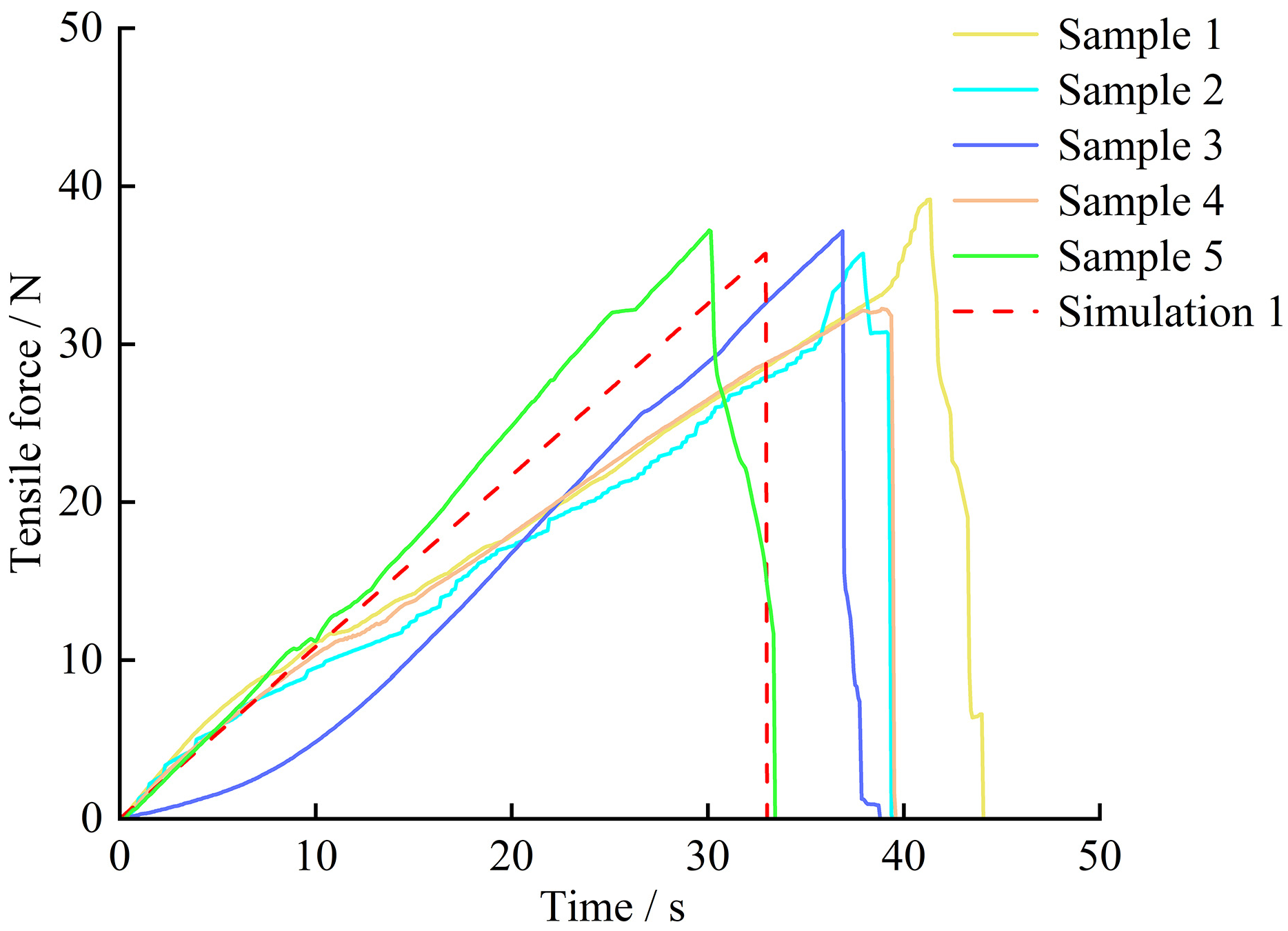
- The parameters of the contact model and bond model were calibrated by establishing an optimization procedure with the stacking angle and peak shear force as key response indicators. In the contact model, the static friction coefficient between root–root, rolling friction coefficient, and restitution coefficient between root–steel significantly influenced the stacking angle. An optimal parameter set, determined through Box–Behnken response surface optimization tests, was identified as 0.571, 0.180, and 0.583. The simulated stacking angle also achieved with these parameters was 26.496°, with a relative error of only 0.43% compared to the actual stacking angle. In the bonding model, the effects of normal contact stiffness and shear contact stiffness on the peak shear force were significant, leading to an optimal parameter solution of 3.57 × 1010 N/m3 for normal contact stiffness and 3.84 × 1010 N/m3 for shear contact stiffness. The simulated peak shear force of the coaxial diameter main root under this parameter combination was 480.40 N, matching the actual measurement exactly, with a relative error of just 1.22%. Additionally, the simulated maximum destructive tensile force of the lateral root was found to be 32.780 N, presenting a relative error of 1.40% when compared to the measured value.
- (3)
- Utilizing the calibrated root model parameters, a simulation model representing root–soil complexes was constructed to reflect actual harvesting conditions, enabling the verification of root pull-up force. The results obtained indicated an average pull-up force of 452.79 N across five trials, which was comparable to the field test value of 436.39 N, resulting in a 3.76% relative error. This evidence highlights the validity of the root model in simulating complex root–soil interactions. The research findings provide a theoretical foundation and reliable data to support the structural design and optimization of operational parameters for cotton stalk harvesting equipment.
- (4)
- The modeling approach proposed in this study provides a feasible and effective flexible root model for the simulation-based design and optimization of whole-stalk cotton stalk harvesters. Additionally, the parameter calibration and optimization have further enriched the DEM parameter database in this field. It should be noted that the field experiments on root extraction force were conducted under specific soil conditions (sandy loam) and moisture content. Whether the root model can maintain its accuracy after adjusting soil-specific parameters requires further validation through more extensive testing. To enhance the applicability of the parameters across different soil types and moisture levels, follow-up studies will include systematic sensitivity analyses involving various cotton field soil types and different moisture gradients. This will help verify and extend the reliability and generalizability of the root model.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Cai, C.; Wang, Z.; Ma, L.; Xu, Z.; Yu, J.; Li, F. Cotton stalk valorization towards bio-based materials, chemicals, and biofuels: A review. Renew. Sustain. Energy Rev. 2024, 202, 114651. [Google Scholar] [CrossRef]
- Zhu, Y.; Zheng, B.; Luo, Q.; Jiao, W.; Yang, Y. Uncovering the drivers and regional variability of cotton yield in China. Agriculture 2023, 13, 2132. [Google Scholar] [CrossRef]
- Zeng, F.; Diao, H.; Cui, J.; Ye, W.; Bai, H.; Li, X. Establishment and Parameter Calibration of a Simulation Model of Coated Cotton Seeds and Soil. Processes 2024, 12, 521. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, Z.; Cai, J.; Yeerbolati, T.; Rui, Z.; Wang, Y. Design and experiments of cotton stalk pulling machine with horizontal-counter rollers. Trans. CSAE 2021, 37, 43–53. [Google Scholar] [CrossRef]
- Xie, J.; Wu, S.; Cao, S.; Zhang, Y.; Zhao, W.; Zhou, J. Design and test of clamping-roller cotton stalk pulling device. Trans. CSAM 2023, 54, 101–111. [Google Scholar] [CrossRef]
- Tamás, K.; Bernon, L. Role of particle shape and plant roots in the discrete element model of soil–sweep interaction. Biosyst. Eng. 2021, 211, 77–96. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, P.; Zhang, H.; Tan, C.; Wan, W.; Wang, Y. Discrete Element Simulation Parameters Calibration for Xinjiang Cotton Straw. Trans. CSAM 2024, 55, 76–84. [Google Scholar] [CrossRef]
- Liu, H.; Cao, S.; Han, D.; He, L.; Li, Y.; Cai, J.; Meng, H.; Wang, S. Parametric Analysis and Numerical Optimization of Root-Cutting Shovel of Cotton Stalk Harvester Using Discrete Element Method. Agriculture 2024, 14, 1451. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, X.; Liu, D.; Xie, F.; Ashwehmbom, L.; Zhang, Z.; Tang, Q. Calibration of discrete element parameters and experimental verification for modelling subsurface soils. Biosyst. Eng. 2021, 212, 215–217. [Google Scholar] [CrossRef]
- Horabik, J.; Molenda, M. Parameters and contact models for DEM simulations of agricultural granular materials: A review. Biosyst. Eng. 2016, 147, 206–225. [Google Scholar] [CrossRef]
- Chen, Y.; Munkholm, L.; Nyord, T. A discrete element model for soil–sweep interaction in three different soils. Soil Tillage Res. 2013, 126, 34–41. [Google Scholar] [CrossRef]
- Ma, Z.; Traore, S.; Zhu, Y.; Li, Y.; Xu, L.; En, L.; Li, Y. DEM simulations and experiments investigating of grain tank discharge of a rice combine harvester. Comput. Electron. Agric. 2022, 198, 107060. [Google Scholar] [CrossRef]
- Zhao, J.; Yu, J.; Sun, K.; Wang, Y.; Liang, L.; Sun, Y.; Zhou, L.; Yu, Y. A discrete element method model and experimental verification for wheat root systems. Biosyst. Eng. 2024, 244, 146–165. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, J.; Yin, B.; Ma, Z.; Hao, J.; Yang, X.; Feng, X.; Ma, Y. Discrete element modelling of the yam root–soil complex and its verification. Biosyst. Eng. 2022, 220, 55–72. [Google Scholar] [CrossRef]
- Zou, L.; Yan, D.; Niu, Z.; Jin, Y.; Cheng, H.; Zheng, H. Parametric analysis and numerical optimisation of spinach root vibration shovel cutting using discrete element method. Comput. Electron. Agric. 2023, 212, 108138. [Google Scholar] [CrossRef]
- Zhang, S.; Zhao, L.; Wang, X.; Huang, D. Quantifying the effects of elongation and flatness on the shear behavior of realistic 3D rock aggregates based on DEM modeling. Adv. Powder Technol. 2021, 32, 1318–1332. [Google Scholar] [CrossRef]
- Li, C.; Zhou, X. Visualization of stick-slip shear failure process of granite by 3D reconstruction technique and DEM. Tribol. Int. 2022, 176, 107923. [Google Scholar] [CrossRef]
- Wang, L.; Yang, H.; Wang, Z.; Wang, Q.; Lu, C.; Wang, C.; He, J. Calibration of DEM Polyhedron Model for Wheat Seed Based on Angle of Repose Test and Semi-Resolved CFD-DEM Coupling Simulation. Agriculture 2025, 15, 506. [Google Scholar] [CrossRef]
- Ligier, K.; Vrublevskyi, O.; Napiorkowski, J. Optimisation of calibration parameters for a discrete element method (DEM) model of plant-origin grains with a low elasticity modulus. Powder Technol. 2024, 444, 120009. [Google Scholar] [CrossRef]
- Xie, K.; Zhang, Z.; Wang, F.; Yu, X.; Wang, C.; Jiang, S. Calibration and experimental verification of discrete element parameters of Panax notoginseng root. Int. J. Agric. Biol. Eng. 2024, 17, 12–23. [Google Scholar] [CrossRef]
- Jiang, D.; Chen, X.; Yan, L.; Gou, H.; Yang, J.; Li, Y. Parameter calibration of discrete element model for cotton rootstalk–soil mixture at harvest stage in Xinjiang cotton field. Agriculture 2023, 13, 1344. [Google Scholar] [CrossRef]
- GB/T 5262-2008; General Provisions on Methods for Determining Test Conditions of Agricultural Machinery. China Standard Press: Beijing, China, 2008.
- Wang, X.; Zhang, Q.; Huang, Y.; Ji, J. An efficient method for determining DEM parameters of a loose cohesive soil modelled using hysteretic spring and linear cohesion contact models. Biosyst. Eng. 2022, 215, 283–294. [Google Scholar] [CrossRef]
- Ma, Y.; Song, C.; Xuan, C.; Wang, H.; Yang, S.; Wu, P. Parameters calibration of discrete element model for alfalfa straw compression simulation. Trans. CSAE 2020, 36, 22–30. [Google Scholar] [CrossRef]
- Fang, M.; Yu, Z.; Zhang, W.; Jiang, C.; Liu, W. Friction coefficient calibration of corn stalk particle mixtures using Plackett-Burman design and response surface methodology. Powder Technol. 2022, 396, 731–742. [Google Scholar] [CrossRef]
- Li, X.; Du, Y.; Liu, L.; Mao, E.; Yang, F.; Wu, J.; Wang, L. Research on the constitutive model of low-damage corn threshing based on DEM. Comput. Electron. Agric. 2022, 194, 106722. [Google Scholar] [CrossRef]
- Li, S.; Diao, P.; Miao, H.; Zhao, Y.; Li, X.; Zhao, H. Modeling the fracture process of wheat straw using a discrete element approach. Powder Technol. 2024, 439, 119726. [Google Scholar] [CrossRef]
- He, X.; Zhang, X.; Zhao, Z.; Shang, S.; Wang, D.; Yuan, X. Design and Test of Resistance-reducing Excavation Device of Cyperus edulis Based on Discrete Element Method. Trans. Chin. Soc. Agric. Mach. 2021, 52, 124–133. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.; Du, D.; Long, S.; Wang, Y.; Han, C.; Xu, Y. Optimization and validation of root-cutting device for Chinese cabbage harvester based on discrete element method. Comput. Electron. Agric. 2023, 214, 108314. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, F.; Dong, J.; Chen, X.; Liu, Y.; Mi, G.; Wang, T.; Jia, X.; Huang, Y.; Wang, X. Calibration of discrete element parameters of maize root and its mixture with soil. Processes 2022, 10, 2433. [Google Scholar] [CrossRef]
- Cai, J.; Zhang, J.; Gao, Z.; Wang, X.; Guo, G.; Baikeli, Y.; Tang, X.; Wang, Y. Design and test of a wheel-belt type cotton stalk puller. Int. J. Agric. Biol. Eng. 2024, 17, 102–108. [Google Scholar] [CrossRef]
- Song, S.; Tang, Z.; Zheng, X.; Liu, J.; Meng, X.; Liang, Y. Calibration of the discrete element parameters for the soil model of cotton field after plowing in Xinjiang of China. Trans. CSAE 2021, 37, 63–70. [Google Scholar]
- Fang, W.; Wang, X.; Han, D.; Zang, N.; Chen, X.; Ohiemi, I. Parameter optimization and disturbance analysis of the film picking device of the chain-type plough layer residual film recovery machine based on DEM-MBD coupling. Comput. Electron. Agric. 2024, 222, 109041. [Google Scholar] [CrossRef]







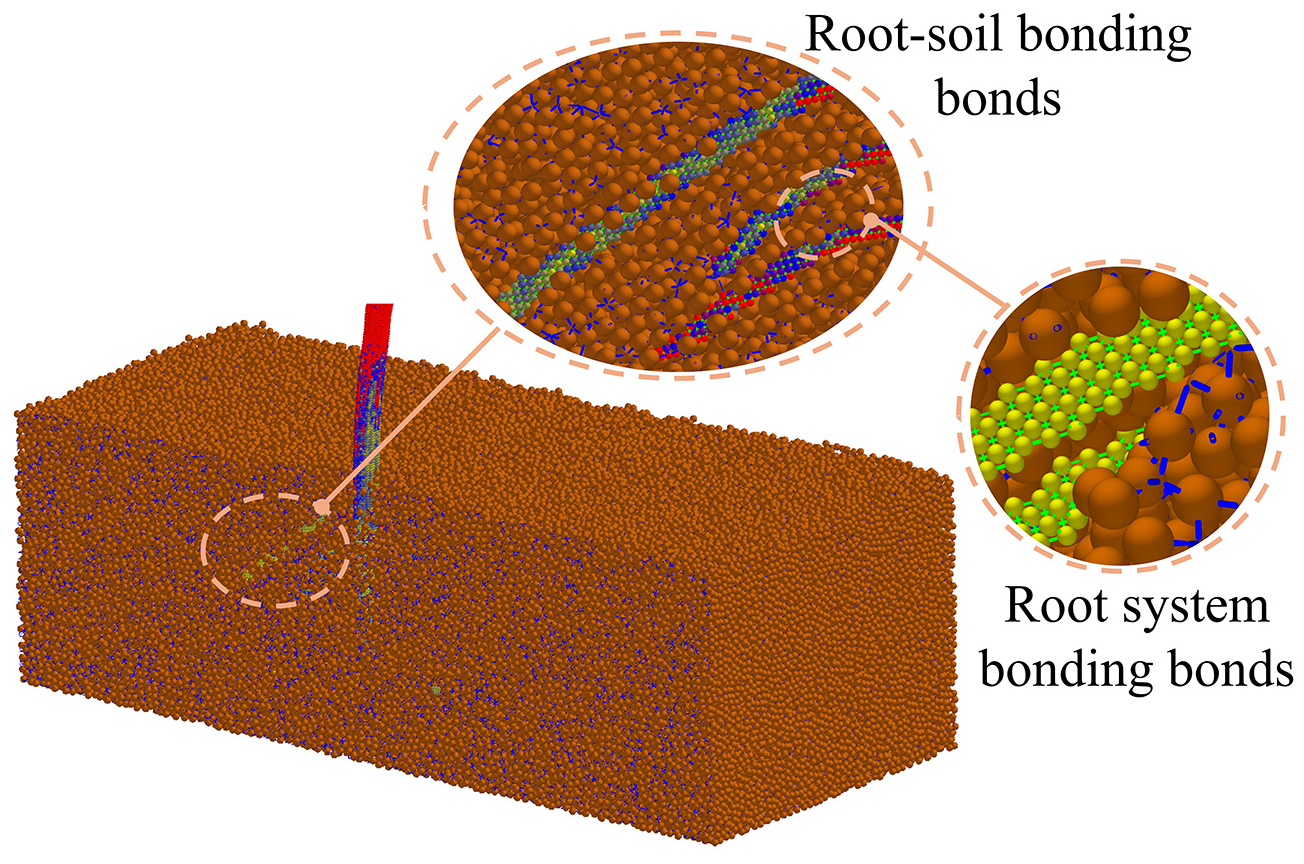
| Parameters | Value | Note | |
|---|---|---|---|
| Primary root | Upper average diameter (mm) | 11.26 | Segment length 27.83 mm |
| Upper-middle average diameter (mm) | 9.12 | Segment length 23.57 mm | |
| Middle average diameter (mm) | 7.24 | Segment length 22.61 mm | |
| Lower-middle average diameter (mm) | 5.72 | Segment length 24.73 mm | |
| Lower average diameter (mm) | 3.98 | Segment length 25.61 mm | |
| Average length (mm) | 124.34 | ||
| Lateral root | Average diameter (mm) | 3.16 | |
| Average length (mm) | 68.44 | ||
| Average quantity (mm) | 6.3 | ||
| Root branching order | 2 | ||
| Average branching angle (°) | 60 | ||
| Average width (mm) | 126.8 | ||
| Parameters | Primary Roots | Lateral Roots | Steel |
|---|---|---|---|
| Density (kg·m−3) | 885 | 861 | 7850 |
| Poisson’s ratio | 0.37 | 0.41 | 0.30 |
| Shear modulus (Pa) | 6.93 × 108 | 5.27 × 106 | 7.94 × 1010 |
| Simulation Parameters | Symbol | Low Level (−1) | High Level (+1) |
|---|---|---|---|
| Restitution coefficient of root–root | X1 | 0.239 | 0.428 |
| Static friction coefficient of root–root | X2 | 0.481 | 0.702 |
| Rolling friction coefficient of root–root | X3 | 0.050 | 0.250 |
| Restitution coefficient of root–steel | X4 | 0.429 | 0.612 |
| Static friction coefficient of root–steel | X5 | 0.563 | 0.616 |
| Rolling friction coefficient of root–steel | X6 | 0.050 | 0.085 |
| Simulation Parameter | Symbol | Low Level (−1) | High Level (+1) |
|---|---|---|---|
| Normal stiffness per unit area of cotton root (N·m−3) | X7 | 2.50 × 1010 | 4.15 × 1010 |
| Shear stiffness per unit area of cotton root (N·m−3) | X8 | 3.0 × 1010 | 5.6 × 1010 |
| Critical normal stress of cotton root (MPa) | X9 | 10 | 40 |
| Critical shear stress of cotton root (MPa) | X10 | 10 | 50 |
| Coding | X7 (N·m−3) | X8 (N·m−3) | X9 (MPa) | X10 (MPa) |
|---|---|---|---|---|
| −2 | 2.5 × 1010 | 3.0 × 1010 | 10 | 10 |
| −1 | 2.91 × 1010 | 3.65 × 1010 | 17.5 | 20 |
| 0 | 3.33 × 1010 | 4.3 × 1010 | 25 | 30 |
| 1 | 3.74 × 1010 | 4.95 × 1010 | 32.5 | 40 |
| 2 | 4.15 × 1010 | 5.6 × 1010 | 40 | 50 |
| Serial No. | Factors | θ′ (°) | |||||
|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | X6 | ||
| 1 | −1 | −1 | −1 | 1 | −1 | 1 | 21.51° |
| 2 | 1 | −1 | −1 | −1 | 1 | −1 | 24.63° |
| 3 | 1 | −1 | 1 | 1 | −1 | 1 | 25.41° |
| 4 | 1 | 1 | 1 | −1 | −1 | −1 | 25.74° |
| 5 | 1 | 1 | −1 | −1 | −1 | 1 | 24.85° |
| 6 | −1 | −1 | −1 | −1 | −1 | −1 | 23.13° |
| 7 | −1 | 1 | −1 | 1 | 1 | −1 | 25.83° |
| 8 | 1 | 1 | −1 | 1 | 1 | 1 | 25.73° |
| 9 | −1 | 1 | 1 | 1 | −1 | −1 | 26.03° |
| 10 | 1 | −1 | 1 | 1 | 1 | −1 | 26.86° |
| 11 | −1 | −1 | 1 | −1 | 1 | 1 | 26.94° |
| 12 | −1 | 1 | 1 | −1 | 1 | 1 | 30.53° |
| Parameters | Standardized Effects | Sum of Squares | F-Value | p-Value | Significance Ranking |
|---|---|---|---|---|---|
| X1 | −0.125 | 0.0469 | 0.0531 | 0.8269 | 6 |
| X2 | 1.705 | 8.72 | 9.88 | 0.0256 | 3 |
| X3 | 2.638 | 20.88 | 23.65 | 0.0046 | 1 |
| X4 | −0.742 | 1.65 | 1.87 | 0.2299 | 4 |
| X5 | 2.308 | 15.99 | 18.10 | 0.0081 | 2 |
| X6 | 0.458 | 0.6302 | 0.7137 | 0.4368 | 5 |
| Serial No. | X2 | X3 | X5 | θ′ (°) | φ (%) |
|---|---|---|---|---|---|
| 1 | 0.481 | 0.05 | 0.563 | 22.31° | 16.16% |
| 2 | 0.536 | 0.10 | 0.577 | 24.71° | 7.14% |
| 3 | 0.592 | 0.15 | 0.590 | 25.52° | 4.10% |
| 4 | 0.647 | 0.20 | 0.603 | 28.18° | 5.90% |
| 5 | 0.702 | 0.25 | 0.616 | 29.55° | 11.05% |
| Serial No. | Factors | θ′ (°) | ||
|---|---|---|---|---|
| X2 | X3 | X5 | ||
| 1 | −1 | 0 | −1 | 24.55 |
| 2 | 1 | −1 | 0 | 24.12 |
| 3 | 0 | 1 | 1 | 30.23 |
| 4 | 1 | 1 | 0 | 28.51 |
| 5 | 0 | 0 | 0 | 26.91 |
| 6 | 0 | −1 | −1 | 23.35 |
| 7 | −1 | 1 | 0 | 26.99 |
| 8 | 0 | 0 | 0 | 27.12 |
| 9 | 0 | 0 | 0 | 26.84 |
| 10 | 1 | 0 | 1 | 28.58 |
| 11 | 1 | 0 | −1 | 25.77 |
| 12 | 0 | −1 | 1 | 25.75 |
| 13 | 0 | 0 | 0 | 26.44 |
| 14 | −1 | 0 | 1 | 27.76 |
| 15 | 0 | 1 | −1 | 26.65 |
| 16 | 0 | 0 | 0 | 26.69 |
| 17 | −1 | −1 | 0 | 23.60 |
| Parameters | Degree of Freedom | Mean Square | F-Value | p-Value | Significance |
|---|---|---|---|---|---|
| Model | 9 | 5.94 | 161.13 | <0.0001 | ** |
| X2 | 1 | 2.08 | 56.46 | 0.0001 | ** |
| X3 | 1 | 30.26 | 821.12 | <0.0001 | ** |
| X5 | 1 | 18.00 | 488.37 | <0.0001 | ** |
| X2X3 | 1 | 0.25 | 6.78 | 0.0352 | * |
| X2X5 | 1 | 0.04 | 1.09 | 0.3322 | |
| X3X5 | 1 | 0.3481 | 9.44 | 0.0180 | * |
| 1 | 0.7164 | 19.44 | 0.0031 | ** | |
| 1 | 1.43 | 38.76 | 0.0004 | ** | |
| 1 | 0.3242 | 8.80 | 0.0209 | * | |
| Residual | 7 | 0.0369 | |||
| Lack of fit | 3 | 0.0001 | 0.9070 | ||
| Pure error | 4 | 0.0644 | |||
| Total | 16 |
| Serial No. | Factors | Fmax (N) | |||
|---|---|---|---|---|---|
| X7 | X8 | X9 | X10 | ||
| 1 | 1 | −1 | 1 | 1 | 480.66 |
| 2 | −1 | 1 | 1 | −1 | 442.38 |
| 3 | 1 | −1 | −1 | −1 | 479.18 |
| 4 | 1 | −1 | 1 | −1 | 476.77 |
| 5 | 0 | 2 | 0 | 0 | 468.53 |
| 6 | −1 | 1 | −1 | 1 | 443.10 |
| 7 | −1 | 1 | 1 | 1 | 443.97 |
| 8 | 0 | −2 | 0 | 0 | 440.64 |
| 9 | 0 | 0 | 0 | 0 | 466.85 |
| 10 | −1 | −1 | −1 | 1 | 434.61 |
| 11 | 1 | 1 | −1 | 1 | 492.55 |
| 12 | 1 | 1 | −1 | −1 | 491.67 |
| 13 | −1 | −1 | 1 | 1 | 433.39 |
| 14 | −2 | 0 | 0 | 0 | 416.03 |
| 15 | 0 | 0 | 2 | 0 | 468.29 |
| 16 | 0 | 0 | 0 | 2 | 468.41 |
| 17 | 0 | 0 | −2 | 0 | 466.87 |
| 18 | 1 | 1 | 1 | −1 | 490.83 |
| 19 | −1 | −1 | −1 | −1 | 437.75 |
| 20 | −1 | 1 | −1 | −1 | 442.05 |
| 21 | 0 | 0 | 0 | −2 | 470.43 |
| 22 | −1 | −1 | 1 | −1 | 435.60 |
| 23 | 0 | 0 | 0 | 0 | 467.76 |
| 24 | 1 | 1 | 1 | 1 | 496.57 |
| 25 | 1 | −1 | −1 | 1 | 479.58 |
| 26 | 2 | 0 | 0 | 0 | 505.12 |
| 27 | 0 | 0 | 0 | 0 | 466.76 |
| Parameters | Degree of Freedom | Mean Square | F-Value | p-Value |
|---|---|---|---|---|
| Model | 14 | 998.73 | 345.44 | <0.0001 |
| X7 | 1 | 12,748.49 | 4409.46 | <0.0001 |
| X8 | 1 | 832.61 | 287.98 | <0.0001 |
| X9 | 1 | 0.2646 | 0.0915 | 0.7674 |
| X10 | 1 | 0.7211 | 0.2494 | 0.6265 |
| X7X8 | 1 | 39.94 | 13.82 | 0.0029 |
| X7X9 | 1 | 1.01 | 0.3493 | 0.5654 |
| X7X10 | 1 | 11.59 | 4.01 | 0.0684 |
| X8X9 | 1 | 5.15 | 1.78 | 0.2066 |
| X8X10 | 1 | 6.66 | 2.30 | 0.1551 |
| X9X10 | 1 | 6.03 | 2.08 | 0.1744 |
| 1 | 63.13 | 21.83 | 0.0005 | |
| 1 | 220.88 | 76.40 | <0.0001 | |
| 1 | 0.0206 | 0.0071 | 0.9342 | |
| 1 | 5.14 | 1.78 | 0.2070 | |
| Residual | 12 | 2.89 | ||
| Lack of fit | 10 | 3.41 | 11.14 | 0.0852 |
| Pure error | 2 | 0.3060 | ||
| Total | 26 |
| Type | Parameter | Value | Unite |
|---|---|---|---|
| Soil | Poisson’s ratio | 0.36 | |
| Shear modulus | 1.3 × 106 | Pa | |
| Density | 1250 | kg·m−3 | |
| Soil–soil | Restitution coefficient | 0.48 | |
| Static friction coefficient | 0.45 | ||
| Rolling friction coefficient | 0.24 | ||
| Normal stiffness per unit area | 1.15 × 108 | N·m−3 | |
| Shear stiffness per unit area | 3.06 × 108 | N·m−3 | |
| Critical normal stress | 6.9 × 105 | Pa | |
| Critical shear stress | 6.7 × 105 | Pa | |
| Soil–cotton roots | Restitution coefficient | 0.45 | |
| Static friction coefficient | 0.62 | ||
| Rolling friction coefficient | 0.70 | ||
| Bond stiffness | 6.97 × 106 | N·m−3 | |
| Bond stress | 2.13 × 106 | Pa | |
| Bond radius | 1.39 | mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, Y.; Xing, R.; Baikeli, Y.; Xu, H.; Ma, W.; Guo, L. Systematic Calibration and Validation of Discrete Element Model Parameters for Cotton Root Systems. Agriculture 2025, 15, 1827. https://doi.org/10.3390/agriculture15171827
Yue Y, Xing R, Baikeli Y, Xu H, Ma W, Guo L. Systematic Calibration and Validation of Discrete Element Model Parameters for Cotton Root Systems. Agriculture. 2025; 15(17):1827. https://doi.org/10.3390/agriculture15171827
Chicago/Turabian StyleYue, Yong, Rensheng Xing, Yasenjiang Baikeli, Haodong Xu, Weibin Ma, and Liehong Guo. 2025. "Systematic Calibration and Validation of Discrete Element Model Parameters for Cotton Root Systems" Agriculture 15, no. 17: 1827. https://doi.org/10.3390/agriculture15171827
APA StyleYue, Y., Xing, R., Baikeli, Y., Xu, H., Ma, W., & Guo, L. (2025). Systematic Calibration and Validation of Discrete Element Model Parameters for Cotton Root Systems. Agriculture, 15(17), 1827. https://doi.org/10.3390/agriculture15171827





