Abstract
This study employs a Super-SBM model to construct a comprehensive evaluation framework—encompassing input factors, desirable outputs, and undesirable outputs—to measure agricultural green total factor productivity (AGTFP) in the Tibet Autonomous Region in the period 2002–2021. We then apply kernel density estimation and Dagum Gini coefficient decomposition to examine its spatiotemporal evolution. The main findings are as follows: (1) AGTFP in Tibet rose overall from 0.949 in 2002 to 1.068 in 2021, with a compound annual growth rate of 0.78%, yet remained below the national average; (2) significant regional heterogeneity emerged, with three typical evolution patterns identified: continual improvement (Nagqu, Qamdo), stable fluctuation (Lhasa, Xigazê), and risk of decline (Lhoka, Nyingchi, Ngari); (3) gains in pure technical efficiency were the primary driver of AGTFP growth, while insufficient scale efficiency was a key constraint; (4) AGTFP exhibited a “convergence–divergence–reconvergence” dynamic, with interregional disparities widening but structural patterns stabilizing; and (5) interregional inequality was the main source of overall disparity—its importance grew over the study period, with the largest gap observed between agrarian and pastoral zones. On this basis, we recommend a “gradient advancement” strategy that prioritizes pure technical efficiency and regional coordination, while promoting zone-specific support tools tailored to local ecological conditions and institutional capacities to ensure inclusive green productivity growth.
1. Introduction
1.1. Global Environmental Pressures on Agriculture
Since the dawn of civilization, agriculture has underpinned human survival and development. Although it represents a relatively small share of the global economy, agriculture bears the primary responsibility for food security and plays a crucial role in supporting economic growth in low-income countries [1]. Yet, modern agricultural practices represent a heavy environmental burden: dependence on fossil fuels generates substantial greenhouse gas emissions [2], excessive use of fertilizers and pesticides leads to non-point-source pollution [3], and inappropriate land use exacerbates soil erosion and ecosystem degradation [4]. In the context of climate change, these problems are becoming ever more acute. Agriculture accounts for roughly 25 percent of global greenhouse gas emissions [5] and is a key driver of global warming [6]. Finding ways to safeguard food security while reducing environmental impacts has emerged as one of the world’s most pressing challenges [7]. This challenge sits squarely within the broader evolution of the sustainable development paradigm, which has undergone successive refinements from early ecological–economic balances to today’s integrated, justice-oriented frameworks [8,9].
1.2. High-Altitude Vulnerabilities and Regional Context
High-altitude regions are home to unique agricultural systems shaped by their distinct geography and climate [10]. These areas, however, face heightened ecological vulnerability. Warming in high-elevation zones can exceed twice the global average rate [11]. Climate change in these regions not only alters glacier and water resource distribution but also affects crop yields, livestock health, and ecosystem services [12]. As rising temperatures drive species migrations and agricultural activities to higher elevations, vital mountain ecosystem services—such as water regulation—are degrading significantly [13], putting irrigation security and production stability at risk [14,15].
The Tibet Autonomous Region exemplifies the complexities of high-altitude agriculture, where fragile ecosystems and the intermingling of farming and pastoralism create intricate resource–environment interactions [16]. Although Tibet has achieved notable gains in crop yields and technical efficiency in recent years, the intensification of production has driven rapid increases in carbon emissions and non-point pollution, undermining those achievements [17]. Under such conditions, conventional total factor productivity (TFP) measures fall short of capturing the true quality of agricultural growth. Green total factor productivity (GTFP) has therefore emerged as a more appropriate metric, integrating desirable outputs with undesirable ones—such as carbon and pollutant emissions—within a single efficiency framework to better reflect sustainability objectives [18].
1.3. Advancements in Green Total Factor Productivity Measurement
In recent years, building on foundational debates around sustainable development—ranging from early notions of “limits to growth” to contemporary calls for socio-ecological justice [9]—the emphasis has shifted toward integrating environmental constraints into productivity metrics. In this context, agricultural green total factor productivity (AGTFP) has emerged as a core indicator of agriculture’s sustainability and has become a frontier topic in environmental economics and agricultural policy research. Traditional TFP measures have been criticized for ignoring environmental and resource costs [19], whereas GTFP integrates undesirable outputs—such as carbon emissions and non-point-source pollution—into the production function, thereby establishing a dual framework of economic growth and environmental constraint [20]. Methodologically, the directional distance function (DDF) has been widely adopted because it can simultaneously capture expansion in desirable outputs and contraction in undesirable outputs [18]. However, the inherent radial and angular biases of the DDF may lead to an overestimation of efficiency scores [21]. To address this shortcoming, Tone (2001) proposed the non-radial, non-angular slacks-based measure (SBM) model, which directly handles slack in inputs and outputs and thereby significantly improves precision in efficiency evaluation [22]. The subsequent Super-SBM model further overcomes the inability of traditional DEA to differentiate among fully efficient decision-making units, making it particularly suitable for complex systems that include undesirable outputs [23]. Since then, scholars have successfully applied SBM and Super-SBM to measure carbon performance [24], ecological efficiency [25], and energy efficiency [26], and they have demonstrated clear advantages in assessing agricultural environmental efficiency [27].
The intensification of global climate change and tightening environmental constraints [28] have driven differentiated policy responses under sustainable development goals [29]. Researchers have increasingly recognized that examining GTFP solely at the aggregate level cannot accurately capture regional variations in green growth [30]. Consequently, analyzing GTFP evolution along spatial and temporal dimensions and revealing its regional divergence, clustering patterns, and driving forces have become key focus points in environmental economics [31,32]. At national and provincial scales, studies have employed spatial autocorrelation (Moran’s I and LISA) [33], spatial Markov chains [34], convergence tests [35], kernel density estimation [36], and Dagum Gini decomposition [37] to map GTFP’s spatiotemporal dynamics and its determinants. These investigations indicate that agricultural credit, digitalization, and green technologies significantly enhance regional GTFP, yet resource endowments and institutional environments produce marked heterogeneity in growth rates and spillover effects [38,39]. Distribution dynamics tools such as spatial Markov chains and kernel density estimation further uncover differentiation trends and “convergence clubs” in GTFP [36]. To strengthen robustness, many studies supplement DEA with bootstrap tests [40] and mitigate endogeneity in second-stage regressions through instrumental variables or dynamic panel GMM [38]. Such multi-method, multi-perspective analyses offer valuable insights for finely characterizing GTFP dynamics in highland agriculture.
1.4. Research Gaps and Study Contributions
Despite these advances, studies of AGTFP in high-altitude, ecologically fragile regions remain scarce. In the Tibet Autonomous Region, highland cropping, natural grassland grazing, and overlapping ecological compensation policies interact in ways that likely produce distinct stages and spatial variation in efficiency evolution compared to lowland areas [41]. Specifically, valley farmlands benefit from superior water resources and infrastructure, resulting in efficiency trajectories that differ sharply from those in pastoral zones and transitional areas [42]. Pastoral zones, influenced by climate variability and grass–livestock balance policies, often experience short-term efficiency fluctuations [43], while agro-pastoral transition zones combine the characteristics of both. Uncovering the mechanisms behind these differences requires an integrated approach that combines efficiency measurement with distribution dynamics and spatial structure analysis.
This study uses data from seven prefectures in the Tibet Autonomous Region and constructs a tripartite analytical framework of efficiency measurement, temporal dynamics, and spatial decomposition. First, we apply the Super-SBM model to measure AGTFP for 2002–2021 and decompose improvements into technical efficiency, scale efficiency, and pure technical efficiency. Second, we employ kernel density estimation to trace changes in AGTFP distribution—examining peak positions, kurtosis, and tail behavior—to reveal whether efficiency evolution follows convergence, divergence, or mixed trajectories. Finally, we classify the seven prefectures into valley farmland, high-altitude pastoral, and agro-pastoral transition zones and use Dagum Gini decomposition to quantify the contributions of within-zone, between-zone, and overlapping effects to the overall spatial disparity. This comprehensive analysis seeks to elucidate the spatiotemporal evolution of AGTFP on the Tibetan Plateau, uncover the underlying drivers and constraints across ecological zones, and offer empirically grounded insights to inform ecological compensation mechanisms, prioritize high-altitude adaptive agricultural technologies, and guide the formulation of differentiated regional policy strategies.
2. Research Area and Data Sources
2.1. Overview of the Study Area
The Tibet Autonomous Region lies at the heart of the Qinghai–Tibet Plateau, covering approximately 1.2284 million km2 with an average elevation exceeding 4000 m, making it the highest and most extensive cold-climate agricultural region in the world. The terrain slopes downward from northwest to southeast and comprises three main units: the mid-to-lower Yarlung Tsangpo River valley (elevation ca. 2800–3500 m), the northern Tibetan Plateau grasslands (above 4000 m), and the transitional Hengduan Mountains of southern Tibet. Mean annual precipitation shows pronounced spatial variation; the southern river valleys receive 800–1200 mm, making them suitable for crop cultivation, whereas the northern plateau records only 200–300 mm and is dominated by natural grasslands. Traditional leading industries include wheat, rapeseed, and vegetable cultivation in the Yarlung Tsangpo valley; high-altitude barley, wheat, and forage production; and pastoralism of sheep and yak on the northern grasslands—together forming a composite “agriculture–pastoralism–mixed” production system.
Based on the 400 mm annual precipitation isohyet, the seven prefectures of Tibet are classified into three ecological zones, detailed as follows.
Farmland Zone (annual precipitation > 400 mm): Qamdo and Nyingchi, located in the warm and humid southeast, receive over 400 mm of rainfall annually. Soil moisture conditions are sufficient to support reliable rainfed agriculture, favoring both crop cultivation and under-forest economic activities.
Agro-Pastoral Transition Zone (annual precipitation 200–400 mm): Lhasa, Lhoka, and Xigazê lie in the semi-humid to semi-arid central region, where rainfall ranges from 200 to 400 mm. These areas can sustain limited dryland farming alongside pastoralism, enabling a mixed production mode.
Pastoral Zone (annual precipitation < 200 mm): Nagqu and Ngari belong to the typical arid plateau zone, with less than 200 mm of highly unevenly distributed rainfall. Such conditions preclude extensive cropping, and natural grasslands and alpine meadows serve as the primary ecological production base, making livestock husbandry dominant.
2.2. Data Sources
This study uses the seven prefectures of the Tibet Autonomous Region as the sample and covers the period 2002–2021. Data on non-point-source pollution, carbon emissions, and input–output indicators were primarily drawn from the Tibet Statistical Yearbook (2003–2022) [44]. These sources follow consistent statistical standards and are released annually by national or regional statistical authorities, allowing for cross-year and cross-region comparability. Environmental constraint parameters—such as fertilizer loss rates and carbon emission coefficients—were set according to the Second National Pollution Source Census Manual for Agricultural Sources and the 2019 Revised IPCC National Greenhouse Gas Inventory Guidelines, using region-specific factors for Tibet. To address occasional missing values in the panel data, we applied linear interpolation for variables with one or two missing years. The proportion of missing values per variable was consistently below 5% of total observations, and interpolation was conducted using adjacent-year values to preserve data continuity. This method ensures completeness of the dataset without introducing artificial volatility or bias. Although some data limitations remain—particularly in the resolution of environmental variables and policy indicators—we believe the dataset offers a robust foundation for tracking long-term trends in agricultural green productivity.
In this study, we adopt a full-coverage approach rather than a sampling framework. Specifically, all seven prefecture-level administrative units (Lhasa, Xigazê, Nyingchi, Nagqu, Ngari, Qamdo, and Lhoka) within the Tibet Autonomous Region are included as decision-making units (DMUs). This complete inclusion strategy is appropriate because the region comprises a small number of well-defined and heterogeneous ecological zones. Therefore, our selection captures the entire population of relevant spatial units, avoiding sampling bias and enhancing the representativeness of the spatiotemporal analysis.
3. Model Selection and Construction of the Indicator System
3.1. Model Selection
3.1.1. Super-SBM Model
All computations in this study were performed using MaxDEA 7.0, a widely used software platform for Data Envelopment Analysis, which supports Super-SBM models with undesirable outputs.
In this study, each decision-making unit (DMU) is assumed to operate a production system characterized by three vectors: an input vector , a desirable output vector and an undesirable output vector . Suppose there are DMUs in total. We collect the input and output data for all units into the following matrices:
denotes the value of the th input for the th DMU; denotes the value of the th desirable output for the th DMU; and denotes the value of the th undesirable output for the th DMU.
By introducing the weight vector , the production possibility set can be defined as follows:
Here, if a DMU’s actual desirable output is lower than the frontier’s ideal desirable output level, or its actual undesirable output is higher than the frontier’s undesirable output level, then the DMU exhibits efficiency loss [45]. Based on the production possibility set, the SBM model incorporated slack amounts for both inputs and outputs into the evaluation [22]. Its nonlinear form before linearization is as follows:
Here, , , and denote the slack variables for inputs, desirable outputs, and undesirable outputs, respectively. The objective function value represents the efficiency score of a DMU and ranges between 0 and 1. When and all slack variables are zero, the DMU lies on the efficient frontier; when , the DMU is inefficient, indicating that its inputs and outputs require adjustment.
To address the challenge of nonlinear computation, the Charnes–Cooper transformation can be used to convert the model into an equivalent linear program [46]. In most efficiency evaluations, it is common to observe multiple decision-making units achieving a 100% efficiency score. Distinguishing among these fully efficient units and identifying their driving factors is therefore critical. To differentiate units that all attain full efficiency under the conventional model, this study employs Super-SBM model [23]. Its formulation is as follows:
Under the assumption of constant returns to scale, the Super-SBM model relaxes the upper bound on efficiency scores, allowing leading decision-making units to exceed a score of one and enabling fine differentiation among tied optimal units. Simultaneously, the model quantifies input and output slacks at a higher resolution, accurately delineating the spatiotemporal evolution of AGTFP in the seven prefectures of Tibet from 2002 to 2021. The Super-SBM model provides a robust methodological basis for uncovering regional disparities in technological progress and resource allocation efficiency. The rationale for its selection in this study is further reinforced by its successful application in related empirical contexts, such as carbon performance evaluations across Chinese provinces [47] and agricultural environmental efficiency analyses incorporating non-point-source pollution and carbon inputs [48].
3.1.2. Kernel Density Estimation
Building on the static decomposition provided by the Super-SBM model, this study employs kernel density estimation to uncover patterns of clustering, dispersion, and polarization in the distribution of AGTFP [49]. The analysis divides the study period into four phases:
The period from 2002 to 2006, which corresponds to China’s Tenth Five-Year Plan, ; the period from 2007 to 2011, which corresponds to the Eleventh Five-Year Plan, ; the period from 2012 to 2016, which corresponds to the Twelfth Five-Year Plan, ; and the period from 2017 to 2021, which corresponds to the Thirteenth Five-Year Plan, .
Let period comprise observed years. Then, the total number of AGTFP observations for the seven prefectures in that period is , and we denote each observation . For any real number , the kernel density estimate for the period is defined as
Here, denotes the smoothed distribution density of AGTFP in period ; ; represents the AGTFP of the th prefecture in period ; and is the bandwidth, using the Gaussian kernel function .
3.1.3. Dagum Gini Coefficient and Its Decomposition
To investigate the sources of AGTFP disparities across different ecological zones, this study employs Dagum’s (1997) Gini coefficient and decomposition method [50]. The overall disparity is expressed as the sum of within-group inequality, between-group inequality, and transvariation density. Mathematically, this is given by
Here, denotes the number of ecological zone categories; is the number of prefectures in the group (farmland zone, agro-pastoral zone, pastoral zone); is the total number of prefectures; is the AGTFP of the th prefecture in the group ; and is the mean AGTFP for the entire region. According to Dagum’s decomposition framework, the overall Gini coefficient can be partitioned into three components:
The within-group inequality contribution is calculated by , where is the weight of group , is the mean AGTFP of group , and is the conventional Gini coefficient within that group.
The net between-group disparity contribution is calculated by , where denotes the relative weight of the mean difference between group and group , and denotes the corresponding mean difference between the two groups.
The transvariation density contribution is calculated by and measures the asymmetric polarization effect generated by the overlap and separation that occur during the process of inter-group disparity.
Through this decomposition, we can precisely identify the share of disparity that arises from diversity within the same ecological zone (), the share attributable to differences in mean levels between different ecological zones (), and the share resulting from transvariation density, which captures the effects of overlapping distributions across zones (). This method provides a quantitative foundation for the formulation of targeted regional green agriculture policies.
3.2. Construction of the Indicator System
An agricultural production system must maximize output under constraints of resource and energy inputs while fully accounting for environmental pollution and its negative externalities on ecosystems and social welfare. Therefore, in constructing the empirical model, we select resource constraint variables—including land, labor, capital, and energy—from the input side and introduce environmental negative externality indicators such as carbon dioxide emissions and agricultural non-point-source pollution. At the same time, carbon sequestration is incorporated as a desirable output to measure the carbon absorption capacity and positive external benefits of the agricultural ecosystem, thereby comprehensively capturing the multidimensional determinants of AGTFP (as shown in Table 1).

Table 1.
Input–output indicator system for evaluating agricultural green total factor productivity in Tibet.
3.2.1. Input Variables
Since the classical theory of factor inputs was proposed, research on agricultural inputs has evolved through trinity and quaternary frameworks [51]. Building on the four-factor production model, this study expands to include five key inputs: labor, land, capital, water resources, and energy. These inputs are both indispensable for agricultural operations and essential constraints when assessing green production efficiency.
Labor input: Because agriculture and animal husbandry account for approximately 98 percent of Tibet’s primary industry, labor input is measured by the year-end number of employees in agriculture, forestry, animal husbandry, and fisheries.
Land input: Total annual sown area is used to avoid measurement bias from idle or fallow land that affects arable land statistics [52].
Capital input: Capital is defined broadly to include both physical and non-radial inputs. Specifically, we use the pure nutrient content of nitrogen, phosphorus, potassium, and compound fertilizers, along with year-end livestock numbers, as core capital factors. We also include pesticide consumption and agricultural plastic film usage to capture their effects on input–output efficiency [53].
Water resource input is defined as the effective irrigated area measuring the intensity of water use in agricultural production [54].
Energy input: In the absence of separate data on fuel consumption or machine-operation hours, total agricultural machinery power is adopted as a proxy for the power–energy input [55].
3.2.2. Desirable Outputs
- (1)
- Gross Output Value of Agriculture and Animal Husbandry
Given that agriculture and animal husbandry account for more than 95 percent of Tibet’s primary sector, this study uses the combined output value of crop farming and livestock production as the primary desirable output to comprehensively reflect the region’s economic output capacity. To eliminate the influence of price fluctuations, the output values are deflated using the agricultural producer price index published by the National Bureau of Statistics and converted to constant 1993 prices.
- (2)
- Agricultural Carbon Sequestration
Agricultural carbon sequestration refers to the total amount of carbon dioxide absorbed and fixed by crops through photosynthesis during their growth cycles. It reflects the net carbon removal capacity of agricultural systems and is also considered a component of agricultural ecological welfare [56]. In this study, carbon sequestration is estimated for major food and cash crops based on their biological characteristics and production volumes [57]. The calculation formula is as follows:
Here, denotes the total annual carbon sequestration of all crops; denotes the annual carbon sequestration of crop ; is the number of crop species included in the calculation; is the amount of carbon absorbed by crop per unit of organic matter synthesized via photosynthesis; is the annual yield of crop ; is the moisture content of crop at maturity; and is the conversion coefficient for the economic yield of crop . This study focuses on the major crops characterized by large sown areas, high yields, and substantial economic value (see Table 2).

Table 2.
Economic conversion coefficients and carbon sequestration parameters for major crops in Tibet.
3.2.3. Undesirable Outputs
There is no consensus on the measurement of agricultural undesirable outputs. Some researchers argue that non-point-source pollution should serve as the primary indicator of agricultural undesirable outputs [64,65]. Non-point-source pollution encompasses the diffuse losses of fertilizers, pesticide residues, animal excreta, and agricultural and domestic wastes. Unlike point-source industrial discharges, these pollutants are dispersed over wide areas, contributing significantly to water eutrophication and ecosystem degradation and presenting substantial remediation challenges [66]. From an environmental risk perspective, non-point-source pollution is undoubtedly a critical component of agricultural undesirable outputs.
Concurrently, the IPCC recommends including carbon emissions from agricultural production processes as undesirable outputs, since these emissions—excluding nutrient elements such as nitrogen and phosphorus—constitute a pure environmental burden [67]. Agricultural machinery operations, fertilizer application, and pesticide use generate substantial greenhouse gases, which drive climate change. Incorporating agricultural carbon emissions into the evaluation framework supports sustainable development objectives. In China, agricultural carbon emissions account for approximately 17 percent of the nation’s total emissions, making agriculture a non-negligible source of greenhouse gases [68]. However, some scholars caution that relying solely on carbon emissions as the undesirable output indicator may be biased and insufficient to reflect the full spectrum of agricultural environmental pressures [69].
Based on these considerations, this study incorporates both non-point-source pollution and carbon emissions as undesirable outputs to more comprehensively capture the environmental impacts of agricultural activities. Specifically, we develop accounting systems to quantify fertilizer and pesticide runoff, livestock pollution intensity, and total agricultural greenhouse gas emissions, thereby providing richer and more accurate environmental constraint information for AGTFP analysis.
- (1)
- Agricultural Non-Point-Source Pollution
This study adopts Tsinghua University’s Inventory Analysis Method to systematically quantify agricultural non-point-source pollution in Tibet, focusing on the primary pollutant sources of fertilizer application and livestock husbandry. We construct an emission coefficient database using the applied pure nutrient equivalents of chemical nitrogen and phosphorus fertilizers and the year-end stock of cattle and sheep [70]. These coefficients are then used to calculate emissions of total nitrogen (TN), total phosphorus (TP), and chemical oxygen demand (COD). Given the ecological lifestyles of rural residents in Tibet, pollution from domestic waste is negligible, and all crop residues are used as livestock fodder, resulting in no significant agricultural solid waste emissions. Accordingly, we deliberately omit the “domestic waste” and “agricultural solid waste” source categories. This approach ensures a comprehensive assessment of non-point-source pollution while accurately reflecting local ecological conditions and production practices. A detailed inventory of agricultural non-point-source pollution accounting is presented in Table 3.

Table 3.
Inventory of agricultural non-point-source pollution in Tibet.
In this study, non-point-source pollution from agricultural fertilizers is calculated based on the applied pure nutrient equivalents of nitrogen and phosphorus fertilizers, combined with loss rate parameters from the Second National Pollution Source Census Manual for Agricultural Sources (State Council Office for the Second National Pollution Source Census, 2022) to estimate the annual total emissions of total nitrogen (TN) and total phosphorus (TP). For livestock waste, we focus on the year-end stocks of cattle (including yak), sheep, and pigs; these three categories together account for over 98 percent of Tibet’s total livestock output value and are predominantly managed through free-range and intensive pasture systems. Using region-specific measured “waste generation coefficients” and “pollution emission coefficients” from the same manual, we calculate manure and wastewater contributions for each species.
Concerning parameter acquisition and model framework, we build on the general formula proposed by Liang (2009) [71] and adopt the emission coefficients provided in the Second National Pollution Source Census Manual for Agricultural Sources. Accordingly, our accounting model for agricultural non-point-source pollution is as follows:
Here, denotes the quantity of pollutant source (for example, the amount of fertilizer applied or the year-end livestock inventory), and denotes the corresponding pollution intensity coefficient. The annual total emissions for each of the three pollutant categories (COD, TN, TP) are then calculated as follows:
Then, following the Class III limits of the Surface Water Environmental Quality Standard (GB3838-2002) (COD 20 mg/L, TN 1 mg/L, TP 0.2 mg/L), the emissions are converted to equivalent standard discharge loads as follows:
Finally, by summing the three standardized discharge loads, we derive the composite non-point-source pollution indicator:
- (2)
- Agricultural Carbon Emissions
Based on IPCC (2006) and related studies [72], this research classifies agricultural carbon sources into four categories: fertilizer application, pesticide use, agricultural film usage, and tillage operations. Emissions are estimated using the activity level multiplied by the emission factor method proposed by Li Bo (2011) [73]:
In the above equation, denotes the total agricultural carbon emissions (kg CO2e), represents the activity level of the th carbon source, and is the corresponding emission factor. Reference values compiled from the literature are given in Table 4.

Table 4.
Agricultural carbon emission sources, coefficients, and references.
- (3)
- Livestock Carbon Emissions
Livestock farming is a major source of agricultural carbon emissions, primarily through methane (CH4) produced by enteric fermentation and both methane (CH4) and nitrous oxide (N2O) released during manure management and treatment. Following the 2019 Revised IPCC Guidelines for National Greenhouse Gas Inventories, this study focuses on three major livestock types—pigs, cattle (including yak), and sheep. Their annual carbon emissions are calculated as follows:
In the equation, represents the total annual carbon emissions from livestock farming (kg CO2e); denotes the year-end inventory of livestock type ; refer to the emission factors for enteric CH4, manure CH4, and manure N2O, respectively; and , . Table 5 presents the CH4 and N2O emission factors for major livestock species, along with their corresponding CO2-equivalent intensities.

Table 5.
Enteric and manure-based carbon emission factors for major livestock species in Tibet.
4. Research Results and Analysis
4.1. Measurement of AGTFP and Decomposition of Results
Based on the input–output evaluation framework for agricultural green total factor productivity established above, we used MaxDEA 7.0 software to calculate AGTFP for the seven prefectures of the Tibet Autonomous Region over the period 2002–2021.
4.1.1. Analysis of AGTFP Estimates for Tibet
Figure 1 illustrates that the agricultural green total factor productivity (AGTFP) across the seven prefectures of the Tibet Autonomous Region increased overall from 2002 to 2021. Efficiency scores fluctuated between a low of 0.457 (Nagqu in 2007) and a high of 1.139 (Qamdo in 2021), yielding a maximum interregional gap of 128.2 percent in 2003. This wide range reflects pronounced spatial heterogeneity in resource allocation and pollution control across the plateau. Region-wide AGTFP rose from 0.949 in 2002 to 1.068 in 2021, with a compound annual growth rate (CAGR) of 0.78 percent—substantially below the national agricultural average of approximately 1.6 percent [74]—underscoring the challenges of agricultural transformation in cold, high-altitude areas. Growth accelerated after 2010, with a CAGR of 4.13 percent between 2010 and 2021, closely associated with policies such as the Tibet Ecological Security Barrier Protection and Construction Plan (2008–2030).
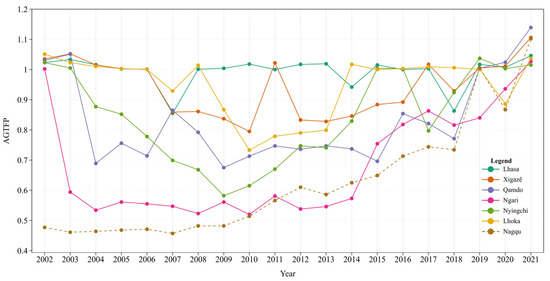
Figure 1.
Temporal trends in agricultural green total factor productivity (AGTFP) across seven prefectures in Tibet, 2002–2021. (Note: A super-efficiency score of at least 1 indicates that the decision-making unit (DMU) lies on the production frontier, meaning its resource allocation is optimal under the given technology, and no input reduction or output expansion is required to achieve full efficiency. A super-efficiency score below 1 indicates that the DMU experiences efficiency loss and must reduce redundant inputs or limit undesirable outputs to move toward the production frontier).
Further examination of the AGTFP trend reveals a clear phase-based dynamic pattern in regional disparities. In 2002, AGTFP values across prefectures were relatively tightly clustered, indicating limited initial differences; between 2004 and 2010, values dispersed, and interregional gaps widened; and from 2017 to 2021—particularly in 2020–2021—the distribution reconverged, signaling a narrowing of disparities. This “convergence–divergence–reconvergence” trajectory reflects complex regional interactions in Tibet’s green agricultural development.
Based on temporal evolution, numerical trends, and the coefficient of variation (CV), the seven prefectures can be classified into three categories, detailed as follows.
Continuous Improvement Type (Nagqu and Qamdo): Nagqu’s AGTFP rose from 0.477 in 2002 to 1.102 in 2021 (CAGR = 4.51 percent), exhibiting three phases, which were an initial valley, gradual ascent, and breakthrough surge. The leap forward owes much to the grassland ecological compensation policy, which reduced livestock overstocking through grazing–livestock balance incentives, and to the shift toward penned, mechanized livestock production that alleviated overgrazing pressure. Qamdo’s AGTFP increased from 1.030 to 1.139 (CAGR = 0.53 percent), accelerating after 2015 (CAGR = 8.56 percent). Its efficiency curve formed a pronounced U shape: from 2002 to 2015 (CAGR = −2.97 percent), pure-nutrient fertilizer application grew 2.4-fold, pesticide use 1.6-fold, and plastic film use 287-fold, while the sown area expanded only 1.06-fold. Excessive input intensity relative to land expansion undermined efficiency and increased environmental risk, causing AGTFP decline. From 2016 to 2021, Qamdo significantly improved resource efficiency through ecological restoration and water-saving irrigation projects in the Lancang River basin; carbon sequestration pilots and green subsidies reduced the carbon sequestration slack variable from −0.012 to 0 and cut undesirable output slack by 73 percent, driving AGTFP growth at an average annual rate of 8.6 percent.
Stable Fluctuation Type (Lhasa and Xigazê): Lhasa’s AGTFP exhibited a W-shaped fluctuation from 2002 to 2021 but maintained a low CV of 0.051, well below the regional average of 0.187, indicating overall stability. Between 2002 and 2013, AGTFP hovered around 1.003 ± 0.02, reflecting strong advantages in intensive resource use; from 2014 to 2018, structural adjustments and external shocks drove it down to 0.863; and from 2019 to 2021, technical subsidies and ecological compensation policies restored it to approximately 1.046. Xigazê experienced larger early-stage volatility—declining from 1.022 in 2002 to 0.795 in 2010—highlighting the vulnerability of traditional agricultural systems. After 2010, organic fertilizer subsidies, standardized base construction, and the Gangba yak geographical indication certification propelled its AGTFP to 1.106, demonstrating the effectiveness of specialty industries combined with green technology in facilitating agricultural transformation on the plateau.
Decline Risk Type (Lhoka, Nyingchi, and Ngari): Lhoka’s AGTFP remained above 1 from 2002 to 2006 before falling sharply from 0.928 in 2007 to 0.799 in 2013, reaching a low of 0.733 in 2010. During this period, total agricultural machinery power grew by 238 percent and fertilizer use by 81 percent, while the sown area increased by only 6.6 percent, and primary industry employment fell by 26.5 percent. The mismatch between intensified mechanization and chemical inputs and declining labor led to inefficiencies and AGTFP decline. From 2014 to 2021, AGTFP stabilized, rebounding to 1.017 in 2014 and 1.037 in 2021, with a brief dip to 0.885 in 2020, indicating that production factor allocation and technology adjustments gradually restored and slightly improved efficiency. Nyingchi underwent a steep decline followed by a prolonged recovery, dropping from 1.023 in 2002 to 0.582 in 2009 (an annual decline of 7.74 percent), then taking twelve years to return to 1.015 by 2021 (annual growth of 3.5 percent), far slower than its rate of decline, underscoring structural constraints on recovery in ecologically fragile zones. Ngari’s decline was even deeper; AGTFP plunged from 1.002 in 2002 to 0.520 in 2010 (CAGR = −7.87 percent) and recovered to 1.027 only by 2021, reflecting the fragility and uncertainty of recovery under extreme environmental constraints. Both prefectures require enhanced adaptive technology investments to shorten the efficiency restoration cycle.
4.1.2. Decomposition of AGTFP Efficiency in Tibet
Figure 2a presents a heat map of technical efficiency (TE) for the Tibet Autonomous Region and its seven prefectures over the 2002–2021 period. The color gradient spans from deep purple, indicating low efficiency (around 0.4), to bright yellow, indicating high efficiency (around 1.2), thereby conveying both absolute levels and temporal trends. Nagqu exhibited extremely low TE at the outset (0.4775 in 2002, reaching a minimum of 0.4569 in 2007) but then improved steadily to 1.1022 by 2021, a 118.39 percent increase, which is the most pronounced gain of all regions. By comparison, Lhasa, Xigazê, and Qamdo maintained relatively high TE throughout the period, with Qamdo achieving the highest value of 1.1393 in 2021. Overall, the region’s TE followed a fluctuating upward trajectory, notably rising by 14.36 percent in 2019, underscoring the effectiveness of recent green agricultural development policies.
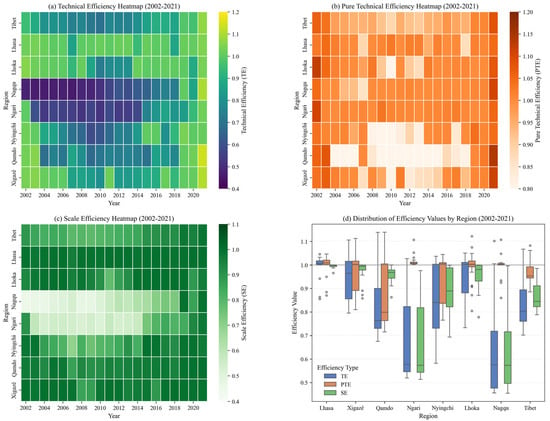
Figure 2.
Spatiotemporal decomposition of agricultural efficiency in Tibet, 2002–2021. (Note: (a) shows the spatiotemporal heat map of technical efficiency (TE) for the Tibet Autonomous Region and its seven prefectures from 2002 to 2021. The color gradient from deep purple to bright yellow represents efficiency scores from low to high (0.4–1.2); (b) shows the spatiotemporal heat map of pure technical efficiency (PTE) for the Tibet Autonomous Region and its seven prefectures from 2002 to 2021. The color gradient from light orange to dark brown represents efficiency scores from low to high (0.8–1.2); (c) shows the spatiotemporal heat map of scale efficiency (SE) for the Tibet Autonomous Region and its seven prefectures from 2002 to 2021. The color gradient from light green to dark green represents efficiency scores from low to high (0.4–1.1); (d) presents box plots of the three efficiency measures for the Tibet Autonomous Region and its seven prefectures from 2002 to 2021: blue for technical efficiency (TE), orange for pure technical efficiency (PTE), and green for scale efficiency (SE). Boxes indicate interquartile ranges; lines are medians; whiskers are 1.5 times the interquartile range; and dots are outliers).
The pure technical efficiency (PTE) heat map in orange tones illustrates efficiency distribution after removing scale effects (Figure 2b). The gradient from light orange (low efficiency, around 0.8) to dark brown (high efficiency, around 1.2) indicates generally high efficiency levels. The mean PTE for Tibet’s prefectures (0.9447) is significantly higher than the mean TE (0.8523), implying that scale inefficiencies are the primary constraint on overall technical efficiency. Qamdo exhibits pronounced polarization, recording both the lowest PTE (0.7154 in 2015) and the highest (1.1394 in 2021) during the study period. Notably, PTE and TE are highly correlated in most regions—for example, Lhasa’s correlation reaches 0.9931—underscoring that pure technical progress drives overall efficiency gains. While aggregate AGTFP has generally improved over the study period, sub-efficiency components reveal divergent patterns across regions. For example, Nagqu and Ngari consistently exhibit low levels of pure technical efficiency (PTE), with values often below 0.9, and even declining in some years. This suggests that technological or managerial inefficiencies remain prevalent in these high-altitude, resource-constrained areas, limiting their capacity to convert inputs into outputs efficiently.
The scale efficiency (SE) heat map in shades of green depicts how closely actual production scales match their optima (Figure 2c). The gradient from light green (low efficiency, around 0.4) to dark green (high efficiency, around 1.1) reveals significant improvement in some areas. Nagqu’s SE rose from a low of 0.4557 in 2002 to 0.9952 in 2021—a 118.39 percent increase—indicating a fundamental restructuring of its agricultural scale. Lhasa shows the most stable and high SE, reaching the ideal value of 1.0000 in 2011 and averaging 0.9815 over the period. Ngari records the lowest mean SE (0.8424) but posts a solid 7.77 percent increase from 2002 to 2021. Overall, the region’s mean SE (0.8996) remains below its mean PTE, confirming that optimizing production scale is critical to raising AGTFP. In the context of this study, scale efficiency reflects not firm-level returns to scale, but rather the degree to which a prefecture’s agricultural structure—such as the concentration of farmland, land fragmentation, and organization of production—enables or limits the effective deployment of green technologies. Higher concentration may foster efficiency gains by lowering marginal adoption costs, while fragmented or small-scale systems may impede scale economies in resource use and ecological transition.
The box plots in Figure 2d summarize the statistical distributions of TE (blue), PTE (orange), and SE (green). Nagqu exhibits the greatest variability—with standard deviations of 0.2121 for TE and 0.2088 for SE—while Lhasa’s efficiency measures are most tightly clustered (TE standard deviation = 0.0476), signaling stable performance. Median TE values rank highest in Lhasa (0.9960), Xigazê (0.9935), and Nyingchi (0.9798) and lowest in Nagqu (0.7677) and Ngari (0.8815). In every prefecture, median PTE exceeds median SE, reaffirming that scale inefficiencies remain the main bottleneck to improving AGTFP in Tibet.
4.2. Temporal Evolution of AGTFP Distribution in Tibet
The evolution of the province-wide kernel density curves (Figure 3) reveals that the AGTFP distribution shifted from a left-skewed profile during the Tenth Five-Year Plan period to a right-skewed, high-peak profile during the Thirteenth Five-Year Plan period. This shift indicates not only an overall improvement in green production efficiency but also the emergence of high-efficiency clusters, consistent with the S-shaped diffusion pattern of technological adoption. Moreover, the increasingly pronounced peak suggests a convergence trend, as regional disparities in green total factor productivity diminish over time.
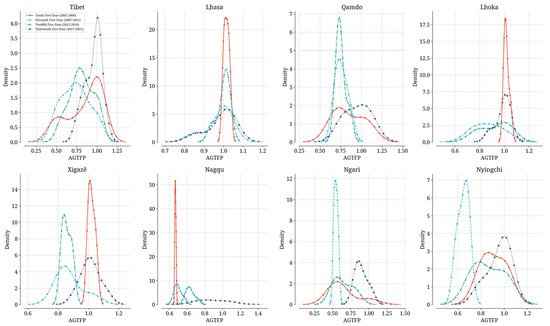
Figure 3.
Kernel density evolution of AGTFP across Tibetan prefectures during successive Five-Year Plans (2002–2021). (In this study, we adjust the Five-Year Plan periods as follows: the “Tenth Five-Year Plan” period is defined as 2002–2006, the “Eleventh Five-Year Plan” as 2007–2011, the “Twelfth Five-Year Plan” as 2012–2016, and the “Thirteenth Five-Year Plan” as 2017–2021. Although China’s official plan cycles ran from 2001–2005 (Tenth) and 2006–2010 (Eleventh), we extended each period by one year. This adjustment reflects the common phenomenon of policy inertia and institutional lag; even after a new plan is issued, government departments often continue to implement tools and frameworks from the previous planning cycle during its first year. For example, although the Tenth Plan was released in 2001, many policies formulated under the Ninth Plan remained in effect throughout that year).
Lhasa consistently exhibits a high AGTFP distribution across all four plan periods, with the main kernel density peak shifting markedly to the right. During the Thirteenth Five-Year Plan, Lhasa’s density curve even shows a slight multimodal pattern, suggesting internal stratification of efficiency levels. As the regional capital, Lhasa benefits from superior policy support, funding, and technology, making it a frontline area for green agricultural innovation. The emergence of multiple peaks in its AGTFP distribution reflects a “club convergence” phenomenon, where agricultural actors at different efficiency tiers form distinct convergence clubs—an outcome of heterogeneous resource endowments and differential technology adoption capacities within the city.
Xigazê’s AGTFP distribution remains relatively stable, with a clear upward shift in its median but without dramatic fluctuations. Its density curve concentrates to the left during the Eleventh and Twelfth Five-Year Plans then shifts rightward in the Thirteenth Plan, overlapping with the high-value region of the Tenth Plan. This pattern indicates steady median improvement and balanced development, rather than abrupt growth.
Qamdo experiences a pronounced efficiency gain and distribution concentration in the Twelfth Plan, exhibiting a single high peak. However, in the Thirteenth Plan, its density becomes bimodal, with one peak in the lower-efficiency range and another in the higher-efficiency range. This suggests that short-term gains driven by policy initiatives have subsequently diverged, revealing instability in the diffusion of green technologies and path-dependent characteristics.
Nyingchi’s AGTFP is highly concentrated during the Eleventh Plan. Although its overall level increases in the Twelfth and Thirteenth Plans—i.e, the density curve shifts rightward—the distribution becomes more dispersed, and the peak height declines. This evolution indicates a transition from a concentrated to a diversified green development model, likely reflecting the influence of a more varied industrial structure and differentiated development strategies. Despite the flattening distribution, the rightward shift confirms overall efficiency gains.
Lhoka’s AGTFP distribution is high and concentrated during the Tenth Plan, then declines and disperses through the Eleventh and Twelfth Plans, before recovering and reconcentrating in the Thirteenth Plan, forming a U-shaped rebound. This volatility likely reflects an adaptation and adjustment phase during the region’s green agricultural transformation, ultimately leading to renewed intensive and efficient development under sustained policy support.
Nagqu, representing the pastoral zone, shows a persistently left-skewed and flat kernel density across all periods, indicating uniformly low green efficiency and significant spatial disparities; the green transition remains a formidable challenge. Ngari’s AGTFP distribution mirrors Nagqu’s pattern, being overall low but with a slight rightward shift, suggesting pockets of green development breakthroughs that nevertheless remain constrained by harsh natural conditions.
From the evolution of the kernel density curves, it is clear that although AGTFP has risen overall in the Tibet Autonomous Region, significant disparities persist among prefectures, and a pattern of structural polarization in green efficiency gains has emerged. Some areas—such as Lhasa and Nyingchi—have already entered a phase of high-efficiency green development, whereas remote pastoral zones like Nagqu and Ngari lag behind. This spatial heterogeneity in the green transition calls for targeted policy interventions. A “gradient advancement” strategy should be developed, tailoring differentiated technology diffusion pathways to the distinct AGTFP distribution profiles of each region, while paying close attention to the critical thresholds for technology adoption and optimizing diffusion network structures.
4.3. Spatial Decomposition of AGTFP Disparities in Tibet
From 2002 to 2020, the overall Gini coefficient for AGTFP in the Tibet Autonomous Region increased from 0.165 to 0.260, representing a 57.6 percent rise, indicating a persistent intensification of regional development imbalances (Table 6). A segmented analysis reveals that the Gini coefficient rose slowly between 2002 and 2008. During the intensive period of modernization policies and technology dissemination from 2008 to 2017, inequality expanded more rapidly. Although the coefficient stabilized somewhat between 2017 and 2020, the overall gap continued to widen.

Table 6.
Decomposition of AGTFP inequality by source and Gini contribution (Tibet, 2002–2020).
Between 2002 and 2020, within-region inequality rose from 0.068 to 0.105—a 54.4 percent increase—although its share of the total Gini coefficient edged down slightly from 41.2 percent to 40.4 percent. Meanwhile, between-region inequality increased from 0.085 to 0.140—a 64.7 percent rise—and its share climbed from 51.5 percent to 53.8 percent. These trends indicate that disparities across ecological zones are the primary driver of AGTFP inequality and that their relative importance has grown over the study period. Although intra-regional imbalances have also widened, their relative contribution has declined modestly, suggesting more uniform productivity distributions within each zone.
Transvariation density remained positive throughout, increasing slightly from 0.012 in 2002 to 0.015 in 2020, but its share of the overall Gini coefficient fell from 7.3 percent to 5.8 percent. The positive transvariation density indicates that AGTFP distributions in different zones partially overlap rather than being completely separated. Overall, from 2002 to 2020, Tibet’s AGTFP inequality exhibited a “three increases, one decrease” pattern: the overall Gini coefficient rose continuously; both within- and between-region disparities expanded significantly, with between-region disparity growing fastest and contributing an increasing share; and transvariation density, while positive, accounted for a declining proportion, showing that cross-zone overlap effects have weakened.
Between 2002 and 2020, the Gini coefficients within Tibet’s three ecological zones all trended upward (Table 7), albeit with varying magnitudes and absolute levels. In the farmland zone, the coefficient rose from 0.025 to 0.033—a 32 percent increase—indicating a modest intensification of internal inequality. The agro-pastoral transition zone’s coefficient grew from 0.035 to 0.045—a 28.6 percent increase—placing it between the other two zones. The pastoral zone experienced the highest inequality increase, from 0.048 to 0.062 (a 29.2 percent rise), demonstrating the most pronounced internal disparity. Overall, although all three zones have narrowed the gap with their leading areas, structural divergence remains most acute in the pastoral zone.

Table 7.
Within- and between-zone Gini coefficients across Tibet’s three agro-ecological regions, 2002–2020.
Concerning between-region disparities, the farmland–pastoral Gini coefficient is the highest, rising from 0.068 to 0.090, underscoring the substantial differences in resource endowments, infrastructure, and industry technology between these zones. The Agro-Pastoral–Pastoral Gini follows, increasing from 0.052 to 0.065, while the farmland–agro-pastoral Gini remains the lowest, rising only from 0.042 to 0.055, reflecting the relative proximity of their geographic and economic conditions. The overall Gini coefficient climbed from 0.165 to 0.260, with between-region disparities contributing more than 50 percent and their share steadily increasing and far exceeding the roughly 40 percent contributed by within-region disparities. Transvariation density remained between 6 percent and 7 percent but trended downward, indicating that although there is partial overlap between ecological zones, this cross-zone effect is becoming less effective at mitigating overall inequality. The spatial gradient in AGTFP disparities across Tibet is pronounced, suggesting an urgent need to bridge the structural gap between the farmland and pastoral zones while reinforcing balanced development within each zone.
5. Discussion
5.1. Spatiotemporal Evolution Mechanisms of AGTFP in Tibet
Between 2002 and 2021, AGTFP in the Tibet Autonomous Region exhibited an upward trend overall, accompanied by pronounced spatial divergence. Temporally, the region’s compound annual growth rate (CAGR) of 0.78 percent lagged behind China’s national agricultural average of approximately 1.6 percent [74]. This finding aligns with Hu’s (2024) and Huang et al.’s (2022) conclusions regarding significant regional disparities and relative underperformance in western China’s green agricultural productivity [75,76]. Notably, AGTFP growth accelerated markedly after 2010 (CAGR = 4.13 percent), coinciding with the implementation of key policies such as the Tibet Ecological Security Barrier Protection and Construction Plan (2008–2030). This temporal inflection supports Huang et al.’s (2024) assertion that institutional change and appropriate policy frameworks play decisive roles in fostering resource-efficient and environmentally friendly agriculture [77,78].
Spatially, AGTFP displayed strong heterogeneity not only in absolute levels but also in evolutionary trajectories. Agricultural zones such as Lhasa and Xigazê consistently maintained efficiencies above one, whereas pastoral regions like Nagqu and Ngari experienced significant jumps from low to high efficiency. This differentiation echoes Huang et al.’s (2022) emphasis on the foundational influence of geography—through its effects on resource accessibility and ecological carrying capacity—on agricultural green productivity [75]. However, our study demonstrates that spatial divergence in Tibet is not solely determined by natural endowments. Targeted ecological compensation and production transformation policies—for example, grassland ecological subsidies in Nagqu and the promotion of penned husbandry in cold-pastoral zones—have reshaped resource use and alleviated ecological pressures, directly driving pastoral AGTFP leaps (Nagqu’s CAGR = 4.51 percent from 2002 to 2021). This outcome corroborates Engel et al.’s (2008) finding that ecological compensation policies significantly enhance agricultural environmental performance [79] and encourages empirical support for policy interventions breaking through natural constraints in high-altitude pastoral areas [80,81].
Efficiency decomposition analysis further uncovers a dual-driven mechanism behind AGTFP growth. On one hand, improvements in pure technical efficiency are the primary growth contributor, consistent with the consensus that technological advancement is the core driver of agricultural efficiency [82]. On the other hand, persistently low scale efficiency constitutes a critical bottleneck. Such scale inefficiency stems from the plateau’s rigid environmental constraints: short effective growing seasons, severe land fragmentation (average plot size under 0.2 ha), and extremely limited ecological carrying capacity preclude economies of scale through intensification. Instead, intensified inputs can exacerbate diseconomies of scale—for instance, overgrazing accelerates desertification, and expanding herd sizes may increase livestock mortality [83]. Under these constraints, Tibet’s agricultural green transition has effectively bypassed a scale-expansion phase, relying directly on technological innovation and management optimization to achieve efficiency gains. This pattern exemplifies the “technology substituting for scale” model in ecologically fragile zones [84] and aligns with the classical interpretation that improvements in technical efficiency can occur independently of scale efficiency [85].
5.2. Regional Divergence and Convergence Characteristics of AGTFP in Tibet
Kernel density analysis indicates that AGTFP in the Tibet Autonomous Region was left-skewed during the Tenth Five-Year Plan, gradually evolving into a right-skewed, high-peak distribution by the Thirteenth Plan and forming high-efficiency clusters. This overall efficiency improvement and technology diffusion follows an S-shaped adoption curve [86], reflecting the club convergence theory: a few pioneering prefectures achieve green technology breakthroughs first, which then diffuse to other areas and stabilize within high-efficiency clubs [87]. However, pastoral zones such as Nagqu and Ngari have persistently low and flat AGTFP distributions, demonstrating that extreme natural conditions, limited technology access, and inadequate infrastructure constrain green productivity gains and produce structural polarization alongside high-efficiency clusters. Previous studies report that many western provinces in China also exhibit relatively low and slow-growing AGTFP due to ecological fragility and resource constraints [88,89], a pattern similar to that of Tibet. Overall, Tibet’s AGTFP displays severe structural polarization in line with theories of unequal regional development [90], indicating that conventional policies are insufficient to balance efficiency increases. Instead, tiered and differentiated green technology diffusion strategies should be tailored to the specific club distributions and geographic conditions of each prefecture.
The prefectures exhibit a convergence–divergence–reconvergence dynamic in AGTFP evolution, reflecting complex regional interactions in Tibet’s green agricultural development. This dynamic mirrors the trend in the Gini coefficient. Although the overall Gini coefficient rose from 0.165 in 2002 to 0.260 in 2020—a 57.6 percent increase—this growth followed a nonlinear path—from initial equilibrium to divergence and then to a new equilibrium—consistent with the core periphery-rebalancing framework in economic geography [91]. Decomposition shows that between-region disparities accounted for 51.5 percent of total inequality in 2002 and increased to 53.8 percent by 2020, corroborating findings on China’s regional inequality that structural factors are the primary drivers [92]. Among ecological types, differences between the farmland and pastoral zones were the largest, with the Gini rising from 0.068 to 0.090, underscoring the deep-seated constraints imposed by ecological conditions on green development. Meanwhile, transvariation density remained positive but declined from 7.3 percent to 5.8 percent, indicating that cross-zone complementarities and spillovers are weakening, consistent with the convergence club phenomenon [93], according to which distinct convergence clubs may form, and gaps between them prove resistant to elimination. The recent convergence observed in 2020–2021 may signal the beginning of a new phase in Tibet’s green agricultural development, as prefectures move from differentiated growth toward a renewed regional balance. These findings provide important insights into the long-term dynamics of plateau agriculture transformation, suggesting that policy interventions and technology diffusion may have varying balancing effects at different stages of development.
5.3. Research Limitations and Future Directions
Although this study applies a combination of Super-SBM modeling, kernel density evolution analysis, and Dagum Gini decomposition to systematically characterize the spatiotemporal dynamics of AGTFP on the Tibetan Plateau—covering efficiency measurement, temporal evolution, and spatial differentiation—several limitations and opportunities for further research remain. First, in terms of data coverage and indicator completeness, the panel data used in this study are primarily derived from statistical yearbooks and literature-based estimations. As such, the analysis does not incorporate higher-resolution data on climate, hydrology, soil, or plot-level inputs and outputs, which limits our ability to examine underlying micro-level mechanisms. Moreover, undesirable outputs are restricted to carbon emissions and non-point-source pollution, omitting other important environmental factors such as residual agricultural plastics and heavy metal accumulation. Second, regarding model assumptions and robustness, the Super-SBM model assumes that all decision-making units share a common production frontier. However, heterogeneity in geography and policy across prefectures in the plateau region may result in distinct frontiers. Future research could apply group-specific DEA or geographically weighted DEA models. Additionally, the results of kernel density estimation and Dagum decomposition may be sensitive to bandwidth selection and group classification schemes, requiring comparative testing and sensitivity analyses to ensure robustness. Third, this study has limitations in both modeling and contextualization. Spatial spillover effects were not captured due to the use of a non-parametric framework, and institutional factors such as policy support, land tenure, and cultural norms were not included due to data constraints. Future work should integrate spatial econometric approaches and contextual data to strengthen explanatory power and policy utility. This study does not examine the short-term impacts of climatic variability or extreme events (e.g., drought, frost) on AGTFP or the resilience of the agricultural system.
Future research could be expanded in the following directions: (1) integration of high-resolution data from remote sensing, meteorological sources, and geographic information systems (GIS) to construct AGTFP models at the village or plot level, enabling the analysis of environmental, technological, and policy effects at the micro scale; (2) employing spatial dynamic panel GMM or spatial Durbin dynamic models to quantify interregional technology diffusion, policy coordination, and ecological compensation spillover effects and exploring the path dependence and cumulative mechanisms underlying AGTFP in plateau regions; (3) investigation of AGTFP’s responses and recovery trajectories in the face of frequent climatic extremes in highland areas and development of agricultural system resilience indicators to assess the timeliness and adaptability of policy responses; and (4) expansion of efficiency assessment frameworks to include multidimensional sustainability goals such as carbon sources and sinks, water footprints, and biodiversity and adoption of multi-objective DEA or integrated sustainability scoring systems to provide more comprehensive performance metrics for policymaking. Furthermore, the incorporation of dynamic institutional and socio-economic variables could help us to better understand the mechanisms underlying the spatial heterogeneity and temporal evolution of agricultural green efficiency in Tibet. By addressing these limitations and advancing the analytical framework, future studies can deepen our understanding of the multiple drivers and resilience dynamics shaping green agricultural growth in high-altitude ecologically fragile regions and offer more targeted empirical support for optimizing sustainable development policies.
6. Conclusions and Policy Recommendations
6.1. Main Findings
This study employs a super-efficiency SBM model to measure AGTFP in the Tibet Autonomous Region from 2002 to 2021 and analyzes its spatiotemporal dynamics in depth. The main conclusions are as follows:
- (1)
- AGTFP in Tibet has shown an overall upward trend, but growth remains below the national average. During the study period, AGTFP in the region increased from 0.949 in 2002 to 1.068 in 2021, yielding a compound annual growth rate (CAGR) of 0.78 percent, which is lower than the national agricultural average of approximately 1.6 percent. Growth accelerated significantly after 2010 (CAGR = 4.13 percent), coinciding with the implementation of key policies such as the Tibet Ecological Security Barrier Protection and Construction Plan (2008–2030), indicating that an appropriate policy framework plays a decisive role in fostering resource-efficient and environmentally sustainable agriculture. Notably, the effects of policy interventions may not appear immediately. In remote, high-altitude regions like Tibet, labor substitution with mechanization often unfolds slowly and may take years to yield measurable productivity gains. This highlights the need for sustained long-term monitoring to assess policy outcomes effectively.
- (2)
- Tibet’s AGTFP exhibits pronounced regional heterogeneity, which can be categorized into three typical evolutionary patterns. The continuous improvement type (Nagqu and Qamdo) follows a three-phase pattern—an initial trough, gradual rise, and rapid leap—primarily driven by grassland ecological compensation and the adoption of penned livestock systems in cold pastoral zones. The stable fluctuation type (Lhasa and Xigazê) maintains consistently high efficiency levels but with considerable volatility. The decline risk type (Lhoka, Nyingchi, and Ngari) is characterized by an initial drop followed by stabilization, or a deep decline with slow recovery, reflecting systemic vulnerability.
- (3)
- Improvements in pure technical efficiency are the primary drivers of AGTFP growth in Tibet, while low scale efficiency remains a major constraint. Efficiency decomposition shows that the mean pure technical efficiency across regions (0.9447) is significantly higher than the mean technical efficiency (0.8523), highlighting scale inefficiency as a key limiting factor. This is primarily due to rigid environmental constraints on the plateau, including short growing seasons caused by cold climates, severe land fragmentation, and limited ecological carrying capacity—all of which undermine the foundational assumptions of economies of scale.
- (4)
- AGTFP in Tibet follows a “convergence–divergence–reconvergence” dynamic pattern, with widening regional disparities but a trend toward structural stabilization. Kernel density analysis shows that the AGTFP distribution shifted from a left-skewed pattern during the Tenth Five-Year Plan to a right-skewed, high-peak structure by the Thirteenth Plan, indicating not only overall improvements in green productivity but also the formation of high-efficiency clusters. Gini coefficient analysis reveals that overall inequality increased substantially, with the coefficient rising from 0.165 in 2002 to 0.260 in 2020—an increase of 57.6 percent—suggesting that regional development imbalances have continued to intensify.
- (5)
- Interregional disparities are the dominant source of AGTFP inequality in Tibet, and their importance has grown over time. Gini decomposition results show that interregional inequality rose from 0.085 in 2002 to 0.140 in 2020—an increase of 64.7 percent—and its share of total inequality rose from 51.5 percent to 53.8 percent, significantly exceeding the contribution from intraregional differences (around 40 percent). Among ecological zones, the farmland–pastoral divide exhibited the highest Gini coefficient (increasing from 0.068 to 0.090), highlighting substantial gaps in resource endowment, infrastructure, and agricultural technology levels between these areas.
Although notable progress has been made in advancing agricultural green productivity in Tibet, the uneven performance across ecological zones and the limited convergence observed during certain periods suggest that structural disparities and localized barriers remain. Future policies must therefore move beyond one-size-fits-all approaches and address region-specific challenges such as ecological fragility, technological diffusion gaps, and institutional capacity constraints. These findings also align closely with the United Nations Sustainable Development Goals (SDGs). Specifically, targeted interventions to reduce spatial disparities contribute to SDG 10 (Reduced Inequalities), while the promotion of environmentally sustainable and socially inclusive agricultural practices in high-altitude areas supports SDG 11 (Sustainable Cities and Communities). The proposed “gradient advancement” strategy reinforces the global imperative of fostering territorial equity, ecological resilience, and sustainable rural transformation.
6.2. Policy Recommendations
Based on the above findings, the following policy recommendations are proposed to enhance AGTFP and promote coordinated regional development in Tibet:
- (1)
- Development of a “staged advancement” strategy for green development, with differentiated technology diffusion pathways tailored to regional AGTFP profiles. For farmland zones (e.g., Qamdo and Nyingchi), priority should be given to promoting water-saving irrigation technologies and organic agriculture certification to enhance value-added production. In agro-pastoral transition zones (e.g., Lhasa, Lhoka, and Xigazê), efforts should focus on integrated crop–livestock circular production systems to improve resource use efficiency. For pastoral zones (e.g., Nagqu and Ngari), ecological compensation mechanisms should be further strengthened, and enclosed livestock systems adapted to alpine environments should be promoted to relieve grazing pressure on grasslands.
- (2)
- Prioritization of the enhancement of pure technical efficiency and overcoming scale-efficiency constraints. Given Tibet’s unique natural conditions, traditional scale expansion strategies should be set aside in favor of technological innovation and managerial optimization to drive productivity gains. Emphasis should be placed on developing precision agriculture technologies suited to high-altitude conditions, environmentally friendly agro-pastoral production models, and value-added processing for specialty agricultural products. Technological progress should be leveraged to compensate for the limitations of scale economies.
- (3)
- Strengthening regional coordination to narrow the structural gap between farmland and pastoral zones. Institutional mechanisms for interregional technology diffusion and resource sharing should be established to facilitate the spread of advanced production techniques from high-efficiency to low-efficiency areas. Infrastructure connectivity should be improved to enhance production conditions and market accessibility in pastoral zones, thereby enabling more efficient circulation, processing, and value-adding of agro-pastoral products.
Author Contributions
M.Z.—concepts, ideas, research design, data collection and analysis, and writing. J.X.—literature collection and organization, and extraction of key insights. C.Y.—ideas, research design, interpretation of the results, and editing. All authors have read and agreed to the published version of the manuscript.
Funding
Zhongba County Agricultural Green Development Pilot Support System Observation Station Construction Project (E11M3600AL) and the Measurement and Analysis of the Contribution Rate of Regional and Agricultural Technological Progress in Lhasa (LSKJ202427).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Data are available upon request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Alston, J.M.; Pardey, P.G. Agriculture in the Global Economy. J. Econ. Perspect. 2014, 28, 121–146. [Google Scholar] [CrossRef]
- Tubiello, F.N.; Rosenzweig, C.; Conchedda, G.; Karl, K.; Gütschow, J.; Xueyao, P.; Obli-Laryea, G.; Wanner, N.; Qiu, S.Y.; Barros, J.D.; et al. Greenhouse gas emissions from food systems: Building the evidence base. Environ. Res. Lett. 2021, 16, 065007. [Google Scholar] [CrossRef]
- Steffen, W.; Richardson, K.; Rockström, J.; Cornell, S.E.; Fetzer, I.; Bennett, E.M.; Biggs, R.; Carpenter, S.R.; de Vries, W.; de Wit, C.A.; et al. Planetary boundaries: Guiding human development on a changing planet. Science 2015, 347, 1259855. [Google Scholar] [CrossRef] [PubMed]
- Borrelli, P.; Robinson, D.A.; Panagos, P.; Lugato, E.; Yang, J.E.; Alewell, C.; Wuepper, D.; Montanarella, L.; Ballabio, C. Land use and climate change impacts on global soil erosion by water (2015–2070). Proc. Natl. Acad. Sci. USA 2020, 117, 21994–22001. [Google Scholar] [CrossRef]
- Yang, Y.; Tilman, D.; Jin, Z.; Smith, P.; Barrett, C.B.; Zhu, Y.-G.; Burney, J.; D’Odorico, P.; Fantke, P.; Fargione, J.; et al. Climate change exacerbates the environmental impacts of agriculture. Science 2024, 385, eadn3747. [Google Scholar] [CrossRef]
- Rosenzweig, C.; Mbow, C.; Barioni, L.G.; Benton, T.G.; Herrero, M.; Krishnapillai, M.; Liwenga, E.T.; Pradhan, P.; Rivera-Ferre, M.G.; Sapkota, T.; et al. Climate change responses benefit from a global food system approach. Nat. Food 2020, 1, 94–97. [Google Scholar] [CrossRef]
- Rockström, J.; Williams, J.; Daily, G.; Noble, A.; Matthews, N.; Gordon, L.; Wetterstrand, H.; DeClerck, F.; Shah, M.; Steduto, P.; et al. Sustainable intensification of agriculture for human prosperity and global sustainability. Ambio 2017, 46, 4–17. [Google Scholar] [CrossRef]
- Manioudis, M.; Meramveliotakis, G. Broad strokes towards a grand theory in the analysis of sustainable development: A return to the classical political economy. New Political Econ. 2022, 27, 866–878. [Google Scholar] [CrossRef]
- Klarin, T. The Concept of Sustainable Development: From its Beginning to the Contemporary Issues. Zagreb Int. Rev. Econ. Bus. 2018, 21, 67–94. [Google Scholar] [CrossRef]
- Altieri, M.A.; Koohafkan, P. Enduring Farms: Climate Change, Smallholders and Traditional Farming Communities; Third World Network (TWN): Penang, Malaysia, 2008; Volume 6. [Google Scholar]
- Pepin, N.; Bradley, R.S.; Diaz, H.F.; Baraer, M.; Caceres, E.B.; Forsythe, N.; Fowler, H.; Greenwood, G.; Hashmi, M.Z.; Liu, X.D.; et al. Elevation-dependent warming in mountain regions of the world. Nat. Clim. Change 2015, 5, 424–430. [Google Scholar] [CrossRef]
- Cuni-Sanchez, A.; Aneseyee, A.B.; Baderha, G.K.R.; Batumike, R.; Bitariho, R.; Imani, G.; Jha, N.; Kaganzi, K.R.; Kaplin, B.A.; Klein, J.A.; et al. Perceived climate change impacts and adaptation responses in ten African mountain regions. Nat. Clim. Change 2025, 15, 153–161. [Google Scholar] [CrossRef]
- Dullinger, S.; Gattringer, A.; Thuiller, W.; Moser, D.; Zimmermann, N.E.; Guisan, A.; Willner, W.; Plutzar, C.; Leitner, M.; Mang, T.; et al. Extinction debt of high-mountain plants under twenty-first-century climate change. Nat. Clim. Change 2012, 2, 619–622. [Google Scholar] [CrossRef]
- Pauli, H.; Halloy, S.R.P. High Mountain Ecosystems Under Climate Change. In Oxford Research Encyclopedia of Climate Science; Oxford University Press: Oxford, UK, 2019. [Google Scholar] [CrossRef]
- Viviroli, D.; Kummu, M.; Meybeck, M.; Kallio, M.; Wada, Y. Increasing dependence of lowland populations on mountain water resources. Nat. Sustain. 2020, 3, 917–928. [Google Scholar] [CrossRef]
- Zhou, Y.; Yuan, G.; Cong, Z.; Wang, X. Priorities for the sustainable development of the ecological environment on the Tibetan Plateau. Fundam. Res. 2021, 1, 329–333. [Google Scholar] [CrossRef]
- Li, D.; Tian, P.; Luo, H.; Hu, T.; Dong, B.; Cui, Y.; Khan, S.; Luo, Y. Impacts of land use and land cover changes on regional climate in the Lhasa River basin, Tibetan Plateau. Sci. Total Environ. 2020, 742, 140570. [Google Scholar] [CrossRef]
- Chung, Y.H.; Färe, R.; Grosskopf, S. Productivity and Undesirable Outputs: A Directional Distance Function Approach. J. Environ. Manag. 1997, 51, 229–240. [Google Scholar] [CrossRef]
- Lansink, A.O.; Ondersteijn, C. Energy Productivity Growth in the Dutch Greenhouse Industry. Am. J. Agric. Econ. 2006, 88, 124–132. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S.; Pasurka, C.A. Environmental production functions and environmental directional distance functions. Energy 2007, 32, 1055–1066. [Google Scholar] [CrossRef]
- Oh, S.-C.; Shin, J. The impact of mismeasurement in performance benchmarking: A Monte Carlo comparison of SFA and DEA with different multi-period budgeting strategies. Eur. J. Oper. Res. 2015, 240, 518–527. [Google Scholar] [CrossRef]
- Tone, K. A slacks-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef]
- Tone, K. A slacks-based measure of super-efficiency in data envelopment analysis. Eur. J. Oper. Res. 2002, 143, 32–41. [Google Scholar] [CrossRef]
- Zhaofeng, W.; Yaoyao, D. Spatiotemporal Variations and Influencing Factors of Carbon Emission Efficiency in Hunan Province Based on the SBM-DEA Model. Geogr. Sci. 2019, 39, 797–806. [Google Scholar] [CrossRef]
- Zhou, C.; Shi, C.; Wang, S.; Zhang, G. Estimation of eco-efficiency and its influencing factors in Guangdong province based on Super-SBM and panel regression models. Ecol. Indic. 2018, 86, 67–80. [Google Scholar] [CrossRef]
- Wang, J.; Wang, S.; Li, S.; Cai, Q.; Gao, S. Evaluating the energy-environment efficiency and its determinants in Guangdong using a slack-based measure with environmental undesirable outputs and panel data model. Sci. Total Environ. 2019, 663, 878–888. [Google Scholar] [CrossRef]
- Cheng, C.; Yu, X.; Hu, H.; Su, Z.; Zhang, S. Measurement of China’s Green Total Factor Productivity Introducing Human Capital Composition. Int. J. Environ. Res. Public Health 2022, 19, 13563. [Google Scholar] [CrossRef]
- Rockström, J.; Steffen, W.; Noone, K.; Persson, Å.; Chapin, F.S.; Lambin, E.F.; Lenton, T.M.; Scheffer, M.; Folke, C.; Schellnhuber, H.J.; et al. A safe operating space for humanity. Nature 2009, 461, 472–475. [Google Scholar] [CrossRef]
- Sachs, J.D.; Schmidt-Traub, G.; Mazzucato, M.; Messner, D.; Nakicenovic, N.; Rockström, J. Six Transformations to achieve the Sustainable Development Goals. Nat. Sustain. 2019, 2, 805–814. [Google Scholar] [CrossRef]
- Shen, Z.; Boussemart, J.-P.; Leleu, H. Aggregate green productivity growth in OECD’s countries. Int. J. Prod. Econ. 2017, 189, 30–39. [Google Scholar] [CrossRef]
- Lv, T.; Fu, S.; Zhang, X.; Hu, H.; Zhang, Y. Spatiotemporal evolution and convergence of agricultural eco-efficiency in the middle reaches of the Yangtze River. Phys. Chem. Earth Parts A/B/C 2023, 131, 103438. [Google Scholar] [CrossRef]
- Liu, Y.; Qi, X.; Guo, Y. Spatiotemporal coupling analysis between green total factor productivity and urban e-commerce development in China’s eight urban clusters. Sci. Rep. 2024, 14, 22816. [Google Scholar] [CrossRef]
- Yu, Z.; Lin, Q.; Huang, C. Re-Measurement of Agriculture Green Total Factor Productivity in China from a Carbon Sink Perspective. Agriculture 2022, 12, 2025. [Google Scholar] [CrossRef]
- He, J.; Han, M. Analysis of spatial and temporal characteristics and evolution of green total factor productivity in agriculture in the lower Yellow River basin. Front. Sustain. Food Syst. 2024, 8, 1474813. [Google Scholar] [CrossRef]
- Bao, H.; Liu, X.; Xu, X.; Shan, L.; Ma, Y.; Qu, X.; He, X. Spatial-temporal evolution and convergence analysis of agricultural green total factor productivity-evidence from the Yangtze River Delta Region of China. PLoS ONE 2023, 18, e0271642. [Google Scholar] [CrossRef] [PubMed]
- Zhao, P.; Wu, H.; Lu, Z.; Kou, J.; Du, J. Spatial differences, distributional dynamics, and driving factors of green total factor productivity in China. Front. Environ. Sci. 2022, 10, 1058612. [Google Scholar] [CrossRef]
- Zhou, F.; Wen, C. Research on the Level of Agricultural Green Development, Regional Disparities, and Dynamic Distribution Evolution in China from the Perspective of Sustainable Development. Agriculture 2023, 13, 1441. [Google Scholar] [CrossRef]
- Wang, F.; Du, L.; Tian, M. Does Agricultural Credit Input Promote Agricultural Green Total Factor Productivity? Evidence from Spatial Panel Data of 30 Provinces in China. Int. J. Environ. Res. Public Health 2023, 20, 529. [Google Scholar] [CrossRef]
- Liu, S.; Lei, P.; Li, X.; Li, Y. A nonseparable undesirable output modified three-stage data envelopment analysis application for evaluation of agricultural green total factor productivity in China. Sci. Total Environ. 2022, 838, 155947. [Google Scholar] [CrossRef]
- Simar, L.; Wilson, P.W. Estimation and inference in two-stage, semi-parametric models of production processes. J. Econom. 2007, 136, 31–64. [Google Scholar] [CrossRef]
- Cui, X.; Graf, H.-F. Recent land cover changes on the Tibetan Plateau: A review. Clim. Change 2009, 94, 47–61. [Google Scholar] [CrossRef]
- Adelabu, D.B.; Clark, V.R.; Bredenhand, E. Potential for Sustainable Mountain Farming: Challenges and Prospects for Sustainable Smallholder Farming in the Maloti–Drakensberg Mountains. Mt. Res. Dev. 2020, 40, A1–A11. [Google Scholar] [CrossRef]
- Zhou, T.; Yang, H.; Qiu, X.; Sun, H.; Song, P.; Yang, W. China’s grassland ecological compensation policy achieves win-win goals in Inner Mongolia. Environ. Res. Commun. 2023, 5, 031007. [Google Scholar] [CrossRef]
- Tibet Statistical Yearbook 2003–2022; China Statistics Press: Beijing, China, 2022.
- Li, H.; Fang, K.; Yang, W.; Wang, D.; Hong, X. Regional environmental efficiency evaluation in China: Analysis based on the Super-SBM model with undesirable outputs. Math. Comput. Model. 2013, 58, 1018–1031. [Google Scholar] [CrossRef]
- Cooper, W.W.; Seiford, L.M.; Tone, K. Data Envelopment Analysis: A Comprehensive Text with Models, Applications, References and DEA-Solver Software; Springer: Berlin/Heidelberg, Germany, 2007; Volume 2. [Google Scholar]
- Zhang, Y.; Yu, Z.; Zhang, J. Analysis of carbon emission performance and regional differences in China’s eight economic regions: Based on the super-efficiency SBM model and the Theil index. PLoS ONE 2021, 16, e0250994. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.; Guo, H.; Xu, S.; Pan, C. Environmental regulations and agricultural carbon emissions efficiency: Evidence from rural China. Heliyon 2024, 10, e25677. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Routledge: Oxfordshire, UK, 2018. [Google Scholar]
- Dagum, C. Decomposition and interpretation of Gini and the generalized entropy inequality measures. Statistica 1997, 57, 295–308. [Google Scholar] [CrossRef]
- Hayami, Y.; Ruttan, V. Agricultural Development: An International Perspective; The Johns Hopkins Press: Baltimore, MD, USA; London, UK, 1971; p. 123. [Google Scholar]
- Liu, Y.; Lu, C.; Chen, X. Dynamic analysis of agricultural green development efficiency in China: Spatiotemporal evolution and influencing factors. J. Arid Land 2023, 15, 127–144. [Google Scholar] [CrossRef]
- Anik, A.R.; Rahman, S.; Sarker, J.R. Agricultural Productivity Growth and the Role of Capital in South Asia (1980–2013). Sustainability 2017, 9, 470. [Google Scholar] [CrossRef]
- Le, N.T.; Thinh, N.A.; Ha, N.T.V.; Tien, N.D.; Lam, N.D.; Hong, N.V.; Tuan, N.T.; Hanh, T.V.; Khanh, N.N.; Thanh, N.N.; et al. Measuring water resource use efficiency of the Dong Nai River Basin (Vietnam): An application of the two-stage data envelopment analysis (DEA). Environ. Dev. Sustain. 2022, 24, 12427–12445. [Google Scholar] [CrossRef]
- Wen, L.; Li, H. Estimation of agricultural energy efficiency in five provinces: Based on data envelopment analysis and Malmquist index model. Energy Sources Part A Recovery Util. Environ. Eff. 2022, 44, 2900–2913. [Google Scholar] [CrossRef]
- Lal, R. Soil carbon sequestration to mitigate climate change. Geoderma 2004, 123, 1–22. [Google Scholar] [CrossRef]
- Kroodsma, D.A.; Field, C.B. CARBON SEQUESTRATION IN CALIFORNIA AGRICULTURE, 1980–2000. Ecol. Appl. 2006, 16, 1975–1985. [Google Scholar] [CrossRef] [PubMed]
- Peltonen-Sainio, P.; Muurinen, S.; Rajala, A.; Jauhiainen, L. Variation in harvest index of modern spring barley, oat and wheat cultivars adapted to northern growing conditions. J. Agric. Sci. 2008, 146, 35–47. [Google Scholar] [CrossRef]
- Eggleston, H.; Buendia, L.; Miwa, K.; Ngara, T.; Tanabe, K. 2006 IPCC Guidelines for National Greenhouse Gas Inventories; Institute for Global Environmental Strategies: Hayama, Japan, 2006. [Google Scholar]
- Ronghua, J.; Wei, L.; Zhengang, Y. A Study on the Carbon Balance of Household Production Systems in Typical Agro-Pastoral Transition Zones of Gansu Province from a Carbon Neutrality Perspective. Crop Res. 2023, 37, 259–266. [Google Scholar]
- Hütsch, B.W.; Schubert, S. Chapter Two—Harvest Index of Maize (Zea mays L.): Are There Possibilities for Improvement? In Advances in Agronomy; Sparks, D.L., Ed.; Academic Press: Cambridge, UK, 2017; Volume 146, pp. 37–82. [Google Scholar]
- Rathke, G.W.; Behrens, T.; Diepenbrock, W. Integrated nitrogen management strategies to improve seed yield, oil content and nitrogen efficiency of winter oilseed rape (Brassica napus L.): A review. Agric. Ecosyst. Environ. 2006, 117, 80–108. [Google Scholar] [CrossRef]
- AL-agele, H.A.; Proctor, K.; Murthy, G.; Higgins, C. A Case Study of Tomato (Solanum lycopersicon var. Legend) Production and Water Productivity in Agrivoltaic Systems. Sustainability 2021, 13, 2850. [Google Scholar] [CrossRef]
- Carpenter, S.R.; Caraco, N.F.; Correll, D.L.; Howarth, R.W.; Sharpley, A.N.; Smith, V.H. Nonpoint pollution of surface waters with phosphorus and nitrogen. Ecol. Appl. 1998, 8, 559–568. [Google Scholar] [CrossRef]
- Novotny, V. Water Quality: Diffuse Pollution and Watershed Management; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Zhu, K.-W.; Cheng, Y.-C.; Yang, Z.-M.; Huang, L.; Zhang, S.; Lei, B. Research trends of agricultural non-point source pollution risk assessment based on bibliometric method. J. Ecol. Rural Environ. 2020, 36, 425–432. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2007-Mitigation of Climate Change:Working Group III Contribution to the Fourth Assessment Report of the IPCC.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007. [Google Scholar]
- Ming, G.; Hongyuan, S. Spatial Convergence and Divergence of Carbon Emission Efficiency in Chinese Agriculture: An Empirical Analysis Based on the Malmquist–Luenberger Index and Spatial Econometrics. Econ. Geogr. 2015, 35, 142–148+185. [Google Scholar] [CrossRef]
- Yiqing, C.; Huarui, W.; Chunfeng, T. Evaluation of Agricultural Production Efficiency and Its Influencing Factors in Jiangxi Province. East China Econ. Manag. 2016, 30, 21–28. [Google Scholar]
- Fu, D.; Gong, Y.; Chen, C.; Gui, X.; Liu, H.; Chen, S.; Ren, J.; Hou, B. Nitrogen and Phosphorus Loading Characteristics of Agricultural Non-Point Sources in the Tuojiang River Basin. Water 2023, 15, 3503. [Google Scholar] [CrossRef]
- Liutao, L. A Study on the Spatiotemporal Characteristics and Evolutionary Patterns of the Rural Ecological Environment. Doctor Nanjing Agricultural University: Nanjing, China, 2009. [Google Scholar]
- Dubey, A.; Lal, R. Carbon Footprint and Sustainability of Agricultural Production Systems in Punjab, India, and Ohio, USA. J. Crop Improv. 2009, 23, 332–350. [Google Scholar] [CrossRef]
- Bo, L.; Junbiao, Z.; Haipeng, L. Spatiotemporal Characteristics and Decomposition of Influencing Factors of Agricultural Carbon Emissions in China. China Popul. Resour. Environ. 2011, 21, 80–86. [Google Scholar]
- Changliang, S. The Impact of Land Transfers on High-Quality Agricultural Development from a Green Total Factor Productivity Perspective. J. Nat. Resour. 2024, 39, 1418–1433. [Google Scholar]
- Huang, X.; Feng, C.; Qin, J.; Wang, X.; Zhang, T. Measuring China’s agricultural green total factor productivity and its drivers during 1998–2019. Sci. Total Environ. 2022, 829, 154477. [Google Scholar] [CrossRef]
- Hu, J. Green productivity growth and convergence in Chinese agriculture. J. Environ. Plan. Manag. 2024, 67, 1775–1804. [Google Scholar] [CrossRef]
- Huang, L.; Zhou, X.; Chi, L.; Meng, H.; Chen, G.; Shen, C.; Wu, J. Stimulating innovation or enhancing productivity? The impact of environmental regulations on agricultural green growth. J. Environ. Manag. 2024, 370, 122706. [Google Scholar] [CrossRef]
- Sun, Y. Environmental regulation, agricultural green technology innovation, and agricultural green total factor productivity. Front. Environ. Sci. 2022, 10, 955954. [Google Scholar] [CrossRef]
- Engel, S.; Pagiola, S.; Wunder, S. Designing payments for environmental services in theory and practice: An overview of the issues. Ecol. Econ. 2008, 65, 663–674. [Google Scholar] [CrossRef]
- Pagiola, S.; Arcenas, A.; Platais, G. Can Payments for Environmental Services Help Reduce Poverty? An Exploration of the Issues and the Evidence to Date from Latin America. World Dev. 2005, 33, 237–253. [Google Scholar] [CrossRef]
- Hayes, T.M. Payment for ecosystem services, sustained behavioural change, and adaptive management: Peasant perspectives in the Colombian Andes. Environ. Conserv. 2012, 39, 144–153. [Google Scholar] [CrossRef]
- Jin, S.; Ma, H.; Huang, J.; Hu, R.; Rozelle, S. Productivity, efficiency and technical change: Measuring the performance of China’s transforming agriculture. J. Product. Anal. 2010, 33, 191–207. [Google Scholar] [CrossRef]
- Harris, R.B. Rangeland degradation on the Qinghai-Tibetan plateau: A review of the evidence of its magnitude and causes. J. Arid Environ. 2010, 74, 1–12. [Google Scholar] [CrossRef]
- Nayak, A.K.; Rahul, T.; Dhal, B.; Nayak, A.D.; Vijayakumar, S.; Satpathy, B.; Chatterjee, D.; Swain, C.K.; Moharana, K.C.; Nayak, P.K.; et al. Eco-efficiency and technical efficiency of different integrated farming systems in eastern India. Int. J. Agric. Sustain. 2023, 21, 2270250. [Google Scholar] [CrossRef]
- Kumbhakar, S.C.; Lovell, C.K. Stochastic Frontier Analysis; Cambridge University Press: Cambridgeshire, UK, 2003. [Google Scholar]
- Rogers, E. Diffusion of Innovations, 5th ed.; Free Press: Tampa, FL, USA, 2003. [Google Scholar]
- Phillips, P.C.; Sul, D. Transition modeling and econometric convergence tests. Econometrica 2007, 75, 1771–1855. [Google Scholar] [CrossRef]
- Haihong, G.; Xinmin, L. Spatiotemporal Evolution of China’s Agricultural Green Total Factor Productivity. China Manag. Sci. 2020, 28, 66–75. [Google Scholar] [CrossRef]
- Yafei, W.; Qijia, Z.; Ying, B. China’s Agricultural Green Total Factor Productivity and Its Spatiotemporal Evolution. Stat. Decis. 2022, 38, 98–102. [Google Scholar] [CrossRef]
- Myrdal, G.; Sitohang, P. Economic Theory and Under-Developed Regions; Gerald Duckworth & Co., Ltd.: London, UK, 1957; Available online: http://revistas.bancomext.gob.mx/rce/magazines/567/12/RCE11.pdf (accessed on 25 November 2024).
- Krugman, P. What’s New About the New Economic Geography? Oxf. Rev. Econ. Policy 1998, 14, 7–17. Available online: https://www.jstor.org/stable/23606492 (accessed on 25 November 2024). [CrossRef]
- Xie, Y.; Zhou, X. Income inequality in today’s China. Proc. Natl. Acad. Sci. USA 2014, 111, 6928–6933. [Google Scholar] [CrossRef]
- Quah, D.T. Twin Peaks: Growth and Convergence in Models of Distribution Dynamics. Econ. J. 1996, 106, 1045–1055. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).