Effect of Angle Between Center-Mounted Blades and Disc on Particle Trajectory Correction in Side-Throwing Centrifugal Spreaders
Abstract
1. Introduction
2. Materials and Methods
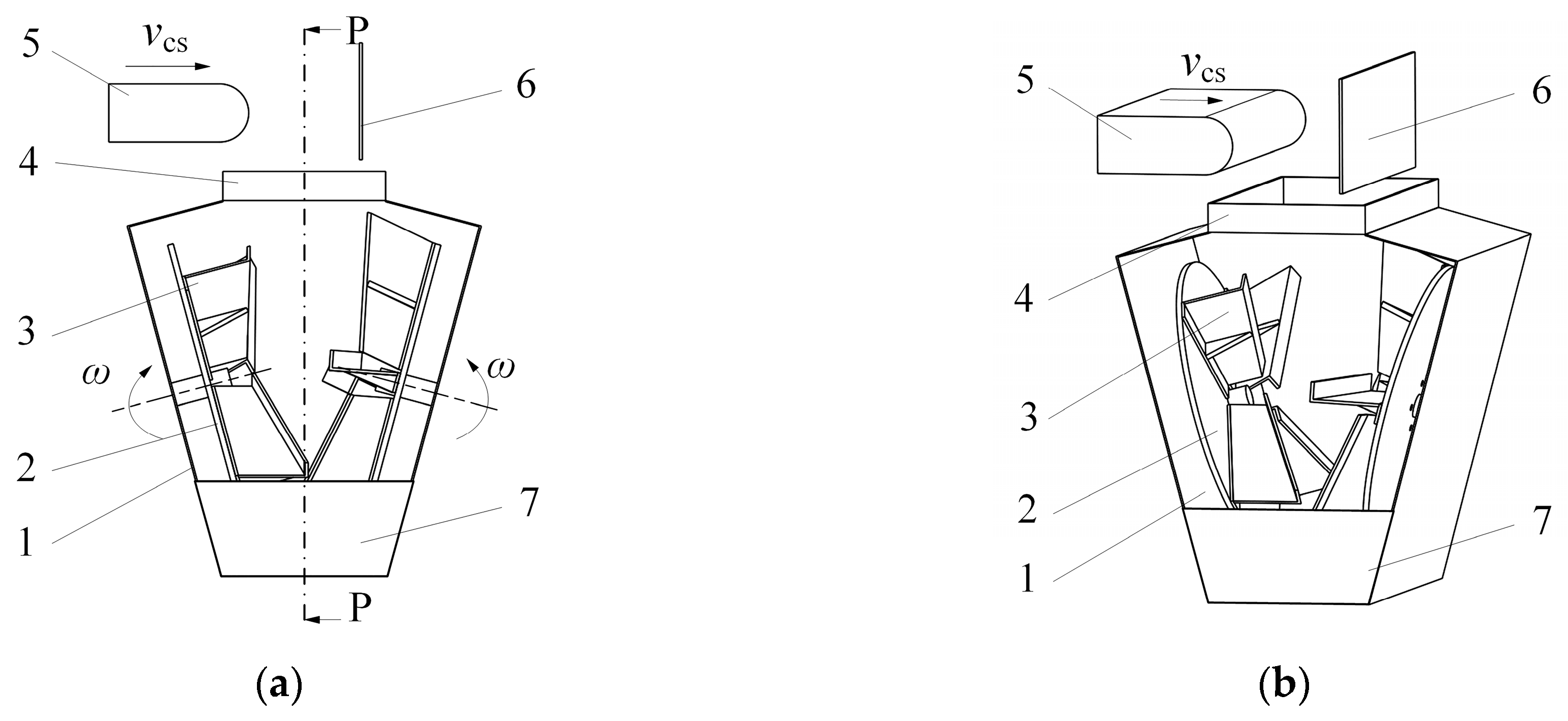
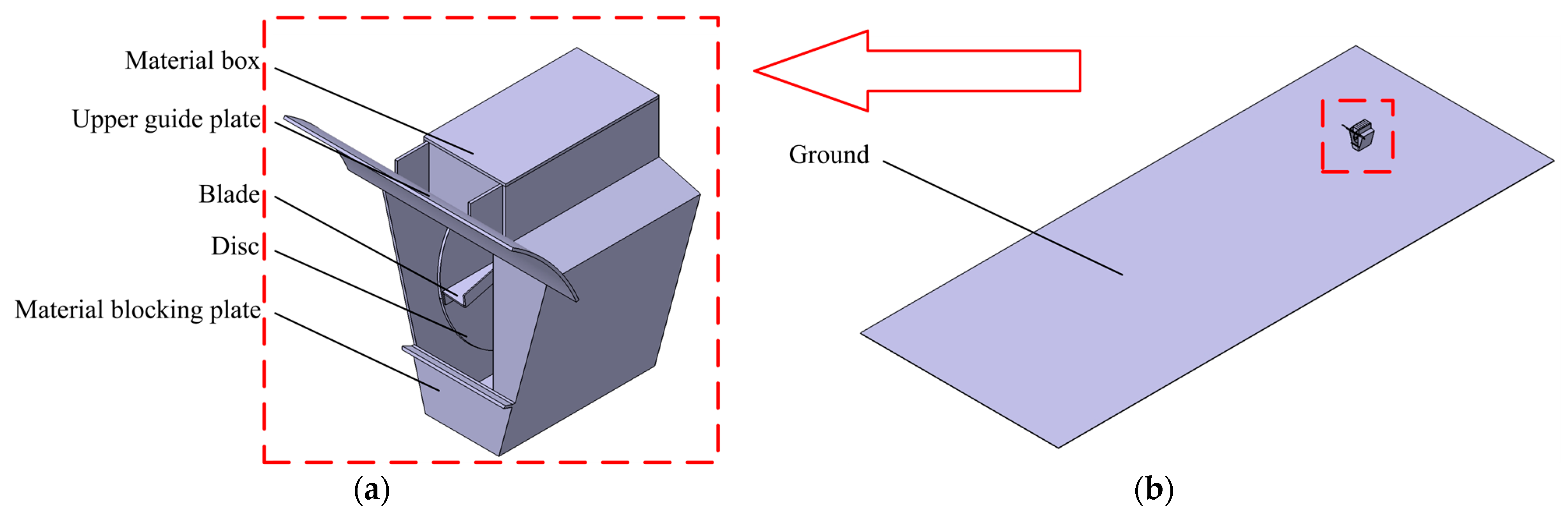
2.1. Structural Configuration and Operational Principles of Centrifugal Spreader
- Disc diameter (R): 500 mm;
- Disc inclination angle (α): 75°;
- Blade–disc angle (τ): 320 mm.
- Operational parameters:
- Disc rotation speed (ω): 700 rpm;
- Machine travel speed (VNCC): 3.6 m/s;
- Feed rate (mcs): 6 kg/s.
- Material properties:
- Particle mass (m): 4 × 10−4 kg;
- Friction coefficient (kf): 0.11 (steel surface);
- Gravitational acceleration (g): 9.81 m/s2.
2.2. Theoretical Analysis of Organic Fertilizer Particle Projection by the Main Throwing Unit
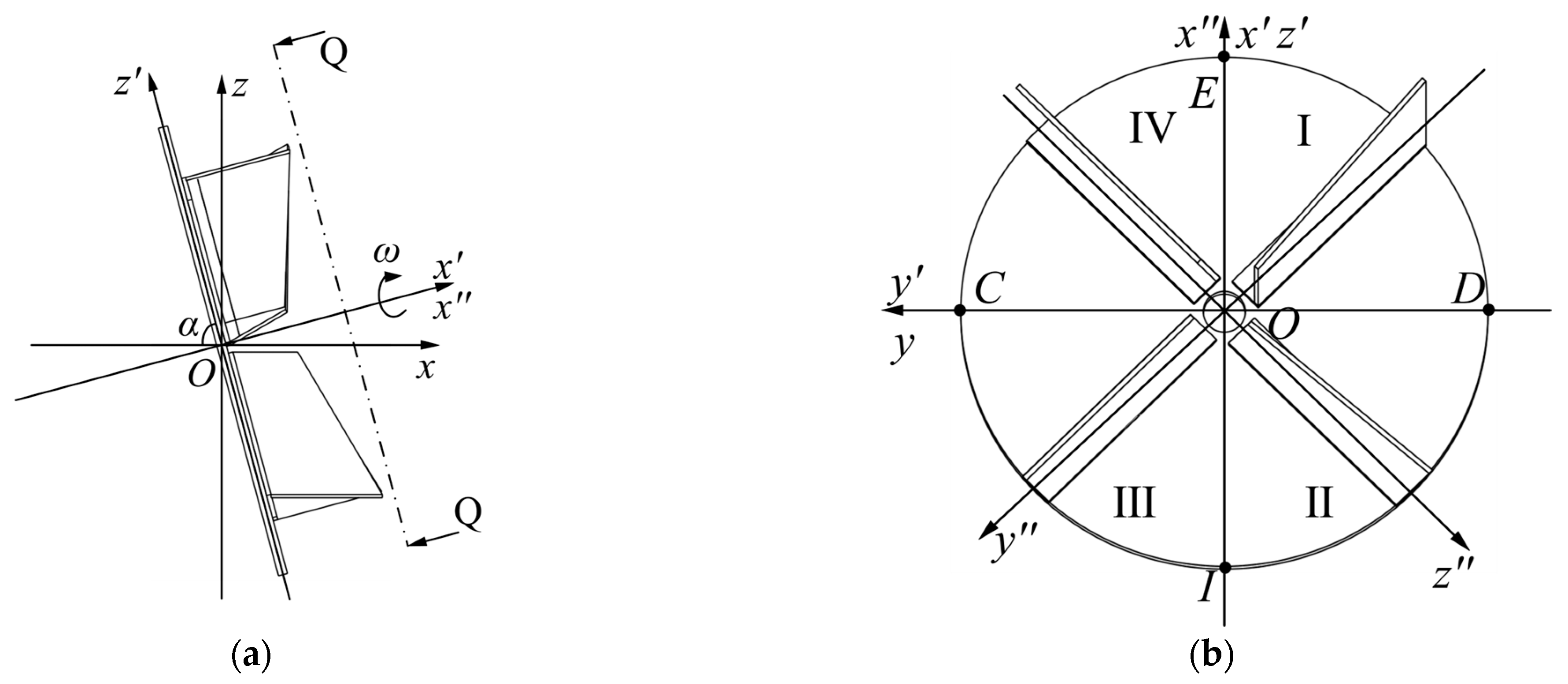
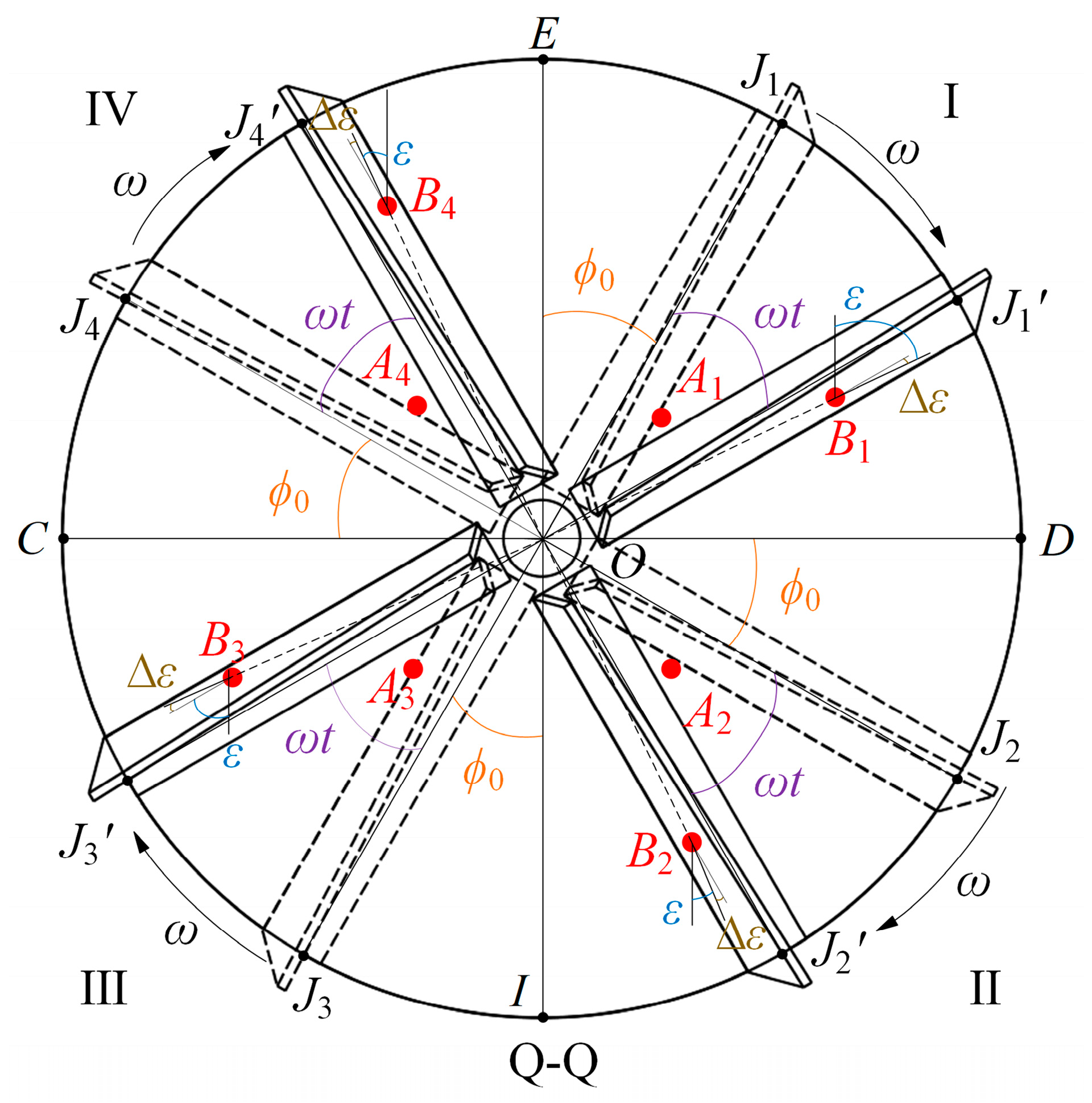
2.2.1. Reference Coordinate System Establishment
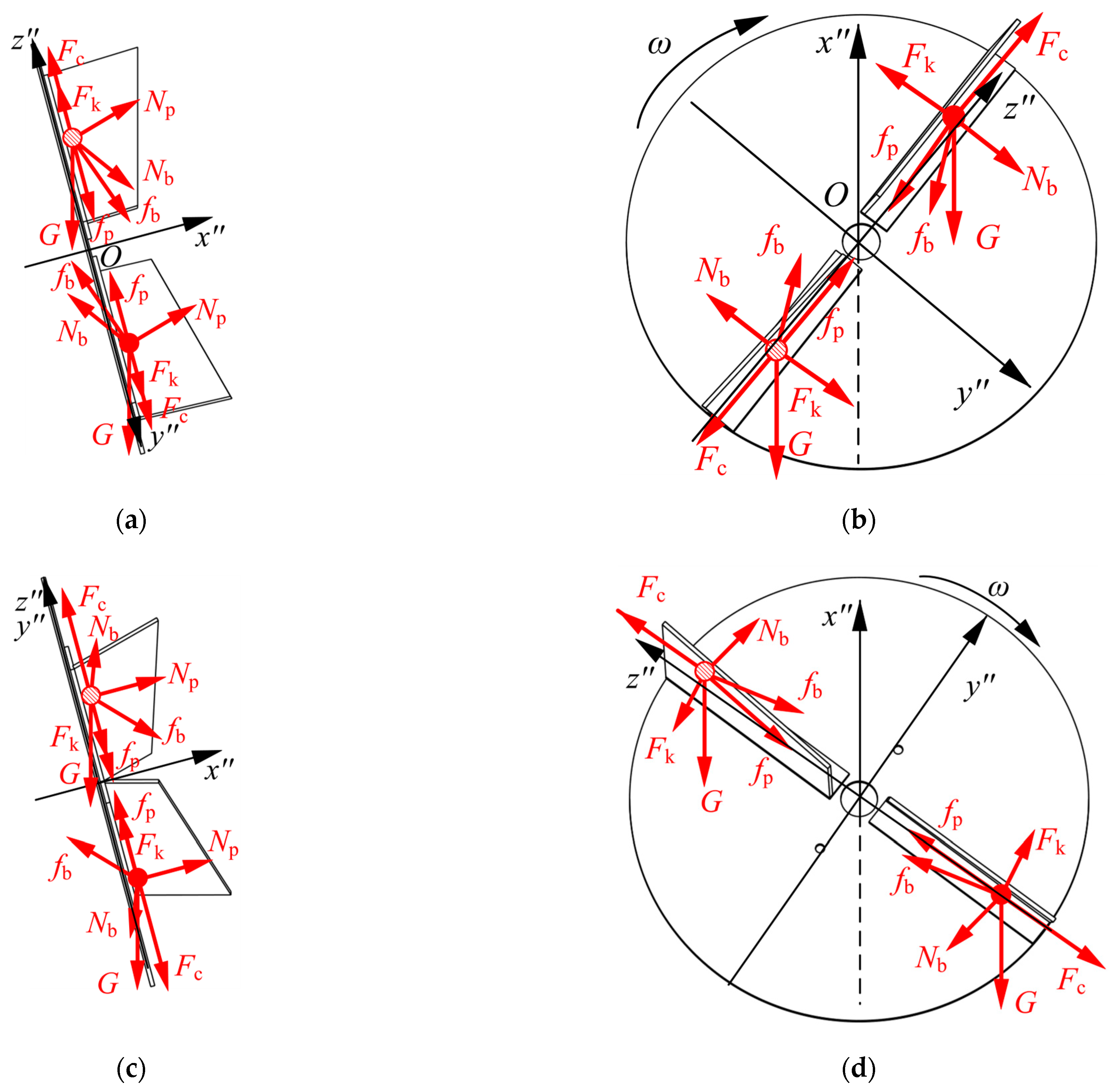
2.2.2. Kinematic and Dynamic Analysis of Particles Under Force
2.2.3. Establishment of Mechanical Equations for Organic Fertilizer Granules
2.3. Analytical Solution of the Mechanical Equations
2.4. Virtual Simulation
2.4.1. Simulation Model Development
2.4.2. Simulation Parameter Settings
2.5. Experimental Setup and Testing
2.5.1. Experimental Setup and Materials
2.5.2. Experimental Methodology
3. Results
3.1. Numerical Analysis
3.2. Virtual Simulation Evaluation Index Measurement Methods
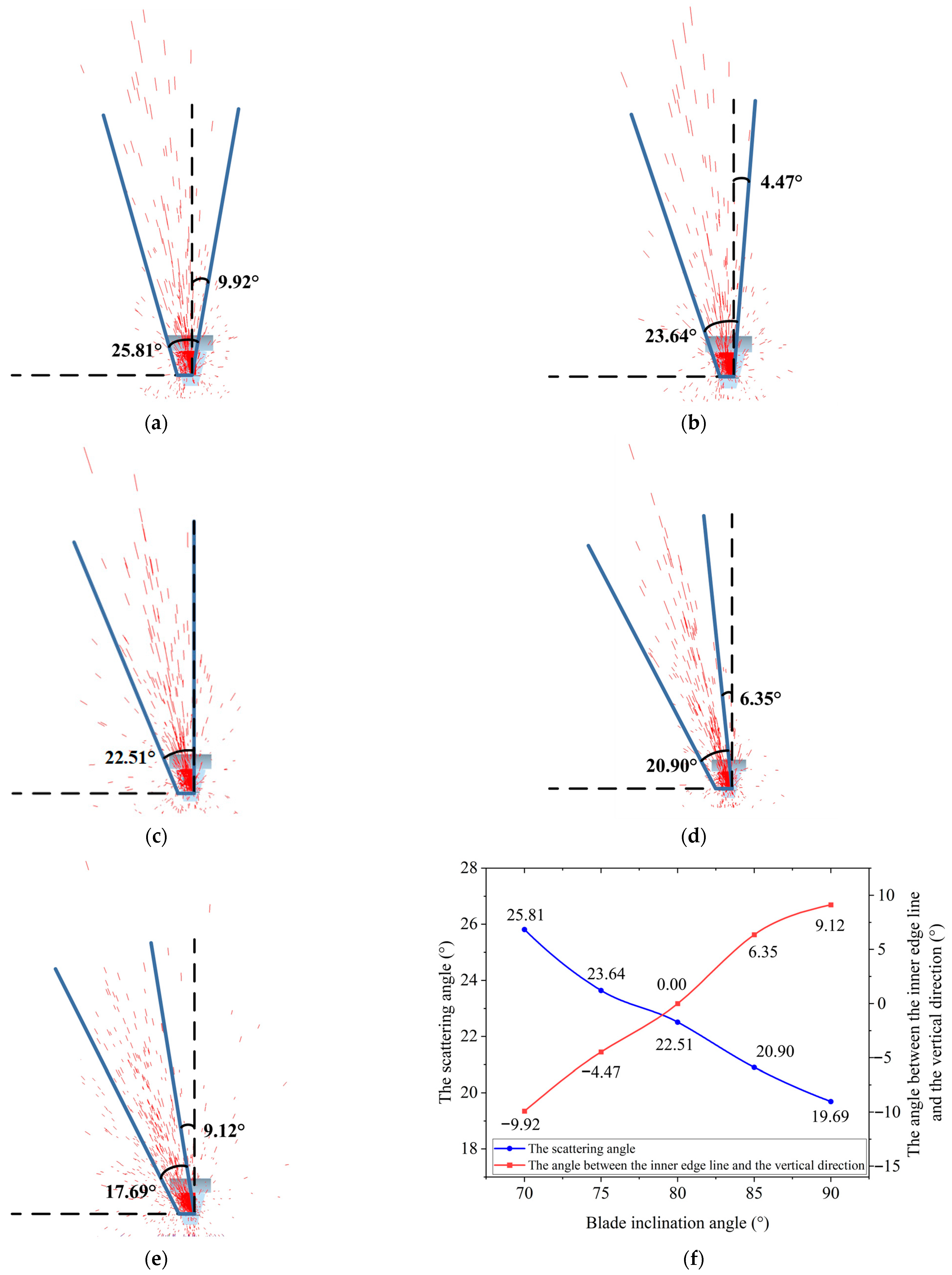
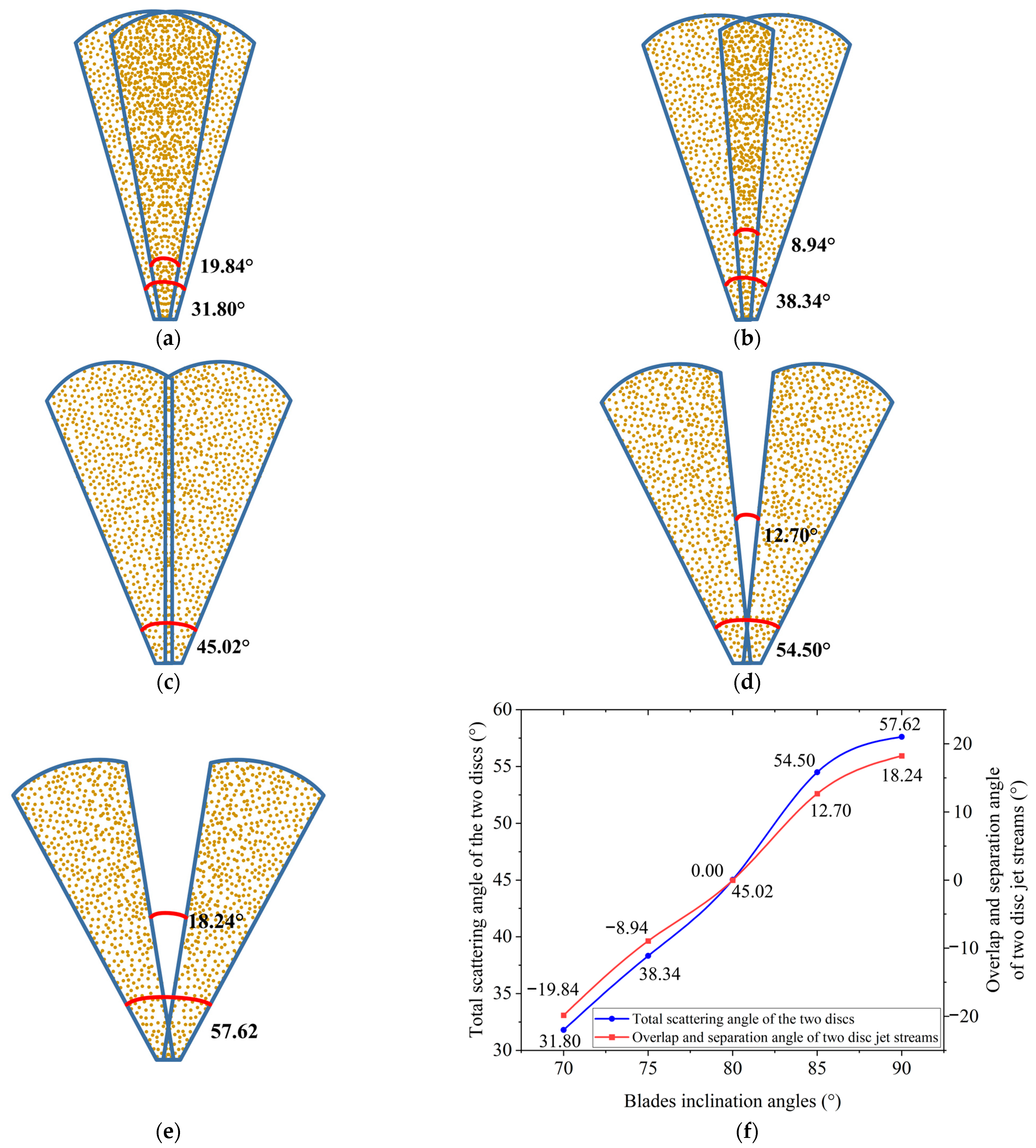
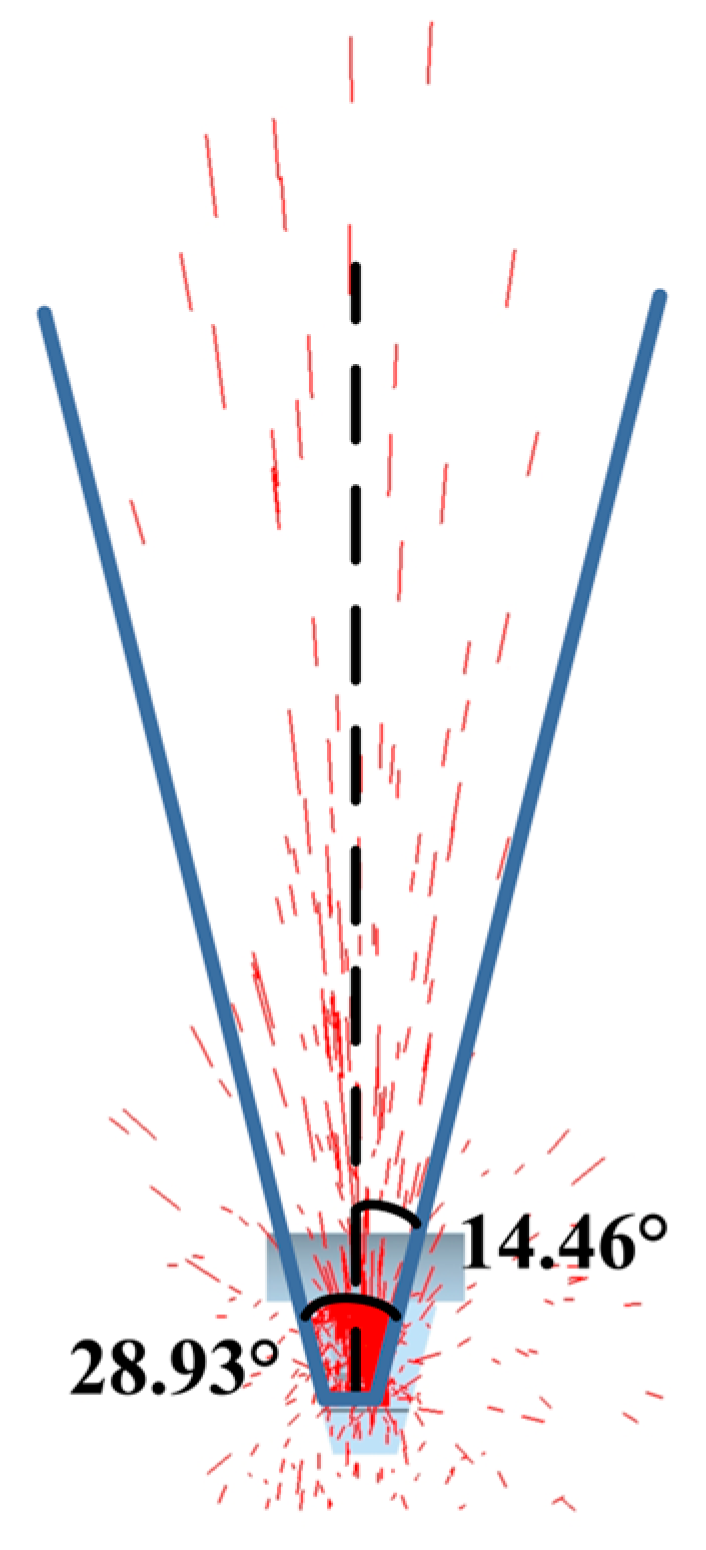
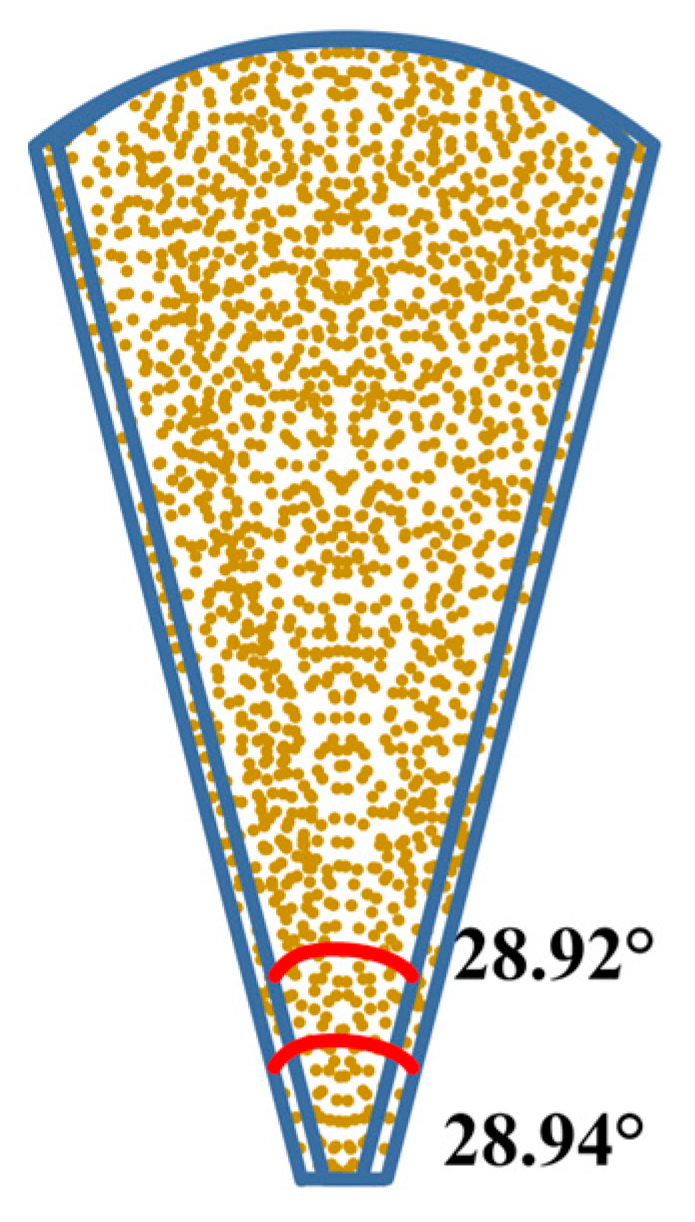
3.2.1. Jet Flow Pattern Analysis
3.2.2. Particle Trajectory Analysis on the Blade
3.3. Analysis of Experimental Results
4. Discussion
4.1. Mathematical Modeling and Numerical Analysis
4.2. Discrete Element Simulation
4.3. Experimental Testing
5. Conclusions
- (1)
- The spatial coordinate system established with the blade as the reference frame, which rotates with the disc, can describe the complex relative motion of particles on the blade under the dual inclination of the disc and the blade. By analyzing the forces and motion of particles in each quadrant during the particle throwing process on the inclined disc, a mathematical model describing the force acting on the particles by the main throwing components is obtained. This model can describe the resultant force acting on the particles on the blade at any given moment. By further deriving the model equations, it becomes possible to qualitatively and quantitatively calculate the displacement, velocity, and force variation in particles on the blade when parameters such as disc inclination, disc rotational speed, blade mounting angle, and blade inclination are known.
- (2)
- When the particle mass m = 4 × 10−4 kg, the disc inclination α = 75°, the sliding friction coefficient between the particle and the steel surface kf = 0.4, and the disc rotational speed ω = 700 rpm, after 0.025 s of motion on the blade, the change in particle velocity for different blade inclinations demonstrates that adjusting the blade inclination can effectively correct the motion trajectory of the particles on the blade.
- (3)
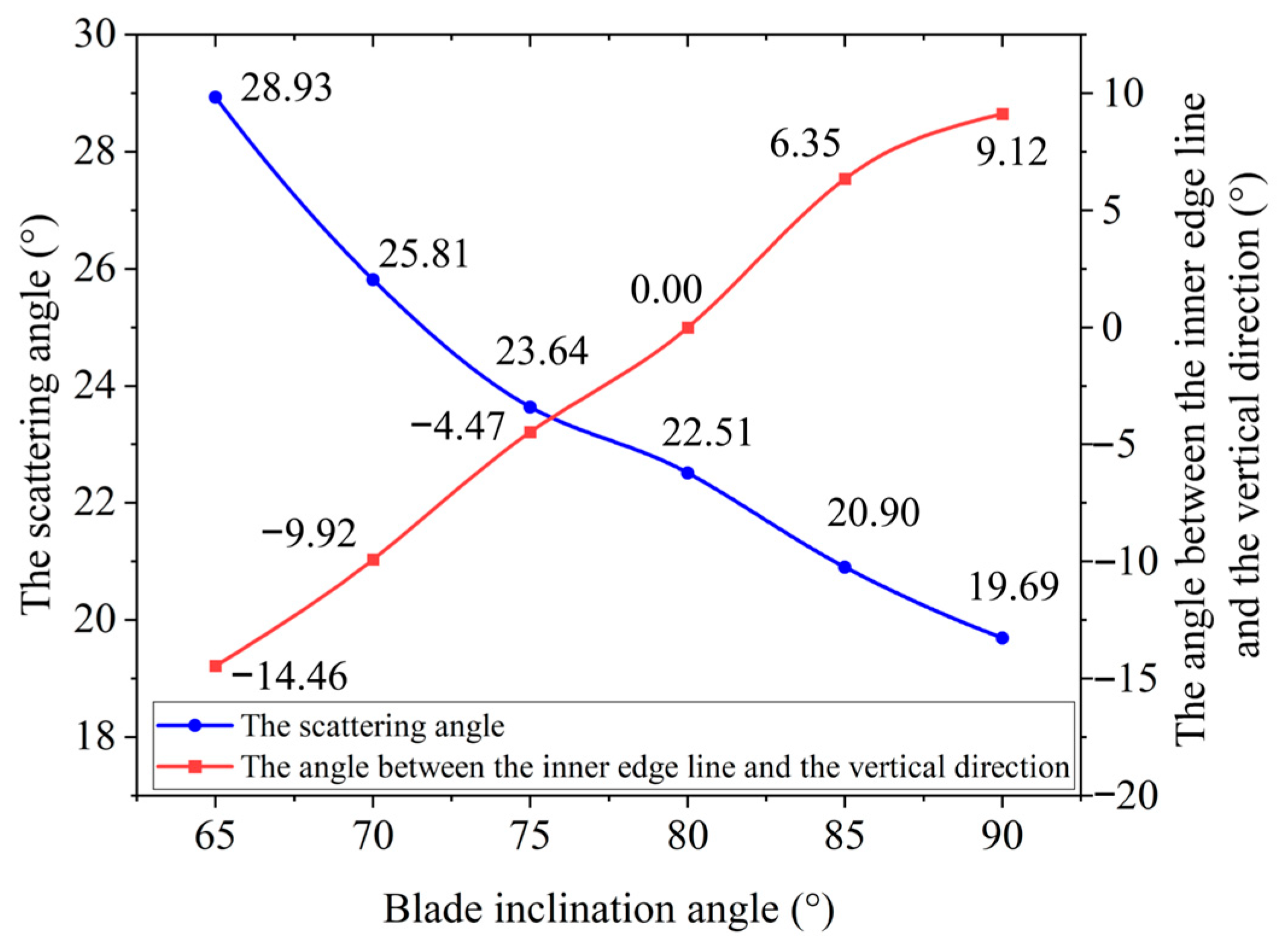
- For a side-throwing device with a disc radius of 500 mm, disc inclination of 75°, center-to-center distance between the two discs of 320 mm, disc rotational speed of 700 rpm, and blades mounted concentrically, within the blade inclination range from 65° to 85°, as the blade inclination increases, the scattering angle of the jet stream formed by the single disc gradually decreases, while the scattering angle of the overall jet stream formed by both discs gradually increases. The jet streams from the two discs transition from crossing to separation. When the blade inclination is 65°, the jet streams from both discs nearly overlap, and at an inclination of 80°, the jet streams from both discs approach the critical point of overlap and separation.
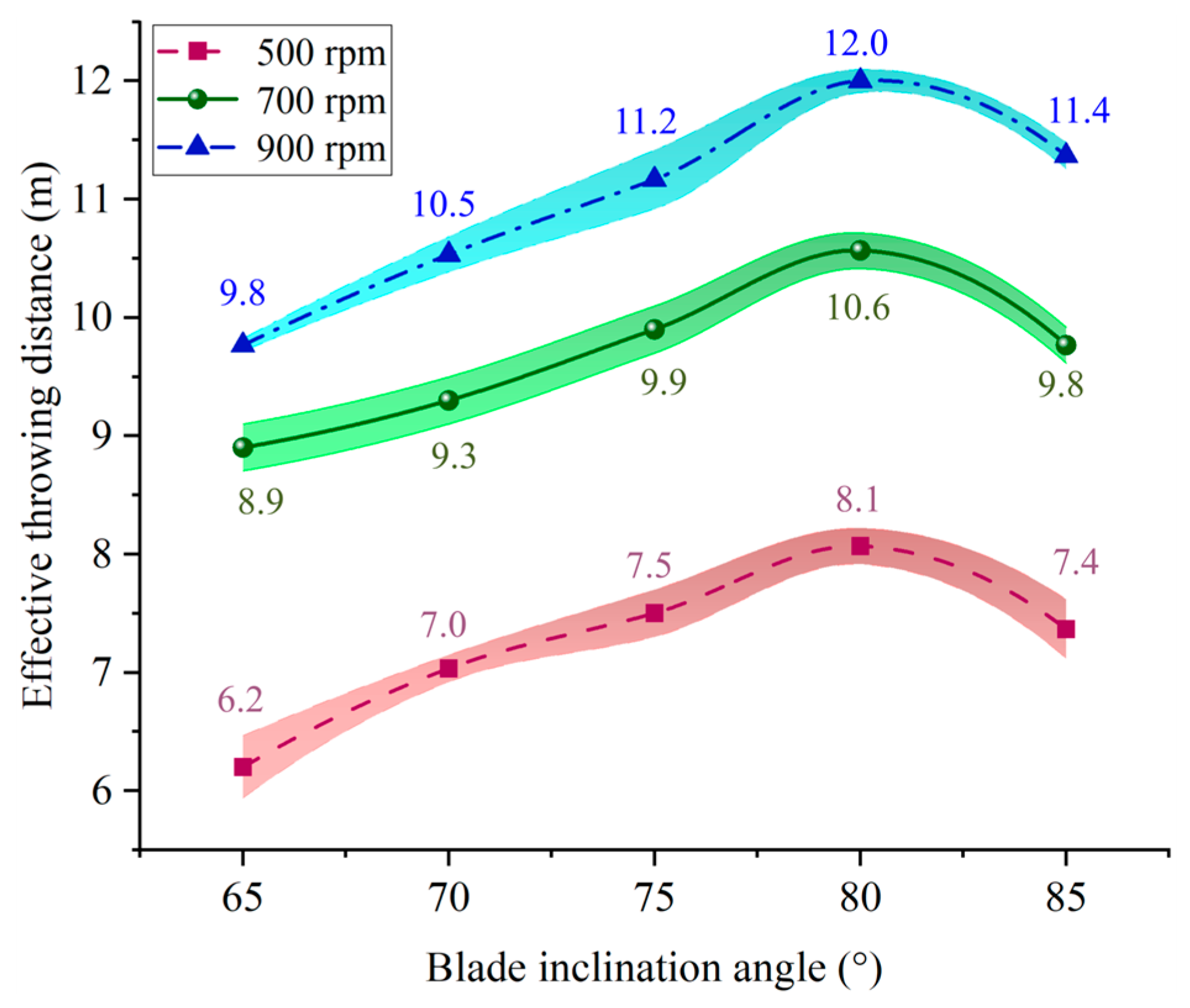
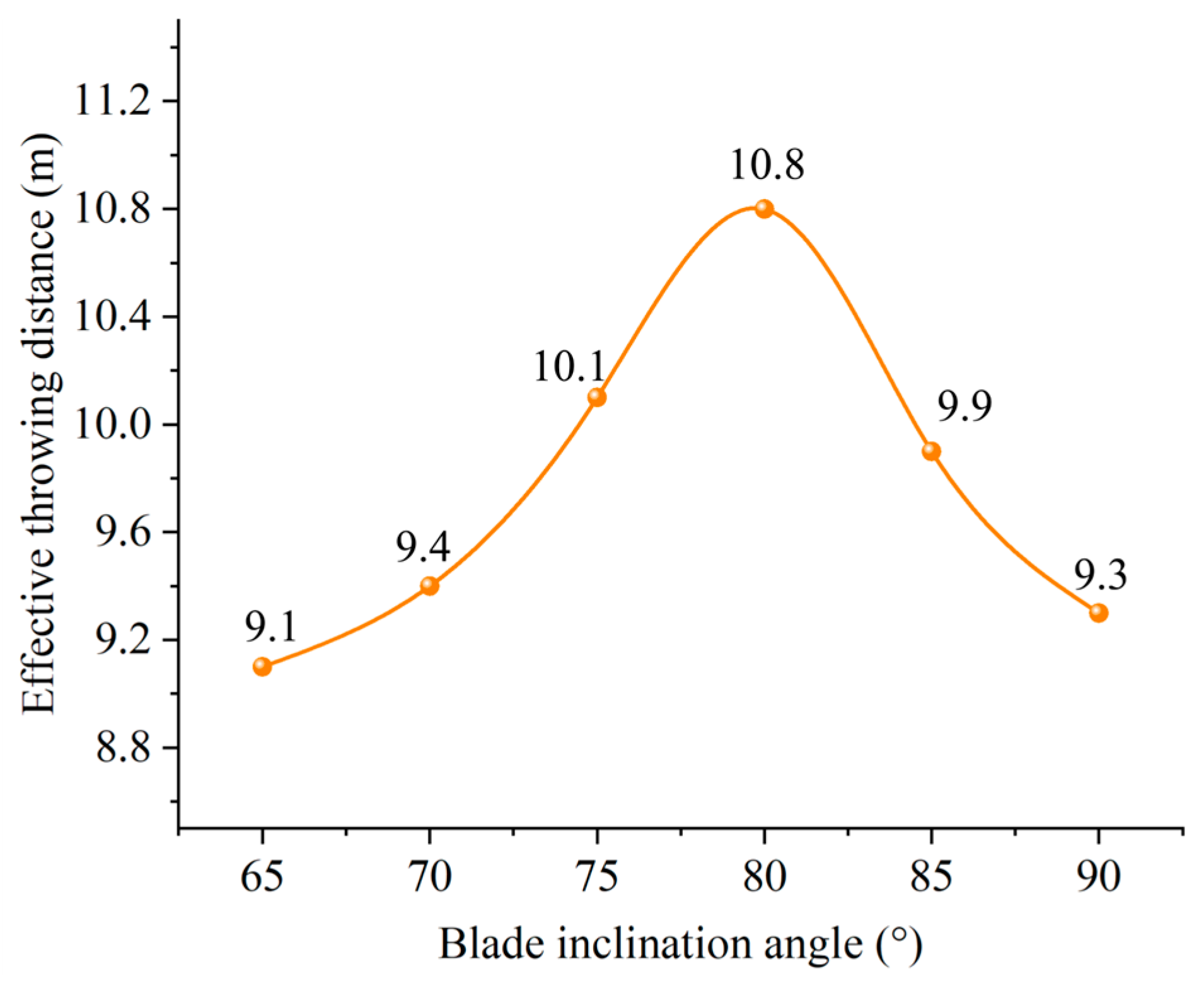
- (4)
- For the same side-throwing device, when the blade inclination range is between 65° and 85°, the device with a 65° blade produces the minimum scattering angle for the overall jet stream formed by both discs, the smallest absolute velocity when the particles leave the blade, and the shortest effective throwing distance on the distribution surface. The device with an 80° blade produces the maximum absolute velocity when the particles leave the blade and the longest effective throwing distance. The device with an 85° blade results in the largest scattering angle for the overall jet stream formed by both discs. Changing the disc rotation speed does not alter the above trends, and it has a non-significant impact on the scattering angle but a significant impact on the effective throwing distance. The mathematical model, virtual simulation, and prototype testing corroborate each other, further clarifying that the blade inclination can influence the overall jet stream morphology by correcting the particle motion path on the blade. This not only lays a foundation for further exploring the control capabilities of the inclined disc side-throwing device in terms of jet stream morphology, but also presents a universal mathematical framework and methodology applicable to centrifugal spreading systems in various engineering fields.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Fan, C.S.; He, R.Y.; Shi, Y.Y.; He, L.N. Structure and operation mode of centrifugal side-throwing organic fertilizer spreader for greenhouses. Powder Technol. 2024, 438, 119457. [Google Scholar] [CrossRef]
- Li, A.Q.; Jia, F.G.; Chu, Y.H.; Han, Y.L.; Li, H.; Sun, Z.; Ji, S.Y.; Li, Z.Z. Simulation of the movement of rice grains in a centrifugal huller by discrete element method and the influence of blade shape. Biosyst. Eng. 2023, 236, 54–70. [Google Scholar] [CrossRef]
- Sharipov, G.M.; Heiß, A.; Eshkabilov, S.L.; Griepentrog, H.W.; Paraforos, D.S. Considering field topography in the model-based assessment of a centrifugal spreader’s variable rate application accuracy. Comput. Electron. Agric. 2023, 213, 108234. [Google Scholar] [CrossRef]
- Gerakari, M.; Mitkou, D.; Antoniadis, C.; Giannakoula, A.; Stefanou, S.; Hilioti, Z.; Chatzidimopoulos, M.; Tsiouni, M.; Pavloudi, A.; Xynias, I.N.; et al. Evaluation of Commercial Tomato Hybrids for Climate Resilience and Low-Input Farming: Yield and Nutritional Assessment Across Cultivation Systems. Agronomy 2025, 15, 929. [Google Scholar] [CrossRef]
- Zinkevičienė, R.; Jotautienė, E.; Juostas, A.; Comparetti, A.; Vaiciukevičius, E. Simulation of granular organic fertilizer application by centrifugal spreader. Agronomy 2021, 11, 247. [Google Scholar] [CrossRef]
- Kömekçi, F.; Kömekçi, C.; Doğu, D.; Aykas, E. Effects of number of vanes, vane angle and disc peripheral speed on the distribution uniformity of twin-disc granular fertilizer broadcaster. Heliyon 2024, 10, 18. [Google Scholar] [CrossRef]
- Li, L.; Peng, L.; Zhao, W. Effects of process parameters on the spreading morphology of disc surface and aluminium powder produced by centrifugal atomisation. Powder Metall. 2023, 66, 509–518. [Google Scholar] [CrossRef]
- Wen, Y.J.; Zhang, J.C.; Yang, N.; Wang, X.H.; Shi, X.Y.; Wang, J.L. Effects of the long-term application of organic fertilization and straw returning on the components of soil organic carbon and pores. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2024, 40, 74–81, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Jiao, J.C.; An, X.H.; Xu, C.X.; Li, T.L.; Meng, H.S.; Zhang, J.; Hao, X.J. Effects of organic fertilizer combined with Pseudomonas fluorescein on maize yield and phosphorus activity in reclaimed soil. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2024, 40, 79–87, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Deng, S.S.; Yan, H.F.; Zhang, C.; Wang, G.Q.; Zhang, J.Y.; Liang, S.W.; Jiang, J.H. Effects of irrigation amounts and nitrogen reduction combined with organic fertilizer pattern on greenhouse cucumber and soil. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2023, 39, 93–102, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Zhu, X.H.; Li, H.C.; Li, X.D.; Liang, J.H.; Zang, J.J.; Zhao, H.S.; Guo, W.C. Mechanized ring-furrow fertilization of organic fertilizers in orchards. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2023, 39, 60–70, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Chen, G.B.; Wang, Q.J.; Li, H.W.; He, J.; Lu, C.Y.; Zhang, X.Y. Design and experiment of solid organic fertilizer crushing and striping machines. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2023, 39, 13–24, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Wang, Y.; Tan, Y.; Zeng, S.; Zeng, H.; Zhao, Z.; Li, L.; Zhang, J.; Liu, W.; Ying, Z. Design and experimental study of the fertilizer applicator with vertical spiral fluted rollers. Int. J. Agric. Biol. Eng. 2023, 16, 80–87. [Google Scholar] [CrossRef]
- Bivainis, V.; Jotautienė, E.; Lekavičienė, K.; Mieldažys, R.; Juodišius, G. Theoretical and Experimental Verification of Organic Granular Fertilizer Spreading. Agriculture 2023, 13, 1135. [Google Scholar] [CrossRef]
- Guan, Z.H.; Mu, S.L.; Jiang, T.; Li, H.T.; Zhang, M.; Wu, C.Y.; Jin, M. Development of Centrifugal Disc Spreader on Tracked Combine Harvester for Rape Undersowing Rice Based on DEM. Agriculture 2022, 12, 562. [Google Scholar] [CrossRef]
- Sharipov, G.M.; Heiß, A.; Eshkabilov, S.L.; Griepentrog, H.W.; Paraforos, D.S. Variable rate application accuracy of a centrifugal disc spreader using ISO 11783 communication data and granule motion modeling. Comput. Electron. Agric. 2021, 182, 106006. [Google Scholar] [CrossRef]
- Hwang, S.J.; Nam, J.S. DEM simulation model to optimise shutter hole position of a centrifugal fertiliser distributor for precise application. Biosyst. Eng. 2021, 204, 326–345. [Google Scholar] [CrossRef]
- Liu, H.X.; Du, C.L.; Yin, L.W.; Zhang, G.F. Shooting flow shape and control of organic fertilizer sidethrowing on inclined opposite discs. Trans. Chin. Soc. Agric. Mach. 2022, 53, 168–177, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Liu, H.X.; Zhao, Y.J.; Xie, Y.T.; Zhang, Y.M.; Shang, J.J. Design and experiment of spiral blades auxiliary roller of organic fertilizer side throwing device. Trans. Chin. Soc. Agric. Mach. 2023, 54, 107–119, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Liu, H.X.; Wang, C.; Wang, J.X.; Fu, L.L. Design and experiment study on portable in-vehicle device of farmyard manure collecting. J. Northeast. Agric. Univ. 2017, 48, 59–71+96, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Liu, H.X.; Wang, J.X.; Su, H.; An, J.Y. Design on side type discharge organic fertilizer spreader with inclined opposite discs and research on its key components. J. Northeast Agric. Univ. 2018, 49, 83–90+98, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Cerović, V.B.; Petrović, D.V.; Radojević, R.L.; Barać, S.R.; Vuković, A. On the fertilizer particle motion along the vane of a centrifugal spreader disc assuming pure sliding of the particle. J. Agric. Sci. 2018, 63, 83–97. [Google Scholar] [CrossRef]
- Tomantschger, K.; Petrović, D.V.; Cerović, V.B.; Dimitrijević, Ž.A.; Radojević, R.L. Prediction of a fertilizer particle motion along a vane of a centrifugal spreader disc assuming its pure rolling. FME Trans. 2018, 46, 544–551. [Google Scholar] [CrossRef]
- Martínez-Rodríguez, A.; Gómez-Águila, M.V.; Soto Escobar, M. Model and Software for the Parameters Calculation in Centrifugal Disk of Fertilizer Spreaders. Rev. Cienc. Técnicas Agropecu. 2021, 30, 82–101. [Google Scholar]
- Zhang, G.Z.; Wang, Y.; Liu, H.P.; Ji, C.; Hou, Q.X.; Zhou, Y. Design and experiments of the centrifugal side throwing fertilizer spreader for lotus root fields. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2018, 34, 21–27, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Liu, C.L.; Zhang, F.Y.; Du, X.; Jiang, M.; Yuan, H.; Liu, Q. Design and experiment of precision fertilizer distribution mechanism with horizontal turbine blades. Trans. Chin. Soc. Agric. Mach. 2020, 51, 165–174, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Zeng, Z.W.; Ma, X.; Cao, X.L.; Li, Z.H.; Wang, X.C. Critical review of applications of discrete element method in agricultural engineering. Trans. Chin. Soc. Agric. Mach. 2021, 52, 1–20, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Qi, Z.Y.; Liu, C.L.; Wang, Y.; Zhang, Z.W.; Sun, X.B. Design and Experimentation of Targeted Deep Fertilization Device for Corn Cultivation. Agriculture 2024, 14, 1645. [Google Scholar] [CrossRef]
- Huan, X.L.; Li, S.B.; Wang, L.; Wang, D.C.; You, Y. Study on silage mixing device of King Grass stalk particles based on DEM simulation and bench test. Powder Technol. 2024, 437, 119581. [Google Scholar] [CrossRef]
- Chen, G.; Wang, Q.; Li, H.; He, J.; Lu, C.; Xu, D.; Sun, M. Experimental research on a propeller blade fertilizer transport device based on a discrete element fertilizer block model. Comput. Electron. Agric. 2023, 208, 107781. [Google Scholar] [CrossRef]

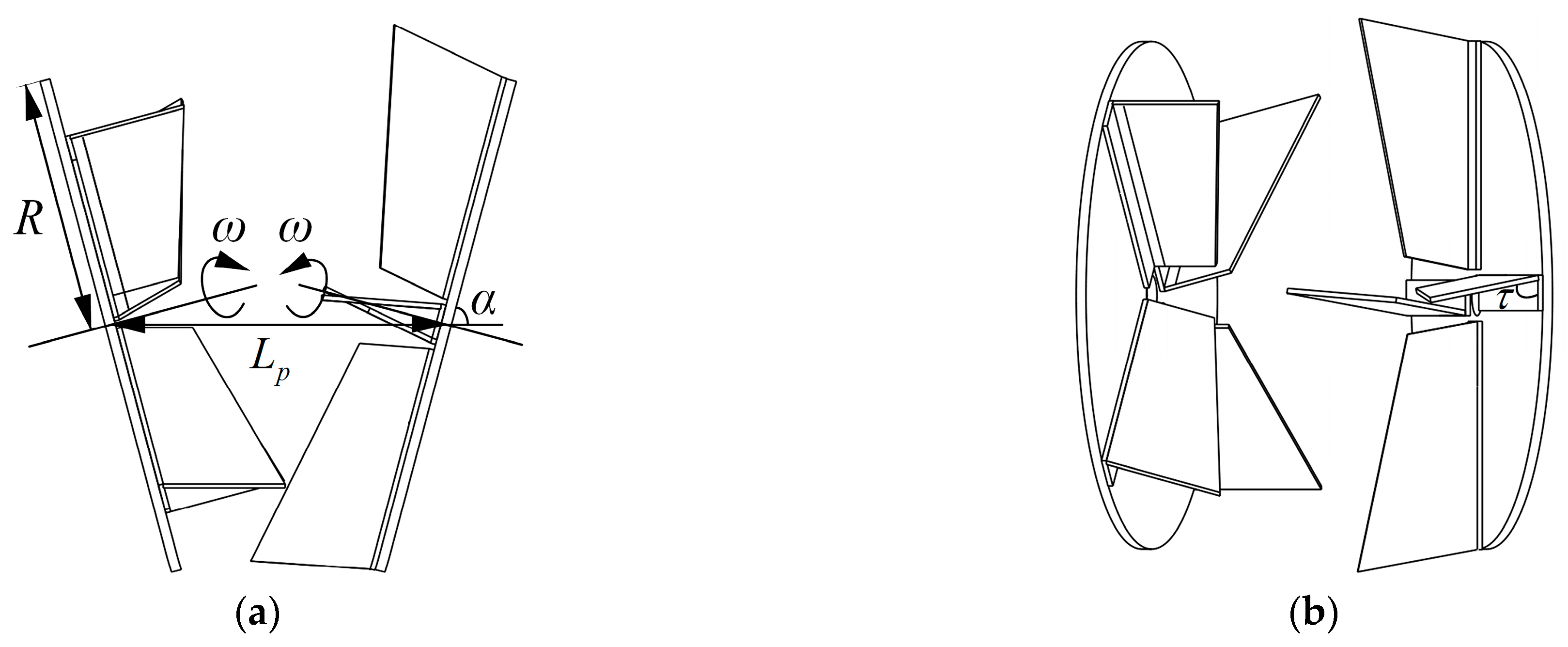








| Parameter | Symbol | Dimension | Value (Range) |
|---|---|---|---|
| Organic fertilizer particle mass | m | kg | 4 × 10−4 |
| Friction coefficient between the fertilizer particle and the main throwing component | kf | 0.11 | |
| Gravitational acceleration | g | m·s−2 | 9.81 |
| Disc diameter | R | mm | 500 |
| Disc tilt angle | α | ° | 75 |
| Angle between the blade and the disc | τ | ° | 65–90 |
| Distance between the centers of two discs | Lp | mm | 320 |
| Disc rotation speed | ω | rpm | 700 |
| Machine travel speed | VNCC | m·s−1 | 3.6 |
| Feed rate of the material conveying device | mcs | kg·s−1 | 6 |
| Actual Particle Size (mm) | Simulated Particle Size (mm) | Mass Fraction (%) |
|---|---|---|
| 0.00–0.50 | 1.25 | 41.60 |
| 0.50–1.00 | 3.75 | 26.15 |
| 1.00–2.00 | 7.50 | 15.15 |
| 2.00–5.00 | 12.50 | 14.40 |
| >5.00 | 25 | 2.70 |
| Item | Parameter | Value |
|---|---|---|
| Fertilizer | Poisson’s ratio | 0.4 |
| Shear modulus (Pa) | 2 × 106 | |
| Density (kg·m−3) | 800 | |
| Steel | Poisson’s ratio | 0.31 |
| Shear modulus (Pa) | 7 × 1010 | |
| Density (kg·m−3) | 7900 | |
| Soil | Poisson’s ratio | 0.3 |
| Shear modulus (Pa) | 5 × 107 | |
| Density (kg·m−3) | 2600 | |
| Fertilizer–fertilizer | Coefficient of restitution | 0.6 |
| Coefficient of static friction | 0.65 | |
| Coefficient of rolling friction | 0.1 | |
| Surface energy (J·m−2) | 0.45 | |
| Fertilizer–steel | Coefficient of restitution | 0.6 |
| Coefficient of static friction | 0.7 | |
| Coefficient of rolling friction | 0.11 | |
| Surface energy (J·m−2) | 0.0225 | |
| Fertilizer–soil | Coefficient of restitution | 0.4 |
| Coefficient of static friction | 0.66 | |
| Coefficient of rolling friction | 0.18 | |
| Surface energy (J·m−2) | 0.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Liu, H.; Shang, J.; Guo, L.; Zheng, G. Effect of Angle Between Center-Mounted Blades and Disc on Particle Trajectory Correction in Side-Throwing Centrifugal Spreaders. Agriculture 2025, 15, 1392. https://doi.org/10.3390/agriculture15131392
Xie Y, Liu H, Shang J, Guo L, Zheng G. Effect of Angle Between Center-Mounted Blades and Disc on Particle Trajectory Correction in Side-Throwing Centrifugal Spreaders. Agriculture. 2025; 15(13):1392. https://doi.org/10.3390/agriculture15131392
Chicago/Turabian StyleXie, Yongtao, Hongxin Liu, Jiajie Shang, Lifeng Guo, and Guoxiang Zheng. 2025. "Effect of Angle Between Center-Mounted Blades and Disc on Particle Trajectory Correction in Side-Throwing Centrifugal Spreaders" Agriculture 15, no. 13: 1392. https://doi.org/10.3390/agriculture15131392
APA StyleXie, Y., Liu, H., Shang, J., Guo, L., & Zheng, G. (2025). Effect of Angle Between Center-Mounted Blades and Disc on Particle Trajectory Correction in Side-Throwing Centrifugal Spreaders. Agriculture, 15(13), 1392. https://doi.org/10.3390/agriculture15131392









