Calibration and Testing of Discrete Elemental Simulation Parameters for Pod Pepper Seeds

Abstract

The discrete elemental parameters of pod pepper seeds were calibrated for future numerical optimization of the pod pepper seed cleaning device. The study concentrates on calibrating the intrinsic and contact parameters of pod pepper seeds utilizing the discrete element method. Compression tests were performed to ascertain intrinsic parameters such as Poisson’s ratio and the seeds’ elastic modulus. The static friction coefficient and collision restitution coefficient between the seeds and steel plates were identified through incline and free-fall tests. Plackett–Burman, steepest ascent, and Box–Behnken experiments were performed to establish a second-order regression model correlating significant parameters with the angle of repose. The optimal parameter combination, based on the measured angle of repose (32.45°), yielded static friction coefficients between seeds, rolling friction coefficients between seeds, and static friction coefficients between seeds and steel plates of 0.608, 0.018, and 0.787, respectively. The two-sample t-test of the physical and simulated repose angles yielded p > 0.05, and the relative error of the physical and simulated repose angles was 0.68%, which confirmed the reliability of the calibration parameters. The findings indicate that the calibration method for pod pepper seeds effectively informs the calibration of parameters for other irregular crops.

1. Introduction

Pod pepper is a kind of vegetable widely grown in China, but its seed scavenging and separation efficiency is low and the separation effect is poor, which limits the development of the pod pepper industry to some extent. In recent years, advancements in computer technology have led to the increasingly widespread application of the discrete element method (DEM) in agricultural equipment research [1,2,3]. Using the discrete element method to study the interactivity features among pod pepper seeds, as well as between the seeds and crucial components of the cleaning and separating machine, can provide valuable reference data for the future design and optimization of pod pepper seed cleaning and separating devices. This approach helps improve research and development efficiency while reducing costs.

Currently, experts at home and abroad mainly focus on the precise calibration of discrete elemental simulation parameters for various types of regularly shaped crops such as corn, fruits, soybeans, mung beans, potatoes, and so on [4]. For instance, Wang et al. [5] developed a mathematical regression model to calibrate the static friction coefficient and rolling friction coefficient among corn seed particles. Coetzee et al. [6] calibrated the friction and stiffness coefficients of maize particles using shear and lateral compression tests, followed by experimental validation. Guo et al. [7] combined physical and simulation experiments to establish a mechanical model of banana stalks and studied their biomechanical properties. Ghodki et al. [8] adjusted the DEM input parameters of the soybean Hertz–Mindlin model by contrasting experimental findings with numerical simulation results, employing a custom-made box apparatus. Zhang et al. [9] conducted simulation measurements and empirical tests, which included bottomless cylinder lifting and slip stacking. The authors fine-tuned the static and rolling friction coefficients between different species of seed models, varying the radii of filled ball particles. They utilized the surface response method, with the angle of repose serving as an indicator. Additionally, Zhang et al. [10] utilized EDEM discrete element simulation software and adopted the Hertz–Mindlin bonding model, which created a model for mung bean seed particles. They calibrated the contact parameters of the treated mung bean seeds and optimized the data based on the relative error between the simulated and actual angles of repose. Liu et al. [11] utilized a combination of experimental measurements and simulation experiments to calibrate discrete meta-simulation parameters of miniature potatoes. Using the discrete element method, Santos et al. [12] obtained the dynamic repose angle of dried cherries through central composite experimental design and rotary drum tests, and calibrated and optimized the parameters required for DEM simulation. In summary, the current research on discrete element simulation parameters mainly focuses on corn, soybeans, fruit and other agricultural products with regular shapes. However, there is a lack of research on the determination and calibration of discrete element simulation parameters for irregularly shaped vegetable seeds, such as pod pepper seeds.

This paper combines physical experiments with simulation experiments. The values obtained from physical experiments form the foundation for choosing simulation parameters. The research focuses on exploring the intrinsic and contact parameters of pod pepper seeds, with the angle of repose of pod pepper seeds serving as an evaluation index. Sequentially, Plackett–Burman experiments, steepest ascent experiments, and Box–Behnken experiments are carried out to calibrate and adjust the discrete element simulation parameters of pod pepper seeds. Subsequently, the discrete meta-simulation parameters of pod pepper seeds are validated using the cylinder lifting method and a two-sample t-test. The primary goal of this research is to establish a foundation for calibrating discrete element simulation parameters for other agriculturally irregularly shaped products, while also offering a theoretical framework for numerically optimizing future equipment designed for cleaning and separating pod pepper seeds.

2. Materials and Methods

2.1. Basic Parameters of Pod Pepper Seeds

In this study, the freshly picked pod pepper in the Xuzhou area was crushed and cleaned to obtain clean pod pepper seeds as the research object. A total of 100 randomly selected seeds were measured for their dimensions along the three axes using the 111N-101-40 absolute origin digital caliper (accuracy: 0.01 mm), as depicted in Figure 1. The mean measurements, as presented in

Table 1. Pod pepper seed triaxial size.

Three-Dimensional Size	General Size/mm	Percent/%	Maximum/mm	Minimum/mm	Average/mm	Standard Deviation
Length	4.02~4.57	88.74	5.17	3.93	4.30	0.342
Width	2.94~3.65	91.42	3.92	2.49	3.31	0.319
Thickness	0.97~1.28	96.15	1.42	0.82	1.09	0.296

, indicate that the pod pepper seeds had lengths, widths, and thicknesses of 4.30, 3.31, and 1.09 mm, respectively, with corresponding standard deviations of 0.342, 0.319, and 0.296 mm. The seeds displayed an elliptical form.

2.2. Measurement of Moisture Content and Density of Pod Pepper Seeds

We randomly sampled 1000 pod pepper seeds and measured their combined mass using an electronic scale accurate to 0.01 g. This procedure was replicated five times, yielding an average mass of 6.37 g per thousand seeds. Additionally, the volume of 1000 pod pepper seeds was measured using the displacement method. This measurement was also repeated five times, yielding an average volume of 5.95 cm³. By performing calculations, the density of pod pepper seeds was determined to be 1070.59 kg/m³.

A randomly selected sample of 1000 seeds of pod pepper were put into a B0D-75-Ⅱ type electric constant temperature blast drying oven, dried at 105 °C for 10 h until the quality no longer changed. Then, we replaced the material, and repeated the experiment five times, calculated by the Formula (1) pod pepper seed moisture content of 20.34%.

$$M_{\mathrm{d}}=\frac{{\mathrm{m}}_{\mathrm{w}}-{\mathrm{m}}_{\mathrm{s}}}{{\mathrm{m}}_{\mathrm{w}}}\times 100\mathrm{\%}$$

(1)

where $M_{\mathrm{d}}$ represents the moisture content of pod pepper seeds, (%); ${\mathrm{m}}_{\mathrm{w}}$ denotes the weight of seeds before drying, (g); ${\mathrm{m}}_{\mathrm{s}}$ denotes the weight of seeds after drying, (g).

2.3. Measurement of Intrinsic Parameters of Pod Pepper Seeds

Establishing the inherent characteristics of pod pepper seeds includes assessing elastic modulus, Poisson’s ratio, and shear modulus. Compression tests were carried out on pod pepper seeds employing a TA.XTPLUS (Stable Micro Systems, Godalming, Surrey, UK) texture analyzer, as illustrated in Figure 2. Throughout the experiment, the pod pepper seeds were positioned horizontally on the compression plate. A 5 mm diameter circular probe was employed to apply loading in the thickness direction at a rate of 0.2 mm/s. After a 3 s loading period, the machine was halted. The average load-displacement during the compression tests of the seeds was determined across six repetitions using the post-processing module of the software. By applying Equation (2), the modulus of elasticity of pod pepper seeds was assessed to be E = 2.36 × 10⁷ Pa.

$$E=\frac{\sigma }{\epsilon }$$

(2)

where $E$ represents the elastic modulus of pod pepper seeds, (Pa); $\sigma$ denotes the maximum compressive stress, (Pa); $\epsilon$ signifies the linear strain.

Poisson’s ratio defines the ratio of lateral strain to axial strain experienced by a material under uniaxial tension or compression. Also referred to as the lateral deformation coefficient, it indicates the material’s elasticity in terms of lateral deformation. We randomly selected 10 pod pepper seeds from the samples and conducted compression tests on them using a texture analyzer. During the test, we applied loading in the thickness direction to the pod pepper seeds at a speed of 0.2 mm/s, ceased loading after 3 s, and measured the deformation of the width-directional positive strain using an absolute origin digital caliper [13]. We calculated the Poisson’s ratio of pod pepper seeds using Equation (3). The mean of the values from 10 tests was determined to be 0.35 ± 0.024.

$$\mu =\frac{\left|{\epsilon }_x\right|}{{\epsilon }_y}=\frac{W_2-W_1}{{\mathrm{T}}_1-T_2}$$

(3)

where $\mu$ represents Poisson’s ratio; ${\epsilon }_x$ denotes the deformation in the width direction of the pod pepper seeds, (mm); ${\epsilon }_y$ indicates the deformation along the thickness direction of the pod pepper seeds, (mm); $W_1$ stands for the width of the pod pepper seeds before loading, (mm); $W_2$ represents the width of the pod pepper seeds after loading, (mm); $T_1$ denotes the thickness of the pod pepper seeds before loading, (mm); $T_2$ signifies the thickness of the pod pepper seeds after loading, (mm).

Equation (4) is the formula for calculating the shear modulus of pod pepper seeds.

$$G=\frac{E}{2(1+\mathsf{\mu })}$$

(4)

where $G$ represents the shear modulus of the seeds, (Pa). The average value of the shear modulus for pod pepper seeds was determined to be 8.75 × 10⁶ Pa.

2.4. Measurement of Contact Parameters of Pod Pepper Seeds

2.4.1. Static Friction Coefficient Determination Test

The static friction coefficient is the ratio of the frictional force between two surfaces to the normal pressure when the surfaces are at rest relative to each other. It is a physical quantity used to describe the nature of friction between surfaces [14]. The coefficient of static friction of pod pepper seeds is determined using an incline plane apparatus, as shown in Figure 3. Prior to the experiment, a steel plate is attached to the incline plane apparatus, and 10 pod pepper seeds are placed on the steel plate. Subsequently, the incline plane apparatus is slowly raised, and the angle of the incline plane is recorded when each seed begins to slide. Seeds are replaced, and the experiment is conducted five times. Using Equation (5), the mean coefficient of static friction between the pod pepper seeds and the steel plate surface is determined to be 0.70 ± 0.035.

$${\mathsf{\mu }}_0=\tan \phi$$

(5)

where ${\mathsf{\mu }}_0$ represents the static friction coefficient of the material; $\phi$ denotes the angle of the pod pepper seeds when they are on the verge of sliding on the inclined surface, (°).

In order to determine the static friction coefficient between seeds of pod pepper, adhesive glue was used to adhere a population of tested seeds onto the measurement plane. Tweezers were then used to place 10 pod pepper seeds at various positions on the population plate. The population plate was slowly raised, following the method for testing the static friction coefficient between the steel plate and pod pepper seeds. This determined the static friction coefficient between the pod pepper seeds to be 0.60 ± 0.031.

2.4.2. Measurement of Rolling Friction Coefficient

Because of the small, elliptical, and flattened nature of pod pepper seeds, measuring the rolling friction coefficient experimentally poses challenges. Hence, this experiment used a simulated repose angle approximation method to calibrate the rolling friction coefficients between pod pepper seeds, and between the seeds and a steel plate. The material angle of repose is influenced by various factors such as the particles’ inherent characteristics and environmental conditions, reflecting the material’s scattering behavior and frictional properties [15,16]. Hence, physical tests for the angle of repose are frequently employed to calibrate discrete element parameters for particles [17]. In order to obtain the accurate rolling friction coefficients, this research utilized physical experiments to obtain the actual repose angle for pod pepper seeds. In the simulation experiments, the rolling friction coefficients between the seeds and the seeds, and between the seeds and the steel plate were gradually adjusted so that the simulated angle of repose of the seed of the pod pepper was consistent with the actual repose angle. This helps to accurately determine the coefficient of rolling friction between pod pepper seeds, and between the seeds and steel plates.

2.4.3. Measurement Test of Coefficient of Restitution

The restitution coefficient is the ratio of the relative velocity of the colliding objects after the collision to the relative velocity before the collision [18]. The current study investigates the interaction between pod pepper seeds, and between seeds and a steel plate. The parameter was measured using a high-speed camera and a steel ruler, and the process of determining the restitution coefficient of the pod pepper seeds is depicted in Figure 4.

Because the pod pepper seeds are lighter, falling from a greater height will be affected by more air resistance; therefore, the pod pepper seeds from a height of H = 15 cm free fall, with a steel plate and a pod pepper seed stock plate as a horizontal contact plate for measurement, and rebound after the measurement of the rebound height of h. According to Newton’s law of collision, the coefficient of restitution e for the collision of two objects is determined by the ratio of their relative velocity to their relative approach velocity before the collision [19,20], as expressed in Equation (6).

$$e=\frac{v_2^{\prime }-v_1^{\prime }}{v_1-v_2}$$

(6)

If object 1 falls freely and collides with object 2, after the collision, object 1 springs up freely, during the fall and rise of object 1, with only object 1’s own gravity doing the work. Therefore, the velocity $v_2$, $v_2^{\prime }$ before and after the collision of object 2 is 0.$v_1^{\prime }=\sqrt{2gh}$,$v_1=\sqrt{2gH}$ (where $g$ represents the acceleration due to gravity, m/s²). From this, the restitution coefficient can be generalized to Equation (7).

$$e=\sqrt{\frac{h}{H}}$$

(7)

The photographs captured were transferred to the computer, and the restitution coefficient between pod pepper seeds and between seeds and steel plate were determined using Equation (7). To ensure accuracy, each experiment was repeated 10 times. The average coefficient of restitution was found to be 0.28 ± 0.041 between pod pepper seeds and 0.39 ± 0.065 between pod pepper seeds and the steel plate.

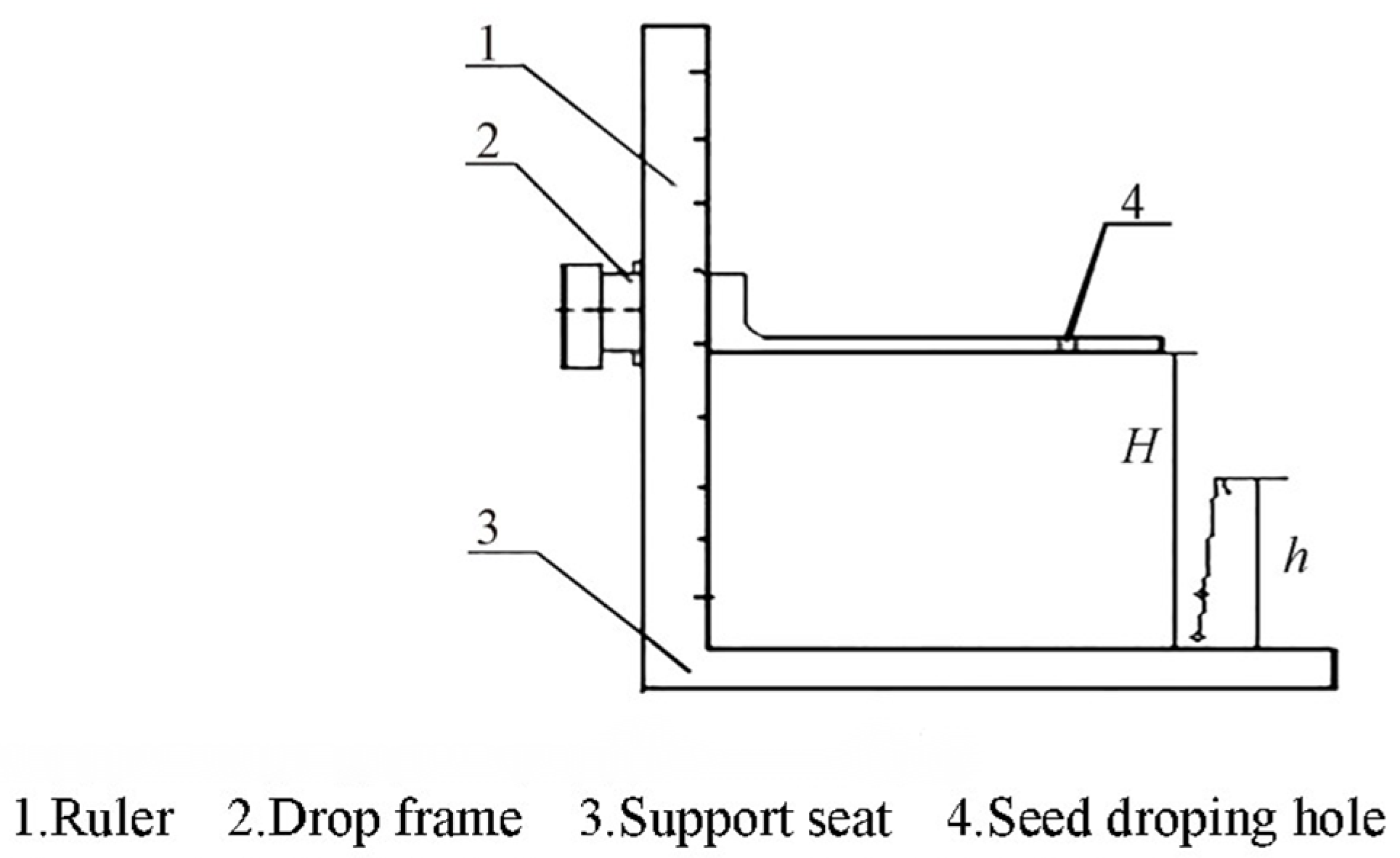
2.5. Determination of the Actual Repose Angle of Pod Pepper Seeds

Considering the flow characteristics of pod pepper seeds, the cylindrical lifting method was selected to determine the experimental angle of repose of the seeds [21,22]. To more precisely ascertain the rolling friction coefficient of pod pepper seeds, a repose experiment was conducted using a steel cylinder. The steel cylinder utilized in the experiment had an inner diameter of 50 mm and a height of 200 mm. It was filled with 20 g of pod pepper seeds and positioned vertically on a horizontal steel plate. After achieving stability, the cylinder was uniformly lifted at a speed of 0.02 m/s. Under the influence of gravity, the pod pepper seeds naturally fell and accumulated, forming a conical pile with a base angle known as the angle of repose of pod pepper seeds. The experiment was repeated five times. A high-definition camera was employed to capture a front-view image of the seed repose. Subsequently, the image of the seed repose underwent processing in MATLAB R2018b, which included grayscale conversion, binarization, extraction of boundary contours, and obtaining a fitted line. This facilitated the calculation of the slope of the fitted line and determination of the angle of the particle pile’s contour edge in MATLAB [23]. The image of the seeds piled on one side is shown in Figure 5a. The process of measuring the repose angle was shown in Figure 5. The average measured repose angle was determined to be 32.45°.

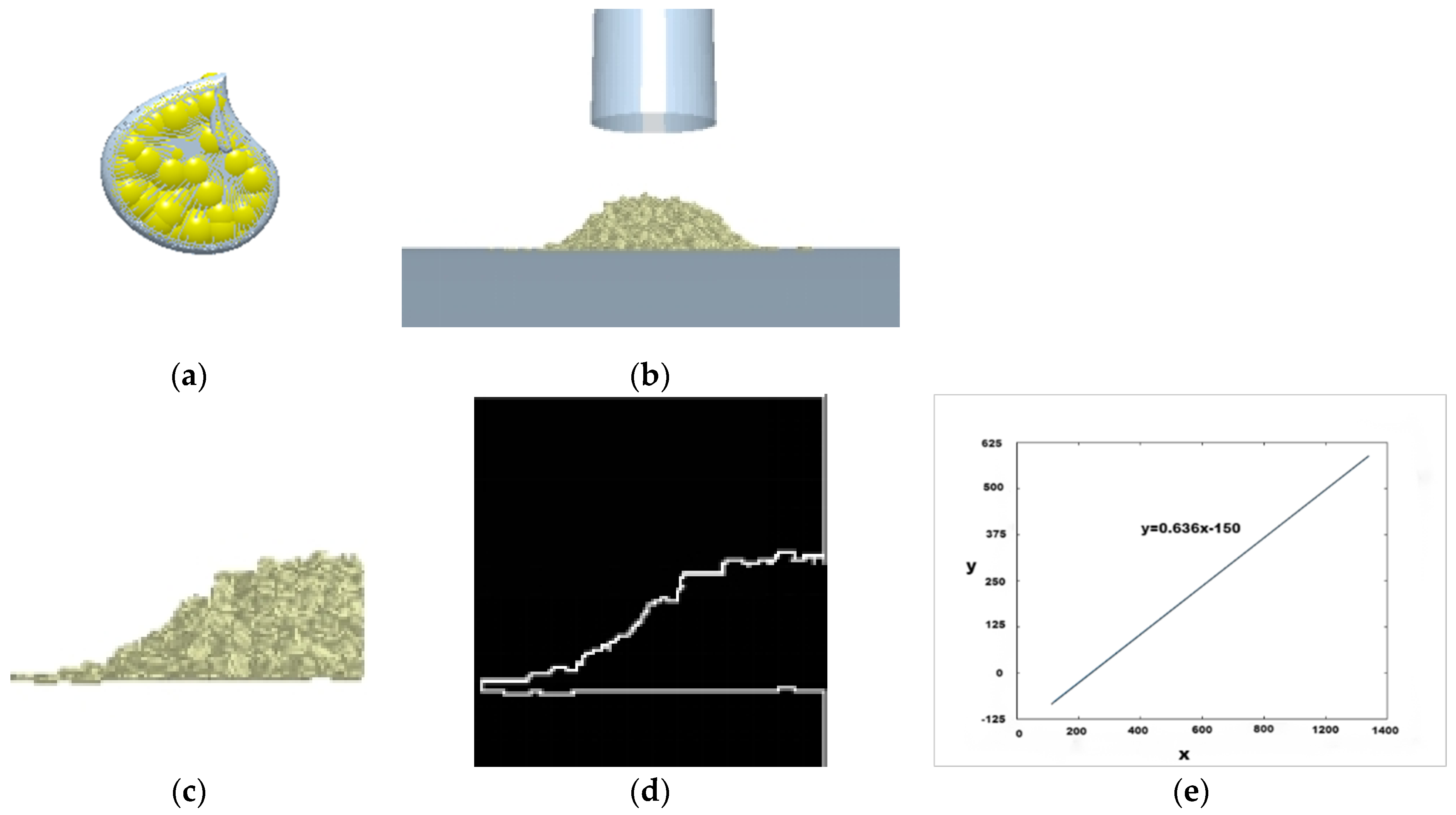
2.6. DEM Model of Pod Pepper Seed for Simulation

Pod pepper seeds are categorized as granular materials, and their flow characteristics can be simulated using the Hertz–Mindlin model [24]. The basic physical parameters of pod pepper seeds and the steel plate were obtained through multiple pre-simulation experiments and combined with relevant domestic and international literature [25,26,27], as shown in

Table 2. Basic physical parameters of pod pepper seeds and plates.

Parameters	Value
Poisson’s ratio of pod pepper seed (${\mathrm{X}}_1$)	0.35
Shear modulus of pod pepper seed/MPa (${\mathrm{X}}_2$)	8.75
Density of pod pepper seed/(kg·m−3)	1071.3
Poisson’s ratio of steel plate /Pa	0.3
Shear modulus of steel plate /Pa	1.1 × 1010
Density of steel plate/(kg·m−3)	7 850
Static friction coefficient between pod pepper seed and seed (${\mathrm{X}}_3$)	0.60
Rolling friction coefficient between pod pepper seed and seed (${\mathrm{X}}_4$)	0.01~0.03
Restitution coefficient between pod pepper seed and seed (${\mathrm{X}}_5$)	0.28
Static friction coefficient between pod pepper seed and steel plate (${\mathrm{X}}_6$)	0.70
Rolling friction coefficient between pod pepper seed and steel plate (${\mathrm{X}}_7$)	0.005~0.020
Restitution coefficient between pod pepper seed and steel plate (${\mathrm{X}}_8$)	0.39

. The geometric model (particle template) of pod pepper seeds was created using SolidWorks 2020 software based on the measured average dimensions and shape in three axes. The pod pepper seed model was subsequently converted to STL format and imported into EDEM, a discrete component simulation software. In order to streamline the model and enhance simulation efficiency, the 3D model of pod pepper seeds was densely packed using individual spherical particles in the EDEM software, as illustrated in Figure 6a.

In the EDEM 2020 software, simulation experiments were conducted by creating models of a steel cylinder and base plate with parameters consistent with the physical experiments. Above the cylinder, a polygon virtual particle plane was established to generate pod pepper seed particles, with a particle generation rate of 10 g/s for 2 s. Once the particles were fully generated and settled at the bottom of the cylinder, the cylinder was lifted at the same speed as in the physical experiments. The time stride is set to 25% of the Rayleigh time stride, and the grid size was set to six times the minimum particle radius. The simulation time was set to 5 s and 10 trials were repeated in order to improve the accuracy of the simulation experiment. The outcomes of the EDEM simulation experiment are depicted in Figure 6b, while the image processing of the simulation experiment is displayed in Figure 6.

3. Result and Discussion

3.1. Plackett–Burman Experiment

The Plackett–Burman experiment utilized the repose angle of pod pepper seeds as the response variable. By analyzing the correlation between the angle of repose and each simulation parameter, we identified the simulation parameters significantly influencing the response variable [28,29]. The range of simulation test parameters is shown in

Table 3. Factors and levels of Plackett–Burman test.

Test Parameters	Low Level (−1)	Hight Level (+1)
${\mathrm{X}}_1$	0.25	0.45
${\mathrm{X}}_2$/MPa	7.75	9.75
${\mathrm{X}}_3$	0.50	0.70
${\mathrm{X}}_4$	0.01	0.03
${\mathrm{X}}_5$	0.18	0.38
${\mathrm{X}}_6$	0.65	0.85
${\mathrm{X}}_7$	0.005	0.02
${\mathrm{X}}_8$	0.29	0.49

. By measuring the values on the left and right sides of the simulated angle of repose of the pod pepper seeds and averaging them, the results are presented in

Table 4. Plackett–Burman experimental design and results.

No.	Test Parameters								Simulated Angle of Repose θ′/(°)
	${\mathbf{X}}_1$	${\mathbf{X}}_2$/MPa	${\mathbf{X}}_3$	${\mathbf{X}}_4$	${\mathbf{X}}_5$	${\mathbf{X}}_6$	${\mathbf{X}}_7$	${\mathbf{X}}_8$
1	−1	1	−1	1	1	−1	1	1	31.48
2	1	1	1	−1	−1	−1	1	−1	29.54
3	1	−1	1	1	1	−1	−1	−1	33.07
4	−1	1	1	−1	1	1	1	−1	32.43
5	1	1	−1	−1	−1	1	−1	1	29.65
6	−1	−1	−1	−1	−1	−1	−1	−1	29.25
7	1	1	−1	1	1	1	−1	−1	32.73
8	−1	−1	−1	1	−1	1	1	−1	32.82
9	−1	−1	1	−1	1	1	−1	1	31.95
10	−1	1	1	1	−1	−1	−1	1	33.12
11	1	−1	−1	−1	1	−1	1	1	29.76
12	1	−1	1	1	−1	1	1	1	34.21

.

Utilizing Design-Expert 13.0 software, a variance analysis was performed on the experimental outcomes, and the significance of various simulation parameters was determined, as illustrated in

Table 5. Significance analysis of the parameters of the Plackett–Burman experiment.

Parameters	Effects	Sum of Squares	Contribution Rate/%	Significance Ranking
${\mathrm{X}}_1$	−0.35	0.36	0.89	6
${\mathrm{X}}_2$	−0.35	0.37	0.91	5
${\mathrm{X}}_3$	1.44	6.21	15.23	2
${\mathrm{X}}_4$	2.48	18.38	45.1	1
${\mathrm{X}}_5$	0.48	0.67	1.64	4
${\mathrm{X}}_6$	1.26	4.78	11.72	3
${\mathrm{X}}_7$	0.078	0.018	0.045	7
${\mathrm{X}}_8$	0.055	0.009	0.022	8

. The coefficient of static friction between pod pepper seeds (X₃), the coefficient of rolling friction between pod pepper seeds (X₄), and the coefficient of static friction between pod pepper seeds and the steel plate (X₆) were found to have a notable influence on the repose angle. Consequently, only these three factors were taken into account for the steepest ascent test.

3.2. Steepest Ascent Test Design

The steepest ascent test was conducted according to the three significantly affected parameters identified from the Plackett–Burman screening test: seed-to-seed coefficient of static friction (X₃), seed-to-seed coefficient of rolling friction (X₄), and seed-to-steel plate coefficient of static friction (X₆) of pod pepper. All other non-significant parameters were selected as mean values derived from physical tests. The relative errors between the simulated and actual repose angles of pod pepper seeds was used as the response value to determine the optimal range interval of the significance parameter in the simulation test [30], and the steepest ascent test design scheme and results are shown in

Table 6. Steepest ascent experiment design and results.

No.	${\mathbf{X}}_3$	${\mathbf{X}}_4$	${\mathbf{X}}_6$	Simulated Angle of Repose θ′/(°)	Relative Errors Y/%
1	0.50	0.01	0.65	29.55	8.94
2	0.55	0.015	0.7	30.95	4.62
3	0.60	0.02	0.75	32.75	0.92
4	0.65	0.025	0.8	33.64	3.67
5	0.70	0.03	0.85	34.05	4.93

.

According to Table 6, with the gradual increase of the three test factors, the relative error of the simulated angle of repose of pod pepper seeds shows a tendency of decreasing and then increasing. Of these, the relative error of the angle of repose for Test 3 was the smallest, measuring at 0.92%. Based on the steepest ascent test, it was established that each parameter in Test 3 would serve as the center point for subsequent tests, with 2 and 4 as the low and high levels, respectively. The Box–Behnken response surface test was used to verify the significance relationship of the model and optimized to obtain the optimal combination of parameters. The relative error Y between the simulated repose angle ${\theta }^{\prime }$ and the actual repose angle θ of the pod pepper seeds was determined using Equation (8).

$$\mathrm{Y}=\frac{{\theta }^{\prime }-\theta }{\theta }\times 100\%$$

(8)

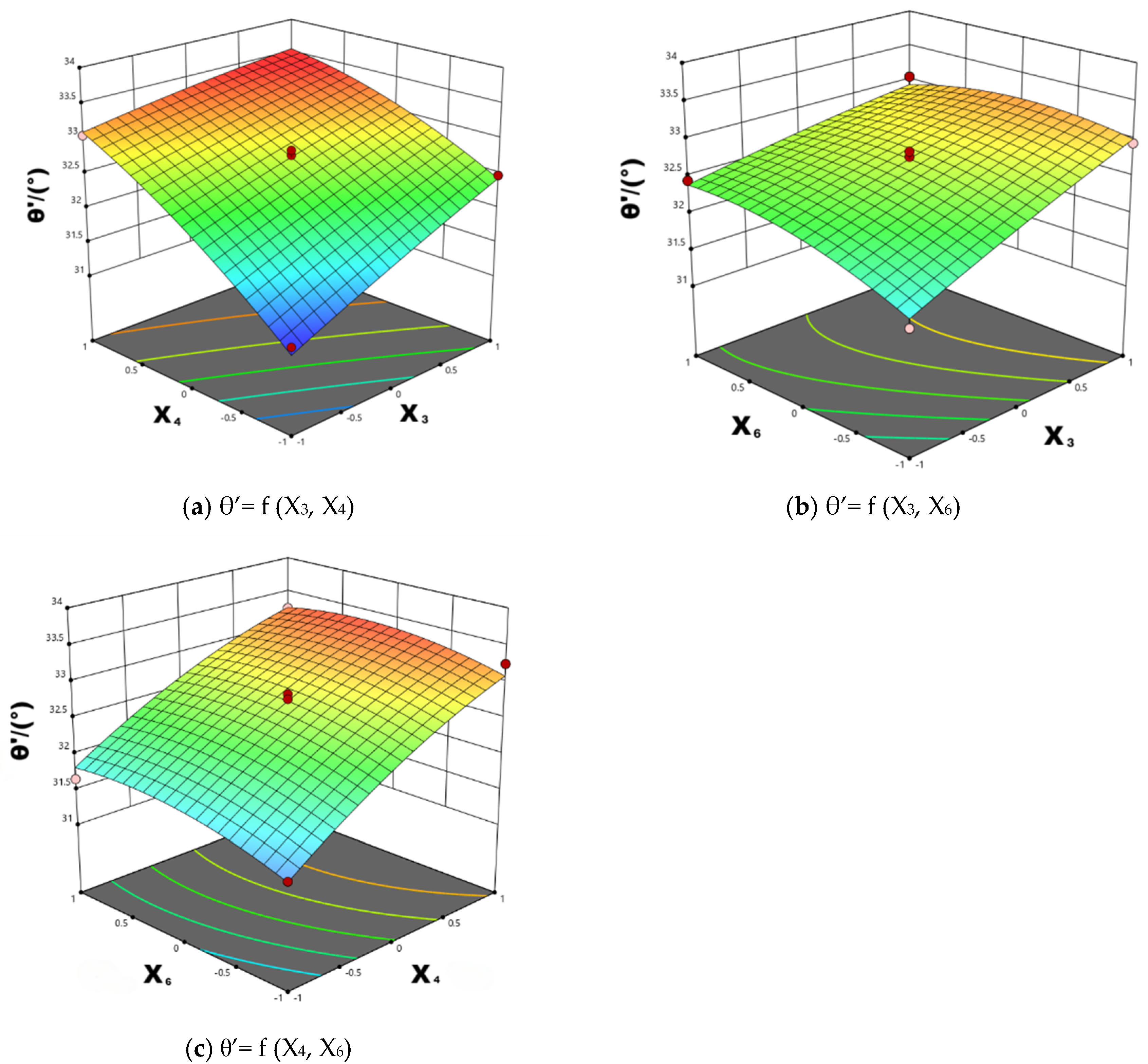
3.3. Box–Behnken Design of Experiments

Design-Expert 13 performed a three-factor, three-level response surface experimental design, resulting in a total of 17 sets of simulation experiments [22,31,32]. The experimental design and results are presented in

Table 7. Box–Behnken experimental design and results.

No.	${\mathbf{X}}_3$	${\mathbf{X}}_4$	${\mathbf{X}}_6$	Simulated Angle of Repose θ′/(°)	Relative Errors Y/%
1	0	1	1	33.25	2.47
2	−1	0	1	32.45	0
3	0	0	0	32.77	0.99
4	0	−1	1	31.65	2.47
5	0	0	0	32.73	0.86
6	−1	−1	0	31.22	3.79
7	1	0	−1	32.95	1.54
8	0	1	−1	33.25	2.47
9	0	0	0	32.72	0.83
10	−1	0	−1	31.65	2.47
11	1	0	1	33.05	1.85
12	0	−1	−1	31.45	3.08
13	1	1	0	33.44	3.05
14	1	−1	0	32.48	0.09
15	0	0	0	32.65	0.62
16	0	0	0	32.84	1.20
17	−1	1	0	33.05	1.69

. From the Box–Behnken experiment results, a multiple regression fit was performed to obtain a second-order regression equation between the repose angle of the pod pepper seed simulation experiment and the three significance parameters, as Equation (9).

$$\begin{gathered} {\mathsf{\theta }}^{\prime }=32.74+0.4438X_3+0.7738X_4+0.1375X_6-0.2175X_3{X}_4-0.175X_3{X}_6 \\ -0.05X_4{X}_6-0.0348X_3^2-0.1598X_4^2-0.1822X_6^2 \end{gathered}$$

(9)

The results of the analysis of variance (ANOVA) of this

Table 8. Variation analysis of Box–Behnken quadratic model.

Source of Variance	Sum of Square	Degree of Freedom	Mean Square	F-Value	p-Value
Model	7.11	9	0.7901	40.95	<0.0001 ***
${\mathrm{X}}_3$	1.58	1	1.58	81.65	<0.0001 ***
${\mathrm{X}}_4$	4.79	1	4.79	248.24	<0.0001 ***
${\mathrm{X}}_6$	0.1512	1	0.1512	7.84	0.0265 **
${\mathrm{X}}_3{\mathrm{X}}_4$	0.1892	1	0.1892	9.81	0.0166 **
${\mathrm{X}}_3{\mathrm{X}}_6$	0.1225	1	0.1225	6.35	0.0398 **
${\mathrm{X}}_4{\mathrm{X}}_6$	0.01	1	0.01	0.5183	0.4949
${\mathrm{X}}_3^2$	0.0051	1	0.0051	0.2635	0.6235
${\mathrm{X}}_4^2$	0.1075	1	0.1075	5.57	0.0503
${\mathrm{X}}_6^2$	0.1399	1	0.1399	7.25	0.031 **
Residual	0.1351	7	0.0193
Lack of fit	0.1156	3	0.0385	7.91	0.0371
Pure error	0.0195	4	0.0049
Sum	7.25	16

Note: ** indicates significant (0.01 < p < 0.05), *** indicates highly significant (p < 0.01).

show that the effects of ${\mathrm{X}}_3$ and ${\mathrm{X}}_4$ on the repose angle are highly significant, while the effects of ${\mathrm{X}}_6$, ${\mathrm{X}}_3{\mathrm{X}}_4$, ${\mathrm{X}}_3{\mathrm{X}}_6$, and ${\mathrm{X}}_6^2$ are significant. Conversely, the effects of ${\mathrm{X}}_4{\mathrm{X}}_6$, ${\mathrm{X}}_3^2$ and ${\mathrm{X}}_4^2$ on the angle of repose are found to be insignificant. The regression model for the repose angle fits well with p < 0.0001 and a non-significant misfit term (p = 0.5136 > 0.05), indicating a satisfactory fit without misfit. The regression equation coefficient of determination R² is 0.9814, corrected determination coefficient (adjusted R²) is 0.9574, the variation coefficient (CV) is 0.4265%, and the precision (Adeq Precision) is 22.8569. These results collectively signify that the regression model is highly significant, accurately reflects the real-world scenario, and can be effectively utilized for further predictive analysis of the target repose angle.

Design-Expert 13 software was utilized to generate Figure 7, illustrating the response surface of the simulated repose angle resulting from the interaction of the three significant factors. In Figure 7a, it is evident that the simulated angle of repose increases notably with the rise in both the seed-to-seed coefficient of static friction and the seed-to-seed coefficient of rolling friction of the pod pepper. Moreover, the effects of these two factors on the simulated angle of repose are largely similar. Conversely, Figure 7b depicts a relatively flat response surface, indicating that the simulated angle of repose experiences gradual increments with increasing static friction coefficient between the pod pepper seeds, while the static friction coefficient between the seeds and the steel plate exerts minimal influence on the simulated repose angle. Furthermore, Figure 7c reveals a distinct trend in the simulated angle of repose with the variation of the coefficient of rolling friction between pod pepper seeds and seeds, which significantly impacts the angle of repose. Conversely, alterations in the static friction coefficient between pod pepper seeds and the steel plate do not significantly affect the simulated angle of repose when the rolling friction coefficient between pod pepper seeds and seeds remains constant.

3.4. Parameter Optimization and Simulation Test Check

The second-order regression equation (Equation (9)) was optimally solved by the optimization module of Design-Expert 13 software, using the actual angle of repose of pod pepper seeds as the response value (32.45°) to make the simulated angle of repose of pod pepper seeds the closest to the angle of repose of the physical experiment. The optimal combination of simulation parameters was obtained for pod pepper seeds is as follows: the static friction coefficient (X₃) between pod pepper seeds and seeds is 0.608; the rolling friction coefficient (X₄) between seeds is 0.018; the static friction coefficient (X₆) between seeds and steel plate is 0.787. For other non-significant parameters are set to the mean values obtained from the physical experiments.

To verify the veracity of the calibrated discrete element simulation parameters post-calibration for pod pepper seeds, three simulation experiments were conducted using the aforementioned parameters as the EDEM simulation parameters. The resulting repose angles of pod pepper seeds were 31.80°, 32.30°, and 33.90°, respectively. A two-sample T-test was performed comparing these values with the repose angle obtained from the physical test. The resulting p-value of 0.462 (>0.05) indicated no significant difference between the repose angles of the physical and simulation tests post-parameter calibration. The average value of the simulated angle of repose was found to be 32.67°, with a relative error of 0.68% compared to the mean value of the physical angle of repose (32.45°). This further confirms the reliability and realism of the simulation results. The comparison of the angle of repose test results for pod pepper seeds is depicted in Figure 8.

4. Conclusions

The aim of this study is to calibrate and determine the intrinsic and contact parameters of pod pepper seeds using the discrete element method, and to provide a reliable parametric basis for future discrete element numerical simulations of pod pepper seed scavenging devices. Here are the outcomes of our investigation:

(1)

The intrinsic and contact parameters (including three-dimensional dimensions, thousand-seed mass, moisture content, density, modulus of elasticity, Poisson’s ratio, shear modulus, and coefficient of friction) of pod pepper seeds were established through physical experiments. Additionally, the mean values of the coefficients of static friction and coefficient of restitution between pod pepper seeds were determined using an inclinometer and a high-speed video camera, resulting in values of 0.60 ± 0.031 and 0.28 ± 0.041, respectively. The mean values of the static friction coefficient and coefficient of restitution between pod pepper seeds and steel plates were 0.70 ± 0.035 and 0.39 ± 0.065, respectively. The ranges of rolling friction coefficients between pod pepper seeds and between pod pepper seeds and steel plates were determined through simulation approximation and prediction methods, ranging from 0.01 to 0.03 and from 0.005 to 0.020, respectively. From compression tests conducted by the texture analyzer, the mean values of Poisson’s ratio and shear modulus of pod pepper seeds were obtained as 0.35 ± 0.024 and 8.75 × 106 Pa, respectively.

(2)

Identification of the physical parameters of pod pepper seeds through physical experiments is the basis for selecting the parameters of the simulation tests. Results from the Plackett–Burman test revealed that the coefficients of static friction between seeds, static friction between seeds and steel plates, and rolling friction between pod pepper seeds were significant parameters affecting the repose angle. These three parameters were identified for the steepest ascent experiment to ascertain the optimal range intervals for simulation test parameters through the Plackett–Burman stacking test.

(3)

Based on the results of the Box–Behnken experiment, a secondary regression model was established correlating the significant parameters with the simulated angle of repose. The optimal simulation parameters for pod pepper seeds were identified through the optimization module of Design-Expert 13 software: the coefficient of static friction between pod pepper seeds (X₃) was 0.608; the coefficient of rolling friction between seeds (X₄) was 0.018; and the coefficient of static friction between seeds and steel plates (X₆) was 0.787.

(4)

The two-sample T test yielded a p-value of 0.462, indicating that there was no significant difference between the simulated and actual angles of repose of pod pepper seeds. The relative error between the mean values of the simulated and actual inclinations was 0.68%, further confirming the reliability of the calibrated parameters for pod pepper seeds. The results of the study indicated that the calibration of material parameters of podded chili seeds by the discrete element method is a feasible and reasonable approach. It can provide a valuable reference for the calibration of parameters of other small irregular crops.