Soil-Specific Calibration Using Plate Compression Filling Technique and Monitoring Soil Biomass Degradation Based on Dielectric Properties
Abstract
1. Introduction
2. Materials and Methods
2.1. Soil Sampling
2.2. Preparation of Soil Samples
- (1)
- Loose filling: The soil sample is gently poured into the PVC container without any compaction;
- (2)
- Uniform compaction by layer (compaction state 1): After each layer of soil sample was added, a flat plate was positioned over the soil sample and then gently tapped with a rubber hammer to ensure the absence of visible air gaps and significant density variations within the test material;
- (3)
- Flat plate compression filling (compaction state 2): The entire soil sample was poured into a PVC container, which was then shaken to eliminate some excess pores in the soil sample. After placing a flat plate over the soil sample, a certain pressure was administered and maintained to ensure that the sample attained the same dry bulk density as in method (2).
2.3. Measurements of the Apparent Dielectric Constant
2.4. Data Processing and Analysis
3. Results and Discussion
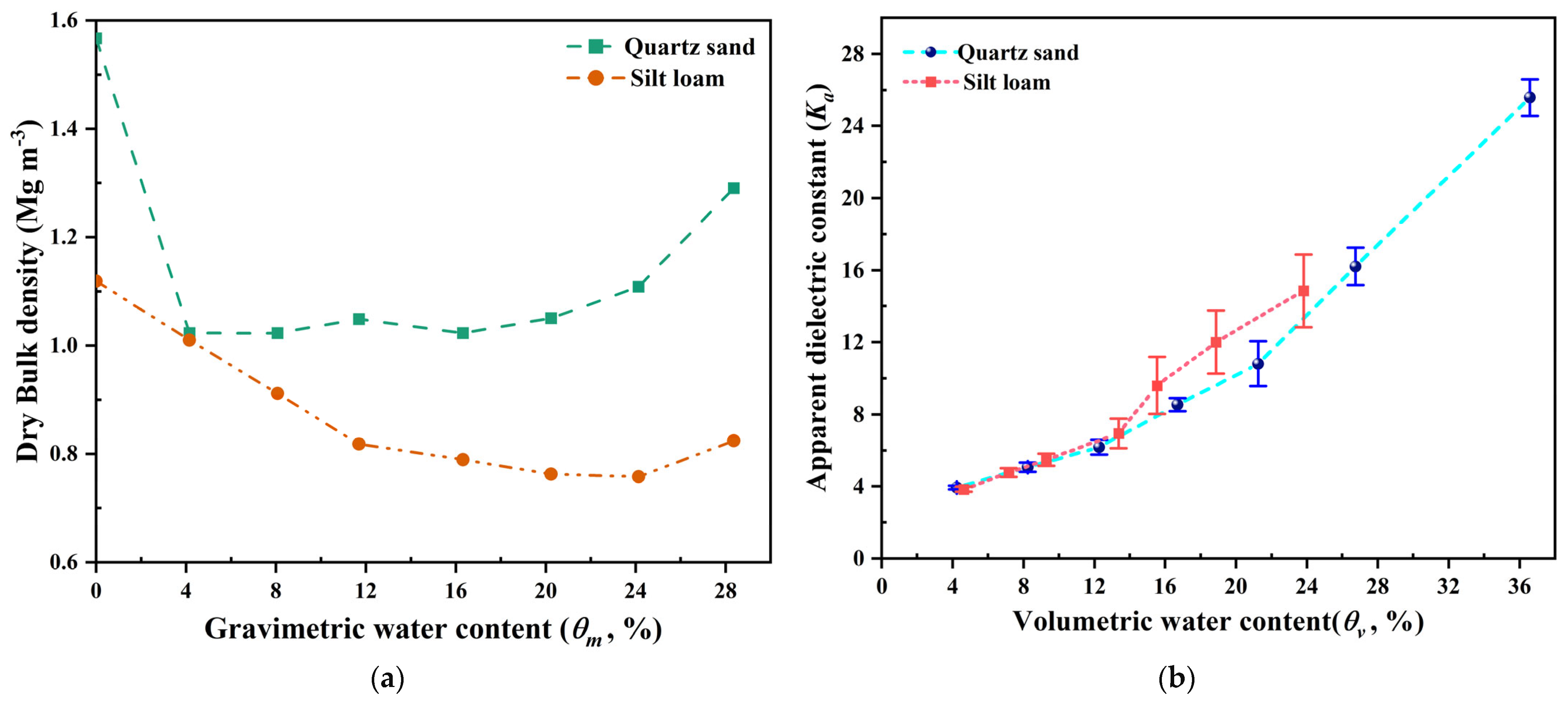
3.1. Variation of Dry Bulk Density and Dielectric Constant of Samples under Loose Filling Conditions
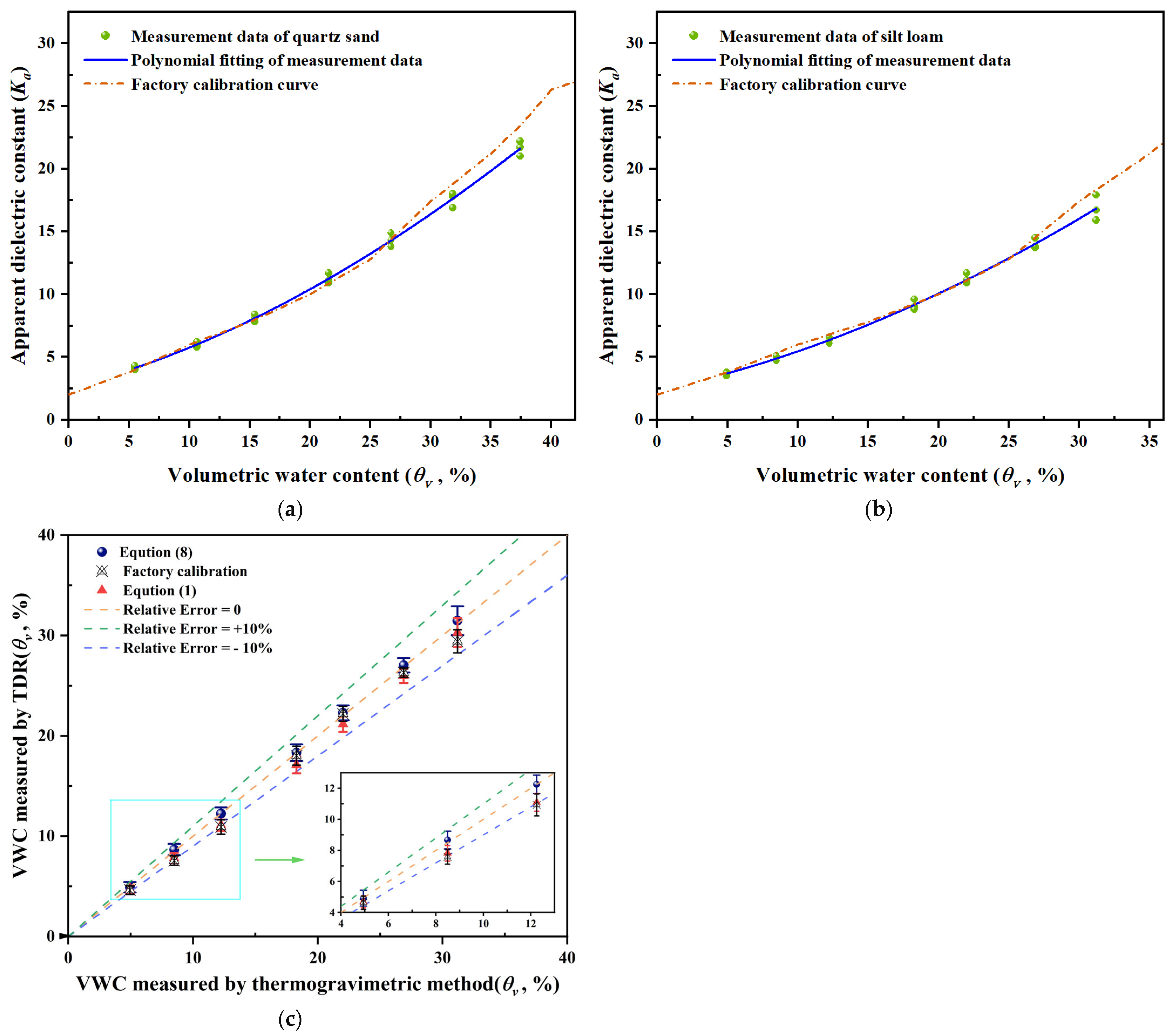
3.2. Developing Soil-Specific Calibration Equation Using Compression Filling Method
3.3. Biomass Degradation
- (1)
- The degradation of biomass leads to the conversion of a portion of soil water into constitution water or crystalline water, where constitution water exists in the form of H+, (OH)-, (H3O)+, while crystalline water refers to neutral water molecules occupying specific positions within mineral lattices. This occurs through changes in the formation of organic hydrates and/or the mineral molecular structure, thereby consuming a portion of water in the soil samples [35]. More specifically, organic matter is broken down into smaller organic molecules via hydrolysis reactions [57]. These reactions can involve the action of enzymes that break down water molecules and bind them to organic substances, resulting in the formation of constitution water. After microbial decomposition in the soil, organic matter further undergoes biotransformation processes to produce inorganic material, which may lead to the formation of crystalline water [58];
- (2)
- Interactions between organic molecules produced during biomass degradation and water molecules alter the distribution and arrangement of water in the soil, resulting in the conversion of some free water into bound water [30]. This results in a reduction in the overall polarizability of the water, which is reflected in the measured decrease in the dielectric constant;
- (3)
- Biomass degradation affects soil grain aggregation through various mechanisms and at different scales [31]. This, in turn, affects the specific surface area of the soil and the connectivity of the soil pores, significantly affecting the soil dielectric constant. More specifically, the decomposition products of organic matter, the binding effects of organic matter, and metabolic byproducts of microbial activity all play a significant role in the formation of soil aggregates during soil biomass degradation.
4. Conclusions
- Soil samples have shown variable levels of expansion in relation to water content when there is loose filling. Following probe insertion, this expansion creates a tiny space between the probe rod and the soil, which could cause the measured dielectric constant’s coefficient of variation (CV) to rise above 10%. Consequently, the loose packaging is not suitable for soil-specific calibration when the probe is inserted vertically;
- After plate compression filling, the dispersion of the measured dielectric constants of soil samples decreased significantly, with their CV values all measuring less than 6%. A third-order polynomial fitting equation explaining the dependency of the dielectric constant on the volumetric water content was found by applying the least-squares method. The suggested plate compression filling approach produced a mean bias error (MBE) of less than 0.5%, according to the findings of the dielectric measurements; in contrast, the maximum MBE associated with factory calibration and Equation (1) was −1.78% and −1.19%, respectively. These findings indicate that the plate compression filling method serves as an effective, simple, and accurate alternative to the uniform compaction method;
- By studying the impact of biomass degradation on soil dielectric properties at specific water content, it was concluded that a gravimetric water content of 24% (the corresponding saturation ratio is 0.54) was most effective in promoting biomass degradation. The SCVCAs maximum production was also reported for the samples having 24% of gravimetric water content. The correlation between the volumetric water content difference measured by the dielectric method and the measurement results of SCVCAs suggests that employing the dielectric method to measure the volumetric water content of soil samples before and after biodegradation serves as a reliable indicator for evaluating biodegradation.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Abdulraheem, M.I.; Chen, H.; Li, L.; Moshood, A.Y.; Zhang, W.; Xiong, Y.; Zhang, Y.; Taiwo, L.B.; Farooque, A.A.; Hu, J. Recent Advances in Dielectric Properties-Based Soil Water Content Measurements. Remote Sens. 2024, 16, 1328. [Google Scholar] [CrossRef]
- Zhao, Y.; Song, J.; Cheng, K.; Liu, Z.; Yang, F. Migration and remediation of typical contaminants in soil and groundwater: A state of art review. Land Degrad. Dev. 2024, 35, 2700–2715. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, H.; Song, B.; Xue, P.; Zhang, W.; Peth, S.; Lee Hill, R.; Horn, R. Characterizing uncertainty in process-based hydraulic modeling, exemplified in a semiarid Inner Mongolia steppe. Geoderma 2023, 440, 116713. [Google Scholar] [CrossRef]
- Bwambale, E.; Abagale, F.K.; Anornu, G.K. Smart irrigation monitoring and control strategies for improving water use efficiency in precision agriculture: A review. Agric. Water Manag. 2022, 260, 107324. [Google Scholar] [CrossRef]
- He, H.; Aogu, K.; Li, M.; Xu, J.; Sheng, W.; Jones, S.B.; Gonzalez-Teruel, J.D.; Robinson, D.A.; Horton, R.; Bristow, K.; et al. A review of time domain reflectometry (TDR) applications in porous media. In Advances in Agronomy; Sparks, D.L., Ed.; Academic Press: Cambridge, MA, USA, 2021; Volume 168, pp. 83–155. [Google Scholar]
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef]
- Kargas, G.; Soulis, K.X. Performance evaluation of a recently developed soil water content, dielectric permittivity, and bulk electrical conductivity electromagnetic sensor. Agric. Water Manag. 2019, 213, 568–579. [Google Scholar] [CrossRef]
- Tian, Z.C.; Lu, Y.L.; Ren, T.S.; Horton, R.; Heitman, J.L. Improved thermo-time domain reflectometry method for continuous in-situ determination of soil bulk density. Soil Tillage Res. 2018, 178, 118–129. [Google Scholar] [CrossRef]
- Zhang, M.H.; Tian, Z.C.; Zhu, Q.; Chen, J.Z. In-situ assessment of soil shrinkage and swelling behavior and hydro-thermal regimes with a thermo-time domain reflectometry technique. Soil Tillage Res. 2023, 227, 105617. [Google Scholar] [CrossRef]
- Chanzy, A.; Gaudu, J.-C.; Marloie, O. Correcting the Temperature Influence on Soil Capacitance Sensors Using Diurnal Temperature and Water Content Cycles. Sensors 2012, 12, 9773–9790. [Google Scholar] [CrossRef]
- Xiao, Q.L.; Zhao, W.H.; Ju, C.Y.; Peng, K.; Yuan, M.; Tan, Q.Z.; He, R.; Huang, M.B. Effects of Different Tillage Depths on Soil Physical Properties and the Growth and Yield of Tobacco in the Mountainous Chongqing Region of China. Agriculture 2024, 14, 276. [Google Scholar] [CrossRef]
- Li, B.; Wang, C.; Gu, X.; Zhou, X.; Ma, M.; Li, L.; Feng, Z.; Ding, T.; Li, X.; Jiang, T.; et al. Accuracy calibration and evaluation of capacitance-based soil moisture sensors for a variety of soil properties. Agric. Water Manag. 2022, 273, 107913. [Google Scholar] [CrossRef]
- Gasch, C.K.; Brown, D.J.; Brooks, E.S.; Yourek, M.; Poggio, M.; Cobos, D.R.; Campbell, C.S. A pragmatic, automated approach for retroactive calibration of soil moisture sensors using a two-step, soil-specific correction. Comput. Electron. Agric. 2017, 137, 29–40. [Google Scholar] [CrossRef]
- Pečan, U.; Kastelec, D.; Pintar, M. Evaluation of Default, Soil-Specific, and Clay Content Correction Calibration Functions for Dielectric Sensors in Soils with Differing Properties. J. Irrig. Drain. Eng. 2022, 148, 04022016. [Google Scholar] [CrossRef]
- Wan, H.Y.; Qi, H.W.; Shang, S.H. Estimating soil water and salt contents from field measurements with time domain reflectometry using machine learning algorithms. Agric. Water Manag. 2023, 285, 108364. [Google Scholar] [CrossRef]
- Yu, X.; Drnevich, V.P. Soil water content and dry density by time domain reflectometry. J. Geotech. Geoenviron. 2004, 130, 922–934. [Google Scholar] [CrossRef]
- Robinson, D.A.; Jones, S.B.; Blonquist, J.M.; Friedman, S.P. A physically derived water content/permittivity calibration model for coarse-textured, layered soils. Soil Sci. Soc. Am. J. 2005, 69, 1372–1378. [Google Scholar] [CrossRef]
- Mane, S.; Das, N.; Singh, G.; Cosh, M.; Dong, Y. Advancements in dielectric soil moisture sensor Calibration: A comprehensive review of methods and techniques. Comput. Electron. Agric. 2024, 218, 108686. [Google Scholar] [CrossRef]
- Veach, A.M.; Zeglin, L.H. Historical Drought Affects Microbial Population Dynamics and Activity During Soil Drying and Re-Wet. Microb. Ecol. 2020, 79, 662–674. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, K.; Chang, T.; Shaghaleh, H.; Qi, Z.; Zhang, J.; Ye, H.; Hamoud, Y.A. Interactive Effects of Microbial Fertilizer and Soil Salinity on the Hydraulic Properties of Salt-Affected Soil. Plants 2024, 13, 473. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, L.; Zhao, X.; Fan, J. Effects of Biomass and Soil Water Content Distribution on Cosmic Ray Neutron Probe Measurement. Water 2023, 15, 2766. [Google Scholar] [CrossRef]
- Zhu, G.; Yong, L.; Zhao, X.; Liu, Y.; Zhang, Z.; Xu, Y.; Sun, Z.; Sang, L.; Wang, L. Evaporation, infiltration and storage of soil water in different vegetation zones in the Qilian Mountains: A stable isotope perspective. Hydrol. Earth Syst. Sci. 2022, 26, 3771–3784. [Google Scholar] [CrossRef]
- Dai, H.; Liu, Y.; Guadagnini, A.; Yuan, S.; Yang, J.; Ye, M. Comparative Assessment of Two Global Sensitivity Approaches Considering Model and Parameter Uncertainty. Water Resour. Res. 2024, 60, e2023WR036096. [Google Scholar] [CrossRef]
- Ahmed, S.; Hu, J.D.; Naqvi, S.; Zhang, Y.Y.; Li, L.Z.; Iderawumi, A.M. Molecular communication network and its applications in crop sciences. Planta 2022, 255, 128. [Google Scholar] [CrossRef] [PubMed]
- Patel, K.F.; Fansler, S.J.; Campbell, T.P.; Bond-Lamberty, B.; Smith, A.P.; RoyChowdhury, T.; McCue, L.A.; Varga, T.; Bailey, V.L. Soil texture and environmental conditions influence the biogeochemical responses of soils to drought and flooding. Commun. Earth Environ. 2021, 2, 127. [Google Scholar] [CrossRef]
- Jin, X.Y.; Jin, H.J.; Wu, X.D.; Luo, D.L.; Yu, S.; Li, X.Y.; He, R.X.; Wang, Q.F.; Knops, J.M.H. Permafrost Degradation Leads to Biomass and Species Richness Decreases on the Northeastern Qinghai-Tibet Plateau. Plants 2020, 9, 1453. [Google Scholar] [CrossRef]
- Thring, L.M.; Boddice, D.; Metje, N.; Curioni, G.; Chapman, D.N.; Pring, L. Factors affecting soil permittivity and proposals to obtain gravimetric water content from time domain reflectometry measurements. Can. Geotech. J. 2014, 51, 1303–1317. [Google Scholar] [CrossRef]
- Franzluebbers, A.J. Holding water with capacity to target porosity. Agric. Environ. Lett. 2020, 5, e20029. [Google Scholar] [CrossRef]
- Ankenbauer, K.J.; Loheide, S.P. The effects of soil organic matter on soil water retention and plant water use in a meadow of the Sierra Nevada, CA. Hydrol. Process. 2017, 31, 891–901. [Google Scholar] [CrossRef]
- Szyplowska, A.; Lewandowski, A.; Yagihara, S.; Saito, H.; Furuhata, K.; Szerement, J.; Kafarski, M.; Wilczek, A.; Majcher, J.; Woszczyk, A.; et al. Dielectric models for moisture determination of soils with variable organic matter content. Geoderma 2021, 401, 115288. [Google Scholar] [CrossRef]
- Regelink, I.C.; Stoof, C.R.; Rousseva, S.; Weng, L.P.; Lair, G.J.; Kram, P.; Nikolaidis, N.P.; Kercheva, M.; Banwart, S.; Comans, R.N.J. Linkages between aggregate formation, porosity and soil chemical properties. Geoderma 2015, 247, 24–37. [Google Scholar] [CrossRef]
- Blonquist, J.M., Jr.; Jones, S.B.; Lebron, I.; Robinson, D.A. Microstructural and phase configurational effects determining water content: Dielectric relationships of aggregated porous media. Water Resour. Res. 2006, 42, 1–13. [Google Scholar] [CrossRef]
- Czachor, H.; Doerr, S.H.; Lichner, L. Water retention of repellent and subcritical repellent soils: New insights from model and experimental investigations. J. Hydrol. 2010, 380, 104–111. [Google Scholar] [CrossRef]
- Orangi, A.; Narsilio, G.A.; Wang, Y.H.; Ryu, D. Experimental investigation of dry density effects on dielectric properties of soil–water mixtures with different specific surface areas. Acta Geotech. 2020, 15, 1153–1172. [Google Scholar] [CrossRef]
- Owenier, F.; Hornung, J.; Hinderer, M. Substrate-sensitive relationships of dielectric permittivity and water content: Implications for moisture sounding. Near Surf. Geophys. 2018, 16, 128–152. [Google Scholar] [CrossRef]
- Benatti, A.L.T.; Polizeli, M. Lignocellulolytic Biocatalysts: The Main Players Involved in Multiple Biotechnological Processes for Biomass Valorization. Microorganisms 2023, 11, 162. [Google Scholar] [CrossRef]
- Baruah, J.; Nath, B.K.; Sharma, R.; Kumar, S.; Deka, R.C.; Baruah, D.C.; Kalita, E. Recent Trends in the Pretreatment of Lignocellulosic Biomass for Value-Added Products. Front. Energy Res. 2018, 6, 141. [Google Scholar] [CrossRef]
- Viana, M.; Jouannin, P.; Pontier, C.; Chulia, D. About pycnometric density measurements. Talanta 2002, 57, 583–593. [Google Scholar] [CrossRef]
- Silva, B.P.C.; Tassinari, D.; Silva, M.L.N.; Silva, B.M.; Curi, N.; da Rocha, H.R. Nonlinear models for soil moisture sensor calibration in tropical mountainous soils. Sci. Agric. 2022, 79, 1–11. [Google Scholar] [CrossRef]
- Peng, W.; Lu, Y.L.; Xie, X.T.; Ren, T.S.; Horton, R. An Improved Thermo-TDR Technique for Monitoring Soil Thermal Properties, Water Content, Bulk Density, and Porosity. Vadose Zone J. 2019, 18, 1–9. [Google Scholar] [CrossRef]
- Jung, S.; Drnevich, V.P.; Abou Najm, M.R. New Methodology for Density and Water Content by Time Domain Reflectometry. J. Geotech. Geoenviron. 2013, 139, 659–670. [Google Scholar] [CrossRef]
- Kim, J.S.; Lee, Y.Y.; Kim, T.H. A review on alkaline pretreatment technology for bioconversion of lignocellulosic biomass. Bioresour. Technol. 2016, 199, 42–48. [Google Scholar] [CrossRef] [PubMed]
- Daniels, L.W. The Nature and Properties of Soils, 15th ed.; Pearson: London, UK, 2016; Volume 80, p. 1428. [Google Scholar]
- Karicheva, E.; Guseva, N.; Kambalina, M. Determination of water-soluble forms of oxalic and formic acids in soils by ion chromatography. IOP Conf. Ser. Earth Environ. Sci. 2016, 33, 012006. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, L.; Huang, M.; Chen, F.; Niu, J.; Liu, M. Feasibility of soil erosion measurement using time domain reflectometry. CATENA 2022, 218, 106571. [Google Scholar] [CrossRef]
- Wilson, T.B.; Kochendorfer, J.; Diamond, H.J.; Meyers, T.P.; Hall, M.; French, B.; Myles, L.; Saylor, R.D. A field evaluation of the SoilVUE10 soil moisture sensor. Vadose Zone J. 2023, 22, e20241. [Google Scholar] [CrossRef]
- Rasheed, M.W.; Tang, J.L.; Sarwar, A.; Shah, S.; Saddique, N.; Khan, M.U.; Khan, M.I.; Nawaz, S.; Shamshiri, R.R.; Aziz, M.; et al. Soil Moisture Measuring Techniques and Factors Affecting the Moisture Dynamics: A Comprehensive Review. Sustainability 2022, 14, 11538. [Google Scholar] [CrossRef]
- Shimobe, S.; Spagnoli, G. Relationship between dielectric constant of soils with clay content and dry unit weight. Environ. Geotech. 2021, 8, 134–147. [Google Scholar] [CrossRef]
- Majcher, J.; Kafarski, M.; Wilczek, A.; Szyplowska, A.; Lewandowski, A.; Woszczyk, A.; Skierucha, W. Application of a dagger probe for soil dielectric permittivity measurement by TDR. Measurement 2021, 178, 109368. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Q.; Liu, S.; Li, J.; Geng, J.; Wang, L. Key soil properties influencing infiltration capacity after long-term straw incorporation in a wheat (Triticum aestivum L.)–maize (Zea mays L.) rotation system. Agric. Ecosyst. Environ. 2023, 344, 108301. [Google Scholar] [CrossRef]
- Zawilski, B.M.; Granouillac, F.; Claverie, N.; Lemaire, B.; Brut, A.; Tallec, T. Calculation of soil water content using dielectric-permittivity-basedsensors—Benefits of soil-specific calibration. Geosci. Instrum. Methods Data Syst. 2023, 12, 45–56. [Google Scholar] [CrossRef]
- Lekshmi, S.U.S.; Singh, D.N.; Baghini, M.S. A critical review of soil moisture measurement. Measurement 2014, 54, 92–105. [Google Scholar] [CrossRef]
- Cui, J.P.; Tan, F. PLSR-Based Assessment of Soil Respiration Rate Changes under Aerated Irrigation in Relation to Soil Environmental Factors. Agriculture 2023, 13, 68. [Google Scholar] [CrossRef]
- Kashyap, P.; Brzezinska, M.; Keller, N.; Ruppert, A.M. Influence of Impurities in the Chemical Processing Chain of Biomass on the Catalytic Valorisation of Cellulose towards γ-Valerolactone. Catalysts 2024, 14, 141. [Google Scholar] [CrossRef]
- Rahim, A.F.A.; Kutty, S.R.M.; Ezechi, E.H. Volatile Fatty Acids Production through Degradation of Biomass by Anaerobic Digestion (Mesophilic and Thermophilic). Appl. Mech. Mater. 2014, 567, 172–176. [Google Scholar] [CrossRef]
- Wirsching, J.; Pagel, H.; Ditterich, F.; Uksa, M.; Werneburg, M.; Zwiener, C.; Berner, D.; Kandeler, E.; Poll, C. Biodegradation of Pesticides at the Limit: Kinetics and Microbial Substrate Use at Low Concentrations. Front. Microbiol. 2020, 11, 2107. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, J.; Kleber, M. The contentious nature of soil organic matter. Nature 2015, 528, 60–68. [Google Scholar] [CrossRef] [PubMed]
- Whitman, T.; Pepe-Ranney, C.; Enders, A.; Koechli, C.; Campbell, A.; Buckley, D.H.; Lehmann, J. Dynamics of microbial community composition and soil organic carbon mineralization in soil following addition of pyrogenic and fresh organic matter. ISME J. 2016, 10, 2918–2930. [Google Scholar] [CrossRef] [PubMed]
- Negron-Juarez, R.; Ferreira, S.J.F.; Mota, M.C.; Faybishenko, B.; Monteiro, M.T.F.; Candido, L.A.; Ribeiro, R.P.; de Oliveira, R.C.; de Araujo, A.C.; Warren, J.M.; et al. Calibration, measurement, and characterization of soil moisture dynamics in a central Amazonian tropical forest. Vadose Zone J. 2020, 19, e20070. [Google Scholar] [CrossRef]
- Lee, S.H.; Ji, W.; Kang, D.M.; Kim, M.S. Effect of soil water content on heavy mineral oil biodegradation in soil. J. Soils Sediments 2018, 18, 983–991. [Google Scholar] [CrossRef]
- Troquet, J.; Larroche, C.; Dussap, C.-G. Evidence for the occurrence of an oxygen limitation during soil bioremediation by solid-state fermentation. Biochem. Eng. J. 2003, 13, 103–112. [Google Scholar] [CrossRef]
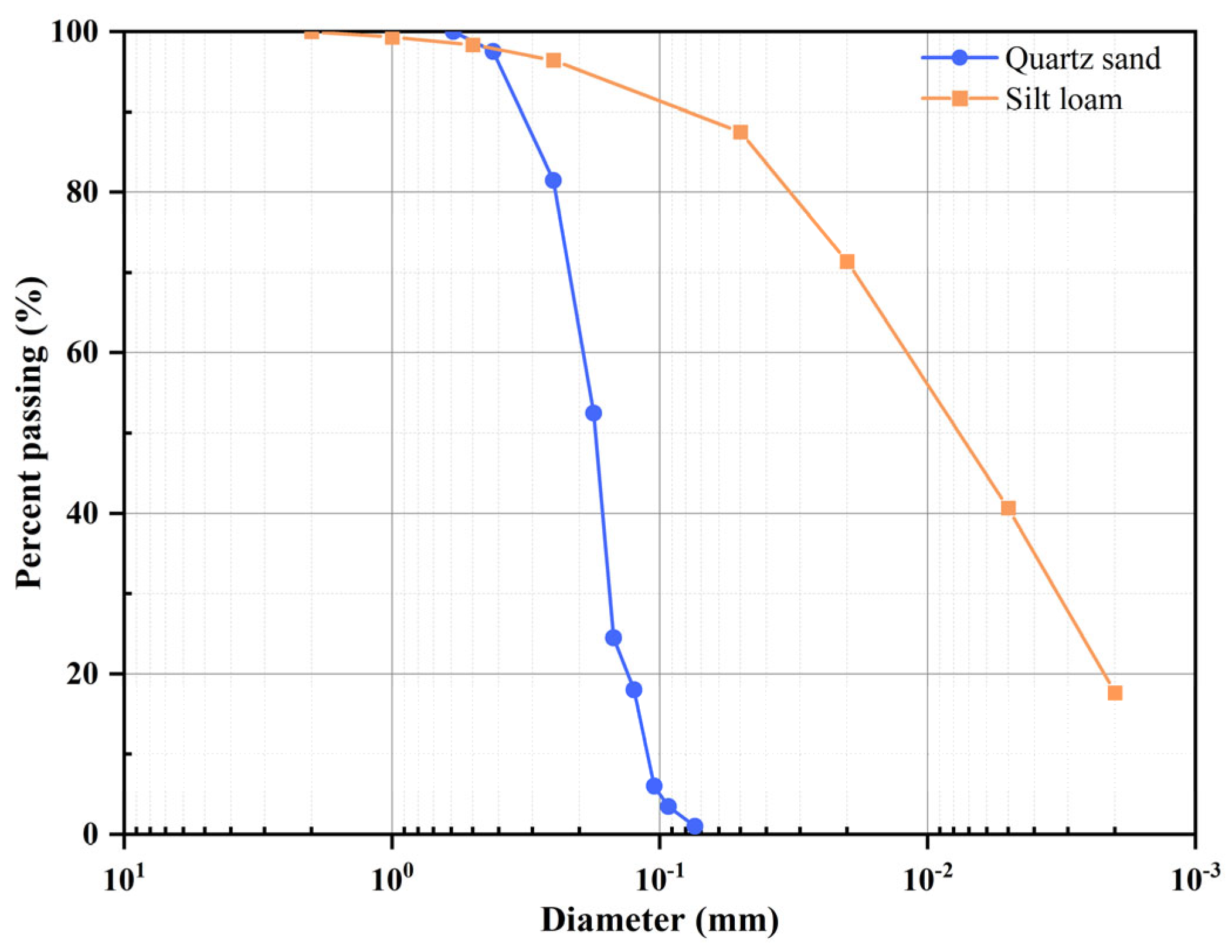

| Soil Name | Clay g kg−1 | Silt g kg−1 | Sand g kg−1 | Texture * | OM g kg−1 | Particle Density , Mg m−3 | Dry Bulk Density , Mg m−3 | Total Porosity , m3 m−3 |
|---|---|---|---|---|---|---|---|---|
| Silt loam | 176.3 | 537.6 | 286.1 | silt loam | 12.3 | 2.63 | 1.12 | 0.574 |
| Quartz sand | 0 | 0 | 100 | sand | 0 | 2.65 | 1.57 | 0.408 |
| Soil Name | % | % | % | % | % | % | % | Dry Bulk Density * , Mg m−3 |
|---|---|---|---|---|---|---|---|---|
| Silt loam | 4.58 | 7.86 | 11.34 | 16.94 | 20.39 | 24.90 | 28.89 | 1.08 |
| Quartz sand | 4.15 | 8.07 | 11.69 | 16.32 | 20.24 | 24.13 | 28.36 | 1.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Awais, M.; Li, L.; Zhang, W.; Abdulraheem, M.I.; Xiong, Y.; Raghavan, V.; Hu, J. Soil-Specific Calibration Using Plate Compression Filling Technique and Monitoring Soil Biomass Degradation Based on Dielectric Properties. Agriculture 2024, 14, 773. https://doi.org/10.3390/agriculture14050773
Chen H, Awais M, Li L, Zhang W, Abdulraheem MI, Xiong Y, Raghavan V, Hu J. Soil-Specific Calibration Using Plate Compression Filling Technique and Monitoring Soil Biomass Degradation Based on Dielectric Properties. Agriculture. 2024; 14(5):773. https://doi.org/10.3390/agriculture14050773
Chicago/Turabian StyleChen, Hongjun, Muhammad Awais, Linze Li, Wei Zhang, Mukhtar Iderawumi Abdulraheem, Yani Xiong, Vijaya Raghavan, and Jiandong Hu. 2024. "Soil-Specific Calibration Using Plate Compression Filling Technique and Monitoring Soil Biomass Degradation Based on Dielectric Properties" Agriculture 14, no. 5: 773. https://doi.org/10.3390/agriculture14050773
APA StyleChen, H., Awais, M., Li, L., Zhang, W., Abdulraheem, M. I., Xiong, Y., Raghavan, V., & Hu, J. (2024). Soil-Specific Calibration Using Plate Compression Filling Technique and Monitoring Soil Biomass Degradation Based on Dielectric Properties. Agriculture, 14(5), 773. https://doi.org/10.3390/agriculture14050773








