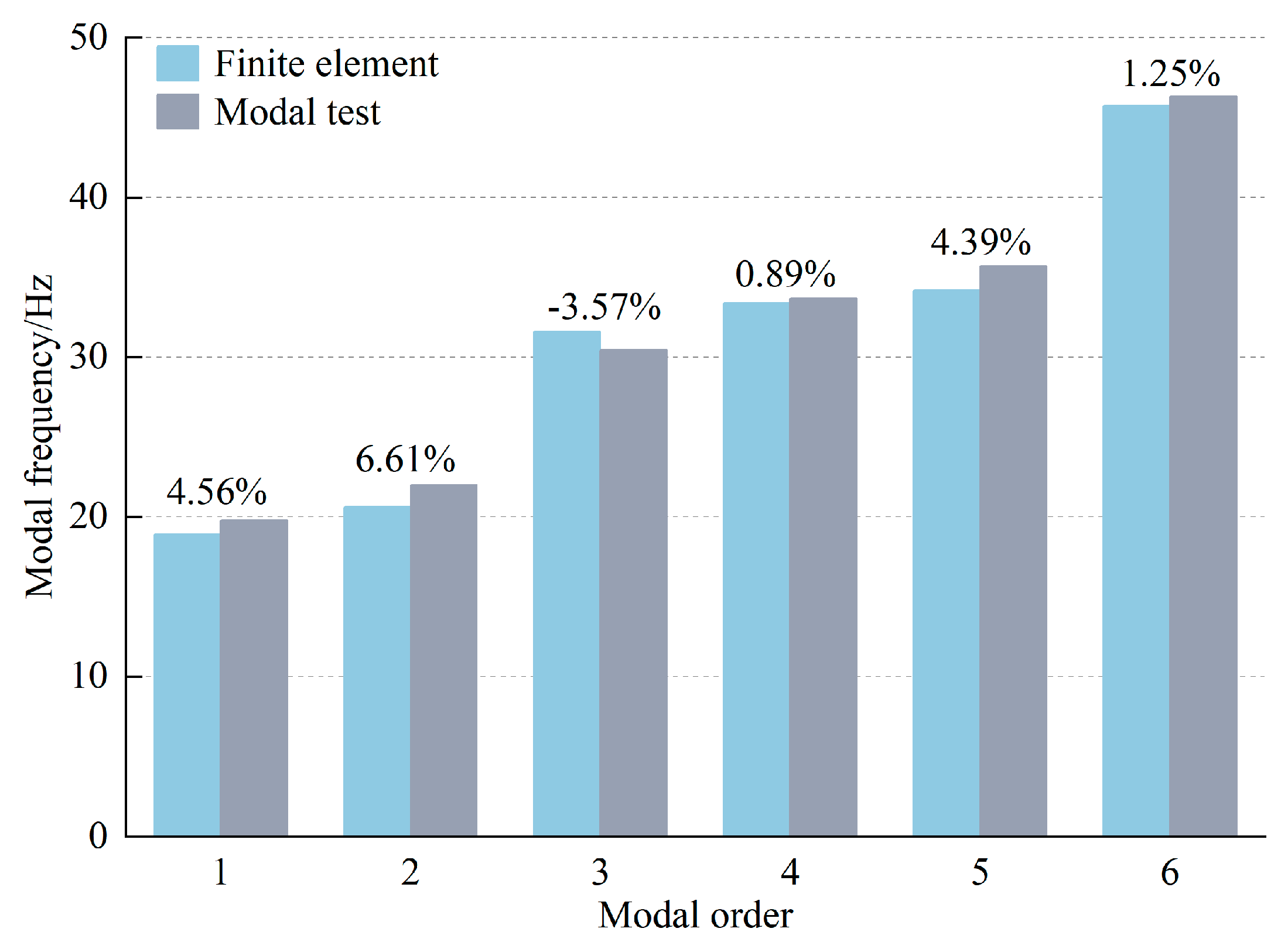Optimization Design of Straw-Crushing Residual Film Recycling Machine Frame Based on Sensitivity and Grey Correlation Degree

Abstract

This paper takes the frame as the research object and explores the vibration characteristics of the frame to address the vibration problem of a 1-MSD straw-crushing and residual film recycling machine in the field operation process, and an accurate identification of the modal parameters of the frame is carried out to solve the resonance problem of the machine, which can achieve cost reduction and increase income to a certain extent. The first six natural frequencies of the frame are extracted by finite element modal identification and modal tests, respectively. The rationality of the modal test results is verified using the comprehensive modal and frequency response confidences. The maximum frequency error of modal frequency results of the two methods is only 6.61%, which provides a theoretical basis for the optimal design of the frame. In order to further analyze the resonance problem of the machine, the external excitation frequency of the machine during normal operation in the field is solved and compared with the first six natural frequencies of the frame. The results show that the first natural frequency of the frame (18.89 Hz) is close to the external excitation generated by the stripping roller (16.67 Hz). The first natural frequency and the volume of the frame are set as the optimization objectives, and the optimal optimization scheme is obtained by using the Optistruct solver, sensitivity method, and grey correlation method. The results indicate the first-order natural frequency of the optimized frame is 21.89 Hz, an increase of 15.882%, which is much higher than the excitation frequency of 16.67 Hz, and resonance can be avoided. The corresponding frame volume is 9.975 × 10⁷ mm³, and the volume reduction is 3.46%; the optimized frame has good dynamic performance, which avoids the resonance of the machine and conforms to the lightweight design criteria of agricultural machinery structures. The research results can provide some theoretical reference for this kind of machine in solving the resonance problem and carrying out related vibration characteristics research.

1. Introduction

Plastic film mulching cultivation technology increases temperature and moisture, saves water and boosts drought resistance, reduces soil salinity, and improves crop yield, all of which are of great significance to agricultural development [1,2]. However, agricultural plastic film is extremely difficult to degrade under natural conditions [3,4], resulting in the transformation of a farmland “white revolution” into “white pollution”. Therefore, it is urgent to control the current situation of residual film pollution [5,6,7,8]. In China, the problem of residual film pollution in cotton fields is mainly treated by residual film recycling machines. The specific models are divided into spring-tooth row, roller, air-suction, follow-up, clamping, etc. [9].

As the main bearing part of the straw-crushing residual film recycling machine, the frame easily bears the extreme load generated by the system and the alternating load generated by other components when it works at high speed without stopping in a complex field terrain [10]. At the same time, there will be related vibration characteristics problems when subjected to vibration, mainly including resonance frequency, natural frequency, damping and amplitude, etc. [11,12]. Research on the vibration characteristics of residual film recycling machines is challenging yet important. To a certain extent, solving the resonance problem can reduce the energy loss of the machine, improve the operation efficiency, and achieve cost reduction and income increase. However, studying the vibration characteristics of the frame system of the straw-crushing and residual film recycling machine with the main purpose of reducing weight and noise is important because it provides a theoretical basis for the in-depth study of the vibration characteristics of the subsequent agricultural machinery.

Some scholars have carried out systematic vibration tests and modal analyses on various types of agricultural machinery and equipment to avoid the resonance problem and reduce the violent vibration phenomenon of the whole machine under complex working conditions and improve driving comfort. Arkadiusz et al. [13] explored the application of accelerometer sensors in the manufacture of low-cost systems for monitoring the vibration of agricultural machinery (such as rotary grass spreaders). Sensors provide useful data on equipment health for agricultural machinery to improve the durability of such machinery. Liu Jiajie et al. [14] optimized the frame design to avoid reducing the stripping machine’s bearing capacity at the working time. Gao et al. [15] explored the vibration characteristics of the chassis frame of the combined harvester by combining NX Nastran with the modal test. Adam et al. [16] collected the vibration signals of the tractor base and the driver’s thigh under the driving condition and the field operation condition. It was found that the vibration energy of the driver in the vertical direction was larger during the field operation, and the seat resonance frequency was 2–3 Hz. Jahanbakhshi et al. [17] conducted a working condition vibration test on the machine to improve the driver’s driving comfort of the combined harvester during operation. Chowdhury et al. [18] explored the vibration characteristics of a radish harvester during field operation to analyze the causes of severe vibration.

At present, there are few studies on the resonance problem and related vibration characteristics of the straw-crushing residual film recycling machine. Therefore, this paper takes the vibration problem of the 1-MSD straw-crushing residual film recovery machine in the field as the background and aims to avoid resonance of the machine based on the relationship between the external excitation of the straw-crushing residual film recovery machine, and its frame mode, sensitivity and grey correlation analyses were combined to analyze the vibration characteristics and optimize the design of the frame of the 1-MSD straw-crushing and residual film recycling machine, providing a theoretical reference for the vibration reduction optimization of the subsequent frame of this kind of machine. To this end, this paper mainly carries out the following work: (1) Establishing the rack model and solving its modal parameters by the finite element method; (2) Extracting the modal parameters of the rack by modal test and comparing it with the results of the finite element method; (3) Analyzing the relationship between the external excitation and the natural frequency of the rack, obtaining the optimized components through sensitivity analysis, establishing the optimization mathematical model and solving; (4) Establishing the optimization scheme based on grey correlation degree and finding the optimal result.

2. Machine Composition and Working Principle

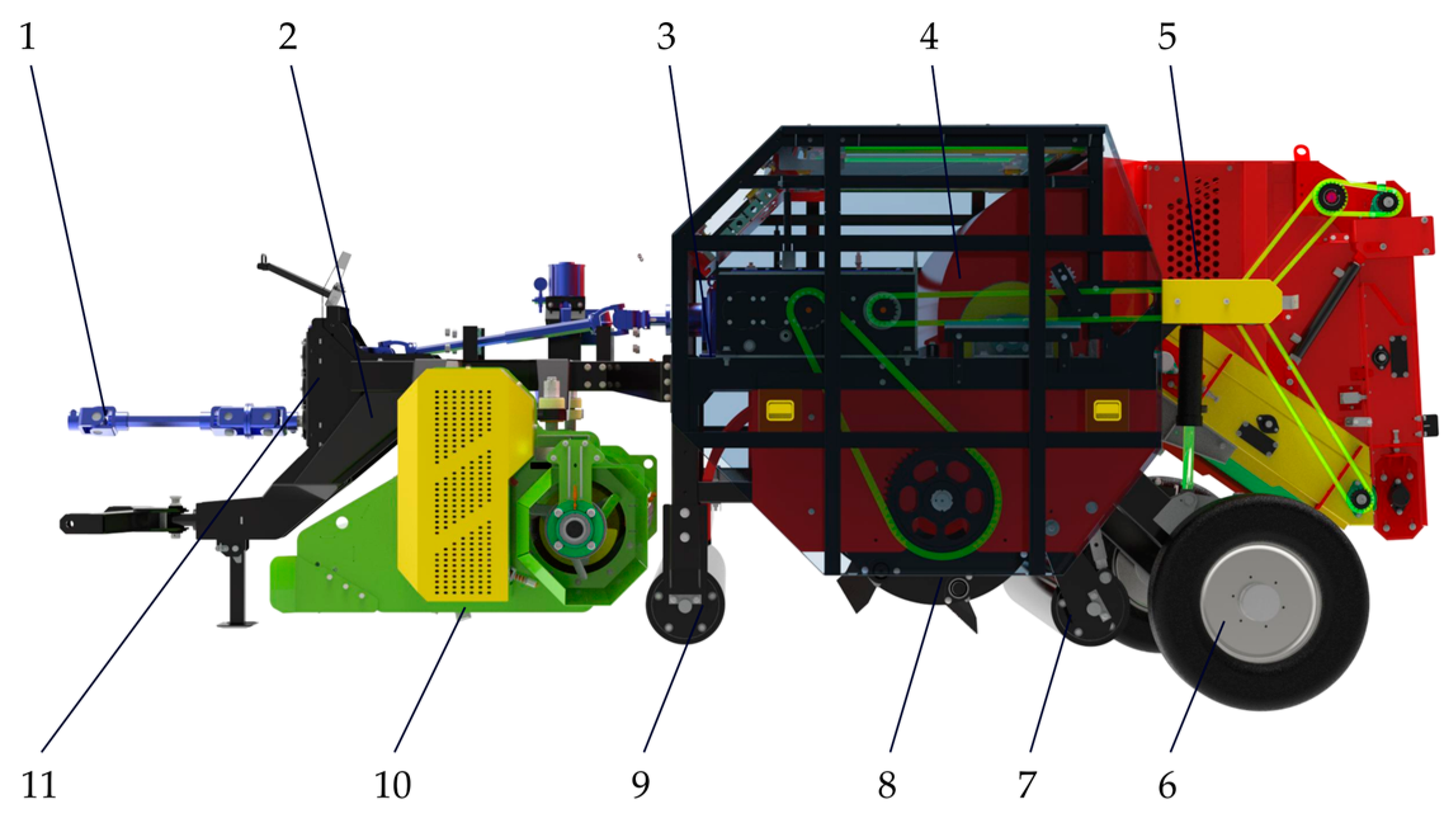
The 1-MSD straw-crushing and residual film recycling machine is shown in Figure 1. The machine is composed of a frame, a straw-crushing and returning device, a film-lifting mechanism, a film-removing mechanism, and a packaging mechanism.

Figure 1. 1-MSD straw-crushing residual film recycling machine. 1. Universal coupling; 2. Frame; 3. Gearbox; 4. Demoulding mechanism; 5. Packing mechanism; 6. Tire; 7. Profile roller; 8. Filming mechanism; 9. Pressing roller; 10. Straw-crushing device; 11. Transfer box.

When the machine works, the tractor pulls the straw-crushing residual film recycling machine along the cotton-planting line. The straw-crushing and returning device cuts the straw and evenly scatters the broken straw into the field. Then, the residual film is picked up by the film-raising mechanism and sent to the film-removal mechanism. Then, the film removal mechanism in the air delivery feeds it to the packaging mechanism. The packaging mechanism continuously accumulates and rubs the residual film, and the diameter of the residual film is transformed from small to large until the film bag is formed. Finally, the hydraulic system opens the packaging warehouse door, and the film bag is discharged into the field, completing the full recovery of straw-crushing residual film.

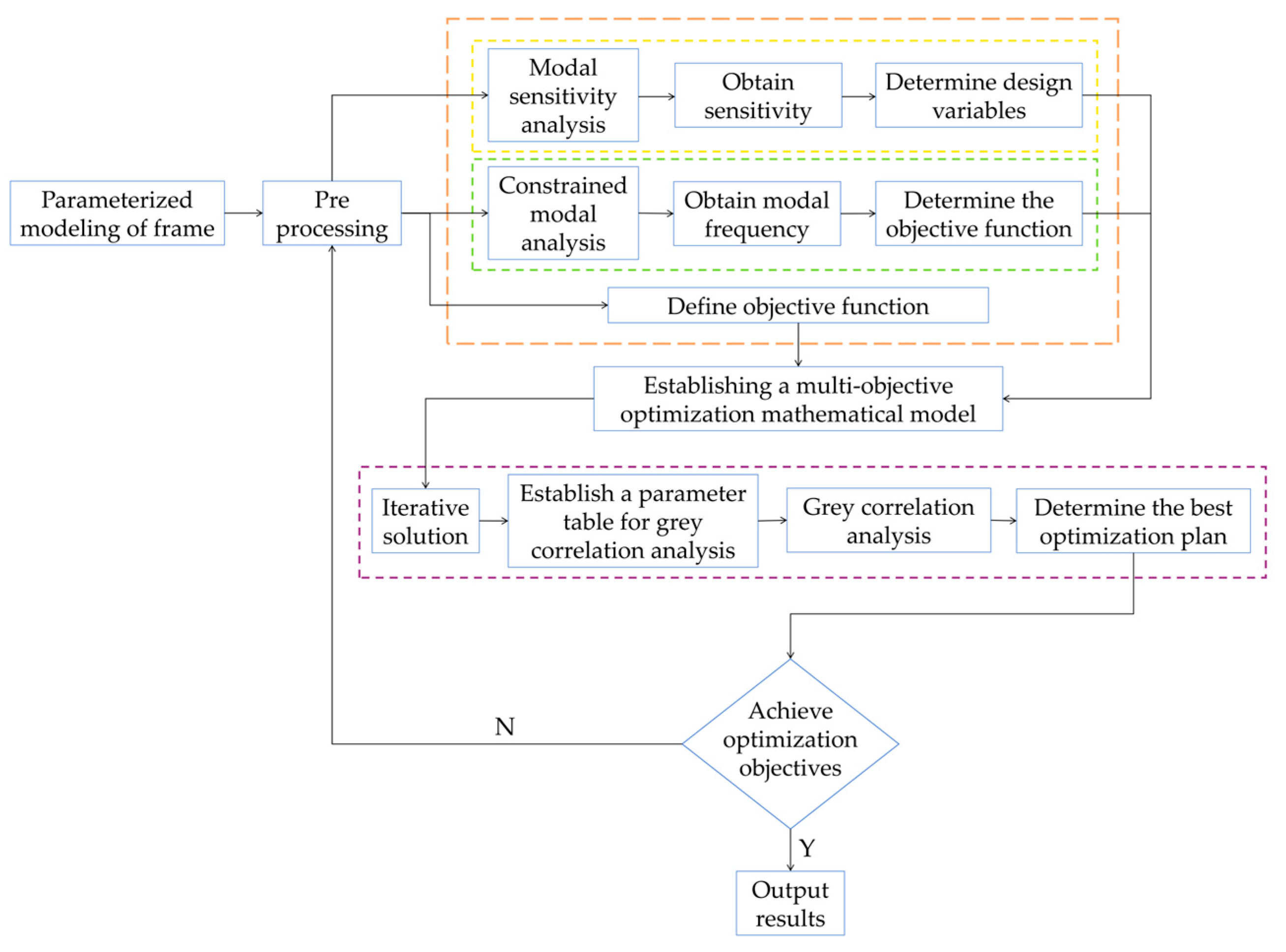
When working in the field, the frame is the main bearing part of the straw-crushing residual film recycling machine, and its bearing capacity is the key factor affecting the quality of straw-returning and residual film recycling. At the same time, the material, size and structure of the frame are important factors affecting its modal [19]. The optimization process of this paper is shown in Figure 2.

Figure 2. Frame Optimization Process.

3. Finite Element Modal Analysis

3.1. Establishment of Finite Element Model

The frame model of the 1-MSD straw-crushing and residual film recycling machine (hereinafter referred to as the frame) was established by using three-dimensional modeling software, and the finite element mesh was divided by Hyper-Mesh 2022 software, as shown in Figure 3.

Figure 3. 1-MSD straw-crushing residual film recycling machine frame. 1. Front joint; 2. Front side plate; 3. Joint arm; 4. Cross beam; 5. Longitudinal beam 1; 6. Rear side plate; 7. Longitudinal beam 2; 8. Longitudinal beam 3; 9. Supporting plate; 10. Lining plate; 11. Beam.

The model is simplified because the accuracy of finite element modeling will directly affect the final analysis results and solution efficiency and cannot affect the final calculation results while shortening the time limit of the software solution. It was simplified by ignoring the impact of welding and the influence of the non-bearing components on the frame and the holes and chamfers with diameters smaller than the mesh size.

Before the division of the frame model, the material of the model is defined as Q235A, the elastic modulus is set to 210 Gpa, the Poisson’s ratio is 0.3, and the mass density is 7850 kg/m³. The multi-zone division method sets the dominant element as the second-order tetrahedral mesh and first-order shell elements. The finite element model of 181,173 elements and 273,507 nodes is obtained (Figure 4).

Figure 4. Frame grid division diagram.

3.2. Finite Element Modal Results

When the external excitation frequency of the machine is close to the natural frequency of the frame, it will produce great deformation and dynamic stress on the frame [20]. Therefore, conducting a modal analysis of the frame is necessary to provide a theoretical basis for the structural optimization of the frame. The modal results should not be disturbed by external factors (noise, wind speed load, etc.) to ensure that the extracted frame modal results have ideal accuracy. Therefore, the modal analysis (finite element method and modal test) for the frame expansion needs to be carried out in the completely free state of the frame without adding any constraints.

In engineering practice, the low-order mode significantly influences the dynamic characteristics of the frame, so it is more important to analyze the low-order vibration mode of the frame for the machine’s operation and the structure’s stability [21]. In this paper, the first six frame modes are solved using the solver Optistruct in Hyper-Mesh 2022, and the modal results are shown in Figure 5.

Figure 5. Vibration mode diagrams of the first six modes of frame. (a) First-order mode shape; (b) Second-order mode shape; (c) Third-order mode shape; (d) Fourth-order mode shape; (e) Fifth-order mode shape; (f) Sixth-order mode shape.

The detailed results of each mode of finite element modal analysis are shown in Table 1. The first six modes are bending and torsion.

Table 1. Finite element analysis modal results.

Mode Order	Frequency/Hz	Mode Shape
1	18.89	First-order torsion along the z-axis
2	20.62	First-order bending forward and backward along the z-axis
3	31.58	Bending-torsion combination
4	33.39	First-order left and right bending along the z-axis
5	34.18	Second-order torsion
6	45.74	Second-order torsion

4. Modal Test Based on PolyMax Method

Verification of the accuracy of the finite element modal analysis method requires a comparison of the modal results of the modal test of the frame to provide theoretical support for the subsequent optimization design of the frame.

4.1. Basic Principle and Mathematical Model of PolyMax Modal Parameter Identification

The modal test is used to obtain accurate modal parameters of the test object through the structural modal parameter identification method. The structural modal parameter identification method can be divided into the frequency, time, and time–frequency domain methods [22,23]. The frequency domain method is used to identify the modal parameters through the frequency response function (FRF) or the structural transfer function. The modal parameter identification is conducted using the time domain method through the actual measurement signal. The time–frequency domain method is used mostly for modal parameter identification of nonlinear and unstable signals. The PolyMax modal parameter identification method can be classified under the frequency domain method. It is a modal parameter identification method that combines the advantages of the least squares complex frequency domain method (LSCF) and the least squares complex exponential method (LSCE) [24]. The discrete time–frequency domain model can avoid the numerical ill-posed problem well, and the obtained modal frequency, modal participation factor, and damping ratio (strong and weak damping applications are ideal) have high accuracy. The results of the steady-state diagram have the advantages of clear and easy extraction.

The dynamic differential equation of the frame is established according to the theory of vibration and described as follows:

$$M\ddot{x}+C\dot{x}+Kx=p$$

(1)

In the formulation, M, C, and K are the mass, damping, and stiffness matrices of the system, respectively. x, ẋ, ẍ, are the displacement, velocity, and acceleration of the system nodes, respectively; and p is the node equivalent load column matrix.

The characteristic equation of Equation (1) is as follows:

$$K+i\omega C-{\omega }^{2}M=0$$

(2)

In the formula, i and ω denote the phase and the characteristic frequency, respectively.

For the modal analysis of the frame, the eigenvalues and corresponding eigenvectors are obtained by solving Equation (2), which corresponds to the natural frequencies and modes of the modal results, respectively. The final analysis object of this paper is the frequency domain signal. The Laplace transform of the system differential Equation (1) is carried out to realize the transformation from the time to the frequency domain, which is described as follows:

$$\begin{array}{c}[M{t}^2+Ct+K]X(t)=F(t)\Rightarrow \\ B(t)X(t)=F(t)\end{array}$$

(3)

The inverse matrix of the system matrix B is solved, and the system displacement frequency response function matrix H is obtained and described as follows:

$$H(t)=B^{-1}(t)=\frac{B^{*}}{\left|B\right|}$$

(4)

where B* and |B| denote the adjoint matrix and determinant of the system matrix B, respectively.

The frequency response function of the ith response vector and the jth reference vector is denoted by H(jω), which is described as follows:

$$H(j\omega )={\displaystyle \sum _{k=1}^m(\frac{B_k}{j\omega -{\lambda }_k}+\frac{B_k^{*}}{j\omega -{\lambda }_k})}$$

(5)

In the formula, m represents the number of dynamic response modes in the analyzed bandwidth of the structure; B_k and $B_K^{*}$ are mutually conjugate matrices, which represent the kth-order modal vector; and λ_k denotes the eigenvalue of order k.

4.2. Modal Test Scheme

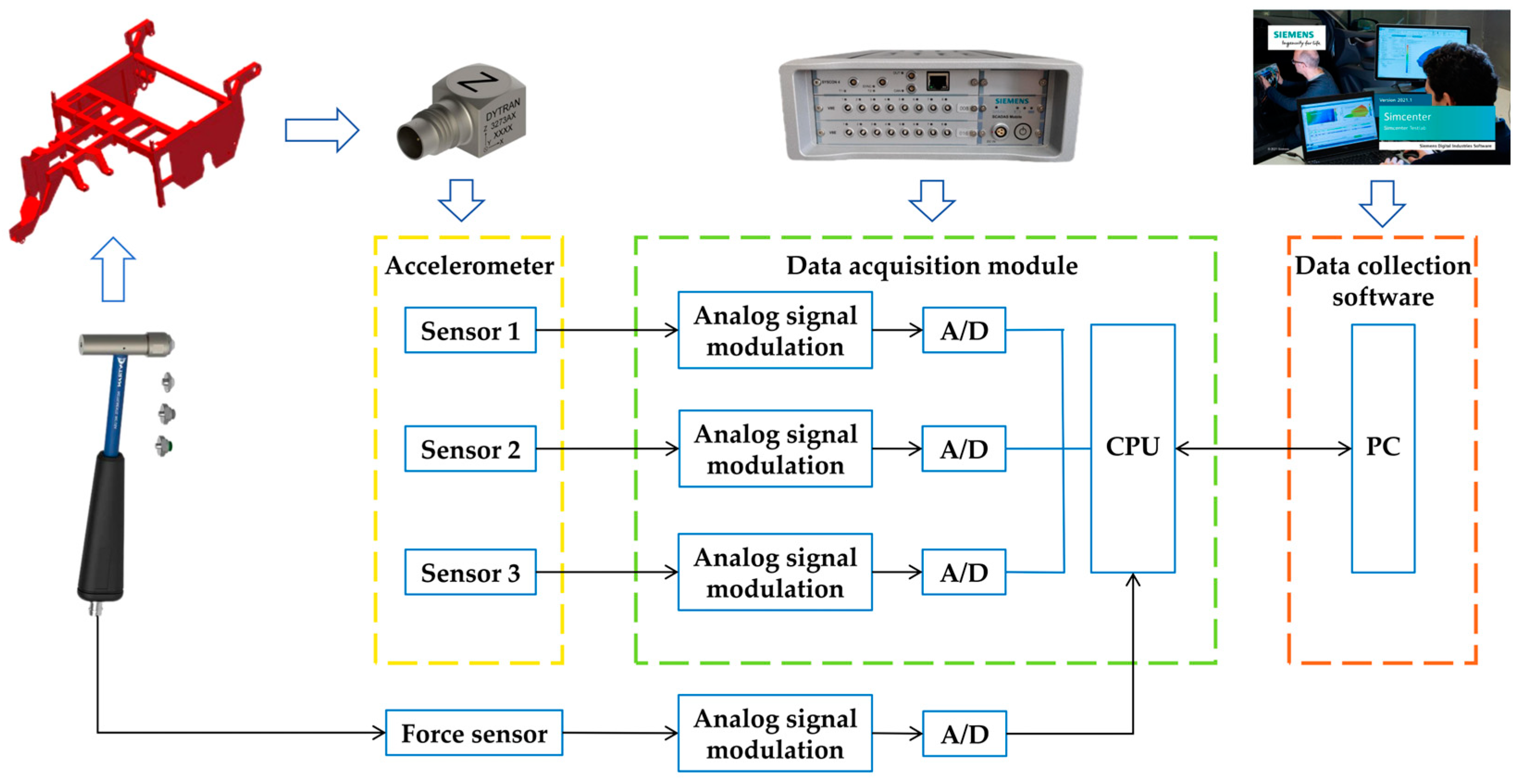
The modal test data acquisition system (Figure 6) in this paper comprises an impact hammer, a three-axis acceleration sensor, a SCADAS data acquisition analyzer, and LMS Test-lab 2021 signal processing and analysis software. The impact hammer is applied to the frame pulse excitation, and the analog signal is fed back to the data acquisition analyzer through the three-axis acceleration sensor. The data acquisition software processes the signal and obtains the frequency response function. The details of the test equipment are shown in Table 2.

Figure 6. Data acquisition system.

Table 2. Modal test equipment.

Equipment Name	Type	Producer	Parameter
Impact hammer	5800B4 (aluminum)	DYTRAN/Chatsworth, CA, USA	10 mV/LbF
Tri-axial accelerometer	3273A4	DYTRAN/Chatsworth, CA, USA	100 mV/g
Data acquisition analyzer	SCADAS (SPM50)	SIEMENS/Munich, Germany	16-channel
Signal Processing Analysis Software	LMS Test Lab	SIEMENS/Munich, Germany	V2021.1

The hammer has three materials: rubber, nylon, and aluminum. After the hammer striking test, the aluminum hammer had the best response effect, and was thus selected for the test.

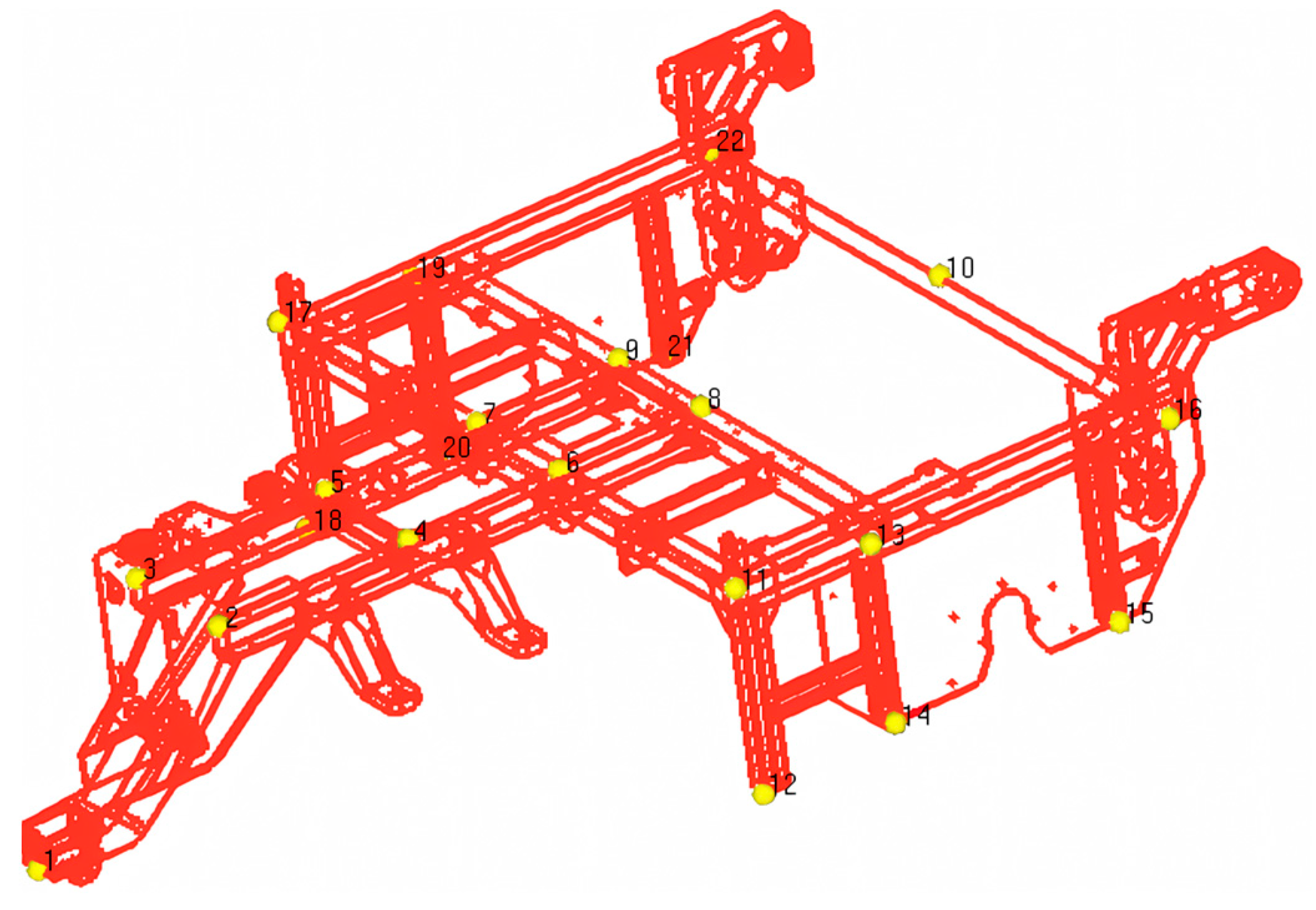
The overall structure of the frame is symmetrical, and the frame is divided into two equal parts along the center line. A total of 22 measuring points are arranged (as shown in Figure 7) to ensure that the measuring points can reflect the shape of the frame structure and ensure that the modal vibration mode of the frame can be fully described. Because the reference point (fixed excitation to place the sensor point) should be able to avoid the node and be easily excited, measuring points 1, 11, and 22 are selected as the reference points. Each reference point is set with a three-axis acceleration sensor, and the remaining points are response points.

Figure 7. Frame modal measuring point model setting.

4.3. Test Steps

(1)

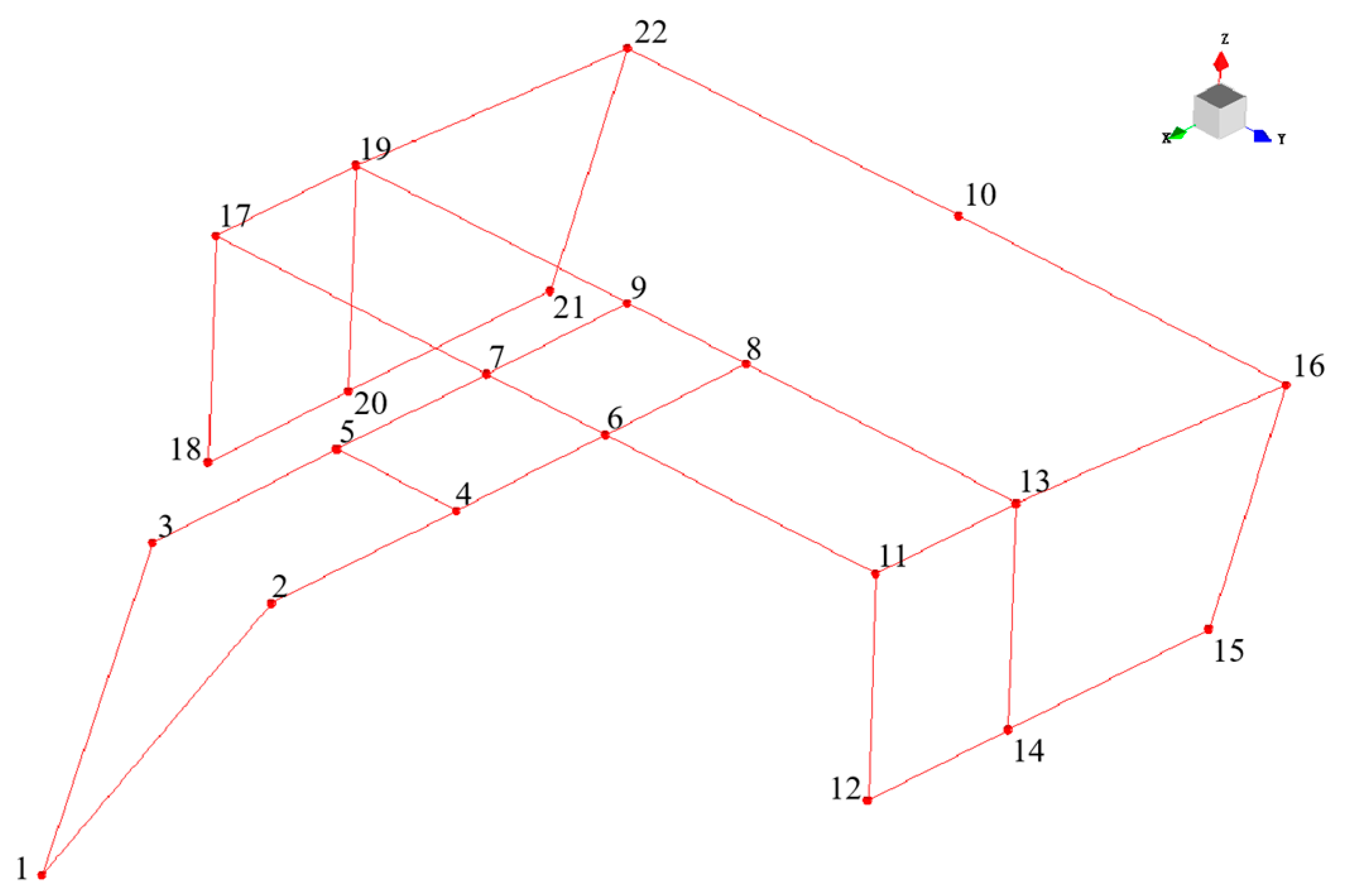
Build a geometric model:

The geometric model of the frame is established in LMS Test-Lab 2021 software based on the layout scheme of the measuring points (Figure 8).

Figure 8. Frame measuring point model.

(2)

Site layout:

The modal test site is arranged, and the frame’s suspension mode and equipment debugging are determined. The modal test was carried out separately in the open hoisting operation area to avoid being affected by other workshop operations (welding, assembly hoisting, etc.) during the test and to ensure that the results have a high signal-to-noise ratio. The gantry crane device is used to lift the frame so that it is in a balanced suspension state (about 20 cm vertical distance from the ground). The horizontal position of the frame is artificially adjusted until the center line of the frame is parallel to the standard operation line of the site. Finally, the data acquisition system is debugged. The specific site layout is shown in Figure 9.

Figure 9. Site layout plan.

(3)

Test process:

The multiple-input multiple-output (MIMO) method [25] was used to test the modal of the frame, and the spectral average method was used to sequentially move the hammer to the X, Y, Z direction of each measuring point five times. The effective excitation ensures that the final FRF function is consistent and that the modal order is complete.

4.4. Analysis of Modal Test Results

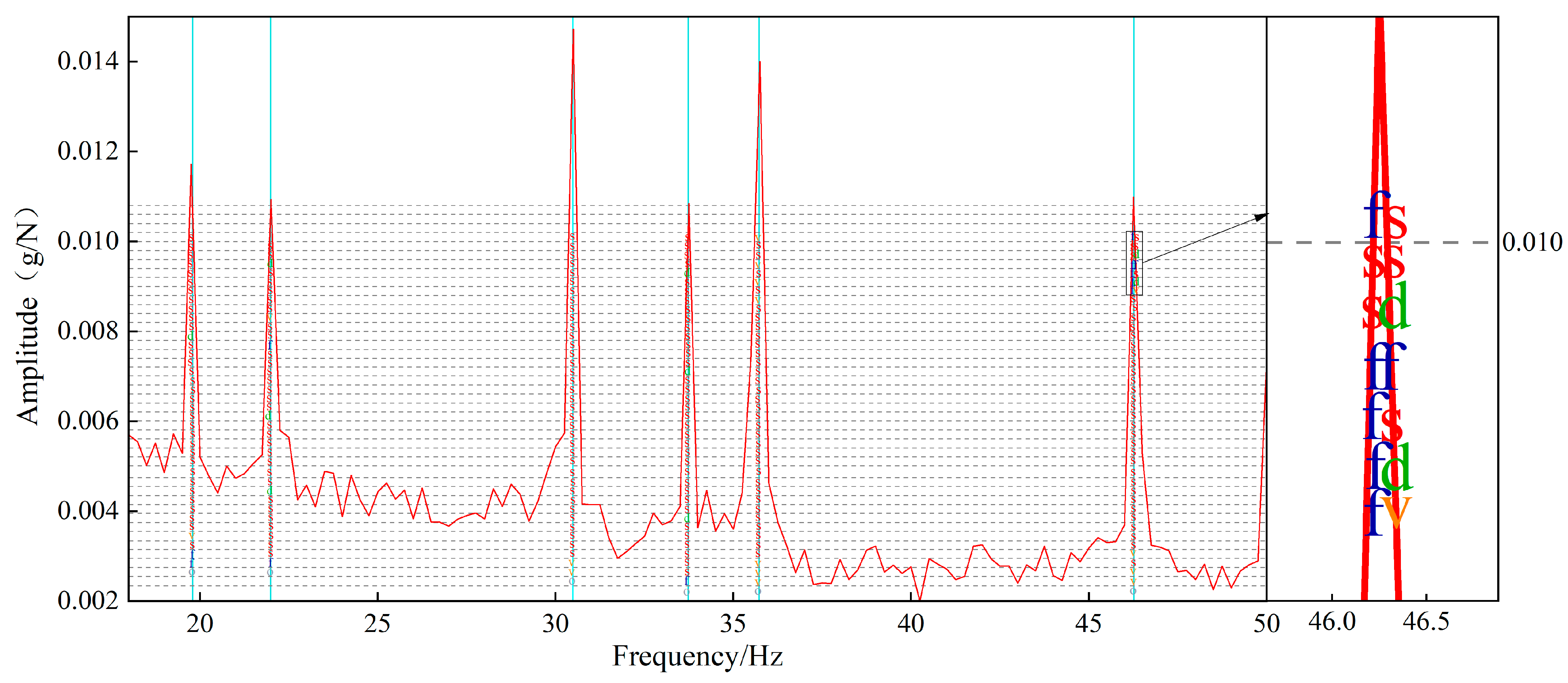
The PolyMax algorithm is used, and 0~200 Hz is selected as the analysis bandwidth to obtain the steady-state diagram (Figure 10).

Figure 10. Stationary result.

In the stabilization interface, the first six peaks are the objects (corresponding to the first six order test modes of the frame). The best pole is selected in the continuous s points near it (the meaning of the pole symbol is shown in Table 3); the more continuous s points, the higher the degree of modal stability extracted near them, and the more realistic the modal parameters obtained. Finally, the first six order modal test parameters of the frame are obtained, as shown in Table 4.

Table 3. Symbolic diagram of modal pole.

Pole	State
o	Pole instability
f	Pole frequency is stable within allowable tolerances
d	Pole damping and frequency stability within allowable tolerances
v	Pole vectors are stable within allowable tolerances
s	Pole frequency, damping, and vector are stable within allowable tolerances

Table 4. Modal test results.

Order	Frequency/Hz	Mode Shape	Damping Ratio/%
1	19.77	First order torsion along the z-axis	0.04
2	21.98	First-order bending forward and backward along the z-axis	0.05
3	30.45	Bending-torsion combination	0.02
4	33.69	First-order left and right bending along the z-axis	0.07
5	35.68	Second-order torsion	0.03
6	46.31	Second-order torsion	0.05

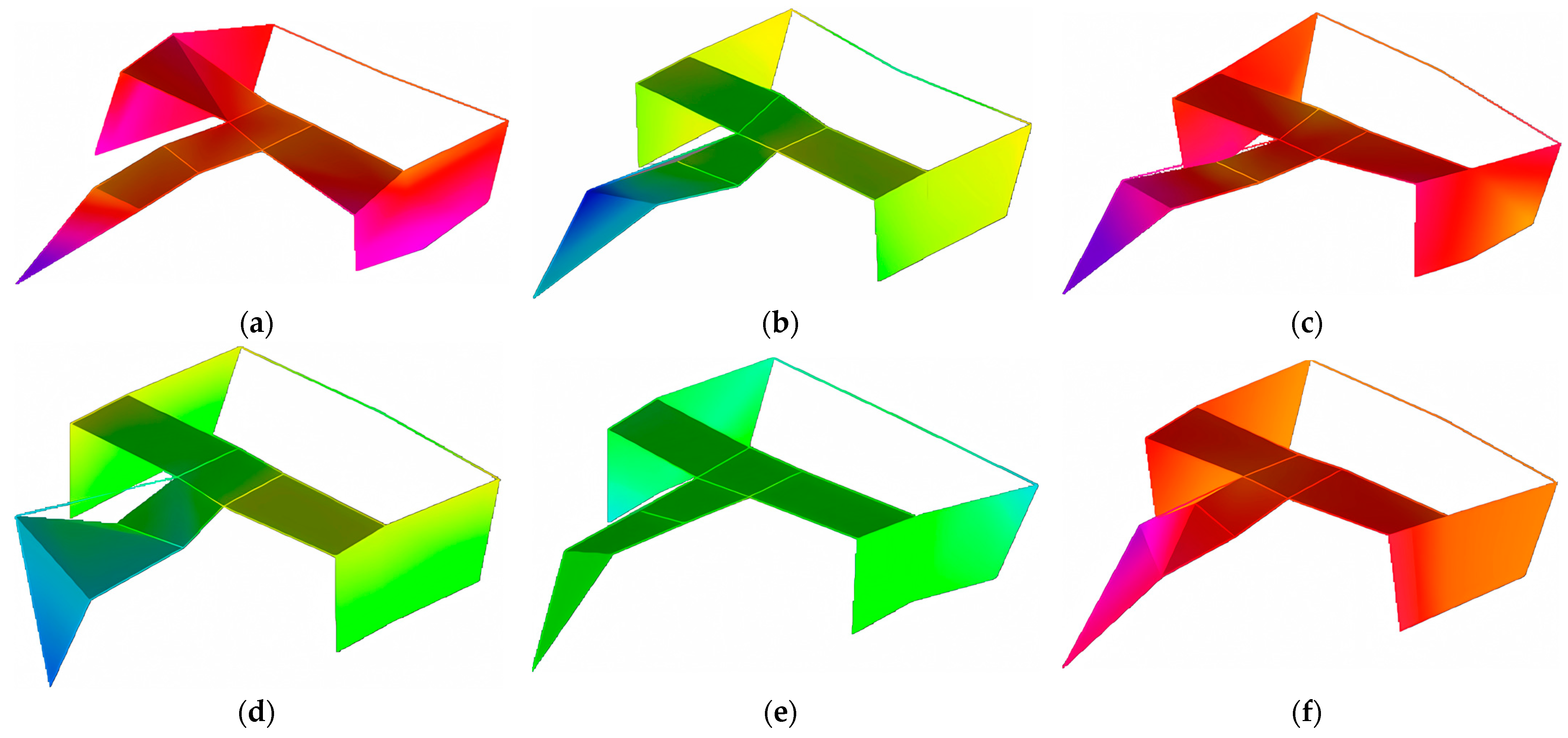
The table shows that the modal frequency of the frame is concentrated in the low-frequency band of 19.77–46.31 Hz, and the first six order modal shapes (as shown in Figure 11) are consistent with the finite element modal analysis results.

Figure 11. Experimental modal vibration mode. (a) First-order mode shape; (b) Second-order mode shape; (c) Third-order mode shape; (d) Fourth-order mode shape; (e) Fifth-order mode shape; (f) Sixth-order mode shape.

Using modal confidence and frequency response confidence analysis, this paper verifies the rationality of modal tests to ensure that the results of modal test parameters are desirable.

4.5. Modal Confidence Analysis

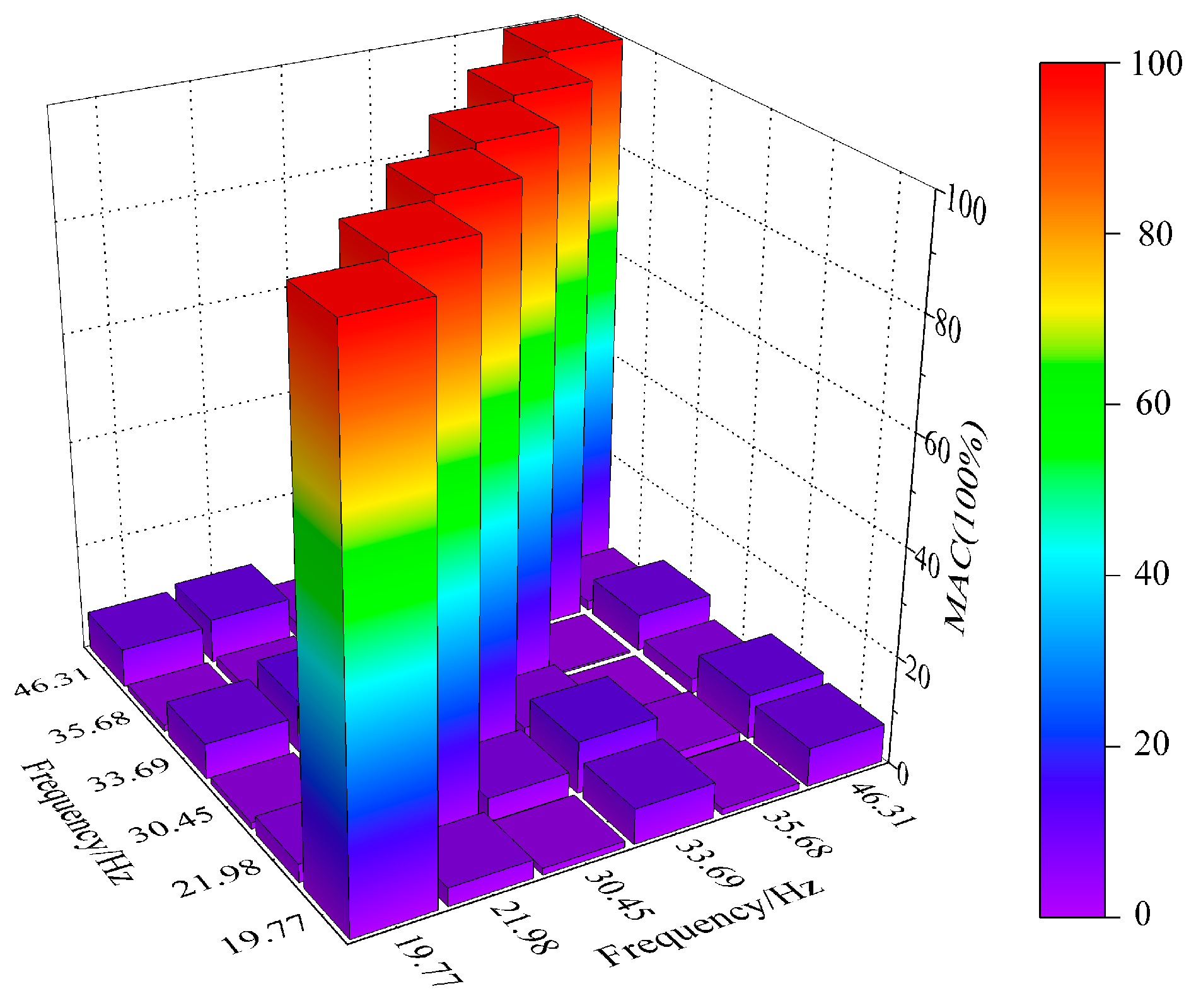
The MAC confidence criterion [26] is used to verify the correlation of the modal results of each order, and the results are shown in Figure 12. The MAC confidence criterion compares two modal shape vectors with any scale. The MAC value should be close to 100% under the same order mode, and the MAC value should be 0 under different order modes. The MAC confidence criterion matrix is expressed as follows:

$${\mathrm{MAC}}_{ij}=\frac{{({\Phi }_i^T{\Phi }_j)}^2}{({\Phi }_i^T{\Phi }_j)({\Phi }_j^T{\Phi }_j)}$$

(6)

Figure 12. Modal test MAC matrix.

In the formula, Φ_i and Φ_j are the ith row and jth column modal vectors in the MAC matrix, respectively. The elements in the MAC matrix reflect the dot product between the vectors of the current modal shape; that is, when the intersection angle of the modal shape vector is 90°, the corresponding MAC value is 0; that is, the correlation between the two is small. Meanwhile, when the modal shape vector intersection angle is 0°, the corresponding MAC value is 1; that is, the correlation between the two is large.

Figure 12 shows that the height of each element of the diagonal corresponds to the MAC value of the same order, which is 100%. The height of the other elements corresponds to the MAC values of different orders, which are close to 0, indicating the absence of a false mode, and the modal confidence is ideal.

4.6. Confidence Analysis of Frequency Response

To further verify the rationality of the extracted modal test parameters, this paper evaluates the frequency response confidence by investigating the correlation and error between the measured FRF and the fitted FRF as a reference. Specifically, the FRF of the interaction between the input and the output measurement points is obtained by solving the Maxwell–Betti reciprocity theorem [27] to ensure that the FRF fitted in multiple ways corresponds to at least one input degree of freedom with a scale modal shape (including modal shape coefficient).

Using the frequency response function fitting criterion:

$$H_{j\omega }={\displaystyle \sum _{r=1}^N(\frac{Q_r{\{\Psi \}}_r{\left\{L\right\}}_r}{j\omega -{\lambda }_r}+\frac{Q_r^{*}{\{\Psi \}}_r^{*}{\left\{L\right\}}_r^{*}}{j\omega -{\lambda }_r^{*}})}+[UR]-\frac{[LR]}{{\omega }^2}$$

(7)

In the formula, H_ij is the frequency response function matrix of i rows and j columns; ψ_r is the rth mode shape; L_r is the modal vector; λ_r is the modal pole; and UR and LR are upper and lower residuals, respectively.

The complex conjugate product of measured FRF and fitted FRF is normalized:

$$Correlation=\frac{{\left|{\displaystyle \sum _i{S}_i\times M_i^{*}}\right|}^2}{\left({\displaystyle \sum _i{S}_i\times S_i^{*}}\right)\left({\displaystyle \sum _i{M}_i\times M_i^{*}}\right)}$$

(8)

In the formula, S_i and M_i represent the complex values of the fitted FRF and the measured FRF at the spectral line i, respectively, and * represents the conjugate.

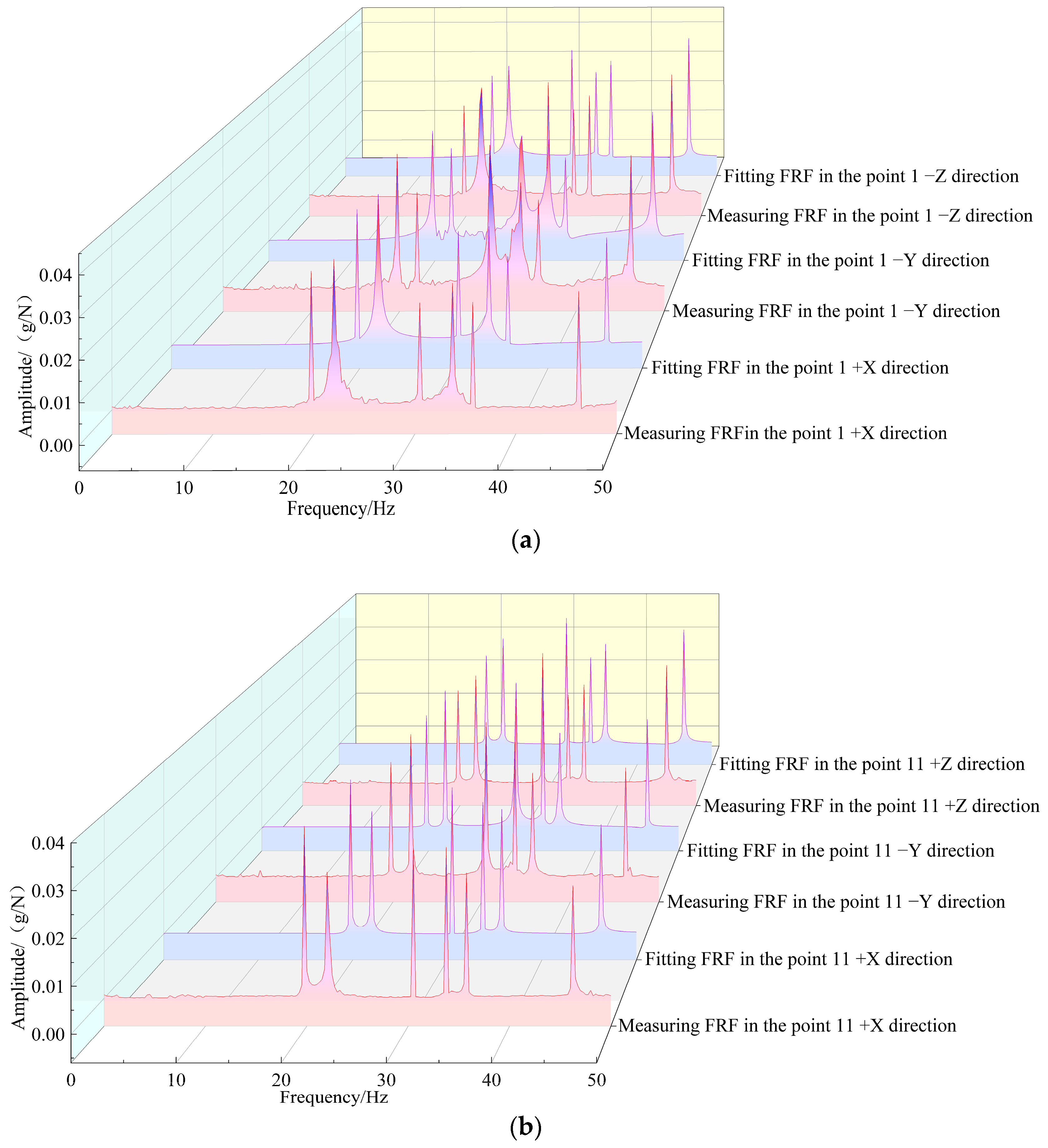
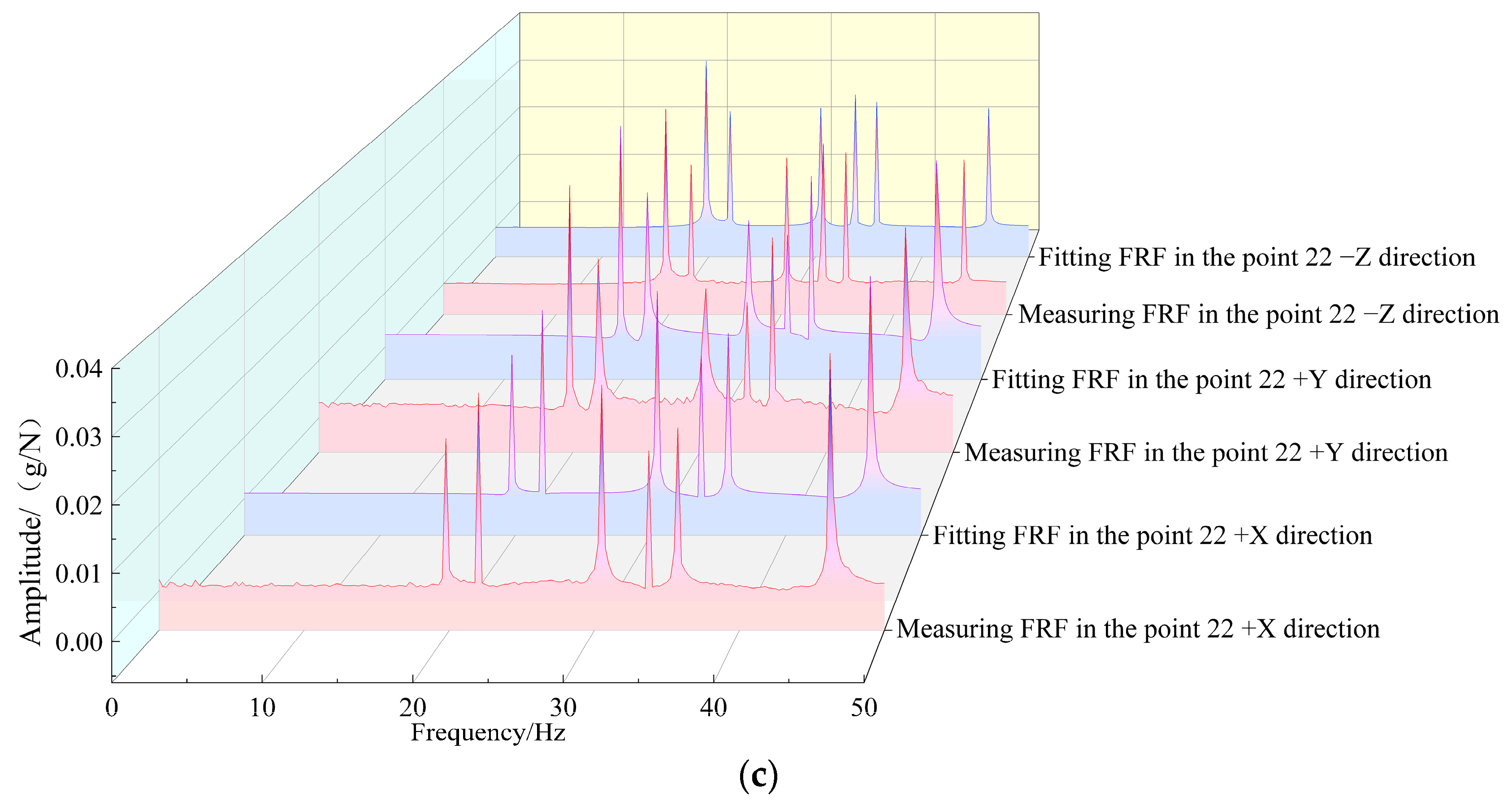
Due to the limited space, only the FRF curves of measuring point 2 (−X, −Y, and −Z directions) and the reference point (points 1, 11, and 22) are compared and verified. The comparison frequency band of the FRF curve is 0~60 Hz. The comparison results of the FRF curve are obtained in modal synthesis (Figure 13).

Figure 13. Frequency response confidence reference. (a) Comparison of point 2−X direction and point 1FRF results; (b) Comparison of point 2−Y direction and point 11FRF results; (c) Comparison of point 2−Z direction and point 22 FRF results.

Figure 13 shows that the trend between the three-way measurement FRF curve of the reference point (points 1, 11, and 22) and the fitted FRF curve is relatively close. The difference of the corresponding amplitude (g/N) at the same frequency (Hz) is small, reflecting that the FRF curve between the measuring point 2 and the reference point has a high correlation and a small error; that is, the frequency response confidence is high.

In summary, from the perspective of modal confidence and frequency response confidence results, the extraction of frame modal test parameters is proven to be effective, and the reliability of test results is high.

4.7. Results Comparison and External Incentive Analysis

The results of the finite element analysis and modal test are compared and analyzed, and the results of the comparison are shown in Figure 14. The figure shows that the frame’s finite element modal analysis results are in good agreement with the modal test results. The maximum relative error of each order’s natural frequency is 6.61%, and the reliability of the finite element modal analysis results is high.

Figure 14. Natural frequency comparison.

The external excitation source (as shown in Table 5) of the straw-crushing residual film recycling machine comes from the vibrations caused by the tractor traction, the work, and the undulation of the field terrain. The power input of the whole machine is provided by a John Deere 1404-A 6-cylinder 4-stroke tractor (rated power is 103 kW), and the external excitation provided by it is:

$$f_T=\frac{2n_{t}z}{60\tau }$$

(9)

Table 5. External excitation frequency.

Vibration Source	Working Rotation Speed/r/min	Excitation Frequency
Tractor	2600	130.00
Field	/	2.96~3.70
Rotary tool axis	3054	50.90
Twist cage	1641	27.35
Filming drum	93	1.55
Stripping roller	1000	16.67

In the formula, f_T is the engine frequency, Hz; n_t is the working speed, r/min; z is the number of engine cylinders; and τ is the number of engine strokes.

The straw-crushing residual film recycling machine operates at a speed of 8~10 m/s in the field, and the external incentives it provides are:

$$f_r=v{n}_r$$

(10)

In the formula, f_r is the path spectrum frequency, Hz; v is the forward speed of the machine, m/s; and n_r is the spatial frequency, Hz.

When the straw-crushing residual film recycling machine operates, the external excitation of the frame by each rotating part is:

$$f_w=\frac{n_w}{60}$$

(11)

In the formula, f_w is the rotation frequency, Hz, and n_w is the working rotation speed.

The modal analysis results show the excitation frequency generated by the stripping roller is close to the first-order natural frequency of the frame. The frame is optimized to avoid the resonance phenomenon of the machine during operation, shorten its service life, and ensure that it meets stiffness and strength requirements. Finally, the machine avoids the external excitation frequency and ensures that the volume of the frame is not too large. Considering that the relative installation positions of the working parts of the 1-MSD straw-crushing and residual film recycling machine have been determined, the cost of changing the overall structure of the frame is too large, and thus, the method of changing the thickness of each part of the frame is used to optimize.

5. Sensitivity and Grey Correlation Analysis

In this paper, the optimization results of the frame are obtained through a joint analysis of sensitivity and grey correlation degree. Specifically, the sensitivity analysis method is used to obtain the sensitivity of each frame component to the first-order natural frequency. At the same time, a multi-objective optimization mathematical model is established, and the Optistruct solver is used to solve it. Finally, a grey correlation evaluation table is constructed, and the optimal results are solved.

5.1. Sensitivity Analysis

Sensitivity analysis is used to explore the degree of influence of changes in structural parameters on mechanical properties [28,29]. In this paper, the sensitivity can be described as the change rate of the natural frequency of the frame caused by the different thicknesses of each part of the frame. The change rate is positive or negative, and the two are positively or negatively correlated. Because the frame is a steel structure, its structural damping is small. It is simplified to a non-damping multi-degree-of-freedom system [30]. The specific dynamic equation is as follows:

$$[m]\left\{\ddot{X}\right\}+[K]\left\{X\right\}=0$$

(12)

where [m] is the mass matrix of the n-order system; [K] is the stiffness matrix of the n-order system; {Ẍ} is an array, indicating acceleration; and {X} is the array, which represents the displacement.

Its characteristic equation is:

$$\left(\left[K\right]-{\omega }_i^2[m]\right)\left\{X_i\right\}=0$$

(13)

where ω_i is the natural frequency of the system and {X_i} is the modal shape vector.

The sensitivity of the natural frequency ω_i of the system to thickness d is calculated by the direct derivative method; that is, the partial derivative of d in the equation is obtained by multiplying {X_i}^T on both sides of the equation.

$${\left\{X_i\right\}}^{\mathrm{T}}([K]-{\omega }_i^2[m])\frac{\partial \left\{X_i\right\}}{\partial d}+{\left\{X_i\right\}}^{\mathrm{T}}(\frac{\partial [K]}{\partial d}-{\omega }_i\frac{\partial [m]}{\partial d}-\frac{\partial {\omega }_i}{\partial d}[m])\left\{X_i\right\}=0$$

(14)

In the formula, d is the thickness of the frame parts, mm.

Derivation of the formula, that is, the derivative sensitivity of the modal frequency, is the following:

$$S=\frac{\partial {\omega }_i}{\partial d}=\frac{{\left\{X_i\right\}}^{\mathrm{T}}(\frac{\partial [K]}{\partial d}-{\omega }_i\frac{\partial [m]}{\partial d})\left\{X_i\right\}}{{\left\{X_i\right\}}^{\mathrm{T}}[m]\left\{X_i\right\}}$$

(15)

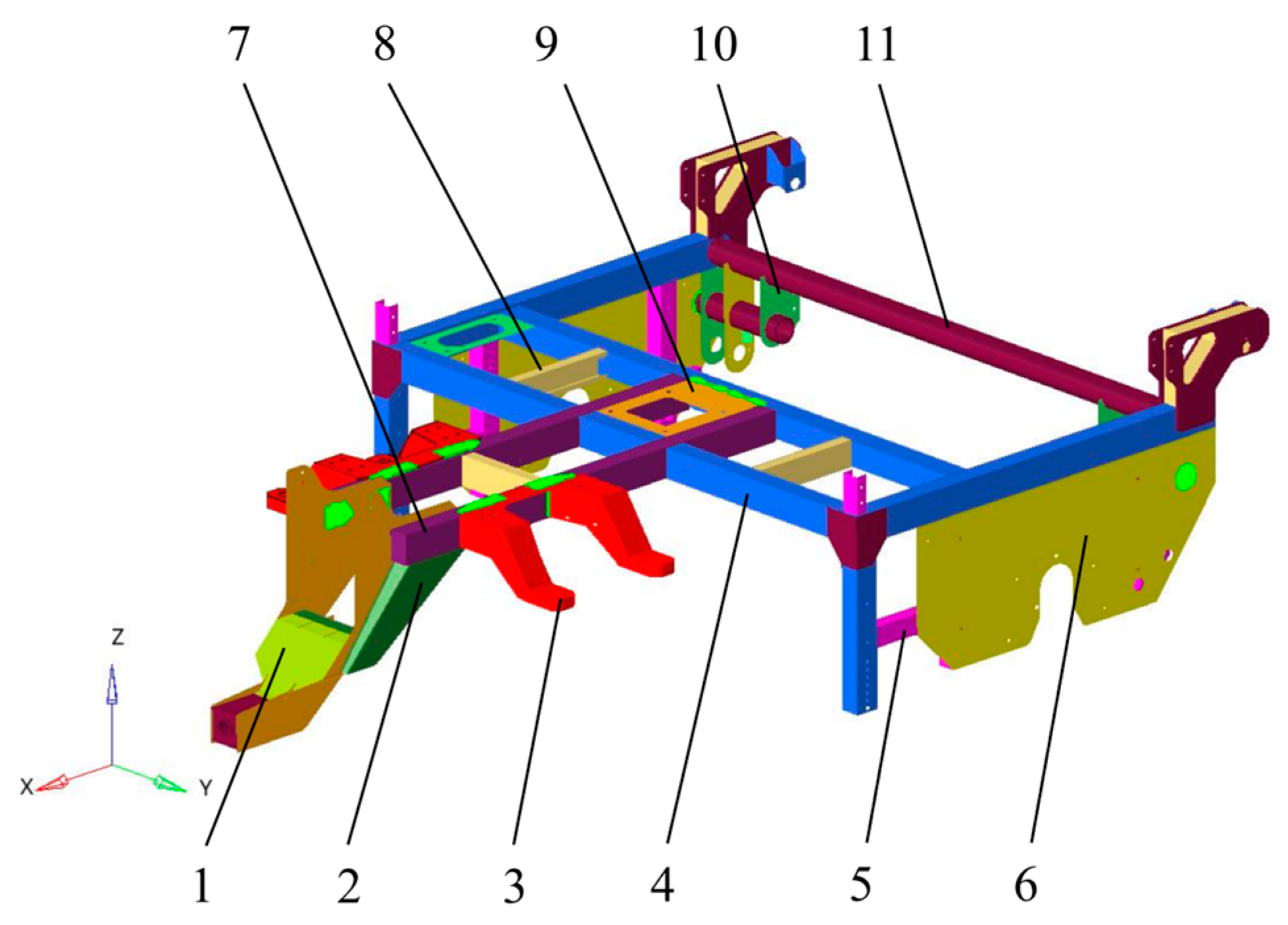
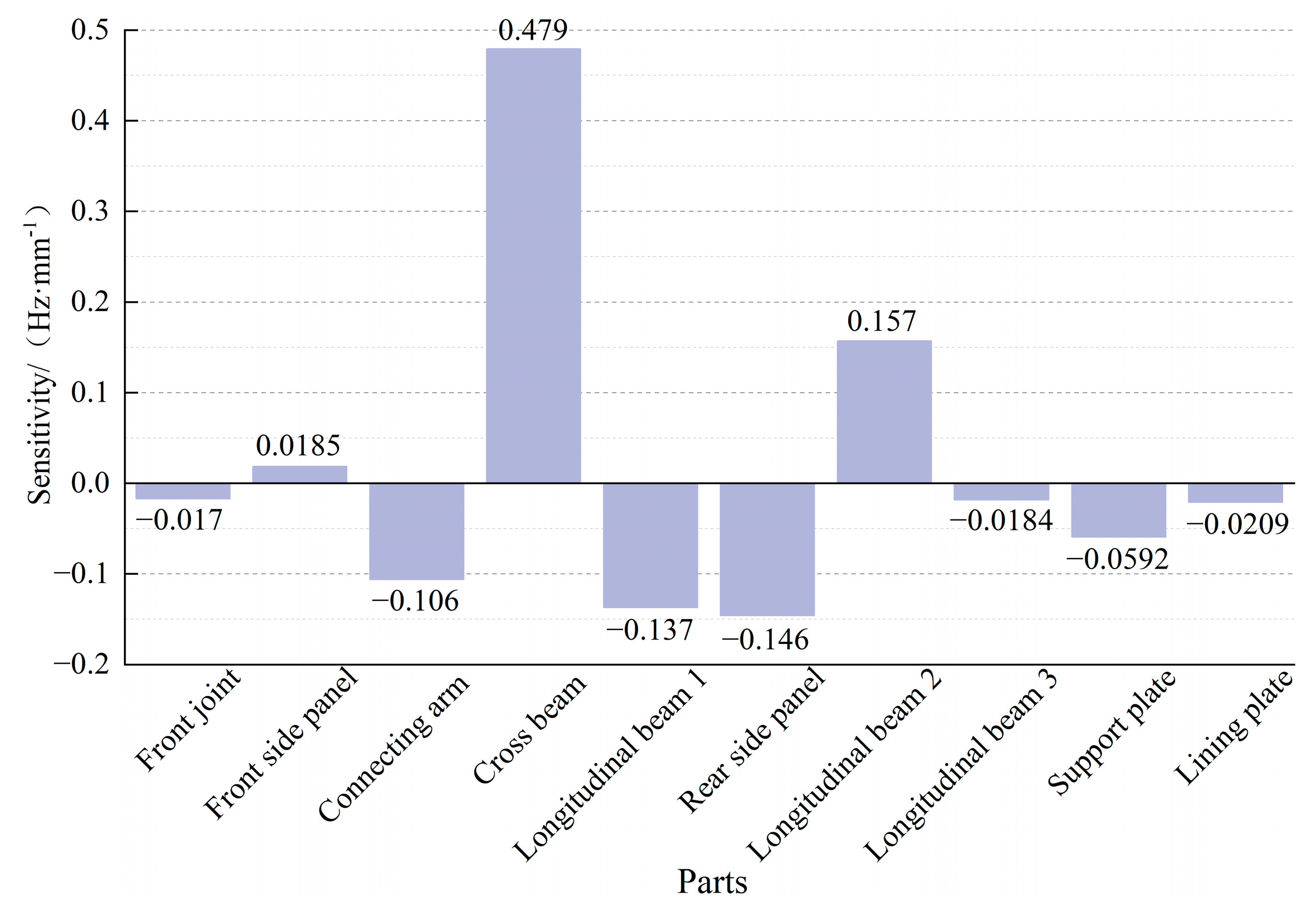
The sensitivity analysis of the 10 components of the frame is conducted according to the requirements of the operation stability of the straw-crushing residual film recycling machine and the results of the modal analysis. The thickness of the frame components is taken as the design variable, and the volume of the frame structure is taken as the optimization target. The lower limit of the first-order modal frequency optimization result is added to calculate the sensitivity of the first-order modal frequency of the frame relative to the thickness of each component. The results are shown in Figure 15.

Figure 15. Sensitivity of the thickness of each component of the frame to the first-order modal frequency.

The sensitivity analysis result shows that the sensitivity of cross beam and longitudinal beam 2 to the first-order modal frequency of the frame is positive; that is, increasing the thickness of the component will increase the first-order modal frequency. The sensitivity of the remaining components to the first-order modal frequency of the frame is negative; that is, reducing the thickness of the component will increase the first-order modal frequency. The thicknesses of the higher-sensitivity parts of the frame are selected as the design variable; in this paper, the parts with the sensitivity result order of magnitude above × 10⁻² are retained for exploration. Finally, the main optimization parts are the connecting arm, cross beam, longitudinal beam 1, rear side panel, and longitudinal beam 2.

5.2. Optimization Modeling and Solving

The first-order natural frequency of the hoist frame should also be as small as possible to meet the requirements of lightweight design of modern agricultural machinery [31]. Therefore, the first-order natural frequency and volume of the frame are taken as the optimization objectives. According to the sensitivity analysis results, the thickness of each frame component is taken as the design variable, and the initial value and limit range of the thickness of each component and the first-order natural frequency are set in Table 6.

Table 6. The thickness of each component of the frame and its first-order natural frequency setting and range of variation.

Variable	x1/mm	x2/mm	x3/mm	x4/mm	x5/mm	Frequency/Hz
Initial value	6	6	12	6	8	18.89
Lower limit	3.5	3.5	9.5	3.5	5.5	22
Upper limit	10.5	10.5	16.5	10.5	12.5	/

Seven design variables are defined in X = (x₁, x₂, x₃, x₄, x₅). The optimization objective function is the volume of the frame, and the optimization response is the first-order natural frequency of the frame. The mathematical model of the optimal design of the frame structure is obtained:

$$\left\{\begin{array}{l}\min F_v(X)=F(x_1,x_2,x_3,x_4,x_5)\\ F_f(X)=F(x_1,x_2,x_3,x_4,x_5)\ge 22\\ \mathrm{s}.\mathrm{t}.\left\{\begin{array}{l}3.5\mathrm{mm}\le x_1\le 10.5\mathrm{mm}\\ 3.5\mathrm{mm}\le x_2\le 10.5\mathrm{mm}\\ 9.5\mathrm{mm}\le x_3\le 16.5\mathrm{mm}\\ 3.5\mathrm{mm}\le x_4\le 10.5\mathrm{mm}\\ 5.5\mathrm{mm}\le x_5\le 12.5\mathrm{mm}\end{array}\right.\end{array}\right.$$

(16)

where x₁ is the connecting arm, mm; x₂ is the cross beam, mm; x₃ is the longitudinal beam 1, mm; x₄ is the back plate, mm; x₅ is the longitudinal beam 2, mm; F_v(X) is the function of the design variable to the volume of the frame; and F_f(X) is the function of design variables to the first-order natural frequency of the frame.

Six groups of non-inferior solutions in the range of (22 ± 0.2) Hz are obtained by iterative calculation using the Optistruct solver (the specific operation process is shown in Figure 16), as shown in matrix R.

$$R=\left[\begin{array}{cccccccc}& K_0& K_1& K_2& K_3& K_4& K_5& K_6\\ C_0:x_0& 6& 5.263& 5.043& 5.040& 5.022& 5.141& 5.342\\ C_1:x_1& 6& 7.451& 7.425& 7.401& 7.532& 7.246& 7.288\\ C_2:x_2& 6& 4.754& 4.843& 4.725& 4.951& 4.660& 4.812\\ C_3:x_3& 12& 10.861& 10.802& 10.924& 10.750& 10.847& 10.912\\ C_4:x_4& 8& 9.461& 9.383& 9.417& 9.421& 9.375& 9.236\\ C_5:x_5& 18.89& 21.92& 21.98& 22.01& 21.89& 21.85& 21.88\\ C_6:x_6& 10.010& 9.998& 9.974& 9.975& 9.743& 9.922& 9.931\end{array}\right]$$

(17)

Figure 16. The specific operation process.

In the formula, K₀ is the initial value column, and K₁~K₆ are six groups of non-inferior solutions.

5.3. Grey Correlation Analysis Method

For the modal evaluation of the frame, the evaluation method should be used to obtain the best design scheme. The purpose is to avoid the incompatibility of the single-index evaluation results in the multi-index decision-making process.

As an important part of grey system theory, grey relational analysis is a method to solve system problems based on fuzzy information [32,33,34]. In this paper, by comparing the grey correlation degree of the optimized multi-group rack design scheme, the primary and secondary relationships between the optimization of the theoretical optimal schemes can be determined. Then, the optimal optimization scheme can be obtained. The steps of grey correlation analysis are as follows:

(1)

Determine the design variables, reference sequence, and comparison sequence.

$$X_0(k)=\{x_0^1,x_0^2,\dots ,x_0^p\},k=1,2,\dots ,p$$

(18)

$$X_i(k)=\{x_i^1,x_i^2,\dots ,x_i^q\},k=1,2,\dots ,q$$

(19)

where X₀(k) is the reference sequence; X_i(k) is the comparison sequence; and p and q represent the dimension of the sequence.

(2)

Reduce the amount of steel treatment.

Because of the different dimensions of the thickness, frequency, and volume of the components in the system, to ensure the accuracy of the calculation results, the analysis data should be removed and tempered before the calculation. The standardization method is adopted in this paper.

$$f(x_k)=\frac{x_k}{x_1},x_1\ne 0$$

(20)

In the formula, any data in each row are divided by the first data in the row.

(3)

Calculate the grey correlation coefficient.

The normalized reference number {X₀(t)} (where t is time) and the comparison number {X_i(t)} are recorded. When t = k, the grey correlation coefficient ξ_i(k) of the system sequence is as follows:

$${\xi }_i(k)=\left|\frac{{\Delta }_{\min }+\rho {\Delta }_{\max }}{{\Delta }_i(k)+\rho {\Delta }_{\max }}\right|$$

(21)

In the formula, Δ_i is the absolute difference between the two series at k time; Δ_min and Δ_max are the minimum difference between the two stages and the maximum difference between the two stages, respectively; and ρ is the resolution coefficient, usually taken as 0.5.

(4)

Calculate grey correlation degree.

$${\gamma }_i=\frac{1}{m}{\displaystyle \sum _{k=1}^m{\xi }_i(k)}$$

(22)

In the formula, γ_i is the grey correlation degree between the evaluation object X_i(k) and X₀(k).

5.4. Optimization Target Grey Correlation Analysis

The six sets of non-inferior solutions obtained by the Optistruct solver constitute M₁~M₆ (comparison sequence). This paper aims to improve the first-order modal frequency of the frame according to the sensitivity analysis results (Figure 15). The minimum value of the connecting arm (x₁), the maximum value of the cross beam (x₂), the minimum value of the longitudinal beam 1 (x₃), the maximum value of the longitudinal beam 2 (x₄), and the minimum value of the rear side plate (x₅) corresponding to M₁~M₆ are selected as the design variables of the reference sequence (M₀). The optimal target frequency is set at 22 Hz, and the volume in the scheme M₄ is selected as the optimal target volume. The above data constitute the reference sequence M₀ and finally form the grey correlation analysis parameter evaluation table, as shown in Table 7.

Table 7. Grey correlation analysis parameter evaluation.

Scheme Number		Reference Sequence/M0	Comparison Sequence
			M1	M2	M3	M4	M5	M6
Design variable	x1/mm	5.040	5.263	5.043	5.040	5.022	5.141	5.342
	x2/mm	7.532	7.451	7.425	7.401	7.532	7.246	7.288
	x3/mm	4.660	4.754	4.843	4.725	4.951	4.660	4.812
	x4/mm	10.750	10.861	10.802	10.924	10.750	10.847	10.912
	x5/mm	9.461	9.461	9.383	9.417	9.421	9.375	9.236
Optimization objectives	Frequency/Hz	22	21.92	21.98	22.01	21.89	21.85	21.88
	Volume/107 mm3	9.743	9.998	9.974	9.975	9.743	9.922	9.931

Through the analysis and processing of the table data through Formulas (6)~(8), the grey correlation degree between M₁~M₆ (comparison sequence), and reference sequence (M₀) is obtained, as shown in Figure 17. The figure shows that the order of the optimal design schemes of the frame is M₄, M₃, M₂, M₅, M₁, M₆, and M₄ is the optimal design scheme.

Figure 17. Grey correlation degree.

The M₄ parameters of the scheme are taken as the optimization results, and the comparison of the frame parameters before and after optimization is shown in Table 8. The table shows that under the condition of meeting the goal of improving the modal frequency of the frame and meeting the lightweight design of the frame, the thickness of the connecting arm (x₁) is 5.022 mm, the thickness of the cross beam (x₂) is 7.532 mm, the thickness of the longitudinal beam 1 (x₃) is 4.951 mm, and the thickness of the longitudinal beam 2 (x₄) is 10.750 mm. The thickness of the rear side plate (x₅) is 9.421 mm. The first-order modal frequency of the frame is increased by 15.88% to 21.89 Hz, which is much higher than the excitation frequency of 16.67 Hz, which can avoid resonance. The volume decreased by 3.46% to 9.743 × 10⁷ mm³.

Table 8. Comparison of parameters before and after optimization.

Scheme	x1/mm	x2/mm	x3/mm	x4/mm	x5/mm	Frequency/Hz	Volume/107 mm3
Before optimization	6	6	6	12	8	18.89	10.092
After optimization	5.022	7.532	4.951	10.750	9.421	21.89	9.743

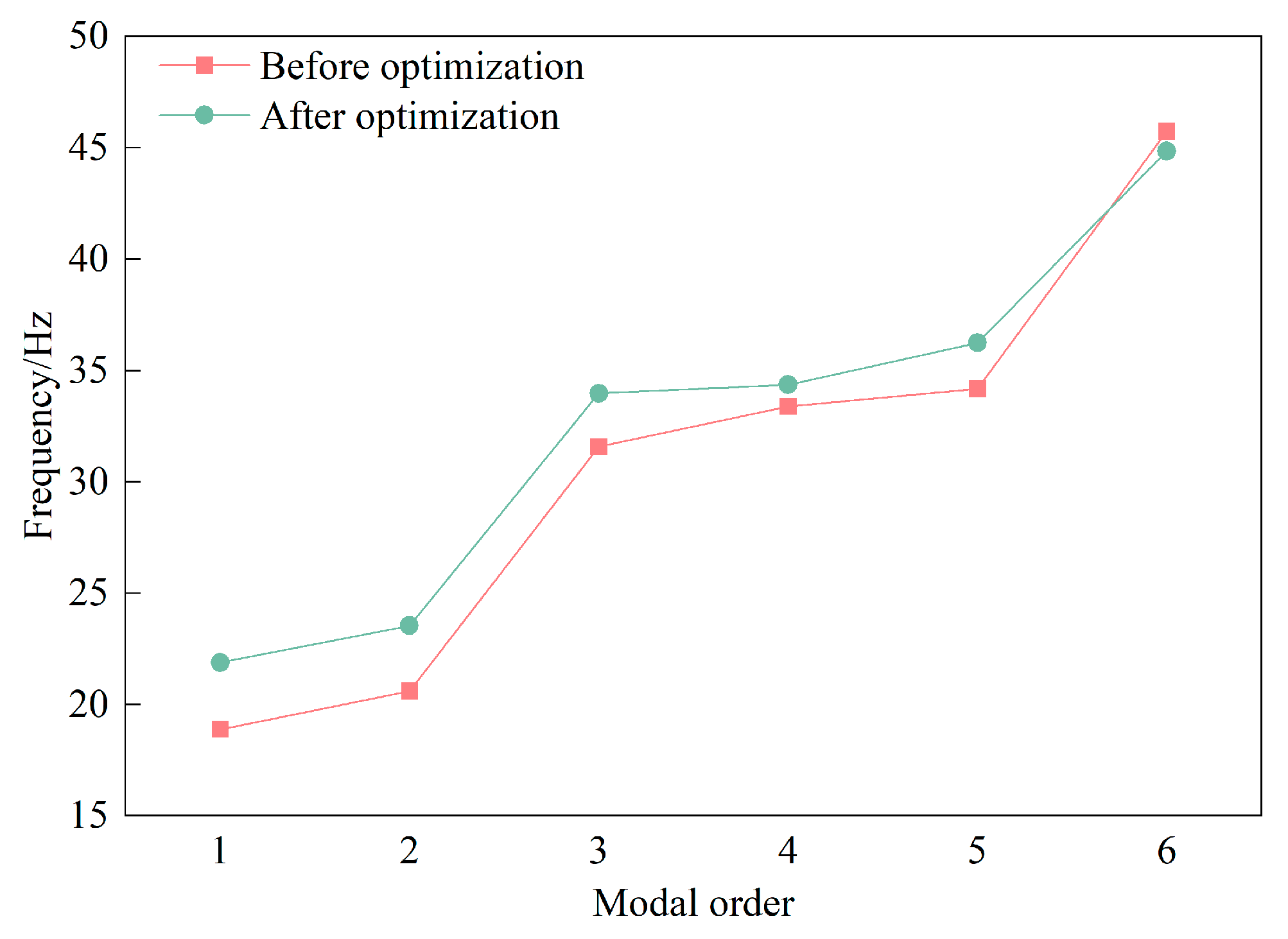
According to the optimization results, the frame is remodeled, and the finite element modal analysis is carried out. Figure 18 compares the first six order modal frequencies of the finite element before and after the frame optimization. The first six natural frequencies of the frame are adjusted to 21.89 Hz, 23.55 Hz, 33.98 Hz, 34.36 Hz, 36.24 Hz, and 44.85 Hz, respectively, all of which avoid the external excitation frequency.

Figure 18. Comparison before and after modal optimization.

Considering the process characteristics of the actual processing, according to the results of the optimized size data of the scheme M₄, the two digits after the decimal point (rounding method) are retained for the frame processing. The optimized frame has a good assembly effect on the 1-MSD straw-crushing residual film recycling machine and the field operation process is stable (as shown in Figure 19).

Figure 19. Optimized frame assembly and field trials. (a) Whole machine assembly; (b) Field operation.

6. Conclusions

(1)

The frame model of the straw-crushing residual film recycling machine was established using three-dimensional modeling software. The frame’s first six natural frequencies and vibration modes were calculated based on the Optistruct solver in HyperMesh.

(2)

The modal test of the frame is carried out based on the PolyMax method, and the modal confidence and frequency response confidence are comprehensively analyzed. It has been proved that the modal test results are ideal, and the reliability of the finite element analysis method in solving the frame mode is further verified.

(3)

By comparing the external excitation frequency with the natural frequency of the frame, it is concluded that the input rotation frequency of the stripping roller is close to the first-order natural frequency of the frame. The sensitivity method obtains the degree of influence of the thickness of each component of the frame on its first-order natural frequency. Taking the thickness of each component of the frame as the design variable and the first-order natural frequency of the frame and the volume of the frame as the objective function, a multi-objective optimization mathematical model is established, and six sets of non-inferior solutions are obtained by using the Optistruct solution method.

(4)

Based on the non-inferior solution results, the grey correlation analysis parameter evaluation table is established, and the best optimization scheme is obtained by the grey correlation evaluation method. The finite element analysis of the optimized frame was carried out. The results showed that the first-order natural frequency of the frame increased by 15.88% to 21.89 Hz, and the rotation frequency of the stripping roller was successfully avoided by 16.67 Hz. The volume decreased by 3.46% to 9.975 × 10⁷ mm³. The frame is well assembled in the 1-MSD straw-crushing residual film recovery machine and runs stably in the field.

7. Discussion and Prospects

Due to the limitation of time and conditions, combined with the current research progress of international scholars on the vibration characteristics of agricultural machinery, there are still some shortcomings in the research work of this paper, which need to be further improved, as follows:

(1)

In the follow-up work, the modal test of the frame should also be carried out under actual conditions, and the finite element modal results should be compared and analyzed to see whether the error is still within a reasonable range.

(2)

Inspired by the research of other scholars, this study should further explore the vibration characteristics of the straw-crushing residual film recycling machine under different working conditions in the future.

(3)

Due to the fact that the recovery time of residual film in the previous year was earlier than the completion time of this study, the machine did not carry out sufficient field verification and comparison. In the follow-up to this study, it is necessary to carry out field tests and comparisons of the machine in a sufficient working area.