Optimization of the Drying Process for Gamma-Irradiated Mushroom Slices Using Mathematical Models and Machine Learning Algorithms
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation and Drying Process
2.2. Dryer Specifications
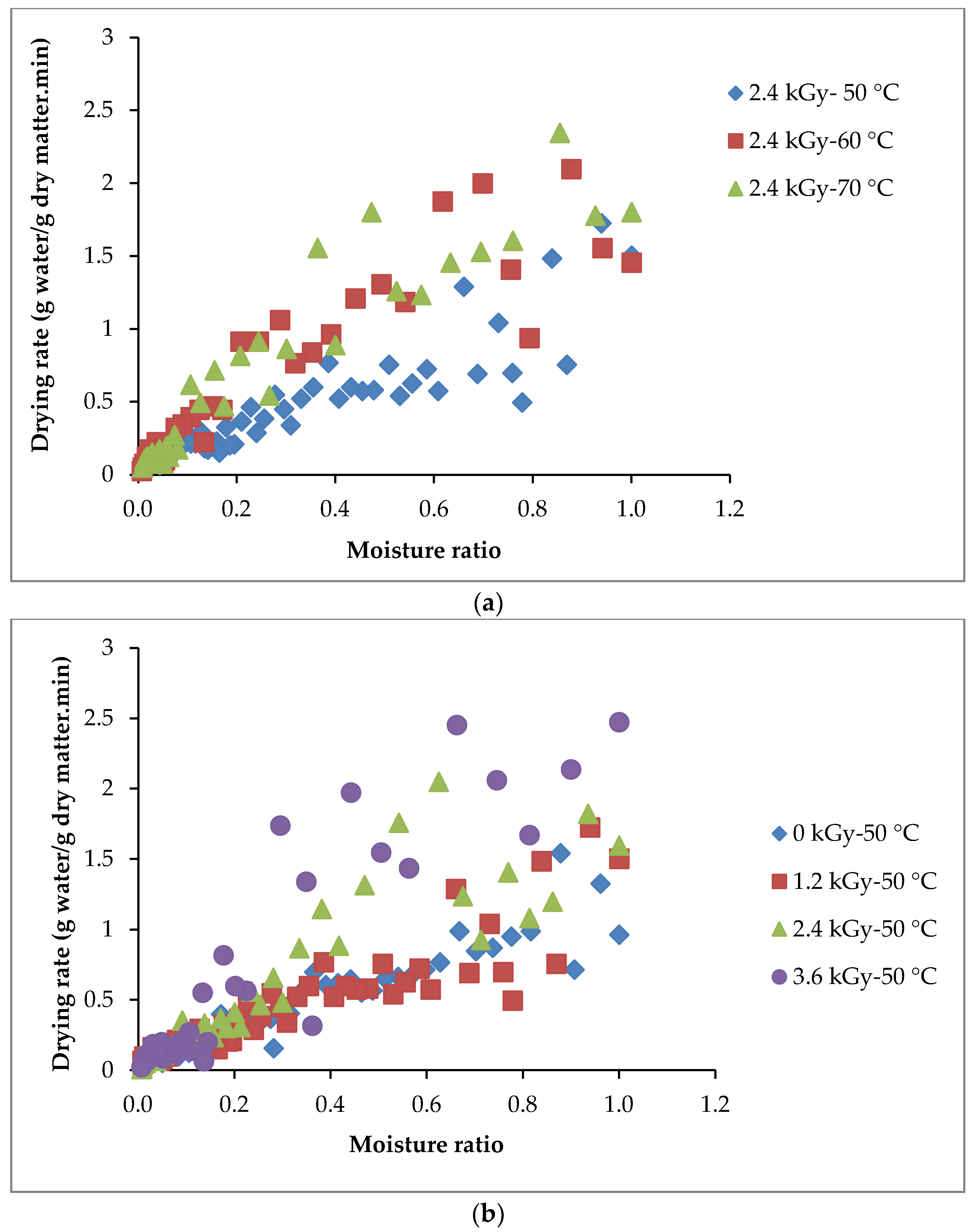
2.3. Drying Rate
2.4. Mathematical Modeling of Drying Curves
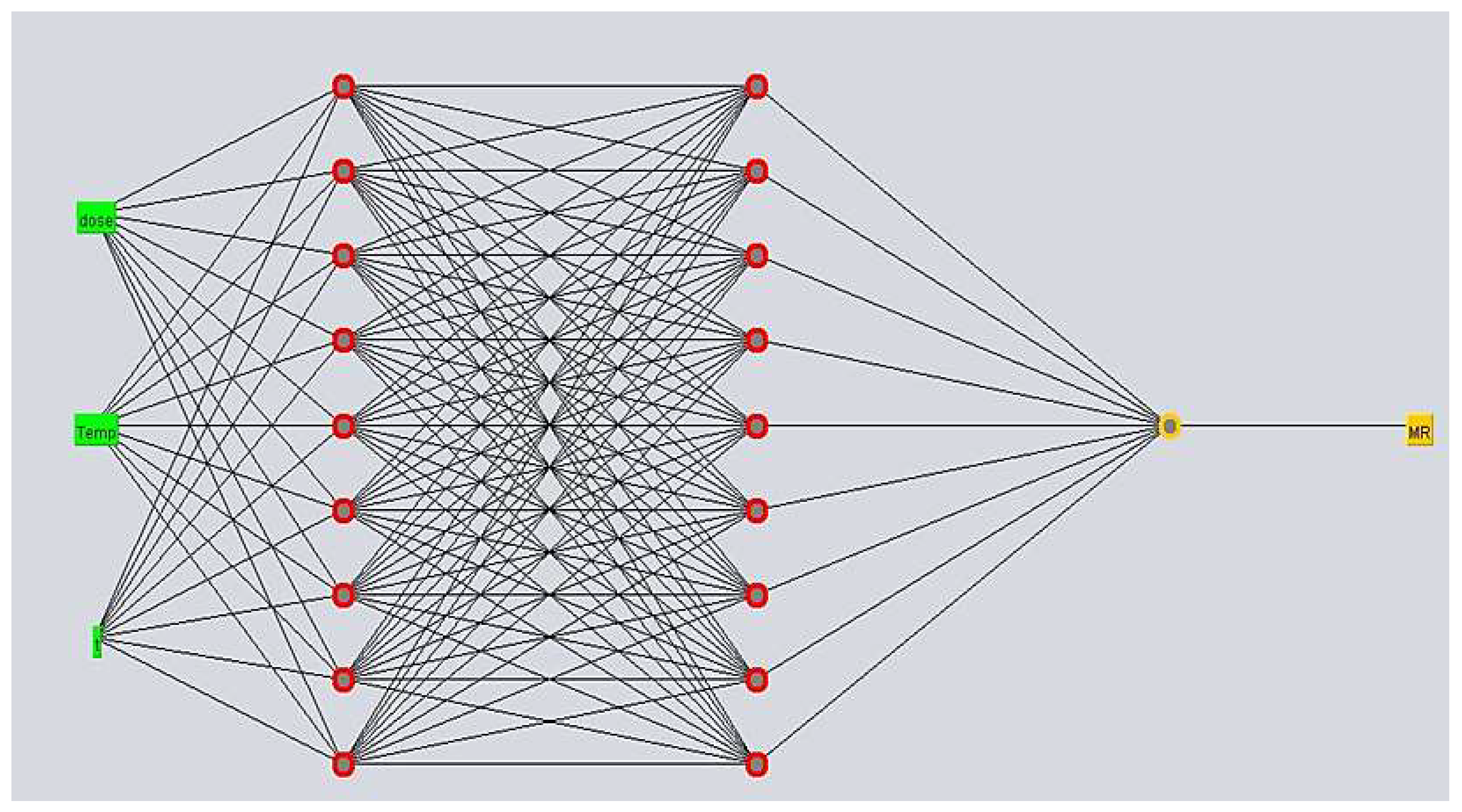
2.5. Artificial Neural Network (ANN)
2.6. Support Vector Machine (SVM)
2.7. k-Nearest Neighbors (kNN)
2.8. Effective Diffusion Coefficient
2.9. Activation Energy
2.10. Heat Utilization Efficiency
3. Results
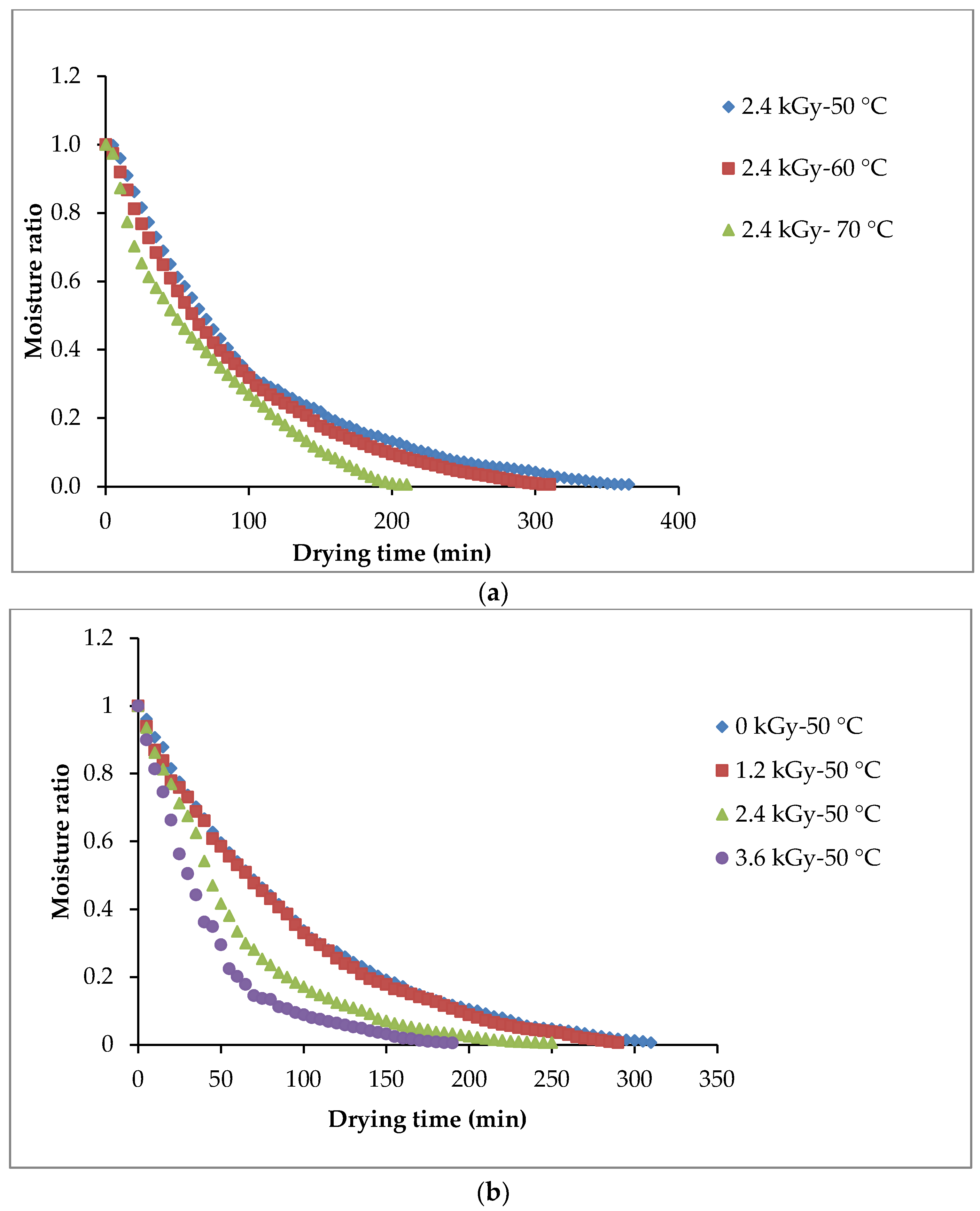
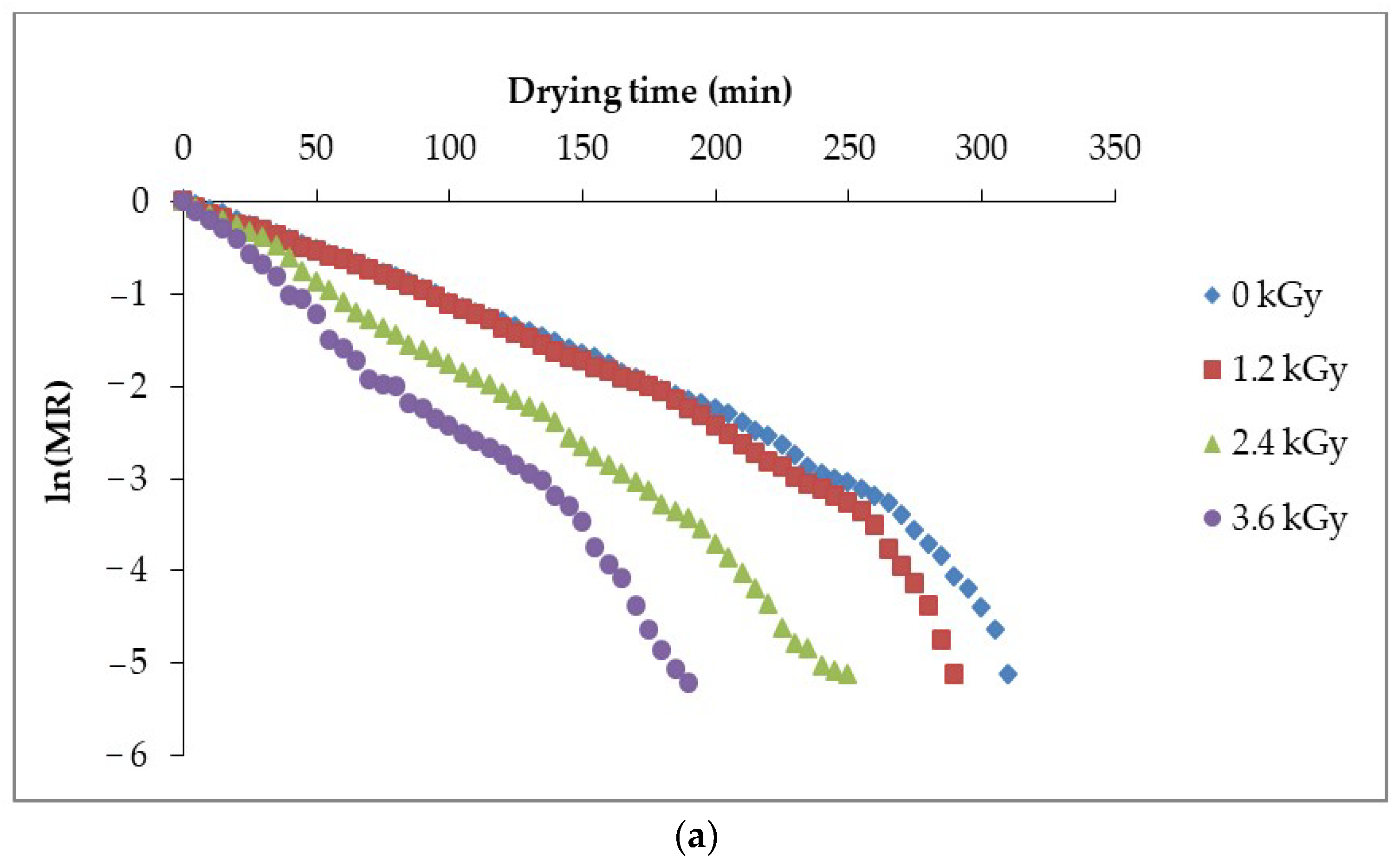
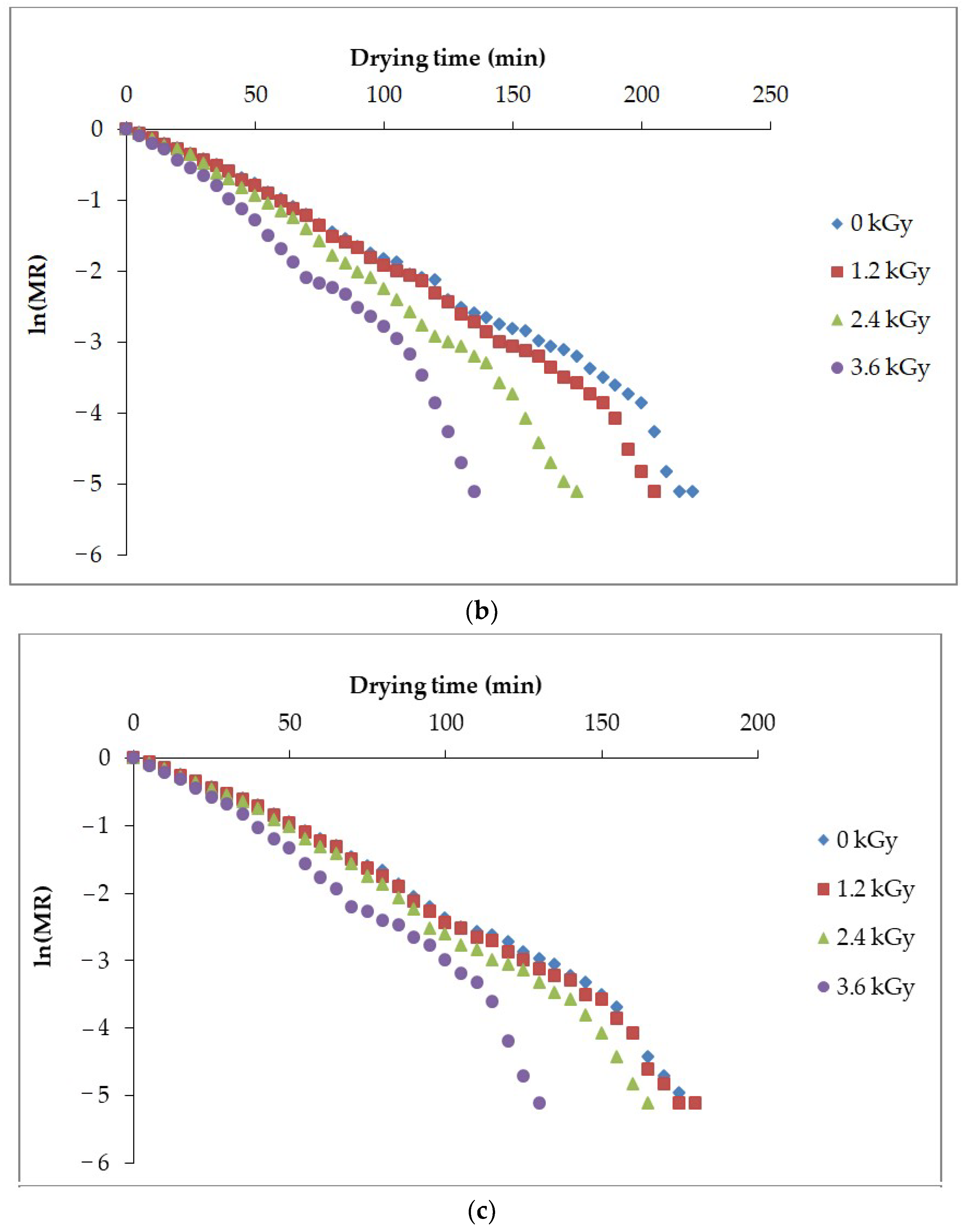
3.1. Drying Kinetics and Drying Rate of Button Mushroom
3.2. Identification of Optimal Mathematical Models for Predicting Temporal Moisture Variations
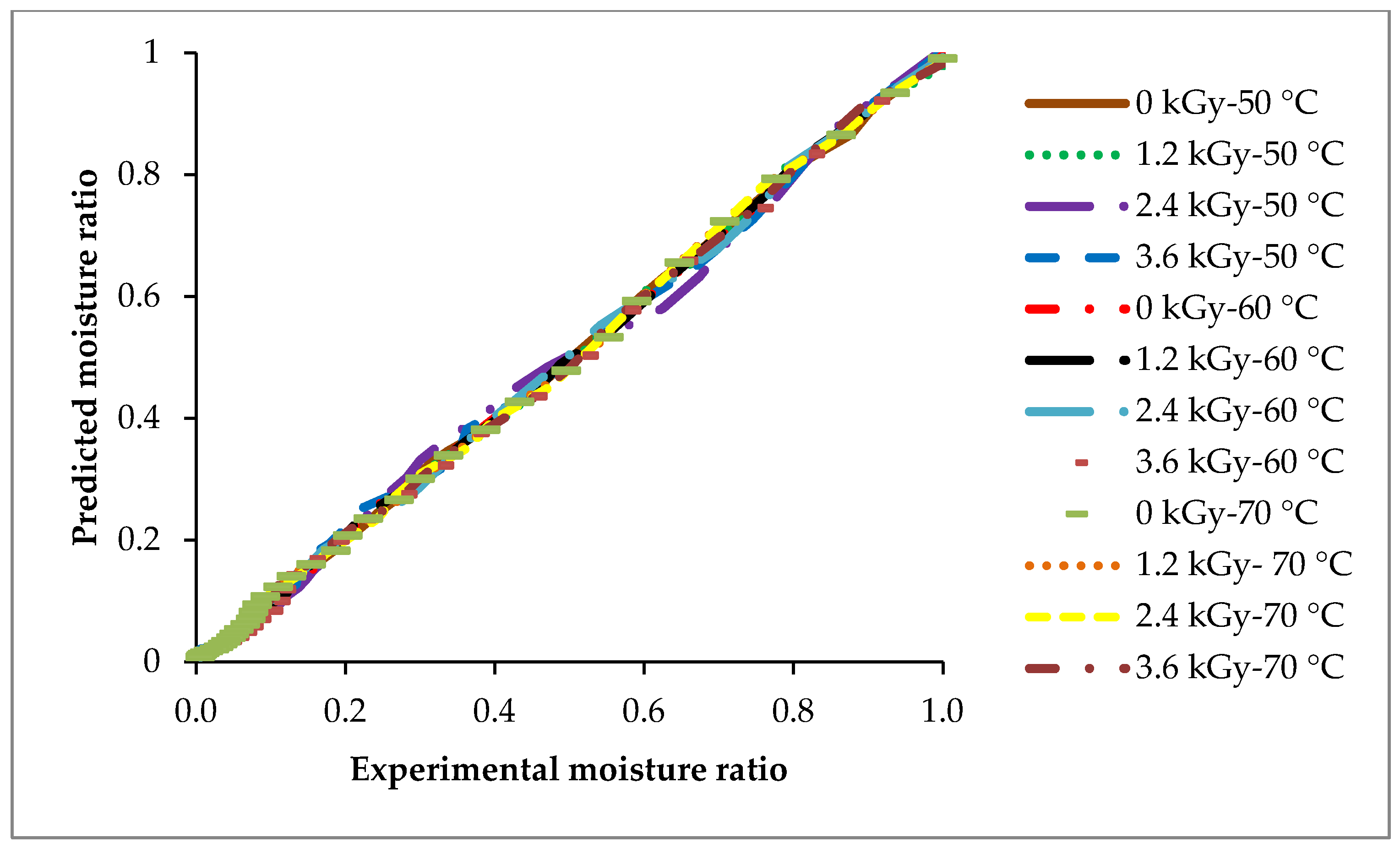
3.3. Moisture Variation Prediction Using Artificial Neural Networks (ANN)
3.4. Moisture Variation Prediction Using Machine Learning Algorithms
3.4.1. Support Vector Machine (SVM)
3.4.2. k-Nearest Neighbors (kNN)
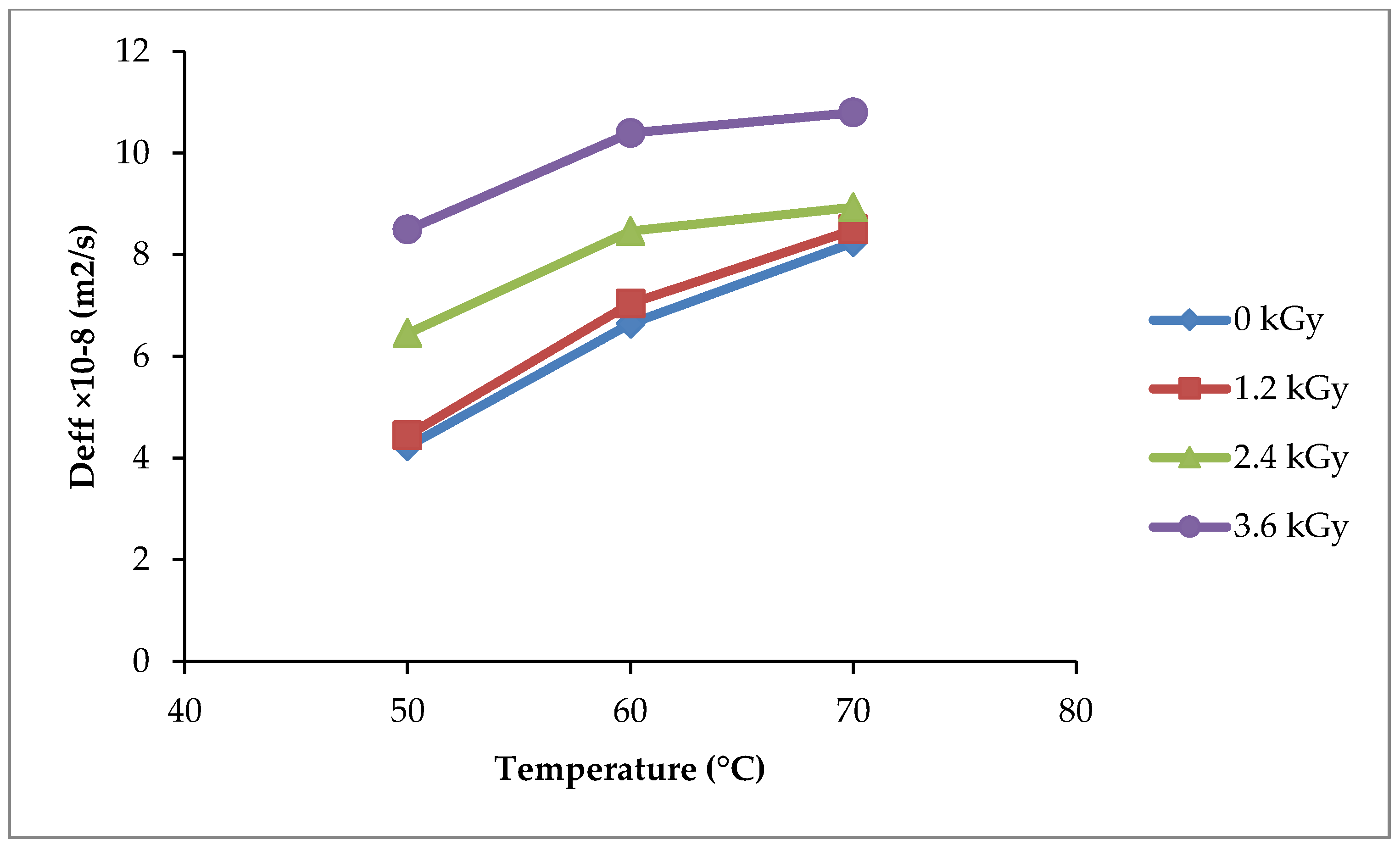
3.5. Effective Moisture Diffusivity
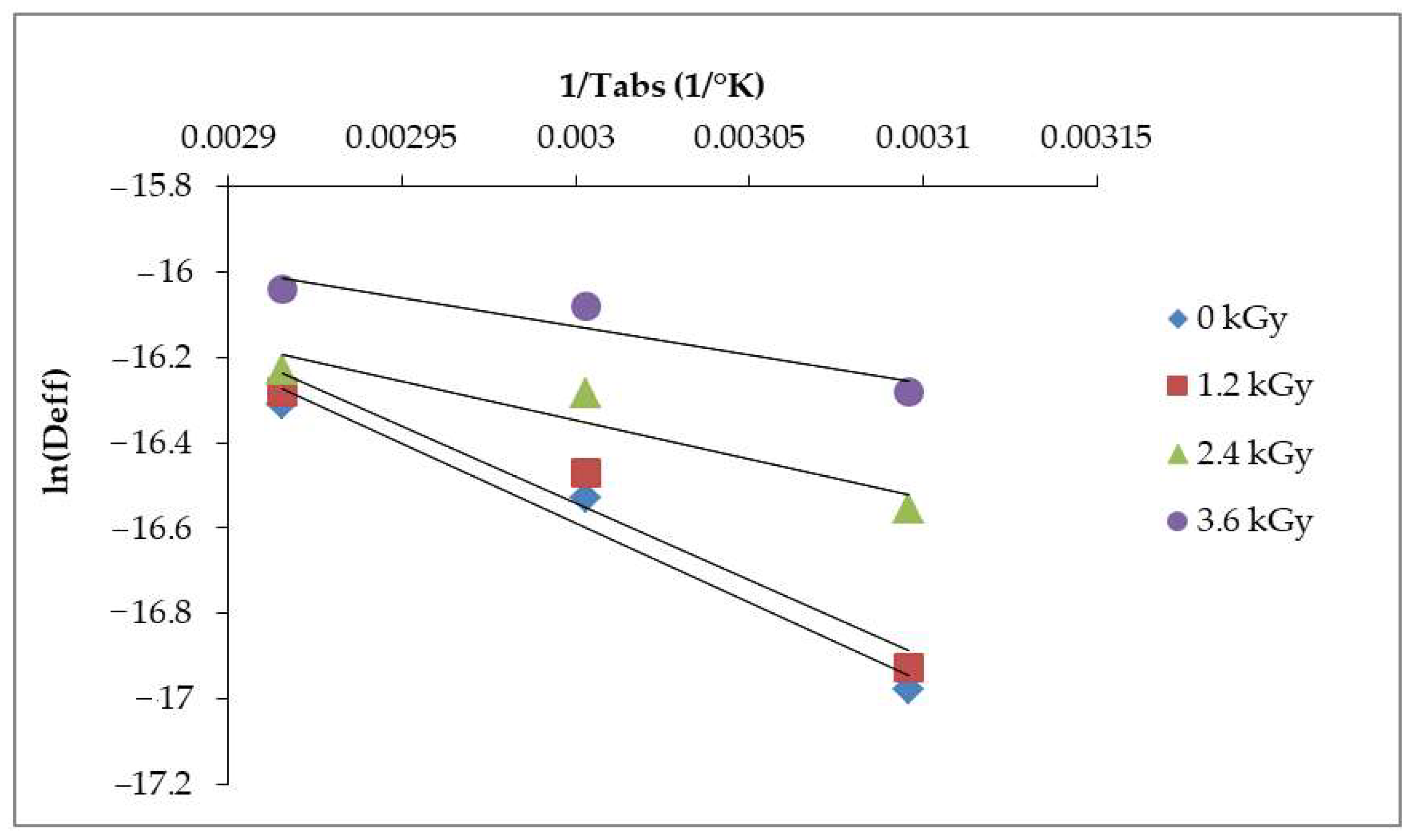
3.6. Activation Energy
3.7. Heat Utilization Efficiency
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Criado, P.; Fraschini, C.; Shankar, S.; Salmieri, S.; Lacroix, M. Influence of cellulose nanocrystals gellan gum-based coating on color and respiration rate of Agaricus bisporus mushrooms. J. Food Sci. 2021, 86, 420–425. [Google Scholar] [CrossRef]
- Gong, M.; Zhang, T.; Wu, Y.; Shang, J.; Su, E.; Cao, Y.; Zhang, J. Synergizing postharvest physiology and nanopackaging for edible mushroom preservation. Food Chem. 2024, 463, 141099. [Google Scholar] [CrossRef] [PubMed]
- Guo, W.; Tang, X.; Cui, S.; Zhang, Q.; Zhao, J.; Mao, B.; Zhang, H. Recent advance in quality preservation of non-thermal preservation technology of fresh mushroom: A review. Crit. Rev. Food Sci. Nutr. 2024, 64, 7878–7894. [Google Scholar] [CrossRef]
- Arsenoaia, V.N.; Vlăduț, V.; Țenu, I.; Voicea, I.; Cârlescu, P.M. Mathematical modeling and numerical simulation of the drying process of seeds in a pilot plant. INMATEH—Agric. Eng. 2019, 57, 55–62. [Google Scholar] [CrossRef]
- Arsenoaia, V.; Vlăduţ, V.; Ţenu, I.; Voicea, I.; Cârlescu, P.M. Drying process modeling with effects of physical parameters on dehydrated seeds. In Proceedings of the 47th International Symposium “Actual Tasks on Agricultural Engineering”, Opatija, Croaţia, 5–7 March 2019. [Google Scholar]
- Sorică, C.; Pătruț, A.; Șovăială, G.H.; Sorică, E.; Vlăduțoiu, L.; Matache, G.; Pavel, I.; Cristea, M. Preliminary researches on some technical-functional parameters of an experimental model of convective dryer with total energy independence. INMATEH—Agric. Eng. 2024, 72, 547–556. [Google Scholar] [CrossRef]
- Huo, J.; Zhang, M.; Wang, D.S.; Mujumdar, A.; Bhandari, B.; Zhang, L. New preservation and detection technologies for edible mushrooms: A review. J. Sci. Food Agric. 2023, 103, 3230–3248. [Google Scholar] [CrossRef]
- Singh, P.; Langowski, H.C.; Wani, A.A.; Saengerlaub, S. Recent advances in extending the shelf life of fresh Agaricus mushrooms: A review. J. Sci. Food Agric. 2010, 90, 1393–1402. [Google Scholar] [CrossRef]
- Wang, J.; Chao, Y. Effect of 60Co irradiation on drying characteristics of apple. J. Food Eng. 2003, 56, 347–351. [Google Scholar] [CrossRef]
- Mahmood, N.; Liu, Y.; Zheng, X.; Munir, Z.; Pandiselvam, R.; Zhang, Y.; Saleemi, M.A.; Yves, H.; Sufyan, M.; Lei, D. Influences of emerging drying technologies on rice quality. Food Res. Int. 2024, 184, 114264. [Google Scholar] [CrossRef] [PubMed]
- Xie, S.; Yang, Z.; Yang, L.; Li, S.; Wang, J.; Yang, M. Performance analysis and technology optimization of infrared drying of sweet potato slice. INMATEH—Agric. Eng. 2024, 64, 119–130. [Google Scholar] [CrossRef]
- Ravindran, R.; Jaiswal, A.K. Wholesomeness and safety aspects of irradiated foods. Food Chem. 2019, 285, 363–368. [Google Scholar] [CrossRef]
- Lester, G.E.; Hallman, G.J.; Pérez, J.A. γ-irradiation dose: Effects on baby-leaf spinach ascorbic acid, carotenoids, folate, α-tocopherol, and phylloquinone concentrations. J. Agric. Food Chem. 2010, 58, 4901–4906. [Google Scholar] [CrossRef]
- World Health Organization (WHO). High-Dose Irradiation: Wholesomeness of Food Irradiatied with Doses Above 10 kGy: Report of a Joint FAO/IAEA/WHO Study Group. No. 890. 1999. Available online: https://www.who.int/publications/i/item/9241208902 (accessed on 10 November 2024).
- International Consultative Group on Food Irradiation (ICGFI). Facts About Food Irradiation; International Consultative Group on Food Irradiation: Buckinghamshire, UK, 1999. [Google Scholar]
- Joseph, T.; Baah, K.; Jahanfar, A.; Dubey, B. A comparative life cycle assessment of conventional hand dryer and roll paper towel as hand drying methods. Sci. Total Environ. 2015, 515, 109–117. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Chao, Y. Drying characteristics of irradiated apple slices. J. Food Eng. 2002, 52, 83–88. [Google Scholar] [CrossRef]
- Cătunescu, G.M.; Muntean, M.; Marian, O.; David, A.P.; Rotar, A.M. Comparative effect of gamma irradiation, drying and freezing on sensory, and hygienic quality of parsley leaves. LWT 2019, 115, 108448. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, H.; Mujumdar, A.S.; Tang, J.; Miao, S.; Wang, Y. Recent developments in high-quality drying of vegetables, fruits, and aquatic products. Crit. Rev. Food Sci. Nutr. 2017, 57, 1239–1255. [Google Scholar] [CrossRef]
- Irchad, A.; Razouk, R.; Ouaabou, R.; Mouhib, M.; Hssaini, L. Effect of 60Co γ-rays on dried figs adsorption isotherms and thermodynamic properties. Front. Nutr. 2022, 9, 940111. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, J. Effect of gamma-ray irradiation on drying characteristics of wheat. Biosyst. Eng. 2006, 95, 219–225. [Google Scholar] [CrossRef]
- Wang, J.; Chao, Y. Effect of gamma irradiation on quality of dried potato. Radiat. Phys. Chem. 2003, 66, 293–297. [Google Scholar] [CrossRef]
- Kortei, N.; Odamtten, G.; Ayim-Akonor, M.; Akonor, P. Modeling the solar drying kinetics of gamma irradiation-pretreated oyster mushrooms (Pleurotus ostreatus). Int. Food Res. J. 2016, 23, 34–39. [Google Scholar]
- Chasiotis, V.K.; Tzempelikos, D.A.; Filios, A.E.; Moustris, K.P. Artificial neural network modelling of moisture content evolution for convective drying of cylindrical quince slices. Comput. Electron. Agric. 2020, 172, 105074. [Google Scholar] [CrossRef]
- Chokphoemphun, S.; Hongkong, S.; Chokphoemphun, S. Evaluation of drying behavior and characteristics of potato slices in multi–stage convective cabinet dryer: Application of artificial neural network. Inf. Process. Agric. 2023, 11, 2214–3173. [Google Scholar] [CrossRef]
- Al-Mashhadany, S.A.; Hasan, H.A.; Al-Sammarraie, M.A. Using machine learning algorithms to predict the sweetness of bananas at different drying times. J. Ecol. Eng. 2024, 25, 231–238. [Google Scholar] [CrossRef]
- Hadjout-Krimat, L.; Belbahi, A.; Dahmoune, F.; Hentabli, M.; Boudria, A.; Achat, S.; Remini, H.; Oukhmanou-Bensidhoum, S.; Spigno, G.; Madani, K. Study of microwave and convective drying kinetics of pea pods (Pisum sativum L.): A new modeling approach using support vector regression methods optimized by dragonfly algorithm techniques. J. Food Process Eng. 2023, 46, e14232. [Google Scholar] [CrossRef]
- Jiang, Q.; Zhang, M.; Mujumdar, A.S. UV induced conversion during drying of ergosterol to vitamin D in various mushrooms: Effect of different drying conditions. Trends Food Sci. Technol. 2020, 105, 200–210. [Google Scholar] [CrossRef]
- Zhao, Y.; Bi, J.; Yi, J.; Jin, X.; Wu, X.; Zhou, M. Evaluation of sensory, textural, and nutritional attributes of shiitake mushrooms (Lentinula edodes) as prepared by five types of drying methods. J. Food Process Eng. 2019, 42, e13029. [Google Scholar] [CrossRef]
- AOAC. International Official Methods of Analysis, 13th ed.; Association of Official Analytical Chemists: Washington, DC, USA, 1990. [Google Scholar]
- Khazaei, N.B.; Tavakoli, T.; Ghassemian, H.; Khoshtaghaza, M.H.; Banakar, A. Applied machine vision and artificial neural network for modeling and controlling of the grape drying process. Comp. Electron. Agricul. 2013, 98, 205–213. [Google Scholar] [CrossRef]
- Zhu, J.F.; Liu, J.Z.; Wu, J.H.; Cheng, J.; Zhou, J.H.; Cen, K.F. Thin-layer drying characteristics and modeling of Ximeng lignite under microwave irradiation. Fuel Process. Technol. 2015, 130, 62–70. [Google Scholar] [CrossRef]
- Zhu, G.; Raghavan, G.S.V.; Li, Z. Predicting the moisture ratio of a hami melon drying process using image processing technology. Foods 2023, 12, 672. [Google Scholar] [CrossRef] [PubMed]
- Man, X.; Li, L.; Fan, X.; Zhang, H.; Lan, H.; Tang, Y.; Zhang, Y. Drying kinetics and mass transfer characteristics of walnut under hot air drying. Agriculture 2024, 14, 182. [Google Scholar] [CrossRef]
- An, J.; Yan, J.; Wei, H.; Liao, X.; Liu, T.; Xie, H. Investigation of the kinetic dynamics in the intermittent microwave–hot-air combined drying of peanut pods. Agriculture 2024, 14, 2259. [Google Scholar] [CrossRef]
- Gomes, F.P.; Resende, O.; de Sousa, E.P.; Célia, J.A.; de Oliveira, K.B. Application of mathematical models and thermodynamic properties in the drying of jambu leaves. Agriculture 2022, 12, 1252. [Google Scholar] [CrossRef]
- Toğrul, İ.T.; Pehlivan, D. Mathematical modelling of solar drying of apricots in thin layers. J. Food Eng. 2002, 55, 209–216. [Google Scholar] [CrossRef]
- Kaleta, A.; Górnicki, K. Some remarks on evaluation of drying models of red beet particles. Energy Convers. Manag. 2010, 51, 2967–2978. [Google Scholar] [CrossRef]
- Ertekin, C.; Yaldiz, O. Drying of eggplant and selection of a suitable thin layer drying model. J. Food Eng. 2004, 63, 349–359. [Google Scholar] [CrossRef]
- da Silva, R.C.; da Silva, W.P.; Gomes, J.P.; de Melo Queiroz, A.J.; de Figueirêdo, R.M.F.; de Lima, A.G.B.; Rocha, A.P.T.; da Silva, L.D.; de Lima Ferreira, J.P.; da Costa Santos, D.; et al. A new empirical model for predicting intermittent and continuous drying of “Neve” melon (Cucumis melo sp.) seeds. Agriculture 2022, 12, 328. [Google Scholar] [CrossRef]
- Carrillo Luis, V.; Beristain Rios, D.; Hernández-Flores, O.A.; Romero-Salazar, C.; Sandoval-Torres, S. Mathematical modeling of goat meat drying kinetics with thermal oscillations. Foods 2024, 13, 3836. [Google Scholar] [CrossRef] [PubMed]
- Taghavifar, H.; Mardani, A.; Taghavifar, L. A hybridized artificial neural network and imperialist competitive algorithm optimization approach for prediction of soil compaction in soil bin facility. Measurement 2013, 46, 2288–2299. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, X.; Xiao, H.; Li, Y.; Yang, T. Effect of combined infrared hot air drying on yam slices: Drying kinetics, energy consumption, microstructure, and nutrient composition. Foods 2023, 12, 3048. [Google Scholar] [CrossRef]
- Koukouch, A.; Idlimam, A.; Asbik, M.; Sarh, B.; Izrar, B.; Bostyn, S.; Bah, A.; Ansari, O.; Zegaoui, O.; Amine, A. Experimental determination of the effective moisture diffusivity and activation energy during convective solar drying of olive pomace waste. Renew. Energy 2017, 101, 565–574. [Google Scholar] [CrossRef]
- Yahya, M.; Fahmi, H.; Hasibuan, R. Experimental performance analysis of a pilot-scale biomass-assisted recirculating mixed-flow dryer for drying paddy. Int. J. Food Sci. 2022, 2022, 4373292. [Google Scholar] [CrossRef] [PubMed]
- He, C.; Wang, H.; Yang, Y.; Huang, Y.; Zhang, X.; Arowo, M.; Ye, J.; Zhang, N.; Xiao, M. Drying behavior and kinetics of drying process of plant-based enteric hard capsules. Pharmaceutics 2021, 13, 335. [Google Scholar] [CrossRef] [PubMed]
- Akpinar, E.; Midilli, A.; Bicer, Y. Single layer drying behaviour of potato slices in a convective cyclone dryer and mathematical modeling. Energy Conv. Manag. 2003, 44, 1689–1705. [Google Scholar] [CrossRef]
- Cao, Z.; Zhou, L.; Bi, J.; Yi, J.; Chen, Q.; Wu, X.; Zheng, J.; Li, S. Effect of different drying technologies on drying characteristics and quality of red pepper (Capsicum frutescens L.): A comparative study. J. Sci. Food Agric. 2016, 96, 3596–3603. [Google Scholar] [CrossRef] [PubMed]
- Pinheiro, M.C.; Madaleno, R.O.; Castro, L.M. Drying kinetics of two fruits Portuguese cultivars (Bravo de Esmolfe apple and Madeira banana): An experimental study. Heliyon 2022, 8, e09341. [Google Scholar] [CrossRef]
- Fikry, M.; Benjakul, S.; Al-Ghamdi, S.; Tagrida, M.; Prodpran, T. Evaluating Kinetics of Convection Drying and Microstructure Characteristics of Asian Seabass Fish Skin without and with Ultrasound Pretreatment. Foods 2023, 12, 3024. [Google Scholar] [CrossRef]
- Akram, K.; Ahn, J.J.; Kwon, J.H. Identification and characterization of gamma-irradiated dried Lentinus edodes using ESR, SEM, and FTIR analyses. J. Food Sci. 2012, 77, 690–696. [Google Scholar] [CrossRef]
- Koorapati, A.; Foley, D.; Pilling, R.; Prakash, A. Electron-beam irradiation preserves the quality of white button mushroom (Agaricus bisporus) slices. J. Food Sci. 2004, 69, 25–29. [Google Scholar] [CrossRef]
- Zhong, Y.; Dong, S.; Cui, Y.; Dong, X.; Xu, H.; Li, M. Recent Advances in Postharvest Irradiation Preservation Technology of Edible Fungi: A Review. Foods 2023, 12, 103. [Google Scholar] [CrossRef] [PubMed]
- Francis, F. Wiley Encyclopedia of Food Science and Technology; Francis, F.J., Ed.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2000; Volume 1. [Google Scholar]
- Feng, H.; Yin, Y.; Tang, J. Microwave drying of food and agricultural materials: Basics and heat and mass transfer modeling. Food Eng. Rev. 2012, 4, 89–106. [Google Scholar] [CrossRef]
- Nadew, T.T.; Tedla, T.S.; Bizualem, Y.D.; Abate, S.N.; Teklehaymanot, L.T. Data on drying kinetics, moisture sorption isotherm, composition study of Ethiopian oyster mushroom (Pleurotus ostreatus mushroom) drying in tray dryer. Data Brief 2024, 56, 110861. [Google Scholar] [CrossRef]
- Tran, T.N.T.; Khoo, K.S.; Chew, K.W.; Phan, T.Q.; Nguyen, H.S.; Nguyen-Sy, T.; Nguyen, T.D.P.; Chen, W.-H.; Show, P.L. Modelling drying kinetic of oyster mushroom dehydration—The optimization of drying conditions for dehydratation of Pleurotus species. Mater. Sci. Energy Technol. 2020, 3, 840–845. [Google Scholar] [CrossRef]
- Khaled, A.Y.; Kabutey, A.; Selvi, K.Ç.; Mizera, Č.; Hrabe, P.; Herák, D. Application of computational intelligence in describing the drying kinetics of persimmon fruit (Diospyros kaki) during vacuum and hot air drying process. Processes 2020, 8, 544. [Google Scholar] [CrossRef]
- Selvi, K.Ç.; Alkhaled, A.Y.; Yıldız, T. Application of artificial neural network for predicting the drying kinetics and chemical attributes of linden (Tilia platyphyllos Scop.) during the infrared drying process. Processes 2022, 10, 2069. [Google Scholar] [CrossRef]
- Shin, J.; Mahmud, M.S.; Rehman, T.U.; Ravichandran, P.; Heung, B.; Chang, Y.K. Trends and prospect of machine vision technology for stresses and diseases detection in precision agriculture. AgriEngineering 2022, 5, 20–39. [Google Scholar] [CrossRef]
- Nath, P.C.; Mishra, A.K.; Sharma, R.; Bhunia, B.; Mishra, B.; Tiwari, A.; Nayak, P.K.; Sharma, M.; Bhuyan, T.; Kaushal, S.; et al. Recent advances in artificial intelligence towards the sustainable future of agri-food industry. Food Chem. 2024, 447, 138945. [Google Scholar] [CrossRef]
- Macedo, L.L.; Vimercati, W.C.; da Silva Araújo, C.; Saraiva, S.H.; Teixeira, L.J.Q. Effect of drying air temperature on drying kinetics and physicochemical characteristics of dried banana. J. Food Process Eng. 2020, 43, e13451. [Google Scholar] [CrossRef]
- Amiri Chayjan, R.; Kaveh, M. Physical parameters and kinetic modeling of fix and fluid bed drying of terebinth seeds. J. Food Process. Preserv. 2014, 38, e12092. [Google Scholar] [CrossRef]
- Lin, X.; Lyng, J.; O’Donnell, C.; Sun, D.W. Effects of dielectric properties and microstructures on microwave-vacuum drying of mushroom (Agaricus bisporus) caps and stipes evaluated by non-destructive techniques. Food Chem. 2022, 367, 130698. [Google Scholar] [CrossRef]
- Salehi, F.; Cheraghi, R.; Rasouli, M. Mass transfer analysis and kinetic modeling of ultrasound-assisted osmotic dehydration of kiwifruit slices. Sci. Rep. 2023, 13, 11859. [Google Scholar] [CrossRef] [PubMed]
- Sawhney, R.; Pangavhane, D.; Sarsavadia, P. Drying studies of single layer thompson seedless grapes. In Proceedings of the International Solar Food Processing Conference, Indore, India, 14–16 January 2009. [Google Scholar]
- Tejeda-Miramontes, J.P.; Espinoza-Paredes, B.C.; Zatarain-Palffy, A.; García-Cayuela, T.; Tejada-Ortigoza, V.; Garcia-Amezquita, L.E. Process modeling and convective drying optimization of raspberry pomace as a fiber-rich functional ingredient: Effect on techno-functional and bioactive properties. Foods 2024, 13, 3597. [Google Scholar] [CrossRef] [PubMed]
- Sousa, E.P.d.; Oliveira, E.N.A.d.; Lima, T.L.S.; Almeida, R.F.; Barros, J.H.T.; Lima, C.M.G.; Giuffrè, A.M.; Wawrzyniak, J.; Wybraniec, S.; Coutinho, H.D.M.; et al. Empirical modeling of the drying kinetics of red beetroot (Beta vulgaris L.; Chenopodiaceae) with peel, and flour stability in laminated and plastic flexible packaging. Foods 2024, 13, 2784. [Google Scholar] [CrossRef] [PubMed]
- Peter, M.; Liu, Z.; Fang, Y.; Dou, X.; Awuah, E.; Soomro, S.A.; Chen, K. Computational intelligence and mathematical modelling in chanterelle mushrooms’ drying process under heat pump dryer. Biosyst. Eng. 2021, 212, 143–159. [Google Scholar] [CrossRef]
- Reyes, A.; Mahn, A.; Vásquez, F. Mushrooms dehydration in a hybrid-solar dryer, using a phase change material. Energy Convers. Manag. 2014, 83, 241–248. [Google Scholar] [CrossRef]
- Barforoosh, M.Y.; Borghaee, A.M.; Rafiee, S.; Minaei, S.; Beheshti, B. Determining the effective diffusivity coefficient and activation energy in thin-layer drying of Haj Kazemi peach slices and modeling drying kinetics using ANFIS. Int. J. Low-Carbon Tech. 2024, 19, 192–206. [Google Scholar] [CrossRef]
- El-Mesery, H.S.; Ashiagbor, K.; Hu, Z.; Rostom, M. Mathematical modeling of thin-layer drying kinetics and moisture diffusivity study of apple slices using infrared conveyor-belt dryer. J. Food Sci. 2024, 89, 1658–1671. [Google Scholar] [CrossRef] [PubMed]
- Tulek, Y. Drying kinetics of oyster mushroom (Pleurotus ostreatus) in a convective hot air dryer. J. Agric. Sci. Technol. 2011, 13, 655–664. [Google Scholar]
- Datt, P. Latent heat of vaporization/condensation. In Encyclopedia of Snow, Ice and Glaciers; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Li, W.; Li, R.; Chen, W.; Feng, J.; Wu, D.; Zhang, Z.; Zhang, J.; Yang, Y. The anabolism of sulphur aroma volatiles responds to enzymatic and non-enzymatic reactions during the drying process of shiitake mushrooms. Food Chem. 2022, 371, 131123. [Google Scholar] [CrossRef] [PubMed]
- Muliterno, M.M.; Rodrigues, D.; Lima, F.S.; Ida, E.I.; Kurozawa, L.E. Conversion/degradation of isoflavones and color alterations during the drying of okara. LWT 2017, 75, 512–519. [Google Scholar] [CrossRef]
| Model Name | Model Equation | Reference |
|---|---|---|
| Newton | MR = exp(−kt) | [34] |
| Page | MR = exp(−ktn) | [35] |
| Henderson and Pabis | MR = a exp(−kt) | [36] |
| Logarithmic | MR = a exp(−kt) + c | [37] |
| Two-term exponential | MR = a exp(−kt) + (1 − a)exp(−kat) | [38] |
| Approach of diffusion | MR = a exp(−kt) + (1 − a)exp(−kbt) | [39] |
| Wang and Sing | MR = 1 + at + bt2 | [40] |
| Midilli | MR = a exp(−ktn) + bt | [41] |
| Model Name | R2 | RMSE | SSE |
|---|---|---|---|
| Newton | 0.9905 | 0.02697 | 0.03886 |
| Page | 0.9954 | 0.01708 | 0.02039 |
| Henderson and Pabis | 0.9924 | 0.02397 | 0.03143 |
| Logarithmic | 0.995 | 0.01703 | 0.01451 |
| Two-term exponential | 0.9955 | 0.01689 | 0.01983 |
| Approximation of diffusion | 0.9912 | 0.0263 | 0.036 |
| Wang and Sing | 0.9783 | 0.04137 | 0.08645 |
| Midilli | 0.998 | 0.01218 | 0.00858 |
| Temp. (°C) | Dose (kGy) | R2 | RMSE | SSE | a | k | b | n |
|---|---|---|---|---|---|---|---|---|
| 50 | 0 | 0.9998 | 0.004366 | 0.001125 | 1.003 | 0.00878 | −8.394 × 10−5 | 1.03 |
| 1.2 | 0.9993 | 0.014200 | 0.007062 | 0.978 | 0.00853 | 1.257 × 10−4 | 1.12 | |
| 2.4 | 0.9969 | 0.016000 | 0.012030 | 1.005 | 0.009567 | 3.49 × 10−5 | 1.14 | |
| 3.6 | 0.9975 | 0.014330 | 0.007184 | 1.002 | 0.01557 | 9.117 × 10−5 | 1.12 | |
| 60 | 0 | 0.9993 | 0.007891 | 0.002553 | 0.996 | 0.006796 | 3.662 × 10−5 | 1.21 |
| 1.2 | 0.9995 | 0.006587 | 0.001649 | 0.992 | 0.006758 | 5.345 × 10−6 | 1.22 | |
| 2.4 | 0.9994 | 0.007905 | 0.002000 | 0.992 | 0.006206 | −1.536 × 10−5 | 1.27 | |
| 3.6 | 0.9988 | 0.010970 | 0.002891 | 0.990 | 0.009661 | 2.7 × 10−5 | 1.25 | |
| 70 | 0 | 09992 | 0.008881 | 0.002603 | 0.990 | 0.008319 | −1.362 × 10−5 | 1.21 |
| 1.2 | 0.9992 | 0.008868 | 0.002595 | 0.987 | 0.008215 | −1.957 × 10−5 | 1.22 | |
| 2.4 | 0.9991 | 0.009615 | 0.002773 | 0.985 | 0.008005 | −2.224 × 10−5 | 1.24 | |
| 3.6 | 0.9988 | 0.011190 | 0.002882 | 0.982 | 0.01028 | 1.379 × 10−5 | 1.24 |
| No. Hidden Layer | No. Neurons | Training | Testing | ||
|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | ||
| 1 | 3 | 0.9961 | 0.0243 | 0.9964 | 0.0266 |
| 1 | 6 | 0.9964 | 0.0280 | 0.9965 | 0.0256 |
| 1 | 9 | 0.9978 | 0.0204 | 0.9966 | 0.0245 |
| 2 | 3, 3 | 0.9928 | 0.0333 | 0.9926 | 0.0452 |
| 2 | 6, 6 | 0.9973 | 0.0207 | 0.9971 | 0.0233 |
| 2 | 9, 9 | 0.9967 | 0.0230 | 0.9969 | 0.0303 |
| 3 | 3, 3, 3 | 0.9932 | 0.0351 | 0.9926 | 0.0457 |
| 3 | 6, 6, 6 | 0.9978 | 0.0182 | 0.9975 | 0.0220 |
| 3 | 9, 9, 9 | 0.9978 | 0.0188 | 0.9973 | 0.0236 |
| Filter Type | Kernel Type | Training | Testing | ||
|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | ||
| Normalize | Polynomial kernel | 0.9161 | 0.1154 | 0.9092 | 0.1261 |
| Normalize | Pearson universal kernel | 0.9979 | 0.0187 | 0.9939 | 0.0344 |
| Normalize | RBF kernel | 0.9164 | 0.1332 | 0.9151 | 0.1505 |
| Standardize | Polynomial kernel | 0.9162 | 0.1152 | 0.9086 | 0.1261 |
| Standardize | Pearson universal kernel | 0.9993 | 0.0112 | 0.9914 | 0.0414 |
| Standardize | RBF kernel | 0.9544 | 0.0929 | 0.9464 | 0.1094 |
| k | Training | Testing | ||
|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | |
| 3 | 0.9998 | 0.0057 | 0.9880 | 0.0458 |
| 5 | 0.9986 | 0.0153 | 0.9824 | 0.0568 |
| 7 | 0.9964 | 0.0254 | 0.9746 | 0.0681 |
| 9 | 0.9931 | 0.0355 | 0.9679 | 0.0784 |
| 11 | 0.9889 | 0.0457 | 0.9581 | 0.0902 |
| Dose (kGy) | 50 °C | 60 °C | 70 °C | |||||
|---|---|---|---|---|---|---|---|---|
| Deff | R2 | Deff | R2 | Deff | R2 | |||
| 0 | 4.2311 | 0.9654 | 6.6385 | 0.9756 | 8.2434 | 0.9779 | ||
| 1.2 | 4.4500 | 0.9824 | 7.0398 | 0.9824 | 8.4988 | 0.9809 | ||
| 2.4 | 6.4561 | 0.9877 | 8.4623 | 0.9772 | 8.9365 | 0.9832 | ||
| 3.6 | 8.4988 | 0.9823 | 10.3956 | 0.9661 | 10.7968 | 0.9676 |
| Ea (kJ/mol) | Ea/R | R2 | D0 (m2/s) | Dose (kGy) |
|---|---|---|---|---|
| 30.81 | 3706.4 | 0.9671 | 0.004216 | 0 |
| 29.91 | 3598.0 | 0.9526 | 0.003190 | 1.2 |
| 15.06 | 1812.4 | 0.8830 | 0.000018 | 2.4 |
| 11.09 | 1334.4 | 0.8769 | 0.000005 | 3.6 |
| Dose (kGy) | Temperature (°C) | Drying Time (min) | Heating Duration (min) | Heat Utilization Efficiency (%) |
|---|---|---|---|---|
| 50 | 310 | 124 | 25.13 | |
| 0 | 60 | 220 | 132 | 23.61 |
| 70 | 180 | 144 | 21.64 | |
| 50 | 290 | 116 | 26.87 | |
| 1.2 | 60 | 205 | 123 | 25.34 |
| 70 | 180 | 144 | 21.64 | |
| 50 | 250 | 100 | 31.17 | |
| 2.4 | 60 | 175 | 105 | 29.68 |
| 70 | 165 | 132 | 23.61 | |
| 50 | 190 | 76 | 41.01 | |
| 3.6 | 60 | 135 | 81 | 38.48 |
| 70 | 130 | 104 | 29.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fartash Naeimi, E.; Khoshtaghaza, M.H.; Selvi, K.Ç.; Ungureanu, N.; Abbasi, S. Optimization of the Drying Process for Gamma-Irradiated Mushroom Slices Using Mathematical Models and Machine Learning Algorithms. Agriculture 2024, 14, 2351. https://doi.org/10.3390/agriculture14122351
Fartash Naeimi E, Khoshtaghaza MH, Selvi KÇ, Ungureanu N, Abbasi S. Optimization of the Drying Process for Gamma-Irradiated Mushroom Slices Using Mathematical Models and Machine Learning Algorithms. Agriculture. 2024; 14(12):2351. https://doi.org/10.3390/agriculture14122351
Chicago/Turabian StyleFartash Naeimi, Ehsan, Mohammad Hadi Khoshtaghaza, Kemal Çağatay Selvi, Nicoleta Ungureanu, and Soleiman Abbasi. 2024. "Optimization of the Drying Process for Gamma-Irradiated Mushroom Slices Using Mathematical Models and Machine Learning Algorithms" Agriculture 14, no. 12: 2351. https://doi.org/10.3390/agriculture14122351
APA StyleFartash Naeimi, E., Khoshtaghaza, M. H., Selvi, K. Ç., Ungureanu, N., & Abbasi, S. (2024). Optimization of the Drying Process for Gamma-Irradiated Mushroom Slices Using Mathematical Models and Machine Learning Algorithms. Agriculture, 14(12), 2351. https://doi.org/10.3390/agriculture14122351








