Performance Analysis and Operation Parameter Optimization of Shaker-Type Harvesting for Camellia Fruits

Abstract

This study aims to address the challenges of achieving a high harvesting rate and low flower bud damage rate during the harvesting of camellia fruits. To this end, a dynamic model of the camellia osmantha tree and a self-developed shaker-type harvesting machine were used as research subjects. The first 24 natural frequencies and mode shapes of the camellia tree were solved using the finite element method, and the effects of vibration frequency, excitation position, and vibration duration on the harvesting rate and flower bud damage rate were quantitatively analyzed through an orthogonal experiment. The numerical analysis results indicate that the camellia tree exhibits good response characteristics at vibration frequencies of 10–15.5 Hz and 38.5 Hz. The three-factors orthogonal experiment figured out that the optimal operational parameters for shaker-type harvesting were determined to be a vibration duration of 30 s, a motor output frequency of 12.5 Hz, and a gripping position height of 50 to 60 cm above the ground. Meanwhile, under these operational parameters, the harvesting efficiency reached 96.97%, while the flower bud damage rate was only 6%.

1. Introduction

The camellia fruit not only produces high-grade natural green health oil, but also serves as an important premium raw material in the food, pharmaceutical, chemical, and cosmetics industries [1,2]. China’s camellia planting area reaches 4.451 million hectares, accounting for more than 95% of the world’s camellia resources [3]. However, the large harvest volume of camellia fruit, combined with harsh working conditions, results in significant challenges. The lack of harvesting equipment leads to prolonged harvesting times and low efficiency, causing severe losses in camellia fruit harvest yields [4,5,6,7].

To improve the efficiency of camellia fruit harvesting, many researchers have begun studying camellia fruit harvesting machinery. Currently, the main mechanical harvesting methods for forest fruit include comb-type and shaker-type methods [8]. The main forest fruit harvesting equipment currently on the market are the olivspeed series produced by the Italian manufacturer BOSCO, the Fruipick series produced by the Italian manufacturer SPEDO, the OLIVATOR series produced by the portable equipment manufacturer ACTIVE of Italy, and the Brumirak series and the Electronic Shakers series produced by Brumi of Italy. The comb type equipment mainly uses a comb structure to contact the forest fruit, breaking the fruit stalk to complete the harvesting operation. Gao et al. developed a comb-type Camellia oleifera harvesting machine and verified the feasibility of this harvesting method through experiments [9]. Wu et al. designed a shaker-type harvesting machine that clamps the branches of the Camellia oleifera tree and vibrates them to cause the fruits to fall off due to inertial force [10]. The above-mentioned harvesting machines have their own adaptability and limitations when facing different crops. It is easy to cause damage to the flower buds and leaves; the comb-type equipment is limited by the length of the comb and this makes it difficult to pick the forest fruit in the inner layer of the tree during the harvesting process.

To improve the operational quality of shaker-type harvesting, scholars have conducted extensive research, proving that the efficiency of harvesting machinery and the rate of flower bud damage are closely related to parameters such as the vibration frequency, excitation position, and vibration duration of the harvesting equipment [3,11,12,13,14]. Gao et al. designed a small raspberry harvesting machine that can fine-tune the excitation frequency and concluded that the harvesting effect is better when the excitation frequency is in the range of 19 Hz to 23 Hz [15]. Gao et al. designed a suspended shaker-type harvester and found that the best harvesting effect was achieved when the excitation frequency was 15 Hz and the clamping height was 1300 mm, while the fruit drop rate and flower drop rate at this time were 95.1% and 4.8%, respectively [16]. Bentahe et al. simulated and analyzed the vibration modes of olive trees under different loading modes. The results demonstrated the feasibility of the finite element model in studying the shaker-type harvesting mechanism [17]. Wang et al. studied the vibration response characteristics of different trained fruit trees under different loading modes. The results showed that the multidirectional excitation loading was more suitable for the spindle tree, while the orbital excitation loading was more suitable for an open-center tree and a vertical plane tree [18]. However, there has been no research that quantitatively analyzes the effects of the vibration frequency, excitation position, and vibration duration on the operational quality of harvesting machinery.

To reveal the influence of operational parameters on the quality of vibration-based harvesting machinery, this study focuses on the Camellia osmantha (henceforth CO) tree and a self-developed contact-type shaker-type harvester. By establishing a finite element model of the CO tree, multi-body dynamic modal tests are conducted to analyze the vibration response characteristics of trees with different morphologies. Through orthogonal experiments, the effects of vibration frequency, excitation position, and vibration duration on the harvesting rate and flower bud damage rate are quantitatively analyzed. The optimal operating parameters, which achieve both a high fruit harvesting rate and a low flower bud damage rate, are identified. This research provides a theoretical foundation and feasible technical solutions for the design of camellia fruit harvesting machinery.

2. Working Principle of Shaker-Type Harvesting Machine for Camellia Fruit

The shaker-type camellia fruit harvester is based on applying mechanical vibration to the branches, causing the fruits to undergo forced vibrations. When the inertial force generated by the vibration is greater than the binding force between the fruit and the fruit stalk, the fruit separates and falls.

Figure 1 shows the vibration mechanism of a CO fruit harvester, which adopts the crank slider mechanism design. The vibration mechanism is the key structure of the CO fruit harvester, and different excitation effects can be achieved by adjusting the speed of the gasoline engine. This design is not limited to gasoline powered shakers, but additional modifications are required if battery power is used.

Figure 2 shows a working diagram of the mechanism in the harvesting mode. During the harvesting process, the loading vibration at the secondary branches of the CO tree is clamped to generate a periodically changing excitation force. Resonance is generated when the excitation frequency is close to the natural frequency of the tree itself. When the force between the fruit and the stalk exceeds the upper limit of the binding force and causes the connection to break [19], the fruit falls off, achieving the purpose of harvesting the camellia fruit.

The primary branches, secondary branches, crown, and main root of the camellia tree form an elastic system, and the camellia tree is discretized into a multi-degree-of-freedom system consisting of multiple units. The material properties of each unit are defined as isotropic, as mentioned earlier. Only the external excitation of the excitation force is considered during the harvesting process.

If M is the integrated mass matrix, K the integrated stiffness matrix of the shaker-type harvester, the $q,$ $\dot{q}$ are the vibration offset vector and velocity vector of each node of the shaker-type harvester relative to the equilibrium position, respectively, then the kinetic energy T and potential energy V of the camellia tree system are, respectively,

$$T={\displaystyle \frac{1}{2}}M{\dot{q}}^2$$

(1)

$$V={\displaystyle \frac{1}{2}}K{q}^2$$

(2)

Considering the biological system of camellia trees is diverse and complex, the damping of the tree is simplified as equivalent viscous damping, and the integrated damping matrix of the system is recorded as C. The Rayleigh dissipation function D of the simplified shaker-type harvester system is:

$$D={\displaystyle \frac{1}{2}}C{\dot{q}}^2$$

(3)

In order to analyze the dynamic characteristics of the elastic system, the Lagrangian function L = T − V, and the external force vector Q of the system are introduced, and Equations (1) to (3) are substituted into the Lagrangian type II dynamics equations (Rasch’s equations)

$${\displaystyle \frac{d}{dt}}({\displaystyle \frac{\partial L}{\partial \dot{q}}})+{\displaystyle \frac{\partial D}{\partial \dot{q}}}-{\displaystyle \frac{\partial L}{\partial q}}=Q$$

(4)

The system can be obtained with damped kinetic equations:

$$M\ddot{q}+C\dot{q}+Kq=Q$$

(5)

where $\ddot{q}$ is the shaker-type harvester acceleration.

In order to improve the efficiency of the CO fruit harvester, it is necessary to analyze the dynamic performance of the CO tree. In this case, the solution of Equation (5) for a given periodic external excitation is the harmonic response analysis in the finite element dynamics problem, which can be used to simulate the dynamic response of a structure when subjected to a simple harmonic load [5]. During the shaker-type harvesting process of the CO tree, a periodic simple harmonic force is usually applied. The finite-element harmonic response analysis can simulate the vibration test and predict the displacement and acceleration response of the CO tree in a specific frequency range. This helps to optimize the parameter settings during shaker-type harvesting of CO fruit, improve fruit harvesting efficiency, and reduce damage to the CO tree from harvesting mechanical devices.

Considering only the excitation force of the shaker and denoting the vibration frequency of this harmonic response exciting force is ω, solving Equation (5), it is not difficult to obtain the vibration response of the shaker-type harvester as

$$q(t)=A\sin \left(\omega t+\phi \right)e^{-\xi \omega t}$$

(6)

where A is the system vibration amplitude vector, ω is the vibration angular frequency, φ is the initial phase angle, and ξ is the system damping ratio.

Furthermore, when the external excitation is zero and the damping effect is neglected, Equation (5) degenerates to:

$$M\ddot{q}+Kq=0$$

(7)

Substituting Equation (6) into Equation (7) and making ξ = 0, the system characteristic equation is obtained as follows:

$$(K-{\omega }^{2}M)A=0$$

(8)

This leads to the system eigenvalue equation as:

$$|K-{\omega }^{2}M|=0$$

(9)

Equation (8) is solved, i.e., the system is analyzed modally.

The vibration destructive effect at resonance can bring about a more ideal separation effect for the fruit and the fruit tree. Modal analysis can more accurately identify the natural frequency and modal vibration shape of the CO tree structure at resonance [20,21], determine the vibration characteristics of a typical CO tree, and provide theoretical references for the design of this type of mechanism.

3. Physical Characteristics of a CO Tree

The different growth characteristics and shapes of a CO tree directly affect the harvesting efficiency of CO fruit harvesting machines [22,23]. In order to improve the operational efficiency, a combination of agricultural machinery and agronomy can be adopted. The shape of a CO tree can be changed by regular pruning of branches, making it suitable for mechanized harvesting [24].

Generally speaking, the morphology of a CO tree after regular pruning is shown in Figure 3, including primary, secondary, and tertiary branches. Among them, the primary branches are usually composed of one to three trunks with a diameter of about 70 mm, the secondary branches are the side branches of the primary branches, usually five to seven, the tertiary branches are the side branches distributed on the secondary branches, and most of the CO fruits and flower buds are distributed on the tertiary branch, with a diameter ranging from 3 to 30 mm.

Different forms of CO tree structures usually have different physical properties. The author and project team members conducted a data survey to determine the shape parameters of the CO tree for subsequent numerical simulation analysis. The experimental samples were the CO tree nurseries planted in Guangxi. On 20 October 2022, five different varieties of CO trees were selected, and three trees of each variety were randomly selected as samples. A total of 15 CO trees were measured for shape parameters. The shape parameters mainly refer to the diameter and length of the trunk and side branches, and the measuring tools are vernier calipers and tape measures, as shown in Figure 4. After measurement, the average value of the 15 sets of data was taken as the shape parameters of the CO tree, and the results are shown in

Table 1. Statistical analysis table for the measurement of the diameter of the main stem and lateral branches of CO tree (unit: mm).

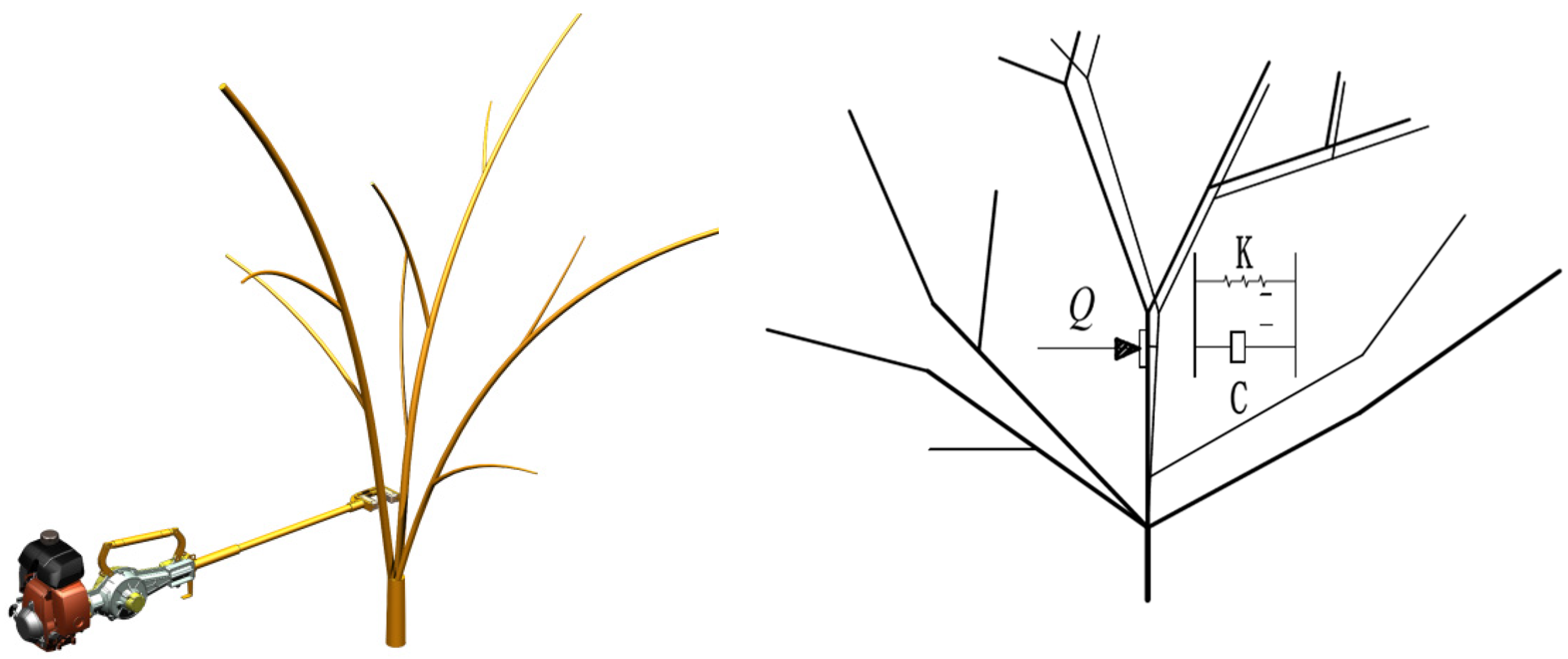
Measuring Part	dmax	dmin	avg	Major Diameter Distribution	Main Diameters in %
first branch	58.7	17.4	34.5	20–35	70%
secondary branch	36.7	10.1	19.9	15–25	80%

:

As shown in Table 1, 70% of the primary branch diameters of the CO tree were distributed in the range of 20–35 mm, and 80% of the secondary branches have a diameter distribution of 15–25 mm. Table 1 can be used as a basis for establishing the geometric model of the CO tree in the following analysis.

The shaker-type harvesting machine for CO fruit is mainly used for the primary and secondary branches of a CO tree, with a diameter range of 10–50 mm. The harvesting process is mainly a movement of the branches in the direction of the force and can therefore be considered as a reciprocating movement of the vibrator in a plane. In order to simplify the complex tree structure and conduct a simple simulation analysis of a CO tree, this paper ignores the orthotropic properties of wood and the bark effect, and regards the CO tree as an isotropic elastic structure, whose vibration characteristics are closely related to the elastic modulus, tensile strength, and density of the CO tree.

The branch test samples were subjected to tensile tests using a SANS electronic universal testing machine, the testing machine model CMT5105. On 21 October 2022, the elastic modulus of tree branches was tested at Guangxi University of Science and Technology, as shown in Figure 5. The precision of the universal testing machine is 0.0001 kN. The universal testing machine displacement control speed was 1.0 mm/mm. Firstly, the diameter of the branch was measured with an accuracy of 0.1 mm, after which the extensometer was tied to the branch. The pitch of the extensometer was 50 mm, and when the tensile test was carried out using an electronic universal testing machine, the small deformation of the extensometer was recorded with an accuracy of 0.001 mm. When the rate of increase in the force of the universal testing machine tends to stabilize, we stop the test. The elastic modulus of the branches was finally obtained to be 18,655.18 MPa.

The density and moisture content of the wood samples were measured at room temperature. The density of some branches of a naturally grown CO tree was measured by first measuring the weight with an electronic scale with an accuracy of 0.01 g, and then measuring the volume of the branches with a measuring cylinder and water with an accuracy of 1 mL. The data of 30 groups of samples were statistically analyzed and the average value was obtained by processing the measured data. The density of CO tree branches was 1.082 g/cm³. Its characteristic Young’s modulus was 18,655.18 MPa and Poisson’s ratio was 0.3. The tree structure was set as an elastic structure and the damping coefficient was taken as 0.0083 [18].

4. Kinetic Characterization of the CO Tree

4.1. Finite Element Model of the CO Tree

Three-dimensional modeling was carried out by referring to the surveying data of the physical samples of a CO tree. At the same time, in order to improve the calculation efficiency, the three-level branches of the CO tree were simplified. Finally, a three-dimensional model of the typical structure of the CO tree was obtained as shown in Figure 6.

The physical properties of CO tree structures with different morphologies are usually different. In order to determine the form parameters of a CO tree, the authors and project team members conducted experimental tests on the actual planted CO tree, and the experimental samples were the CO tree nurseries planted in Guangxi. Five different varieties of CO tree were selected, and three trees of each variety were randomly selected as samples, totaling 15 trees for the determination of form parameters, which mainly refers to the diameter and length of the main stem and lateral branches, and the measuring tool is a vernier caliper. After the measurement, the average value of 15 groups of data was taken as the shape parameter of the CO tree. The three-dimensional model of the CO tree was imported into ANSYS 2022 R1 software for finite element analysis. The solid unit SOLID187 was used to discretize the CO tree, which is suitable for the vibration response characteristic analysis of the CO tree. Since the soil is a multi-point contact action on the root system of fruit trees, the approximation of fixing the root and soil was used to constrain the X, Y, and Z direction degrees of freedom of the roots. Since the established finite element model is large, in order to reduce the calculation time, the finite element grid unit size was set to 0.1 m while meeting the calculation accuracy requirements. A total of 6248 nodes and 2365 units were generated, as shown in Figure 7.

4.2. Modal Analysis of the CO Tree

Considering that the working frequency of the CO fruit harvesting mechanism should not be too high, the modal analysis frequency range of this paper is 0–50 Hz. Using the Lanczos method, the first 26 vibration frequencies of the branches are listed in

Table 2. Frequency table of the main modes of the finite element model of the CO tree.

Order	1	2	3	4	5	6	7	8
Frequency/Hz	3.05	3.15	3.16	3.99	4.13	4.93	4.98	12.46
Order	9	10	11	12	13	14	15	16
Frequency/Hz	12.64	13.79	14.32	14.71	15.56	17.52	18.49	24.64
Order	17	18	19	20	21	22	23	24
Frequency/Hz	25.61	26.97	27.19	32.90	33.70	35.52	36.22	38.5

. In order to give the best vibration form of fruit branch separation, Figure 8 shows the modal vibration shape diagram under the eighth best vibration form.

4.3. Frequency Response Characteristics of the CO Tree

The amplitude of the force at the excitation node is taken as 500 N and the structure is analyzed for its frequency response. Figure 9 gives the characteristic vibration response curves of some key nodes of the CO tree model under a single gyratory type excitation mode, and the frequency range is 0~35 Hz.

It can be seen from Figure 8 that when the excitation frequency is 13 to 15.5 Hz and 38.5 Hz, a more significant vibration response will be triggered. These frequencies are close to the 8th, 9th, 12th, and 24th order modal frequencies of the CO tree mode, respectively. Especially in the range of 12.5 to 15.5 Hz, the vibration response is particularly severe. It should be noted that node responses at other frequencies are beyond the normal working range of the harvester and will not be considered. In actual work, 12.5 Hz is used as the working frequency of the CO fruit harvesting mechanism.

Figure 8. Modal cloud diagrams of the model of the CO tree at typical orders.

Figure 8. Modal cloud diagrams of the model of the CO tree at typical orders.

Figure 9. Characteristic curve of vibration response of CO tree under loading.

Figure 9. Characteristic curve of vibration response of CO tree under loading.

5. Shaker-Type Harvesting Experiment on the CO Tree

5.1. Test Materials and Methods

Generally speaking, the harvesting efficiency of the CO fruit harvesting machinery is related to the loading height, excitation frequency, and excitation duration. In order to study the influence of these setting parameters on the harvesting effect, this section specially constructs an orthogonal test table, with a total of 24 working conditions for harvesting. The experiment was conducted from 25 October to 27 October 2023 and the experimental samples were CO tree nurseries planted in Guangxi. The average tree height was 2.7 m, and the average crown width was 3.9 m². Since the size of the fruit tree and the fruit harvesting season have a great influence on the harvesting effect, 36 CO trees with similar tree size and fruit in the mature stage were selected for the purposes of the experiment.

5.2. Evaluation Criteria for CO Fruit Harvesting Rate and Flower Bud Damage Rate

In order to verify the rationality of the CO fruit harvester, based on practical experience, the harvesting process is evaluated by the harvesting rate and flower bud damage rate.

In this regard, a counting method may be used to calculate the net harvesting rate. Specifically, after each vibration of the CO tree, the fallen fruits are collected and the number is noted as Cr; then, we harvest the unshed fruits from the CO tree and count them as Cu. The net harvesting rate Pn is

$$P_n={\displaystyle \frac{C_r}{C_r+C_u}}\times 100\%$$

(10)

The total number of flower buds recorded before the shaker-type operation was Su. The number of flower buds dropped after the operation is Sr; the number of flower buds should be recorded separately before and after conducting the experiment and the flower bud damage rate should be calculated according to the following equation: Pd is

$$P_d={\displaystyle \frac{S_r}{S_u}}\times 100\%$$

(11)

In order to reduce the complexity of the experiment, a one-factor test was conducted with the objectives of a high CO fruit harvesting rate and a low bud damage rate; the optimal ranges of each factor were optimized to determine the experimental factor codes, as shown in

Table 3. Considerations.

Encodings	Considerations
	Loading Height/cm	Excitation Frequency/Hz	Excitation Time/s
−1	30–40	10	20
0	40–50	12.5	25
1	50–60	15	30

. A BoxBehnken Design (BBD) response surface test with three factors and three levels was designed using Design-Expert 13 software; a total of 17 groups of tests were designed. The relationship between the experimental factors and the experimental evaluation indicators was characterized by fitting a multivariate quadratic equation.

5.3. Results and Discussion

The tree before and after the operation of the picker is shown in Figure 10, and the data on the harvesting of CO fruits under different working conditions are shown in

Table 4. Experimental design and results.

Serial Number	Considerations			Evaluation Indicators
	Load High A/cm	Excitation Frequency B/Hz	Excitation Duration C/s	Harvesting Rate/%	Pod Damage Rate/%
1	30–40	15	25	95.1	14.26
2	40–50	10	30	79.29	10.41
3	50–60	12.5	30	91.58	17.14
4	30–40	12.5	20	90.1	5.26
5	50–60	12.5	20	86.11	12.41
6	50–60	10	25	78.36	8
7	40–50	12.5	25	88.59	10.81
8	50–60	12.5	30	96.97	6
9	30–40	12.5	30	86.95	26.32
10	40–50	12.5	25	84.09	9.52
11	40–50	15	20	92.1	14.29
12	50–60	12.5	30	94.32	20
13	40–50	10	20	74.98	5.56
14	30–40	10	20	79.07	28.38
15	40–50	15	30	92.68	16.25
16	50–60	15	25	96.36	56.41
17	30–40	10	25	83.65	26.92

.

Based on the experimental results obtained in Table 4, a quadratic polynomial regression model was obtained by Design-Expert 13

$$\left\{\begin{array}{l}Y1=86.75+0.2351A+7.70B+1.56C+\hfill \\ 1.23AB+2.65AC-1.34BC+\hfill \\ 3.12A^2-1.71B^2-0.4850C^2\hfill \\ Y2=9.15+1.60A+5.78B+3.02C+\hfill \\ 16.28AB-4.15AC+0.2934BC+\hfill \\ 10.16A^2+7.59B^2-4.61C^2\hfill \end{array}\right.$$

(12)

where Y1 is the harvesting rate; Y2 is the flower bud damage rate; A is the loading height; B is the excitation frequency; C is the excitation duration.

From the analysis of variance of the regression models (

Table 5. Analysis of variance of the quadratic polynomial model for harvesting rate.

Source	Degrees of Freedom	Mean Square	F-Value	p-Value
Model	9	79.24	14.27	0.0010 *
A-loading height	1	0.5279	0.0951	0.7668
B-Excitation frequency	1	500.17	90.08	<0.0001 **
C-Excitation duration	1	23.25	4.19	0.0800 **
AB	1	6.71	1.21	0.3081
AC	1	39.22	7.06	0.0326 *
BC	1	8.05	1.45	0.2677
A2	1	33.87	6.10	0.0428 *
B2	1	10.30	1.86	0.2153
C2	1	0.8186	0.1474	0.7124
Residual	7	5.55
Lack of fit	4	3.55	0.4325	0.7822
Pure error	3	8.22
Cor total	16
Determination R2	0.9483

Note: ** indicates highly significant (p < 0.01); * indicates significant (0.01 ≤ p ≤ 0.05).

and

Table 6. Analysis of variance of the quadratic polynomial model for bud damage rate.

Source	Degrees of Freedom	Mean Square	F-Value	p-Value
Model	9	242.51	5.01	0.0226 *
A-loading height	1	24.41	0.5039	0.5008
B-Excitation frequency	1	281.99	5.82	0.0466 *
C-Excitation duration	1	87.33	1.80	0.2213
AB	1	1182.50	24.41	0.0017 **
AC	1	96.30	1.99	0.2014
BC	1	0.3838	0.0079	0.9316
A2	1	359.37	7.42	0.0296 *
B2	1	203.41	4.20	0.0796
C2	1	73.88	1.52	0.2567
Residual	7	48.45
Lack of fit	4	57.22	1.56	0.3730
Pure error	3	36.75
Cor total	16
Determination R2	0.8655

Note: ** indicates highly significant (p < 0.01); * indicates significant (0.01 ≤ p ≤ 0.05).

), it can be seen that the P values of the regression models for the CO fruit harvesting rate and bud damage rate were 0.001 and 0.0226, respectively, which was less than 0.05. Therefore, the two models were significant; and the coefficients of determination of the models, R², were 0.9483 and 0.8655, respectively, which showed that the models had small errors, and they could be used for analyzing and predicting the harvesting rate of CO fruits and the bud damage rate of a CO tree. It can be used to analyze and predict the harvesting rate and bract damage rate of CO fruits.

From the comparative analysis in

Table 7. Comparison of harvesting rate and bud damage rate data.

Source	Degrees of Freedom	Harvesting Rate			Bud Damage Rate
		Mean Square	F-Value	p-Value	Mean Square	F-Value	p-Value
Model	9	79.24	14.27	0.0010 *	242.51	5.01	0.0226 *
A-loading height	1	0.5279	0.0951	0.7668	24.41	0.5039	0.5008
B-Excitation frequency	1	500.17	90.08	<0.0001 **	281.99	5.82	0.0466 *
C-Excitation duration	1	23.25	4.19	0.0800 **	87.33	1.80	0.2213

Note: ** indicates highly significant (p < 0.01); * indicates significant (0.01 ≤ p ≤ 0.05).

, it can be seen that the excitation frequency has a significant impact on the extraction rate and bud damage rate of CO fruits. The loading height has no significant effect on the harvesting rate and bud damage rate of CO fruits. The duration of excitation has a significant impact on the recovery rate of CO fruits. The main order of factors affecting the harvesting rate of CO fruit and the bud damage rate is the excitation frequency, excitation duration, and blessing height.

Through the analysis of the regression model of the harvesting test by Design-Expert software, it can be seen that when the harvesting time of the harvesting device is 30 s, the motor output frequency is 12.5 Hz, and the clamping position of the clamping claw (the distance from the ground to the clamping center of the clamping tea branch) is 50–60 cm, the harvesting rate is 96.97%, and the flower bud damage rate is 6%. This product was successfully used in the selection and yield measurement of CO tree varieties by the State Forestry and Grassland Administration at the end of 2023. Compared with manual harvesting, both the harvesting time and the flower bud damage rate are less, so this CO fruit shaker-type harvesting machine meets the harvesting requirements.

6. Conclusions

Since the device is still in the experimental stage, there is still a certain gap compared with the real mechanized harvesting of CO fruit. In particular, the bud damage rate needs to be further reduced, which requires the optimization of operating parameters and clamping materials. The research in this paper provides a useful reference for further optimizing operating parameters, but further experiments and improvements are needed to achieve better harvesting results.

In this paper, a combination of finite element modelling and harmonic response simulation experiments is adopted to study the influence of the vibration frequency, excitation position, and vibration duration on the harvesting rate and flower bud damage rate during the shaker-type harvesting of camellia fruit. The experimental results show that:

The CO tree will induce a more significant vibration response when the excitation frequency is 10 to 15.5 Hz and 38.5 Hz. These frequencies correspond to the 8th, 9th, 13th, and 24th order modal frequencies of the CO tree mode, respectively. Especially at 12.5 Hz, the vibration response is the most severe.

The factor that has the greatest impact on the harvesting rate and flower bud damage rate is the motor output frequency, that is, the vibration frequency of the clamping head. The factors with less impact are the clamping position of the clamping head and the harvesting time of the harvesting device.

When the vibration frequency of the CO fruit harvester was 12.5 Hz, the vibration time was 30 s, and the clamping position was 50–60 cm from the ground; the net harvesting rate of the CO fruit was the highest, which was 96.97%, and the flower bud damage rate was 6%.