Color Dominance-Based Polynomial Optimization Segmentation for Identifying Tomato Leaves and Fruits
Abstract
1. Introduction
2. Color Dominance Segmentation Applying Unique Interpolation Polynomial Method
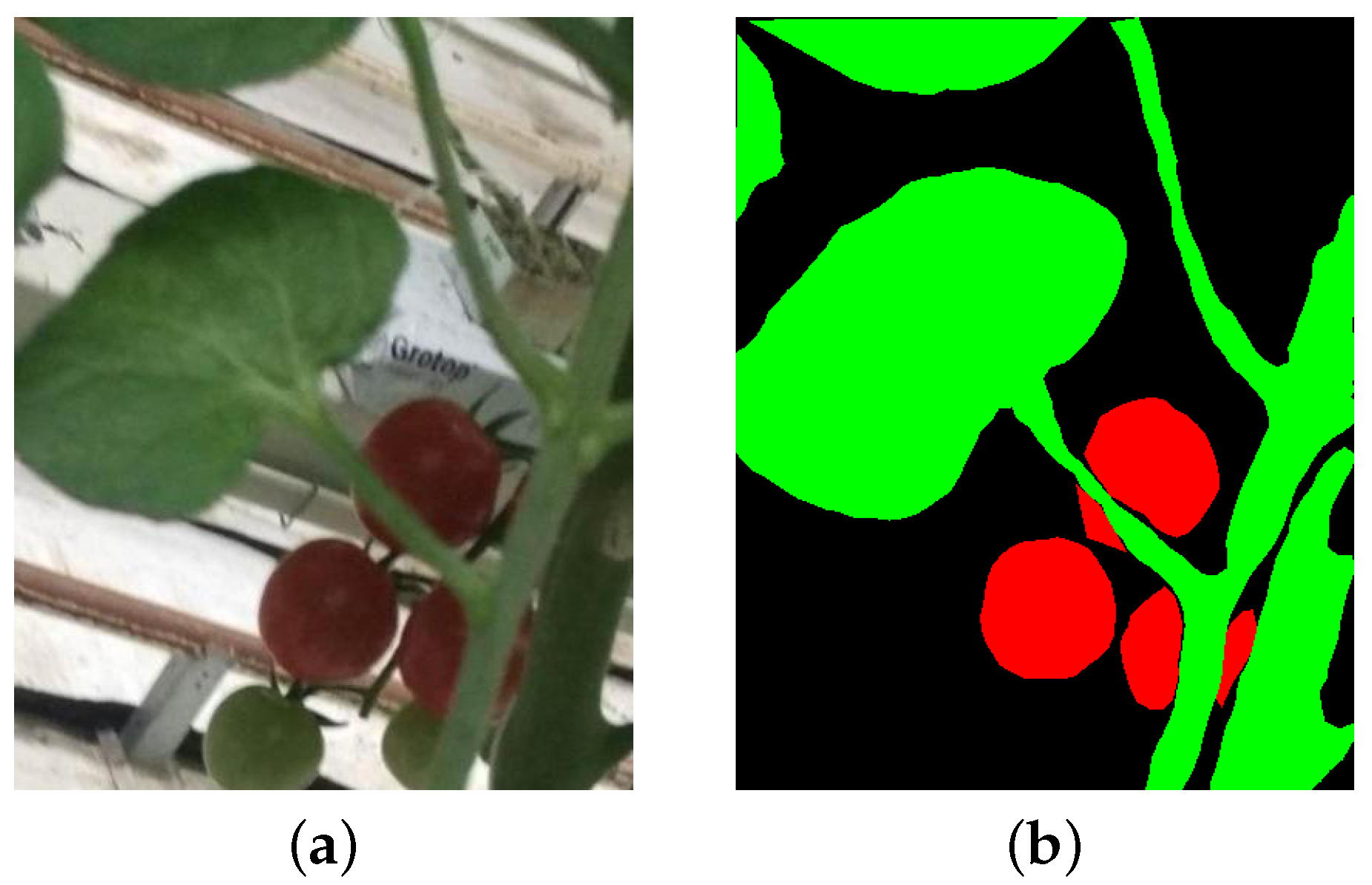
2.1. Segmentation Method by Color Dominance
2.2. Unique Interpolation Polynomial (UIP)
2.3. Dataset
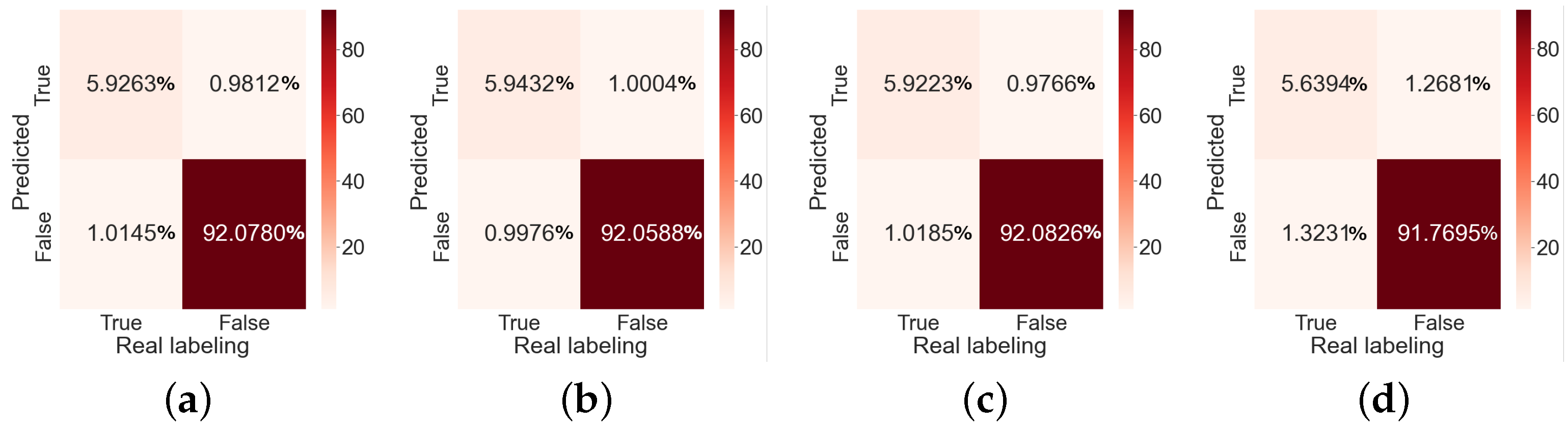
2.3.1. Performance Metrics
- True-Positive are pixels that the segmentation algorithm classifies as belonging to a class and in the mask if they belong to this class.
- True-Negative are pixels that the segmentation algorithm classifies as not belonging to a class and in the mask do not belong to this class.
- False-Positive are pixels that the segmentation algorithm classifies as belonging to a class and in the mask are not.
- False-Negative are pixels that the segmentation algorithm classifies as not belonging to a class, and in the mask they are.
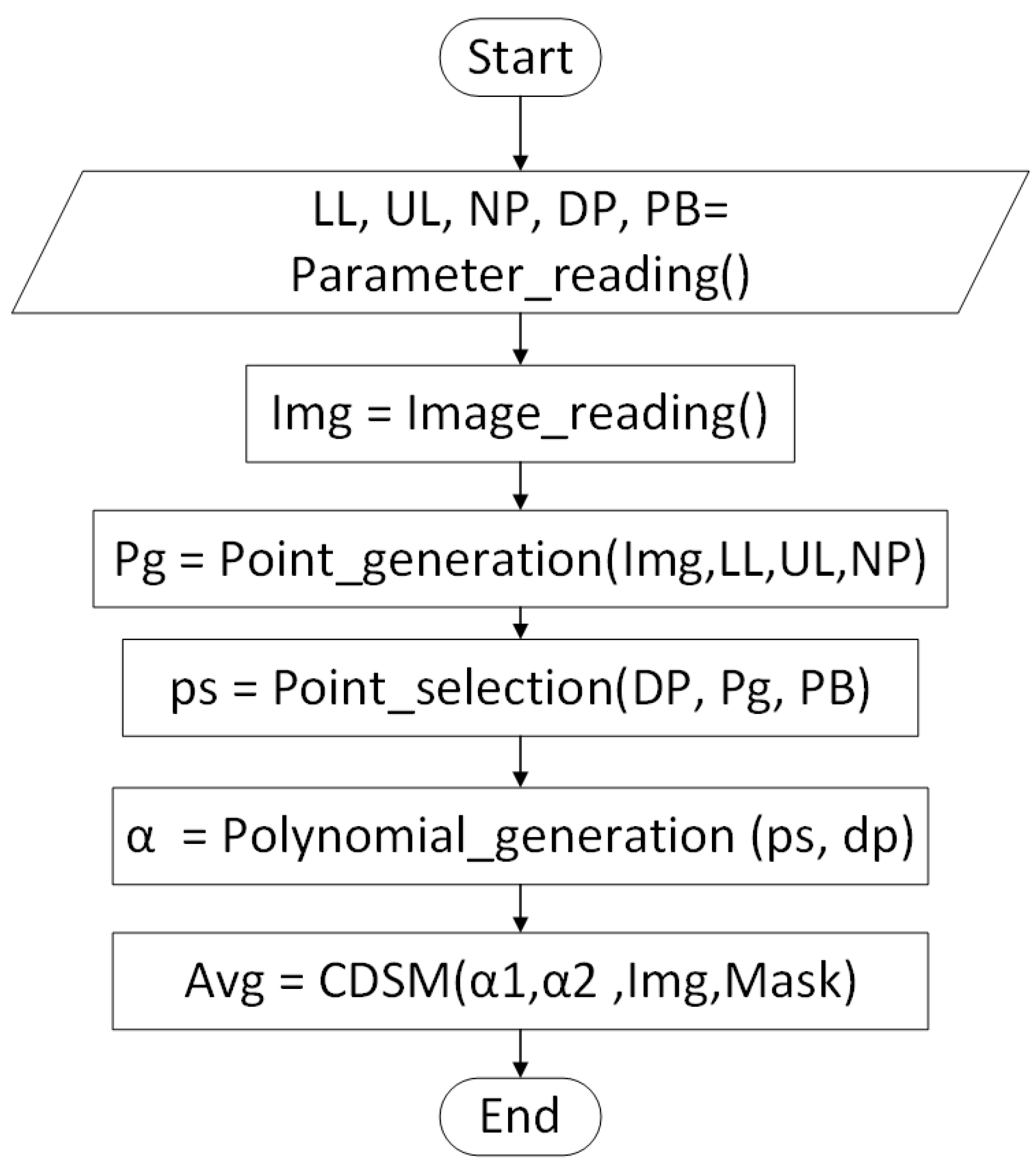
2.4. Polynomial Optimization Method
| Algorithm 1 Basic Algorithm for generation of initial points |
|
| Algorithm 2 Selection of points to interpolate from and |
|
| Algorithm 3 Basic Algorithm for function polynomial generation |
|
| Algorithm 4 Color dominance method of segmentation |
|
3. Experimentation and Results
- Manufacturer: ASUSTeK COMPUTER Inc., Taipei, China
- Modelo: X510UNR
- Processor: Intel® Core™ i7-8550U CPU @ 1.80GHz × 8.
- RAM: 16 GB.
- Operating system: Ubuntu 22.04.2 LTS 64 bits.
4. Comparison of Results Between Interpolation Procedure vs. Greedy Algorithm vs. UNet CNN
| Algorithm 5 Greedy algorithm for determining the optimal values of and |
|
5. Practical Applications
- Crop Monitoring: Efficient segmentation of leaves and fruits allows farmers to more accurately track the condition of their crops, facilitating early detection of issues such as diseases or pests.
- Irrigation and Fertilization Optimization: With a more detailed analysis of vegetation, farmers can adjust irrigation and fertilization practices more effectively, optimizing resource use and improving crop yields.
- Precision Harvesting: Accurate segmentation aids in planning harvests, enabling identification of the optimal time for collection and reducing damage to the plants.
- Plant Health Analysis: By differentiating between healthy and unhealthy leaves, the method can be used to assess the overall health of plants and make informed decisions about crop management.
6. Conclusions
6.1. Limitations
6.2. Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gebbers, R.; Adamchuk, V.I. Precision agriculture and food security. Science 2010, 327, 828–831. [Google Scholar] [CrossRef] [PubMed]
- Rorie, R.L.; Purcell, L.C.; Karcher, D.E.; King, C.A. The assessment of leaf nitrogen in corn from digital images. Crop Sci. 2011, 51, 2174–2180. [Google Scholar] [CrossRef]
- Sun, Y.; Gao, J.; Wang, K.; Shen, Z.; Chen, L. Utilization of Machine Vision to Monitor the Dynamic Responses of Rice Leaf Morphology and Colour to Nitrogen, Phosphorus, and Potassium Deficiencies. J. Spectrosc. 2018, 2018, 1469314. [Google Scholar] [CrossRef]
- Dhingra, G.; Kumar, V.; Joshi, H.D. A novel computer vision based neutrosophic approach for leaf disease identification and classification. Meas. J. Int. Meas. Confed. 2019, 135, 782–794. [Google Scholar] [CrossRef]
- Ireri, D.; Belal, E.; Okinda, C.; Makange, N.; Ji, C. A computer vision system for defect discrimination and grading in tomatoes using machine learning and image processing. Artif. Intell. Agric. 2019, 2, 28–37. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, D.; Zhang, G.; Wang, J. Estimating nitrogen status of rice using the image segmentation of G-R thresholding method. Field Crop. Res. 2013, 149, 33–39. [Google Scholar] [CrossRef]
- Kirk, K.; Andersen, H.J.; Thomsen, A.G.; Jørgensen, J.R.; Jørgensen, R.N. Estimation of leaf area index in cereal crops using red-green images. Biosyst. Eng. 2009, 104, 308–317. [Google Scholar] [CrossRef]
- Sun, Y.; Tong, C.; He, S.; Wang, K.; Chen, L. Identification of Nitrogen, Phosphorus, and Potassium Deficiencies Based on Temporal Dynamics of Leaf Morphology and Color. Sustainability 2018, 10, 762. [Google Scholar] [CrossRef]
- Castillo-Martínez, M.; Gallegos-Funes, F.J.; Carvajal-Gámez, B.E.; Urriolagoitia-Sosa, G.; Rosales-Silva, A.J. Color index based thresholding method for background and foreground segmentation of plant images. Comput. Electron. Agric. 2020, 178, 105783. [Google Scholar] [CrossRef]
- Nakane, T.; Bold, N.; Sun, H.; Lu, X.; Akashi, T.; Zhang, C. Application of evolutionary and swarm optimization in computer vision: A literature survey. IPSJ Trans. Comput. Vis. Appl. 2020, 12, 3. [Google Scholar] [CrossRef]
- Puranik, P.; Bajaj, P.; Abraham, A.; Palsodkar, P.; Deshmukh, A. Human perception-based color image segmentation using comprehensive learning particle swarm optimization. In Proceedings of the 2009 2nd International Conference on Emerging Trends in Engineering and Technology, ICETET, Nagpur, India, 16–18 December 2009; pp. 630–635. [Google Scholar] [CrossRef]
- Ghamisi, P.; Couceiro, M.S.; Martins, F.M.; Benediktsson, J.A. Multilevel image segmentation based on fractional-order darwinian particle swarm optimization. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2382–2394. [Google Scholar] [CrossRef]
- Tao, W.B.; Tian, J.W.; Liu, J. Image segmentation by three-level thresholding based on maximum fuzzy entropy and genetic algorithm. Pattern Recognit. Lett. 2003, 24, 3069–3078. [Google Scholar] [CrossRef]
- Liang, Y.C.; Chen, A.H.L.; Chyu, C.C. Application of a hybrid ant colony optimization for the multilevel thresholding in image processing. In Neural Information Processing, Proceedings of the 13th International Conference, ICONIP 2006, Hong Kong, China, 3–6 October 2006, Proceedings, Part II; Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2006; Volume 4233, pp. 1183–1192. [Google Scholar] [CrossRef]
- Vergés-Llahí, J.; Climent, J.; Sanfeliu, A. Colour image segmentation solving hard-constraints on graph partitioning greedy algorithms. Proc.-Int. Conf. Pattern Recognit. 2000, 15, 625–628. [Google Scholar] [CrossRef]
- Subr, K.; Majumder, A.; Irani, S. Greedy algorithm for local contrast enhancement of images. In Image Analysis and Processing—ICIAP 2005, Proceedings of the 13th International Conference, Cagliari, Italy, 6–8 September 2005. Proceedings 13; Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2005; Volume 3617, pp. 171–179. [Google Scholar] [CrossRef]
- Patil, B.M.; Amarapur, B. Segmentation of leaf images using greedy algorithm. In Proceedings of the 2017 International Conference on Energy, Communication, Data Analytics and Soft Computing, ICECDS 2017, Chennai, India, 1–2 August 2018; pp. 2137–2141. [Google Scholar] [CrossRef]
- Le Guyader, C.; Apprato, D.; Gout, C. Using a level set approach for image segmentation under interpolation conditions. Numer. Algorithms 2005, 39, 221–235. [Google Scholar] [CrossRef]
- Paiement, A.; Mirmehdi, M.; Xie, X.; Hamilton, M.C. Integrated segmentation and interpolation of sparse data. IEEE Trans. Image Process. 2014, 23, 110–125. [Google Scholar] [CrossRef]
- Ge, M.S.; Wu, P.T.; Zhu, D.L.; Zhang, L. Application of different curve interpolation and fitting methods in water distribution calculation of mobile sprinkler machine. Biosyst. Eng. 2018, 174, 316–328. [Google Scholar] [CrossRef]
- Moon, T.; Hong, S.; Choi, H.Y.; Jung, D.H.; Chang, S.H.; Son, J.E. Interpolation of greenhouse environment data using multilayer perceptron. Comput. Electron. Agric. 2019, 166, 105023. [Google Scholar] [CrossRef]
- Guerra Ibarra, J.P.; Cuevas, F.J. Segmentation of Leaves and Fruits of Tomato Plants by Color Dominance. AgriEngineering 2023, 5, 1846–1864. [Google Scholar] [CrossRef]
- Li, J.; Zhang, F.; Qian, X.; Zhu, Y.; Shen, G. Quantification of rice canopy nitrogen balance index with digital imagery from unmanned aerial vehicle. Remote Sens. Lett. 2015, 6, 183–189. [Google Scholar] [CrossRef]
- Nagar, H.; Sharma, R. Pest Detection on Leaf using Image Processing. In Proceedings of the 2021 International Conference on Computer Communication and Informatics (ICCCI), Coimbatore, India, 27–29 January 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, D.; Jia, W.; Ji, W.; Ruan, C.; Sun, Y. Cucumber fruits detection in greenhouses based on instance segmentation. IEEE Access 2019, 7, 139635–139642. [Google Scholar] [CrossRef]
- Kang, H.; Chen, C. Fruit detection and segmentation for apple harvesting using visual sensor in orchards. Sensors 2019, 19, 4599. [Google Scholar] [CrossRef] [PubMed]
- González Perea, R.; Daccache, A.; Rodríguez Díaz, J.A.; Camacho Poyato, E.; Knox, J.W. Modelling impacts of precision irrigation on crop yield and in-field water management. Precis. Agric. 2018, 19, 497–512. [Google Scholar] [CrossRef]
- Jaiswal, S.; Pandey, M.K. A Review on Image Segmentation. Adv. Intell. Syst. Comput. 2021, 1187, 233–240. [Google Scholar] [CrossRef]
- Taheri, M.; Lim, N.; Lederer, J. Balancing Statistical and Computational Precision and Applications to Penalized Linear Regression with Group Sparsity; Department of Computer Sciences and Department of Biostatistics and Medical Informatics: Madison, WI, USA, 2016; pp. 233–240. [Google Scholar]
- Rezatofighi, H.; Tsoi, N.; Gwak, J.; Sadeghian, A.; Reid, I.; Savarese, S. Generalized intersection over union: A metric and a loss for bounding box regression. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 658–666. [Google Scholar] [CrossRef]
- Feo, T.A.; Resende, M.G.C. Greedy Randomized Adaptive Search Procedures. J. Glob. Optim. 1995, 6, 109–133. [Google Scholar] [CrossRef]
- Guerra Ibarra, J.P.; Cuevas de la Rosa, F. Optimization of Color Dominance Factor by Greedy Algorithm for Leaves and Fruit Segmentation of Tomato Plants. In Pattern Recognition; Mezura-Montes, E., Acosta-Mesa, H.G., Carrasco-Ochoa, J.A., Martínez-Trinidad, J.F., Olvera-López, J.A., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 200–209. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. UNet: Convolutional Networks for Biomedical Image Segmentation; Springer: Cham, Switzerland, 2015; Volume 9351, pp. 234–241. [Google Scholar] [CrossRef]
- McNeely-White, D.; Beveridge, J.R.; Draper, B.A. Inception and ResNet features are (almost) equivalent. Cogn. Syst. Res. 2020, 59, 312–318. [Google Scholar] [CrossRef]




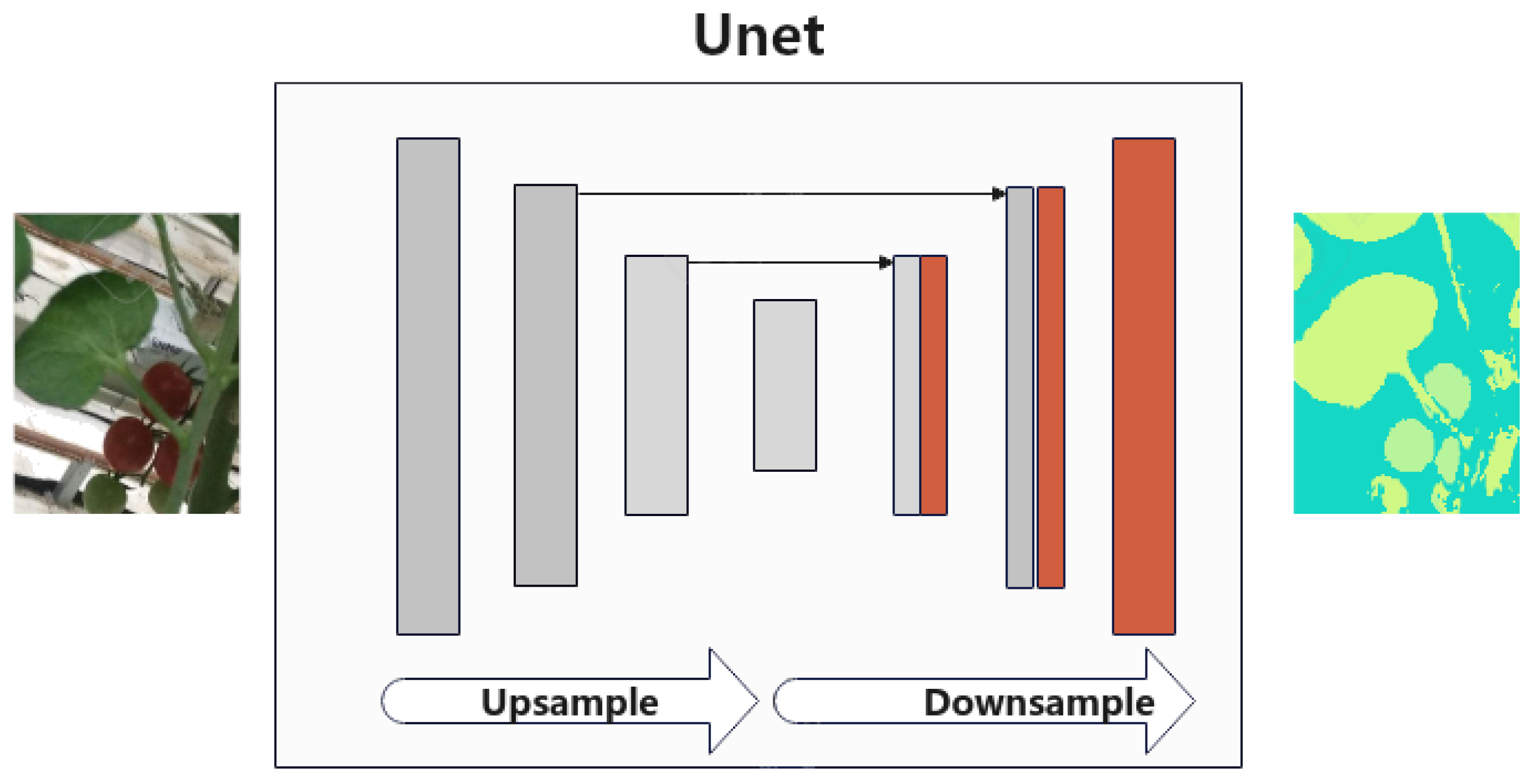

| General Parameter Initial Values | |
|---|---|
| Parameter | Initial value |
| Lower limit (LL) | 1 |
| Upper limit (UL) | 10 |
| NP | 18 |
| Second-degree interpolation | |
| DP | 2 |
| PB | {2, 1, 0} |
| Third-degree interpolation | |
| DP | 3 |
| PB | {3, 2, 1, 0} |
| Leaves | Fruits | ||
|---|---|---|---|
| Value | Average | Value | Average |
| 1 | 0.82810 | 1 | 0.77064 |
| 1.5 | 0.86569 | 1.5 | 0.80076 |
| 2 | 0.88711 | 2 | 0.81728 |
| 2.5 | 0.89840 | 2.5 | 0.82309 |
| 3 | 0.90308 | 3 | 0.81783 |
| 3.5 | 0.90184 | 3.5 | 0.79786 |
| 4 | 0.89481 | 4 | 0.76556 |
| 4.5 | 0.88032 | 4.5 | 0.72516 |
| 5 | 0.85739 | 5 | 0.67627 |
| 5.5 | 0.82693 | 5.5 | 0.63124 |
| 6 | 0.78917 | 6 | 0.58066 |
| 6.5 | 0.74334 | 6.5 | 0.53069 |
| 7 | 0.69495 | 7 | 0.48455 |
| 7.5 | 0.64235 | 7.5 | 0.44542 |
| 8 | 0.59173 | 8 | 0.40557 |
| 8.5 | 0.53794 | 8.5 | 0.37429 |
| 9 | 0.49586 | 9 | 0.34096 |
| 9.5 | 0.45202 | 9.5 | 0.31707 |
| 10 | 0.41148 | 10 | 0.29246 |
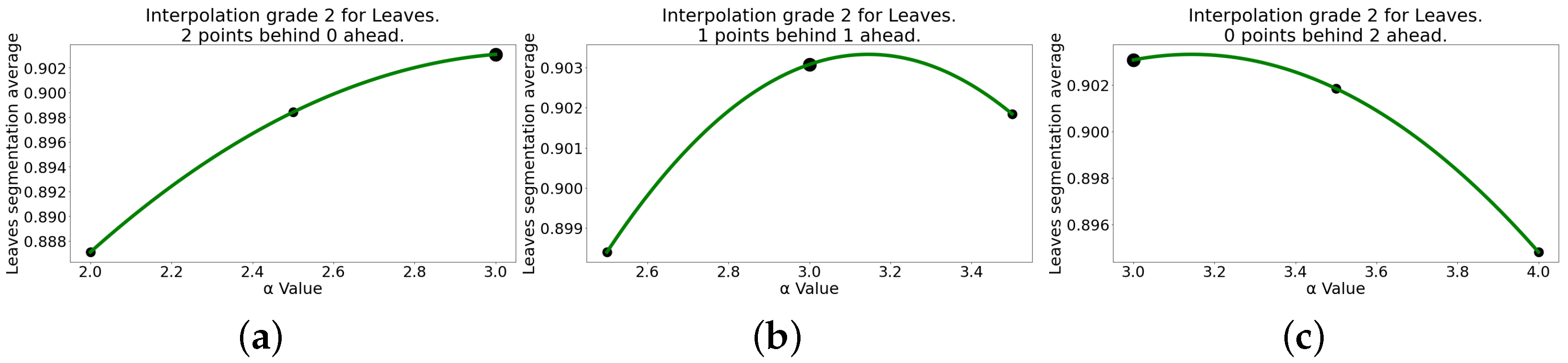
| Second-Degree Interpolation for Leaves | ||||||
|---|---|---|---|---|---|---|
| Points | Points | Polynomial | Derivative | Value α1 | Generated Value | Real Segmenting |
| Behind | Ahead | f(x) | f′(x) | Root | f(α1) | Avg. |
| 2 | 0 | |||||
| 1 | 1 | |||||
| 0 | 2 | |||||
| Second-Degree Interpolation for Fruits | ||||||
|---|---|---|---|---|---|---|
| Points | Points | Polynomial | Derivative | Value α2 | Generated Value | Real Segmenting |
| Behind | Ahead | f(x) | f′(x) | Root | f(α2) | Avg. |
| 2 | 0 | |||||
| 1 | 1 | |||||
| 0 | 2 | |||||
| Third-Degree Interpolation for Leaves | ||||||
|---|---|---|---|---|---|---|
| Points | Points | Polynomial | Derivative | Value α1 | Generated Value | Real Segmenting |
| Behind | Ahead | f(x) | f′(x) | Root | f(α1) | Avg. |
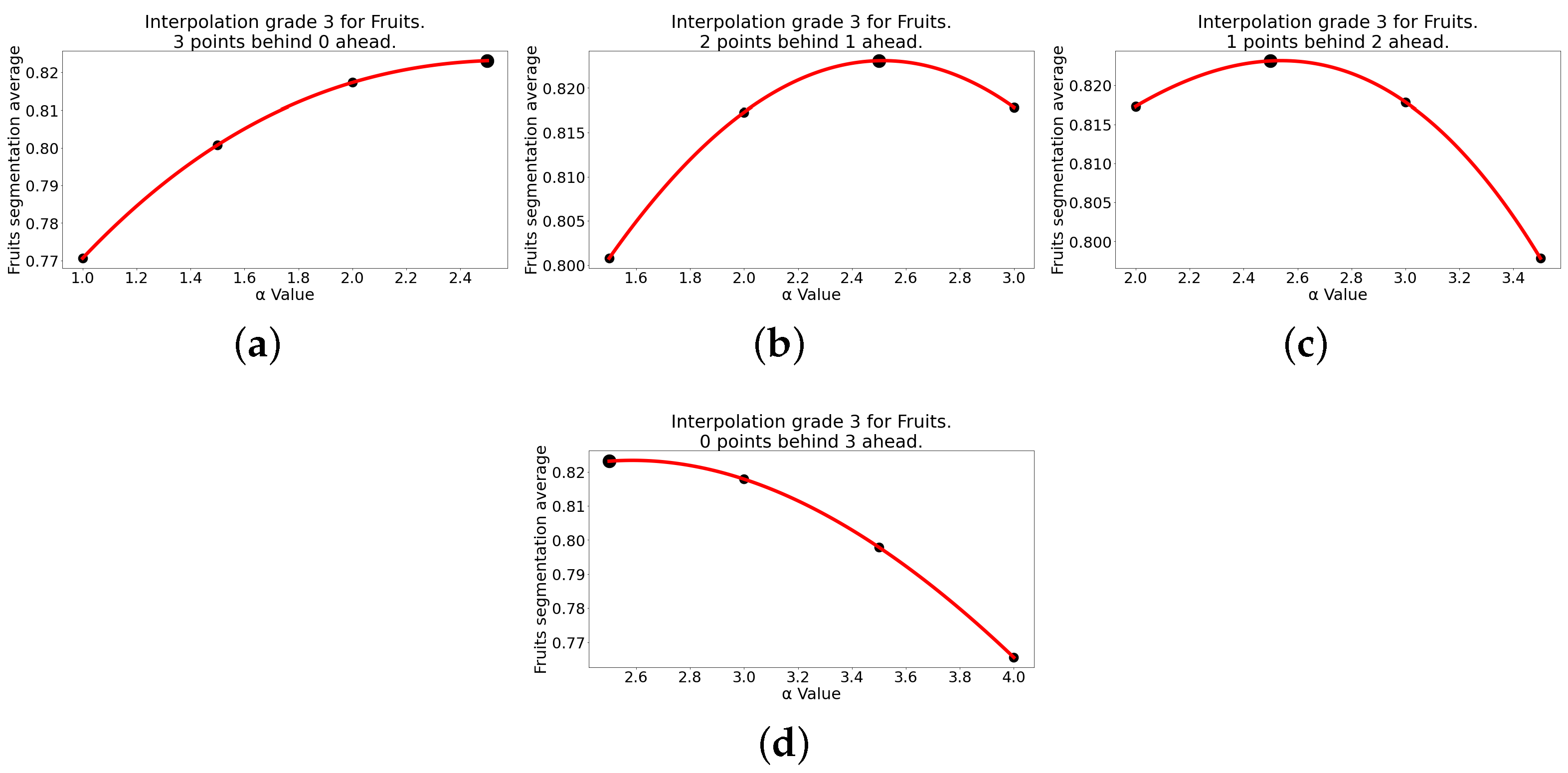
| 3 | 0 | |||||
| 2 | 1 | |||||
| 1 | 2 | |||||
| 0 | 3 | |||||
| Third-Degree Interpolation for Fruits | ||||||
|---|---|---|---|---|---|---|
| Points | Points | Polynomial | Derivative | Value α2 | Generated Value | Real Segmenting |
| Behind | Ahead | f(x) | f′(x) | Root | f(α2) | Avg. |
| 3 | 0 | |||||
| 2 | 1 | |||||
| 1 | 2 | |||||
| 0 | 3 | |||||
| General Parameter for Greedy Algorithm | |
|---|---|
| Parameter | Initial value |
| Lower limit for leaves (LLl) | 1 |
| Upper limit for leaves (ULl) | 10 |
| Lower limit for fruit (LLf) | 1 |
| Upper limit for fruit (ULf) | 10 |
| step | |
| sc | |
| Comparison of Leaves Segmentation Results of Interpolation Method vs. Greedy Algorithm | ||||
|---|---|---|---|---|
| Greedy algorithm | ||||
| Optimum value of real (AR) | Real avg. (RA) | |||
| 3.141900 | 0.903296 | |||
| Interpolation procedure | ||||
| Degree polynomial | Calculated (CA) | Generated avg. (GA) | Error | Error segmentation |
| 2 | 3.145660 | 0.903291 | ||
| 3 | 3.137880 | 0.903292 | ||
| Comparison of Fruits Segmentation Results of Interpolation Method vs. Greedy Algorithm | ||||
|---|---|---|---|---|
| Greedy algorithm | ||||
| Optimum value of real (AR) | Real avg. (RA) | |||
| 2.57940 | 0.823170 | |||
| Interpolation procedure | ||||
| Degree polynomial | Calculated (CA) | Generated avg. (GA) | Error | Error segmentation |
| 2 | ||||
| 3 | ||||
| Method | Leaves | Fruits |
|---|---|---|
| POM Second-degree | 0.903291 | 0.823139 |
| POM Third-degree | 0.903292 | 0.823135 |
| Greedy algorithm | 0.903296 | 0.823170 |
| Unet | 0.880544 | 0.819766 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerra Ibarra, J.P.; Cuevas de la Rosa, F.J.; Linares Ramirez, A. Color Dominance-Based Polynomial Optimization Segmentation for Identifying Tomato Leaves and Fruits. Agriculture 2024, 14, 1911. https://doi.org/10.3390/agriculture14111911
Guerra Ibarra JP, Cuevas de la Rosa FJ, Linares Ramirez A. Color Dominance-Based Polynomial Optimization Segmentation for Identifying Tomato Leaves and Fruits. Agriculture. 2024; 14(11):1911. https://doi.org/10.3390/agriculture14111911
Chicago/Turabian StyleGuerra Ibarra, Juan Pablo, Francisco Javier Cuevas de la Rosa, and Alicia Linares Ramirez. 2024. "Color Dominance-Based Polynomial Optimization Segmentation for Identifying Tomato Leaves and Fruits" Agriculture 14, no. 11: 1911. https://doi.org/10.3390/agriculture14111911
APA StyleGuerra Ibarra, J. P., Cuevas de la Rosa, F. J., & Linares Ramirez, A. (2024). Color Dominance-Based Polynomial Optimization Segmentation for Identifying Tomato Leaves and Fruits. Agriculture, 14(11), 1911. https://doi.org/10.3390/agriculture14111911






