Abstract
When mugwort is mechanically harvested, problems such as a low efficiency and high crushing rate seriously affect the quality of mugwort and restrict the development of the mugwort industry. In order to improve the efficiency of mugwort harvesting and reduce the crushing rate, the finite element method simulation and experiment are combined to study the optimal harvesting method of mugwort. Firstly, the parameters of the components of mugwort, such as the mugwort culm, mugwort stalk, and mugwort leaf, were investigated by tensile and three-point bending methods to determine the values of density, the modulus of elasticity, and Poisson’s ratio, and to establish the material mechanics model of mugwort. Secondly, harvesting of mugwort was simulated through the established three-dimensional model of mugwort, combined with its material mechanics model and using display dynamics. Finally, by conducting harvesting tests on mugwort, the harvesting force of different harvesting directions and harvesting positions were measured to reveal the harvesting mechanism of mugwort and to determine the optimal harvesting direction and position of mugwort leaves. The experimental results showed that the harvesting force was lowest when the harvesting angle was 0° or 90°, and the leaves were least damaged when the harvesting position was close to the stalk. The results of the study can provide data support for the study of the mechanical properties of mugwort and provide a theoretical basis for the research and development of high-efficiency and low-loss mugwort harvesting machinery and the optimisation of harvesting methods.
1. Introduction
The herb mugwort is a high-value-added herb in the Artemisia genus of the Asteraceae family, and mugwort leaves have high economic benefits [1,2,3,4]. Its leaves are dried and crushed to obtain the moxa velvet; the moxa velvet is widely favoured by more and more people, because the moxa velvet has beneficial functions for the human body, such as the effect of haemostasis to drive away cold and dampness to eliminate fatigue, and other efficacies [5,6,7]. However, its price is still high because the current harvesting of mugwort leaves is mainly by manual labour, and the cost of harvesting is high [8,9]. With the increase in the planting area of mugwort, the shortage of labour for mugwort harvesting is becoming more and more prominent. Therefore, it is urgent to design and develop a mugwort harvester. Experts and scholars have also developed some mugwort harvesting machines [10,11,12]; however, mugwort leaves were more broken and also contain more weeds, such as mugwort branches, and it also affected the yield of mugwort leaves [13,14]. Thus, the development of a low-loss and high-efficiency wormwood harvester is necessary. In addition, there has been little research on the mechanical properties of mugwort, leading to a lack of key parameters in research and development, and then affecting the accuracy of research and development results. In addition, broken mugwort leaves and debris, such as mugwort branches and dead mugwort leaves, affect the quality of mugwort leaves and subsequent processing; the subsequent processing includes drying and sieving. So, it is crucial to investigate the breakage mechanism of mugwort leaves in order to obtain high-quality mugwort leaves.
The nature of mugwort leaf breakage is that the harvesting force is higher than the strength of the adhesion of mugwort leaves [15,16], and the adhesion strength of different parts of the mugwort plant is different, and when mechanically harvesting, the different contact positions will affect the harvesting effect. In addition, the harvesting mode also has a significant effect on the harvesting force [17,18]. Thus, harvesting mugwort by different positions and different angles can more accurately analyse the fracture mechanism of mugwort. Whereas the macroscopic and microscopic structures of mugwort are more complex, the more realistic its 3D model is, the more accurate the subsequent finite element-based harvesting simulation will be. Hence, modelling different parts of mugwort separately, such as mugwort leaves, mugwort stems, and mugwort branches, is more conducive to an accurate simulation analysis. In addition, the properties and parameters of mugwort leaves, mugwort stems, and mugwort branches are different. So, it is necessary to model the material mechanics of the mugwort leaf, mugwort stem, and mugwort branch separately through physical tests. Based on the above, we expected to access harvesting mechanisms and determine the best direction and location of mugwort by performing finite element method simulations and experiments.
Therefore, in order to obtain mugwort leaves with a low impurity rate and high quality during efficient mechanical harvesting, this paper takes mugwort as the research object, and firstly, a three-dimensional model of mugwort consisting of the mugwort branch, mugwort stem, and mugwort leaf was constructed. Secondly, on the basis of the physical test of the texture instrument, the mechanical parameters of mugwort branches, mugwort stems, and mugwort leaves were obtained, and the material mechanical model of the above-mentioned components of mugwort was established. Finally, through finite element method simulation and experimental study of the mugwort harvesting process, the fracture mechanism of mugwort leaves was explored, the mugwort harvesting force was obtained, and the optimal direction and position of mugwort leaves were determined. The results provided data support for the study of the mechanical properties of mugwort, and provided a theoretical basis for the development of high-efficiency and low-loss mugwort harvesting machinery and the optimisation of harvesting methods.
2. Materials and Methods
2.1. Three-Dimensional Engineering Modelling of the Branch, Stem, and Leaf of Mugwort
The macroscopic and microscopic structures of mugwort are complex, and the more realistic its 3D model is, the more accurate the subsequent finite element-based harvesting simulation will be. Due to the different mechanical properties of different parts of mugwort, the results of the harvesting simulation and experiments would be affected; therefore, the mugwort was divided into three parts in the modelling, the mugwort branch, mugwort stem, and mugwort leaf, as shown in Figure 1.
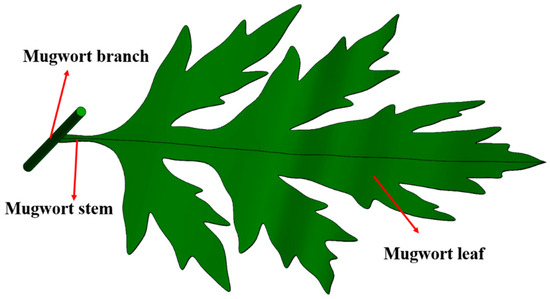
Figure 1.
Mugwort 3D model.
2.2. Physical Tests on Branch, Stem, and Leaf of Mugwort
Density, the modulus of elasticity, and Poisson’s ratio are the basic parameters when mugwort is subjected to finite element method-based harvesting simulations. Density determines the mass distribution and inertia effect for the mass and inertia force of the mugwort structure. The modulus of elasticity determines the response of mugwort when subjected to a force, and Poisson’s ratio is the degree of the lateral deformation of mugwort under tension. They represent the physical properties of mugwort and determine the mechanical properties of mugwort. The modulus of elasticity should be calculated from the stress–strain curves obtained in the physical tests, and using digital vernier callipers (type: MNT-150; measurement range: 0–150 mm; precision: 0.01 mm; manufactured by Shanghai Yingte Trading Co., Shanghai, China) to measure the diameter of the mugwort stem and branch, the tensile test of the mugwort stem and leaves and the bending test of the mugwort branch were carried out by using a mass spectrometer (FTC, type: TMS-Pro; maximum test force: 500N; manufactured by Food Technology Corporation, Sterling, VA, USA). Density can be calculated from the mass and volume of the different parts of mugwort. An analytical balance (type: ME204E; measurement range: 0–220 g; precision: 0.1 mg; manufactured by METTLER TOLEDO, Zurich, Switzerland) was used to measure the mass and a measuring cylinder (type: 10 mL; precision: 0.1 mL; manufactured by ASONE, Osaka, Japan) was used to measure the volume. Poisson’s ratio can be obtained from the relevant literature.
In order to obtain more accurate stress–strain curves, tensile or bending tests should be chosen according to the characteristics of different parts of the mugwort. The tensile test was used for mugwort stems and mugwort leaves, while the three-point bending test was used for mugwort branches. A number of fresh mugwort samples were randomly selected and the branches, stems, and leaves were intercepted, and the tests were repeated five times in order to eliminate errors and the average values were taken. The tensile tests of mugwort stems and leaves are shown in Figure 2 and Figure 3, respectively. The stems and leaves were placed on the fixture used for tensile testing, and the tensile tests were carried out on the mass spectrometer. The bending test of the mugwort branch is shown in Figure 4, in which the red box shows the local enlargement of the test object. The bending test was carried out by placing the mugwort branch on the fixture used for bending on the mass spectrometer.
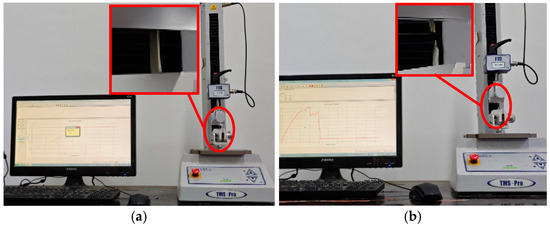
Figure 2.
Physical test of mugwort stem: before test (a); after test (b).

Figure 3.
Physical test of mugwort leaf: before test (a); after test (b).
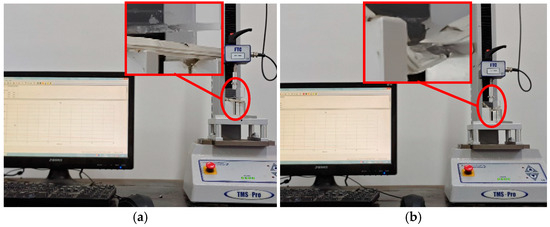
Figure 4.
Physical test of mugwort branch: before test (a); after test (b).
2.3. Mechanical Modelling of Branch, Stem, and Leaf of Mugwort
2.3.1. Elastic Moduli
Physical tests on mugwort were carried out according to references [19,20,21,22], through which it was found that the mechanical properties of mugwort were similar to those of elastoplastic materials. Therefore, the mechanical models of the mugwort branch, mugwort stem, and mugwort leaf were simplified to elastic–plastic models.
The stresses and strains of mugwort stems and mugwort leaves can be calculated according to the following equations, Equations (1) and (2), and references [20,23]:
where σ is the stress of the mugwort stems and mugwort leaves, MPa; F is the load of the test, N; A is the cross-sectional area of the mugwort stems and mugwort leaves, mm2; ε is the strain of the mugwort stems and mugwort leaves, mm·mm−1; ∆l is the change in the length of the mugwort stems and mugwort leaves, mm; and l is the nominal length of the mugwort stems and mugwort leaves, mm.
The modulus of elasticity of mugwort stems and mugwort leaves can be calculated according to Equation (3) based on references [20,23]:
where E is the elastic modulus of the mugwort stems and mugwort leaves, MPa.
The tensile loads and length changes in mugwort stems and mugwort leaves can be obtained from the mass spectrometer, and the nominal lengths can be measured by digital vernier callipers, while the cross-sectional area should be determined based on the shape. The shape of the mugwort stem is similar to a semi-cylinder, so the cross-sectional area of the stem is calculated according to the semi-circular area formula. The cross-section of a mugwort leaf is similar to a rectangle, so the cross-sectional area of a mugwort leaf is calculated according to the rectangular area formula.
The modulus of elasticity of a mugwort branch can be calculated according to Equations (4) and (5) based on references [24,25]:
where I is the moment of inertia of the cross-section of the mugwort branch, mm4; D is the diameter of the mugwort branch, mm; L is the pivot span, which was fixed at 60 mm in the test; ΔF is the change in bending force of the mugwort branch, N; and ΔS is the variation in the bending of the mugwort branch, mm.
The bending force and bending variation in the mugwort branch can be obtained from the mass spectrometer, while the cross-sectional moment of inertia of the mugwort branch should be determined according to the shape. The shape of the mugwort branch is similar to that of a cylinder, so the diameter of the mugwort branch can be measured by digital vernier callipers, and the cross-sectional moment of inertia of the mugwort branch is calculated according to the formula for the moment of inertia of a circular cross-section.
The cross-sectional area of the mugwort stem is the average of the maximum and minimum semi-circular cross-sectional areas of the mugwort stem, and the stress–strain curve of the mugwort stem is shown in Figure 5. Point b is the yield point in the figure, and the elastic stage is between point a and point b, where the mugwort stem deforms linearly. After point b, the mugwort stem enters the yield stage. In the elastic stage, the modulus of elasticity of the mugwort stem can be found according to Equation (3), as shown in Table 1.
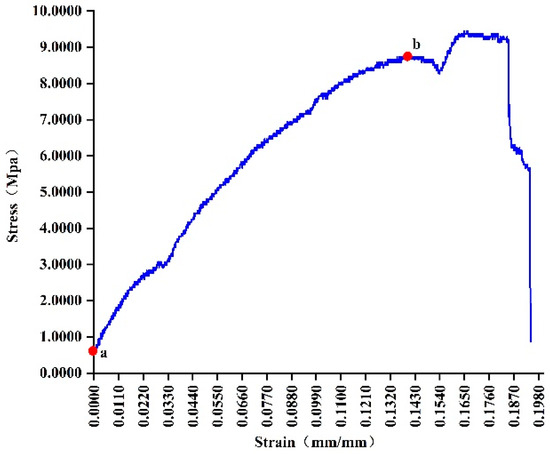
Figure 5.
Stress–strain curve of mugwort stem.

Table 1.
Mechanical parameters of different parts of the mugwort.
The cross-sectional area of a mugwort leaf is the average of its maximum and minimum rectangular cross-sectional areas, and the stress–strain curve of the mugwort leaf is shown in Figure 6. In the figure, point d is the yield point, and the mugwort leaf is deformed linearly in the elastic stage between point c and point d. After point d, the mugwort leaf enters the yield stage. In the elastic stage, the modulus of elasticity of the mugwort leaf can be found according to Equation (3), as shown in Table 1.
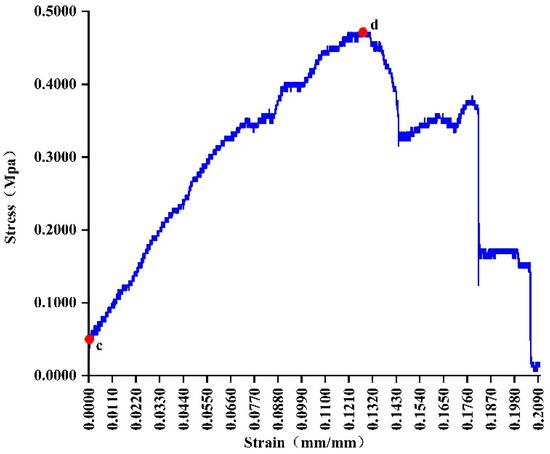
Figure 6.
Stress–strain curve of mugwort leaf.
The bending force–displacement curves of the mugwort branch are shown in Figure 7. In the figure, the elasticity stage is between point e and point f, and the mugwort branch deforms linearly. After point f, the mugwort branch enters the yielding stage. In the elastic phase, the modulus of elasticity of the mugwort branch can be found according to Equation (5), as shown in Table 1.
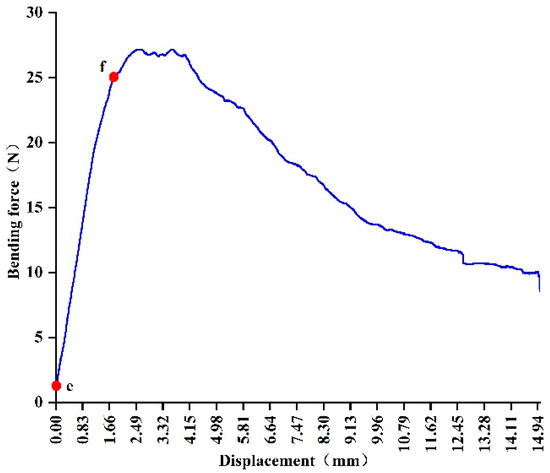
Figure 7.
Bending force–displacement curve of mugwort branch.
2.3.2. Densities
When calculating the volume of different parts of the mugwort plants, the more realistic the assumed shape is, the more accurate the calculated density results will be. Considering the irregularity of the shape of the parts of the mugwort, the drainage method was used to calculate the volume according to reference [26] in order to obtain a more accurate density value. Since the density of each part of mugwort is less than the density of water, a piece of a magnet with a volume of 1000 mm3 was tied to each part of the mugwort as a whole and it was put into a measuring cylinder during the test. The volume of water before and after being put in was recorded and the difference was the volume of each part of the mugwort.
Based on the mass and volume obtained, the density of the mugwort branch, mugwort stem, and mugwort leaf was calculated by the following equation, Equation (6), and the test was repeated three times and the average value was taken. The results are shown in Table 1.
where ρ is the density of the mugwort, kg/m3; m is the mass of the mugwort, kg.
2.3.3. Poisson Ratio
Poisson’s ratio is the ratio of the absolute value of the transverse positive strain to the axial positive strain of a material in a unidirectional compression or tensile test, also known as the transverse deformation coefficient, which is an elastic constant reflecting the transverse deformation of a material [27]. Poisson’s ratio of many materials has been measured by many experts and scholars at home and abroad. Since Poisson’s ratio has a small effect on the simulation results, Poisson’s ratio of each part of the mugwort can be assumed based on Poisson’s ratio of similar materials obtained previously. According to reference [28], Poisson’s ratios of mugwort stems, mugwort leaves, and mugwort branches can be obtained, as shown in Table 1.
2.4. Harvesting Simulation Based on the Finite Element Method
After obtaining the mechanical parameters of each part of mugwort, HyperMesh 2017, HyperView 2017, and Radioss 2017 software were used to simulate its harvesting and to theoretically analyse the defoliation mechanism of mugwort during harvesting. Firstly, the 3D model of mugwort was imported into HyperMesh. Then, mugwort leaves, mugwort stems, and mugwort branches were meshed separately in Components, and each mesh after division was rendered green, while the boundary lines between the meshes were rendered black. Secondly, the mechanical parameters density, modulus of elasticity, and Poisson’s ratio of the different parts of Table 1 were entered in the Materials module, respectively. Finally, the mugwort was fixed in the Load Collectors module, different mugwort stem-to-branch angles were set, and parallel mugwort leaf upward velocities were applied to the upper and lower parts of the mugwort leaf, respectively. The completed pre-processed model was imported into Radioss software for displaying the solution and HyperView was used for the visualisation and analysis of the simulation results.
3. Results and Discussion
3.1. Harvesting Simulation Analysis
Simulation tests at different angles refer to simulation tests conducted from five different directions, including 0°, 30°, 45°, 60°, and 90°, respectively. Simulation tests at different positions were conducted from two different positions such as near the top of the mugwort leaf or the mugwort stem. The position near the top of the mugwort leaf is referred to as the upper part and the position near the mugwort stem is referred to as the lower part. The simulation results of harvesting from different angles and different positions are shown in Figure 8. The output display option of the simulation results is displacement and the value of displacement is the amount of displacement relative to the initial state. The larger the value of displacement, the larger the relative displacement. It displays in real time the relative displacement between the various parts of the harvesting process.

Figure 8.
Mugwort harvesting simulation experiment, (a) mugwort model and simulation results for 0° and different positions, (b) mugwort model and simulation results for 30° and different positions, (c) mugwort model and simulation results for 45° and different positions, (d) mugwort model and simulation results for 60° and different positions, (e) mugwort model and simulation results for 90° and different positions.
In Figure 8, the left side is the mugwort pre-processing model, the upper left side is the mugwort 3D model, the lower left side is the mugwort grid model, and the red box is the local enlargement of the angle between the mugwort stem and the mugwort branch. The right side of the figure shows the simulation visualisation, with the harvesting simulation location on the upper right side in the upper part and the harvesting simulation location on the lower right side in the lower part. The angle between the stem and branch set in Figure 8a is less than 5°, which can be approximated as 0° in the harvesting simulation, and the angles set in Figure 8b–e are 30°, 45°, 60°, and 90°, respectively. The leaf folds appearing in the simulated viewable images are due to the biological properties of mugwort itself, as the naturally grown leaves are not in an absolute plane, whereas the velocity applied when performing the harvesting simulation is in an absolute plane; hence, the folds appear, but they have no effect on the location of leaf breakage.
In the simulations on the upper right side, mugwort leaf breakage occurs on the blades as shown in Figure 8a–e, while their angles are different in the simulations. The results show that when the harvesting position is in the upper part, the breakage of mugwort occurs on the leaf blades at different harvesting angles. In the simulation on the lower right side, the location of mugwort breakage was near the stem; when the harvesting angle was close to 0°, the breakage occurred close to the combination of the mugwort stem and mugwort branch, and when the harvesting angles were 30°, 45°, 60°, and 90°, the breakage occurred close to the combination of the mugwort stem and mugwort leaf. The results showed that when the harvesting position was in the lower part, the fracture occurred close to the mugwort stem at different harvesting angles.
3.2. Field Test Analysis
Harvesting tests of mugwort were conducted from different angles and locations to verify the accuracy of the simulation results. The experimental mugwort was taken from Caohe Town, Herb County, Hubei Province, and harvested on 13 May 2024. Harvesting tests of mugwort were conducted using a texture meter to measure the harvesting force. The harvesting test at different angles refers to the test conducted from five different directions, such as 0°, 30°, 45°, 60°, and 90°, respectively. Harvesting tests at different positions were conducted from two different positions including near the top of the mugwort leaf and the mugwort stem, respectively. The position near the top of the mugwort leaf is referred to as the upper part, and the position near the mugwort stem is referred to as the lower part. The harvesting trials at different angles and different positions are shown in the red dashed circle boxes in Figure 9. The 10 curves in Figure 9a–j are from 10 tests conducted to eliminate errors, while the curves represent the force and displacement. Figure 9a shows that the harvesting angle was 0° and the harvesting position was in the upper position. Figure 9b shows that the harvesting angle was 0° and the harvesting position was in the lower position. Figure 9c shows that the harvesting angle was 30° and the harvesting position was in the upper position. Figure 9d shows that the harvesting angle was 30° and the harvesting position was in the lower position. Figure 9e shows that the harvesting angle was 45° and the harvesting position was in the upper position. Figure 9f shows that the harvesting angle was 45° and the harvesting position was in the lower position. Figure 9g shows that the harvesting angle was 60° and the harvesting position was in the upper position. Figure 9h shows that the harvesting angle was 60° and the harvesting position was in the lower position. Figure 9i shows that the harvesting angle was 90° and the harvesting position was in the upper position. Figure 9j shows that the harvesting angle was 90° and the harvesting position was in the lower position.
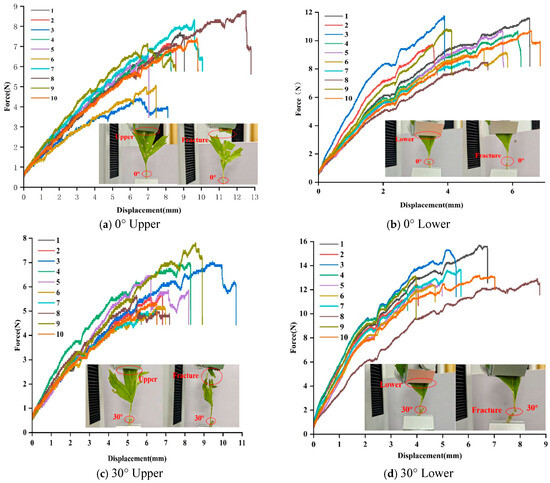
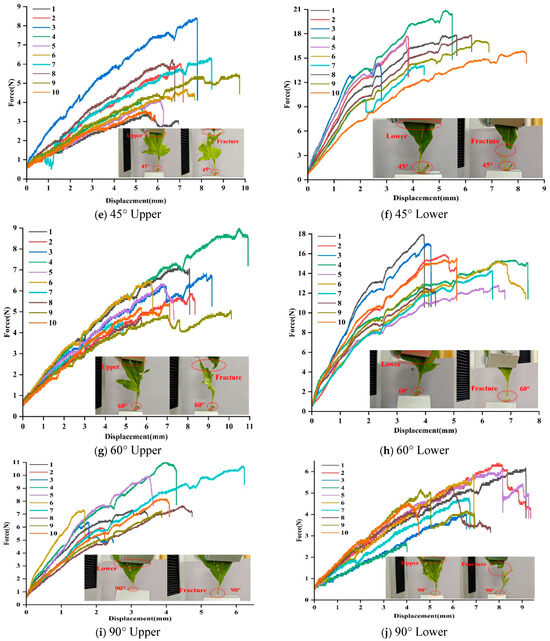
Figure 9.
Harvesting force–displacement curves and samples at different angles and positions.
Harvesting tests at the same angle and at the same position were conducted 10 times in parallel to eliminate random errors, as shown in the curves in Figure 9. The breaking forces of the mugwort at different positions and angles were measured as shown in Table 2. The standard deviation of the data showed that the mean value of each force measured was valid and that for the same harvesting force, the force values were uniformly distributed as shown in Figure 10.

Table 2.
Harvesting force of mugwort in different positions and different angles.
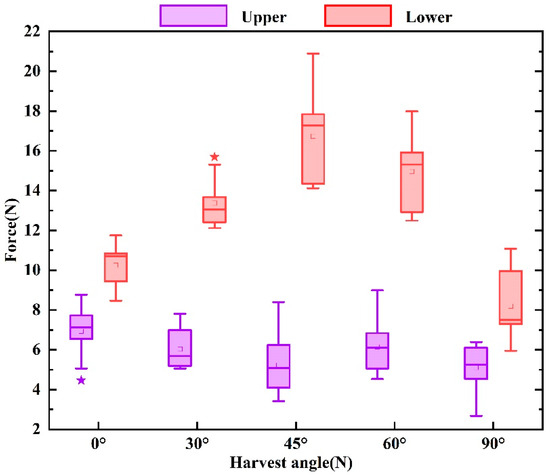
Figure 10.
Mugwort harvesting force box plot.
From the point of view of the harvesting force, it can be seen from Figure 10 that when the harvesting position is in the upper part, the harvesting force is small; at this time, the change in the harvesting angle has little effect on the harvesting force. When the harvesting position is in the lower part, the harvesting force is larger, and the effect of the change in harvesting angle on the harvesting force is more significant; the harvesting force gradually increases from 0° to 45°, and the harvesting force gradually becomes smaller from 45° to 90°, and the harvesting force is the largest when it is around 45°. Under the same harvesting angle, the harvesting force required when the harvesting position is in the lower part is greater than that in the upper part.
Based on the above test results, it can be determined that when mugwort is defoliated, when the harvesting position is near the top of the mugwort leaves, most of the breakages occur at the leaf blades, a few at the combination of the mugwort leaves and the mugwort stems, and very few at the stems or the combination of the mugwort stems and the mugwort branches; when the harvesting position is close to the mugwort stems, most of the breakages occur at the combination of the mugwort stems and the mugwort branches, a few at the stems, and very few at the combination of the mugwort stems and the mugwort leaves, and the different mugwort harvesting angles had little effect on its fracture location. The experimental results were consistent with the simulation results, which further verified the accuracy of the previously established material mechanics model for each part of mugwort.
Therefore, based on the results of this study, the optimal harvesting mode and harvesting position for mechanical harvesting of mugwort can be determined. When harvesting mugwort, impurities such as mugwort stems, dead mugwort, and shredded leaves can affect the overall harvesting of mugwort leaves [13,14]. It illustrated that the harvesting force is different for different harvesting locations and harvesting methods, and the strength of attachment was the major factor that affected the detachment force [15,16]. Therefore, when designing a mugwort harvesting machine, in order to reduce the breakage rate of mugwort leaves, the contact position of the harvesting part with mugwort should be set near the part of the mugwort stem. As the growth angle of mugwort petiole is about 45°, according to Figure 10, the harvesting force is the largest when the harvesting angle is 45°, and the harvesting force is the smallest when the harvesting angle is 0° and 90°, and the harvesting force gradually increases from 0° to 45°, and the harvesting force gradually becomes smaller from 45° to 90°. It also showed that harvesting patterns were also critical for the efficient harvesting from references [17,18,29]. In order to improve the harvesting efficiency, mugwort should be brushed until it is perpendicular or parallel to the mugwort stem before applying the harvesting force. When harvesting mugwort, as long as the harvesting tool is in contact with the mugwort stem first, and then the stem is brushed to 0° or 90°, and then the harvesting force is applied, high-efficiency and low-loss harvesting effects can be achieved.
4. Conclusions
In order to obtain mugwort with a low impurity content and high quality during efficient mechanical harvesting, this study used a combination of finite element method simulation and experimental study to test the harvesting of mugwort at different positions and different angles. Firstly, a three-dimensional model of the mugwort branch, mugwort stem, and mugwort leaf was constructed. Secondly, the mechanical parameters of mugwort leaves, mugwort stems, and mugwort branches were measured according to the physical tests on the mass spectrometer, and the mechanical models of mugwort leaves, mugwort stems, and mugwort branches were established. Finally, the harvesting simulation and experimental study of mugwort were carried out to obtain the harvesting force, determine the harvesting mechanism, and obtain the optimal harvesting direction and position of mugwort. The experimental results showed that the harvesting angle gradually increased from 0° to 45°, the harvesting force gradually became smaller from 45° to 90°, and the harvesting force was maximum at about 45°. Under the same harvesting angle, the harvesting force required when the harvesting position was in the lower part was greater than that in the upper part, and the different harvesting angles of mugwort did not have much effect on its fracture position. Based on the results obtained, the optimum harvesting pattern and harvesting position for mechanical harvesting of mugwort can be determined, which in turn is expected to lead to the design and development of a mugwort harvesting machine that can achieve high-efficiency and low-breakage harvesting results. When designing a mugwort harvesting machine, firstly, the harvesting knives should be set close to the mugwort stems, and then by combing the mugwort leaves until they are perpendicular or parallel to the stems, it is expected to achieve high-efficiency and low-breakage harvesting performance. The results of the study can provide data support for the study of the mechanical properties of mugwort, and can also provide a basis for the optimisation of mugwort harvesting methods.
Author Contributions
Conceptualization, S.W. and D.Z.; methodology, S.W. and D.Z.; software, S.W., D.Z. and R.L.; validation, S.W., D.Z. and X.H.; investigation, S.W., D.Z., X.H. and R.L.; writing—original draft, S.W. and D.Z.; writing—review and editing X.H. and R.L.; visualisation, S.W., D.Z., X.H. and R.L.; funding acquisition, X.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Department of Agriculture and Rural Affairs of Hubei Province [grant number: HBSNYT202220] and the Key Research and Development Program of Hubei Province [grant number: 2022BBA0016].
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Anwar, F.; Ahmad, N.; Alkharfy, K.M.; Gilani, A.-u.-H. Mugwort (Artemisia vulgaris) Oils. In Essential Oils in Food Preservation, Flavor and Safety; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar] [CrossRef]
- Kim, W.-S.; Choi, W.J.; Lee, S.; Kim, W.J.; Lee, D.C.; Sohn, U.D.; Shin, H.-S.; Kim, W. Anti-inflammatory, Antioxidant and Antimicrobial Effects of Artemisinin Extracts from Artemisia annua L. Korean J. Physiol. Pharmacol. 2015, 19, 21–27. [Google Scholar] [CrossRef] [PubMed]
- Pandey, A.K.; Singh, P. The Genus Artemisia: A 2012–2017 Literature Review on Chemical Composition, Antimicrobial, Insecticidal and Antioxidant Activities of Essential Oils. Medicines 2017, 4, 68. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, A.; Gangopadhyay, D.; Chowdhury, T. Economical and Environmental Importance of Mulberry: A Review. Int. J. Plant Environ. 2017, 3, 67–72. [Google Scholar] [CrossRef]
- Szopa, A.; Pajor, J.; Klin, P.; Rzepiela, A.; Elansary, H.; Al-Mana, F.; Mattar, M.; Ekiert, H. Artemisia absinthium L.—Importance in the History of Medicine, the Latest Advances in Phytochemistry and Therapeutical, Cosmetological and Culinary Uses. Plants 2020, 9, 1063. [Google Scholar] [CrossRef] [PubMed]
- Yurchyshyn, O. Search for biologically actuve substances with antimicrobial and antibiotic potentiating properties amoung members of the genus artemisia againts the main pathogens of infectious skin lesions. Art Med. 2021, 5, 84–89. [Google Scholar] [CrossRef]
- Jin, S.; Wang, Y.; Liu, T.; Ning, X.; Liang, R.; Hu, K.; Cao, J. Preparation and Application of Volatilized Wormwood Essence Derived Naturally into Green Insecticide. Molecules 2024, 29, 2877. [Google Scholar] [CrossRef] [PubMed]
- Guyer, D. Mechanical Harvesting. In Advanced Automation for Tree Fruit Orchards and Vineyards; Springer: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Pargi Sanjay, J.; Gupta, P.; Balas, P.R.; Bambhaniya, V.U. Comparison between Manual Harvesting and Mechanical Harvesting. J. Sci. Res. Rep. 2024, 30, 917–934. [Google Scholar] [CrossRef]
- Wang, D. Structural Design and Experimental Analysis of High Efficiency Mugwort Defoliation Machine. Master’s Thesis, Hubei University of Technology, Wuhan, China, 2020. [Google Scholar] [CrossRef]
- Dong, W.T. Design and Experimental Study on the Defoliation Machine of Mugwort. Master’s Thesis, Huazhong Agricultural University, Wuhan, China, 2022. [Google Scholar] [CrossRef]
- Sun, S. Experimental Study on the Influencing Factors of Defoliation Quality of Mugwort Defoliation Machine; Hubei University of Technology: Wuhan, China, 2018; CNKI:CDMD:2.1018.957170. [Google Scholar]
- Hou, J.; Yu, Y.; Tang, Z.; Zhang, L.; Jin, J.; Wang, W. Optimization and experiment on mechanical vibration harvesting process parameters of mulberry. INMATEH Agric. Eng. 2024, 72, 557–568. [Google Scholar] [CrossRef]
- Wang, W.; Lu, H.; Zhang, S.; Yang, Z. Damage caused by multiple impacts of litchi fruits during vibration harvesting. Comput. Electron. Agric. 2019, 162, 732–738. [Google Scholar] [CrossRef]
- Gilman, E. Branch-to-Stem Diameter Ratio Affects Strength of Attachment. J. Arboric. 2003, 29, 291–294. [Google Scholar] [CrossRef]
- Kane, B.; Farrell, R.; Zedaker, S.; Loferski, J.; Smith, D. Failure Mode and Prediction of the Strength of Branch Attachments. Arboric. Urban For. 2008, 34, 308–316. [Google Scholar] [CrossRef]
- Li, J.; Karkee, M.; Zhang, Q.; Xiao, K.; Feng, T. Characterizing apple picking patterns for robotic harvesting. Comput. Electron. Agric. 2016, 127, 633–640. [Google Scholar] [CrossRef]
- Davidson, J.; Silwal, A.; Karkee, M.; Mo, C.; Zhang, Q. Hand-Picking Dynamic Analysis for Undersensed Robotic Apple Harvesting. Trans. ASABE 2016, 59, 745–758. [Google Scholar] [CrossRef]
- Zhao, J.; Tsuchikawa, S.; Ma, T.; Hu, G.; Yun, C.; Wang, Z.; Chen, Q.; Gao, Z.; Chen, J. Modal Analysis and Experiment of a Lycium barbarum L. Shrub for Efficient Vibration Harvesting of Fruit. Agriculture 2021, 11, 519. [Google Scholar] [CrossRef]
- Zhao, J.; Ma, T.; Inagaki, T.; Chen, Q.; Gao, Z.; Sun, L.; Cai, H.; Chen, C.; Li, C.; Zhang, S.; et al. Finite Element Method Simulations and Experiments of Detachments of Lycium barbarum L. Forests 2021, 12, 699. [Google Scholar] [CrossRef]
- Yun, C.; Zhao, J.; Chen, Q.; Chen, J. Simulation for Fitting the Bending Shape of Fruit Branches of Lycium barbarum Based on the Finite Element Method. Horticulturae 2021, 7, 434. [Google Scholar] [CrossRef]
- Zhao, J.; Sugirbay, A.; Chen, Y.; Zhang, S.; Liu, F.; Bu, L.; Yun, C.; Wang, Z.; Chen, J. FEM explicit dynamics simulation and NIR hyperspectral reflectance imaging for determination of impact bruises of Lycium barbarum L. Postharvest Biol. Technol. 2019, 155, 102–110. [Google Scholar] [CrossRef]
- Celik, H.K. Determination of bruise susceptibility of pears (Ankara variety) to impact load by means of FEM-based explicit dynamics simulation. Postharvest Biol. Technol. 2017, 128, 83–97. [Google Scholar] [CrossRef]
- Nie, H.-B. Determination of elastic modulus of cemented carbides by three-point bend tests. Fenmo Yejin Cailiao Kexue Yu Gongcheng/Mater. Sci. Eng. Powder Metall. 2010, 15, 606–610. [Google Scholar]
- Silberschmidt, V. Comprehensive Mechanics of Materials; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar]
- Qing, C.R. Research on Angular Resistance and Plant Structure of Rapeseed Carob and Plucking Mechanism for Low-Loss Mechanised Harvesting; Jiangsu University: Zhenjiang, China, 2021. [Google Scholar]
- The Poisson’s Ratio. Available online: https://baike.baidu.com/item/%E6%B3%8A%E6%9D%BE%E6%AF%94/5920115?fr=aladdin (accessed on 25 May 2021).
- Wang, Y. Abaqus Analysis User’s Guide: Materials Volume, 1st ed.; China Machine Press: Beijing, China, 2018; pp. 27–28. [Google Scholar]
- Bu, L.; Hu, G.; Chen, C.; Sugirbay, A.; Chen, J. Experimental and simulation analysis of optimum picking patterns for robotic apple harvesting. Sci. Hortic. 2019, 261, 108937. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).