Author Contributions
Conceptualisation, E.A.; methodology, E.A., K.A.A. and D.L.A.; software, E.A., K.A.A. and B.V.G.; validation, E.A., D.L.A., K.A.A. and J.Z.; formal analysis, B.V.G., Z.L. and P.M.; investigation, P.M. and Z.L.; data curation, E.A.; writing—original draft preparation, E.A.; writing—review and editing, E.A., K.A.A., D.L.A., J.Z., B.V.G. and P.M.; visualisation, E.A., D.L.A. and K.A.A.; supervision, J.Z.; project administration, J.Z.; funding acquisition, J.Z. All authors have read and agreed to the published version of the manuscript.
Figure 1.
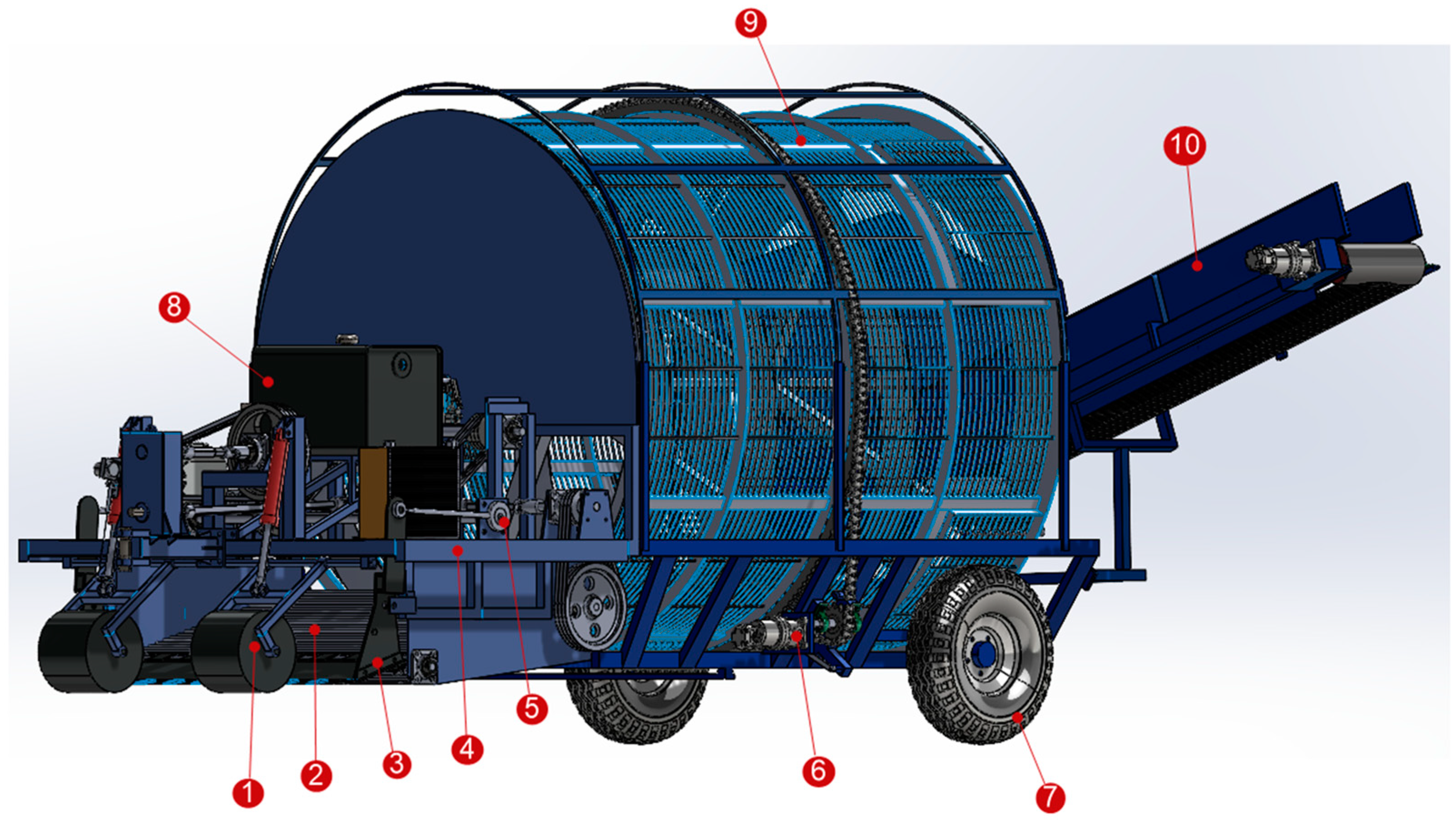
4U-1600A Jerusalem artichoke harvester: (1) diablo rollers (depth adjustment), (2) soil–tuber conveyor, (3) shovel, (4) harvester body, (5) vibration mechanism, (6) hydraulic motor, (7) wheel, (8) hydraulic fluid tank, (9) cleaning cylinder, and (10) tuber conveyor.
Figure 1.
4U-1600A Jerusalem artichoke harvester: (1) diablo rollers (depth adjustment), (2) soil–tuber conveyor, (3) shovel, (4) harvester body, (5) vibration mechanism, (6) hydraulic motor, (7) wheel, (8) hydraulic fluid tank, (9) cleaning cylinder, and (10) tuber conveyor.
Figure 2.
Mechanical and physical properties experiment for Jerusalem artichoke crop: (a) sampled tubers from artichoke field (different sizes and shapes), (b) tuber density determination, (c) uniaxial compression test, (d) inclined plane method for friction coefficients, and (e) root bending test.
Figure 2.
Mechanical and physical properties experiment for Jerusalem artichoke crop: (a) sampled tubers from artichoke field (different sizes and shapes), (b) tuber density determination, (c) uniaxial compression test, (d) inclined plane method for friction coefficients, and (e) root bending test.
Figure 3.
Static angle of repose for soil–crop mass calibration: (a) experiment (the red line is a laser pointer which serves as a visual reference for the angle being measured) and (b) DEM simulation.
Figure 3.
Static angle of repose for soil–crop mass calibration: (a) experiment (the red line is a laser pointer which serves as a visual reference for the angle being measured) and (b) DEM simulation.
Figure 4.
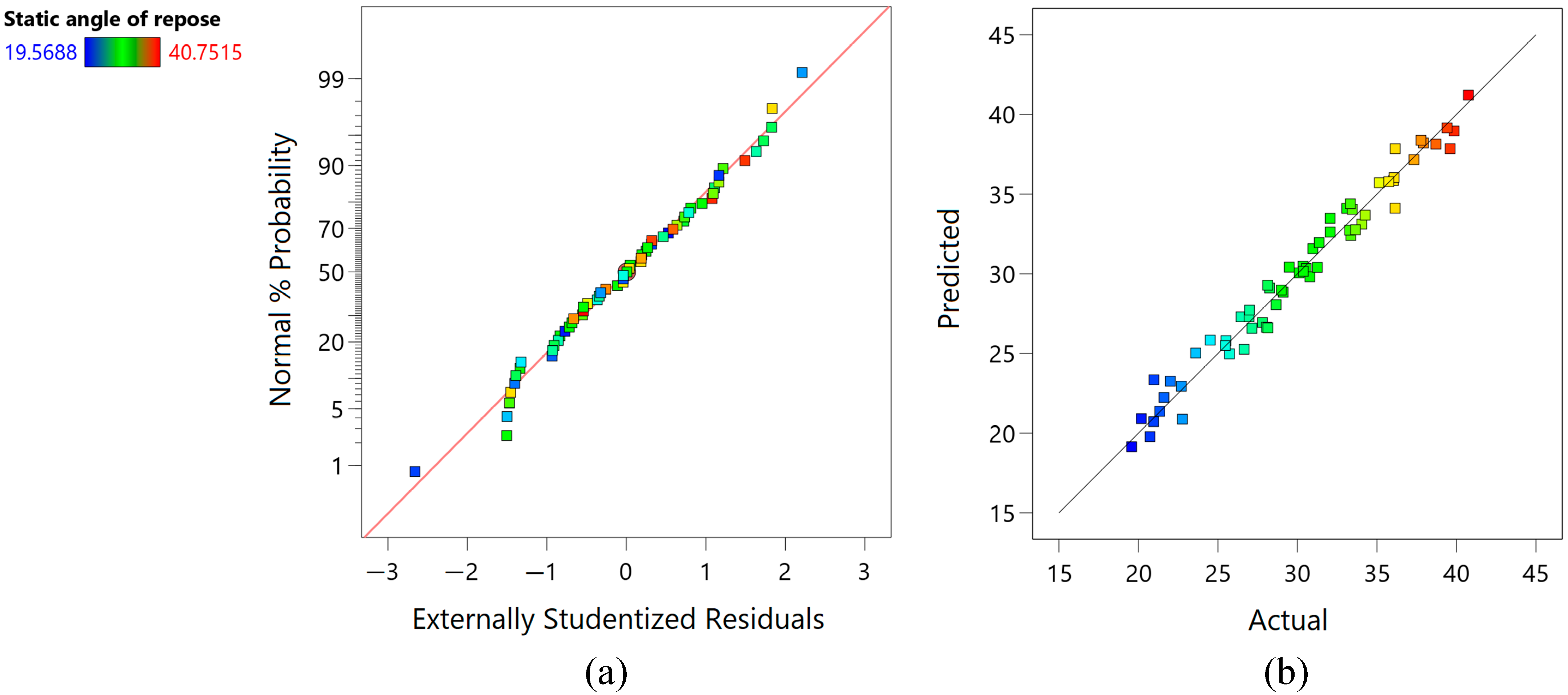
Diagnostic plots: (a) normal plot of residuals and (b) predicted versus actual plot.
Figure 4.
Diagnostic plots: (a) normal plot of residuals and (b) predicted versus actual plot.
Figure 5.
Optimal DEM input parameters from the static angle of repose simulation.
Figure 5.
Optimal DEM input parameters from the static angle of repose simulation.
Figure 6.
DEM crop–modelling technique: (a) Fresh Jerusalem artichoke tuber, (b) 3D computer-aided design model, (c) DEM tuber particle, and (d) DEM crop model.
Figure 6.
DEM crop–modelling technique: (a) Fresh Jerusalem artichoke tuber, (b) 3D computer-aided design model, (c) DEM tuber particle, and (d) DEM crop model.
Figure 7.
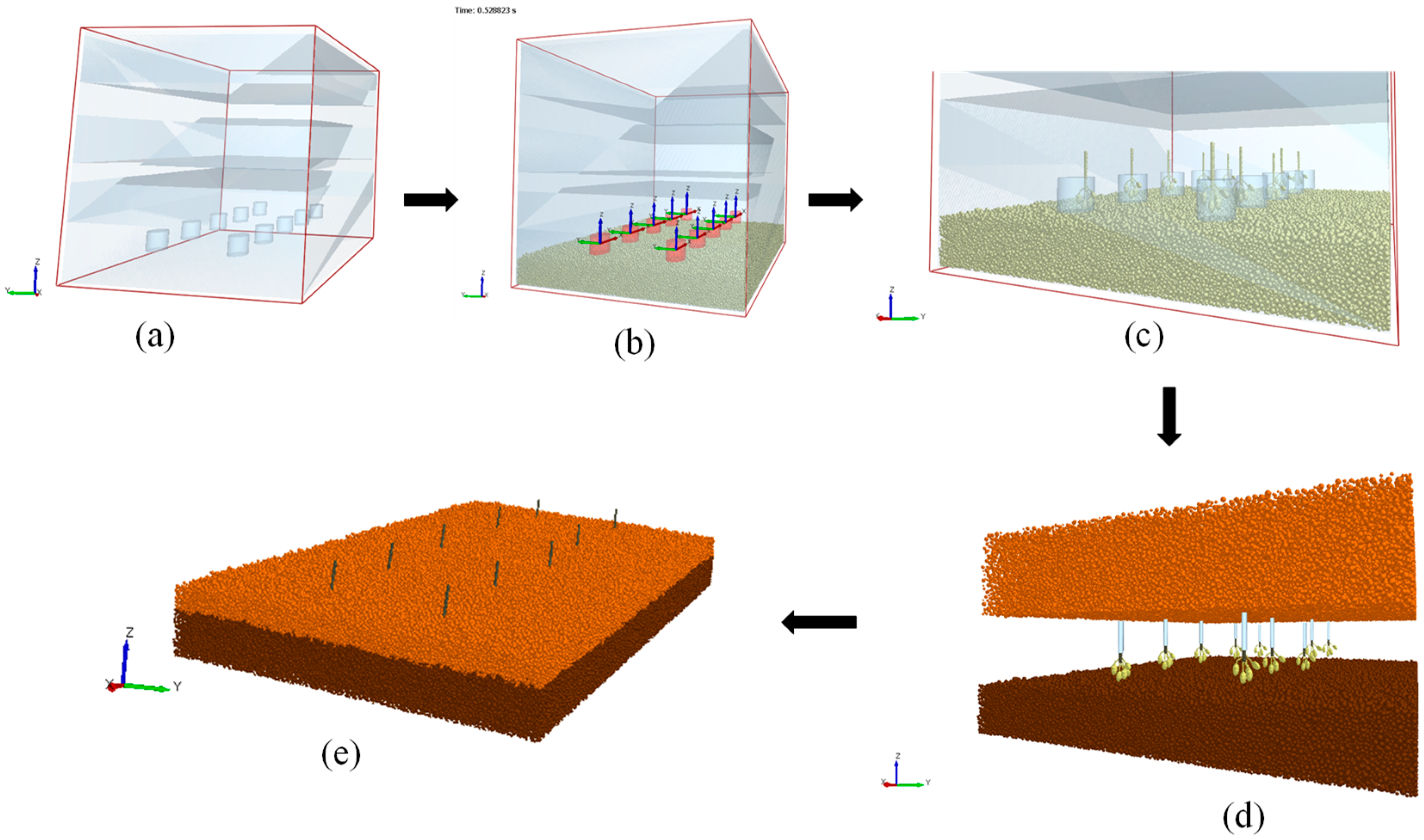
DEM soil–crop mixture model establishment: (a) factory setup, (b) subsoil creation, (c) crop creation, (d) topsoil creation, and (e) soil–crop model.
Figure 7.
DEM soil–crop mixture model establishment: (a) factory setup, (b) subsoil creation, (c) crop creation, (d) topsoil creation, and (e) soil–crop model.
Figure 8.
Tractor–harvester setup used in this study.
Figure 8.
Tractor–harvester setup used in this study.
Figure 9.
The depth of operation for the two field experiments: (a) clay soil field and (b) sandy loam field.
Figure 9.
The depth of operation for the two field experiments: (a) clay soil field and (b) sandy loam field.
Figure 10.
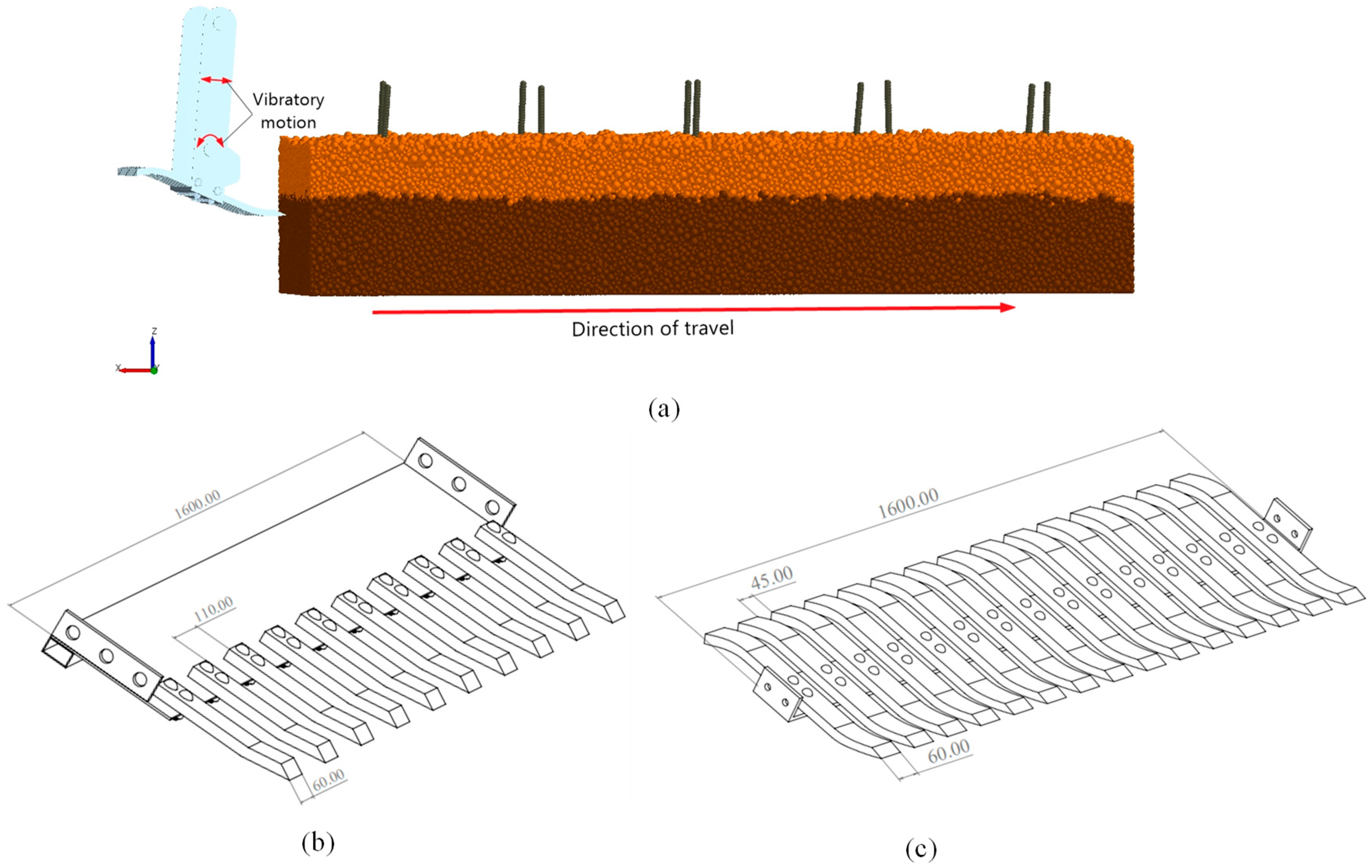
(a) DEM soil–shovel simulation setup, (b) fork-shaped shovel, and (c) S-shaped shovel.
Figure 10.
(a) DEM soil–shovel simulation setup, (b) fork-shaped shovel, and (c) S-shaped shovel.
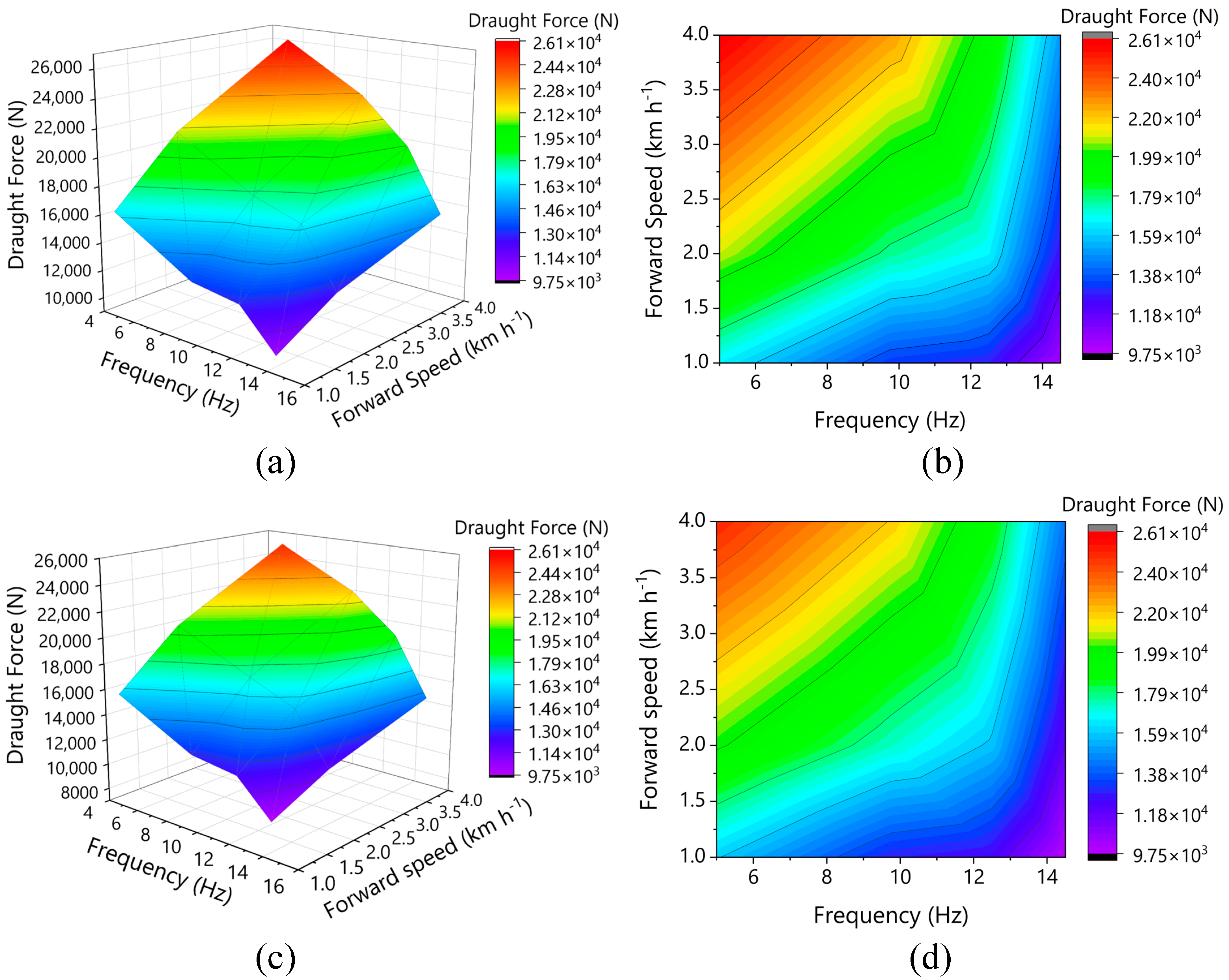
Figure 11.
Effect of forward speed and vibration frequency on draught force: (a,b) clay field experiment 3D and 2D contour plots, and (c,d) DEM simulation 3D and 2D contour plots.
Figure 11.
Effect of forward speed and vibration frequency on draught force: (a,b) clay field experiment 3D and 2D contour plots, and (c,d) DEM simulation 3D and 2D contour plots.
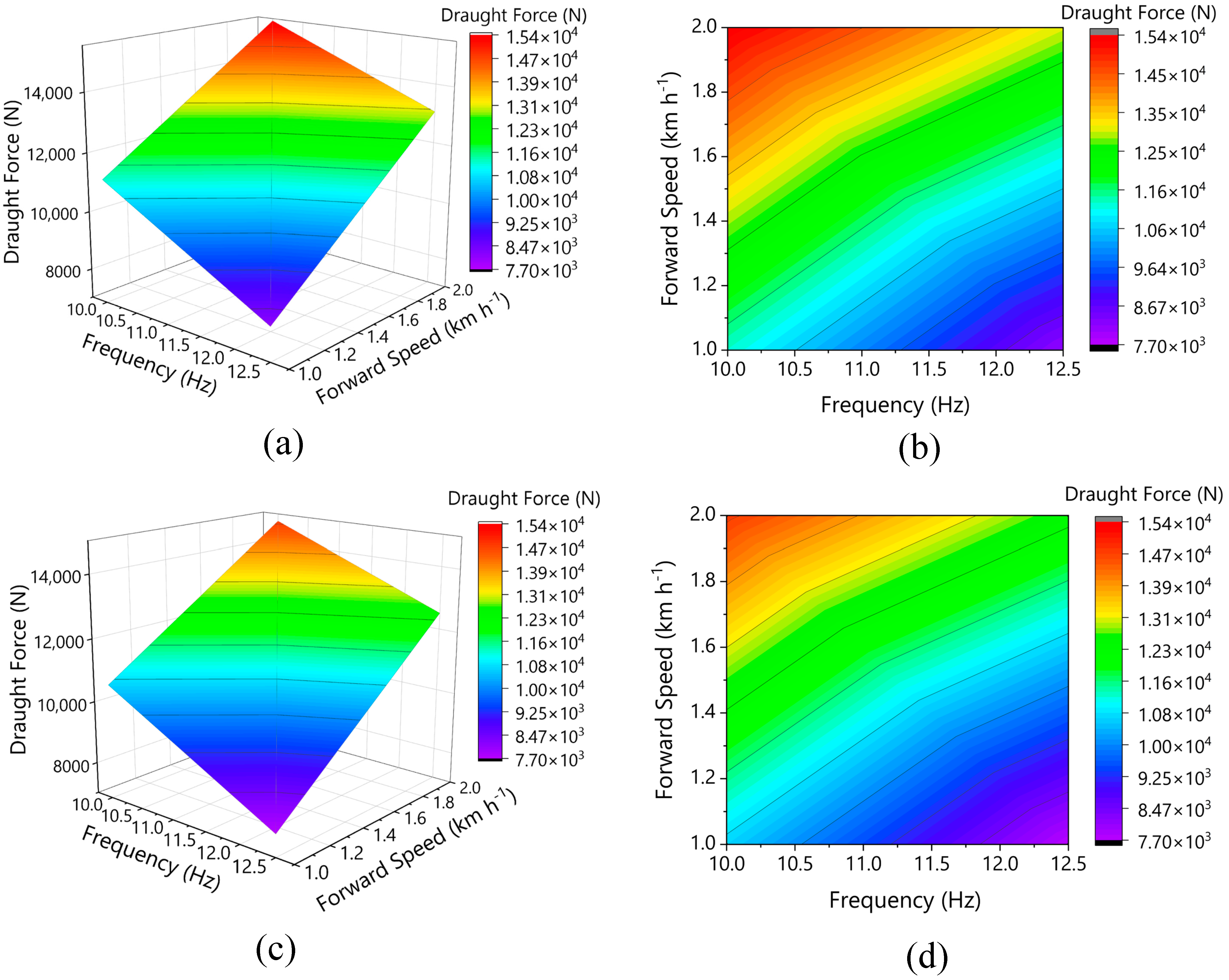
Figure 12.
Effects of forward speed and vibration frequency on draught force: (a,b) sandy loam field experiment 3D and 2D contour plots, and (c,d) DEM simulation 3D and 2D contour plots.
Figure 12.
Effects of forward speed and vibration frequency on draught force: (a,b) sandy loam field experiment 3D and 2D contour plots, and (c,d) DEM simulation 3D and 2D contour plots.
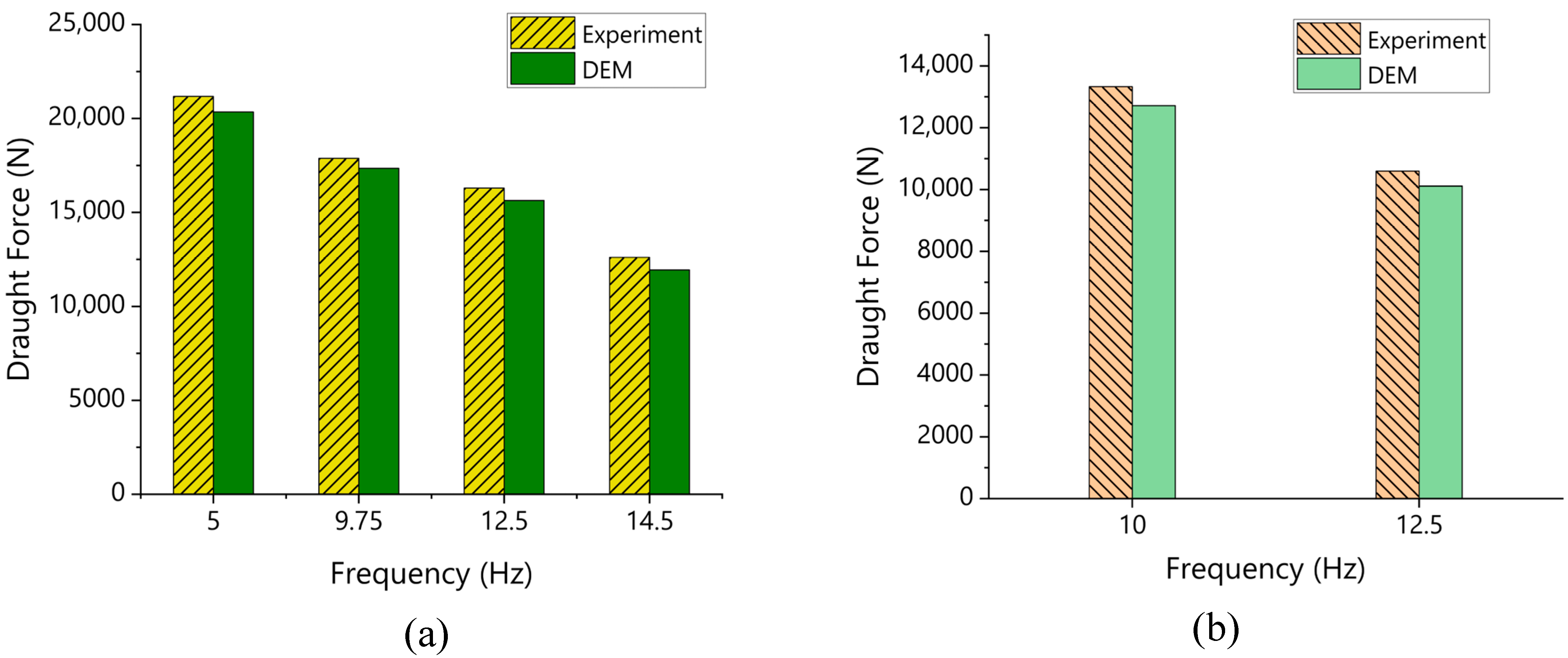
Figure 13.
Effect of vibration frequency on draught force for the experiment and DEM simulation: (a) clay soil and (b) sandy loam.
Figure 13.
Effect of vibration frequency on draught force for the experiment and DEM simulation: (a) clay soil and (b) sandy loam.
Figure 14.
Comparison of field data and DEM for drawbar power: (a,b) clay soil field and DEM results, respectively; (c,d) sandy loam soil field and DEM results, respectively.
Figure 14.
Comparison of field data and DEM for drawbar power: (a,b) clay soil field and DEM results, respectively; (c,d) sandy loam soil field and DEM results, respectively.
Figure 15.
Soil translocation properties of the shovels evaluated in clay soil: (a) field experiment for fork shovel, (b) DEM result for fork-shaped shovel, and (c) DEM result for S-shaped shovel.
Figure 15.
Soil translocation properties of the shovels evaluated in clay soil: (a) field experiment for fork shovel, (b) DEM result for fork-shaped shovel, and (c) DEM result for S-shaped shovel.
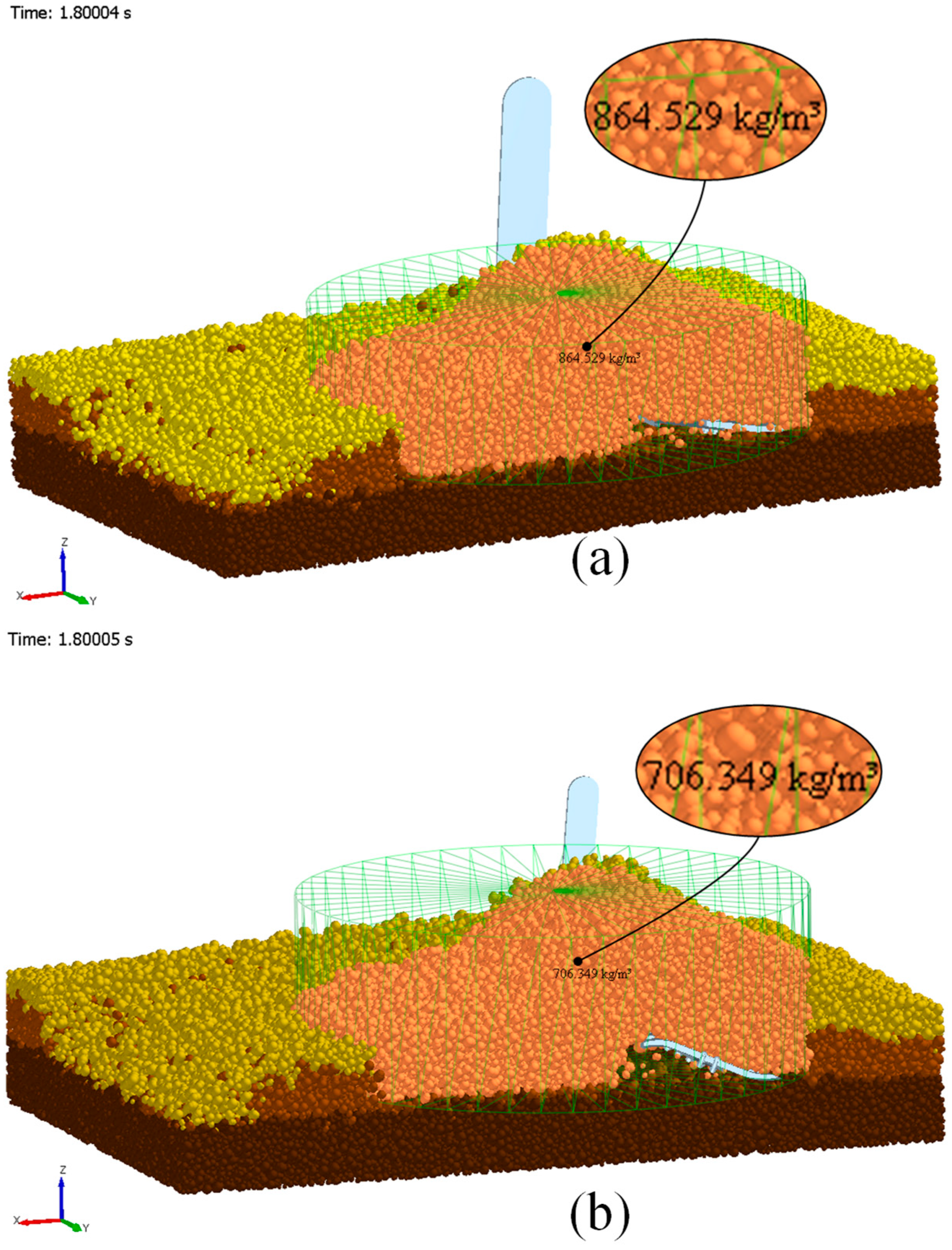
Figure 16.
DEM predicted soil bulk density for clay soil evaluation: (a) fork-shaped shovel and (b) S-shaped shovel.
Figure 16.
DEM predicted soil bulk density for clay soil evaluation: (a) fork-shaped shovel and (b) S-shaped shovel.
Figure 17.
Soil–crop mass translocation properties of the tools evaluated in sandy loam soil: (a) field experiment result, (b,c) DEM result for the fork-shaped shovel, and (d,e) DEM result for the S-shaped shovel.
Figure 17.
Soil–crop mass translocation properties of the tools evaluated in sandy loam soil: (a) field experiment result, (b,c) DEM result for the fork-shaped shovel, and (d,e) DEM result for the S-shaped shovel.
Figure 18.
DEM-predicted bulk density for sandy loam soil evaluation: (a) fork-shaped shovel and (b) S-shaped shovel.
Figure 18.
DEM-predicted bulk density for sandy loam soil evaluation: (a) fork-shaped shovel and (b) S-shaped shovel.
Table 1.
DEM input parameters for the soil–crop mixture model (sandy loam soil).
Table 1.
DEM input parameters for the soil–crop mixture model (sandy loam soil).
| Parameter and Unit | Value | Remarks |
|---|
| Poison’s ratio: soil | 0.3 | Selected |
| Poison’s ratio: steel | 0.3 | [30] |
| Poisson’s ratio: root | 0.38 | Measured |
| Poison’s ratio: tuber | 0.48 | Measured |
| Poison’s ratio: stem | 0.35 | Measured |
| Particles’ solid density (kg m−3) | 2600 | [6] |
| Density of steel (kg m−3) | 7865 | [30] |
| Density of root (kg m−3) | 1132 | Measured |
| Density of tuber (kg m−3) | 1184.4 | Measured |
| Density of stem (kg m−3) | 250.75 | Measured |
| Shear modulus (Pa): soil | | [6] |
| Shear modulus (Pa): steel | | [30] |
| Shear modulus (Pa): root | | Measured |
| Shear modulus (Pa): tuber | | Measured |
| Shear modulus (Pa): stem | | Measured |
| Coefficient of restitution: soil–soil | 0.6 | [6] |
| Coefficient of restitution: soil–steel | 0.6 | [6] |
| Coefficient of restitution: soil–root | 0.439 | Calibrated |
| Coefficient of restitution: soil–tuber | 0.514 | Calibrated |
| Coefficient of restitution: soil–stem | 0.554 | Calibrated |
| Coefficient of restitution: root–steel | 0.32 | Measured |
| Coefficient of restitution: tuber–steel | 0.62 | Measured |
| Coefficient of restitution: stem–steel | 0.53 | Measured |
| Coefficient of static friction: soil–soil | 0.45 | [6] |
| Coefficient of static friction: root–soil | 0.195 | Calibrated |
| Coefficient of static friction: tuber–soil | 0.212 | Calibrated |
| Coefficient of static friction: stem–soil | 0.166 | Calibrated |
| Coefficient of static friction: soil–steel | 0.45 | [6] |
| Coefficient of static friction: root–steel | 0.511 | Measured |
| Coefficient of static friction: tuber–steel | 0.446 | Measured |
| Coefficient of static friction: stem–steel | 0.5 | Measured |
| Coefficient of rolling friction: soil–soil | 0.18 | [6] |
| Coefficient of rolling friction: root–soil | 0.015 | Calibrated |
| Coefficient of rolling friction: tuber–soil | 0.175 | Calibrated |
| Coefficient of rolling friction: stem–soil | 0.069 | Calibrated |
| Coefficient of rolling friction: root–steel | 0.21 | Measured |
| Coefficient of rolling friction: tuber–steel | 0.32 | Measured |
| Coefficient of rolling friction: stem–steel | 0.05 | Measured |
| Normal stiffness per unit area (N m−3) | | Selected |
| Shear stiffness per unit area (N m−3) | | Calibrated |
| Normal strength (Pa) | | Calibrated |
| Shear strength (Pa) | | Calibrated |
| Bonded disk scale | 1 | Selected |
| JKR surface energy (J m−2) | 10 | Selected |
Table 2.
DEM input parameters used for the soil–tool interaction simulation (clay soil).
Table 2.
DEM input parameters used for the soil–tool interaction simulation (clay soil).
| Parameter and Unit | Value | Remarks |
|---|
| Poison’s ratio: soil | 0.3 | Selected |
| Poison’s ratio: steel | 0.3 | [30] |
| Particles’ solid density (kg m−3) | 2600 | Selected |
| Density of steel (kg m−3) | 7865 | [30] |
| Shear modulus (Pa): soil | | Calibrated |
| Shear modulus (Pa): steel | | [30] |
| Yield strength (Pa): soil (single sphere, dual sphere, and triple sphere) | | Default value in EDEM® 2020 |
| Yield strength (Pa): steel | | Default value in EDEM® 2020 |
| Coefficient of restitution: soil–soil | 0.467 | Calibrated |
| Coefficient of restitution: soil–steel | 0.05 | Selected |
| Coefficient of static friction: soil–soil | 0.388 | Calibrated |
| Coefficient of static friction: soil–steel | 0.45 | Selected |
| Coefficient of rolling friction: soil–soil | 0.192 | Calibrated |
| Coefficient of rolling friction: soil–steel | 0.15 | Selected |
| Damping factor | 0.5 | Default value in EDEM® 2020 |
| Stiffness factor | 0.85 | Default value in EDEM® 2020 |
| Cohesive energy density (J m−3) | 20,965.7 | Calibrated |
Table 3.
Regression model fit summary for responses (clay field experiment and DEM simulation).
Table 3.
Regression model fit summary for responses (clay field experiment and DEM simulation).
| Source | Sequential p-Value | Adjusted R2 | Predicted R2 | Remark |
|---|
| Experiment draught force |
| Linear | <0.0001 * | 0.9038 | 0.8475 | |
| 2FI | 0.0798 ** | 0.9280 | 0.7966 | |
| Quadratic | 0.0512 ** | 0.9643 | 0.9324 | Suggested |
| Cubic | 0.0340 * | 0.9947 | 0.9664 | Aliased |
| DEM draught force | | | | |
| Linear | <0.0001 * | 0.9017 | 0.8430 | |
| 2FI | 0.0908 ** | 0.9243 | 0.7748 | |
| Quadratic | 0.0394 * | 0.9657 | 0.9120 | Suggested |
| Cubic | 0.0240 * | 0.9959 | 0.9538 | Aliased |
| Experiment drawbar power |
| Linear | <0.0001 * | 0.9473 | 0.9011 | |
| 2FI | 0.0006 * | 0.9874 | 0.9692 | Suggested |
| Quadratic | 0.0963 ** | 0.9923 | 0.9734 | |
| Cubic | 0.0085 ** | 0.9995 | 0.9977 | Aliased |
| DEM drawbar power |
| Linear | <0.0001 * | 0.9450 | 0.8974 | |
| 2FI | 0.0010 * | 0.9850 | 0.9623 | Suggested |
| Quadratic | 0.0777 ** | 0.9915 | 0.9693 | |
| Cubic | 0.0073 * | 0.9995 | 0.9968 | Aliased |
Table 4.
Regression model fit summary for the sandy loam soil (field and DEM simulation).
Table 4.
Regression model fit summary for the sandy loam soil (field and DEM simulation).
| Source | Experiment Draught Force | DEM Draught Force |
|---|
| Std. Dev. | 368.33 | 362.5 |
| Mean | 11,963.1 | 11,411.15 |
| CoV% | 3.08 | 3.18 |
| R2 | 0.9952 | 0.9951 |
| Adjusted R2 | 0.9857 | 0.9852 |
| Predicted R2 | 0.9235 | 0.9212 |
| Adequacy precision | 22.8498 | 22.4509 |
Table 5.
ANOVA summary result for the clay soil (field and DEM simulation).
Table 5.
ANOVA summary result for the clay soil (field and DEM simulation).
| Experiment Draught Force (Quadratic) | DEM Draught Force (Quadratic) | Experiment Drawbar Power (2FI) | DEM Drawbar Power (2FI) |
|---|
| Source | F-Value | p-Value | Source | F-Value | p-Value | Source | F-Value | p-Value | Source | F-Value | p-Value |
|---|
| Model | 60.51 | <0.0001 * | Model | 62.89 | <0.0001 * | Model | 288.85 | <0.0001 * | Model | 242.23 | <0.0001 * |
| A | 150.65 | <0.0001 * | A | 159.85 | <0.0001 * | A | 66.6 | <0.0001 * | A | 57.39 | 0.0003 * |
| B | 157.21 | <0.0001 * | B | 159.02 | <0.0001 * | B | 810.21 | <0.0001 * | B | 678.05 | <0.0001 * |
| AB | 8.13 | 0.0291 * | AB | 8.15 | 0.029 * | AB | 29.72 | 0.0006 * | AB | 25.06 | 0.0010 * |
| A2 | 5.33 | 0.0603 ** | A2 | 7.54 | 0.0335 * | | | | | | |
| B2 | 4.83 | 0.0.0704 ** | B2 | 4.09 | 0.0895 ** | | | | | | |
| Std.Dev. | 876.40 | | Std.Dev. | 836.44 | | Std.Dev. | 1.01 | | Std.Dev. | 1.06 | |
| Mean | 16,990.08 | | Mean | 16,321.74 | | Mean | 12.07 | | Mean | 11.59 | |
| CoV% | 5.16 | | CoV% | 5.12 | | CoV% | 8.37 | | CoV% | 9.17 | |
Table 6.
Comparison of clay soil field and DEM simulation result for draught force and drawbar power.
Table 6.
Comparison of clay soil field and DEM simulation result for draught force and drawbar power.
| Frequency | Forward Speed | Experiment Draught Force | DEM Draught Force | Experiment Drawbar Power | DEM Drawbar Power | RE |
|---|
| (Hz) | (km h−1) | (N) | (N) | (kW) | (kW) | (%) |
|---|
| 5 | 1 | 16,542.170 | 15,926.626 | 4.595 | 4.424 | 3.721 |
| 5 | 2 | 20,951.889 | 20,105.592 | 11.640 | 11.170 | 4.039 |
| 5 | 4 | 26,036.022 | 25,019.387 | 28.929 | 27.799 | 3.905 |
| 9.75 | 1 | 13,288.189 | 12,867.725 | 3.691 | 3.574 | 3.164 |
| 9.75 | 2 | 17,684.548 | 17,270.654 | 9.825 | 9.595 | 2.340 |
| 9.75 | 4 | 22,677.284 | 21,915.671 | 25.197 | 24.351 | 3.358 |
| 12.5 | 1 | 12,819.620 | 12,362.924 | 3.561 | 3.434 | 3.562 |
| 12.5 | 2 | 16,586.874 | 15,699.174 | 9.215 | 8.722 | 5.352 |
| 12.5 | 4 | 19,479.821 | 18,863.692 | 21.644 | 20.960 | 3.163 |
| 14.5 | 1 | 10,245.086 | 9795.835 | 2.846 | 2.721 | 4.385 |
| 14.5 | 2 | 12,573.063 | 11,794.365 | 6.985 | 6.552 | 6.193 |
| 14.5 | 4 | 14,996.467 | 14,239.182 | 16.663 | 15.821 | 5.050 |
Table 7.
Comparison of sandy loam soil field and DEM simulation result for draught force and drawbar power.
Table 7.
Comparison of sandy loam soil field and DEM simulation result for draught force and drawbar power.
| Frequency | Forward Speed | Experiment Draught Force | DEM Draught Force | Experiment Drawbar Power | DEM Drawbar Power | RE |
|---|
| (Hz) | (km h−1) | (N) | (N) | (kW) | (kW) | (%) |
|---|
| 10 | 1 | 11,232.587 | 10,669.730 | 3.120 | 2.964 | 5.011 |
| 10 | 2 | 15,423.266 | 14,753.971 | 8.568 | 8.197 | 4.340 |
| 12.5 | 1 | 8134.596 | 7705.821 | 2.260 | 2.141 | 5.271 |
| 12.5 | 2 | 13,061.930 | 12,515.067 | 7.257 | 6.953 | 4.187 |