Contributions to the Optimization of the Medicinal Plant Sorting Process into Size Classes
Abstract
1. Introduction
- Identifying the dimensional characteristics of dried and chopped nettle fragments, in order to determine the mesh sizes of the sieve for obtaining the dimensional sorts.
- Variation in several parameters of the plane sieve for plants, in order to optimize the sorting process.
- Evaluation of the quality of the sorting process by calculating the average separation coefficient.
- Determination of multivariable regression functions of the polytropic form, in order to assess the constructive, functional, and qualitative indices of the sieving equipment.
2. Materials and Methods
2.1. Choice of the Medicinal Plant to Be Studied
- -
- Underground part: horizontal elongated rhizomes, from which underground stolons start;
- -
- Aerial stem: develops on the stolons, has 4 obvious edges and is hairy, generally unbranched, empty inside;
- -
- Leaves: arranged opposed, triangular-ovate lamina being 4–7 cm long and half wide, serrated edge with large teeth, hairs on both sides; lower leaves have a long petiole while upper ones have a short petiole;
- -
- Flowers: disposed in cymes at the base of the leaves, with 3–6 white, large flowers, corolla of up to 2 cm, with the upper lip having the form of a helmet, and the lower one the form of a spoon;
- -
- Fruits: nucleus with three edges, brown, grouped 4 in the persistent calyx.
2.2. Granulometric Analysis of Plant Fragments
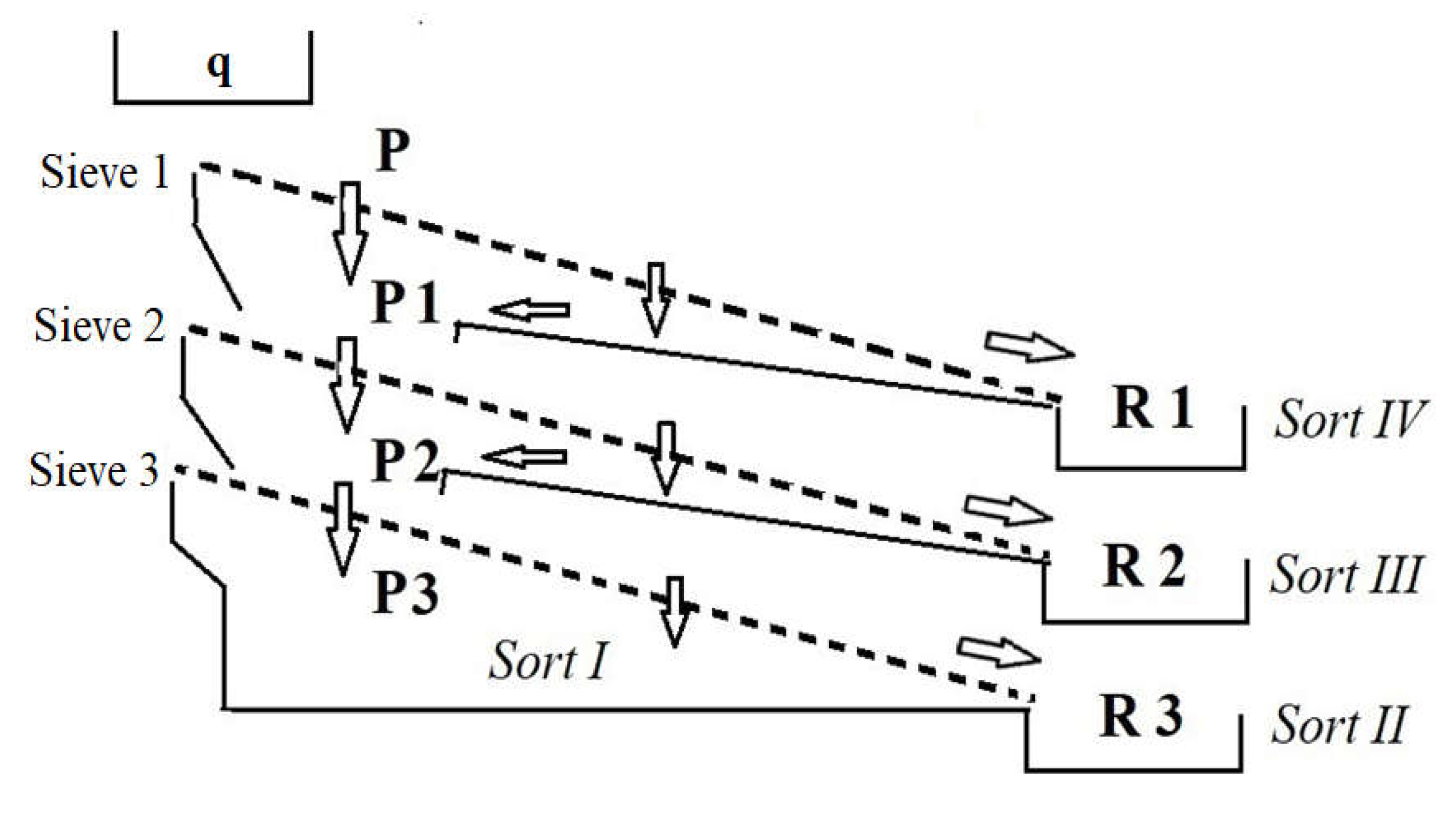
2.3. Plant Sorter Working Methodology
2.4. Calculation of Average Separation Coefficient (Cemed)—Experiment
2.5. The Algorithm for Calculating Multivariate Function Coefficients for Average Separation Coefficient (Cemed)—Mathematical Model
- Speed of sieve drive mechanism (n = 1000 rpm, n = 950 rpm; n = 900 rpm);
- Sieve inclination angle (α = 12.08°, α = 13.33°, α = 14.7°);
- Specific flow of sieve loading with plant material (q = 4–10 kg/dm·h).
3. Results
- Sort 1 (l < 2.8 mm), p1 = 8.22%;
- Sort 2 (l = 2.9–4.0 mm), p2 = 69.15%;
- Sort 3 (l = 4.1–5.6 mm), p3 = 13.18%;
- Sort 4 (l > 5.6 mm), p4 = 9.46%.
- -
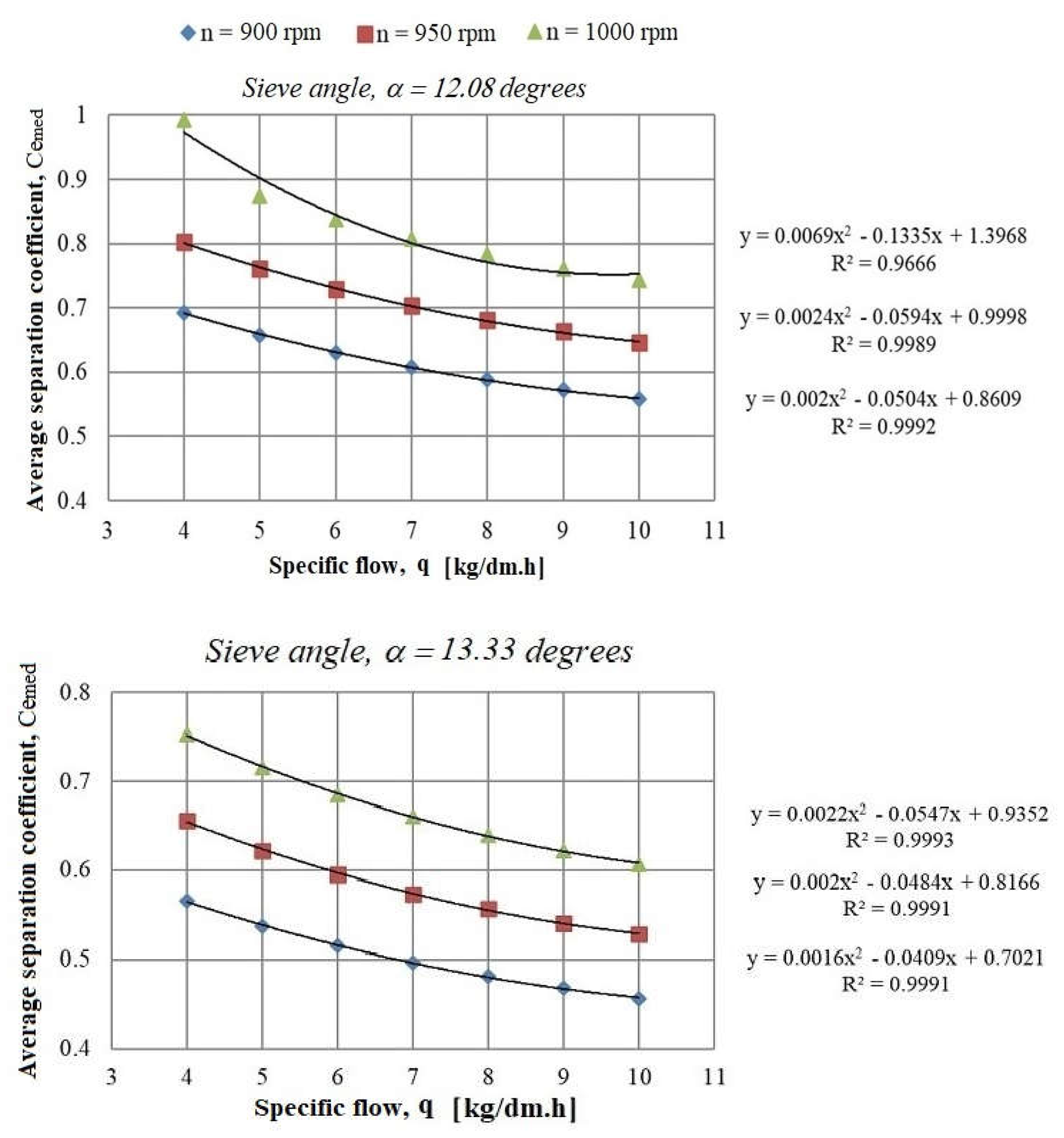
- For α = 12.08°:
- -
- For α = 13.33°:
- -
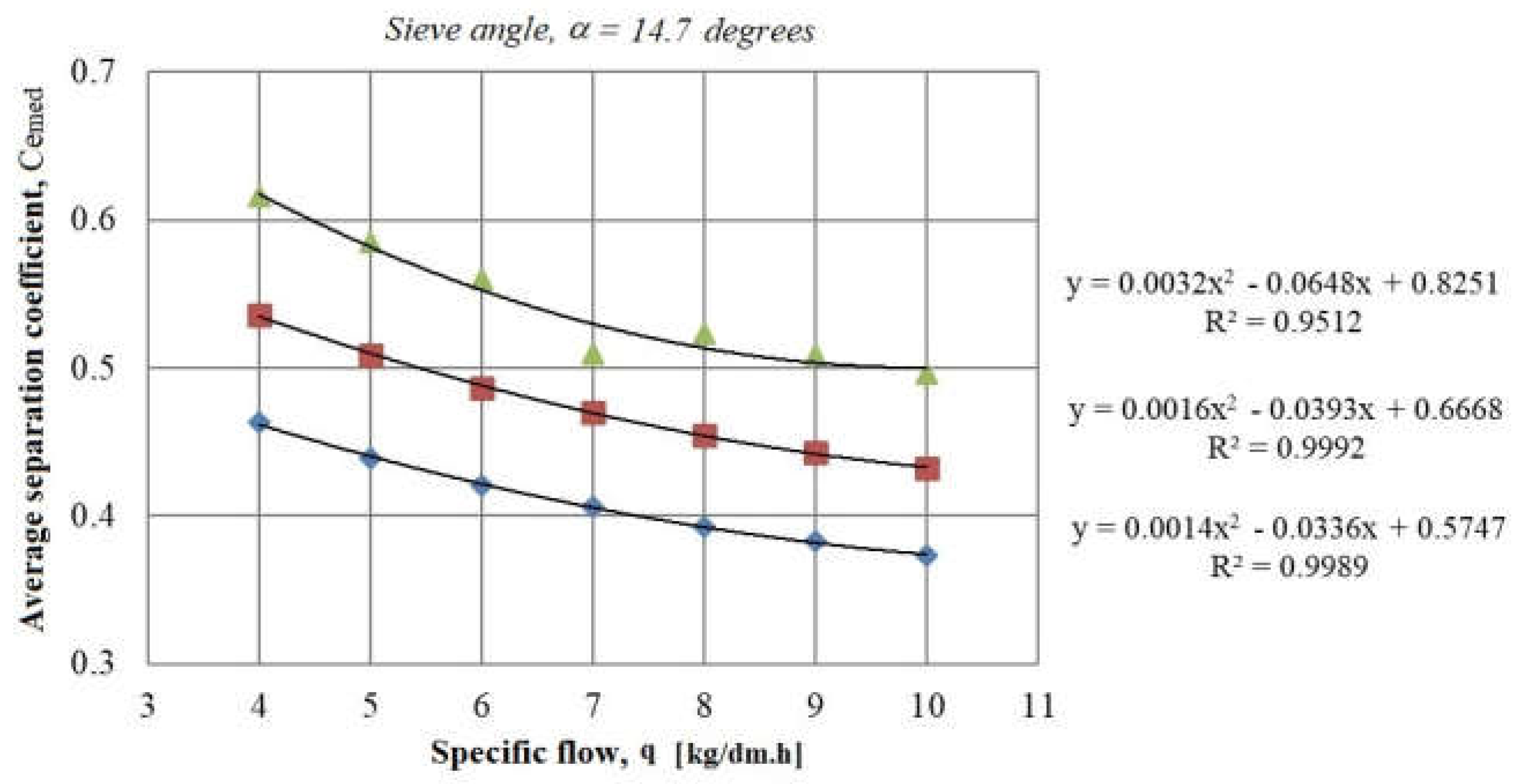
- For α = 14.7°:
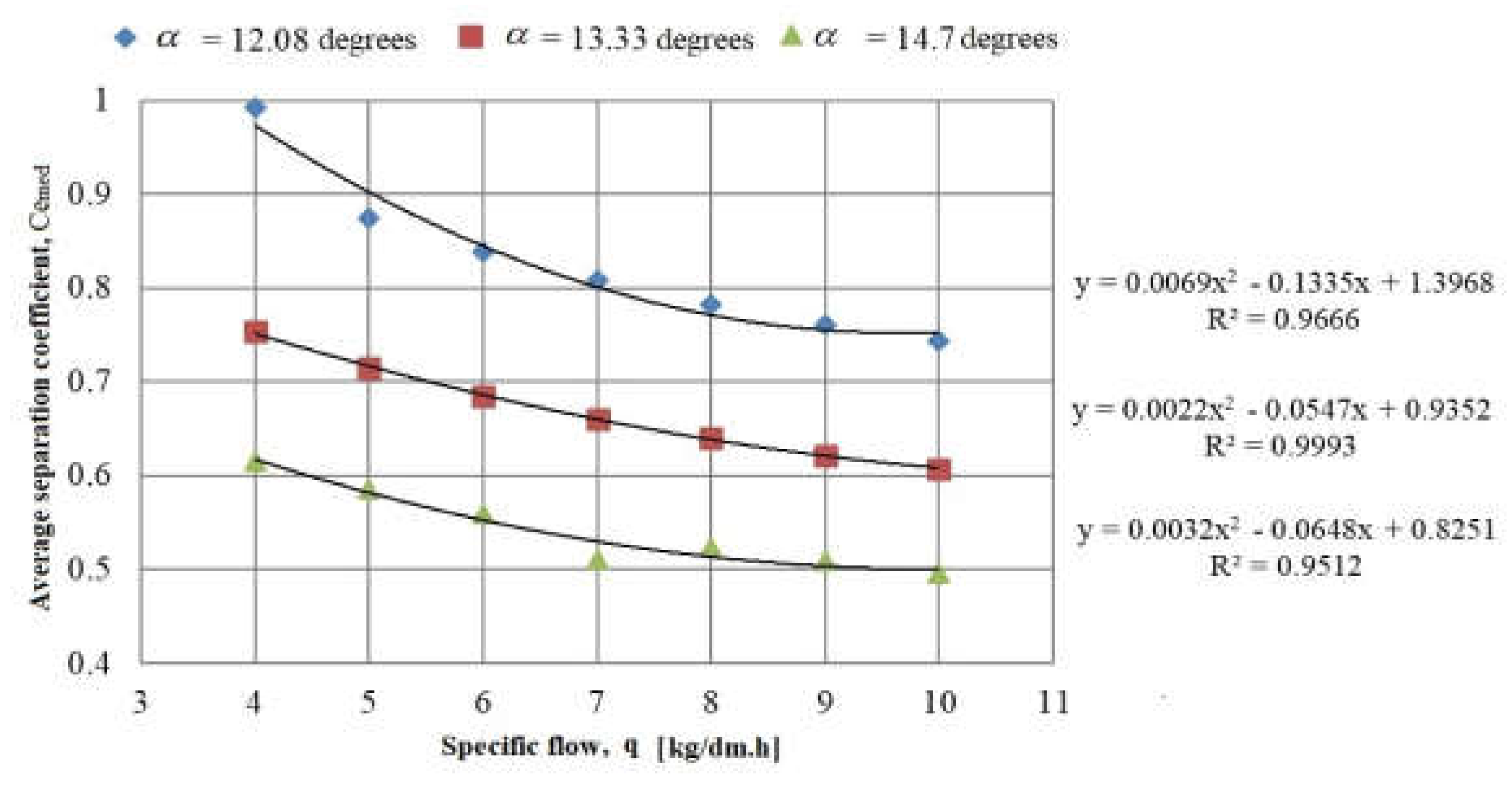
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pruteanu, A. Research on the Sorting Process of Medicinal Plants to Obtain Bioactive Plant Extracts. Ph.D. Thesis, University Politehnica of Bucharest, Bucharest, Romania, 2018. [Google Scholar]
- Tabatabaeefar, A.; Aghagoolzadeh, H.; Mobli, H. Design and development of an auxiliary chickpea second sieving and grading machine. In Agricultural Engineering International: The CIGR Journal of Scientific Research and Development; International Commission of Agricultural Engineering: Liège, Belgium, 2003; Volume 5. [Google Scholar]
- Fouda, T.Z. Engineering studies on the performance of paddy and rice separator. Misr. J. Ag. Eng. 2009, 26, 935–952. [Google Scholar] [CrossRef]
- Kharitonov, M.K.; Gievsky, A.М.; Orobinsky, V.I.; Chernyshov, A.V.; Baskakov, I.V. Studying the design and operational parameters of the sieve module of the grain cleaning machine. IOP Conf. Ser. Earth Environ. Sci. 2020, 488, 012021. [Google Scholar] [CrossRef]
- Moskovskiy, M.; Khamuev, V.; Dorokhov, A.; Gerasimenko, S. Determining optimal kinematic parameters of a screen shoe used for separating breeding seed samples. MATEC Web Conf. 2019, 298, 00044. [Google Scholar] [CrossRef]
- Konopka, S.; Markowski, P.; Kaliniewicz, Z.; Choszcz, D.J.; Lipinski, A.J.; Kusinska, E. Optimization of the separation efficiency of buckwheat seeds andwild radish siliques in a grader with indented pockets. Sustainability 2018, 10, 3870. [Google Scholar] [CrossRef]
- Stoica, D.; Voicu, G.; Popa, L.; Constantin, G.; Tudor, P. Assessment indices for the efficiency of the separation process on a sieve with conical separation surface. INMATEH–Agric. Eng. 2020, 60, 190–200. [Google Scholar] [CrossRef]
- Stoica, D. Frequency dependence on the separation process at a conical screen with vibrating movement. In Proceedings of the 2nd International Electronic Conference on Applied Sciences Session Mechanical Engineering, Online, 15–31 October 2021. [Google Scholar] [CrossRef]
- KeShun, L. Some factors affecting sieving performance and efficiency. Powder Technol. 2009, 193, 208–213. [Google Scholar] [CrossRef]
- Šaršunova, V.A.; Kruglenjab, V.E.; Kamińskic, E.; Kubońd, M. Flax seed separation with vibrating screens. Agric. Eng. 2014, 3, 187–201. [Google Scholar] [CrossRef]
- Alekseev, V.V.; Mitryukhin, E.L.; Mitryukhin, L.K.; Chuchkalov, S.I. Optimization of separation of two-component mixtures of seeds under horizontal vibration. IOP Conf. Ser. Earth Environ. Sci. 2022, 954, 012005. [Google Scholar] [CrossRef]
- Mustafayev, S.K.; Pelipenko, T.V.; Drozdov, A.N.; Kalienko, E.A. Production line intended for implementation of innovative technologies of cleaning and fractionation of raw coriander. Adv. Eng. Res. 2018, 157, 424–428. [Google Scholar] [CrossRef]
- Zhang, B.; Gong, J.; Yuan, W.; Fu, J.; Huang, Y. Intelligent prediction of sieving efficiency in vibrating screens. Hindawi Publ. Corp. Shock. Vib. 2016, 2, 9175417. [Google Scholar] [CrossRef]
- Rebot, D.; Babii, A. Influence of the velocity of the medium layer on its dynamic parameters in the process of vibration separation. UJMEMS 2022, 8, 33–40. [Google Scholar] [CrossRef]
- Wang, G.; Tong, X. Screening efficiency and screen length of a linear vibrating screen using DEM 3D simulation. Int. J. Min. Sci. Technol. 2011, 21, 451–455. [Google Scholar] [CrossRef]
- Vlăduţ, V.; Danciu, A.; Grigore, I.; Herişanu, N.; Dumitru, I.; Sorică, C.; Voicea, I.; Biriş, S.S.; Duţu, M.; Păunescu, D.; et al. The influence of the working regime of oscillations produced by an electrovibrator on the sorting of materials. Appl. Mech. Mater. 2015, 801, 197–201. [Google Scholar] [CrossRef]
- Szymański, T.; Wodziński, P. Screening on a screen with a vibrating sieve. Physicochem. Probl. Miner. Process. 2003, 37, 27–36. [Google Scholar]
- Igathinathane, C.; Pordesimo, L.O.; Columbus, E.P.; Batchelor, W.D.; Sokhansanj, S. Sieveless particle size distribution analysis of particulate materials through computer vision. Comput. Electron. Agric. 2009, 66, 147–158. [Google Scholar] [CrossRef]
- Fang, W.; Wang, X.; Han, D.; Chen, X. Review of material parameter calibration method. Agriculture 2022, 12, 706. [Google Scholar] [CrossRef]
- Bai, S.; Yuan, Y.; Niu, K.; Zhou, L.; Zhao, B.; Wei, L.; Liu, L.; Xiong, S.; Shi, Z.; Ma, Y. Simulation parameter calibration and experimental study of a discrete element model of cotton precision Seed Metering. Agriculture 2022, 12, 87. [Google Scholar] [CrossRef]
- Konopka, S.; Choszcz, D.J.; Markowski, P. Optimization of the separation parameters and indicators of separation efficiency of buckwheat seeds. Sustainability 2017, 9, 2134. [Google Scholar] [CrossRef]
- Song, J.; Lu, S.Z.; Liu, L.H.; Wang, M.; Liu, T.X. Analysis of mechanophysical properties of Fritillaria Ussuriensis Maxim and designing of grade sieve machine. Adv. Mater. Res. Trans Tech Publ. 2013, 764, 165–168. [Google Scholar] [CrossRef]
- Riehlea, P.; Ruschea, N.; Saakeb, B.; Rohna, S. Influence of the leaf content and the herbal particle size on the presence and the extractability of quantitated phenolic compounds in cistus incanus herbal teas. J. Agric. Food Chem. 2014, 62, 10978–10988. [Google Scholar] [CrossRef]
- Chen, Z.; He, L.; Ye, Y.; Chen, J.; Sun, L.; Wu, C.; Chen, L.; Wang, R. Automatic sorting of fresh tea leaves using vision-based recognition method. J. Food Process Eng. 2020, 43, e13474. [Google Scholar] [CrossRef]
- Zhong, Z.; Chunguang, L.; Haibin, W.; Dongfeng, Z.; Mi, S. Design and test of technology improvement on vibrating grizzly before cut leaf tobacco flavoured. J. Anhui Agric. Univ. 2012, 40, 1166–1168. [Google Scholar]
- Voicu, G.; Constantin, G.A.; Ştefan, E.M.; Căsăndroiu, T. Using of granulometric distribution functions in estimating flows of grist sorted in a plansifter compartment. J. EcoAgriTourism 2014, 10, 47–52. [Google Scholar]
- Constantin, G.A.; Voicu, G.; Ştefan, M.E.; Paraschiv, G. Research on the grain milling dimensional characteristics of the second grit in an industrial wheat mill. INMATEH–Agric. Eng. 2013, 39, 71–78. [Google Scholar]
- Yeom, S.B.; Ha, E.-S.; Kim, M.-S.; Jeong, S.H.; Hwang, S.-J.; Choi, D.H. Application of the discrete element method for manufacturing process simulation in the pharmaceutical industry. Pharmaceutics 2019, 11, 414. [Google Scholar] [CrossRef]
- Rogers, A.; Ierapetritou, M. Challenges and opportunities in modeling pharmaceutical manufacturing processes. Comput. Chem. Eng. 2015, 81, 32–39. [Google Scholar] [CrossRef]
- Suresh, P.; Basu, P.K. Improving pharmaceutical product development and manufacturing: Impact on cost of drug development and cost of goods sold of pharmaceuticals. J. Pharm. Innov. 2008, 3, 175–187. [Google Scholar] [CrossRef]
- Ketterhagen, W.R.; am Ende, M.T.; Hancock, B.C. Process modeling in the pharmaceutical industry using the discrete element method. J. Pharm. Sci. 2009, 98, 442–470. [Google Scholar] [CrossRef]
- Ardelean, A.; Mohan, G. Medicinal Flora of Romania; All Publishing House: Bucharest, Romania, 2008; p. 57. [Google Scholar]
- Nencu, I.; Vlase, L.; Istudor, V.; Tămaş, M. Preliminary research regarding Urtica urens L. and Urtica dioica L. Farm. J. 2015, 63, 710–715. [Google Scholar]
- Bodros, E.; Baley, C. Study of the tensile properties of stinging nettle fibres (Urtica dioica). Mater. Lett. 2008, 62, 2143–2145. [Google Scholar] [CrossRef]
- Virgilioa, D.N.; Papazogloub, G.E.; Jankauskienec, Z.; Lonardod, D.S.; Praczyke, M.; Wielgusze, K. The potential of stinging nettle (Urtica dioica L.) as a crop with multiple uses. Ind. Crops Prod. 2015, 68, 42–49. [Google Scholar] [CrossRef]
- Allen, T. Particle Size Analysis by Sieving. In Powder Sampling and Particle Size Determination; Elsevier: Amsterdam, The Netherlands, 2003; Chapter 4; pp. 208–235. [Google Scholar]
- Ipate, G.; Căsăndroiu, T. Physical Properties of Agri-Food Products; Politehnica Press Publishing House: Bucharest, Romania, 2009; pp. 55–62. [Google Scholar]
- Ene, G. Equipment for Classification and Sorting of Polydisperse Solids; Matrix Rom Publishing House: Bucharest, Romania, 2005; p. 173. [Google Scholar]
- Constantin, G.A. Research on the Process of Sifting and Sorting Grain Milling Fractions in an Industrial Mill. Ph.D. Thesis, University Politehnica of Bucharest, Bucharest, Romania, 2014. [Google Scholar]
- Voicu, G.; Constantin, G.A.; Ştefan, E.M.; Voicu, P. Technologies for Processing Agricultural Products; Terra Nostra Publishing House: Iaşi, Romania, 2013; pp. 72–124. [Google Scholar]
- Păunescu, I.; David, L. Basis of Experimental Research on Biotechnical Systems; Printech Publishing House: Bucharest, Romania, 1999; pp. 112–148. [Google Scholar]
- Zagajewski, P.; Dreszer, K.A. The state of theoretical studies on threshing and separation of grain from cereal mass. J. Agric. Eng. Res. 2008, 51, 4–9. [Google Scholar]
- El-Sayed, S.A.; Mostafa, M.E. Analysis of grain size statistic and particle size distribution of biomass powders. Waste Biomass Valor. 2014, 5, 1005–1018. [Google Scholar] [CrossRef]
- Danciu, A.; Postelnicu, E.; Vlăduţ, V.; Voicea, I.; Matache, M.; Ludig, M.; Martinov, M.; Atanasov, A.; Florea, C. Testing the manufacturing technology and equipment for medicinal and aromatic plant processing. Obtaining the active-principle extracts out of medicinal and aromatic plants. INMATEH–Agric. Eng. 2011, 34, 57–66. [Google Scholar]
- Ioancea, L.; Kathrein, I. Conditioning and Superior Capitalisation of Plant Raw Materials for Food Purposes-Technologies and Installations; Ceres Publishing House: Bucharest, Romania, 1988. [Google Scholar]
- Akhmadiev, F.; Gizzyatov, R.; Nazipov, I. Vibration separation of bulk construction mixtures by measurement sizes on sieve classifiers. IOP Conf. Ser. Mater. Sci. Eng. 2020, 890, 012106. [Google Scholar] [CrossRef]
- Nazarenko, I.; Onyshchenko, A.; Oryshchenko, S.; Fedorenko, O.; Tsepelev, S.; Titova, L. Research of technical systems of materials sorting processes. In Dynamic Processes in Technological Technical Systems; РС Тесhnology Сеntеr: Kharkiv, Ukraine, 2021; pp. 43–56. [Google Scholar] [CrossRef]
- Voicu, G.; Casandroiu, T.; Toma, L. Adequate statistical models for distribution appreciation of seeds separation by the 19 cleaning system sieves of the combines. In Proceedings of the International Symposium “Integrated Systems for Agri-Food Production SIPA’05”, Timisoara, Romania, 24–26 November 2005; pp. 185–192. [Google Scholar]
- Tarcolea, C.; Casandroiu, T.; Voicu, G. Stochastic models for simulating seed separation process on sieves. In Proceedings of the 36th International Symposium Actual Tasks on Agricultural Engineering, Opatija, Croatia, 11–15 February 2008; pp. 293–306. [Google Scholar]
- Casandroiu, T.; Popescu, M.; Voicu, G. A developing a mathematical model for simulating the seeds separation process on the 13 plane sieves. U.P.B. Sci. Bull. Ser. D 2009, 71, 17–29. [Google Scholar]
- Voicu, G.; Casandroiu, T.; Toma, L. A multiple logistic regression statistical model to estimate grain losses on sieve 5 cleaning system from combine. In Proceedings of the 34th International Symposium Actual Tasks on Agricultural Engineering, Opatija, Croatia, 21–24 February 2006; pp. 481–491. [Google Scholar]
- Lu, Z.; Hu, X.; Lu, Y. Particle morphology analysis of biomass material based on improved image processing method. Int. J. Anal. Chem. 2017, 2017, 5840690. [Google Scholar] [CrossRef]
- Pruteanu, A.; David, L.; Vlăduţ, V.; Matache, M.; Muscalu, A.; Danciu, A. Research on lavender (Lavandula angustifolia) sorting process quality. INMATEH–Agric. Eng. 2015, 46, 109–114. [Google Scholar]
- Pruteanu, A.; David, L.; Muscalu, A.; Vlăduţ, V. Quality of thymus (Thymus vulgaris) screening process in order to obtain bioactive extracts. In Proceedings of the 44th International Symposium Actual Tasks on Agricultural Engineering, Opatija, Croatia, 23–26 February 2016; pp. 299–310. [Google Scholar]
- Pruteanu, A.; David, L.; Vlăduţ, V.; Muscalu, A. Researches on quality of nettle (Urtica dioica) screening process in order to obtain bioactive extracts. Sci. Bull. Univ. Politeh. Buchar. Ser. D 2017, 79, 267–278. [Google Scholar]
- Pruteanu, A.; Matache, M.; David, L.; Muscalu, A. Research of technological process for medicinal plant separation. In Proceedings of the 16th International Scientific Conference Engineering for Rural Development, Jelgava, Latvia, 24–26 May 2017; pp. 892–897. [Google Scholar] [CrossRef]
- De Carlo, A.; Tarraf, W.; Lambardi, M.; Benelli, C. Temporary immersion system for production of biomass and bioactive compounds from medicinal plants. Agronomy 2021, 11, 2414. [Google Scholar] [CrossRef]
- Belščak-Cvitanović, A.; Komes, D.; Durgo, K.; Vojvodik, A.; Busic, A. Nettle (Urtica dioica L.) extracts as functional ingredients for production of chocolates with improved bioactive composition and sensory properties. J. Food Sci. Technol. 2015, 52, 7723–7734. [Google Scholar] [CrossRef] [PubMed]
- Jeszka-Skowron, M.; Zgoła-Grzeskowiak, A.; Frankowski, R.; Grzeskowiak, T.; Jeszka, A.M. Variation in the content of bioactive compounds in infusions prepared from different parts of wild polish stinging nettle (Urtica dioica L.). Molecules 2022, 27, 4242. [Google Scholar] [CrossRef] [PubMed]



| Characteristic | Unit of Measurement | Values |
|---|---|---|
| Drive | - | 2 electric vibrating motors |
| Electric motors power | kW | 0.15 |
Overall dimensions:
| m | 2.330 1.150 1.530 |
| Number of sieve frames | pieces | 3 |
| Dimensions of changeable sieve frames meshes (9 pcs.) | mm | 1.15; 2.8; 3.15; 4.0; 5.6; 6.3; 8.0; 10.0; 13.2 |
Dimensions of sieve frames
| m | 1.495 0.600 0.040 |
| Maximum revolution speed Amplitudes of sieve oscillations | rpm mm | 1000 1–10 |
| Sieve inclination in three fixed positions, α | ° | 12.08; 13.33; 14.7 |
| Mass | kg | 260 |
| No. | Fraction Limits (mm) | Sort | Sample (g) | Average (g) | Share p (%) | ||||
|---|---|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5 | |||||
| 1 | <2.8 | I | 9.49 | 9.68 | 9.88 | 10.07 | 10.26 | 9.88 | 8.22 |
| 2 | 2.9–4.0 | II | 83.17 | 83.37 | 82.59 | 82.78 | 82.98 | 82.98 | 69.15 |
| 3 | 4.1–5.6 | III | 15.81 | 15.49 | 15.98 | 16.14 | 15.65 | 15.81 | 13.18 |
| 4 | 5.7–8.0 | IV | 8.23 | 7.88 | 8.02 | 7.87 | 8.12 | 8.02 | 6.70 |
| 5 | >8.1 | V | 3.47 | 3.45 | 3.12 | 3.09 | 3.4 | 3.31 | 2.76 |
| Sample mass (g) | 120 | 120 | 120 | 120 | 120 | 120 | 100 | ||
| Sample | Revolution Speed, n (rpm) | Sieve Angle α (°) | Sort 1 P3 (kg) | Sort 2 R3 (kg) | Sort 3 R2 (kg) | Sort 4 R1 (kg) | Mass of Sorts P (kg) |
|---|---|---|---|---|---|---|---|
| 1 | 1000 | 12.08 | 0.00001 | 0.06750 | 0.10400 | 0.07749 | 0.249 |
| 2 | 1000 | 12.08 | 0.00003 | 0.12858 | 0.10187 | 0.11900 | 0.349 |
| 3 | 1000 | 12.08 | 0.00035 | 0.25500 | 0.09400 | 0.13900 | 0.488 |
| 4 | 1000 | 12.08 | 0.00050 | 0.09700 | 0.15000 | 0.25048 | 0.498 |
| 5 | 1000 | 13.33 | 0.00023 | 0.12400 | 0.06700 | 0.05900 | 0.250 |
| 6 | 1000 | 13.33 | 0.00027 | 0.16200 | 0.09300 | 0.09200 | 0.347 |
| 7 | 1000 | 13.33 | 0.00040 | 0.04500 | 0.08000 | 0.22262 | 0.348 |
| 8 | 1000 | 13.33 | 0.00048 | 0.22700 | 0.09600 | 0.11100 | 0.434 |
| 9 | 1000 | 14.7 | 0.00015 | 0.12800 | 0.05900 | 0.06000 | 0.247 |
| 10 | 1000 | 14.7 | 0.00002 | 0.02500 | 0.04300 | 0.18098 | 0.249 |
| 11 | 1000 | 14.7 | 0.00024 | 0.18400 | 0.09000 | 0.10100 | 0.375 |
| 12 | 1000 | 14.7 | 0.00026 | 0.21800 | 0.12400 | 0.11800 | 0.460 |
| 13 | 1000 | 14.7 | 0.00000 | 0.02700 | 0.05000 | 0.38200 | 0.459 |
| 14 | 950 | 12.08 | 0.00035 | 0.20200 | 0.08400 | 0.08900 | 0.375 |
| 15 | 950 | 12.08 | 0.00009 | 0.05800 | 0.10000 | 0.21589 | 0.374 |
| 16 | 950 | 12.08 | 0.00033 | 0.22600 | 0.09100 | 0.14600 | 0.463 |
| 17 | 950 | 13.33 | 0.00020 | 0.13100 | 0.03500 | 0.06200 | 0.228 |
| 18 | 950 | 13.33 | 0.00022 | 0.02580 | 0.05000 | 0.15193 | 0.228 |
| 19 | 950 | 13.33 | 0.00037 | 0.16200 | 0.05200 | 0.09700 | 0.311 |
| 20 | 950 | 13.33 | 0.00020 | 0.03000 | 0.05700 | 0.22380 | 0.311 |
| 21 | 950 | 13.33 | 0.00020 | 0.03500 | 0.07300 | 0.20280 | 0.311 |
| 22 | 950 | 13.33 | 0.00001 | 0.02800 | 0.04800 | 0.23499 | 0.311 |
| 23 | 950 | 13.33 | 0.00010 | 0.03000 | 0.05300 | 0.22790 | 0.311 |
| 24 | 950 | 13.33 | 0.00047 | 0.20300 | 0.12400 | 0.15900 | 0.486 |
| 25 | 950 | 13.33 | 0.00025 | 0.02900 | 0.06400 | 0.39279 | 0.486 |
| 26 | 950 | 14.7 | 0.00019 | 0.19600 | 0.07700 | 0.07100 | 0.344 |
| 27 | 950 | 14.7 | 0.00000 | 0.01650 | 0.03400 | 0.29450 | 0.345 |
| 28 | 950 | 14.7 | 0.00031 | 0.23300 | 0.11800 | 0.14700 | 0.498 |
| 29 | 900 | 12.08 | 0.00035 | 0.03000 | 0.06000 | 0.13664 | 0.227 |
| 30 | 900 | 12.08 | 0.00034 | 0.17500 | 0.08700 | 0.05900 | 0.321 |
| 31 | 900 | 13.33 | 0.00048 | 0.02800 | 0.10000 | 0.28952 | 0.418 |
| 32 | 900 | 13.33 | 0.00018 | 0.16500 | 0.07600 | 0.09500 | 0.336 |
| 33 | 900 | 13.33 | 0.00015 | 0.01550 | 0.04000 | 0.28035 | 0.336 |
| 34 | 900 | 13.33 | 0.00030 | 0.19100 | 0.08700 | 0.11300 | 0.391 |
| 35 | 900 | 14.7 | 0.00005 | 0.00750 | 0.01800 | 0.16441 | 0.190 |
| 36 | 900 | 14.7 | 0.00027 | 0.05680 | 0.07600 | 0.26500 | 0.398 |
| 37 | 900 | 14.7 | 0.00010 | 0.00800 | 0.03010 | 0.35980 | 0.398 |
| No. | Sample | Revolution Speed, n (rpm) | Sieve Angle, α (°) | Specific Flow, q (kg/dm·h) | Average Separation Coefficient Cemed |
|---|---|---|---|---|---|
| 1 | 29 | 900 | 12.08 | 4.54 | 0.70 |
| 2 | 1 | 1000 | 12.08 | 4.98 | 0.87 |
| 3 | 35 | 900 | 14.7 | 3.8 | 0.48 |
| 4 | 10 | 1000 | 14.7 | 4.98 | 0.6 |
| 5 | 31 | 900 | 12.08 | 8.36 | 0.59 |
| 6 | 4 | 1000 | 12.08 | 9.96 | 0.77 |
| 7 | 37 | 900 | 14.7 | 7.96 | 0.4 |
| 8 | 13 | 1000 | 14.7 | 9.18 | 0.52 |
| 9 | 33 | 900 | 13.33 | 6.72 | 0.51 |
| 10 | 7 | 1000 | 13.33 | 6.96 | 0.68 |
| 11 | 27 | 950 | 14.7 | 6.9 | 0.48 |
| 12 | 15 | 950 | 12.08 | 7.48 | 0.71 |
| 13 | 25 | 950 | 13.33 | 9.72 | 0.54 |
| 14 | 18 | 950 | 13.33 | 4.56 | 0.65 |
| 15 | 20 | 950 | 13.33 | 6.22 | 0.61 |
| 16 | 21 | 950 | 13.33 | 6.22 | 0.64 |
| 17 | 22 | 950 | 13.33 | 6.22 | 0.59 |
| 18 | 23 | 950 | 13.33 | 6.22 | 0.60 |
| Regression Coefficients | Testing Coefficients | Coefficients’ Significance |
|---|---|---|
| a1 = 0.0000016 | F1 = 3696.122765650 > 8.2560 | Is significant |
| a2 = 2.7082166 | F2 = 33.109848938 > 8.2560 | Is significant |
| a3 = −2.0532161 | F3 = 66.0598420435 > 8.2560 | Is significant |
| a4 = −0.2362560 | F4 = 21.306697235 > 8.2560 | Is significant |
| No. | Sample | Average Separation Coefficient | Deviation, A (%) | |
|---|---|---|---|---|
| Experimental Cemedexp | Calculated with Equation (16) Cemedc | with Equation (16) | ||
| 1 | 2 | 0.854 | 0.865 | −0.549 |
| 2 | 3 | 0.762 | 0.748 | 1.532 |
| 3 | 5 | 0.679 | 0.668 | 1.830 |
| 4 | 6 | 0.612 | 0.596 | 2.268 |
| 5 | 8 | 0.524 | 0.514 | 1.24 |
| 6 | 9 | 0.622 | 0.598 | 1.967 |
| 7 | 11 | 0.544 | 0.538 | 0.412 |
| 8 | 12 | 0.494 | 0.478 | 2.409 |
| 9 | 14 | 0.697 | 0.679 | 3.028 |
| 10 | 16 | 0.587 | 0.483 | 1.814 |
| 11 | 17 | 0.516 | 0.508 | 0.361 |
| 12 | 19 | 0.492 | 0.476 | 2.777 |
| 13 | 24 | 0.409 | 0.401 | 2.159 |
| 14 | 26 | 0.645 | 0.664 | −2.906 |
| 15 | 28 | 0.587 | 0.602 | −2.488 |
| 16 | 30 | 0.565 | 0.546 | 3.439 |
| 17 | 32 | 0.421 | 0.401 | 4.826 |
| 18 | 34 | 0.7 | 0.668 | 4.627 |
| 19 | 36 | 0.647 | 0.612 | 5.479 |
| Specific Flow, q (kg/dm·h) | α = 12.08° | α = 13.33° | α = 14.7° | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Revolution Speed, n (rpm) | Revolution Speed, n (rpm) | Revolution Speed, n (rpm) | |||||||
| 900 | 950 | 1000 | 900 | 950 | 1000 | 900 | 950 | 1000 | |
| 4 | 0.693 | 0.803 | 0.922 | 0.566 | 0.656 | 0.753 | 0.463 | 0.536 | 0.616 |
| 5 | 0.658 | 0.761 | 0.875 | 0.537 | 0.622 | 0.715 | 0.439 | 0.509 | 0.585 |
| 6 | 0.630 | 0.729 | 0.838 | 0.515 | 0.596 | 0.685 | 0.421 | 0.487 | 0.560 |
| 7 | 0.607 | 0.703 | 0.808 | 0.496 | 0.574 | 0.66 | 0.406 | 0.470 | 0.540 |
| 8 | 0.589 | 0.681 | 0.783 | 0.481 | 0.557 | 0.64 | 0.393 | 0.455 | 0.523 |
| 9 | 0.572 | 0.663 | 0.761 | 0.468 | 0.541 | 0.622 | 0.383 | 0.443 | 0.509 |
| 10 | 0.558 | 0.646 | 0.743 | 0.456 | 0.528 | 0.607 | 0.373 | 0.432 | 0.496 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pruteanu, M.A.; Ungureanu, N.; Vlăduț, V.; Matache, M.-G.; Niţu, M. Contributions to the Optimization of the Medicinal Plant Sorting Process into Size Classes. Agriculture 2023, 13, 645. https://doi.org/10.3390/agriculture13030645
Pruteanu MA, Ungureanu N, Vlăduț V, Matache M-G, Niţu M. Contributions to the Optimization of the Medicinal Plant Sorting Process into Size Classes. Agriculture. 2023; 13(3):645. https://doi.org/10.3390/agriculture13030645
Chicago/Turabian StylePruteanu, Mirabela Augustina, Nicoleta Ungureanu, Valentin Vlăduț, Mihai-Gabriel Matache, and Mihaela Niţu. 2023. "Contributions to the Optimization of the Medicinal Plant Sorting Process into Size Classes" Agriculture 13, no. 3: 645. https://doi.org/10.3390/agriculture13030645
APA StylePruteanu, M. A., Ungureanu, N., Vlăduț, V., Matache, M.-G., & Niţu, M. (2023). Contributions to the Optimization of the Medicinal Plant Sorting Process into Size Classes. Agriculture, 13(3), 645. https://doi.org/10.3390/agriculture13030645









