1. Introduction
Globally, pulses are the second most important crop group after cereals. Lentil is one of the most widely consumed pulses in India and specifically in the Middle East and South Asian regions [
1]. Being a rich source of essential nutrients, it is regarded as a high value crop for ensuring food and nutritional security for millions of people in developing countries. It is drought-tolerant and can also be grown as a rotation crop. Lentils also improve soil fertility by replenishing soil nitrogen levels. [
2]. India contributes around 18% to world lentil production and is one of the major lentil-exporting countries in the world [
3].
Despite being a major producer and consumer, the yield of lentil is considerably low in India compared to other major producing countries. The crop yield is affected by multiple factors such as physical, economic and technological. Morphological characters play a crucial role in yield enhancement as well as reduction. [
4,
5]. A good prediction model explores the complex relationship between different factors and yield. It helps to improve management techniques and boost actual yields. A good prediction model should be reliable, consistent, object-oriented, cost effective and sensitive to extreme events [
6]. Several researchers have attempted to model the crop yield of lentil using different models such as simple correlation [
1], path analysis [
7], multiple linear regression [
8], stepwise regression [
9], factorial analysis [
2] and principle component analysis [
10]. These studies assumed the linear relationship between plant characters and crop yield. However, these models have not been successful in capturing the nonlinear relationship between crop yield and plant characters [
11].
In the past decades, there has been a consistently rising interest in the application of machine learning (ML) techniques such as artificial neural networks (ANNs), support vector regression (SVR) and random forest (RF) in different fields, particularly for modelling nonlinear relationships. Schultz and Wieland [
12] discussed the possibilities of applying neural networks or neural networks in combination with fuzzy techniques in the field of agroecological modelling. Uno et al. [
13] used artificial neural networks to predict corn yield from compact airborne spectrographic imager data. They used statistical and ANN approaches along with various vegetation indices to develop yield prediction models. Lee et al. [
14] and Zhang et al. [
15] found that multivariate adaptive regression spline (MARS) performed better than both statistical parametric methods such as linear discriminant analysis or logistic regression and nonparametric approaches such as neural networks and support vector machines. Khazaei et al. [
16] applied artificial neural network methodology to model the correlation between crop yield and 10 yield components of chickpea (Cicer arietinum L.). They also used the fuzzy c-means clustering technique for the classification of 362 chickpea genotypes based on agronomic and morphological traits. Among the various ANN structures, the 10-14-3-1 ANN structure with a training algorithm of back-propagation and hyperbolic tangent transfer function in the hidden and output layers performed best. Higgins et al. [
17] developed an ANN model for forecasting the maturity of green peas using historical harvest information along with weather and climate forecasts. They implemented and evaluated the model in a large pea growing region in Tasmania, Australia. The model allowed for not only the harvesting of peas closer to their ideal maturity indices, but also the planning of harvest and transportation logistics with a significantly longer lead time. Khairunniza-Bejo et al. [
11] highlighted the prediction accuracy of the ANN model compared to other linear models in crop yield prediction. They showed that the ANN model captured the relationship among the variables much more accurately. Gandhi et al. [
18] used the support vector machine (SVM) model for rice crop yield prediction in India using climatic variables. Deo et al. [
19] applied MARS, least square, SVM and decision tree for drought forecasting in eastern Australia. Garg et al. [
20] forecast rice yield using the fuzzy logic and regression model. They tested four different types of the fuzzy interval with four degrees of regression equations. Ying-Xue et al. [
21] developed a support vector machine-based open crop model (SBOCM) integrating developmental stage and yield prediction models for rice crop yield prediction in China. Klompenburg et al. [
22] and Batool et al. [
23], Cubillas et al. [
24], Bali and Singla [
25] and Ji et al. [
26] reviewed the research works related to crop yield prediction using ML techniques. They explored the different machine learning techniques used in crop yield prediction and their efficiency. The studies reported the increasing trend of hybrid models in crop yield prediction.
The selection of appropriate input variables is an important part of any model such as multiple linear regression models (MLRs) and machine learning models [
27,
28,
29]. Feature selection is an effective way to reduce computation time, improve learning accuracy and facilitate a better understanding of the learning model or data. Many studies [
30,
31,
32] suggested that variable selection reduces the complexity of the model and make it more interpretable. However, each variable (feature) selection strategy is data-based and has its own benefit, drawback and applicability. MARS is based on local regression modelling, which uses spline functions to approximate complex nonlinear relations [
33,
34]. The advantage of MARS is that the relative importance of independent variables to the dependent variable can be captured [
15,
33,
35]. The important variable can be selected based on the relative importance of independent variables. Therefore, MARS was used as a selection model in the present study.
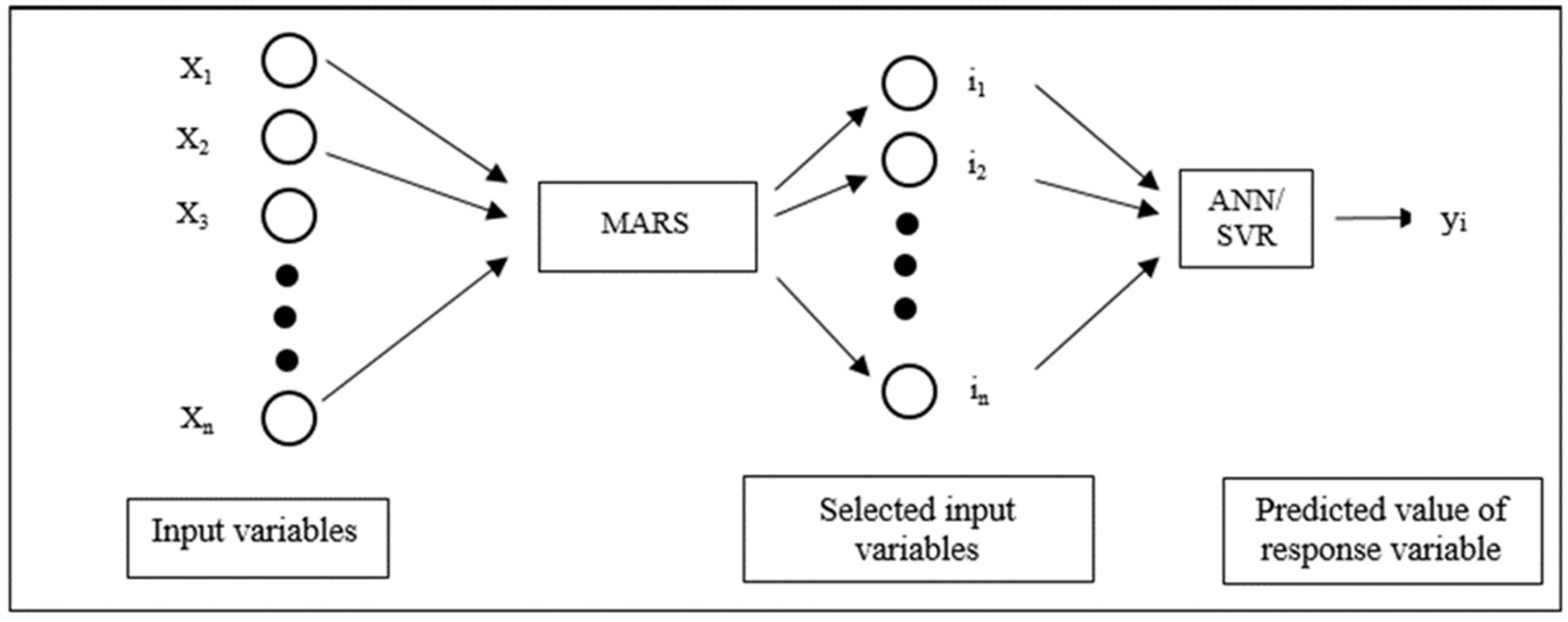
In the literature, most researchers have restricted themselves to using only one method such as ANN in their study. Comparative study and hybrid modelling of soft computing techniques with variable selection on particular datasets is yet to be done. This motivated the present comparative study of different soft computing techniques such as ANN, MARS and SVR. A hybrid model was formulated using MARS and ANN/SVR. These techniques and the proposed hybrid model were applied to the lentil dataset, and their modelling and forecasting performances were compared using different statistical measures. The remaining portion of the paper is divided into materials and methods, results and discussion, and a conclusion section.
5. Conclusions
Modelling and forecasting of complex, multifactorial and nonlinear phenomenon such as crop yield have intrigued researchers for decades. This study is an attempt in the similar direction to contribute to the vast literature of crop-yield modelling. The study proposed novel hybrids based on MARS. The feature extraction ability of MARS was utilized, and efficient forecasting models were developed using ANN and SVR. The utility of the proposed models was illustrated and compared using a lentil dataset with baseline models. As these models do not depend on assumptions about functional form, probability distribution or smoothness and have been proven to be universal approximators.
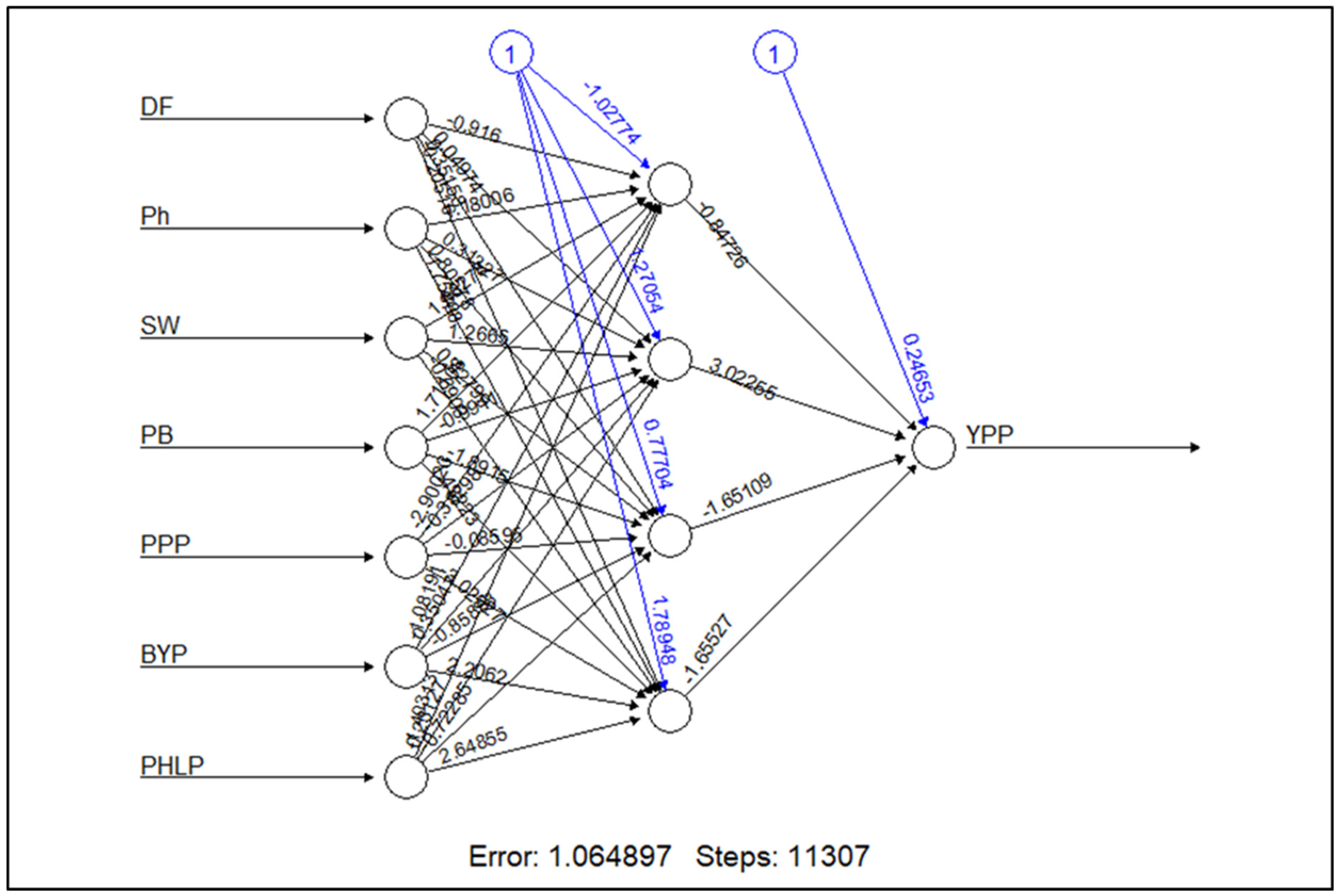
The novel hybrid model was built in two steps, each performing a specialized task. In the first step, important input variables were identified using the MARS model instead of hand-picking variables based on a theoretical framework. In the second step, nonlinear prediction techniques ANN and SVR were used for yield prediction using the selected variables. The performance of the models was compared using fit statistics such as RMSE, MAD, MAPE and ME. The proposed MARS-based hybrid models performed better as compared to the individual models such as MARS, SVR and ANN. This is largely due to the enhanced feature extraction capability of the MARS model coupled with the nonlinear adaptive learning feature of ANN and SVR. This proposed framework can be applied to a variety of datasets to capture the nonlinear relationship between independent and dependent variables. The R packages developed in this study have utility in multifactorial and multivariate experiments such as genomic selection, gene expression analysis, survival analysis, digital soil mappings, etc. Further, efforts can be directed to propose and evaluate hybrids of other soft computing techniques.