Study on Mechanical Properties of Tomatoes for the End-Effector Design of the Harvesting Robot
Abstract
:1. Introduction
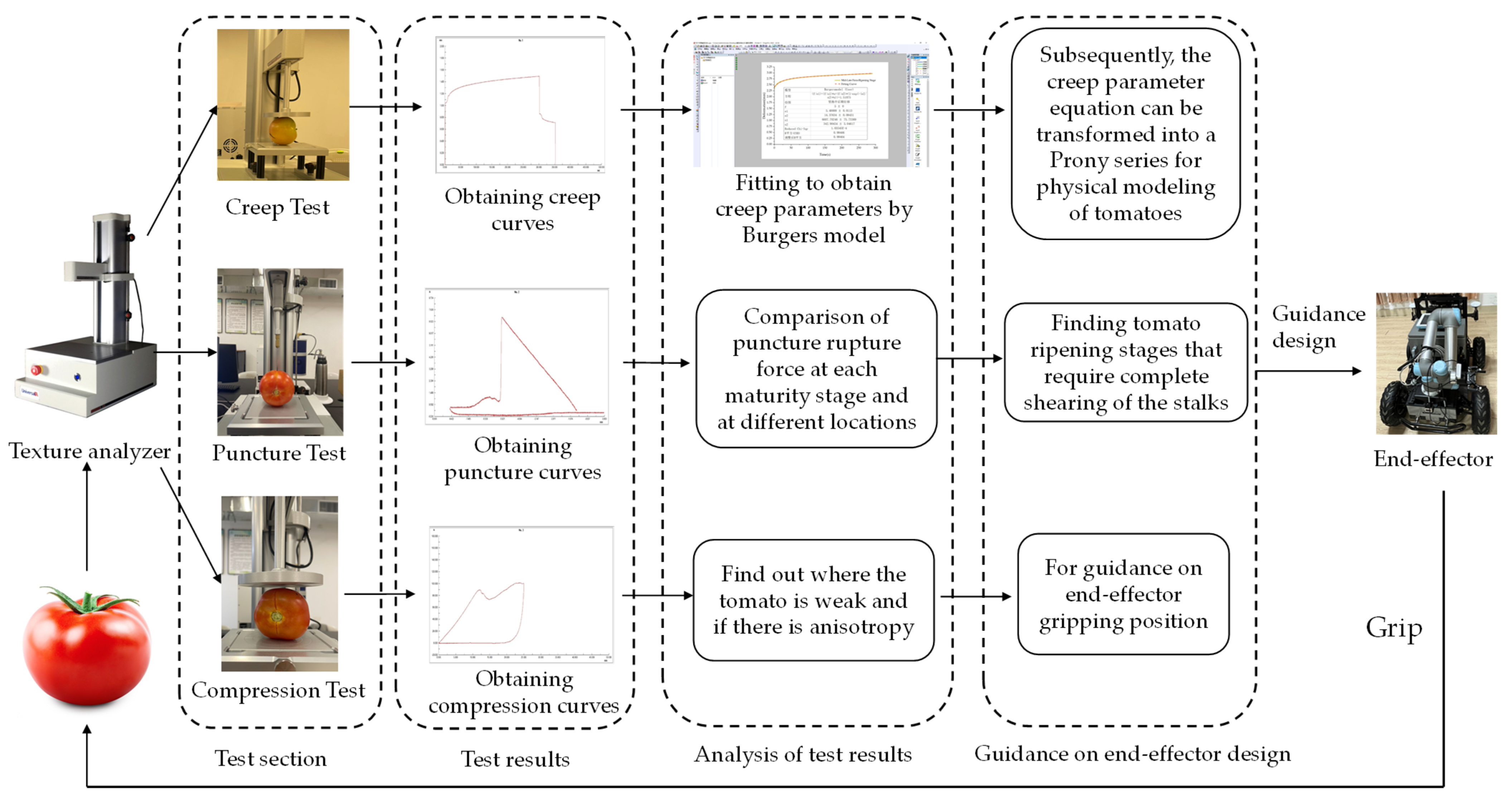
2. Materials and Methods
2.1. Sample Preparation
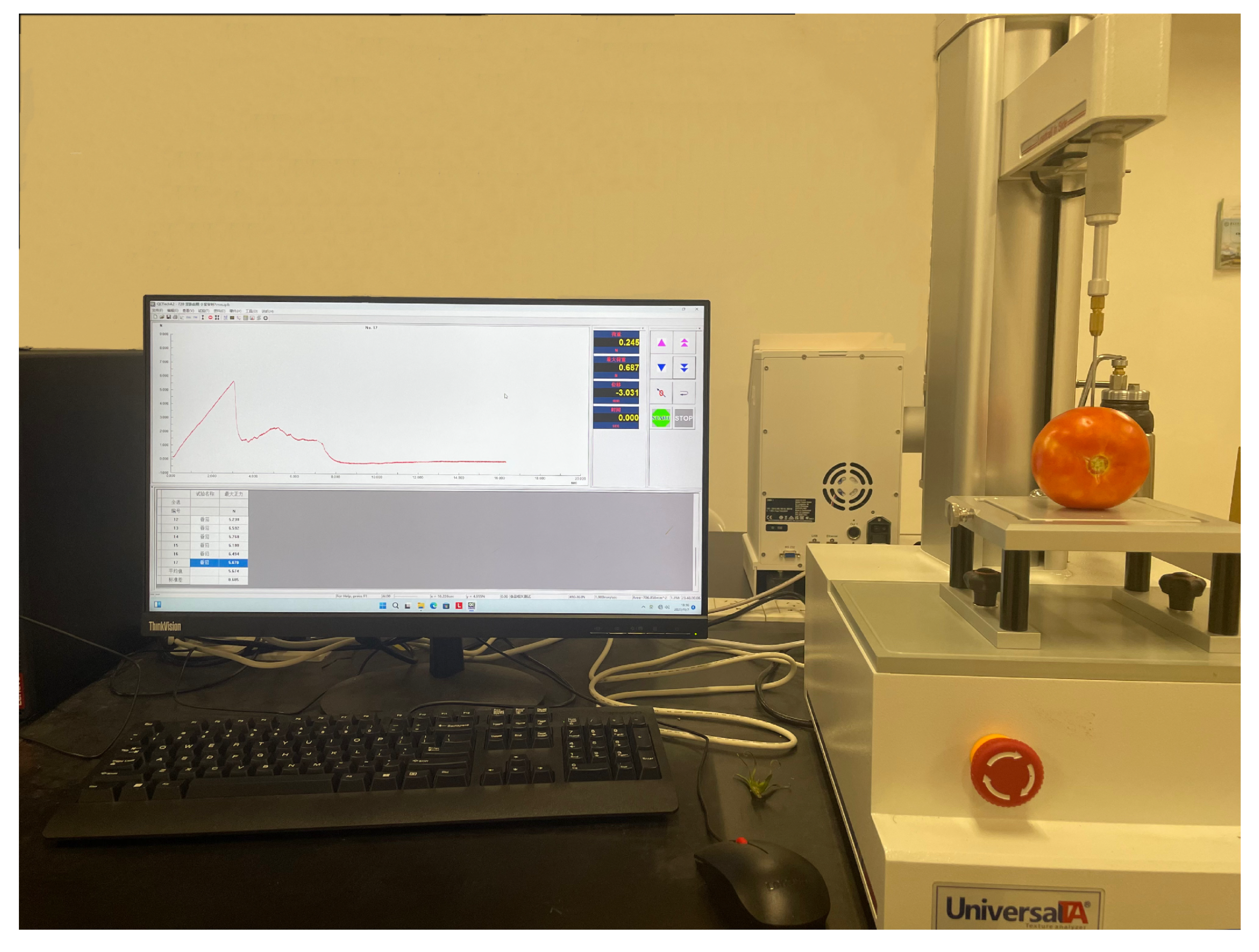
2.2. Texture Analyzer
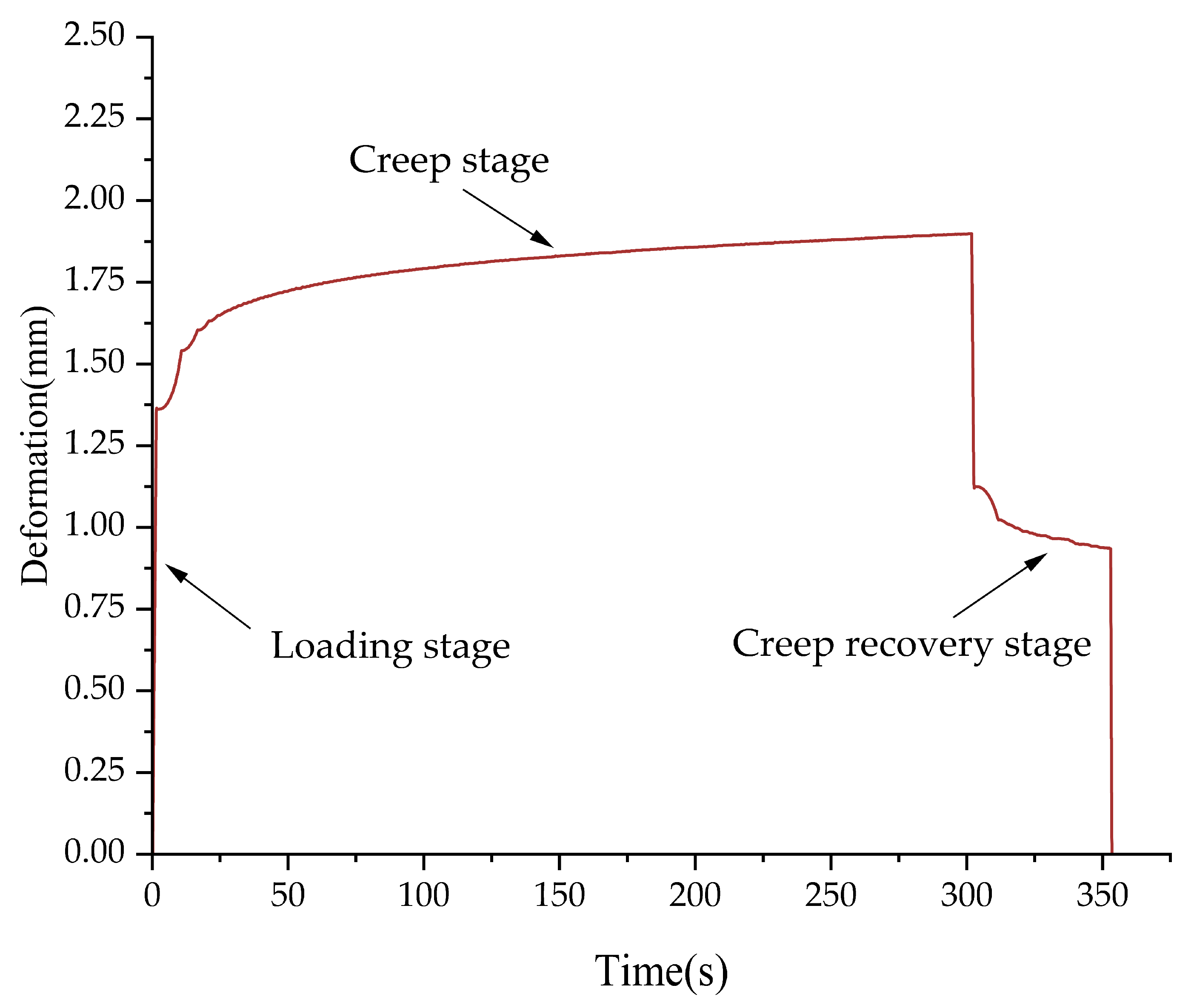
2.3. Creep Test
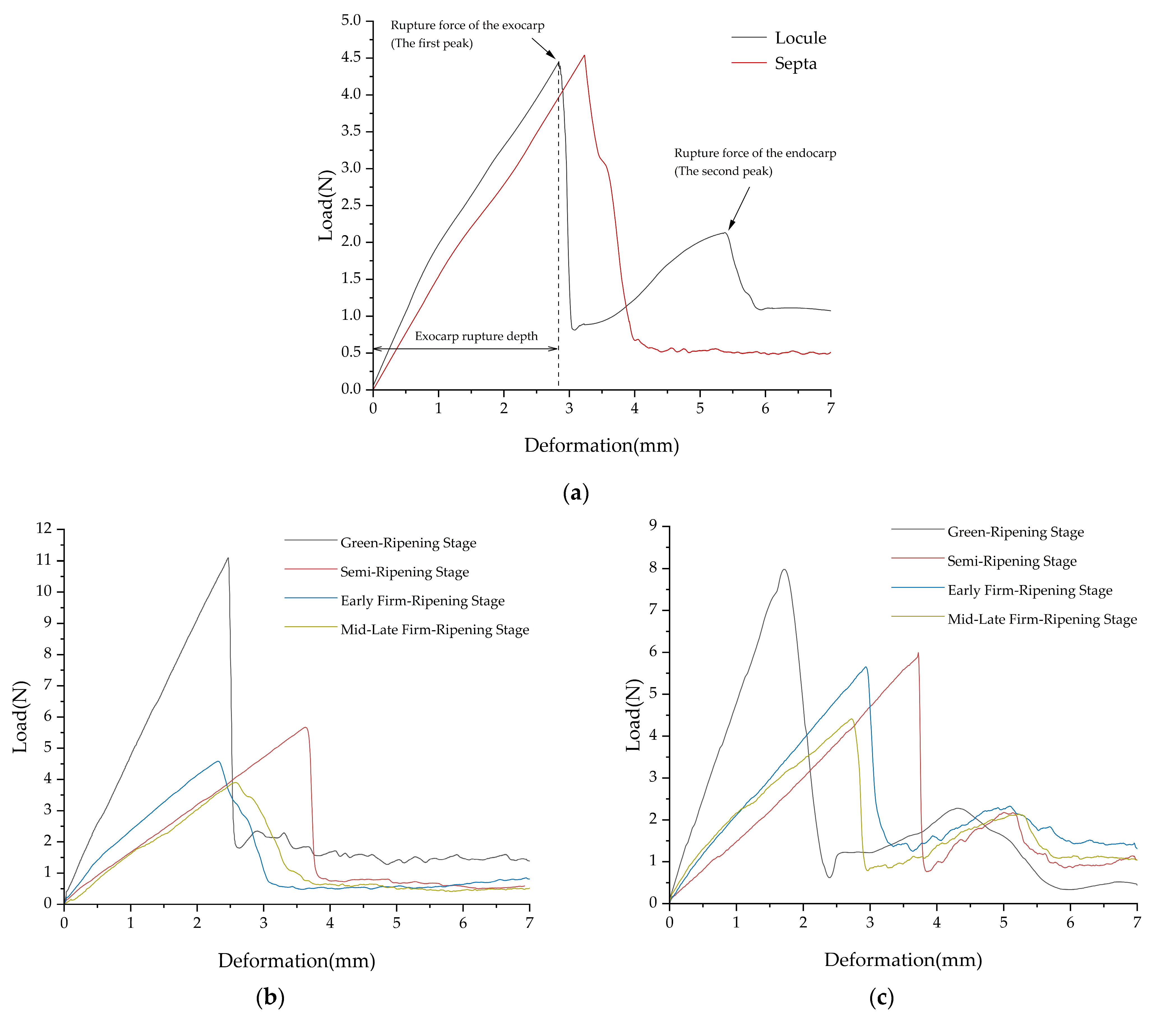
2.4. Puncture Test
2.5. Compression Test
2.6. Creep Model
2.7. Statistical Analysis
3. Results and Discussion
3.1. Creep Test
3.2. Puncture Test
3.3. Compression Test
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, Y.Z.; He, J.; Wei, F. Development and International Competitiveness Evaluation of China’s Tomato Industry in the 13th Five-Year Plan Period. Zhongguo Gua-Cai 2023, 36, 112–116. [Google Scholar]
- Zhang, J.; Liu, S.; Zhu, X.; Chang, Y.; Wang, C.; Ma, N.; Wang, J.; Zhang, X.; Lyu, J.; Xie, J. A Comprehensive Evaluation of Tomato Fruit Quality and Identification of Volatile Compounds. Plants 2023, 12, 2947. [Google Scholar] [CrossRef]
- Malik, M.; Zhang, T.; Li, H. Mature Tomato Fruit Detection Algorithm Based on improved HSV and Watershed Algorithm. In Proceedings of the 6th International Federation of Automatic Control (IFAC) Conference on Bio-Robotics (BIOROBOTICS), Beijing, China, 13–15 July 2018. [Google Scholar]
- Wang, P.C. Research on Tomato Fruit Growth Pose Recognition and Harvesting Control Based on Binocular Vision. Ph.D. Thesis, Zhejiang Sci-Tech University, Hangzhou, China, 1 May 2021. [Google Scholar]
- Samuel, D.V.K. Manually operated tomato harvesting tool for greenhouse. Acta Hortic. 2006, 710, 491–496. [Google Scholar] [CrossRef]
- Evans, W.; Cerven, V.; Winter, N.; Coker, C. A Proposed Alternative Production Regime for Cherry and Grape Tomato Using Compact Plants and Once-over Harvest. HortTechnology 2010, 20, 620–622. [Google Scholar] [CrossRef]
- Yang, Z.; Amin, A.; Zhang, Y.; Wang, X.; Chen, G.; Abdelhamid, M.A. Design of a Tomato Sorting Device Based on the Multisine-FSR Composite Measurement. Agronomy 2023, 13, 1778. [Google Scholar] [CrossRef]
- Tsai, C.; Kao, I.; Shibata, A.; Yoshimoto, K.; Higashimori, M.; Kaneko, M. Experimental study of creep response of viscoelastic contact interface under force control. In Proceedings of the International Conference on Intelligent Robots and Systems, Taipei, China, 18–22 October 2010. [Google Scholar]
- Deng, Y.; Wu, Y.; Li, Y.F. Biomechanical Characteristics and Texture Detection of Fruits and Vegetables During Storage and Transportation. Trans. Chin. Soc. Agric. Eng. 2005, 21, 1–6. [Google Scholar]
- Li, Z.G. Research on Grasping Damage of Tomato Harvesting Robot Based on Tomato Biomechanical Characteristics. Ph.D. Thesis, Jiangsu University, Zhenjiang, China, 15 June 2011. [Google Scholar]
- Zhou, J.; Zhang, N.; Meng, Y.; Wang, M. Online Estimation of Tomato Viscoelastic Parameters for Robot Grasping. Nongye Jixie Xuebao 2017, 48, 26–32. [Google Scholar]
- Wang, B.; Zhang, W.; Feng, Q. Measurement and Analysis of Stem-Clamping Mechanical Properties for Automatic Pruning of Tomatoes. J. Agric. Mech. Res. 2023, 45, 157–163. [Google Scholar]
- Ince, A.; Cevik, M.Y.; Vursavuş, K.K. Effects of Ripening Stages on Textural Mechanical Properties of Tomato. Int. J. Agric. Biol. Eng. 2016, 9, 200–206. [Google Scholar]
- Zhang, B.; Zhou, J.; Meng, Y.; Zhang, N.; Gu, B.; Yan, Z.; Idris, S.I. Comparative study of mechanical damage caused by a two-finger tomato gripper with different robotic grasping patterns for harvesting robots. Biosyst. Eng. 2018, 171, 245–257. [Google Scholar] [CrossRef]
- Pham, Q.; Liou, N. Investigating texture and mechanical properties of Asian pear flesh by compression tests. J. Mech. Sci. Technol. 2017, 31, 3671–3674. [Google Scholar] [CrossRef]
- Stropek, Z.; Golacki, K. Quantity assessment of plastic deformation energy under impact loading conditions of selected apple cultivars. Postharvest Biol. Tec. 2016, 115, 9–17. [Google Scholar] [CrossRef]
- Stropek, Z.; Golacki, K. Bruise susceptibility and energy dissipation analysis in pears under impact loading conditions. Postharvest Biol. Tec. 2020, 163, 111120. [Google Scholar] [CrossRef]
- Shirvani, M.; Ghanbarian, D.; Ghasemi-Varnamkhasti, M. Measurement and evaluation of the apparent modulus of elasticity of apple based on Hooke’s, Hertz’s and Boussinesq’s theories. Measurement 2014, 54, 133–139. [Google Scholar] [CrossRef]
- Bi, C.; Li, D.; Wang, L.; Adhikari, B. Viscoelastic properties and fractal analysis of acid-induced SPI gels at different ionic strength. Carbohydr. Polym. 2013, 92, 98–105. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, N.; Fu, N.; Li, D.; Wang, L.; Chen, X. Mechanical Properties of Hulless Barley Stem with Different Moisture Contents. Int. J. Food. Eng. 2019, 15, 20180033. [Google Scholar] [CrossRef]
- Hou, J.; He, Z.; Liu, D.; Zhu, Z.; Long, Z.; Yue, X.; Wang, W. Mechanical Damage Characteristics and Nondestructive Testing Techniques of Fruits: A Review. Food Sci. Technol. 2023, 43, e001823. [Google Scholar] [CrossRef]
- Jahanbakhshi, A.; Yeganeh, R.; Shahgoli, G. Determination of Mechanical Properties of Banana Fruit under Quasi-Static Loading in Pressure, Bending, and Shearing Tests. Int. J. Fruit Sci. 2020, 20, 314–322. [Google Scholar] [CrossRef]
- Wu, K.; Lou, J.; Li, C.; Luo, W.; Li, C.; Li, J. Creep Modelling of Rootstock during Holding in Watermelon Grafting. Agriculture 2021, 11, 1266. [Google Scholar] [CrossRef]
- Vu, Q.; Ronzhin, A. A Model of Four-Finger Gripper with a Built-in Vacuum Suction Nozzle for Harvesting Tomatoes; Smart Innovation, Systems and Technologies. In Proceedings of the 14th International Conference on Electromechanics and Robotics “Zavalishin’s Readings”, Kursk, Russia, 17–20 April 2019; Spinger: Singapore, 2020; pp. 149–160. [Google Scholar]
- Jun, J.; Kim, J.; Seol, J.; Kim, J. Towards an Efficient Tomato Harvesting Robot: 3D Perception, Manipulation, and End-Effector. IEEE Access 2021, 9, 17631–17640. [Google Scholar] [CrossRef]
- Deimel, R.; Brock, O. A novel type of compliant and underactuated robotic hand for dexterous grasping. Int. J. Robot. Res. 2016, 35, 161–185. [Google Scholar] [CrossRef]
- Yang, M. Rheology of Agricultural Materials; China Agriculture Press: Beijing, China, 2010; pp. 56–83. [Google Scholar]
- Zhuang, M.; Li, G.; Ding, K.; Xu, G. Research on the application of impedance control in flexible grasp of picking robot. Adv. Mech. Eng. 2023, 15, 16878132231161016. [Google Scholar] [CrossRef]
- Psarra, E.; George, C.P. Luffa Cylindrica as a Durable Biofiber Reinforcement for Epoxy Systems. Compos. Sci. Technol. 2021, 203, 108597. [Google Scholar] [CrossRef]
- Wu, X.; Wang, C.; Guo, Y. Effects of the high-pulsed electric field pretreatment on the mechanical properties of fruits and vegetables. J. Food. Eng. 2020, 274, 109837. [Google Scholar] [CrossRef]
- Wei, J.; Tang, C.; Xu, B.; He, G. Contact force modeling and variable damping impedance control of apple harvesting robot. Comput. Electron. Agric. 2022, 198, 107026. [Google Scholar]
- Wei, J.; Ding, Y.; Xu, B.; Chen, G.; Zhao, D. Adaptive Variable Parameter Impedance Control for Apple Harvesting Robot Compliant Picking. Complexity 2020, 2020, 4812657. [Google Scholar] [CrossRef]
- Quintana, S.; Llalla, O.; García-Zapateiro, L.; García-Risco, M.; Fornari, T. Preparation and Characterization of Licorice-Chitosan Coatings for Postharvest Treatment of Fresh Strawberries. Appl. Sci. 2020, 10, 8431. [Google Scholar] [CrossRef]
- Tao, Y.; Zhou, J.; Wang, M.; Zhang, N.; Meng, Y. An optimum strategy for robotic tomato grasping based on real-time viscoelastic parameters estimation. Int. J. Adv. Robot. Syst. 2017, 14, 1–8. [Google Scholar] [CrossRef]
- Qian, Z. Study on Grasping Model and Compliance Control of Gripper of Apple Picking Robot. Master’s Thesis, Jiangsu University, Zhenjiang, China, 10 June 2019. [Google Scholar]
- Bui, H.; Makhlouf, J.; Ratti, C. Postharvest ripening characterization of greenhouse tomatoes. Int. J. Food Prop. 2010, 13, 830–846. [Google Scholar] [CrossRef]
- Sirisomboon, P.; Tanaka, M.; Kojima, T. Evaluation of tomato textural mechanical properties. J. Food Eng. 2012, 111, 618–624. [Google Scholar] [CrossRef]
- Vieira, D.; Caliari, M.; Souza, E.; Soares Júnior, M. Mechanical resistance, biometric and physicochemical characteristics of tomato cultivars for industrial processing. Food Sci. Technol. 2019, 39, 363–370. [Google Scholar] [CrossRef]
- Desmet, M.; Lammertyn, J. The relative influence of stem and fruit properties on stem puncture injury in tomatoes. Postharvest Biol. Tec. 2004, 33, 101–109. [Google Scholar] [CrossRef]
- Xiong, Z.; Li, H.; Hou, L. Study on mechanical properties of cherry tomato for robot picking. Mod. Agric. Equip. 2020, 41, 24–28. [Google Scholar]
- Liu, J.; Li, P.; Li, Z. Experimental study on mechanical properties of tomatoes for robotic harvesting. Nongye Gongcheng Xuebao 2008, 24, 66–70. [Google Scholar]






| Physical Parameters | Green-Ripening Stage | Semi-Ripening Stage | Early Firm-Ripening Stage | Mid-Late Firm-Ripening Stage | |
|---|---|---|---|---|---|
| Diameter (mm) | Max | 80.21 | 72.04 | 86.86 | 83.29 |
| Mean | 70.73 ± 6.18 | 65.83 ± 4.30 | 72.15 ± 8.11 | 71.70 ± 6.69 | |
| Min | 63.27 | 60.04 | 57.25 | 59.11 | |
| Minor Diameter (mm) | Max | 76.92 | 69.95 | 84.45 | 78.98 |
| Mean | 66.63 ± 6.78 | 63.78 ± 3.74 | 69.39 ± 7.65 | 68.54 ± 5.63 | |
| Min | 58.44 | 57.42 | 54.69 | 58.34 | |
| Height (mm) | Max | 65.51 | 71.11 | 112.43 | 132.61 |
| Mean | 57.86 ± 4.74 | 61.77 ± 4.87 | 57.00 ± 3.12 | 62.07 ± 20.44 | |
| Min | 51.38 | 55.04 | 51.35 | 52.90 | |
| Weight (g) | Max | 225.496 | 202.448 | 252.640 | 228.865 |
| Mean | 154.116 ± 41.599 | 151.347 ± 24.799 | 167.489 ± 43.937 | 156.586 ± 44.144 | |
| Min | 110.203 | 111.379 | 88.299 | 55.160 | |
| Quantities | 14 | 14 | 14 | 14 |
| Ripening Stage | /(N mm−1) | /(N mm−1) | /(N s mm−1) | /(N s mm−1) | R2 |
|---|---|---|---|---|---|
| Green-Ripening Stage | 1194.23 | 81.90 | 21808.45 | 2663.27 | 0.998 |
| Semi-Ripening Stage | 151.30 | 21.79 | 8568.42 | 454.63 | 0.996 |
| Early Firm-Ripening Stage | 183.84 | 23.44 | 9271.09 | 587.88 | 0.996 |
| Mid-Late Firm-Ripening Stage | 61.21 | 14.37 | 6607.71 | 342.90 | 0.994 |
| Ripening Stage | End Value | Start Value | Change Value | |||||
|---|---|---|---|---|---|---|---|---|
| Ripening Stage | 1 | −0.674 ** | −0.666 ** | −0.617 ** | −0.674 ** | 0.584 ** | 0.580 ** | 0.559 ** |
| 1 | 0.971 ** | 0.945 ** | 0.958 ** | −0.819 ** | −0.805 ** | −0.808 ** | ||
| 1 | 0.980 ** | 0.995 ** | −0.850 ** | −0.830 ** | −0.856 ** | |||
| 1 | 0.969 ** | −0.892 ** | −0.870 ** | −0.902 ** | ||||
| 1 | −0.821 ** | −0.803 ** | −0.822 ** | |||||
| End value | 1 | 0.995 ** | 0.953 ** | |||||
| Start value | 1 | 0.917 ** | ||||||
| Change value | 1 |
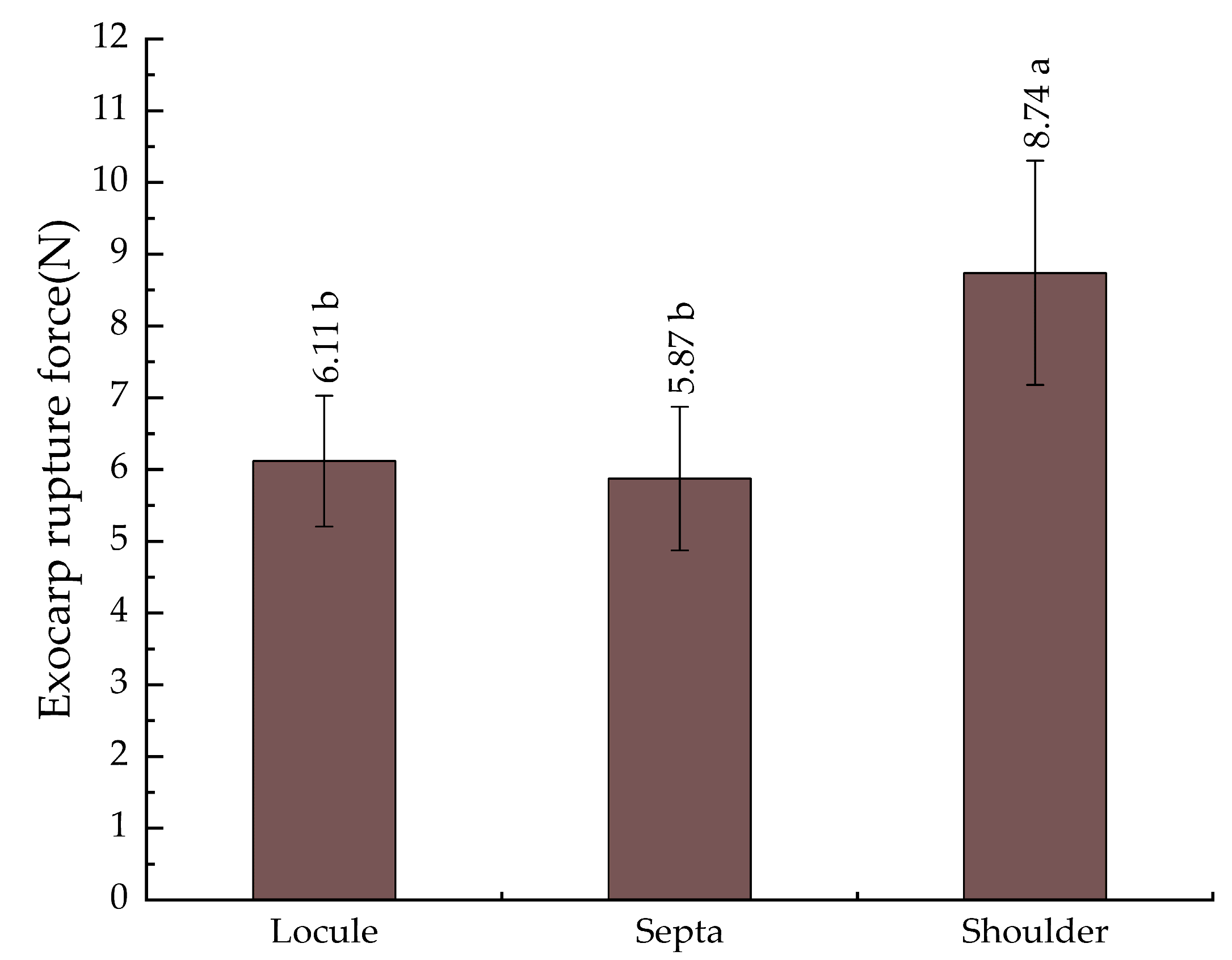
| Ripening Stage | Experimental Results | Exocarp Rupture Force/(N) | Exocarp Rupture Depth/(mm) | Exocarp Brittleness/ (N mm−1) | Exocarp Toughness/ (N mm) |
|---|---|---|---|---|---|
| Green-Ripening Stage | Max | 11.476 | 3.534 | 5.745 | 20.280 |
| Mean | 9.224 ± 0.901 a | 2.016 ± 0.359 d | 4.657 ± 0.621 a | 9.384 ± 2.439 b | |
| Min | 7.415 | 1.488 | 3.247 | 5.634 | |
| Semi-Ripening Stage | Max | 7.651 | 5.157 | 2.604 | 19.314 |
| Mean | 5.996 ± 0.952 b | 3.471 ± 0.730 b | 1.770 ± 0.328 c | 10.598 ± 3.415 a | |
| Min | 3.982 | 2.223 | 1.123 | 5.242 | |
| Early Firm-Ripening Stage | Max | 6.807 | 4.327 | 2.798 | 12.776 |
| Mean | 5.408 ± 0.688 c | 2.822 ± 0.590 c | 1.974 ± 0.359 b | 7.717 ± 2.163 c | |
| Min | 3.884 | 1.668 | 1.349 | 3.239 | |
| Mid-Late Firm-Ripening Stage | Max | 6.415 | 5.697 | 1.769 | 16.258 |
| Mean | 4.521 ± 0.654 d | 3.781 ± 0.758 a | 1.229 ± 0.239 d | 8.651 ± 2.640 bc | |
| Min | 3.315 | 2.657 | 0.855 | 5.230 |
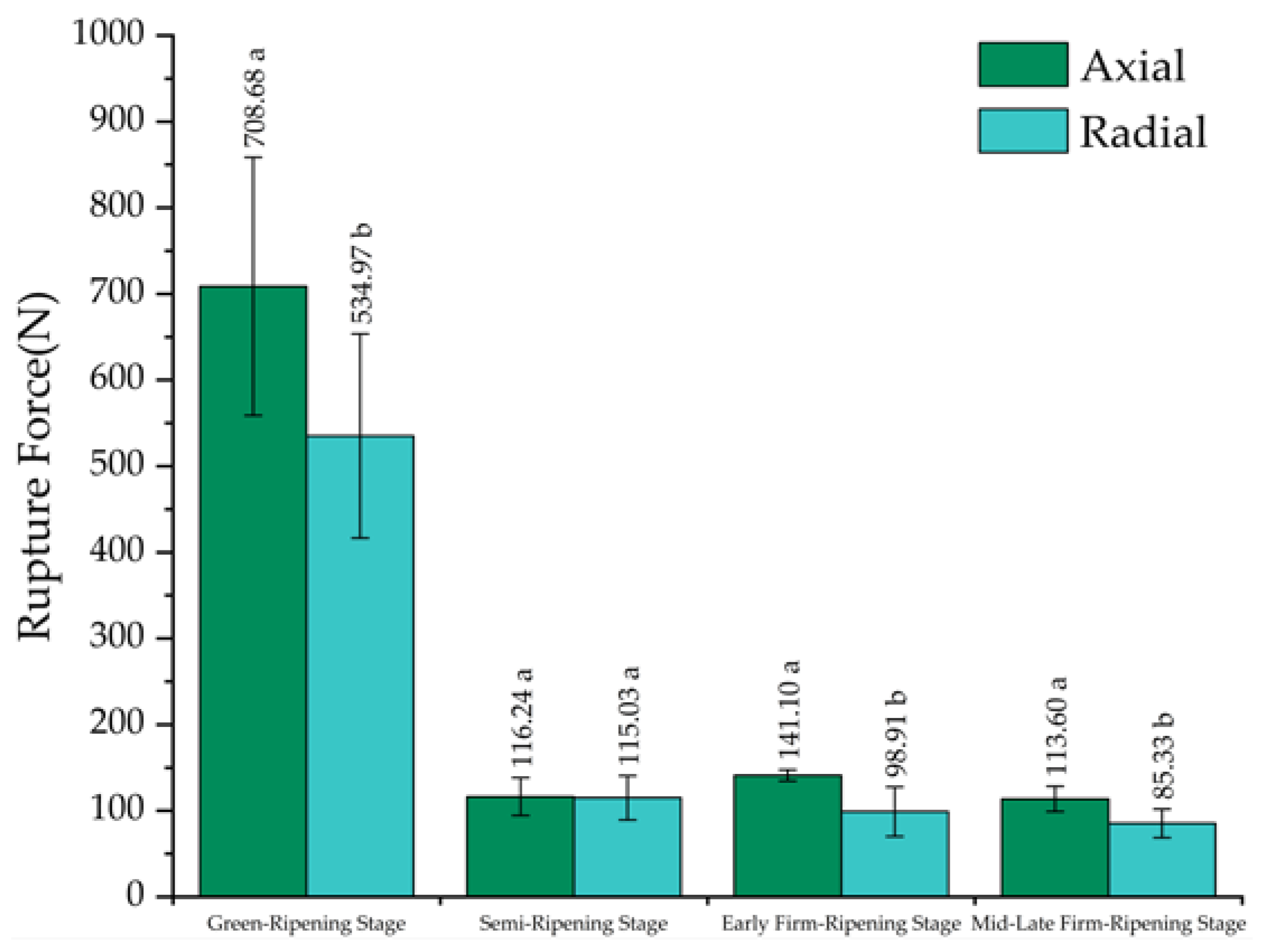
| Loading Direction | Experimental Results | Green-Ripening Stage | Semi-Ripening Stage | Early Firm-Ripening Stage | Mid-Late Firm-Ripening Stage | ||||
|---|---|---|---|---|---|---|---|---|---|
| Rupture Force/(N) | Rupture Deformation/(mm) | Rupture Force/(N) | Rupture Deformation/(mm) | Rupture Force/(N) | Rupture Deformation/(mm) | Rupture Force/(N) | Rupture Deformation/(mm) | ||
| Axial | Max | 991.30 | 29.72 | 143.11 | 16.93 | 148.72 | 16.78 | 136.74 | 18.74 |
| Mean | 708.68 ± 149.89 a | 24.70 ± 2.99 | 116.24 ± 21.90 a | 15.03 ± 1.84 | 141.10 ± 6.41 a | 14.80 ± 1.81 | 113.60 ± 14.72 a | 14.49 ± 2.48 | |
| Min | 540.34 | 20.44 | 84.94 | 11.91 | 131.12 | 12.09 | 99.56 | 12.32 | |
| Radial | Max | 790.41 | 28.14 | 151.37 | 20.26 | 148.04 | 20.94 | 106.23 | 18.86 |
| Mean | 534.97 ± 118.52 b | 24.19 ± 4.16 | 109.71 ± 24.75 b | 16.86 ± 3.04 | 98.91 ± 28.65 b | 17.04 ± 3.02 | 85.33 ± 16.54 b | 16.30 ± 2.69 | |
| Min | 306.21 | 13.63 | 81.22 | 12.03 | 52.67 | 12.09 | 62.13 | 12.49 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, S.; He, M.; Jia, X.; Zheng, Z.; Wu, X.; Weng, W. Study on Mechanical Properties of Tomatoes for the End-Effector Design of the Harvesting Robot. Agriculture 2023, 13, 2201. https://doi.org/10.3390/agriculture13122201
Zheng S, He M, Jia X, Zheng Z, Wu X, Weng W. Study on Mechanical Properties of Tomatoes for the End-Effector Design of the Harvesting Robot. Agriculture. 2023; 13(12):2201. https://doi.org/10.3390/agriculture13122201
Chicago/Turabian StyleZheng, Shuhe, Minglei He, Xuexin Jia, Zebin Zheng, Xinhui Wu, and Wuxiong Weng. 2023. "Study on Mechanical Properties of Tomatoes for the End-Effector Design of the Harvesting Robot" Agriculture 13, no. 12: 2201. https://doi.org/10.3390/agriculture13122201
APA StyleZheng, S., He, M., Jia, X., Zheng, Z., Wu, X., & Weng, W. (2023). Study on Mechanical Properties of Tomatoes for the End-Effector Design of the Harvesting Robot. Agriculture, 13(12), 2201. https://doi.org/10.3390/agriculture13122201




