Facilitating Resilience during an African Swine Fever Outbreak in the Austrian Pork Supply Chain through Hybrid Simulation Modelling
Abstract
1. Introduction
2. State of the Art
3. Methodology
3.1. DES of the Pork Supply Chain
- Breeding farm: produces piglets for rearing or fattening purposes;
- Rearing farm: obtains piglets from breeding farms, raises them, and transport them to fattening farms;
- Fattening farm: obtains piglets from breeding or rearing farms and fattens them until slaughter;
- Combined farm: carries out pig breeding and pig fattening and occasionally obtains mother sows from breeding farms.
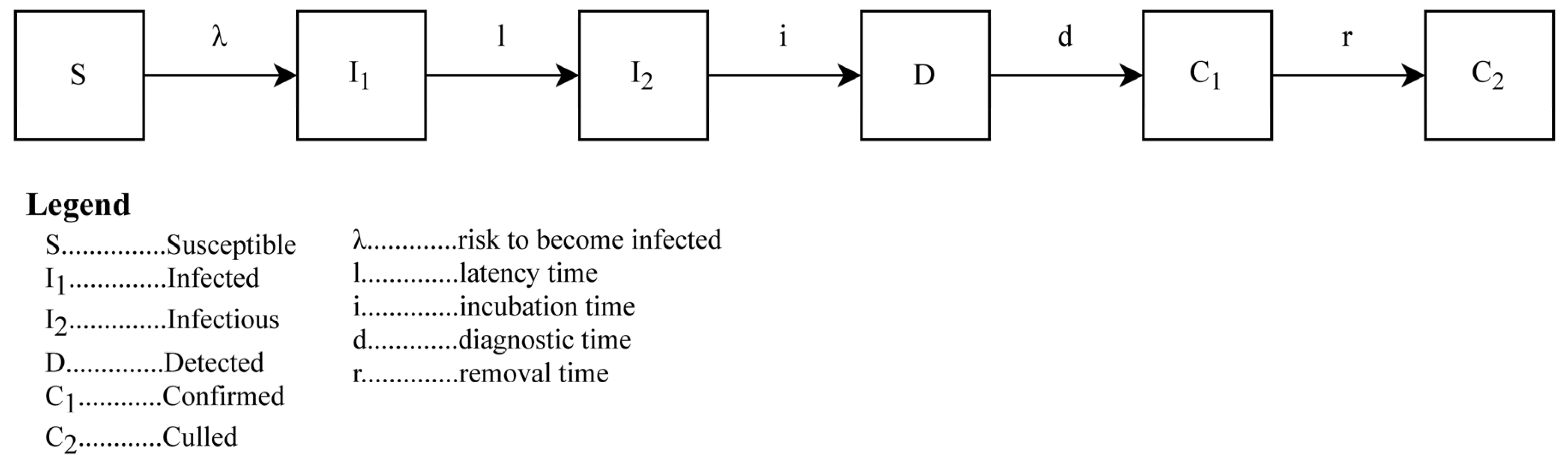
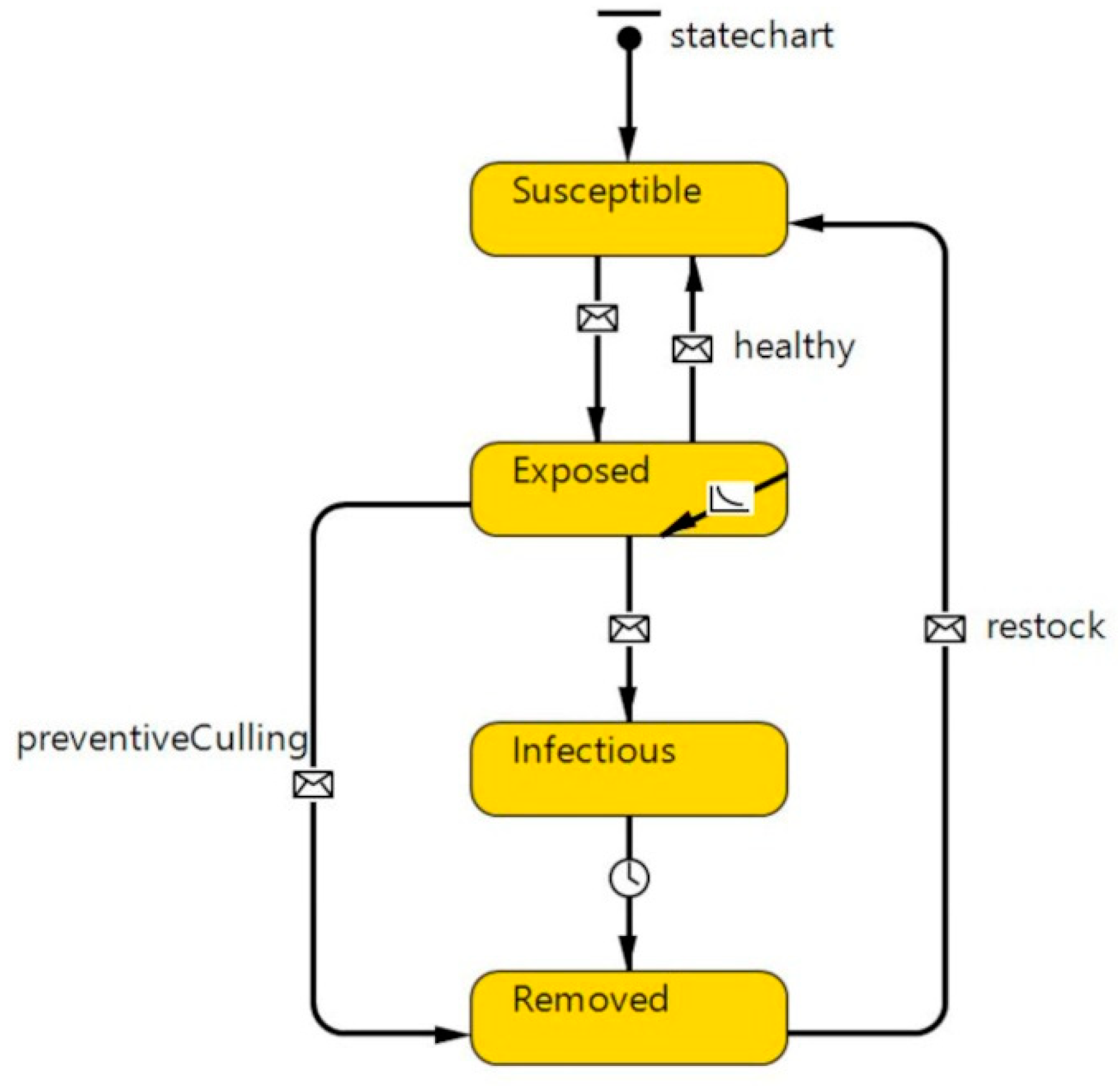
3.2. ABS of the ASF Outbreak
- Culling of all pigs on an infected holding;
- Taking a sufficient number of samples and sending them to a national reference laboratory;
- Destroying all materials (e.g., waste, feeding stuff, meat) that could be contaminated;
- Carrying out epidemiological investigations;
- Establishing a protection zone of 3 km and a surveillance zone of 10 km around the infected holding immediately after confirmation. In these zones:
- Epidemiological investigations are carried out;
- All pigs are kept inside their pens;
- The movement and transport of pigs on public roads (with exceptions is prohibited);
- Finding contact holdings based on epidemiological investigations and applying the same measures as at an infected holding.
4. Numerical Studies
5. Results
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- OIE. African Swine Fever. Available online: https://www.oie.int/en/disease/african-swine-fever/ (accessed on 11 November 2021).
- Beltran-Alcrudo, D.; Arias, M.; Gallardo, C.; Kramer, S.A.; Penrith, M.-L. African Swine Fever: Detection and Diagnosis—A Manual for Veterinarians. FAO Animal Production and Health Manual; FAO: Rome, Italy, 2017; Volume 19. [Google Scholar]
- Nigsch, A.; Costard, S.; Jones, B.A.; Pfeiffer, D.U.; Wieland, B. Stochastic spatio-temporal modelling of African swine fever spread in the European Union during the high risk period. Prev. Vet. Med. 2013, 108, 262–275. [Google Scholar] [CrossRef]
- Rowlands, R.J.; Michaud, V.; Heath, L.; Hutchings, G.; Oura, C.; Vosloo, W.; Dwarka, R.; Onashvili, T.; Albina, E.; Dixon, L.K. African swine fever virus isolate, Georgia, 2007. Emerg. Infect. Dis. 2008, 14, 1870–1874. [Google Scholar] [CrossRef]
- Cwynar, P.; Stojkov, J.; Wlazlak, K. African Swine Fever Status in Europe. Viruses 2019, 11, 310. [Google Scholar] [CrossRef] [PubMed]
- Guinat, C.; Gubbins, S.; Vergne, T.; Gonzales, J.L.; Dixon, L.; Pfeiffer, D.U. Experimental pig-to-pig transmission dynamics for African swine fever virus, Georgia 2007/1 strain. Epidemiol. Infect. 2016, 144, 25–34. [Google Scholar] [CrossRef] [PubMed]
- Szymańska, E.J.; Dziwulaki, M. Development of African Swine Fever in Poland. Agriculture 2022, 12, 119. [Google Scholar] [CrossRef]
- Blome, S.; Franzke, K.; Beer, M. African swine fever-A review of current knowledge. Virus Res. 2020, 287, 198099. [Google Scholar] [CrossRef] [PubMed]
- Dixon, L.K.; Sun, H.; Roberts, H. African swine fever. Antivir. Res. 2019, 165, 34–41. [Google Scholar] [CrossRef]
- Desmecht, D.; Gerbier, G.; Gortázar Schmidt, C.; Grigaliuniene, V.; Helyes, G.; Kantere, M.; Korytarova, D.; Linden, A.; Miteva, A.; Neghirla, I.; et al. Epidemiological analysis of African swine fever in the European Union (September 2019 to August 2020). EFSA J. 2021, 19, 6572. [Google Scholar] [CrossRef]
- FAO. African Swine Fever (ASF) Virology. Available online: https://www.fao.org/ag/againfo/programmes/en/empres/ASF/Virology.html (accessed on 15 November 2021).
- Montgomery, E.R. On a Form of Swine Fever occuring in British East Africa (Kenya Colony). J. Comp. Pathol. Ther. 1921, 34, 159–191. [Google Scholar] [CrossRef]
- Chenais, E.; Depner, K.; Guberti, V.; Dietze, K.; Viltrop, A.; Ståhl, K. Epidemiological considerations on African swine fever in Europe 2014–2018. Porc. Health Manag. 2019, 5, 6. [Google Scholar] [CrossRef]
- Sánchez-Vizcaíno, J.M.; Mur, L.; Gomez-Villamandos, J.C.; Carrasco, L. An update on the epidemiology and pathology of African swine fever. J. Comp. Pathol. 2015, 152, 9–21. [Google Scholar] [CrossRef]
- Guinat, C.; Gogin, A.; Blome, S.; Keil, G.; Pollin, R.; Pfeiffer, D.U.; Dixon, L. Transmission routes of African swine fever virus to domestic pigs: Current knowledge and future research directions. Vet. Rec. 2016, 178, 262–267. [Google Scholar] [CrossRef] [PubMed]
- Woźniakowski, G.; Pejsak, Z.; Jabłoński, A. Emergence of African Swine Fever in Poland (2014–2021). Successes and Failures in Disease Eradication. Agriculture 2021, 11, 738. [Google Scholar] [CrossRef]
- Shreve, C.; Davis, B.; Fordham, M. Integrating animal disease epidemics into disaster risk management. Disaster Prev. Manag. 2016, 25, 506–519. [Google Scholar] [CrossRef]
- Halasa, T.; Boklund, A.; Bøtner, A.; Mortensen, S.; Kjær, L.J. Simulation of transmission and persistence of African swine fever in wild boar in Denmark. Prev. Vet. Med. 2019, 167, 68–79. [Google Scholar] [CrossRef] [PubMed]
- Barongo, M.B.; Bishop, R.P.; Fèvre, E.M.; Knobel, D.L.; Ssematimba, A. A Mathematical Model that Simulates Control Options for African Swine Fever Virus (ASFV). PLoS ONE 2016, 11, e0158658. [Google Scholar] [CrossRef]
- Lee, H.S.; Thakur, K.K.; Bui, V.N.; Pham, T.L.; Bui, A.N.; Dao, T.D.; Thanh, V.T.; Wieland, B. A stochastic simulation model of African swine fever transmission in domestic pig farms in the Red River Delta region in Vietnam. Transbound. Emerg. Dis. 2020, 68, 1384–1391. [Google Scholar] [CrossRef]
- Penrith, M.-L. History of ‘swine fever’ in Southern Africa. J. S. Afr. Vet. Assoc. 2013, 84, 1. [Google Scholar] [CrossRef]
- Bosch, J.; Rodríguez, A.; Iglesias, I.; Muñoz, M.J.; Jurado, C.; Sánchez-Vizcaíno, J.M.; de la Torre, A. Update on the Risk of Introduction of African Swine Fever by Wild Boar into Disease-Free European Union Countries. Transbound. Emerg. Dis. 2017, 64, 1424–1432. [Google Scholar] [CrossRef]
- Jones, A.D.; Ngure, F.M.; Pelto, G.; Young, S.L. What are we assessing when we measure food security? A compendium and review of current metrics. Adv. Nutr. 2013, 4, 481–505. [Google Scholar] [CrossRef]
- FAO. Rome Declaration on World Food Security and World Food Summit Plan of Action; FAO: Rome, Italy, 1996. [Google Scholar]
- FAO. State of Food and Agriculture; FAO: Rome, Italy, 2001. [Google Scholar]
- Hecht, A.A.; Biehl, E.; Barnett, D.J.; Neff, R.A. Urban Food Supply Chain Resilience for Crises Threatening Food Security: A Qualitative Study. J. Acad. Nutr. Diet. 2019, 119, 211–224. [Google Scholar] [CrossRef] [PubMed]
- Holling, C.S. Resilience and Stability of Ecological Systems. Annu. Rev. Ecol. Syst. 1973, 4, 1–23. [Google Scholar] [CrossRef]
- Garnier, E. Lessons learned from the past for a better resilience to contemporary risks. Disaster Prev. Manag. 2019, 28, 786–803. [Google Scholar] [CrossRef]
- Sinclair, K.; Curtis, A.; Mendham, E.; Mitchell, M. Can resilience thinking provide useful insights for those examining efforts to transform contemporary agriculture? Agric. Hum. Values 2014, 31, 371–384. [Google Scholar] [CrossRef]
- ADIS. Outbreaks per Disease: European Commission. Available online: https://ec.europa.eu/food/animals/animal-diseases/animal-disease-information-system-adis_en (accessed on 1 February 2022).
- Sanson, R.L. The Development of a Decision Support System for an Animal Disease Emergency. Ph.D. Thesis, Massey University, Palmerston North, New Zealand, 1993. [Google Scholar]
- Jalvingh, A.W.; Nielen, M.; Dijkhuizen, A.A.; Morris, R.S. EpiMAN: Decision Support System for Contagious Animal Disease Control. IFAC Proc. Vol. 1995, 28, 97–102. [Google Scholar] [CrossRef]
- Martínez-López, B.; Perez, A.M.; Sánchez-Vizcaíno, J.M. A simulation model for the potential spread of foot-and-mouth disease in the Castile and Leon region of Spain. Prev. Vet. Med. 2010, 96, 19–29. [Google Scholar] [CrossRef]
- Jalvingh, A.W.; Nielen, M.; Maurice, H.; Stegeman, A.J.; Elbers, A.R.; Dijkhuizen, A.A. Spatial and stochastic simulation to evaluate the impact of events and control measures on the 1997–1998 classical swine fever epidemic in The Netherlands: I. Description of simulation model. Prev. Vet. Med. 1999, 42, 271–295. [Google Scholar] [CrossRef]
- Nielen, M.; Jalvingh, A.W.; Meuwissen, M.; Horst, S.H.; Dijkhuizen, A.A. Spatial and stochastic simulation to evaluate the impact of events and control measures on the 1997–1998 classical swine fever epidemic in The Netherlands. II. Comparison of control strategies. Prev. Vet. Med. 1999, 42, 297–317. [Google Scholar] [CrossRef]
- Mangen, M.-J.; Jalvingh, A.; Nielen, M.; Mourits, M.; Klinkenberg, D.; Dijkhuizen, A. Spatial and stochastic simulation to compare two emergency-vaccination strategies with a marker vaccine in the 1997/1998 Dutch Classical Swine Fever epidemic. Prev. Vet. Med. 2001, 48, 177–200. [Google Scholar] [CrossRef][Green Version]
- Velthuis, A.G.J.; Mourits, M.C.M. Effectiveness of movement-prevention regulations to reduce the spread of foot-and-mouth disease in The Netherlands. Prev. Vet. Med. 2007, 82, 262–281. [Google Scholar] [CrossRef]
- Boklund, A.; Goldbach, S.G.; Uttenthal, A.; Alban, L. Simulating the spread of classical swine fever virus between a hypothetical wild-boar population and domestic pig herds in Denmark. Prev. Vet. Med. 2008, 85, 187–206. [Google Scholar] [CrossRef] [PubMed]
- Nigsch, A. Simulation von Ausbrüchen der Klassischen Schweinepest in Einer Schweinedichten Region in der Steiermark und die Abschätzung der Wirtschaftlichen Auswirkungen. Ph.D. Dissertation, University of Veterinary Medicine, Vienna, Austria, 2009. [Google Scholar]
- Hiesel, J.A.; Kopacka, I.; Fuchs, R.; Schobesberger, H.; Wagner, P.; Loitsch, A.; Köfer, J. Epidemiological evaluation of different FMD control strategies in two selected regions in Austria. Berl. Münch. Tierärz. Wochenschr. 2016, 129, 484–494. [Google Scholar] [CrossRef]
- Garner, M.G.; Beckett, S.D. Modelling the spread of foot-and-mouth disease in Australia. Aust. Vet. J. 2005, 83, 758–766. [Google Scholar] [CrossRef]
- Roche, S.E.; Garner, M.G.; Wicks, R.M.; East, I.J.; de Witte, K. How do resources influence control measures during a simulated outbreak of foot and mouth disease in Australia? Prev. Vet. Med. 2014, 113, 436–446. [Google Scholar] [CrossRef] [PubMed]
- Pendell, D.L.; Leatherman, J.; Schroeder, T.C.; Alward, G.S. The economic impacts of Foot-and-Mouth disease Outbreak: A regional analysis. J. Agric. Appl. Econ. 2007, 39, 19–33. [Google Scholar] [CrossRef]
- Harvey, N.; Reeves, A.; Schoenbaum, M.A.; Zagmutt-Vergara, F.J.; Dubé, C.; Hill, A.E.; Corso, B.A.; McNab, W.B.; Cartwright, C.I.; Salman, M.D. The North American Animal Disease Spread Model: A simulation model to assist decision making in evaluating animal disease incursions. Prev. Vet. Med. 2007, 82, 176–197. [Google Scholar] [CrossRef]
- Martínez-López, B.; Ivorra, B.; Ngom, D.; Ramos, A.M.; Sánchez-Vizcaíno, J.M. A novel spatial and stochastic model to evaluate the within and between farm transmission of classical swine fever virus: II validation of the model. Vet. Microbiol. 2012, 155, 21–32. [Google Scholar] [CrossRef]
- Halasa, T.; Toft, N.; Boklund, A. Improving the Effect and Efficiency of FMD Control by Enlarging Protection or Surveillance Zones. Front. Vet. Sci. 2015, 2, 70. [Google Scholar] [CrossRef]
- Dórea, F.C.; Nöremark, M.; Widgren, S.; Frössling, J.; Boklund, A.; Halasa, T.; Ståhl, K. Evaluation of Strategies to Control a Potential Outbreak of Foot-and-Mouth Disease in Sweden. Front. Vet. Sci. 2017, 4, 118. [Google Scholar] [CrossRef]
- Halasa, T.; Bøtner, A.; Mortensen, S.; Christensen, H.; Wulff, S.B.; Boklund, A. Modeling the Effects of Duration and Size of the Control Zones on the Consequences of a Hypothetical African Swine Fever Epidemic in Denmark. Front. Vet. Sci. 2018, 5, 49. [Google Scholar] [CrossRef]
- Bradhurst, R.; Garner, G.; Hóvári, M.; de la Puente, M.; Mintiens, K.; Yadav, S.; Federici, T.; Kopacka, I.; Stockreiter, S.; Kuzmanova, I.; et al. Development of a transboundary model of livestock disease in Europe. Transbound. Emerg. Dis. 2021, 1–20. [Google Scholar] [CrossRef]
- Marschik, T.; Kopacka, I.; Stockreiter, S.; Schmoll, F.; Hiesel, J.; Höflechner-Pöltl, A.; Käsbohrer, A.; Pinior, B. The Epidemiological and Economic Impact of a Potential Foot-and-Mouth Disease Outbreak in Austria. Front. Vet. Sci. 2021, 7, 594753. [Google Scholar] [CrossRef] [PubMed]
- Hayes, B.H.; Andraud, M.; Salazar, L.G.; Rose, N.; Vergne, T. Mechanistic modelling of African swine fever: A systematic review. Prev. Vet. Med. 2021, 191, 105358. [Google Scholar] [CrossRef]
- Lee, H.S.; Bui, V.N.; Dao, D.T.; Bui, N.A.; Le, T.D.; Kieu, M.A.; Nguyen, Q.H.; Tran, L.H.; Roh, J.-H.; So, K.-M.; et al. Pathogenicity of an African swine fever virus strain isolated in Vietnam and alternative diagnostic specimens for early detection of viral infection. Porc. Health Manag. 2021, 7, 36. [Google Scholar] [CrossRef] [PubMed]
- Lange, M.; Thulke, H.-H. Elucidating transmission parameters of African swine fever through wild boar carcasses by combining spatio-temporal notification data and agent-based modelling. Stoch. Environ. Res. Risk Assess. 2017, 31, 379–391. [Google Scholar] [CrossRef]
- Halasa, T.; Boklund, A.; Bøtner, A.; Toft, N.; Thulke, H.-H. Simulation of Spread of African Swine Fever, Including the Effects of Residues from Dead Animals. Front. Vet. Sci. 2016, 3, 6. [Google Scholar] [CrossRef] [PubMed]
- De Carvalho Ferreira, H.C.; Backer, J.A.; Weesendorp, E.; Klinkenberg, D.; Stegeman, J.A.; Loeffen, W.L.A. Transmission rate of African swine fever virus under experimental conditions. Vet. Microbiol. 2013, 165, 296–304. [Google Scholar] [CrossRef]
- Halasa, T.; Bøtner, A.; Mortensen, S.; Christensen, H.; Toft, N.; Boklund, A. Simulating the epidemiological and economic effects of an African swine fever epidemic in industrialized swine populations. Vet. Microbiol. 2016, 193, 7–16. [Google Scholar] [CrossRef]
- Andraud, M.; Halasa, T.; Boklund, A.; Rose, N. Threat to the French Swine Industry of African Swine Fever: Surveillance, Spread, and Control Perspectives. Front. Vet. Sci. 2019, 6, 248. [Google Scholar] [CrossRef]
- Croft, S.; Massei, G.; Smith, G.C.; Fouracre, D.; Aegerter, J.N. Modelling Spatial and Temporal Patterns of African Swine Fever in an Isolated Wild Boar Population to Support Decision-Making. Front. Vet. Sci. 2020, 7, 154. [Google Scholar] [CrossRef]
- Yang, A.; Schlichting, P.; Wight, B.; Anderson, W.M.; Chinn, S.M.; Wilber, M.Q.; Miller, R.S.; Beasley, J.C.; Boughton, R.K.; Ver Cauteren, K.C.; et al. Effects of social structure and management on risk of disease establishment in wild pigs. J. Anim. Ecol. 2021, 90, 820–833. [Google Scholar] [CrossRef]
- Taylor, R.A.; Podgórski, T.; Simons, R.R.; Ip, S.; Gale, P.; Kelly, L.A.; Snary, E.L. Predicting spread and effective control measures for African swine fever—Should we blame the boars? Transbound. Emerg. Dis. 2021, 68, 397–416. [Google Scholar] [CrossRef]
- Pietschmann, J.; Guinat, C.; Beer, M.; Pronin, V.; Tauscher, K.; Petrov, A.; Keil, G.; Blome, S. Course and transmission characteristics of oral low-dose infection of domestic pigs and European wild boar with a Caucasian African swine fever virus isolate. Arch. Virol. 2015, 160, 1657–1667. [Google Scholar] [CrossRef] [PubMed]
- Brailsford, S.C.; Eldabi, T.; Kunc, M.; Mustafee, N.; Osorio, A.F. Hybrid simulation modelling in operational research: A state-of-the-art review. Eur. J. Oper. Res. 2019, 278, 721–737. [Google Scholar] [CrossRef]
- Keeling, M.J. Models of foot-and-mouth disease. Proc. Biol. Sci. 2005, 272, 1195–1202. [Google Scholar] [CrossRef] [PubMed]
- Wearing, H.J.; Rohani, P.; Keeling, M.J. Appropriate models for the management of infectious diseases. PLoS Med. 2005, 2, 621–627. [Google Scholar] [CrossRef]
- Adivar, B.; Selen, E.S. Review of research studies on population specific epidemic disasters. Disaster Prev. Manag. 2013, 22, 243–264. [Google Scholar] [CrossRef]
- OpenStreetMap. Available online: https://www.openstreetmap.org/#map=7/48.385/13.966 (accessed on 9 December 2021).
- European Parliament; Council. EU Regulation No 2016/429 (Regulation on Transmissible Animal Diseases and Amending and Repealing Certain Acts in the Area of Animal Health, “Animal Health Law”): Animal Health Law; Official Journal of the European Union: Luxembourg, 2016. [Google Scholar]
- Bundesministerin für Gesundheit und Frauen. ASF-Regulation (Verordnung der Bundesministerin für Gesundheit und Frauen zur Bekämpfung der Afrikanischen Schweinepest bei Haus- und Wildschweinen): ASP-Verordnung 2005; Bundesministerin für Gesundheit und Frauen zur Bekämpfung der Afrikanischen Schweinepest bei Haus- und Wildschweinen: Vienna, Austria, 2005. [Google Scholar]
- Velthuis, A.; de Jong, M.; Kamp, E.; Stockhofe, N.; Verheijden, J. Design and analysis of an Actinobacillus pleuropneumoniae transmission experiment. Prev. Vet. Med. 2003, 60, 53–68. [Google Scholar] [CrossRef]
- AGES. Afrikanische Schweinepest. Available online: https://www.ages.at/themen/krankheitserreger/afrikanische-schweinepest/ (accessed on 18 December 2021).
- Eblé, P.L.; de Koeijer, A.A.; de Jong, M.C.M.; Engel, B.; Dekker, A. A meta-analysis quantifying transmission parameters of FMDV strain O Taiwan among non-vaccinated and vaccinated pigs. Prev. Vet. Med. 2008, 83, 98–106. [Google Scholar] [CrossRef]
- Bundesministerin für Gesundheit und Frauen. Austrian Swine Health Regulation (Schweinegesundheitsverordnung): SchwG-VO; Bundesministerin für Gesundheit und Frauen über Biosicherheitsmaßnahmen, hygienische Anforderungen und die Gesundheitsüberwachung in Schweinehaltungsbetrieben: Vienna, Austria, 2016. [Google Scholar]
- European Parliament Council. EU Regulation (EC) No 1069/2009 of the European Parliament and of the Council of 21 October 2009 Laying Down Health Rules as Regards Animal By-Products and Derived Products Not Intended for Human Consumption and Repealing Regulation (EC) No 1774/2002 (Animal By-Products Regulation); Official Journal of the European Union: Luxembourg, 2009. [Google Scholar]


| Model | Method | Source | Country | Disease |
|---|---|---|---|---|
| EpiMAN | The model combines a database management system (DBMS), a geographic information system (GIS), expert system elements, various models on specific aspects of foot and mouth disease (FMD) epidemiology (InterSpread), and a statistical analysis capability. | Sanson [31] | New Zealand | FMD |
| InterSpread® | Inter-farm spread model using a spatial stochastic simulation operating on the actual geography of the area. | Sanson [31] | New Zealand | FMD |
| Jalvingh et al. [32] | New Zealand | FMD | ||
| Martínez-López et al. [33] | Spain | FMD | ||
| InterCSF | Spatial, temporal, and stochastic simulation model of classic swine fever (CSF), using InterSpread as the basis. | Jalvingh et al. [34] | Netherlands | CSF |
| Nielen et al. [35] | Netherlands | CSF | ||
| Mangen et al. [36] | Netherlands | CSF | ||
| InterFMD | Stochastic and spatial simulation of the spread and control of FMD. | Velthuis and Mourits [37] | Netherlands | FMD |
| InterSpread Plus® | Stochastic, individual-based, discrete time, and spatio-temporal state transition spread of infectious disease model (using InterSpread as the basis). | Boklund et al. [38] | Denmark | CSF |
| Nigsch [39] | Austria | CSF | ||
| Nigsch et al. [3] | European Union | ASF | ||
| Hiesel et al. [40] | Austria | FMD | ||
| AusSpread | Stochastic spatial simulation of the spread and control of FMD at a regional scale. | Garner and Beckett [41] | Australia | FMD |
| Roche et al. [42] | Australia | FMD | ||
| NAADSM | Spatial, stochastic, state transition simulation model. | Pendell et al. [43] | United States of America | FMD |
| Harvey et al. [44] | United States of America and Canada | FMD | ||
| Lee et al. [20] | Vietnam | ASF | ||
| Be-FAST | Discrete time stochastic susceptible-infected model (within farm); spatial stochastic individual-based model (between farms). | Martínez-López et al. [45] | Spain | CSF |
| DTU-DADS | Spatial, stochastic simulation model (between-farm spread simulated using agent-based modelling (ABM), within-farm spread modelled using a compartmental model). | Halasa et al. [46] | Denmark | FMD |
| Dórea et al. [47] | Sweden | FMD | ||
| Halasa et al. [48] | Denmark | ASF | ||
| EuFMDis | Multi-country spatially explicit simulation model with equation-based (spread within a herd) and data-driven individual-based modelling (spread between herds). | Bradhurst et al. [49] | European Union | FMD |
| Marschik et al. [50] | Austria | FMD |
| Component | Value | Unit | Description | Source |
|---|---|---|---|---|
| latency time [l] | 4 | Day | Period from infection to onset of infectivity | Guinat et al. [6] Guinat et al. [15] Pietschmann et al. [61] |
| incubation time [i] | 15 | Day | Period from infection to onset of symptoms | Austrian Agency for Health and Food Safety [70] |
| diagnostic time [d] | 24 | Hour | Period from onset of symptoms to receiving laboratory result | Information from reference laboratory |
| transmission rate within holding [β] | 0.3 | - | Number of secondary infections originating from an infectious entity per time unit | Guinat et al. [6] Eblé et al. [71] |
| radius protection zone | 3 | Kilometre | Certain disease eradication measures in this zone come into force | ASF-Regulation 2005 [68] Regulation (EU) 2016/429 [67] |
| radius surveillance zone | 10 | Kilometre | Certain disease eradication measures in this zone come into force | ASF-Regulation 2005 [68] Regulation (EU) 2016/429 [67] |
| radius infection zone | 40 | Kilometre | Zone in which the disease can be spread | Assumption by the authors |
| transmission rate infection zone | 0–10 | ‰ | See description of β | Assumption by the authors |
| transmission rate infection zone after confirmation | 0–10 | ‰ | See description of β | Assumption by the authors |
| initial farm type | 1–4 | - | Farm type of first infected pig holding (1 breeding farm, 2 rearing farm, 3 fattening farm, 4 combined farm) | Austrian Swine Health Regulation 2016 [72] |
| federal state | 1–4 | - | Federal state of first outbreak (1 Lower Austria, 2 Upper Austria, 3 Styria, 4 Carinthia) | - |
| outbreak start time | 987 | Day | Time when first pig becomes infected | Assumption by the authors |
| outbreak duration | 365 | Day | The transmission rate remains at the set level for this duration. Afterwards it is set to zero | Assumption by the authors |
| Initial Farm Type | Federal State | Municipality | Transmission Rate | Control Strategy | ||||
|---|---|---|---|---|---|---|---|---|
| Abbr. | Number of Farms | Number of Pigs | Nr. | Infection Zone | Infection Zone after Confirmation | |||
| 1 2 3 4 | Lower Austria | A | 56 | 47,527 | 1 | 1‰ | 0.1‰ | SS SC |
| 2 | 2‰ | 0.2‰ | ||||||
| B | 15 | 2755 | 3 | 3‰ | 0.3‰ | |||
| 4 | 4‰ | 0.4‰ | ||||||
| C | 15 | 963 | 5 | 5‰ | 0.5‰ | |||
| 6 | 1% | 1‰ | ||||||
| 1 2 3 4 | Upper Austria | D | 70 | 33,573 | 1 | 1‰ | 0.1‰ | SS SC |
| 2 | 2‰ | 0.2‰ | ||||||
| E | 38 | 18,419 | 3 | 3‰ | 0.3‰ | |||
| 4 | 4‰ | 0.4‰ | ||||||
| F | 12 | 570 | 5 | 5‰ | 0.5‰ | |||
| 6 | 1% | 1‰ | ||||||
| 1 2 3 4 | Styria | G | 139 | 48,249 | 1 | 1‰ | 0.1‰ | SS SC |
| 2 | 2‰ | 0.2‰ | ||||||
| H | 38 | 4233 | 3 | 3‰ | 0.3‰ | |||
| 4 | 4‰ | 0.4‰ | ||||||
| I | 9 | 412 | 5 | 5‰ | 0.5‰ | |||
| 6 | 1% | 1‰ | ||||||
| 1 2 3 4 | Carinthia | J | 32 | 10,185 | 1 | 1‰ | 0.1‰ | SS SC |
| 2 | 2‰ | 0.2‰ | ||||||
| K | 30 | 687 | 3 | 3‰ | 0.3‰ | |||
| 4 | 4‰ | 0.4‰ | ||||||
| L | 11 | 100 | 5 | 5‰ | 0.5‰ | |||
| 6 | 1% | 1‰ | ||||||
| Mun. | SS | |||||||||||||
| Number of Infected Farms | Number of Culled Pigs | |||||||||||||
| Transmission Rate | µ | Transmission Rate | µ | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 | |||
| A | 32 | 74 | 103 | 130 | 164 | 277 | 130 | 7472 | 34,289 | 50,510 | 45,272 | 31,088 | 72,210 | 40,140 |
| B | 102 | 183 | 274 | 387 | 472 | 813 | 372 | 11,576 | 19,286 | 40,517 | 43,152 | 56,213 | 97,674 | 44,736 |
| C | 39 | 73 | 110 | 140 | 174 | 296 | 139 | 18,838 | 27,026 | 44,486 | 35,627 | 50,903 | 87,134 | 44,002 |
| D | 104 | 215 | 324 | 416 | 503 | 920 | 414 | 30,110 | 79,480 | 118,456 | 137,306 | 177,721 | 320,340 | 143,902 |
| E | 97 | 205 | 300 | 384 | 497 | 888 | 395 | 27,435 | 55,379 | 84,161 | 113,867 | 146,631 | 269,025 | 116,083 |
| F | 98 | 203 | 324 | 412 | 524 | 940 | 417 | 48,344 | 37,871 | 50,981 | 89,482 | 103,567 | 111,461 | 88,126 |
| G | 74 | 145 | 219 | 282 | 351 | 635 | 284 | 18,357 | 38,882 | 67,278 | 87,807 | 92,622 | 177,093 | 80,340 |
| H | 73 | 136 | 204 | 267 | 313 | 595 | 264 | 12,564 | 20,162 | 32,755 | 40,761 | 55,489 | 97,957 | 43,281 |
| I | 23 | 44 | 60 | 84 | 94 | 171 | 79 | 505 | 1581 | 1889 | 3591 | 2700 | 6232 | 2749 |
| J | 48 | 95 | 148 | 198 | 229 | 416 | 189 | 5364 | 9868 | 13,066 | 18,124 | 20,476 | 33,230 | 16,688 |
| K | 43 | 84 | 114 | 152 | 204 | 359 | 159 | 1793 | 2642 | 4838 | 5490 | 9526 | 13,076 | 6227 |
| L | 34 | 63 | 92 | 130 | 155 | 277 | 125 | 431 | 990 | 1746 | 2491 | 2681 | 5076 | 2202 |
| Mun. | SC | |||||||||||||
| Number of Infected Farms | Number of Culled Pigs | |||||||||||||
| Transmission Rate | µ | Transmission Rate | µ | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 | |||
| A | 33 | 66 | 96 | 121 | 158 | 274 | 125 | 7992 | 16,329 | 29,044 | 33,163 | 36,071 | 75,078 | 32,946 |
| B | 100 | 177 | 269 | 375 | 451 | 839 | 369 | 7427 | 34,289 | 50,510 | 45,272 | 31,088 | 72,210 | 40,140 |
| C | 34 | 72 | 99 | 131 | 164 | 302 | 134 | 12,313 | 17,605 | 29,344 | 32,006 | 41,700 | 98,802 | 38,628 |
| D | 102 | 203 | 315 | 427 | 501 | 917 | 411 | 34,009 | 65,124 | 99,049 | 150,449 | 163,148 | 314,547 | 137,721 |
| E | 90 | 190 | 286 | 401 | 466 | 900 | 389 | 35,850 | 58,677 | 79,542 | 112,113 | 129,433 | 265,302 | 113,486 |
| F | 100 | 208 | 319 | 417 | 519 | 917 | 413 | 15,722 | 38,449 | 54,055 | 86,934 | 104,556 | 188,144 | 81,310 |
| G | 86 | 146 | 210 | 287 | 347 | 624 | 283 | 20,342 | 41,969 | 57,829 | 83,659 | 94,812 | 168,389 | 77,833 |
| H | 63 | 134 | 206 | 257 | 331 | 580 | 262 | 13,174 | 23,934 | 37,351 | 41,578 | 52,544 | 97,330 | 44,318 |
| I | 22 | 38 | 56 | 80 | 96 | 170 | 77 | 757 | 1287 | 2734 | 2572 | 3984 | 7528 | 3144 |
| J | 54 | 92 | 146 | 186 | 220 | 429 | 188 | 5799 | 9005 | 12,562 | 16,413 | 19,112 | 35,754 | 16,441 |
| K | 42 | 84 | 115 | 159 | 175 | 356 | 155 | 1817 | 2661 | 4774 | 5935 | 6612 | 15,347 | 6024 |
| L | 29 | 69 | 92 | 132 | 149 | 265 | 123 | 516 | 1072 | 2334 | 2485 | 4270 | 5400 | 2679 |
| Transmission Rate | 1 | 2 | 3 | |||||||||||||||
| Strategy | SS | SC | SS | SC | SS | SC | ||||||||||||
| Number of Days When RP Is Overutilized | ||||||||||||||||||
| Rendering Plant | Rendering Plant | Rendering Plant | ||||||||||||||||
| Municipality | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| A | 1 | 2 | 0 | 1 | 2 | 0 | 12 | 13 | 7 | 3 | 4 | 2 | 8 | 11 | 2 | 5 | 6 | 1 |
| B | 1 | 2 | 0 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 3 | 0 | 2 | 5 | 1 | 1 | 4 | 1 |
| C | 7 | 12 | 6 | 1 | 4 | 0 | 6 | 6 | 4 | 1 | 6 | 0 | 7 | 11 | 4 | 4 | 8 | 0 |
| D | 2 | 4 | 0 | 2 | 4 | 1 | 3 | 13 | 0 | 4 | 13 | 2 | 9 | 16 | 3 | 9 | 13 | 2 |
| E | 1 | 4 | 0 | 7 | 9 | 6 | 2 | 11 | 1 | 12 | 18 | 9 | 2 | 11 | 1 | 4 | 11 | 2 |
| F | 5 | 12 | 2 | 0 | 3 | 0 | 1 | 11 | 1 | 1 | 6 | 0 | 5 | 12 | 3 | 3 | 7 | 1 |
| G | 2 | 1 | 0 | 2 | 2 | 1 | 4 | 1 | 1 | 6 | 4 | 3 | 8 | 6 | 0 | 8 | 6 | 1 |
| H | 2 | 2 | 1 | 3 | 2 | 1 | 1 | 1 | 0 | 2 | 1 | 0 | 3 | 2 | 1 | 6 | 4 | 1 |
| I | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| K | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| L | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Transmission Rate | 4 | 5 | 6 | |||||||||||||||
| Strategy | SS | SC | SS | SC | SS | SC | ||||||||||||
| Number of Days When RP Is Overutilized | ||||||||||||||||||
| Rendering Plant | Rendering Plant | Rendering Plant | ||||||||||||||||
| Municipality | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| A | 16 | 21 | 9 | 5 | 9 | 5 | 2 | 5 | 1 | 4 | 5 | 0 | 7 | 15 | 5 | 6 | 12 | 5 |
| B | 2 | 4 | 0 | 0 | 2 | 0 | 1 | 5 | 0 | 1 | 4 | 1 | 3 | 13 | 3 | 1 | 14 | 0 |
| C | 3 | 4 | 2 | 2 | 6 | 0 | 9 | 18 | 2 | 5 | 16 | 3 | 6 | 27 | 2 | 6 | 24 | 5 |
| D | 6 | 25 | 1 | 7 | 27 | 3 | 8 | 30 | 2 | 9 | 28 | 3 | 20 | 64 | 8 | 17 | 54 | 8 |
| E | 2 | 19 | 0 | 5 | 14 | 1 | 9 | 26 | 1 | 9 | 21 | 3 | 14 | 55 | 3 | 9 | 54 | 2 |
| F | 4 | 13 | 2 | 4 | 12 | 3 | 3 | 15 | 0 | 3 | 13 | 1 | 7 | 38 | 1 | 5 | 33 | 1 |
| G | 13 | 8 | 5 | 11 | 5 | 1 | 9 | 4 | 0 | 12 | 4 | 1 | 25 | 9 | 2 | 26 | 8 | 2 |
| H | 4 | 2 | 0 | 6 | 1 | 1 | 5 | 3 | 1 | 6 | 3 | 0 | 9 | 3 | 0 | 10 | 3 | 1 |
| I | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J | 2 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 2 | 0 | 0 |
| K | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| L | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kummer, Y.; Fikar, C.; Burtscher, J.; Strobl, M.; Fuchs, R.; Domig, K.J.; Hirsch, P. Facilitating Resilience during an African Swine Fever Outbreak in the Austrian Pork Supply Chain through Hybrid Simulation Modelling. Agriculture 2022, 12, 352. https://doi.org/10.3390/agriculture12030352
Kummer Y, Fikar C, Burtscher J, Strobl M, Fuchs R, Domig KJ, Hirsch P. Facilitating Resilience during an African Swine Fever Outbreak in the Austrian Pork Supply Chain through Hybrid Simulation Modelling. Agriculture. 2022; 12(3):352. https://doi.org/10.3390/agriculture12030352
Chicago/Turabian StyleKummer, Yvonne, Christian Fikar, Johanna Burtscher, Martina Strobl, Reinhard Fuchs, Konrad J. Domig, and Patrick Hirsch. 2022. "Facilitating Resilience during an African Swine Fever Outbreak in the Austrian Pork Supply Chain through Hybrid Simulation Modelling" Agriculture 12, no. 3: 352. https://doi.org/10.3390/agriculture12030352
APA StyleKummer, Y., Fikar, C., Burtscher, J., Strobl, M., Fuchs, R., Domig, K. J., & Hirsch, P. (2022). Facilitating Resilience during an African Swine Fever Outbreak in the Austrian Pork Supply Chain through Hybrid Simulation Modelling. Agriculture, 12(3), 352. https://doi.org/10.3390/agriculture12030352






