1. Introduction
Agriculture was and is the most important sector of our country’s national economy. Agribusiness must meet the growing needs of the population for food as well as of industry for raw materials [
1,
2]. Modern production implies a highly efficient use of the production potential of the agro-industrial complex with technical, quality, and, especially, reliability upgrades of agricultural machinery to reduce losses and improve the quality of agricultural products [
3,
4,
5,
6,
7,
8,
9,
10,
11].
Modern agriculture is unthinkable without the cultivation and production of grain crops. Grain crops occupy an area of over 40 million hectares in the Russian Federation, which is 10% of the world’s land area. Grain is the main and indispensable product in the diets of humans as well as productive farm animals and is the main element of food security [
12,
13,
14]. Grain crops have high nutritional, taste, and dietary properties. Grain production achievements are essentially one of the most important indicators of the development level of agriculture in general.
The leading role among grain crops belongs to wheat and barley. They occupy more than half of the global acreage. This explains the close attention to all issues in one way or another related to the production and harvesting of these crops [
15,
16,
17].
Plants of these crops at the time of maturation contain a grain in the ear, which, in natural conditions and in the full ripeness phase, gradually loses mechanical connection with it and crumbles in the field. For the harvest of full-grown grain, it is necessary to carry out timely harvesting before it falls off by artificially forcing grain separation from the ear [
18,
19]. In addition, a promising way to get a crop with high quality indicators is to harvest it in the phase of early ripeness. Studies [
1,
2,
20] show that grain ripening reduces its nutritional and fodder value: there is a decrease in the amount of protein, micro- and macroelements, and essential amino acids. Therefore, harvesting crops in the early ripeness stages will almost completely eliminate biological and significantly reduce mechanical losses of grain.
Combine harvesters are now used everywhere for harvesting. To date, they are the main machine use for crop harvesting. Their designs implement a method of threshing and primary separation of the harvested heap. This method, invented more than a century ago, involves cutting the entire crop and feeding it into a threshing machine, where it is subjected to the drum beater’s impact while being dragged through a rigid grid. Up to 80% of the power is spent on threshing and grinding the straw, and about 7% of the energy is used to separate the grain from the receptacle [
3,
5].
This impact mode on the processed mass in combines, necessary for the extraction of grain and its separation from the ears of plants through the deck, has serious drawbacks: it is energy-consuming and leads to an overall high level of grain injury up to 20–30% of the entire threshed mass of grain.
Injured grain has reduced germination, and pathogens develop in the resulting cracks during storage. This often makes it impossible to obtain quality seed material, and when a certain level of the concentration of microtoxins is reached, the grain is unsuitable not only for the production of baked goods, but also for animal feed [
5,
21,
22,
23].
Moreover, the self-drainage process can occur in grain crops due to insufficient connection of the grain to the ear during untimely harvesting. This also causes grain losses, which amount to millions of tons per year [
6].
Thirdly, combine harvesting technology assumes fully matured grain collection and does not allow for harvesting crops in the early phases of ripeness, since the grain that has not reached full ripeness has a strong connection with the ear. It is technically impossible to separate such grains from the ear by threshing.
Thus, the pressing issue of the day is to ensure low-energy and low-traumatic forced grain extraction from the ear as well as grain extraction from the ear at the early ripeness phase.
For this purpose, it is necessary not only to improve the existing methods of grain harvesting [
24,
25], but also to develop new, highly effective physical–mechanical methods of its harvesting and, accordingly, to design the appropriate equipment [
7,
8,
9,
26].
The most suitable method, which ensures low grain trauma as well as the ability to harvest crops in the early stages of ripeness, is the method of combing at the root. However, the design for the harvesting of grain crops must be further refined to ensure the full harvesting of grain crops, including in the early stages of ripeness, and thus the design of the combing cutterbars should be further developed. For this purpose, it is necessary to determine the natural resonance frequencies and fluctuation forms, where the grain’s release from the ear occurs. The ripeness phase at which the grain is harvested affects the presence or absence of grain connection with the ear: in the early ripeness stages, the grain is attached to the stalk and has a strong connection with the ear, while at maturity the grain is held in the ear only by the scales. Therefore, the natural resonance frequencies for fully mature and early ripening grains will differ significantly [
27,
28].
The solution to this problem requires the development and creation of adequate analytical and numerical physical–mechanical models, including models based on CAD–CAE complexes, which are able to describe the interaction between the elements of the stem–column–grain system. At the same time, there are physical–mechanical models of the process of working bodies of grain harvesting equipment and their impact on the stem–spike–grain system [
10,
11,
29,
30,
31,
32]. Obtaining such models will make it possible to substantiate the design and kinematic parameters of a new harvesting unit by the root combing method. Due to the data obtained, for the first time, the method of grain crops harvesting in the early stages of ripeness will be substantiated, aimed at achieving the Sustainable Development Goals formulated by the UN, including the elimination of hunger, ensuring food security and improved nutrition, and the promotion of sustainable agricultural development.
2. Materials and Methods
A block theory can be considered as an approximate mathematical model considering the peculiarities of the geometry. Herewith, in the general case, the section characteristics and mechanical properties depend on the longitudinal coordinate of the beam, which leads to boundary value problems with variable coefficients that can be solved analytically only in particular cases. A simpler model is a beam consisting of two homogeneous parts (stem and spike); in this case, the solution can be constructed analytically in both static and harmonic analysis [
33,
34,
35,
36,
37].
2.1. Ear and Grain Fluctuation Mathematical Model Based on the Beam Theory
2.1.1. Continuous One-Dimensional Ear Fluctuation Model
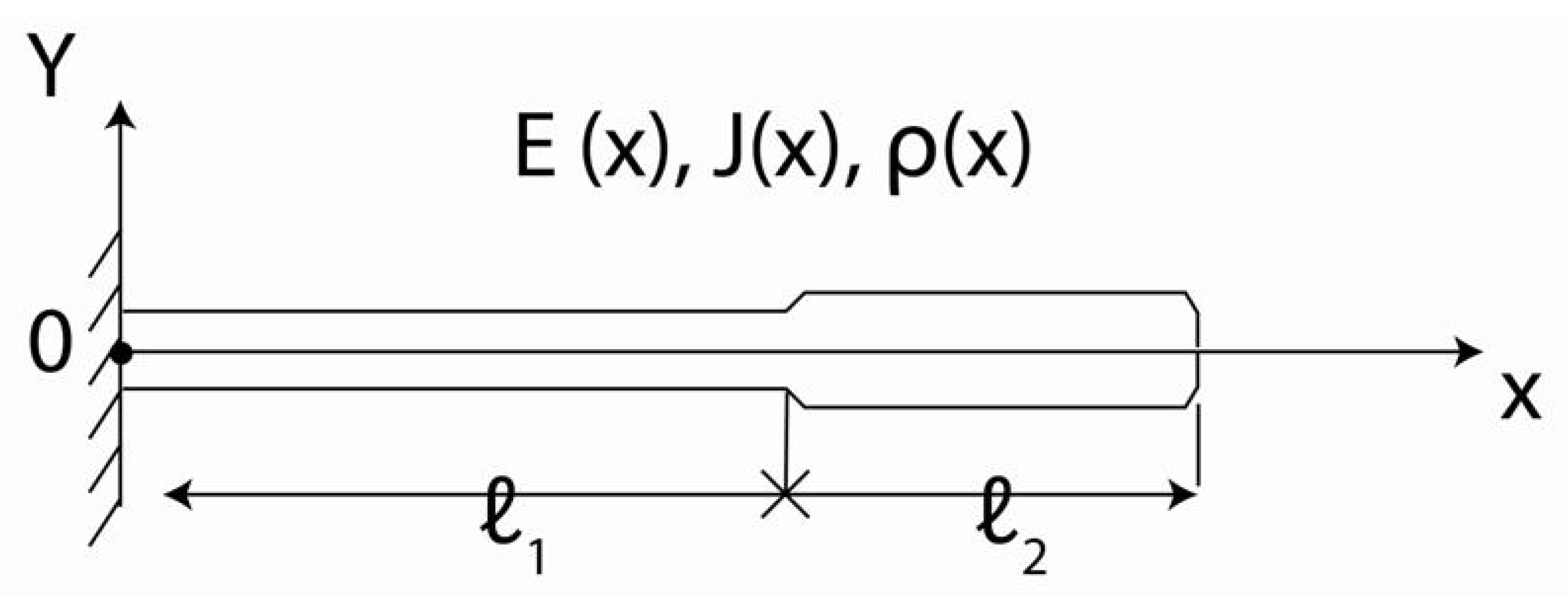
Ear fluctuations are considered within the Euler–Bernoulli beam theory. The ear model is represented by an inhomogeneous beam with variable cross-section, density, and elastic modulus (
Figure 1).
The lower end of the rod is fixed and a distributed pressure or a concentrated force acts on its surface, which in the general case depends on a time variable, and in special cases is a harmonic influence with circular frequency. The fluctuation equation has a form with respective transverse displacements and appears as follows:
where
is the Young’s modulus,
is the moment of inertia, and
is the density.
The boundary conditions are as follows:
The initial conditions correspond to the absence of motion at the initial moment of time:
In the general case of the parameters’ dependence of the ear model on the axial coordinate, the solution of the initial boundary value problem (Equations (1)–(3)) can be constructed numerically, particular in computer mathematical systems such as Maple or MATLAB mathematical packages, using the built-in numerical integration procedures of differential equations.
According to
Figure 1, the rod consists of two main parts, where, in a simplified version, its characteristics can be considered constant. In this case, the mathematical Equation (4) consists of a differential equations system with constant coefficients and boundary conditions (Equation (2)), which has the following form:
where
is the Young’s modulus,
is the moment of inertia, and
is the density, which are constant values at each site.
The docking equations at
are
For the harmonic excitation of fluctuations with a circular frequency
, the system of Equation (4), respecting the amplitude of fluctuations, appears as below:
The homogeneous () boundary values of Equations (2), (5), and (6) are considered to find the resonant natural frequencies.
2.1.2. Relative Grain Motion Equations
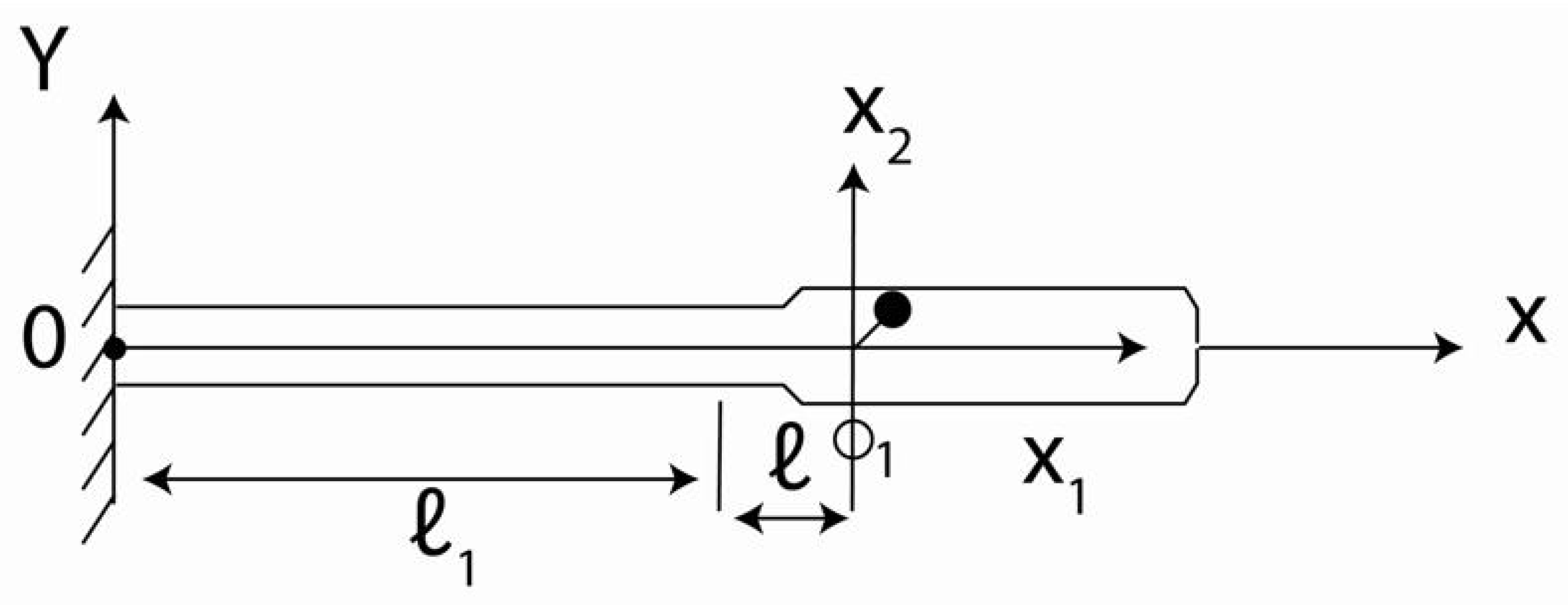
Figure 2 shows the layout of the grain in question and the mobile coordinate system
.
Figure 3 shows the scheme of grain attachment to the ear (3a, on the stem; 3b, without stem). Grain dynamics is investigated in two variants: the first model does not take into account grain size and considers a material point; the second model considers a solid body with a given inertia matrix.
The linear stiffness spring and the spiral stiffness spring simulate the grain and ear relationship; moreover, the linear spring corresponds to the stem’s presence and the spiral spring corresponds to the scales’ interaction.
Choosing a mobile coordinate system coherent with the translational transverse motion of the point (
) of grain to ear attachment, grain acceleration can be represented as follows:
where
are the transfer acceleration and the relative acceleration, respectively.
Here, the transport acceleration is found from the solution of the corresponding boundary value problems of
Section 2.1.
Then, the motion of the grain equation with mass
in the mobile coordinate system
with initial conditions will take the following form:
where
is the radius vector of the grain mass center in motion,
is the radius vector of the grain mass center before the commencement of motion, and
represents the resultant force of the weight and elasticity forces of the linear and circular springs, respectively.
When moving in the plane
, the vector Equation (9) is reduced to a system (taking into account the notations
):
where
are the initial coordinates of the grain mass center,
is the fluctuations’ circular frequency of the ear, and
is the point fluctuations’ amplitude
center of grain attachment (
Figure 3).
Equations (9) and (10) are nonlinear differential equations and their solutions can be numerically constructed. As a result, maximum elastic force
, moment of elasticity
, and their effects
in the increasing section
and
can be found as
In turn, these are compared to similar data obtained in experiments on grain extraction from the ear [
27,
28,
38].
2.1.3. Analytical Solution to the Problem
The solution of the homogeneous boundary value problem from of Equations (2), (5) and (6) will be found in the following form (here and below,
is denoted by
, and
by
, respectively):
where, to simplify the notation, we use the following:
, where
and
are hyperbolic cosine and sine, respectively. The constants
are found further from the boundary and coupling conditions.
Satisfying the boundary conditions at the ends of the beam, we obtain
The docking Equation (5) lead to a linear system:
Matrix
A of the system (16) is represented by the following:
Equality to zero of the determinant of matrix
A,
D = det(A) = 0, is the equation aimed at finding natural frequencies.
In particular, with
, the dependence of the normalized value of the determinant
on the parameter
appears as in
Figure 4.
The first three roots are equal, respectively:
Analysis of the natural waveforms shows that the form corresponding to the second natural frequency () is characterized by intensive movement of the part of the ear containing grains, which agrees with the results obtained in the next paragraph of this article by the finite element method. The frequency interval corresponding to the second natural frequency can be called the low-frequency range, in which effective grain extraction from the ear is possible. It should be noted that this mode can be implemented directly in the field during the harvesting of grain crops when the ear is not separated from the stem and the stem is not cut.
3. Numerical Experiments
The second frequency range, in which effective grain extraction from the ear is possible, is the range of intense grain vibrations itself in the ear. Here, it should be noted that there are several modes associated with different grain maturity degrees, namely, the grain is attached to the stalk and the grain is held by the scales. This frequency range can be called the high-frequency range because it is a kilohertz interval.
To carry out numerical calculations on the developed mathematical model, experimental data on the deformation and destruction of plant elements obtained earlier were used [
27,
28,
38].
Numerical experiments to determine the grain motion characteristics in this range were carried out in the finite element analysis software package ACELAN [
39,
40]. This software has the status of freeware. Its developer is the Southern Federal University, Rostov-on-Don, Russia. The fourth author of this article is one of its developers.
About 25,000 tetragonal 3D finite elements were used for the calculation. The dimensions of the finite elements were chosen from the following condition: at least six elements per half wavelength. The finite-element mesh thickened until the results of the calculations became independent of its shape. The inaccuracy of the resulting finite-element solution was estimated from the characteristic size of the element and the order of approximation. On a PC with an Intel i7processor, 8 GB of RAM, and a 1 TB HDD, the calculation time of one option was about 5–10 min.
In a numerical experiment, the fluctuations of an individual grain at different stages of its maturation were considered in the cases of its connection with the ear (early stage) and in the absence of such a connection (late stage).
Modal analysis was carried out and natural resonance frequencies and forms of fluctuations were found.
Figure 5,
Figure 6,
Figure 7,
Figure 8 and
Figure 9 show the results for the frequencies at which the fluctuations of the grain contribute to its separation from the ear.
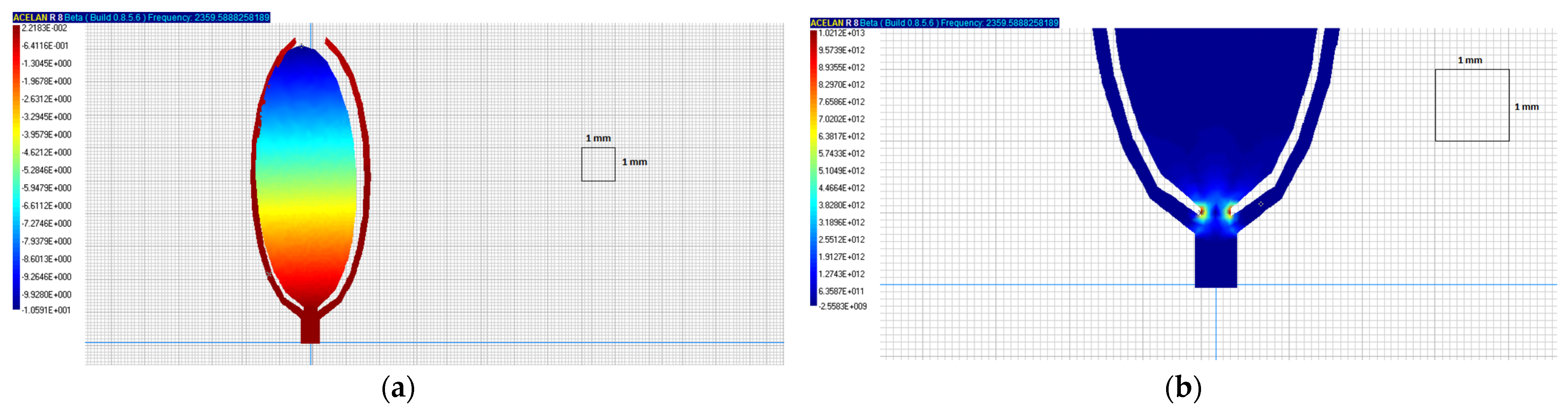
Thus,
Figure 5a,b shows distributions of the stress–strain state (DSS) of the grain at its own frequency of 2.36 kHz, in the case of it not interacting with the scales, in the presence of a connection of the grain with the ear through the stalk. The characteristic of movement corresponds to the fluctuation of the grain at the stalk (
Figure 5a), in which the maximum stresses arise (
Figure 5b); this may serve as the basis for its detachment from the ear.
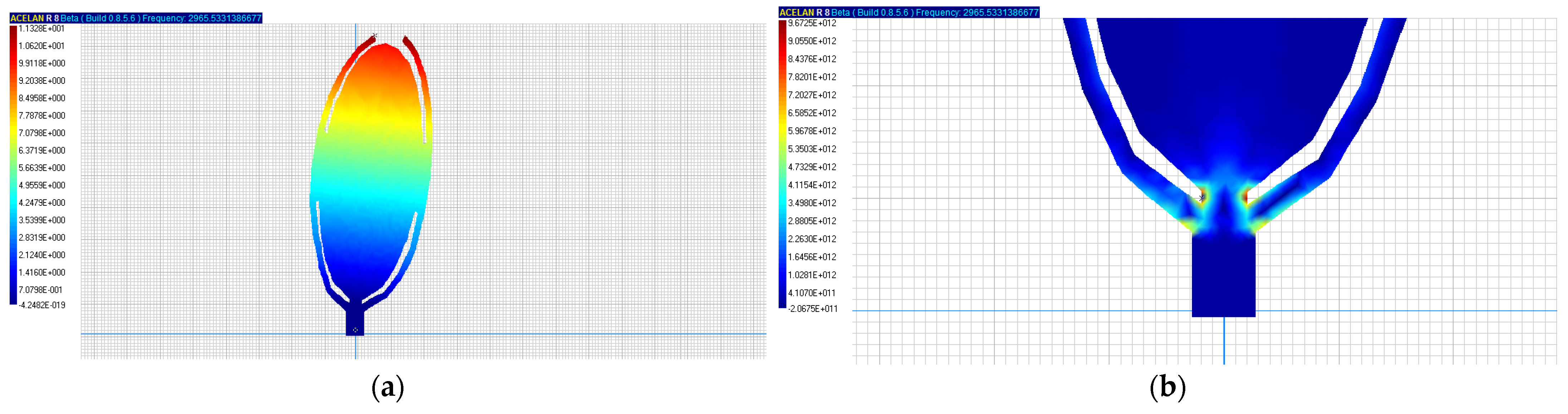
Figure 6a,b shows similar results with a rigid connection between the grain and the scales; due to their rigidity, the frequency increases compared to the previous case. There is a qualitative overlap of DSS characteristics with the previous case.
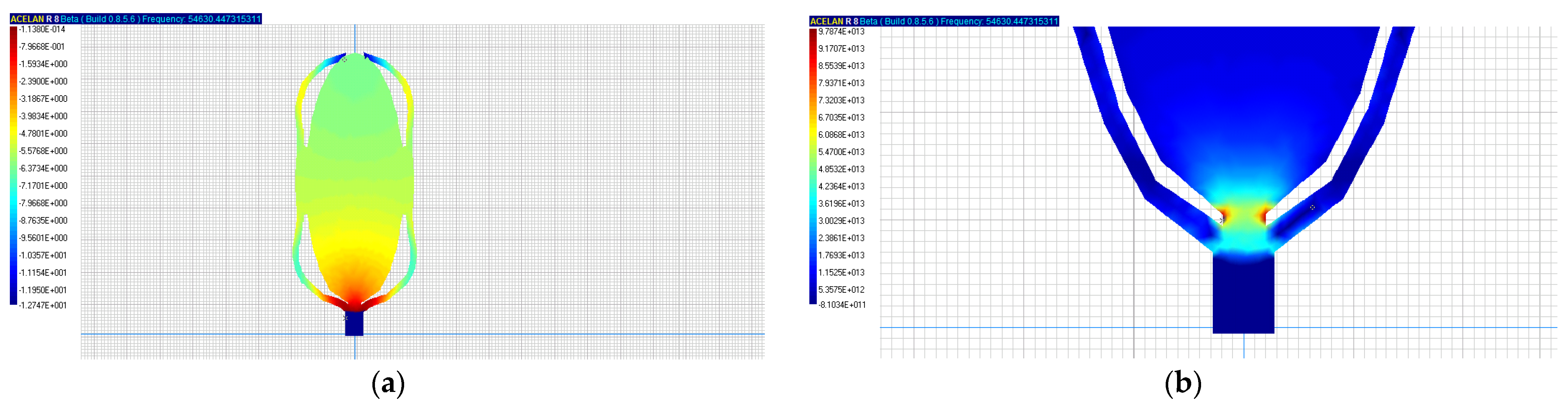
Figure 7a,b shows results in the presence of a rigid connection to the scales. The natural frequency in this case is slightly lower and is 54.63 kHz. The maximum stress levels, as in the previous case, occur in the stalk.
Figure 8a,b shows the results of bending grain fluctuations in the second maturity stage (no connection with the stalk); the maximum stresses occur at the base of the scales, which may be a sign of their destruction if the fluctuations’ amplitude is sufficient.
The figures below show the fluctuation forms and characteristics of the stress–strain state during vertical movement of the grain without connection with the scales and in the presence of this connection. It should be noted that the natural sequences in this case are much higher than the previous bending modes.
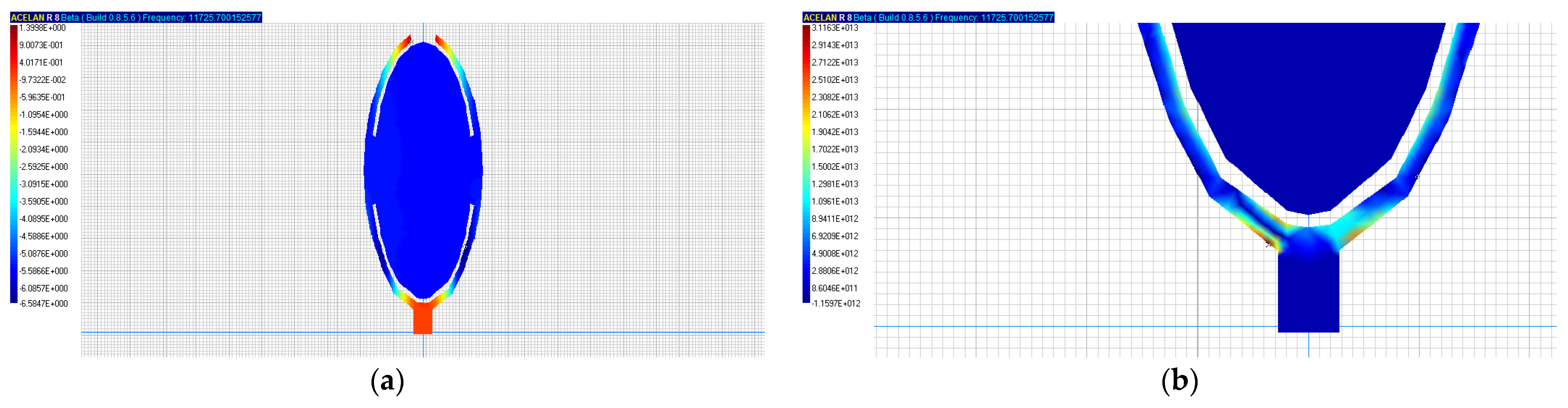
Figure 9a,b shows vertical displacements and stress intensity distributions in the absence of the peduncle, but with the grain connection with the scales, at the natural frequency of 11.73 kHz, which, due to the lower rigidity of the scales compared to the peduncle, is much lower than in the case in which there is a peduncle. The maximum stresses, as before, occur at the place where the scales are attached to the spike, which will also lead to their detachment.
4. Results and Discussion
Studies conducted earlier by other researchers have mainly been aimed at modeling the process of grain threshing and separation after its detachment from the ear. Research on mathematical modeling and numerical calculations has been carried out for the first time [
41,
42,
43,
44]. The use of the applied beam theory and the general continuum formulation within the linear theory of the elasticity framework made it possible to determine the natural forms and frequencies of the grain crops’ ears. Thus, at the natural frequency of 5.868 kHz, there is an intensive ear movement that contributes to the release of grain from it. The frequency interval corresponding to the second natural frequency can be called the low-frequency range. This mode can be used for grain crops harvesting when the ear is not separated from the stem and the stem is not cut.
Numerical experiments aimed at natural ear fluctuation frequency determination were carried out; natural ear fluctuation frequencies contribute to the release of grain at different degrees of maturity.
Grain in the early stages of ripeness has a strong connection with the stem, so for harvesting grain at this stage, vertical and bending forms of grain fluctuation on the stem with and without connection with the scales were considered.
When considering the bending forms of grain fluctuations on the stalk without connection with the scales (
Figure 5a,b), the maximum stresses occur at the fluctuation frequency of 2.36 kHz, which may serve as the basis for its detachment from the ear. When considering the bending forms of fluctuations on the stalk with the connection between the grain and scales (
Figure 6a,b), due to the increase of stiffness, the natural frequency increases to 2.97 kHz, at which the grain detachment from the ear occurs.
Assessment of the grain vibration forms on the peduncle with and without connection with the scales was considered for the grain extraction from the ear in two cases: in the first case, grain was extracted from the ear by breaking the connection of the grain with the peduncle and the scales; in the second case, the grain connection with the peduncle only was broken by the impact of resonant frequencies, which can lead to grain release through breaking off scales from the spike, leaving the scales on the spike unbroken. From the energy-saving point of view, the latter is more advantageous; the frequency of vibrations aimed only at breaking the connection with the stalk was 0.61 kHz lower than the frequency of vibrations aimed at breaking the connection of the grain with the stalk and with the scales.
In reviewing the vertical forms of grain fluctuation on the stem without connection with the scales, the maximum stress is in the material of the stem, which contributes to its destruction. The fluctuation frequency in this case was 56.01 kHz. When considering the presence of a rigid connection with the scales, (
Figure 7a,b) the natural frequency of fluctuations in this case was slightly lower at 54.63 kHz. Maximum stresses also occur in the stalk.
At full maturity, the grain is held in the ear only by the scales; the grain has no connection with the stalk. Assessing the bending form of fully ripe grain fluctuations (
Figure 8a,b), the maximum stresses occurred at the base of the scales, which may be a sign of their destruction with s sufficient amplitude of fluctuations. Grain release from the ear was observed at the natural frequency of 0.95 kHz.
When analyzing the distribution of vertical displacements and stress intensity of the grain in the ear (
Figure 9a,b), the maximum stresses, as in bending forms of fluctuation, occurred in the place of attachment of the scales to the ear, which will also lead to their detachment. The natural frequency of fluctuations in this case was 11.73 kHz.
5. Conclusions
The use of resonant frequencies for grain extraction from the ear is a highly effective physical and mechanical method of its harvesting. To design agricultural harvesting machinery using resonant frequencies, it is necessary to have data on the interaction between the elements of the stem–column–grain system, as well as physical and mechanical models of the process of harvesting machinery working tools and their impact on this system.
This article presented fluctuation models of the stem with the spike and the individual grain in the spike. The applied beam theory and the general continuum formulation within the framework of linear elasticity theory were used for this purpose. Analysis of the fluctuations’ natural forms showed that, at a natural frequency equal to 5.868 kHz, there is an intensive movement of the part of the ear containing grains. The data obtained are consistent with the results obtained by numerical experiments.
Numerical experiments have shown that the separation of grain from the ear at full ripeness, when the grain in the ear is held only by scales and there is no connection with the stalk, in the bending fluctuation form had a natural frequency at which the grain can be separated of 0.95 kHz. With the vertical form of grain, the vibrations’ natural frequencies increased to 11.73 kHz, which is more energy consuming. Therefore, it is advisable to apply bending forms of grain fluctuations at its full ripeness.
When considering the effect of resonant frequencies on the grain of the early phases of ripeness, when the grain has a strong connection with the ear with the help of the stalk, the natural frequencies of the grain, at which its release from the ear can occur, increase.
Thus, in the bending forms of grain fluctuation on the peduncle without connection with the scales, the natural frequency of fluctuation was 2.36 kHz. At bending forms of grain fluctuations on the peduncle with a connection with the scales, the natural frequencies increased to 2.97 kHz.
The vertical forms of grain fluctuation on the stalk with and without scales sharply increased the natural frequencies at which grain is released from the ear. The natural frequency of grain vibrations in the case of the impact of resonant vibrations on the stalk and scales was 54.63 kHz. The natural frequency of grain on the peduncle fluctuations without connection with the scales was 56.01 kHz.
The results show that the bending form of grain fluctuation both at full ripeness and in the early phases of ripeness is the least energy-consuming form.
Author Contributions
Conceptualization, B.M., Y.L., V.P. and D.R.; methodology, A.M., A.S. and I.P.; software, I.P. and A.M.; validation, A.M. and A.S.; formal analysis, I.P. and T.M.; investigation, D.R. and V.P.; resources B.M., Y.L., V.P. and D.R.; data curation, A.M. and A.S.; writing—original draft preparation, T.M. and D.R.; writing—review and editing, A.M., A.S. and V.P.; visualization, A.M., A.S. and V.P.; supervision, B.M., Y.L. and V.P.; project administration, D.R.; funding acquisition, B.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Don State Technical University; This work was carried out within the framework of the Presidential grant of the Russian Federation for state support of young Russian scientists (MK-1700.2021.5, agreement No. 075-15-2021-179).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work was carried out within the framework of the Presidential grant of the Russian Federation for state support of young Russian scientists (MK-1700.2021.5, agreement No. 075-15-2021-179).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Berihuete-Azorín, M.; Stika, H.-P.; Hallama, M.; Valamoti, S.M. Distinguishing ripe spelt from processed green spelt (Grünkern) grains: Methodological aspects and the case of early La Tène Hochdorf (Vaihingen a.d. Enz, Germany). J. Arch. Sci. 2020, 118, 105143. [Google Scholar] [CrossRef]
- Kraska, P.; Andruszczak, P.K.S.; Dziki, D.; Stocki, M.; Stocka, N.; Rozyło, K.; Gierasimiuk, R. Green Grain of Spelt (Triticum aestivum Ssp. Spelta) Harvested at the Stage of Milk-Dough As a Rich Source of Valuable Nutrients. Emir. J. Food Agric. 2019, 31, 263–270. [Google Scholar] [CrossRef]
- Huang, T.; Li, B.; Shen, D.; Cao, J.; Mao, B. Analysis of the grain loss in harvest based on logistic regression. Proc. Comp. Sci. 2017, 122, 698–705. [Google Scholar] [CrossRef]
- Risius, H.; Prochnow, A.; Ammon, C.; Mellmann, J.; Hoffmann, T. Appropriateness of on-combine moisture measurement for the management of harvesting and postharvest operations and capacity planning in grain harvest. Biosyst. Eng. 2017, 156, 120–135. [Google Scholar] [CrossRef]
- Yu, H.; Li, B.; Shen, D.; Cao, J.; Mao, B. Study on prediction model of grain post-harvest loss. Procedia Comp. Sci. 2017, 122, 122–129. [Google Scholar] [CrossRef]
- Buryanov, A.; Kostylenko, O. On the dynamics of winter wheat grain shedding under weather conditions in 2013. In Development of Innovative Technologies and Technical Means for the Agro-Industrial Complex: Collection of Scientific Papers of the 9th International Scientific Practical Conference in 2 Parts, Zernograd, Russia, 28–29 May 2014; Khlystunov, V.F., Rykov, V., Buryanov, A., Bespamyatnova, N., Kambulov, S., Kushnarev, A., Eds.; North Caucasian Research Institute of Mechanization and Electrification of Agriculture: Zernograd, Russia, 2014; pp. 121–128. [Google Scholar]
- Lysenok, O.; Matrosov, A. Evaluation of the efficiency of the comb of the conveyor of the feeder chamber of the combine. In Proceedings of the 7th International Scientific-Practical Conference, State and Prospects for the Development of Agricultural Engineering, Rostov-on-Don, Russia, 25–27 February 2014; pp. 86–87. [Google Scholar]
- Lachuga, U.; Pakhomov, V.; Buryanov, A. Ocher: Technology, technique, prospects. In Innovative Technologies in Science and Education. ITNO-2013: Collection of Scientific Works of Scientific and Methodical Conference (Rostov-on-Don—Divnomorskoye, 12–15 September 2013); GNU SKNIIMESH Rosselkhozakademiya: Rostov-on-Don, Russia; Zernograd, Russia, 2013; pp. 47–51. [Google Scholar]
- Korotky, A.; Marchenko, E.; Ivanov, V.; Popov, S.; Marchenko, J.; Dontsov, N. Model of forming vibration mechanochemical solid lubrication coating on surface of steel rope. IOP Conf. Ser. Earth Environ. Sci. 2019, 403, 012116. [Google Scholar] [CrossRef]
- Pakhomov, V.; Braginets, S.; Bakhchevnikov, O.; Rudoy, D.; Chernutsky, M.V. Research results of vibration extraction of grain from the ear possibility of Polytheme Network. Electron. Sci. J. Kuban State Agrar. Univ. 2020, 155, 25–42. [Google Scholar]
- Lachuga, F.; Matrosov, A.; Panfilov, I.; Pakhomov, V.; Rudoy, D. Mathematical model of wheat ear dynamics. In Mathematical Modeling and Biomechanics in Modern University; Springer: Berlin/Heidelberg, Germany, 2019; p. 91. [Google Scholar]
- Pakhomov, V.; Rykov, V.; Kambulov, S.; Kambulov, I.; Demina, E.; Kolesnik, V. Grain quality of winter wheat depending on cultivation technologies. Russ. Grain Farming 2016, 6, 55–59. [Google Scholar]
- Pakhomov, V.; Rykov, V.; Kambulov, S.; Shevchenko, N.; Revyakin, E. Experience of Winter Wheat Cultivation in Insufficient Moisture Conditions; Rosinformagrotech: Moscow, Russia, 2015; p. 160. [Google Scholar]
- Rybas, I.; Gureeva, A. Winter soft wheat spike productivity in the southern part of the Rostov region in the ecological plasticity indicators. Int. Sci. Res. J. 2016, 5, 52–56. [Google Scholar]
- Rykov, V.; Kambulov, S.; Kambulov, I.; Kolesnik, V.; Demina, E.; Ridnyi, S. Cultivation technologies effect on winter wheat grain toxicity indicators. Sci. Cent. Russ. 2016, 6, 36–42. [Google Scholar]
- Sokolova, E.; Orobets, V.; Sevostyanova, O.; Gorchakov, E.; Rudoy, D.; Olshevskaya, A.; Babajanyan, A. Toxicological evaluation of a new iron-containing preparation for farm animals with alimentary anemia. E3S Web Conf. 2020, 175, 03015. [Google Scholar] [CrossRef]
- Buryanov, M.; Buryanov, A.; Chervyakov, I. Methods of mathematical modeling of the process of grain movement in the transporting channel of the stripping header. Tract. Agric. Mach. 2015, 10, 27–30. [Google Scholar]
- Bello, R.S. Agricultural Machinery & Mechanization; Dominion Services: Lagos, Nigeria, 2012; p. 355. [Google Scholar]
- Buryanov, A.; Buryanov, M.; Goryachev, Y.; Kostylenko, O. The effect of the grain loss value by harvesting machines on their efficiency. In State and Prospects of Agricultural Engineering Development: Collection of Scientific Works of the 8th International Scientific-Practical Conference, within the 18th International Agroindustrial Exhibition "Interagromash-2015", Rostov-on-Don, Russia, 3–6 March 2015; DSTU “PRINT”: Rostov-on-Don, Russia, 2015; pp. 19–22. [Google Scholar]
- Özkaya, B.; Turksoy, S.; Özkaya, H.; Baumgartner, B.; Özkeser, İ.; Köksel, H. Changes in the functional constituents and phytic acid contents of firiks produced from wheats at different maturation stages. Food Chem. 2018, 246, 150–155. [Google Scholar] [CrossRef] [PubMed]
- Ziegler, V.; Paraginski, R.T.; Ferreira, C.D. Grain storage systems and effects of moisture, temperature and time on grain quality—A review. J. Stored Prod. Res. 2021, 91, 101770. [Google Scholar] [CrossRef]
- Matumba, L.; Namaumbo, S.; Ngoma, T.; Meleke, N.; Boevre, M.D.; Logrieco, A.F.; Saeger, S.D. Five keys to prevention and control of mycotoxins in grains: A proposal. Glob. Food Secur. 2021, 30, 100562. [Google Scholar] [CrossRef]
- Bendinelli, W.E.; Su, C.T.; Péra, T.G.; Filho, J.V.C. What are the main factors that determine post-harvest losses of grains? Sustain. Prod. Consum. 2020, 21, 228–238. [Google Scholar] [CrossRef]
- Kolesnikov, D.A.; Matrosov, A.A. Calculation of strength characteristics and service life of the rear axle of the combine. In Proceedings of the 3rd International Scientific-Practical Conference, State and Prospects for the Development of Agricultural Engineering: Materials, Rostov-on-Don, Russia, 4–5 March 2010; pp. 200–202. [Google Scholar]
- Miu, P. Combine Harvesters: Theory, Modeling, and Design; CRC Press: Boca Raton, FL, USA; Taylor and Francis: Abingdon, UK, 2015. [Google Scholar] [CrossRef]
- Ivanov, Y.; Pakhomov, V.; Kambulov, S.; Rudoi, D. Determination of the parameters of the hydrodynamic mixer. MATEC Web Conf. 2018, 224, 05023. [Google Scholar] [CrossRef] [Green Version]
- Shack, Y.; Pakhomov, V.; Buryanov, A. Innovative Technologies in Science and Education—ITNO-2013; DSTU “PRINT”: Rostov-on-Don, Russia, 2013; pp. 47–51. [Google Scholar]
- Matrosov, M.; Nizhnik, D.; Panfilov, I.; Pakhomov, V.; Serebryanaya, I.; Soloviev, A.; Rudoy, D. Calculation of the movement trajectory of the grain mass in the field stripper. E3S Web Conf. 2020, 210, 08015. [Google Scholar] [CrossRef]
- Lachuga, Y.; Alabushev, A.; Pakhomov, V.; Ionova, E.; Khliystunov, V. Physico-mechanical characteristics of connections and biological features of separating grain from ear. IOP Conf. Ser. Earth Environ. Sci. 2019, 403, 012050. [Google Scholar] [CrossRef]
- Soloviev, A.; Matrosov, A.; Panfilov, I.; Meskhi, B.; Polushkin, O.; Rudoy, D.; Chebanenko, V. Mathematical and laboratory modeling of resonant impact on the spike for the purpose of grain selection. E3S Web Conf. 2020, 210, 05017. [Google Scholar] [CrossRef]
- Ziborov, E.N.; Matrosov, A.A. Calculation of strength characteristics and service life of the front axle of a combine. In Proceedings of the 3rd International Scientific-Practical Conference, State and Prospects for the Development of Agricultural Engineering, Rostov-on-Don, Russia, 4–5 March 2010; pp. 199–200. [Google Scholar]
- Meskhi, B.; Pakhomov, V.; Rudoy, D.; Butovchenko, A.; Soloviev, A.; Olshevskaya, A.; Doroshenko, A. Organizational and Technological Design Bases in Agricultural Production; DSTU: Rostov-on-Don, Russsia, 2019; p. 548. [Google Scholar]
- Korotun, A.A.; Matrosov, A.A. Calculation of strength characteristics and service life of the combine frame. In Proceedings of the 3rd International Scientific-Practical Conference, State and Prospects for the Development of Agricultural Engineering, Rostov-on-Don, Russia, 4–5 March 2010; p. 217. [Google Scholar]
- Pinder, G.F. Numerical Methods for Solving Partial Differential Equations, A Comprehensive Introduction for Scientists and Engineers; Wiley: Hoboken, NJ, USA, 2018; p. 309. [Google Scholar]
- Menter, F.R.; Egorov, Y. The Scale-Adaptive Simulation Method for Unsteady Turbulent Flow Predictions. Part 1: Theory and Model Description. J. Flow Turbul. Combust. 2010, 85, 113–138. [Google Scholar] [CrossRef]
- Bayin, S.S. Essentials of Mathematical Methods in Science and Engineering; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2019; p. 960. [Google Scholar]
- Ivanov, V.; Popov, S.; Dontsov, N.; Ekinil, G.; Oleynikova, J.; Denisenko, J. Mechanical coating formed under conditions of vibration exposure. E3S Web Conf. 2020, 175, 05023. [Google Scholar] [CrossRef]
- Lachuga, Y.; Soloviev, A.; Matrosov, A.; Panfilov, I.; Pakhomov, V.; Rudoy, D. Analytical model of ear dynamics and conditions for efficient grain extraction. IOP Conf. Ser. Earth Environ. Sci. 2019, 403, 012055. [Google Scholar] [CrossRef]
- Belokon, A.; Nasedkin, A.; Solovyev, A. New schemes for the finite-element dynamic analysis of piezoelectric devices. J. Appl. Math. Mech. 2002, 66, 481–490. [Google Scholar] [CrossRef]
- Belokon, A.; Eremeyev, V.; Nasedkin, A.; Solovyev, A. Partitioned schemes of the finite-element method for dynamic problems of acoustoelectroelasticity. J. Appl. Math. Mech. 2000, 64, 367–377. [Google Scholar] [CrossRef] [Green Version]
- Miu, P.I.; Kutzbach, H.-D. Modeling and simulation of grain threshing and separation in threshing units—Part I. Comput. Electron. Agric. 2008, 60, 96–104. [Google Scholar] [CrossRef]
- Miu, P.I.; Kutzbach, H.-D. Modeling and simulation of grain threshing and separation in axial threshing units: Part II. Application to tangential feeding. Comput. Electron. Agric. 2008, 60, 105–109. [Google Scholar] [CrossRef]
- Lenaerts, B.; Aertsen, T.; Tijskens, E.; Ketelaere, B.D.; Ramon, H.; Baerdemaeker, J.D.; Saeys, W. Simulation of grain–straw separation by Discrete Element Modeling with bendable straw particles. Comput. Electron. Agric. 2014, 101, 24–33. [Google Scholar] [CrossRef] [Green Version]
- Hong, G.; Li, J.; Dong, J.; Ning, Y.; Pan, J. Frequency-dependent characteristics of grain-beam system: Negative mass and jump behaviour. Int. J. Mech. Sci. 2021, 209, 106706. [Google Scholar] [CrossRef]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).