Soybean Yield Estimation and Its Components: A Linear Regression Approach
Abstract
1. Introduction
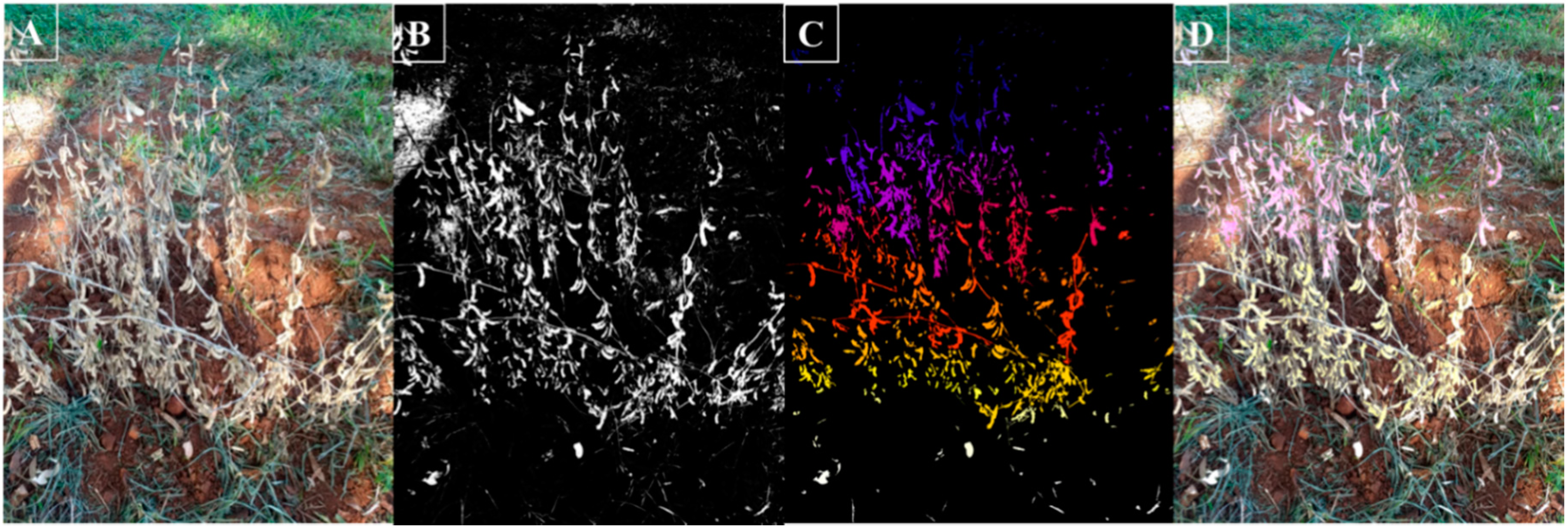
2. Materials and Methods
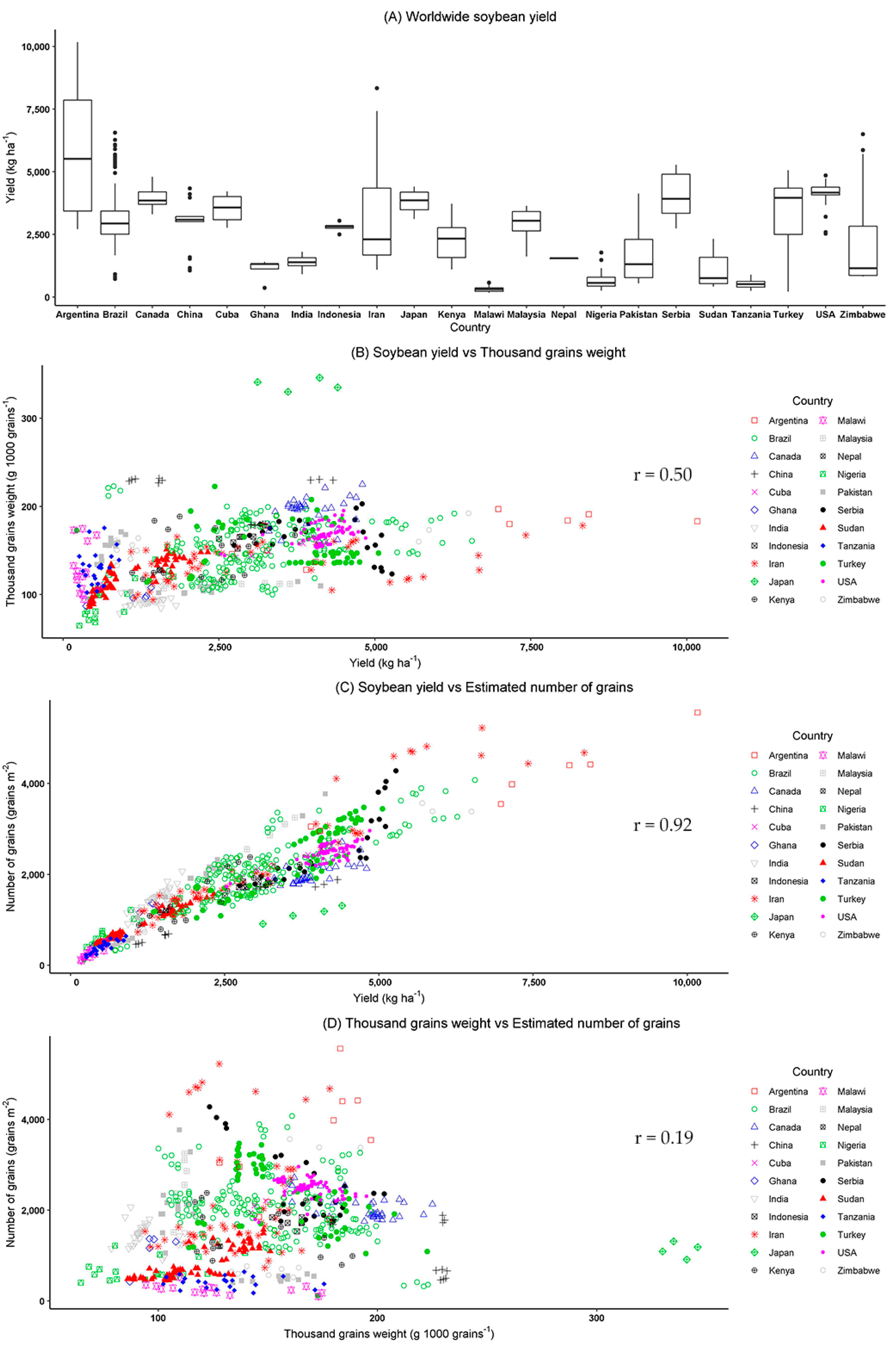
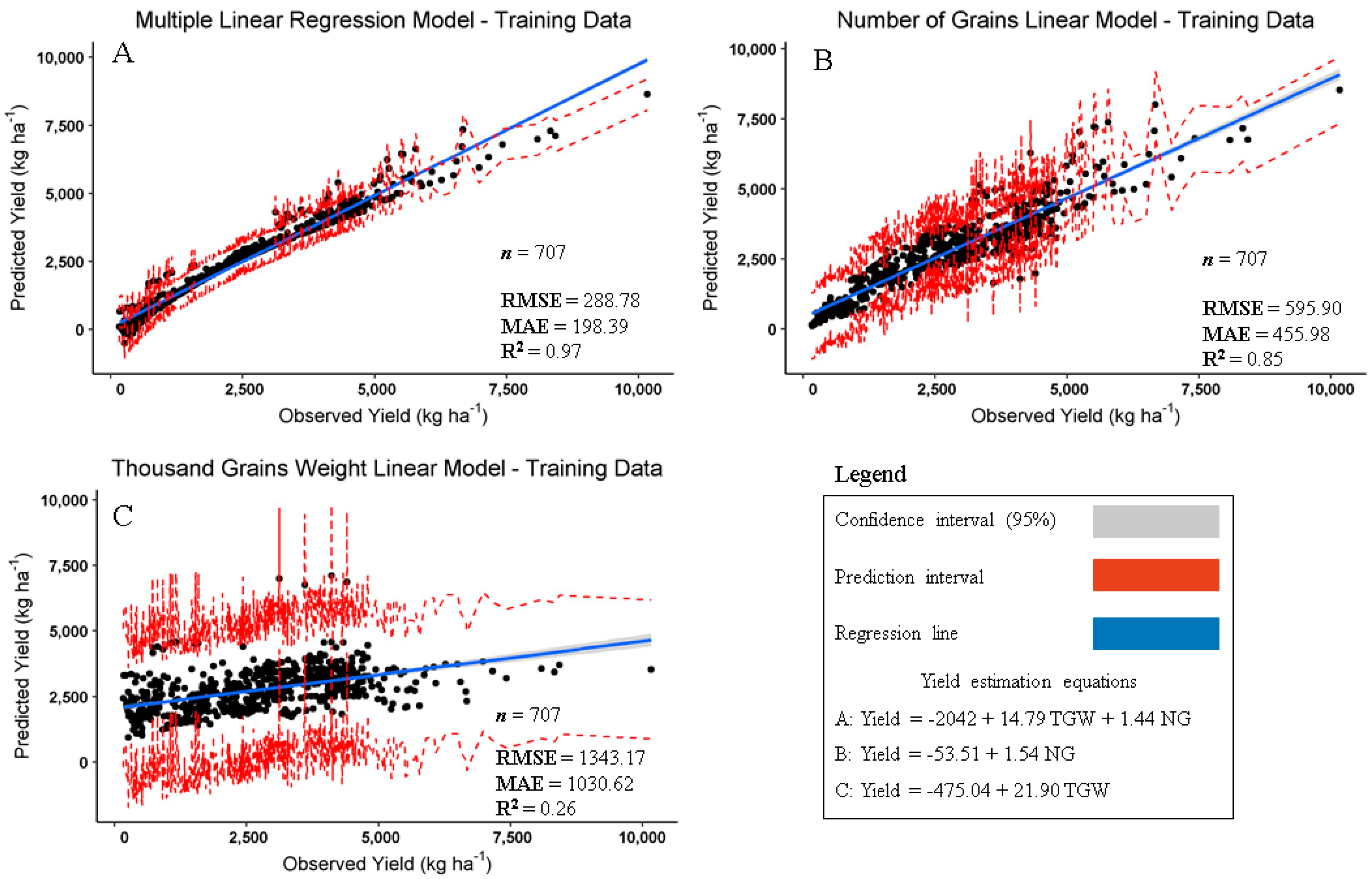
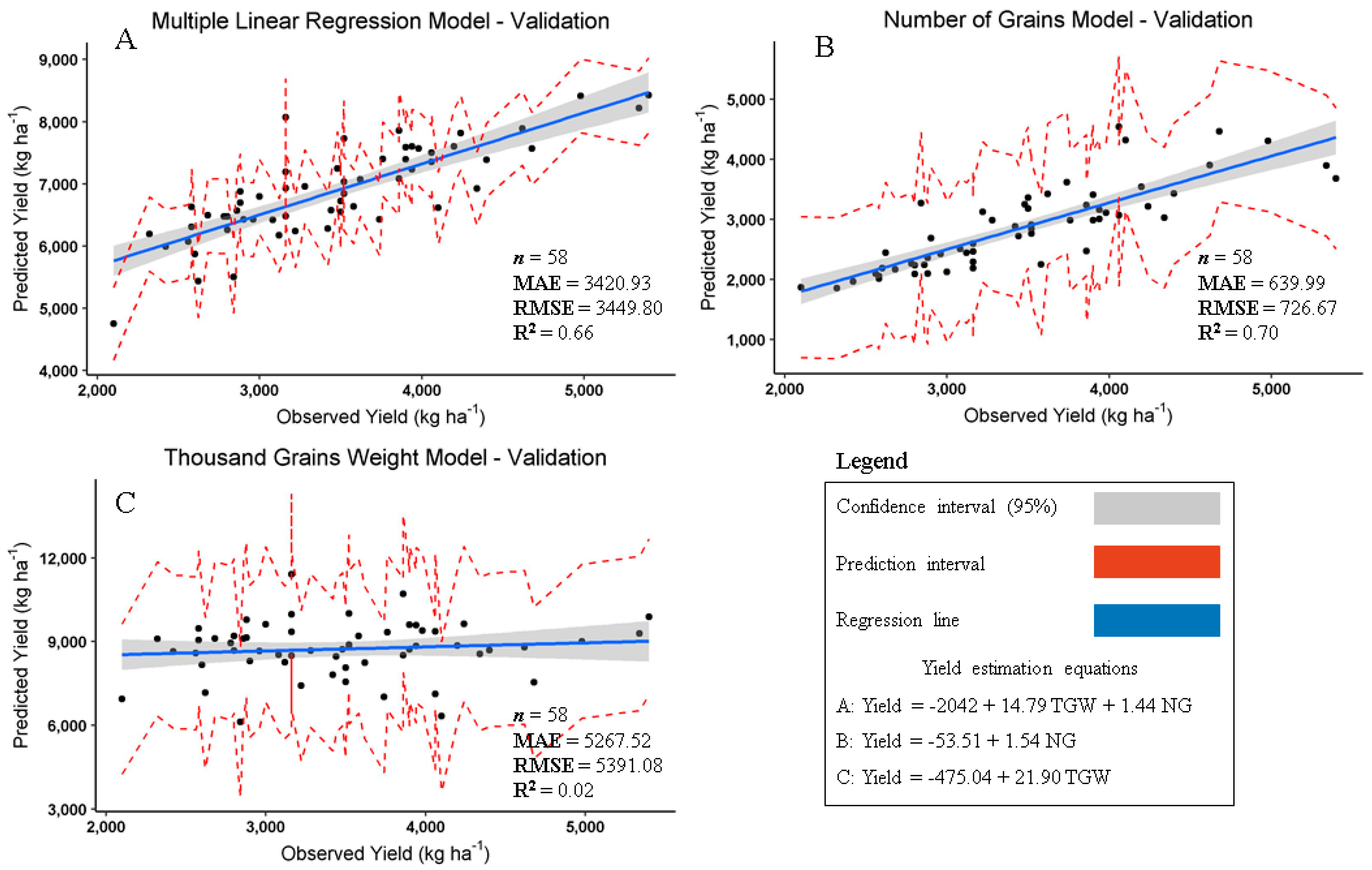
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fritz, S.; See, L.; Bayas, J.C.L.; Waldner, F.; Jacques, D.; Becker-Reshef, I.; Rembold, F. A comparison of global agricultural monitoring systems and current gaps. Agric. Syst. 2019, 168, 258–272. [Google Scholar] [CrossRef]
- Fulton, J.; Hawkins, E.; Taylor, R.; Franzen, A. Yield monitor data: Collection, management, and usage. Crops Soils 2018, 51, 4–51. [Google Scholar] [CrossRef]
- Fulton, J.; Hawkins, E.; Taylor, R.; Franzen, A. Yield monitoring and mapping. In Precision Agriculture Basics; Shannon, D.K., Clay, D.E., Kitchen, N.R., Eds.; ASA, CSSA, and SSSA: Madison, WI, USA, 2018; pp. 63–78. [Google Scholar]
- Betbeder, J.; Fieuzal, R.; Baup, F. Assimilation of LAI and dry biomass data from optical and SAR images into an agro-meteorological model to estimate soybean yield. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2540–2553. [Google Scholar] [CrossRef]
- Figueiredo, G.K.; Brunsell, N.A.; Higa, B.H.; Rocha, J.V.; Augusto, R.; Lamparelli, C. Correlation maps to assess soybean yield from EVI data in Paraná State, Brazil. Sci. Agric. 2016, 73, 462–470. [Google Scholar] [CrossRef]
- Maestrini, B.; Basso, B. Predicting spatial patterns of within-field crop yield variability. Field Crops Res. 2018, 219, 106–112. [Google Scholar] [CrossRef]
- You, J.; Li, X.; Low, M.; Lobell, D.; Ermon, S. Deep gaussian process for crop yield prediction based on remote sensing data. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Al-Gaadi, K.A.; Hassaballa, A.A.; Tola, E.; Kayad, A.G.; Madugundu, R.; Alblewi, B.; Assiri, F. Prediction of potato crop yield using precision agriculture techniques. PLoS ONE 2016, 11, e0162219. [Google Scholar] [CrossRef]
- Coelho, A.P.; De Faria, R.T.; Leal, F.T.; de Arruda Barbosa, J.; Dalri, A.B.; Rosalen, D.L. Estimation of irrigated oats yield using spectral indices. Agri. Water Manag. 2019. [Google Scholar] [CrossRef]
- Setiyono, T.D.; Quicho, E.D.; Gatti, L.; Campos-Taberner, M.; Busetto, L.; Collivignarelli, F.; García-Haro, F.J.; Boschetti, M.; Khan, N.I.; Holecz, F. Spatial rice yield estimation based on MODIS and Sentinel-1 SAR data and ORYZA crop growth model. Remote Sens. 2018, 10, 293. [Google Scholar] [CrossRef]
- Syngenta. Syngenta Crop Challenge in Analytics. 2018. Available online: https://www.ideaconnection.com/syngenta-crop-challenge/challenge.php (accessed on 20 January 2020).
- Khaki, S.; Wang, L. Crop yield prediction using deep neural networks. Front. Plant Sci. 2019, 10. [Google Scholar] [CrossRef]
- Romero, J.R.; Roncallo, P.F.; Akkiraju, P.C.; Ponzoni, I.; Echenique, V.C.; Carballido, J.S. Using classification algorithms for predicting durum wheat yield in the province of Buenos Aires. Comput. Electron. Agric. 2013, 96, 173–179. [Google Scholar] [CrossRef]
- Aggelopoulou, A.; Bochtis, D.; Fountas, S.; Swain, K.C.; Gemtos, T.; Nanos, G.D. Yield prediction in apple orchards based on image processing. Precis. Agric. 2011, 12, 448–456. [Google Scholar] [CrossRef]
- Kurosaki, H.; Yumoto, S. Effects of low temperature and shading during flowering on the yield components in soybeans. Plant Prod. Sci. 2003, 6, 17–23. [Google Scholar] [CrossRef]
- Hao, D.; Cheng, H.; Yin, Z.; Cui, S.; Zhang, D.; Wang, H.; Yu, D. Identification of single nucleotide polymorphisms and haplotypes associated with yield and yield components in soybean (Glycine max) landraces across multiple environments. Theor. Appl. Genet. 2012, 124, 447–458. [Google Scholar] [CrossRef]
- Caverzan, A.; Giacomin, R.; Muller, M.; Biazus, C.; Langaro, N.D.; Chavarria, G. How does seed vigor affect soybean yield components? Agron. J. 2018, 110, 1318–1327. [Google Scholar] [CrossRef]
- MacMillan, K.P.; Guiden, R.H. Effect of seeding date, environment and cultivar on soybean seed yield, yield components, and seed quality in the Northern Great Plains. Agron. J. 2020, 112, 1666–1678. [Google Scholar] [CrossRef]
- Stein, M.; Bargoti, S.; Underwood, J. Image based mango fruit detection, localisation and yield estimation using multiple view geometry. Sensors 2016, 16, 1915. [Google Scholar] [CrossRef]
- Reza, M.N.; Na, I.S.; Baek, S.W.; Lee, K.-H. Rice yield estimation based on K-means clustering with graph-cut segmentation using low-altitude UAV images. Biosyst. Eng. 2018, 177, 109–121. [Google Scholar] [CrossRef]
- Tedesco-Oliveira, D.; da Silva, R.P.; Maldonado, W., Jr.; Zerbato, C. Convolutional neural networks in predicting cotton yield from images of commercial fields. Comput. Electron. Agric. 2020, 171, 105307. [Google Scholar] [CrossRef]
- Egli, D.B.; Yu, Z. Crop growth rate and seeds per unit area in soybean. Crop Sci. 1991, 31, 439–442. [Google Scholar] [CrossRef]
- Lindsey, L. Agronomic Crops Network: Estimating Soybean Yield. 2020. Available online: https://agcrops.osu.edu/newsletter/corn-newsletter/2015-26/estimating-soybean-yield (accessed on 28 January 2020).
- Gromping, U. Variable importance assessment in regression: Linear regression versus random forest. Am. Stat. 2009, 63, 309–319. [Google Scholar] [CrossRef]
- R Foundation for Statistical Computing. R: A Language and Environment for Statistical Computing, version 3.6.0; R Core Team: Vienna, Austria, 2019. [Google Scholar]
- Abbasi, M.K.; Majeed, A.; Sadiq, A.; Khan, S.R. Application of Bradyrhizobium japonicum and phosphorus fertilization improved growth, yield and nodulation of soybean in the sub-humid hilly region of Azad Jammu and Kashmir, Pakistan. Plant Prod. Sci. 2008, 11, 368–376. [Google Scholar] [CrossRef]
- Afzal, A.; Bano, A.; Fatima, M. Higher soybean yield by inoculation with N-fixing and P-solubilizing bacteria. Agron. Sustain. Dev. 2010, 30, 487–495. [Google Scholar] [CrossRef]
- Almaz, M.G.; Halim, R.A.; Martini, M.Y. Effect of combined application of poultry manure and inorganic fertilizer on yield and yield components of maize intercropped with soybean. Pertanika J. Trop. Agric. Sci. 2017, 40, 173–184. [Google Scholar]
- Ambrosini, V.G.; Fontoura, S.M.V.; De Moraes, R.P.; Tamagno, S.; Ciampitti, I.A.; Bayer, C. Soybean yield response to Bradyrhizobium strains in fields with inoculation history in Southern Brazil. J. Plant Nutr. 2019, 42, 1941–1951. [Google Scholar] [CrossRef]
- Arslan, H.; Karakus, M.; Hatipoglu, H.; Arslan, D.; Bayraktar, O.V. Assessment of performances of yield and factors affecting the yield in some soybean varieties/lines grown under semi-arid climate conditions. Appl. Ecol. Env. Res. 2018, 16, 4289–4298. [Google Scholar] [CrossRef]
- Belkheir, A.M.; Zhou, X.; Smith, D.L. Variability in yield and yield component responses to genistein pre-incubated Bradyrhizobium japonicum by soybean [Glycine max (L.) Merr] cultivars. Plant Soil 2001, 229, 41–46. [Google Scholar] [CrossRef]
- Bertham, R.R.; Arifin, Z.; Nusantara, A.D. The improvement of yield and quality of soybeans in a coastal area using low input technology based on biofertilizers. Int. J. Adv. Sci. Eng. Inf. Technol. 2019, 9, 787–791. [Google Scholar] [CrossRef]
- Bryant, C.J.; Krutz, L.J.; Nuti, R.C.; Truman, C.C.; Locke, M.A.; Falconer, R.; Atwill, L.; Wood, C.W.; Spencer, G.D. Furrow diking as Mid-Southern USA irrigation strategy: Soybean grain yield, irrigation water use efficiency, and net returns above furrow diking costs. Crop. Forage Turfgrass Manag. 2019, 5, 180076. [Google Scholar] [CrossRef]
- Carciochi, W.D.; Schwalbert, R.; Andrade, F.H.; Corassa, G.M.; Carter, P.; Gaspar, A.P.; Schmidt, J.; Ciampitti, I.A. Soybean seed yield response to plant density by yield environment in North America. Agron. J. 2019, 111, 1923–1932. [Google Scholar] [CrossRef]
- Chirchir, G.J. Seed Quality of Soybean (Glycine max [L.] Merrill) Genotypes under Varying Storage and Priming Methods, Mother Plant Nutrient Profiles and Agro-Ecologies in Keyna. Master’s Thesis, Kenyatta University, Nairobi, Keyna, 2011. [Google Scholar]
- Crusciol, A.A.C.; Nascente, A.S.; Borghi, E.; Soratto, R.P.; Martins, P.O. Improving soil fertility and crop yield in a tropical region with palisadegrass cover crops. Agron. J. 2015, 107, 2271–2280. [Google Scholar] [CrossRef]
- De Freitas, R.M.S.; De Lima, L.E.; Silva, R.S.; Campos, H.D.; Perin, A. Fluxapyroxad in the asian soybean rust control in the Cerrado biome. Rev. Caatinga 2016, 29, 619–628. [Google Scholar] [CrossRef]
- De Luca, M.J.; Hungría, M. Plant densities and modulation of symbiotic nitrogen fixation in soybean. Sci. Agric. 2014, 71, 181–187. [Google Scholar] [CrossRef]
- Dos Santos, H.P.; Fontaneli, R.S.; Pires, J.; Lampert, E.A.; Vargas, A.M.; Verdi, A.C. Grain yield and agronomic traits in soybean according to crop rotation systems. Bragantia 2014, 73, 263–273. [Google Scholar] [CrossRef][Green Version]
- Ekhtiari, S.; Kobraee, S.; Shamsi, K. Soybean yield under water deficit conditions. J. Biodivers. Env. Sci. 2013, 3, 46–52. [Google Scholar]
- Felisberto, G.; Bruzi, A.T.; Zuffo, A.M.; Zambiazzi, E.V.; Soares, I.O.; De Rezende, P.M.; Botelho, F.B.S. Agronomic performance of RR® soybean cultivars using different pre-sowing desiccation periods and distinct post-emergence herbicides. Afr. J. Agric. Res. 2015, 10, 3445–3452. [Google Scholar] [CrossRef]
- Ferreira, A.S.; Balbinot, A.A., Jr.; Werner, F.; Zucareli, C.; Franchini, J.C.; Debiasi, H. Plant density and mineral nitrogen fertilization influencing yield, yield components and concentration of oil and protein in soybean grains. Bragantia 2016, 75, 362–370. [Google Scholar] [CrossRef]
- Franchini, J.C.; Balbinot, A.A., Jr.; Debiasi, H.; Procópio, S.O. Intercropping of soybean cultivars with Urochloa. Pesq. Agropec. Trop. 2014, 44, 119–126. [Google Scholar] [CrossRef]
- Gai, Z.; Zhang, J.; Li, C. Effects of starter nitrogen fertilizer on soybean root activity, leaf photosynthesis and grain yield. PLoS ONE 2017, 12. [Google Scholar] [CrossRef]
- Galindo, F.S.; Filho, M.C.T.; Buzetti, S.; Santini, J.M.K.; Ludkiewicz, M.G.Z.; Baggio, G. Modes of application of cobalt, molybdenum and Azospirillum brasilense on soybean yield and profitability. Rev. Bras. Eng. Agric. Ambient. 2017, 21, 180–185. [Google Scholar] [CrossRef]
- Gaspar, A.P.; Conley, S.P. Responses of canopy reflectance, light interception, and soybean seed yield to replanting suboptimal stands. Crop Sci. 2015, 55, 377–385. [Google Scholar] [CrossRef]
- Gerçek, S.; Boydak, E.; Okant, M.; Dikilita, S. Water pillow irrigation compared to furrow irrigation for soybean production in a semi-arid area. Agric. Water Manag. 2008, 96, 87–92. [Google Scholar] [CrossRef]
- Ghassemi-Golezani, K.; Lotfi, R. Response of soybean cultivars to water stress at reproductive stages. Int. J. Plant. Anim. Environ. Sci. 2012, 2, 198–202. [Google Scholar]
- Gulluoglu, L.; Bakal, H.; Arioglu, H. The effects of twin-row planting pattern and plant population on seed yield and yield components of soybean at late double-cropped planting in Cukurova region. Turk. J. Field Crop 2016, 21, 59–65. [Google Scholar] [CrossRef]
- Hayder, G.; Mumtaz, S.S.; Khan, A.; Khan, S. Maize and soybean intercropping under various levels of soybean seed rates. Asian J. Plant Sci. 2003, 2, 339–341. [Google Scholar]
- Hernández, M.; Cuevas, F. The effect of inoculating with arbuscular Mycorrhiza and Bradyrhizobium strains on soybean (Glycine max (L) Merrill) crop development. Cult. Trop. 2003, 24, 19–21. [Google Scholar]
- Ibrahim, S.E. Agronomic studies on irrigated soybeans in central Sudan: II. Effect of sowing date on grain yield and yield components. Int. J. Agric. Sci. 2012, 2, 766–773. [Google Scholar]
- Jephter, B.F.M.; Mumba, P.; Bokosi, J.M. Assessment of the agronomic productivity and protein content in 16 soybean genotypes. Afr. J. Food Agric. Nutr. Dev. 2017, 17, 12600–12613. [Google Scholar] [CrossRef]
- Kaschuk, G.; Nogueira, M.A.; De Luca, M.J.; Hungria, M. Response of determinate and indeterminate soybean cultivars to basal and topdressing N fertilization compared to sole inoculation with Bradyrhizobium. Field Crops Res. 2016, 195, 21–27. [Google Scholar] [CrossRef]
- Keramati, S.; Pirdashti, H.; Esmaili, M.A.; Abbasian, A.; Habibi, M. The critical period of weed control in soybean (Glycine max (L.) Merr.) in north of Iran conditions. Pak. J. Biol. Sci. 2008, 11, 463–467. [Google Scholar]
- Kumar, M.; Das, T.K. Integrated weed management for system productivity and economics in soybean (Glycine max)—Wheat (Triticum aestivum) system. Indian J. Agron. 2008, 53, 189–194. [Google Scholar]
- Lamptey, S.; Yeboah, S.; Sakodie, K.; Berdjour, A. Growth and yield response of soybean under different weeding regimes. Asian J. Agric. Food Sci. 2015, 3, 155–163. [Google Scholar]
- Leblanc, M.L.; Cloutier, D.C. Susceptibility of row-planted soybean (Glycine max) to the rotary hoe. J. Sustain. Agric. 2011, 18, 53–61. [Google Scholar] [CrossRef]
- Liu, X.; Rahman, T.; Song, C.; Su, B.; Yang, F.; Yong, T.; Wu, Y.; Zhang, C.; Yang, W. Changes in light environment, morphology, growth and yield of soybean in maize-soybean intercropping systems. Field Crops Res. 2017, 200, 38–46. [Google Scholar] [CrossRef]
- Lyimo, L.D.; Tamba, M.R.; Madege, R.R. Effects of genotype on yield and yield components of soybean (Glycine max (L) Merrill). Afr. J. Agric. Res. 2016, 10, 1930–1936. [Google Scholar] [CrossRef]
- Maleki, A.; Naderi, A.; Naseri, R.; Fathi, A.; Bahamin, S.; Maleki, R. Physiological performance of soybean cultivars under drought stress. Bull. Env. Pharmacol. Life Sci. 2013, 2, 38–44. [Google Scholar]
- Mandal, K.G.; Hati, K.M.; Misra, A.K. Biomass yield and energy analysis of soybean production in relation to fertilizer-NPK and organic manure. Biomass Bioenergy 2009, 33, 1670–1679. [Google Scholar] [CrossRef]
- Madanzi, T.; Chiduza, C.; Kageler, S.J.R.; Muziri, T. Effects of different plant populations on yield of different soybean (Glycine Max (L.) Merrill) varieties in a smallholder sector of Zimbabwe. J. Agron. 2012, 11, 9–16. [Google Scholar] [CrossRef]
- Mandić, V.; Simić, A.; Krnjaja, V.; Bijelić, Z.; Tomić, Z.; Stanojković, A.; Muslić, D.R. Effect of foliar fertilization on soybean grain yield. Biotech. Anim. Husb. 2015, 31, 133–143. [Google Scholar] [CrossRef]
- Mbah, E.U.; Muoneke, C.O.; Okpara, D.A. Effect of compound fertilizer on the yield and productivity of soybean and maize in soybean/maize intercrop in southeastern Nigeria. Trop. Subtrop. Agroecosyst. 2007, 7, 87–95. [Google Scholar]
- Moosavi, S.S.; Mirhadi, S.M.J.; Imani, A.A.; Khaneghah, A.M.; Moghanlou, B.S. Study of effect of planting date on vegetative traits, reproductive traits and grain yield of soybean cultivars in cold region of Ardabil (Iran). Afr. J. Agric. Res. 2011, 6, 4879–4883. [Google Scholar]
- Mostafavi, K. Grain yield and yield components of soybean upon application of different micronutrient foliar fertilizers at different growth stages. Int. J. Agric. Res. Rev. 2012, 2, 389–394. [Google Scholar]
- Muoneke, C.O.; Ogwuche, M.A.O.; Kalu, B.A. Effect of maize planting density on the performance of maize/soybean intercropping system in a guinea savannah agroecosystem. Afr. J. Agric. Res. 2007, 2, 667–677. [Google Scholar]
- Nico, M.; Miralles, D.J.; Kantolic, A.G. Post-flowering photoperiod and radiation interaction in soybean yield determination: Direct and indirect photoperiodic effects. Field Crops Res. 2015, 176, 45–55. [Google Scholar] [CrossRef]
- Orlowski, J.M.; Haverkamp, B.J.; Laurenz, R.G.; Marburger, D.A.; Wilson, E.W.; Casteel, S.N.; Conley, S.P.; Naeve, S.L.; Nafziger, E.D.; Roozeboom, K.L.; et al. High-input management systems effect on soybean seed yield, yield components and economic break-even probabilities. Crop Sci. 2016, 56, 1988–2004. [Google Scholar] [CrossRef]
- Paudel, B.; Karki, T.B.; Shah, S.C.; Chaudhary, N.K. Yield and economics of maize (Zea mays) + soybean (Glycin max L. Merrill) intercropping system under different tillage methods. World J. Agric. Res. 2015, 3, 74–77. [Google Scholar] [CrossRef]
- Rosa, C.B.; Marchetti, M.E.; Serra, A.P.; De Souza, L.C.F.; Ensinas, S.C.; Da Silva, E.F.; Lourente, E.R.P.; Dupas, E.; De Moraes, E.M.; Mattos, F.A.; et al. Soybean agronomic performance in narrow and wide row spacing associated with NPK fertilizer under no-tillage. Afr. J. Agric. Res. 2016, 11, 2947–2956. [Google Scholar] [CrossRef]
- Salehi, M. Effect of foliar application of methanol on the growth and yield of soybean. Environ. Treat. Tech. 2013, 1, 122–125. [Google Scholar]
- Sharma, O.P.; Tiwari, S.C.; Raghuwanshi, R.K. Effect of doses and sources of sulphur on nodulation, yield, oil and protein content of soybean and soil properties. Soybean Res. 2004, 2, 35–40. [Google Scholar]
- Souza, R.; Teixeira, I.; Reis, E.; Silva, A. Soybean morphophysiology and yield response to seeding systems and plant populations. Chil. J. Agric. Res. 2016, 76. [Google Scholar] [CrossRef]
- Popović, V.; Vidić, M.; Jocković, D.; Ikanović, J.; Jakšić, S.; Cvijanović, G. Variability and correlations between yield components of soybean [Glycine max (L.) Merr.]. Genetika 2012, 44, 33–45. [Google Scholar] [CrossRef]
- Taheri, N.; Zarghami, R.; Oveysi, M.; Tarighaleslami, M. The effect of source limitations on yield and yield components of soybean (Glycine max L.) under drought stress. World Appl. Sci. J. 2012, 18, 788–795. [Google Scholar] [CrossRef]
- Tonello, E.S.; Fabbian, N.L.; Sacon, D.; Netto, A.; Silva, V.N.; Milanesi, P.M. Soybean seed origin effects on physiological and sanitary quality and crop yield. Semin. Ciências Agrárias 2019, 40, 1789–1804. [Google Scholar] [CrossRef]
- Uchino, H.; Iwama, K.; Jitsuyama, Y.; Yudate, T.; Nakamura, S. Yield losses of soybean and maize by competition with interseeded cover crops and weeds in organic-based cropping systems. Field Crops Res. 2009, 113, 342–351. [Google Scholar] [CrossRef]
- Yari, V.; Frnia, A.; Maleki, A.; Moradi, M.; Naseri, R.; Ghasemi, M.; Lotfi, A. Yield and yield components of soybean cultivars as affected by planting date. Bull. Env. Pharmacol. Life Sci. 2013, 2, 85–90. [Google Scholar]
- Zuffo, A.M.; Bruzi, A.T.; De Rezende, P.M.; Bianchi, M.C.; Zambiazzi, E.V.; Soares, I.O.; Ribeiro, A.B.M.; Vilela, G.L.D. Morphoagronomic and productive traits of RR® soybean due to inoculation via Azospirillum brasilense grove. Afr. J. Micr. Res. 2016, 10, 438–444. [Google Scholar] [CrossRef]
- United States Department of Agriculture (USDA). Foreign Agricultural Service: Soybeans. Available online: https://www.fas.usda.gov/commodities/soybeans (accessed on 5 July 2020).
- Empresa Brasileira de Pesquisa Agropecuária (EMBRAPA). Embrapa Soja. 2020. Available online: https://www.embrapa.br/soja/cultivos/soja1 (accessed on 5 July 2020). (In Portuguese).
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine learning in agriculture: A review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef]
- Board, J.E. Yield components related to seed yield in determinate soybean. Crop Sci. 1987, 27, 1296–1297. [Google Scholar] [CrossRef]
- De Bruin, J.L.; Pedersen, P. Soybean seed yield response to planting date and seeding rate in the upper Midwest. Agron. J. 2008, 100, 696–703. [Google Scholar] [CrossRef]
- Robinson, A.P.; Conley, S.P.; Volenec, J.J.; Santini, J.B. Analysis of high yielding, early-planted soybean in Indiana. Agron. J. 2009, 101, 131–139. [Google Scholar] [CrossRef]
- Zhang, C.; Kovacs, J.M. The application of small unmanned aerial systems for precision agriculture: A review. Precis. Agric. 2012, 13, 693–712. [Google Scholar] [CrossRef]
- Palmer, P.B.; O`Connell, D.G. Regression analysis for prediction: Understanding the process. Cardiopulm. Phys. Ther. J. 2009, 20, 23–26. [Google Scholar] [CrossRef] [PubMed]
- Smidt, E.R.; Conley, S.P.; Zhu, J.; Arriage, F.J. Identifying field attributes that predict soybean yield using random forest analysis. Agron. J. 2016, 108, 637–646. [Google Scholar] [CrossRef]
- Marko, O.; Brdar, S.; Panic, M.; Lugonja, P.; Crnojevic, V. Soybean varieties portfolio optimisation based on yield prediction. Comput. Electron. Agric. 2016, 127, 467–474. [Google Scholar] [CrossRef]
- Christenson, B.S.; Schapaugh, W.T.; An, N.; Price, K.P.; Prasad, V.; Fritz, A.K. Predicting soybean relative maturity and seed yield using canopy reflectance. Crop Sci. 2016, 56, 625–643. [Google Scholar] [CrossRef]
- Patrício, D.I.; Rieder, R. Computer vision and artificial intelligence in precision agriculture for grain crops: A systematic review. Comput. Electron. Agric. 2018, 153, 69–81. [Google Scholar] [CrossRef]
- Barbedo, J.G.A. Digital image processing techniques for detecting, quantifying and classifying plant diseases. SpringerPlus 2013, 2, 660. [Google Scholar] [CrossRef]
- Vithu, P.; Moses, J.A. Machine vision system for food grain quality evaluation: A review. Trends Food Sci. Technol. 2016, 56, 13–20. [Google Scholar] [CrossRef]
- Uzal, L.C.; Grinblat, G.L.; Namías, R.; Larese, M.G.; Bianchi, J.S.; Morandi, E.N.; Granitto, P.M. Seed-per-pod estimation for plant breeding using deep learning. Comput. Electron. Agric. 2018, 150, 196–204. [Google Scholar] [CrossRef]
- Li, Y.; Jia, J.; Khattak, A.M.; Sun, S.; Gao, W.; Wang, M. Soybean seed counting based on pod image using two-column convolution neural network. IEEE Access 2019, 7, 64177–64185. [Google Scholar] [CrossRef]
- Liu, X.; Jia, W.; Ruan, C.; Zhao, D.; Gu, Y.; Chen, W. The recognition of apple fruits in plastic bags based on block classification. Precis. Agric. 2018, 19, 735–749. [Google Scholar] [CrossRef]
- Qureshi, W.S.; Payne, A.; Walsh, K.B.; Linker, R.; Cohen, O.; Dailey, M.N. Machine vision for counting fruit on mango tree canopies. Precis. Agric. 2017, 18, 224–244. [Google Scholar] [CrossRef]
- Ramos, P.J.; Prieto, F.A.; Montoya, E.C.; Oliveros, C.E. Automatic fruit count on coffee branches using computer vision. Comput. Electron. Agric. 2017, 137, 9–22. [Google Scholar] [CrossRef]
- Sa, I.; Ge, Z.; Dayoub, F.; Upcroft, B.; Perez, T.; Mccool, C. Deepfruits: A fruit detection system using deep neural networks. Sensors 2016, 16, 1222. [Google Scholar] [CrossRef] [PubMed]
| Measurement | Training Dataset | Validation Dataset | ||||
|---|---|---|---|---|---|---|
| Yield (kg ha−1) | TGW (g 1000 Grains−1) | NG (Grains m−2) | Yield (kg ha−1) | TGW (g 1000 Grains−1) | NG (Grains m−2) | |
| n | 707.0 | 707.0 | 707.0 | 58.0 | 58.0 | 58.0 |
| Minimum | 167.1 | 64.7 | 100.0 | 2100.0 | 301.5 | 1236.0 |
| Median | 2819.0 | 148.4 | 1849.0 | 3460.0 | 423.3 | 1888.0 |
| Mean | 2764.9 | 148.0 | 1826.0 | 3463.8 | 420.4 | 1889.0 |
| Maximum | 10,170.0 | 346.0 | 5557.0 | 5400.0 | 542.9 | 2975.0 |
| Standard Deviation | 1557.6 | 35.9 | 932.0 | 736.6 | 44.6 | 444.0 |
| Sample Variance | 2,425,981.0 | 1291.6 | 868,565.2 | 542,588.9 | 1991.8 | 196,958.0 |
| CV (%) | 56.3 | 24.3 | 51.1 | 21.3 | 10.6 | 23.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, M.C.F.; Molin, J.P. Soybean Yield Estimation and Its Components: A Linear Regression Approach. Agriculture 2020, 10, 348. https://doi.org/10.3390/agriculture10080348
Wei MCF, Molin JP. Soybean Yield Estimation and Its Components: A Linear Regression Approach. Agriculture. 2020; 10(8):348. https://doi.org/10.3390/agriculture10080348
Chicago/Turabian StyleWei, Marcelo Chan Fu, and José Paulo Molin. 2020. "Soybean Yield Estimation and Its Components: A Linear Regression Approach" Agriculture 10, no. 8: 348. https://doi.org/10.3390/agriculture10080348
APA StyleWei, M. C. F., & Molin, J. P. (2020). Soybean Yield Estimation and Its Components: A Linear Regression Approach. Agriculture, 10(8), 348. https://doi.org/10.3390/agriculture10080348






