Abstract
Soybean yield estimation is either based on yield monitors or agro-meteorological and satellite imagery data, but they present several limiting factors regarding on-farm decision level. Aware that machine learning approaches have been largely applied to estimate soybean yield and the availability of data regarding soybean yield and its components (number of grains (NG) and thousand grains weight (TGW)), there is an opportunity to study their relationships. The objective was to explore the relationships between soybean yield and its components, generate equations to estimate yield and evaluate its prediction accuracy. The training dataset was composed of soybean yield and its components’ data from 2010 to 2019. Linear regression models based on NG, TGW and yield were fitted on the training dataset and applied to a validation dataset composed of 58 on-field collected samples. It was found that globally TGW and NG presented weak (r = 0.50) and strong (r = 0.92) linear relationships with yield, respectively. In addition to that, applying the fitted models to the validation dataset, model based on NG presented the highest accuracy, coefficient of determination (R2) of 0.70, mean absolute error (MAE) of 639.99 kg ha−1 and root mean squared error (RMSE) of 726.67 kg ha−1.
1. Introduction
Yield is a quantitative measurement of the crop and it is an important feature that can benefit decision makers by supporting and improving their crop management [1]. The common approach to estimate grain yield with higher spatial resolution providing farm level data is using harvesters coupled to yield monitors [2]. Yield is computed through the convergence of yield monitor flow, global navigation satellite system (GNSS) receiver and moisture sensor data [3]. Grain yield monitor estimation accuracy is affected by many factors such as: (i) mass flow sensor, (ii) cleanness of the system, (iii) wiring harnesses and (iv) moisture sensor. Hence, constant inspection of the sensor system and calibration is required before the start of harvesting to achieve higher accuracy rates and obtain reliable data of estimated yield [3].
Other approaches have also been developed to estimate grain yield, but they have a lower spatial resolution, limiting its application on a farm level. Among these approaches, the most common is the application of remote sensing techniques based on agro-meteorological [4] and satellite imagery data [5,6]. Regarding this kind of data, efforts have also been made applying advanced algorithms to estimate yield [7].
Worldwide, researchers are making efforts to apply machine learning (ML) techniques in different databases to estimate crop yield. Most of these databases are composed of spectral band/vegetation indices from crop canopies [8,9], chlorophyll index [9], fusion of chemical and physical soil properties, historical weather conditions and historical crop yield [10]. For example, Syngenta Crop Challenge [11] supplied a database with 2267 experimental corn hybrids planted in different locations across Canada and the United States between 2008 and 2016. Using that database to feed a deep learning neural network, the corn hybrid yield of 2017 was successfully predicted with a 12% root mean squared error compared to the average yield [12].
However, to support on-farm decision making, it is necessary to apply methods to gather higher spatial resolution data and the application of new sensor technologies and remote sensing techniques relying on the concepts of high-throughput phenotyping research could be suitable for this situation [3]. In this sense, some researchers have already applied ML techniques to analyze yield and its components. For example, Romero et al. [13] predicted durum wheat yield based on its plant height, peduncle length, spikelet number per ear, grain number per ear and grain weight per ear applying different ML decision trees. Aggelopoulou et al. [14] predicted apple tree yield based on its yield components, in their case, full bloom. The prediction was made by applying an image processing-based algorithm which learned texture patterns and correlated them to its yield.
Soybean yield components can be affected by several factors such: shading and temperature [15], genotype and environmental conditions [16], seed vigor [17] and seeding date, environment and cultivar [18]. Despite that, yield prediction through its components is becoming more popular in crops whose yield component is the product to be marketed, for example, mango [19] and rice [20], highlighting the possibility of applying it to soybean crops since the final product is grain.
Therefore, due to the ability to predict crop yield through its components (cotton [21] and rice [20]), large application of ML techniques in agriculture and soybean yield and its components’ data availability, there is an opportunity to investigate the possibility to forecast soybean yield based on its components in a global scale, unlike the common approach which relies on vegetation indices. In this sense, this paper aimed to (i) explore soybean yield and yield components’ relations from data published around the world, (ii) generate a global equation to estimate soybean yield and (iii) evaluate linear regressions prediction accuracy.
2. Materials and Methods
The training dataset was composed of published data from 2010 to 2019 that contained soybean yield and thousand grains weight (TGW) or hundred grains weight (HGW). In cases where HGW data was available instead of TGW, HGW values were multiplied by 10 to convert them to TGW. It was decided to use the training dataset relying on available data because it allowed the analysis of soybean yield and its components’ relations on a global perspective since the dataset came from different locations of study, treatments, soybean varieties and year of study.
Based on literature reviews [22,23], Equation (1) was used to estimate the number of soybean grains (grains m−2) because normally this data is not available and it is known that soybean yield (kg ha−1) is a function of the number of grains in a certain area (grains m−2) and the average weight per grain [22], in this case, it was adapted to thousand grains weight (g 1000 grains−1).
where, NG is the number of grains (grains m−2) and TGW is the weight of a thousand grains (g 1000 grains−1).
A descriptive analysis (number of observations, minimum, median, mean and maximum values, standard deviation, sample variance and coefficient of variation) and scatterplot (yield versus country, yield versus TGW and yield versus NG) were applied to the training dataset to provide better data visualization and inference. In addition to the scatterplots, Pearson’s correlation (r) between soybean yield and its components was also calculated.
Linear regression models were used to predict yield because the number of observations was larger than the number of variables [24]. All yield observations, TGW and NG from the training dataset were used to fit three linear regression models: (A) Yield as function of TGW and NG, (B) yield as function of NG and (C) yield as function of TGW.
As linear regression allows formulation of the equation to predict the desired parameter, in our case, yield, it was also gathered from each model using the equation. Linear regression models generated from the training dataset were further applied to the validation dataset to predict soybean yield.
The validation dataset was composed of 58 randomly selected on-field samples of 1 m2 from a soybean field (cultivar TMG 7062) collected at Piracicaba, Brazil (22.7356° S, 47.6479° W) in March of 2019. Number of grains (grains m−2) was carefully and manually counted grain by grain, thousand grains weight (g 1000 grains−1) and yield (kg ha−1) were obtained from these samples after the drying process (105 °C for 72 h in a forced circulation air oven).
Overall performance of the fitted equations was evaluated by comparing their root mean squared error (RMSE), mean absolute error (MAE) and coefficient of determination (R2) for both the training and validation datasets. All the statistical analysis was performed in R environment [25].
3. Results and Discussion
In 707 observations of soybean data (training dataset) it was found that they contained at least “yield” and “thousand grains weight” or “hundred grains weight” from 56 eligible papers [26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81] across the world, as presented in Table 1. A large difference between soybean yield and its yield components between countries is observed. Yield presented a range from 167.1 to 10,170 kg ha−1. Different yield values found across the world highlight the regional variability inherent among environment and genotype. Furthermore, note that the coefficient of variation of yield and number of grains are higher than 50% and thousand grains weight is approximately 24%. These values indicate that TGW presents less variance than yield and NG in a worldwide range. The validation dataset, also shown in Table 1, presents variability among samples which is higher for both yield and NG than TGW when looking at the coefficient of variation.

Table 1.
Descriptive analysis of the soybean training dataset obtained from [26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81] and validation dataset.
Soybean yield variability among countries despite year, genotype and treatments can be seen in Figure 1. Figure 1A (worldwide soybean yield) shows soybean yield distribution among countries. Note that within country there are large yield differences representing yield variability at a country level which is expected, as we can see in several governmental reports, for example, in the US and Brazil, United States Department of Agriculture—USDA [82] and Brazilian Agricultural Research Corporation—EMBRAPA [83], respectively, that are responsible for forecasting and presenting harvested yield by location.
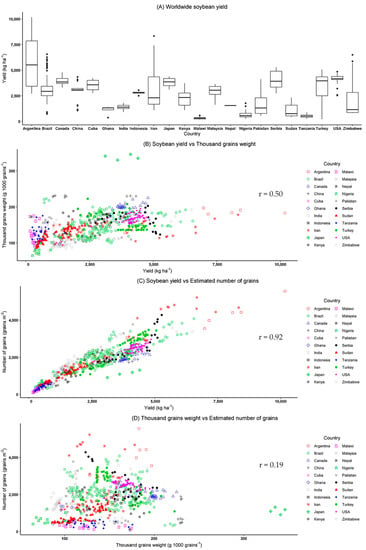
Figure 1.
Boxplot and scatterplots of observed soybean yield (kg ha−1) and its yield components by country. (A) Worldwide soybean yield (kg ha−1) by country, (B) thousand grains weight (g 1000 grains−1), (C) number of grains (grains m−2) and (D) thousand grains weight (g 1000 grains−1) versus number of grains (grains m−2). r = correlation coefficient.
The graphic of Figure 1B (soybean yield versus TGW) shows that there is weak linear relationship (r = 0.50) between these two variables which will further negatively impact the linear regression model prediction accuracy. On the other hand, Figure 1C (soybean yield versus NG) presents a strong linear relationship between yield and NG (r = 0.92). Comparing TGW and NG data (Figure 1D), there is a weak linear relationship (r = 0.19) indicating that there is no collinearity between them.
Based on Figure 1, it shows an opportunity to further investigate the possibility of applying machine learning techniques to estimate soybean yield based on its components. Corroborating the idea that yield prediction is one of the most important topics in precision agriculture and that ML techniques have widely been applied in agriculture, this paper also applied ML techniques to forecast yield [84], but relying on the use of its components as predictor variables.
Yield is a function of the number of pods (np), grain number per pod (gnp) and grain weight (gw), as presented in Equation (2) adapted from Egli and Zhen-wen [22] and Lindsey [23]. Combining np and gnp, a new variable is generated, which is the number of grains (NG), providing Equation (3). Based on that, soybean yield is a direct function of NG and gw. Regarding these two variables related to yield, number of grains (grains m−2) has more influence on yield than grain weight/thousand grains weight [34,85,86,87] which corroborates with the findings in Figure 1.
where, np, ngp and gw are number of pods (unit ha−1), number of grains per pod (grain unit−1) and grain weight (kg grain−1), respectively.
where, NG and gw are, respectively, number of grains (grain ha−1) and grain weight (kg grain−1).
Figure 2 presents the relation between observed and predicted soybean yields. The linear models were generated from the training dataset. Model A (Figure 2A) presents the highest R2 (0.97) and lowest RMSE (288.78 kg ha−1), model B (Figure 2B) presents R2 of 0.85 and RMSE of 455.98 kg ha−1, and model C (Figure 2C) presents the lowest R2 (0.26) and the highest RMSE (1343.17 kg ha−1), as expected due to the weak linear relationship between yield and TGW. Higher R2 and lower MAE values are found for models A and B and not for model C because NG has more global influence than TGW to predict yield, as seen previously in Figure 1. Hence, it is expected that models A and B present a better overall performance compared to model C when applied to the validation dataset.
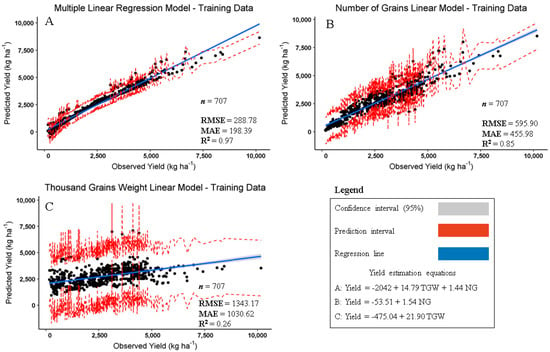
Figure 2.
Scatterplot of soybean observed and predicted yields (kg ha−1) applied to training dataset. (A) Yield estimation based on thousand grains weight (TGW in g 1000 grains−1) and number of grains (NG in grain m−2), (B) yield estimation as function of number of grains (NG in grains m−2) and (C) yield estimation as functions of thousand grains weight (TGW in g 1000 grains−1). n = number of observations; MAE = mean absolute error (kg ha−1); RMSE = root mean squared error (kg ha−1); R2 = multiple R-squared; Yield = soybean yield (kg ha−1); TGW = thousand grains weight (g 1000 grains−1); NG = number of grains (grains m−2).
Results of the fitted models A, B and C application to the validation dataset is shown in Figure 3. R2 values for models A (Figure 3A), B (Figure 3B) and C (Figure 3C) are 0.66, 0.70 and 0.02, respectively. Model B presents the highest R2, lowest MAE (639.99 kg ha−1) and RMSE (726.67 kg ha−1) followed by model A (MAE—3420.93 kg ha−1 and RMSE—3449.80 kg ha−1) and model C (MAE—5267.52 kg ha−1 and RMSE—5391.08 kg ha−1). These results indicate that model B presents higher accuracy rate to predict soybean yield based on number of grains from data collected in a single field. Therefore, in this case, yield prediction based on NG can support on-farm decision making which is the scale of precision agriculture actions that deals with the variability within field levels [88]. Note that, to achieve a good accuracy rate, both predicted and observed yields should present, not only high R2, low RMSE and MAE, but also, the amplitude ratio between predicted and observed yield values as close as possible to one (R2 = 1.00), meaning that there was a perfect prediction without error and unexplained variance [89].
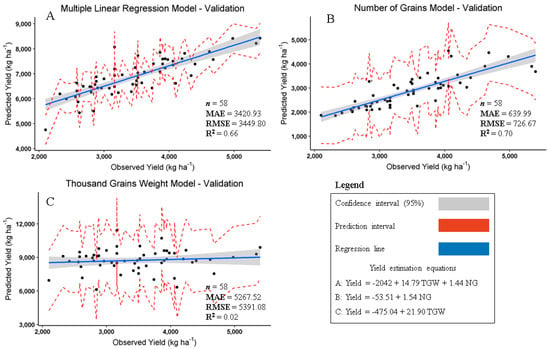
Figure 3.
Scatterplot of soybean observed and predicted yields (kg ha−1) applied to validation dataset. (A) Yield estimation based on thousand grains weight (TGW in g 1000 grains−1) and number of grains (NG in grains m−2), (B) yield estimation as function of number of grains (NG in grains m−2) and (C) yield estimation as functions of thousand grains weight (TGW in g 1000 grains−1). n = number of observations; MAE = mean absolute error (kg ha−1); RMSE = root mean squared error (kg ha−1); R2 = multiple R-squared; Yield = soybean yield (kg ha−1); TGW = thousand grains weight (g 1000 grains−1); NG = number of grains (grains m−2).
This paper presents a novel model to predict soybean yield based on its components and data published worldwide by applying linear regression models different from those published based on soil properties [90], historical data about soil, yield and soybean variety [91] and vegetation indices [92]. Model B, based on the number of grains per m2 which presented the highest R2, demonstrated its potential to predict soybean yield.
Currently, our soybean yield estimations are either based on agro-meteorological/crop models or based on yield monitors. Agro-meteorological/crop models are restricted by their spatial resolution and, most of the time, they do not represent farm-level support for on-farm decision making. On the other hand, yield monitors have a higher spatial resolution compared to agro-meteorological/crop models, but they are limited due to operational limitations and several error factors. These factors can be caused by different sources such miss calibration, sensor system errors and many others [3].
As stated by Patrício and Rieder [93], the application of computer vision, machine learning and high-performance computing together are considered as one of the main drivers to solving different problems in agriculture; we have to look for options considering these applications that will deliver better data and information to farmers to support and improve their decision making regarding their crop at farm level.
Efforts have been made in digital image processing techniques related to plant diseases [94] and reviews about computer vision systems to evaluate grain quality [95]. In this sense, there are several researchers working on grain quality and plant disease diagnosis by applying computer vision, which is expected since its evaluations are based on the visualization. Hence, being aware that there is a strong linear relation of number of grains per m2 with soybean yield (r = 0.92) in a worldwide range and that computational processing techniques are becoming more efficient, it is highlighted that there is an opportunity to apply computer vision techniques to gather these data to estimate soybean yield instead of looking for indirect factors to estimate its yield.
The proposed model in this paper can be suitable for different approaches from on-farm yield sampling for genetic plot trials to punctual yield scouting. The implication of applying this model is to acquire the predictor variable (NG) which is not easy at the moment. However, there are researchers working on high-throughput phenotyping, specifically, estimating the number of grains per pod of soybean plants [96] and number of grains [97], both under controlled environmental conditions.
Uzal et al. [96] developed an approach based on convolutional neural networks and support vector machines to estimate seed per pod for soybean plants through image processing resulting in R2 of validation and test ranging from 0.90 to 0.95 and 0.50 to 0.86, respectively. Li et al. [97] estimated soybean seed based on deep learning techniques, in their case, applying two convolution neural networks reaching MAE and MSE values of 13.21 and 17.62 number of seeds per image, respectively.
Considering non-controlled environmental conditions and targeting a yield component such as grain, Reza et al. [20] looking to estimate rice yield based on its components, in their case rice grain area, they applied a graph-cut algorithm with K-means clustering in images obtained from an unmanned aerial vehicle and found a coefficient of determination of 0.98 comparing the ground-truth and the proposed method. Thus, computer vision application in agriculture presents the potential to obtain yield components data, like rice grain which can be extrapolated to soybean grain.
Figure 4 represents an example of computer vision technique application to gather the number of grains of a sample. It shows the potential of applying computer vision techniques to obtain soybean number of grains. Note that in this paper our focus is not to demonstrate how to implement computer vision, but highlight that soybean yield can be accurately predicted through its components, in our suggested model by the number of grains per m2, and one possible method to reach these components data is by applying computer vision techniques. Indeed, more research applying computer vision to acquire soybean number of grains is required, but we must rely on technological and computational advances in agriculture that have been improving in large steps.
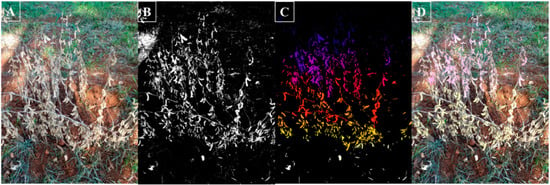
Figure 4.
Example of computer vision technique application to gather soybean number of grains on-field situations. (A) Original soybean image, (B) soybean image transformation, (C) surface object detection image and (D) original soybean image overlaid with surface object detection image.
Being aware that yield monitors present several time consuming steps for calibration to improve their accuracy estimation [3] and that soybean yield can be accurately estimated by model B (based on the number of grains per m2), efforts should be made aiming at achieving accurate numbers of grains in on-field situations without harvesting the crop to apply model B to forecast soybean yield. Therefore, in accordance that computer vision techniques are being applied to estimate crop components related to yield [98,99,100,101] and the example of Figure 4, it is highlighted that computer vision is a promising method that will support how soybean number of grains are gathered on-field in a fast, reliable and accurate way.
4. Conclusions
In this work, considering the dataset used, it can be concluded that globally soybean yield presents a strong linear relationship with number of grains even for different varieties, countries and treatments and presents a weak linear relationship with thousand grains weight. It was possible to estimate soybean yield based on two equations, one dependent on thousand grains weight and number of grains (model A) and another dependent only on the number of grains (model B). Model B, yield as function of number of grains, applied to the validation dataset presented the best prediction accuracy compared to models A and C, highest R2 (0.70), lowest MAE (639.99 kg ha−1) and RMSE (726.67 kg ha−1).
Despite the suitability of fit of model B to predict soybean yield, it is worth noting that, currently, it is difficult and time-consuming to access NG data to use the proposed model. However, as the implementation of technology in agriculture advances, the proposed method corroborates towards the use and development of computer vision application to estimate crop yield, in this case, soybean yield.
Author Contributions
Conceptualization, M.C.F.W. and J.P.M.; methodology, M.C.F.W. and J.P.M.; validation, M.C.F.W. and J.P.M., investigation, M.C.F.W. and J.P.M.; writing—original draft preparation, M.C.F.W. and J.P.M.; writing—review and editing, M.C.F.W. and J.P.M.; visualization, M.C.F.W. and J.P.M.; supervision, J.P.M. All authors have read and agreed to the published version of the manuscript.
Funding
The authors are grateful to CAPES and CNPq (process number: 130968/2019-6) for the scholarship support to M.W. (Masters student, University of Sao Paulo) and to Fundação de Estudos Agrários Luiz de Queiroz (FEALQ) for supporting the publication fee.
Acknowledgments
We thank Horst Bremer Neto that allowed us to collect the soybean samples on-field and Ricardo Chan for proofreading the English manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fritz, S.; See, L.; Bayas, J.C.L.; Waldner, F.; Jacques, D.; Becker-Reshef, I.; Rembold, F. A comparison of global agricultural monitoring systems and current gaps. Agric. Syst. 2019, 168, 258–272. [Google Scholar] [CrossRef]
- Fulton, J.; Hawkins, E.; Taylor, R.; Franzen, A. Yield monitor data: Collection, management, and usage. Crops Soils 2018, 51, 4–51. [Google Scholar] [CrossRef]
- Fulton, J.; Hawkins, E.; Taylor, R.; Franzen, A. Yield monitoring and mapping. In Precision Agriculture Basics; Shannon, D.K., Clay, D.E., Kitchen, N.R., Eds.; ASA, CSSA, and SSSA: Madison, WI, USA, 2018; pp. 63–78. [Google Scholar]
- Betbeder, J.; Fieuzal, R.; Baup, F. Assimilation of LAI and dry biomass data from optical and SAR images into an agro-meteorological model to estimate soybean yield. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2540–2553. [Google Scholar] [CrossRef]
- Figueiredo, G.K.; Brunsell, N.A.; Higa, B.H.; Rocha, J.V.; Augusto, R.; Lamparelli, C. Correlation maps to assess soybean yield from EVI data in Paraná State, Brazil. Sci. Agric. 2016, 73, 462–470. [Google Scholar] [CrossRef]
- Maestrini, B.; Basso, B. Predicting spatial patterns of within-field crop yield variability. Field Crops Res. 2018, 219, 106–112. [Google Scholar] [CrossRef]
- You, J.; Li, X.; Low, M.; Lobell, D.; Ermon, S. Deep gaussian process for crop yield prediction based on remote sensing data. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Al-Gaadi, K.A.; Hassaballa, A.A.; Tola, E.; Kayad, A.G.; Madugundu, R.; Alblewi, B.; Assiri, F. Prediction of potato crop yield using precision agriculture techniques. PLoS ONE 2016, 11, e0162219. [Google Scholar] [CrossRef]
- Coelho, A.P.; De Faria, R.T.; Leal, F.T.; de Arruda Barbosa, J.; Dalri, A.B.; Rosalen, D.L. Estimation of irrigated oats yield using spectral indices. Agri. Water Manag. 2019. [Google Scholar] [CrossRef]
- Setiyono, T.D.; Quicho, E.D.; Gatti, L.; Campos-Taberner, M.; Busetto, L.; Collivignarelli, F.; García-Haro, F.J.; Boschetti, M.; Khan, N.I.; Holecz, F. Spatial rice yield estimation based on MODIS and Sentinel-1 SAR data and ORYZA crop growth model. Remote Sens. 2018, 10, 293. [Google Scholar] [CrossRef]
- Syngenta. Syngenta Crop Challenge in Analytics. 2018. Available online: https://www.ideaconnection.com/syngenta-crop-challenge/challenge.php (accessed on 20 January 2020).
- Khaki, S.; Wang, L. Crop yield prediction using deep neural networks. Front. Plant Sci. 2019, 10. [Google Scholar] [CrossRef]
- Romero, J.R.; Roncallo, P.F.; Akkiraju, P.C.; Ponzoni, I.; Echenique, V.C.; Carballido, J.S. Using classification algorithms for predicting durum wheat yield in the province of Buenos Aires. Comput. Electron. Agric. 2013, 96, 173–179. [Google Scholar] [CrossRef]
- Aggelopoulou, A.; Bochtis, D.; Fountas, S.; Swain, K.C.; Gemtos, T.; Nanos, G.D. Yield prediction in apple orchards based on image processing. Precis. Agric. 2011, 12, 448–456. [Google Scholar] [CrossRef]
- Kurosaki, H.; Yumoto, S. Effects of low temperature and shading during flowering on the yield components in soybeans. Plant Prod. Sci. 2003, 6, 17–23. [Google Scholar] [CrossRef]
- Hao, D.; Cheng, H.; Yin, Z.; Cui, S.; Zhang, D.; Wang, H.; Yu, D. Identification of single nucleotide polymorphisms and haplotypes associated with yield and yield components in soybean (Glycine max) landraces across multiple environments. Theor. Appl. Genet. 2012, 124, 447–458. [Google Scholar] [CrossRef]
- Caverzan, A.; Giacomin, R.; Muller, M.; Biazus, C.; Langaro, N.D.; Chavarria, G. How does seed vigor affect soybean yield components? Agron. J. 2018, 110, 1318–1327. [Google Scholar] [CrossRef]
- MacMillan, K.P.; Guiden, R.H. Effect of seeding date, environment and cultivar on soybean seed yield, yield components, and seed quality in the Northern Great Plains. Agron. J. 2020, 112, 1666–1678. [Google Scholar] [CrossRef]
- Stein, M.; Bargoti, S.; Underwood, J. Image based mango fruit detection, localisation and yield estimation using multiple view geometry. Sensors 2016, 16, 1915. [Google Scholar] [CrossRef]
- Reza, M.N.; Na, I.S.; Baek, S.W.; Lee, K.-H. Rice yield estimation based on K-means clustering with graph-cut segmentation using low-altitude UAV images. Biosyst. Eng. 2018, 177, 109–121. [Google Scholar] [CrossRef]
- Tedesco-Oliveira, D.; da Silva, R.P.; Maldonado, W., Jr.; Zerbato, C. Convolutional neural networks in predicting cotton yield from images of commercial fields. Comput. Electron. Agric. 2020, 171, 105307. [Google Scholar] [CrossRef]
- Egli, D.B.; Yu, Z. Crop growth rate and seeds per unit area in soybean. Crop Sci. 1991, 31, 439–442. [Google Scholar] [CrossRef]
- Lindsey, L. Agronomic Crops Network: Estimating Soybean Yield. 2020. Available online: https://agcrops.osu.edu/newsletter/corn-newsletter/2015-26/estimating-soybean-yield (accessed on 28 January 2020).
- Gromping, U. Variable importance assessment in regression: Linear regression versus random forest. Am. Stat. 2009, 63, 309–319. [Google Scholar] [CrossRef]
- R Foundation for Statistical Computing. R: A Language and Environment for Statistical Computing, version 3.6.0; R Core Team: Vienna, Austria, 2019. [Google Scholar]
- Abbasi, M.K.; Majeed, A.; Sadiq, A.; Khan, S.R. Application of Bradyrhizobium japonicum and phosphorus fertilization improved growth, yield and nodulation of soybean in the sub-humid hilly region of Azad Jammu and Kashmir, Pakistan. Plant Prod. Sci. 2008, 11, 368–376. [Google Scholar] [CrossRef]
- Afzal, A.; Bano, A.; Fatima, M. Higher soybean yield by inoculation with N-fixing and P-solubilizing bacteria. Agron. Sustain. Dev. 2010, 30, 487–495. [Google Scholar] [CrossRef]
- Almaz, M.G.; Halim, R.A.; Martini, M.Y. Effect of combined application of poultry manure and inorganic fertilizer on yield and yield components of maize intercropped with soybean. Pertanika J. Trop. Agric. Sci. 2017, 40, 173–184. [Google Scholar]
- Ambrosini, V.G.; Fontoura, S.M.V.; De Moraes, R.P.; Tamagno, S.; Ciampitti, I.A.; Bayer, C. Soybean yield response to Bradyrhizobium strains in fields with inoculation history in Southern Brazil. J. Plant Nutr. 2019, 42, 1941–1951. [Google Scholar] [CrossRef]
- Arslan, H.; Karakus, M.; Hatipoglu, H.; Arslan, D.; Bayraktar, O.V. Assessment of performances of yield and factors affecting the yield in some soybean varieties/lines grown under semi-arid climate conditions. Appl. Ecol. Env. Res. 2018, 16, 4289–4298. [Google Scholar] [CrossRef]
- Belkheir, A.M.; Zhou, X.; Smith, D.L. Variability in yield and yield component responses to genistein pre-incubated Bradyrhizobium japonicum by soybean [Glycine max (L.) Merr] cultivars. Plant Soil 2001, 229, 41–46. [Google Scholar] [CrossRef]
- Bertham, R.R.; Arifin, Z.; Nusantara, A.D. The improvement of yield and quality of soybeans in a coastal area using low input technology based on biofertilizers. Int. J. Adv. Sci. Eng. Inf. Technol. 2019, 9, 787–791. [Google Scholar] [CrossRef]
- Bryant, C.J.; Krutz, L.J.; Nuti, R.C.; Truman, C.C.; Locke, M.A.; Falconer, R.; Atwill, L.; Wood, C.W.; Spencer, G.D. Furrow diking as Mid-Southern USA irrigation strategy: Soybean grain yield, irrigation water use efficiency, and net returns above furrow diking costs. Crop. Forage Turfgrass Manag. 2019, 5, 180076. [Google Scholar] [CrossRef]
- Carciochi, W.D.; Schwalbert, R.; Andrade, F.H.; Corassa, G.M.; Carter, P.; Gaspar, A.P.; Schmidt, J.; Ciampitti, I.A. Soybean seed yield response to plant density by yield environment in North America. Agron. J. 2019, 111, 1923–1932. [Google Scholar] [CrossRef]
- Chirchir, G.J. Seed Quality of Soybean (Glycine max [L.] Merrill) Genotypes under Varying Storage and Priming Methods, Mother Plant Nutrient Profiles and Agro-Ecologies in Keyna. Master’s Thesis, Kenyatta University, Nairobi, Keyna, 2011. [Google Scholar]
- Crusciol, A.A.C.; Nascente, A.S.; Borghi, E.; Soratto, R.P.; Martins, P.O. Improving soil fertility and crop yield in a tropical region with palisadegrass cover crops. Agron. J. 2015, 107, 2271–2280. [Google Scholar] [CrossRef]
- De Freitas, R.M.S.; De Lima, L.E.; Silva, R.S.; Campos, H.D.; Perin, A. Fluxapyroxad in the asian soybean rust control in the Cerrado biome. Rev. Caatinga 2016, 29, 619–628. [Google Scholar] [CrossRef][Green Version]
- De Luca, M.J.; Hungría, M. Plant densities and modulation of symbiotic nitrogen fixation in soybean. Sci. Agric. 2014, 71, 181–187. [Google Scholar] [CrossRef]
- Dos Santos, H.P.; Fontaneli, R.S.; Pires, J.; Lampert, E.A.; Vargas, A.M.; Verdi, A.C. Grain yield and agronomic traits in soybean according to crop rotation systems. Bragantia 2014, 73, 263–273. [Google Scholar] [CrossRef][Green Version]
- Ekhtiari, S.; Kobraee, S.; Shamsi, K. Soybean yield under water deficit conditions. J. Biodivers. Env. Sci. 2013, 3, 46–52. [Google Scholar]
- Felisberto, G.; Bruzi, A.T.; Zuffo, A.M.; Zambiazzi, E.V.; Soares, I.O.; De Rezende, P.M.; Botelho, F.B.S. Agronomic performance of RR® soybean cultivars using different pre-sowing desiccation periods and distinct post-emergence herbicides. Afr. J. Agric. Res. 2015, 10, 3445–3452. [Google Scholar] [CrossRef]
- Ferreira, A.S.; Balbinot, A.A., Jr.; Werner, F.; Zucareli, C.; Franchini, J.C.; Debiasi, H. Plant density and mineral nitrogen fertilization influencing yield, yield components and concentration of oil and protein in soybean grains. Bragantia 2016, 75, 362–370. [Google Scholar] [CrossRef]
- Franchini, J.C.; Balbinot, A.A., Jr.; Debiasi, H.; Procópio, S.O. Intercropping of soybean cultivars with Urochloa. Pesq. Agropec. Trop. 2014, 44, 119–126. [Google Scholar] [CrossRef]
- Gai, Z.; Zhang, J.; Li, C. Effects of starter nitrogen fertilizer on soybean root activity, leaf photosynthesis and grain yield. PLoS ONE 2017, 12. [Google Scholar] [CrossRef]
- Galindo, F.S.; Filho, M.C.T.; Buzetti, S.; Santini, J.M.K.; Ludkiewicz, M.G.Z.; Baggio, G. Modes of application of cobalt, molybdenum and Azospirillum brasilense on soybean yield and profitability. Rev. Bras. Eng. Agric. Ambient. 2017, 21, 180–185. [Google Scholar] [CrossRef]
- Gaspar, A.P.; Conley, S.P. Responses of canopy reflectance, light interception, and soybean seed yield to replanting suboptimal stands. Crop Sci. 2015, 55, 377–385. [Google Scholar] [CrossRef]
- Gerçek, S.; Boydak, E.; Okant, M.; Dikilita, S. Water pillow irrigation compared to furrow irrigation for soybean production in a semi-arid area. Agric. Water Manag. 2008, 96, 87–92. [Google Scholar] [CrossRef]
- Ghassemi-Golezani, K.; Lotfi, R. Response of soybean cultivars to water stress at reproductive stages. Int. J. Plant. Anim. Environ. Sci. 2012, 2, 198–202. [Google Scholar]
- Gulluoglu, L.; Bakal, H.; Arioglu, H. The effects of twin-row planting pattern and plant population on seed yield and yield components of soybean at late double-cropped planting in Cukurova region. Turk. J. Field Crop 2016, 21, 59–65. [Google Scholar] [CrossRef]
- Hayder, G.; Mumtaz, S.S.; Khan, A.; Khan, S. Maize and soybean intercropping under various levels of soybean seed rates. Asian J. Plant Sci. 2003, 2, 339–341. [Google Scholar]
- Hernández, M.; Cuevas, F. The effect of inoculating with arbuscular Mycorrhiza and Bradyrhizobium strains on soybean (Glycine max (L) Merrill) crop development. Cult. Trop. 2003, 24, 19–21. [Google Scholar]
- Ibrahim, S.E. Agronomic studies on irrigated soybeans in central Sudan: II. Effect of sowing date on grain yield and yield components. Int. J. Agric. Sci. 2012, 2, 766–773. [Google Scholar]
- Jephter, B.F.M.; Mumba, P.; Bokosi, J.M. Assessment of the agronomic productivity and protein content in 16 soybean genotypes. Afr. J. Food Agric. Nutr. Dev. 2017, 17, 12600–12613. [Google Scholar] [CrossRef]
- Kaschuk, G.; Nogueira, M.A.; De Luca, M.J.; Hungria, M. Response of determinate and indeterminate soybean cultivars to basal and topdressing N fertilization compared to sole inoculation with Bradyrhizobium. Field Crops Res. 2016, 195, 21–27. [Google Scholar] [CrossRef]
- Keramati, S.; Pirdashti, H.; Esmaili, M.A.; Abbasian, A.; Habibi, M. The critical period of weed control in soybean (Glycine max (L.) Merr.) in north of Iran conditions. Pak. J. Biol. Sci. 2008, 11, 463–467. [Google Scholar]
- Kumar, M.; Das, T.K. Integrated weed management for system productivity and economics in soybean (Glycine max)—Wheat (Triticum aestivum) system. Indian J. Agron. 2008, 53, 189–194. [Google Scholar]
- Lamptey, S.; Yeboah, S.; Sakodie, K.; Berdjour, A. Growth and yield response of soybean under different weeding regimes. Asian J. Agric. Food Sci. 2015, 3, 155–163. [Google Scholar]
- Leblanc, M.L.; Cloutier, D.C. Susceptibility of row-planted soybean (Glycine max) to the rotary hoe. J. Sustain. Agric. 2011, 18, 53–61. [Google Scholar] [CrossRef]
- Liu, X.; Rahman, T.; Song, C.; Su, B.; Yang, F.; Yong, T.; Wu, Y.; Zhang, C.; Yang, W. Changes in light environment, morphology, growth and yield of soybean in maize-soybean intercropping systems. Field Crops Res. 2017, 200, 38–46. [Google Scholar] [CrossRef]
- Lyimo, L.D.; Tamba, M.R.; Madege, R.R. Effects of genotype on yield and yield components of soybean (Glycine max (L) Merrill). Afr. J. Agric. Res. 2016, 10, 1930–1936. [Google Scholar] [CrossRef]
- Maleki, A.; Naderi, A.; Naseri, R.; Fathi, A.; Bahamin, S.; Maleki, R. Physiological performance of soybean cultivars under drought stress. Bull. Env. Pharmacol. Life Sci. 2013, 2, 38–44. [Google Scholar]
- Mandal, K.G.; Hati, K.M.; Misra, A.K. Biomass yield and energy analysis of soybean production in relation to fertilizer-NPK and organic manure. Biomass Bioenergy 2009, 33, 1670–1679. [Google Scholar] [CrossRef]
- Madanzi, T.; Chiduza, C.; Kageler, S.J.R.; Muziri, T. Effects of different plant populations on yield of different soybean (Glycine Max (L.) Merrill) varieties in a smallholder sector of Zimbabwe. J. Agron. 2012, 11, 9–16. [Google Scholar] [CrossRef]
- Mandić, V.; Simić, A.; Krnjaja, V.; Bijelić, Z.; Tomić, Z.; Stanojković, A.; Muslić, D.R. Effect of foliar fertilization on soybean grain yield. Biotech. Anim. Husb. 2015, 31, 133–143. [Google Scholar] [CrossRef]
- Mbah, E.U.; Muoneke, C.O.; Okpara, D.A. Effect of compound fertilizer on the yield and productivity of soybean and maize in soybean/maize intercrop in southeastern Nigeria. Trop. Subtrop. Agroecosyst. 2007, 7, 87–95. [Google Scholar]
- Moosavi, S.S.; Mirhadi, S.M.J.; Imani, A.A.; Khaneghah, A.M.; Moghanlou, B.S. Study of effect of planting date on vegetative traits, reproductive traits and grain yield of soybean cultivars in cold region of Ardabil (Iran). Afr. J. Agric. Res. 2011, 6, 4879–4883. [Google Scholar]
- Mostafavi, K. Grain yield and yield components of soybean upon application of different micronutrient foliar fertilizers at different growth stages. Int. J. Agric. Res. Rev. 2012, 2, 389–394. [Google Scholar]
- Muoneke, C.O.; Ogwuche, M.A.O.; Kalu, B.A. Effect of maize planting density on the performance of maize/soybean intercropping system in a guinea savannah agroecosystem. Afr. J. Agric. Res. 2007, 2, 667–677. [Google Scholar]
- Nico, M.; Miralles, D.J.; Kantolic, A.G. Post-flowering photoperiod and radiation interaction in soybean yield determination: Direct and indirect photoperiodic effects. Field Crops Res. 2015, 176, 45–55. [Google Scholar] [CrossRef]
- Orlowski, J.M.; Haverkamp, B.J.; Laurenz, R.G.; Marburger, D.A.; Wilson, E.W.; Casteel, S.N.; Conley, S.P.; Naeve, S.L.; Nafziger, E.D.; Roozeboom, K.L.; et al. High-input management systems effect on soybean seed yield, yield components and economic break-even probabilities. Crop Sci. 2016, 56, 1988–2004. [Google Scholar] [CrossRef]
- Paudel, B.; Karki, T.B.; Shah, S.C.; Chaudhary, N.K. Yield and economics of maize (Zea mays) + soybean (Glycin max L. Merrill) intercropping system under different tillage methods. World J. Agric. Res. 2015, 3, 74–77. [Google Scholar] [CrossRef]
- Rosa, C.B.; Marchetti, M.E.; Serra, A.P.; De Souza, L.C.F.; Ensinas, S.C.; Da Silva, E.F.; Lourente, E.R.P.; Dupas, E.; De Moraes, E.M.; Mattos, F.A.; et al. Soybean agronomic performance in narrow and wide row spacing associated with NPK fertilizer under no-tillage. Afr. J. Agric. Res. 2016, 11, 2947–2956. [Google Scholar] [CrossRef][Green Version]
- Salehi, M. Effect of foliar application of methanol on the growth and yield of soybean. Environ. Treat. Tech. 2013, 1, 122–125. [Google Scholar]
- Sharma, O.P.; Tiwari, S.C.; Raghuwanshi, R.K. Effect of doses and sources of sulphur on nodulation, yield, oil and protein content of soybean and soil properties. Soybean Res. 2004, 2, 35–40. [Google Scholar]
- Souza, R.; Teixeira, I.; Reis, E.; Silva, A. Soybean morphophysiology and yield response to seeding systems and plant populations. Chil. J. Agric. Res. 2016, 76. [Google Scholar] [CrossRef]
- Popović, V.; Vidić, M.; Jocković, D.; Ikanović, J.; Jakšić, S.; Cvijanović, G. Variability and correlations between yield components of soybean [Glycine max (L.) Merr.]. Genetika 2012, 44, 33–45. [Google Scholar] [CrossRef]
- Taheri, N.; Zarghami, R.; Oveysi, M.; Tarighaleslami, M. The effect of source limitations on yield and yield components of soybean (Glycine max L.) under drought stress. World Appl. Sci. J. 2012, 18, 788–795. [Google Scholar] [CrossRef]
- Tonello, E.S.; Fabbian, N.L.; Sacon, D.; Netto, A.; Silva, V.N.; Milanesi, P.M. Soybean seed origin effects on physiological and sanitary quality and crop yield. Semin. Ciências Agrárias 2019, 40, 1789–1804. [Google Scholar] [CrossRef]
- Uchino, H.; Iwama, K.; Jitsuyama, Y.; Yudate, T.; Nakamura, S. Yield losses of soybean and maize by competition with interseeded cover crops and weeds in organic-based cropping systems. Field Crops Res. 2009, 113, 342–351. [Google Scholar] [CrossRef]
- Yari, V.; Frnia, A.; Maleki, A.; Moradi, M.; Naseri, R.; Ghasemi, M.; Lotfi, A. Yield and yield components of soybean cultivars as affected by planting date. Bull. Env. Pharmacol. Life Sci. 2013, 2, 85–90. [Google Scholar]
- Zuffo, A.M.; Bruzi, A.T.; De Rezende, P.M.; Bianchi, M.C.; Zambiazzi, E.V.; Soares, I.O.; Ribeiro, A.B.M.; Vilela, G.L.D. Morphoagronomic and productive traits of RR® soybean due to inoculation via Azospirillum brasilense grove. Afr. J. Micr. Res. 2016, 10, 438–444. [Google Scholar] [CrossRef]
- United States Department of Agriculture (USDA). Foreign Agricultural Service: Soybeans. Available online: https://www.fas.usda.gov/commodities/soybeans (accessed on 5 July 2020).
- Empresa Brasileira de Pesquisa Agropecuária (EMBRAPA). Embrapa Soja. 2020. Available online: https://www.embrapa.br/soja/cultivos/soja1 (accessed on 5 July 2020). (In Portuguese).
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine learning in agriculture: A review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef]
- Board, J.E. Yield components related to seed yield in determinate soybean. Crop Sci. 1987, 27, 1296–1297. [Google Scholar] [CrossRef]
- De Bruin, J.L.; Pedersen, P. Soybean seed yield response to planting date and seeding rate in the upper Midwest. Agron. J. 2008, 100, 696–703. [Google Scholar] [CrossRef]
- Robinson, A.P.; Conley, S.P.; Volenec, J.J.; Santini, J.B. Analysis of high yielding, early-planted soybean in Indiana. Agron. J. 2009, 101, 131–139. [Google Scholar] [CrossRef]
- Zhang, C.; Kovacs, J.M. The application of small unmanned aerial systems for precision agriculture: A review. Precis. Agric. 2012, 13, 693–712. [Google Scholar] [CrossRef]
- Palmer, P.B.; O`Connell, D.G. Regression analysis for prediction: Understanding the process. Cardiopulm. Phys. Ther. J. 2009, 20, 23–26. [Google Scholar] [CrossRef] [PubMed]
- Smidt, E.R.; Conley, S.P.; Zhu, J.; Arriage, F.J. Identifying field attributes that predict soybean yield using random forest analysis. Agron. J. 2016, 108, 637–646. [Google Scholar] [CrossRef]
- Marko, O.; Brdar, S.; Panic, M.; Lugonja, P.; Crnojevic, V. Soybean varieties portfolio optimisation based on yield prediction. Comput. Electron. Agric. 2016, 127, 467–474. [Google Scholar] [CrossRef]
- Christenson, B.S.; Schapaugh, W.T.; An, N.; Price, K.P.; Prasad, V.; Fritz, A.K. Predicting soybean relative maturity and seed yield using canopy reflectance. Crop Sci. 2016, 56, 625–643. [Google Scholar] [CrossRef]
- Patrício, D.I.; Rieder, R. Computer vision and artificial intelligence in precision agriculture for grain crops: A systematic review. Comput. Electron. Agric. 2018, 153, 69–81. [Google Scholar] [CrossRef]
- Barbedo, J.G.A. Digital image processing techniques for detecting, quantifying and classifying plant diseases. SpringerPlus 2013, 2, 660. [Google Scholar] [CrossRef]
- Vithu, P.; Moses, J.A. Machine vision system for food grain quality evaluation: A review. Trends Food Sci. Technol. 2016, 56, 13–20. [Google Scholar] [CrossRef]
- Uzal, L.C.; Grinblat, G.L.; Namías, R.; Larese, M.G.; Bianchi, J.S.; Morandi, E.N.; Granitto, P.M. Seed-per-pod estimation for plant breeding using deep learning. Comput. Electron. Agric. 2018, 150, 196–204. [Google Scholar] [CrossRef]
- Li, Y.; Jia, J.; Khattak, A.M.; Sun, S.; Gao, W.; Wang, M. Soybean seed counting based on pod image using two-column convolution neural network. IEEE Access 2019, 7, 64177–64185. [Google Scholar] [CrossRef]
- Liu, X.; Jia, W.; Ruan, C.; Zhao, D.; Gu, Y.; Chen, W. The recognition of apple fruits in plastic bags based on block classification. Precis. Agric. 2018, 19, 735–749. [Google Scholar] [CrossRef]
- Qureshi, W.S.; Payne, A.; Walsh, K.B.; Linker, R.; Cohen, O.; Dailey, M.N. Machine vision for counting fruit on mango tree canopies. Precis. Agric. 2017, 18, 224–244. [Google Scholar] [CrossRef]
- Ramos, P.J.; Prieto, F.A.; Montoya, E.C.; Oliveros, C.E. Automatic fruit count on coffee branches using computer vision. Comput. Electron. Agric. 2017, 137, 9–22. [Google Scholar] [CrossRef]
- Sa, I.; Ge, Z.; Dayoub, F.; Upcroft, B.; Perez, T.; Mccool, C. Deepfruits: A fruit detection system using deep neural networks. Sensors 2016, 16, 1222. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).