Research Status and Prospects on Plant Canopy Structure Measurement Using Visual Sensors Based on Three-Dimensional Reconstruction
Abstract
:1. Introduction
2. 3D Plant Canopy Data Measurement Technology
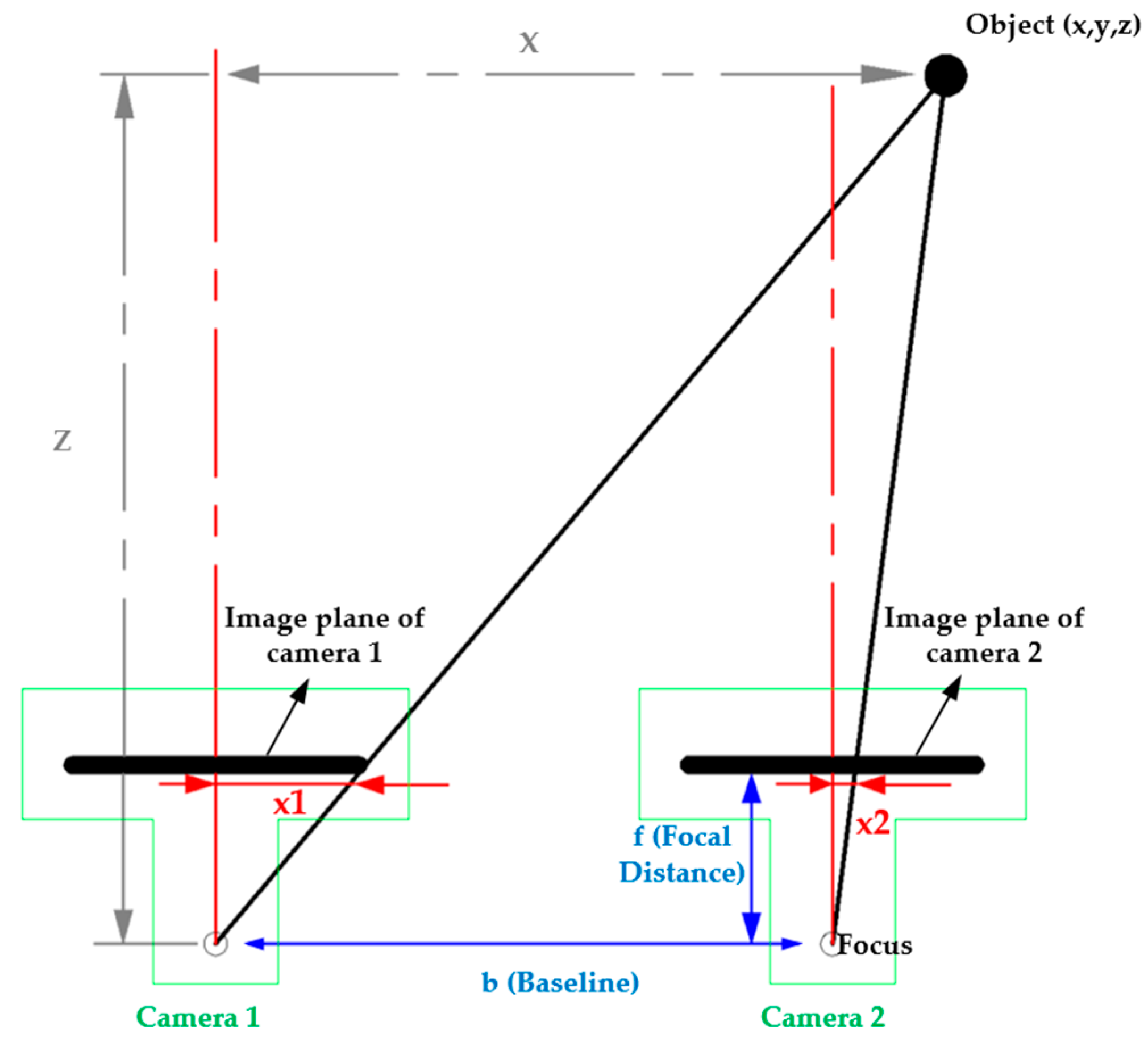
2.1. Binocular Stereo Vision Technology and Equipment
2.2. Multi-View Vision Technology
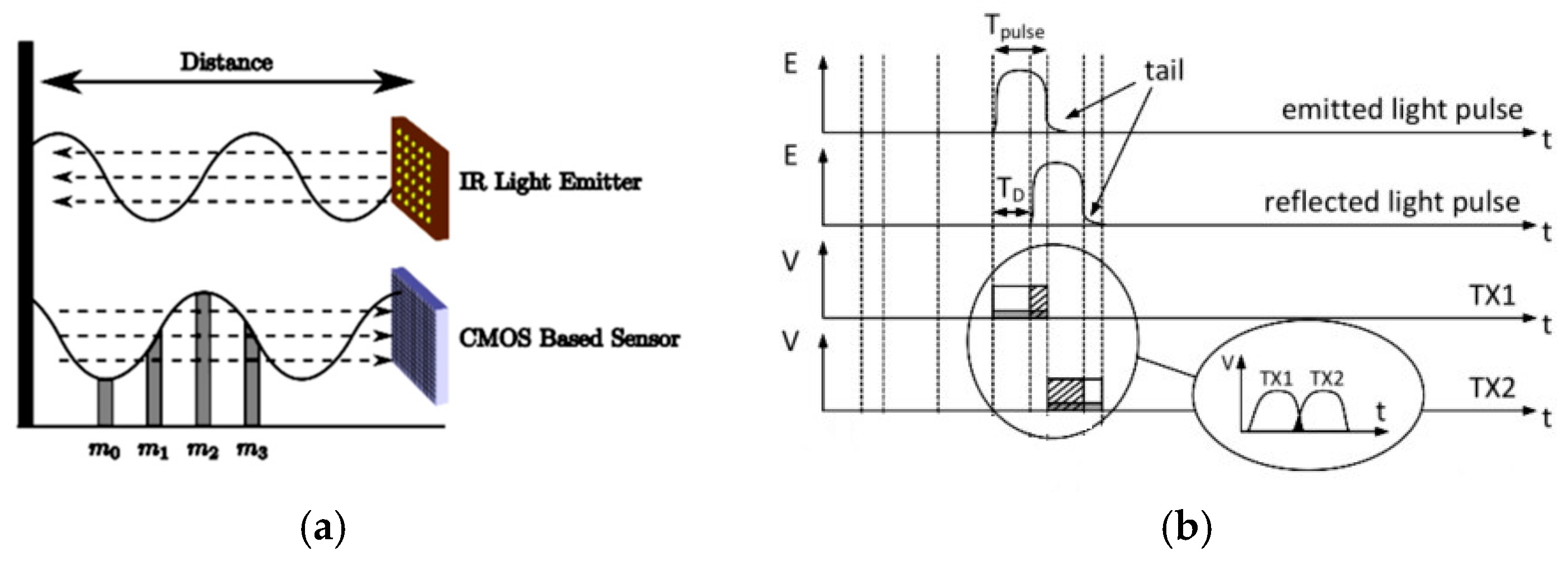
2.3. Time of Flight Technology
2.3.1. Time of Flight Cameras
2.3.2. LiDAR Scanning Equipment Based on ToF
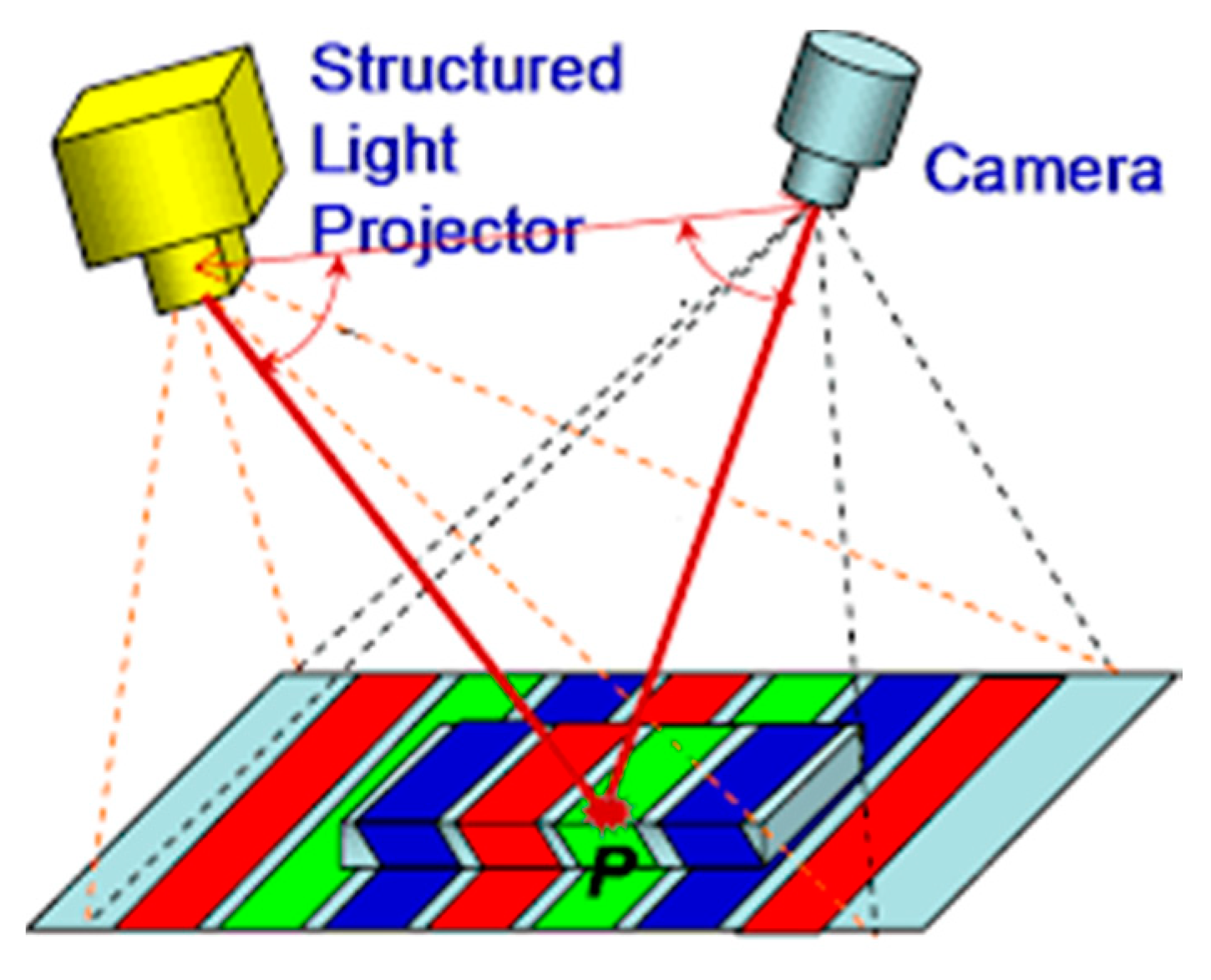
2.4. Structured Light Technology and Equipment
2.5. Comparison of Main Measurement Technologies
3. Plant Canopy Structure Measurement Based on 3D Reconstruction
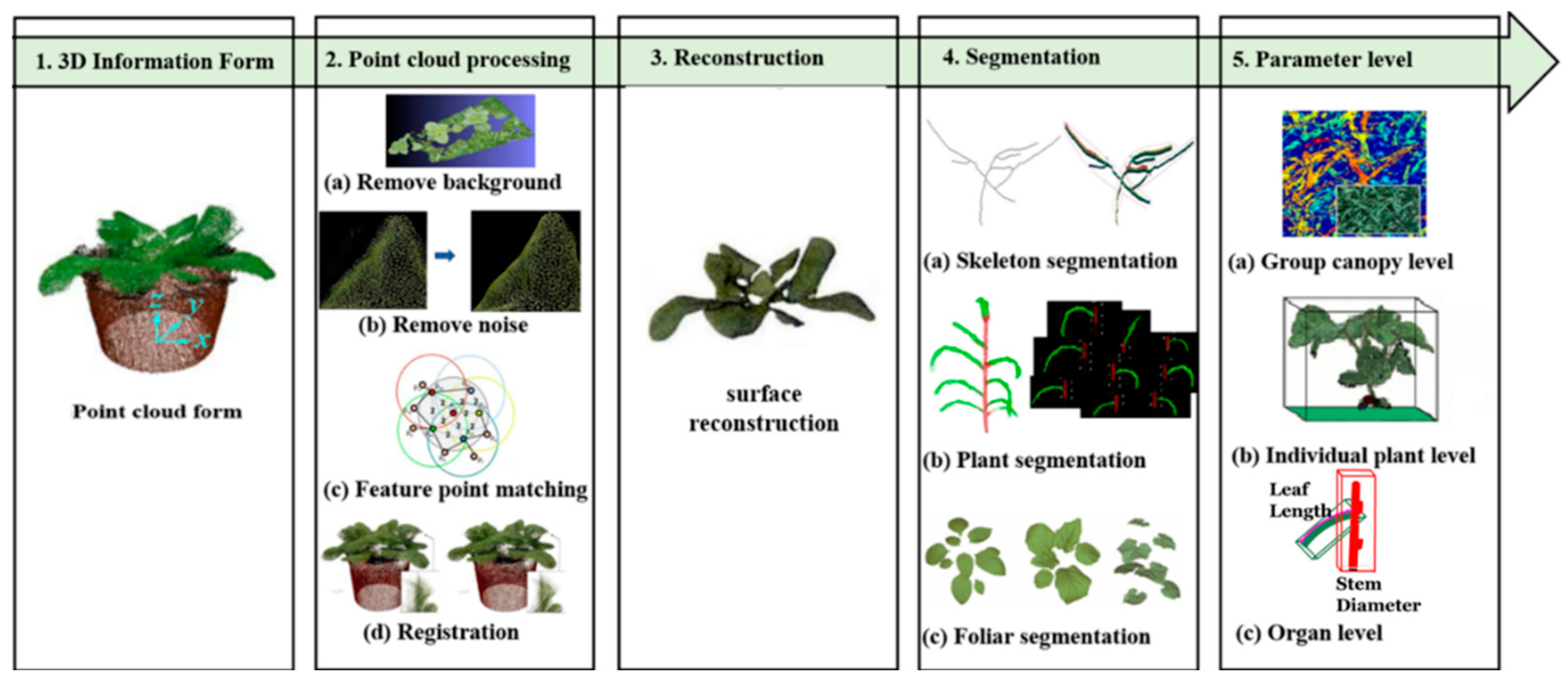
3.1. 3D Plant Data Acquisition
3.2. 3D Plant Canopy Point Clouds Preprocessing
3.2.1. Background Subtraction
3.2.2. Outlier Removal and Plant Point Clouds Noise Reduction
3.3. 3D Plant Canopy Reconstruction
3.3.1. Plant Point Clouds Registration
3.3.2. Plant Point Clouds Surface Reconstruction
3.4. Plant Canopy Segmentation
3.5. Plant Canopy Structure Parameters Extraction
3.5.1. Leaf Inclination Angles
3.5.2. Leaf Area Density (LAD)
3.5.3. Plant Area Density (PAD)
4. Conclusions
4.1. Poor Standardization of Algorithms
4.2. 3D Reconstruction Operation Is Slow
4.3. Plant 3D Reconstruction Is Inaccurate
4.4. High Equipment Collection Cost
5. Prospection
5.1. Establishing a Standard System of 3D Plant Canopy Structure Data
5.2. Speeding Up the 3D Plant Canopy Structure Reconstruction
5.3. Improving the Accuracy of the 3D Structure Index of Canopy Reconstruction
Author Contributions
Funding
Conflicts of Interest
References
- Li, D.; Yang, H. State-of-the-art review for internet of things in agriculture. Trans. Chin. Soc. Agric. Mach. 2018, 49, 1–20. [Google Scholar]
- Rahman, A.; Mo, C.; Cho, B.-K. 3-D image reconstruction techniques for plant and animal morphological analysis—A review. J. Biosyst. Eng. 2017, 42, 339–349. [Google Scholar]
- Tsai, R. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses. IEEE J. Robot. Autom. 1987, 3, 323–344. [Google Scholar] [CrossRef] [Green Version]
- Faugeras, O.; Toscani, G. Camera calibration for 3D computer vision. In Proceedings of the International Workshop on Industrial Application of Machine Vision and Machine Intelligence, Tokyo, Japan, 2–5 February 1987; pp. 240–247. [Google Scholar]
- Martins, H.; Birk, J.R.; Kelley, R.B. Camera models based on data from two calibration planes. Comput. Gr. Image Process. 1981, 17, 173–180. [Google Scholar] [CrossRef]
- Pollastri, F. Projection center calibration by motion. Pattern Recognit. Lett. 1993, 14, 975–983. [Google Scholar] [CrossRef]
- Caprile, B.; Torre, V. Using vanishing points for camera calibration. Int. J. Comput. Vis. 1990, 4, 127–139. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef] [Green Version]
- Qi, W.; Li, F.; Zhenzhong, L. Review on camera calibration. In Proceedings of the 2010 Chinese Control and Decision Conference, Xuzhou, China, 26–28 May 2010; pp. 3354–3358. [Google Scholar]
- Andersen, H.J.; Reng, L.; Kirk, K. Geometric plant properties by relaxed stereo vision using simulated annealing. Comput. Electron. Agric. 2005, 49, 219–232. [Google Scholar] [CrossRef]
- Malekabadi, A.J.; Khojastehpour, M.; Emadi, B. Disparity map computation of tree using stereo vision system and effects of canopy shapes and foliage density. Comput. Electron. Agric. 2019, 156, 627–644. [Google Scholar] [CrossRef]
- Li, L.; Yu, X.; Zhang, S.; Zhao, X.; Zhang, L. 3D cost aggregation with multiple minimum spanning trees for stereo matching. Appl. Opt. 2017, 56, 3411–3420. [Google Scholar] [CrossRef]
- Bao, Y.; Tang, L.; Breitzman, M.W.; Salas Fernandez, M.G.; Schnable, P.S. Field-based robotic phenotyping of sorghum plant architecture using stereo vision. J. Field Robot. 2019, 36, 397–415. [Google Scholar] [CrossRef]
- Baweja, H.S.; Parhar, T.; Mirbod, O.; Nuske, S. Stalknet: A deep learning pipeline for high-throughput measurement of plant stalk count and stalk width. In Field and Service Robotics; Springer: Cham, Switzerland, 2018; pp. 271–284. [Google Scholar]
- Dandrifosse, S.; Bouvry, A.; Leemans, V.; Dumont, B.; Mercatoris, B. Imaging wheat canopy through stereo vision: Overcoming the challenges of the laboratory to field transition for morphological features extraction. Front. Plant Sci. 2020, 11, 96. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vázquez-Arellano, M.; Griepentrog, H.W.; Reiser, D.; Paraforos, D.S. 3-D imaging systems for agricultural applications—A review. Sensors 2016, 16, 618. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, C.; Zheng, Y.F. Passive and active stereo vision for smooth surface detection of deformed plates. IEEE Trans. Ind. Electron. 1995, 42, 300–306. [Google Scholar] [CrossRef]
- Jin, H.; Soatto, S.; Yezzi, A.J. Multi-view stereo reconstruction of dense shape and complex appearance. Int. J. Comput. Vis. 2005, 63, 175–189. [Google Scholar] [CrossRef] [Green Version]
- Smith, M.; Carrivick, J.; Quincey, D. Structure from motion photogrammetry in physical geography. Prog. Phys. Geogr. 2016, 40, 247–275. [Google Scholar] [CrossRef]
- Malambo, L.; Popescu, S.C.; Murray, S.C.; Putman, E.; Pugh, N.A.; Horne, D.W.; Richardson, G.; Sheridan, R.; Rooney, W.L.; Avant, R.; et al. Multitemporal field-based plant height estimation using 3D point clouds generated from small unmanned aerial systems high-resolution imagery. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 31–42. [Google Scholar] [CrossRef]
- Tsai, M.; Chiang, K.; Huang, Y.; Lin, Y.; Tsai, J.; Lo, C.; Lin, Y.; Wu, C. The development of a direct georeferencing ready UAV based photogrammetry platform. In Proceedings of the 2010 Canadian Geomatics Conference and Symposium of Commission I, Calgary, AB, Canada, 15–18 June 2010. [Google Scholar]
- Turner, D.; Lucieer, A.; Wallace, L. Direct georeferencing of ultrahigh-resolution UAV imagery. IEEE Trans. Geosci. Remote Sens. 2013, 52, 2738–2745. [Google Scholar] [CrossRef]
- Rose, J.; Paulus, S.; Kuhlmann, H. Accuracy analysis of a multi-view stereo approach for phenotyping of tomato plants at the organ level. Sensors 2015, 15, 9651–9665. [Google Scholar] [CrossRef] [Green Version]
- Süss, A.; Nitta, C.; Spickermann, A.; Durini, D.; Varga, G.; Jung, M.; Brockherde, W.; Hosticka, B.J.; Vogt, H.; Schwope, S. Speed considerations for LDPD based time-of-flight CMOS 3D image sensors. In Proceedings of the 2013 the ESSCIRC (ESSCIRC), Bucharest, Romania, 16–20 September 2013; pp. 299–302. [Google Scholar]
- Iddan, G.J.; Yahav, G. Three-dimensional imaging in the studio and elsewhere. In Proceedings of the Three-Dimensional Image Capture and Applications IV, San Jose, CA, USA, 13 April 2001; pp. 48–55. [Google Scholar]
- Foix, S.; Alenya, G.; Torras, C. Lock-in time-of-flight (ToF) cameras: A survey. IEEE Sens. J. 2011, 11, 1917–1926. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Wang, L.; Xiang, L.; Wu, Q.; Jiang, H. Automatic non-destructive growth measurement of leafy vegetables based on kinect. Sensors 2018, 18, 806. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Si, Y.; Wanlin, G.; Jiaqi, M.; Mengliu, W.; Minjuan, W.; Lihua, Z. Method for measurement of vegetable seedlings height based on RGB-D camera. Trans. Chin. Soc. Agric. Mach. 2019, 50, 128–135. [Google Scholar]
- Vázquez-Arellano, M.; Paraforos, D.S.; Reiser, D.; Garrido-Izard, M.; Griepentrog, H.W. Determination of stem position and height of reconstructed maize plants using a time-of-flight camera. Comput. Electron. Agric. 2018, 154, 276–288. [Google Scholar] [CrossRef]
- Bao, Y.; Tang, L.; Srinivasan, S.; Schnable, P.S. Field-based architectural traits characterisation of maize plant using time-of-flight 3D imaging. Biosyst. Eng. 2019, 178, 86–101. [Google Scholar] [CrossRef]
- Liu, S.; Yao, J.; Li, H.; Qiu, C.; Liu, R. Research on 3D skeletal model extraction algorithm of branch based on SR4000. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2019; p. 022059. [Google Scholar]
- Hu, C.; Li, P.; Pan, Z. Phenotyping of poplar seedling leaves based on a 3D visualization method. Int. J. Agric. Biol. Eng. 2018, 11, 145–151. [Google Scholar] [CrossRef] [Green Version]
- Kadambi, A.; Bhandari, A.; Raskar, R. 3d depth cameras in vision: Benefits and limitations of the hardware. In Computer Vision and Machine Learning with RGB-D Sensors; Springer: Cham, Switzerland, 2014; pp. 3–26. [Google Scholar]
- Verbyla, D.L. Satellite Remote Sensing of Natural Resources; CRC Press: Cleveland, OH, USA, 1995; Volume 4. [Google Scholar]
- Garrido, M.; Paraforos, D.S.; Reiser, D.; Vázquez Arellano, M.; Griepentrog, H.W.; Valero, C. 3D maize plant reconstruction based on georeferenced overlapping LiDAR point clouds. Remote Sens. 2015, 7, 17077–17096. [Google Scholar] [CrossRef] [Green Version]
- Shen, D.A.Y.; Liu, H.; Hussain, F. A lidar-based tree canopy detection system development. In Proceedings of the 2018 the 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 10361–10366. [Google Scholar]
- Shen, Y.; Addis, D.; Liu, H.; Hussain, F. A LIDAR-Based Tree Canopy Characterization under Simulated Uneven Road Condition: Advance in Tree Orchard Canopy Profile Measurement. J. Sens. 2017, 2017, 8367979. [Google Scholar] [CrossRef] [Green Version]
- Yuan, H.; Bennett, R.S.; Wang, N.; Chamberlin, K.D. Development of a peanut canopy measurement system using a ground-based lidar sensor. Front. Plant Sci. 2019, 10, 203. [Google Scholar] [CrossRef] [Green Version]
- Qiu, Q.; Sun, N.; Wang, Y.; Fan, Z.; Meng, Z.; Li, B.; Cong, Y. Field-based high-throughput phenotyping for Maize plant using 3D LiDAR point cloud generated with a “Phenomobile”. Front. Plant Sci. 2019, 10, 554. [Google Scholar] [CrossRef] [Green Version]
- Jin, S.; Su, Y.; Wu, F.; Pang, S.; Gao, S.; Hu, T.; Liu, J.; Guo, Q. Stem–leaf segmentation and phenotypic trait extraction of individual maize using terrestrial LiDAR data. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1336–1346. [Google Scholar] [CrossRef]
- Geng, J. Structured-light 3D surface imaging: A tutorial. Adv. Opt. Photonics 2011, 3, 128–160. [Google Scholar] [CrossRef]
- Chéné, Y.; Rousseau, D.; Lucidarme, P.; Bertheloot, J.; Caffier, V.; Morel, P.; Belin, É.; Chapeau-Blondeau, F. On the use of depth camera for 3D phenotyping of entire plants. Comput. Electron. Agric. 2012, 82, 122–127. [Google Scholar] [CrossRef]
- Azzari, G.; Goulden, M.L.; Rusu, R.B. Rapid characterization of vegetation structure with a Microsoft Kinect sensor. Sensors 2013, 13, 2384–2398. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, T.; Slaughter, D.; Max, N.; Maloof, J.; Sinha, N. Structured light-based 3D reconstruction system for plants. Sensors 2015, 15, 18587–18612. [Google Scholar] [CrossRef] [Green Version]
- Syed, T.N.; Jizhan, L.; Xin, Z.; Shengyi, Z.; Yan, Y.; Mohamed, S.H.A.; Lakhiar, I.A. Seedling-lump integrated non-destructive monitoring for automatic transplanting with Intel RealSense depth camera. Artif. Intell. Agric. 2019, 3, 18–32. [Google Scholar] [CrossRef]
- Vit, A.; Shani, G. Comparing RGB-D sensors for close range outdoor agricultural phenotyping. Sensors 2018, 18, 4413. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Yuan, Y.; Zhou, Y.; Zhu, X.; Syed, T.N. Experiments and analysis of close-shot identification of on-branch citrus fruit with realsense. Sensors 2018, 18, 1510. [Google Scholar] [CrossRef] [Green Version]
- Milella, A.; Marani, R.; Petitti, A.; Reina, G. In-field high throughput grapevine phenotyping with a consumer-grade depth camera. Comput. Electron. Agric. 2019, 156, 293–306. [Google Scholar] [CrossRef]
- Perez-Sanz, F.; Navarro, P.J.; Egea-Cortines, M. Plant phenomics: An overview of image acquisition technologies and image data analysis algorithms. GigaScience 2017, 6, gix092. [Google Scholar] [CrossRef] [Green Version]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. Structure-from-Motion photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef] [Green Version]
- Klose, R.; Penlington, J.; Ruckelshausen, A. Usability study of 3D time-of-flight cameras for automatic plant phenotyping. Bornimer Agrartech. Ber. 2009, 69, 12. [Google Scholar]
- Ma, X.; Zhu, K.; Guan, H.; Feng, J.; Yu, S.; Liu, G. High-throughput phenotyping analysis of potted soybean plants using colorized depth images based on a proximal platform. Remote Sens. 2019, 11, 1085. [Google Scholar] [CrossRef] [Green Version]
- Sun, G.; Wang, X. Three-dimensional point cloud reconstruction and morphology measurement method for greenhouse plants based on the kinect sensor self-calibration. Agronomy 2019, 9, 596. [Google Scholar] [CrossRef] [Green Version]
- Paproki, A.; Sirault, X.; Berry, S.; Furbank, R.; Fripp, J. A novel mesh processing based technique for 3D plant analysis. BMC Plant Biol. 2012, 12, 63. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scharr, H.; Briese, C.; Embgenbroich, P.; Fischbach, A.; Fiorani, F.; Müller-Linow, M. Fast high resolution volume carving for 3D plant shoot reconstruction. Front. Plant Sci. 2017, 8, 1680. [Google Scholar] [CrossRef] [Green Version]
- Kumar, P.; Connor, J.; Mikiavcic, S. High-throughput 3D reconstruction of plant shoots for phenotyping. In Proceedings of the 2014 13th International Conference on Control Automation Robotics and Vision (ICARCV), Singapore, 10–12 December 2014; pp. 211–216. [Google Scholar]
- Gibbs, J.A.; Pound, M.; French, A.P.; Wells, D.M.; Murchie, E.; Pridmore, T. Plant phenotyping: An active vision cell for three-dimensional plant shoot reconstruction. Plant Physiol. 2018, 178, 524–534. [Google Scholar] [CrossRef] [Green Version]
- Neubert, B.; Franken, T.; Deussen, O. Approximate image-based tree-modeling using particle flows. In Proceedings of the ACM SIGGRAPH 2007 Papers, San Diego, CA, USA, 5–9 August 2007. [Google Scholar]
- Aggarwal, A.; Guibas, L.J.; Saxe, J.; Shor, P.W. A linear-time algorithm for computing the Voronoi diagram of a convex polygon. Discret. Comput. Geom. 1989, 4, 591–604. [Google Scholar] [CrossRef]
- Srihari, S.N. Representation of three-dimensional digital images. ACM Comput. Surv. 1981, 13, 399–424. [Google Scholar] [CrossRef]
- Vandenberghe, B.; Depuydt, S.; Van Messem, A. How to Make Sense of 3D Representations for Plant Phenotyping: A Compendium of Processing and Analysis Techniques; OSF Preprints: Charlottesville, VA, USA, 2018. [Google Scholar] [CrossRef] [Green Version]
- Klodt, M.; Herzog, K.; Töpfer, R.; Cremers, D. Field phenotyping of grapevine growth using dense stereo reconstruction. BMC Bioinf. 2015, 16, 143. [Google Scholar] [CrossRef] [Green Version]
- Guo, K.; Zou, D.; Chen, X. 3D mesh labeling via deep convolutional neural networks. ACM Trans. Graph. 2015, 35, 1–12. [Google Scholar] [CrossRef]
- Gai, J.; Tang, L.; Steward, B. Plant recognition through the fusion of 2D and 3D images for robotic weeding. In 2015 ASABE Annual International Meeting; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2015. [Google Scholar]
- Andújar, D.; Dorado, J.; Fernández-Quintanilla, C.; Ribeiro, A. An approach to the use of depth cameras for weed volume estimation. Sensors 2016, 16, 972. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mitra, N.J.; Nguyen, A. Estimating surface normals in noisy point cloud data. In Proceedings of the Nineteenth Annual Symposium on Computational Geometry, San Diego, CA, USA, 8–10 June 2003; pp. 322–328. [Google Scholar]
- Hawkins, D.M. Identification of Outliers; Springer: Cham, Switzerland, 1980; Volume 11. [Google Scholar]
- Johnson, T.; Kwok, I.; Ng, R.T. Fast Computation of 2-Dimensional Depth Contours. In KDD; Citeseer: Princeton, NJ, USA, 1998; pp. 224–228. [Google Scholar]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data clustering: A review. ACM Comput. Surv. 1999, 31, 264–323. [Google Scholar] [CrossRef]
- Knorr, E.M.; Ng, R.T.; Tucakov, V. Distance-based outliers: Algorithms and applications. VLDB J. 2000, 8, 237–253. [Google Scholar] [CrossRef]
- Breunig, M.M.; Kriegel, H.-P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 16–18 May 2000; pp. 93–104. [Google Scholar]
- Fleishman, S.; Cohen-Or, D.; Silva, C.T. Robust moving least-squares fitting with sharp features. ACM Trans. Graph. 2005, 24, 544–552. [Google Scholar] [CrossRef]
- Wu, J.; Xue, X.; Zhang, S.; Qin, W.; Chen, C.; Sun, T. Plant 3D reconstruction based on LiDAR and multi-view sequence images. Int. J. Precis. Agric. Aviat. 2018, 1. [Google Scholar] [CrossRef]
- Wolff, K.; Kim, C.; Zimmer, H.; Schroers, C.; Botsch, M.; Sorkine-Hornung, O.; Sorkine-Hornung, A. Point cloud noise and outlier removal for image-based 3D reconstruction. In Proceedings of the 2016 the Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 118–127. [Google Scholar]
- Xia, C.; Shi, Y.; Yin, W. Obtaining and denoising method of three-dimensional point cloud data of plants based on TOF depth sensor. Trans. Chin. Soc. Agric. Eng. 2018, 34, 168–174. [Google Scholar]
- Zhou, Z.; Chen, B.; Zheng, G.; Wu, B.; Miao, X.; Yang, D.; Xu, C. Measurement of vegetation phenotype based on ground-based lidar point cloud. J. Ecol. 2020, 39, 308–314. [Google Scholar]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Proceedings of the Sensor Fusion IV: Control Paradigms and Data Structures, Boston, MA, USA, 30 April 1992; pp. 586–606. [Google Scholar]
- Jian, B.; Vemuri, B.C. A robust algorithm for point set registration using mixture of Gaussians. In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05), Beijing, China, 17–21 October 2005; Volume 1, pp. 1246–1251. [Google Scholar]
- Chui, H.; Rangarajan, A. A new point matching algorithm for non-rigid registration. Comput. Vis. Image Underst. 2003, 89, 114–141. [Google Scholar] [CrossRef]
- Jia, H.; Meng, Y.; Xing, Z.; Zhu, B.; Peng, X.; Ling, J. 3D model reconstruction of plants based on point cloud stitching. Appl. Sci. Technol. 2019, 46, 19–24. [Google Scholar]
- Boissonnat, J.-D. Geometric structures for three-dimensional shape representation. ACM Trans. Graph. 1984, 3, 266–286. [Google Scholar] [CrossRef]
- Curless, B.; Levoy, M. A volumetric method for building complex models from range images. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, New York, NY, USA, 4–9 August 1996; pp. 303–312. [Google Scholar]
- Edelsbrunner, H.; Mücke, E.P. Three-dimensional alpha shapes. ACM Trans. Graph. 1994, 13, 43–72. [Google Scholar] [CrossRef]
- Amenta, N.; Choi, S.; Dey, T.K.; Leekha, N. A simple algorithm for homeomorphic surface reconstruction. In Proceedings of the Sixteenth Annual Symposium on Computational Geometry, Kowloon, Hong Kong, China, 12–14 June 2000; pp. 213–222. [Google Scholar]
- Forero, M.G.; Gomez, F.A.; Forero, W.J. Reconstruction of surfaces from points-cloud data using Delaunay triangulation and octrees. In Proceedings of the Vision Geometry XI, Seattle, WA, USA, 24 November 2002; pp. 184–194. [Google Scholar]
- Liang, J.; Park, F.; Zhao, H. Robust and efficient implicit surface reconstruction for point clouds based on convexified image segmentation. J. Sci. Comput. 2013, 54, 577–602. [Google Scholar] [CrossRef]
- Carr, J.C.; Beatson, R.K.; Cherrie, J.B.; Mitchell, T.J.; Fright, W.R.; McCallum, B.C.; Evans, T.R. Reconstruction and representation of 3D objects with radial basis functions. In Proceedings of the 28th Annual ACM Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 12–17 August 2001; pp. 67–76. [Google Scholar]
- Alexa, M.; Behr, J.; Cohen-Or, D.; Fleishman, S.; Levin, D.; Silva, C.T. Point set surfaces. In Proceedings of the IEEE Conference on Visualization ’01, San Diego, CA, USA, 21–26 October 2001; pp. 21–28. [Google Scholar]
- Ohtake, Y.; Belyaev, A.; Alexa, M.; Turk, G.; Seidel, H.-P. Multi-level partition of unity implicits. In ACM Siggraph 2005 Courses; Association for Computing Machinery: New York, NY, USA, 2005. [Google Scholar]
- Kazhdan, M.; Bolitho, M.; Hoppe, H. Poisson surface reconstruction. In Proceedings of the Fourth Eurographics Symposium on Geometry Processing, Cagliari, Sardinia, Italy, 26–28 June 2006; Eurographics Association: Goslar, Germany, 2006; pp. 60–66. [Google Scholar]
- Boissonnat, J.-D.; Flototto, J. A local coordinate system on a surface. In Proceedings of the Seventh ACM Symposium on Solid Modeling and Applications, Saarbrücken, Germany, 17–21 June 2002; pp. 116–126. [Google Scholar]
- Jay, S.; Rabatel, G.; Hadoux, X.; Moura, D.; Gorretta, N. In-field crop row phenotyping from 3D modeling performed using Structure from Motion. Comput. Electron. Agric. 2015, 110, 70–77. [Google Scholar] [CrossRef] [Green Version]
- Andújar, D.; Ribeiro, A.; Fernández-Quintanilla, C.; Dorado, J. Using depth cameras to extract structural parameters to assess the growth state and yield of cauliflower crops. Comput. Electron. Agric. 2016, 122, 67–73. [Google Scholar] [CrossRef]
- Martinez-Guanter, J.; Ribeiro, Á.; Peteinatos, G.G.; Pérez-Ruiz, M.; Gerhards, R.; Bengochea-Guevara, J.M.; Machleb, J.; Andújar, D. Low-cost three-dimensional modeling of crop plants. Sensors 2019, 19, 2883. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, P.; Guo, Y.; Li, B.; Zhu, J.; Ma, Y. Three-dimensional reconstruction and its precision evaluation of plant architecture based on multiple view stereo method. Trans. Chin. Soc. Agric. Eng. 2015, 31, 209–214. [Google Scholar]
- Pound, M.P.; French, A.P.; Murchie, E.H.; Pridmore, T.P. Automated recovery of three-dimensional models of plant shoots from multiple color images. Plant. Physiol. 2014, 166, 1688–1698. [Google Scholar] [CrossRef] [Green Version]
- Kato, A.; Schreuder, G.F.; Calhoun, D.; Schiess, P.; Stuetzle, W. Digital surface model of tree canopy structure from LIDAR data through implicit surface reconstruction. In Proceedings of the ASPRS 2007 Annual Conference, Tampa, FL, USA, 7–11 May 2007; Citeseer: Princeton, NJ, USA, 2007. [Google Scholar]
- Tahir, R.; Heuvel, F.V.D.; Vosselmann, G. Segmentation of point clouds using smoothness constraint. Int. Arch. Photogramm. Remote Sens. SPATIAL Inf. Sci. 2006, 36, 248–253. [Google Scholar]
- Ng, A.Y.; Jordan, M.I.; Weiss, Y. On spectral clustering: Analysis and an algorithm. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2002; pp. 849–856. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Marton, Z.C.; Beetz, M. Aligning point cloud views using persistent feature histograms. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3384–3391. [Google Scholar]
- Mehnert, A.; Jackway, P. An improved seeded region growing algorithm. Pattern Recognit. Lett. 1997, 18, 1065–1071. [Google Scholar] [CrossRef]
- Paulus, S.; Dupuis, J.; Mahlein, A.-K.; Kuhlmann, H. Surface feature based classification of plant organs from 3D laserscanned point clouds for plant phenotyping. BMC Bioinf. 2013, 14, 238. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Cao, Y.; Tang, X.-S.; Yan, S.; Cai, X. Leaf segmentation on dense plant point clouds with facet region growing. Sensors 2018, 18, 3625. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dey, D.; Mummert, L.; Sukthankar, R. Classification of plant structures from uncalibrated image sequences. In Proceedings of the 2012 IEEE Workshop on the Applications of Computer Vision (WACV), Breckenridge, CO, USA, 9–11 January 2012; pp. 329–336. [Google Scholar]
- Lalonde, J.F.; Vandapel, N.; Huber, D.F.; Hebert, M. Natural terrain classification using three-dimensional ladar data for ground robot mobility. J. Field Robot. 2006, 23, 839–861. [Google Scholar] [CrossRef]
- Gélard, W.; Herbulot, A.; Devy, M.; Debaeke, P.; McCormick, R.F.; Truong, S.K.; Mullet, J. Leaves segmentation in 3d point cloud. In International Conference on Advanced Concepts for Intelligent Vision Systems; Springer: Cham, Switzerland, 2017; pp. 664–674. [Google Scholar]
- Piegl, L.; Tiller, W. Symbolic operators for NURBS. Comput. Aided Design 1997, 29, 361–368. [Google Scholar] [CrossRef]
- Santos, T.T.; Koenigkan, L.V.; Barbedo, J.G.A.; Rodrigues, G.C. 3D plant modeling: Localization, mapping and segmentation for plant phenotyping using a single hand-held camera. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2014; pp. 247–263. [Google Scholar]
- Müller-Linow, M.; Pinto-Espinosa, F.; Scharr, H.; Rascher, U. The leaf angle distribution of natural plant populations: Assessing the canopy with a novel software tool. Plant Methods 2015, 11, 11. [Google Scholar] [CrossRef] [Green Version]
- Zhu, B.; Liu, F.; Zhu, J.; Guo, Y.; Ma, Y. Three-dimensional quantifications of plant growth dynamics in field-grown plants based on machine vision method. Trans. Chin. Soc. Agric. Mach. 2018, 49, 256–262. [Google Scholar]
- Sodhi, P.; Hebert, M.; Hu, H. In-Field Plant Phenotyping Using Model-Free and Model-Based Methods. Master’s Thesis, Carnegie Mellon University Pittsburgh, Pittsburgh, PA, USA, 2017. [Google Scholar]
- Hosoi, F.; Omasa, K. Estimating vertical plant area density profile and growth parameters of a wheat canopy at different growth stages using three-dimensional portable lidar imaging. ISPRS J. Photogramm. Remote Sens. 2009, 64, 151–158. [Google Scholar] [CrossRef]
- Cornea, N.D.; Silver, D.; Min, P. Curve-skeleton properties, applications, and algorithms. IEEE Trans. Vis. Comput. Graph. 2007, 13, 530. [Google Scholar] [CrossRef] [Green Version]
- Biskup, B.; Scharr, H.; Schurr, U.; Rascher, U. A stereo imaging system for measuring structural parameters of plant canopies. Plant Cell Environ. 2007, 30, 1299–1308. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Smith, G.; Jonckheere, I.; Coppin, P. Review of methods for in situ leaf area index (LAI) determination: Part II. Estimation of LAI, errors and sampling. Agric. For. Meteorol. 2004, 121, 37–53. [Google Scholar] [CrossRef]
- Hosoi, F.; Omasa, K. Voxel-based 3-D modeling of individual trees for estimating leaf area density using high-resolution portable scanning lidar. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3610–3618. [Google Scholar] [CrossRef]
- Liang, J.; Edelsbrunner, H.; Fu, P.; Sudhakar, P.V.; Subramaniam, S. Analytical shape computation of macromolecules: I. Molecular area and volume through alpha shape. Proteins Struct. Function Bioinf. 1998, 33, 1–17. [Google Scholar] [CrossRef]
- Chalidabhongse, T.; Yimyam, P.; Sirisomboon, P. 2D/3D vision-based mango’s feature extraction and sorting. In Proceedings of the 2006 the 9th International Conference on Control, Automation, Robotics and Vision, Singapore, 5–8 December 2006; pp. 1–6. [Google Scholar]
- SANTOS, T.; Ueda, J. Automatic 3D plant reconstruction from photographies, segmentation and classification of leaves and internodes using clustering. In Embrapa Informática Agropecuária-Resumo em anais de congresso (ALICE); Finnish Society of Forest Science: Vantaa, Finland, 2013. [Google Scholar]
- Embgenbroich, P. Bildbasierte Entwicklung Eines Dreidimensionalen Pflanzenmodells am Beispiel von Zea Mays. Master’s Thesis, Helmholtz Association of German Research Centers, Berlin, Germany, 2015. [Google Scholar]
- Lorensen, W.E.; Cline, H.E. Marching cubes: A high resolution 3D surface construction algorithm. ACM Siggraph Comput. Graph. 1987, 21, 163–169. [Google Scholar] [CrossRef]
- Song, Y.; Maki, M.; Imanishi, J.; Morimoto, Y. Voxel-based estimation of plant area density from airborne laser scanner data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, 38, W12. [Google Scholar] [CrossRef] [Green Version]
- Lati, R.N.; Filin, S.; Eizenberg, H. Plant growth parameter estimation from sparse 3D reconstruction based on highly-textured feature points. Precis. Agric. 2013, 14, 586–605. [Google Scholar] [CrossRef]
- Itakura, K.; Hosoi, F. Automatic leaf segmentation for estimating leaf area and leaf inclination angle in 3D plant images. Sensors 2018, 18, 3576. [Google Scholar] [CrossRef] [Green Version]
- Zhao, C. Big data of plant phenomics and its research progress. J. Agric. Big Data 2019, 1, 5–14. [Google Scholar]
- Zhou, J.; Guo, X.; Wu, S.; Du, J.; Zhao, C. Research progress on 3D reconstruction of plants based on multi-view images. China Agric. Sci. Technol. Rev. 2018, 21, 9–18. [Google Scholar]
- Marton, Z.C.; Rusu, R.B.; Beetz, M. On fast surface reconstruction methods for large and noisy point clouds. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3218–3223. [Google Scholar]
- Lou, L.; Liu, Y.; Han, J.; Doonan, J.H. Accurate multi-view stereo 3D reconstruction for cost-effective plant phenotyping. In International Conference Image Analysis and Recognition; Springer: Cham, Switzerland, 2014; pp. 349–356. [Google Scholar]
- Apelt, F.; Breuer, D.; Nikoloski, Z.; Stitt, M.; Kragler, F. Phytotyping4D: A light-field imaging system for non-invasive and accurate monitoring of spatio-temporal plant growth. Plant J. 2015, 82, 693–706. [Google Scholar] [CrossRef]
- Itakura, K.; Hosoi, F. Estimation of leaf inclination angle in three-dimensional plant images obtained from lidar. Remote Sens. 2019, 11, 344. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; Liu, Z.; Guo, B. Three-dimensional digital image correlation method based on a light field camera. Opt. Lasers Eng. 2019, 116, 19–25. [Google Scholar] [CrossRef]
- Hu, Y. Research on Three-Dimensional Reconstruction and Growth Measurement of Leafy Crops based on Depth Camera; Zhejiang University: Hangzhou, China, 2018. [Google Scholar]
- Henke, M.; Junker, A.; Neumann, K.; Altmann, T.; Gladilin, E. Automated alignment of multi-modal plant images using integrative phase correlation approach. Front. Plant Sci. 2018, 9, 1519. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Myint, K.N.; Aung, W.T.; Zaw, M.H. Research and analysis of parallel performance with MPI odd-even sorting algorithm on super cheap computing cluster. In Seventeenth International Conference on Computer Applications; University of Computer Studies, Yangon under Ministry of Education: Yangon, Myanmar, 2019; pp. 99–106. [Google Scholar]
- Dong, J.; Burnham, J.G.; Boots, B.; Rains, G.; Dellaert, F. 4D crop monitoring: Spatio-temporal reconstruction for agriculture. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3878–3885. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Liu, W.; Sun, J.; Li, W.; Hu, T.; Wang, P. Deep learning on point clouds and its application: A survey. Sensors 2019, 19, 4188. [Google Scholar] [CrossRef] [PubMed] [Green Version]






| Camera | Bumblebee2-03S2 | Zed2 | PM802(PERCIPIO) |
|---|---|---|---|
| RGB resolution and frame rate | 648 × 488, 48 fps 1024 × 768, 18 fps | 4416 × 1242, 15 fps 3480 × 1080, 30 fps 2560 × 720, 60 fps | 2560 × 1920, 1 fps 1280 × 960, 1 fps 640 × 480, 1 fps |
| Depth resolution and frame rate | 648 × 488, 48 fps | 2560 × 720, 15 fps (Ultra mode) | 1280 × 1920, 1 fps 640 × 480, 1 fps |
| Baseline | 120 mm | 120 mm | 450 mm |
| Focal length | 2.5 mm | 2.12 mm | N.A. |
| Size (mm) | 157 × 36 × 47.4 | 175 × 30 × 33 | 538.4 × 85.5 × 89.6 |
| Weight (g) | 342 | 135 | 2000 |
| Measurable range (m) | N.A. | 0.5–20 | 0.85–4.2 |
| Field of view (vertical × horizontal) | 66° × 43° | 110° × 70° | 56° × 46° |
| Accuracy | N.A. | <1% up to 3 m <5% up to 15 m | 0.04–1% |
| Special or limitations | Extendable | 1. Inertial Measurement Unit (IMU) 2. Depending on high-performance equipment | 1. Protection: IP54 2. Applying for industry equipment |
| Price ($) | 116 | 449 | 11766 |
| Project | Colmap | GPUlma + Fusibile | HPMVS | MICMAC | MVE | OpenMVS | PMVS |
|---|---|---|---|---|---|---|---|
| Language | C++ CUDA | C++ CUDA | C++ | C++ | C++ | C++ CUDA | C++ CUDA |
| Name | Function | Company |
|---|---|---|
| ContextCapture | Create detailed 3D models quickly with simple photos | Bentley Acute3D |
| PhotoMesh | Construct full-element, fine, textured three-dimensional mesh models from a set of standard, disordered two-dimensional photographs. | SkyLine |
| StreetFactory | Enabling rapid and fully automatic process of images from any aerial or street camera for the generation of a 3D textured database and distortion-free imagery | AirBus |
| PhotoScan | Performing photogrammetric processing of digital images and generates 3D spatial data to be used in geographic information system (GIS) applications | AgiSoft |
| Pix4DMapper | Transform images in digital maps and 3D models. | Pix4D |
| RealityCapture | Extracts accurate 3D models from a set of ordinary images and/or laser scans | RealityCapture |
| Camera | CAMCUBE 3 | SR-4000 | Kinect V2 | IFM Efector 3D (O3D303) |
|---|---|---|---|---|
| Manufacturer | PMD Technologies GmbH | Mesa Imaging AG | Microsoft | IFM |
| Principle | Continuous-wave modulation | Continuous-wave modulation | Continuous-wave modulation | Continuous-wave modulation |
| V (vertical) × H (horizontal) field of view | 40° × 40° | N.A. | 70° × 60° | 60° × 45° |
| Frame rate and depth resolution | 40 fps, 200 × 200 | 54 fps, 176 × 144 | 30 fps, 512 × 424 | 40 fps, 352 × 264 |
| Measurable range (m) | 0.03–7.5 | 0.03–7.5 | 0.5–5 | 0.03–8 |
| Focal length (m) | 0.013 | 0.008 | 0.525 | N.A. |
| Signal wavelength (nm) | 870 | 850 | 827–850 | 850 |
| Advantages | Strong resistance to ambient light, high precision | High precision and light weight | Rich development resource bundle | Not affected by light, detection of scenes and object without 3D images of motion blur |
| Disadvantages | High cost | Not for outdoor light | Low measurement accuracy; not suitable for very close object recognition | High cost |
| Performance Parameters | LMS 111 [35] | UTM30LX [36,37] | LMS291-S05 [38] | Velodyne HDL64E-S3 [39] | FARO Focus 3D X 330 HDR [40] |
|---|---|---|---|---|---|
| Measurement range (m) | 0.5–20 | 0.1–30 | 0.2–80 | 0.02–120 | 0.6–330 |
| Field of view (vertical × horizontal) | 270° (H) | 270° (H) | 180° (H) | 26.9° × 360° (V × H) | 300° × 360° (V × H) |
| Light source | Infrared (905 nm) | Laser Semicon-ductor (905 nm) | Infrared (905 nm) | Infrared (905 nm) | Infrared (1550 nm) |
| Scanning frequency (Hz) | 25 | 40 | 75 | 20 | 97 |
| Angular resolution (°) | 0.5 | 0.25 | 0.25 | 0.35 | 0.009 |
| Systematic error | ±30 mm | N.A. | ±35 mm | N.A. | ±2 mm |
| Statistical error | ±12 mm | N.A. | ±10 mm | N.A. | N.A. |
| Laser class | Class 1 (IEC 60825-1) | Class 1 | Class 1 (EN/IEC 60825-1) | Class 1 (Eye-safe) | Class 1 |
| Weight (kg) | 1.1 | 0.21 | 4.5 | 12.7 | 5.2 |
| LiDAR specifications | 2D | 2D | 2D | 3D | 3D |
| Performance Parameters | Kinect V1 | RealSense SR300 | Orbbec Astra | Occipital Structure |
|---|---|---|---|---|
| Measurable range (m) | 0.5–4.5 | 0.2–2 | 0.6–8 | 0.4–3.5 |
| V × H field of view | 57° × 43° | 71.5° × 55° | 60° × 49.5° | 58° × 45° |
| Frame rate and depth resolution | 30 fps, 320 × 240 | 60 fps, 640 × 480 | 30 fps, 640 × 480 | 60 fps, 320 × 240 |
| Price ($) | 199 | 150 | 150 | 499 |
| Size (mm) | 280 × 64 × 38 | 14 × 20 × 4 | 165 × 30 × 40 | 119.2 × 28 × 29 |
| Category | Advantages | Disadvantages |
|---|---|---|
| Binocular stereo vision technology [49] | (1) Get depth image quickly and plant’s slight movement does not affect the precision (2) Low cost (3) Obtains deep and color data at the same time (4) No further auxiliary equipment | (1) Affected by scene lighting (2) High computer performance and complicated algorithm (3) Complex 3D scene reconstruction (4) Not for homogeneous color (5) False boundary problem |
| Structure-from- motion technology [50] | (1) Operates easily and low cost (2) Open source and commercial software for 3D reconstruction (3) Suitable for aerial applications, excellent portability | (1) Not suitable for real-time applications |
| Time-of-flight technology [49,51] | (1) No external light (2) Single viewpoint to compute depth | (1) Poor depth resolution (2) Not work in bright light (3) Short distance measurement |
| LiDAR scanning technology | (1) Fast image collection (2) Can work at night (3) Can work in severe weather (rain, snow, fog, etc.) for advanced laser scanning (4) Works over long distances (more than 100 m) | (1) Poor edge detection (3D point clouds of edges of plant organs like leaves, for instance, are blurry) (2) Needs warm-up time (3) Need for movement to obtain the depth data of the detected object |
| Structured light technology | (1) Accuracy and high depth resolution (2) Get depth image quickly (3) Captures large area | (1) Indoor plant imaging (2) Stationary object |
| Type | Name | Function | Reference URL |
|---|---|---|---|
| Open source library | Point Cloud Library | Large cross-platform open-source C++ programming library providing a full set of point cloud data processing modules to implement a large number of general point-cloud-related algorithms and efficient data structures | http://pointclouds.org/ |
| Point Data Abstraction Library | C++ BSD (the Berkeley software distribution) library for translation and manipulation of point cloud data | https://pdal.io/ | |
| Liblas | Libraries for reading and writing plain LiDAR formats | https://liblas.org/ | |
| Entwine | Data organization library for a large number of point clouds, designed to manage hundreds of millions of point and desktop-scale point clouds | https://github.com/connormanning/entwine/ | |
| PotreeConverter | Data organization library that generates data for data used in Potree (a large network-based point cloud renderer) network viewer | https://github.com/potree/PotreeConverter | |
| Open source software | Paraview | Multi-platform data analysis and visualization application | https://www.paraview.org/ |
| Meshlab | Open source for unstructured 3D triangular mesh processing and editing; portable and scalable system | http://meshlab.sourceforge.net/ | |
| CloudCompare | 3D point cloud and grid processing software open source project | http://www.danielgm.net/cc/ | |
| OpenFlipper | Multi-platform application and programming framework designed to process, model, and render geometric data | http://www.openflipper.org/ | |
| PotreeDesktop | Desktop/portable version of the web-based point cloud viewer Potree | https://github.com/potree/PotreeDesktop | |
| Point Cloud Magic | The first set of free point cloud data processing “point cloud cube” software developed by the Chinese Academy of Sciences for remote sensing of the earth, LiDAR statistical parameters, extraction of vegetation height, biomass, etc., based on statistical regression methods and single tree segmentation | http://lidar.radi.ac.cn/ |
| RMSE | Cotton [123] | Sunflower [123] | Black Eggplant [123] | Tomato [123] | Maize [30] | Palm Tree Seedling [124] | Leafy Vegetable [27] |
|---|---|---|---|---|---|---|---|
| Plant height | 1.7 cm | 1.1 cm | 1 cm | 1.3 cm | 0.058 m | / | 0.6957 cm |
| Leaf area (cm2) | 80 | 30 | 10 | 10 | / | 3.23 | 72.43 |
| Leaf inclination angles (°) | / | / | / | / | 3.455 | 2.68 | / |
| Stem diameter | / | / | / | / | 5.3 mm | / | / |
| Volume | / | / | / | / | / | / | 2.522 cm3 |
| LAD | PAD | |
|---|---|---|
| Tree | MAPE: 17.2–55.3% [116] | R2: 0.818 [122] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zhang, Y.; Gu, R. Research Status and Prospects on Plant Canopy Structure Measurement Using Visual Sensors Based on Three-Dimensional Reconstruction. Agriculture 2020, 10, 462. https://doi.org/10.3390/agriculture10100462
Wang J, Zhang Y, Gu R. Research Status and Prospects on Plant Canopy Structure Measurement Using Visual Sensors Based on Three-Dimensional Reconstruction. Agriculture. 2020; 10(10):462. https://doi.org/10.3390/agriculture10100462
Chicago/Turabian StyleWang, Jizhang, Yun Zhang, and Rongrong Gu. 2020. "Research Status and Prospects on Plant Canopy Structure Measurement Using Visual Sensors Based on Three-Dimensional Reconstruction" Agriculture 10, no. 10: 462. https://doi.org/10.3390/agriculture10100462
APA StyleWang, J., Zhang, Y., & Gu, R. (2020). Research Status and Prospects on Plant Canopy Structure Measurement Using Visual Sensors Based on Three-Dimensional Reconstruction. Agriculture, 10(10), 462. https://doi.org/10.3390/agriculture10100462





