Modelling the Evolution of COVID-19 in High-Incidence European Countries and Regions: Estimated Number of Infections and Impact of Past and Future Intervention Measures
Abstract
1. Introduction
2. Methods
2.1. Data Collection
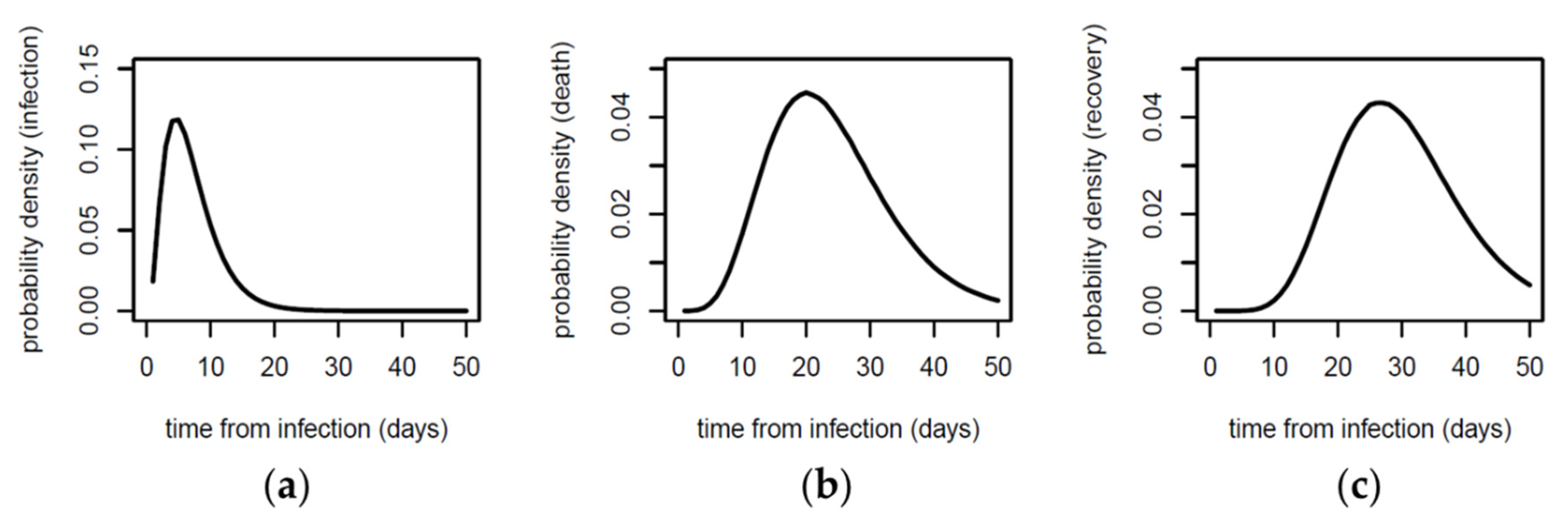
2.2. Estimating New Infections and Deaths over Time
2.3. Model Fitting
2.4. Predictive Model from a Given Set of Parameters
2.5. Estimating Active Cases from Model Predictions
3. Results
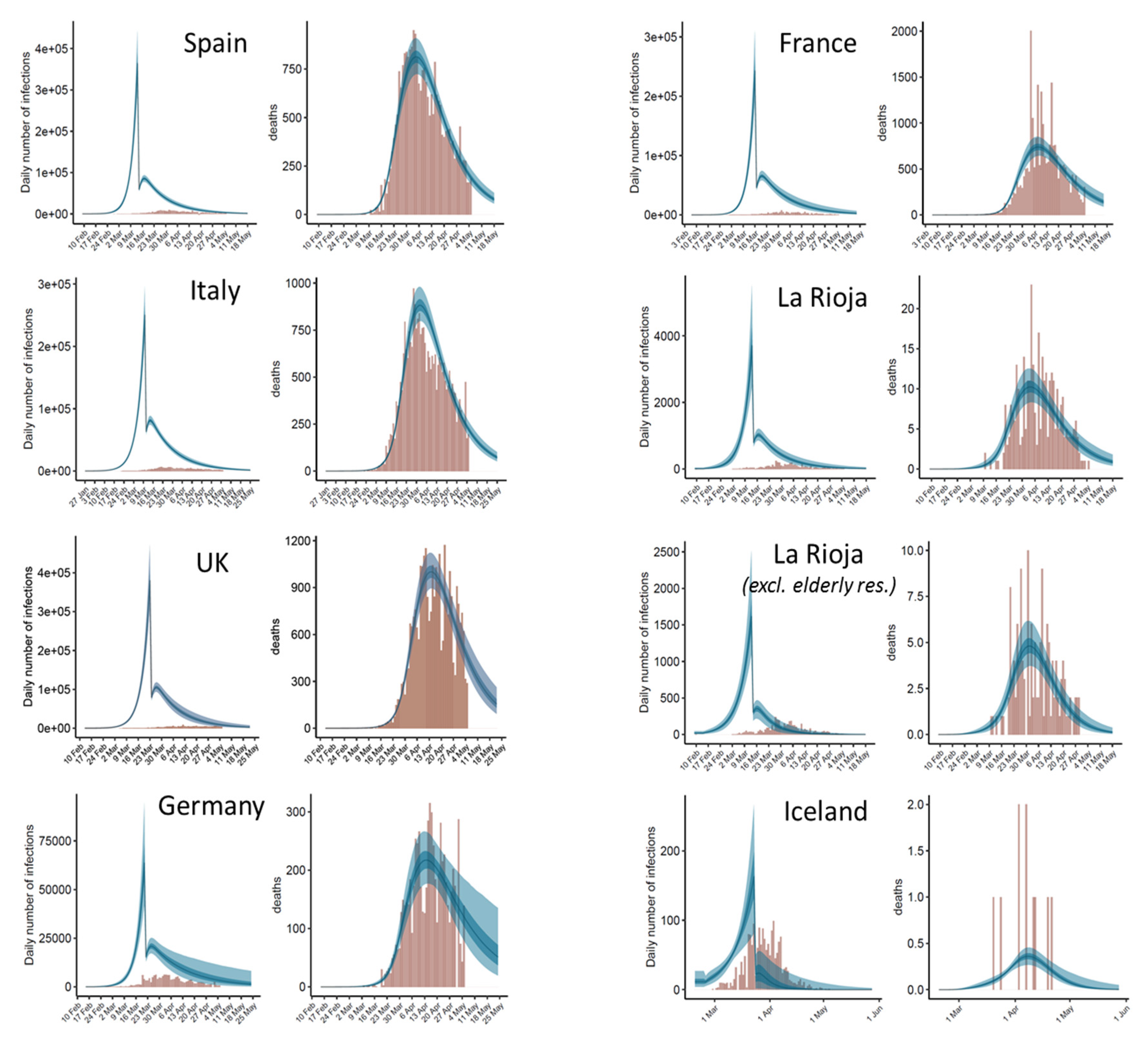
3.1. Model Suggests a Significant Impact of Intervention Measures on Disease Transmission
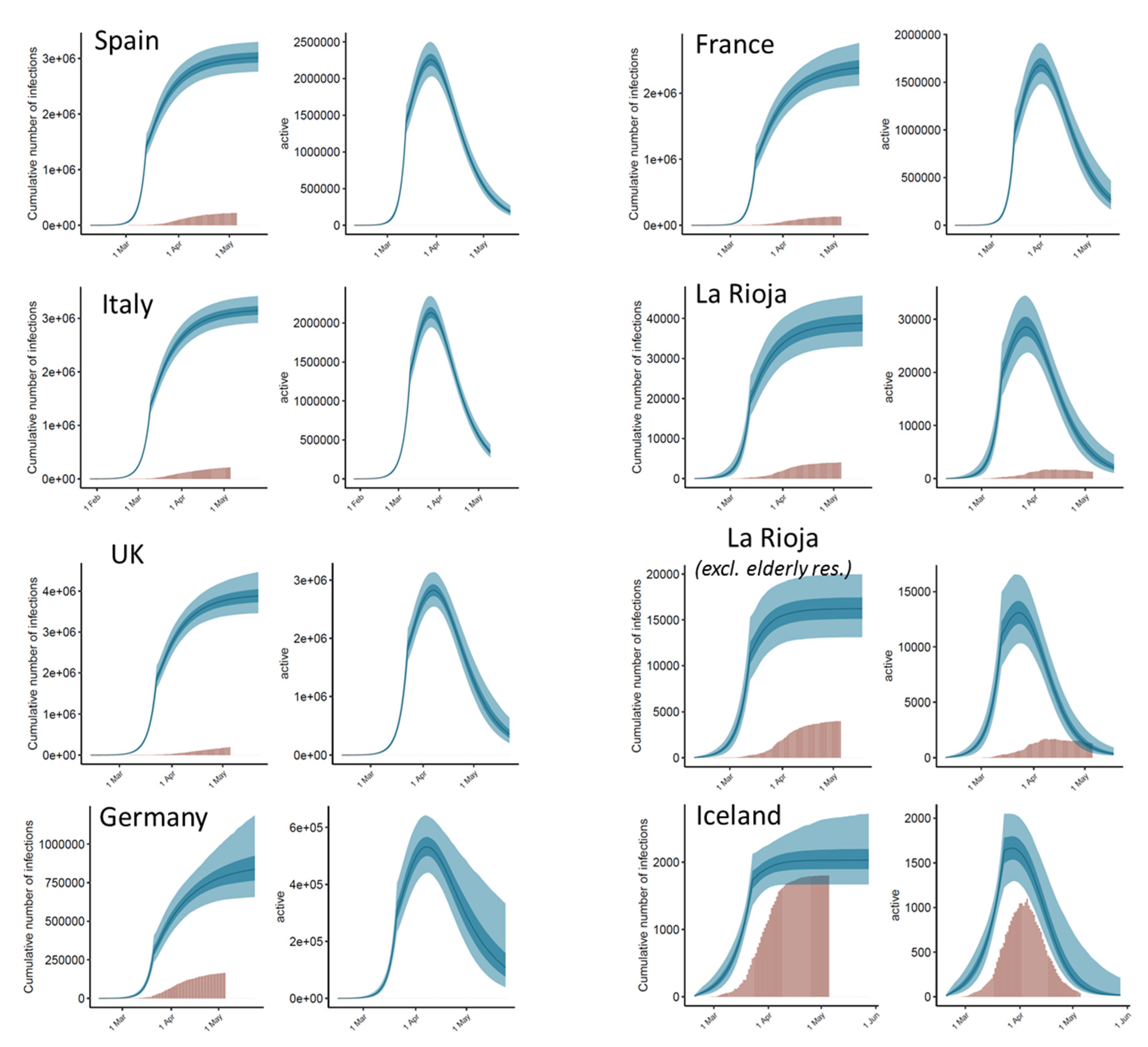
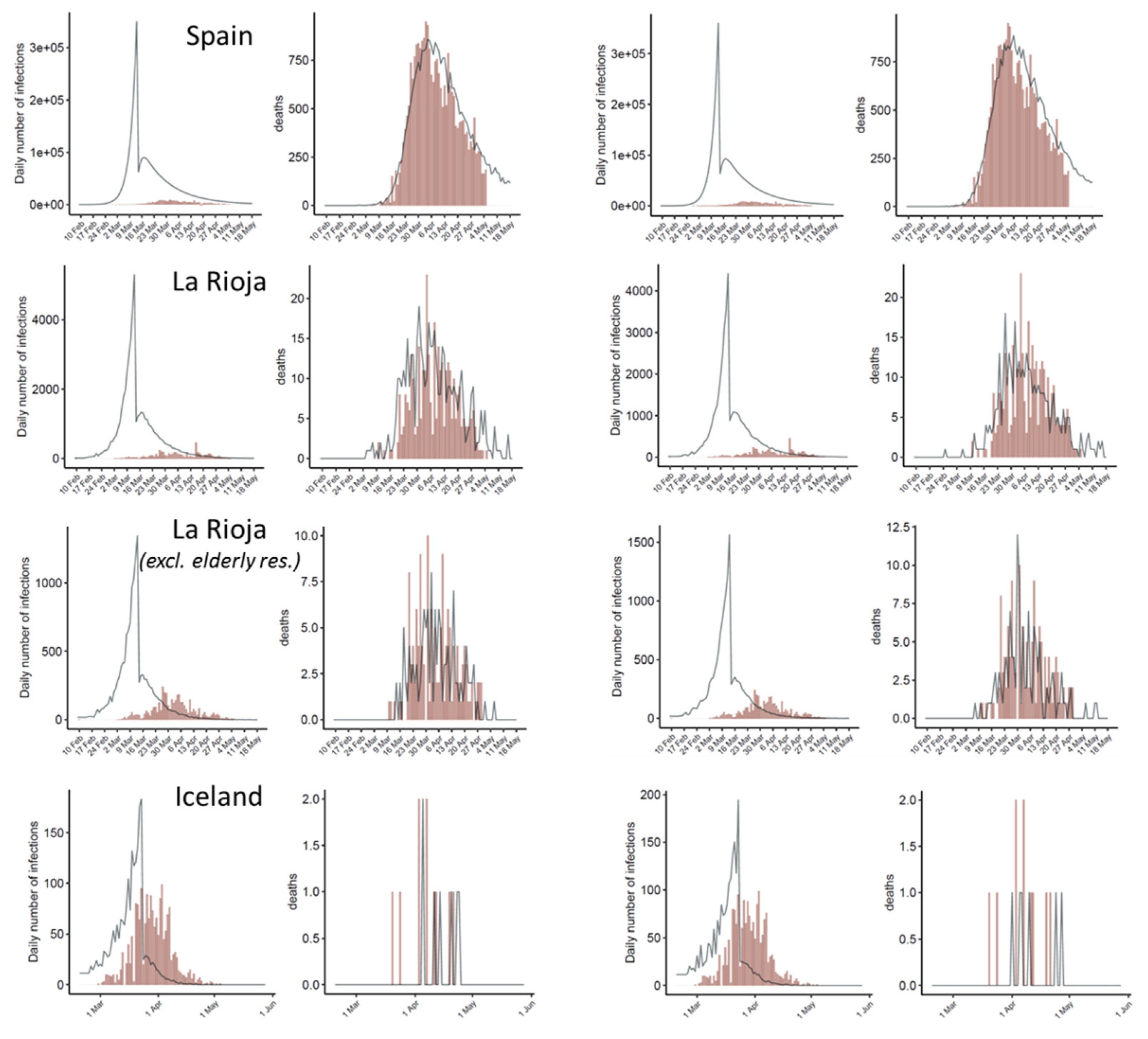
3.2. Estimated Number of Total Infections and Active Cases
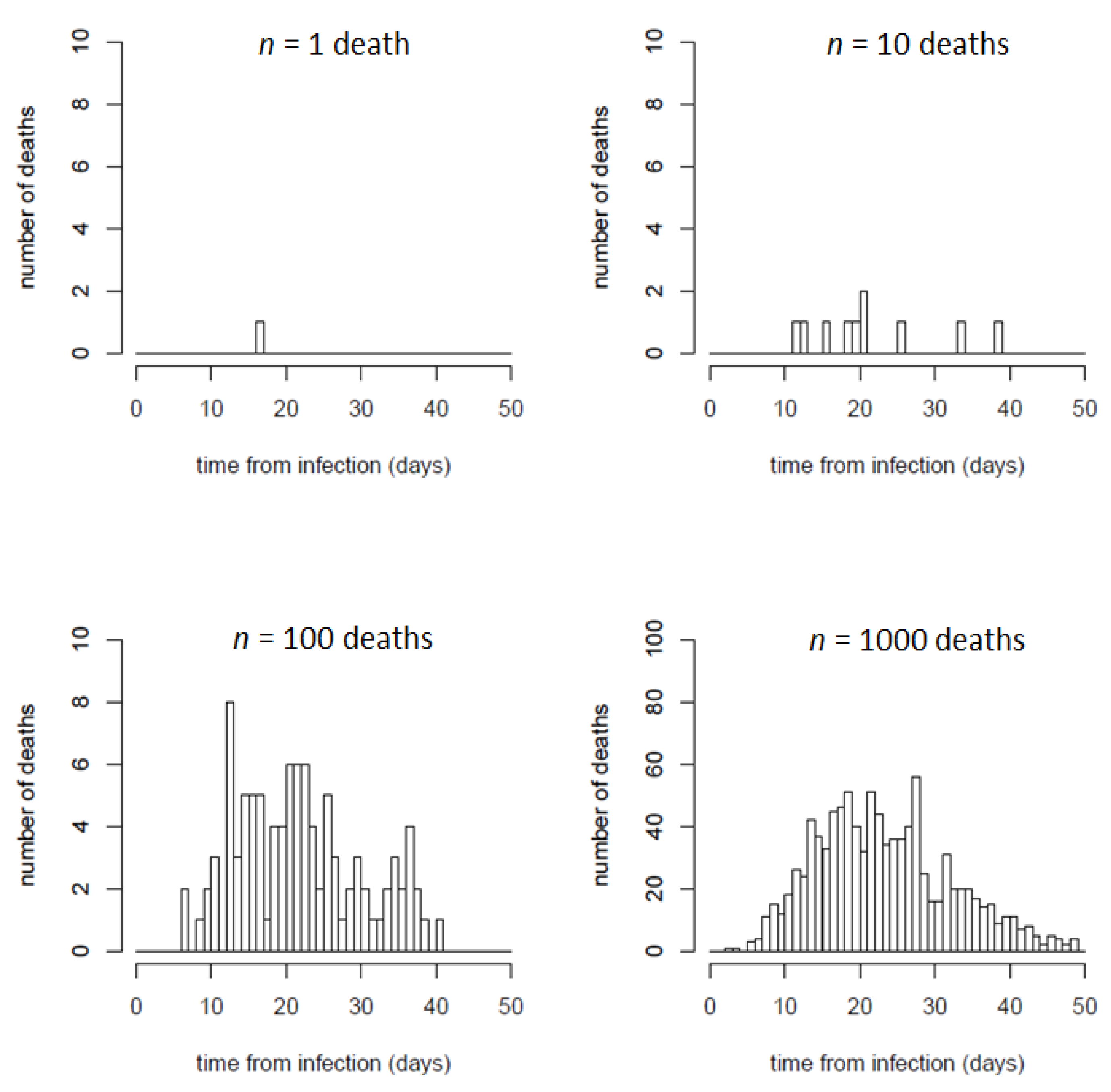
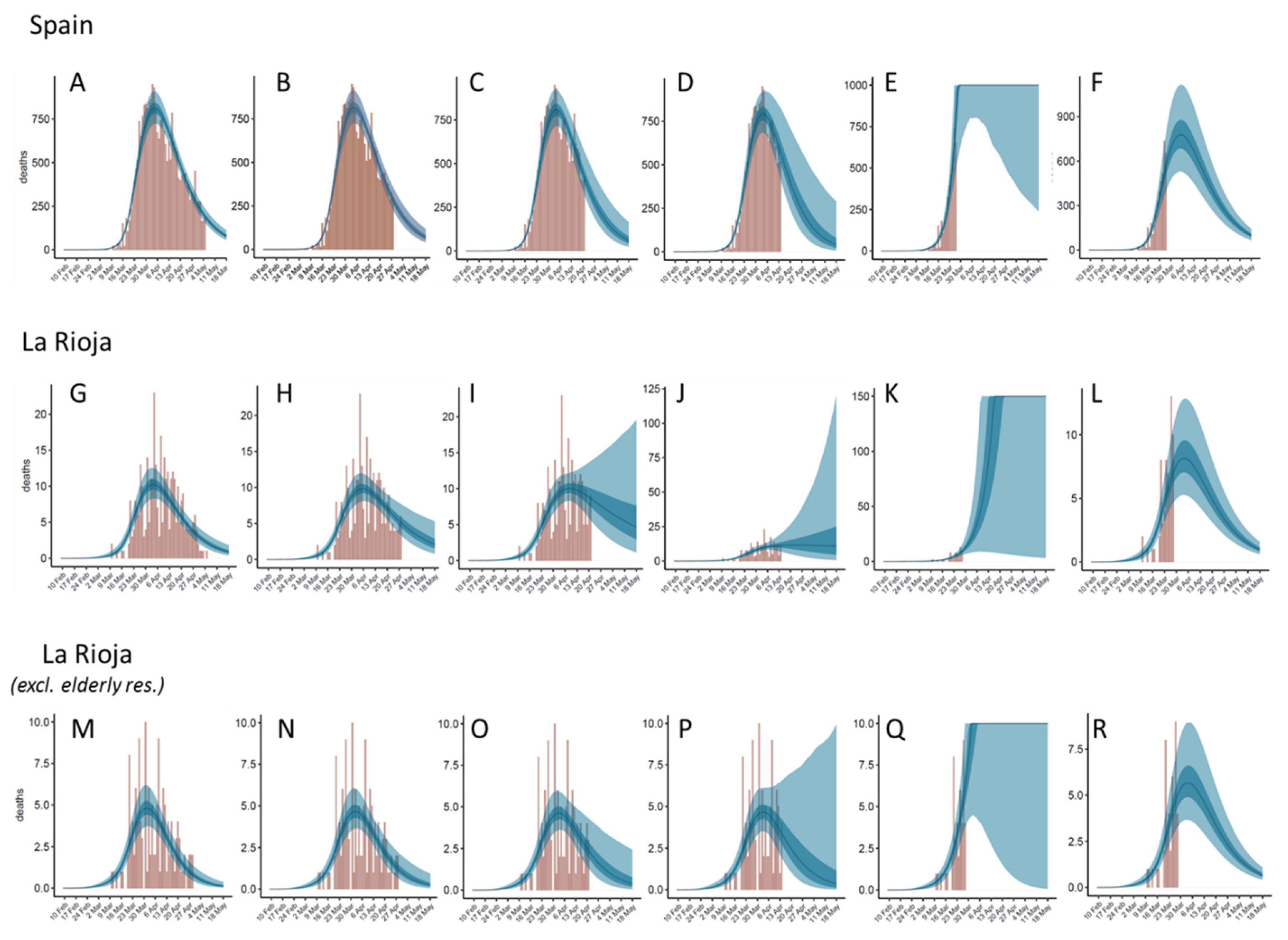
3.3. Predicting Discrete Distributions of Infections and Deaths
3.4. The Reliability of the Predictions Depends on the Stage of the Epidemic Outbreak
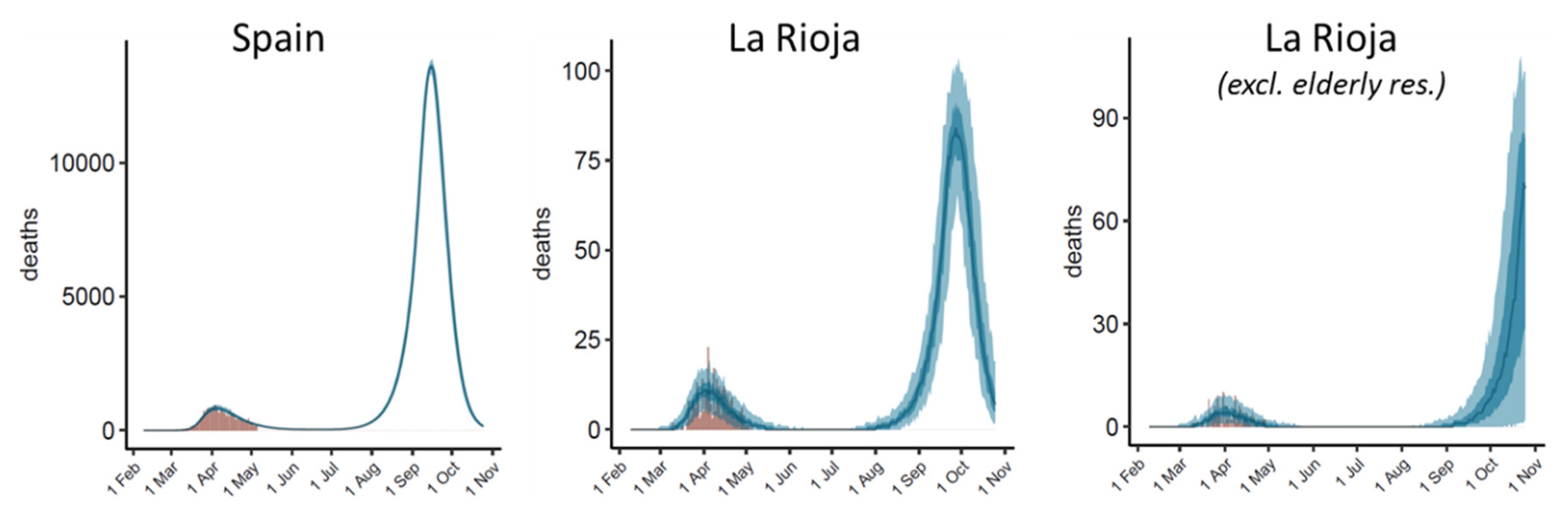
3.5. Modelling Long-Term Disease Progression in Different Scenarios
4. Discussion
5. Conclusions
Supplementary Materials
Funding
Conflicts of Interest
References
- World Health Organization. Coronavirus Disease 2019 (COVID-19) Situation Report—106 (WHO, 2020). Available online: https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200505covid-19-sitrep-106.pdf?sfvrsn=47090f63_2 (accessed on 5 May 2020).
- Kissler, S.M.; Tedijanto, C.; Goldstein, E.; Grad, Y.H.; Lipsitch, M. Projecting the transmission dynamics of SARS-CoV-2 through the postpandemic period. Science. (in press). [CrossRef]
- Li, R.; Pei, S.; Chen, B.; Song, Y.; Zhang, T.; Yang, W.; Shaman, J. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV2). Science. (in press). [CrossRef]
- Flaxman, S.; Mishra, S.; Gandy, A.; Unwin, H.J.T.; Coupland, H.; Mellan, T.; Zhu, H.; Berah, T.; Eaton, J.; Perez Guzman, P.; et al. (2020) Estimating the Number of Infections and the Impact of Non-Pharmaceutical Interventions on COVID-19 in 11 European Countries. Imperial College London, MRC Centre for Global Infectious Disease Analysis, Report 13 (30 March 2020). Available online: https://www.imperial.ac.uk/mrc-global-infectious-disease-analysis/covid-19/report-13-europe-npi-impact/ (accessed on 5 May 2020).
- Google COVID-19 Community Mobility Reports. Available online: https://www.google.com/covid19/mobility/ (accessed on 5 May 2020).
- Ferguson, N.; Laydon, D.; Nedjati-Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunubá, Z.; Cuomo-Dannenburg, G.; et al. (2020) Impact of Non-Pharmaceutical Interventions (NPIs) to Reduce COVID-19 Mortality and Healthcare Demand. Imperial College London, MRC Centre for Global Infectious Disease Analysis, Report 9. Available online: https://www.imperial.ac.uk/mrc-global-infectious-disease-analysis/news--wuhan-coronavirus/report-9-impact-of-npis-on-covid-19/ (accessed on 5 May 2020).
- Verity, R.; Okell, L.C.; Dorigatti, I.; Winskill, P.; Whittaker, C.; Imai, N.; Cuomo-Dannenburg, G.; Thompson, H.; Walker, P.G.; Fu, H.; et al. Estimates of the severity of coronavirus disease 2019: A model-based analysis. Lancet Infect. Dis. (in press). [CrossRef]
- Lourenço, J.; Paton, R.; Ghafari, M.; Kraemer, M.; Thompson, C.; Simmonds, P.; Klenerman, P.; Gupta, S. Fundamental principles of epidemic spread highlight the immediate need for large-scale serological surveys to assess the stage of the SARS-CoV-2 epidemic. medRxiv 2020. [Google Scholar]
- Oke, J.; Heneghan, C. Global Covid-10 Case Fatality Rates. CEBM Research. Report 17 March 2020 (updated 30 April 2020). 2020. Available online: https://www.cebm.net/covid-19/global-covid-19-case-fatality-rates/ (accessed on 5 May 2020).
- City of New York. COVID-19: Data. Available online: https://www1.nyc.gov/site/doh/covid/covid-19-data.page (accessed on 5 May 2020).
- Robert Koch Institute COVID-19 Daily Situation Report 5 May 2020. Available online: https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Situationsberichte/2020-05-05-en.pdf?__blob=publicationFile (accessed on 5 May 2020).
- Robert Koch Institute COVID-19 Daily Situation Report 22 April 2020. Available online: https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Situationsberichte/2020-04-22-en.pdf?__blob=publicationFile (accessed on 5 May 2020).
- Directorate of Health and the Department of Civil Protection and Emergency Management. Available online: https://www.covid.is/data (accessed on 5 May 2020).
- Spanish Health Ministry. Press Release 27 April 2020. Available online: https://www.mscbs.gob.es/en/gabinete/notasPrensa.do?metodo=detalle&id=4883 (accessed on 5 May 2020).
- Gobierno de La Rioja. Available online: https://actualidad.larioja.org/coronavirus/datos (accessed on 5 May 2020).
- He, X.; Lau, E.H.Y.; Wu, P.; Deng, X.; Wang, J.; Hao, X.; Lau, Y.; Wong, J.Y.; Guan, Y.; Tan, X.; et al. Temporal dynamics in viral shedding and transmissibility of COVID-19. medRxiv 2020. [Google Scholar]
- Linton, N.M.; Kobayashi, T.; Yang, Y.; Hayashi, K.; Akhmetzhanov, A.R.; Jung, S.M.; Yuan, B.; Kinoshita, R.; Nishiura, H. Incubation Period and Other Epidemiological Characteristics of 2019 Novel Coronavirus Infections with Right Truncation: A Statistical Analysis of Publicly Available Case Data. J. Clin. Med. 2020, 9, 538. [Google Scholar] [CrossRef] [PubMed]
- Nishiura, H.; Lintona, N.M.; Akhmetzhanov, A.R. Serial interval of novel coronavirus (COVID-19) infections. Int. J. Inf. Dis. 2020, 93, 284–286. [Google Scholar] [CrossRef] [PubMed]
- Lauer, S.A.; Grantz, K.H.; Bi, Q.; Jones, F.K.; Zheng, Q.; Meredith, H.R.; Azman, A.S.; Reich, N.G.; Lessler, J. The Incubation Period of Coronavirus Disease 2019 (COVID-19) From Publicly Reported Confirmed Cases: Estimation and Application. Ann. Int. Med. (in press). [CrossRef] [PubMed]
- Bastolla, U. How lethal is the novel coronavirus, and how many undetected cases there are? The importance of being tested. medRxiv 2020. [Google Scholar]
- Gatto, M.; Bertuzzo, E.; Mari, L.; Miccoli, S.; Carraro, L.; Casagrandi, R.; Rinaldo, A. Spread and dynamics of the COVID-19 epidemic in Italy: Effects of emergency containment measures. Proc. Natl. Acad. Sci. USA 2020, 117, 10484–10491. [Google Scholar] [CrossRef] [PubMed]
- Díez-Fuertes, F.; Caballero, M.I.; Monzón, S.; Jiménez, P.; Varona, S.; Cuesta, I.; Zaballos, Á.; Thomson, M.M.; Jiménez, M.; Pérez, J.G.; et al. Phylodynamics of SARS-CoV-2 transmission in Spain. bioRxiv 2020. [Google Scholar]
| Country/Region | Total Detected Cases | Cases per 100 k People | Total Reported Deaths |
|---|---|---|---|
| Spain | 219,329 | 469 | 25,613 |
| Italy | 211,938 | 351 | 29,079 |
| UK | 190,584 | 287 | 28,734 |
| Germany | 163,860 | 198 | 6831 |
| France | 131,863 | 197 | 25,201 |
| La Rioja (Spain) | 3969 | 1256 | 336 |
| La Rioja (Spain) 1 | 2988 | 952 | 143 |
| Iceland | 1799 | 509 | 10 |
| Country/Region | Time of Intervention | Days from First 100 Cases to Intervention Time | IFR |
|---|---|---|---|
| Spain | 14 March | 11 | 0.926% |
| Italy | 11 March | 16 | 1.090% |
| UK | 24 March | 18 | 0.919% |
| Germany | 22 March | 20 | 1.093% |
| France | 17 March | 15 | 1.153% |
| La Rioja | 14 March | 5 | 0.926% |
| Iceland | 24 March | 8 | 0.556% |
| Country/Region | R0 | Rt after Intervention | Estimated Infections in First 6 Days |
|---|---|---|---|
| Spain | 4.82 (4.18–5.51) | 0.58 (0.52–0.65) | 396 (153–819) |
| Italy | 3.14 (2.93–3.38) | 0.65 (0.60–0.70) | 623 (370–964) |
| UK | 3.60 (3.26–3.95) | 0.60 (0.50–0.70) | 749 (396–1276) |
| Germany | 3.68 (2.91–4.57) | 0.71 (0.54–0.89) | 314 (70–876) |
| France | 4.47 (3.93–5.06) | 0.64 (0.55–0.74) | 113 (43–242) |
| La Rioja | 3.29 (2.41–4.48) | 0.57 (0.45–0.70) | 72 (8–239) |
| La Rioja 1 | 2.55 (2.06–3.34) | 0.41 (0.21–0.59) | 123 (27–279) |
| Iceland | 1.84 (1.37–2.38) | 0.26 (0.01–0.69) | 75 (24–162) |
| Country/Region | Estimated Total Infections | Detection Rate | % Population Infected | Estimated Active Cases |
|---|---|---|---|---|
| Spain | 2990K (2742K–3269K) | 7.3% (6.7–8.0%) | 6.4% (5.9–7.0%) | 415K (329K–538K) |
| Italy | 3094K (2868K–3358K) | 6.9% (6.3–7.4%) | 5.1% (4.7–5.6%) | 445K (365K–551K) |
| UK | 3800K (3406K–4292K) | 5.0% (4.4–5.6%) | 5.6% (5.0–6.3%) | 998K (739K–1369K) |
| Germany | 793K (641K–1024K) | 20.6% (16.0–25.6%) | 0.9% (0.8–1.2%) | 245K (142K–451K) |
| France | 2351K (2089K–2693K) | 5.6% (4.9–6.3%) | 3.6% (3.2–4.1%) | 482K (341K–715K) |
| La Rioja | 38,505 (32,850–45,155) | 10.3% (8.8–12.1%) | 12.2% (10.4–14.3%) | 4746 (2821–8088) |
| La Rioja 1 | 16,205 (13,095–19,972) | 18.4% (15.0–22.8%) | 5.2% (4.2–6.4%) | 945 (464–2059) |
| Iceland | 2029 (1669–2647) | 88.7% (68.0–100%) | 0.6% (0.5–0.7%) | 141 (78–605) |
| Country/Region | Forecast Start Time | R0 | Rt | Deaths 29 April–5 May |
|---|---|---|---|---|
| Spain | 1791 (real) | |||
| 5 May (last day, original model) | 4.82 (4.18–5.51) | 0.58 (0.52–0.65) | 1653 (1386–1980) | |
| 28 April (1 week to last) | 4.87 (4.20–5.63) | 0.57 (0.48–0.65) | 1562 (1178–2048) | |
| 21 April (2 weeks to last) | 4.88 (4.13–5.69) | 0.54 (0.40–0.70) | 1470 (853–2466) | |
| 14 April (3 weeks to last) | 4.90 (4.03–5.84) | 0.50 (0.23–0.78) | 1344 (430–3435) | |
| 27 March (1 week to peak) | 4.08 (3.28–5.06) | 2.99 (0.78–4.37) | off-limits (2972–off) | |
| 27 March (1 week to peak) locked Rt | 4.56 (3.57–5.66) | 0.625 | 1864 (1223–2666) | |
| La Rioja | 10 (real) | |||
| 5 May (last day, original model) | 3.29 (2.41–4.48) | 0.57 (0.45–0.70) | 19 (13–28]) | |
| 28 April (1 week to last) | 3.00 (2.33–4.17) | 0.71 (0.55-0.88) | 31 (18–50) | |
| 21 April (2 weeks to last) | 2.81 (2.24–3.83) | 0.84 (0.61–1.10) | 52 (22–111) | |
| 14 April (3 weeks to last) | 2.72 (2.17–3.74) | 0.98 (0.54–1.44) | 108 (16–358) | |
| 28 March (1 week to peak) | 2.76 (2.22–3.69) | 2.29 (0.80–3.35) | off-limits (37-off) | |
| 28 March (1 week to peak) locked Rt | 2.86 (2.22–4.00) | 0.625 | 19 (11–29) | |
| La Rioja (excluding elderly residences) | 2 (real) | |||
| 5 May (last day, original model) | 2.55 (2.06–3.34) | 0.41 (0.21–0.59) | 5 (2–8) | |
| 28 April (1 week to last) | 2.46 (1.97–3.15) | 0.51 (0.29–0.72) | 7 (3–13) | |
| 21 April (2 weeks to last) | 2.45 (1.93–3.14) | 0.58 (0.28–0.87) | 10 (3–24) | |
| 14 April (3 weeks to last) | 2.44 (1.87–3.12) | 0.58 (0.14–1.10) | 13 (2–57) | |
| 28 March (1 week to peak) | 2.53 (2.04–3.34) | 1.88 (0.32–2.88) | off-limits (3–off) | |
| 28 March (1 week to peak) locked Rt | 2.61 (2.06–3.59) | 0.625 | 13 (8–20) | |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández-Recio, J. Modelling the Evolution of COVID-19 in High-Incidence European Countries and Regions: Estimated Number of Infections and Impact of Past and Future Intervention Measures. J. Clin. Med. 2020, 9, 1825. https://doi.org/10.3390/jcm9061825
Fernández-Recio J. Modelling the Evolution of COVID-19 in High-Incidence European Countries and Regions: Estimated Number of Infections and Impact of Past and Future Intervention Measures. Journal of Clinical Medicine. 2020; 9(6):1825. https://doi.org/10.3390/jcm9061825
Chicago/Turabian StyleFernández-Recio, Juan. 2020. "Modelling the Evolution of COVID-19 in High-Incidence European Countries and Regions: Estimated Number of Infections and Impact of Past and Future Intervention Measures" Journal of Clinical Medicine 9, no. 6: 1825. https://doi.org/10.3390/jcm9061825
APA StyleFernández-Recio, J. (2020). Modelling the Evolution of COVID-19 in High-Incidence European Countries and Regions: Estimated Number of Infections and Impact of Past and Future Intervention Measures. Journal of Clinical Medicine, 9(6), 1825. https://doi.org/10.3390/jcm9061825





