Morphological State Transition Dynamics in EGF-Induced Epithelial to Mesenchymal Transition
Abstract
1. Introduction
2. Methods
2.1. Cell Lines and Culture Conditions
2.2. Phalloidin-FITC Staining
2.3. Immunofluorescence
2.4. Quantitative PCR
2.5. Quantitative Image Analysis
2.6. Migration Assay
2.7. Western Blotting
2.8. Flow Cytometry
2.9. Live and Dead Cell Estimation
2.10. Cell Viability Assay
2.11. Mathematical Model
2.12. Data Analysis
3. Results
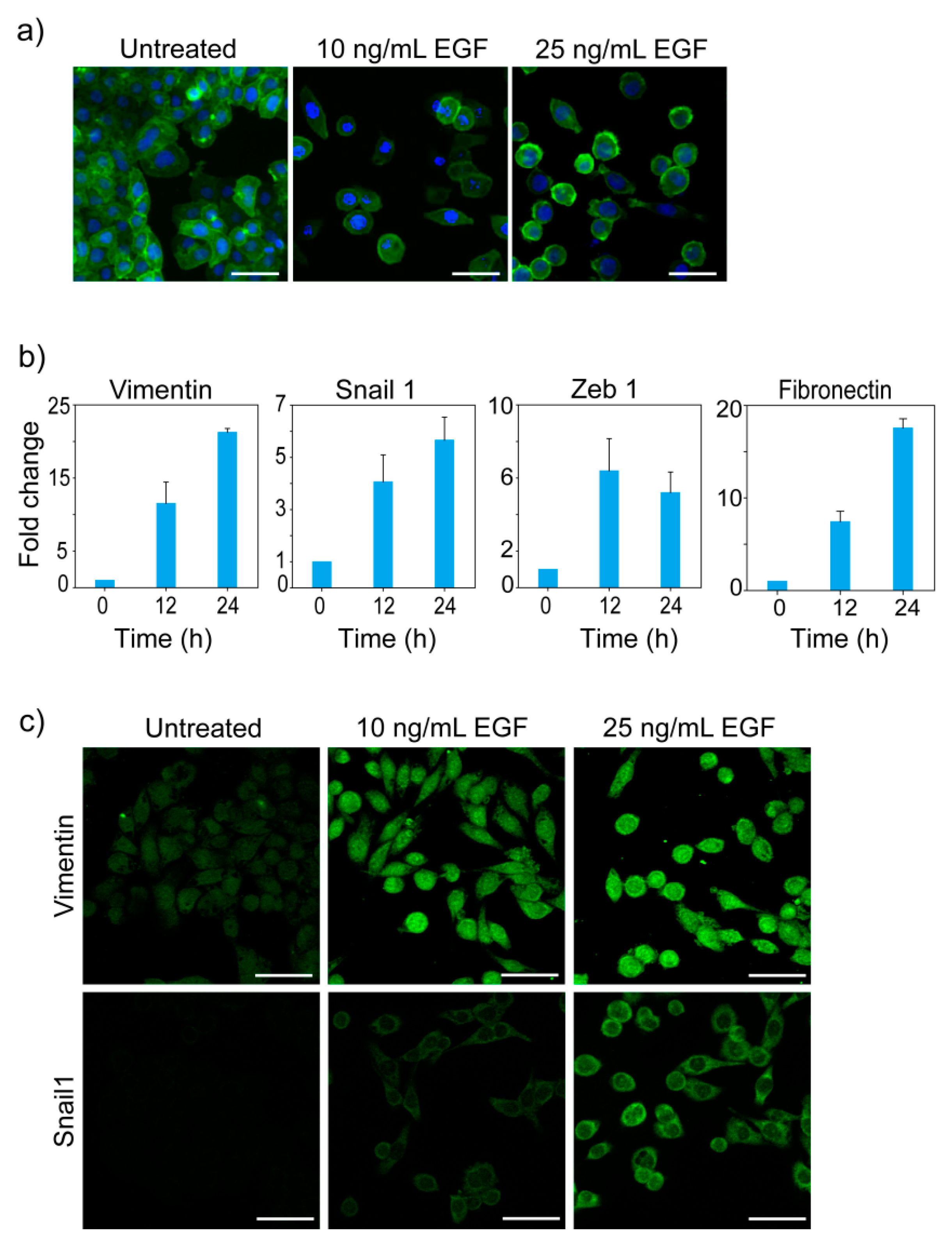
3.1. EGF-Induced EMT
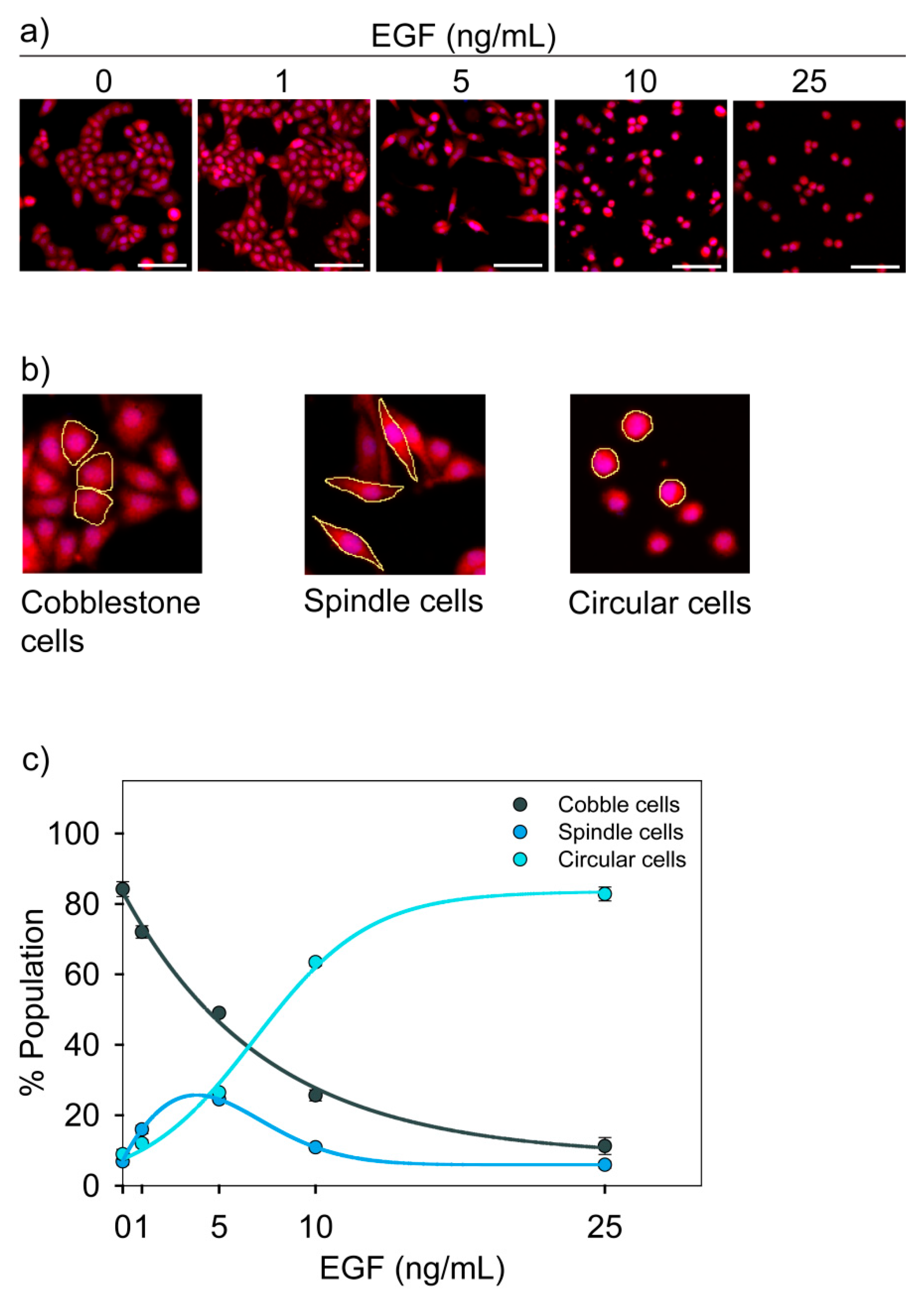
3.2. Morphological States of MDA-MB-468 Cells
3.3. Functional Characterization of Three Cell States
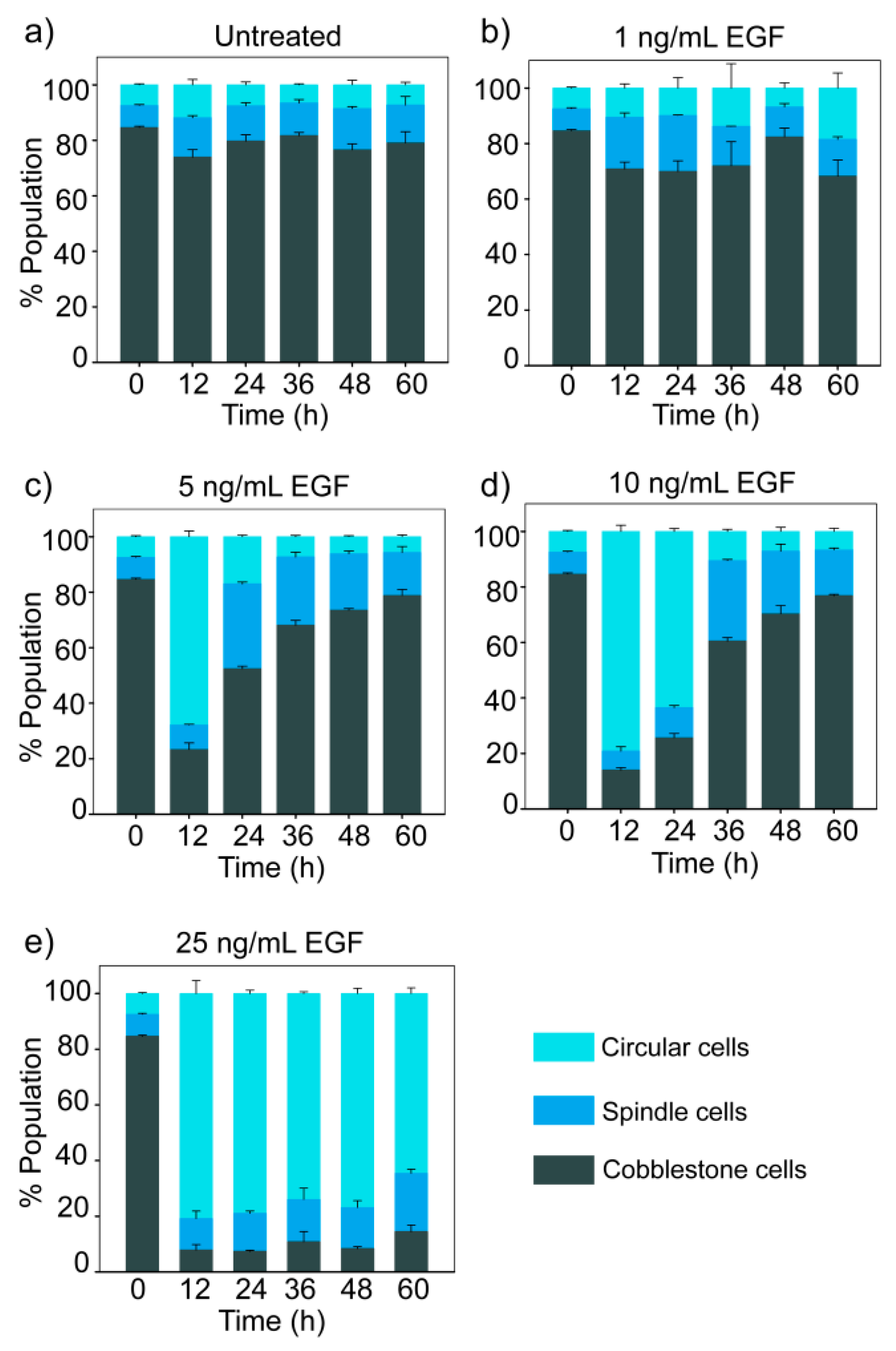
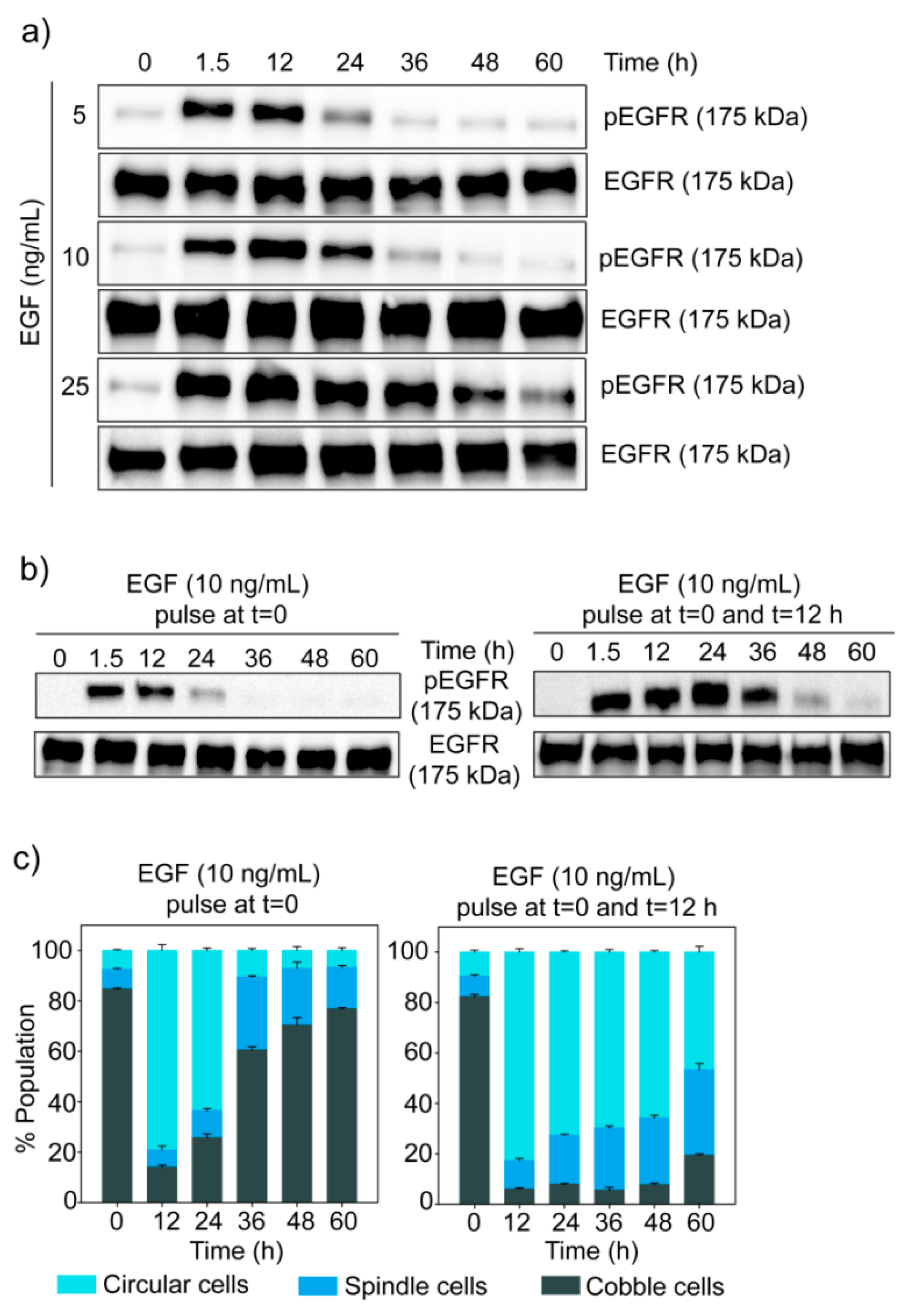
3.4. Dose-Dependent Temporal Dynamics of State Transition
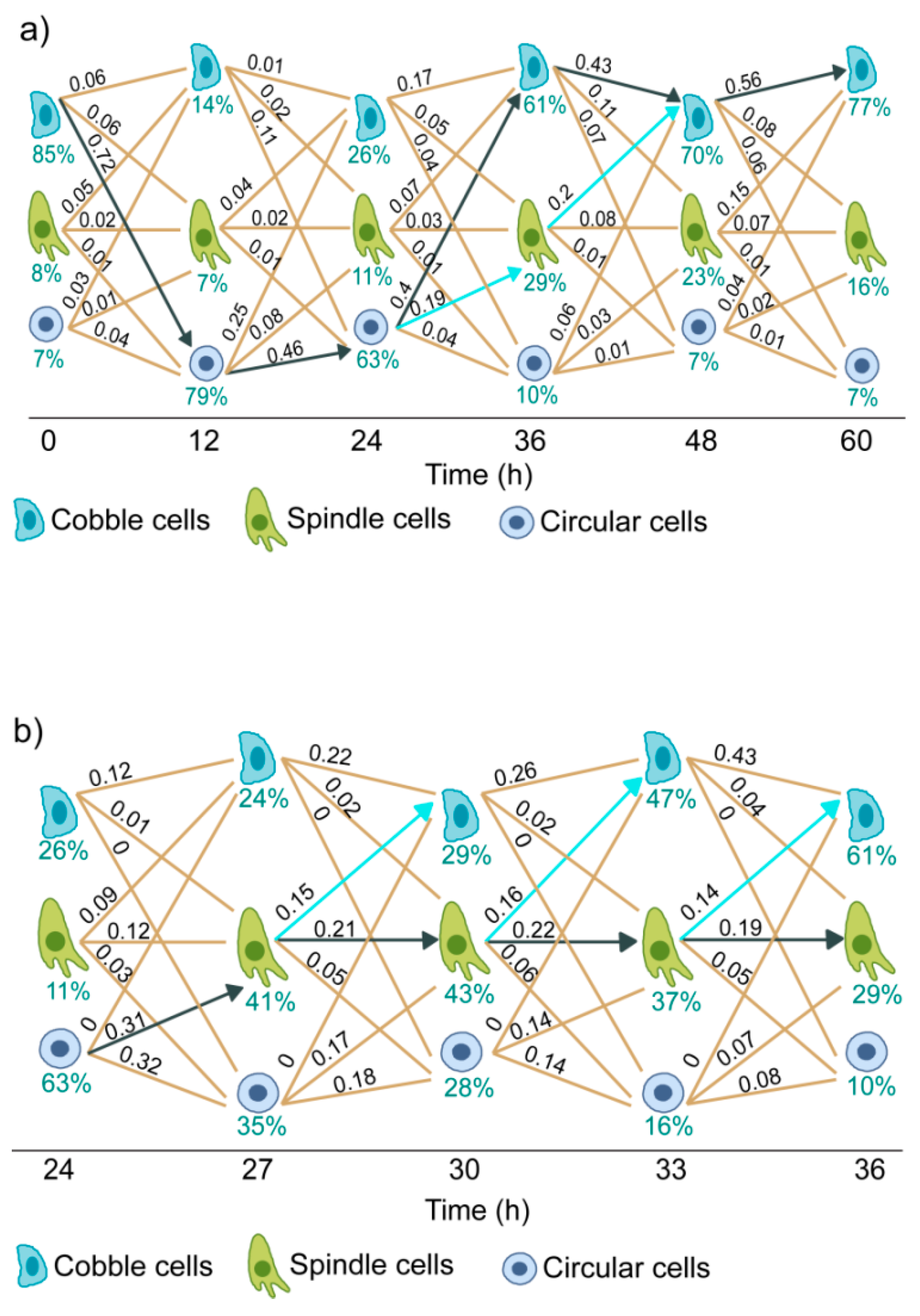
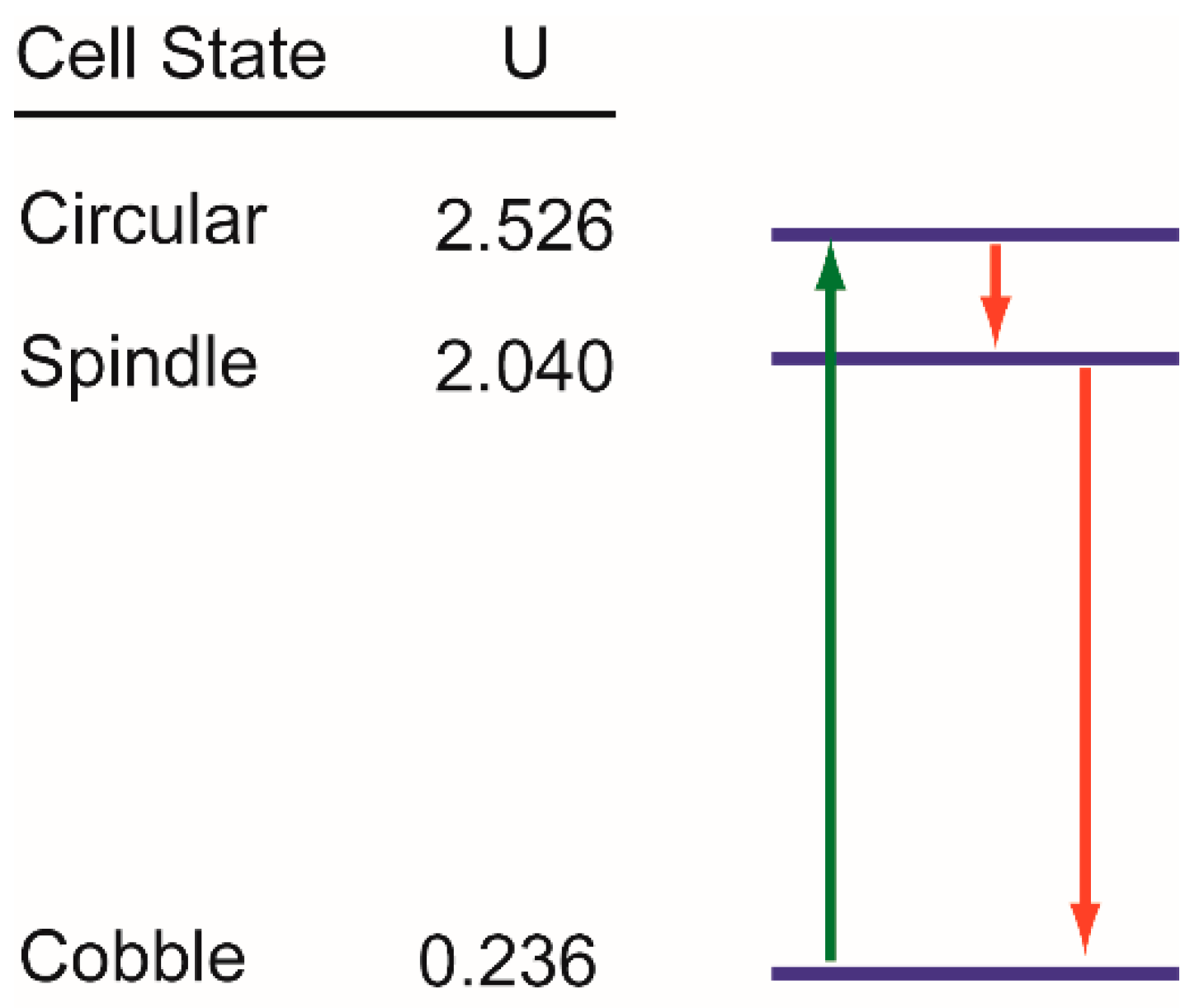
3.5. Trajectories of Cell State Transition
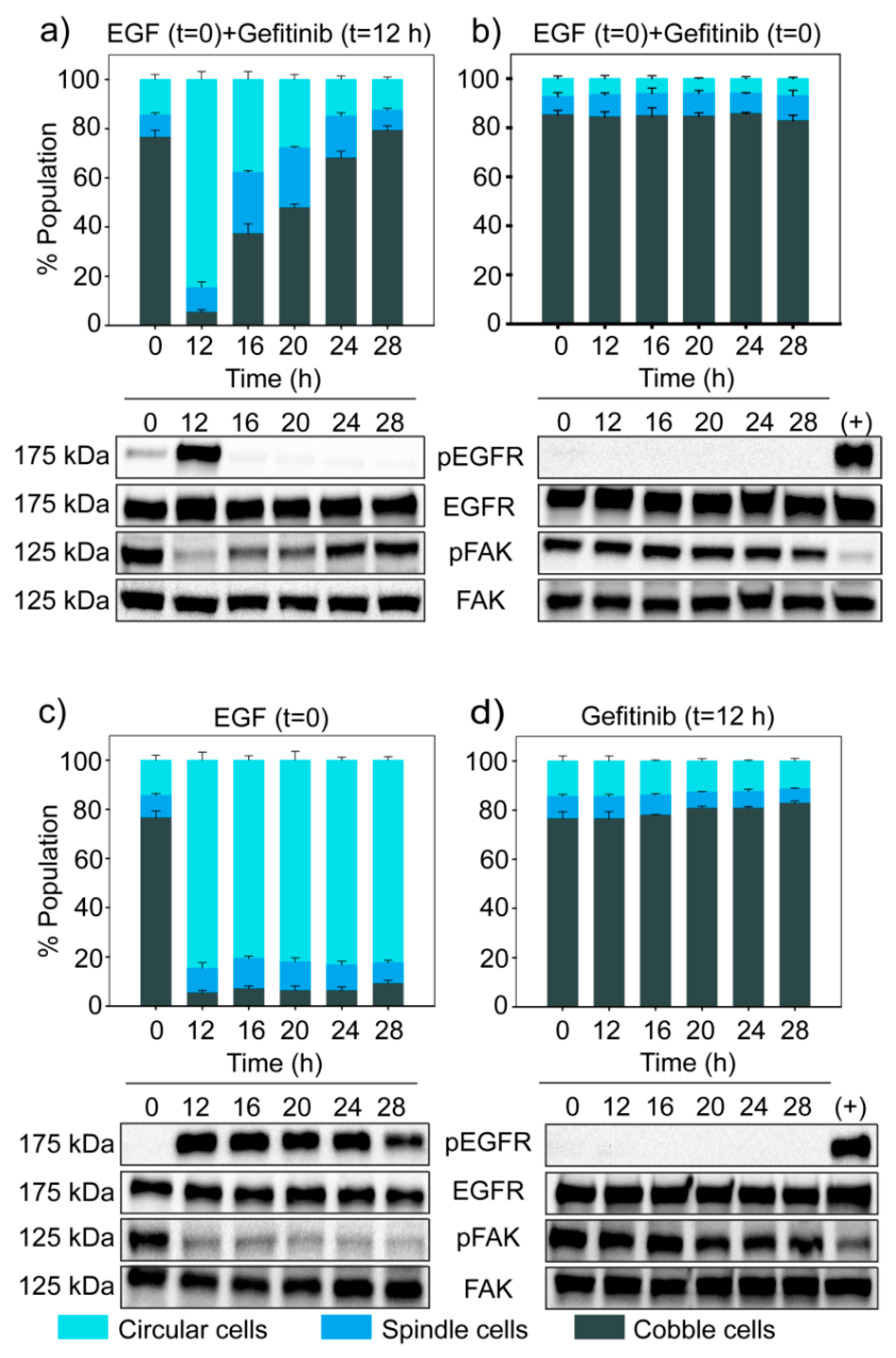
3.6. Dynamics of EGF Signaling Drives the State Transition
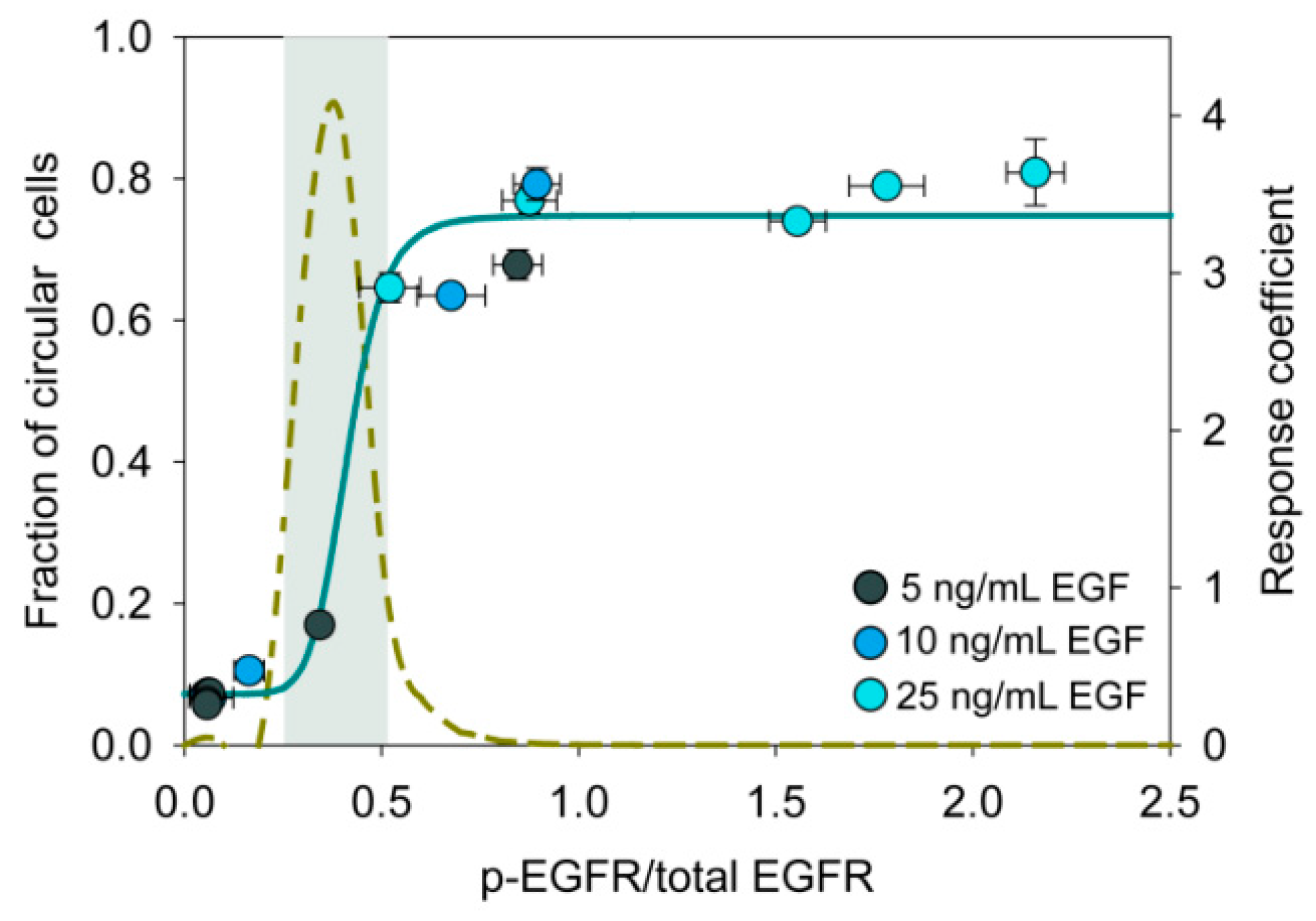
3.7. An Ultrasensitive Switch-Like Response in State Transition
4. Discussion
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Lamouille, S.; Xu, J.; Derynck, R. Molecular mechanisms of epithelial-mesenchymal transition. Nat. Rev. Mol. Cell Biol. 2014, 15, 178–196. [Google Scholar] [CrossRef]
- Xu, J.; Lamouille, S.; Derynck, R. TGF-beta-induced epithelial to mesenchymal transition. Cell Res. 2009, 19, 156–172. [Google Scholar] [CrossRef]
- Lo, H.C.; Zhang, X.H. EMT in Metastasis: Finding the Right Balance. Dev. Cell 2018, 45, 663–665. [Google Scholar] [CrossRef]
- Mittal, V. Epithelial Mesenchymal Transition in Tumor Metastasis. Annu. Rev. Pathol. 2018, 13, 395–412. [Google Scholar] [CrossRef] [PubMed]
- Tsai, J.H.; Yang, J. Epithelial-mesenchymal plasticity in carcinoma metastasis. Genes Dev. 2013, 27, 2192–2206. [Google Scholar] [CrossRef]
- Hong, T.; Watanabe, K.; Ta, C.H.; Villarreal-Ponce, A.; Nie, Q.; Dai, X. An Ovol2-Zeb1 Mutual Inhibitory Circuit Governs Bidirectional and Multi-step Transition between Epithelial and Mesenchymal States. PLoS Comput. Biol. 2015, 11, e1004569. [Google Scholar] [CrossRef] [PubMed]
- Jolly, M.K.; Tripathi, S.C.; Jia, D.; Mooney, S.M.; Celiktas, M.; Hanash, S.M.; Mani, S.A.; Pienta, K.J.; Ben-Jacob, E.; Levine, H. Stability of the hybrid epithelial/mesenchymal phenotype. Oncotarget 2016, 7, 27067–27084. [Google Scholar] [CrossRef] [PubMed]
- Jolly, M.K.; Tripathi, S.C.; Somarelli, J.A.; Hanash, S.M.; Levine, H. Epithelial/mesenchymal plasticity: How have quantitative mathematical models helped improve our understanding? Mol. Oncol. 2017, 11, 739–754. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, X.J.; Zhang, H.; Teng, Y.; Li, R.; Bai, F.; Elankumaran, S.; Xing, J. TGF-beta-induced epithelial-to-mesenchymal transition proceeds through stepwise activation of multiple feedback loops. Sci. Signal 2014, 7, ra91. [Google Scholar] [CrossRef]
- Jia, D.; Jolly, M.K.; Kulkarni, P.; Levine, H. Phenotypic Plasticity and Cell Fate Decisions in Cancer: Insights from Dynamical Systems Theory. Cancers 2017, 9, 70. [Google Scholar] [CrossRef]
- Marr, C.; Zhou, J.X.; Huang, S. Single-cell gene expression profiling and cell state dynamics: Collecting data, correlating data points and connecting the dots. Curr. Opin. Biotechnol. 2016, 39, 207–214. [Google Scholar] [CrossRef]
- Mojtahedi, M.; Skupin, A.; Zhou, J.; Castano, I.G.; Leong-Quong, R.Y.; Chang, H.; Trachana, K.; Giuliani, A.; Huang, S. Cell Fate Decision as High-Dimensional Critical State Transition. PLoS Biol. 2016, 14, e2000640. [Google Scholar] [CrossRef]
- Gupta, P.B.; Fillmore, C.M.; Jiang, G.; Shapira, S.D.; Tao, K.; Kuperwasser, C.; Lander, E.S. Stochastic state transitions give rise to phenotypic equilibrium in populations of cancer cells. Cell 2011, 146, 633–644. [Google Scholar] [CrossRef]
- Waddington, C.H. The Strategy of the Genes: A Discussion of Some Aspects of Theoretical Biology; Allen & Unwin: London, UK, 1957. [Google Scholar]
- Wang, J.; Zhang, K.; Xu, L.; Wang, E. Quantifying the Waddington landscape and biological paths for development and differentiation. Proc. Natl. Acad. Sci. USA 2011, 108, 8257–8262. [Google Scholar] [CrossRef] [PubMed]
- Sha, Y.; Haensel, D.; Gutierrez, G.; Du, H.; Dai, X.; Nie, Q. Intermediate cell states in epithelial-to-mesenchymal transition. Phys. Boil. 2019, 16, 021001. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Balazsi, G. A landscape view on the interplay between EMT and cancer metastasis. NPJ Syst. Biol. Appl. 2018, 4, 34. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Hong, T.; Nie, Q. Quantifying the landscape and kinetic paths for epithelial-mesenchymal transition from a core circuit. Phys. Chem. Chem. Phys. 2016, 18, 17949–17956. [Google Scholar] [CrossRef]
- Biswas, K.; Jolly, M.K.; Ghosh, A. Stability and mean residence times for hybrid epithelial/mesenchymal phenotype. Phys. Biol. 2019, 16, 025003. [Google Scholar] [CrossRef]
- Su, Y.; Wei, W.; Robert, L.; Xue, M.; Tsoi, J.; Garcia-Diaz, A.; Homet Moreno, B.; Kim, J.; Ng, R.H.; Lee, J.W.; et al. Single-cell analysis resolves the cell state transition and signaling dynamics associated with melanoma drug-induced resistance. Proc. Natl. Acad. Sci. USA 2017, 114, 13679–13684. [Google Scholar] [CrossRef]
- Hormoz, S.; Singer, Z.S.; Linton, J.M.; Antebi, Y.E.; Shraiman, B.I.; Elowitz, M.B. Inferring Cell-State Transition Dynamics from Lineage Trees and Endpoint Single-Cell Measurements. Cell Syst. 2016, 3, 419–433.e418. [Google Scholar] [CrossRef] [PubMed]
- Pisco, A.O.; Brock, A.; Zhou, J.; Moor, A.; Mojtahedi, M.; Jackson, D.; Huang, S. Non-Darwinian dynamics in therapy-induced cancer drug resistance. Nat. Commun. 2013, 4, 2467. [Google Scholar] [CrossRef] [PubMed]
- Jang, S.; Choubey, S.; Furchtgott, L. Dynamics of embryonic stem cell differentiation inferred from single-cell transcriptomics show a series of transitions through discrete cell states. eLife 2017, 6. [Google Scholar] [CrossRef]
- Kimmel, J.C.; Chang, A.Y.; Brack, A.S.; Marshall, W.F. Inferring cell state by quantitative motility analysis reveals a dynamic state system and broken detailed balance. PLoS Comput. Biol. 2018, 14, e1005927. [Google Scholar] [CrossRef] [PubMed]
- Moreno-Bueno, G.; Peinado, H.; Molina, P.; Olmeda, D.; Cubillo, E.; Santos, V.; Palacios, J.; Portillo, F.; Cano, A. The morphological and molecular features of the epithelial-to-mesenchymal transition. Nat. Protoc. 2009, 4, 1591–1613. [Google Scholar] [CrossRef] [PubMed]
- Marklein, R.A.; Lam, J.; Guvendiren, M.; Sung, K.E.; Bauer, S.R. Functionally-Relevant Morphological Profiling: A Tool to Assess Cellular Heterogeneity. Trends Biotechnol. 2018, 36, 105–118. [Google Scholar] [CrossRef]
- Leggett, S.E.; Sim, J.Y.; Rubins, J.E.; Neronha, Z.J.; Williams, E.K.; Wong, I.Y. Morphological single cell profiling of the epithelial-mesenchymal transition. Integr. Biol. 2016, 8, 1133–1144. [Google Scholar] [CrossRef]
- Mandal, M.; Ghosh, B.; Anura, A.; Mitra, P.; Pathak, T.; Chatterjee, J. Modeling continuum of epithelial mesenchymal transition plasticity. Integr. Biol. 2016, 8, 167–176. [Google Scholar] [CrossRef] [PubMed]
- Neve, R.M.; Chin, K.; Fridlyand, J.; Yeh, J.; Baehner, F.L.; Fevr, T.; Clark, L.; Bayani, N.; Coppe, J.P.; Tong, F.; et al. A collection of breast cancer cell lines for the study of functionally distinct cancer subtypes. Cancer Cell 2006, 10, 515–527. [Google Scholar] [CrossRef]
- Chavez, K.J.; Garimella, S.V.; Lipkowitz, S. Triple negative breast cancer cell lines: One tool in the search for better treatment of triple negative breast cancer. Breast Dis. 2010, 32, 35–48. [Google Scholar] [CrossRef] [PubMed]
- Davis, F.M.; Parsonage, M.T.; Cabot, P.J.; Parat, M.-O.; Thompson, E.W.; Roberts-Thomson, S.J.; Monteith, G.R. Assessment of gene expression of intracellular calcium channels, pumps and exchangers with epidermal growth factor-induced epithelial-mesenchymal transition in a breast cancer cell line. Cancer Cell Int. 2013, 13, 76. [Google Scholar] [CrossRef]
- Bonnomet, A.; Syne, L.; Brysse, A.; Feyereisen, E.; Thompson, E.W.; Noël, A.; Foidart, J.-M.; Birembaut, P.; Polette, M.; Gilles, C. A dynamic in vivo model of epithelial-to-mesenchymal transitions in circulating tumor cells and metastases of breast cancer. Oncogene 2012, 31, 3741. [Google Scholar] [CrossRef] [PubMed]
- Lo, H.W.; Hsu, S.C.; Xia, W.; Cao, X.; Shih, J.Y.; Wei, Y.; Abbruzzese, J.L.; Hortobagyi, G.N.; Hung, M.C. Epidermal growth factor receptor cooperates with signal transducer and activator of transcription 3 to induce epithelial-mesenchymal transition in cancer cells via up-regulation of TWIST gene expression. Cancer Res. 2007, 67, 9066–9076. [Google Scholar] [CrossRef]
- Davis, F.M.; Azimi, I.; Faville, R.A.; Peters, A.A.; Jalink, K.; Putney, J.W., Jr.; Goodhill, G.J.; Thompson, E.W.; Roberts-Thomson, S.J.; Monteith, G.R. Induction of epithelial–mesenchymal transition (EMT) in breast cancer cells is calcium signal dependent. Oncogene 2014, 33, 2307. [Google Scholar] [CrossRef] [PubMed]
- Davis, F.M.; Peters, A.A.; Grice, D.M.; Cabot, P.J.; Parat, M.O.; Roberts-Thomson, S.J.; Monteith, G.R. Non-stimulated, agonist-stimulated and store-operated Ca2+ influx in MDA-MB-468 breast cancer cells and the effect of EGF-induced EMT on calcium entry. PLoS ONE 2012, 7, e36923. [Google Scholar] [CrossRef] [PubMed]
- Verma, N.; Keinan, O.; Selitrennik, M.; Karn, T.; Filipits, M.; Lev, S. PYK2 sustains endosomal-derived receptor signalling and enhances epithelial-to-mesenchymal transition. Nat. Commun. 2015, 6, 6064. [Google Scholar] [CrossRef]
- Ramakers, C.; Ruijter, J.M.; Deprez, R.H.; Moorman, A.F. Assumption-free analysis of quantitative real-time polymerase chain reaction (PCR) data. Neurosci. Lett. 2003, 339, 62–66. [Google Scholar] [CrossRef]
- Kamentsky, L.; Jones, T.R.; Fraser, A.; Bray, M.A.; Logan, D.J.; Madden, K.L.; Ljosa, V.; Rueden, C.; Eliceiri, K.W.; Carpenter, A.E. Improved structure, function and compatibility for CellProfiler: Modular high-throughput image analysis software. Bioinformatics 2011, 27, 1179–1180. [Google Scholar] [CrossRef]
- Jones, T.R.; Carpenter, A.E.; Lamprecht, M.R.; Moffat, J.; Silver, S.J.; Grenier, J.K.; Castoreno, A.B.; Eggert, U.S.; Root, D.E.; Golland, P.; et al. Scoring diverse cellular morphologies in image-based screens with iterative feedback and machine learning. Proc. Natl. Acad. Sci. USA 2009, 106, 1826–1831. [Google Scholar] [CrossRef]
- Lowry, O.H.; Rosebrough, N.J.; Farr, A.L.; Randall, R.J. Protein measurement with the Folin phenol reagent. J. Biol. Chem. 1951, 193, 265–275. [Google Scholar]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef]
- Dengler, W.A.; Schulte, J.; Berger, D.P.; Mertelsmann, R.; Fiebig, H.H. Development of a propidium iodide fluorescence assay for proliferation and cytotoxicity assays. Anticancer Drugs 1995, 6, 522–532. [Google Scholar] [CrossRef]
- Wan, C.P.; Sigh, R.V.; Lau, B.H. A simple fluorometric assay for the determination of cell numbers. J. Immunol. Methods 1994, 173, 265–272. [Google Scholar] [CrossRef]
- Mosmann, T. Rapid colorimetric assay for cellular growth and survival: Application to proliferation and cytotoxicity assays. J. Immunol. Methods 1983, 65, 55–63. [Google Scholar] [CrossRef]
- Davis, F.M.; Kenny, P.A.; Soo, E.T.L.; van Denderen, B.J.W.; Thompson, E.W.; Cabot, P.J.; Parat, M.-O.; Roberts-Thomson, S.J.; Monteith, G.R. Remodeling of purinergic receptor-mediated Ca2+ signaling as a consequence of EGF-induced epithelial-mesenchymal transition in breast cancer cells. PLoS ONE 2011, 6, e23464. [Google Scholar] [CrossRef] [PubMed]
- Franchi, M.; Masola, V.; Bellin, G.; Onisto, M.; Karamanos, K.A.; Piperigkou, Z. Collagen Fiber Array of Peritumoral Stroma Influences Epithelial-to-Mesenchymal Transition and Invasive Potential of Mammary Cancer Cells. J. Clin. Med. 2019, 8, 213. [Google Scholar] [CrossRef] [PubMed]
- Buder, T.; Deutsch, A.; Seifert, M.; Voss-Bohme, A. CellTrans: An R Package to Quantify Stochastic Cell State Transitions. Bioinform. Biol. Insights 2017, 11. [Google Scholar] [CrossRef]
- Lu, Z.; Jiang, G.; Blume-Jensen, P.; Hunter, T. Epidermal growth factor-induced tumor cell invasion and metastasis initiated by dephosphorylation and downregulation of focal adhesion kinase. Mol. Cell. Biol. 2001, 21, 4016–4031. [Google Scholar] [CrossRef]
- Matsumoto, K.; Ziober, B.L.; Yao, C.C.; Kramer, R.H. Growth factor regulation of integrin-mediated cell motility. Cancer Metastasis Rev. 1995, 14, 205–217. [Google Scholar] [CrossRef] [PubMed]
- Turner, C.E. Paxillin and focal adhesion signalling. Nat. Cell Biol. 2000, 2, E231–E236. [Google Scholar] [CrossRef]
- Clark, E.A.; Brugge, J.S. Integrins and signal transduction pathways: The road taken. Science 1995, 268, 233–239. [Google Scholar] [CrossRef]
- Kholodenko, B.N.; Hoek, J.B.; Westerhoff, H.V.; Brown, G.C. Quantification of information transfer via cellular signal transduction pathways. FEBS Lett. 1997, 414, 430–434. [Google Scholar]
- Goldbeter, A.; Koshland, D.E. Sensitivity amplification in biochemical systems. Q. Rev. Biophys. 1982, 15, 555–591. [Google Scholar] [CrossRef]
- Chang, H.H.; Hemberg, M.; Barahona, M.; Ingber, D.E.; Huang, S. Transcriptome-wide noise controls lineage choice in mammalian progenitor cells. Nature 2008, 453, 544–547. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.Y.; Lin, J.R.; Cimprich, K.A.; Meyer, T. A two-dimensional ERK-AKT signaling code for an NGF-triggered cell-fate decision. Mol. Cell 2012, 45, 196–209. [Google Scholar] [CrossRef] [PubMed]
- Moris, N.; Pina, C.; Arias, A.M. Transition states and cell fate decisions in epigenetic landscapes. Nat. Rev. Genet. 2016, 17, 693–703. [Google Scholar] [CrossRef] [PubMed]
- Ferrell, J.E., Jr.; Machleder, E.M. The biochemical basis of an all-or-none cell fate switch in Xenopus oocytes. Science 1998, 280, 895–898. [Google Scholar] [CrossRef]
- Narula, J.; Devi, S.N.; Fujita, M.; Igoshin, O.A. Ultrasensitivity of the Bacillus subtilis sporulation decision. Proc. Natl. Acad. Sci. USA 2012, 109, E3513–E3522. [Google Scholar] [CrossRef]
- Huang, C.Y.; Ferrell, J.E., Jr. Ultrasensitivity in the mitogen-activated protein kinase cascade. Proc. Natl. Acad. Sci. USA 1996, 93, 10078–10083. [Google Scholar] [CrossRef]
- Melen, G.J.; Levy, S.; Barkai, N.; Shilo, B.Z. Threshold responses to morphogen gradients by zero-order ultrasensitivity. Mol. Syst. Biol. 2005, 1. [Google Scholar] [CrossRef]
- Wang, J.; Li, C.; Wang, E. Potential and flux landscapes quantify the stability and robustness of budding yeast cell cycle network. Proc. Natl. Acad. Sci. USA 2010, 107, 8195–8200. [Google Scholar] [CrossRef]
- Sisan, D.R.; Halter, M.; Hubbard, J.B.; Plant, A.L. Predicting rates of cell state change caused by stochastic fluctuations using a data-driven landscape model. Proc. Natl. Acad. Sci. USA 2012, 109, 19262–19267. [Google Scholar] [CrossRef] [PubMed]
- Atkins, P.; de Paula, J. Atkin’s Physical Chemistry, 8th ed.; W. H. Freeman and Company: New York, NY, USA, 2006. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Devaraj, V.; Bose, B. Morphological State Transition Dynamics in EGF-Induced Epithelial to Mesenchymal Transition. J. Clin. Med. 2019, 8, 911. https://doi.org/10.3390/jcm8070911
Devaraj V, Bose B. Morphological State Transition Dynamics in EGF-Induced Epithelial to Mesenchymal Transition. Journal of Clinical Medicine. 2019; 8(7):911. https://doi.org/10.3390/jcm8070911
Chicago/Turabian StyleDevaraj, Vimalathithan, and Biplab Bose. 2019. "Morphological State Transition Dynamics in EGF-Induced Epithelial to Mesenchymal Transition" Journal of Clinical Medicine 8, no. 7: 911. https://doi.org/10.3390/jcm8070911
APA StyleDevaraj, V., & Bose, B. (2019). Morphological State Transition Dynamics in EGF-Induced Epithelial to Mesenchymal Transition. Journal of Clinical Medicine, 8(7), 911. https://doi.org/10.3390/jcm8070911




