Frequency-Dependent Amplification of Head Motion in Infant Rockers: A Segmental IMU-Based Signal Analysis
Highlights
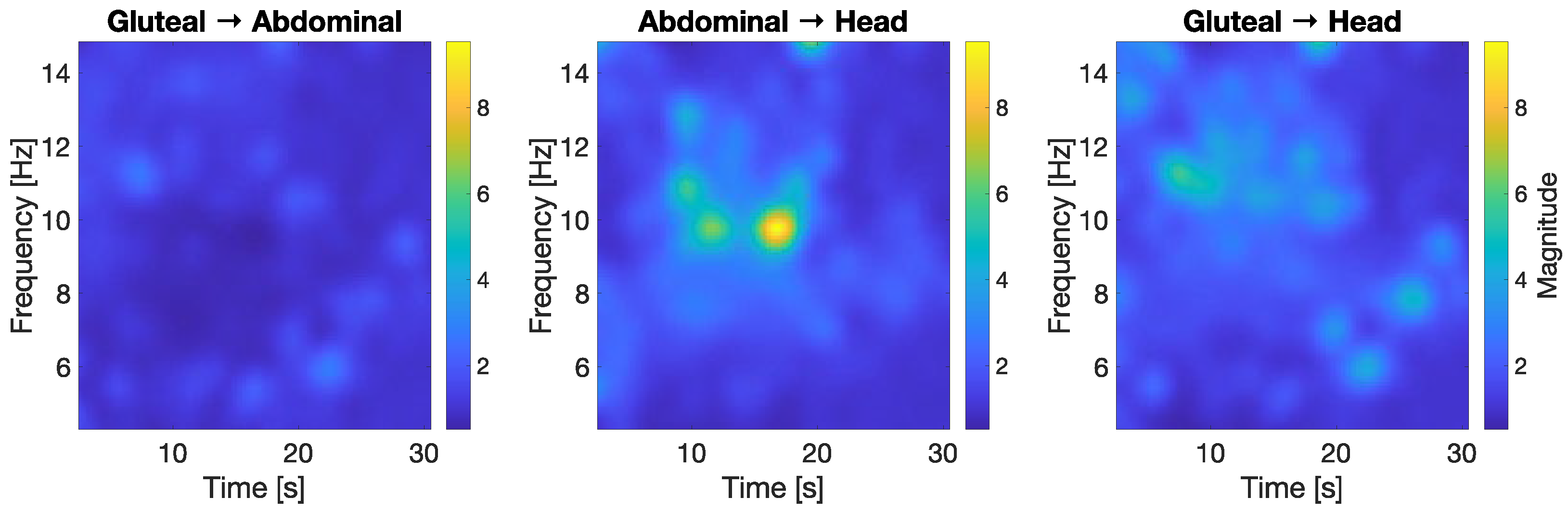
- Head motion in infant rockers demonstrates strong frequency-dependent amplification, with the highest angular displacements and peak accelerations occurring in the head segment.
- The abdomen acts as a damping transition zone, while the gluteal region remains almost static, serving as the mechanical input.
- A distinct amplification of motion energy is observed in the 10–12 Hz range, indicating inertial and potentially resonant effects.
- Even seemingly gentle rocking can lead to significant dynamic loading at the head due to upward frequency-dependent amplification.
- These results highlight the need to consider segmental dynamics and resonance effects when designing infant rockers.
- The findings have ergonomic and safety implications, especially for younger infants with more vulnerable neuromuscular control.
Abstract
1. Introduction
- Quantify segmental motion patterns during passive rocking using IMUs;
- Compare dynamic responses across head, abdominal, and gluteal regions;
- Analyze frequency-specific energy transmission using wavelet and transfer function analysis;
- Explore implications for rocker safety and infant biomechanics.
2. Materials and Methods
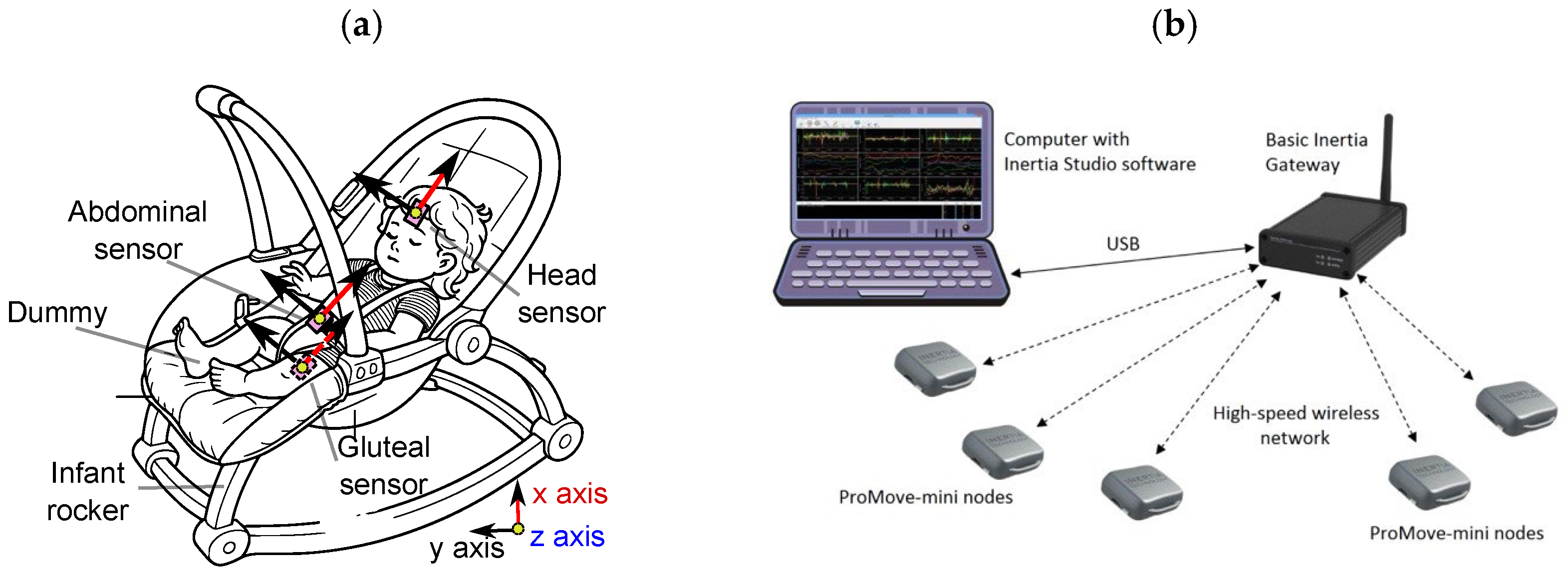
2.1. Experimental Measurement Setup
2.2. Wavelet Analysis Theory
- —is the wavelet function in the time domain—a localized waveform used to analyze the structure of the signal at various scales and positions,
- —is a normalization constant that ensures the wavelet has unit energy. This allows for meaningful comparison of energy across different scales,
- —is the complex sinusoidal carrier—it defines the oscillatory behavior of the wavelet, centered at a frequency determined by the parameter . This component allows the wavelet to extract frequency-specific information from the signal,
- —is the Gaussian envelope, which ensures that the wavelet is localized in time. This time localization is what gives the Morlet wavelet its ability to detect transient features and changing frequency content in non-stationary signals,
- —is the central (dimensionless) frequency of the wavelet. A common choice is which provides a good balance between time and frequency resolution. Smaller values improve time localization at the expense of frequency resolution, and vice versa.
3. Results
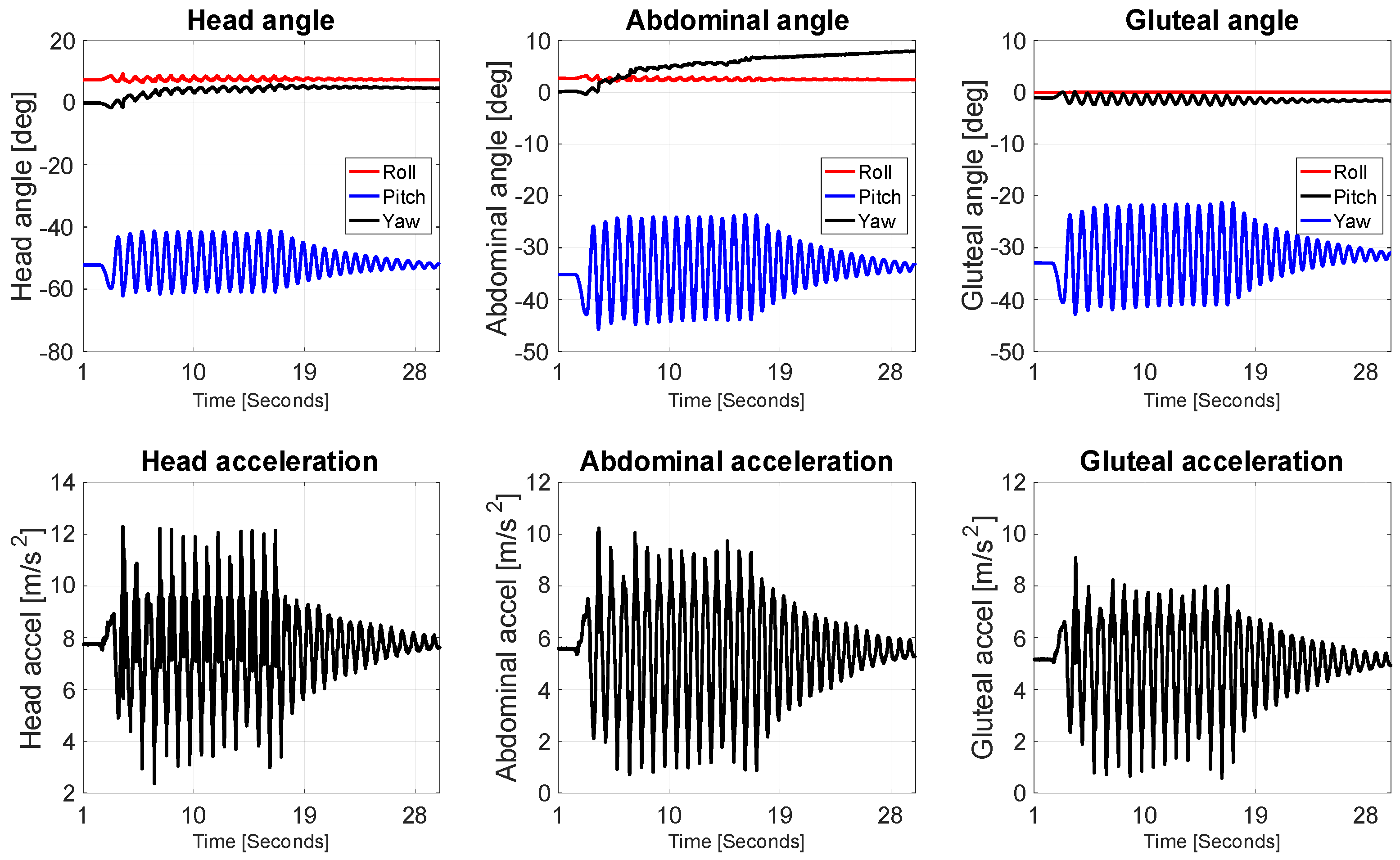
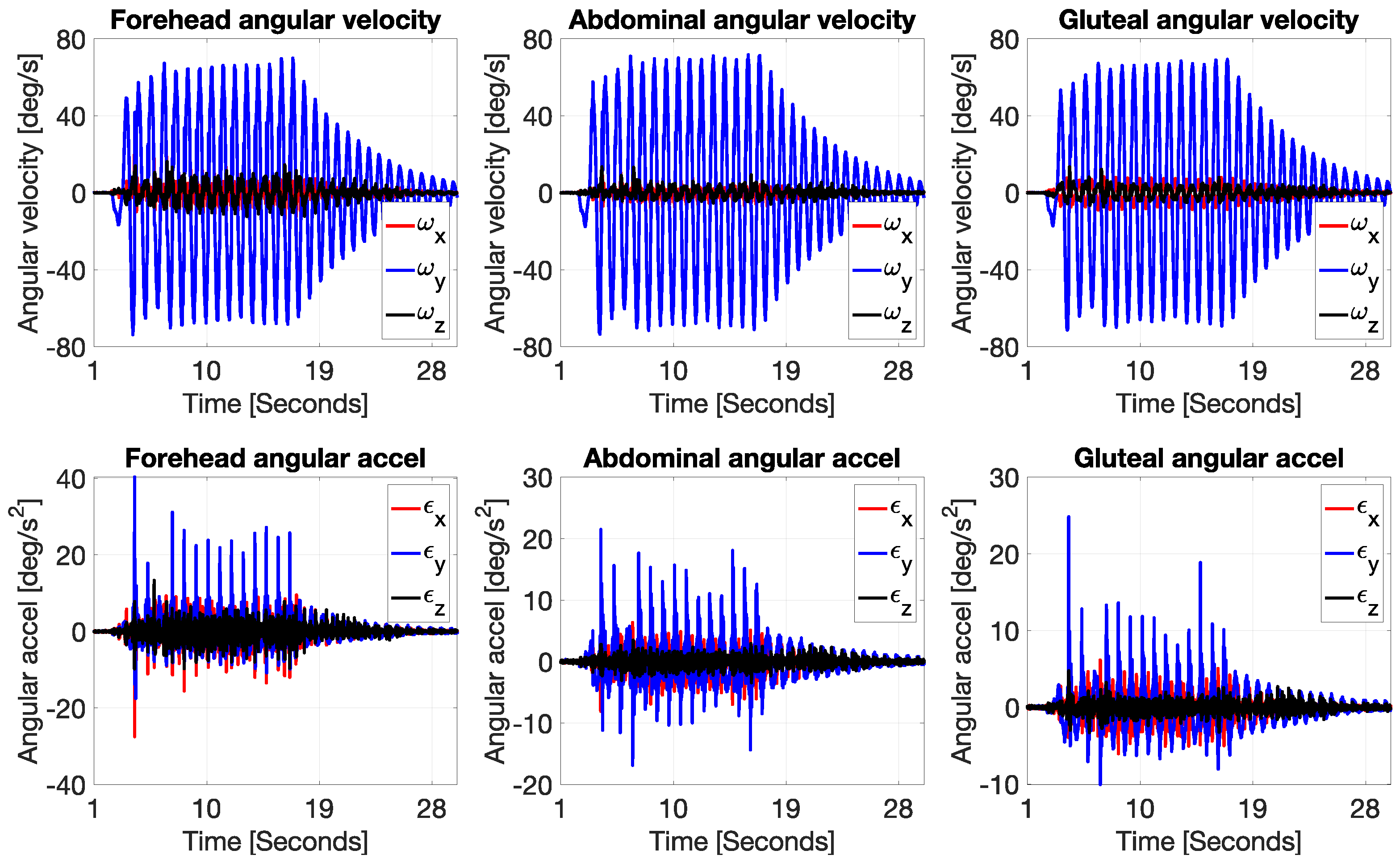
3.1. Kinematic Analysis
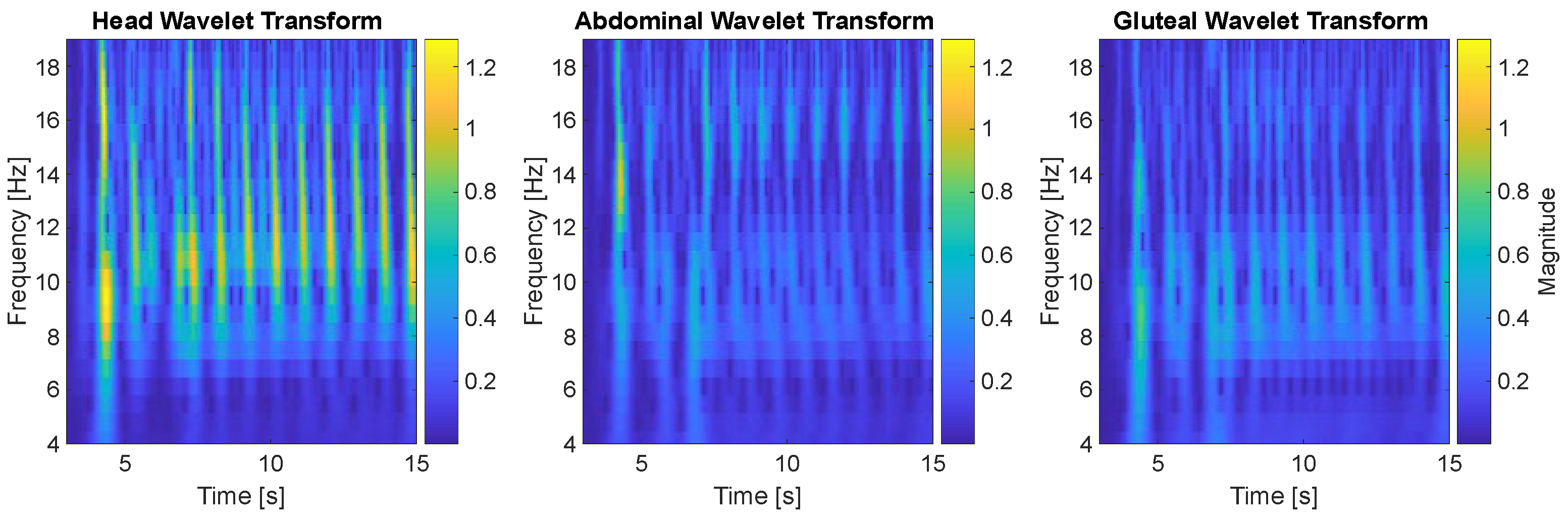
3.2. Wavelet Analysis
4. Discussion
5. Limitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yadav, J.P.; Agrawal, A.; Sawant, V.D. Effect of facilitated rocking movement in reducing vaccination-induced pain in young infants: A randomized control trial. Bull. Natl. Res. Cent. 2022, 46, 117. [Google Scholar] [CrossRef]
- Obladen, M. Two Millennia of Debating the Cradle. Neonantology 2021, 118, 198–205. [Google Scholar] [CrossRef]
- Sydor, M.; Pop, J.; Jasińska, A.; Zabłocki, M. Anthropo-Mechanical Cradles: A Multidisciplinary Review. Int. J. Env. Res. Public. Healh 2022, 19, 15759. [Google Scholar] [CrossRef]
- Coats, B.; Margulies, S.S. Material properties of human infant skull and suture at high rates. J. Neurotrauma 2006, 23, 1222–1232. [Google Scholar] [CrossRef]
- Moore, L.; Bourne, A.J.; Beal, S.; Collett, M.; Byard, R.W. Unexpected infant death in association with suspended rocking cradles. Am. J. Forensic Med. Pathol. 1995, 16, 177–180. [Google Scholar] [CrossRef] [PubMed]
- de San Lazaro, C.; Harvey, R.; Ogden, A. Shaking infant trauma induced by misuse of a baby chair. Arch. Dis. Child. 2003, 88, 632–634. [Google Scholar] [CrossRef]
- Bandak, F.A. Shaken baby syndrome: A biomechanics analysis of injury mechanisms. Forensic Sci. Int. 2005, 151, 71–79. [Google Scholar] [CrossRef]
- Glowinski, S.; Majdanik, S.; Glowinska, A.; Majdanik, E. Trauma in a shaken infant? A case study. Aggress. Violent Behav. 2020, 55, 101515. [Google Scholar] [CrossRef]
- Mannen, E.M.; Siegel, D.; Goldrod, S.; Bossart, A.; Lujan, T.J.; Wilson, C.; Whitaker, B.; Carrol, J. Seated Products Characterization and Testing; Report; United States Consumer Product Safety Comission: Bethesda, MA, USA, 2023; p. 218.
- Ko, Y.H.; Ooi, L.E.; Lee, Y.K.; Ko, C.W.; Leong, K.R.; Lim, C.B.; Ung, I.K.L. Vibration Analysis of Electronic Baby Hammock. Trans. Sci. Technol. 2016, 3, 328–335. [Google Scholar]
- Consumer Product Safety Commission. Available online: https://www.federalregister.gov/documents/2023/10/26/2023-23322/safety-standard-for-infant-and-infanttoddler-rockers (accessed on 10 April 2025).
- Worobey, J.; Vetrini, N.R.; Rozo, E.M. Mechanical measurement of infant activity: A cautionary note. Infant. Behav. Dev. 2009, 32, 167–172. [Google Scholar] [CrossRef] [PubMed]
- Malcuit, G.; Pomerleau, A.; Brosseau, N. Cardiac and behavioral responses to rocking stimulations in one- and three-month-old infants. Percept. Mot. Ski. 1988, 66, 207–217. [Google Scholar] [CrossRef] [PubMed]
- Margulies, S.S.; Thibault, K. Infant Skull and Suture Properties: Measurements and Implications for Mechanisms of Pediatric Brain Injury. J. Biomech. Eng. 2000, 122, 364–371. [Google Scholar] [CrossRef] [PubMed]
- Meaney, D.F.; Morrison, B.; Dale Bass, C. The mechanics of traumatic brain injury: A review of what we know and what we need to know for reducing its societal burden. J. Biomech. Eng. 2014, 136, 021008. [Google Scholar] [CrossRef]
- Siegel, D.N.; Goldrod, S.; Wilson, C.; Bossert, A.; Lujan, T.J.; Whitaker, B.N.; Carroll, J.L.; Mannen, E.M. Commercial infant products influence body position and muscle use. Early Hum. Dev. 2024, 198, 106122. [Google Scholar] [CrossRef]
- Glowinski, S.; Głowińska, A. Unveiling the Abusive Head Trauma and Shaken baby Syndrome: A Comprehensive Wavelet Analysis. Biomed. Signal Process. Control 2025, 107, 107862. [Google Scholar] [CrossRef]
- Duda-Goławska, J.; Rogowski, A.; Laudańska, Z.; Żygierewicz, J.; Tomalski, P. Identifying Infant Body Position from Inertial Sensors with Machine Learning: Which Parameters Matter? Sensors 2024, 24, 7809. [Google Scholar] [CrossRef]
- Franchak, J.M.; Tang, M.; Rousey, H.; Luo, C. Long-form recording of infant body position in the home using wearable inertial sensors. Behav. Res. Methods 2024, 56, 4982–5001. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Inertia Technology. Available online: https://inertia-technology.com (accessed on 10 June 2025).
- Akujuobi, C.M. Wavelets and Wavelet Transform Systems and Their Applications A Digital Signal Processing Approach; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Boako, G.; Alagidede, P. Co-movement of Africa’s equity markets: Regional and global analysis in the frequency–time domains. Phys. A Stat. Mech. Appl. 2017, 468, 359–380. [Google Scholar] [CrossRef]
- Rihar, A.; Mihelj, M.; Pašič, J. Infant trunk posture and arm movement assessment using pressure mattress, inertial and magnetic measurement units (IMUs). J. Neuroeng. Rehabil. 2014, 11, 133. [Google Scholar] [CrossRef]
- Airaksinen, M.; Vaaras, E.; Haataja, L.; Räsänen, O.; Vanhatalo, S. Automatic assessment of infant carrying and holding using at-home wearable recordings. Sci. Rep. 2024, 14, 4852. [Google Scholar] [CrossRef]
- Lloyd, J.; Willey, E.N.; Galaznik, J.G.; Lee, W.; Luttner, S.E. Biomechanical evaluation of head kinematics during infant shaking versus pediatric activities of daily living. J. Forensic Biomech. 2011, 2, 1–9. [Google Scholar] [CrossRef]
- Reimann, R.J. Fundamental Limits of Shaking a Baby. J. Forensic Sci. 2018, 63, 1864–1866. [Google Scholar] [CrossRef]
- Alvarez, V.S.; Kleiven, S. Effect of pediatric growth on cervical spine kinematics and deformations in automotive crashes. J. Biomech. 2018, 71, 76–83. [Google Scholar] [CrossRef] [PubMed]
- Coats, B.; Binenbaum, G.; Smith, C.; Peiffer, R.L.; Christian, C.W.; Duhaime, A.C.; Margulies, S.S. Cyclic Head Rotations Produce Modest Brain Injury in Infant Piglets. J. Neurotrauma 2017, 34, 235–247. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, N.G.; Ralston, J.; Smith, C.; Margulies, S.S. Physiological and pathological responses to head rotations in toddler piglets. J. Neurotrauma 2010, 27, 1021–1035. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Głowińska, A.; Glowinski, S. Frequency-Dependent Amplification of Head Motion in Infant Rockers: A Segmental IMU-Based Signal Analysis. J. Clin. Med. 2025, 14, 8301. https://doi.org/10.3390/jcm14238301
Głowińska A, Glowinski S. Frequency-Dependent Amplification of Head Motion in Infant Rockers: A Segmental IMU-Based Signal Analysis. Journal of Clinical Medicine. 2025; 14(23):8301. https://doi.org/10.3390/jcm14238301
Chicago/Turabian StyleGłowińska, Alina, and Sebastian Glowinski. 2025. "Frequency-Dependent Amplification of Head Motion in Infant Rockers: A Segmental IMU-Based Signal Analysis" Journal of Clinical Medicine 14, no. 23: 8301. https://doi.org/10.3390/jcm14238301
APA StyleGłowińska, A., & Glowinski, S. (2025). Frequency-Dependent Amplification of Head Motion in Infant Rockers: A Segmental IMU-Based Signal Analysis. Journal of Clinical Medicine, 14(23), 8301. https://doi.org/10.3390/jcm14238301






