Sex Differentiation of Trabecular Bone Structure Based on Textural Analysis of Pelvic Radiographs
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset Description
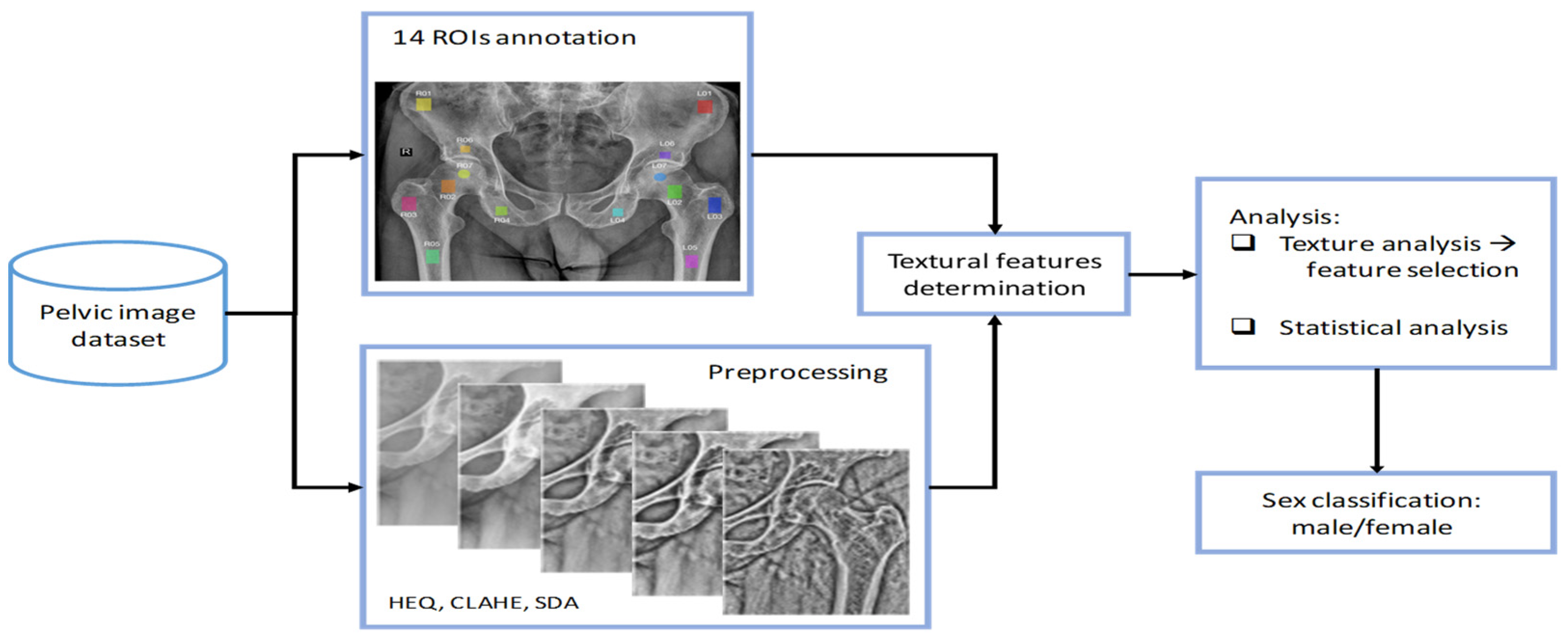
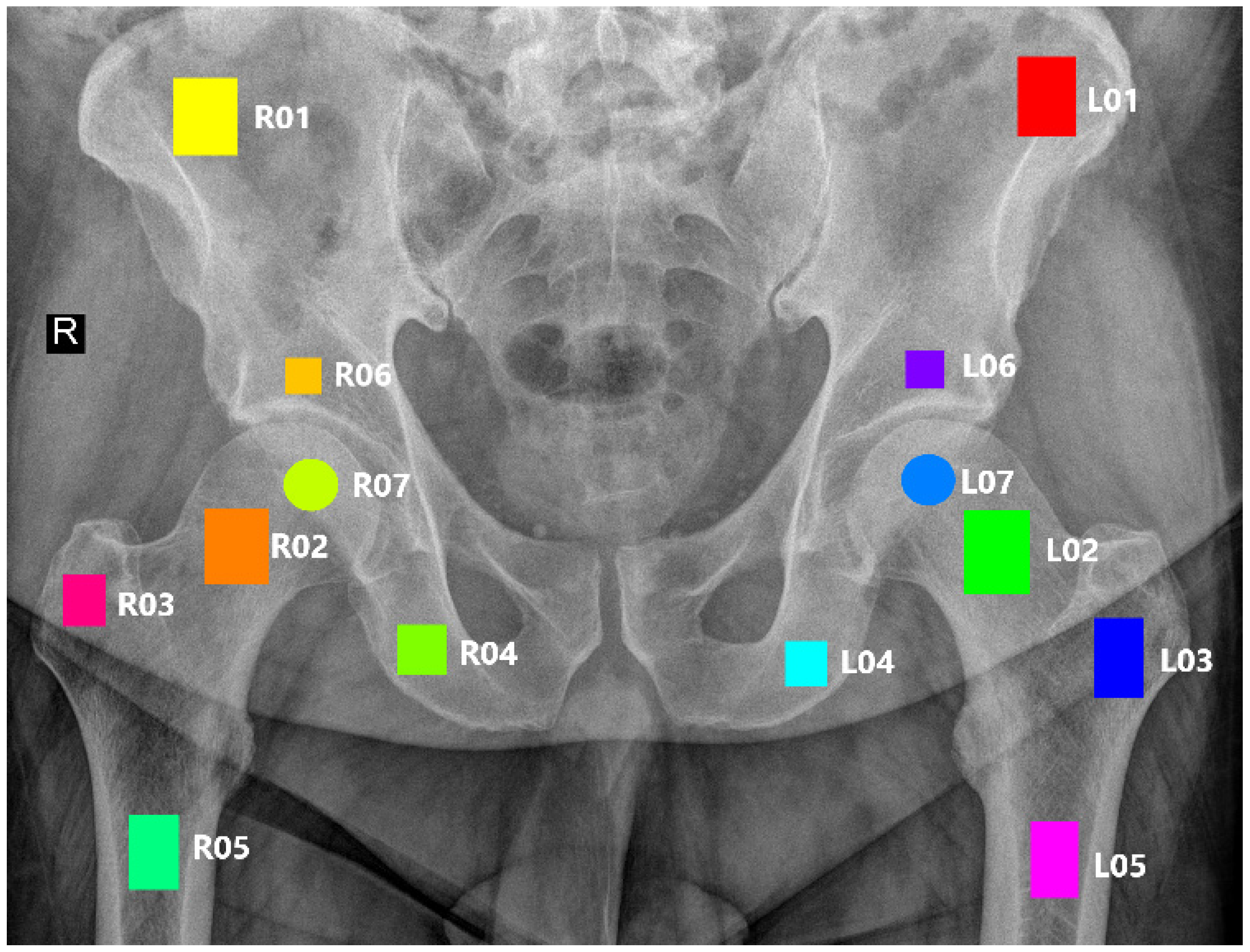
2.2. ROI Annotation
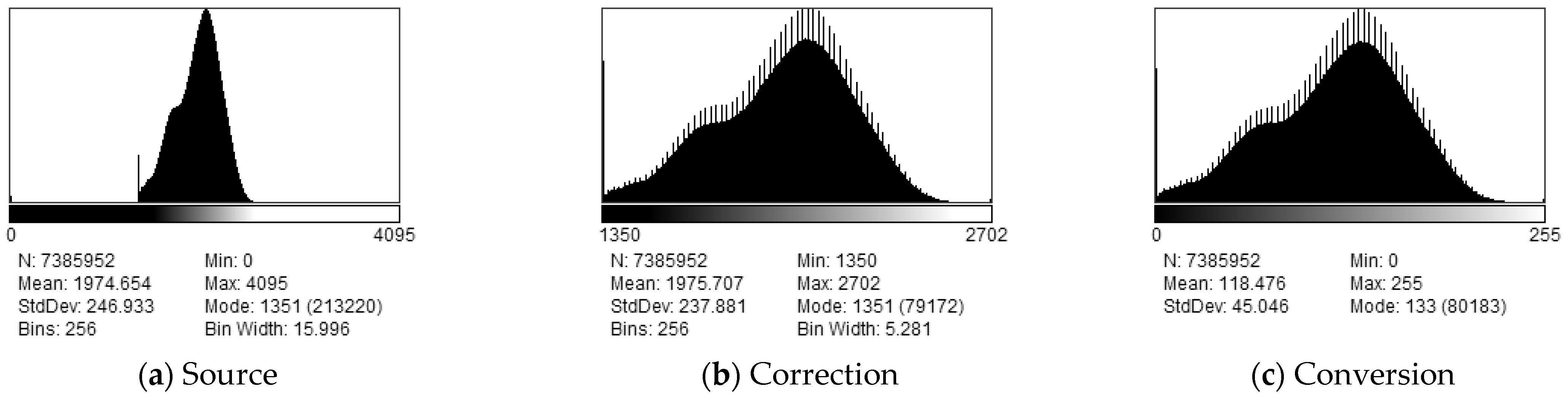
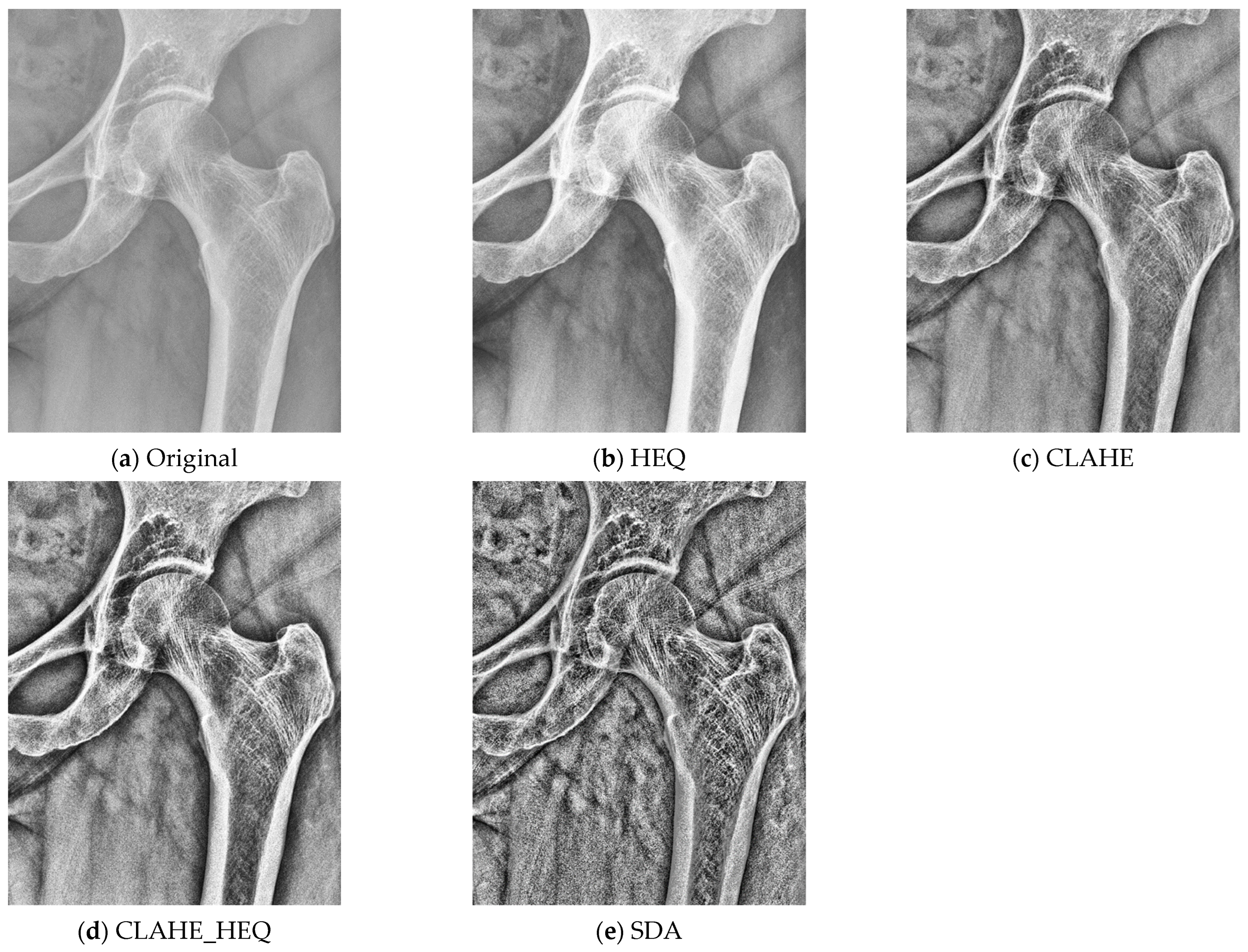
2.3. Preprocessing
2.4. Textural Features
- After designating all the regions of interest (ROIs), we proceeded with the determination of textural features based on pyRadiomics [21]. All available textural parameters were computed. In the following text, we will limit ourselves to a concise list of the primary methods employed in our research. The set of parameters was derived from various statistical image descriptors and comprised the following groups (as described in refs. [21,26]):
- First-order features (FOFs) are based on simple statistical information that can be determined from an image histogram. These features include the 10th percentile, 90th percentile, energy, total energy, entropy, minimum, maximum, mean, median, range, inter-quartile range, mean absolute deviation, robust mean absolute deviation, root mean squared, kurtosis, skewness, standard deviation, uniformity, and variance.
- The gray-level co-occurrence matrix (GLCM) derives textural information by considering the spatial distribution of pixel brightness in the image. It consists of the following features: autocorrelation, joint average, cluster prominence, cluster shade, cluster tendance, contrast, correlation, difference average, difference entropy, difference variance, joint energy, joint entropy, informational measure of correlation (IMC) 1, informational measure of correlation (IMC) 2, inverse difference moment, maximal correlation coefficient, inverse difference moment normalized, inverse difference, inverse difference normalized, inverse variance, maximum probability, sum entropy, and the sum of squares.
- The grey-level size zone matrix (GLSZM) provides a statistical representation by estimating a bivariate conditional probability density function of the image distribution values. This matrix takes into account various aspects such as minor area emphasis, significant area emphasis, grey-level non-uniformity, size-zone non-uniformity, zone percentage, grey-level variance, zone variance, zone entropy, low grey-level zone emphasis, high grey-level zone emphasis, small-area low grey-level emphasis, small-area high grey-level emphasis, large-area low grey-level emphasis, and large-area high grey-level emphasis.
- The grey-level run length matrix (GLRLM) considers that images with more frequent changes in pixel brightness next to each other have better contrast, while those where one color is kept longer are blurred. Therefore, the length of pixels with the same color in a linear neighborhood is considered as basic information and used to calculate the following features: short-run emphasis, long-run emphasis, grey-level non-uniformity, grey-level non-uniformity normalized, run length non-uniformity, run length non-uniformity normalized, run percentage, grey-level variance, run variance, run entropy, low grey-level run emphasis, high grey-level run emphasis, short-run low grey-level emphasis, short-run high grey-level emphasis, long-run low grey-level emphasis, and long-run high-grey level emphasis.
- The gray-level dependence matrix (GLDM) evaluates the relationships between the brightness of neighboring pixels in a rectangular area. The following features are derived from this analysis: small dependence emphasis, large dependence emphasis, gray-level non-uniformity, dependence non-uniformity, dependence non-uniformity normalized, gray-level variance, dependence variance, dependence entropy, low gray-level emphasis, high gray-level emphasis, small dependence low gray-level emphasis, small dependence high-gray level emphasis, large dependence low gray-level emphasis, and large dependence high gray-level emphasis.
- The neighboring grey tone difference matrix (NGTDM) determines image information by analyzing the rectangular region and comparing its central pixel brightness with the average one for the whole area. It calculates coarseness, contrast, business, complexity, and strength.
- The gradient map features derive information from the changing magnitude within an ROI. This method calculates five parameters: mean, variance, skewness, kurtosis, and nonzeros.
- The first-order autoregressive model assumes the dependence of pixel intensities of adjacent pixels and aims to find weights of gradient directions that best correlate to the region’s pixel distributions. In consequence, four parameters are calculated.
- The Haar wavelet transform decomposes the image into several sub bands of energies and calculates their frequency characteristics. There are four scale transformations, and the features describe spatial combinations of the resulting low-pass and high-pass values.
- The Gabor transform decomposes the image into frequency components. The valid frequencies are found by convolving the image with proper complex number kernels, while stored parameters describe the Gaussian envelope’s frequency, orientation, and standard deviation.
- The histogram of oriented gradients determines the features from histograms representing the frequency of orientations found in the image. The feature vector constitutes a normalized histogram.
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nieves, J.W.; Formica, C.; Ruffing, J.; Zion, M.; Garrett, P.; Lindsay, R.; Cosman, F. Males Have Larger Skeletal Size and Bone Mass than Females, Despite Comparable Body Size. J. Bone Miner. Res. 2004, 20, 529–535. [Google Scholar] [CrossRef] [PubMed]
- Seeman, E. The structural and biochemical basis of the gain and loss of bone strength in women and men. Endocrinol. Metab. Clin. N. Am. 2003, 32, 25–38. [Google Scholar] [CrossRef] [PubMed]
- Seeman, E. Sexual dimorphism in skeletal size, density and strength. J. Clin. Endocrinol. Metab. 2001, 86, 4576–4584. [Google Scholar] [CrossRef]
- Khosla, S.; Oursler, M.J.; Monroe, D.G. Estrogen and the Skeleton. Trends Endocrinol. Metab. 2012, 23, 576–581. [Google Scholar] [CrossRef] [PubMed]
- Noirrit-Esclassan, E.; Valera, M.-C.; Tremollieres, F.; Arnal, J.-F.; Lenfant, F.; Fontaine, C.; Vinel, A. Critical Role of Estrogens on Bone Homeostasis in Both Male and Female: From Physiology to Medical Implications. Int. J. Mol. Sci. 2021, 22, 1568. [Google Scholar] [CrossRef] [PubMed]
- Demontiero, O.; Vidal, C.; Duque, G. Aging and bone loss: New insights for the clinician. Ther. Adv. Musculoskelet. Dis. 2011, 4, 61–76. [Google Scholar] [CrossRef]
- Hannan, M.T.; Tucker, K.L.; Dawson-Hughes, B.; Cupples, L.A.; Felson, D.T.; Kiel, D.P. Effect of Dietary Protein on Bone Loss in Elderly Men and Women: The Framingham Osteoporosis Study. J. Bone Miner. Res. 2000, 15, 2504–2512. [Google Scholar] [CrossRef] [PubMed]
- Christen, P.; Ito, K.; Ellouz, R.; Boutroy, S.; Sornay-Rendu, E.; Chapurlat, R.D.; van Rietbergen, B. Bone remodelling in humans is load-driven but not lazy. Nat. Commun. 2014, 5, 4855. [Google Scholar] [CrossRef]
- Kamiński, P.; Obuchowicz, R.; Stępień, A.; Lasek, J.; Pociask, E.; Piórkowski, A. Correlation of Bone Textural Parameters with Age in the Context of Orthopedic X-ray Studies. Appl. Sci. 2023, 13, 6618. [Google Scholar] [CrossRef]
- Lewis, C.L.; Laudicina, N.M.; Khuu, A.; Loverro, K.L. The Human Pelvis: Variation in Structure and Function During Gait. Anat. Rec. 2017, 300, 633–642. [Google Scholar] [CrossRef] [PubMed]
- Rajasekhar, S.; Vasudha, T.K.; Aravindhan, K. Sex Determination by Biometry of Anterior Features of Human Hip Bones in South Indian Population. J. Clin. Diagn. Res. 2017, 11, AC13–AC16. [Google Scholar] [CrossRef] [PubMed]
- Spradley, M.K. Metric Methods for the Biological Profile in Forensic Anthropology: Sex, Ancestry, and Stature. Acad. Forensic Pathol. 2016, 6, 391–399. [Google Scholar] [CrossRef] [PubMed]
- de Boer, H.H.; Roberts, J.; Delabarde, T.; Mundorff, A.Z.; Blau, S. Disaster victim identification operations with fragmented, burnt, or commingled remains: Experience-based recommendations. Forensic Sci. Res. 2020, 5, 191–201. [Google Scholar] [CrossRef] [PubMed]
- Bhardwaj, V.; Kumar, I.; Aggarwal, P.; Singh, P.K.; Shukla, R.; Verma, A. Demystifying the Radiography of Age Estimation in Criminal Jurisprudence: A Pictorial Review. Indian J. Radiol. Imaging 2024. [Google Scholar] [CrossRef]
- Nurzynska, K.; Piórkowski, A.; Strzelecki, M.; Kociołek, M.; Banyś, R.P.; Obuchowicz, R. Differentiating age and sex in vertebral body CT scans—Texture analysis versus deep learning approach. Biocybern. Biomed. Eng. 2024, 44, 20–30. [Google Scholar] [CrossRef]
- Paschall, A.; Ross, A.H. Biological sex variation in bone mineral density in the cranium and femur. Sci. Justice 2018, 58, 287–291. [Google Scholar] [CrossRef] [PubMed]
- Sakaran, R.; Alias, A.; Woon, C.K.; Ku Mohd Noor, K.M.; Zaidun, N.H.; Zulkiflee, N.D.I.; Lin, N.W.; Chung, E. Sex estimation on thoracic vertebrae: A systematic review. Transl. Res. Anat. 2023, 31, 100243. [Google Scholar] [CrossRef]
- Romagnoli, E.; Carnevale, V.; Nofroni, I.; D’Erasmo, E.; Paglia, F.; De Geronimo, S.; Pepe, J.; Raejntroph, N.; Maranghi, M.; Minisola, S. Quality of life in ambulatory postmenopausal women: The impact of reduced bone mineral density and subclinical vertebral fractures. Osteoporos Int. 2004, 15, 975–980. [Google Scholar] [CrossRef] [PubMed]
- Buller, L.T.; Best, M.J.; Quinnan, S.M. A nationwide analysis of pelvic ring fractures: Incidence and trends in treatment, length of stay, and mortality. Geriatr. Orthop. Surg. Rehabil. 2016, 7, 9–17. [Google Scholar] [CrossRef] [PubMed]
- Oura, P.; Junno, J.A.; Hunt, D.; Lehenkari, P.; Tuukkanen, J.; Maijanen, H. Deep learning in sex estimation from knee radiographs—A proof-of-concept study utilizing the Terry Anatomical Collection. Leg. Med. 2023, 61, 102211. [Google Scholar] [CrossRef] [PubMed]
- van Griethuysen, J.J.M.; Fedorov, A.; Parmar, C.; Hosny, A.; Aucoin, N.; Narayan, V.; Beets-Tan, R.G.H.; Fillion-Robin, J.-C.; Pieper, S.; Aerts, H.J.W.L. Computational Radiomics System to Decode the Radiographic Phenotype. Cancer Res. 2017, 77, e104–e107. [Google Scholar] [CrossRef] [PubMed]
- Szczypiński, P.M.; Strzelecki, M.; Materka, A.; Klepaczko, A. MaZda—The Software Package for Textural Analysis of Bio-medical Images. In Computers in Medical Activity; Kącki, E., Rudnicki, M., Stempczyńska, J., Eds.; Advances in Soft Computing; Springer: Berlin/Heidelberg, Germany, 2009; Volume 65, pp. 73–84. ISBN 978-3-642-04461-8. [Google Scholar]
- Pizer, S.; Amburn, E.; Austin, J.; Cromartie, R. Adaptive histogram equalization and its variations. Comput. Vis. Graph. Image Process. 1987, 39, 355–368. [Google Scholar] [CrossRef]
- Piorkowski, A. A Statistical Dominance Algorithm for Edge Detection and Segmentation of Medical Images. In Proceedings of the Information Technologies in Medicine: 5th International Conference, ITIB 2016, Kamień Śląski, Poland, 20–22 June 2016; Springer International Publishing: Cham, Switzerland, 2016. AISC Volume 471. Volume 1, pp. 3–14. [Google Scholar]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Obuchowicz, R.; Nurzynska, K.; Pierzchała, M.; Piorkowski, A.; Strzelecki, M. Texture analysis for the bone age assessment from MRI images of adolescent wrists in boys. J. Clin. Med. 2023, 12, 2762. [Google Scholar] [CrossRef]
- Kociołek, M.; Strzelecki, M.; Obuchowicz, R. Does image normalization and intensity resolution impact texture classification? Comput. Med. Imaging Graph. 2020, 81, 101716. [Google Scholar] [CrossRef] [PubMed]
- Mazur, P. The Influence of Bit-Depth Reduction on Correlation of Texture Features with a Patient’s Age. In Progress in Image Processing, Pattern Recognition and Communication Systems; Choraś, M., Choraś, R.S., Kurzyński, M., Trajdos, P., Pejaś, J., Hyla, T., Eds.; Lecture Notes in Networks and Systems; Springer International Publishing: Cham, Switzerland, 2022; Volume 255, pp. 191–198. [Google Scholar]
- Strzelecki, M.; Kociołek, M.; Materka, A. On the Influence of Image Features Wordlength Reduction on Texture Classification. In Proceedings of the International Conference on Information Technologies in Biomedicine, ITIB 2018, Kamień Śląski, Poland, 18–20 June 2018; Advances in Intelligent Systems and Computing. Springer: Cham, Switzerland, 2016; Volume 762, pp. 15–26. [Google Scholar] [CrossRef]
- Bruzek, J.; Murail, P. Methodology and reliability of sex determination from the skeleton. In Forensic Anthropology and Medicine; Humana Press: Totowa, NJ, USA, 2006; pp. 225–242. [Google Scholar] [CrossRef]
- Bytheway, J.A.; Ross, A.H. A geometric morphometric approach to sex determination of the human adult os coxa. J. Forensic Sci. 2010, 55, 859–864. [Google Scholar] [CrossRef]
- Fukuta, M.; Kato, C.; Biwasaka, H.; Usui, A.; Horita, T.; Kanno, S.; Kato, H.; Aoki, Y. Sex estimation of the pelvis by deep learning of two-dimensional depth images generated from homologous models of three-dimensional computed tomography images. Forensic Sci. Int. Rep. 2020, 2, 100129. [Google Scholar] [CrossRef]
- Poole, K.E.S.; Treece, G.M.; Mayhew, P.M.; Vaculík, J.; Dungl, P.; Horák, M.; Štěpán, J.J.; Gee, A.H. Cortical Thickness Mapping to Identify Focal Osteoporosis in Patients with Hip Fracture. PLoS ONE 2012, 7, e38466. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Wang, L.; Hao, Y.; Wang, Z.; Wang, M.; Ge, S. Analysis of trabecular distribution of the proximal femur in patients with fragility fractures. BMC Musculoskelet. Disord. 2013, 14, 130. [Google Scholar] [CrossRef] [PubMed]
- Purkait, R. Sex determination from femoral head measurements: A new approach. Leg. Med. 2003, 5, S347–S350. [Google Scholar] [CrossRef]
- DiGirolamo, D.J.; Clemens, T.L.; Kousteni, S. The Skeleton as an Endocrine Organ. Nat. Rev. Rheumatol. 2012, 8, 674–683. [Google Scholar] [CrossRef] [PubMed]
- Telfer, S.; Brunnquell, C.L.; Allen, J.D.; Linnau, K.F.; Zamora, D.; Kleweno, C.P. The Effect of Age and Sex on Pelvic Bone Density Measured Opportunistically in Clinical CT Scans. J. Orthop. Res. 2021, 39, 485–492. [Google Scholar] [CrossRef] [PubMed]
- Willett, T.L.; Dapaah, D.Y.; Uppuganti, S.; Granke, M.; Nyman, J.S. Bone Collagen Network Integrity and Transverse Fracture Toughness of Human Cortical Bone. Bone 2019, 120, 187–193. [Google Scholar] [CrossRef] [PubMed]
- Saito, M.; Fujii, K.; Soshi, S.; Tanaka, T. Reductions in Degree of Mineralization and Enzymatic Collagen Cross-Links and Increases in Glycation-Induced Pentosidine in the Femoral Neck Cortex in Cases of Femoral Neck Fracture. Osteoporos. Int. 2006, 17, 986–995. [Google Scholar] [CrossRef] [PubMed]
- Ebraheim, N.; Sabry, F.F.; Nadim, Y.; Xu, R.; Yeasting, R.A. Internal Architecture of the Sacrum in the Elderly. Spine 2000, 25, 292–297. [Google Scholar] [CrossRef] [PubMed]
- Ni, Q.; Nyman, J.S.; Wang, X.; Santos, A.D.L.; Nicolella, D.P. Assessment of Water Distribution Changes in Human Cortical Bone by Nuclear Magnetic Resonance. Meas. Sci. Technol. 2007, 18, 715–723. [Google Scholar] [CrossRef]
- Kirchhoff, C.; Braunstein, V.; Milz, S.; Sprecher, C.M.; Kirchhoff, S.; Graw, M.; Imhoff, A.B.; Hinterwimmer, S. Age and Gender as Determinants of the Bone Quality of the Greater Tuberosity: A HR-PQCT Cadaver Study. BMC Musculoskelet. Disord. 2012, 13, 221. [Google Scholar] [CrossRef] [PubMed]
- Greenwood, C.; Clement, J.; Dicken, A.; Evans, P.; Lyburn, I.; Martin, R.M.; Stone, N.; Zioupos, P.; Rogers, K. Age-Related Changes in Femoral Head Trabecular Microarchitecture. Aging Dis. 2018, 9, 976. [Google Scholar] [CrossRef] [PubMed]
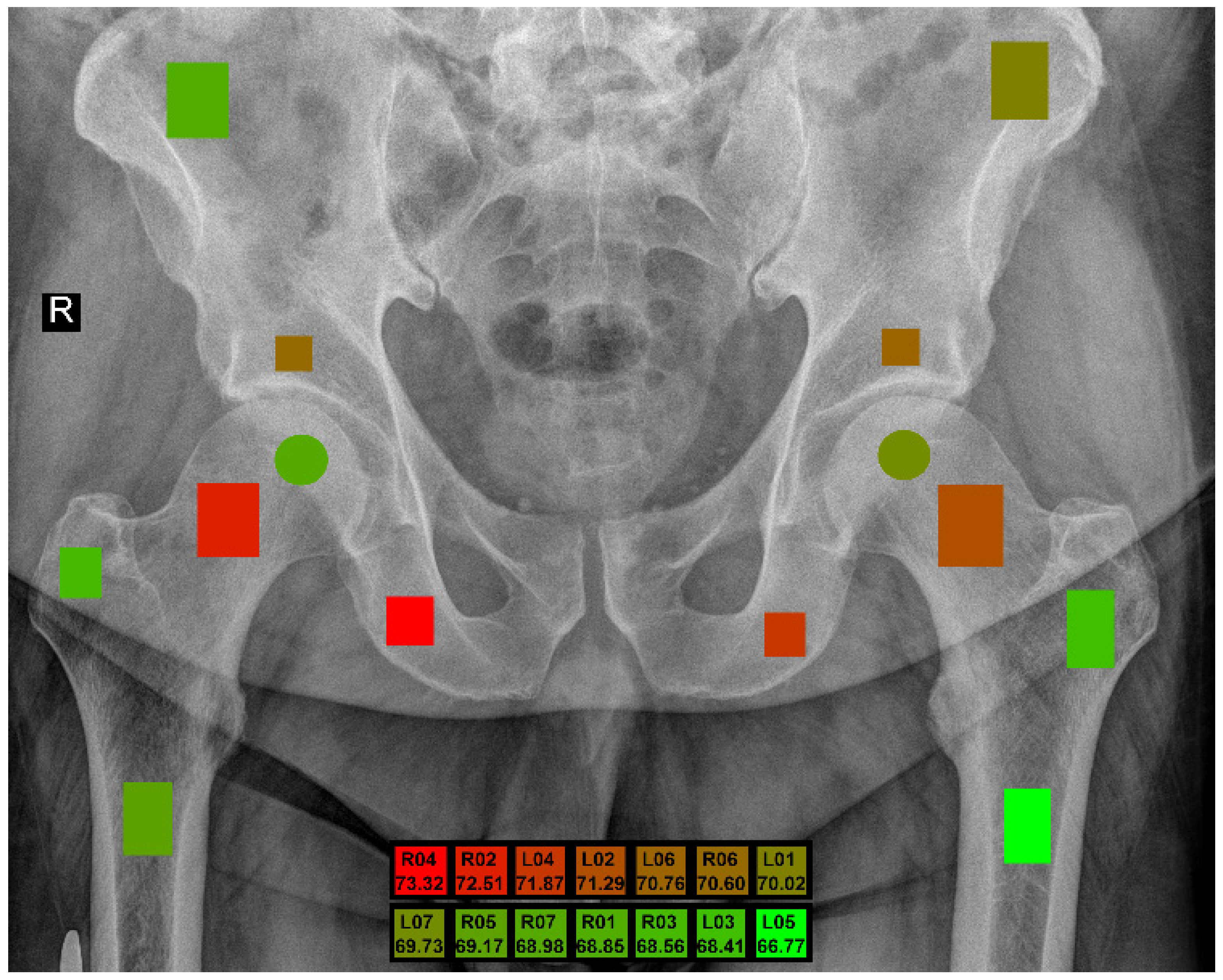
| ROI Left | ROI Right | Anatomical Structure |
|---|---|---|
| L01 | R01 | Wing of ilium |
| L02 | R02 | Neck of femur |
| L03 | R03 | Greater trochanter |
| L04 | R04 | Ischium |
| L05 | R05 | Shaft of femur |
| L06 | R06 | Hip bone above the acetabulum |
| L07 | R07 | Femur head (center) |
| ROI | 5 Bit | 6 Bit | 7 Bit | 8 Bit | Max | Avg |
|---|---|---|---|---|---|---|
| L01 | 66.23 | 68.86 | 69.19 | 70.02 | 70.02 | 68.58 |
| L02 | 71.29 | 70.46 | 70.03 | 70.26 | 71.29 | 70.51 |
| L03 | 68.10 | 68.41 | 67.41 | 68.01 | 68.41 | 67.98 |
| L04 | 71.87 | 71.46 | 71.21 | 71.37 | 71.87 | 71.48 |
| L05 | 64.99 | 66.77 | 63.63 | 63.63 | 66.77 | 64.76 |
| L06 | 70.76 | 68.31 | 68.72 | 69.11 | 70.76 | 69.23 |
| L07 | 69.65 | 69.59 | 69.73 | 69.16 | 69.73 | 69.53 |
| R01 | 67.04 | 68.85 | 67.34 | 66.81 | 68.85 | 67.51 |
| R02 | 71.78 | 71.59 | 72.51 | 71.30 | 72.51 | 71.80 |
| R03 | 68.56 | 66.46 | 67.47 | 68.38 | 68.56 | 67.72 |
| R04 | 73.32 | 70.48 | 72.64 | 71.30 | 73.32 | 71.94 |
| R05 | 69.17 | 67.42 | 67.57 | 68.98 | 69.17 | 68.29 |
| R06 | 67.92 | 68.78 | 70.60 | 69.11 | 70.60 | 69.10 |
| R07 | 66.70 | 67.40 | 68.98 | 67.27 | 68.98 | 67.59 |
| ROI | Bit | Preproc | Filter | Classifier | Accuracy | BACC | Sensitivity | Specificity | F1-Score |
|---|---|---|---|---|---|---|---|---|---|
| L02 | 5 | CLAHE | multi-MIM | SVM_linear | 68.83 | 71.29 | 75.11 | 67.47 | 56.63 |
| 6 | CLAHE | multi-MIM | SVM_rbf | 66.23 | 70.46 | 77.63 | 63.28 | 54.71 | |
| 6 | CLAHE | multi-MIM | SVM_rbf_p | 66.23 | 70.46 | 77.63 | 63.28 | 54.71 | |
| 5 | SDAr50 | multi-CIFE | RF_d4_l5 | 72.05 | 70.36 | 64.87 | 75.85 | 54.62 | |
| 8 | CLAHE | multi-JMI | SVM_rbf | 67.70 | 70.26 | 74.50 | 66.02 | 54.96 | |
| 8 | CLAHE | multi-JMI | SVM_rbf_p | 67.70 | 70.26 | 74.50 | 66.02 | 54.96 | |
| 5 | CLAHE+HEQ | uni-Kendall | LR_d | 68.85 | 70.13 | 70.52 | 69.74 | 54.53 | |
| 6 | SDAr50 | multi-CIFE | SVM_rbf | 68.24 | 70.06 | 72.89 | 67.23 | 54.19 | |
| 6 | SDAr50 | multi-CIFE | SVM_rbf_p | 68.24 | 70.06 | 72.89 | 67.23 | 54.19 | |
| 7 | CLAHE | multi-JMI | SVM_rbf | 66.81 | 70.03 | 75.67 | 64.40 | 54.68 | |
| L04 | 5 | none | uni-Pearson | RF_d4_l5 | 72.04 | 71.87 | 68.96 | 74.79 | 56.61 |
| 5 | none | uni-Pearson | SVM_rbf | 71.75 | 71.74 | 69.06 | 74.43 | 56.28 | |
| 5 | none | uni-Pearson | SVM_rbf_p | 71.75 | 71.74 | 69.06 | 74.43 | 56.28 | |
| 6 | HEQ | multi-MIM | SVM_linear | 68.53 | 71.46 | 75.33 | 67.59 | 55.76 | |
| 6 | HEQ | uni-Fisher | LR_d | 70.29 | 71.45 | 71.32 | 71.58 | 55.07 | |
| 5 | HEQ | PCA | SVM_linear | 69.99 | 71.37 | 72.07 | 70.67 | 55.84 | |
| 8 | CLAHE+HEQ | PCA | LR_d | 70.55 | 71.37 | 71.10 | 71.64 | 54.79 | |
| 8 | CLAHE+HEQ | PCA | SVM_linear | 70.55 | 71.37 | 71.10 | 71.64 | 54.79 | |
| 5 | HEQ | PCA | LR_d | 69.40 | 71.30 | 73.12 | 69.47 | 55.71 | |
| 6 | HEQ | uni-Fisher | SVM_linear | 70.00 | 71.26 | 71.32 | 71.19 | 54.77 | |
| R02 | 7 | SDAr50 | multi-JMI | SVM_rbf | 67.43 | 72.51 | 80.41 | 64.60 | 58.26 |
| 7 | SDAr50 | multi-JMI | SVM_rbf_p | 67.43 | 72.51 | 80.41 | 64.60 | 58.26 | |
| 7 | SDAr50 | multi-JMI | LR_d | 69.16 | 72.42 | 76.92 | 67.93 | 57.46 | |
| 5 | SDAr50 | multi-CIFE | LR_d | 70.00 | 71.78 | 73.59 | 69.97 | 56.40 | |
| 5 | SDAr50 | PCA | SVM_rbf | 71.75 | 71.67 | 68.96 | 74.38 | 56.16 | |
| 5 | SDAr50 | PCA | SVM_rbf_p | 71.75 | 71.67 | 68.96 | 74.38 | 56.16 | |
| 7 | SDAr50 | PCA | LR_d | 67.95 | 71.62 | 77.23 | 66.01 | 55.71 | |
| 6 | CLAHE+HEQ | PCA | LR_d | 70.02 | 71.59 | 72.16 | 71.02 | 55.85 | |
| 7 | SDAr50 | PCA | SVM_linear | 67.66 | 71.45 | 77.23 | 65.66 | 55.57 | |
| 6 | CLAHE+HEQ | PCA | SVM_rbf | 70.89 | 71.44 | 69.95 | 72.93 | 55.95 | |
| R04 | 5 | CLAHE+HEQ | multi-CIFE | SVM_rbf | 70.58 | 73.32 | 77.31 | 69.33 | 57.94 |
| 5 | CLAHE+HEQ | multi-CIFE | SVM_rbf_p | 70.58 | 73.32 | 77.31 | 69.33 | 57.94 | |
| 7 | CLAHE+HEQ | multi-CIFE | SVM_rbf | 69.12 | 72.64 | 78.25 | 67.03 | 57.03 | |
| 7 | CLAHE+HEQ | multi-CIFE | SVM_rbf_p | 69.12 | 72.64 | 78.25 | 67.03 | 57.03 | |
| 5 | CLAHE+HEQ | multi-CIFE | RF_d4_l5 | 72.33 | 71.41 | 67.48 | 75.33 | 56.30 | |
| 8 | CLAHE+HEQ | multi-CIFE | SVM_rbf | 67.38 | 71.30 | 77.29 | 65.31 | 55.93 | |
| 8 | CLAHE+HEQ | multi-CIFE | SVM_rbf_p | 67.38 | 71.30 | 77.29 | 65.31 | 55.93 | |
| 5 | none | uni-Pearson | SVM_rbf | 68.88 | 70.66 | 72.22 | 69.11 | 56.22 | |
| 5 | none | uni-Pearson | SVM_rbf_p | 68.88 | 70.66 | 72.22 | 69.11 | 56.22 | |
| 6 | CLAHE+HEQ | multi-CIFE | SVM_rbf | 66.81 | 70.48 | 76.08 | 64.88 | 54.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamiński, P.; Nurzynska, K.; Kwiecień, J.; Obuchowicz, R.; Piórkowski, A.; Pociask, E.; Stępień, A.; Kociołek, M.; Strzelecki, M.; Augustyniak, P. Sex Differentiation of Trabecular Bone Structure Based on Textural Analysis of Pelvic Radiographs. J. Clin. Med. 2024, 13, 1904. https://doi.org/10.3390/jcm13071904
Kamiński P, Nurzynska K, Kwiecień J, Obuchowicz R, Piórkowski A, Pociask E, Stępień A, Kociołek M, Strzelecki M, Augustyniak P. Sex Differentiation of Trabecular Bone Structure Based on Textural Analysis of Pelvic Radiographs. Journal of Clinical Medicine. 2024; 13(7):1904. https://doi.org/10.3390/jcm13071904
Chicago/Turabian StyleKamiński, Paweł, Karolina Nurzynska, Joanna Kwiecień, Rafał Obuchowicz, Adam Piórkowski, Elżbieta Pociask, Aleksandra Stępień, Marcin Kociołek, Michał Strzelecki, and Piotr Augustyniak. 2024. "Sex Differentiation of Trabecular Bone Structure Based on Textural Analysis of Pelvic Radiographs" Journal of Clinical Medicine 13, no. 7: 1904. https://doi.org/10.3390/jcm13071904
APA StyleKamiński, P., Nurzynska, K., Kwiecień, J., Obuchowicz, R., Piórkowski, A., Pociask, E., Stępień, A., Kociołek, M., Strzelecki, M., & Augustyniak, P. (2024). Sex Differentiation of Trabecular Bone Structure Based on Textural Analysis of Pelvic Radiographs. Journal of Clinical Medicine, 13(7), 1904. https://doi.org/10.3390/jcm13071904










