Deep Learning and Machine Learning with Grid Search to Predict Later Occurrence of Breast Cancer Metastasis Using Clinical Data
Abstract
1. Background
2. Methods
2.1. Datasets
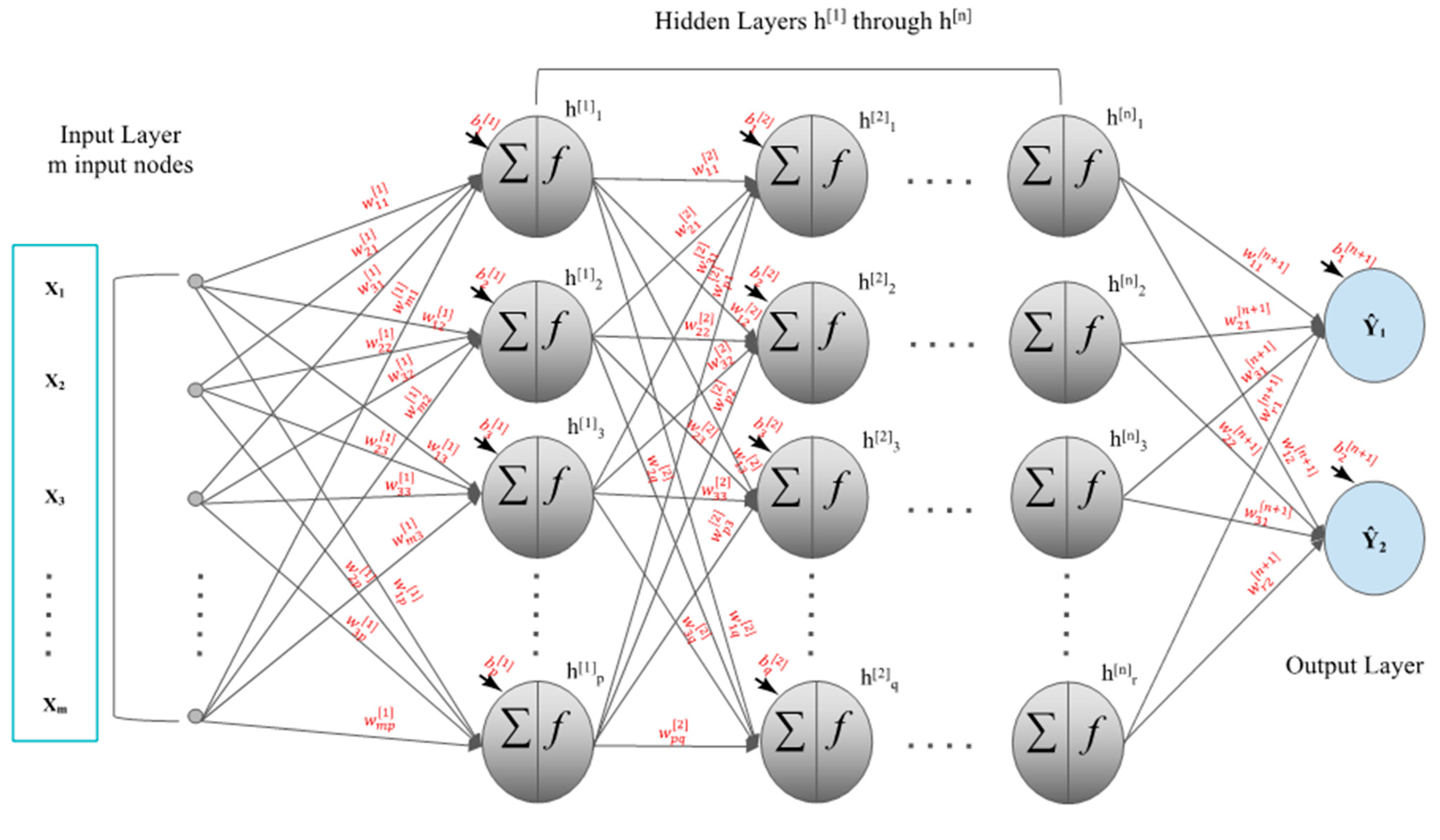
2.2. Feedforward Neural Networks
2.3. Hyperparameter Tuning with Grid Search
2.4. Overfitting
2.4.1. Performance Metrics and 5-Fold Cross-Validation
2.4.2. Comparison to 9 Other Machine Learning Methods
2.4.3. Statistical Testing
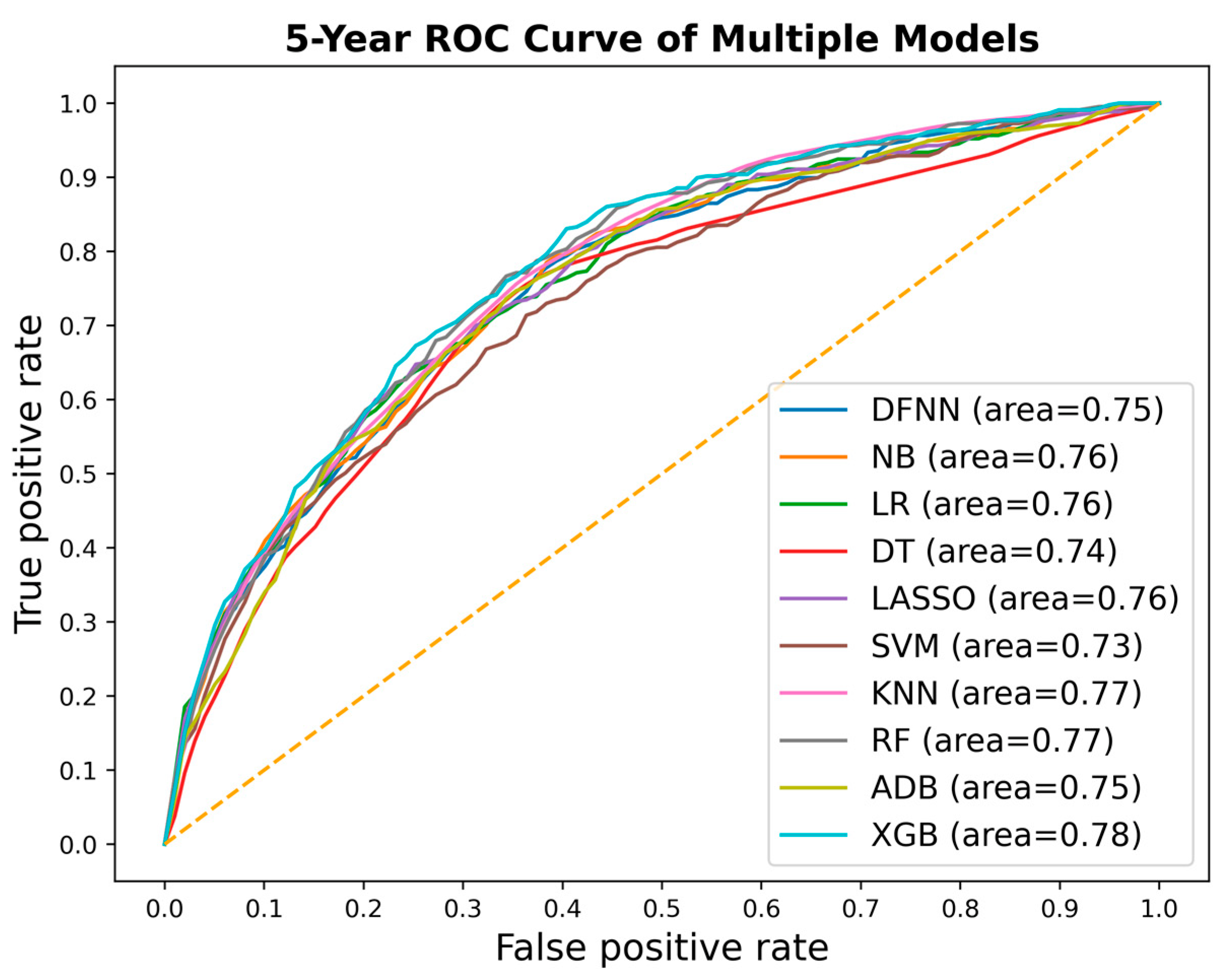
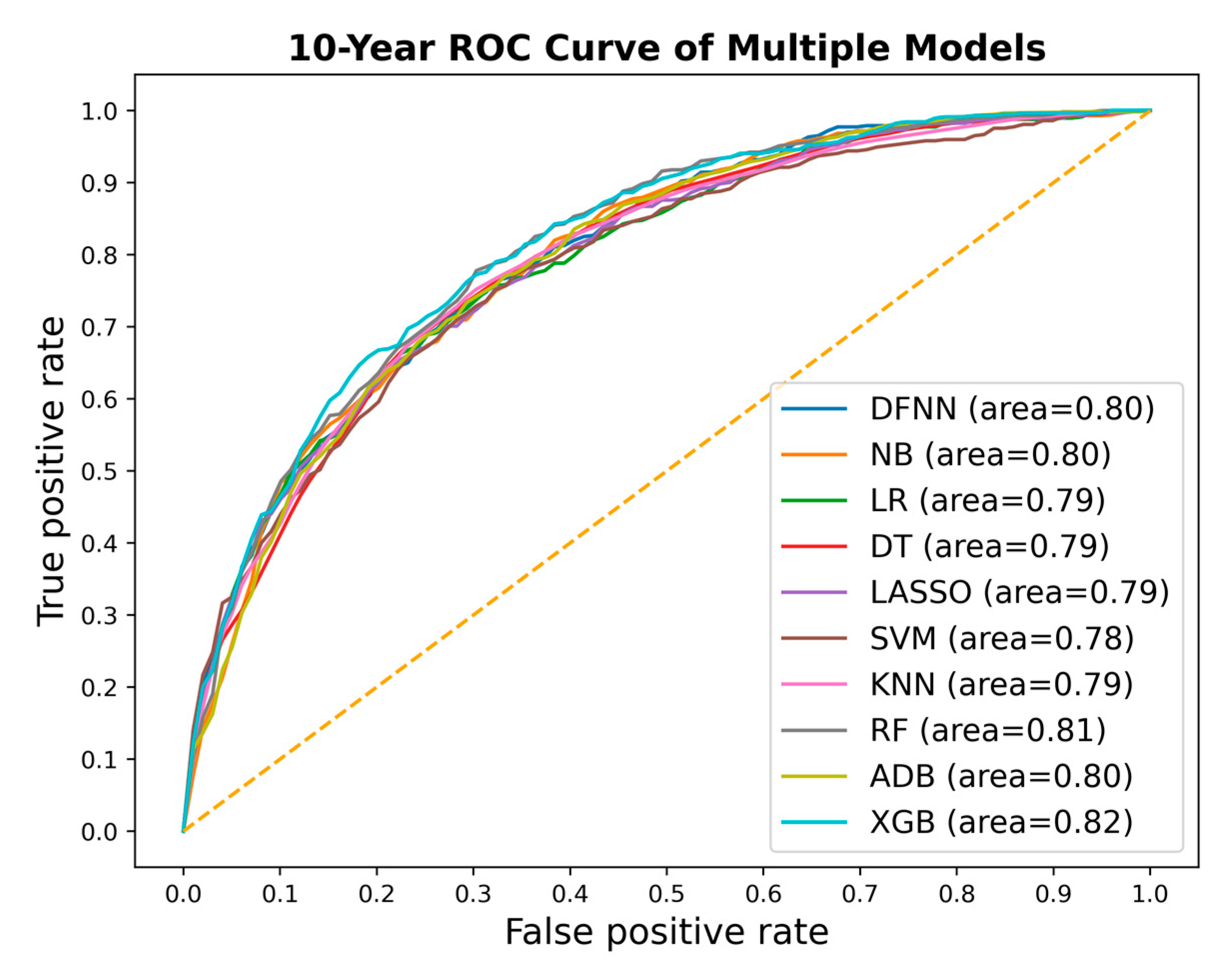
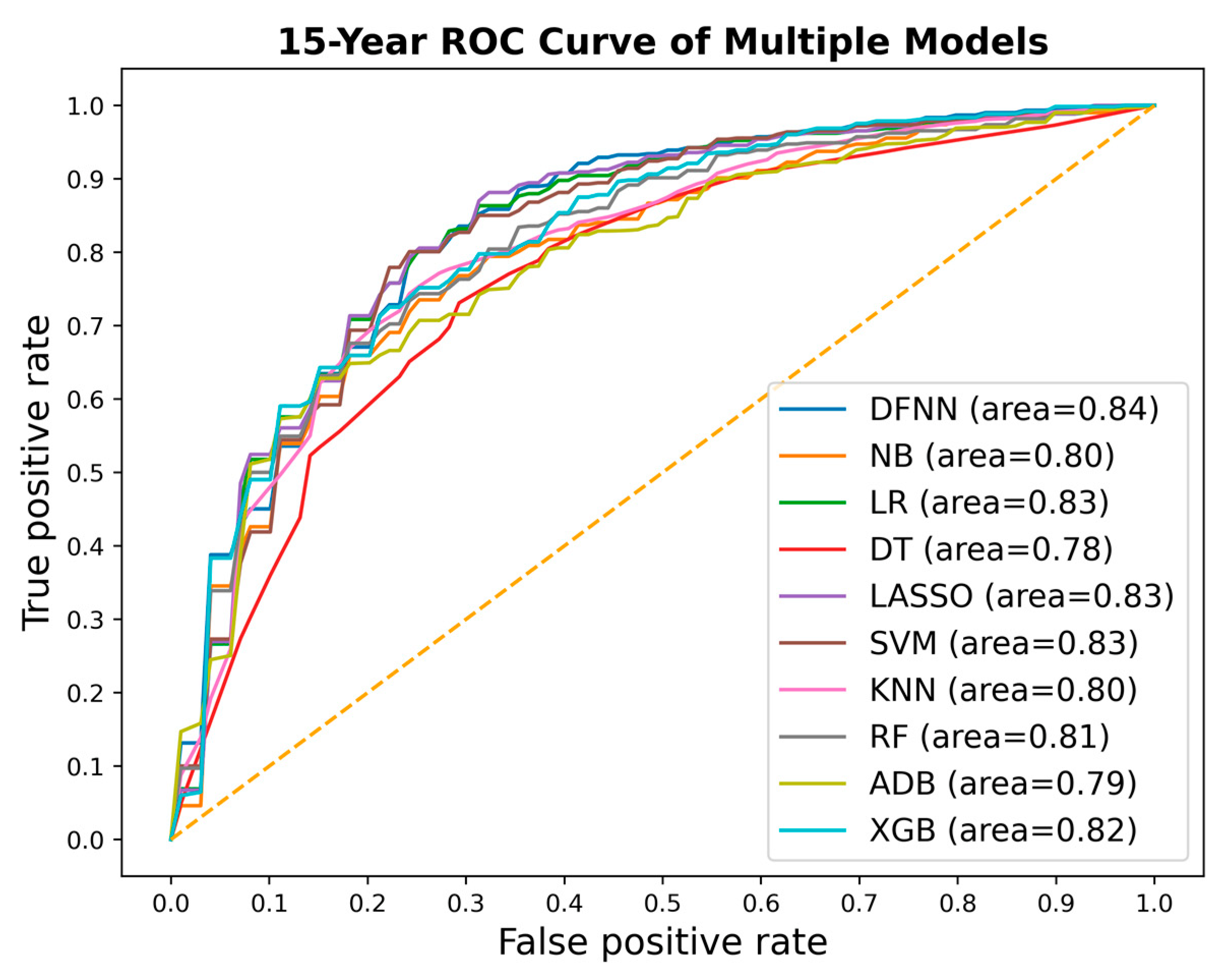
3. Results
4. Discussion
4.1. The Potential Effects of Data Imbalance
4.2. Computation Time
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global Cancer Statistics 2020: GLOBOCAN Estimates of Incidence and Mortality Worldwide for 36 Cancers in 185 Countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef] [PubMed]
- Rahib, L.; Wehner, M.R.; Matrisian, L.M.; Nead, K.T. Estimated Projection of US Cancer Incidence and Death to 2040. JAMA Netw. Open 2021, 4, e214708. [Google Scholar] [CrossRef] [PubMed]
- American Cancer Society. Cancer Facts & Figures. 2021. Available online: https://www.cancer.org/research/cancer-facts-statistics/all-cancer-facts-figures/cancer-facts-figures-2021.html (accessed on 8 July 2021).
- DeSantis, C.E.; Ma, J.; Gaudet, M.M.; Newman, L.A.; Miller, K.D.; Goding Sauer, A.; Jemal, A.; Siegel, R.L. Breast cancer statistics, 2019. CA Cancer J. Clin. 2019, 69, 438–451. [Google Scholar] [CrossRef] [PubMed]
- Afifi, A.; Saad, A.M.; Al-Husseini, M.J.; Elmehrath, A.O.; Northfelt, D.W.; Sonbol, M.B. Causes of death after breast cancer diagnosis: A US population-based analysis. Cancer 2019, 126, 1559–1567. [Google Scholar] [CrossRef]
- Siegel, R.L.; Miller, K.D.; Jemal, A. Cancer statistics, 2020. CA Cancer J. Clin. 2020, 70, 7–30. [Google Scholar] [CrossRef]
- Gupta, G.P.; Massagué, J. Cancer Metastasis: Building a Framework. Cell 2006, 127, 679–695. [Google Scholar] [CrossRef]
- Weigelt, B.; Horlings, H.; Kreike, B.; Hayes, M.; Hauptmann, M.; Wessels, L.; de Jong, D.; Van de Vijver, M.; Veer, L.V.; Peterse, J. Refinement of breast cancer classification by molecular characterization of histological special types. J. Pathol. 2008, 216, 141–150. [Google Scholar] [CrossRef]
- Carey, L.A.; Dees, E.C.; Sawyer, L.; Gatti, L.; Moore, D.T.; Collichio, F.; Ollila, D.W.; Sartor, C.I.; Graham, M.L.; Perou, C.M. The Triple negative paradox: Primary tumor chemosensitivity of breast cancer subtypes. Clin. Cancer Res. 2007, 13, 2329–2334. [Google Scholar] [CrossRef]
- The Cancer Genome Atlas (TCGA) Research Network. Comprehensive molecular portraits of human breast tumours. Nature 2012, 490, 61–70. [Google Scholar] [CrossRef]
- Fisher, B.; Anderson, S.; Bryant, J.; Margolese, R.G.; Deutsch, M.; Fisher, E.R.; Jeong, J.-H.; Wolmark, N. Twenty-Year Follow-up of a Randomized Trial Comparing Total Mastectomy, Lumpectomy, and Lumpectomy plus Irradiation for the Treatment of Invasive Breast Cancer. N. Engl. J. Med. 2002, 347, 1233–1241. [Google Scholar] [CrossRef]
- Zeng, Z.; Espino, S.; Roy, A.; Li, X.; Khan, S.A.; Clare, S.E.; Jiang, X.; Neapolitan, R.E.; Luo, Y. Using natural language processing and machine learning to identify breast cancer local recurrence. BMC Bioinform. 2018, 19, 498. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, K.-Y.; Wong, S.T. Cancer classification and prediction using logistic regression with Bayesian gene selection. J. Biomed. Inform. 2004, 37, 249–259. [Google Scholar] [CrossRef]
- Cai, B.; Jiang, X. Computational methods for ubiquitination site prediction using physicochemical properties of protein sequences. BMC Bioinform. 2016, 17, 116. [Google Scholar] [CrossRef]
- Lee, S.; Jiang, X. Modeling miRNA-mRNA interactions that cause phenotypic abnormality in breast cancer patients. PLoS ONE 2017, 12, e0182666. [Google Scholar] [CrossRef]
- Long, Q.; Chung, M.; Moreno, C.S.; Johnson, B.A. Risk prediction for prostate cancer recurrence through regularized estimation with simultaneous adjustment for nonlinear clinical effects. Ann. Appl. Stat. 2011, 5, 2003–2023. [Google Scholar] [CrossRef]
- Golub, T.R.; Slonim, D.K.; Tamayo, P.; Huard, C.; Gaasenbeek, M.; Mesirov, J.P.; Coller, H.; Loh, M.L.; Downing, J.R.; Caligiuri, M.A.; et al. Molecular Classification of Cancer: Class Discovery and Class Prediction by Gene Expression Monitoring. Science 1999, 286, 531–537. [Google Scholar] [CrossRef]
- Wang, Y.; Makedon, F.S.; Ford, J.C.; Pearlman, J. HykGene: A hybrid approach for selecting marker genes for phenotype classification using microarray gene expression data. Bioinformatics 2005, 21, 1530–1537. [Google Scholar] [CrossRef]
- Mcculloch, W.S.; Pitts, W.H. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Farley, B.; Clark, W. Simulation of self-organizing systems by digital computer. IRE Prof. Group Inf. Theory 1954, 4, 76–84. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning. In Encyclopedia of Machine Learning and Data Mining; Sammut, C., Webb, G.I., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1–11. [Google Scholar]
- Neapolitan, R.E.; Jiang, X. Deep Learning in neural networks: An overview. In Artificial Intelligence; Routledge: London, UK, 2018. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Mcclelland, J.L.; PDP Research Group. A General framework for Parallel Distributed Processing. In PParallel Distributed Processing: Explorations in the Microstructure of Cognition; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Lancashire, L.J.; Powe, D.G.; Reis-Filho, J.S.; Rakha, E.; Lemetre, C.; Weigelt, B.; Abdel-Fatah, T.M.; Green, A.; Mukta, R.; Blamey, R.; et al. A validated gene expression profile for detecting clinical outcome in breast cancer using artificial neural networks. Breast Cancer Res. Treat. 2010, 120, 83–93. [Google Scholar] [CrossRef]
- Belciug, S.; Gorunescu, F. A hybrid neural network/genetic algorithm applied to breast cancer detection and recurrence. Expert Syst. 2013, 30, 243–254. [Google Scholar] [CrossRef]
- Steriti, R.; Fiddy, M. Regularized image reconstruction using SVD and a neural network method for matrix inversion. IEEE Trans. Signal Process. 1993, 41, 3074–3077. [Google Scholar] [CrossRef]
- Hua, J.; Lowey, J.; Xiong, Z.; Dougherty, E.R. Noise-injected neural networks show promise for use on small-sample expression data. BMC Bioinform. 2006, 7, 274. [Google Scholar] [CrossRef]
- Saritas, I. Prediction of Breast Cancer Using Artificial Neural Networks. J. Med. Syst. 2012, 36, 2901–2907. [Google Scholar] [CrossRef]
- Ran, L.; Zhang, Y.; Zhang, Q.; Yang, T. Convolutional neural network-based robot navigation using uncalibrated spherical images. Sensors 2017, 17, 1341. [Google Scholar] [CrossRef]
- Deng, L.; Tur, G.; He, X.; Hakkani-Tur, D. Use of kernel deep convex networks and end-to-end learning for spoken language understanding. In Proceedings of the 2012 IEEE Spoken Language Technology Workshop (SLT), Miami, FL, USA, 2–5 December 2012; pp. 210–215. [Google Scholar] [CrossRef]
- Fernández, S.; Graves, A.; Schmidhuber, J. An Application of Recurrent Neural Networks to Discriminative Keyword Spotting. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2007; pp. 220–229. [Google Scholar] [CrossRef]
- Naik, N.; Madani, A.; Esteva, A.; Keskar, N.S.; Press, M.F.; Ruderman, D.; Agus, D.B.; Socher, R. Deep learning-enabled breast cancer hormonal receptor status determination from base-level H&E stains. Nat. Commun. 2020, 11, 5727. [Google Scholar] [CrossRef]
- Min, S.; Lee, B.; Yoon, S. Deep learning in bioinformatics. Brief. Bioinform. 2016, 18, 851–869. [Google Scholar] [CrossRef]
- Lundervold, A.S.; Lundervold, A. An overview of deep learning in medical imaging focusing on MRI. Z. Med. Phys. 2018, 29, 102–127. [Google Scholar] [CrossRef]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. J. Mach. Learn. Res. 2010, 9, 249–256. [Google Scholar]
- NIH. The Promise of Precision Medicine. Available online: https://www.nih.gov/about-nih/what-we-do/nih-turning-discovery-into-health/promise-precision-medicine (accessed on 9 June 2021).
- Jiang, X.; Wells, A.; Brufsky, A.; Neapolitan, R. A clinical decision support system learned from data to personalize treatment recommendations towards preventing breast cancer metastasis. PLoS ONE 2019, 14, e0213292. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Wells, A.; Brufsky, A.; Shetty, D.; Shajihan, K.; Neapolitan, R.E. Leveraging Bayesian networks and information theory to learn risk factors for breast cancer metastasis. BMC Bioinform. 2020, 21, 298. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Chereda, H.; Bleckmann, A.; Menck, K.; Perera-Bel, J.; Stegmaier, P.; Auer, F.; Kramer, F.; Leha, A.; Beißbarth, T. Explaining decisions of graph convolutional neural networks: Patient-specific molecular subnetworks responsible for metastasis prediction in breast cancer. Genome Med. 2021, 13, 42. [Google Scholar] [CrossRef]
- Lee, Y.-W.; Huang, C.-S.; Shih, C.-C.; Chang, R.-F. Axillary lymph node metastasis status prediction of early-stage breast cancer using convolutional neural networks. Comput. Biol. Med. 2020, 130, 104206. [Google Scholar] [CrossRef]
- Papandrianos, N.; Papageorgiou, E.; Anagnostis, A.; Feleki, A. A deep-learning approach for diagnosis of metastatic breast cancer in bones from whole-body scans. Appl. Sci. 2020, 10, 997. [Google Scholar] [CrossRef]
- Zhou, L.-Q.; Wu, X.-L.; Huang, S.-Y.; Wu, G.-G.; Ye, H.-R.; Wei, Q.; Bao, L.-Y.; Deng, Y.-B.; Li, X.-R.; Cui, X.-W.; et al. Lymph node metastasis prediction from primary breast cancer US images using deep learning. Radiology 2020, 294, 19–28. [Google Scholar] [CrossRef]
- Yang, X.; Wu, L.; Ye, W.; Zhao, K.; Wang, Y.; Liu, W.; Li, J.; Li, H.; Liu, Z.; Liang, C. Deep Learning Signature Based on Staging CT for Preoperative Prediction of Sentinel Lymph Node Metastasis in Breast Cancer. Acad. Radiol. 2020, 27, 1226–1233. [Google Scholar] [CrossRef]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; van der Laak, J.A.W.M.; van Ginneken, B.; Sánchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef]
- Hossain, M.D.Z.; Sohel, F.; Shiratuddin, M.F.; Laga, H. A Comprehensive Survey of Deep Learning for Image Captioning. ACM Comput. Surv. 2019, 51, 1–36. [Google Scholar] [CrossRef]
- Mohanty, S.P.; Hughes, D.P.; Salathé, M. Using deep learning for image-based plant disease detection. Front. Plant Sci. 2016, 7, 1419. [Google Scholar] [CrossRef]
- Szandała, T. Review And comparison of commonly used activation functions for deep neural networks. In Bio-Inspired Neurocomputing; Part of Studies in Computational Intelligence Book Series; Springer: Berlin/Heidelberg, Germany, 2021; pp. 203–224. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Douglass, M.J.J. Book Review: Hands-on Machine Learning with Scikit-Learn, Keras, and Tensorflow, 2nd edition by Aurélien Géron. Phys. Eng. Sci. Med. 2020, 43, 1135–1136. [Google Scholar] [CrossRef]
- Stancin, I.; Jovic, A. An overview and comparison of free Python libraries for data mining and big data analysis. In Proceedings of the 2019 42nd International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 20–24 May 2019. [Google Scholar] [CrossRef]
- Kim, L.S. Understanding the difficulty of training deep feedforward neural networks Xavier. In Proceedings of the International Joint Conference on Neural Networks, Nagoya, Japan, 25–29 October 1993; Volume 2. [Google Scholar]
- Shen, H. Towards a Mathematical Understanding of the Difficulty in Learning with Feedforward Neural Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 811–820. [Google Scholar] [CrossRef]
- Brownlee, J. How to Grid Search Hyperparameters for Deep Learning Models in Python with Keras. Available online: https://machinelearningmastery.com/grid-search-hyperparameters-deep-learning-models-python-keras/ (accessed on 28 June 2022).
- Liashchynskyi, P.; Liashchynskyi, P. Grid Search, Random Search, Genetic Algorithm: A Big Comparison for NAS. arXiv 2019, arXiv:1912.06059. [Google Scholar]
- Alibrahim, H.; Ludwig, S.A. Hyperparameter Optimization: Comparing Genetic Algorithm against Grid Search and Bayesian Optimization. In Proceedings of the 2021 IEEE Congress on Evolutionary Computation (CEC), Kraków, Poland, 28 June–1 July 2021; pp. 1551–1559. [Google Scholar] [CrossRef]
- Ghojogh, B.; Crowley, M. The Theory Behind Overfitting, Cross Validation, Regularization, Bagging, and Boosting: Tuto-Rial. May 2019. Available online: https://arxiv.org/abs/1905.12787v1 (accessed on 8 August 2021).
- Li, Z.; Kamnitsas, K.; Glocker, B. Overfitting of Neural Nets Under Class Imbalance: Analysis and Improvements for Segmentation. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics; Springer: Berlin/Heidelberg, Germany, 2019; pp. 402–410. [Google Scholar] [CrossRef]
- Ying, X. An Overview of Overfitting and its Solutions. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
- Friedman, N.; Geiger, D.; Goldszmidt, M. Bayesian Network Classifiers. Mach. Learn. 1997, 29, 131–163. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Neapolitan, R. Learning Bayesian Networks; Prentice Hall: Hoboken, NJ, USA, 2004; Available online: https://www.amazon.com/Learning-Bayesian-Networks-Richard-Neapolitan/dp/0130125342/ref=sr_1_3?dchild=1&keywords=Learning+Bayesian+Networks&qid=1628620634&sr=8-3 (accessed on 7 October 2021).
- McCallum, A.; Nigam, K. A Comparison of Event Models for Naive Bayes Text Classification. In Proceedings of the AAAI/ICML-98 Workshop on Learning for Text Categorization, Madison, WI, USA, 26–27 July 1998. [Google Scholar]
- Ng, A.Y.; Jordan, M.I. On discriminative vs. Generative classifiers: A comparison of logistic regression and naive bayes. In Advances in Neural Information Processing Systems; Deitterich, T.G., Becker, S., Ghahramani, Z., Eds.; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting. Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Safavian, S.; Landgrebe, D. A Survey of Decision Tree Classifier Methodology. IEEE Trans. Syst. Man Cybern. 1991, 21, 660–674. [Google Scholar] [CrossRef]
- Ho, T.K. Random Decision Forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition (ICDAR), Montreal, QC, Canada, 14–16 August 1995. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Vandewalle, J. Least Squares Support Vector Machine Classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Osuna, E.; Freund, R.; Girosit, F. Training support vector machines: An application to face detection. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, PR, USA, 17–19 June 1997. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Yang, Z.R. Biological applications of support vector machines. Brief. Bioinform. 2004, 5, 328–338. [Google Scholar] [CrossRef] [PubMed]
- Hsu, C.-W.; Chang, C.-C.; Lin, C.-J. A Practical Guide to Support Vector Classification; Department of Computer Science, National Taiwan University: Taipei, Taiwan, 2003. [Google Scholar]
- Wang, H.; Zheng, B.; Yoon, S.W.; Ko, H.S. A support vector machine-based ensemble algorithm for breast cancer diagnosis. Eur. J. Oper. Res. 2018, 267, 687–699. [Google Scholar] [CrossRef]
- Parikh, K.S.; Shah, T.P. Support Vector Machine—A Large Margin Classifier to Diagnose Skin Illnesses. Procedia Technol. 2016, 23, 369–375. [Google Scholar] [CrossRef]
- Tibshirani, R.; Saunders, M.; Rosset, S.; Zhu, J.; Knight, K. Sparsity and smoothness via the fused lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 91–108. [Google Scholar] [CrossRef]
- Weinberger, K.Q.; Blitzer, J.; Saul, L.K. Distance metric learning for large margin nearest neighbor classification. In Advances in Neural Information Processing Systems 18; Weiss, Y., Schölkopf, B., Platt, J.C., Eds.; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Yang, Y.; Liu, X. A re-examination of text categorization methods. In Proceedings of the 22nd Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Berkeley, CA, USA, 15–19 August 1999. [Google Scholar] [CrossRef]
- Weinberger, K.Q.; Saul, L.K. Distance metric learning for large margin nearest neighbor classification. J. Mach. Learn. Res. 2009, 10, 207–244. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.C., Jr.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
- Opitz, D.; Maclin, R. Popular Ensemble Methods: An Empirical Study. J. Artif. Intell. Res. 1999, 11, 169–198. [Google Scholar] [CrossRef]
- Dietterich, T.G. Ensemble methods in machine learning. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1857. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Viola, P.; Jones, M.J. Robust Real-Time Face Detection. Int. J. Comput. Vis. 2004, 57, 137–154. [Google Scholar] [CrossRef]
- Viola, P.; Jones, M. Rapid object detection using a boosted cascade of simple features. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2001), Kauai, HI, USA, 8–14 December 2001; Volume 1. [Google Scholar] [CrossRef]
- Zięba, M.; Tomczak, S.K.; Tomczak, J.M. Ensemble boosted trees with synthetic features generation in application to bankruptcy prediction. Expert Syst. Appl. 2016, 58, 93–101. [Google Scholar] [CrossRef]
- Torlay, L.; Perrone-Bertolotti, M.; Thomas, E.; Baciu, M. Machine learning—XGBoost analysis of language networks to classify patients with epilepsy. Brain Inform. 2017, 4, 159–169. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.; Liu, C.; Li, Y.; Liu, N. A boosted decision tree approach using Bayesian hyper-parameter optimization for credit scoring. Expert Syst. Appl. 2017, 78, 225–241. [Google Scholar] [CrossRef]
- Mousa, S.; Bakhit, P.R.; Osman, O.A.; Ishak, S. A comparative analysis of tree-based ensemble methods for detecting imminent lane change maneuvers in connected vehicle environments. Transp. Res. Rec. J. Transp. Res. Board 2018, 2672, 268–279. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, L.; Ai, H.; Zhang, H.; Fan, Y.; Zhao, Q.; Liu, H. HLPI-Ensemble: Prediction of human lncRNA-protein interactions based on ensemble strategy. RNA Biol. 2018, 15, 797–806. [Google Scholar] [CrossRef]
- Ribeiro, M.H.D.M.; dos Santos Coelho, L. Ensemble approach based on bagging, boosting and stacking for short-term prediction in agribusiness time series. Appl. Soft Comput. 2020, 86, 105837. [Google Scholar] [CrossRef]
- Torres-Barrán, A.; Alonso, Á.; Dorronsoro, J.R. Regression tree ensembles for wind energy and solar radiation prediction. Neurocomputing 2019, 326–327, 151–160. [Google Scholar] [CrossRef]
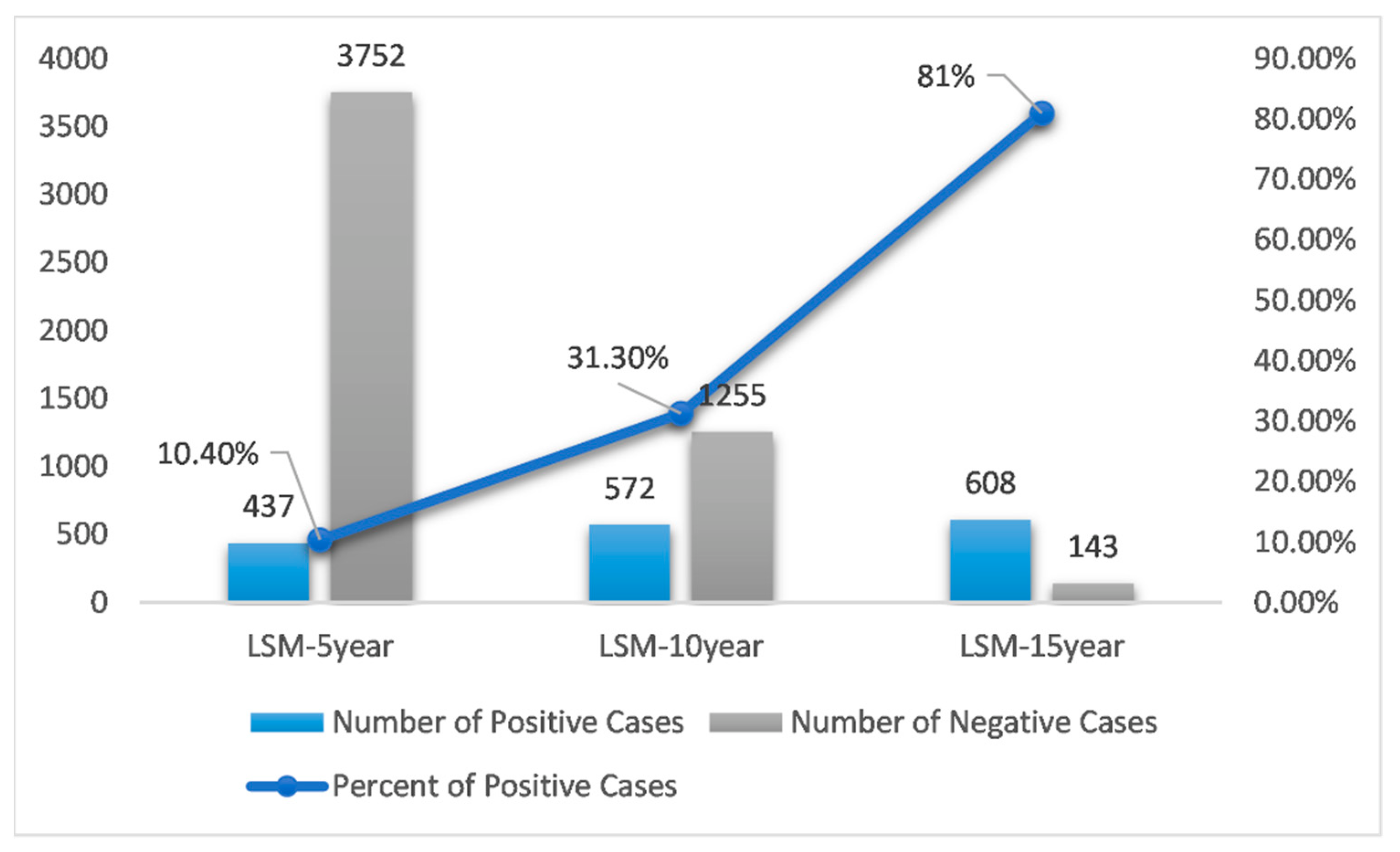
| Total # of Cases | # Positive Cases | # Negative Cases | |
|---|---|---|---|
| LSM-5year | 4189 | 437 | 3752 |
| LSM-10year | 1827 | 572 | 1255 |
| LSM-15year | 751 | 608 | 143 |
| Hyperparameter | Description | Values |
|---|---|---|
| # of Hidden Layers | The depth of a DFNN | 1, 2, 3, 4 |
| # of Hidden Nodes | Number of neurons in a hidden layer | 10, 20, …, 70, 75, 80, 90, … 120, 200, 300, …, 1100 |
| Optimizer | Optimizes internal model parameters towards minimizing the loss | SGD (stochastic gradient descent), AdaGrad |
| Learning rate | Used by both SGD and AdaGrad | 0.001 to 0.3, step size: 0.001 |
| Momentum | Smooths out the curve of gradients by moving average. Used by SGD. | 0, 0.4, 0.5, 0.9 |
| Iteration-based decay | Iteration-based decay; updating learning rate by a decreasing factor in each epoch | 0 0.0001, 0.0002, …, 0.001, 0.002, …, 0.01 |
| Dropout rate | Manage overfitting and training time by randomly selecting nodes to ignore | 0, 0.4, 0.5 |
| Epochs | Number of times model is trained by each of the training set samples exactly once | 20, 30, 50, 80, 100, 200, …, 800 |
| Batch_size | Unit number of samples fed to the optimizer before updating weights | 1, 10, 20, …, 100 |
| L1 (Lebesgue 1) | Sparsity regularization | 0, 0.0005, 0.0008, 0.001, 0.002, 0.005, 0.008, 0.01, 0.02, 0.05, 0, 0.1, 0.2, 0.5 |
| L2 (Lebesgue 2) | Weight decay regularization; it penalizes large weights to adjust the weight updating step | 0, 0.0005, 0.0008, 0.001, 0.002, 0.005, 0.008, 0.01, 0.02, 0.05, 0, 0.1, 0.2, 0.5 |
| L1ORL2 | Using L1 and L2 combinations to regularize overfitting | L1 only, L2 only, L1 and L2 |
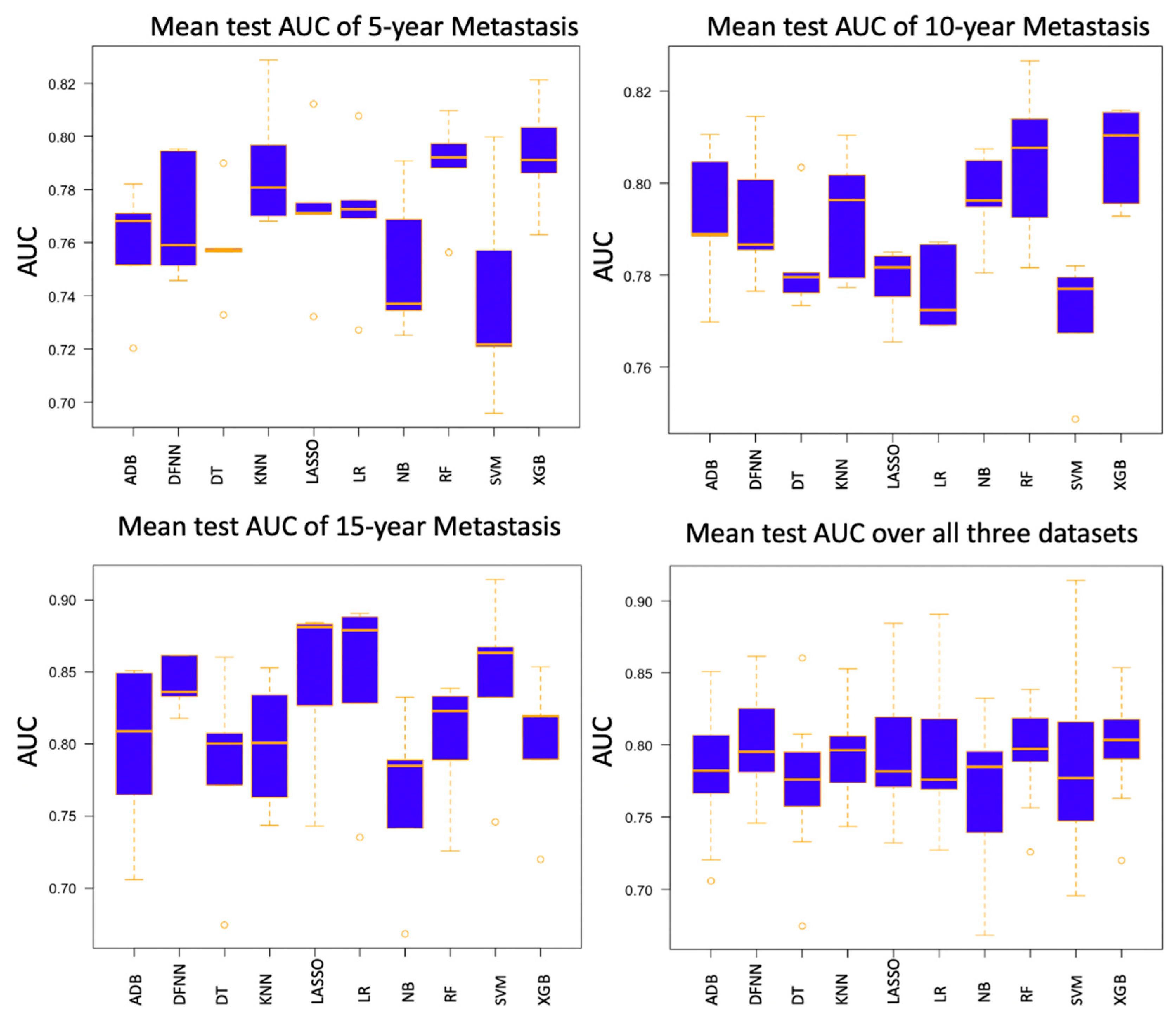
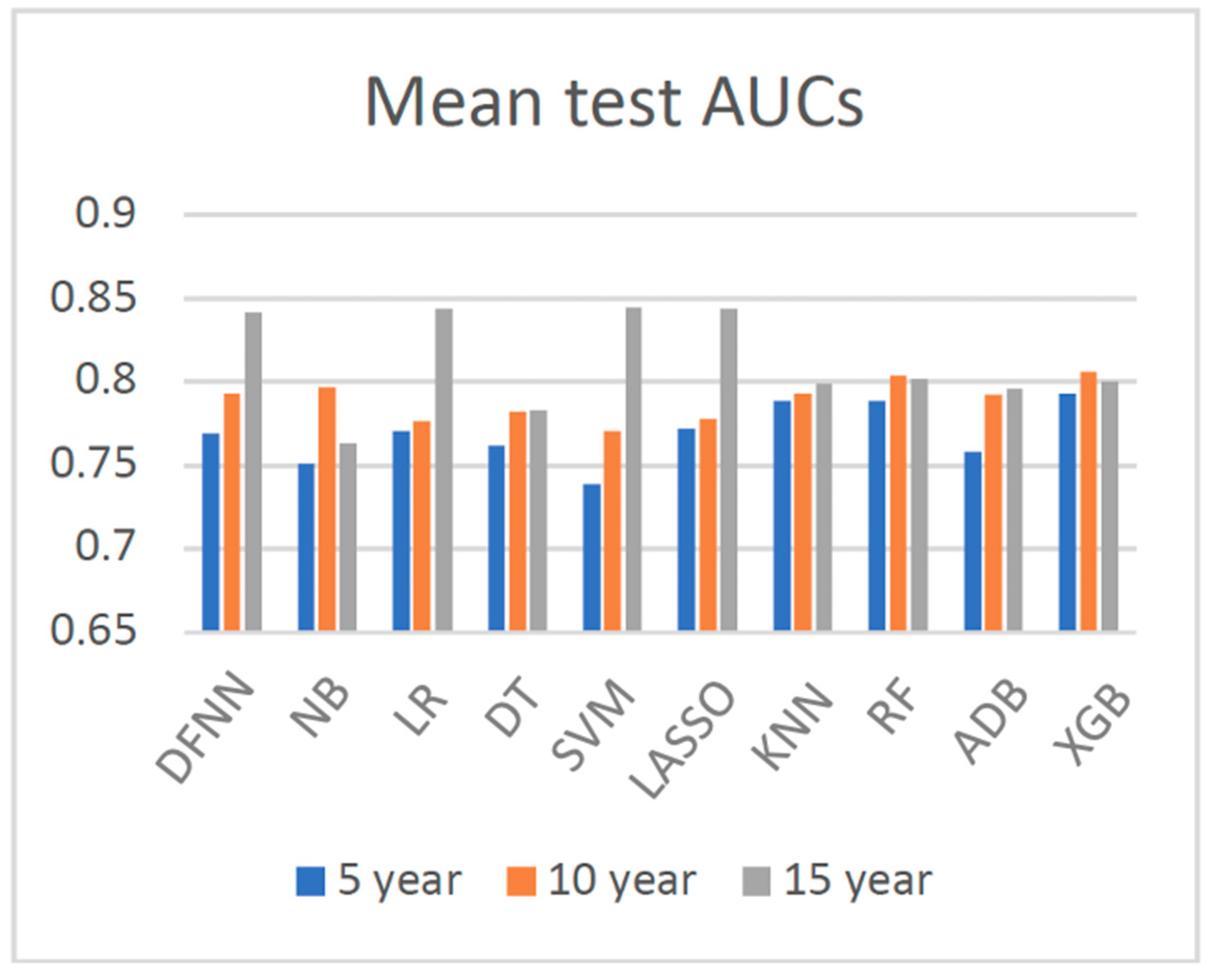
| Mean Test AUC/Mean Train AUC | LSM-5 Year | LSM-10 Year | LSM-15 Year |
|---|---|---|---|
| DFNN | 0.769/0.806 | 0.793/0.830 | 0.842/0.873 |
| NB | 0.751/0.753 | 0.797/0.798 | 0.763/0.826 |
| LR | 0.771 /0.773 | 0.777/0.809 | 0.844/0.884 |
| DT | 0.762/0.780 | 0.783/0.827 | 0.783/0.838 |
| SVM | 0.739/0.811 | 0.771/0.808 | 0.845/0.867 |
| LASSO | 0.772/0.774 | 0.778/0.806 | 0.844/0.887 |
| KNN | 0.789/0.816 | 0.793/0.819 | 0.799/0.832 |
| RF | 0.789/0.801 | 0.804/0.840 | 0.802/0.849 |
| ADB | 0.759/0.754 | 0.792/0.800 | 0.796/0.829 |
| XGB | 0.793/0.813 | 0.806/0.845 | 0.800/0.854 |
| Hyperparameter Values of the Best-Performing Model | LSM-5 Year | LSM-10 Year | LSM-15 Year |
|---|---|---|---|
| Number of hidden layers. | 2 | 1 | 3 |
| Number of hidden nodes | {75, 75} | {75} | {300, 300, 300} |
| Kernel initializer | he_normal | he_normal | he_normal |
| Optimizer | SGD | SGD | SGD |
| Learning rate | 0.005 | 0.01 | 0.005 |
| Momentum Beta | 0.9 | 0.9 | 0.9 |
| Iteration-based decay | 0.01 | 0.01 | 0.01 |
| Dropout rate | 0.5 | 0.5 | 0.5 |
| Epochs | 100 | 100 | 100 |
| L1 (Lebesgue 1) | 0 | 0 | 0 |
| L2 (Lebesgue 1) | 0.008 | 0.008 | 0.008 |
| L1 and L2 combined | No | No | No |
| Method | LSM-5 (Sec) | LSM-10 (Sec) | LSM-15 (Sec) | # of Models Trained | Total Time (Days) |
|---|---|---|---|---|---|
| DFNN | 117.430 | 45.021 | 20.212 | 24,111 | 50.974 |
| NB | 0.060 | 0.046 | 0.026 | 18,109 | 0.028 |
| LR | 0.563 | 0.353 | 0.253 | 22,399 | 0.303 |
| DT | 0.048 | 0.037 | 0.032 | 107,351 | 0.145 |
| LASSO | 0.860 | 0.372 | 0.189 | 1024 | 0.017 |
| SVM | 12.197 | 2.876 | 0.362 | 1799 | 0.321 |
| KNN | 1.636 | 0.436 | 0.132 | 42,341 | 1.080 |
| RF | 0.774 | 0.603 | 0.549 | 27,000 | 0.602 |
| ADB | 0.655 | 0.508 | 0.403 | 13 | 0.000 |
| XGB | 4.710 | 4.566 | 3.850 | 46,980 | 7.137 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X.; Xu, C. Deep Learning and Machine Learning with Grid Search to Predict Later Occurrence of Breast Cancer Metastasis Using Clinical Data. J. Clin. Med. 2022, 11, 5772. https://doi.org/10.3390/jcm11195772
Jiang X, Xu C. Deep Learning and Machine Learning with Grid Search to Predict Later Occurrence of Breast Cancer Metastasis Using Clinical Data. Journal of Clinical Medicine. 2022; 11(19):5772. https://doi.org/10.3390/jcm11195772
Chicago/Turabian StyleJiang, Xia, and Chuhan Xu. 2022. "Deep Learning and Machine Learning with Grid Search to Predict Later Occurrence of Breast Cancer Metastasis Using Clinical Data" Journal of Clinical Medicine 11, no. 19: 5772. https://doi.org/10.3390/jcm11195772
APA StyleJiang, X., & Xu, C. (2022). Deep Learning and Machine Learning with Grid Search to Predict Later Occurrence of Breast Cancer Metastasis Using Clinical Data. Journal of Clinical Medicine, 11(19), 5772. https://doi.org/10.3390/jcm11195772






