Forecasting Postoperative Delirium in Older Adult Patients with Fast-and-Frugal Decision Trees
Abstract
1. Introduction
2. Materials and Methods
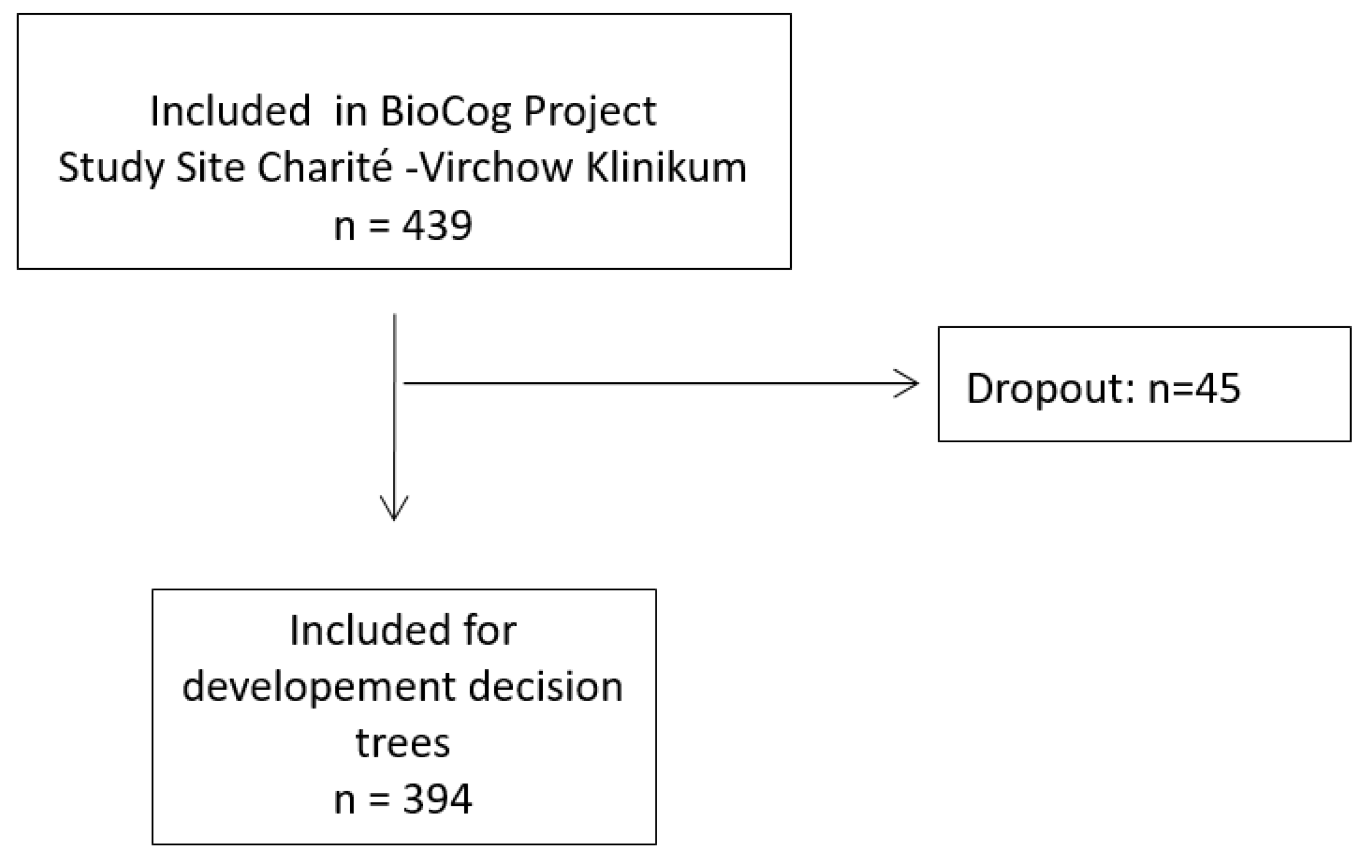
2.1. Overview of the Present Study
2.2. Assessment of Postoperative Delirium
- ≥2 cumulative points on the Nursing Delirium Screening Scale (Nu-DESC) and/or a positive Confusion Assessment Method (CAM) score;
- a positive CAM score for the Intensive Care Unit (CAM-ICU);
- a patient chart review that showed descriptions of delirium (e.g., confused, agitated, drowsy, disorientated, delirious, received antipsychotic therapy).
2.3. Cues
2.4. Model Comparison
2.4.1. Training and Test Set
2.4.2. Model Comparison Procedure
3. Results
3.1. Patient Characteristics
3.2. Model Comparison
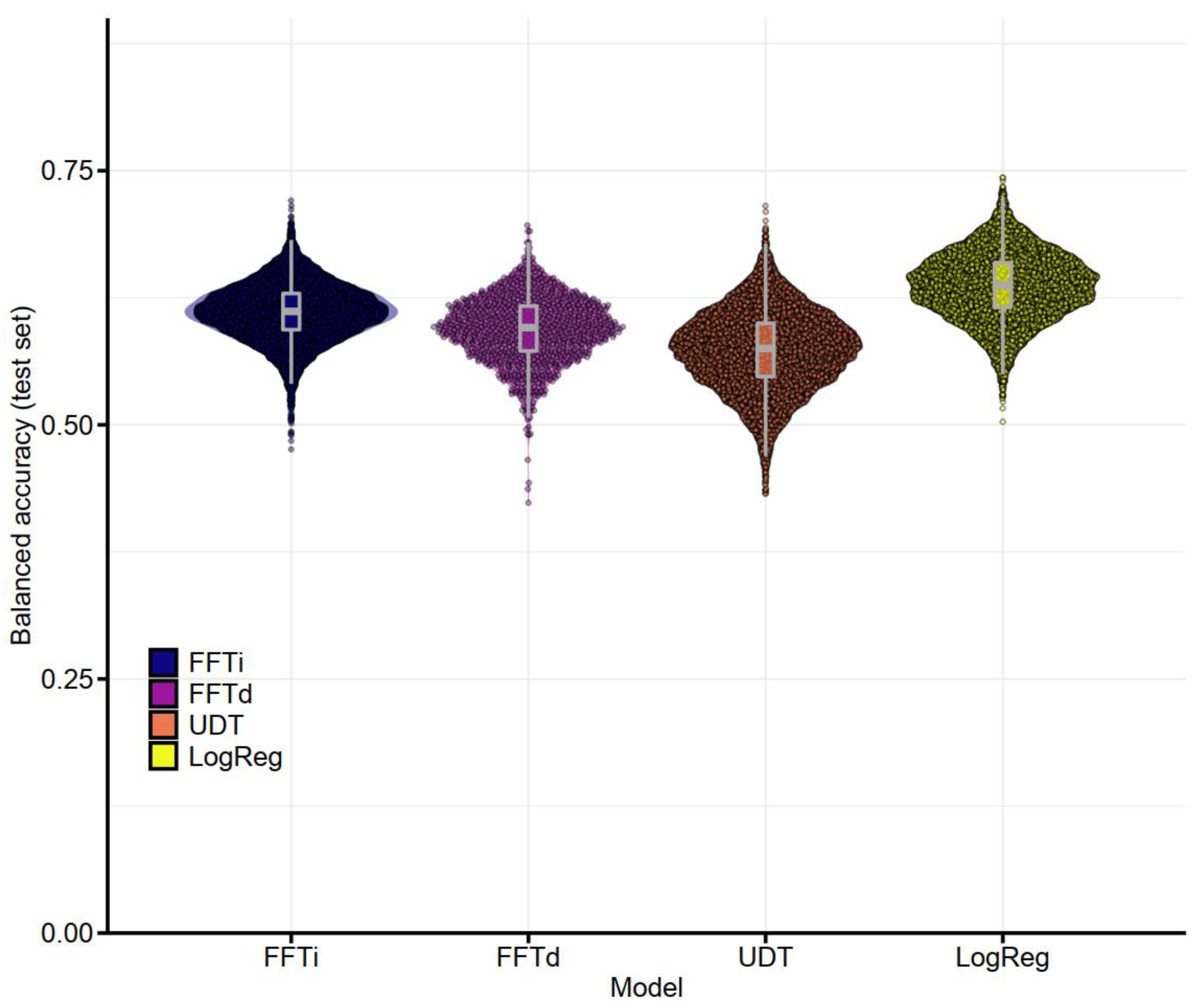
3.2.1. Performance of Pre-Operative Models
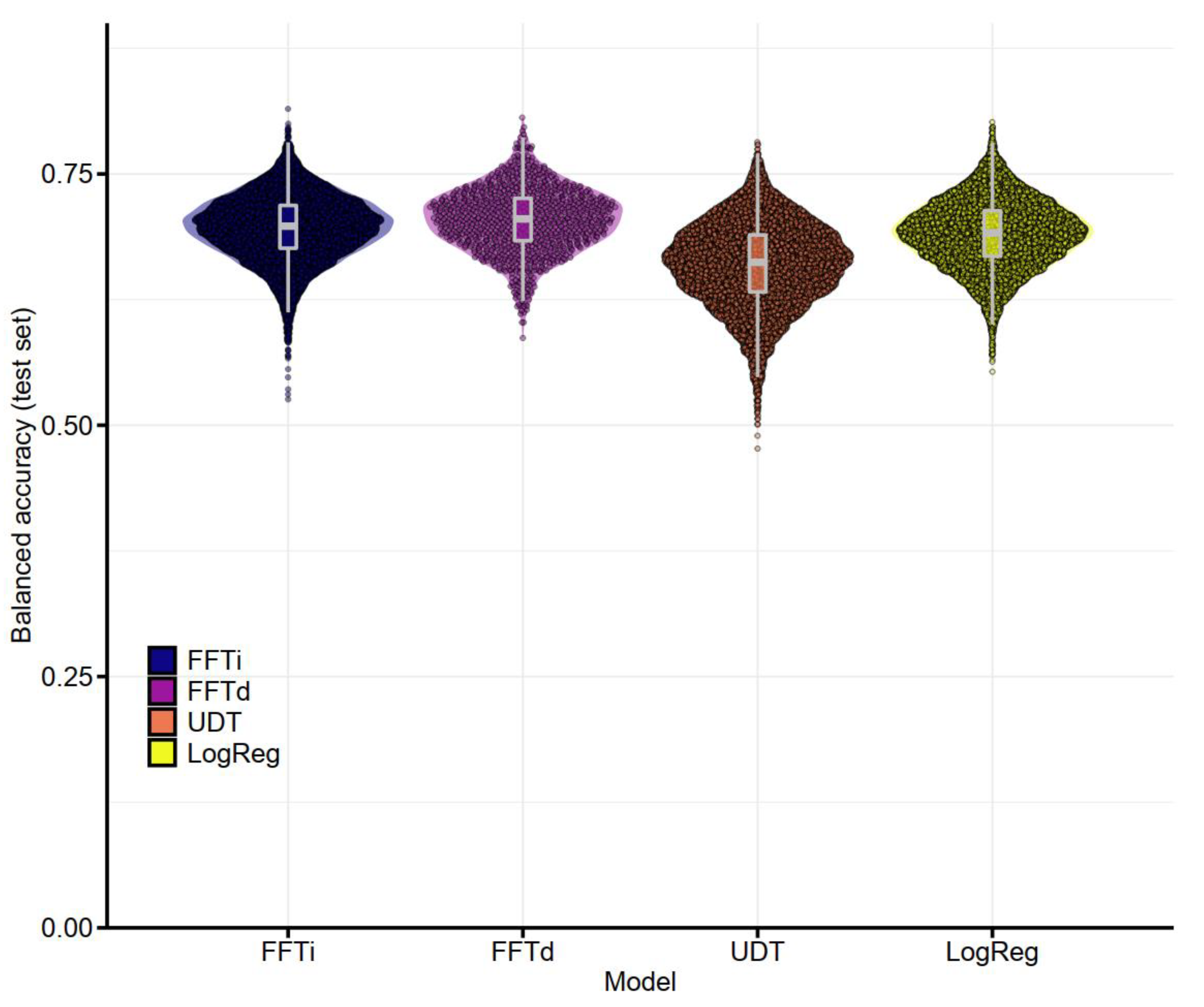
3.2.2. Performance of Postoperative Models
3.3. Decision Trees Based on Full Dataset
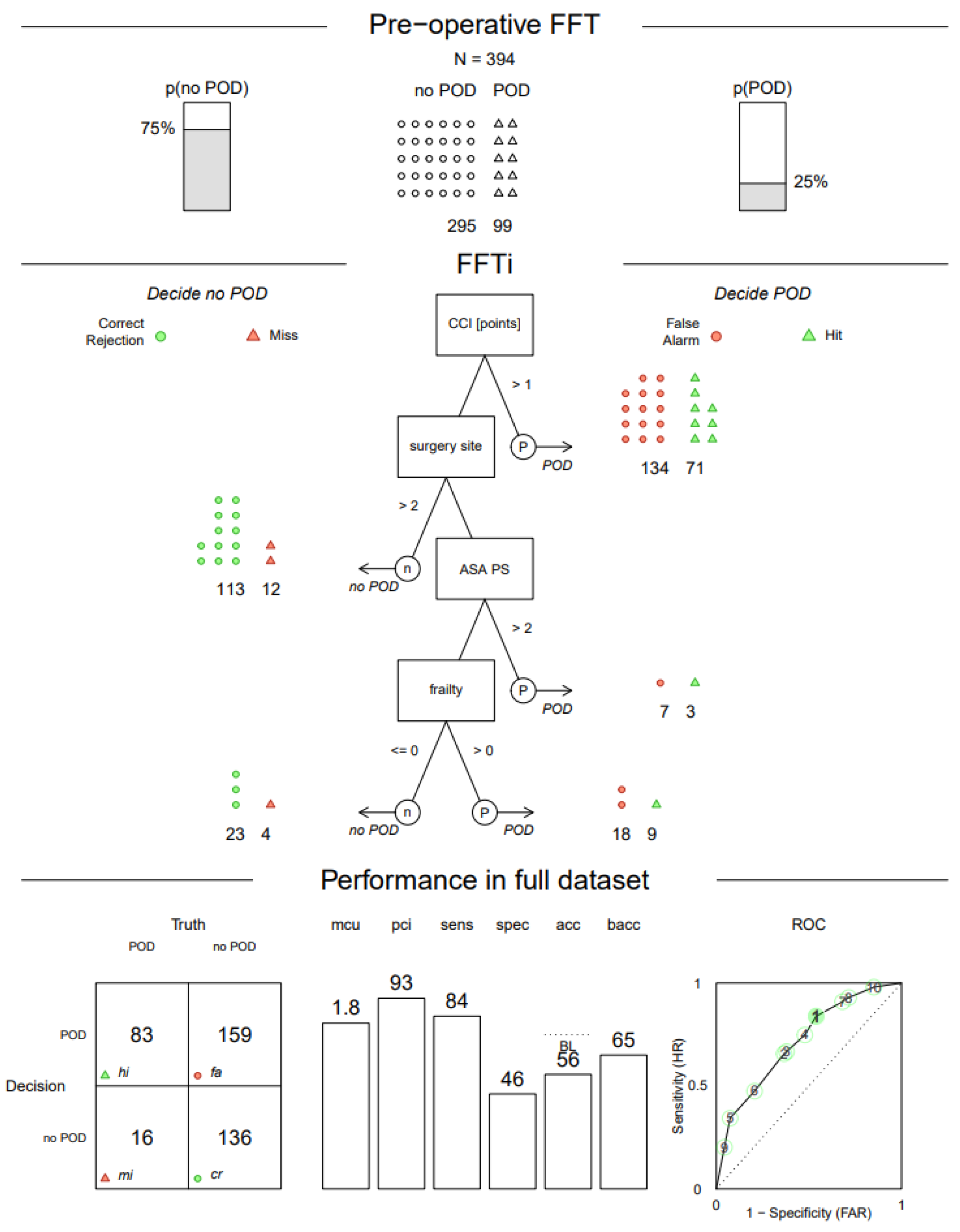
3.3.1. Pre-Operative FFTree
3.3.2. Postoperative FFTree
4. Discussion
Strength and Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hewer, W.; Thomas, C.; Drach, L.M. Delir Beim Alten Menschen; W. Kohlhammer GmbH: Stuttgart, Germany, 2016; Volume 1. [Google Scholar]
- Rengel, K.F.; Pandharipande, P.P.; Hughes, C.G. Postoperative delirium. Presse Med. 2018, 47 Pt 2, e53–e64. [Google Scholar] [CrossRef] [PubMed]
- Bickel, H.; Gradinger, R.; Kochs, E.; Forstl, H. High risk of cognitive and functional decline after postoperative delirium. A three-year prospective study. Dement. Geriatr. Cogn. Disord. 2008, 26, 26–31. [Google Scholar] [CrossRef] [PubMed]
- Moskowitz, E.E.; Overbey, D.M.; Jones, T.S.; Jones, E.L.; Arcomano, T.R.; Moore, J.T.; Robinson, T.N. Post-operative delirium is associated with increased 5-year mortality. Am. J. Surg. 2017, 214, 1036–1038. [Google Scholar] [CrossRef] [PubMed]
- Davis, D.H.; Muniz Terrera, G.; Keage, H.; Rahkonen, T.; Oinas, M.; Matthews, F.E.; Cunningham, C.; Polvikoski, T.; Sulkava, R.; MacLullich, A.M.; et al. Delirium is a strong risk factor for dementia in the oldest-old: A population-based cohort study. Brain A J. Neurol. 2012, 135, 2809–2816. [Google Scholar] [CrossRef]
- Daiello, L.A.; Racine, A.M.; Yun Gou, R.; Marcantonio, E.R.; Xie, Z.; Kunze, L.J.; Vlassakov, K.V.; Inouye, S.K.; Jones, R.N.; Alsop, D.; et al. Postoperative Delirium and Postoperative Cognitive Dysfunction: Overlap and Divergence. Anesthesiology 2019, 131, 477–491. [Google Scholar] [CrossRef]
- Sprung, J.; Roberts, R.O.; Weingarten, T.N.; Nunes Cavalcante, A.; Knopman, D.S.; Petersen, R.C.; Hanson, A.C.; Schroeder, D.R.; Warner, D.O. Postoperative delirium in elderly patients is associated with subsequent cognitive impairment. Br. J. Anaesth. 2017, 119, 316–323. [Google Scholar] [CrossRef]
- Wang, J.; Li, Z.; Yu, Y.; Li, B.; Shao, G.; Wang, Q. Risk factors contributing to postoperative delirium in geriatric patients postorthopedic surgery. Asia-Pac. Psychiatry Off. J. Pac. Rim Coll. Psychiatr. 2015, 7, 375–382. [Google Scholar] [CrossRef]
- Berian, J.R.; Zhou, L.; Russell, M.M.; Hornor, M.A.; Cohen, M.E.; Finlayson, E.; Ko, C.Y.; Rosenthal, R.A.; Robinson, T.N. Postoperative Delirium as a Target for Surgical Quality Improvement. Ann. Surg. 2017, 268, 93–99. [Google Scholar] [CrossRef]
- Inouye, S.K. Predisposing and precipitating factors for delirium in hospitalized older patients. Dement. Geriatr. Cogn. Disord. 1999, 10, 393–400. [Google Scholar] [CrossRef]
- Aldecoa, C.; Bettelli, G.; Bilotta, F.; Sanders, R.D.; Audisio, R.; Borozdina, A.; Cherubini, A.; Jones, C.; Kehlet, H.; MacLullich, A.; et al. European Society of Anaesthesiology evidence-based and consensus-based guideline on postoperative delirium. Eur. J. Anaesthesiol. 2017, 34, 192–214. [Google Scholar] [CrossRef]
- Ho, M.H.; Nealon, J.; Igwe, E.; Traynor, V.; Chang, H.R.; Chen, K.H.; Montayre, J. Postoperative Delirium in Older Patients: A Systematic Review of Assessment and Incidence of Postoperative Delirium. Worldviews Evid. Based Nurs. 2021, 18, 290–301. [Google Scholar] [CrossRef] [PubMed]
- Maldonado, J.R. Neuropathogenesis of delirium: Review of current etiologic theories and common pathways. Am. J. Geriatr. Psychiatry Off. J. Am. Assoc. Geriatr. Psychiatry 2013, 21, 1190–1222. [Google Scholar] [CrossRef]
- Saller, T.; Hofmann-Kiefer, K. Kenntnis und Umsetzung der S3-Leitlinie zum Delirmanagement in Deutschland. Anaesthesist 2016, 65, 755–762. [Google Scholar] [CrossRef] [PubMed]
- Cherak, S.J.; Soo, A.; Brown, K.N.; Ely, E.W.; Stelfox, H.T.; Fiest, K.M. Development and validation of delirium prediction model for critically ill adults parameterized to ICU admission acuity. PLoS ONE 2020, 15, e0237639. [Google Scholar] [CrossRef] [PubMed]
- de la Varga-Martínez, O.; Gómez-Pesquera, E.; Muñoz-Moreno, M.F.; Marcos-Vidal, J.M.; López-Gómez, A.; Rodenas-Gómez, F.; Ramasco, F.; Álvarez-Refojo, F.; Tamayo, E.; Gómez-Sánchez, E. Development and validation of a delirium risk prediction preoperative model for cardiac surgery patients (DELIPRECAS): An observational multicentre study. J. Clin. Anesth. 2021, 69, 110158. [Google Scholar] [CrossRef] [PubMed]
- Inouye, S.K.; Viscoli, C.M.; Horwitz, R.I.; Hurst, L.D.; Tinetti, M.E. A predictive model for delirium in hospitalized elderly medical patients based on admission characteristics. Ann. Intern. Med. 1993, 119, 474–481. [Google Scholar] [CrossRef]
- Pagali, S.R.; Miller, D.; Fischer, K.; Schroeder, D.; Egger, N.; Manning, D.M.; Lapid, M.I.; Pignolo, R.J.; Burton, M.C. Predicting Delirium Risk Using an Automated Mayo Delirium Prediction Tool: Development and Validation of a Risk-Stratification Model. Mayo Clin. Proc. 2021, 96, 1229–1235. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, L.; Qi, Y.; Chen, G.; Zhou, J.; Zhu, H.; Hao, Y. Development and Validation of a Postoperative Delirium Prediction Model for Elderly Orthopedic Patients in the Intensive Care Unit. J. Healthc. Eng. 2021, 2021, 9959077. [Google Scholar] [CrossRef]
- Wassenaar, A.; van den Boogaard, M.; van Achterberg, T.; Slooter, A.J.; Kuiper, M.A.; Hoogendoorn, M.E.; Simons, K.S.; Maseda, E.; Pinto, N.; Jones, C.; et al. Multinational development and validation of an early prediction model for delirium in ICU patients. Intensive Care Med. 2015, 41, 1048–1056. [Google Scholar] [CrossRef]
- Green, L.; Mehr, D. What alters physicians’ decisions to admit to the coronary care unit? J. Fam. Pract. 1997, 45, 219–226. [Google Scholar]
- Phillips, N.; Neth, H.; Woike, J.K.; Gaissmaier, W. FFTrees: A toolbox to create, visualize, and evaluate fast-and-frugal decision trees. Judgm. Decis. Mak. 2017, 12, 344–368. [Google Scholar]
- Wegwarth, O. Deciding the Fast & Frugal Way on the Application of Pharmacodiagnostic Tests in Cancer Care? A Comparative Study of Oncologists’, Pathologists’, and Cancer Patients’ Decision Making in Germany and the USA. Ph.D. Thesis, Humboldt University, Berlin, Germany, 2007. [Google Scholar]
- Wegwarth, O.; Day, R.W.; Gigerenzer, G. Decisions on pharmacogenomic tests in the USA and Germany. J. Eval. Clin. Pract. 2011, 17, 228–235. [Google Scholar] [CrossRef] [PubMed]
- Woike, J.K.; Hoffrage, U.; Martignon, L. Integrating and testing natural frequencies, naïve Bayes, and fast-and-frugal trees. Decision 2017, 4, 234–260. [Google Scholar] [CrossRef]
- Pitt, M.A.; Myung, I.J.; Zhang, S. Toward a method of selecting among computational models of cognition. Psychol. Rev. 2002, 109, 472–491. [Google Scholar] [CrossRef] [PubMed]
- Gigerenzer, G.; Todd, P.M. The ABC Research Group. Simple Heuristics that Makes Us Smart; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Gigerenzer, G.; Goldstein, D.G. Reasoning the fast and frugal way: Models of bounded rationality. Psychol. Rev. 1996, 103, 650–669. [Google Scholar] [CrossRef] [PubMed]
- Martignon, L.; Katsikopoulos, K.V.; Woike, J.K. Categorization with limited resources: A family of simple heuristics. J. Math. Psychol. 2008, 52, 352–361. [Google Scholar] [CrossRef]
- Heinrich, M.; Müller, A.; Lammers-Lietz, F.; Borchers, F.; Mörgeli, R.; Kruppa, J.; Zacharias, N.; Winterer, G.; Slooter, A.J.C.; Spies, C.D. Radiological, Chemical, and Pharmacological Cholinergic System Parameters and Neurocognitive Disorders in Older Presurgical Adults. J. Gerontol. A Biol. Sci. Med. Sci. 2021, 76, 1029–1036. [Google Scholar] [CrossRef]
- American Psychiatric Association Publishing. American Psychiatric Association: Diagnostic and Statistical Manual of Mental Disorders, 5th ed.; American Psychiatric Association Publishing: Washington, DC, USA, 2013. [Google Scholar] [CrossRef]
- Charlson, M.E.; Pompei, P.; Ales, K.L.; MacKenzie, C.R. A new method of classifying prognostic comorbidity in longitudinal studies: Development and validation. J. Chronic Dis. 1987, 40, 373–383. [Google Scholar] [CrossRef]
- UNESCO Institute for Statistics. International Standard Classification of Education ISCED 2011; UNESCO Institute for Statistics: Montreal, QC, Canada, 2012; Available online: http://uis.unesco.org/sites/default/files/documents/international-standard-classification-of-education-isced-2011-en.pdf (accessed on 2 May 2020).
- Mahoney, F.I.; Barthel, D.W. Functional evaluation: The barthel index. Md. State Med. J. 1965, 14, 61–65. [Google Scholar]
- Lawton, M.P.; Brody, E.M. Assessment of older people: Self-maintaining and instrumental activities of daily living. Gerontologist 1969, 9, 179–186. [Google Scholar] [CrossRef]
- Guigoz, Y.; Vellas, B.; Garry, P.J. Assessing the nutritional status of the elderly: The Mini Nutritional Assessment as part of the geriatric evaluation. Nutr. Rev. 1996, 54, S59–S65. [Google Scholar] [CrossRef] [PubMed]
- Yesavage, J.A.; Brink, T.L.; Rose, T.L.; Lum, O.; Huang, V.; Adey, M.; Leirer, V.O. Development and validation of a geriatric depression screening scale: A preliminary report. J. Psychiatr. Res. 1982, 17, 37–49. [Google Scholar] [CrossRef]
- Saunders, J.B.; Aasland, O.G.; Babor, T.F.; de la Fuente, J.R.; Grant, M. Development of the Alcohol Use Disorders Identification Test (AUDIT): WHO Collaborative Project on Early Detection of Persons with Harmful Alcohol Consumption—II. Addiction 1993, 88, 791–804. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees, 1st ed.; Routledge: London, UK, 1984. [Google Scholar] [CrossRef]
- Therneau, T.; Atkinson, B. Recursive Partitioning and Regression Trees. R Package Version 4.1-16. 2019. Available online: https://CRAN.R-project.org/package=rpart (accessed on 2 May 2020).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: https://www.R-project.org/ (accessed on 2 May 2020).
- Luan, S.; Schooler, L.J.; Gigerenzer, G. A signal-detection analysis of fast-and-frugal trees. Psychol. Rev. 2011, 118, 316–338. [Google Scholar] [CrossRef]
- Radtke, F.M.; Franck, M.; MacGuill, M.; Seeling, M.; Lütz, A.; Westhoff, S.; Neumann, U.; Wernecke, K.D.; Spies, C.D. Duration of fluid fasting and choice of analgesic are modifiable factors for early postoperative delirium. Eur. J. Anaesthesiol. 2010, 27, 411–416. [Google Scholar] [CrossRef]
- Robinson, T.N.; Raeburn, C.D.; Tran, Z.V.; Angles, E.M.; Brenner, L.A.; Moss, M. Postoperative delirium in the elderly: Risk factors and outcomes. Ann. Surg. 2009, 249, 173–178. [Google Scholar] [CrossRef]
- Marcantonio, E.R.; Goldman, L.; Mangione, C.M.; Ludwig, L.E.; Muraca, B.; Haslauer, C.M.; Donaldson, M.C.; Whittemore, A.D.; Sugarbaker, D.J.; Poss, R.; et al. A clinical prediction rule for delirium after elective noncardiac surgery. Jama 1994, 271, 134–139. [Google Scholar] [CrossRef] [PubMed]
- van den Boogaard, M.; Pickkers, P.; Slooter, A.J.; Kuiper, M.A.; Spronk, P.E.; van der Voort, P.H.; van der Hoeven, J.G.; Donders, R.; van Achterberg, T.; Schoonhoven, L. Development and validation of PRE-DELIRIC (PREdiction of DELIRium in ICu patients) delirium prediction model for intensive care patients: Observational multicentre study. BMJ 2012, 344, e420. [Google Scholar] [CrossRef]
- Kim, E.M.; Li, G.; Kim, M. Development of a Risk Score to Predict Postoperative Delirium in Patients With Hip Fracture. Anesth. Analg. 2020, 130, 79–86. [Google Scholar] [CrossRef]
- Rasmussen, L.S.; Larsen, K.; Houx, P.; Skovgaard, L.T.; Hanning, C.D.; Moller, J.T. The assessment of postoperative cognitive function. Acta Anaesthesiol. Scand. 2001, 45, 275–289. [Google Scholar] [CrossRef]
- Fried, L.P.; Tangen, C.M.; Walston, J.; Newman, A.B.; Hirsch, C.; Gottdiener, J.; Seeman, T.; Tracy, R.; Kop, W.J.; Burke, G.; et al. Frailty in older adults: Evidence for a phenotype. J. Gerontol. Ser. A Biol. Sci. Med. Sci. 2001, 56, M146–M156. [Google Scholar] [CrossRef] [PubMed]
- Vellas, B.; Guigoz, Y.; Garry, P.J.; Nourhashemi, F.; Bennahum, D.; Lauque, S.; Albarede, J.L. The Mini Nutritional Assessment (MNA) and its use in grading the nutritional state of elderly patients. Nutrition 1999, 15, 116–122. [Google Scholar] [CrossRef]
- Ensrud, K.E.; Ewing, S.K.; Cawthon, P.M.; Fink, H.A.; Taylor, B.C.; Cauley, J.A.; Dam, T.-T.; Marshall, L.M.; Orwoll, E.S.; Cummings, S.R.; et al. A comparison of frailty indexes for the prediction of falls, disability, fractures, and mortality in older men. J. Am. Geriatr. Soc. 2009, 57, 492–498. [Google Scholar] [CrossRef]
- Rockwood, K.; Andrew, M.; Mitnitski, A. A comparison of two approaches to measuring frailty in elderly people. J. Gerontol. Ser. A Biol. Sci. Med. Sci. 2007, 62, 738–743. [Google Scholar] [CrossRef]
- Siscovick, D.S.; Fried, L.; Mittelmark, M.; Rutan, G.; Bild, D.; O’Leary, D.H. Exercise intensity and subclinical cardiovascular disease in the elderly. The Cardiovascular Health Study. Am. J. Epidemiol. 1997, 145, 977–986. [Google Scholar] [CrossRef] [PubMed]
- Podsiadlo, D.; Richardson, S. The timed “Up & Go”: A test of basic functional mobility for frail elderly persons. J. Am. Geriatr. Soc. 1991, 39, 142–148. [Google Scholar] [CrossRef] [PubMed]

| Characteristic | POD (n = 99) 25.10% | Non POD (n = 295) 74.90% | p |
|---|---|---|---|
| n = 394 | |||
| Age (years) | 74 [71;77] | 72 [68;76] | 0.004 a |
| Sex | |||
| Female | 51 (41.5%) | 145 (49.2%) | 0.684 b |
| ASA PS | <0.001 b | ||
| 1–2 | 43 (43.4%) | 203 (68.8%) | |
| 3–4 | 56 (56.6%) | 92 (31.2%) | |
| Charlson Comorbidity Index | 2.14 ±1.5 c | 1.43 ± 1.6 c | <0.001 a |
| Frailty status | <0.001 b | ||
| Pre-frail | 50 (51.0%) | 143 (49.1%) | |
| frail | 30 (30.6%) | 30 (10.3%) | |
| Site of surgery | <0.001 b | ||
| intracranial | 2 (2.0%) | 7 (2.4%) | |
| intrathoracic, intra-abdominal or pelvic | 67 (67.7%) | 122 (41.4%) | |
| peripheral | 30 (30.3%) | 166 (56.3%) | |
| Duration of Anaesthesia (min) | 360 [220;495] | 157 [100;260] | <0.001 b |
| Training | Prediction | ||||||
|---|---|---|---|---|---|---|---|
| Sensitivity | Specificity | Bal. Accuracy | Sensitivity | Specificity | Bal. Accuracy | ||
| FFTi | M | 0.693 | 0.682 | 0.688 | 0.578 | 0.644 | 0.611 |
| SE | (0.0013) | (0.0013) | (0.0002) | (0.0015) | (0.0014) | (0.0003) | |
| FFTd | M | 0.751 | 0.689 | 0.720 | 0.562 | 0.625 | 0.593 |
| SE | (0.0037) | (0.0037) | (0.0007) | (0.0044) | (0.0040) | (0.0011) | |
| UDT | M | 0.868 | 0.738 | 0.803 | 0.52 | 0.626 | 0.573 |
| SE | (0.0006) | (0.0006) | (0.0002) | (0.0010) | (0.0007) | (0.0004) | |
| LogReg | M | 0.737 | 0.747 | 0.742 | 0.581 | 0.692 | 0.637 |
| SE | (0.0004) | (0.0003) | (0.0003) | (0.0007) | (0.0004) | (0.0003) | |
| Training | Prediction | ||||||
|---|---|---|---|---|---|---|---|
| Sensitivity | Specificity | Bal. Accuracy | Sensitivity | Specificity | Bal. Accuracy | ||
| FFTi | M | 0.767 | 0.723 | 0.745 | 0.698 | 0.695 | 0.696 |
| SE | (0.0008) | (0.0008) | (0.0002) | (0.0011) | (0.0009) | (0.0003) | |
| FFTd | M | 0.815 | 0.756 | 0.786 | 0.698 | 0.71 | 0.704 |
| SE | (0.0025) | (0.0024) | (0.0007) | (0.0032) | (0.0028) | (0.0010) | |
| UDT | M | 0.896 | 0.784 | 0.840 | 0.625 | 0.694 | 0.660 |
| SE | (0.0005) | (0.0005) | (0.0002) | (0.0010) | (0.0007) | (0.0004) | |
| LogReg | M | 0.792 | 0.803 | 0.798 | 0.632 | 0.749 | 0.690 |
| SE | (0.0004) | (0.0003) | (0.0003) | (0.0007) | (0.0004) | (0.0003) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heinrich, M.; Woike, J.K.; Spies, C.D.; Wegwarth, O. Forecasting Postoperative Delirium in Older Adult Patients with Fast-and-Frugal Decision Trees. J. Clin. Med. 2022, 11, 5629. https://doi.org/10.3390/jcm11195629
Heinrich M, Woike JK, Spies CD, Wegwarth O. Forecasting Postoperative Delirium in Older Adult Patients with Fast-and-Frugal Decision Trees. Journal of Clinical Medicine. 2022; 11(19):5629. https://doi.org/10.3390/jcm11195629
Chicago/Turabian StyleHeinrich, Maria, Jan K. Woike, Claudia D. Spies, and Odette Wegwarth. 2022. "Forecasting Postoperative Delirium in Older Adult Patients with Fast-and-Frugal Decision Trees" Journal of Clinical Medicine 11, no. 19: 5629. https://doi.org/10.3390/jcm11195629
APA StyleHeinrich, M., Woike, J. K., Spies, C. D., & Wegwarth, O. (2022). Forecasting Postoperative Delirium in Older Adult Patients with Fast-and-Frugal Decision Trees. Journal of Clinical Medicine, 11(19), 5629. https://doi.org/10.3390/jcm11195629






