New Methods for the Acoustic-Signal Segmentation of the Temporomandibular Joint
Abstract
:1. Introduction
2. Materials and Methods
2.1. Database
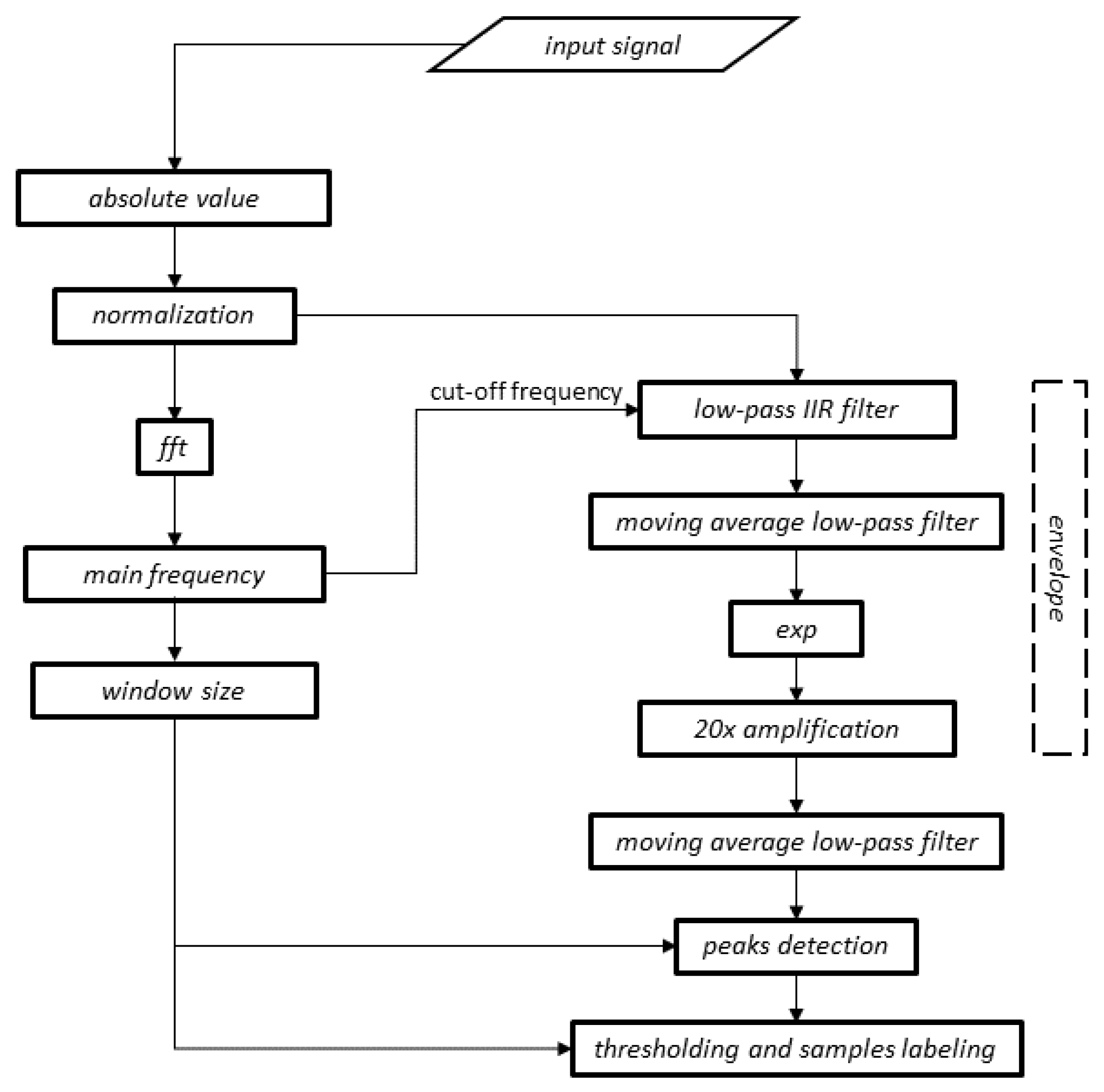
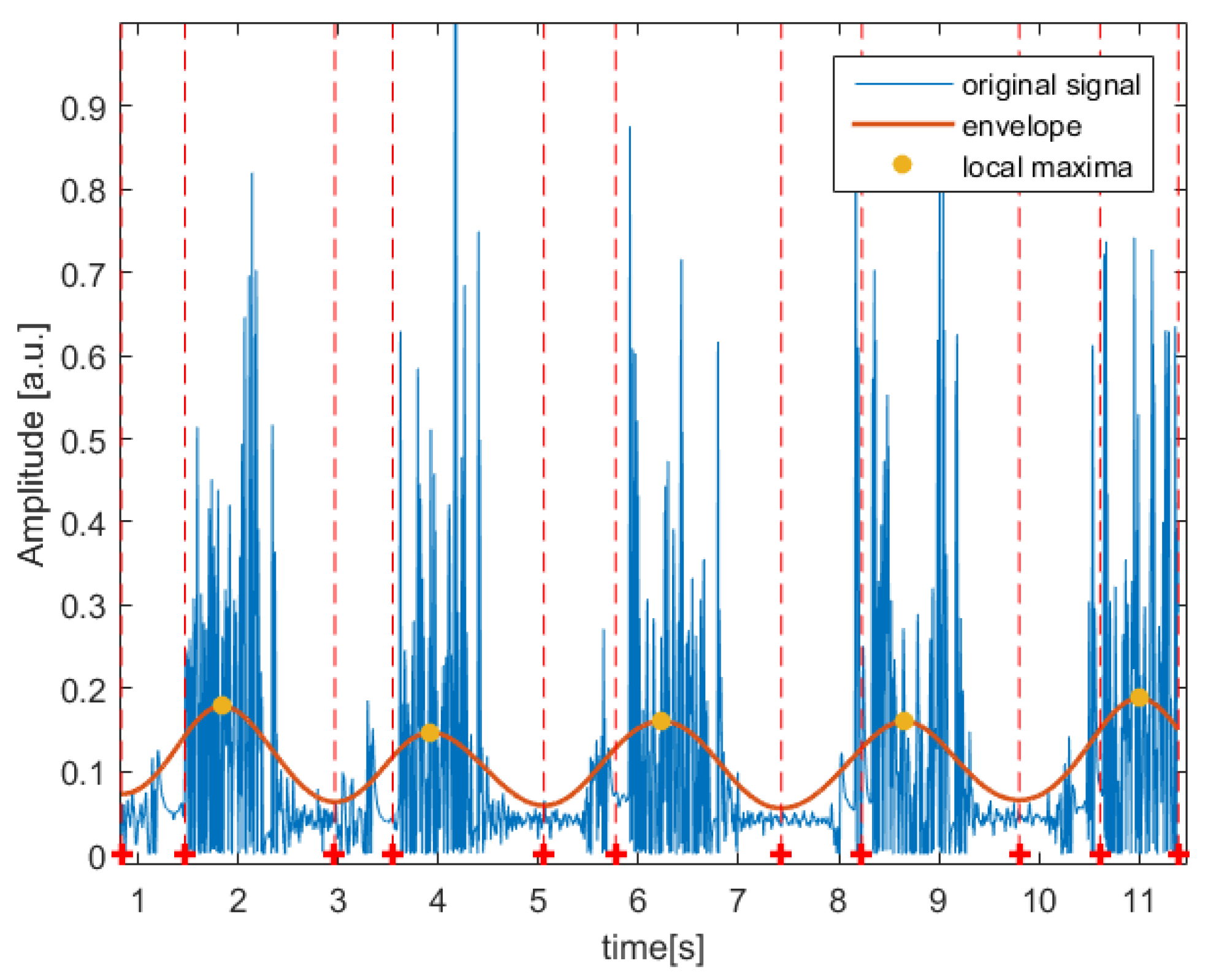
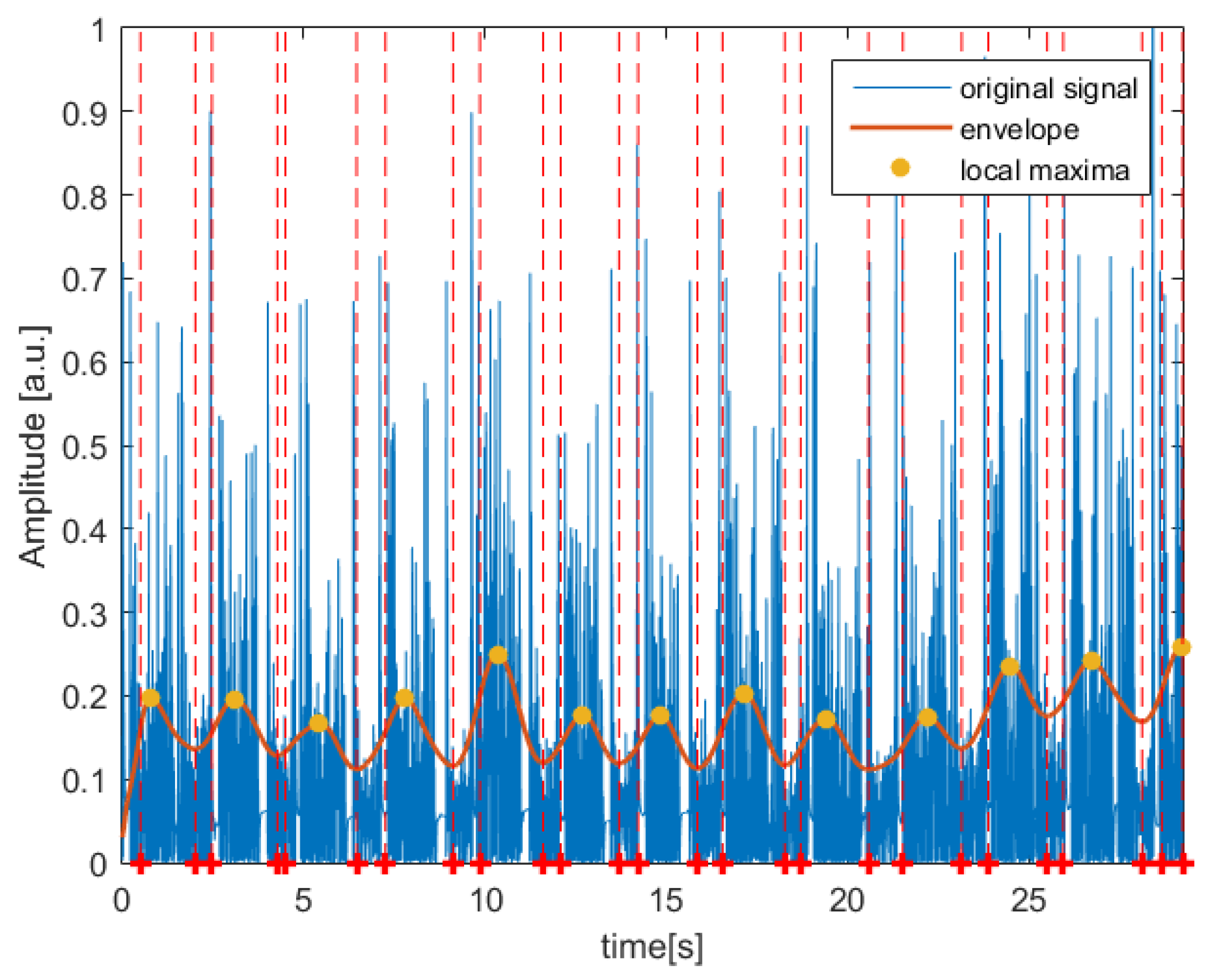
2.2. Digital Signal-Processing Method
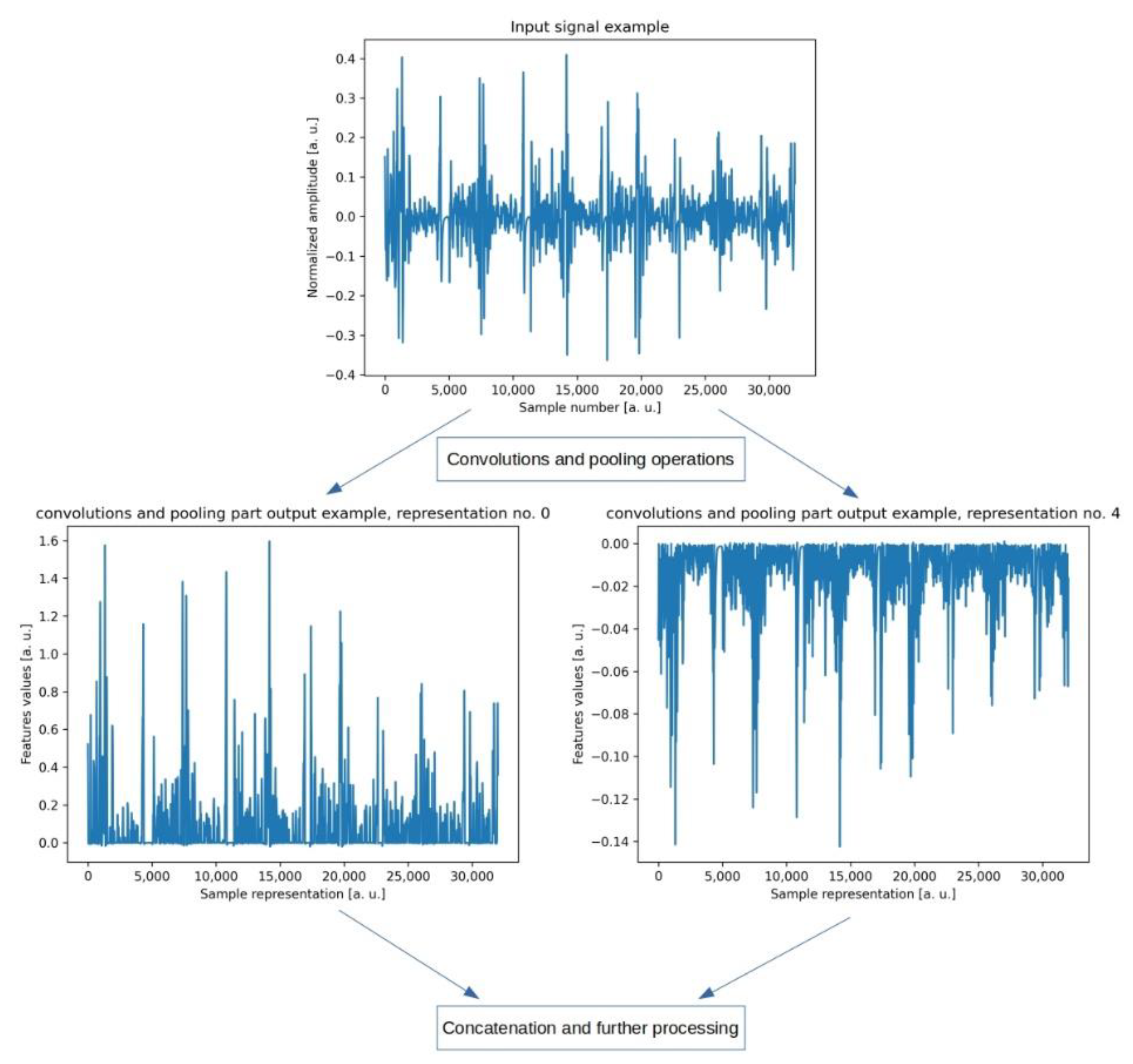
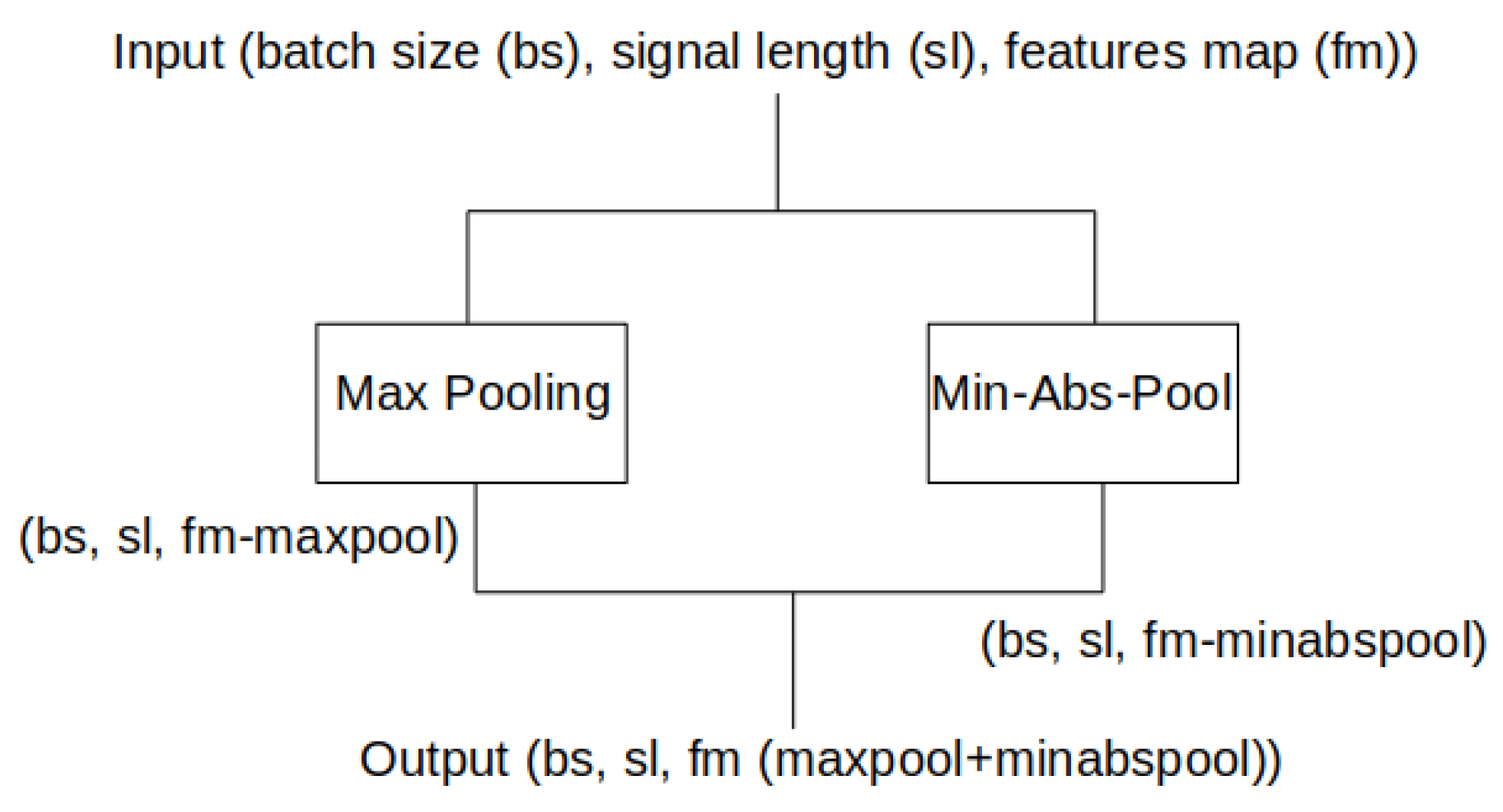
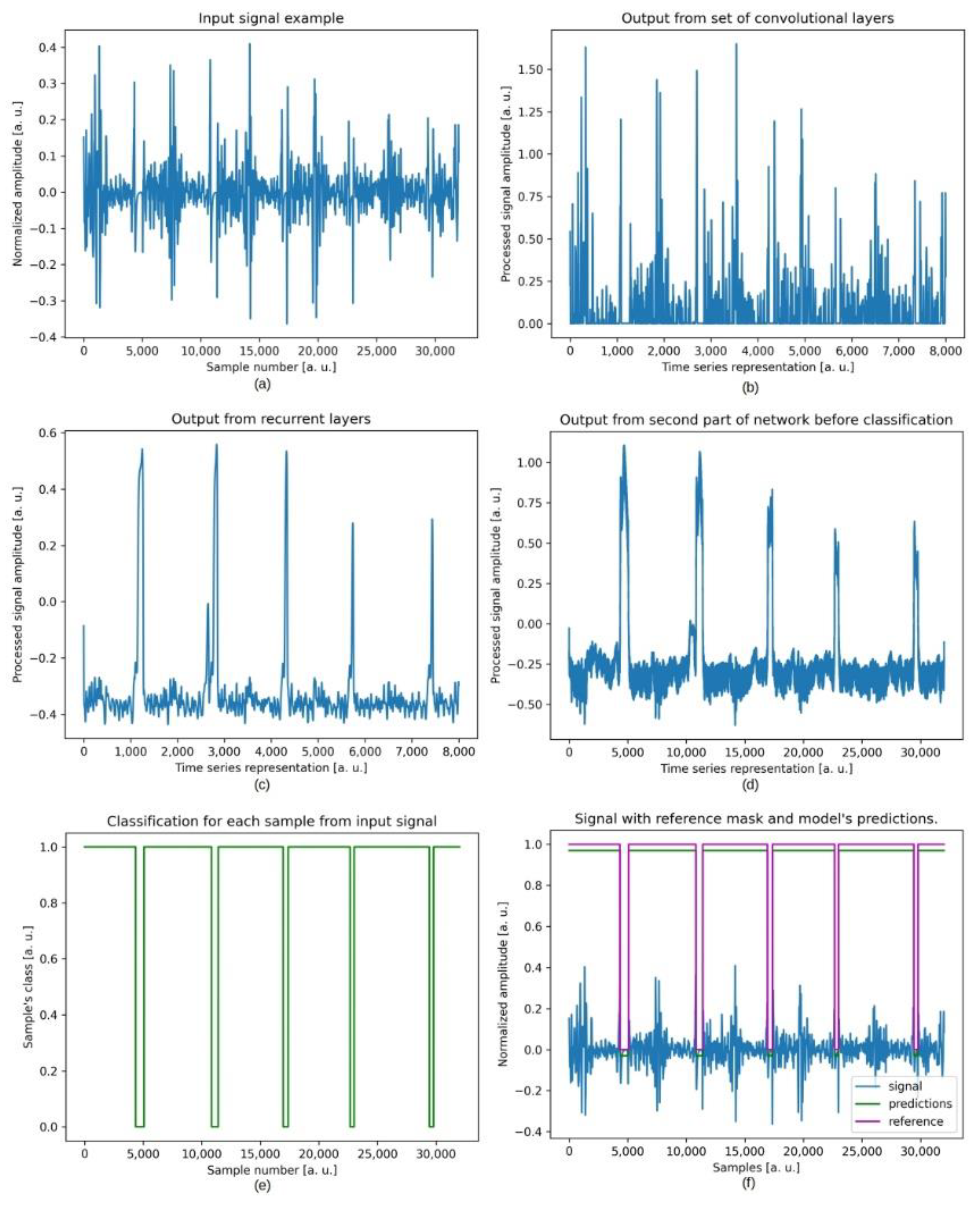
2.3. Deep Learning Method
2.4. Evaluation
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Djurdjanovic, D.; Widmalm, S.E.; Williams, W.J.; Koh, C.K.H.; Yang, K.P. Computerized Classification of Temporomandibular Joint Sounds. IEEE Trans. Biomed. Eng. 2000, 47, 977–984. [Google Scholar] [CrossRef] [PubMed]
- Yoo, S.; Boston, J.R.; Rudy, T.E.; Greco, C.M.; Leader, J.K. Time-Frequency Analysis of Temporomandibular Joint (TMJ) Clicking Sounds Using Radially Gaussian Kernels. IEEE Trans. Biomed. Eng. 2001, 48, 936–939. [Google Scholar] [CrossRef] [PubMed]
- Arafa, A.F.; Mostafa, N.M.; Moussa, S.A. Assessment of Schoolchildren’s Temporomandibular Joint Sounds Associated with Bruxism. J. Dent. Oral Disord. Ther. 2019, 7, 1–6. [Google Scholar] [CrossRef]
- Lavigne, G.J.; Khoury, S.; Abe, S.; Yamaguchi, T.; Raphael, K. Bruxism Physiology and Pathology: An Overview for Clinicians*. J. Oral Rehabil. 2008, 35, 476–494. [Google Scholar] [CrossRef] [PubMed]
- Ciavarella, D.; Tepedino, M.; Laurenziello, M.; Guida, L.; Troiano, G.; Montaruli, G.; Illuzzi, G.; Chimenti, C.; Lo Muzio, L. Swallowing and Temporomandibular Disorders in Adults. J. Craniofac. Surg. 2018, 29, e262–e267. [Google Scholar] [CrossRef]
- Gauer, R.; Semidey, M.J. Diagnosis and Treatment of Temporomandibular Disorders. Am. Fam. Physician 2015, 91, 378–386. [Google Scholar]
- Kucharski, D.; Grochala, D.; Kajor, M.; Kańtoch, E. A Deep Learning Approach for Valve Defect Recognition in Heart Acoustic Signal. In Information Systems Architecture and Technology, Proceedings of the 38th International Conference on Information Systems Architecture and Technology—ISAT 2017, Szklarska Poręba, Poland, 17–19 September 2017; Borzemski, L., Świątek, J., Wilimowska, Z., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 3–14. [Google Scholar]
- Sun, S.; Jiang, Z.; Wang, H.; Fang, Y. Automatic Moment Segmentation and Peak Detection Analysis of Heart Sound Pattern via Short-Time Modified Hilbert Transform. Comput. Methods Programs Biomed. 2014, 114, 219–230. [Google Scholar] [CrossRef]
- Varghees, V.N.; Ramachandran, K.I. A Novel Heart Sound Activity Detection Framework for Automated Heart Sound Analysis. Biomed. Signal Process. Control 2014, 13, 174–188. [Google Scholar] [CrossRef]
- Tang, H.; Li, T.; Qiu, T.; Park, Y. Segmentation of Heart Sounds Based on Dynamic Clustering. Biomed. Signal Process. Control 2012, 7, 509–516. [Google Scholar] [CrossRef]
- Sedighian, P.; Subudhi, A.W.; Scalzo, F.; Asgari, S. Pediatric Heart Sound Segmentation Using Hidden Markov Model. IEEE Eng. Med. Biol. Soc. 2014, 2014, 5490–5493. [Google Scholar] [CrossRef]
- Zhong, L.; Guo, X.; Ji, A.; Ding, X. A Robust Envelope Extraction Algorithm for Cardiac Sound Signal Segmentation. In Proceedings of the 2011 5th International Conference on Bioinformatics and Biomedical Engineering, Wuhan, China, 10–12 May 2011; pp. 1–5. [Google Scholar]
- Wu, Y.; Chen, P.; Luo, X.; Huang, H.; Liao, L.; Yao, Y.; Wu, M.; Rangayyan, R.M. Quantification of Knee Vibroarthrographic Signal Irregularity Associated with Patellofemoral Joint Cartilage Pathology Based on Entropy and Envelope Amplitude Measures. Comput. Methods Programs Biomed. 2016, 130, 1–12. [Google Scholar] [CrossRef] [PubMed]
- An, F.-P.; Liu, Z.-W. Medical Image Segmentation Algorithm Based on Feedback Mechanism CNN. Contrast Media Mol. Imaging 2019, 2019, 6134942. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Girum, K.B.; Créhange, G.; Hussain, R.; Lalande, A. Fast Interactive Medical Image Segmentation with Weakly Supervised Deep Learning Method. Int. J. Comput. Assist. Radiol. Surg. 2020, 15, 1437–1444. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention, Proceedings of the 18th International Conference, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Zhang, Z.; Wu, C.; Coleman, S.; Kerr, D. DENSE-INception U-Net for Medical Image Segmentation. Comput. Methods Programs Biomed. 2020, 192, 105395. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Lu, X. A Speech Recognition Acoustic Model Based on LSTM-CTC. In Proceedings of the 2018 IEEE 18th International Conference on Communication Technology (ICCT), Chongqing, China, 13–16 October 2021; pp. 1052–1055. [Google Scholar]
- Yadav, S.; Yang, Y.; Dutra, E.H.; Robinson, J.L.; Wadhwa, S. Temporomandibular Joint Disorders in Older Adults. J. Am. Geriatr. Soc. 2018, 66, 1213–1217. [Google Scholar] [CrossRef]
- Perez, C. Temporomandibular Disorders in Children and Adolescents. Gen. Dent. 2018, 66, 51–55. [Google Scholar] [PubMed]
- Osiewicz, M.A.; Lobbezoo, F.; Loster, B.W.; Wilkosz, M.; Naeije, M.; Ohrbach, R. Research Diagnostic Criteria for Temporomandibular Disorders (RDC/TMD): The Polish Version of a Dual-Axis System for the Diagnosis of TMD.* RDC/TMD Form. J. Stomatol. 2013, 66, 576–649. [Google Scholar] [CrossRef]
- Dammling, C.; Abramowicz, S.; Kinard, B. The Use of Pharmacologic Agents in the Management of Temporomandibular Joint Disorder. Front. Oral Maxillofac. Med. 2021, 1–7. [Google Scholar] [CrossRef]
- Kijak, E.; Szczepek, A.J.; Margielewicz, J. Association between Anatomical Features of Petrotympanic Fissure and Tinnitus in Patients with Temporomandibular Joint Disorder Using CBCT Imaging: An Exploratory Study. Pain Res. Manag. 2020, 2020, e1202751. [Google Scholar] [CrossRef]
- Meng, Q.; Yuan, M.; Yang, Z.; Feng, H. An Empirical Envelope Estimation Algorithm. In Proceedings of the 2013 6th International Congress on Image and Signal Processing (CISP), Hangzhou, China, 16–18 December 2013; Volume 2, pp. 1132–1136. [Google Scholar]
- Caetano, M.; Rodet, X. Improved Estimation of the Amplitude Envelope of Time-Domain Signals Using True Envelope Cepstral Smoothing. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4244–4247. [Google Scholar]
- Johnson, C.R., Jr.; Sethares, W.A.; Klein, A.G. Software Receiver Design: Build Your Own Digital Communication System in Five Easy Steps; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Lyons, R. Streamlining Digital Signal Processing; John Wiley & Sons, Inc.: New York, NY, USA, 2006; pp. 23–54. [Google Scholar]
- Chen, Y.; Lv, J.; Sun, Y.; Jia, B. Heart Sound Segmentation via Duration Long–Short Term Memory Neural Network. Appl. Soft Comput. 2020, 95, 106540. [Google Scholar] [CrossRef]
- Fernando, T.; Ghaemmaghami, H.; Denman, S.; Sridharan, S.; Hussain, N.; Fookes, C. Heart Sound Segmentation Using Bidirectional LSTMs with Attention. IEEE J. Biomed. Health Inform. 2020, 24, 1601–1609. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Y.; Sun, Y.; Lv, J.; Jia, B.; Huang, X. End-to-End Heart Sound Segmentation Using Deep Convolutional Recurrent Network. Complex Intell. Syst. 2021, 7, 2103–2117. [Google Scholar] [CrossRef]
- Tuijt, M.; Koolstra, J.H.; Lobbezoo, F.; Naeije, M. Biomechanical Modeling of Open Locks of the Human Temporomandibular Joint. Clin. Biomech. 2012, 27, 749–753. [Google Scholar] [CrossRef] [PubMed]
- Clifford, G.D.; Liu, C.; Moody, B.; Springer, D.; Silva, I.; Li, Q.; Mark, R.G. Classification of Normal/Abnormal Heart Sound Recordings: The PhysioNet/Computing in Cardiology Challenge 2016. In Proceedings of the 2016 Computing in cardiology conference (CinC), Vancouver, BC, Canada, 11–14 September 2016; pp. 609–612. [Google Scholar]
- Rojas, R. The Backpropagation Algorithm. In Neural Networks: A Systematic Introduction; Rojas, R., Ed.; Springer: Berlin/Heidelberg, Germany, 1996; pp. 149–182. ISBN 978-3-642-61068-4. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; Curran Associates, Inc.: New York, NY, USA, 2012; Volume 25. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. arXiv 2014, arXiv:1409.4842. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. arXiv 2016, arXiv:1506.02640. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation. arXiv 2014, arXiv:1311.2524. [Google Scholar]
- Frishman, W.H. Is the Stethoscope Becoming an Outdated Diagnostic Tool? Am. J. Med. 2015, 128, 668–669. [Google Scholar] [CrossRef]
- Montinari, M.R.; Minelli, S. The First 200 Years of Cardiac Auscultation and Future Perspectives. J. Multidiscip. Healthc. 2019, 12, 183. [Google Scholar] [CrossRef] [Green Version]
- Evora, P.R.B.; Schmidt, A.; Braile, D.M. Even Considering the Existing High Technology, Do Not Forget That the Old Stethoscope Is Still a Useful Tool for the Heart Team. Braz. J. Cardiovasc. Surg. 2018, 33, I–II. [Google Scholar] [CrossRef] [PubMed]
- Allwood, G.; Du, X.; Webberley, K.M.; Osseiran, A.; Marshall, B.J. Advances in Acoustic Signal Processing Techniques for Enhanced Bowel Sound Analysis. IEEE Rev. Biomed. Eng. 2018, 12, 240–253. [Google Scholar] [CrossRef] [PubMed]


| Metric | DSP Method | Deep Learning Method |
|---|---|---|
| Positive Predictivity (PP) | 0.93 | 0.98 |
| Specificity (Sp) | 0.65 | 0.67 |
| Sensitivity (Se) | 0.91 | 0.98 |
| Negative Predictivity (NP) | 0.67 | 0.74 |
| Dice coefficient (Dice) | 0.86 | 0.85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kajor, M.; Kucharski, D.; Grochala, J.; Loster, J.E. New Methods for the Acoustic-Signal Segmentation of the Temporomandibular Joint. J. Clin. Med. 2022, 11, 2706. https://doi.org/10.3390/jcm11102706
Kajor M, Kucharski D, Grochala J, Loster JE. New Methods for the Acoustic-Signal Segmentation of the Temporomandibular Joint. Journal of Clinical Medicine. 2022; 11(10):2706. https://doi.org/10.3390/jcm11102706
Chicago/Turabian StyleKajor, Marcin, Dariusz Kucharski, Justyna Grochala, and Jolanta E. Loster. 2022. "New Methods for the Acoustic-Signal Segmentation of the Temporomandibular Joint" Journal of Clinical Medicine 11, no. 10: 2706. https://doi.org/10.3390/jcm11102706
APA StyleKajor, M., Kucharski, D., Grochala, J., & Loster, J. E. (2022). New Methods for the Acoustic-Signal Segmentation of the Temporomandibular Joint. Journal of Clinical Medicine, 11(10), 2706. https://doi.org/10.3390/jcm11102706






