Neutralization Dialysis for Phenylalanine and Mineral Salt Separation. Simple Theory and Experiment
Abstract
1. Introduction
2. Theoretical
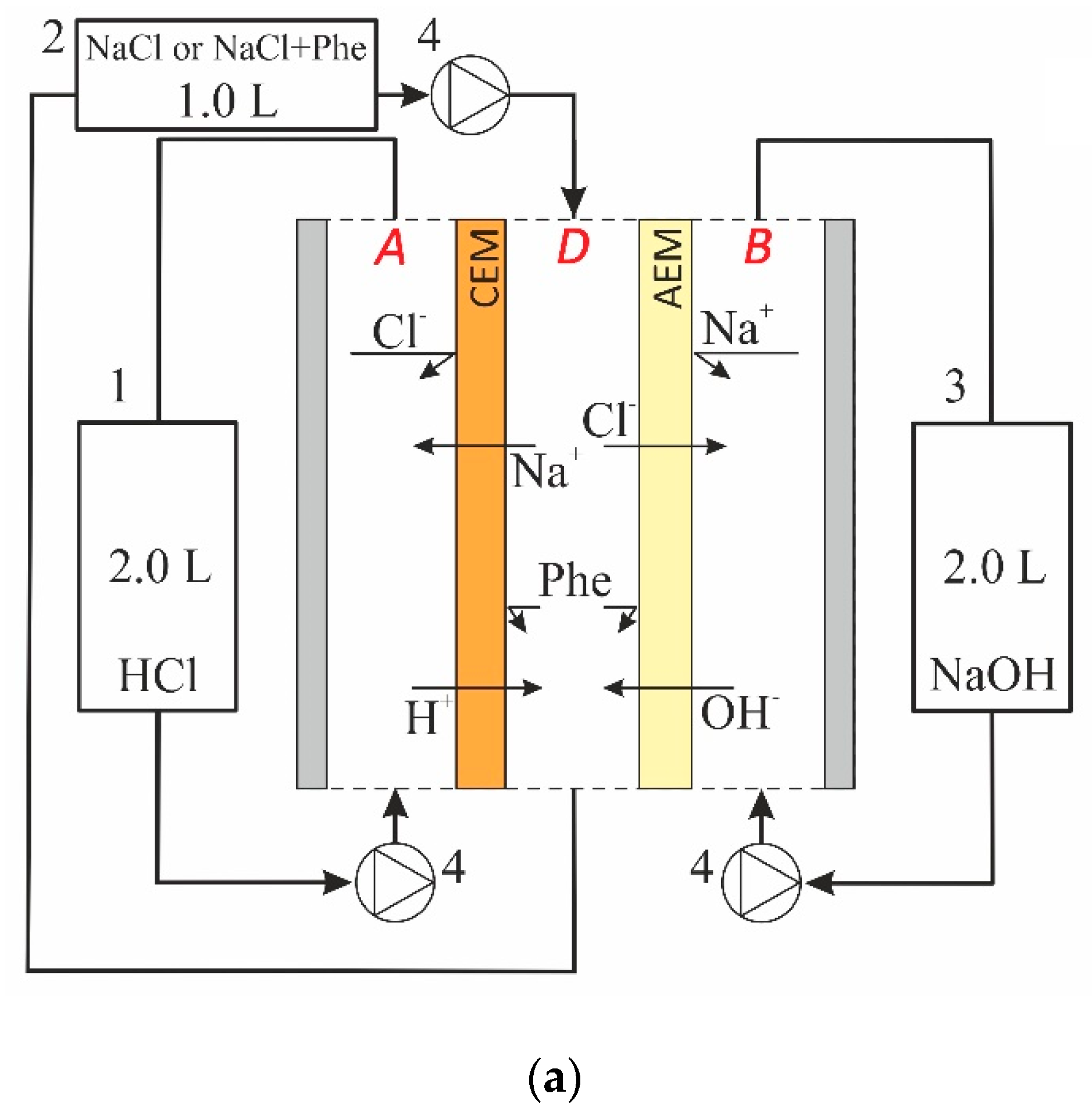
2.1. System under Study
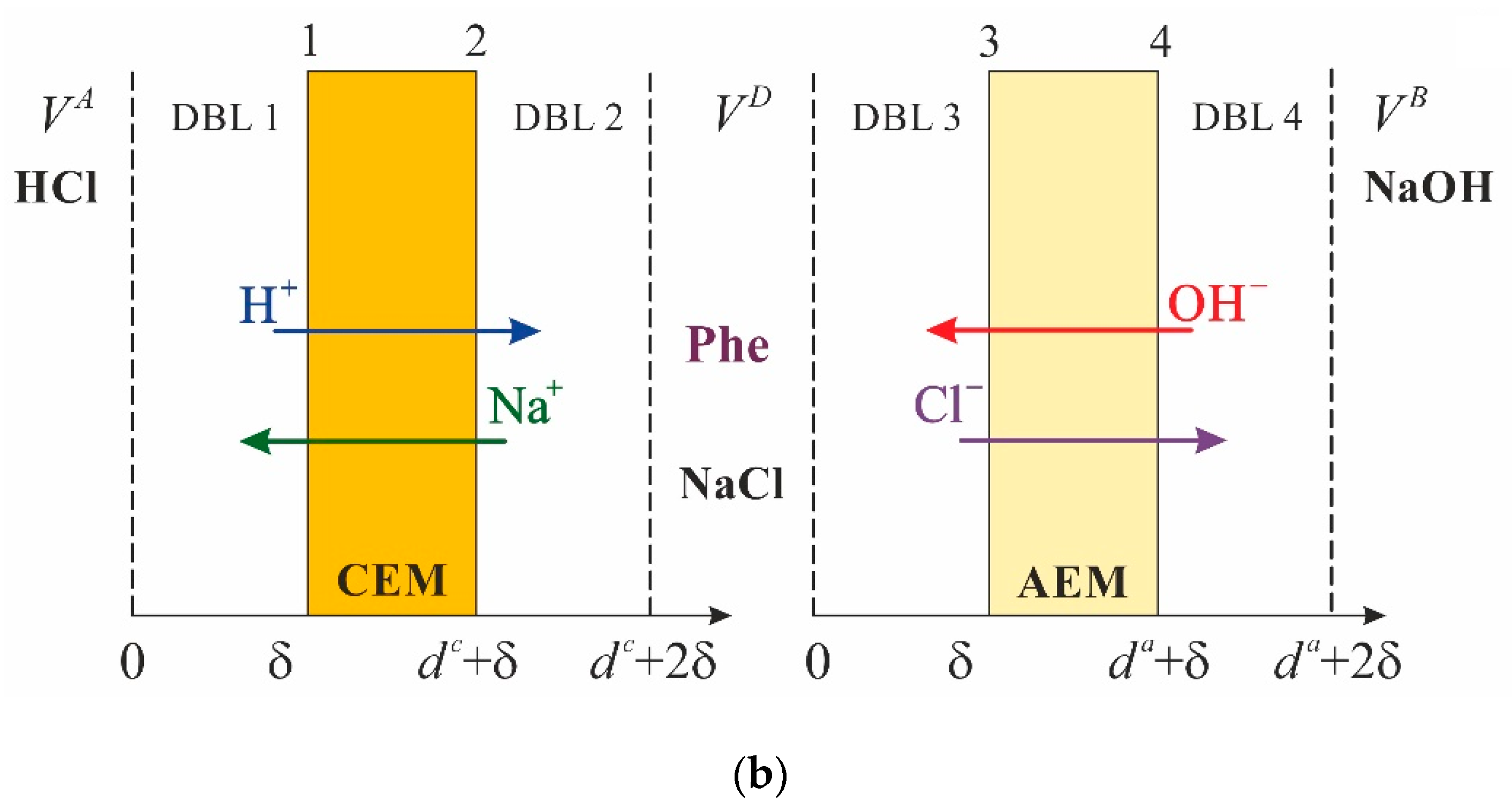
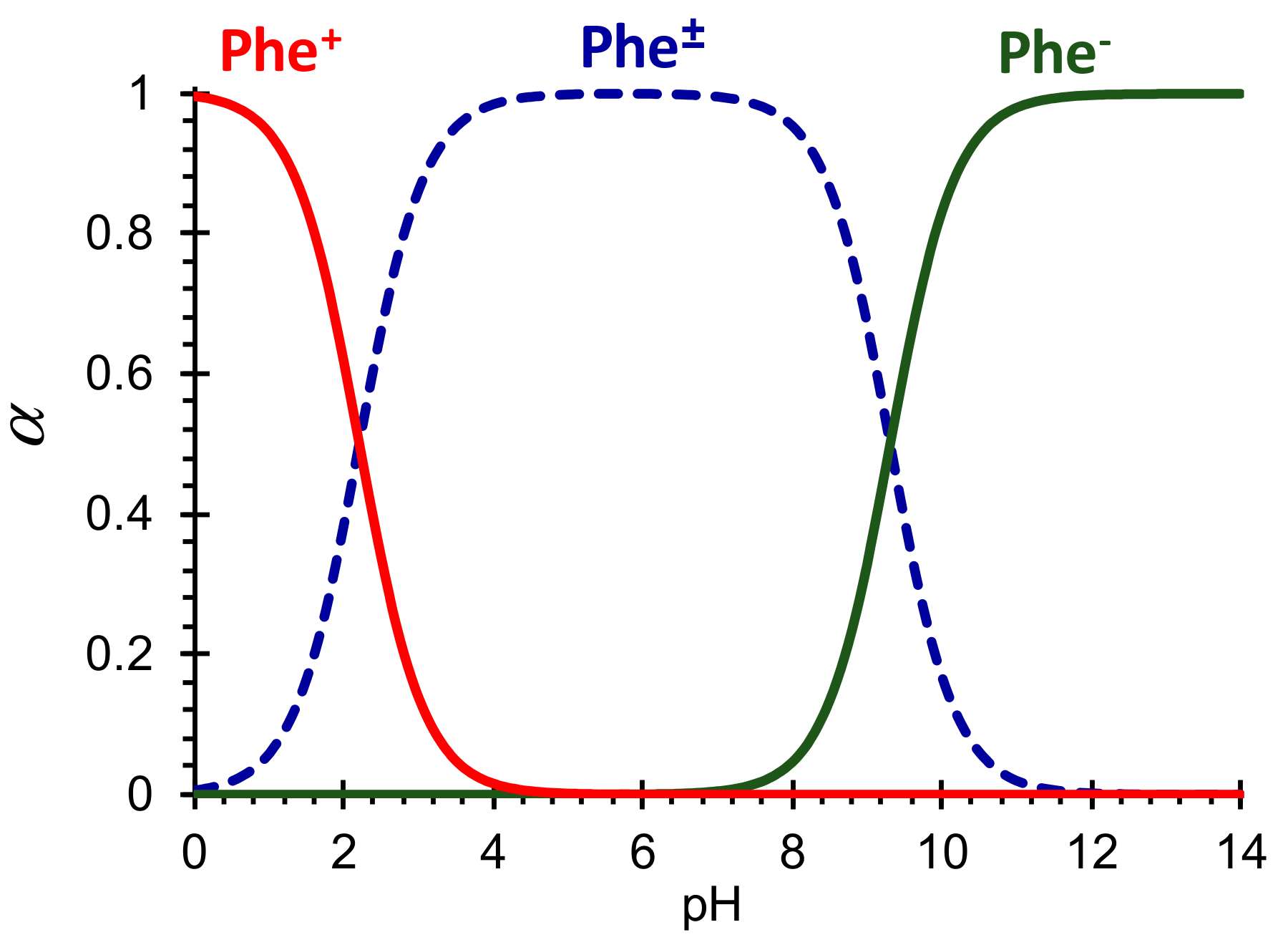
2.2. Problem Formulation
3. Experiment
4. Parameters of the Model
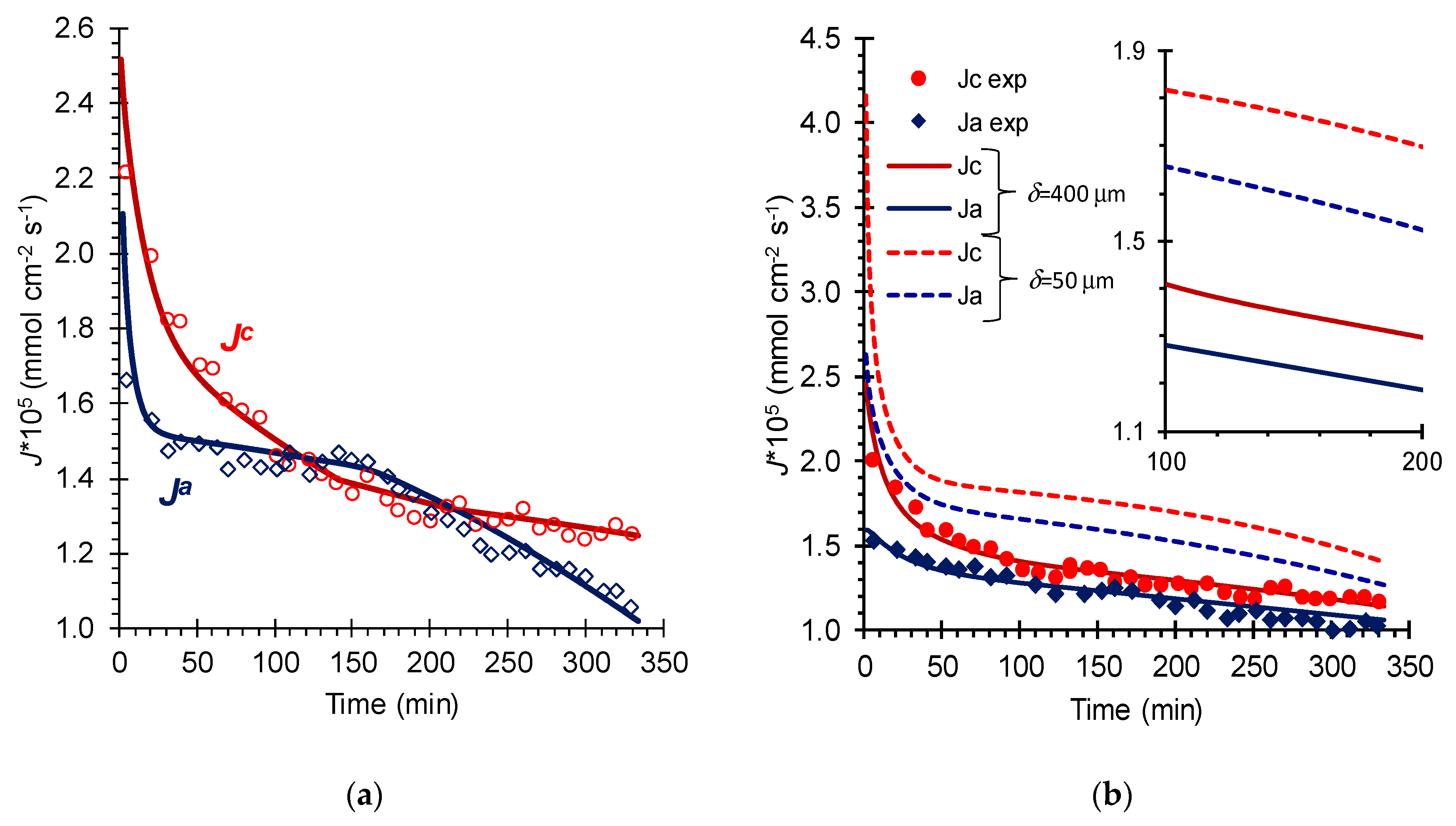
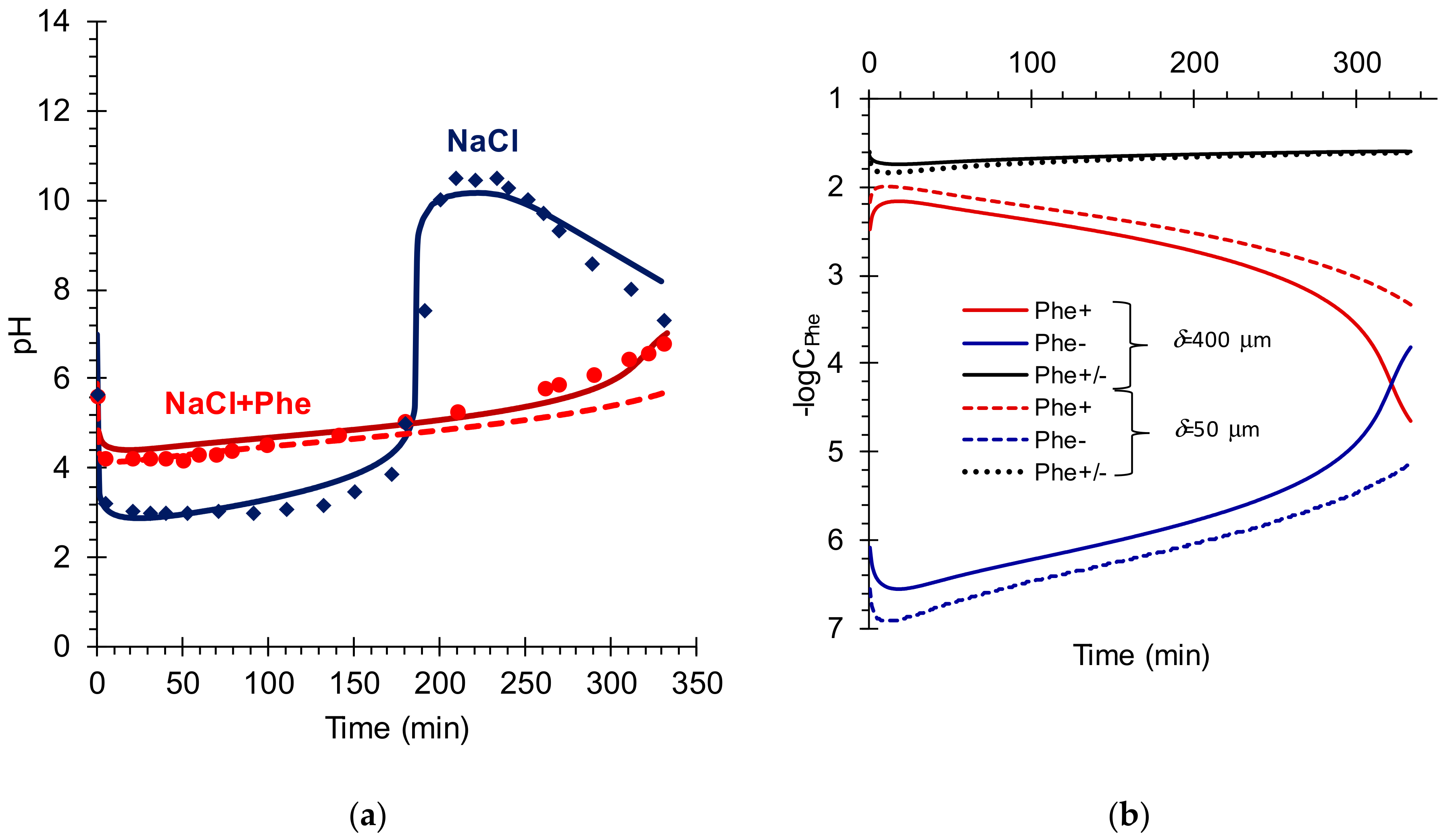
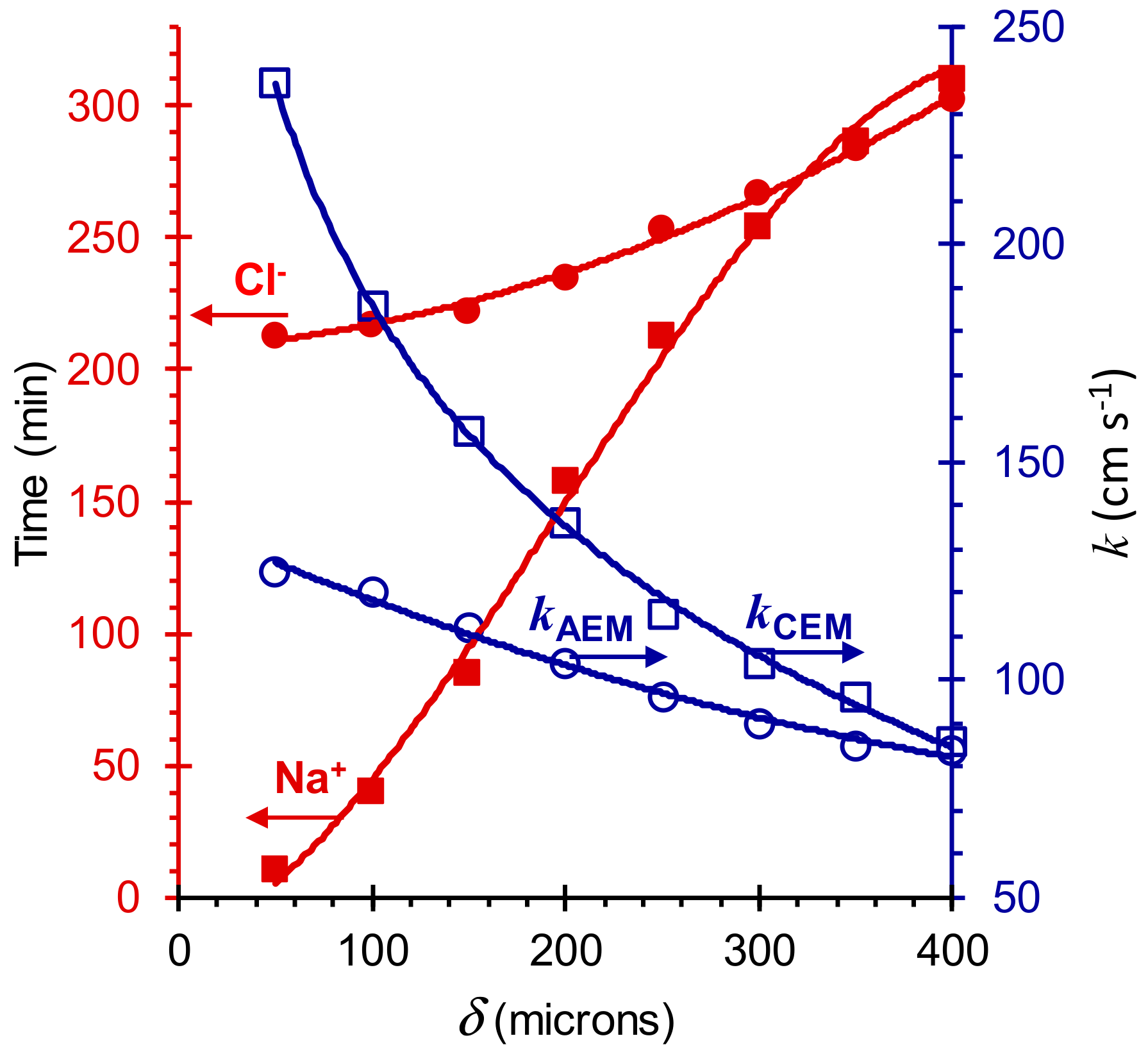
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Parameter | Value | Description |
|---|---|---|
| 2.7 × 10−6 cm2 s−1 | H+ and Na+ ions diffusion coefficients in the MK-40prof | |
| 7.88 × 10−7 cm2 s−1 | ||
| 9.6 × 10−7 cm2 s−1 | OH− and Cl− ions diffusion coefficients in the MA-40prof | |
| 3.03 × 10−7 cm2 s−1 | ||
| and | 590 and 650 µm | Thickness of the MA-40prof and MK-40prof, respectively |
| 9.3 × 10−5 cm2 s−1 | H+, OH−, Na+ and Cl− ions diffusion coefficients in solution at infinite dilution | |
| 5.3 × 10−5 cm2 s−1 | ||
| 1.33 × 10−5 cm2 s−1 | ||
| 2.03 × 10−5 cm2 s−1 | ||
| 0.3 mmol cm−3 | H+ and OH− ions initial concentrations in the A and B circuits, respectively | |
| 0.3 mmol cm−3 | ||
| 0.025 mmol cm−3 | Na+, Cl−, H+ and OH− ions initial concentrations in the D circuit | |
| 0.025 mmol cm−3 | ||
| 10−5.9 mmol cm−3 | ||
| 10−8.1 mmol cm−3 | ||
| 0.025 mmol cm−3 | Initial concentration of phenylalanine in the D circuit | |
| 1.7 mmol cm−3 | Ion-exchange capacity of the MK-40prof and MA-40prof | |
| 2.4 mmol cm−3 | ||
| 1.0 | Nikolskii equilibrium constant (upper indexes “c” and “a” denote the MK-40prof and MA-40prof membranes, respectively) | |
| (i = 1,2) | = 6.31 × 10−3 mol L−1 = 4.90 × 10−10 mol L−1 | Equilibrium constants for the phenylalanine protonation/deprotonation chemical reactions in Equations (6) and (7) denoted by ( ) and ( ), respectively |
| 2000 cm3 | Solution volumes in A, B and D circuits | |
| 2000 cm3 | ||
| 1000 cm3 | ||
| S | 7.14 cm2 | Working surface area of membrane |
| F | 96.485 C mmol−1 | Faraday constant |
| R | 8.314 × 10−3 J mmol−1 K−1 | Gas constant |
| T | 298 K | Absolute temperature |
References
- Amrane, C.; Lalmi, A.; Bouhidel, K.E. Coupling diffusion dialysis with precipitation-cementation to separate and recover nitric acid, Cu++, Zn++ and Pb++ from the wastewater of a brass pickling bath. Int. J. Glob. Warm. 2017, 11, 337–357. [Google Scholar]
- Kerr, C. Sustainable technologies for the regeneration of acidic tin stripping solutions used in PCB fabrication. Circuit World 2004, 30, 51–58. [Google Scholar] [CrossRef]
- Luo, J.; Wu, C.; Xu, T.; Wu, Y. Diffusion dialysis-concept, principle and applications. J. Membr. Sci. 2011, 366, 1–16. [Google Scholar] [CrossRef]
- Janiszewska, M.; Arguillarena, A.; Wajs, M.; Staszak, K.; Regel-Rosocka, M. Application of diffusion dialysis for reduction of acidity of real pregnant leach solutions containing Ni and Co ions. Sep. Sci. Technol. 2019. [Google Scholar] [CrossRef]
- Khan, M.I.; Mondal, A.N.; Cheng, C.; Pan, J.; Emmanuel, K.; Wu, L.; Xu, T. Porous BPPO-based membranes modified by aromatic amine for acid recovery. Sep. Purif. Technol. 2016, 157, 27–34. [Google Scholar] [CrossRef]
- Xiao, H.-F.; Chen, Q.; Cheng, H.; Li, X.M.; Qin, W.M.; Chen, B.S.; Xiao, D.; Zhang, W.M. Selective removal of halides from spent zinc sulfate electrolyte by diffusion dialysis. J. Membr. Sci. 2017, 537, 111–118. [Google Scholar] [CrossRef]
- Noubli, A.; Akretche, D.E.; Crespo, J.G.; Velizarov, S. Complementary membrane-based processes for recovery and preconcentration of phosphate from industrial wastewater. Sep. Purif. Technol. 2020, 234, 116123. [Google Scholar] [CrossRef]
- Skopinska-Wisniewska, J.; Olszewski, K.; Bajek, A.; Rynkiewicz, A.; Sionkowska, A. Dialysis as a method of obtaining neutral collagen gels. Mater. Sci. Eng. C 2014, 40, 65–70. [Google Scholar] [CrossRef]
- Vasil’eva, V.I.; Goleva, E.A. Selective separation of sodium ions from a mixture with phenylalanine by Donnan dialysis with a profiled sulfogroup cation exchange membrane. Rus. J. Phys. Chem. A 2013, 87, 1895–1901. [Google Scholar] [CrossRef]
- Stamatialis, D.F.; Papenburg, B.J.; Gironés, M.; Saiful, S.; Bettahalli, S.N.M.; Schmitmeier, S.; Wessling, M. Medical applications of membranes: Drug delivery, artificial organs and tissue engineering. J. Membr. Sci. 2008, 308, 1–34. [Google Scholar] [CrossRef]
- Tijink, M.S.L.; Wester, M.; Sun, J.; Saris, A.; Bolhuis-Versteeg, L.A.M.; Saiful, S.; Joles, J.A.; Borneman, Z.; Wessling, M.; Stamatialis, D.F. A novel approach for blood purification: Mixed-matrix membranes combining diffusion and adsorption in one step. Acta Biomater. 2012, 8, 2279–2287. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, N.; Miyamoto, K.; Murata, T.; Ishikawa, E.; Horiuchi, T. Newly developed neutralized pH icodextrin dialysis fluid: nonclinical evaluation. Artif. Organs 2016, 40, E158–E166. [Google Scholar] [CrossRef] [PubMed]
- Stancheva, K.A. Applications of dialysis. Oxid. Commun. 2008, 31, 758–775. [Google Scholar]
- Radke, W. Consequences of on-line dialysis on polyelectrolyte molar masses determined by size-exclusion chromatography with light scattering detection. J. Sep. Sci. 2016, 39, 696–702. [Google Scholar] [CrossRef] [PubMed]
- Huang, R.L.; Tan, Z.L.; Xing, T.X.; Pan, Y.F.; Li, T.J. An in vitro method for the estimation of ileal crude protein and amino acids digestibility using the dialysis tubing for pig feedstuffs. Anim. Feed Sci. Tech. 2000, 88, 79–89. [Google Scholar] [CrossRef]
- Wijmans, J.G.; Baker, R.W. The solution-diffusion model: a review. J. Membr. Sci. 1995, 107, 1–21. [Google Scholar] [CrossRef]
- Ring, S.; Hasson, D.; Shemer, H.; Semiat, R. Simple modeling of Donnan separation processes. J. Membr. Sci. 2015, 476, 348–355. [Google Scholar] [CrossRef]
- Agarwal, C.; Goswami, A. Nernst Planck approach based on non-steady state flux for transport in a Donnan dialysis process. J. Membr. Sci. 2016, 507, 119–125. [Google Scholar] [CrossRef]
- Szczepański, P.; Szczepańska, G. Donnan dialysis—A new predictive model for non−steady state transport. J. Membr. Sci. 2017, 525, 277–289. [Google Scholar] [CrossRef]
- Szczepański, P. Chemometric method for Donnan dialysis physicochemical model simplification. Prediction of: Transport, recovery, concentration, and desalination efficiency. Desalination 2018, 444, 6–12. [Google Scholar]
- Prado-Rubio, O.A.; Møllerhøj, M.; Jørgensen, S.B.; Jonsson, G. Modeling Donnan dialysis separation for carboxylic anion recovery. Comput. Chem. Eng. 2010, 34, 1567–1579. [Google Scholar] [CrossRef]
- Vasil’eva, V.; Goleva, E.; Pismenskaya, N.; Kozmai, A.; Nikonenko, V. Effect of surface profiling of a cation-exchange membrane on the phenylalanine and NaCl separation performances in diffusion dialysis. Sep. Purif. Technol. 2019, 210, 48–59. [Google Scholar] [CrossRef]
- Štěpánek, V.; Palatý, Z.; Bendová, H. Numerical analysis of dialysis with chemical reaction at steady state. Irreversible second-order reaction. Chem. Eng. Process. 2015, 95, 362–371. [Google Scholar] [CrossRef]
- Igawa, M.; Echizenya, K.; Hayashita, T.; Seno, M. Neutralization dialysis for deionization. Bull. Chem. Soc. Jpn. 1987, 60, 381–383. [Google Scholar] [CrossRef]
- Igawa, M.; Mikami, K.; Okochi, H. Transport characteristics of neutralization dialysis and desalination of tap water. Bull. Chem. Soc. Jpn. 2003, 76, 437–441. [Google Scholar] [CrossRef]
- Bleha, M.; Tishchenko, G.A. Neutralization dialysis for desalination. J. Membr. Sci. 1992, 73, 305–311. [Google Scholar] [CrossRef]
- Tanabe, H.; Okochi, H.; Igawa, M. Separation of weak acids and bases by neutralization dialysis. Ind. Eng. Chem. Res. 1995, 34, 2450–2454. [Google Scholar] [CrossRef]
- Zheleznov, A.; Windmöller, D.; Körner, S.; Böddeker, K.W. Dialytic transport of carboxylic acids through an anion exchange membrane. J. Membr. Sci. 1998, 139, 137–143. [Google Scholar] [CrossRef]
- Ueno, K.; Doi, T.; Nanzai, B.; Igawa, M. Selective transport of neutral amino acids across a double-membrane system comprising cation and anion exchange membranes. J. Membr. Sci. 2017, 537, 344–352. [Google Scholar] [CrossRef]
- Wang, G.; Tanabe, H.; Igawa, M. Transport of glycine by neutralization dialysis. J. Membr. Sci. 1995, 106, 207–211. [Google Scholar] [CrossRef]
- Wang, M.; Hou, S.; Liu, Y.; Xu, X.; Lu, T.; Zhao, R.; Pan, L. Capacitive neutralization deionization with flow electrodes. Electrochim. Acta 2016, 216, 211–218. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Y.; Ou-Yang, W.; Bastos Sales, B.; Sun, Z.; Liu, F.; Zhao, R. Capacitive neutralization dialysis for direct energy generation. Envir. Sci. Tech. 2017, 51, 9363–9370. [Google Scholar] [CrossRef] [PubMed]
- Chérif, M.; Mkacher, I.; Ghalloussi, R.; Chaabane, L.; Ben Salah, A.; Walha, K.; Dammak, L.; Grande, D. Experimental investigation of neutralization dialysis in three-compartment membrane stack. Desalin. Water Treat. 2015, 56, 2567–2575. [Google Scholar] [CrossRef]
- Chérif, M.; Mkacher, I.; Dammak, L.; Ben Salah, A.; Walha, K.; Grande, D.; Nikonenko, V. Water desalination by neutralization dialysis with ion-exchange membranes: Flow rate and acid/alkali concentration effects. Desalination 2015, 361, 13–24. [Google Scholar] [CrossRef]
- Tsukahara, S.; Nanzai, B.; Igawa, M. Selective transport of amino acids across a double membrane system composed of a cation- and an anion-exchange membrane. J. Membr. Sci. 2013, 448, 300–307. [Google Scholar] [CrossRef]
- Sato, K.; Yonemoto, T.; Tadaki, T. Modeling of ionic transport in neutralization dialytic deionization. J. Chem. Eng. Jpn. 1993, 26, 68–74. [Google Scholar] [CrossRef]
- Denisov, G.A.; Tishchenko, G.A.; Bleha, M.; Shataeva, L.K. Theoretical analysis of neutralization dialysis in the three-compartment membrane cell. J. Membr. Sci. 1995, 98, 13–25. [Google Scholar] [CrossRef]
- Chérif, M.; Korchane, S.; Chaabane, L.; Dammak, L.; Ben Salah, A.; Walha, K.; Kozmai, A. Reconstituted and brackish waters desalination by neutralization dialysis process with ion-exchange membranes. Desalin. Water Treat. 2017, 65, 52–59. [Google Scholar] [CrossRef]
- Kozmai, A.; Chérif, M.; Dammak, L.; Bdiri, M.; Larchet, C.; Nikonenko, V. Modelling non-stationary ion transfer in neutralization dialysis. J. Membr. Sci. 2017, 540, 60–70. [Google Scholar] [CrossRef]
- Lide, D.R. Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2005; ISBN 0849304873. [Google Scholar]
- Zabolotskii, V.I.; Loza, S.A.; Sharafan, M.V. Physicochemical properties of profiled heterogeneous ion-exchange membranes. Russ. J. Electrochem. 2005, 41, 1053–1060. [Google Scholar] [CrossRef]
- Berezina, N.P.; Kononenko, N.A.; Dyomina, O.A.; Gnusin, N.P. Characterization of ion-exchange membrane materials: Properties vs structure. Adv. Colloid Interfac. 2008, 139, 3–28. [Google Scholar] [CrossRef] [PubMed]
- Vermaas, D.A.; Kunteng, D.; Saakes, M.; Nijmeijer, K. Fouling in reverse electrodialysis under natural conditions. Water Res. 2013, 47, 1289–1298. [Google Scholar] [CrossRef] [PubMed]
- Gnusin, N.P.; Karpenko, L.V.; Demina, O.A.; Berezina, N.P. Calculation of the ion-exchange equilibrium constant for MK-40 sulfo cation-exchange membranes from conductometric data. Rus. J. Phys. Chem. 2001, 75, 1550–1554. [Google Scholar]
- Kozmai, A.E.; Nikonenko, V.V.; Zyryanova, S.; Pismenskaya, N.D.; Dammak, L.; Baklouti, L. Modelling of anion-exchange membrane transport properties with taking into account the change in exchange capacity and swelling when varying bathing solution concentration and pH. J. Membr. Sci. 2019, 590, 117291. [Google Scholar] [CrossRef]
- Sousa, P.; Soares, A.; Monteiro, E.; Roubo, A. A CFD study of the hydrodynamics in a desalination membrane filled with spacers. Desalination 2014, 349, 22–30. [Google Scholar] [CrossRef]
| Membranes | MK-40prof | MA-40prof |
|---|---|---|
| Maximum 1 thickness in swollen state (cm) | 0.065 ± 0.0005 [22] | 0.059 ± 0.0005 |
| Minimum 2 thickness in swollen state (cm) | 0.030 ± 0.0005 | 0.030 ± 0.0005 |
| Water content (wt %) | 42 ± 1 [22] | 44 ± 2 |
| Ion-exchange capacity (meq cm−3 wet membrane) | 1.7 ± 0.1 [22] | 2.4 ± 0.1 |
| Electric conductivity in 0.1 M NaCl (S m−1) | 0.58 [22] | 0.39 [41] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kozmai, A.; Goleva, E.; Vasil’eva, V.; Nikonenko, V.; Pismenskaya, N. Neutralization Dialysis for Phenylalanine and Mineral Salt Separation. Simple Theory and Experiment. Membranes 2019, 9, 171. https://doi.org/10.3390/membranes9120171
Kozmai A, Goleva E, Vasil’eva V, Nikonenko V, Pismenskaya N. Neutralization Dialysis for Phenylalanine and Mineral Salt Separation. Simple Theory and Experiment. Membranes. 2019; 9(12):171. https://doi.org/10.3390/membranes9120171
Chicago/Turabian StyleKozmai, Anton, Elena Goleva, Vera Vasil’eva, Victor Nikonenko, and Natalia Pismenskaya. 2019. "Neutralization Dialysis for Phenylalanine and Mineral Salt Separation. Simple Theory and Experiment" Membranes 9, no. 12: 171. https://doi.org/10.3390/membranes9120171
APA StyleKozmai, A., Goleva, E., Vasil’eva, V., Nikonenko, V., & Pismenskaya, N. (2019). Neutralization Dialysis for Phenylalanine and Mineral Salt Separation. Simple Theory and Experiment. Membranes, 9(12), 171. https://doi.org/10.3390/membranes9120171







