Glucose Can Protect Membranes against Dehydration Damage by Inducing a Glassy Membrane State at Low Hydrations
Abstract
1. Introduction
2. Materials and Methods
2.1. Preparation of Multi-Lamellar, Solid Supported Membranes
2.2. X-ray Diffraction
2.3. Calculating Electron Densities
2.4. Molecular Dynamics Simulations
2.5. Molecular Dynamics Analysis
3. Results
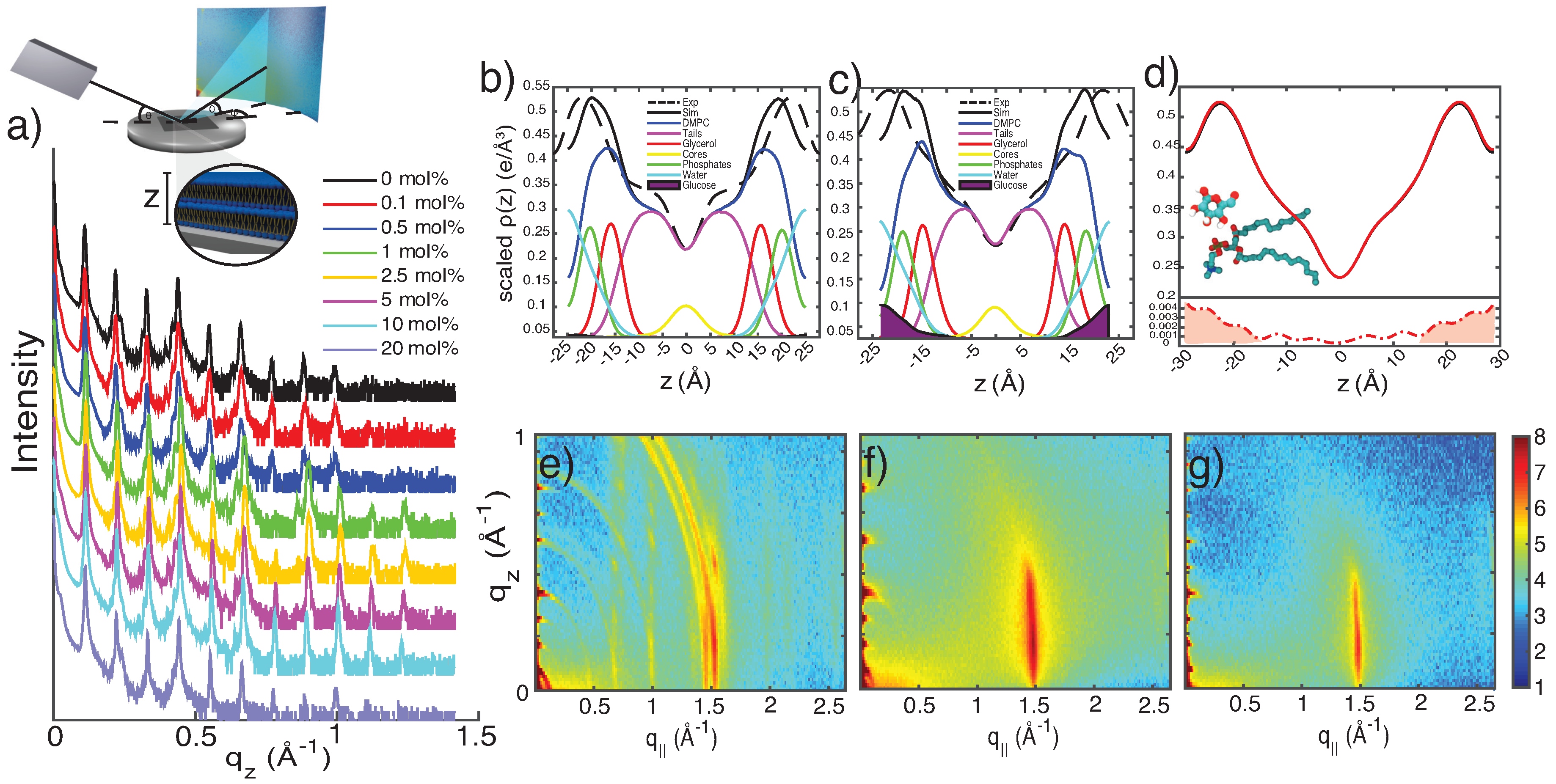
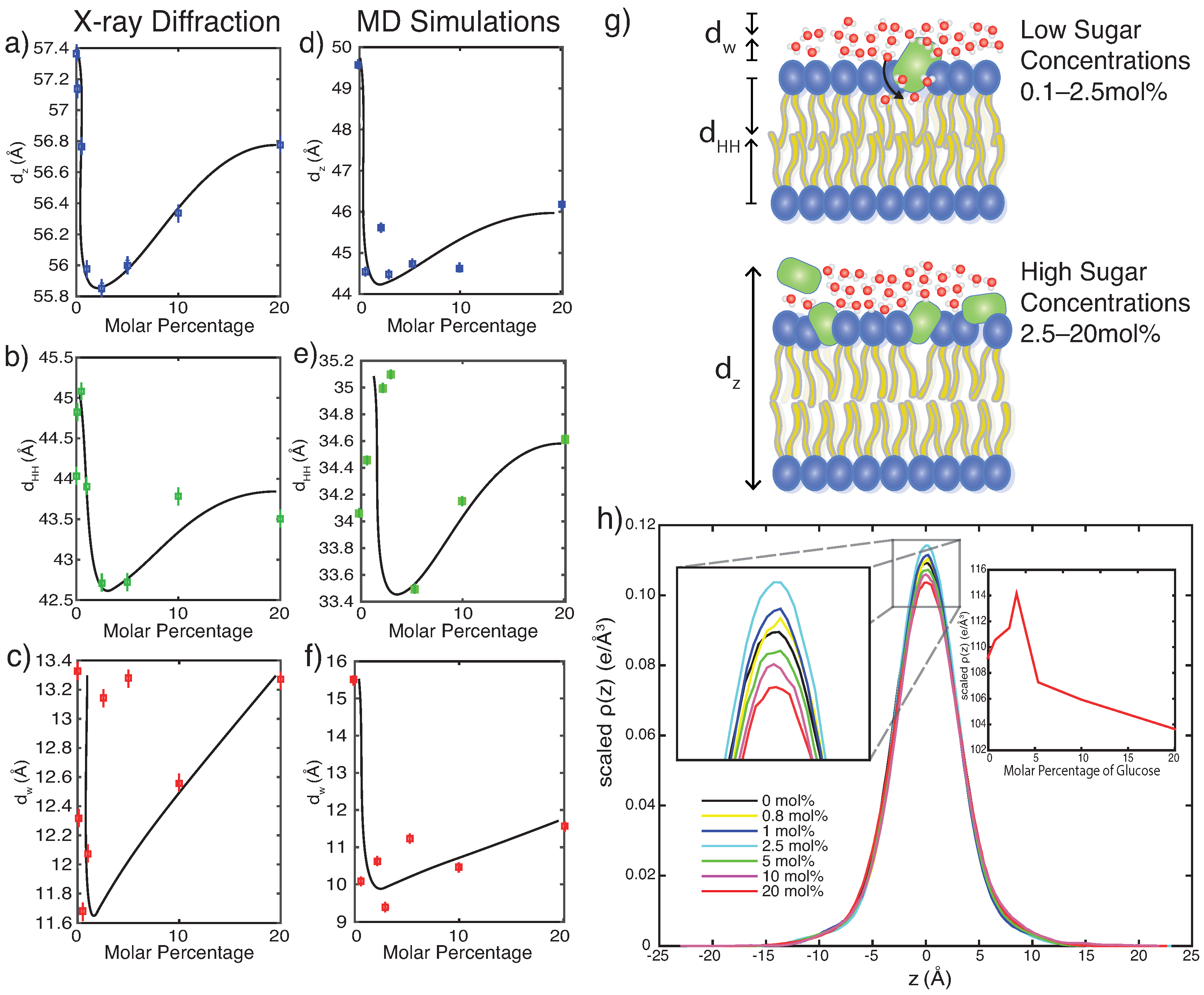
3.1. X-ray Diffraction
3.2. Molecular Dynamics Simulations
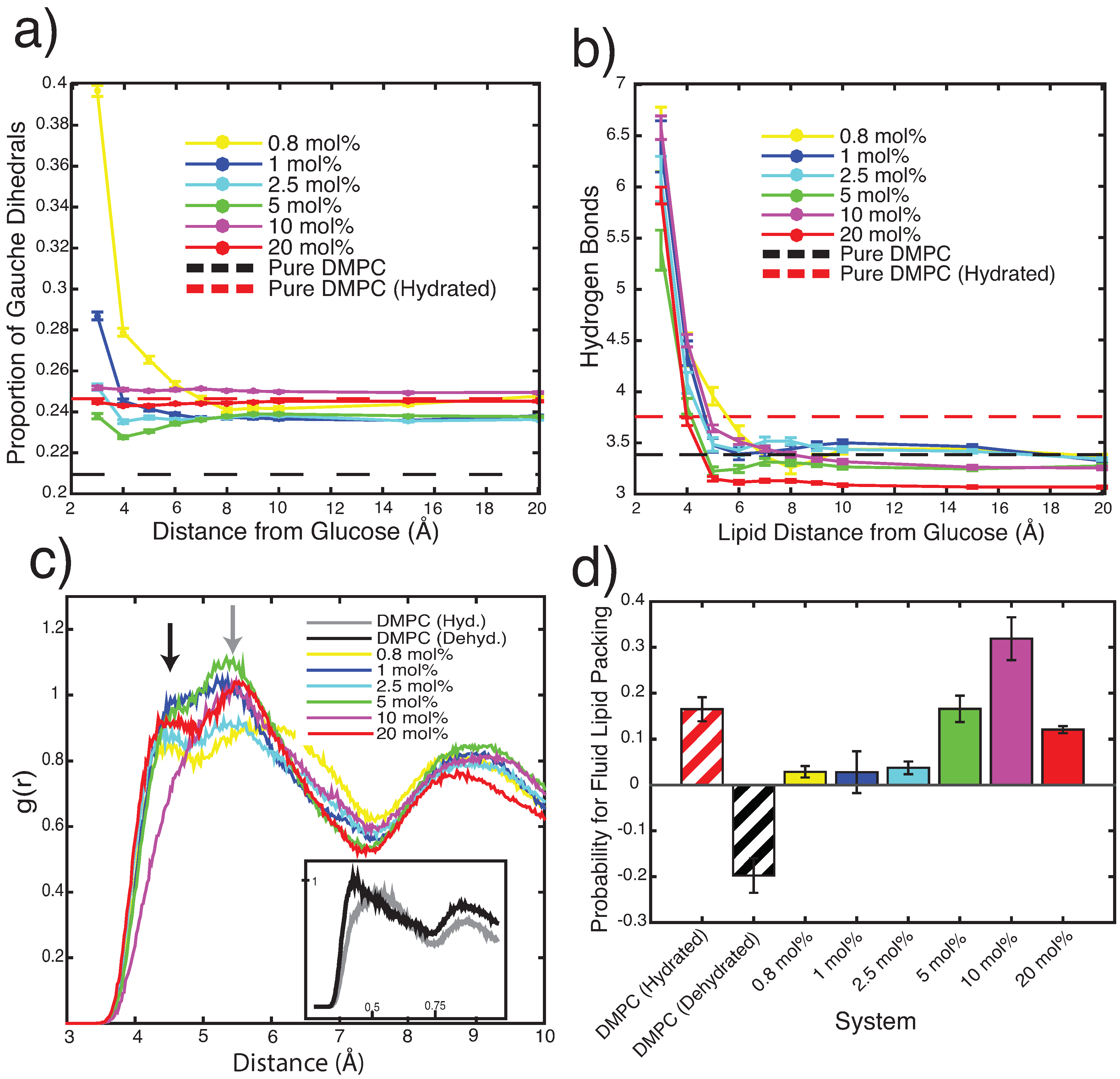
3.2.1. Molecular Dynamics: Structural Analysis
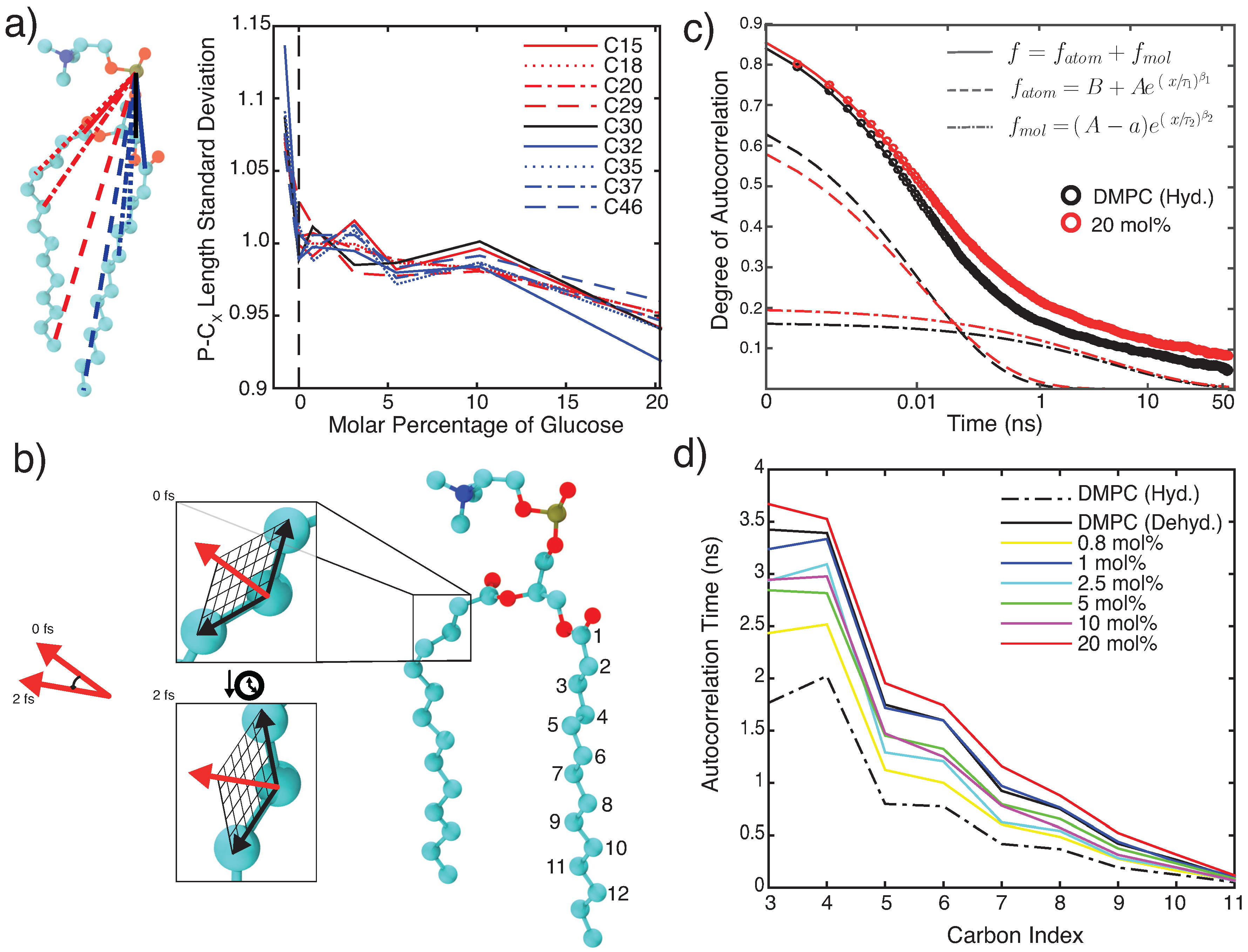
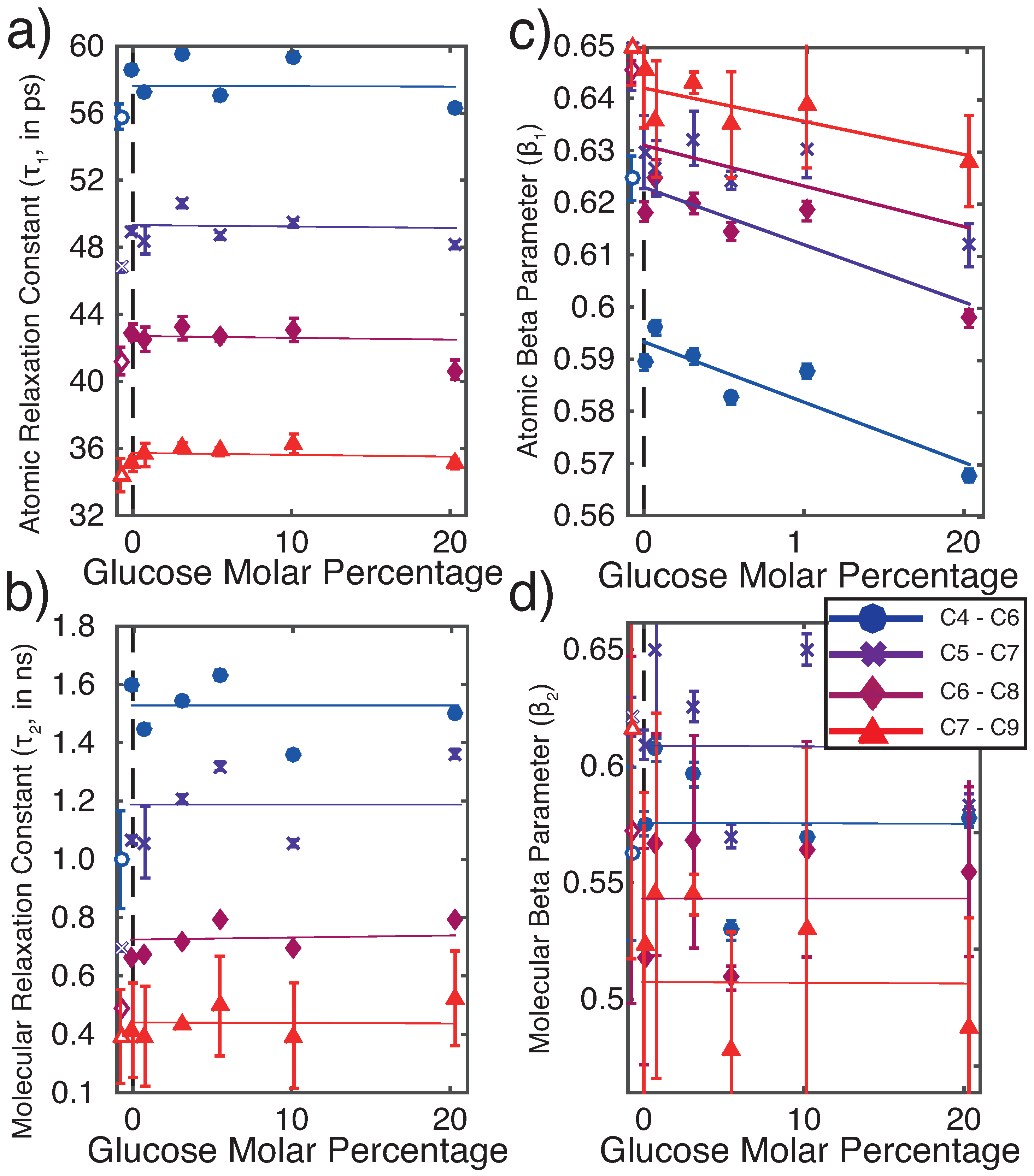
3.2.2. Molecular Dynamics: Dynamical Analysis
4. Discussion
4.1. Glucose Slows Down Lipid Bilayer Dynamics
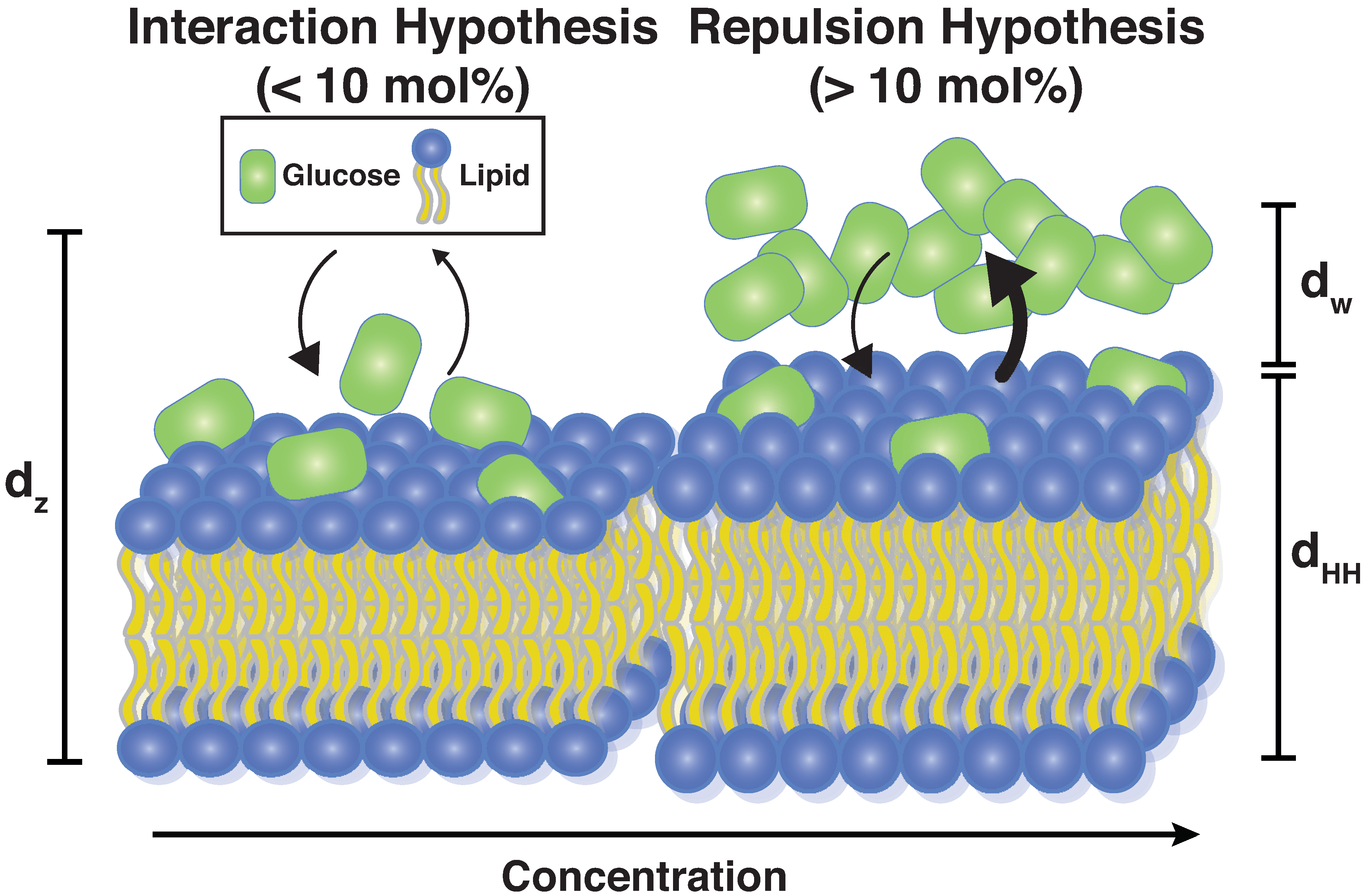
4.2. Glucose Has a Non-Monotonic Effect on Bilayer Spacings
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Crowe, J.H.; Crowe, L.M.; Chapman, D. Preservation of membranes in anhydrobiotic organisms: The role of trehalose. Science 1984, 223, 701–703. [Google Scholar] [CrossRef] [PubMed]
- Crowe, J.H.; Whittam, M.A.; Chapman, D.; Crowe, L.M. Interactions of phospholipid monolayers with carbohydrates. Biochim. Biophys. Acta (BBA) Biomembr. 1984, 769, 151–159. [Google Scholar] [CrossRef]
- Nagase, H.; Ueda, H.; Nakagaki, M. Effect of water on lamellar structure of DPPC/sugar systems. Biochim. Biophys. Acta (BBA)-Biomembranes 1997, 1328, 197–206. [Google Scholar] [CrossRef]
- Rudolph, A.S.; Goins, B. The effect of hydration stress solutes on the phase behavior of hydrated dipalmitoylphosphatidylcholine. Biochim. Biophys. Acta (BBA) Biomembr. 1991, 1066, 90–94. [Google Scholar] [CrossRef]
- Vereyken, I.J.; Chupin, V.; Islamov, A.; Kuklin, A.; Hincha, D.K.; de Kruijff, B. The effect of fructan on the phospholipid organization in the dry state. Biophys. J. 2003, 85, 3058–3065. [Google Scholar] [CrossRef]
- Roy, A.; Dutta, R.; Kundu, N.; Banik, D.; Sarkar, N. A Comparative Study of the Influence of Sugars Sucrose, Trehalose and Maltose on the Hydration and Diffusion of DMPC Lipid Bilayer at Complete Hydration: Investigation of Structural and Spectroscopic Aspect of Lipid-Sugar Interaction. Langmuir 2016, 32, 5124–5134. [Google Scholar] [CrossRef]
- Koster, K.L.; Lei, Y.P.; Anderson, M.; Martin, S.; Bryant, G. Effects of vitrified and nonvitrified sugars on phosphatidylcholine fluid-to-gel phase transitions. Biophys. J. 2000, 78, 1932–1946. [Google Scholar] [CrossRef]
- Stümpel, J.; Vaz, W.L.; Hallmann, D. An X-ray diffraction and differential scanning calorimetric study on the effect of sucrose on the properties of phosphatidylcholine bilayers. Biochim. Biophys. Acta (BBA) Biomembr. 1985, 821, 165–168. [Google Scholar] [CrossRef]
- Luzardo, M.D.C.; Amalfa, F.; Nunez, A.; Diaz, S.; De Lopez, A.B.; Disalvo, E. Effect of trehalose and sucrose on the hydration and dipole potential of lipid bilayers. Biophys. J. 2000, 78, 2452–2458. [Google Scholar] [CrossRef]
- Söderlund, T.; Alakoskela, J.M.I.; Pakkanen, A.L.; Kinnunen, P.K. Comparison of the effects of surface tension and osmotic pressure on the interfacial hydration of a fluid phospholipid bilayer. Biophys. J. 2003, 85, 2333–2341. [Google Scholar] [CrossRef]
- Demé, B.; Dubois, M.; Zemb, T. Swelling of a lecithin lamellar phase induced by small carbohydrate solutes. Biophys. J. 2002, 82, 215–225. [Google Scholar] [CrossRef]
- Demé, B.; Zemb, T. Measurement of sugar depletion from uncharged lamellar phases by SANS contrast variation. J. Appl. Crystallogr. 2000, 33, 569–573. [Google Scholar] [CrossRef]
- Nagle, J.F.; Jablin, M.S.; Tristram-Nagle, S. Sugar does not affect the bending and tilt moduli of simple lipid bilayers. Chem. Phys. Lipids 2016, 196, 76–80. [Google Scholar] [CrossRef] [PubMed]
- Caffrey, M.; Fonseca, V.; Leopold, A.C. Lipid-Sugar Interactions Relevance to Anhydrous Biology. Plant Physiol. 1988, 86, 754–758. [Google Scholar] [CrossRef] [PubMed]
- Andersen, H.D.; Wang, C.; Arleth, L.; Peters, G.H.; Westh, P. Reconciliation of opposing views on membrane–sugar interactions. Proc. Natl. Acad. Sci. USA 2011, 108, 1874–1878. [Google Scholar] [CrossRef] [PubMed]
- Madden, T.D.; Bally, M.B.; Hope, M.J.; Cullis, P.R.; Schieren, H.P.; Janoff, A.S. Protection of large unilamellar vesicles by trehalose during dehydration: Retention of vesicle contents. Biochim. Biophys. Acta (BBA) Biomembranes 1985, 817, 67–74. [Google Scholar] [CrossRef]
- Payen, R. Variations des teneurs en glycogène et en tréhalose pendant le séchage de la levure. Can. J. Res. 1949, 27, 749–756. [Google Scholar] [CrossRef]
- Sussman, A.S.; Lingappa, B.T. Role of trehalose in ascospores of Neurospora tetrasperma. Science 1959, 130, 1343. [Google Scholar] [CrossRef] [PubMed]
- Crowe, J.H. Trehalose as a ”chemical chaperone”. In Molecular Aspects of the Stress Response: Chaperones, Membranes and Networks; Springer: Berlin, Germany, 2007; pp. 143–158. [Google Scholar]
- LeNeveu, D.M.; Rand, R. Measurement and modification of forces between lecithin bilayers. Biophys. J. 1977, 18, 209. [Google Scholar] [CrossRef]
- Gaber, B.; Chandrasekhar, I.; Pattiabiraman, N. Molecular Modeling of the Interaction of Trehalose with the Phospholipid-Bilayer. Biophys. J. 1986, 49, A435. [Google Scholar]
- Lee, C.W.; Waugh, J.S.; Griffin, R.G. Solid-state NMR study of trehalose/1, 2-dipalmitoyl-sn-phosphatidylcholine interactions. Biochemistry 1986, 25, 3737–3742. [Google Scholar] [CrossRef] [PubMed]
- Koster, K.L.; Webb, M.S.; Bryant, G.; Lynch, D.V. Interactions between soluble sugars and POPC (1-palmitoyl-2-oleoylphosphatidylcholine) during dehydration: Vitrification of sugars alters the phase behavior of the phospholipid. Biochim.Biophys. Acta (BBA) Biomembranes 1994, 1193, 143–150. [Google Scholar] [CrossRef]
- Sun, W.Q.; Leopold, A.C.; Crowe, L.M.; Crowe, J.H. Stability of dry liposomes in sugar glasses. Biophys. J. 1996, 70, 1769. [Google Scholar] [CrossRef]
- Crowe, L.M.; Womersley, C.; Crowe, J.H.; Reid, D.; Appel, L.; Rudolph, A. Prevention of fusion and leakage in freeze-dried liposomes by carbohydrates. Biochim. Biophys. Acta (BBA) Biomembr. 1986, 861, 131–140. [Google Scholar] [CrossRef]
- Crowe, J.H.; Crowe, L.M.; Carpenter, J.F.; Rudolph, A.; Wistrom, C.A.; Spargo, B.; Anchordoguy, T. Interactions of sugars with membranes. Biochim. Biophys. Acta (BBA) Rev. Biomembr. 1988, 947, 367–384. [Google Scholar] [CrossRef]
- Lambruschini, C.; Relini, A.; Ridi, A.; Cordone, L.; Gliozzi, A. Trehalose interacts with phospholipid polar heads in Langmuir monolayers. Langmuir 2000, 16, 5467–5470. [Google Scholar] [CrossRef]
- Lairion, F.; Disalvo, E.A. Effect of trehalose on the contributions to the dipole potential of lipid monolayers. Chem. Phys. Lipids 2007, 150, 117–124. [Google Scholar] [CrossRef] [PubMed]
- Leekumjorn, S.; Sum, A.K. Molecular dynamics study on the stabilization of dehydrated lipid bilayers with glucose and trehalose. J. Phys. Chem. B 2008, 112, 10732–10740. [Google Scholar] [CrossRef] [PubMed]
- Cevc, G. Effect of lipid headgroups and (nonelectrolyte) solution on the structural and phase properties of bilayer membranes. Berichte der Bunsengesellschaft für Physikalische Chemie 1988, 92, 953A–961A. [Google Scholar] [CrossRef]
- Montañés, F.; Olano, A.; Ibáñez, E.; Fornari, T. Modeling solubilities of sugars in alcohols based on original experimental data. AIChE J. 2007, 53, 2411–2418. [Google Scholar] [CrossRef]
- Rheinstädter, M.; Toppozini, L.; Dies, H. The Interaction of Bio-Molecules with Lipid Membranes Studied by X-ray Diffraction. Zeitschrift für Physikalische Chemie 2014, 228, 1105–1120. [Google Scholar] [CrossRef]
- Barrett, M.A.; Zheng, S.; Roshankar, G.; Alsop, R.J.; Belanger, R.K.; Huynh, C.; Kučerka, N.; Rheinstädter, M.C. Interaction of aspirin (acetylsalicylic acid) with lipid membranes. PLoS ONE 2012, 7, e34357. [Google Scholar] [CrossRef] [PubMed]
- Alsop, R.J.; Armstrong, C.L.; Maqbool, A.; Toppozini, L.; Dies, H.; Rheinstädter, M.C. Cholesterol expels ibuprofen from the hydrophobic membrane core and stabilizes lamellar phases in lipid membranes containing ibuprofen. Soft Matter 2015, 11, 4756–4767. [Google Scholar] [CrossRef] [PubMed]
- Alsop, R.J.; Schober, R.M.; Rheinstädter, M.C. Swelling of phospholipid membranes by divalent metal ions depends on the location of the ions in the bilayers. Soft Matter 2016, 12, 6737–6748. [Google Scholar] [CrossRef] [PubMed]
- Khondker, A.; Dhaliwal, A.; Alsop, R.J.; Tang, J.; Backholm, M.; Shi, A.C.; Rheinstädter, M.C. Partitioning of caffeine in lipid bilayers reduces membrane fluidity and increases membrane thickness. Phys. Chem. Chem. Phys. 2017, 19, 7101–7111. [Google Scholar] [CrossRef] [PubMed]
- Alsop, R.J.; Dhaliwal, A.; Rheinstadter, M.C. Curcumin Protects Membranes Through Carpet or Insertion Model Depending on Hydration. Langmuir 2017, 33, 8516–8524. [Google Scholar] [CrossRef] [PubMed]
- Tieleman, D.P.; Sansom, M.S.; Berendsen, H.J. Alamethicin helices in a bilayer and in solution: Molecular dynamics simulations. Biophys. J. 1999, 76, 40–49. [Google Scholar] [CrossRef]
- Lins, R.D.; Hünenberger, P.H. A new GROMOS force field for hexopyranose-based carbohydrates. J. Comput. Chem. 2005, 26, 1400–1412. [Google Scholar] [CrossRef]
- Scott, A.P.; Radom, L. Harmonic vibrational frequencies: An evaluation of Hartree-Fock, Møller-Plesset, quadratic configuration interaction, density functional theory, and semiempirical scale factors. J. Phys. Chem. 1996, 100, 16502–16513. [Google Scholar] [CrossRef]
- Berendsen, H.J.; Postma, J.P.; van Gunsteren, W.F.; Hermans, J. Interaction models for water in relation to protein hydration. In Intermolecular Forces; Springer: Berlin, Germany, 1981; pp. 331–342. [Google Scholar]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar] [CrossRef]
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef] [PubMed]
- Schmid, N.; Eichenberger, A.P.; Choutko, A.; Riniker, S.; Winger, M.; Mark, A.E.; van Gunsteren, W.F. Definition and testing of the GROMOS force-field versions 54A7 and 54B7. Eur. Biophys. J. 2011, 40, 843–856. [Google Scholar] [CrossRef] [PubMed]
- Berger, O.; Edholm, O.; Jähnig, F. Molecular dynamics simulations of a fluid bilayer of dipalmitoylphosphatidylcholine at full hydration, constant pressure, and constant temperature. Biophys. J. 1997, 72, 2002. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N · log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.; Fraaije, J.G. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Evans, D.J.; Holian, B.L. The nose–hoover thermostat. J. Chem. Phys. 1985, 83, 4069–4074. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Boggara, M.B.; Krishnamoorti, R. Partitioning of nonsteroidal antiinflammatory drugs in lipid membranes: A molecular dynamics simulation study. Biophys. J. 2010, 98, 586–595. [Google Scholar] [CrossRef]
- Hess, B. Determining the shear viscosity of model liquids from molecular dynamics simulations. J. Chem. Phys. 2002, 116, 209–217. [Google Scholar] [CrossRef]
- Saito, H.; Shinoda, W. Cholesterol effect on water permeability through DPPC and PSM lipid bilayers: A molecular dynamics study. J. Phys. Chem. B 2011, 115, 15241–15250. [Google Scholar] [CrossRef]
- Hofsäß, C.; Lindahl, E.; Edholm, O. Molecular dynamics simulations of phospholipid bilayers with cholesterol. Biophys. J. 2003, 84, 2192–2206. [Google Scholar] [CrossRef]
- Venable, R.M.; Brooks, B.R.; Pastor, R.W. Molecular dynamics simulations of gel (LβI) phase lipid bilayers in constant pressure and constant surface area ensembles. J. Chem. Phys. 2000, 112, 4822–4832. [Google Scholar] [CrossRef]
- Ryckaert, J.P.; Bellemans, A. Molecular dynamics of liquid alkanes. Faraday Discuss. Chem. Soc. 1978, 66, 95–106. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Rifici, S.; D’Angelo, G.; Crupi, C.; Branca, C.; Conti Nibali, V.; Corsaro, C.; Wanderlingh, U. Influence of Alcohols on the Lateral Diffusion in Phospholipid Membranes. J. Phys. Chem. B 2016, 120, 1285–1290. [Google Scholar] [CrossRef] [PubMed]
- Abraham, M.; van der Spoel, D.; Lindahl, E.; Hess, B. GROMACS User Manual Version 5.1.1. Available online: ftp://ftp.gromacs.org/pub/manual/manual-5.1.1.pdf (accessed on 10 January 2019).
- Pluhackova, K.; Kirsch, S.A.; Han, J.; Sun, L.; Jiang, Z.; Unruh, T.; Böckmann, R.A. A Critical Comparison of Biomembrane Force Fields: Structure and Dynamics of Model DMPC, POPC, and POPE Bilayers. J. Phys. Chem. B 2016, 120, 3888–3903. [Google Scholar] [CrossRef]
- Armstrong, C.L.; Marquardt, D.; Dies, H.; Kučerka, N.; Yamani, Z.; Harroun, T.A.; Katsaras, J.; Shi, A.C.; Rheinstädter, M.C. The observation of highly ordered domains in membranes with cholesterol. PLoS ONE 2013, 8, e66162. [Google Scholar] [CrossRef]
- Mills, T.T.; Toombes, G.E.; Tristram-Nagle, S.; Smilgies, D.M.; Feigenson, G.W.; Nagle, J.F. Order parameters and areas in fluid-phase oriented lipid membranes using wide angle X-ray scattering. Biophys. J. 2008, 95, 669–681. [Google Scholar] [CrossRef]
- Phillips, J.C. Stretched exponential relaxation in molecular and electronic glasses. Rep. Prog. Phys. 1996, 59, 1133–1207. [Google Scholar] [CrossRef]
- Gawrisch, K. The dynamics of membrane lipids. In The Structure of Biological Membranes; CRC Press: Boca Raton, FL, USA, 2004; pp. 153–177. [Google Scholar]

| # DMPC Molecules | # Glucose Molecules | Water/Lipid (sim) | Glucose mol% (exp) | Run Time (ns) | Temperature (K) |
|---|---|---|---|---|---|
| 128 | 0 | 27 | 0 | 200 | 300 |
| 128 | 0 | 7 | 0 | 500 | 300 |
| – | – | – | 0.1 | – | 300 |
| – | – | – | 0.5 | – | 300 |
| 128 | 1 | 7 | 1 | 200 | 300 |
| 128 | 3 | 7 | 1 | 200 | 300 |
| 128 | 4 | 7 | 2.5 | 200 | 300 |
| 128 | 7 | 7 | 5 | 200 | 300 |
| 128 | 13 | 7 | 10 | 200 | 300 |
| 128 | 26 | 7 | 20 | 200 | 300 |
| 128 | 0 | 27 | – | 200 | 280 |
| 128 | 0 | 7 | 0 | 200 | 280 |
| 128 | 1 | 7 | 1 | 200 | 280 |
| 128 | 3 | 7 | 1 | 200 | 280 |
| 128 | 4 | 7 | 2.5 | 200 | 280 |
| 128 | 7 | 7 | 5 | 200 | 280 |
| 128 | 13 | 7 | 10 | 200 | 280 |
| 128 | 26 | 7 | 20 | 200 | 280 |
| Glucose (mol%) | (Å2) | (Å) | (Å) | (Å) | |
|---|---|---|---|---|---|
| X-ray diffraction | |||||
| 0 | 7 | – | 57.4 | 44.0 | 13.3 |
| 0.1 | 7 | – | 57.1 | 44.8 | 12.3 |
| 0.5 | 7 | – | 56.8 | 45.1 | 11.7 |
| 1 | 7 | – | 56.0 | 43.9 | 12.1 |
| 2.5 | 7 | – | 55.9 | 42.7 | 13.1 |
| 5 | 7 | – | 56.0 | 42.7 | 13.3 |
| 10 | 7 | – | 56.3 | 43.8 | 12.6 |
| 20 | 7 | – | 56.8 | 43.5 | 13.3 |
| MD simulations | |||||
| 0 | 25 | 63.0 | 41.6 | 21.4 | |
| 0 | 7 | 49.6 | 34.1 | 15.5 | |
| 0.8 | 7 | 44.5 | 34.5 | 10.1 | |
| 1 | 7 | 45.6 | 35.0 | 10.6 | |
| 2.5 | 7 | 44.5 | 35.1 | 9.4 | |
| 5 | 7 | 44.7 | 33.5 | 11.2 | |
| 10 | 7 | 44.6 | 34.2 | 10.5 | |
| 20 | 7 | 46.2 | 34.6 | 11.6 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhaliwal, A.; Khondker, A.; Alsop, R.; Rheinstädter, M.C. Glucose Can Protect Membranes against Dehydration Damage by Inducing a Glassy Membrane State at Low Hydrations. Membranes 2019, 9, 15. https://doi.org/10.3390/membranes9010015
Dhaliwal A, Khondker A, Alsop R, Rheinstädter MC. Glucose Can Protect Membranes against Dehydration Damage by Inducing a Glassy Membrane State at Low Hydrations. Membranes. 2019; 9(1):15. https://doi.org/10.3390/membranes9010015
Chicago/Turabian StyleDhaliwal, Alexander, Adree Khondker, Richard Alsop, and Maikel C. Rheinstädter. 2019. "Glucose Can Protect Membranes against Dehydration Damage by Inducing a Glassy Membrane State at Low Hydrations" Membranes 9, no. 1: 15. https://doi.org/10.3390/membranes9010015
APA StyleDhaliwal, A., Khondker, A., Alsop, R., & Rheinstädter, M. C. (2019). Glucose Can Protect Membranes against Dehydration Damage by Inducing a Glassy Membrane State at Low Hydrations. Membranes, 9(1), 15. https://doi.org/10.3390/membranes9010015







