Grain Boundary Segregation in Pd-Cu-Ag Alloys for High Permeability Hydrogen Separation Membranes
Abstract
:1. Introduction
2. Methodology
3. Results
3.1. Structure and Stability of Pure Pd GB Models
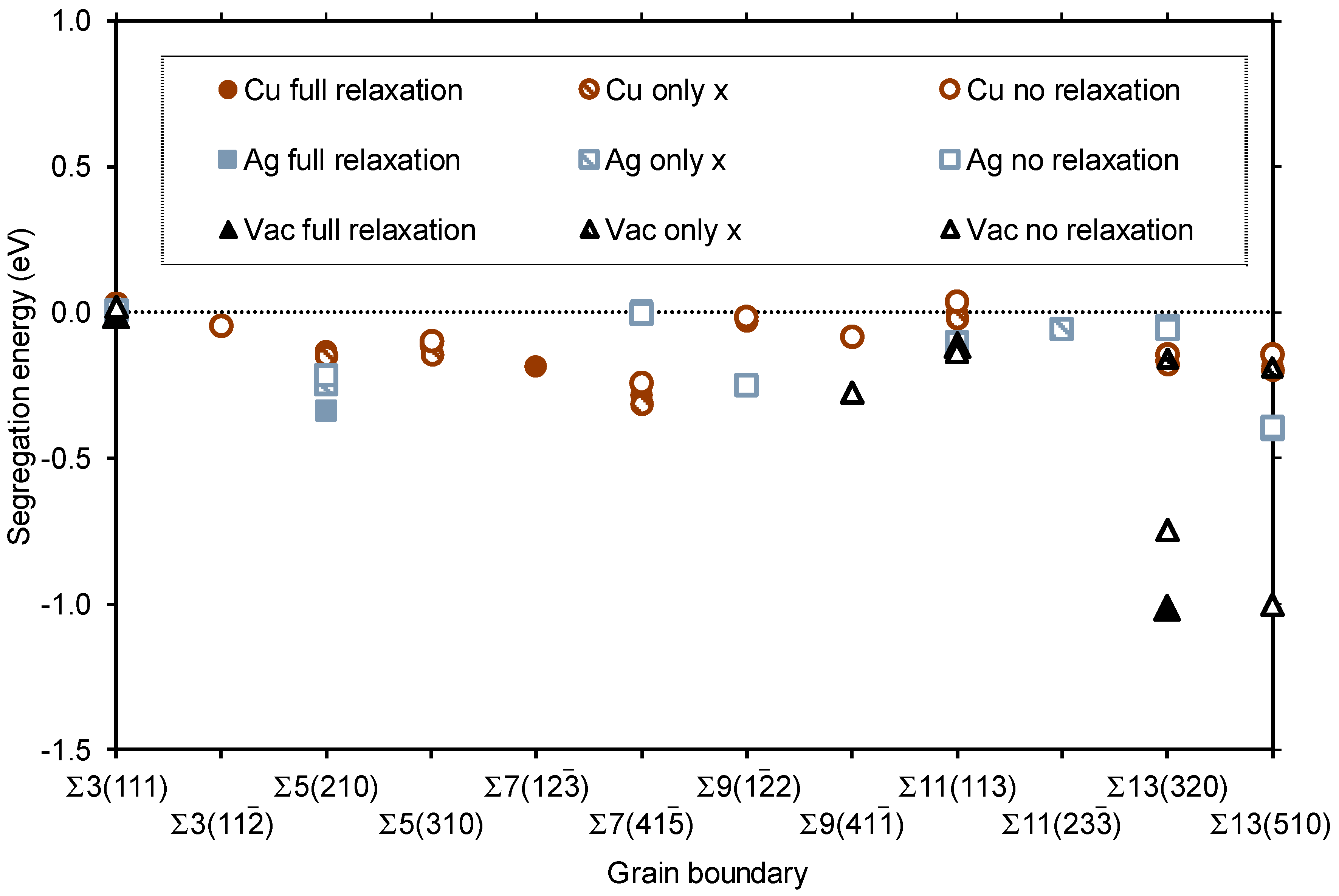
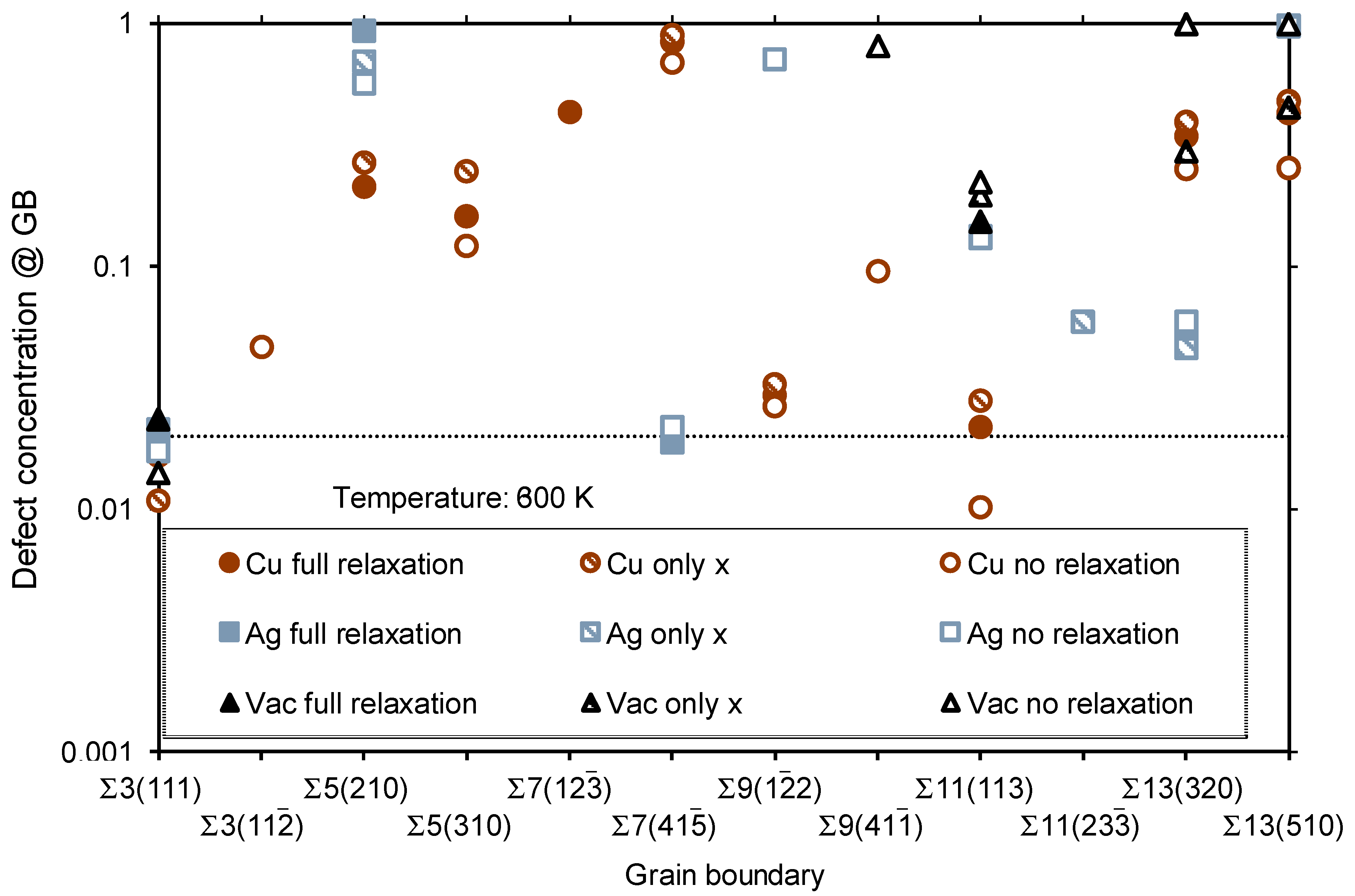
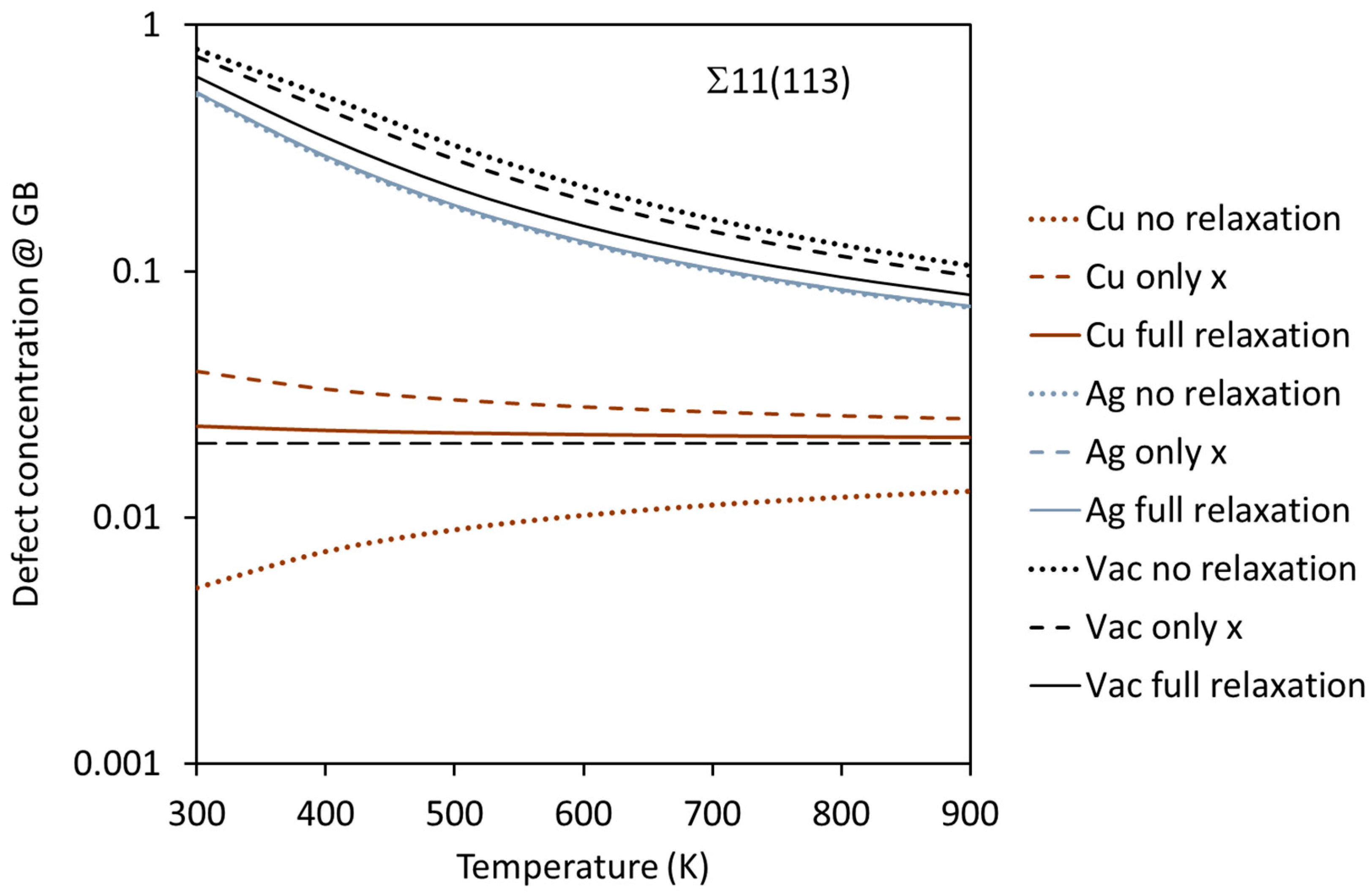
3.2. Segregation of Single Point Defects
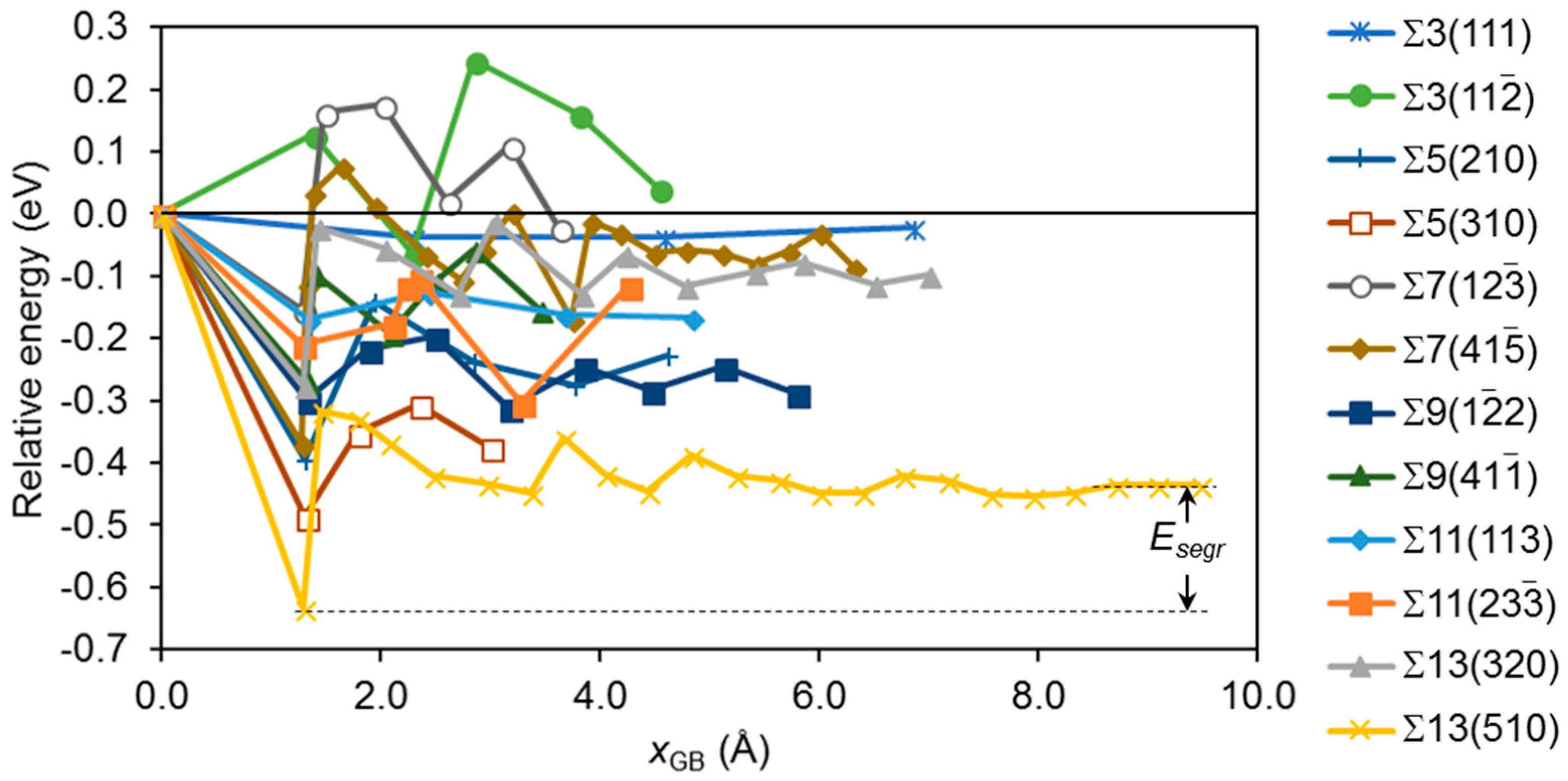
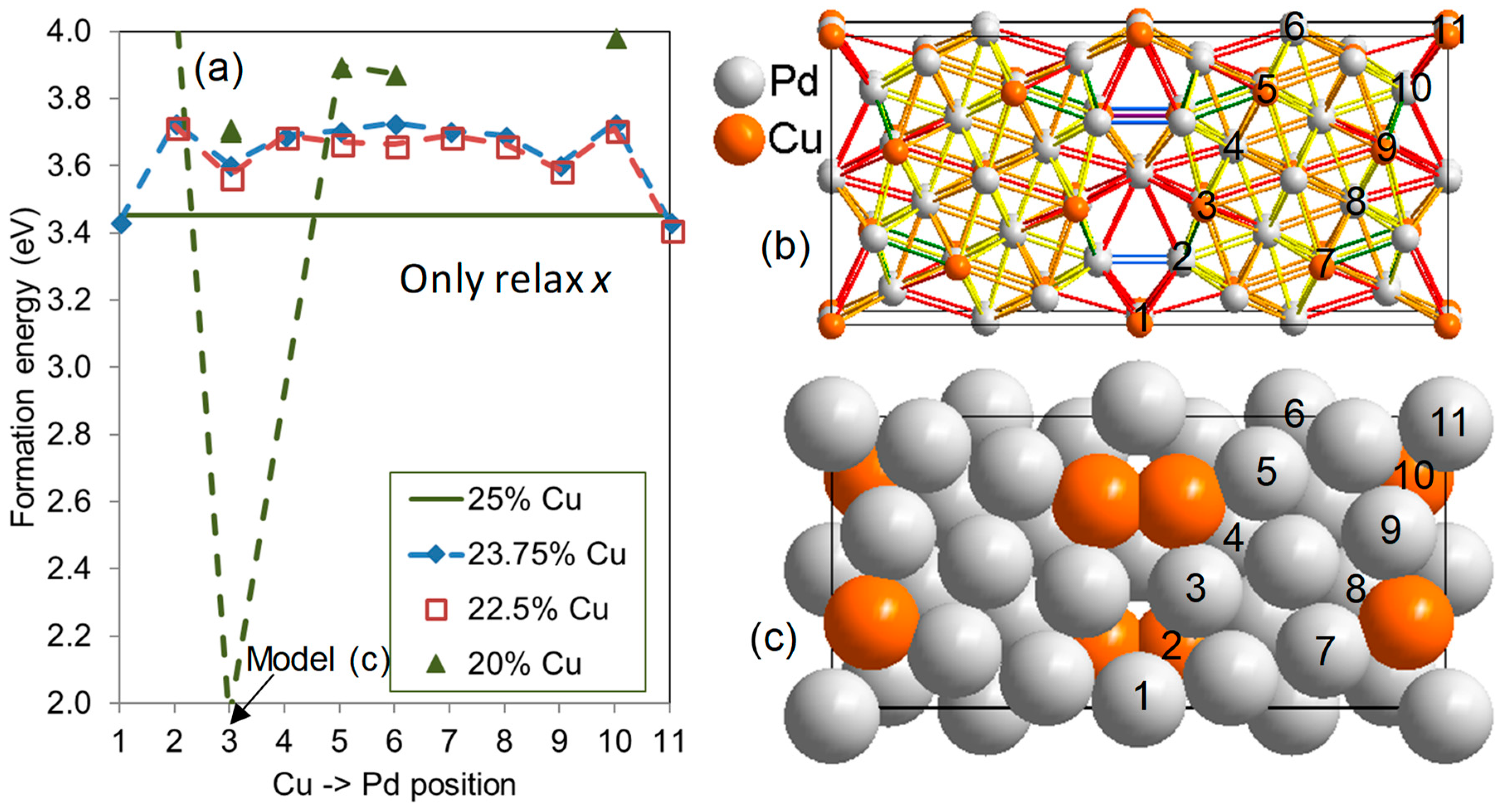
3.3. Binary Systems with More Than One Impurity Atom
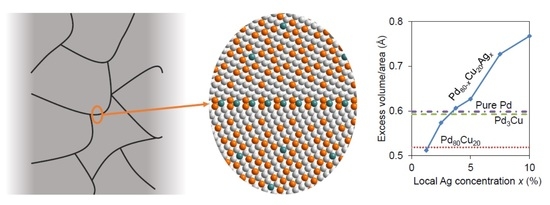
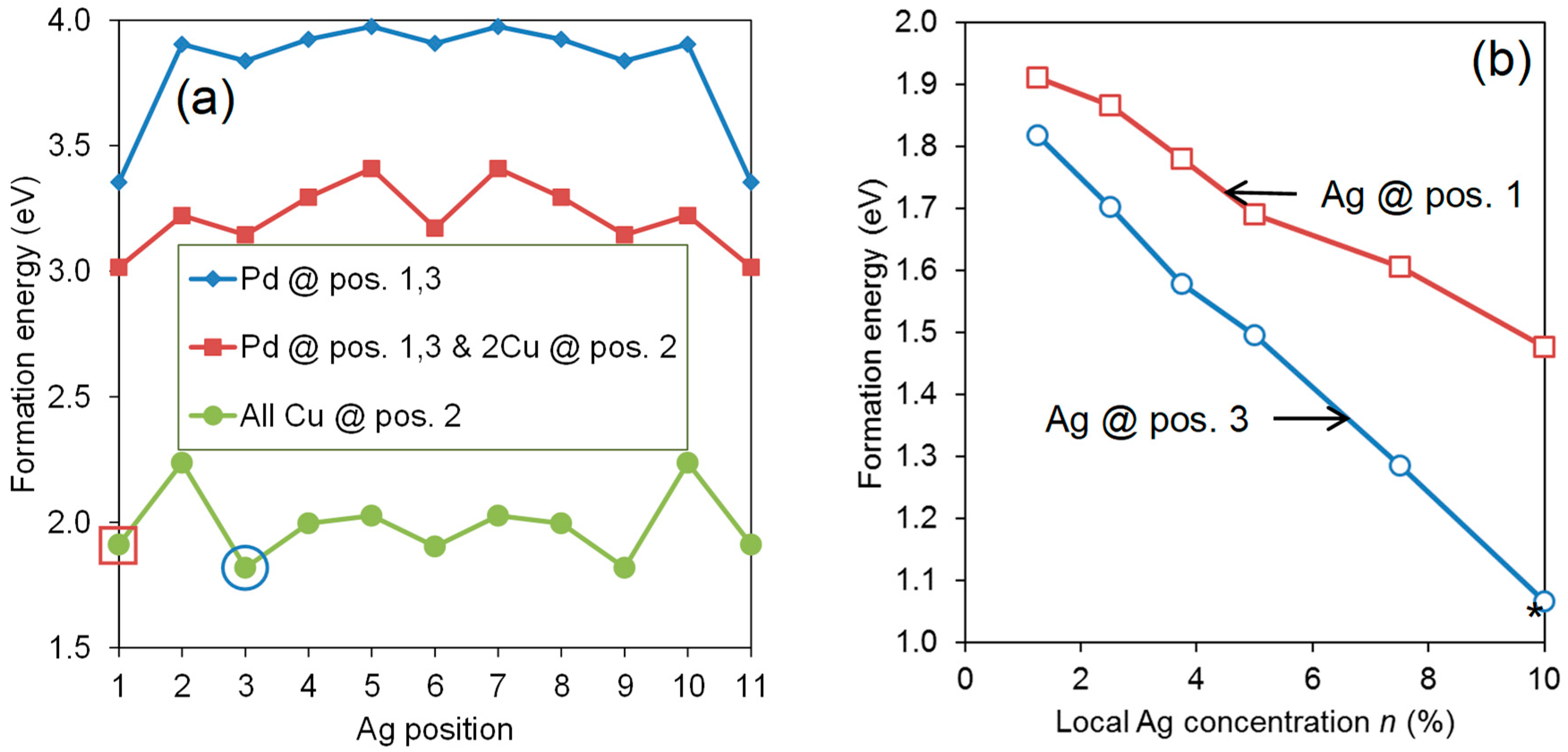
3.4. Segregation in Ternary Pd-Cu-Ag Alloys
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gallucci, F.; Fernandez, E.; Corengia, P.; Annaland, M.v.S. Recent advances on membranes and membrane reactors for hydrogen production. Chem. Eng. Sci. 2013, 92, 40–66. [Google Scholar] [CrossRef]
- Al-Mufachi, N.A.; Rees, N.V.; Steinberger-Wilkens, R. Hydrogen selective membranes: A review of palladium-based dense metal membranes. Renew. Sustain. Energy Rev. 2015, 47, 540–551. [Google Scholar] [CrossRef]
- Li, P.; Wang, Z.; Liu, Z.Y.; Cao, X.; Li, W.; Wang, J.; Wang, S. Recent developments in membranes for efficient hydrogen purification. J. Membr. Sci. 2015, 495, 130–168. [Google Scholar] [CrossRef]
- Lu, G.Q.; Diniz da Costa, J.C.; Duke, M.; Giessler, S.; Socolow, R.; Williams, R.H.; Kreutz, T. Inorganic membranes for hydrogen production and purification: A critical review and perspective. J. Colloid Interface Sci. 2007, 314, 589–603. [Google Scholar] [CrossRef] [PubMed]
- Bredesen, R.; Peters, T.A.; Boeltken, T.; Dittmeyer, R. Pd-Based Membranes in Hydrogen Production for Fuel cells. In Process Intensification for Sustainable Energy Conversion; John Wiley & Sons, Ltd.: West Sussex, UK, 2015; pp. 209–242. [Google Scholar]
- Peters, T.A.; Stange, M.; Bredesen, R. Development of thin Pd-23%Ag/Stainless Steel composite membranes for application in Water Gas Shift membrane reactors. In Carbon Dioxide Capture for Storage in Deep Geological Formations; Eide, L.I., Ed.; CPL Press and BP: Berkshire, UK, 2010; pp. 135–155. [Google Scholar]
- Uemiya, S. State-of-the-Art of Supported Metal Membranes for Gas Separation. Sep. Purif. Rev. 1999, 28, 51–85. [Google Scholar] [CrossRef]
- Oertel, M.; Schmitz, J.; Weirich, W.; Jendryssek-Neumann, D.; Schulten, R. Steam reforming of natural gas with intergrated hydrogen separation for hydrogen production. Chem. Eng. Technol. 1987, 10, 248–255. [Google Scholar] [CrossRef]
- Coulter, K.E.; Way, J.D.; Gade, S.K.; Chaudhari, S.; Sholl, D.S.; Semidey-Flecha, L. Predicting, Fabricating, and Permeability Testing of Free-Standing Ternary Palladium-Copper-Gold Membranes for Hydrogen Separation. J. Phys. Chem. C 2010, 114, 17173–17180. [Google Scholar] [CrossRef]
- Galipaud, J.; Martin, M.H.; Roue, L.; Guay, D. Pulsed Laser Deposition of PdCuAu Alloy Membranes for Hydrogen Absorption Study. J. Phys. Chem. C 2015, 119, 26451–26458. [Google Scholar] [CrossRef]
- Kim, D.W.; Park, Y.J.; Woo, B.I.; Kang, S.M.; Park, J.S. Study on the perm-selectivity of thin Pd-Cu-Ni ternary alloy membrane for hydrogen purification and separation. Jpn. J. Appl. Phys. 2010, 49, 018003. [Google Scholar] [CrossRef]
- Nayebossadri, S.; Speight, J.; Book, D. Effects of low Ag additions on the hydrogen permeability of Pd-Cu-Ag hydrogen separation membranes. J. Membr. Sci. 2014, 451, 216–225. [Google Scholar] [CrossRef]
- Peters, T.A.; Kaleta, T.; Stange, M.; Bredesen, R. Development of ternary Pd-Ag-TM alloy membranes with improved sulphur tolerance. J. Membr. Sci. 2013, 429, 448–458. [Google Scholar] [CrossRef]
- Peters, T.A.; Kaleta, T.; Stange, M.; Bredesen, R. Development of thin binary and ternary Pd-based alloy membranes for use in hydrogen production. J. Membr. Sci. 2011, 383, 124–134. [Google Scholar] [CrossRef]
- Ryi, S.K.; Park, J.S.; Kim, S.H.; Cho, S.H.; Kim, D.W.; Um, K.Y. Characterization of Pd-Cu-Ni ternary alloy membrane prepared by magnetron sputtering and Cu-reflow on porous nickel support for hydrogen separation. Separ. Purif. Technol. 2006, 50, 82–91. [Google Scholar] [CrossRef]
- Chen, F.L.; Kinari, Y.; Sakamoto, Y. The hydrogen miscibility gaps in hydrogenated Pd-Y-In(Sn, Pb) ternary alloys. J. Alloys Compd. 1994, 205, 119–124. [Google Scholar] [CrossRef]
- Ling, C.; Semidey-Flecha, L.; Sholl, D.S. First-principles screening of PdCuAg ternary alloys as H-2 purification membranes. J. Membr. Sci. 2011, 371, 189–196. [Google Scholar] [CrossRef]
- Pati, S.; Jat, R.A.; Anand, N.S.; Derose, D.J.; Karn, K.N.; SMukerjee, K.; Parida, S.C. Pd-Ag-Cu dense metallic membrane for hydrogen isotope purification and recovery at low pressures. J. Membr. Sci. 2017, 522, 151–158. [Google Scholar] [CrossRef]
- Tarditi, A.M.; Cornaglia, L.M. Novel PdAgCu ternary alloy as promising materials for hydrogen separation membranes: Synthesis and characterization. Surf. Sci. 2011, 605, 62–71. [Google Scholar] [CrossRef]
- Zhao, L.F.; Goldbach, A.; Bao, C.; Xu, H.Y. Structural and Permeation Kinetic Correlations in PdCuAg Membranes. ACS Appl. Mater. Interfaces 2014, 6, 22408–22416. [Google Scholar] [CrossRef] [PubMed]
- Gao, M.C.; Ouyang, L.; Dogan, O.N. First principles screening of B2 stabilizers in CuPd-based hydrogen separation membranes: (1) Substitution for Pd. J. Alloys Compd. 2013, 574, 368–376. [Google Scholar] [CrossRef]
- Bredesen, R.; Klette, H. Method of Manufacturing Thin Metal Membranes. US Patent 6,086,729, 11 July 2000. [Google Scholar]
- Peters, T.A.; Stange, M.; Bredesen, R. 2-Fabrication of palladium-based membranes by magnetron sputtering. In Palladium Membrane Technology for Hydrogen Production, Carbon Capture and Other Applications; Woodhead Publishing: Cambridge, UK, 2015; pp. 25–41. [Google Scholar]
- Nicholson, K.M.; Chandrasekhar, N.; Sholl, D.S. Powered by DFT: Screening Methods That Accelerate Materials Development for Hydrogen in Metals Applications. Acc. Chem. Res. 2014, 47, 3275–3283. [Google Scholar] [CrossRef] [PubMed]
- Chandrasekhar, N.; Sholl, D.S. Large-Scale Computational Screening of Binary Intermetallics for Membrane-Based Hydrogen Separation. J. Phys. Chem. C 2015, 119, 26319–26326. [Google Scholar] [CrossRef]
- Kamakoti, P.; Sholl, D.S. Towards first principles-based identification of ternary alloys for hydrogen purification membranes. J. Membr. Sci. 2006, 279, 94–99. [Google Scholar] [CrossRef]
- Semidey-Flecha, L.; Ling, C.; Sholl, D.S. Detailed first-principles models of hydrogen permeation through PdCu-based ternary alloys. J. Membr. Sci. 2010, 362, 384–392. [Google Scholar] [CrossRef]
- Lovvik, O.M.; Peters, T.A.; Bredesen, R. First-principles calculations on sulfur interacting with ternary Pd-Ag-transition metal alloy membrane alloys. J. Membr. Sci. 2014, 453, 525–531. [Google Scholar] [CrossRef]
- Kirchheim, R.; Kownacka, I.; Filipek, S.M. Hydrogen segregation at grain-boundaries in nanocrystalline nickel. Scr. Metall. Mater. 1993, 28, 1229–1234. [Google Scholar] [CrossRef]
- Lemier, C.; Weissmueller, J. Grain boundary segregation, stress and stretch: Effects on hydrogen absorption in nanocrystalline palladium. Acta Mater. 2007, 55, 1241–1254. [Google Scholar] [CrossRef]
- Siegel, D.J.; Hamilton, J.C. Computational study of carbon segregation and diffusion within a nickel grain boundary. Acta Mater. 2005, 53, 87–96. [Google Scholar] [CrossRef]
- Aksyonov, D.A.; Lipnitskii, A.G.; Kolobov, Y.R. Grain boundary segregation of C, N and O in hexagonal close-packed titanium from first principles. Model. Simul. Mater. Sci. Eng. 2013, 21, 12. [Google Scholar] [CrossRef]
- Lejcek, P.; Sob, M. An analysis of segregation-induced changes in grain boundary cohesion in bcc iron. J. Mater. Sci. 2014, 49, 2477–2482. [Google Scholar] [CrossRef]
- Yazdandoost, F.; Mirzaeifar, R. Tilt grain boundaries energy and structure in NiTi alloys. Comput. Mater. Sci. 2017, 131, 108–119. [Google Scholar] [CrossRef]
- Yan, J.Y.; Ehteshami, H.; Korzhavyi, P.A.; Borgenstam, A. Sigma 3(111) grain boundary of body-centered cubic Ti-Mo and Ti-V alloys: First-principles and model calculations. Phys. Rev. Mater. 2017, 1, 023602. [Google Scholar] [CrossRef]
- Zhao, Z.M.; Wan, J.F.; Wang, J.N. Ab-Initio Study of Electronic Structure of Martensitic Twin Boundary in Ni2MnGa Alloy. Mater. Trans. 2016, 57, 477–480. [Google Scholar] [CrossRef]
- Kim, Y.K.; Jung, W.S.; Lee, B.J. Modified embedded-atom method interatomic potentials for the Ni-Co binary and the Ni-Al-Co ternary systems. Model. Simul. Mater. Sci. Eng. 2015, 23, 055004. [Google Scholar] [CrossRef]
- Kiyohara, S.; Mizoguchi, T. Investigation of Segregation of Silver at Copper Grain Boundaries by First Principles and Empirical Potential Calculations. AIP Conf. Proc. 2016, 1763, 040001. [Google Scholar]
- Zhang, P.B.; Li, X.J.; Zhao, J.J.; Zheng, P.F.; Chen, J.M. Atomic investigation of alloying Cr, Ti, Y additions in a grain boundary of vanadium. J. Nucl. Mater. 2016, 468, 147–152. [Google Scholar] [CrossRef]
- Basha, D.A.; Sahara, R.; Somekawa, H.; Rosalie, J.M.; Singh, A.; Tsuchiya, K. Interfacial segregation induced by severe plastic deformation in a Mg-Zn-Y alloy. Scr. Mater. 2016, 124, 169–173. [Google Scholar] [CrossRef]
- Piochaud, J.B.; Becquart, C.S.; Domain, C. Ab initio and Atomic kinetic Monte Carlo modelling of segregation in concentrated FeCrNi alloys. In Proceedings of the Sna + Mc 2013—Joint International Conference on Supercomputing in Nuclear Applications + Monte Carlo, Paris, France, 27–31 October 2013. [Google Scholar]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics for liquid-metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Ranganathan, S. On geometry of coincidence-site lattices. Acta Crystallogr. 1966, 21, 197. [Google Scholar] [CrossRef]
- Olmsted, D.L.; Foiles, S.M.; Holm, E.A. Survey of computed grain boundary properties in face-centered cubic metals: I. Grain boundary energy. Acta Mater. 2009, 57, 3694–3703. [Google Scholar] [CrossRef]
- Dontsova, E.; Rottler, J.; Sinclair, C.W. Solute-defect interactions in Al-Mg alloys from diffusive variational Gaussian calculations. Phys. Rev. B 2014, 90, 174102. [Google Scholar] [CrossRef]
- Mekonnen, W.; Arstad, B.; Klette, H.; Walmsley, J.C.; Bredesen, R.; Venvik, H.; Holmestad, R. Microstructural characterization of self-supported 1.6 μm Pd/Ag membranes. J. Membr. Sci. 2008, 310, 337–348. [Google Scholar] [CrossRef]
- Peters, T.A.; Tucho, W.M.; Ramachandran, A.; Stange, M.; Walmsley, J.C.; Holmestad, R.; Borg, A.; Bredesen, R. Thin Pd-23%Ag/stainless steel composite membranes: Long-term stability, life-time estimation and post-process characterisation. J. Membr. Sci. 2009, 326, 572–581. [Google Scholar] [CrossRef]
- Lovvik, O.M.; Opalka, S.M. Reversed surface segregation in palladium-silver alloys due to hydrogen adsorption. Surf. Sci. 2008, 602, 2840–2844. [Google Scholar] [CrossRef]

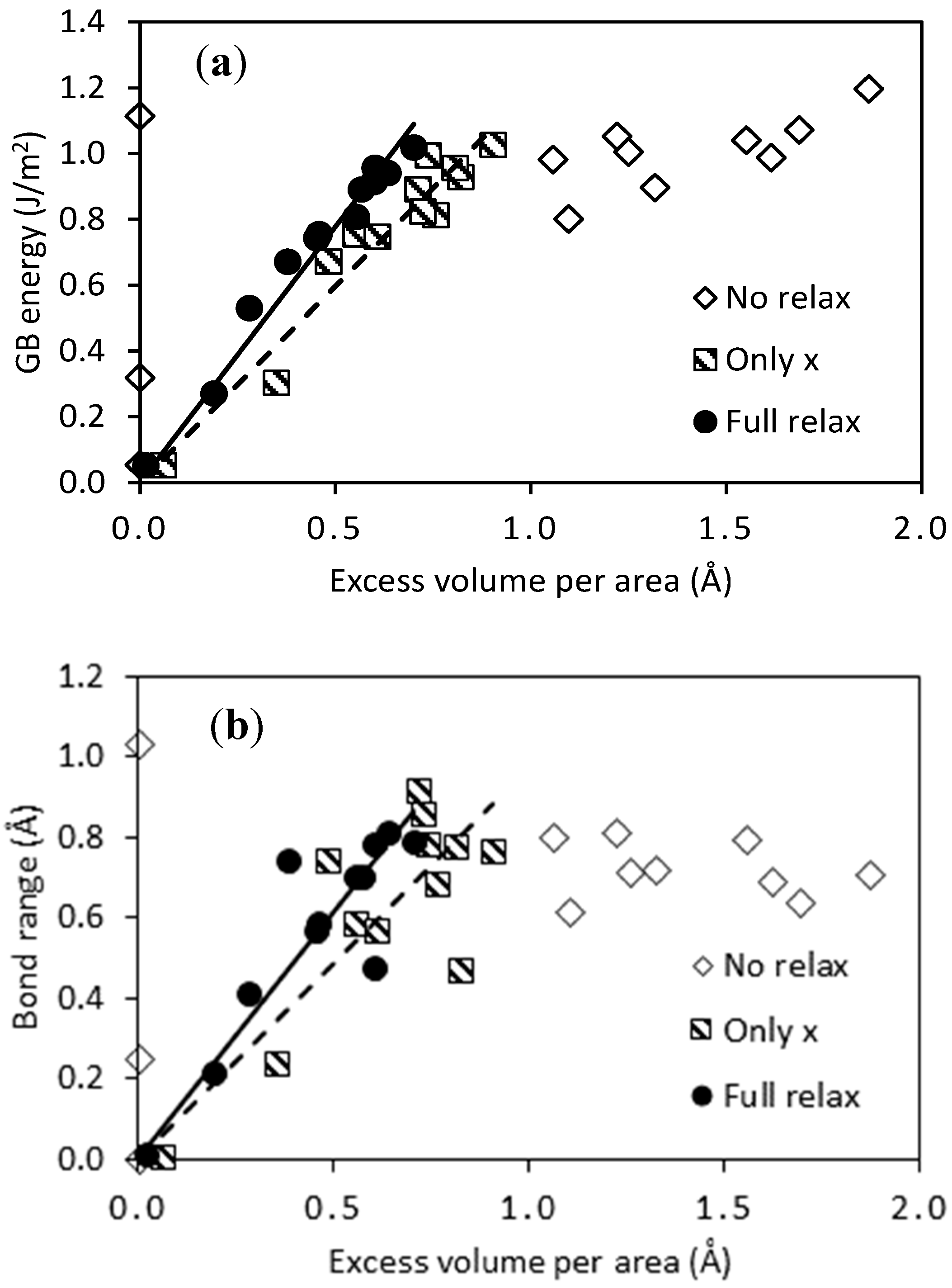

| GB Model | # of Atoms | Excess Volume/Area (Å) | GB Energy (J/m2) | Bond Range (Å) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| No Relax | Only x | Full Relax | No Relax | Only x | Full Relax | No Relax | Only x | Full Relax | |||
| 48 | 13.7 | 0.00 | 0.06 | 0.01 | 0.05 | 0.05 | 0.05 | 0.01 | 0.01 | 0.02 | |
| 44 | 19.4 | 1.61 | 0.48 | 0.38 | 0.99 | 0.67 | 0.67 | 0.69 | 0.75 | 0.75 | |
| 80 | 17.7 | 0.00 | 0.82 | 0.60 | 1.11 | 0.93 | 0.91 | 1.04 | 0.48 | 0.48 | |
| 72 | 12.5 | 1.25 | 0.71 | 0.57 | 1.01 | 0.89 | 0.89 | 0.72 | 0.92 | 0.71 | |
| 78 | 14.8 | 1.06 | 0.81 | 0.63 | 0.98 | 0.96 | 0.94 | 0.80 | 0.78 | 0.82 | |
| 80 | 25.6 | 1.22 | 0.90 | 0.70 | 1.05 | 1.03 | 1.02 | 0.82 | 0.77 | 0.79 | |
| 68 | 23.7 | 1.32 | 0.76 | 0.55 | 0.90 | 0.81 | 0.81 | 0.72 | 0.69 | 0.71 | |
| 64 | 16.8 | 1.86 | 0.55 | 0.46 | 1.20 | 0.76 | 0.76 | 0.71 | 0.59 | 0.59 | |
| 88 | 26.2 | 0.00 | 0.35 | 0.19 | 0.32 | 0.30 | 0.27 | 0.26 | 0.24 | 0.22 | |
| 80 | 18.6 | 1.69 | 0.72 | 0.28 | 1.07 | 0.82 | 0.53 | 0.64 | 0.86 | 0.42 | |
| 100 | 28.5 | 1.10 | 0.61 | 0.45 | 0.80 | 0.75 | 0.74 | 0.62 | 0.57 | 0.57 | |
| 100 | 40.3 | 1.55 | 0.74 | 0.60 | 1.04 | 1.00 | 0.96 | 0.80 | 0.79 | 0.79 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Løvvik, O.M.; Zhao, D.; Li, Y.; Bredesen, R.; Peters, T. Grain Boundary Segregation in Pd-Cu-Ag Alloys for High Permeability Hydrogen Separation Membranes. Membranes 2018, 8, 81. https://doi.org/10.3390/membranes8030081
Løvvik OM, Zhao D, Li Y, Bredesen R, Peters T. Grain Boundary Segregation in Pd-Cu-Ag Alloys for High Permeability Hydrogen Separation Membranes. Membranes. 2018; 8(3):81. https://doi.org/10.3390/membranes8030081
Chicago/Turabian StyleLøvvik, Ole Martin, Dongdong Zhao, Yanjun Li, Rune Bredesen, and Thijs Peters. 2018. "Grain Boundary Segregation in Pd-Cu-Ag Alloys for High Permeability Hydrogen Separation Membranes" Membranes 8, no. 3: 81. https://doi.org/10.3390/membranes8030081
APA StyleLøvvik, O. M., Zhao, D., Li, Y., Bredesen, R., & Peters, T. (2018). Grain Boundary Segregation in Pd-Cu-Ag Alloys for High Permeability Hydrogen Separation Membranes. Membranes, 8(3), 81. https://doi.org/10.3390/membranes8030081