Emulsification Characteristics Using a Dynamic Woven Metal Microscreen Membrane
Abstract
:1. Introduction
2. Materials and Methods
2.1. Emulsion Stabilization
2.1.1. Surfactant-Stabilized Emulsion
2.1.2. Pickering Emulsions (PE)
2.2. Emulsion Preparation and Characterization
3. Results and Discussion
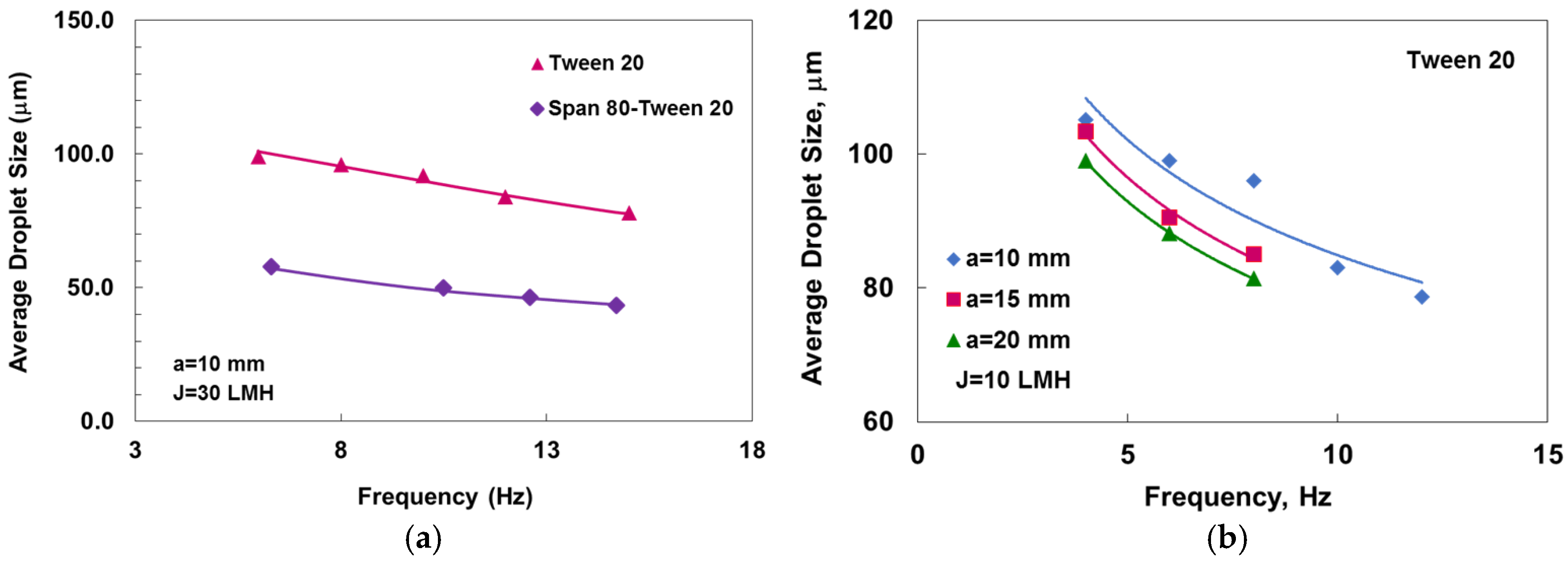
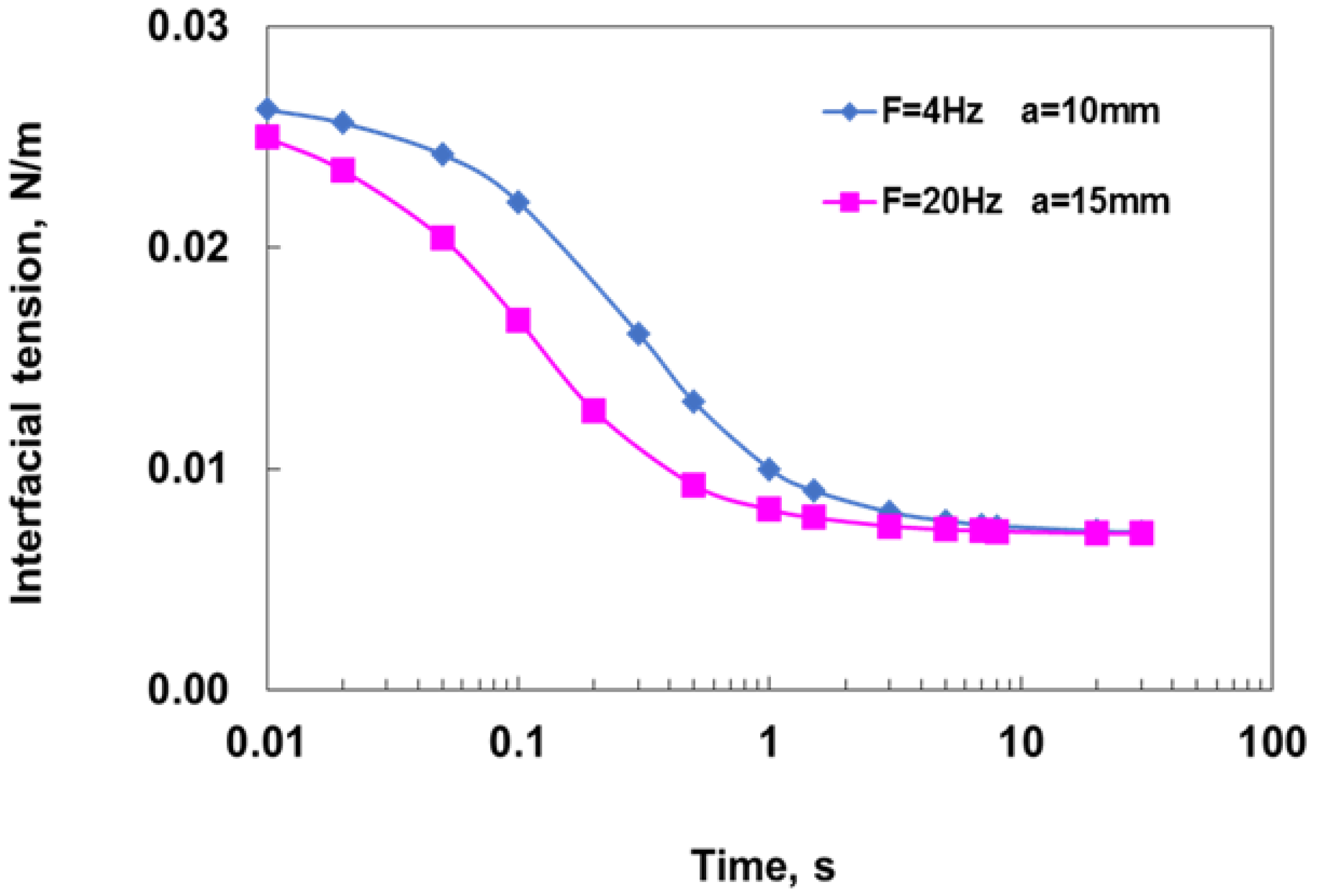
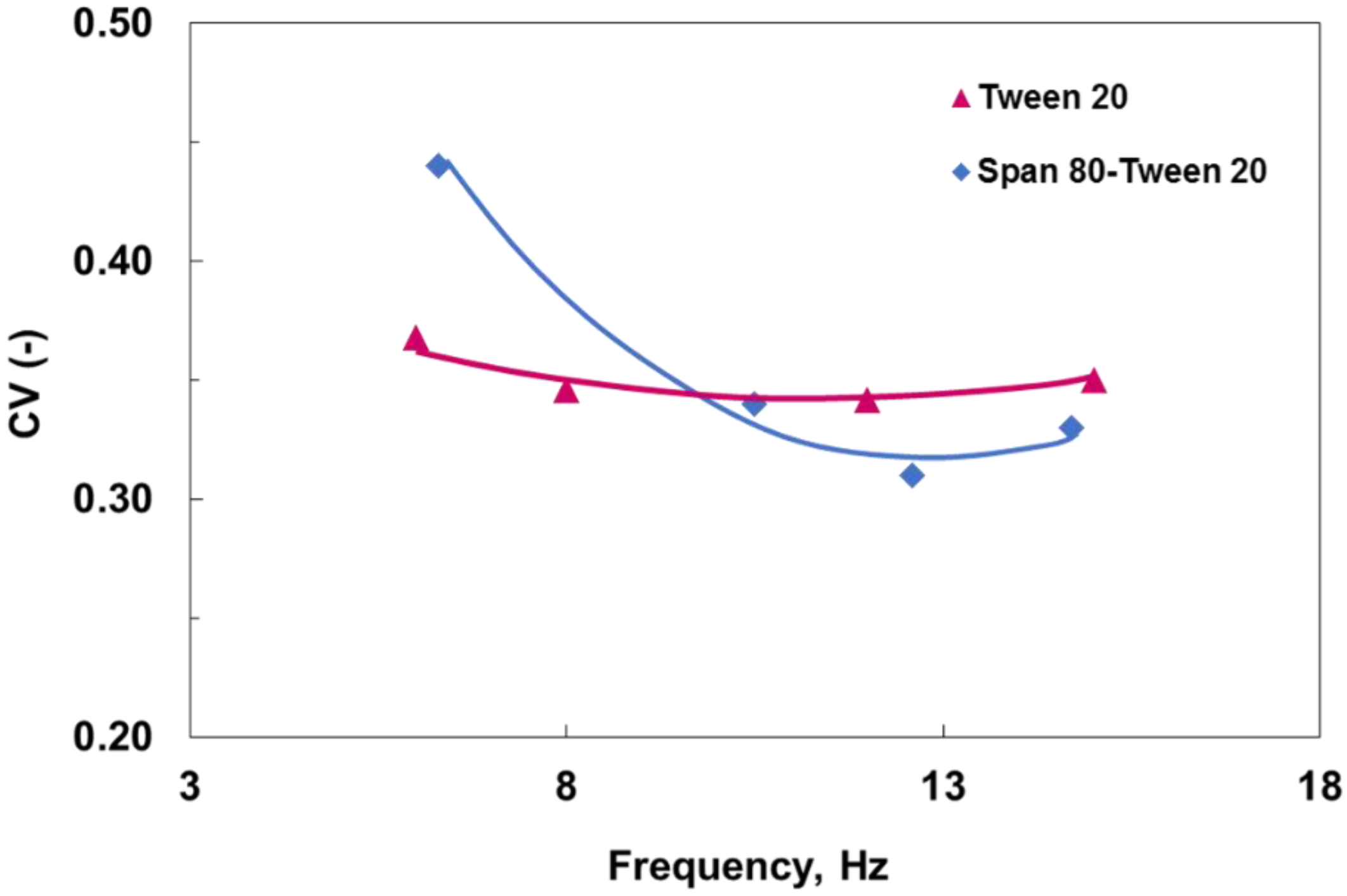
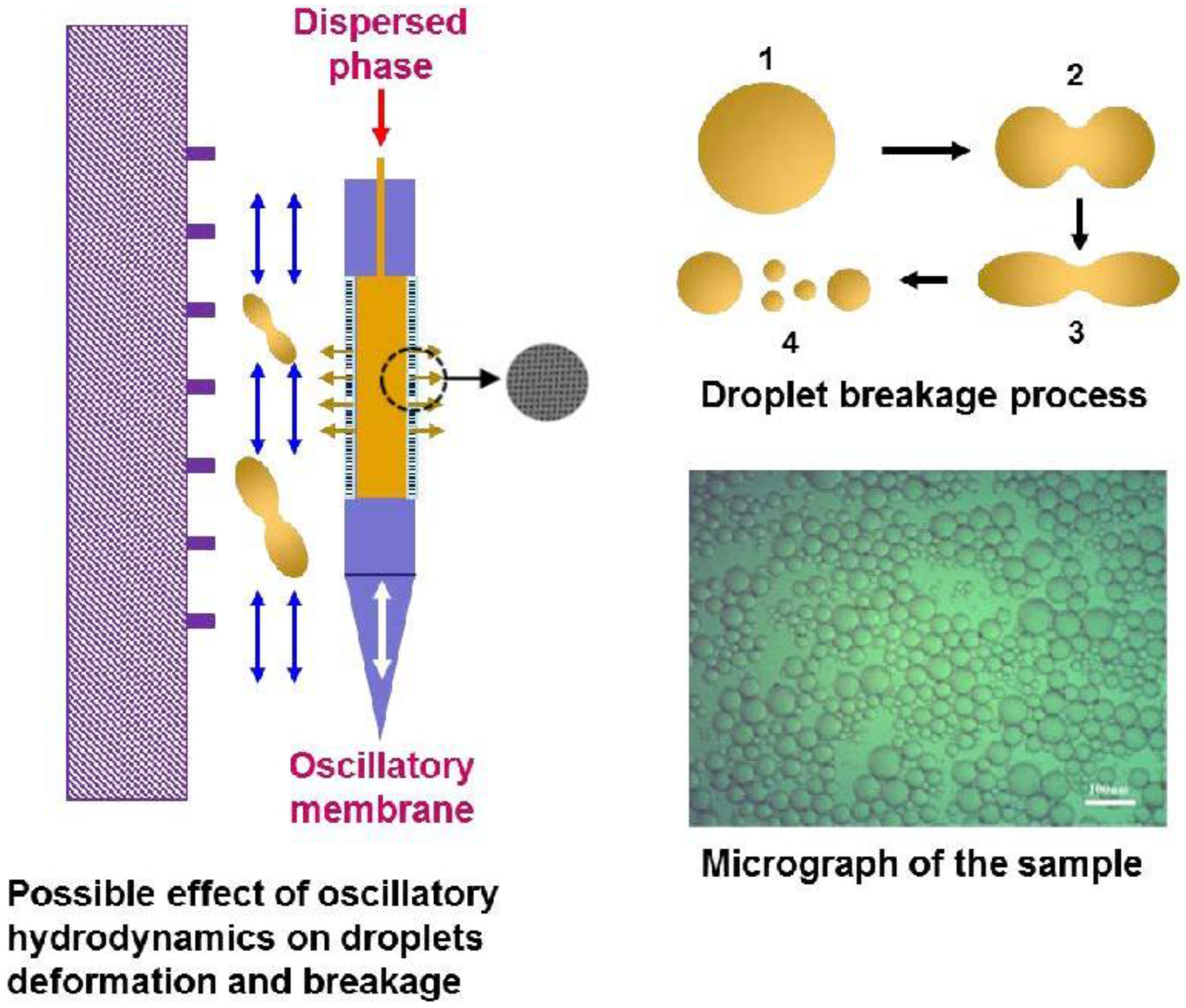
3.1. The Effect of Oscillation
3.1.1. Surfactant-Stabilized Emulsions
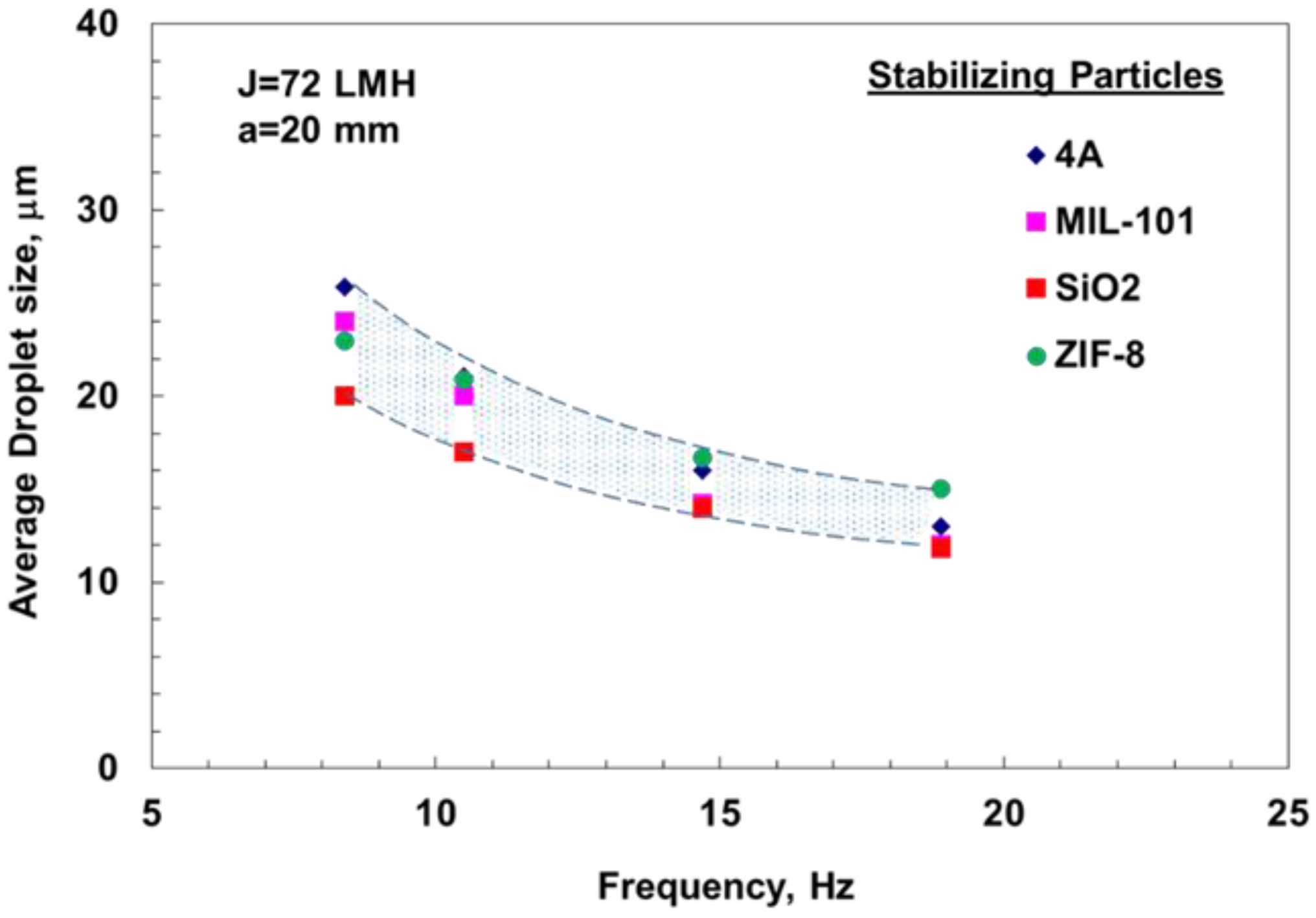
3.1.2. Particle-Stabilized Emulsions
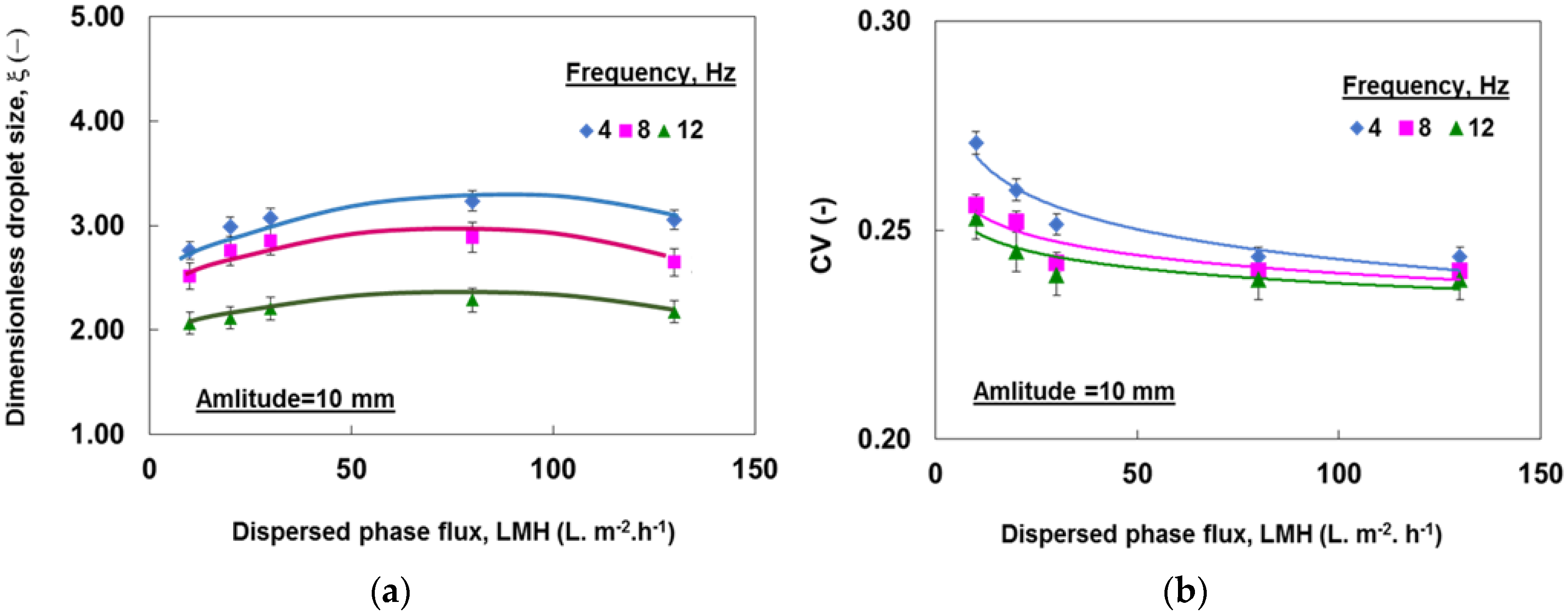
3.2. The Effect of Dispersed Phase Flux
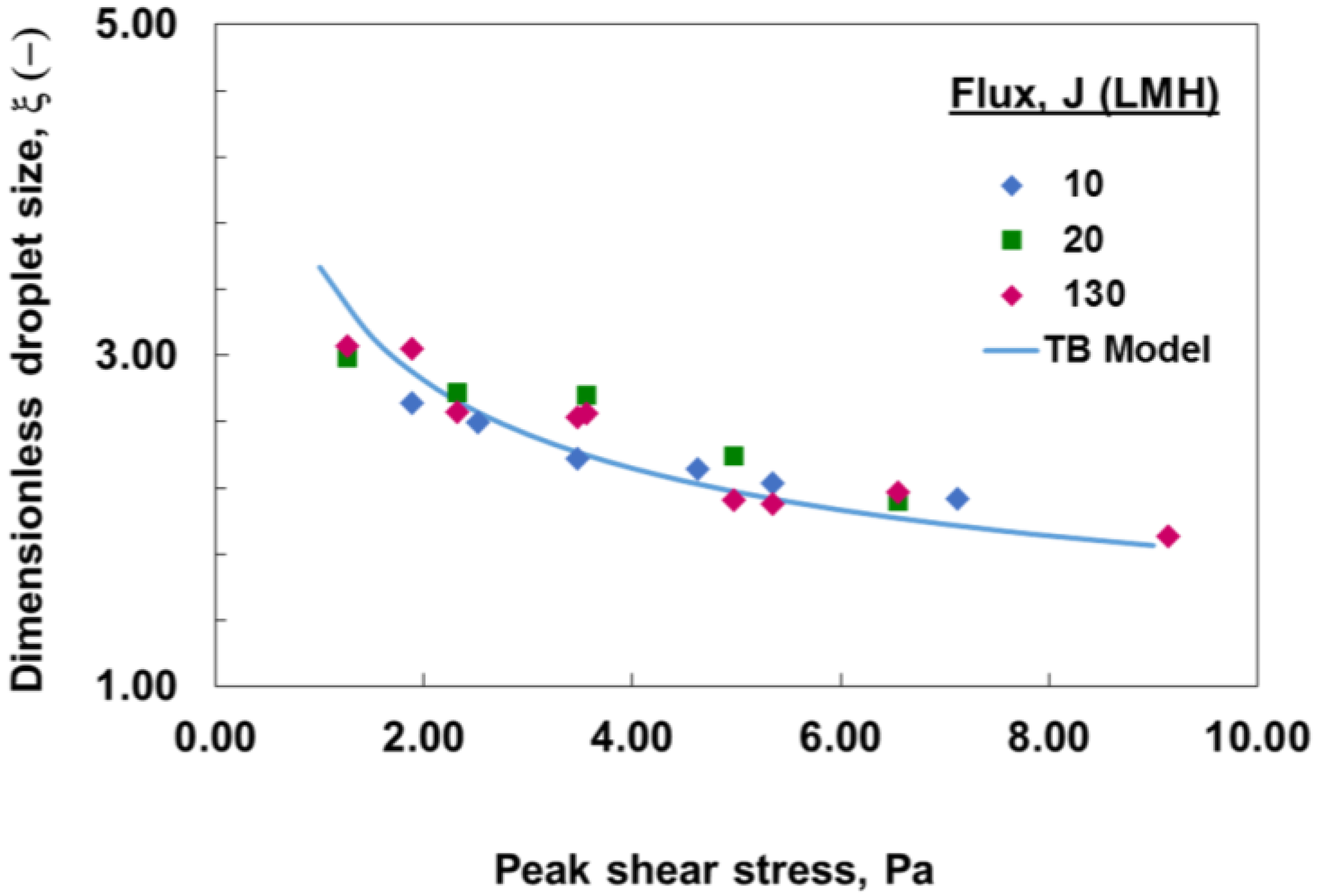
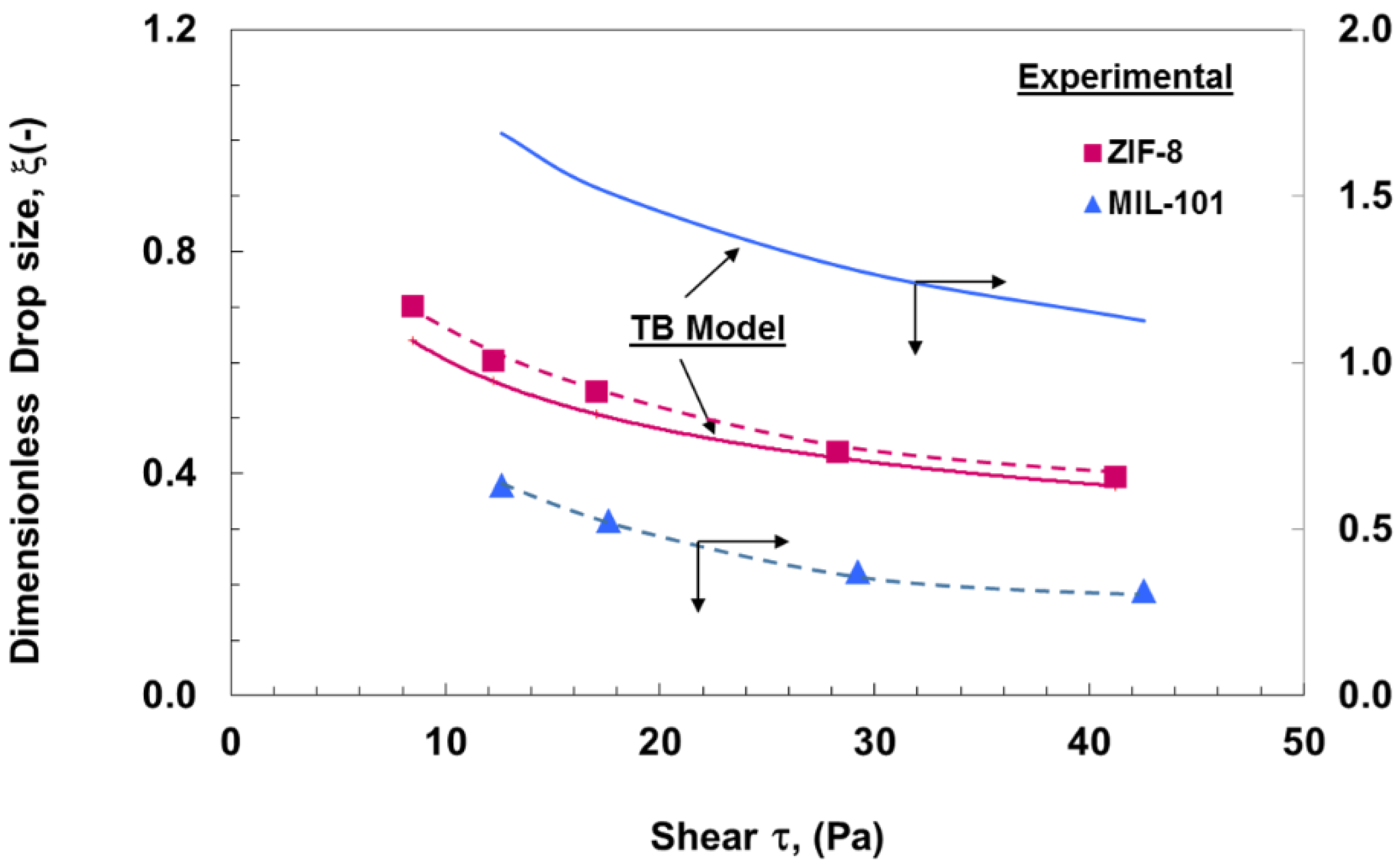
3.3. Drop Size Modeling
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CV | coefficient of variation |
| DME | dynamic membrane emulsification |
| LMH | liter per meter square per hour |
| MOFs | metal organic frameworks |
| PE | Pickering emulsions |
| TB | torque balance |
| WMMS | woven metal microscreen |
References
- Vladisavljević, G.T.; Williams, R.A. Recent developments in manufacturing emulsions and particulate products using membranes. Adv. Colloid Interface Sci. 2005, 113, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Gijsbertsen-Abrahamse, A.J.; van der Padt, A.; Boom, R.M. Status of cross-flow membrane emulsification and outlook for industrial application. J. Membr. Sci. 2004, 230, 149–159. [Google Scholar] [CrossRef]
- Egidi, E.; Gasparini, G.; Holdich, R.G.; Vladisavljević, G.T.; Kosvintsev, S.R. Membrane emulsification using membranes of regular pore spacing: Droplet size and uniformity in the presence of surface shear. J. Membr. Sci. 2008, 323, 414–420. [Google Scholar] [CrossRef]
- Thompson, K.L.; Armes, S.P.; York, D.W. Preparation of pickering emulsions and colloidosomes with relatively narrow size distributions by stirred cell membrane emulsification. Langmuir 2011, 27, 2357–2363. [Google Scholar] [CrossRef] [PubMed]
- Vladisavljević, G.T.; Williams, R.A. Manufacture of large uniform droplets using rotating membrane emulsification. J. Colloid Interface Sci. 2006, 266, 396–402. [Google Scholar] [CrossRef] [PubMed]
- Schadler, V.; Windhab, E.J. Continuous membrane emulsification by using a membrane system with controlled pore distance. Desalination 2006, 189, 130–135. [Google Scholar] [CrossRef]
- Manga, M.S.; Cayre, O.J.; Williams, R.A.; Biggs, S.; York, D.W. Production of solid-stabilised emulsions through rotational membrane emulsification: Influence of particle adsorption kinetics. Soft Matter 2012, 8, 1532–1538. [Google Scholar] [CrossRef]
- Aryanti, N.; Hou, R.; Williams, R.A. Performance of a rotating membrane emulsifier for production of coarse droplets. J. Membr. Sci. 2009, 326, 9–18. [Google Scholar] [CrossRef]
- Gomaa, H.G.; Al-Taweel, A.M. Intensification of inter-phase mass transfer: The combined effect of oscillatory motion and turbulence promoters. Heat Mass Transf. 2007, 43, 371–379. [Google Scholar] [CrossRef]
- Zhu, J.; Barrow, D. Analysis of droplet size during crossflow membrane emulsification using stationary and vibrating micromachined silicon nitride membranes. J. Membr. Sci. 2005, 261, 136–144. [Google Scholar] [CrossRef]
- Holdich, R.G.; Dragosavac, M.M.; Vladisavljević, G.T.; Kosvintsev, S.R. Membrane emulsification with oscillating and stationary membranes. Ind. Eng. Chem. Res. 2010, 49, 3810–3817. [Google Scholar] [CrossRef]
- Kelder, J.D.; Jansen, J.J.M.; Boom, R.M. Membrane emulsification with vibrating membranes: A numerical study. J. Membr. Sci. 2007, 304, 50–59. [Google Scholar] [CrossRef]
- Silva, P.S.; Dragosavac, M.M.; Vladisavljević, G.T.; Bandulasena, H.C.H.; Holdich, R.G.; Stillwell, M.; Williams, B. Azimuthally oscillating membrane emulsification for controlled droplet production. AIChE J. 2015, 61, 3607–3615. [Google Scholar] [CrossRef]
- Piacentini, E.; Drioli, E.; Giorno, L. Pulsed back-and-forward cross-flow batch membrane emulsification with high productivity to obtain highly uniform and concentrate emulsions. J. Membr. Sci. 2014, 453, 119–125. [Google Scholar] [CrossRef]
- Sun, G.; Li, Y.; Lu, Y.; Khan, B.; Tompa, G.S. Investigation of efficiency improvement on silicon solar cells due to porous layers. Mater. Res. Soc. Symp. Proc. 1995, 358, 593–598. [Google Scholar] [CrossRef]
- Pestryakov, A.N.; Fyodorov, A.A.; Shurov, V.A.; Gaisinovich, M.S.; Fyodorov, I.V. Foam metal catalysts with intermediate support for deep oxidation of hydrocarbons. React. Kinet. Catal. Lett. 1994, 53, 347–352. [Google Scholar] [CrossRef]
- Aveyard, R.; Binks, B.P.; Clint, J.H. Emulsions stabilized solely by colloiadal particles. Adv. Colloid Interface Sci. 2003, 100–102, 503–546. [Google Scholar] [CrossRef]
- Huo, J.; Marcello, M.; Garai, A.; Bradshaw, D. MOF-polymer composite microcapsules derived from pickering emulsions. Adv. Mater. 2013, 25, 2717–2722. [Google Scholar] [CrossRef] [PubMed]
- Hartmann, M.; Fischer, M. Amino-functionalized basic catalysts with MIL-101. Microporous Mesoporous Mater. 2012, 164, 38–43. [Google Scholar] [CrossRef]
- Schlichiting, H. Boundary-Layer Theory, 7th ed.; McGraw-Hill: New York, NY, USA, 1979; p. 93. [Google Scholar]
- Van der Graaf, S.; Schroen, C.; van der Sman, R.; Boom, R.M. Influence of dynamic interfacial tension on droplet formation during membrane emulsification. J. Colloid Interface Sci. 2004, 277, 456–463. [Google Scholar] [CrossRef] [PubMed]
- Rayner, M.; Trägårdh, G.; Trägårdh, C. The impact of mass transfer and interfacial expansion rate on droplet size in membrane emulsification processes. Colloids Surfaces A Physicochem. Eng. Asp. 2005, 266, 1–17. [Google Scholar] [CrossRef]
- Gomaa, H.G.; Rao, S.; Al-Taweel, A.M. Intensification of membrane microfiltration using oscillatory motion. Sep. Purif. Technol. 2011, 78, 336–344. [Google Scholar] [CrossRef]
- Jiang, S.; Chen, Q.; Tripathy, M.; Luijten, E.; Schweizer, K.S.; Granick, S. Janus particle synthesis and assembly. Adv. Mater. 2010, 22, 1060–1071. [Google Scholar] [CrossRef] [PubMed]
- Chevalier, Y.; Bolzinger, M.A. Emulsions stabilized with solid nanoparticles: Pickering emulsions. Colloids Surfaces A Physicochem. Eng. Asp. 2013, 439, 23–34. [Google Scholar] [CrossRef]
- Vladisavljevi´c, G.T.; Lambrich, U.; Nakajima, M.; Schubert, H. Production of O–W emulsions using SPG membranes, ceramic α-aluminium oxide membranes, microfluidizer and a silicon microchannel plate a comparative study. Colloids Surfaces A Physicochem. Eng. Asp. 2004, 232, 199–207. [Google Scholar] [CrossRef]
- Abrahamse, A.J.; van Lierop, R.; van der Sman, R.G.M.; van der Padt, A.; Boom, R.M. Analysis of droplet formation and interactions during cross-flow membrane emulsification. J. Membr. Sci. 2002, 204, 125–137. [Google Scholar] [CrossRef]
- Abrahamse, A.J.; van der Padt, A.; Boom, R.M. Influence of membrane morphology on pore activation in membrane emulsification. J. Membr. Sci. 2003, 217, 141–150. [Google Scholar] [CrossRef]
- Kosvintsev, S.R.; Gasparini, G.; Holdich, R.G. Membrane emulsification: Droplet size and uniformity in the absence of surface shear. J. Membr. Sci. 2008, 313, 182–189. [Google Scholar] [CrossRef]
- De Luca, G.; Sindona, A.; Giorno, L.; Drioli, E. Quantitative analysis of coupling effects in cross-flow membrane emulsification. J. Membr. Sci. 2004, 229, 199–209. [Google Scholar] [CrossRef]
- Van der Graaf, S.; Steegmans, M.L.J.; van der Sman, R.G.M.; Schroën, C.G.P.H.; Boom, R.M. Droplet formation in a T-shaped microchannel junction: A model system for membrane emulsification. Colloids Surfaces. A Physicochem. Eng. Asp. 2005, 266, 106–116. [Google Scholar] [CrossRef]
- Xu, J.H.; Luo, G.S.; Chen, G.G.; Wang, J.D. Experimental and theoretical approaches on droplet formation from a micrometer screen hole. J. Membr. Sci. 2005, 266, 121–131. [Google Scholar] [CrossRef]
- Peng, S.J.; Williams, R.A. Controlled production of emulsions using a crossflow membrane—Part I: Droplet formation from a single pore. Trans. IChemE 1998, 76, 894–901. [Google Scholar] [CrossRef]
- Goldman, A.J.; Cox, R.G.; Brenner, H. Slow viscous motion of a sphere parallel to a plane wall—II Couette flow. Chem. Eng. Sci. 1967, 22, 653–660. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, L.; Zhang, W.; Luo, G. Mass-transfer-controlled dynamic interfacial tension in microfluidic emulsification processes. Langmuir 2016, 32, 3174–3185. [Google Scholar] [CrossRef] [PubMed]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabouni, R.; Gomaa, H.G.; Liu, J.; Zhu, J. Emulsification Characteristics Using a Dynamic Woven Metal Microscreen Membrane. Membranes 2016, 6, 34. https://doi.org/10.3390/membranes6020034
Sabouni R, Gomaa HG, Liu J, Zhu J. Emulsification Characteristics Using a Dynamic Woven Metal Microscreen Membrane. Membranes. 2016; 6(2):34. https://doi.org/10.3390/membranes6020034
Chicago/Turabian StyleSabouni, Rana, Hassan G. Gomaa, Jiangshan Liu, and Jesse Zhu. 2016. "Emulsification Characteristics Using a Dynamic Woven Metal Microscreen Membrane" Membranes 6, no. 2: 34. https://doi.org/10.3390/membranes6020034
APA StyleSabouni, R., Gomaa, H. G., Liu, J., & Zhu, J. (2016). Emulsification Characteristics Using a Dynamic Woven Metal Microscreen Membrane. Membranes, 6(2), 34. https://doi.org/10.3390/membranes6020034





