Influence of Global and Local Membrane Curvature on Mechanosensitive Ion Channels: A Finite Element Approach
Abstract
:1. Introduction
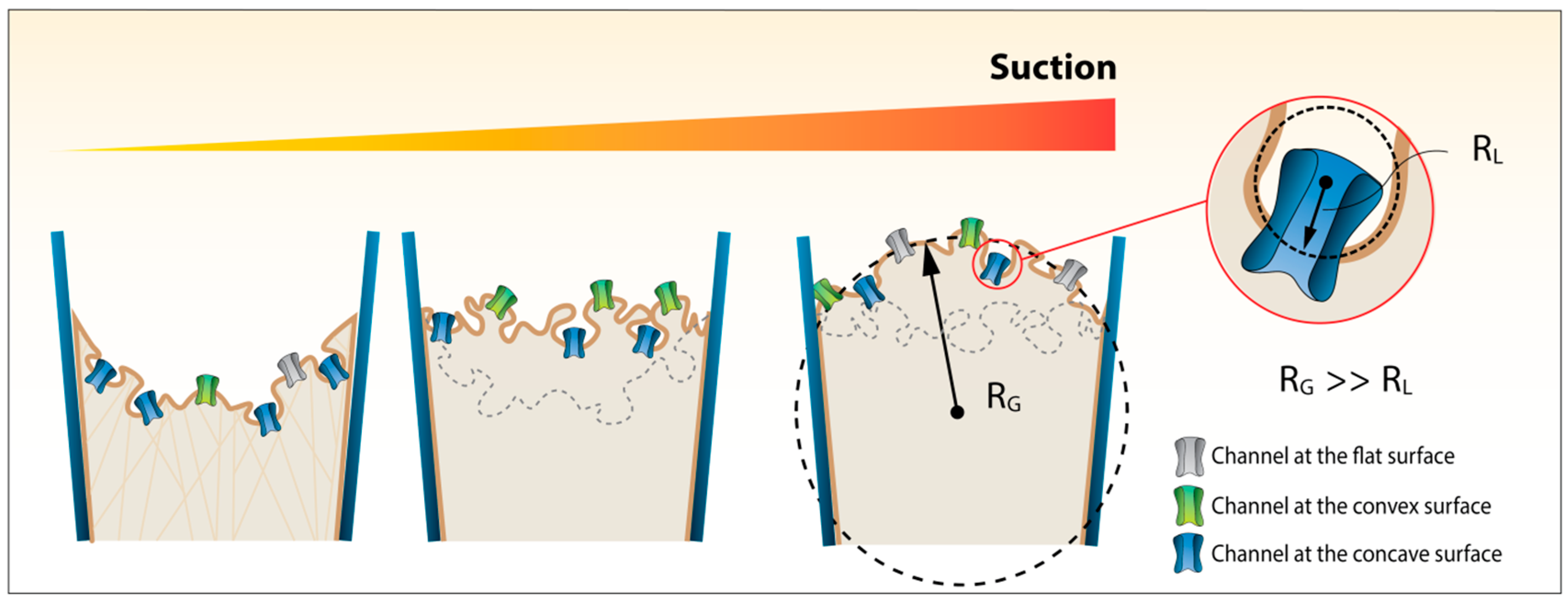
2. Materials and Methods
2.1 A More General and Accurate Approach for Tension Calculations

2.2. Finite Element (FE) Model
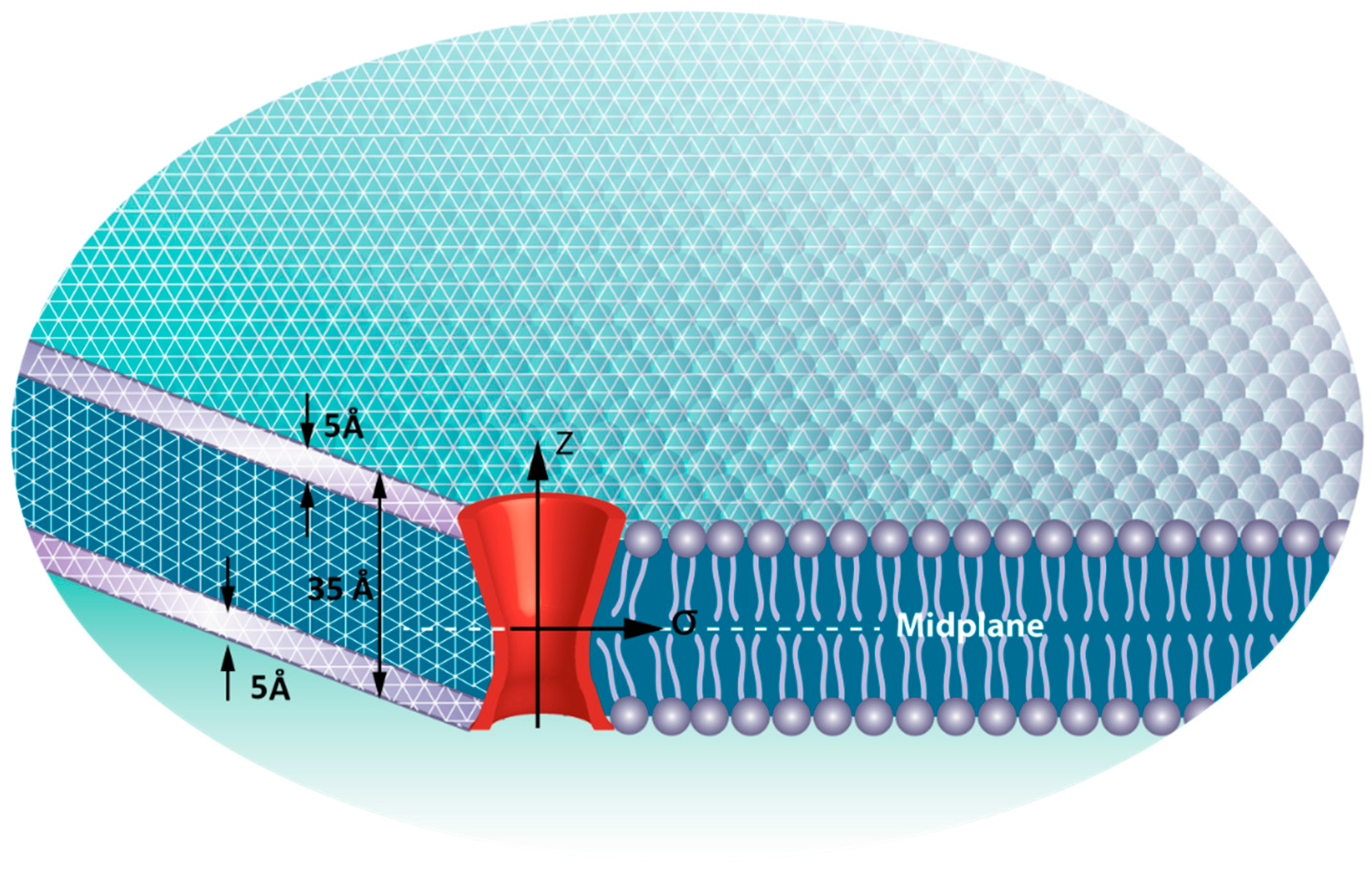
2.3. Patch Clamping
3. Results
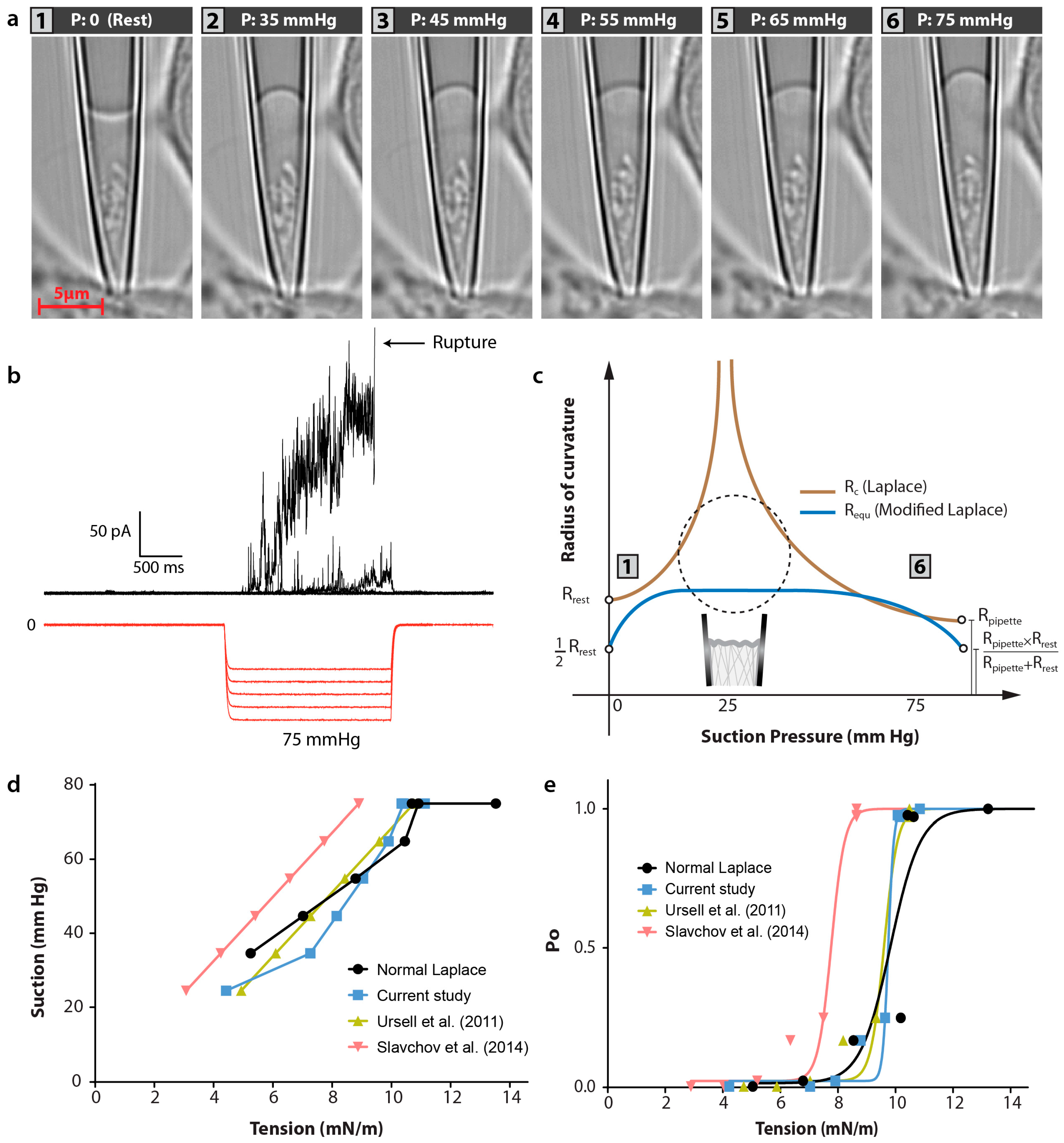
3.1. Calculating Tension in a Membrane Patch
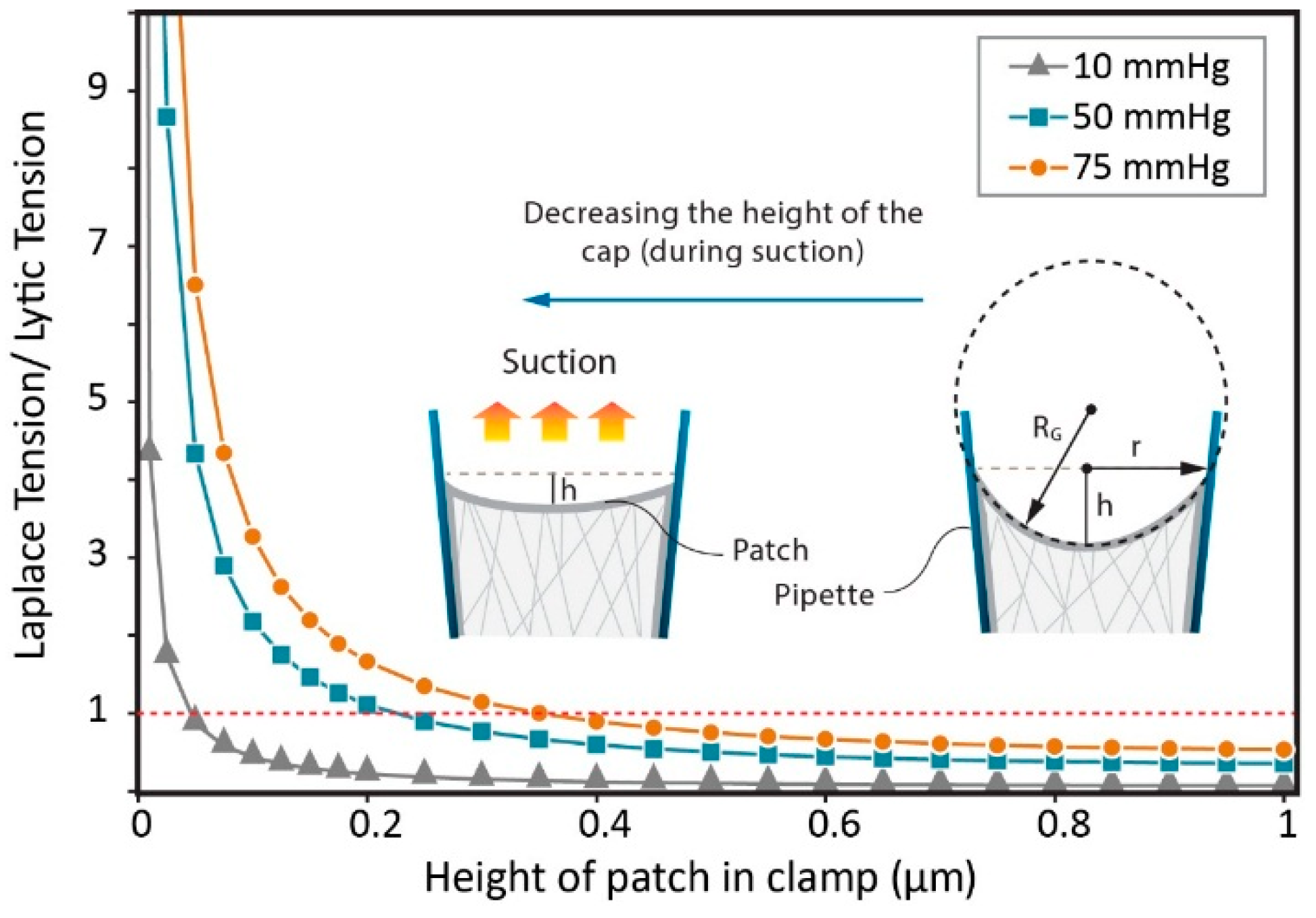
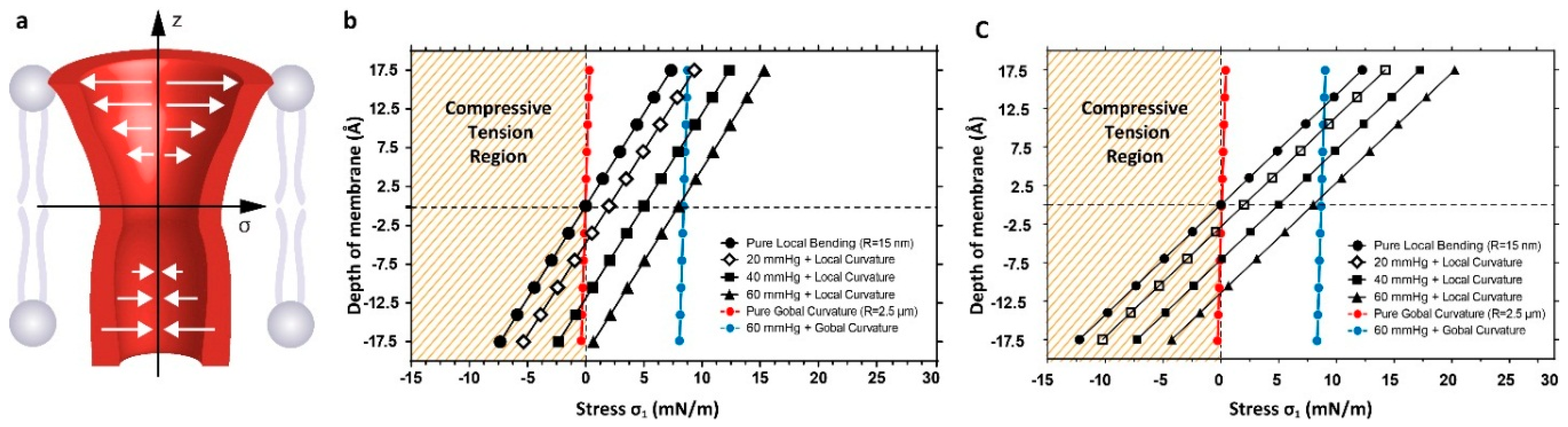
3.2. Estimation of Stress in Regions of High Local Curvature
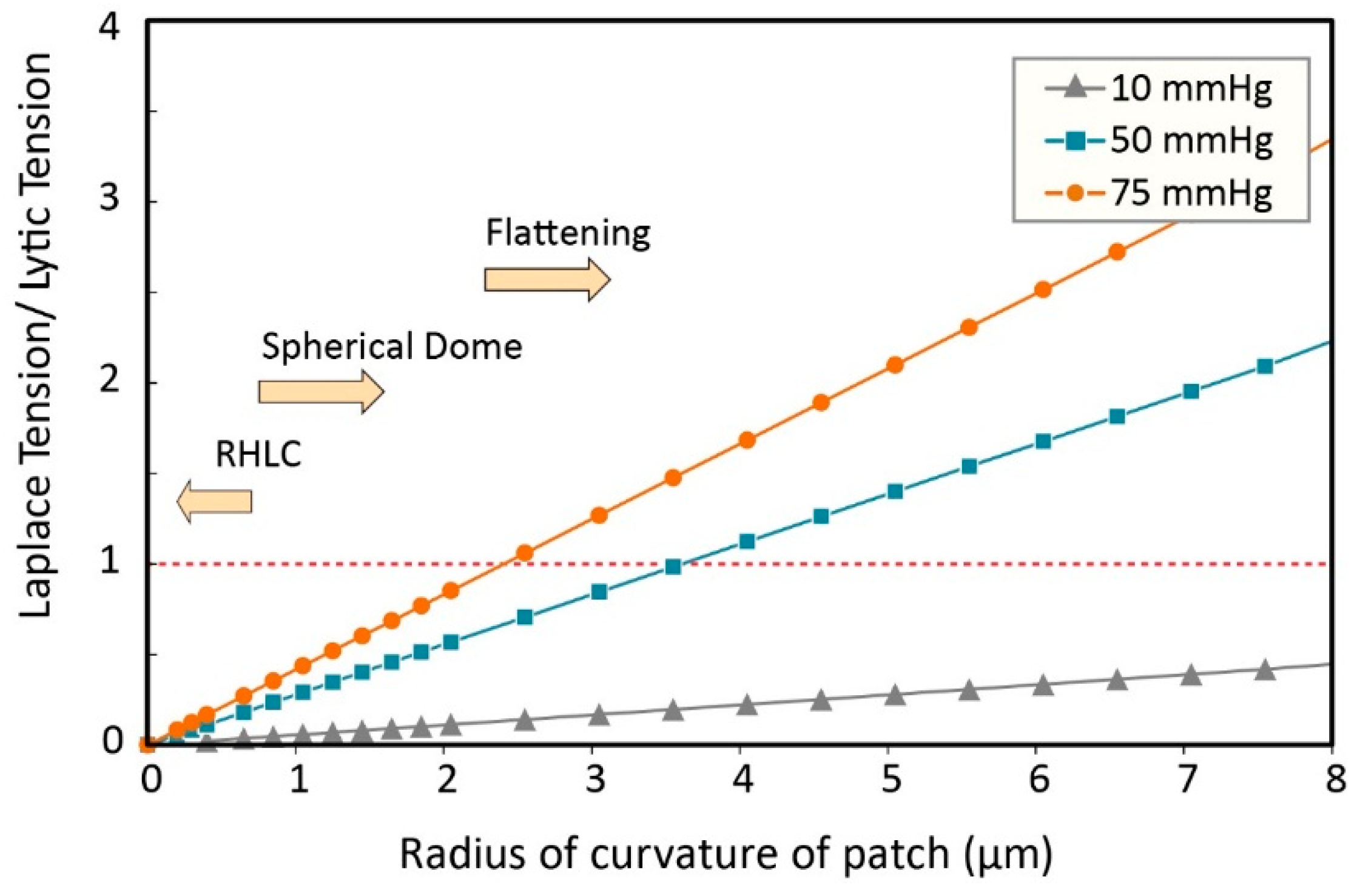
3.3. Modified Laplace’s Equation and Equivalent Membrane Patch Model
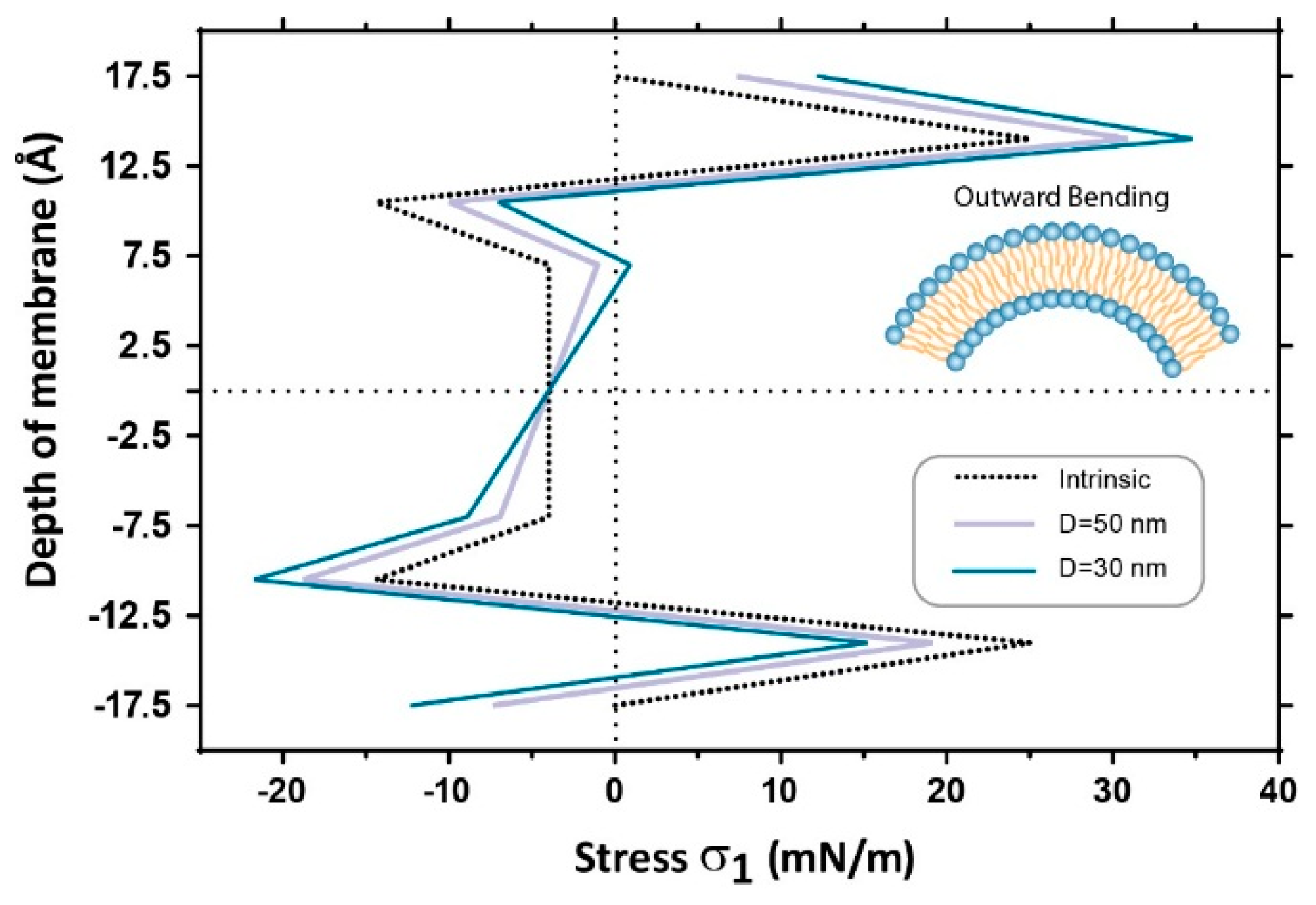
4. Discussion
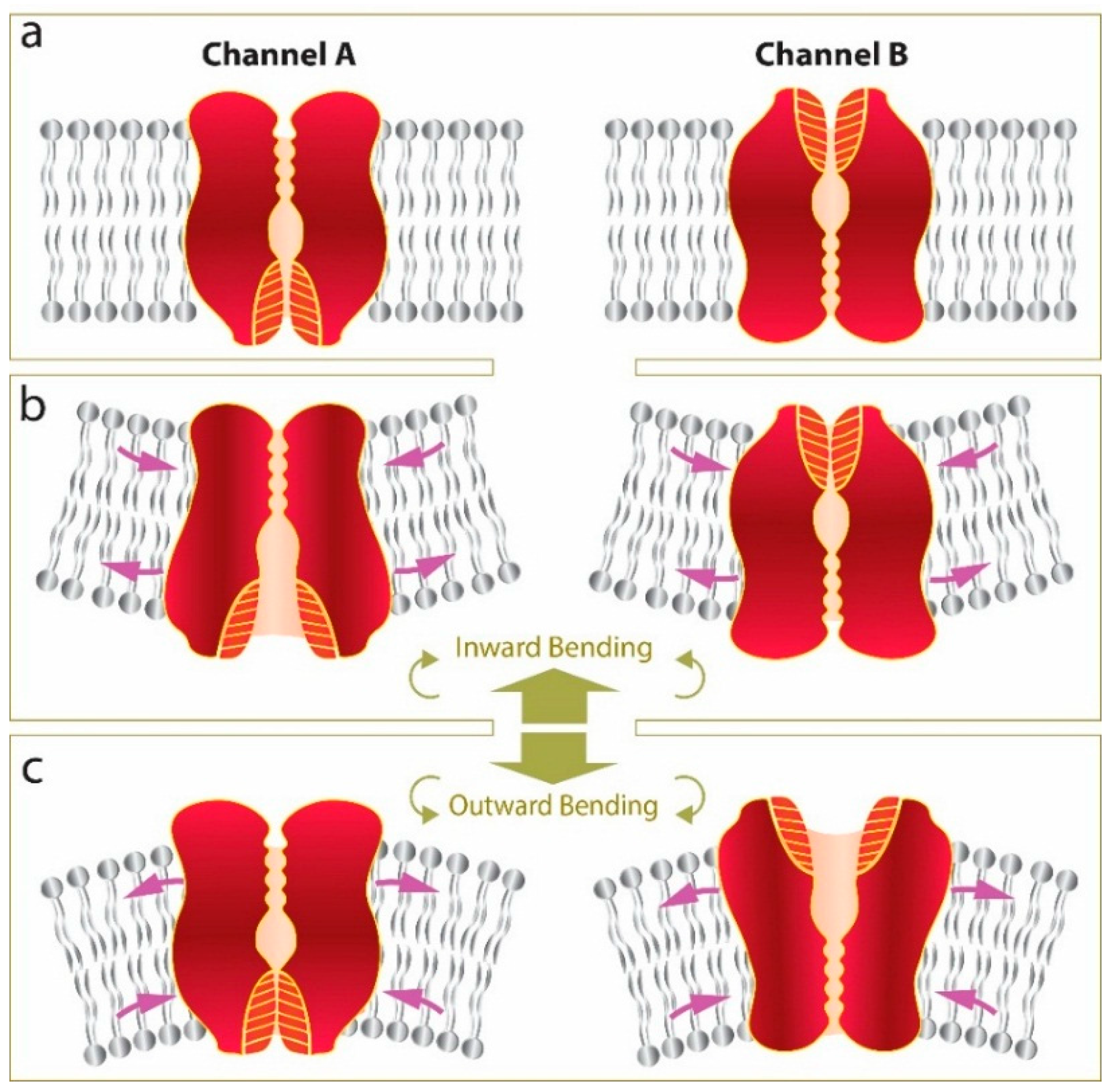
5. Conclusions
Conflicts of Interest
References
- McMahon, H.T.; Boucrot, E. Membrane curvature at a glance. J Cell Sci. 2015, 128, 1065–1070. [Google Scholar] [CrossRef] [PubMed]
- Zimmerberg, J.; Kozlov, M.M. How proteins produce cellular membrane curvature. Nat. Rev. Mol. Cell Biol. 2006, 7, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Martinac, B.; Adler, J.; Kung, C. Mechanosensitive ion channels of E. coli activated by amphipaths. Nature 1990, 348, 261–263. [Google Scholar] [CrossRef] [PubMed]
- Perozo, E.; Cortes, D.M.; Sompornpisut, P.; Kloda, A.; Martinac, B. Open channel structure of MscL and the gating mechanism of mechanosensitive channels. Nature 2002, 418, 942–948. [Google Scholar] [CrossRef] [PubMed]
- Nomura, T.; Cranfield, C.G.; Deplazes, E.; Owen, D.M.; Macmillan, A.; Battle, A.R.; Constantine, M.; Sokabe, M.; Martinac, B. Differential effects of lipids and lyso-lipids on the mechanosensitivity of the mechanosensitive channels MscL and MscS. Proc. Natl. Acad. Sci. USA 2012, 109, 8770–8775. [Google Scholar] [CrossRef] [PubMed]
- Lesage, F.; Terrenoire, T.; Romey, G.; Lazdunski, M. Human TREK2, a 2P domain mechano-sensitive K+ channel with multiple regulations by polyunsaturated fatty acids, lysophospholipids, and Gs, Gi, and Gq protein-coupled receptors. J. Biol. Chem. 2000, 275, 28398–28405. [Google Scholar] [CrossRef] [PubMed]
- Patel, A.J.; Honoré, E.; Maingret, F.; Lesage, F.; Fink, M.; Duprat, F.; Lazdunski, M. A mammalian two pore domain mechano-gated S-like K+ channel. EMBO J. 1998, 17, 4283–4290. [Google Scholar] [CrossRef] [PubMed]
- Sachs, F. Stretch-activated ion channels: what are they? Physiology 2010, 25, 50–56. [Google Scholar] [CrossRef] [PubMed]
- Morris, C.E. Voltage-gated channel mechanosensitivity: fact or friction? Front. Physiol. 2011, 2, 25. [Google Scholar] [CrossRef] [PubMed]
- Cox, C.D.; Bae, C.; Ziegler, L.; Hartley, S.; Nikolova-Krstevski, V.; Rphde, P.R.; Ng, C.-A.; Sachs, F.; Gottlieb, P.A.; Martinac, B. Removal of the mechanoprotective influence of the cytoskeleton reveals PIEZO1 is gated by bilayer tension. Nat. Commun. 2015. [Google Scholar] [CrossRef] [PubMed]
- Coste, B.; Xiao, B.; Santos, J.S.; Syeda, R.; Grandl, J.; Spencer, K.S.; Kim, S.E.; Schmidt, M.; Mathur, J.; Dubin, A.E.; et al. Piezo proteins are pore-forming subunits of mechanically activated channels. Nature 2012, 483, 176–181. [Google Scholar] [CrossRef] [PubMed]
- Teng, J.; Loukin, S.; Anishkin, A.; Kung, C. The force-from-lipid (FFL) principle of mechanosensitivity, at large and in elements. Pflügers Archiv- Eur. J. Physiol. 2015, 467, 27–37. [Google Scholar] [CrossRef] [PubMed]
- Vásquez, V.; Krieg, M.; Lockhead, D.; Goodman, M.B. Phospholipids that contain polyunsaturated fatty acids enhance neuronal cell mechanics and touch sensation. Cell Rep. 2014, 6, 70–80. [Google Scholar] [CrossRef] [PubMed]
- Katta, S.; Krieg, M.; Goodman, M.B. Feeling Force: Physical and Physiological Principles Enabling Sensory Mechanotransduction. Annu. Rev. Cell Dev. Biol. 2015, 31, 347–371. [Google Scholar] [CrossRef] [PubMed]
- Battle, A.; Ridone, P.; Bavi, N.; Nakayama, Y.; Nikolaev, Y.A.; Martinac, B. Lipid–protein interactions: Lessons learned from stress. Biochim. Biophys. Acta (BBA)-Biomembranes 2015, 1848, 1744–1756. [Google Scholar] [CrossRef] [PubMed]
- Sachs, F. Mechanical transduction by ion channels: A cautionary tale. World J. Neurol. 2015, 5, 74–87. [Google Scholar] [CrossRef]
- Suchyna, T.M.; Markin, V.S.; Sachs, F. Biophysics and structure of the patch and the gigaseal. Biophys. J. 2009, 97, 738–747. [Google Scholar] [CrossRef] [PubMed]
- Bavi, N.; Nakayama, Y.; Bavi, O.; Cox, C.D.; Qin, Q.-H.; Martinac, B. Biophysical implications of lipid bilayer rheometry for mechanosensitive channels. Proc. Natl. Acad. Sci. USA 2014, 111, 13864–13869. [Google Scholar] [CrossRef] [PubMed]
- Besch, S.R.; Suchyna, T.; Sachs, F. High-speed pressure clamp. Pflügers Arch. 2002, 445, 161–166. [Google Scholar] [CrossRef] [PubMed]
- Pliotas, C.; Dahl, A.C.E.; Rasmussen, T.; Mahendran, K.R.; Smith, T.K.; Marius, P.; Gault, J.; Banda, T.; Rasmussen, A.; Miller, S.; et al. The role of lipids in mechanosensation. Nat. Struct. Mol. Biol. 2015, 22, 991–998. [Google Scholar] [CrossRef] [PubMed]
- Lewis, A.H.; Grandl, J. Mechanical sensitivity of Piezo1 ion channels can be tuned by cellular membrane tension. eLife 2015, 4, e12088. [Google Scholar] [CrossRef] [PubMed]
- Brohawn, S.G.; Su, Z.; MacKinnon, R. Mechanosensitivity is mediated directly by the lipid membrane in TRAAK and TREK1 K+ channels. Proc. Natl. Acad. Sci. USA 2014, 111, 3614–3619. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Bae, C.; Sachs, F.; Sychyna, T.M. Caveolae regulation of mechanosensitive channel function in myotubes. PLoS ONE 2013, 8, e72894. [Google Scholar] [CrossRef] [PubMed]
- Lo, H.P.; Nixon, S.J.; Hall, T.E.; Cowling, B.S.; Ferguson, C.; Morgan, G.P.; Schieber, N.L.; Fernandez-Rojo, M.A.; Bastiani, M.; Floetenmeyer, M.; et al. The caveolin-cavin system plays a conserved and critical role in mechanoprotection of skeletal muscle. J. Cell Biol. 2015, 210, 833–849. [Google Scholar] [CrossRef] [PubMed]
- Ventsel, E.; Krauthammer, T.; Carrera, E. Thin Plates and Shells: Theory, Analysis, and Applications. Appl. Mech. Rev. 2002, 55, B72. [Google Scholar] [CrossRef]
- Chen, X.; Cui, Q.; Tang, Y.; Yoo, J.; Yethiraj, A. Gating mechanisms of mechanosensitive channels of large conductance, I: a continuum mechanics-based hierarchical framework. Biophys. J. 2008, 95, 563–580. [Google Scholar] [CrossRef] [PubMed]
- Bavi, N.; Nomura, T.; Qin, Q.; Martinac, B. Gating Mechanism of Mechanosensitive Ion Channels Studied by Continuum Mechanics. Biophys. J. 2014, 106, 554a–555a. [Google Scholar] [CrossRef]
- Bavi, O.; Vossoughi, M.; Naghdabadi, R.; Jamali, Y. The effect of local bending on gating of MscL using a representative volume element and finite element simulation. Channels 2014, 8, 344–349. [Google Scholar] [CrossRef] [PubMed]
- Sukharev, S.I.; Blount, P.; Martinac, B.; Blattner, F.R.; Kung, C. A large-conductance mechanosensitive channel in E. coli encoded by mscL alone. Nature 1994, 368, 265–268. [Google Scholar] [CrossRef] [PubMed]
- Berrier, C.; Pozza, A.; Lavalette, A.L.; Chardonnet, A.; Mesneau, A.; Jaxel, C.; Maire, M.; Ghazi, A. The purified mechanosensitive channel TREK-1 is directly sensitive to membrane tension. J. Biol. Chem. 2013, 288, 27307–27314. [Google Scholar] [CrossRef] [PubMed]
- Brohawn, S.G.; Campbell, E.B.; MacKinnon, R. Physical mechanism for gating and mechanosensitivity of the human TRAAK K+ channel. Nature 2014, 516, 126–130. [Google Scholar] [CrossRef] [PubMed]
- Sokabe, M.; Sachs, F.; Jing, Z.Q. Quantitative video microscopy of patch clamped membranes stress, strain, capacitance, and stretch channel activation. Biophys. J. 1991, 59, 722–728. [Google Scholar] [CrossRef]
- Suchyna, T.M.; Sachs, F. Mechanosensitive channel properties and membrane mechanics in mouse dystrophic myotubes. J. Physiol. 2007, 581, 369–387. [Google Scholar] [CrossRef] [PubMed]
- Shaikh, S.; Cox, C.D.; Nomura, T.; Martinac, B. Energetics of gating MscS by membrane tension in azolectin liposomes and giant spheroplasts. Channels 2014, 8, 321–326. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.H.; Frangos, J.A. Effects of amyloid β-peptides on the lysis tension of lipid bilayer vesicles containing oxysterols. Biophys. J. 2008, 95, 620–628. [Google Scholar] [CrossRef] [PubMed]
- Ursell, T.; Kondev, J.; Reeves, D.; Wiggins, P.A.; RobPhillips, R. Role of lipid bilayer mechanics in mechanosensation, in Mechanosensitive Ion Channels. In Mechanosensitive Ion Channels (Series Mechanosensitivity in Cells and Tissues); Springer: Berlin, Germany, 2008; Volume 1, pp. 37–70. [Google Scholar]
- Perozo, E.; Kloda, A.; Cortes, D.M.; Martinac, B. Physical principles underlying the transduction of bilayer deformation forces during mechanosensitive channel gating. Nat. Struct. Mol. Biol. 2002, 9, 696–703. [Google Scholar]
- Honoré, E.; Patel, A.J.; Chemin, J.; Suchyna, T.; Sachs, F. Desensitization of mechano-gated K2P channels. Proc. Natl. Acad. Sci. USA 2006, 103, 6859–6864. [Google Scholar]
- Lim, C.T.; Zhou, E.H.; Quek, S.T. Mechanical models for living cells--a review. J. Biomech. 2006, 39, 195–216. [Google Scholar] [CrossRef] [PubMed]
- Hamill, O. Twenty odd years of stretch-sensitive channels. Pflügers Arch. Eur. J. Physiol. 2006, 453, 333–351. [Google Scholar] [CrossRef] [PubMed]
- Thorn, H.; Stenkula, K.G.; Karlsson, M.; Örtegren, U.; Nystrom, F.H.; Gustavsson, J.; Strålfors, P. Cell surface orifices of caveolae and localization of caveolin to the necks of caveolae in adipocytes. Mol. Biol. Cell 2003, 14, 3967–3976. [Google Scholar] [CrossRef] [PubMed]
- Ursell, T.; Agrawal, A.; Phillips, R. Lipid bilayer mechanics in a pipette with glass-bilayer adhesion. Biophys. J. 2011, 101, 1913–1920. [Google Scholar] [CrossRef] [PubMed]
- Slavchov, R.I.; Nomura, T.; Martinac, B.; Sokabe, M.; Sachs, F. Gigaseal Mechanics: Creep of the Gigaseal under the Action of Pressure, Adhesion, and Voltage. J. Phys. Chem. B 2014, 118, 12660–12672. [Google Scholar] [CrossRef] [PubMed]
- Predescu, S.A.; Predescu, D.N.; Malik, A.B. Molecular determinants of endothelial transcytosis and their role in endothelial permeability. Am. J. Physiol.-Lung Cell. Mol. Physiol. 2007, 293, L823–L842. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Tiruppathi, C.; Minshall, R.D.; Malik, A.B. Size and dynamics of caveolae studied using nanoparticles in living endothelial cells. ACS Nano 2009, 3, 4110–4116. [Google Scholar] [CrossRef] [PubMed]
- Nomura, T.; Cox, C.D.; Bavi, A.; Sokabe, M.; Martinac, B. Unidirectional incorporation of a bacterial mechanosensitive channel into liposomal membranes. FASEB J. 2015, 29, 4334–4345. [Google Scholar] [CrossRef] [PubMed]
- Böttcher, B.; Prazak, V.; Rasmussen, A.; Black, S.S.; Rasmussen, T. The Structure of YnaI Implies Structural and Mechanistic Conservation in the MscS Family of Mechanosensitive Channels. Structure 2015, 23, 1705–1714. [Google Scholar]
- Wilson, M.E.; Maksaev, G.; Haswell, E.S. MscS-like mechanosensitive channels in plants and microbes. Biochemistry 2013, 52, 5708–5722. [Google Scholar] [CrossRef] [PubMed]
- Booth, I.R.; Blount, P. The MscS and MscL families of mechanosensitive channels act as microbial emergency release valves. J. Bacteriol. 2012, 194, 4802–4809. [Google Scholar] [CrossRef] [PubMed]
- Cox, C.D.; Nakayama, Y.; Nomura, T.; Martinac, B. The evolutionary 'tinkering' of MscS-like channels: generation of structural and functional diversity. Pflügers Arch. Eur. J. Physiol. 2015, 467, 3–13. [Google Scholar] [CrossRef] [PubMed]
- Malcolm, H.R.; Maurer, J.A. The mechanosensitive channel of small conductance (MscS) superfamily: not just mechanosensitive channels anymore. Biochemistry 2012, 13, 2037–2043. [Google Scholar] [CrossRef] [PubMed]
- Ingber, D.E. Cellular mechanotransduction: putting all the pieces together again. FASEB J. 2006, 20, 811–827. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, N.; Jose, M.D.; Birkner, J.P.; Walko, M.; Ingólfsson, H.I.; Dimitrova, A.; Arnarez, C.; Marrink, S.J.; Koçer, A. The activation mode of the mechanosensitive ion channel, MscL, by lysophosphatidylcholine differs from tension-induced gating. FASEB J. 2014, 28, 4292–4302. [Google Scholar] [CrossRef] [PubMed]
- Kocer, A. Mechanisms of mechanosensing-mechanosensitive channels, function and re-engineering. Curr. Opin. Chem. Biol. 2015, 29, 120–127. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bavi, O.; Cox, C.D.; Vossoughi, M.; Naghdabadi, R.; Jamali, Y.; Martinac, B. Influence of Global and Local Membrane Curvature on Mechanosensitive Ion Channels: A Finite Element Approach. Membranes 2016, 6, 14. https://doi.org/10.3390/membranes6010014
Bavi O, Cox CD, Vossoughi M, Naghdabadi R, Jamali Y, Martinac B. Influence of Global and Local Membrane Curvature on Mechanosensitive Ion Channels: A Finite Element Approach. Membranes. 2016; 6(1):14. https://doi.org/10.3390/membranes6010014
Chicago/Turabian StyleBavi, Omid, Charles D. Cox, Manouchehr Vossoughi, Reza Naghdabadi, Yousef Jamali, and Boris Martinac. 2016. "Influence of Global and Local Membrane Curvature on Mechanosensitive Ion Channels: A Finite Element Approach" Membranes 6, no. 1: 14. https://doi.org/10.3390/membranes6010014
APA StyleBavi, O., Cox, C. D., Vossoughi, M., Naghdabadi, R., Jamali, Y., & Martinac, B. (2016). Influence of Global and Local Membrane Curvature on Mechanosensitive Ion Channels: A Finite Element Approach. Membranes, 6(1), 14. https://doi.org/10.3390/membranes6010014




