Efficient Separation of a Novel Microbial Chassis, Vibrio natriegens, from High-Salt Culture Broth Using Ceramic Ultrafiltration Membranes
Abstract
1. Introduction
2. Materials and Methods
2.1. Production of Fermentation Broth
2.2. Feed Solutions for Filtration with the Ceramic Membrane
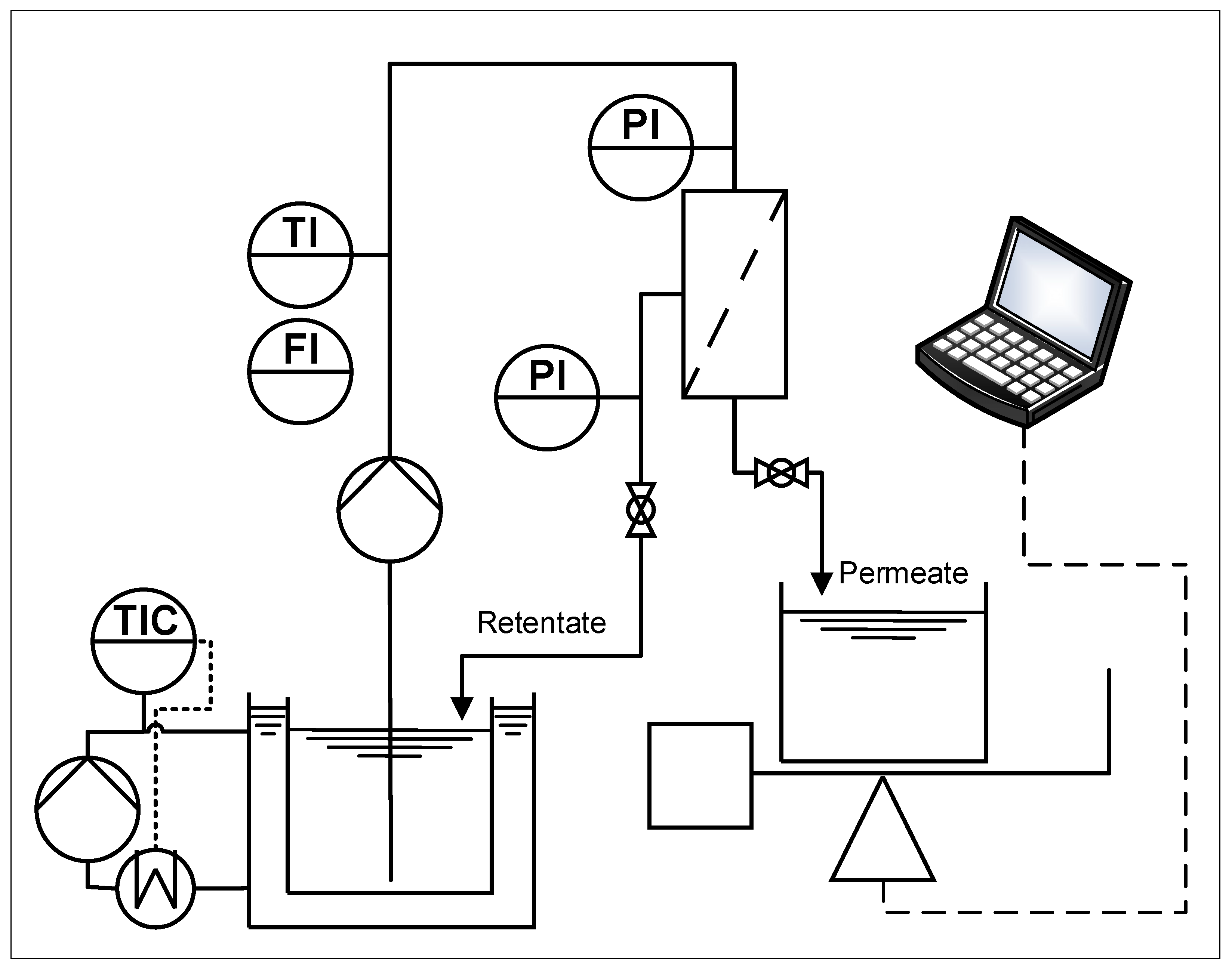
2.3. Filtration Plant
2.4. General Procedure for the Filtration Experiments
2.5. Filtration Experiments to Determine the Compressibility Index
2.6. Chemical Cleaning of Ceramic Membranes
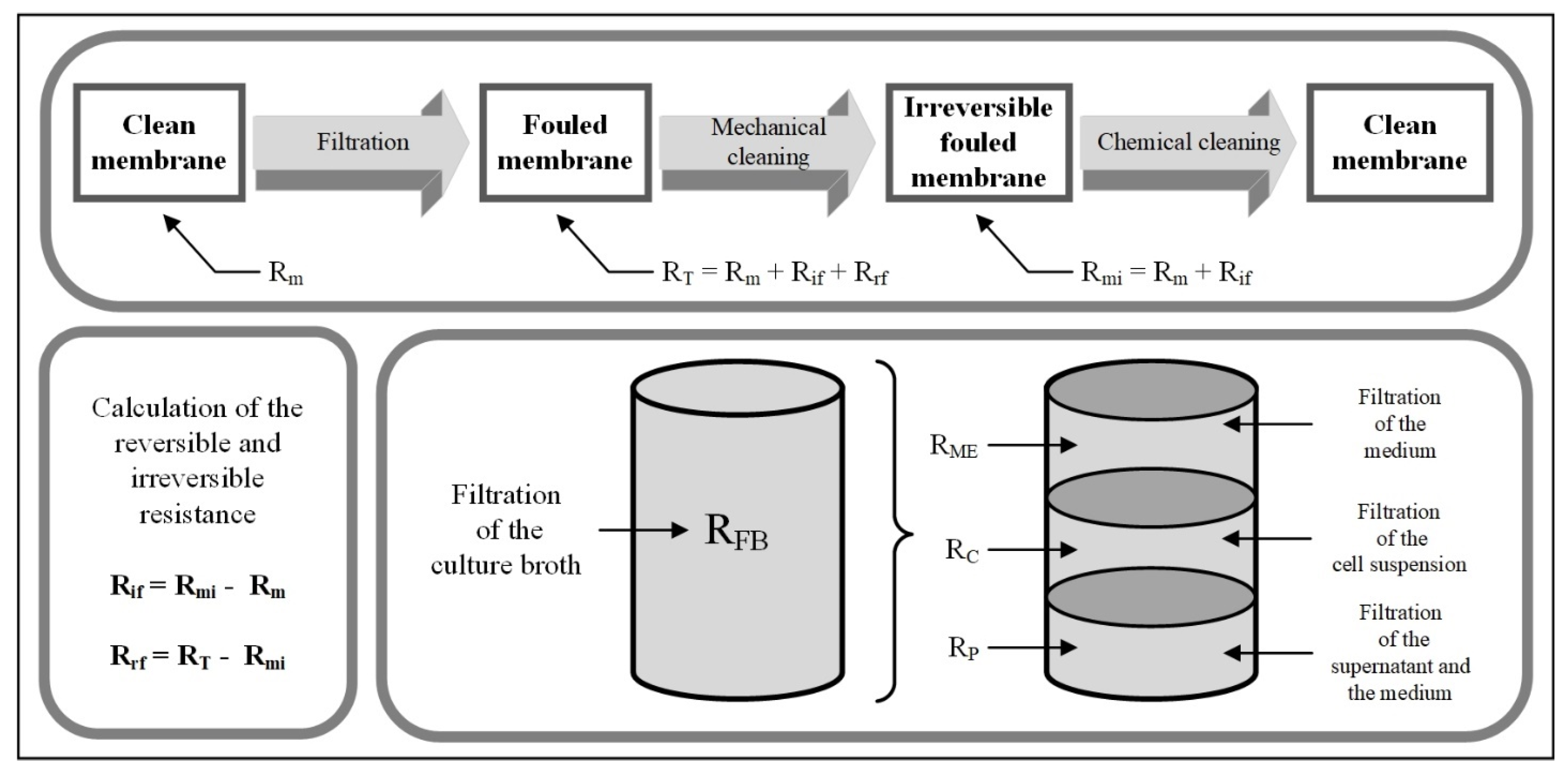
2.7. Data Analysis
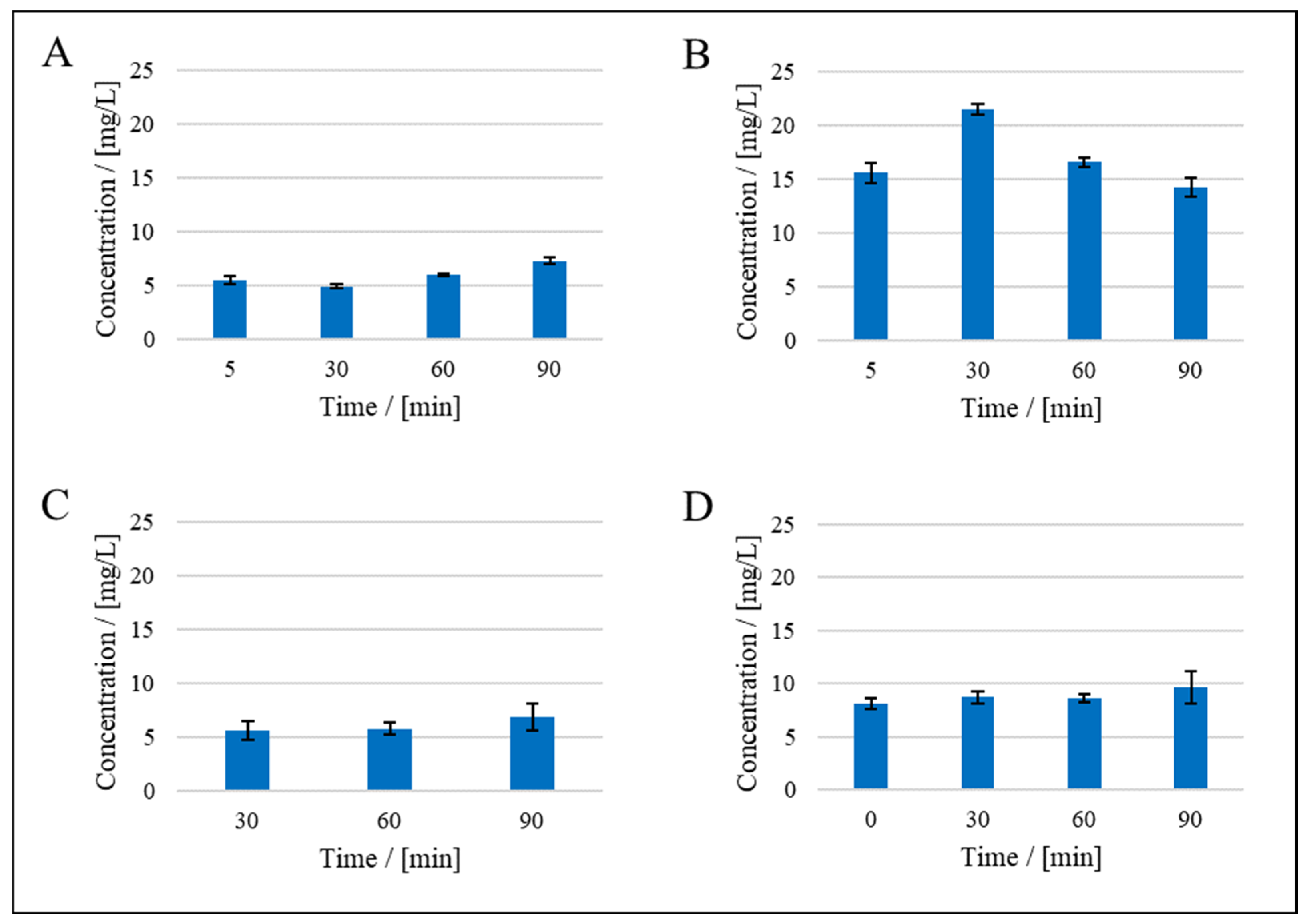
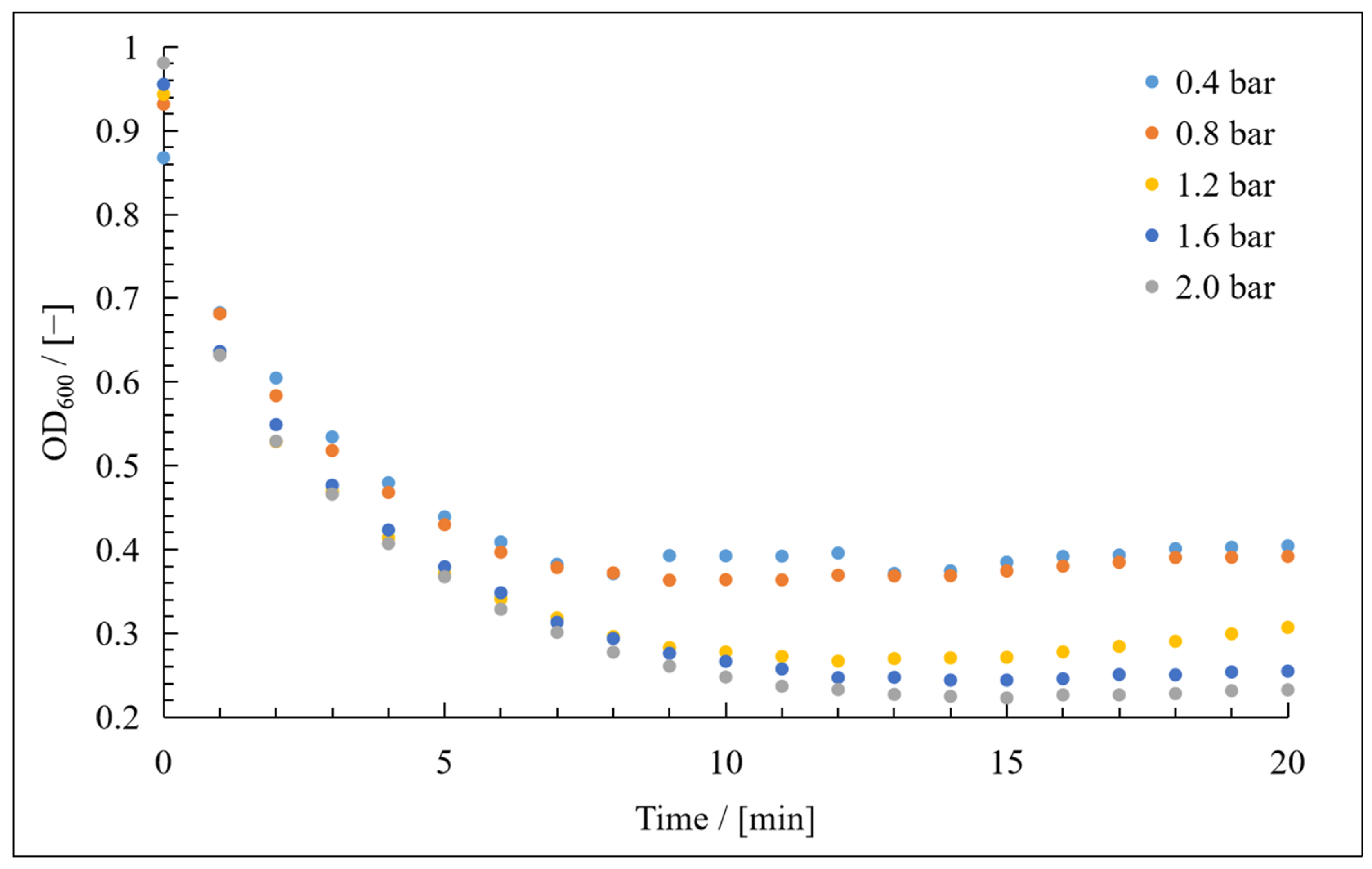
3. Results
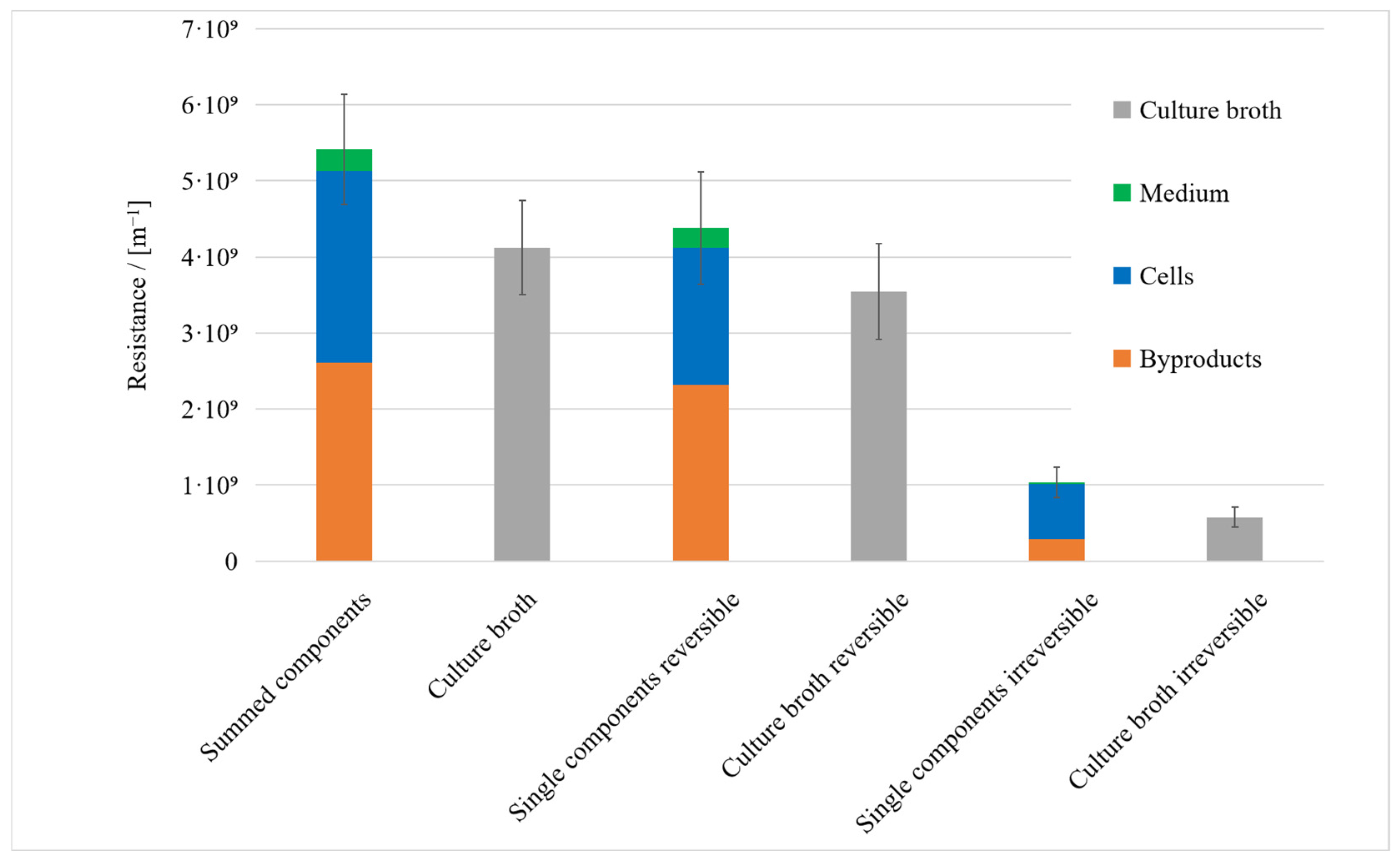
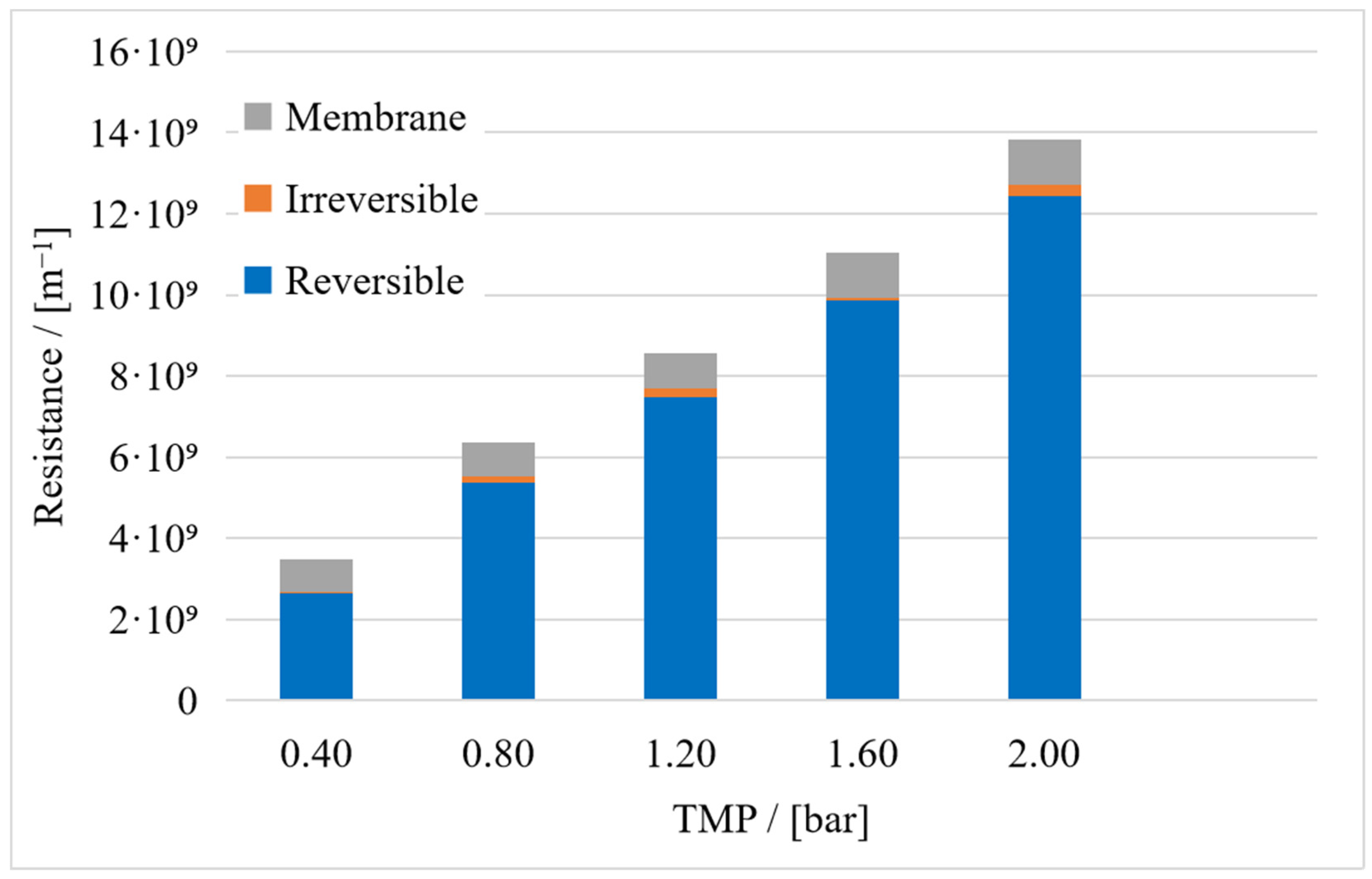
3.1. Resistance in Series Model
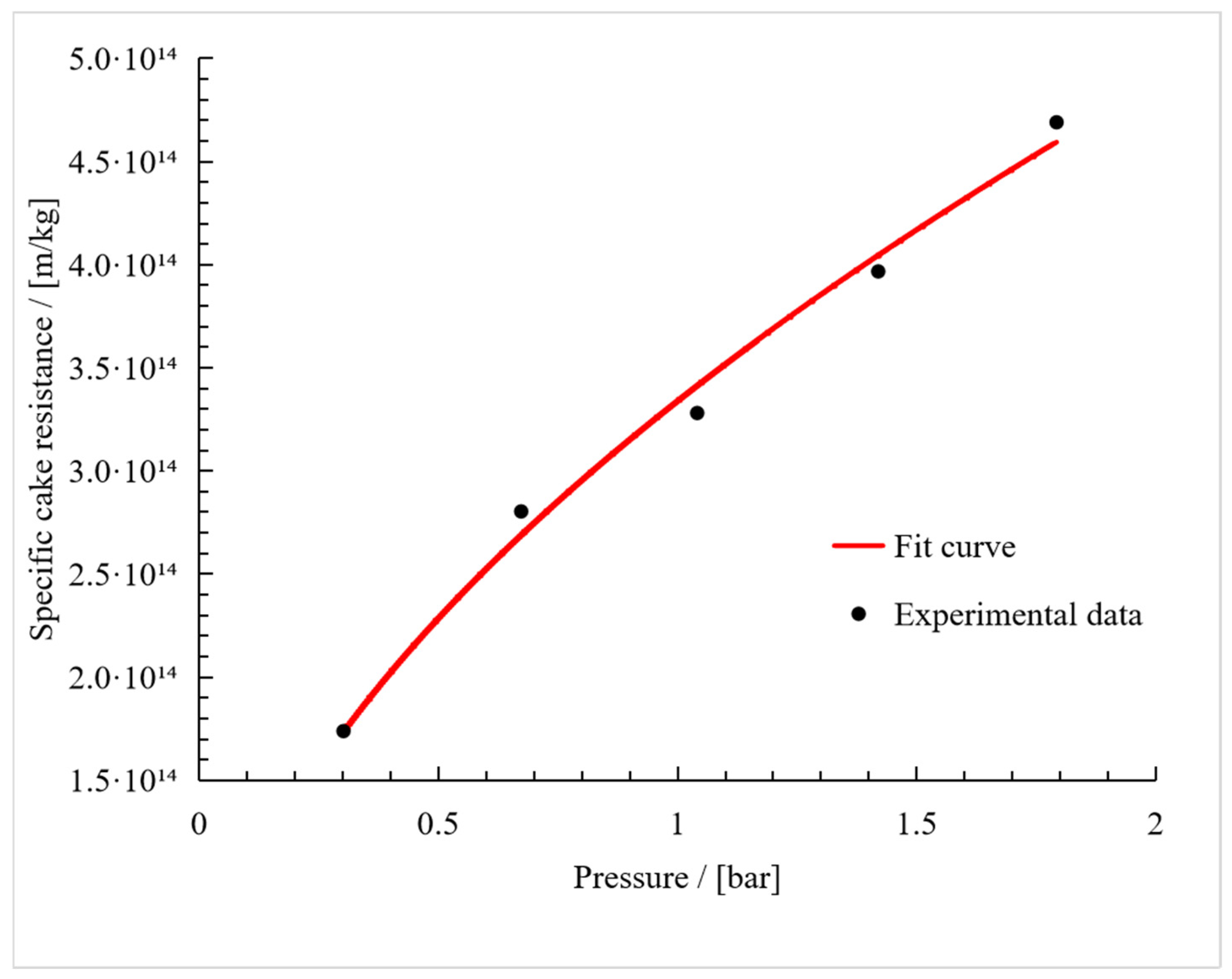
3.2. Compressibility Index
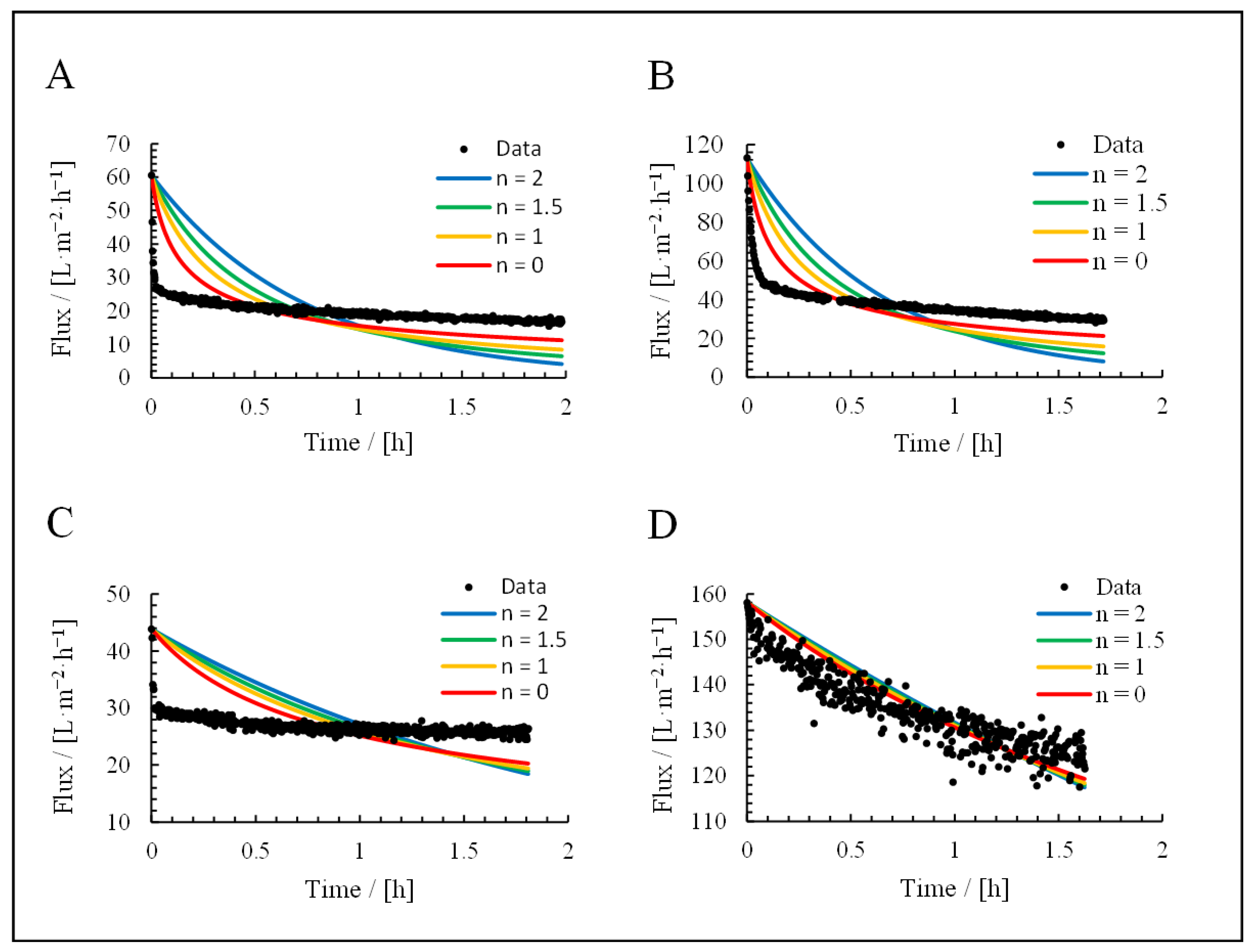
3.3. Application of Hermia’s Laws
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Austin, B.; Zachary, A.; Colwell, R.R. Recognition of Beneckea natriegens (Payne et al.) Baumann et al. as a member of the genus vibrio, as previously proposed by Webb and Payne. Int. J. Syst. Bacteriol. 1978, 28, 315–317. [Google Scholar] [CrossRef]
- Payne, W.J. Studies on bacterial utilization of uronic acids. III. Induction of oxidative enzymes in a marine isolate. J. Bacteriol. 1958, 76, 301–307. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Dong, F.; Wu, M.; Tao, R.; Yang, J.; Wu, M.; Jiang, Y.; Yang, S.; Yang, L. Vibrio natriegens as a pET-Compatible Expression Host Complementary to Escherichia coli. Front. Microbiol. 2021, 12, 627181. [Google Scholar] [CrossRef]
- Eagon, R.G. Pseudomonas natriegens, a marine bacterium with a generation time of less than 10 minutes. J. Bacteriol. 1962, 83, 736–737. [Google Scholar] [CrossRef]
- Maida, I.; Bosi, E.; Perrin, E.; Papaleo, M.C.; Orlandini, V.; Fondi, M.; Fani, R.; Wiegel, J.; Bianconi, G.; Canganella, F. Draft genome sequence of the fast-growing bacterium Vibrio natriegens strain DSMZ 759. Genome Announc. 2013, 1, e00648-13. [Google Scholar] [CrossRef]
- Hoffart, E.; Grenz, S.; Lange, J.; Nitschel, R.; Müller, F.; Schwentner, A.; Feith, A.; Lenfers-Lücker, M.; Takors, R.; Blombach, B. High substrate uptake rates empower Vibrio natriegens as production host for industrial biotechnology. Appl. Environ. Microbiol. 2017, 83, e01614-17. [Google Scholar] [CrossRef]
- Schwarz, S.; Gerlach, D.; Fan, R.; Czermak, P. GbpA as a secretion and affinity purification tag for an antimicrobial peptide produced in Vibrio natriegens. Electron. J. Biotechnol. 2022, 56, 75–83. [Google Scholar] [CrossRef]
- Díaz, E.; Blázquez, M.L.; Fernández-Llamosas, H.; Carmona, M.; Castro, L. Speeding up bioproduction of selenium nanoparticles by using Vibrio natriegens as microbial factory. Sci. Rep. 2017, 7, 16046. [Google Scholar] [CrossRef]
- Eichmann, J.; Oberpaul, M.; Weidner, T.; Gerlach, D.; Czermak, P. Selection of High Producers From Combinatorial Libraries for the Production of Recombinant Proteins in Escherichia coli and Vibrio natriegens. Front. Bioeng. Biotechnol. 2019, 7, 254. [Google Scholar] [CrossRef]
- Becker, W.; Wimberger, F.; Zangger, K. Vibrio natriegens: An Alternative Expression System for the High-Yield Production of Isotopically Labeled Proteins. Biochemistry 2019, 58, 2799–2803. [Google Scholar] [CrossRef]
- Schleicher, L.; Muras, V.; Claussen, B.; Pfannstiel, J.; Blombach, B.; Dibrov, P.; Fritz, G.; Steuber, J. Vibrio natriegens as host for expression of multisubunit membrane protein complexes. Front. Microbiol. 2018, 9, 2537. [Google Scholar] [CrossRef] [PubMed]
- Weinstock, M.T.; Hesek, E.D.; Wilson, C.M.; Gibson, D.G. Vibrio natriegens as a fast-growing host for molecular biology. Nat. Methods 2016, 13, 849–851. [Google Scholar] [CrossRef] [PubMed]
- Des Soye, B.J.; Davidson, S.R.; Weinstock, M.T.; Gibson, D.G.; Jewett, M.C. Establishing a High-Yielding Cell-Free Protein Synthesis Platform Derived from Vibrio natriegens. ACS Synth. Biol. 2018, 7, 2245–2255. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.H.; Ostrov, N.; Wong, B.G.; Gold, M.A.; Khalil, A.S.; Church, G.M. Functional genomics of the rapidly replicating bacterium Vibrio natriegens by CRISPRi. Nat. Microbiol. 2019, 4, 1105–1113. [Google Scholar] [CrossRef]
- Stadler, K.A.; Becker, W.; Darnhofer, B.; Birner-Gruenberger, R.; Zangger, K. Overexpression of recombinant proteins containing non-canonical amino acids in Vibrio natriegens: P-azido-L-phenylalanine as coupling site for 19F-tags. Amino Acids 2022, 54, 1041–1053. [Google Scholar] [CrossRef]
- Jørgensen, C.E.; Abrahamsen, R.K.; Rukke, E.O.; Johansen, A.G.; Schüller, R.B.; Skeie, S.B. Optimization of protein fractionation by skim milk microfiltration: Choice of ceramic membrane pore size and filtration temperature. J. Dairy Sci. 2016, 99, 6164–6179. [Google Scholar] [CrossRef]
- Cimini, A.; Moresi, M. Beer Clarification by Novel Ceramic Hollow-Fiber Membranes: Effect of Pore Size on Product Quality. J. Food Sci. 2016, 81, E2521–E2528. [Google Scholar] [CrossRef]
- Moreno-García, J.; García-Martínez, T.; Mauricio, J.C.; Moreno, J. Yeast immobilization systems for alcoholic wine fermentations: Actual trends and future perspectives. Front. Microbiol. 2018, 9, 241. [Google Scholar] [CrossRef]
- Oppermann, T. Mannheimia haemolytica—Bioprocess improvement of leukotoxin production using a fed-batch process and a ceramic membrane based downstream strategy. Ph.D. Thesis, Justus-Liebig-Universität Gießen, Giessen, Germany, 2018. [Google Scholar]
- Ebrahimi, M.; Busse, N.; Kerker, S.; Schmitz, O.; Hilpert, M.; Czermak, P. Treatment of the bleaching effluent from sulfite pulp production by ceramic membrane filtration. Membranes 2015, 6, 7. [Google Scholar] [CrossRef]
- Tomczak, W.; Gryta, M. Clarification of 1,3-propanediol fermentation broths by using a ceramic fine UF membrane. Membranes 2020, 10, 319. [Google Scholar] [CrossRef]
- Persson, A.; Jönsson, A.S.; Zacchi, G. Separation of lactic acid-producing bacteria from fermentation broth using a ceramic microfiltration membrane with constant permeate flow. Biotechnol. Bioeng. 2001, 72, 269–277. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimi, M.; Kerker, S.; Daume, S.; Geile, M.; Ehlen, F.; Unger, I.; Schütz, S.; Czermak, P. Innovative ceramic hollow fiber membranes for recycling/reuse of oilfield produced water. Desalin. Water Treat. 2015, 55, 3554–3567. [Google Scholar] [CrossRef]
- Hoffmann, D.; Leber, J.; Loewe, D.; Lothert, K.; Oppermann, T.; Zitzmann, J.; Weidner, T.; Salzig, D.; Wolff, M.; Czermak, P. Purification of New Biologicals Using Membrane-Based Processes; Elsevier Inc.: Amsterdam, The Netherlands, 2018. [Google Scholar] [CrossRef]
- Maguire, N.A.P.; Ebrahimi, M.; Fan, R.; Gießelmann, S.; Ehlen, F.; Schütz, S.; Czermak, P. Influence of Ceramic Membrane Surface Characteristics on the Flux Behavior of a Complex Fermentation Broth. Membranes 2021, 11, 402. [Google Scholar] [CrossRef] [PubMed]
- McCarthy, A.A.; Walsh, P.K.; Foley, G. Experimental techniques for quantifying the cake mass, the cake and membrane resistances and the specific cake resistance during crossflow filtration of microbial suspensions. J. Memb. Sci. 2002, 201, 31–45. [Google Scholar] [CrossRef]
- Di Bella, G.; Di Trapani, D. A brief review on the resistance-in-series model in membrane bioreactors (MBRs). Membranes 2019, 9, 24. [Google Scholar] [CrossRef]
- Mota, M.; Teixeira, J.A.; Yelshin, A. Influence of cell-shape on the cake resistance in dead-end and cross-flow filtrations. Sep. Purif. Technol. 2002, 27, 137–144. [Google Scholar] [CrossRef]
- Riesmeier, B.; Kroner, K.H.; Kula, M.R. Studies on secondary layer formation and its characterization during cross-flow filtration of microbial cells. J. Memb. Sci. 1987, 34, 245–266. [Google Scholar] [CrossRef]
- Tanaka, T.; Tsuneyoshi, S.I.; Kitazawa, W.; Nakanishi, K. Characteristics in Crossflow Filtration Using Different Yeast Suspensions. Sep. Sci. Technol. 1997, 32, 1885–1898. [Google Scholar] [CrossRef]
- Vyas, H.K.; Mawson, A.J.; Bennett, R.J.; Marshall, A.D. A new method for estimating cake height and porosity during crossflow filtration of particulate suspensions. J. Memb. Sci. 2000, 176, 113–119. [Google Scholar] [CrossRef]
- Diez, V.; Ezquerra, D.; Cabezas, J.L.; García, A.; Ramos, C. A modified method for evaluation of critical flux, fouling rate and in situ determination of resistance and compressibility in MBR under different fouling conditions. J. Memb. Sci. 2014, 453, 1–11. [Google Scholar] [CrossRef]
- Gul, A.; Hruza, J.; Yalcinkaya, F. Fouling and chemical cleaning of microfiltration membranes: A mini-review. Polymers 2021, 13, 846. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Tal, G.; Hankins, N.P.; Gitis, V. Fouling and cleaning of ultrafiltration membranes: A review. J. Water Process Eng. 2014, 1, 121–138. [Google Scholar] [CrossRef]
- Slimane, F.Z.; Ellouze, F.; Amar, N. Ben Fouling mechanism and screening of backwash parameters: Seawater ultrafiltration case. Environ. Eng. Res. 2019, 24, 298–308. [Google Scholar] [CrossRef]
- Liang, J.; Yu, L.; Wu, J. The dynamic change of specific cake resistance in membrane bioreactor due to periodical cake relaxation. J. Environ. Chem. Eng. 2020, 8, 103837. [Google Scholar] [CrossRef]
- Ghaffour, N.; Qamar, A. Membrane fouling quantification by specific cake resistance and flux enhancement using helical cleaners. Sep. Purif. Technol. 2020, 239, 116587. [Google Scholar] [CrossRef]
- Fane, A.G.; Fell, C.J.D.; Hodgson, P.H.; Leslie, G.; Marshall, K. Microfiltration of biomass and biofluids: Effects of membrane morphology and operating conditions. Filtr. Sep. 1991, 28, 332–340. [Google Scholar] [CrossRef]
- Nakanish, K.; Tadokoro, T.; Matsuno, R. On the Specific Resistance of Cakes of Microorganisms. Chem. Eng. Commun. 1987, 62, 187–201. [Google Scholar] [CrossRef]
- Tanaka, T.; Abe, K.I.; Asakawa, H.; Yoshida, H.; Nakanishi, K. Filtration characteristics and structure of cake in crossflow filtration of bacterial suspension. J. Ferment. Bioeng. 1994, 78, 455–461. [Google Scholar] [CrossRef]
- Loginov, M.; Doudiès, F.; Hengl, N.; Pignon, F.; Gésan-Guiziou, G. Influence of membrane resistance on swelling and removal of colloidal filter cake after filtration pressure release. J. Memb. Sci. 2020, 595, 117498. [Google Scholar] [CrossRef]
- Sørensen, B.L.; Sørensen, P.B. Structure Compression in Cake Filtration. J. Environ. Eng. 1997, 123, 345–353. [Google Scholar] [CrossRef]
- Kujundzic, E.; Greenberg, A.R.; Fong, R.; Moore, B.; Kujundzic, D.; Hernandez, M. Biofouling potential of industrial fermentation broth components during microfiltration. J. Memb. Sci. 2010, 349, 44–55. [Google Scholar] [CrossRef]
- Fonseca, A.C.; Summers, R.S.; Greenberg, A.R.; Hernandez, M.T. Extra-cellular polysaccharides, soluble microbial products, and natural organic matter impact on nanofiltration membranes flux decline. Environ. Sci. Technol. 2007, 41, 2491–2497. [Google Scholar] [CrossRef] [PubMed]
- Rushton, A. (Ed.) Mathematical Models and Design Methods in Solid-Liquid Separation; Springer: Dordrecht, The Netherlands, 1985. [Google Scholar] [CrossRef]
- Bowen, W.R.; Calvo, J.I.; Hernández, A. Steps of membrane blocking in flux decline during protein microfiltration. J. Memb. Sci. 1995, 101, 153–165. [Google Scholar] [CrossRef]
- Burghardt, J.P.; Coletta, L.A.; van der Bolt, R.; Ebrahimi, M.; Gerlach, D.; Czermak, P. Development and characterization of an enzyme membrane reactor for fructo-oligosaccharide production. Membranes 2019, 9, 148. [Google Scholar] [CrossRef]
- Field, R.W.; Wu, D.; Howell, J.A.; Gupta, B.B. Critical flux concept for microfiltration fouling. J. Memb. Sci. 1995, 100, 259–272. [Google Scholar] [CrossRef]
- Gunde-Cimerman, N.; Plemenitaš, A.; Oren, A. Strategies of adaptation of microorganisms of the three domains of life to high salt concentrations. FEMS Microbiol. Rev. 2018, 42, 353–375. [Google Scholar] [CrossRef]
- Gregory, G.J.; Boyd, E.F. Stressed out: Bacterial response to high salinity using compatible solute biosynthesis and uptake systems, lessons from Vibrionaceae. Comput. Struct. Biotechnol. J. 2021, 19, 1014–1027. [Google Scholar] [CrossRef]
- Magpusao, J.; Oey, I.; Kebede, B. Opportunities and Challenges of Algal Protein Extraction and Production. Innov. Food Process. Technol. A Compr. Rev. 2020, 3, 216–233. [Google Scholar] [CrossRef]
- Liu, D.; Wu, C.; Wu, R.; Huang, J.; Liao, B.; Lei, M.; Zhang, Y.; He, H. Comprehensive analysis of the phylogeny and extracellular proteases in genus Vibrio strain. Microb. Pathog. 2019, 131, 1–8. [Google Scholar] [CrossRef]
- Thoma, F.; Blombach, B. Metabolic engineering of Vibrio natriegens. Essays Biochem. 2021, 65, 381–392. [Google Scholar] [CrossRef]
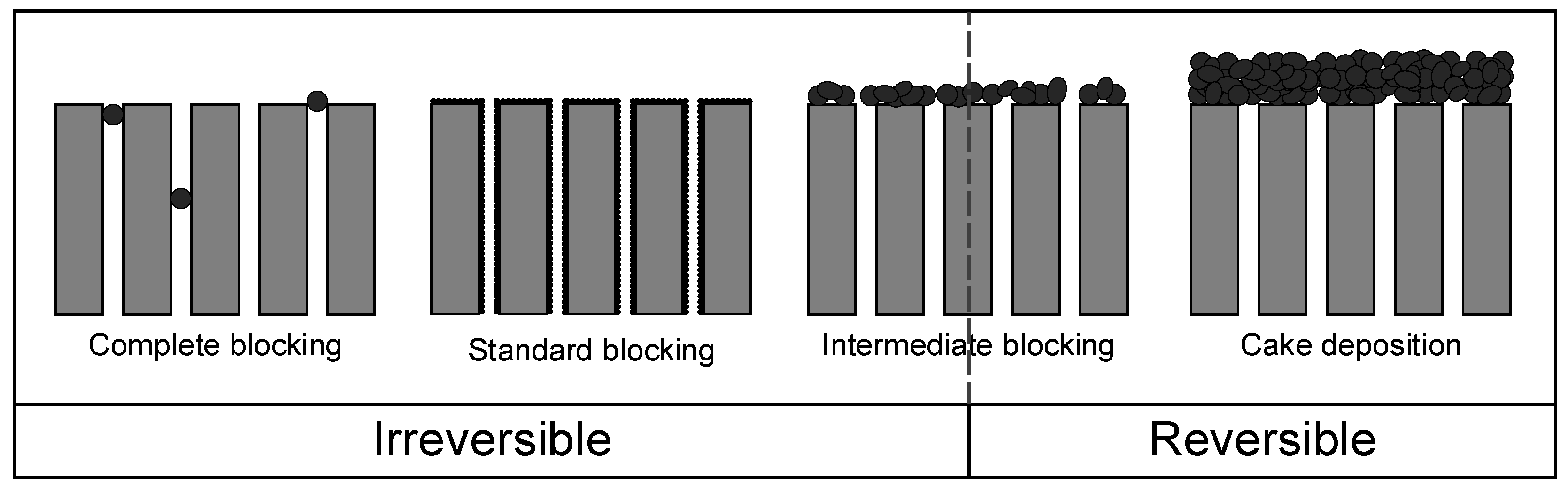
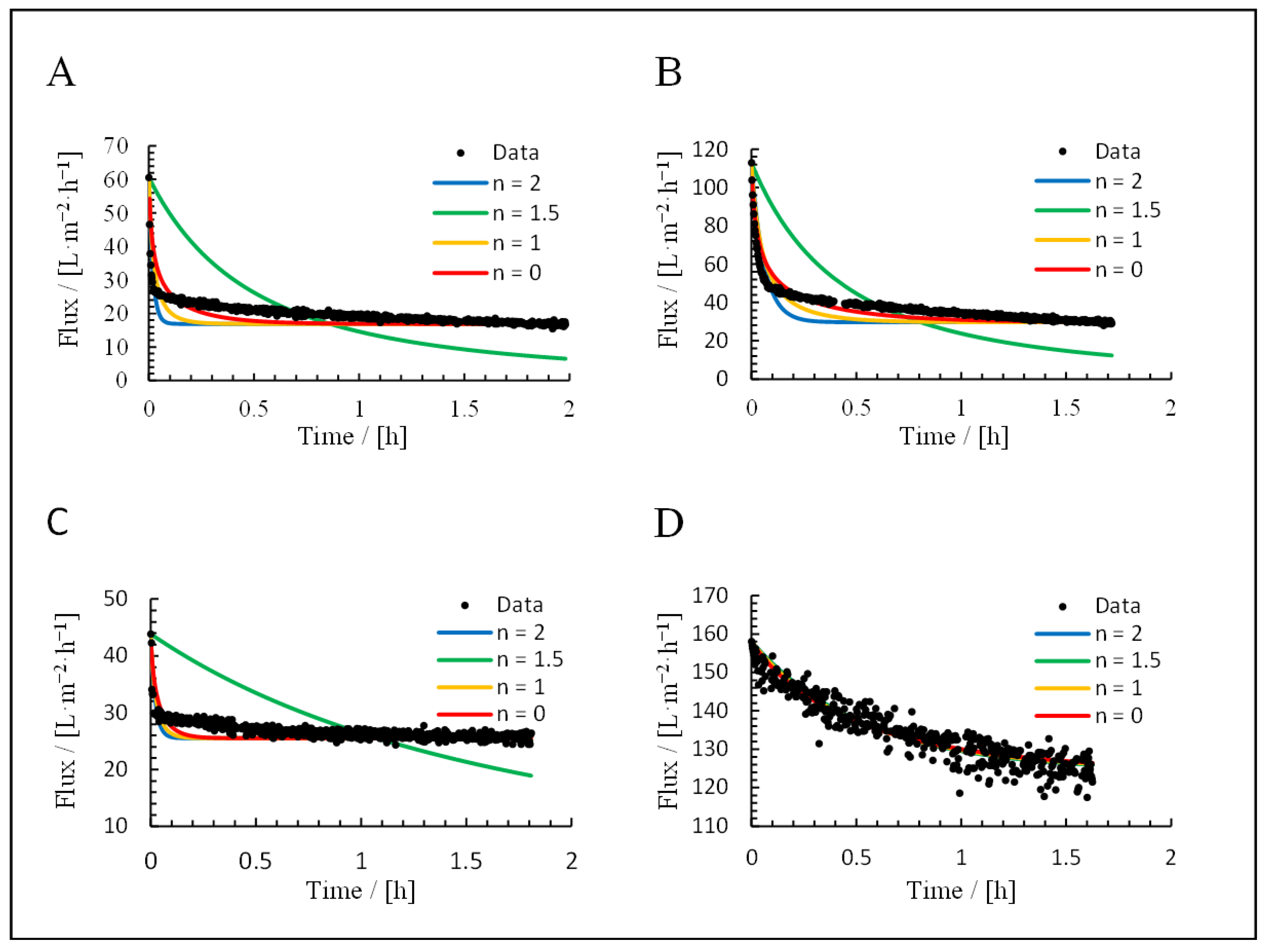
| Mechanism | n | Equation | |
|---|---|---|---|
| Complete blocking | 2 | (12) | |
| Standard blocking | 1.5 | (13) | |
| Intermediate blocking | 1 | (14) | |
| Cake deposition | 0 | (15) |
| Mechanism | n | Equation | |
|---|---|---|---|
| Complete blocking | 2 | (17) | |
| Standard blocking | 1.5 | (18) | |
| Intermediate blocking | 1 | (19) | |
| Cake deposition | 0 | (20) |
| Fit Model | R2 of the Fit | |||
|---|---|---|---|---|
| Culture Broth | Cells | Supernatant | Medium | |
| Complete blocking | 0.53 | 0.81 | 0.50 | 0.88 |
| Standard blocking | 0.74 | 0.74 | 0.58 | 0.88 |
| Intermediate blocking | 0.61 | 0.88 | 0.53 | 0.88 |
| Cake filtration | 0.72 | 0.92 | 0.51 | 0.88 |
| Fit Model | R2 of the Fit | |||
|---|---|---|---|---|
| Culture Broth | Cells | Supernatant | Medium | |
| Complete blocking | 0.71 | 0.69 | 0.56 | 0.86 |
| Standard blocking | 0.74 | 0.74 | 0.58 | 0.87 |
| Intermediate blocking | 0.31 | 0.14 | 0.30 | 0.87 |
| Cake filtration | 0.88 | 0.88 | 0.71 | 0.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schwarz, S.; Fan, R.; Ebrahimi, M.; Czermak, P. Efficient Separation of a Novel Microbial Chassis, Vibrio natriegens, from High-Salt Culture Broth Using Ceramic Ultrafiltration Membranes. Membranes 2025, 15, 121. https://doi.org/10.3390/membranes15040121
Schwarz S, Fan R, Ebrahimi M, Czermak P. Efficient Separation of a Novel Microbial Chassis, Vibrio natriegens, from High-Salt Culture Broth Using Ceramic Ultrafiltration Membranes. Membranes. 2025; 15(4):121. https://doi.org/10.3390/membranes15040121
Chicago/Turabian StyleSchwarz, Stefan, Rong Fan, Mehrdad Ebrahimi, and Peter Czermak. 2025. "Efficient Separation of a Novel Microbial Chassis, Vibrio natriegens, from High-Salt Culture Broth Using Ceramic Ultrafiltration Membranes" Membranes 15, no. 4: 121. https://doi.org/10.3390/membranes15040121
APA StyleSchwarz, S., Fan, R., Ebrahimi, M., & Czermak, P. (2025). Efficient Separation of a Novel Microbial Chassis, Vibrio natriegens, from High-Salt Culture Broth Using Ceramic Ultrafiltration Membranes. Membranes, 15(4), 121. https://doi.org/10.3390/membranes15040121







