Abstract
CO2 capture by membrane gas absorption technology has been considered a promising alternative to mitigate or stabilize atmospheric CO2 concentrations. The non-isothermal nature of the CO2 absorption process in hollow fiber membrane contactors is a critical factor that significantly influences CO2 removal performance. In the present study, a non-isothermal mathematical model and a two-dimensional computational simulation were carried out to evaluate the CO2 separation by three typical absorbents in a polyvinylidene fluoride hollow fiber membrane contactor under non-wetting operation mode. The simulation results exhibited good matching with the published experimental data with the deviations in the range of lower than 5%, which validated the reliability of the developed numerical model. A significant temperature increase ranging from 2 to 15 K was observed along the length of the hollow fiber membrane contactor, which further facilitated the absorption and reaction process in this study. The results showed that potassium glycinate exhibited the highest absorption capacity, followed by monoethanolamine and 1-ethyl-3-methylimidazolium. In addition, the mass transfer could be enhanced by increasing the liquid flow rate, absorbent concentration, module length, and membrane porosity, while increasing the gas velocity and CO2 inlet concentration were unfavorable for the CO2 removal process.
1. Introduction
The carbon dioxide generated during the combustion process of fossil fuels is a major contributor to greenhouse gas emissions. The resulting global warming has brought severe challenges to global food security, water resources, ecological systems, energy supplies, human health, and large-scale infrastructure. To address this issue, it is particularly imperative to implement effective measures to limit CO2 emission from large-scale industrial sources [1]. According to the Energy Technology Perspectives 2020 report issued by the International Energy Agency [2], renewable energy generation, bioenergy, hydrogen energy, and carbon dioxide capture and storage have been identified as key technologies to achieve global net zero emissions. Among them, carbon dioxide capture and storage is the only technology which can directly stabilize or even reduce the atmospheric carbon dioxide concentrations in the short term.
The CO2 post-combustion capture system is currently the most advanced technology to capture CO2 from the flue gas of coal-fired power plants or other large CO2 emission sources without the significant retrofitting of existing infrastructure. Chemical absorption is the most well-established technology and has been extensively utilized in the gas separation industry for decades. However, conventional gas absorption towers and scrubbers are generally encountered with challenges of flooding, absorbent losses, entrainment, liquid channeling, foaming, and other operation problems [3]. The applications of another promising membrane gas separation technology are generally limited by the tradeoff between permeability and selectivity, even though it has the advantages of a high specific surface area, flexible design, and compact and simple structure [4]. Consequently, researchers have extensively explored the integration of two or more CO2 separation technologies, with the aim of enhancing the CO2 removal efficiency and eliminating the operational challenges.
Membrane gas absorption technology is a hybrid process that combines the advantages of gas absorption technology with membrane separation technology, which has been considered a promising approach in the field of CO2 separation [5,6]. Compared with conventional absorption towers or columns, the absorbent and flue gas in a hollow fiber membrane contactor flow in the tube side and shell side, respectively, thus avoiding the operational problems such as flooding, channeling, entrainment, and foaming. Furthermore, membrane gas absorption technology has the advantages of a compact structure, large specific surface area, good operational flexibility, modular design, low energy consumption, and easy linear scaling [7]. The main drawback of membrane gas absorption technology is the membrane wetting over long-time operation, which can be prohibited by the superhydrophobic surface modification of porous polymer membranes [8]. Unlike traditional membrane gas separation, in this process, the hollow fiber membrane does not provide CO2 selectivity but rather serves as the contact interface between the gas and liquid phases. The selectivity is provided by the absorbent flowing on the tube side of the membrane contactor. Therefore, the selection of an absorbent is a critical factor in improving CO2 removal efficiency and reducing the energy consumption. Alkanolamines, pure alkaline solutions, amino acid salts, and ionic liquids have been extensively used as the absorbents for CO2 removal by the hollow fiber membrane contactors [9,10,11].
Mathematical modeling and simulation are crucial methods to predict the mass transfer performance and CO2 removal efficiency, which plays an important role in the design and scale-up of the CO2 separation process by the membrane contactor. A variety of research projects have been carried out to investigate the influences of different absorbents and operating parameters on CO2 removal efficiency based on isothermal mathematical models under the non-wetting mode. Nakhjiri et al. [12,13,14,15] compared the effects of different liquid absorbents on CO2 separation in polyvinylidene fluoride (PVDF) and polypropylene (PP) hollow fiber membrane contactors. The numerical results showed that CO2 concentration at the outlet was reduced from 4 mol/m3 to 0.76, 0.45 and 0.71 mol/m3 using ethylenediamine, (piperazinyl-1)-2-ethylamine, and polystyrene as absorbents, respectively. Compared with NaOH and triethylamine, monoethanolamine (MEA) showed better efficiency in removing CO2, and 2-tert-butylaminoethanol can achieve a decarbonization effect similar to that of MEA [16]. The addition of nanoparticles can enhance Brownian motion and grazing effects. Ghasem et al. [17] developed a two-dimensional mathematical model to simulate the CO2 absorption process of water-based nanofluids enhanced by carbon nanotubes in hollow fiber membrane contactors. The simulation results showed that the CO2 removal rate increased by about 20% after adding 0.5 wt. % carbon nanotubes. Furthermore, the addition of montmorillonite nanoparticles and SiO2 nanoparticles can also improve the CO2 removal rate [18,19]. Vaezi et al. [20] and Bozonc et al. [21] proposed a two-dimensional mathematical model to evaluate the CO2 removal efficiency in a porous hydrophobic polytetrafluoroethylene and PP hollow fiber membrane using 3-diethylaminopropylamine and MEA as the absorbent. The influences of amine concentration, liquid and gas flow rate, liquid temperature, CO2 partial pressure, membrane tortuosity, packing density, and hollow fiber numbers on CO2 absorption performance were studied. Xia et al. [22] developed a two-dimensional mass transfer model to compare the CO2 absorption by ammonia, MEA, and diethanolamine under different operating conditions and membrane geometric properties. Bozonc et al. [23] simulated the CO2 absorption process using MEA in a hollow fiber membrane contactor and studied the effects of operating parameters on the removal process. All above simulation models have been developed under isothermal conditions for simplification. However, the absorption process of CO2 by absorbents is non-isothermal and exothermic, during which the reaction heat is accumulated as the absorbent moves toward the outlet. The non-isothermal process definitely influences the subsequent CO2 absorption process, and a non-isothermal model shall be developed to present a more realistic approach that is relevant to the CO2 absorption by reactive absorbents in hollow fiber membrane contactors.
There have been very limited non-isothermal models to estimate the influences of temperature variations on reaction kinetics. Sohaib et al. [24] developed a two-dimensional non-isothermal model to investigate the non-isothermal behaviors of the CO2 absorption process and its influences on the reaction kinetics, by using four amino acid-based ionic liquids in a hydrophobic polypropylene membrane contactor. A 10–25 K temperature increase was observed along the membrane contactor length, which was attributed to the release of dissolution reaction energy, which further affected relevant parameters including diffusive solubility, rate constants, and reaction rates. The simulation results of Zaidiza et al. [25] also found that, the temperature profiles along the membrane contactor were increased by nearly 30 K, which further enhanced the reaction rate of MEA with CO2 by 5%. Evidently, the non-isothermal nature of the CO2 absorption process should be taken into account to evaluate the CO2 removal performance using absorbents in hollow fiber membrane contactors. Therefore, it is correspondingly the interest of the present study to develop a two-dimensional non-isothermal model, with the aim of providing a more realistic approach towards the CO2 absorption process using three typical absorbents in a PVDF hollow fiber membrane contactor. Potassium glycinate (PG), MEA, and 1-ethyl-3-methylimidazolium acetate ([EMIM][Ac]) were selected as the absorbents to represent the amino acid salt, amine solution, and ionic liquid, respectively. Furthermore, the influences of various operational parameters and hollow fiber module specifications on CO2 removal performance were studied using the proposed model.
2. Methodology
2.1. Model Development
In this study, a two-dimensional finite element mathematical model was developed to simulate the non-isothermal CO2 separation process from flue gas using three typical absorbents in a hollow fiber membrane contactor operating under a non-wetted mode. COMSOL software version 6.1 was employed to evaluate the CO2 removal efficiency and concentration distribution within the gas–liquid membrane contactor. PVDF was selected as the hydrophobic porous membrane, mainly due to its intrinsic hydrophobicity, affordability, and exceptional thermal and chemical stability. Three representative aqueous solutions representing alkanolamines, amino acid salts, and ionic liquids were selected as the chemical absorbents, named MEA, PG, and [EMIM][Ac], respectively.
The schematic diagram of the hollow fiber membrane contactor used for model development is presented in Figure 1. The flue gas composed of CO2 and N2 enters the shell side of the hollow fiber membrane contactor from the top (Z = L) and flows downward, while the absorbent enters the tube side from the bottom (Z = 0), flowing in the opposite direction. Driven by the concentration gradient, CO2 in the flue gas mixture diffuses through the membrane pores to the gas–liquid contact interface, and it is further absorbed into the liquid phase by the absorbent. The model in this study is established based on the Happel free surface model, which had been extensively used for hollow fiber membrane contactors [26]. This model considers only a portion of the fluid surrounding the hollow fibers, approximating it as an annular cross section.
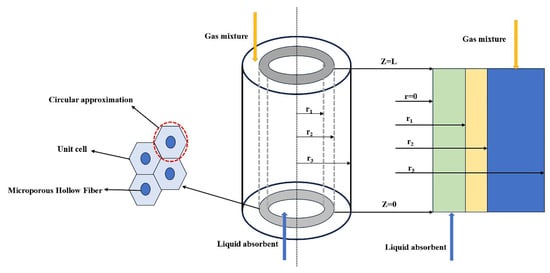
Figure 1.
Schematic diagram of CO2 absorption in a hollow fiber membrane contactor.
The model is developed based on the following assumptions: the CO2 removal process occurs under steady-state conditions, with both the gas flowing in the shell side and liquid flowing in the tube side being laminar; Henry’s Law is applied to determine the gas–liquid equilibrium at the interfacial boundary. The gas phase on the shell side is treated as an ideal gas.
The specifications for the PVDF hollow fiber membrane contactor used in this study are detailed in Table 1. The simulations were conducted at a temperature of 303.15 K and a pressure of 0.1 MPa.

Table 1.
Specification of the hollow fiber membrane contactor.
2.2. Governing Equations and Boundary Conditions
The continuity equation for the component i can be expressed as follows [27]:
where Ci is the concentration, mol/m3; Di is the diffusion coefficient, m2/s; Ri is the reaction rate of component i along the axial direction, and the reaction only occurs in the liquid phase, mol/m3·s; VZ is the axial velocity, m/s; and t is time, s.
2.2.1. Shell Side Equations
The continuity equation for the gas side in the shell compartment under a steady state can be expressed as follows [28]:
where DCO2,shell is the diffusion coefficient of component CO2, m2/s; CCO2,shell is the concentration of component CO2 in the shell compartment, mol/m3; and VZ,shell is the velocity in the shell compartment, m/s.
When the gas phase is assumed under a laminar state, the velocity distribution of the gas phase in the shell side can be calculated based on the Happel model, which can be expressed by the following [29]:
where is the shell-side average velocity, m/s; r2 is the hollow fiber outer diameter, mm; r3 is the effective radius of the shell side, which can be expressed by the following [30]:
where φ is the volume fraction of the void, expressed by the following Equation [12]:
where n is the number of hollow fibers and R is the inner diameter of the module, mm.
The thermal balance equation in the shell compartment is presented as follows:
where is the thermal conductivity of the gas phase in the shell compartment, W/m·K; Tg,shell is the temperature of the gas phase in the shell compartment, K; Cp,g is the specific heat of gas phase in the shell compartment, J/mol·K.
2.2.2. Membrane Side Equations
When the membrane pores are filled with gas, the mass transfer resistance of the membrane is typically neglected, which corresponds to the non-wetting operation mode considered in this study. Under these conditions, CO2 diffuses from the outer surface of the hollow fiber to the gas–liquid contact interface through the microporous pores. Thus, the steady-state continuity equation within the hollow fiber membrane can be expressed as follows [18]:
where DCO2,mem is the diffusion coefficient of CO2 within the membrane pores, m2/s; CCO2,mem is the concentration of CO2 inside the membrane pores, mol/m3. The diffusion coefficient of the CO2 inside the membrane pores is influenced by the membrane tortuosity and porosity. The diffusion coefficient of CO2 inside the membrane pores can be expressed as follows [31,32]:
The thermal balance equation of CO2 at the membrane side can be presented by the following:
where is the thermal conductivity of CO2 within the membrane pores, W/m·K; is the thermal conductivity of membrane material, W/m·K; TCO2,mem is the temperature of CO2 within the membrane pores, K; and ε is the membrane porosity.
2.2.3. Tube Side Equations
The steady-state continuity equation for CO2 in the tube compartment consists of convection, diffusion, and chemical reaction, which can be expressed by the following [33]:
where DCO2,tube is the CO2 diffusion coefficient in the tube compartment, m2/s; CCO2,tube is the CO2 axial concentration in the tube compartment, mol/m3; VZ,tube is the CO2 axial velocity in the tube compartment, m/s; and is the reaction rate of CO2 in the liquid phase in the tube side, mol/m3·s.
Since radial convection is significantly lower than axial convection, only axial convection is considered in the model. The velocity distribution of the laminar flow in the tube is denoted by the following [30]:
where v is the liquid velocity at the inlet, m/s.
The thermal balance equation of CO2 in the tube compartment is presented as follows:
where is the thermal conductivity of the liquid phase in the tube side, W/m·K; TL,tube is the temperature of the liquid phase in the tube side, K; is the enthalpy change of the absorption process, J/mol; Cp,L is the liquid phase specific heat in the tube compartment, J/mol·K; and is the reaction rate of absorbent in the tube side, mol/m3·s.
2.2.4. Boundary Conditions
According to the research results obtained by Lee et al. [34], the effect of temperature on the absorbent performance is negligible in the temperature range of 293.15 K to 323.15 K. In this study, parameter values at 303.15 K are used in the simulation. Table 2, Table 3 and Table 4 provide the corresponding boundary conditions applied in the simulation for the shell side, membrane side, and tube side, respectively. These boundary conditions are crucial for accurately modeling the CO2 separation process within the hollow fiber membrane contactor. The partition coefficient m is defined as the ratio of the CO2 concentration in the liquid phase to that in the gas phase at the interface. In the simulation, the value of m is usually considered as a constant value.

Table 2.
Absorbent properties.

Table 3.
Boundary conditions of mass transfer equation.

Table 4.
Boundary condition of energy equations.
2.3. Reaction Mechanism
In the MEA-CO2-H2O system, the reaction between MEA and CO2 is described by a zwitterionic mechanism, which proceeds by forming zwitterions as intermediates.
The intermediate zwitterion loses a proton by reacting with the MEA molecule.
Therefore, the total reaction between MEA and CO2 is as follows:
The reaction between the amino acid salt PG solution and CO2 is also described by the zwitterion mechanism. The formation of zwitterions follows the following reaction:
The deprotonation of zwitterions by bases also follows the following reaction:
The chemisorption mechanism is proposed by Gurau et al. The basic chemistry of [Emim][Ac] IL and CO2 is described by the following reversible reaction:
The CO2 removal efficiency is a critical indicator for evaluating the separation performance of the membrane contactor. It can be expressed by the following equation:
where Cin and Cout are the concentration of CO2 at the inlet and outlet of the membrane contactor, respectively, mol/m3.
2.4. Verification of Grid Independence
Figure 2 illustrates the triangular meshing technique used to analyze the behavior of gas and liquid solutions within a microporous hollow fiber membrane contactor. The PARDISO solver, known for its memory efficiency, was employed to enhance the computational efficiency and accuracy. A finer mesh size and higher degree of aggregation near the membrane wall were utilized to capture the reactions and gas–liquid interactions occurring within the membrane pores, thereby improving the fidelity of the mathematical model and reducing computational discrepancies. It is important to note that increasing the number of grids can reduce computational errors and improve accuracy. However, this also results in a longer computational time. Therefore, an optimum mesh grid number must be determined.
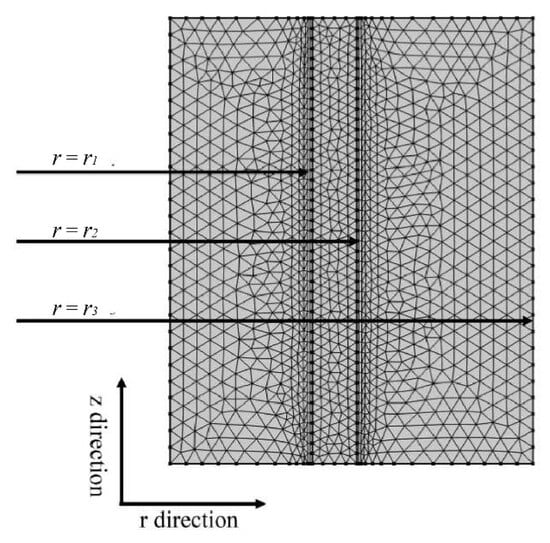
Figure 2.
Triangular mesh division of shell, membrane, and tube sides in HFMC.
Figure 3 shows the effect of the number of grids on the CO2 concentration at the shell side outlet. As depicted, the number of grids has a significant impact on simulation results when increasing from 800 to 1134. However, beyond 1134 grids, further increases have no noticeable effect on the results, indicating that the calculation accuracy becomes independent of the number of grids at this point. Therefore, to balance accuracy and computational cost, the number of grids used in this study were determined to be 1134.
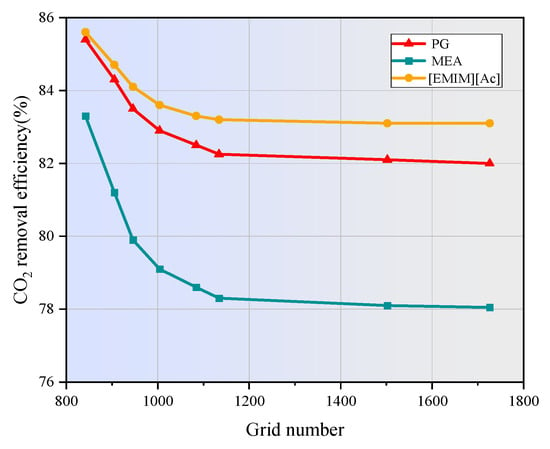
Figure 3.
Effect of grid number on CO2 removal efficiency.
2.5. Numerical Model Validation
To validate the reliability of the developed numerical model, the numerical results of CO2 removal efficiency using MEA in a PVDF hollow fiber membrane contactor under non-wetting mode were compared with the experimental results published in the literature [40]. As shown in Figure 4, the numerical simulation results exhibit a strong correlation with the experimental data, with an average error margin of less than 5%. The observed deviations between the experimental and simulation results are likely attributable to the estimation of certain constants and reaction kinetics during the development of the mathematical model. These findings suggest that the numerical method developed in this study is both reliable and accurate to predict the performance of the hollow fiber membrane contactor.
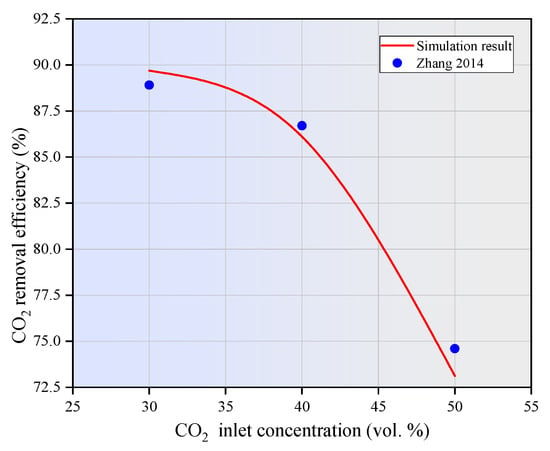
Figure 4.
Comparison between simulation results and experimental data [40]. CL = 10 wt.%, Vg = 0.32 m/s, VL = 0.06 m/s, T = 298.15 K, p = 0.1 MPa.
3. Results and Discussion
3.1. CO2 Concentration Distribution in the Shell Side
The CO2 concentration distribution in the shell side of the hollow fiber membrane contactor is presented in Figure 5. When the mixture gas of CO2 and N2 is introduced into the shell side from the top the hollow fiber membrane contactor at Z = L, the CO2 concentration in the shell side reaches its maximum value. It is assumed that the CO2 concentration in the tube side is zero at Z = 0. As the flue gas flows through the shell side, the mass transfer of CO2 is initially influenced by axial convection, driven by the laminar gas flow that carries CO2 downward at a certain velocity. Concurrently, CO2 molecules diffuse towards the hollow fiber membrane surface through molecular diffusion driven by the concentration gradient, as described by Fick’s Law. As depicted in Figure 5, the CO2 concentration gradually decreases in both the axial and radial directions as the gas moves toward the outlet. This decrease is attributed to the comprehensive effects of convective transport, molecular diffusion towards the membrane pores, permeation through the membrane pores, and subsequent reaction with the absorbent flowing countercurrent in the tube side. Under identical operating conditions, the highest axial variation in CO2 concentration is observed when PG is used as the absorbent, followed by MEA, with [EMIM][Ac] exhibiting the least variation. This trend corresponds to the relative CO2 absorption capacities of the absorbents, with PG having the highest absorption capacity, followed by MEA, and [EMIM][Ac] showing the lowest capacity.
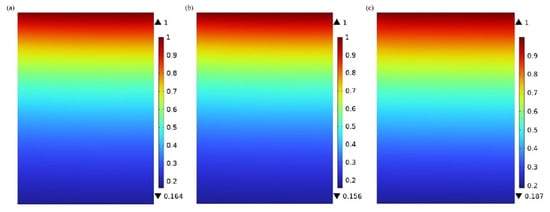
Figure 5.
Concentration distribution of CO2 in the shell side: (a) MEA; (b) PG; and (c) [EMIM][Ac]. CCO2 = 1 mol/m3, CL = 1600 mol/m3, Vg = 0.4 m/s, VL = 1 m/s, T = 303.15 K, p = 0.1 MPa.
3.2. Absorbent Concentration Distribution in the Tube Side
Figure 6 shows the axial concentration distributions of MEA, PG, and [EMIM][Ac] in the tube side of the membrane contactor operating under the non-wetting mode. As CO2 diffuses through the membrane pores to the gas–liquid interface, it undergoes a chemical reaction with the absorbent flowing in the tube side. As shown in Figure 6, the concentration of the absorbent at the gas–liquid interface decreases significantly due to the substantial consumption by the chemical absorption reaction with CO2. In contrast, the absorbent farther from the gas–liquid interface retains a relatively high concentration, as it cannot react with CO2 immediately due to the slower diffusion rate of CO2. Additionally, under the same operating conditions, the concentration of MEA, PG, and [EMIM][Ac] decreases from 1600 mol/m3 to 755 mol/m3, 766 mol/m3, and 921 mol/m3, respectively. This phenomenon reflects the relative CO2 removal performance of the absorbents, with MEA exhibiting the best performance, followed by PG, and [EMIM][Ac] showing the lowest performance among the absorbents studied. Furthermore, along the axial direction of the membrane module, the concentration of the absorbent gradually decreases as it moves through the tube side. That is because the gaseous CO2 continuously diffuses into the liquid phase and reacts chemically with the absorbent as it progresses along the tube.
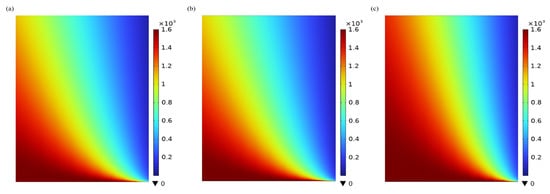
Figure 6.
Concentration distribution of (a) MEA; (b) PG; and (c) [EMIM][Ac]. CCO2 = 1 mol/m3, CL = 1600 mol/m3, Vg = 0.4 m/s, VL = 1 m/s, T = 303.15 K, p = 0.1 MPa.
3.3. Influence of Reaction Heat on CO2 Removal Efficiency
The reaction between CO2 and the studied absorbent is exothermic, leading to an increase in the liquid phase temperature. Figure 7 shows the axial temperature distributions of the three absorbents at an inlet temperature of 303.15 K, with temperature increases ranging from 2 to 15 K at the outlet. The maximum temperatures at the outlet for MEA, PG, and [EMIM][Ac] are 304.8 K, 313 K, and 318 K, respectively. The variation in temperature increase among the different absorbents is influenced by their specific heat capacities and the energy released during the absorption reaction, with reaction enthalpy being the primary contributor of the temperature rise. As the reaction occurs at the gas–liquid interface and the reactants move axially along with the absorbent, the thermal energy released by the chemical reaction gradually accumulates along the length of the membrane contactor, resulting in an overall increase in temperature. The radial temperature gradient in the three absorbents is negligible due to efficient heat dissipation facilitated by the liquid flow.
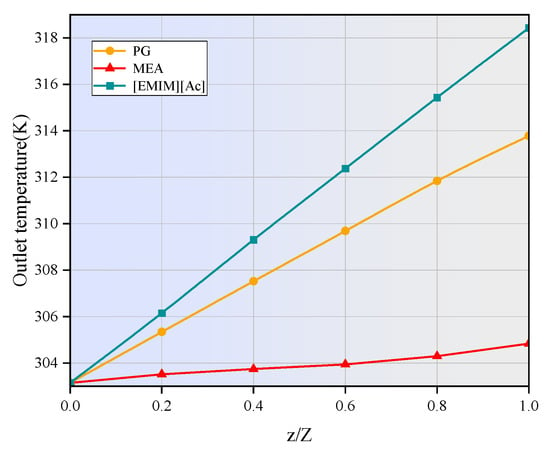
Figure 7.
Axial temperature distribution in the tube side. CCO2 = 1 mol/m3, CL = 1600 mol/m3, Vg = 0.4 m/s, VL = 1 m/s, T = 303.15 K, p = 0.1 MPa.
The effect of reaction heat on the absorption performance of MEA, PG, and [EMIM][Ac] is illustrated in Figure 8. The results indicate that the CO2 removal efficiency predicted by the non-isothermal model is superior to that of the isothermal model. The reaction between CO2 and the three absorbents is reversible, which releases heat during absorption and absorbs heat during desorption. The increase in temperature along the membrane length intensifies molecular motion in the absorption liquid, leading to a higher frequency of molecular collisions. This enhances the mass transfer rate of CO2, allowing it to dissolve more rapidly into the absorption liquid and thereby increase the CO2 absorption rate. Additionally, the reaction rate constant increases with temperature, as described by the Arrhenius Equation, further promoting the CO2 reaction rate. Figure 8 also demonstrates that the CO2 removal efficiency is highly dependent on the membrane module length. As the membrane module length increases from 100 mm to 500 mm, the CO2 removal efficiency improves from 50.4% to 95.6% for MEA, from 50.6% to 95.7% for PG, and from 50.8% to 93.2% for [EMIM][Ac], respectively. Longer membrane modules provide extended contact time and a larger surface area, which contribute to a higher CO2 removal efficiency.
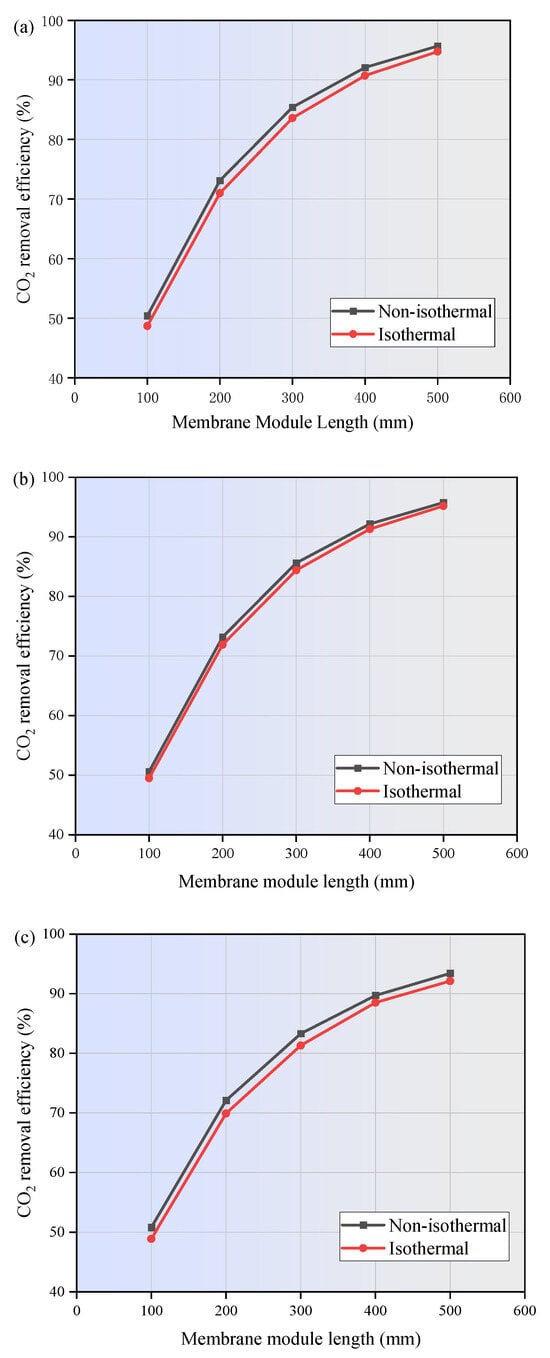
Figure 8.
Effect of reaction heat on the absorption properties of (a) MEA; (b) PG; and (c) [EMIM][Ac]. CCO2 = 1 mol/m3, CL = 1600 mol/m3, Vg = 0.4 m/s, VL = 1 m/s, T = 303.15 K, p = 0.1 MPa.
3.4. Effect of Gas Flow Rate and CO2 Inlet Concentration on CO2 Removal
The effect of gas velocity on CO2 removal efficiency in the hollow fiber membrane contactor was investigated across a gas velocity range of 0.2 m/s to 1 m/s, with the results shown in Figure 9. As shown, the CO2 removal efficiency for all three absorbents decreases as the gas flow rate increases. Specifically, the CO2 removal efficiency decreases from 96.6% to 54.8% for MEA, from 96.9% to 55.7% for PG, and from 76.1% to 28.9% for [EMIM][Ac]. At a given liquid phase flow rate, increasing the gas phase flow rate results in a gradual decline in CO2 removal efficiency. This is because a higher gas phase flow rate significantly reduces the residence time of the gas within the membrane contactor. As a result, CO2 in the flue gas has insufficient time to diffuse into the membrane tube side to react with the absorption liquid. This results in a higher CO2 concentration at the outlet of the membrane contactor, ultimately reducing the overall removal efficiency.
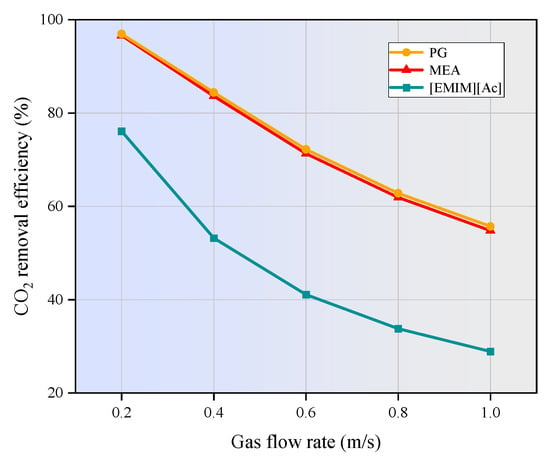
Figure 9.
Effect of inlet gas flow rate on CO2 removal efficiency. CCO2 = 1 mol/m3, CL = 1600 mol/m3, VL = 1 m/s, T = 303.15 K, p = 0.1 MPa.
Figure 10 illustrates the variation in CO2 removal efficiency with changing CO2 inlet concentrations.
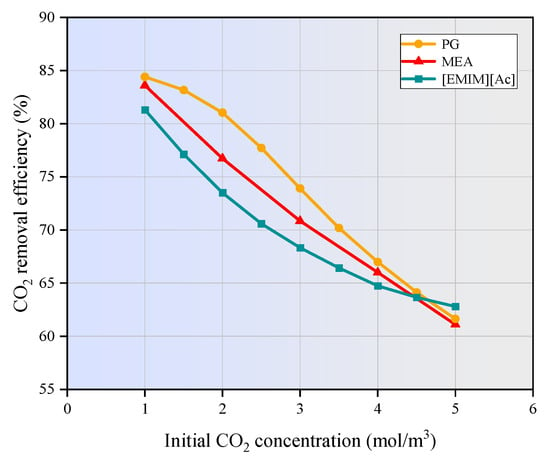
Figure 10.
Effect of inlet CO2 concentration on absorption properties of the liquid phase. CL = 1600 mol/m3, Vg = 0.4 m/s, VL = 1 m/s, T = 303.15 K, p = 0.1 MPa.
The liquid phase flow rate was maintained at 1 m/s, the gas phase flow rate at 0.4 m/s, and the CO2 concentration in the inlet gas ranged from 1 mol/m3 to 5 mol/m3. As depicted in Figure 10, the CO2 removal efficiency gradually decreases as the CO2 inlet concentration increases. Higher CO2 concentrations intensify the concentration gradient between the shell and tube sides of the membrane contactor, causing more CO2 to diffuse into the liquid phase and react with the absorbent. When the flow rate of the absorption liquid is constant, the absorbent becomes insufficient to fully capture the increased CO2 load, resulting in a decrease in CO2 removal efficiency.
3.5. Effect of Liquid Flow Rate on CO2 Removal
Figure 11 illustrates the relationship between the CO2 removal efficiency and liquid flow rate. As the liquid flow rate increases from 1 m/s to 5 m/s, the CO2 removal efficiency gradually increases from 83.6 to 84.1% for MEA, from 84.4% to 84.9% for PG, and from 81.3% to 83.2% for [EMIM][Ac], respectively. A higher liquid flow rate enhances the turbulent disturbance of the absorbent, which allows the reaction products of CO2 and the absorbent to diffuse quickly into the bulk liquid and be removed. Additionally, it replenishes the consumed absorbent at the gas–liquid interface more promptly, increasing the CO2 concentration gradient between the gas and liquid phases, thereby facilitating the diffusion of CO2 into the liquid phase. These factors comprehensively lead to an improvement in CO2 removal efficiency.
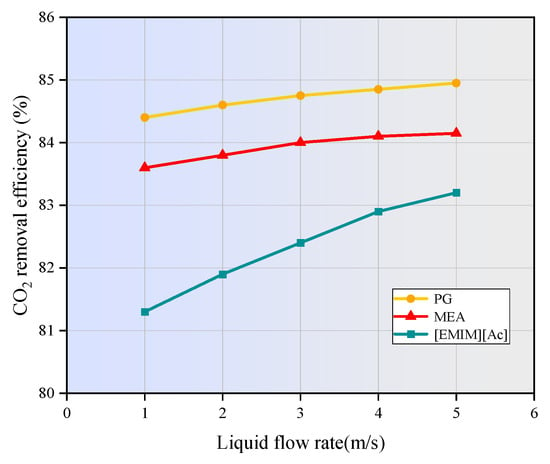
Figure 11.
Effect of absorbent flow rate on absorption properties of the liquid phase. CCO2 = 1 mol/m3, CL = 1600 mol/m3, Vg = 0.4 m/s, T = 303.15 K, p = 0.1 MPa.
It can also be observed form Figure 11 that, at a given liquid flow rate, the absorption efficiency of the chemical absorbents PG and MEA is significantly higher than that of [EMIM][Ac]. PG exhibits the highest absorption efficiency, which, according to Yan et al. [41], is due to its strong affinity for CO2 and efficient mass transfer properties. MEA is slightly less efficient than PG due to differences in reaction dynamics. In contrast, [EMIM][Ac] demonstrates the lowest absorption efficiency. This is likely because its combination of physical and chemical absorption mechanisms is less effective, and its higher viscosity increases mass transfer resistance.
3.6. Effect of Absorbent Concentration on CO2 Removal
Figure 12 shows the effect of absorbent concentration on CO2 removal efficiency. Obviously, increasing the concentration of the chemical absorbent in a hollow fiber membrane contactor significantly enhances CO2 removal from the flue gas. Higher absorbent concentrations provide more reactive components, enabling faster and more efficient reactions with CO2 as it diffuses through the microporous membrane into the liquid phase. This rapid reaction reduces the CO2 concentration on the liquid side, thereby creating a greater concentration gradient that drives additional CO2 from the gas phase into the liquid. Consequently, the dissolution rate of CO2 in the absorbent increases, leading to an improvement in overall CO2 removal efficiency. However, it is important to balance the absorbent concentration with operational factors such as viscosity and potential pressure drop to ensure the optimal performance of the membrane contactor [42]. In contrast to Figure 8, the CO2 removal efficiency of [emim][Ac] is significantly lower than that of MEA and PG. This can be attributed to the slower reaction rate of [emim][Ac], and the fact that more stay time is needed to achieve the same efficiency as MEA and PG [43].
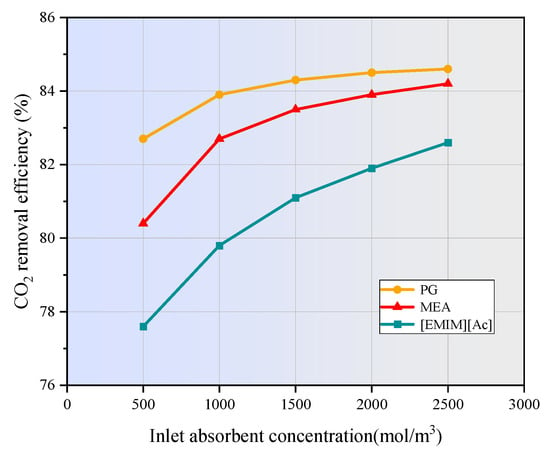
Figure 12.
Effect of absorbent concentration on CO2 removal efficiency. CCO2 = 1 mol/m3, Vg = 0.3 m/s, VL = 0.1 m/s, T = 303.15 K, p = 0.1 MPa.
3.7. Effect of Membrane Porosity on CO2 Removal
Figure 13 shows the effect of hollow fiber membrane porosity on the CO2 absorption performance of MEA, PG, and [EMIM][Ac] under the non-wetting operation mode. The CO2 removal efficiency is enhanced with increasing membrane porosity. Specifically, when the membrane porosity increases from 0.1 to 0.9, the removal efficiency for MEA improves from 10.5% to approximately 95.6%, from 10.6% to 99.1% for PG, and from 11.5% to around 93.5% for [EMIM][Ac], respectively. This enhancement is attributed to the fact that higher porosity results in a greater effective diffusion coefficient of CO2 within the membrane pores. Consequently, the mass-transfer resistance is reduced, and CO2 diffuses more rapidly and efficiently through the membrane, thereby improving the overall separation efficiency. However, excessively high porosity may decrease the membrane wettability, making it easier for solvents to penetrate the membrane pores, which can increase mass transfer resistance and potentially counteract the benefits of higher porosity. Furthermore, increasing porosity can also compromise the structural integrity of the membrane, reducing its self-supporting ability. This can make membrane fabrication more challenging and affect the long-term stability and durability of the membrane contactor [44]. Therefore, the porosity should be optimized to balance the improvement in CO2 removal efficiency with potential challenges related to membrane wettability and structural integrity.
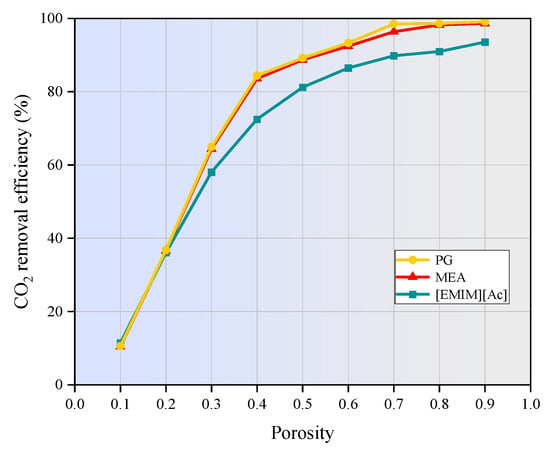
Figure 13.
Effect of membrane porosity on CO2 removal efficiency. CCO2 = 1 mol/m3, CL = 1600 mol/m3, Vg = 1 m/s, VL = 0.1 m/s, T = 303.15 K, p = 0.1 MPa.
4. Conclusions
In this study, the finite element method was applied to numerically investigate the CO2 separation by three typical absorbents in a PVDF hollow fiber membrane contactor. The performance of the non-isothermal model was compared with that of the isothermal model. The effects of operating parameters on CO2 removal efficiency were studied. The main conclusion can be drawn as follows:
- (1)
- The temperatures along the membrane contactor length for three studied absorbents all show an upward trend, with an increase of 2 to 15 K. This temperature increase intensifies the molecular motion in the absorbent, leading to a higher frequency of molecular collisions. Consequently, the mass transfer of CO2 is enhanced, allowing it to dissolve more rapidly into the absorption liquid and thereby increasing the CO2 absorption rate.
- (2)
- As the gas flow rate and CO2 inlet concentration increase, the CO2 removal efficiency decreases significantly. When the gas velocity increases from 1m/s to 5m/s, the CO2 removal efficiency of MEA and PG is decreased by 41.8% and 41.2%, respectively. [EMIM][Ac] is more susceptible to the influence of gas velocity, and the corresponding CO2 removal efficiency is decreased by nearly 47%. When the CO2 inlet concentration increases from 1 mol/m3 to 5 mol/m3, the CO2 removal efficiency of three absorption systems are decreased by around 20%.
- (3)
- The increase in liquid velocity and absorbent concentration has a limited positive effect on CO2 removal. When the liquid velocity increases from 1 m/s to 5 m/s, the CO2 removal efficiency of MEA, PG, and [EMIM][Ac] is only increased by 0.5%, 0.5%, and 1.9%. While the absorbent concentration increased from 500 mol/m3 to 2500 mol/m3, the CO2 removal rates of MEA, PG, and [EMIM][Ac] is increased by 3.8%, 1.9%, and 5%.
- (4)
- When the membrane length increases from 100 mm to 500 mm, the CO2 removal efficiency of MEA, PG, and [EMIM][Ac] is increased from 50% to 95.7%, 95.7%, and 93.2%. When the porosity increases from 0.1 to 0.9, the CO2 removal efficiency of MEA, PG, and [EMIM][Ac] is increased by 85.1%, 88%, and 82% respectively.
- (5)
- In this study, PG exhibits the highest absorption capacity, followed by MEA and [EMIM][Ac], and [EMIM][Ac] is more sensitive to changes in various parameters compared to the other two absorbents.
Author Contributions
Y.J.: writing—original draft, methodology, software, and investigation; L.W.: writing—review and editing, conceptualization, and project administration; J.B.: validation, formal analysis, and visualization; W.Z.: validation, investigation, and software; H.Z.: formal analysis, investigation, and visualization; Y.L.: writing—review and editing, funding acquisition, supervision, and methodology; X.C.: investigation and data curation. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Natural Science Foundation of Shandong Province (No. ZR2021ME174).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gkotsis, P.; Peleka, E.; Zouboulis, A. Membrane-Based Technologies for Post-Combustion CO2 Capture from Flue Gases: Recent Progress in Commonly Employed Membrane Materials. Membranes 2023, 13, 898. [Google Scholar] [CrossRef] [PubMed]
- IEA. 2020. Available online: https://www.iea.org/reports/energy-technology-perspectives-2020 (accessed on 15 January 2024).
- Li, J.; Zhang, H.D.; Gao, Z.P.; Fu, J.; Ao, W.Y.; Dai, J.J. Experimental and Theoretical Studies on Mass Transfer Performance for CO2 Absorption into Aqueous N,N-Dimethylethanolamine Solution in the Polytetrafluoroethylene Hollow-Fiber Membrane Contactor. Ind. Eng. Chem. Res. 2018, 57, 16862–16874. [Google Scholar]
- Miroshnichenko, D.; Shalygin, M.; Bazhenov, S. Simulation of the Membrane Process of CO2 Capture from Flue Gas via Commercial Membranes While Accounting for the Presence of Water Vapor. Membranes 2023, 13, 692. [Google Scholar] [CrossRef]
- Li, F.; Lv, Y.; Bi, J.; Zhang, H.; Zhao, W.; Su, Y.; Du, T.; Mu, J. Environmental Impact Evaluation of CO2 Absorption and Desorption Enhancement by Membrane Gas Absorption: A Life Cycle Assessment Study. Energies 2024, 17, 2371. [Google Scholar] [CrossRef]
- Mu, J.; Bi, J.; Lv, Y.; Su, Y.; Zhao, W.; Zhang, H.; Li, F.; Du, T.; Zhou, H. Techno-economic evaluation on solar-assisted post-combustion CO2 capture in hollow fiber membrane contactors. Energies 2024, 17, 2139. [Google Scholar] [CrossRef]
- Lu, G.; Wang, Z.; Bhatti, U.H.; Fan, X. Recent progress in carbon dioxide capture technologies: A review. Clean Energy Sci. Technol. 2023, 1, 32. [Google Scholar] [CrossRef]
- Lv, Y.; Yu, X.; Jia, J.; Tu, S.; Yan, J.; Dahlquist, E. Fabrication and Characterization of Superhydrophobic Polypropylene Hollow Fiber Membranes for Carbon Dioxide Absorption. Appl. Energy 2012, 1, 167–174. [Google Scholar] [CrossRef]
- Tran, M.L.; Nguyen, C.H.; Chu, K.-Y.; Juang, R.-S. A Simplified Kinetic Modeling of CO2 Absorption into Water and Monoethanolamine Solution in Hollow-Fiber Membrane Contactors. Membranes 2023, 13, 494. [Google Scholar] [CrossRef] [PubMed]
- Lv, Y.; Yu, X.; Tu, S.; Yan, J.; Dahlquist, E. Experimental studies on simultaneous removal of CO2 and SO2 in a polypropylene hollow fiber membrane contactor. Appl. Energy 2012, 97, 283–288. [Google Scholar] [CrossRef]
- Sumayli, A.; Mahdi, W.A.; Alshahrani, S.M. Numerical evaluation of CO2 molecular removal from CO2/N2 mixture utilizing eco-friendly [emim][OAc] and [emim][MeSO4] ionic liquids inside membrane contactor. J. Mol. Liq. 2024, 396, 123958. [Google Scholar] [CrossRef]
- Nakhjiri, A.T.; Heydarinasab, A. Computational simulation and theoretical modeling of CO2 separation using EDA, PZEA and PS absorbents inside the hollow fiber membrane contactor. J. Ind. Eng. Chem. 2019, 78, 106–115. [Google Scholar] [CrossRef]
- Nakhjiri, A.T.; Heydarinasab, A.; Bakhtiari, O.; Mohammadi, T. The effect of membrane pores wettability on CO2 removal from CO2/CH4 gaseous mixture using NaOH, MEA and TEA liquid absorbents in hollow fiber membrane contactor. Chin. J. Chem. Eng. 2018, 26, 1845–1861. [Google Scholar] [CrossRef]
- Nakhjiri, A.T.; Heydarinasab, A. Efficiency evaluation of novel liquid potassium lysinate chemical solution for CO2 molecular removal inside the hollow fiber membrane contactor: Comprehensive modeling and CFD simulation. J. Mol. Liq. 2020, 297, 111561. [Google Scholar] [CrossRef]
- Nakhjiri, A.T.; Heydarinasab, A.; Bakhtiari, O.; Mohammadi, T. Numerical simulation of CO2/H2S simultaneous removal from natural gas using potassium carbonate aqueous solution in hollow fiber membrane contactor. J. Environ. Chem. Eng. 2020, 8, 104130. [Google Scholar] [CrossRef]
- Ao, D.; Ma, G.; Zang, C.; Qin, Y.; Qi, Y.; Wan, W. A Numerical Study on Removal of CO2 by 2-(tert-Butylamino) Ethanol in a Hollow Fiber Membrane Contactor. Ind. Eng. Chem. Res. 2022, 61, 3685–3693. [Google Scholar] [CrossRef]
- Hajilary, N.; Rezakazemi, M. CFD modeling of CO2 capture by water-based nanofluids using hollow fiber membrane contactor. Int. J. Greenh. Gas Control. 2018, 77, 88–95. [Google Scholar] [CrossRef]
- Ansaripour, M.; Haghshenasfard, M.; Moheb, A. Experimental and numerical investigation of CO2 absorption using nanofluids in a hollow-fiber membrane contactor. Chem. Eng. Technol. 2018, 41, 367–378. [Google Scholar] [CrossRef]
- Rezakazemi, M.; Darabi, M.; Soroush, E.; Mesbah, M. CO2 absorption enhancement by water-based nanofluids of CNT and SiO2 using hollow-fiber membrane contactor. Sep. Purif. Technol. 2019, 210, 920–926. [Google Scholar] [CrossRef]
- Vaezi, M.; Sanaeepur, H.; Amooghin, A.E.; Nakhjiri, A.T. Modeling of CO2 absorption in a membrane contactor containing 3-diethylaminopropylamine (DEAPA) solvent. Int. J. Greenh. Gas Control. 2023, 127, 103938. [Google Scholar] [CrossRef]
- Bozonc, A.C.; Cormos, A.M.; Dragan, S.; Dinca, C.; Cormos, C.C. Dynamic Modeling of CO2 Absorption Process Using Hollow-Fiber Membrane Contactor in MEA Solution. Energies 2022, 15, 7241. [Google Scholar] [CrossRef]
- Xia, J.; Zhang, Z.; Wang, L.; Wang, F.; Miao, H.; Zhang, H.; Xia, L.; Yuan, J. Performance evaluation and optimization of hollow fiber membrane contactors for carbon dioxide absorption: A comparative study of ammonia, ethanolamine, and diethanolamine solvents. J. Environ. Chem. Eng. 2023, 11, 111354. [Google Scholar] [CrossRef]
- Bozonc, A.C.; Sandu, V.C.; Cormos, C.C.; Cormos, A.M. 3D-CFD Modeling of Hollow-Fiber Membrane Contactor for CO2 Absorption Using MEA Solution. Membranes 2024, 14, 86. [Google Scholar] [CrossRef]
- Sohaib, Q.; Muhammad, A.; Younas, M.; Rezakazemi, M.; Druon-Bocquet, S.; Sanchez-Marcano, J. Rigorous non-isothermal modeling approach for mass and energy transport during CO2 absorption into aqueous solution of amino acid ionic liquids in hollow fiber membrane contactors. Sep. Purif. Technol. 2021, 254, 117644. [Google Scholar] [CrossRef]
- Zaidiza, D.A.; Wilson, S.G.; Belaissaoui, B.; Rode, S.; Castel, C.; Roizard, D.; Favre, E. Rigorous modelling of adiabatic multicomponent CO2 post-combustion capture using hollow fibre membrane contactors. Chem. Eng. Sci. 2016, 145, 45–58. [Google Scholar] [CrossRef]
- Happel, J. Viscous flow relative to arrays of cylinders. AIChE J. 1959, 5, 174–177. [Google Scholar] [CrossRef]
- Faiz, R.; Al-Marzouqi, M. Insights on natural gas purification: Simultaneous absorption of CO2 and H2S using membrane contactors. Sep. Purif. Technol. 2011, 76, 351–361. [Google Scholar] [CrossRef]
- Al-Marzouqi, M.H.; El-Naas, M.H.; Marzouk, S.A.; Al-Zarooni, M.A.; Abdullatif, N.; Faiz, R. Modeling of CO2 absorption in membrane contactors. Sep. Purif. Technol. 2008, 59, 286–293. [Google Scholar] [CrossRef]
- Cao, F.; Gao, H.; Ling, H.; Huang, Y.; Liang, Z. Theoretical modeling of the mass transfer performance of CO2 absorption into DEAB solution in hollow fiber membrane contactor. J. Membr. Sci. 2020, 593, 117439. [Google Scholar] [CrossRef]
- Faiz, R.; Al-Marzouqi, M. Mathematical modeling for the simultaneous absorption of CO2 and H2S using MEA in hollow fiber membrane contactors. J. Membr. Sci. 2009, 342, 269–278. [Google Scholar] [CrossRef]
- Nakhjiri, A.T.; Heydarinasab, A.; Bakhtiari, O.; Mohammadi, T. Experimental investigation and mathematical modeling of CO2 sequestration from CO2/CH4 gaseous mixture using MEA and TEA aqueous absorbents through polypropylene hollow fiber membrane contactor. J. Membr. Sci. 2018, 565, 1–13. [Google Scholar] [CrossRef]
- Ghobadi, J.; Ramirez, D.; Khoramfar, S.; Kabir, M.M.; Jerman, R.; Saeed, M. Mathematical modeling of CO2 separation using different diameter hollow fiber membranes. Int. J. Greenh. Gas Control. 2021, 104, 103204. [Google Scholar] [CrossRef]
- Bakhshali, N.; Tahery, R.; Banazadeh, H. Modelling and simulation of mass transfer in tubular gas-liquid membrane contactors for turbulent flow conditions and comparison of results with laminar flow conditions. Middle-East J. Sci. 2013, 10, 1419–1430. [Google Scholar]
- Lee, H.J.; Kim, M.K.; Park, J.H.; Magnone, E. Temperature and pressure dependence of the CO2 absorption through a ceramic hollow fiber membrane contactor module. Chem. Eng. Process. Process Intensif. 2020, 150, 107871. [Google Scholar] [CrossRef]
- Keshavarz, P.; Fathikalajahi, J.; Ayatollahi, S. Analysis of CO2 separation and simulation of a partially wetted hollow fiber membrane contactor. J. Hazard. Mater. 2008, 152, 1237–1247. [Google Scholar] [CrossRef]
- Paul, S.; Ghoshal, A.K.; Mandal, B. Removal of CO2 by single and blended aqueous alkanolamine solvents in hollow-fiber membrane contactor: Modeling and simulation. Ind. Eng. Chem. Res. 2007, 46, 2576–2588. [Google Scholar] [CrossRef]
- Park, S.W.; Choi, B.S.; Lee, J.W. Chemical absorption of carbon dioxide with triethanolamine in non-aqueous solutions. Korean J. Chem. Eng. 2006, 23, 138–143. [Google Scholar] [CrossRef]
- Lv, B.; Xia, Y.; Shi, Y.; Liu, N.; Li, W.; Li, S. A novel hydrophilic amino acid ionic liquid [C2OHmim][Gly] as aqueous sorbent for CO2 capture. Int. J. Greenh. Gas Control. 2016, 46, 1–6. [Google Scholar] [CrossRef]
- Masoumi, S.; Keshavarz, P.; Ayatollahi, S.; Mehdipour, M.; Rastgoo, Z. Enhanced carbon dioxide separation by amine-promoted potassium carbonate solution in a hollow fiber membrane contactor. Energy Fuels 2013, 27, 5423–5432. [Google Scholar] [CrossRef]
- Zhang, Z.; Yan, Y.; Zhang, L.; Chen, Y.; Ran, J.; Pu, G.; Qin, C. Theoretical study on CO2 absorption from biogas by membrane contactors: Effect of operating parameters. Ind. Eng. Chem. Res. 2014, 53, 14075–14083. [Google Scholar] [CrossRef]
- Yan, S.P.; Fang, M.X.; Zhang, W.F.; Wang, S.Y.; Xu, Z.K.; Luo, Z.Y.; Cen, K.F. Experimental study on the separation of CO2 from flue gas using hollow fiber membrane contactors without wetting. Fuel Process. Technol. 2007, 88, 501–511. [Google Scholar] [CrossRef]
- Zareie-kordshouli, F.; Lashani-zadehgan, A.; Darvishi, P. Comparative evaluation of CO2 capture from flue gas by [Emim][Ac] ionic liquid, aqueous potassium carbonate (without activator) and MEA solutions in a packed column. Int. J. Greenh. Gas Control. 2016, 52, 305–318. [Google Scholar] [CrossRef]
- Yin, Y.; Gao, H.; Liang, Z. Experimental and Numerical Analysis for Improving CO2 Mass Transfer Performance of Blended Solvents in Hollow Fiber Membrane Contactors. Ind. Eng. Chem. Res. 2023, 62, 13458–13469. [Google Scholar] [CrossRef]
- Shirazian, S.; Taghvaie Nakhjiri, A.; Heydarinasab, A.; Ghadiri, M. Theoretical investigations on the effect of absorbent type on carbon dioxide capture in hollow-fiber membrane contactors. PLoS ONE 2020, 15, e0236367. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).