Bi-Objective Optimization of Techno-Economic and Environmental Performance for Membrane-Based CO2 Capture via Single-Stage Membrane Separation
Abstract
1. Introduction
2. Materials and Methods
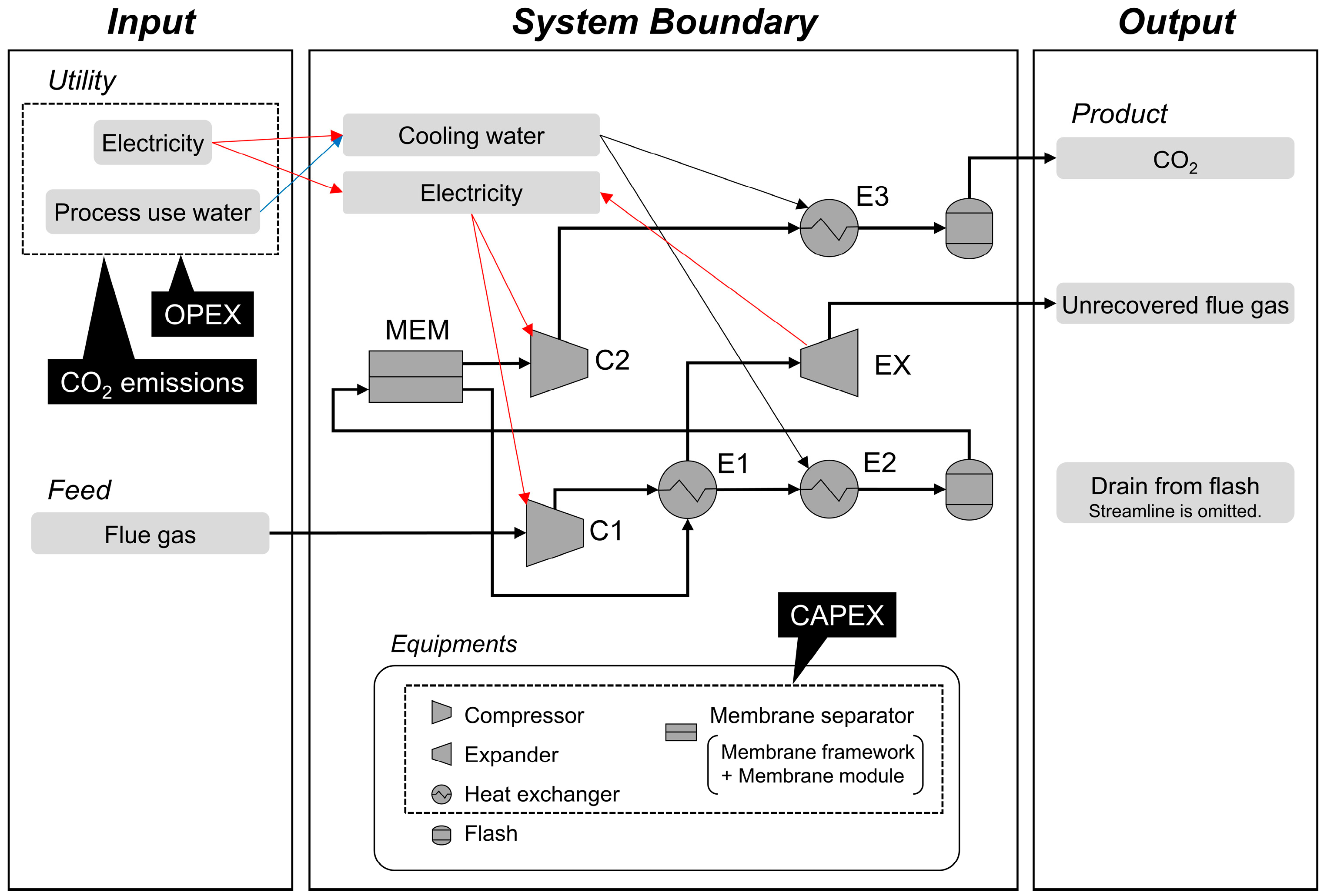
2.1. Boundary and Process Simulation Settings
2.2. Analyses of Evaluation Indexes
2.3. MLB-MOGABO
2.4. Case Study Settings
3. Results
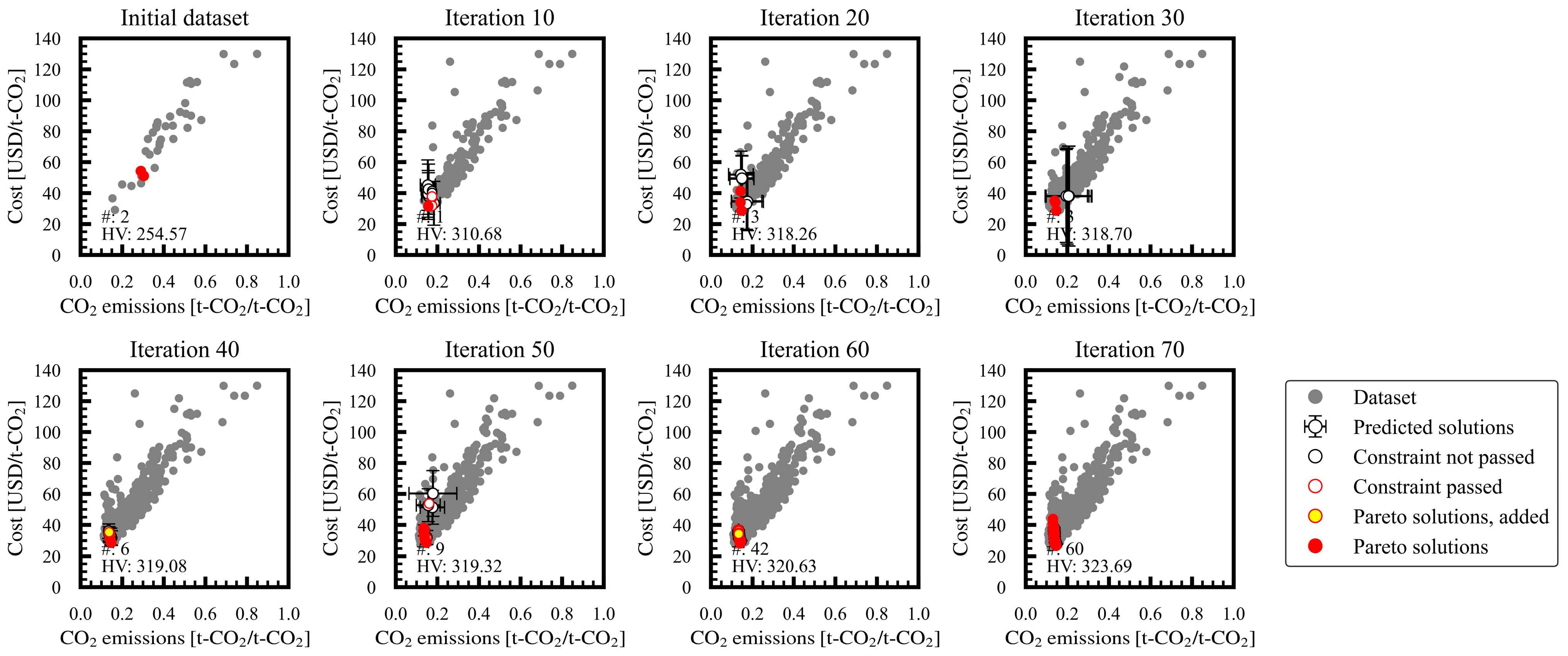
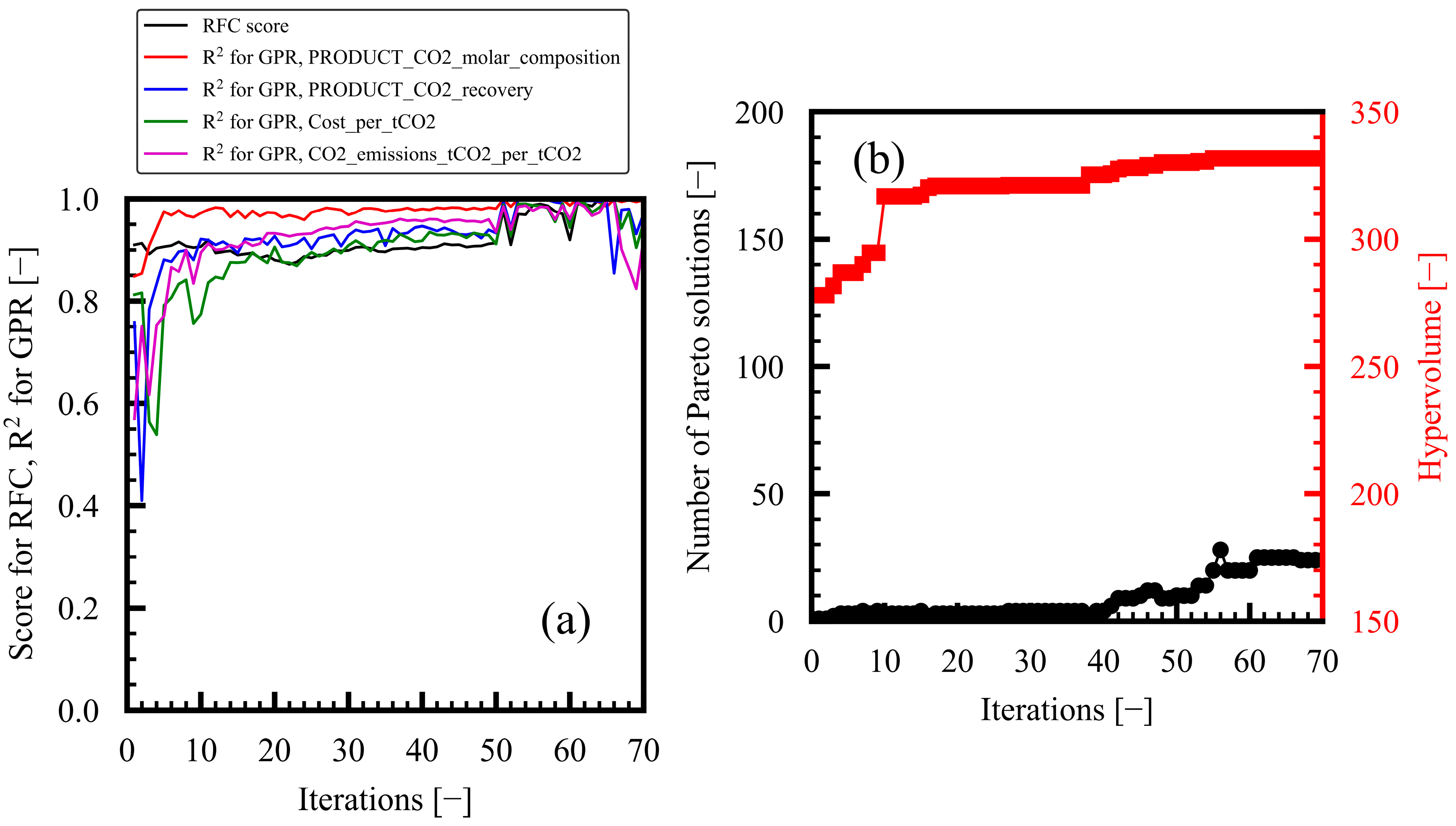
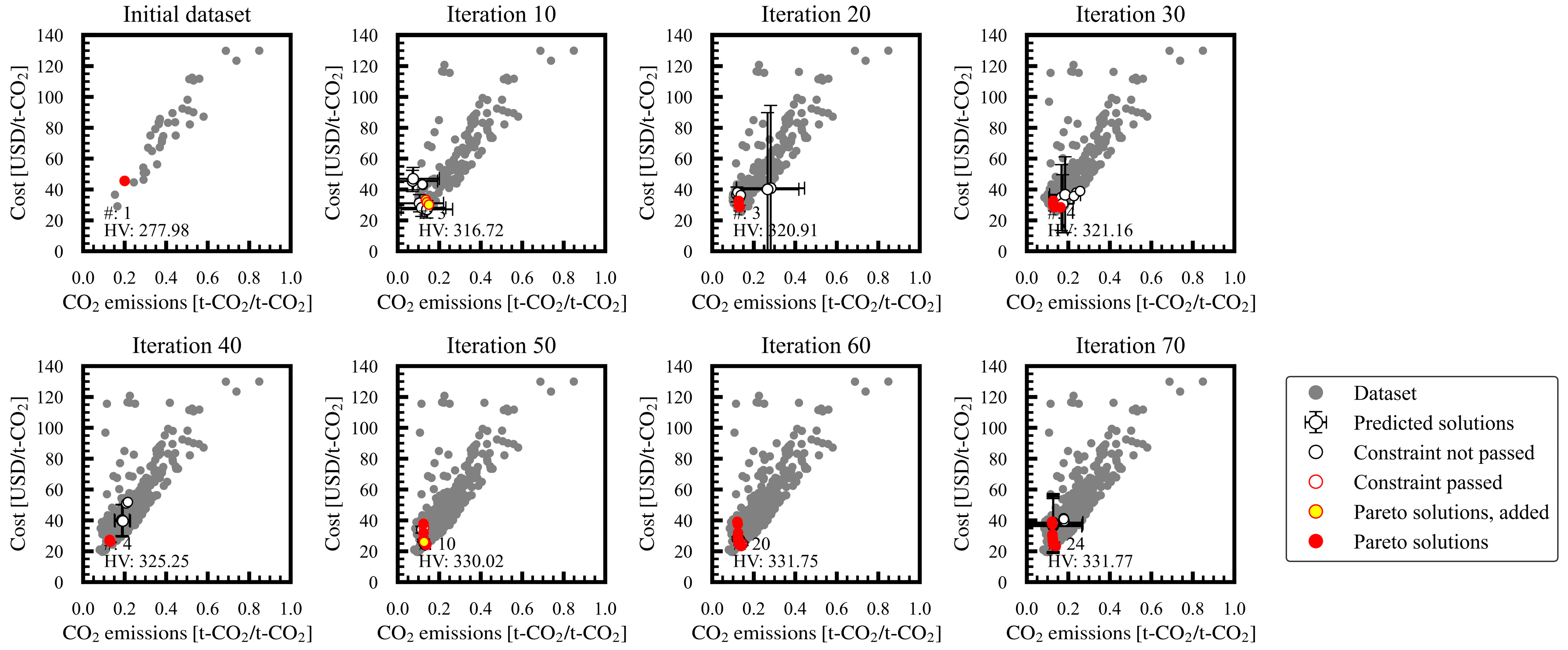
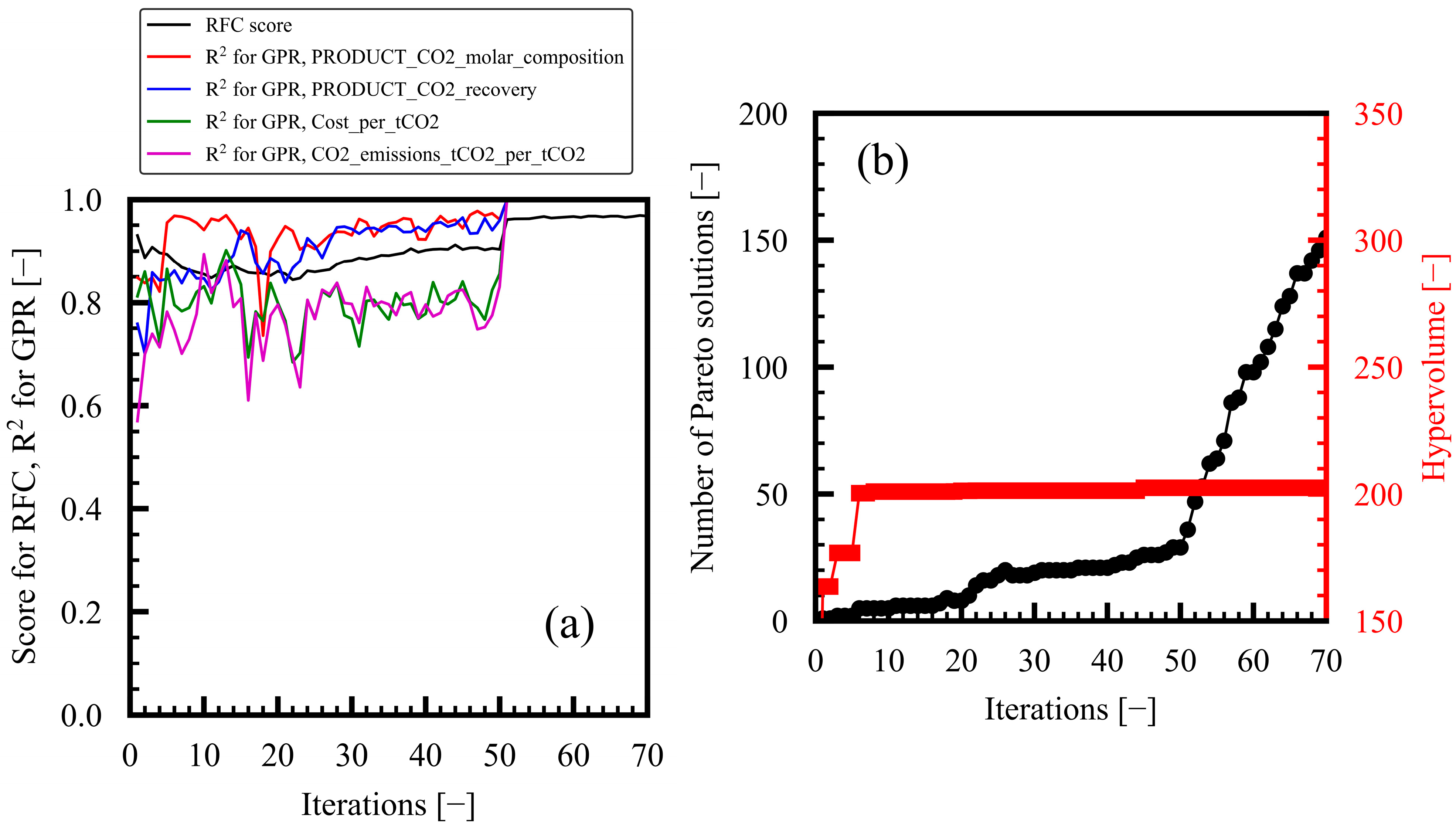
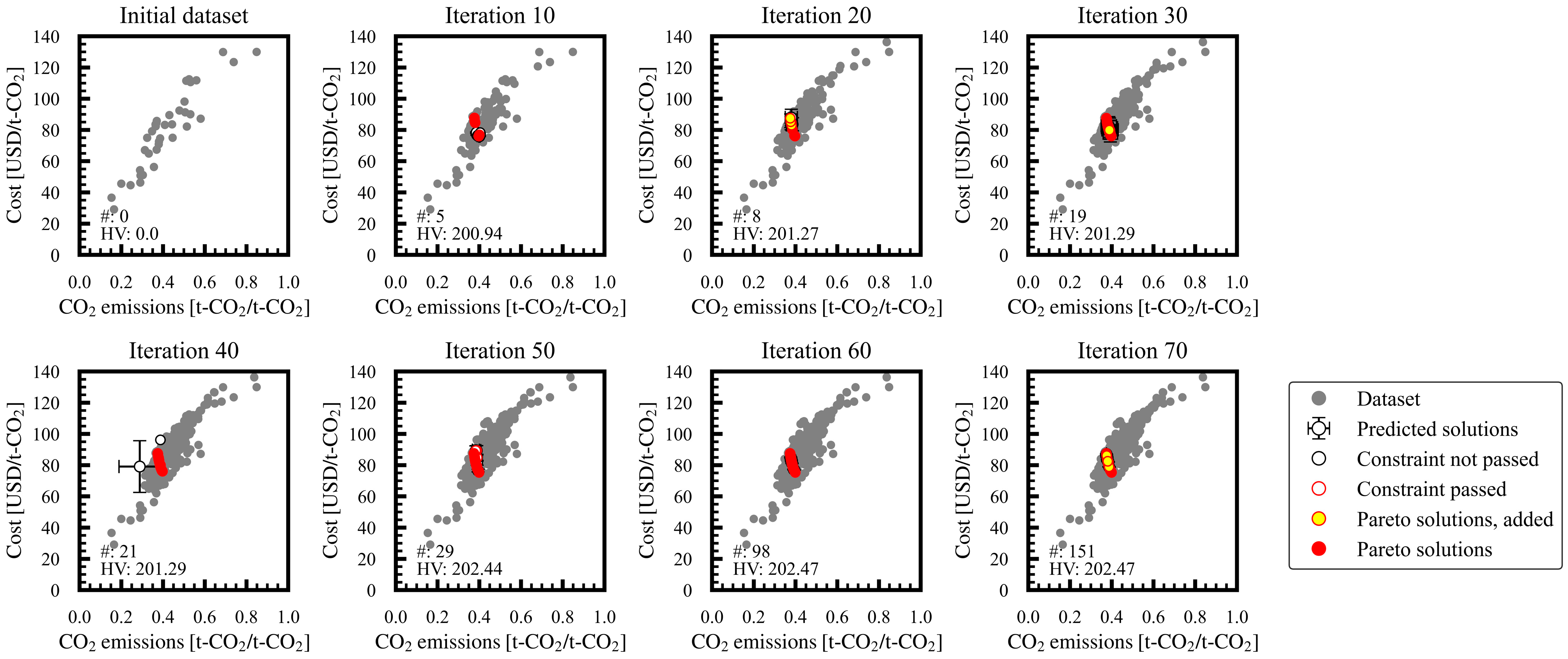
3.1. Progress of Bi-Objective Optimization
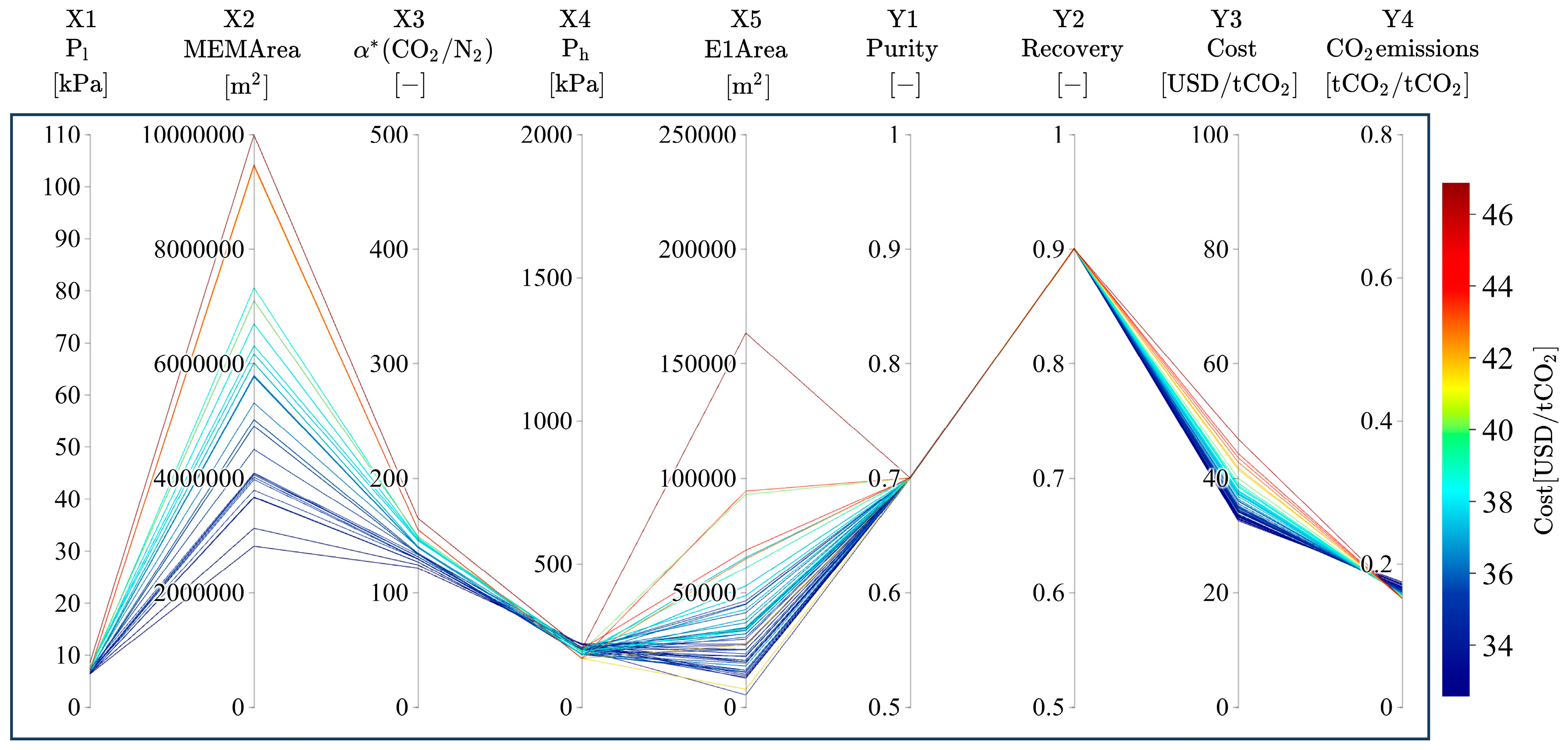
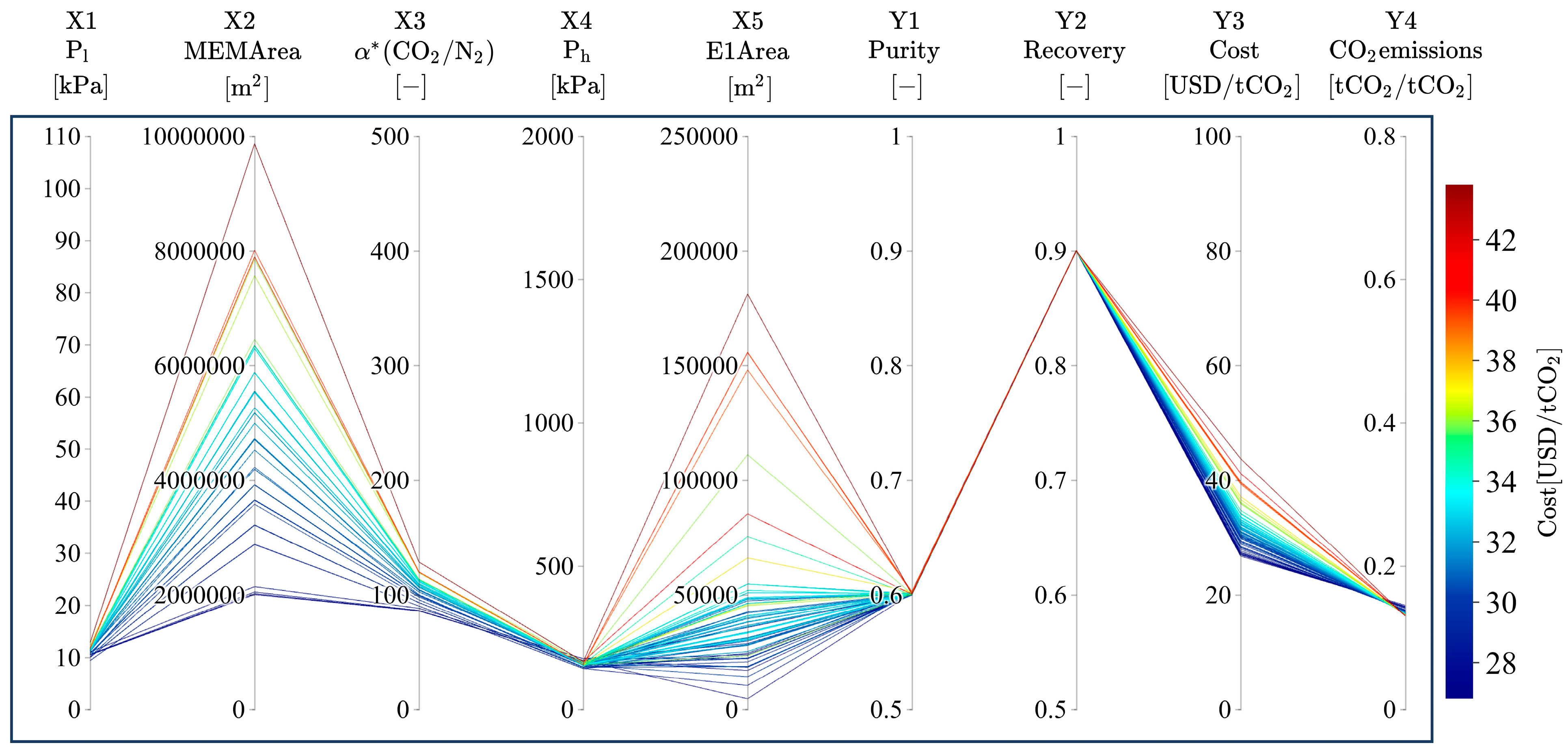
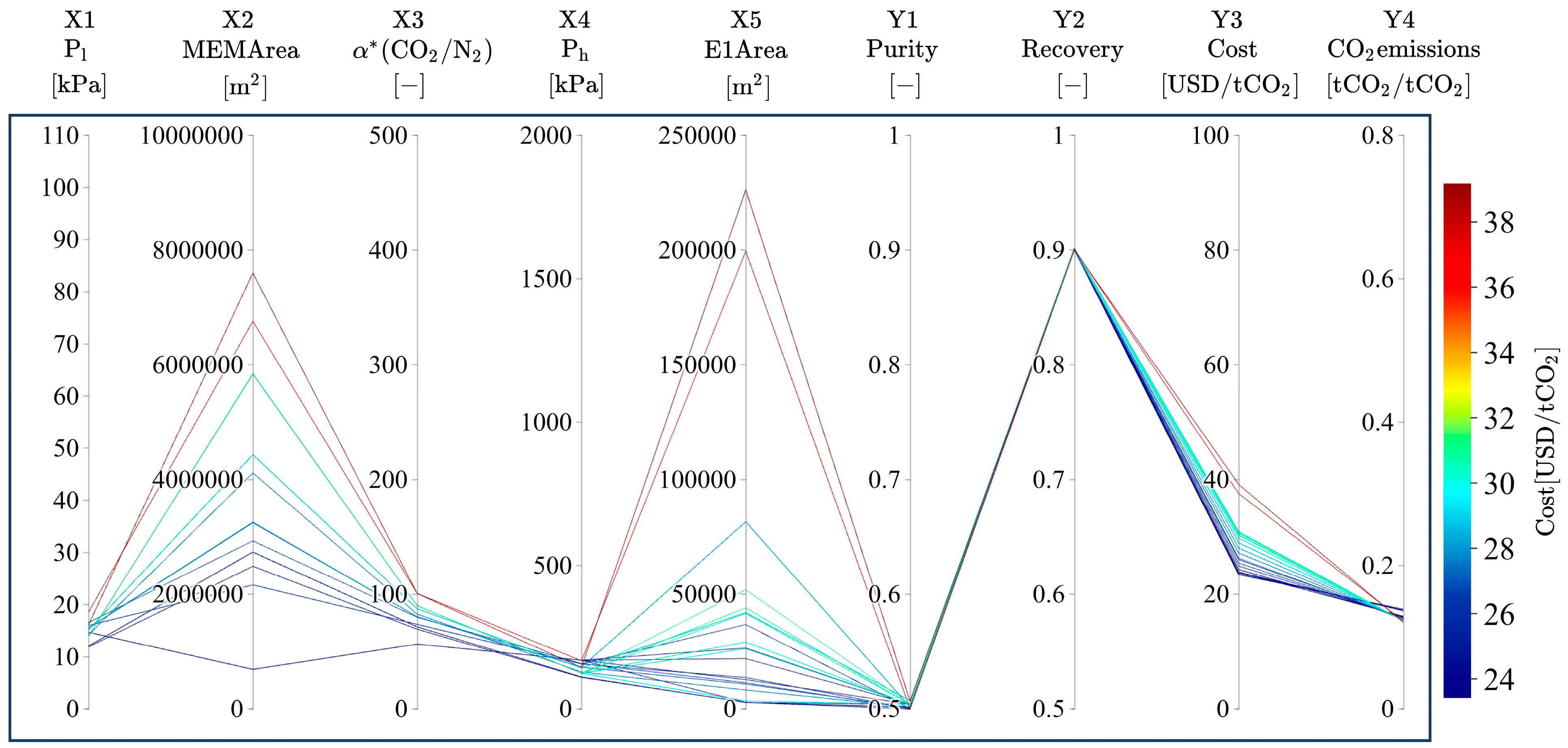
3.2. Trends of Pareto Solutions
3.3. Relationship of Product CO2 Purity with α*(CO2/N2), Ph, Pl, and Dimensionless Numbers
3.4. Relationship of Product CO2 Purity with Membrane Area and Power Consumption
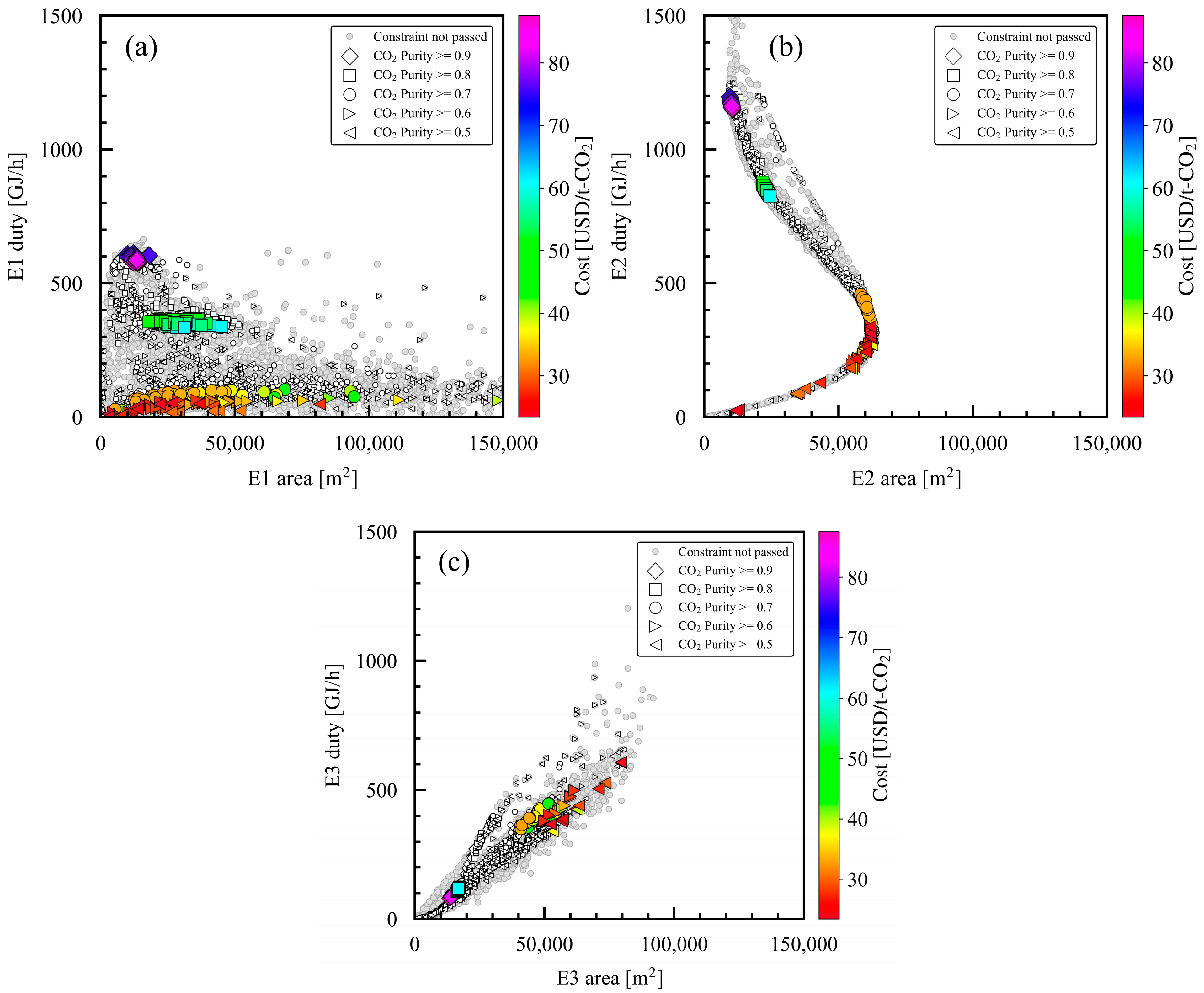
3.5. Relationship of Product CO2 Purity with Area in Heat Exchangers
4. Implications and Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
- The following abbreviations are used in this manuscript:
| Nomenclature | |
| CAPEX | Capital expenditure, USD/t-CO2 |
| CEPCI | Chemical engineering plant cost index |
| CRF | Capital recovery factor |
| CTM | Total module cost, USD |
| FBM | Bare-module factor |
| OPEX | Operational expenditure, USD/t-CO2 |
| Ph | Feed-side pressure, kPa |
| Pl | Permeate-side pressure, kPa |
| Pr | Pressure ratio (Ph/Pl) |
| R2 | Coefficient of determination |
| U-value | Overall heat-transfer coefficient, kW/m2K |
| Equipment | |
| C | Compressor |
| E | Heat exchanger |
| Ex | Expander |
| MEM | Membrane separator |
| Acronyms | |
| ADoE | Adaptive design of experiments |
| CAPCOST | Capital equipment-costing program |
| CCUS | Carbon dioxide capture, utilization, and storage |
| GPR | Gaussian process regression |
| LCA | Life cycle assessment |
| ML | Machine learning |
| MLB-MOGABO | Machine learning-based multi-objective genetic algorithm Bayesian optimization |
| RFC | Random forest classification |
Appendix A. Progress of Bi-Objective Optimization Implemented by MLB-MOGABO

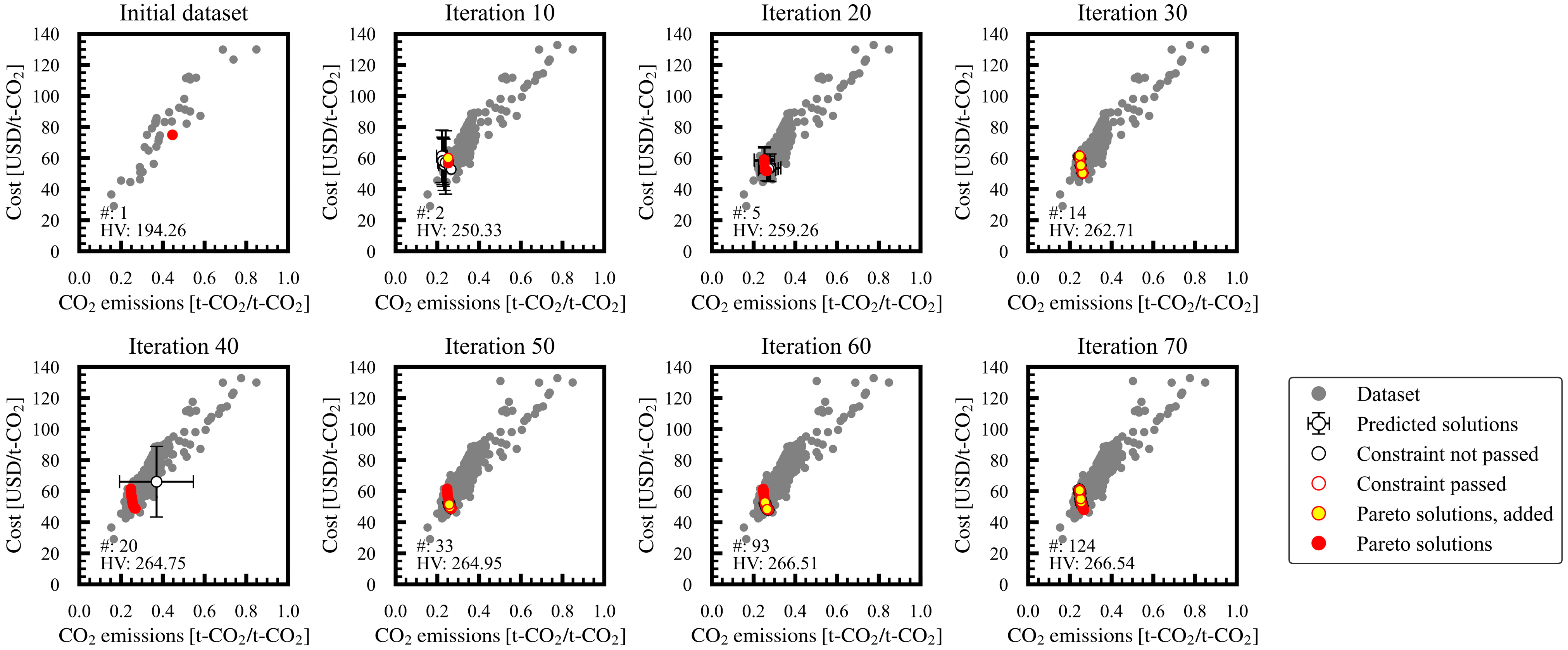

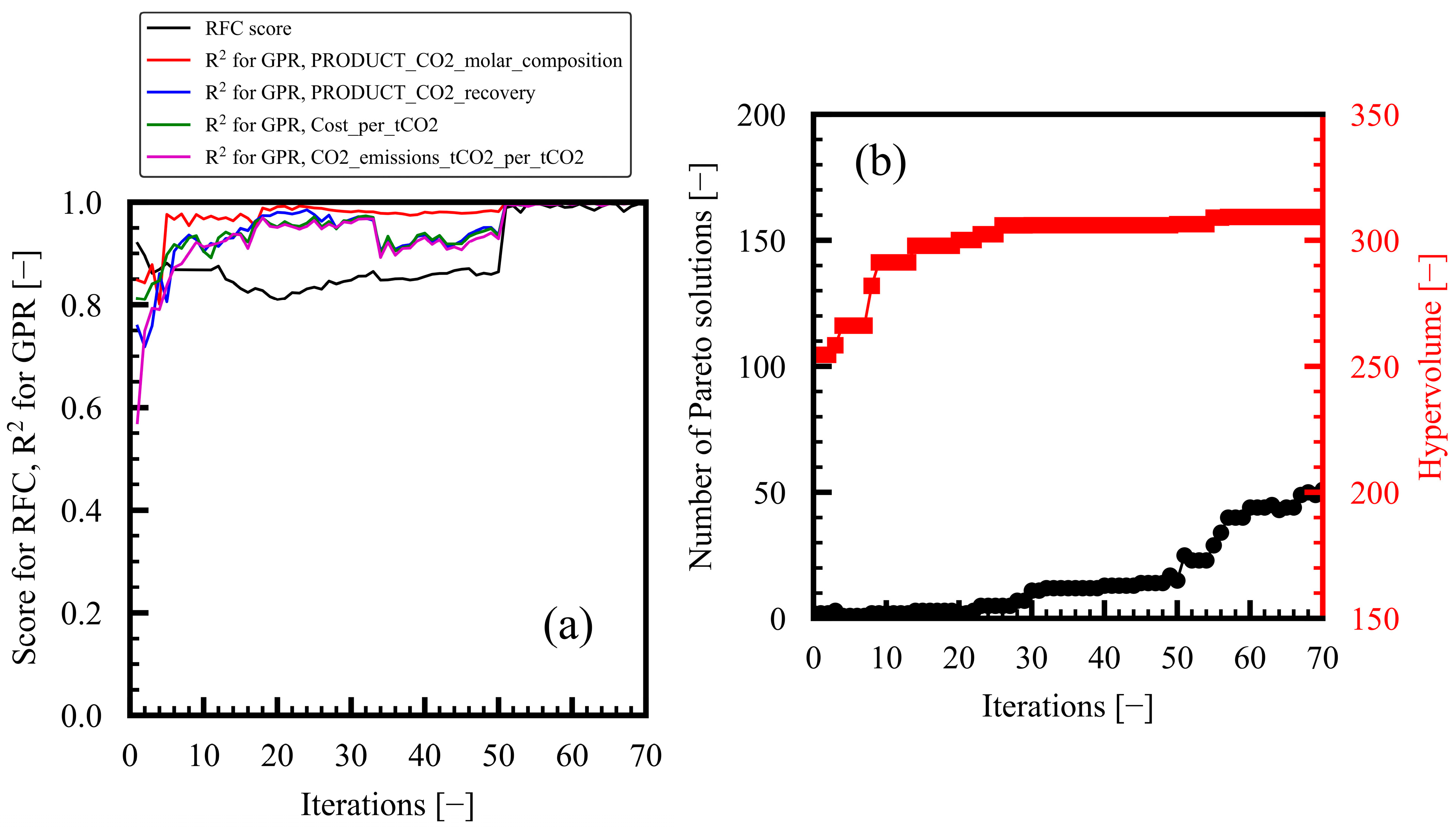

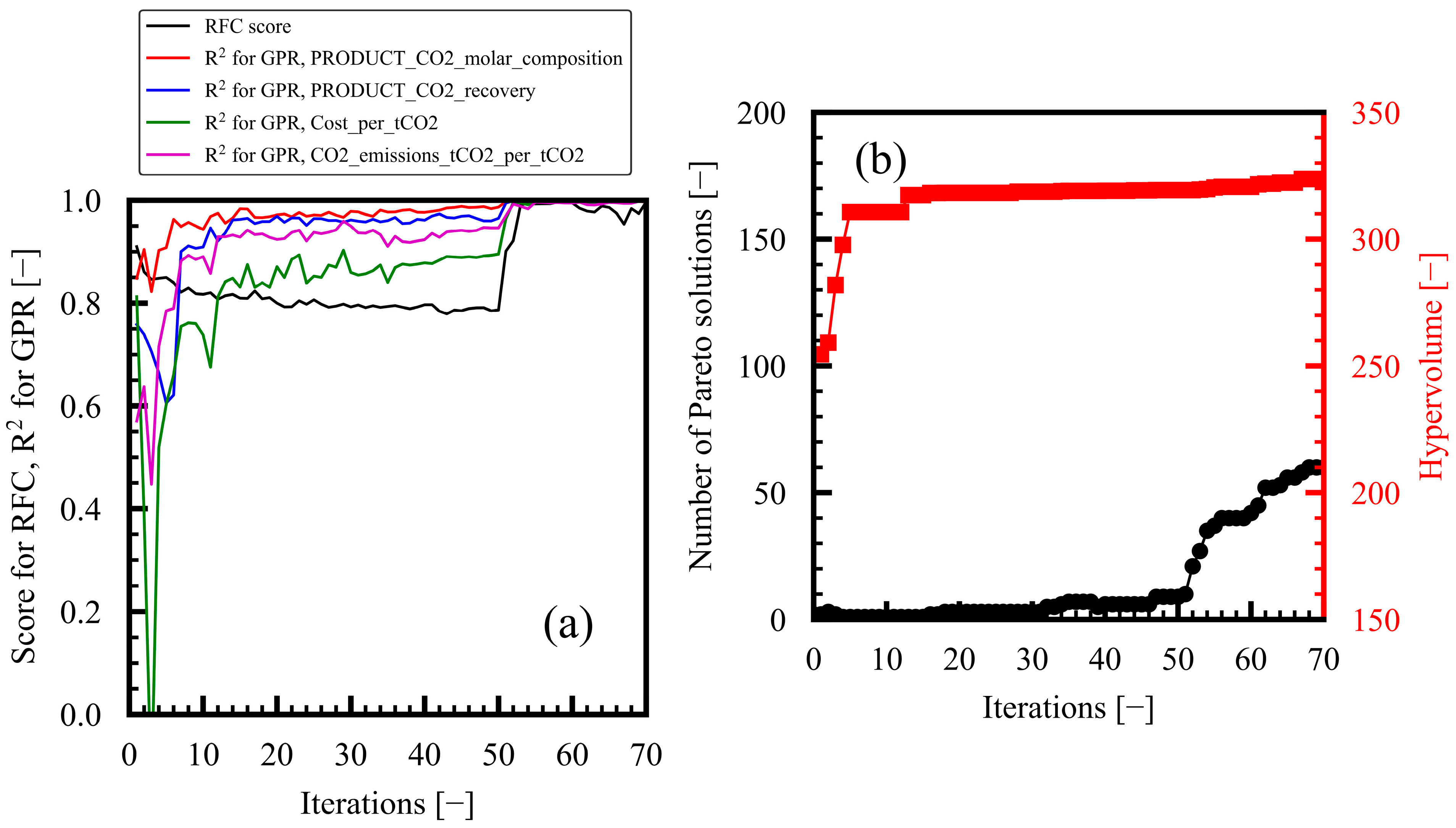
References
- Osman, A.I.; Hefny, M.; Maksoud, M.I.A.A.; Elgarahy, A.M.; Rooney, D.W. Recent advances in carbon capture storage and utilisation technologies: A review. Environ. Chem. Lett. 2021, 19, 797–849. [Google Scholar] [CrossRef]
- Kenarsari, S.D.; Yang, D.L.; Jiang, G.D.; Zhang, S.J.; Wang, J.J.; Russell, A.G.; Wei, Q.; Fan, M.H. Review of recent advances in carbon dioxide separation and capture. RSC. Adv. 2013, 3, 22739–22773. [Google Scholar] [CrossRef]
- Han, Y.; Ho, W.S.W. Moving beyond 90% Carbon Capture by Highly Selective Membrane Processes. Membranes 2022, 12, 399. [Google Scholar] [CrossRef] [PubMed]
- Favre, E. Membrane Separation Processes and Post-Combustion Carbon Capture: State of the Art and Prospects. Membranes 2022, 12, 884. [Google Scholar] [CrossRef] [PubMed]
- Kancherla, R.; Nazia, S.; Kalyani, S.; Sridhar, S. Modeling and simulation for design and analysis of membrane-based separation processes. Comput. Chem. Eng. 2021, 148, 107258. [Google Scholar] [CrossRef]
- Kárászová, M.; Zach, B.; Petrusová, Z.; Cervenka, V.; Bobák, M.; Syc, M.; Izák, P. Post-combustion carbon capture by membrane separation, Review. Sep. Purif. Technol. 2020, 238, 116448. [Google Scholar] [CrossRef]
- Han, Y.; Yang, Y.T.; Ho, W.S.W. Recent Progress in the Engineering of Polymeric Membranes for CO2 Capture from Flue Gas. Membranes 2020, 10, 365. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.Y.; Wu, H.Y.; Wang, Z.; Qiao, Z.H.; Zhao, S.; Wang, J.X. Recent advances on the membrane processes for CO2 separation. Chin. J. Chem. Eng. 2018, 26, 2280–2291. [Google Scholar] [CrossRef]
- Olabi, A.G.; Wilberforce, T.; Elsaid, K.; Sayed, E.T.; Maghrabie, H.M.; Abdelkareem, M.A. Large scale application of carbon capture to process industries—A review. J. Clean. Prod. 2022, 362, 132300. [Google Scholar] [CrossRef]
- Chatziasteriou, C.C.; Kikkinides, E.S.; Georgiadis, M.C. Recent advances on the modeling and optimization of CO2 capture processes. Comput. Chem. Eng. 2022, 165, 107938. [Google Scholar] [CrossRef]
- Tapia, J.F.D.; Lee, J.Y.; Ooi, R.E.H.; Foo, D.C.Y.; Tan, R.R. A review of optimization and decision-making models for the planning of CO2 capture, utilization and storage (CCUS) systems. Sustain. Prod. Consump. 2018, 13, 1–15. [Google Scholar] [CrossRef]
- Hara, N.; Taniguchi, S.; Yamaki, T.; Nguyen, T.T.H.; Kataoka, S. Bi-objective optimization of post-combustion CO2 capture using methyldiethanolamine. Int. J. Greenh. Gas Control 2023, 122, 103815. [Google Scholar] [CrossRef]
- Hara, N.; Taniguchi, S.; Yamaki, T.; Nguyen, T.T.H.; Kataoka, S. Impacts of hydrogen price and carbon dioxide emission factor on bi-objective optimizations of absorption and subsequent methanation processes of carbon dioxide capture, utilization, and storage. J. Clean. Prod. 2024, 456, 142358. [Google Scholar] [CrossRef]
- Shindo, Y.; Hakuta, T.; Yoshitome, H.; Inoue, H. Calculation Methods for Multicomponent Gas Separation by Permeation. Sep. Sci. Technol. 1985, 20, 445–459. [Google Scholar] [CrossRef]
- Merkel, T.C.; Lin, H.Q.; Wei, X.T.; Baker, R. Power plant post-combustion carbon dioxide capture: An opportunity for membranes. J. Membr. Sci. 2010, 359, 126–139. [Google Scholar] [CrossRef]
- Huang, Y.; Merkel, T.C.; Baker, R.W. Pressure ratio and its impact on membrane gas separation processes. J. Membr. Sci. 2014, 463, 33–40. [Google Scholar] [CrossRef]
- Ramasubramanian, K.; Verweij, H.; Ho, W.S.W. Membrane processes for carbon capture from coal-fired power plant flue gas: A modeling and cost study. J. Membr. Sci. 2012, 421, 299–310. [Google Scholar] [CrossRef]
- Li, Q.H.; Wu, H.Y.; Wang, Z.; Wang, J.X. Analysis and optimal design of membrane processes for flue gas CO2 capture. Sep. Purif. Technol. 2022, 298, 121584. [Google Scholar] [CrossRef]
- Xu, J.Y.; Wang, Z.; Qiao, Z.H.; Wu, H.Y.; Dong, S.L.; Zhao, S.; Wang, J.X. Post-combustion CO2 capture with membrane process: Practical membrane performance and appropriate pressure. J. Membr. Sci. 2019, 581, 195–213. [Google Scholar] [CrossRef]
- Vandersluijs, J.P.; Hendriks, C.A.; Blok, K. Feasibility of Polymer Membranes for Carbon-Dioxide Recovery from Flue-Gases. Energy Conv. Manag. 1992, 33, 429–436. [Google Scholar] [CrossRef]
- Micari, M.; Dakhchoune, M.; Agrawal, K.V. Techno-economic assessment of postcombustion carbon capture using high-performance nanoporous single-layer graphene membranes. J. Membr. Sci. 2021, 624, 119103. [Google Scholar] [CrossRef]
- Roussanaly, S.; Anantharaman, R.; Lindqvist, K.; Zhai, H.B.; Rubin, E. Membrane properties required for post-combustion CO2 capture at coal-fired power plants. J. Membr. Sci. 2016, 511, 250–264. [Google Scholar] [CrossRef]
- Mat, N.C.; Lipscomb, G.G. Membrane process optimization for carbon capture. Int. J. Greenh. Gas Control 2017, 62, 1–12. [Google Scholar] [CrossRef]
- Arias, A.M.; Mussati, M.C.; Mores, P.L.; Scenna, N.J.; Caballero, J.A.; Mussati, S.F. Optimization of multi-stage membrane systems for CO2 capture from flue gas. Int. J. Greenh. Gas Control 2016, 53, 371–390. [Google Scholar] [CrossRef]
- Chiwaye, N.; Majozi, T.; Daramola, M.O. On optimisation of N2 and CO2-selective hybrid membrane process systems for post-combustion CO2 capture from coal-fired power plants. J. Membr. Sci. 2021, 638, 119691. [Google Scholar] [CrossRef]
- Ramezani, R.; Randon, A.; Di Felice, L.; Gallucci, F. Using a superstructure approach for techno-economic analysis of membrane processes. Chem. Eng. Res. Des. 2023, 199, 296–311. [Google Scholar] [CrossRef]
- Asadi, J.; Kazempoor, P. Sustainability Enhancement of Fossil-Fueled Power Plants by Optimal Design and Operation of Membrane-Based CO2 Capture Process. Atmosphere 2022, 13, 14. [Google Scholar] [CrossRef]
- Yuyama, S.; Kaneko, H. Simultaneous Design of Gas Separation Membranes and Schemes through Combined Process and Materials Informatics. Ind. Eng. Chem. Res. 2023, 62, 18541–18551. [Google Scholar] [CrossRef]
- Towler, G.; Sinnot, R. Chemical Engineering Design, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 2022. [Google Scholar]
- AVEVA PRO/II Simulation v2022. Available online: https://www.aveva.com/en/products/pro-ii-simulation/ (accessed on 23 January 2023).
- Turton, R.; Shaeiwitz, J.A.; Bhattacharyya, D.; Whiting, W.B. Analysis, Synthesis, and Design of Chemical Processes, 5th ed.; Pearson Education, Inc.: London, UK, 2018. [Google Scholar]
- CEPCI. Economic Indicators. Chem. Eng. 2022, 72. Available online: http://www.chemengonline.com (accessed on 23 January 2023).
- U.S. Energy Information Administration, Electric Power Annual 2021. 2022. Available online: https://www.eia.gov/electricity/annual/ (accessed on 23 January 2023).
- U.S. Energy Information Administration, How Much Carbon Dioxide Is Produced per Kilowatthour of U.S. Electricity Generation? 2021. Available online: https://www.eia.gov/tools/faqs/faq.php?id=74&t=11 (accessed on 10 November 2023).
- SimaPro PRe Sustainability, SimaPro v9.4.0. Available online: https://support.simapro.com (accessed on 20 January 2023).
- Misra, S.; Nikolaou, M. Adaptive design of experiments for model order estimation in subspace identification. Comput. Chem. Eng. 2017, 100, 119–138. [Google Scholar] [CrossRef]
- Kaneko, H. Adaptive design of experiments based on Gaussian mixture regression. Chemometr. Intell. Lab. 2021, 208, 104226. [Google Scholar] [CrossRef]
- Kennard, R.W.; Stone, L.A. Computer Aided Design of Experiments. Technometrics 1969, 11, 137. [Google Scholar] [CrossRef]
- Scikit-Learn Random Forest Classifier. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html (accessed on 21 June 2023).
- Kaneko, H. Python_Doe_Kspub. Available online: https://github.com/hkaneko1985/python_doe_kspub (accessed on 14 February 2022).
- Kaneko, H. Examining variable selection methods for the predictive performance of regression models and the proportion of selected variables and selected random variables. Heliyon 2021, 7, e07356. [Google Scholar] [CrossRef]
- Verma, S.; Pant, M.; Snasel, V. A comprehensive review on NSGA-II for multi-objective combinatorial optimization problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
- Srinivas, N.; Krause, A.; Kakade, S.M.; Seeger, M.W. Information-Theoretic Regret Bounds for Gaussian Process Optimization in the Bandit Setting. IEEE Trans. Inform. Theory 2012, 58, 3250–3265. [Google Scholar] [CrossRef]
- Wang, X.L.; Jin, Y.C.; Schmitt, S.; Olhofer, M. An adaptive Bayesian approach to surrogate-assisted evolutionary multi-objective optimization. Inform. Sci. 2020, 519, 317–331. [Google Scholar] [CrossRef]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2001. [Google Scholar]
- Shang, K.; Ishibuchi, H.; He, L.J.; Pang, L.M. A survey on the hypervolume indicator in evolutionary multiobjective optimization. IEEE Trans. Evolut. Comput. 2021, 25, 1–20. [Google Scholar] [CrossRef]
- Yang, D.X.; Wang, Z.; Wang, J.X.; Wang, S.C. Potential of Two-Stage Membrane System with Recycle Stream for CO2 Capture from Postcombustion Gas. Energy Fuels 2009, 23, 4755–4762. [Google Scholar] [CrossRef]
- Baker, R.W. Membrane Technology and Applications, 3rd ed.; John Wiley and Sons Ltd.: London, UK, 2012. [Google Scholar]
- He, X.Z.; Fu, C.; Hagg, M.B. Membrane system design and process feasibility analysis for CO2 capture from flue gas with a fixed-site-carrier membrane. Chem. Eng. J. 2015, 268, 1–9. [Google Scholar] [CrossRef]
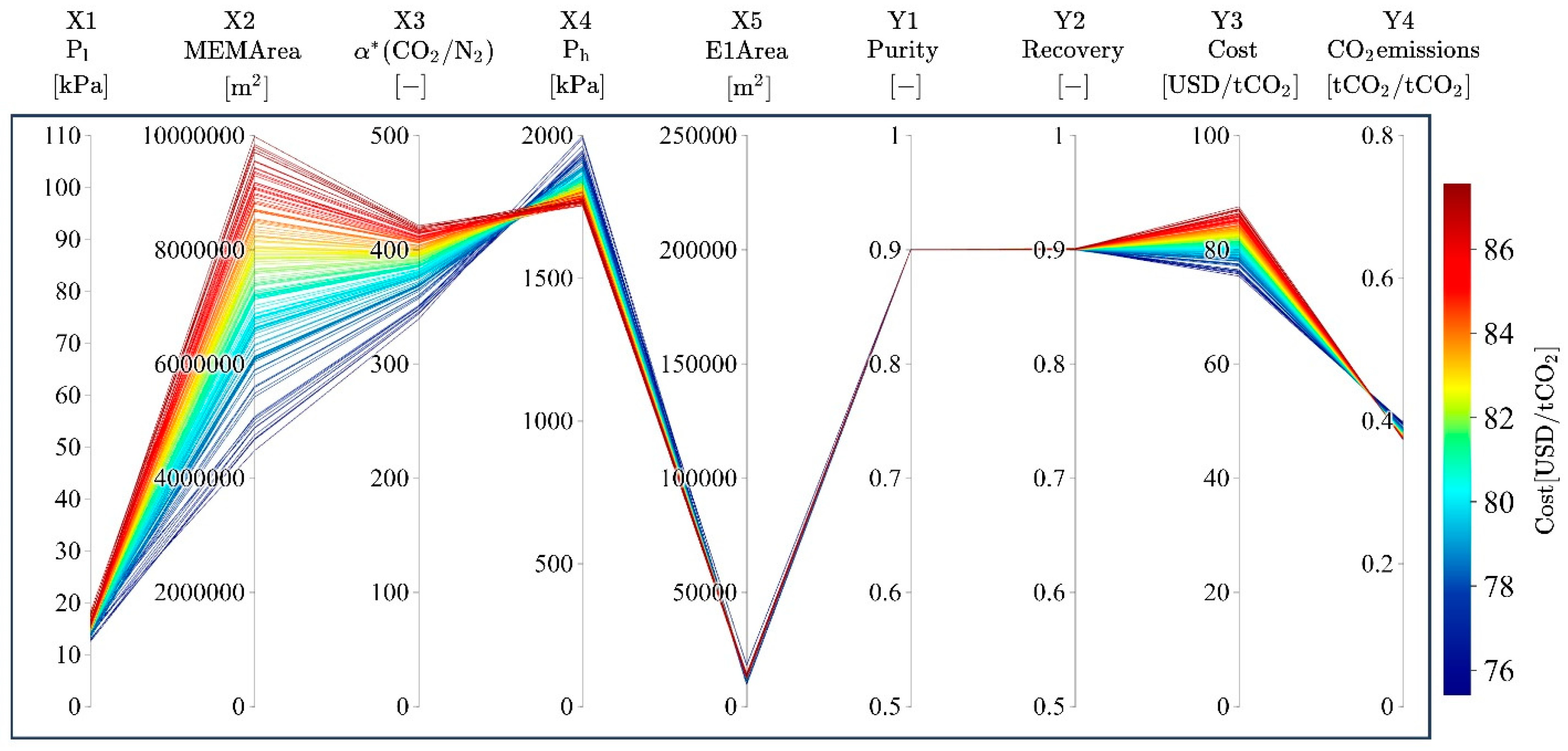

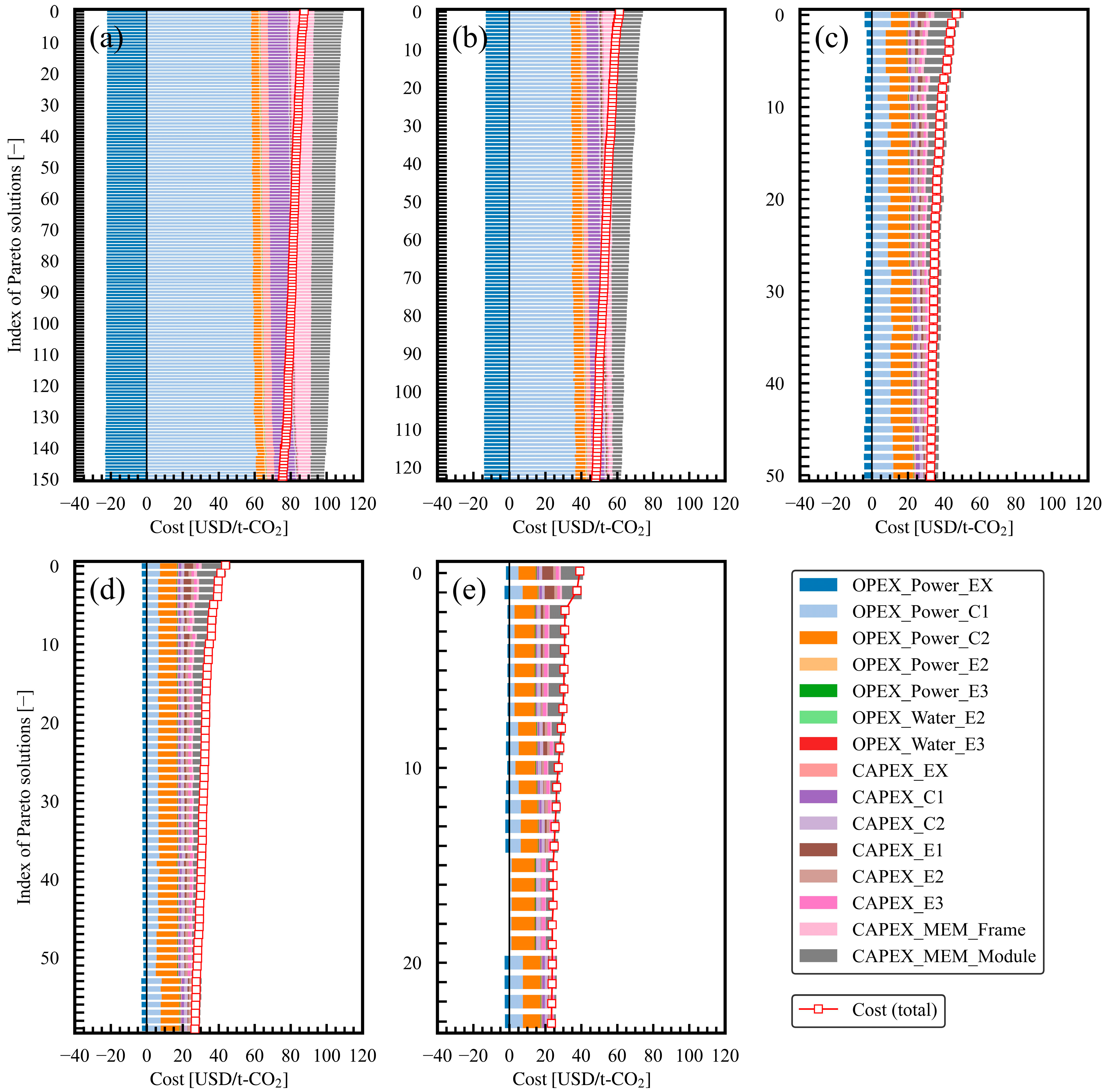
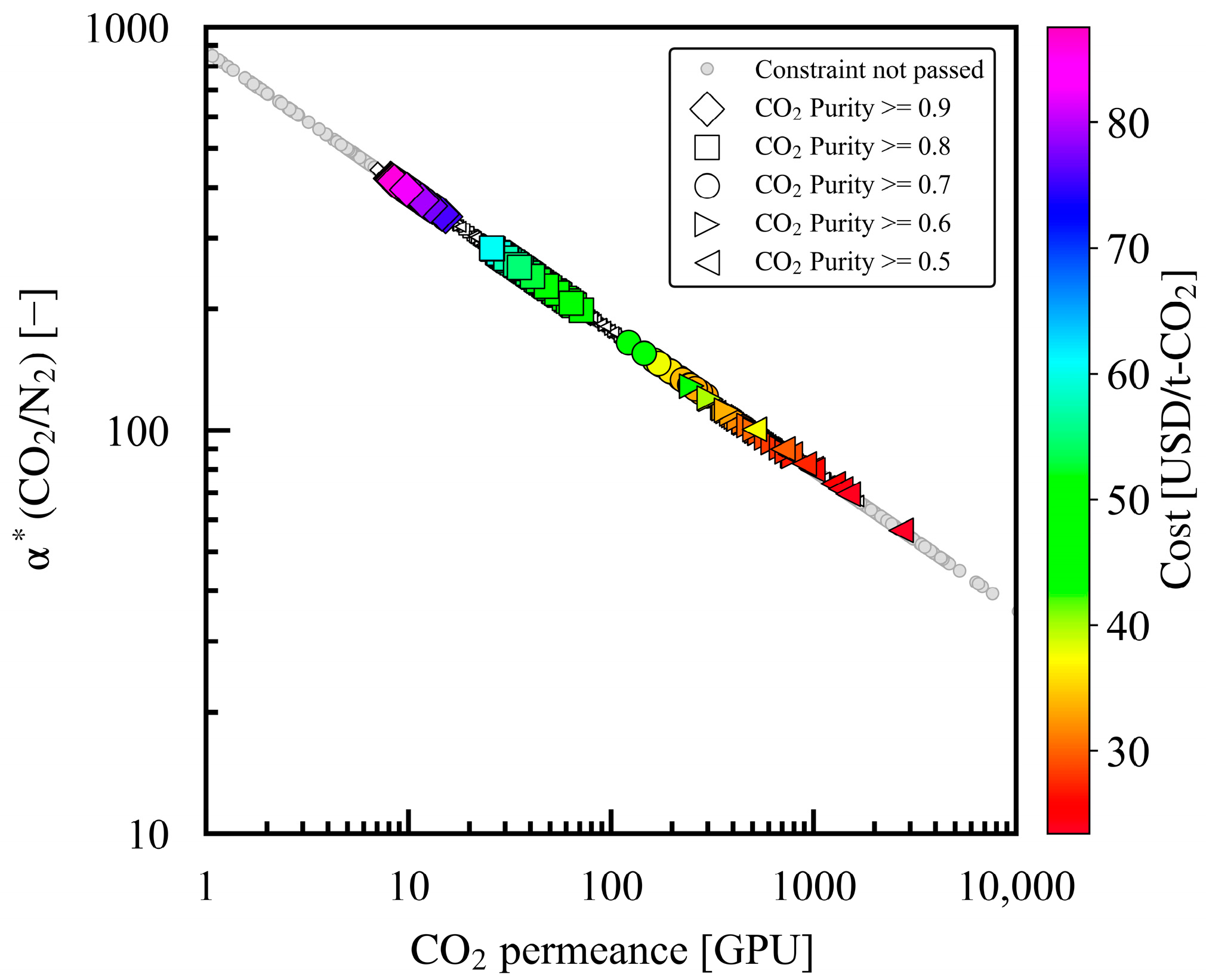
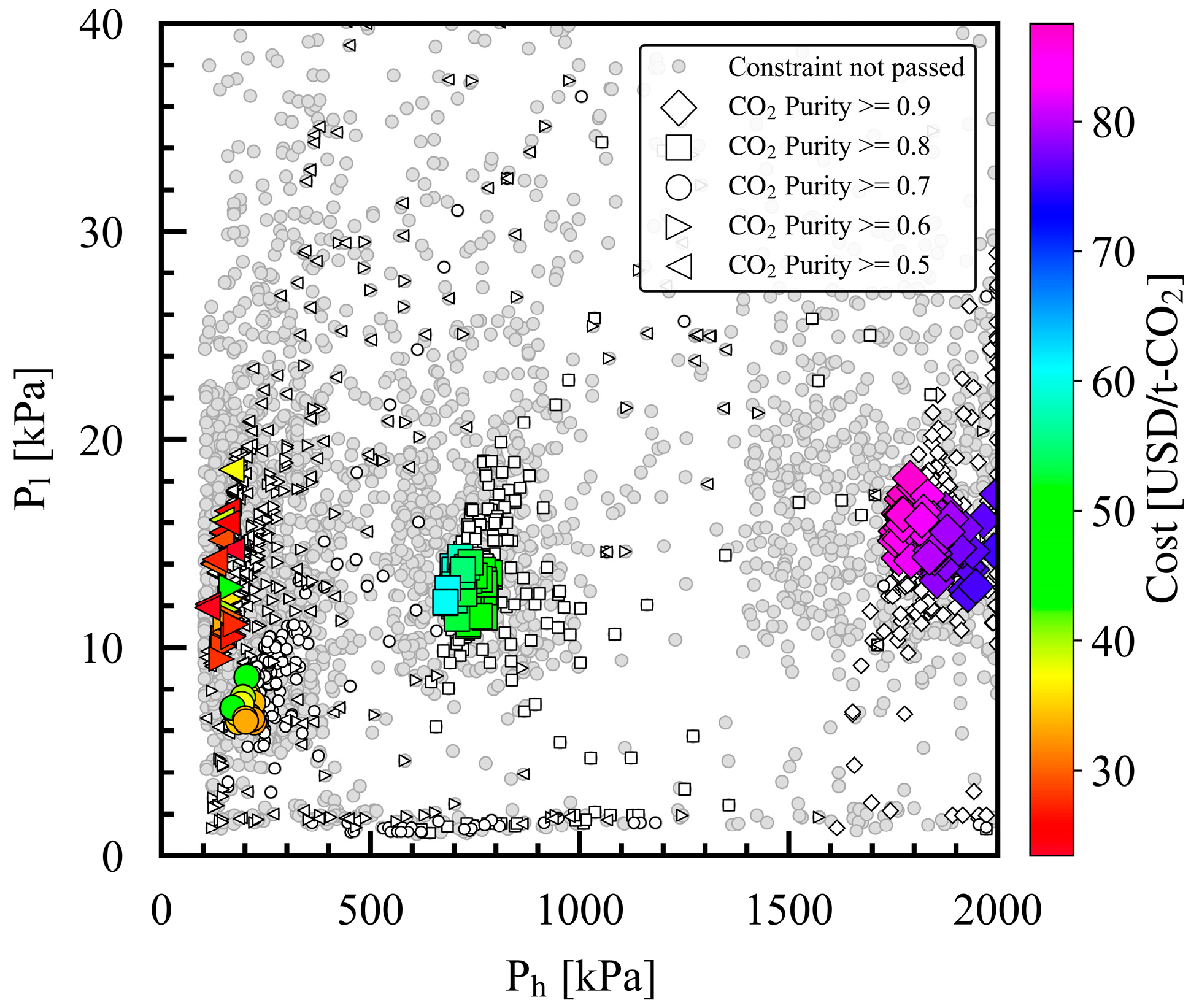


| Equipment Code | Equipment Type | Setting for Process Simulation | Setting for CAPEX Evaluation | ||||
|---|---|---|---|---|---|---|---|
| Method | Capacity | ||||||
| Unit | Min. | Max. | |||||
| C1, C2 | Compressor | Adiabatic efficiency: 75% | CAPCOST [31], centrifugal, axial, and reciprocating | Fluid power, kW | 450 | 3000 | |
| EX | Expander | Adiabatic efficiency: 75% | CAPCOST [31], radial gas/liquid expanders | Fluid power, kW | 100 | 1500 | |
| E1, E3 | Heat exchanger | Hot side: gas; cold side: gas; solved using minimum internal temperature approach (ΔT: 10 °C); U-value determined by pressure [13] | CAPCOST [31], floating head | Area, m2 | 10 | 1000 | |
| E2 | Heat exchanger | Hot side: gas (product temperature: 40 °C); cold side: cooling water (inlet temperature: 30 °C, outlet temperature: 40 °C); U-value determined by pressure [13] | CAPCOST [31], floating head | Area, m2 | 10 | 1000 | |
| MEM | Membrane separator | Membrane framework | Calculated based on cross-flow model; pressure in both feed and permeate sides, membrane area, and permeance for all gas components used for calculation | Estimated based on previously published equation [22]; reference cost converted from EUR to USD at USD/EUR = 0.75 | Area, m2 | 0 | 25,000 |
| Membrane module | Estimated by multiplying capacity and membrane module price | Area, m2 | 0 | - | |||
| Parameter | Value | Unit | Remark |
|---|---|---|---|
| CAPEX | |||
| Annual operation hour | 8000 | h/year | The annual production rate was calculated using the hourly production rate obtained from the process simulation multiplied by the annual operation hour |
| CEPCI2001 | 397.0 | - | CEPCI for year 2001 [31]; used as base year |
| CEPCI2014 | 576.1 | - | CEPCI for 2014 [32]; used as base year for evaluation of membrane framework |
| CEPCI2021 | 708.0 | - | CEPCI for year 2021 [32]. |
| CRFst | 0.098 | - | Capital recovery factor calculated from service life: 25 years; interest rate: 0.08; used as standard values |
| CRFMemModule | 0.250 | - | Capital recovery factor calculated from service life: 5 years; interest rate: 0.08; used for membrane module |
| Membrane module price | 50 | USD/m2 | Changed in case studies |
| OPEX | |||
| Electricity | 0.0718 | USD/kWh | Average price in US industrial sector in year 2021 [33] |
| Process use water | 0.177 | USD/1000 kg | [31] |
| CO2 emissions factor | |||
| Electricity | 0.656 | kg-CO2/kWh | Calculated from the total CO2 emissions divided by the total electricity generation from coal, natural gas, and petroleum in the US in year 2021 [34] |
| Process use water | - | kg-CO2/1000 kg | Evaluated using SimaPro for water, completely softened [35]; value hidden as per terms and conditions of SimaPro |
| Code | Design Variable | Unit | Setting for Bi-Objective Optimization | |||
|---|---|---|---|---|---|---|
| Range for Generating Initial Sample Dataset | Limit of Optimization Range | |||||
| Min. | Max. | Min | Max | |||
| X1 | MEM permeate-side pressure, Pl | kPa | 1 | 101 | 1 | 101 |
| X2 | MEM area | m2 | 100,000 | 10,000,000 | 1 | 10,000,000 |
| X3 | MEM ideal separation factor, α*(CO2/N2) | - | 10 | 1000 | 10 | 1000 |
| X4 | C1 outlet pressure, Ph | kPa | 200 | 2000 | 101 | 2000 |
| X5 | E1 area | m2 | 10 | 1000 | 1 | 100,000 |
| Code | Objective Variable | Unit | Remark | Setting for ML Model Building | Setting for Bi-Objective Optimization | ||
|---|---|---|---|---|---|---|---|
| Dataset | Method | Objective | Constraint | ||||
| Y0 | Convergence | - | Convergence of process simulation (1/0) | All data were used | RFC | - | =1 |
| Y1 | Product CO2 purity | - | Molar concentration of CO2 in the product | Only the converged data were used | GPR | - | ≥0.9, 0.8, 0.7, 0.6, 0.5 |
| Y2 | Product CO2 recovery | - | Recovery of CO2 in the product | - | ≥0.9 | ||
| Y3 | Cost | USD/t-CO2 | Cost per tCO2 in product | Minimize | - | ||
| Y4 | CO2 emissions | t-CO2/t-CO2 | CO2 emissions per tCO2 in product | Minimize | - | ||
| - | MEM ideal separation factor (CO2/N2) | - | Used as constraint in case studies 8, 9, and 10 | - | - | - | ≤50 |
| Case Study Number | Setting | Result | |
|---|---|---|---|
| Product CO2 Purity | Number of Pareto Solutions | Hypervolume | |
| 1 | ≥0.9 | 151 | 202.5 |
| 2 | ≥0.8 | 124 | 266.5 |
| 3 | ≥0.7 | 51 | 309.3 |
| 4 | ≥0.6 | 60 | 323.7 |
| 5 | ≥0.5 | 24 | 331.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hara, N.; Taniguchi, S.; Yamaki, T.; Nguyen, T.T.H.; Kataoka, S. Bi-Objective Optimization of Techno-Economic and Environmental Performance for Membrane-Based CO2 Capture via Single-Stage Membrane Separation. Membranes 2025, 15, 57. https://doi.org/10.3390/membranes15020057
Hara N, Taniguchi S, Yamaki T, Nguyen TTH, Kataoka S. Bi-Objective Optimization of Techno-Economic and Environmental Performance for Membrane-Based CO2 Capture via Single-Stage Membrane Separation. Membranes. 2025; 15(2):57. https://doi.org/10.3390/membranes15020057
Chicago/Turabian StyleHara, Nobuo, Satoshi Taniguchi, Takehiro Yamaki, Thuy T. H. Nguyen, and Sho Kataoka. 2025. "Bi-Objective Optimization of Techno-Economic and Environmental Performance for Membrane-Based CO2 Capture via Single-Stage Membrane Separation" Membranes 15, no. 2: 57. https://doi.org/10.3390/membranes15020057
APA StyleHara, N., Taniguchi, S., Yamaki, T., Nguyen, T. T. H., & Kataoka, S. (2025). Bi-Objective Optimization of Techno-Economic and Environmental Performance for Membrane-Based CO2 Capture via Single-Stage Membrane Separation. Membranes, 15(2), 57. https://doi.org/10.3390/membranes15020057







