Microscopic Exploration of Water Permeation and Ion Rejection for Edge Amine-Functionalized GO Nanoslits
Abstract
1. Introduction
2. Simulation Models and Methods
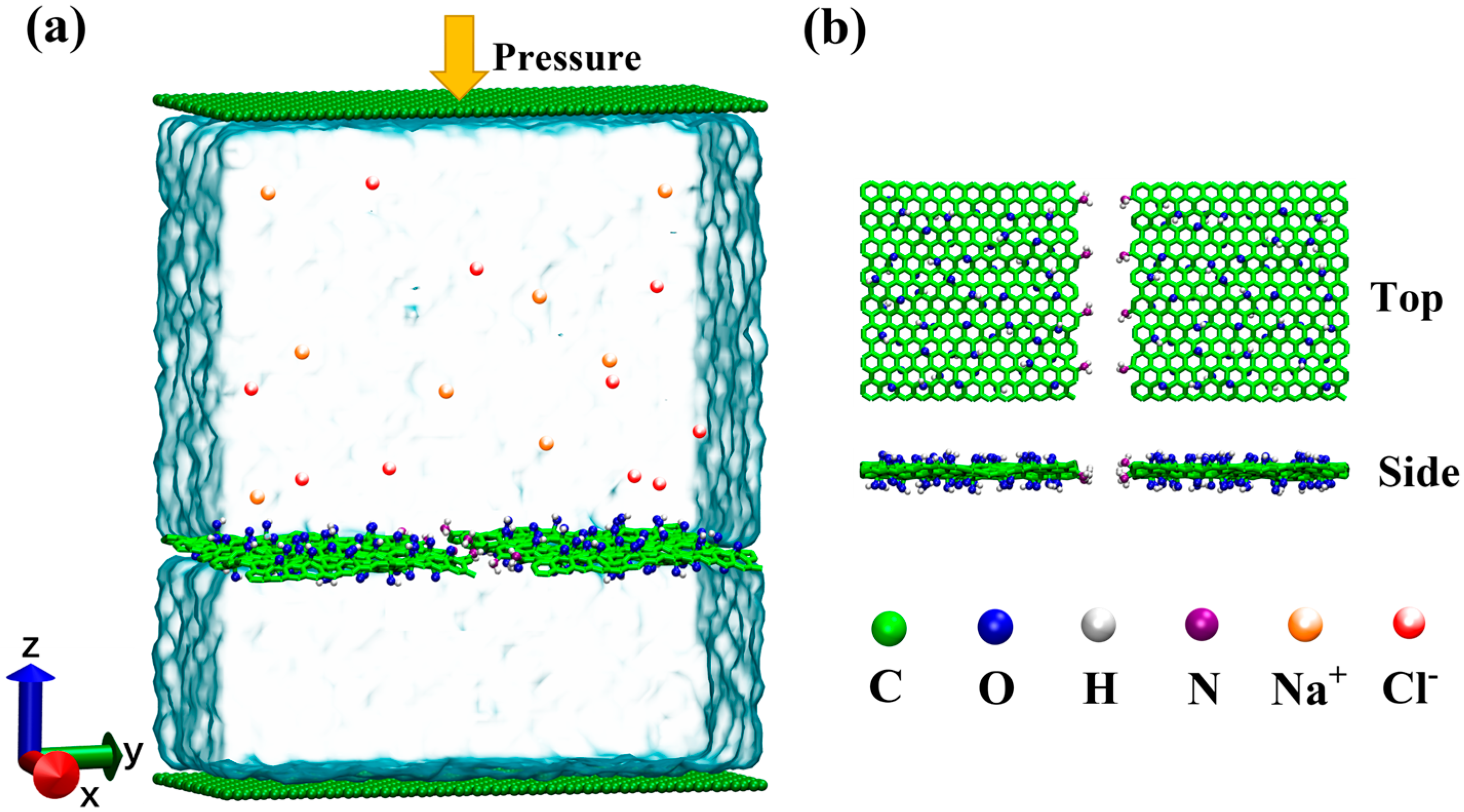
2.1. Simulation Models
2.2. Force Field and Simulation Details
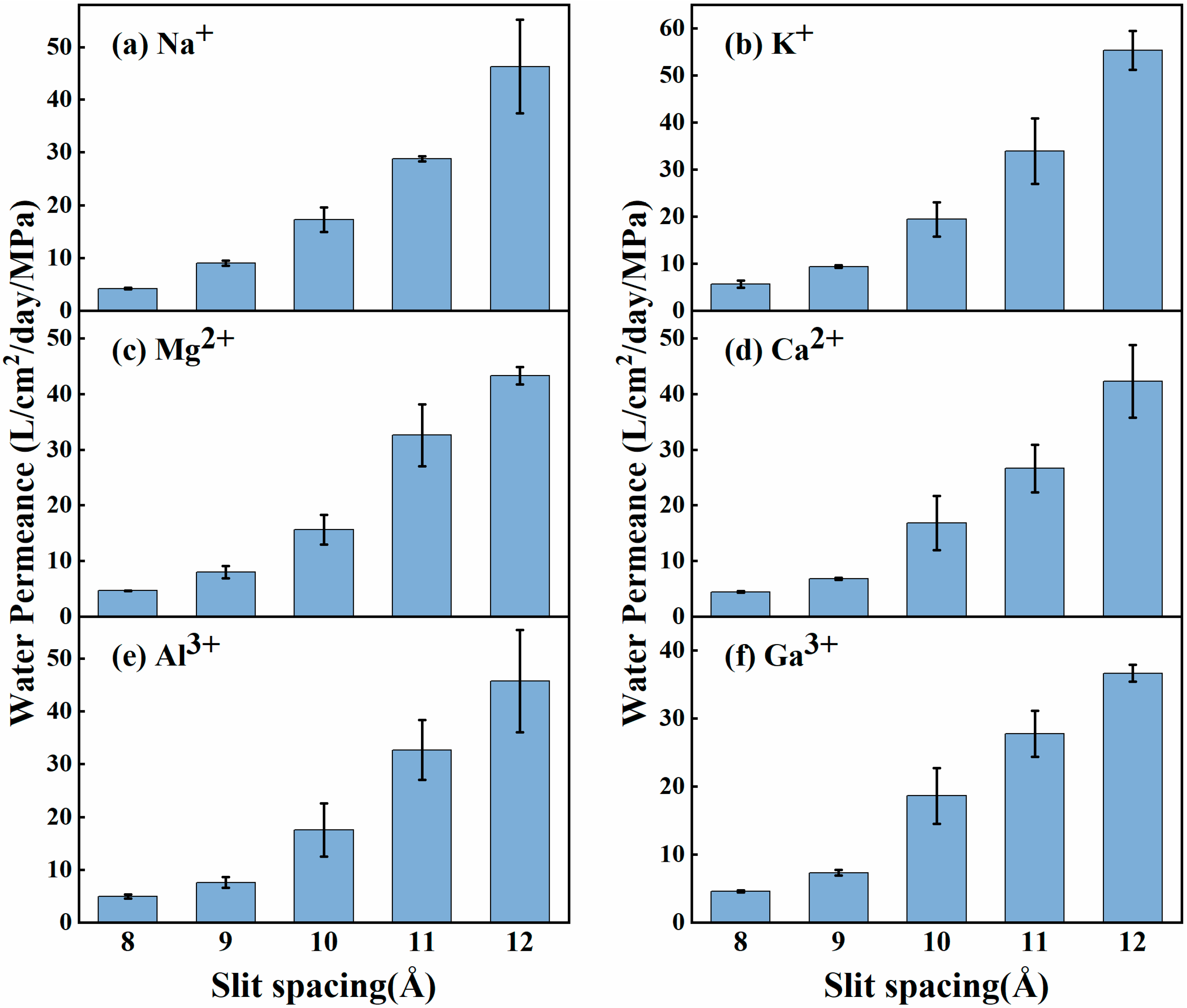
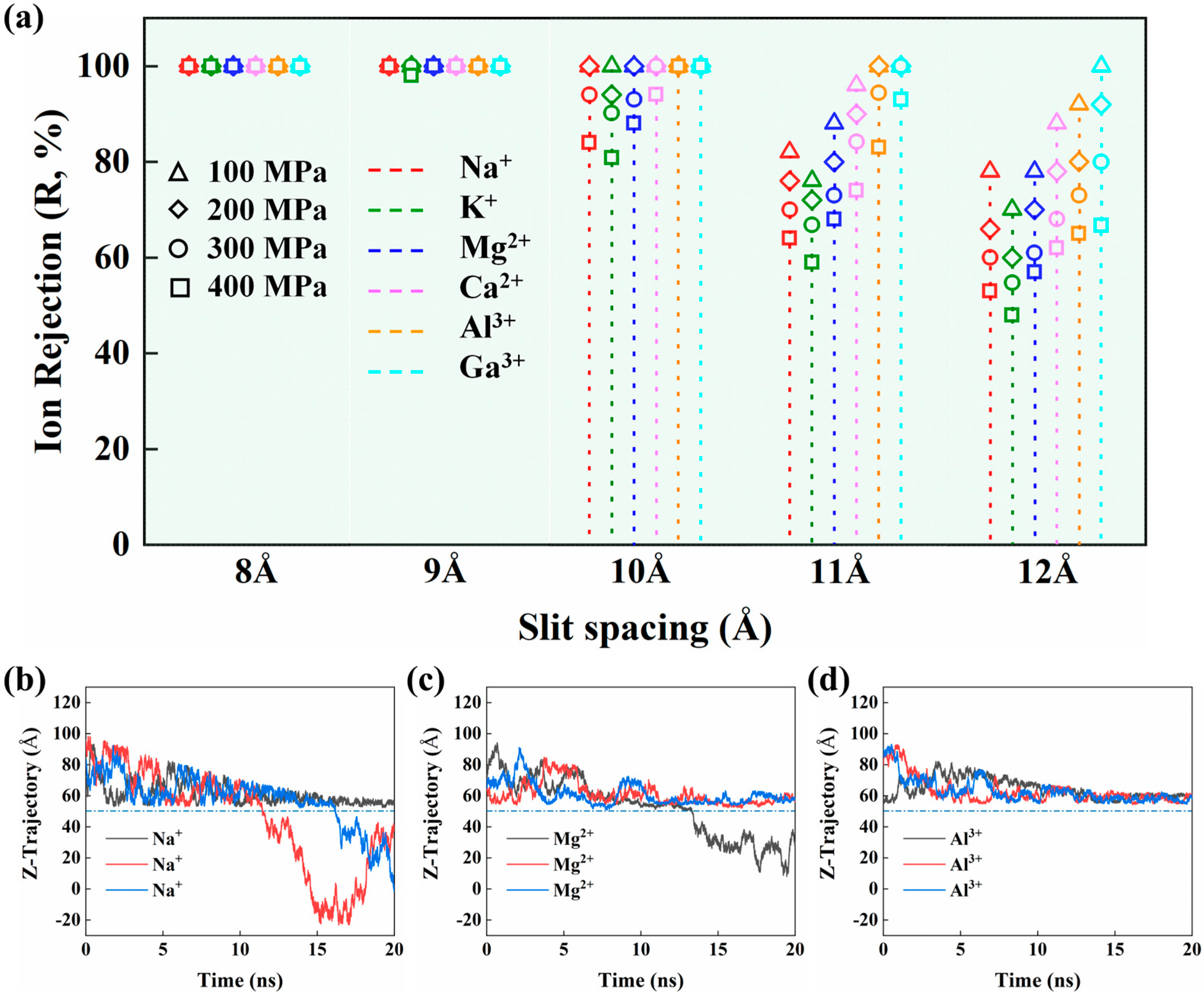
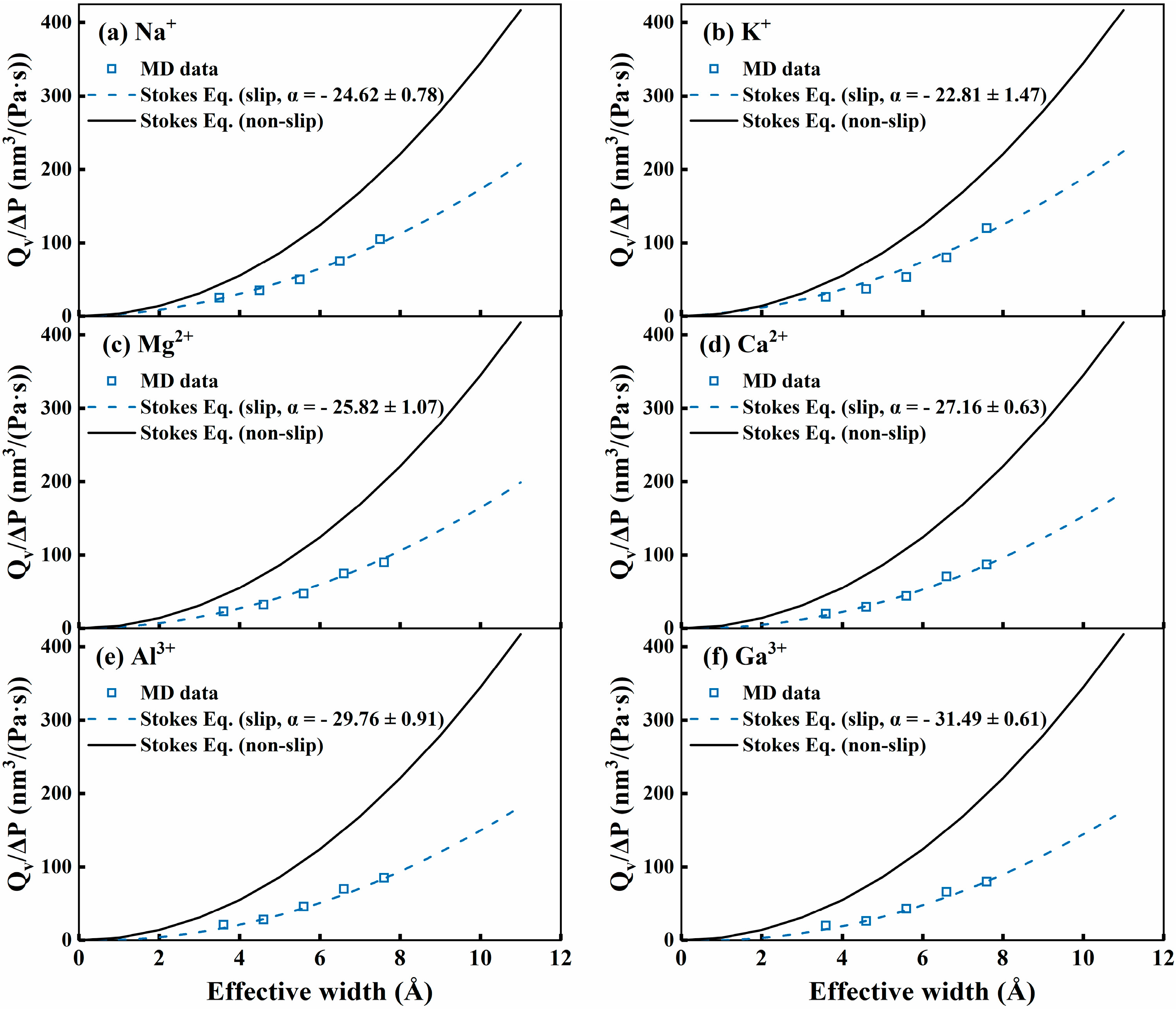
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Werber, J.R.; Osuji, C.O.; Elimelech, M. Materials for next-generation desalination and water purification membranes. Nat. Rev. Mater. 2016, 1, 16018. [Google Scholar] [CrossRef]
- Gin, D.L.; Noble, R.D. Designing the next generation of Chemical Separation Membranes. Science 2011, 332, 674–676. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, F.E.; Khalil, A.; Hilal, N. Emerging desalination technologies: Current status, challenges and future trends. Desalination 2021, 517, 115183. [Google Scholar] [CrossRef]
- Asif, M.B.; Iftekhar, S.; Maqbool, T.; Pramanik, B.K.; Tabraiz, S.; Sillanpää, M.; Zhang, Z. Two-dimensional nanoporous and lamellar membranes for water purification: Reality or a myth? Chem. Eng. J. 2022, 432, 134335. [Google Scholar] [CrossRef]
- Johnson, D.J.; Hilal, N. Nanocomposite nanofiltration membranes: State of play and recent advances. Desalination 2022, 524, 115480. [Google Scholar] [CrossRef]
- Dervin, S.; Dionysiou, D.D.; Pillai, S.C. 2D nanostructures for water purification: Graphene and beyond. Nanoscale 2016, 8, 15115–15131. [Google Scholar] [CrossRef]
- Liu, B.; Zhou, K. Recent progress on graphene-analogous 2D nanomaterials: Properties, modeling and applications. Prog. Mater. Sci. 2019, 100, 99–169. [Google Scholar] [CrossRef]
- Wei, N.; Peng, X.; Xu, Z. Understanding Water Permeation in Graphene Oxide Membranes. ACS Appl. Mater. Interfaces 2014, 6, 5877–5883. [Google Scholar] [CrossRef]
- Chen, B.; Jiang, H.; Liu, X.; Hu, X. Molecular Insight into Water Desalination across Multilayer Graphene Oxide Membranes. ACS Appl. Mater. Interfaces 2017, 9, 22826–22836. [Google Scholar] [CrossRef] [PubMed]
- Dahanayaka, M.; Liu, B.; Srikanth, N.; Zhou, K. Ionised graphene oxide membranes for seawater desalination. Desalination 2020, 496, 114637. [Google Scholar] [CrossRef]
- Liang, S.; Wang, S.; Chen, L.; Fang, H. Controlling interlayer spacings of graphene oxide membranes with cationic for precise sieving of mono-/multi-valent ions. Sep. Purif. Technol. 2020, 241, 116738. [Google Scholar] [CrossRef]
- Wei, Y.; Pastuovic, Z.; Shen, C.; Murphy, T.; Gore, D.B. Ion beam engineered graphene oxide membranes for mono-/di-valent metal ions separation. Carbon 2020, 158, 598–606. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, L.; Cui, X.; Zhang, Q.; Hu, W.; Du, J.; Zeng, H.; Xu, Q. 2D Material Nanofiltration Membranes: From Fundamental Understandings to Rational Design. Adv. Sci. 2021, 8, 2102493. [Google Scholar] [CrossRef]
- Willcox, J.A.L.; Kim, H.J. Molecular Dynamics Study of Water Flow across Multiple Layers of Pristine, Oxidized, and Mixed Regions of Graphene Oxide. ACS Nano 2017, 11, 2187–2193. [Google Scholar] [CrossRef]
- Muscatello, J.; Jaeger, F.; Matar, O.K.; Müller, E.A. Optimizing Water Transport through Graphene-Based Membranes: Insights from Nonequilibrium Molecular Dynamics. ACS Appl. Mater. Interfaces 2016, 8, 12330–12336. [Google Scholar] [CrossRef]
- Qin, L.; Tobiason, J.E.; Huang, H. Water and humic acid transport in graphene-derived membrane: Mechanisms and implications to functional membrane design. J. Membr. Sci. 2020, 613, 118441. [Google Scholar] [CrossRef]
- Song, N.; Gao, X.; Ma, Z.; Wang, X.; Wei, Y.; Gao, C. A review of graphene-based separation membrane: Materials, characteristics, preparation and applications. Desalination 2018, 437, 59–72. [Google Scholar] [CrossRef]
- Wang, L.; Wang, N.; Li, J.; Li, J.; Bian, W.; Ji, S. Layer-by-layer self-assembly of polycation/GO nanofiltration membrane with enhanced stability and fouling resistance. Sep. Purif. Technol. 2016, 160, 123–131. [Google Scholar] [CrossRef]
- Pandey, R.P.; Shahi, V.K. Sulphonated imidized graphene oxide (SIGO) based polymer electrolyte membrane for improved water retention, stability and proton conductivity. J. Power Sources 2015, 299, 104–113. [Google Scholar] [CrossRef]
- Zhang, B.; Cao, Y.; Jiang, S.; Li, Z.; He, G.; Wu, H. Enhanced proton conductivity of Nafion nanohybrid membrane incorporated with phosphonic acid functionalized graphene oxide at elevated temperature and low humidity. J. Membr. Sci. 2016, 518, 243–253. [Google Scholar] [CrossRef]
- Yang, J.; Gong, D.; Li, G.; Zeng, G.; Wang, Q.; Zhang, Y.; Liu, G.; Wu, P.; Vovk, E.; Peng, Z.; et al. Self-Assembly of Thiourea-Crosslinked Graphene Oxide Framework Membranes toward Separation of Small Molecules. Adv. Mater. 2018, 30, 1705775. [Google Scholar] [CrossRef] [PubMed]
- Hung, W.S.; Tsou, C.H.; Guzman, M.D.; An, Q.F.; Liu, Y.L.; Zhang, Y.M.; Hu, C.C.; Lee, K.R.; Lai, J.Y. Cross-Linking with Diamine Monomers To Prepare Composite Graphene Oxide-Framework Membranes with Varying d-Spacing. Chem. Mater. 2014, 26, 2983–2990. [Google Scholar] [CrossRef]
- Qiu, R.; Xiao, J.; Chen, X.D.; Selomulya, C.; Zhang, X.; Woo, M.W. Comparison of the effects of edge functionalized graphene oxide membranes on monovalent cation selectivity. J. Membr. Sci. 2021, 620, 118892. [Google Scholar] [CrossRef]
- Qian, Y.; Shang, J.; Liu, D.; Yang, G.; Wang, X.; Chen, C.; Kou, L.; Lei, W. Enhanced Ion Sieving of Graphene Oxide Membranes via Surface Amine Functionalization. J. Am. Chem. Soc. 2021, 143, 5080–5090. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Jiang, T.J.; Wang, Y.; Liu, J.H.; Li, L.N.; Chen, X.; Huang, X.J. Enhanced electrochemical sensing arsenic(III) with excellent anti-interference using amino-functionalized graphene oxide decorated gold microelectrode: XPS and XANES evidence. Sens. Actuators B Chem. 2017, 245, 230–237. [Google Scholar] [CrossRef]
- Wang, C.; Lan, Y.; Yu, W.; Li, X.; Qian, Y.; Liu, H. Preparation of amino-functionalized graphene oxide/polyimide composite films with improved mechanical, thermal and hydrophobic properties. Appl. Surf. Sci. 2016, 362, 11–19. [Google Scholar] [CrossRef]
- Su, Z.; Wang, H.; Tian, K.; Xu, F.; Huang, W.; Tian, X. Simultaneous reduction and surface functionalization of graphene oxide with wrinkled structure by diethylenetriamine (DETA) and their reinforcing effects in the flexible poly (2-ethylhexyl acrylate) (P2EHA) films. Composites Part A 2016, 84, 64–75. [Google Scholar] [CrossRef]
- Sethi, J.; Suhail, A.; Safarzadeh, M.; Sattar, A.; Wei, Y.; Pan, G. NH2 linker for femtomolar label-free detection with reduced graphene oxide screen-printed electrodes. Carbon 2021, 179, 514–522. [Google Scholar] [CrossRef]
- Ching, K.; Lian, B.; Leslie, G.; Chen, X.; Zhao, C. Metal-cation-modified graphene oxide membranes for water permeation. Carbon 2020, 170, 646–657. [Google Scholar] [CrossRef]
- Staff, K.; Brown, M.B.; Chilcott, R.P.; Hider, R.C.; Jones, S.A.; Kong, X.L. Ga(III) complexes—The effect of metal coordination on potential systemic absorption after topical exposure. Toxicol. Lett. 2011, 202, 155–160. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Wang, J.; Zhang, X.; Hu, M.; Xu, Q.; Xie, Y.; Liu, Y.; Lu, R. Confined lamellar channels structured by multilayer graphene for high-efficiency desalination. Desalination 2022, 530, 115681. [Google Scholar] [CrossRef]
- Safaei, S.; Tavakoli, R. On the design of graphene oxide nanosheets membranes for water desalination. Desalination 2017, 422, 83–90. [Google Scholar] [CrossRef]
- Li, J.; Li, Q.; Xu, Z.; Yang, X. Molecular simulation of adsorption behavior for phenol aqueous solution into layered graphene oxides. Sep. Purif. Technol. 2024, 335, 126215. [Google Scholar] [CrossRef]
- Liu, G.; Shen, J.; Liu, Q.; Liu, G.; Xiong, J.; Yang, J.; Jin, W. Ultrathin two-dimensional MXene membrane for pervaporation desalination. J. Membr. Sci. 2018, 548, 548–558. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Tersoff, J. Modeling solid-state chemistry: Interatomic potentials for multicomponent systems. Phys. Rev. B 1989, 39, 5566. [Google Scholar] [CrossRef]
- Lindsay, L.; Broido, D.A. Optimized Tersoff and Brenner empirical potential parameters for lattice dynamics and phonon thermal transport in carbon nanotubes and graphene. Phys. Rev. B 2010, 81, 205441. [Google Scholar] [CrossRef]
- Konatham, D.; Striolo, A. Molecular design of stable graphene nanosheets dispersions. Nano Lett. 2008, 8, 4630–4641. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Damm, W.; Frontera, A.; Tirado-Rives, J.; Jorgensen, W.L. OPLS all-atom force field for carbohydrates. J. Comput. Chem. 1997, 18, 1955–1970. [Google Scholar] [CrossRef]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M.; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar] [CrossRef]
- Vafa, N.; Firoozabadi, B.; Pishkenari, H.N. Hybrid graphene oxide-graphene membrane for efficient water desalination: Insights from molecular dynamics simulation. J. Mol. Liq. 2024, 407, 125241. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The missing term in effective pair potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Dang, L.X. Mechanism and thermodynamics of ion selectivity in aqueous-solutions of 18-crown-6 ether: A molecular dynamics study. J. Chem. Phys. 1995, 117, 6954–6960. [Google Scholar] [CrossRef]
- Chowdhuri, S.; Chandra, A. Hydration structure and diffusion of ions in supercooled water: Ion size effects. J. Chem. Phys. 2003, 118, 9719–9725. [Google Scholar] [CrossRef]
- Larentzos, J.P.; Criscenti, L.J. A molecular dynamics study of alkaline earth metal-chloride complexation in aqueous solution. J. Phys. Chem. B 2008, 112, 14243–14250. [Google Scholar] [CrossRef] [PubMed]
- Faro, T.M.C.; Thim, G.P.; Skaf, M.S. A Lennard-Jones plus Coulomb potential for Al3+ ions in aqueous solutions. J. Chem. Phys. 2010, 132, 114509. [Google Scholar] [CrossRef]
- Kowall, T.; Caravan, P.; Bourgeois, H.; Helm, L.; Rotzinger, F.P.; Merbach, A.E. Interpretation of activation volumes for water exchange reactions revisited: Ab initio calculations for Al3+, Ga3+, and In3+, and new experimental data. J. Am. Chem. Soc. 1998, 120, 6569–6577. [Google Scholar] [CrossRef]
- Werder, T.; Walther, J.H.; Jaffe, R.L.; Halicioglu, T.; Koumoutsakos, P. On the water-carbon interaction for use in molecular dynamics simulations of graphite and carbon nanotubes. J. Phys. Chem. B 2003, 107, 1345–1352. [Google Scholar] [CrossRef]
- Eastwood, J.W.; Hockney, R.W.; Lawrence, D.N. P3M3DP-the three-dimensional periodic particle-particle/particle-mesh program. Comput. Phys. Commun. 1980, 19, 215–261. [Google Scholar] [CrossRef]
- Shi, J.X.; Natsuki, T.; Lei, X.W.; Ni, Q.Q. Equivalent Young’s modulus and thickness of graphene sheets for the continuum mechanical models. Appl. Phys. Lett. 2014, 104, 223101. [Google Scholar] [CrossRef]
- Kou, J.; Zhou, X.; Lu, H.; Wu, F.; Fan, J. Graphyne as the membrane for water desalination. Nanoscale 2014, 6, 1865–1870. [Google Scholar] [CrossRef]
- Suk, M.E.; Aluru, N.R. Modeling Water Flow Through Carbon Nanotube Membranes with Entrance/Exit Effects. Nanoscale Microscale Thermophys. Eng. 2017, 21, 247–262. [Google Scholar] [CrossRef]
- Gupta, K.M.; Zhang, K.; Jiang, J. Water Desalination through Zeolitic Imidazolate Framework Membranes: Significant Role of Functional Groups. Langmuir 2015, 31, 13230–13237. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Yang, X. Pyridinic nitrogen doped nanoporous graphene as desalination membrane: Molecular simulation study. J. Membr. Sci. 2015, 496, 108–117. [Google Scholar] [CrossRef]
- Cohen-Tanugi, D.; Grossman, J.C. Water Desalination across Nanoporous Graphene. Nano Lett. 2012, 12, 3602–3608. [Google Scholar] [CrossRef]
- Manikandan, D.; Chakraborty, S. Massively Improved Water Desalination Performance Using Phase-Engineered MoS2 Nanopores. Nano Lett. 2025, 25, 10870–10878. [Google Scholar] [CrossRef] [PubMed]
- Xue, Q.; Lim, Y.J.; Zhang, K. Engineering multi-channel water transport in surface-porous MXene nanosheets for high-performance thin-film nanocomposite membranes. J. Membr. Sci. 2025, 728, 124151. [Google Scholar] [CrossRef]
- Gu, Z.; Lin, G.; Xie, G. Carbon nitride (C3N) nanoslits guided membrane for efficient seawater desalination. Appl. Surf. Sci. 2022, 582, 152460. [Google Scholar] [CrossRef]
- Ma, X.; Zhu, X.; Huang, C.; Fan, J. Exploring the potential of MXene nanoslit for water desalination through molecular dynamics simulations. Desalination 2023, 556, 116560. [Google Scholar] [CrossRef]
- Liu, T.; Lyv, J.; Xu, Y.; Zheng, C.; Liu, Y.; Fu, R.; Liang, L.; Wu, J.; Zhang, Z. Graphene-based woven filter membrane with excellent strength and efficiency for water desalination. Desalination 2022, 533, 115775. [Google Scholar] [CrossRef]
- Yang, X.; Yang, X. Molecular simulation of water permeation and salt rejection for MoS2 nanoslit membranes. Desalination 2023, 564, 116787. [Google Scholar] [CrossRef]
- Zheng, B.; Tian, Y.; Jia, S.; Zhao, X.; Li, H. Molecular dynamics study on applying layered graphene oxide membranes for separating cadmium ions from water. J. Membr. Sci. 2020, 603, 117996. [Google Scholar] [CrossRef]
- Hasimoto, H. On the flow of a viscous fluid past a thin screen at small Reynolds numbers. J. Phys. Soc. Jpn. 1958, 13, 633–639. [Google Scholar] [CrossRef]
- Xu, T.; Zhang, M.; Xu, Z.; Yang, X. Molecular Insight into Water Transport through Heterogeneous GO-based Two-Dimensional Nanocapillary. ACS Appl. Mater. Interfaces 2019, 11, 33409–33418. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Feng, Q.; Javadpour, F.; Yang, Y.-B. Breakdown of Fast Mass Transport of Methane through Calcite Nanopores. J. Phys. Chem. C 2016, 120, 14260–14269. [Google Scholar] [CrossRef]
- Zhang, J.; Kwok, D.Y. Apparent slip over a solid-liquid interface with a no-slip boundary condition. Phys. Rev. E 2004, 70, 056701. [Google Scholar] [CrossRef]
- Cieplak, M.; Koplik, J.; Banavar, J.R. Boundary Conditions at a Fluid-Solid Interface. Phys. Rev. Lett. 2001, 86, 803. [Google Scholar] [CrossRef]
- Brehm, M.; Kirchner, B. TRAVIS—A Free Analyzer and Visualizer for Monte Carlo and Molecular Dynamics Trajectories. J. Chem. Inf. Model. 2011, 51, 2007–2023. [Google Scholar] [CrossRef] [PubMed]
- Guàrdia, E.; Rey, R.; Padró, J.A. Potential of mean force by constrained molecular dynamics: A sodium chloride ion-pair in water. Chem. Phys. 1991, 155, 187–195. [Google Scholar] [CrossRef]
- Xu, Z.; Yang, X.; Yang, Z. A Molecular Simulation Probing of Structure and Interaction for Supramolecular Sodium Dodecyl Sulfate/Single-Wall Carbon Nanotube Assemblies. Nano Lett. 2010, 10, 985–991. [Google Scholar] [CrossRef] [PubMed]


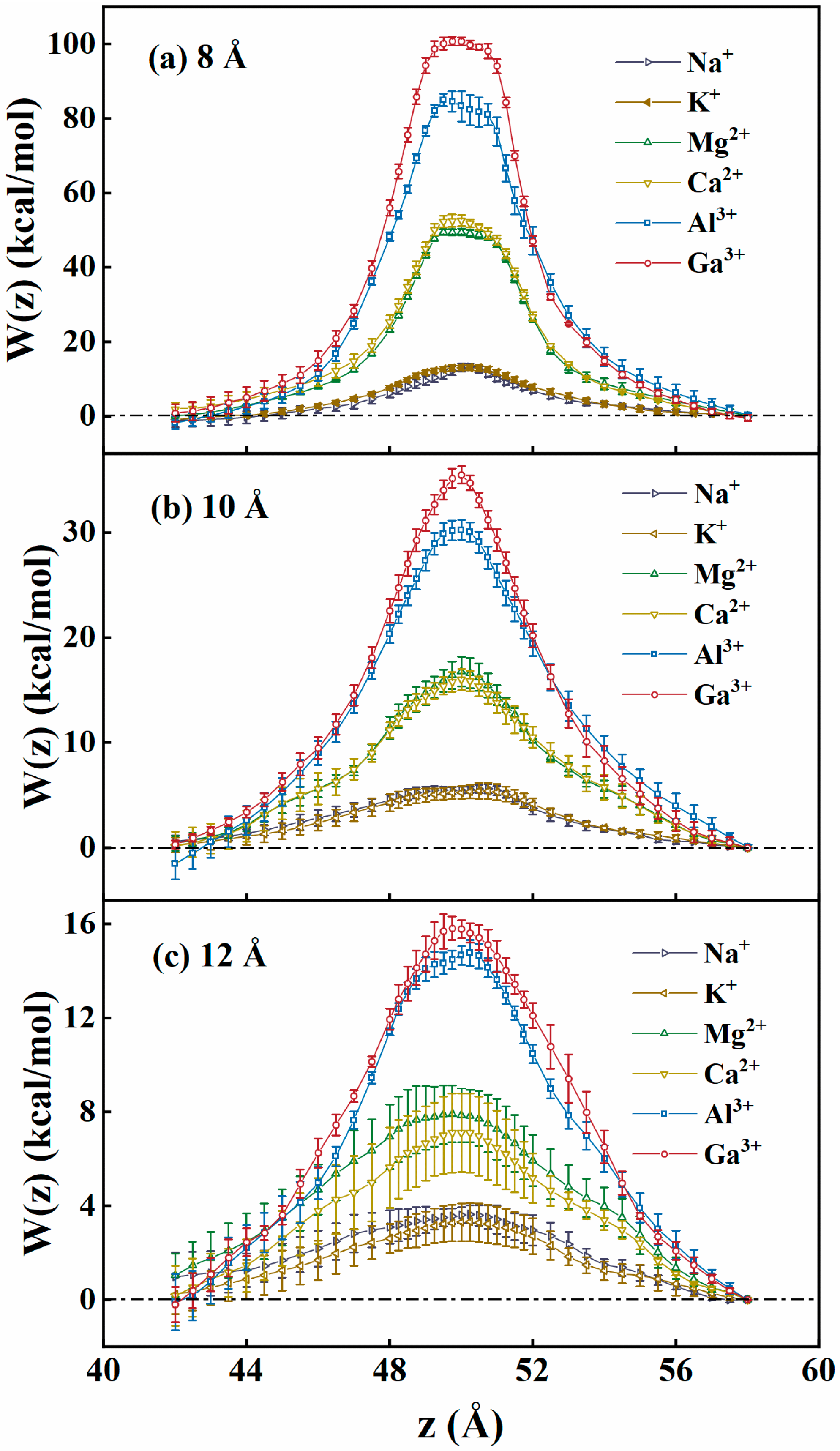
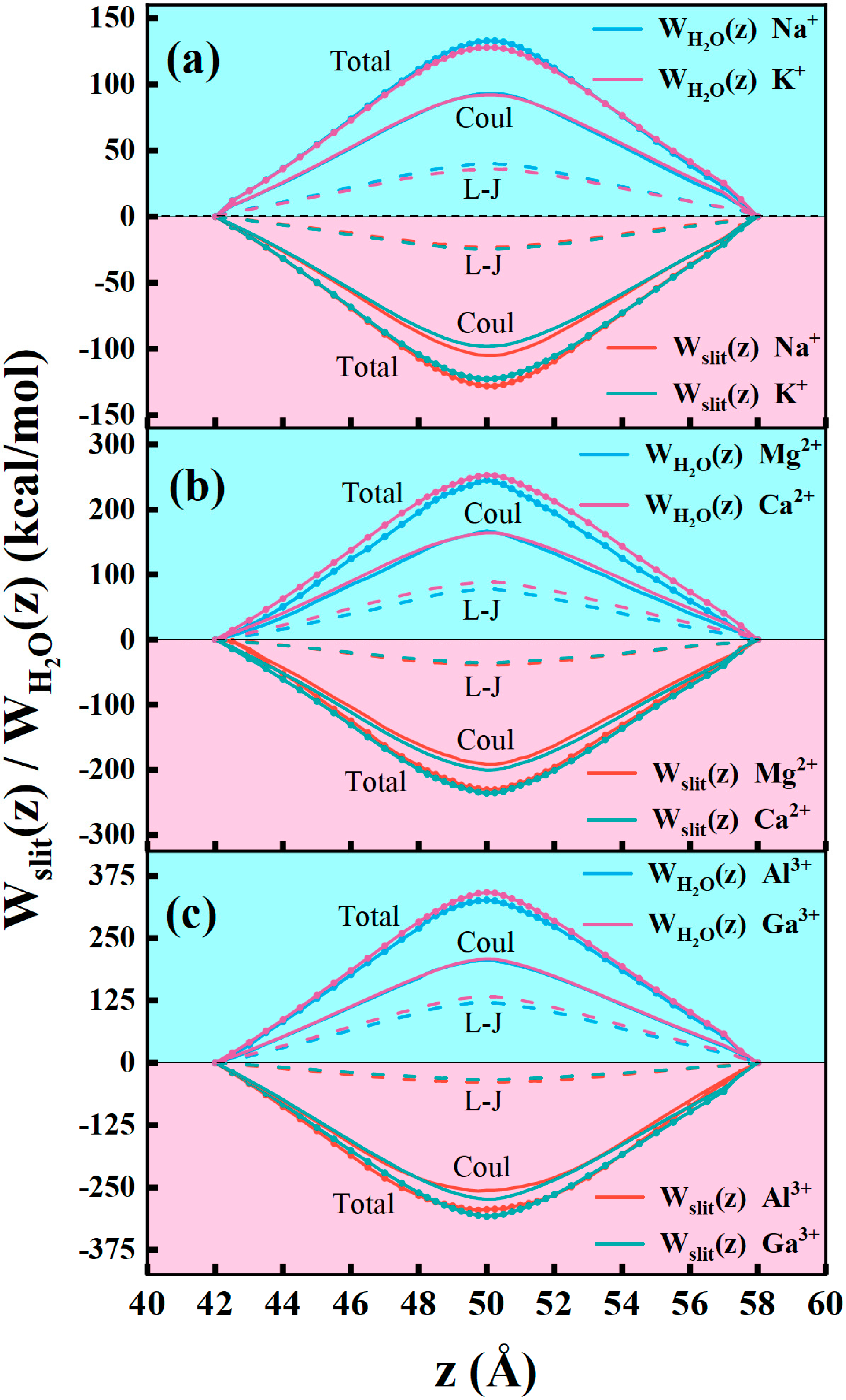
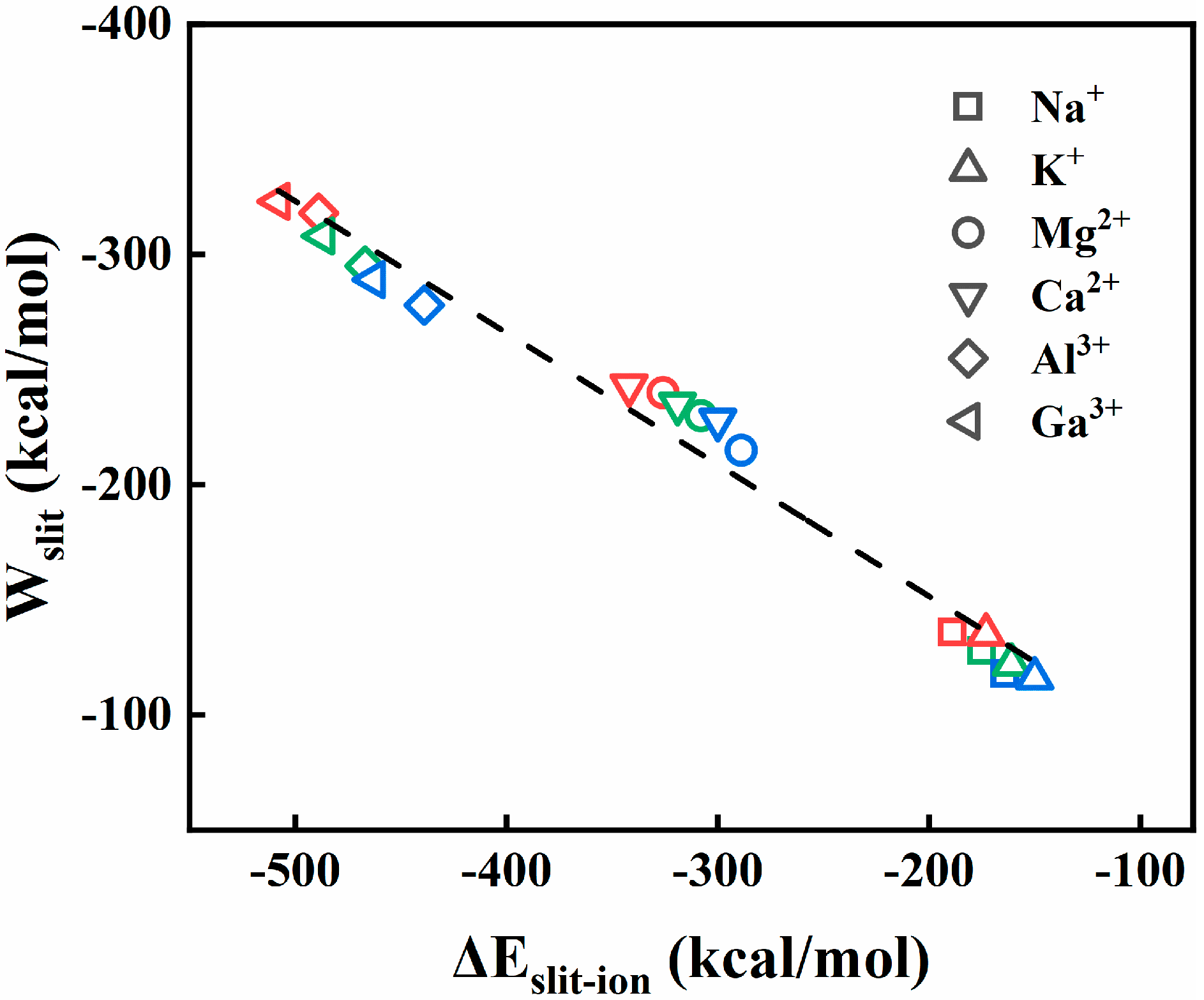
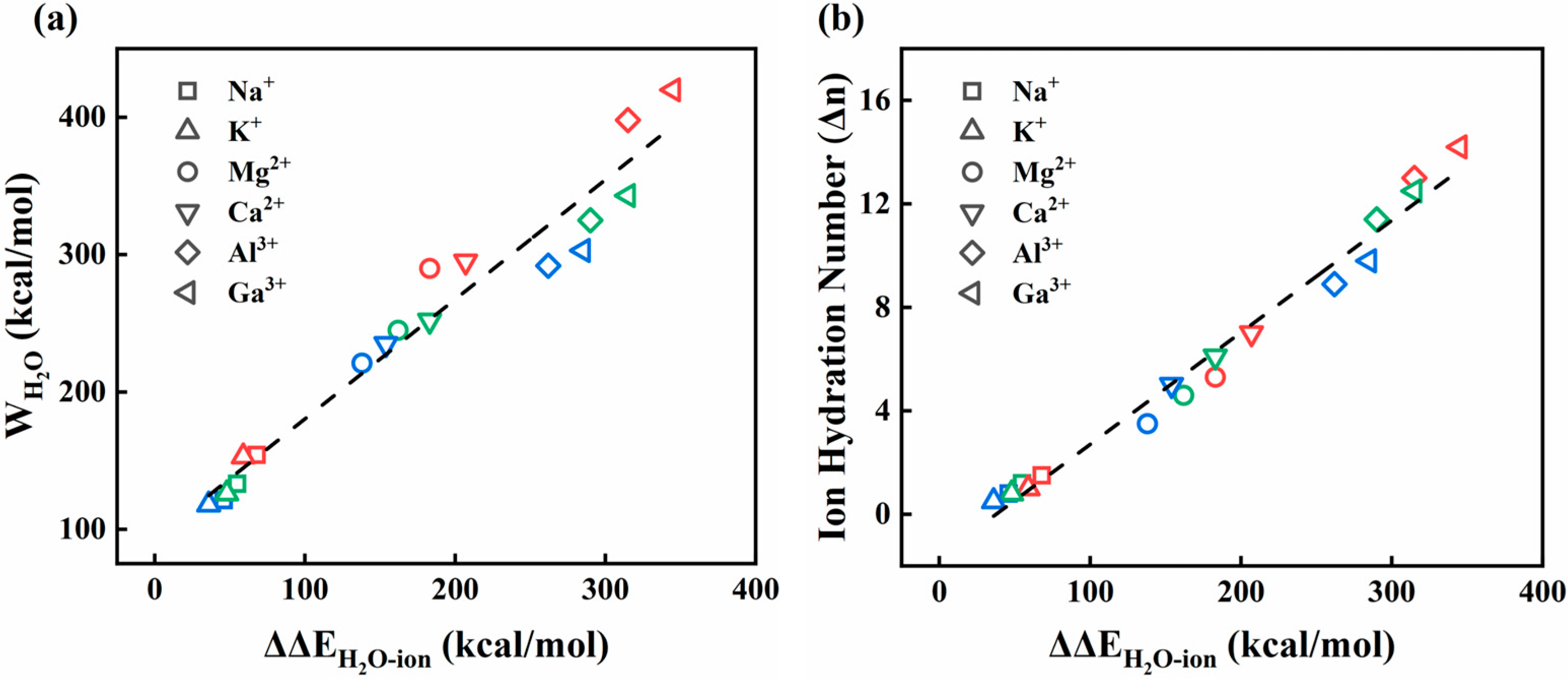
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pei, Y.; Li, W.; Yang, X. Microscopic Exploration of Water Permeation and Ion Rejection for Edge Amine-Functionalized GO Nanoslits. Membranes 2025, 15, 334. https://doi.org/10.3390/membranes15110334
Pei Y, Li W, Yang X. Microscopic Exploration of Water Permeation and Ion Rejection for Edge Amine-Functionalized GO Nanoslits. Membranes. 2025; 15(11):334. https://doi.org/10.3390/membranes15110334
Chicago/Turabian StylePei, Yinfeng, Wenjin Li, and Xiaoning Yang. 2025. "Microscopic Exploration of Water Permeation and Ion Rejection for Edge Amine-Functionalized GO Nanoslits" Membranes 15, no. 11: 334. https://doi.org/10.3390/membranes15110334
APA StylePei, Y., Li, W., & Yang, X. (2025). Microscopic Exploration of Water Permeation and Ion Rejection for Edge Amine-Functionalized GO Nanoslits. Membranes, 15(11), 334. https://doi.org/10.3390/membranes15110334




