Hydrodynamic Evaluation of a Filtering Hydrocyclone for Solid Particle/Water Separation
Abstract
1. Introduction
2. Methodology
2.1. Problem Description
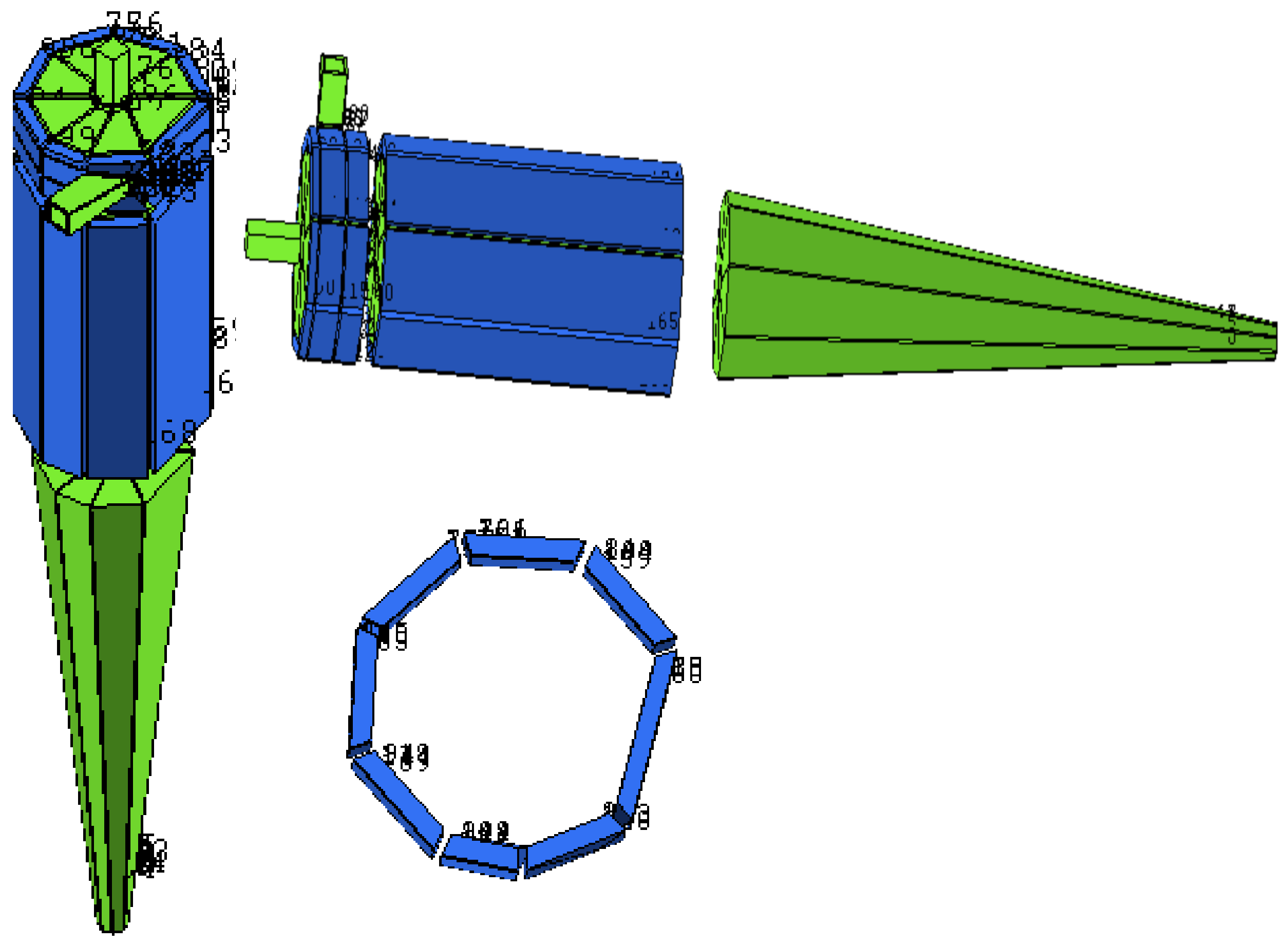
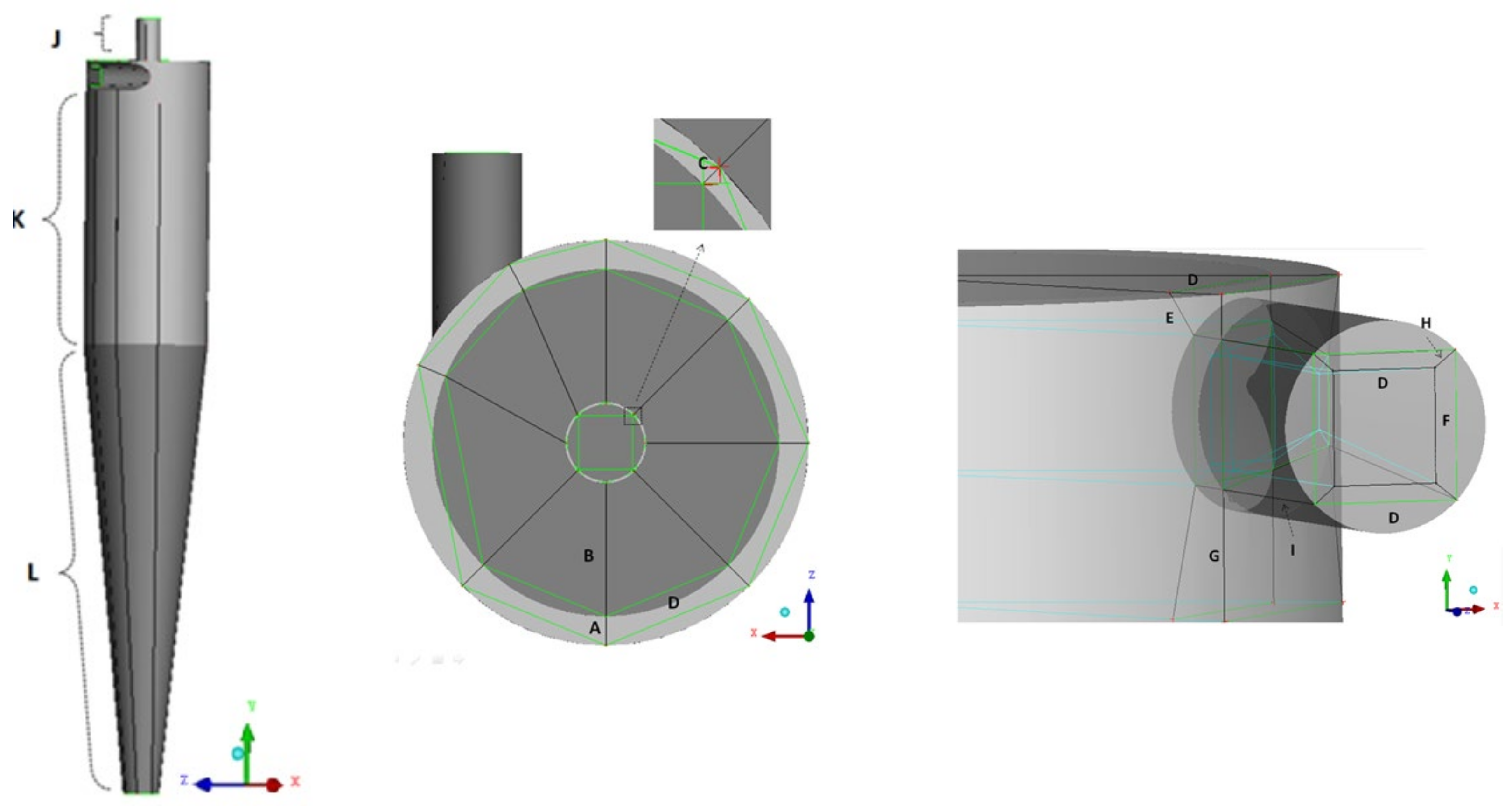
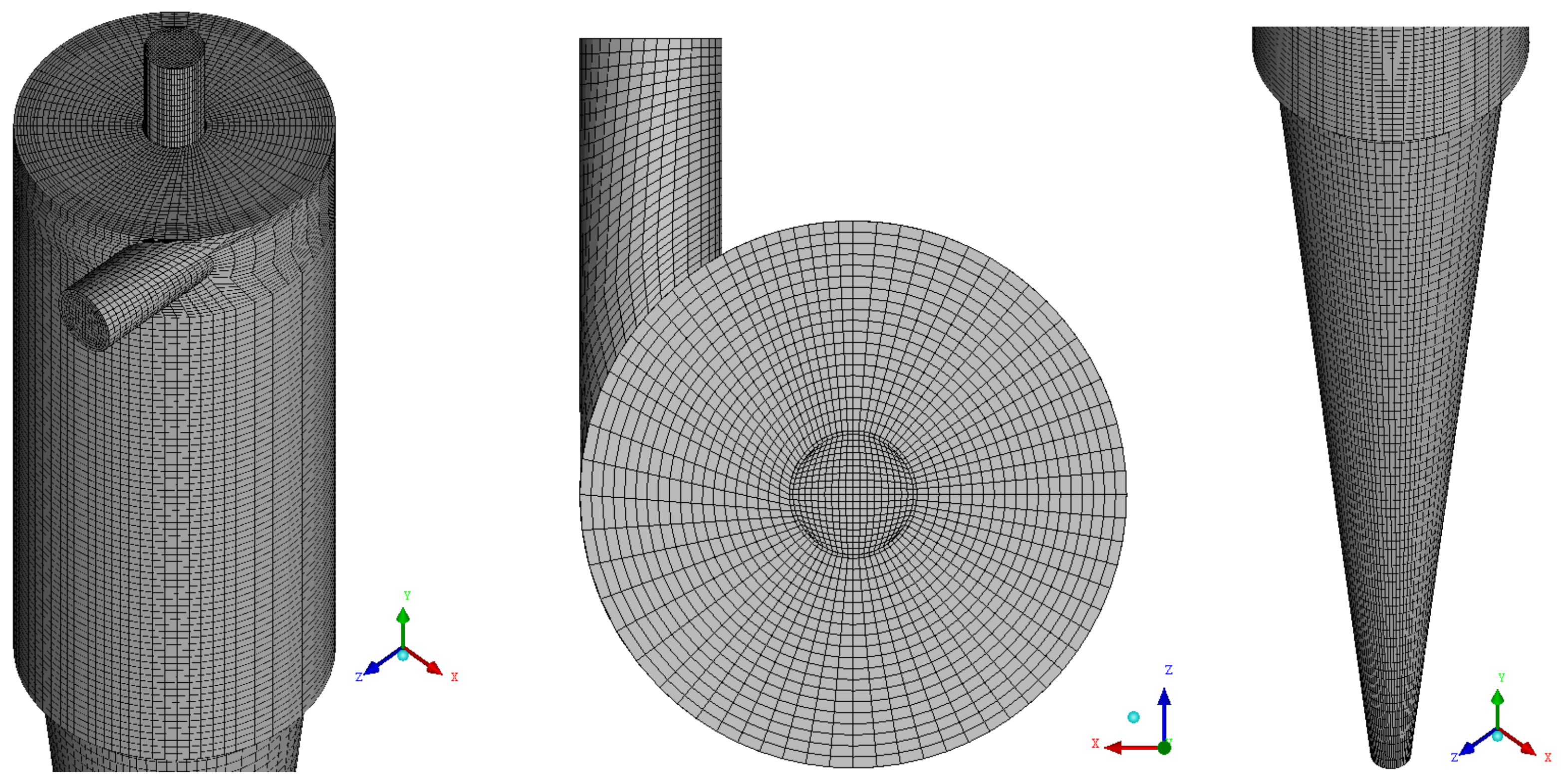
2.2. Computational Domain
- (a)
- Definition of a set of points and curves to represent the geometry;
- (b)
- Selection of a set of blocks through division, merging, boundary definitions, face modifications, and vertex movements;
- (c)
- Verification of block quality to ensure that the blocking generated a high-quality mesh;
- (d)
- Assessment of mesh quality.
2.3. Mathematical Modeling
2.3.1. The Model
- (a)
- Incompressible, steady, and isothermal flow.
- (b)
- Water as the continuous phase, and solid particles as the dispersed phase.
- (c)
- Particles were assumed to be spherical with a diameter of 9.34 μm [28].
- (d)
- Flow with constant physical and chemical properties.
- (e)
- There is no mass source.
- (f)
- Porosity and permeability were assumed to be uniformly distributed in the porous medium.
- (a)
- Mass Conservation
- (b) Linear Momentum Conservation
- (c) Turbulence Model
- (d) Porous Medium Model
2.3.2. Boundary Conditions Used in Simulations
- (a)
- Inlet
- (b)
- Walls
- (c) Outlets
2.3.3. Thermophysical and Chemical Parameters of Materials Used in Simulations
2.3.4. Auxiliary Equations
- (a)
- Pressure Drop
- (b) Filtrate Flow
- (c) Euler Number
- (d) Liquid Ratio
- (e) Total Efficiency
2.4. Studied Case
3. Results and Discussion
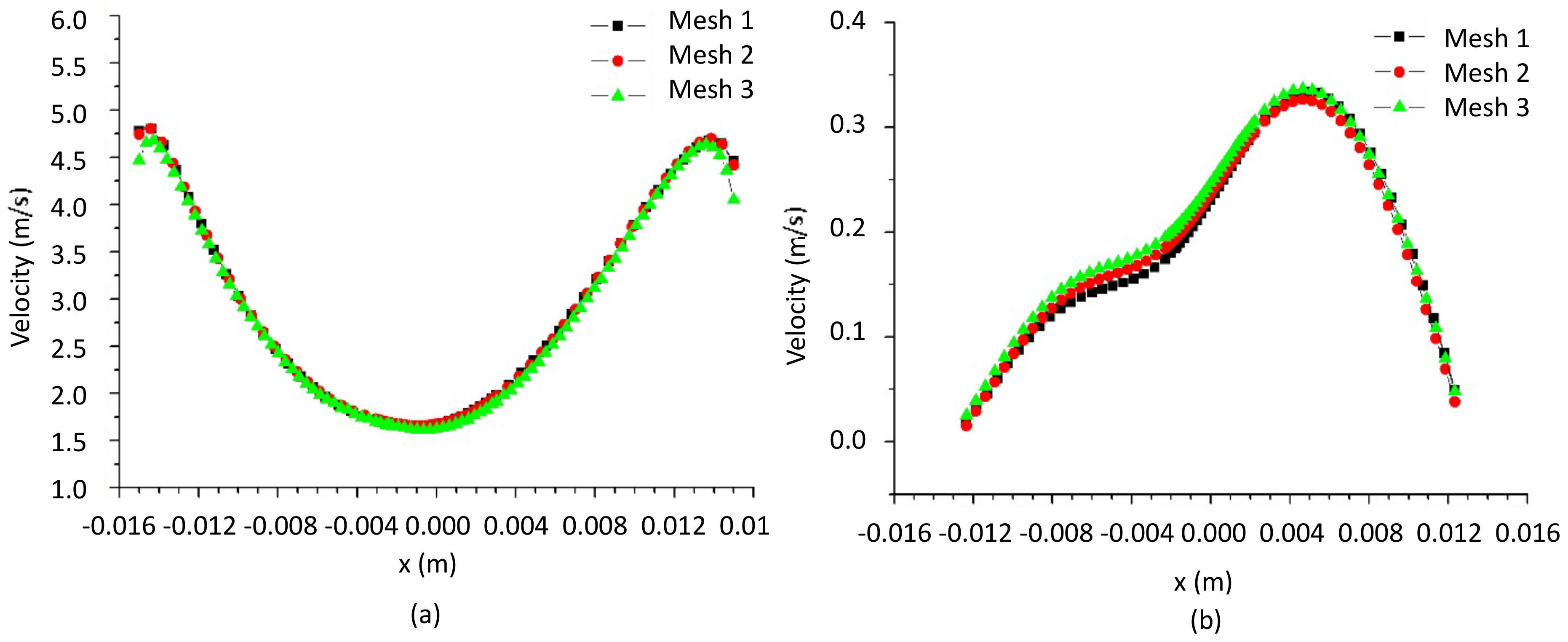
3.1. Mesh Quality Assessment
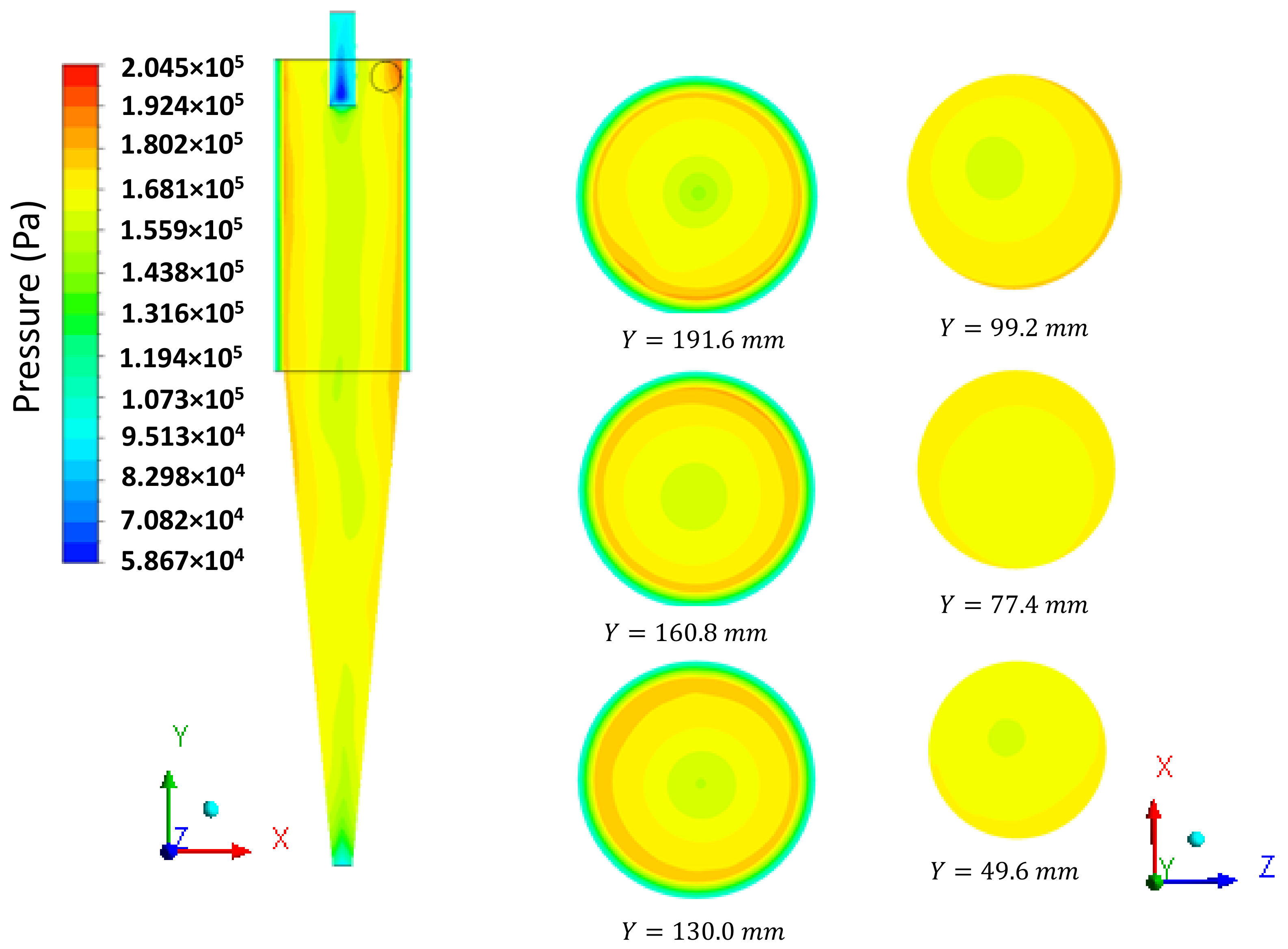
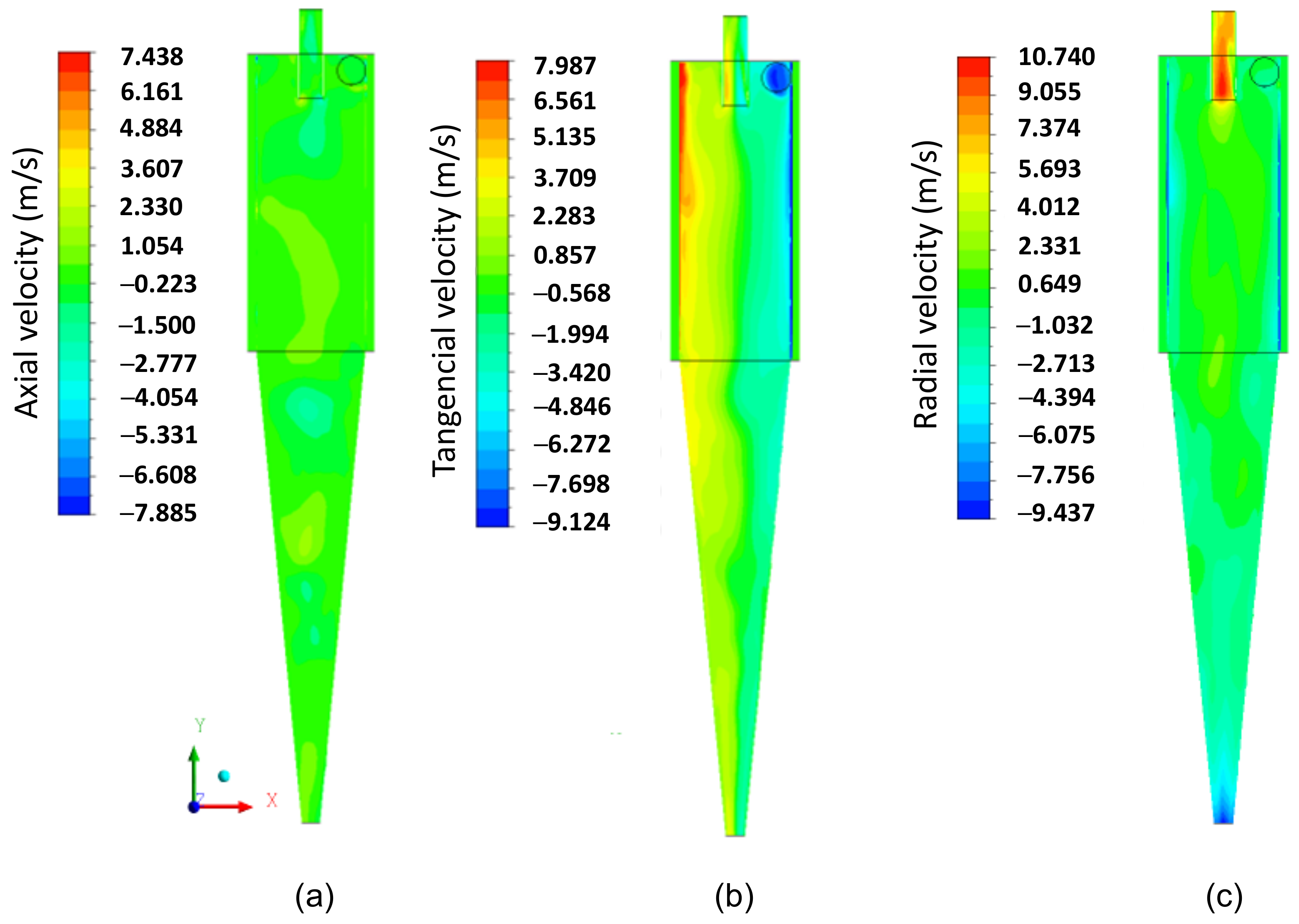
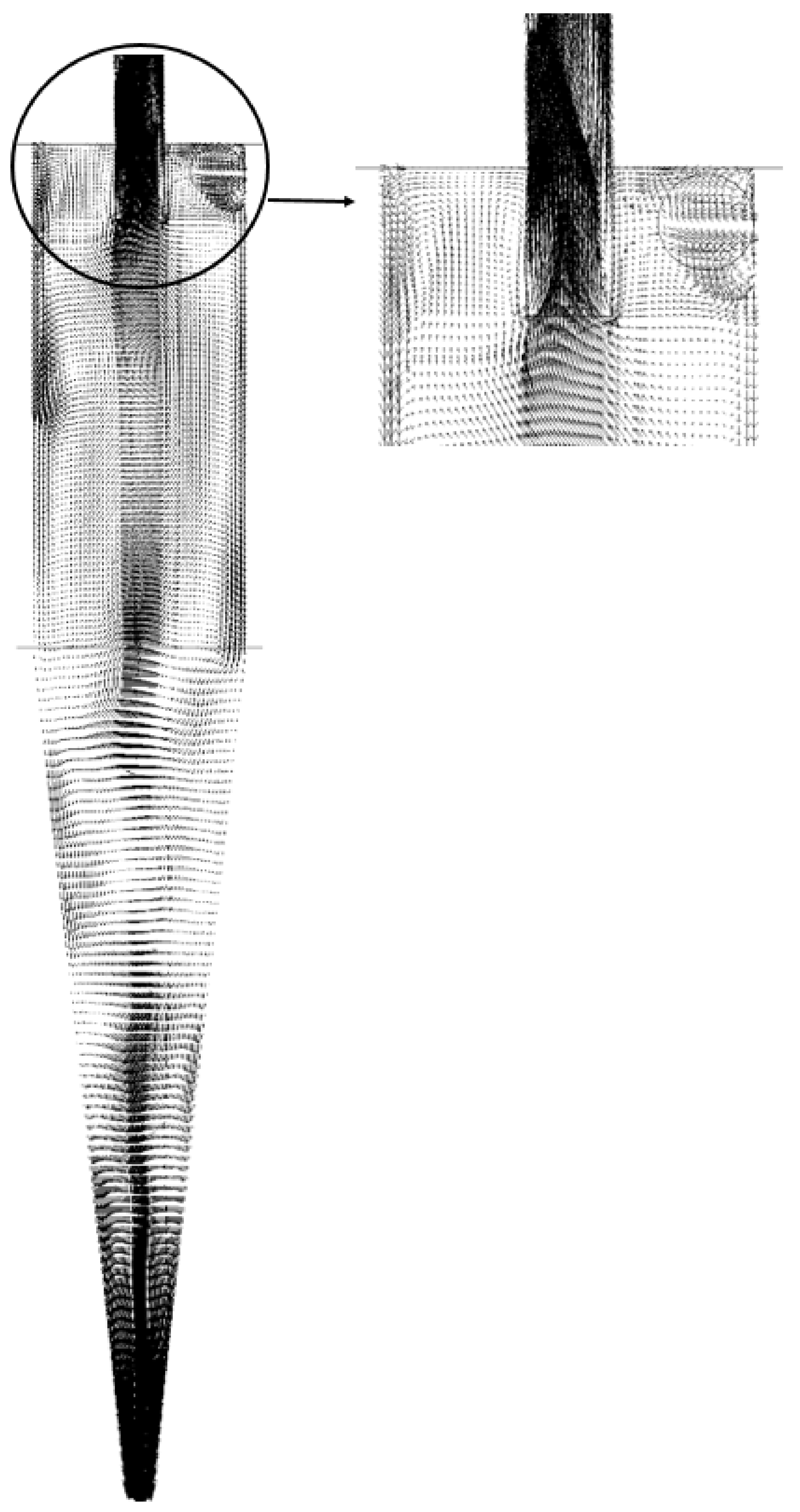
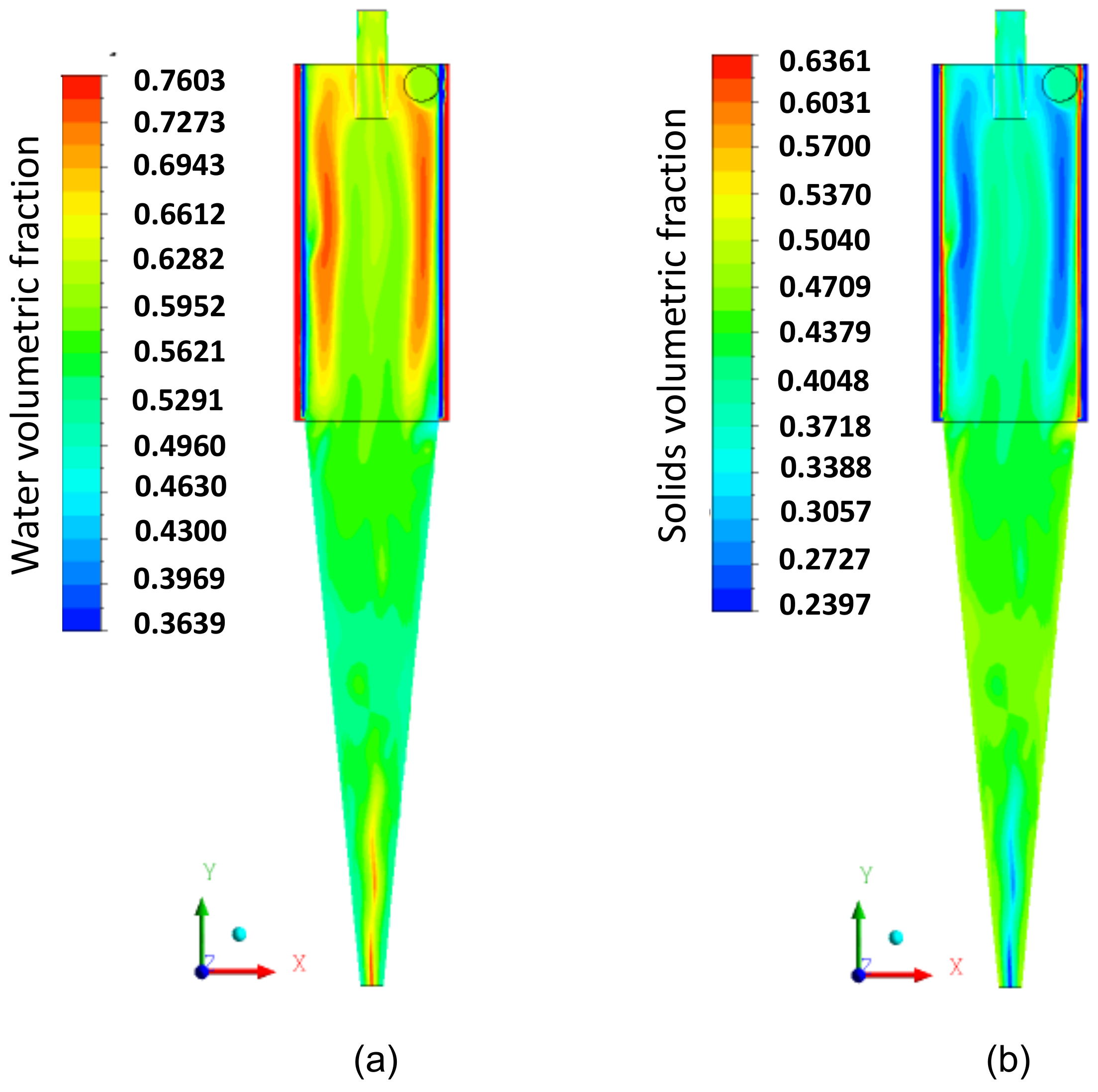
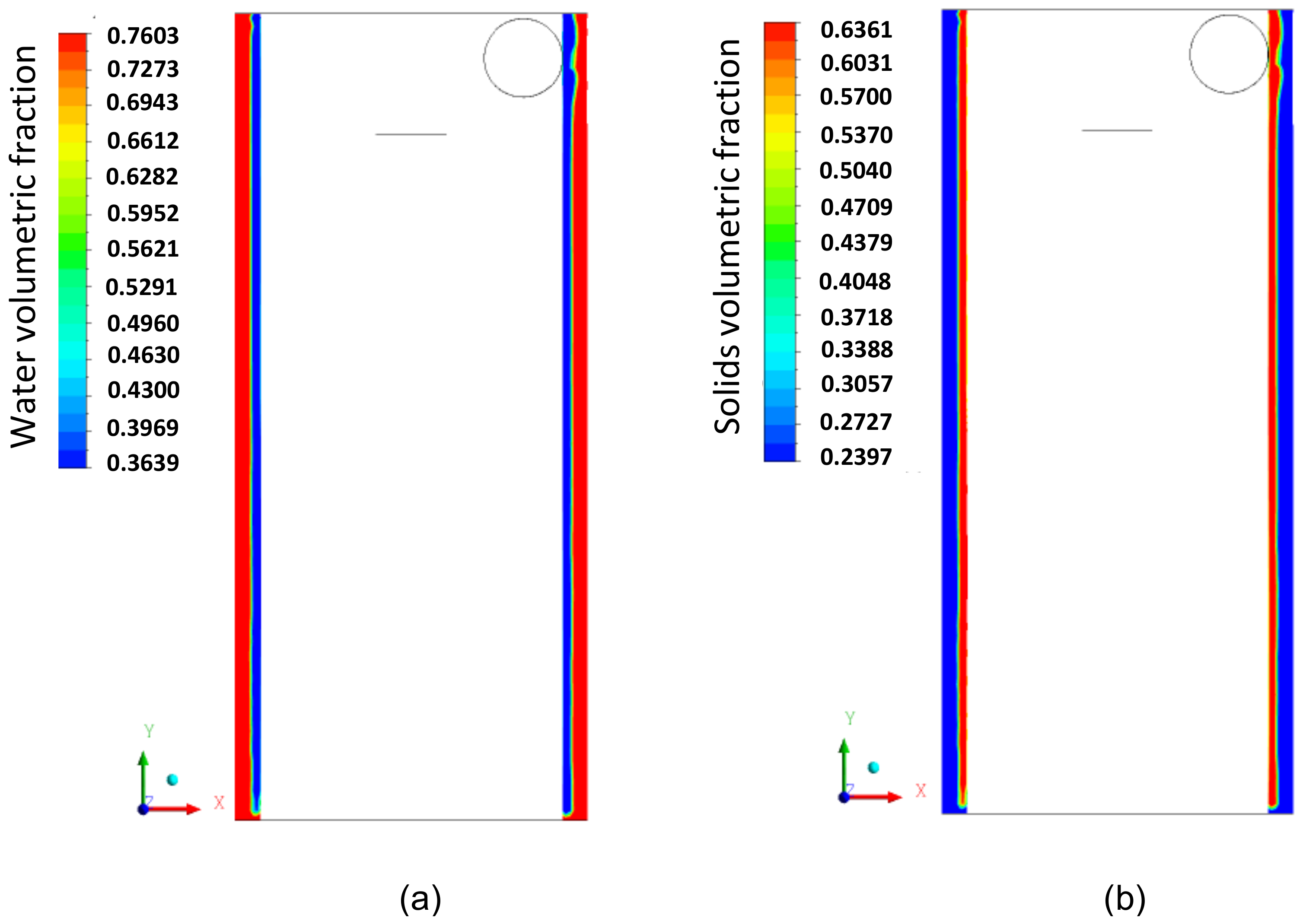
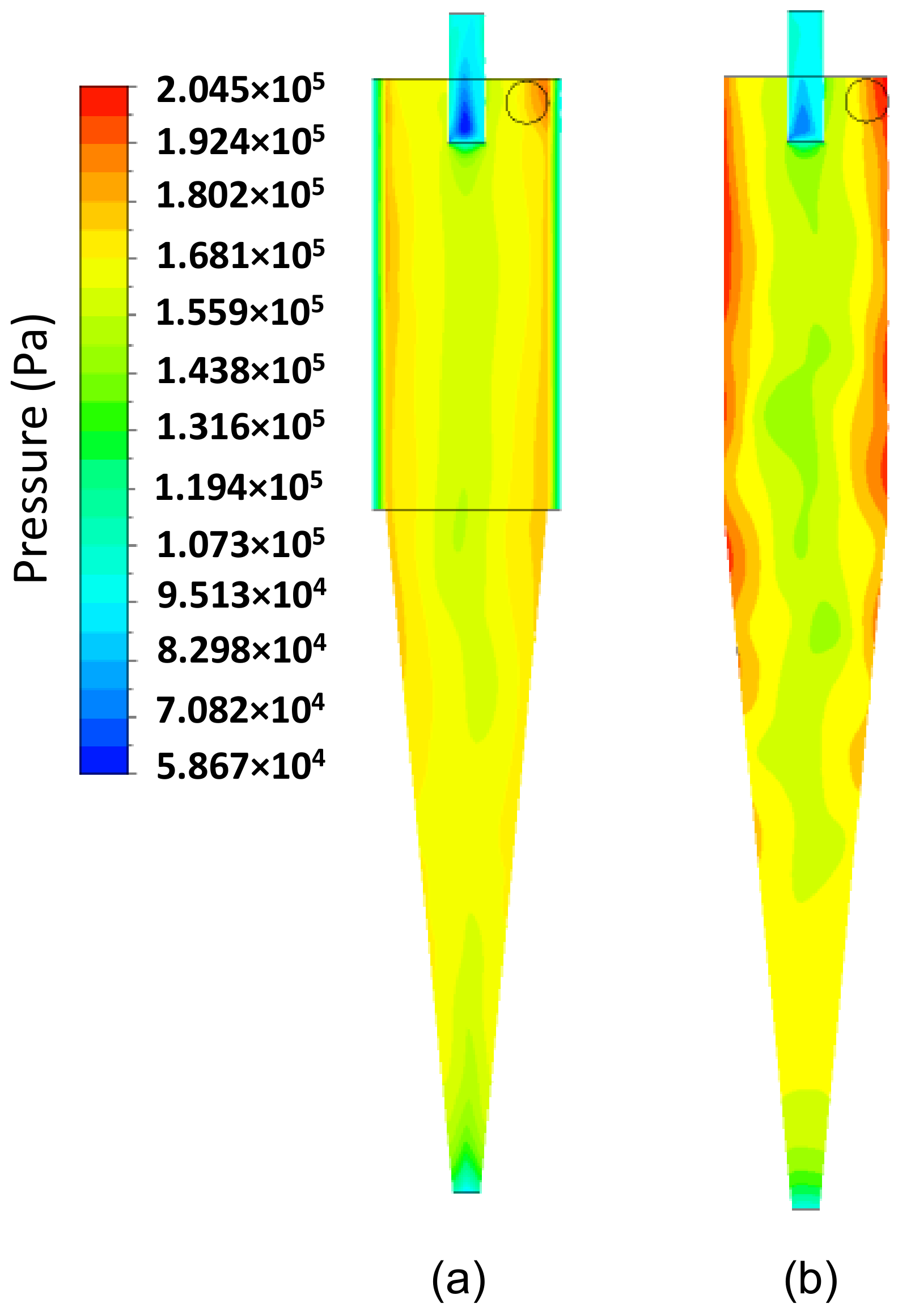
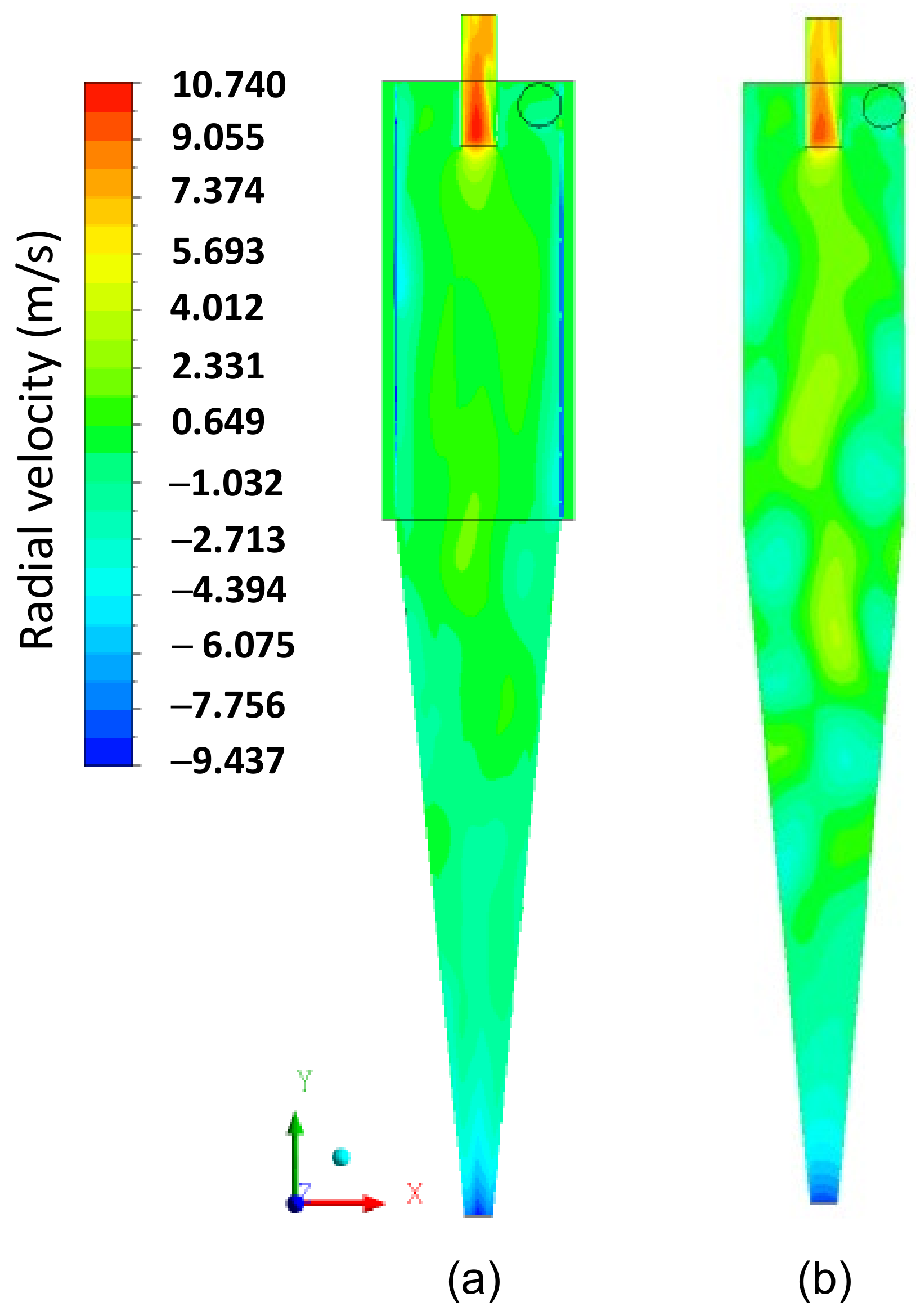
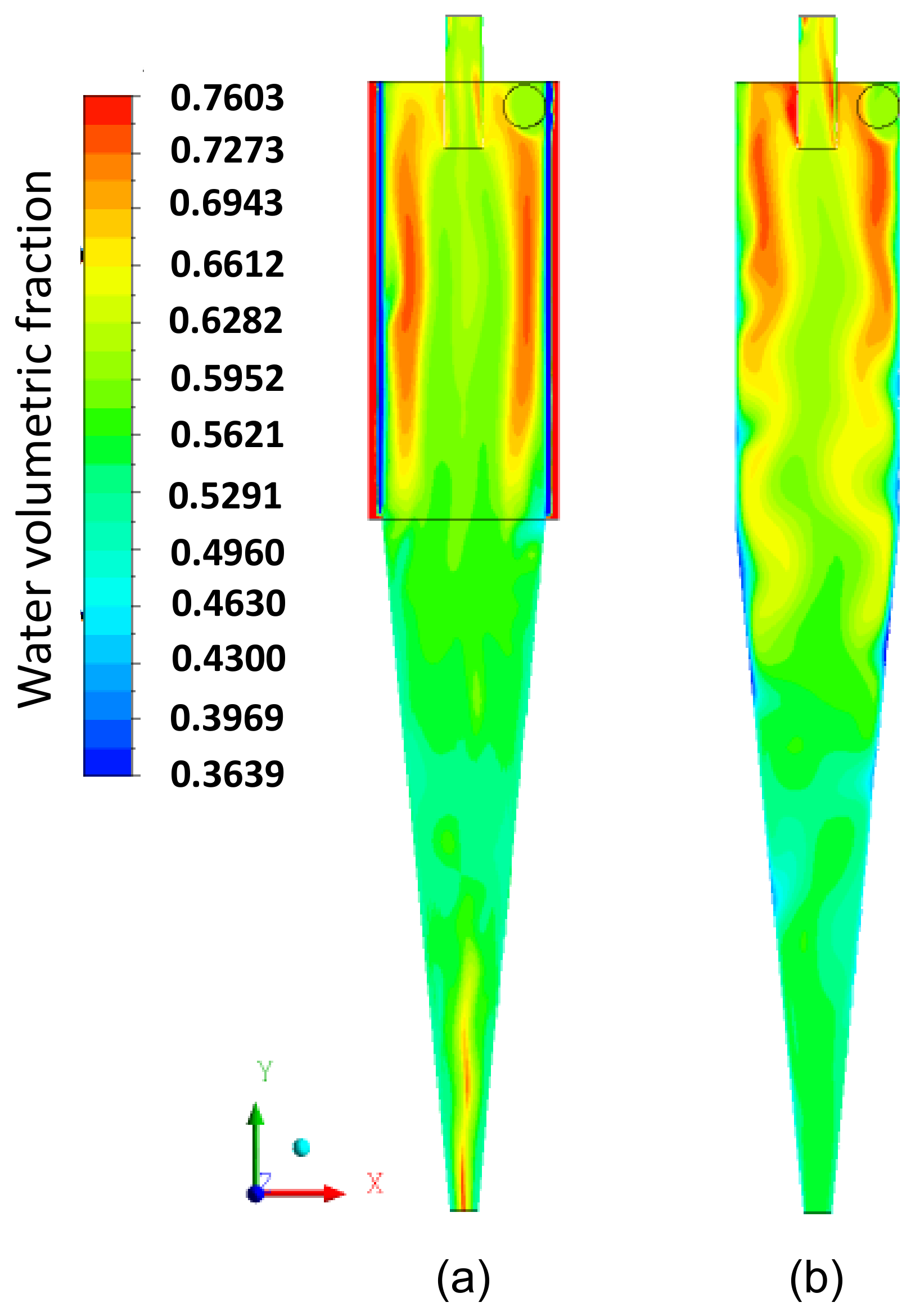
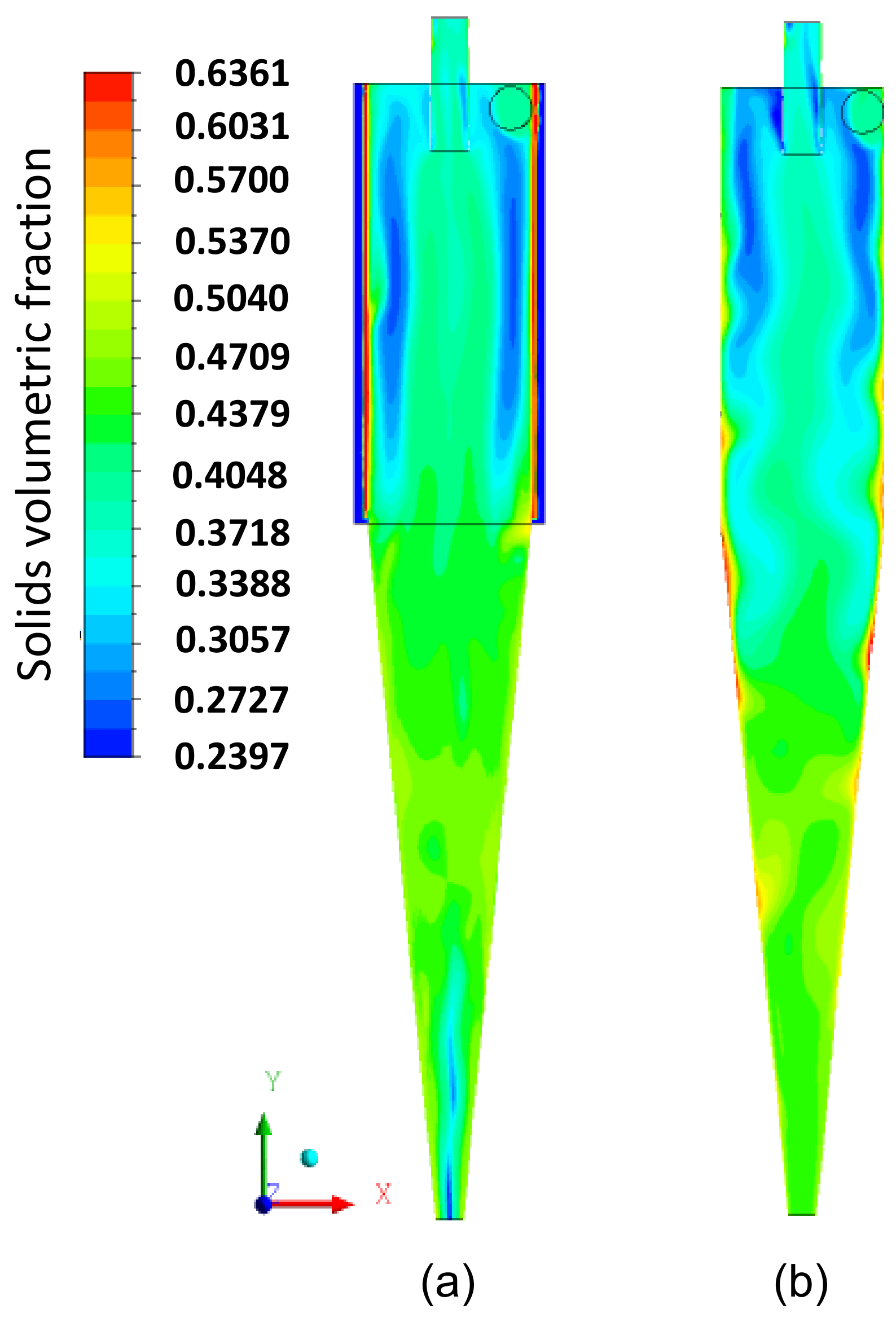
3.2. Flow Dynamics in the Hydrocyclone with Cylindrical Filtering Medium
3.3. A Comparison between the Conventional and Filtering Hydrocyclones
3.4. Advances and Challenges to Increase the Performance of Filtering Hydrocyclones
- (a)
- Regarding the membranes: Implementing porous membranes in hydrocyclones involves addressing practical challenges such as construction planning and managing pressure gradients across the device. Effective materials selection, considering mechanical, thermal, and hydric properties like rupture and flexural stresses, thermal conductivity, thermal diffusivity, specific heat, porosity and permeability, is crucial for optimizing filtering hydrocyclone performance and reliability.
- (b)
- Regarding the others fixed part of the filtering hydrocyclone: Construction planning and economic analysis involving the inlet and outlet types, the shape and dimensions of fixed parts, such as overflow, underflow, and cylindrical and conical parts, play an important role in increasing the separation performance of filtration devices.
- (c)
- Regarding numerical simulation: The robustness of the mathematical modeling and advanced and innovative numerical simulation tools can significantly improve the understanding related to the interactions between solid and fluid particles during the isothermal and non-isothermal flows in the filtering hydrocyclone. These powerful tools allow excellent predictions and easy control of physical and thermal effects, ensuring the safety of the filtration device and helping to make safe decisions.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rosa, J.J. Treatment of Oily Effluents by In-Line Pneumatic Flocculation and Separation by Flotation—FF Process. Ph.D. Thesis, PPGEM-UFRGS, Porto Alegre, Brazil, 2002. (In Portuguese). [Google Scholar]
- Rego, F.C.A. Study of the Cylindrical Hydrocyclone of a Centrifugal Flotation Unit with the Aid of Computational Fluid Dynamics. Master’s Thesis, Chemical and Biochemical Process Technology, Federal University of Rio de Janeiro, Rio de Janeiro, Brazil, 2008. [Google Scholar]
- Hargreaves, J.H.; Silvester, R.S. Computational Fluid Dynamics Applied to the Analysis of Deoiling Hydrocyclone Performance. Chem. Eng. Res. Des. 1990, 68, 365–383. [Google Scholar]
- Simões, A.M.B.M.; Farias Neto, S.R.; Cavalcanti, R.S. Evaluation of Turbulent Intensity in a Cylindrical-Conical Body via CFX. In Proceedings of the XV Brazilian Congress of Chemical Engineering, Curitiba, Brazil, 26–27 September 2004. [Google Scholar]
- Husveg, T.; Rambeau, O.; Drengstig, T.; Bilstad, T. Performance of Deoiling Hydrocyclone during Variable Flow Rates. Miner. Eng. 2007, 20, 368–379. [Google Scholar] [CrossRef]
- Vieira, L.G.M.; Damasceno, J.J.R.; Barrozo, M.A.S. Improvement of Hydrocyclone Separation Performance by Incorporating a Conical Filtering Wall. Chem. Eng. Process. Process Intensif. 2007, 49, 460–467. [Google Scholar] [CrossRef]
- Simões, A.M.B.M. Separation of Spilled Water-Oil in the Sea Using a Hydrocyclone: A Numerical Study of the Turbulence Intensity Caused by the Feed Duct. Master’s Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2008. (In Portuguese). [Google Scholar]
- Mousavian, S.M.; Najafi, A.F. Numerical Simulations of Gas-Liquid-Solid Flows in a Hydrocyclone Separator. Arch. Appl. Mech. 2008, 79, 395–409. [Google Scholar] [CrossRef]
- Buriti, C.J.O. Application of a Hydrocyclone in the Separation Process of Multiphase Fluids Oil/Water/Sand During Oil Production; Monograph; PRH-25/ANP-UFCG: Campina Grande, Brazil, 2009. (In Portuguese) [Google Scholar]
- Farias, F.P.M.; Lima, A.G.B.; Neto, S.R.F. Influence of the Lower Outlet Duct of the Cyclone Used as a Dryer: Modeling and Simulation. In Proceedings of the XVII Brazilian Congress of Chemical Engineering (COBEQ2008), Recife, Brazil, 14–17 September 2008; pp. 1–8. (In Portuguese). [Google Scholar]
- Farias, F.P.M.; Neto, S.R.F.; Lima, A.G.B.; Buriti, C.J.O. Performance of the Water/Glycerine Separation by Hydrocyclone. In Proceedings of the 8th World Congress on Computational Mechanics (WCCM 2008) & 5th European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2008), Venice, Italy, 30 June–5 July 2008. [Google Scholar]
- Farias, F.P.M.; Buriti, C.J.O.; Lima, W.C.P.B.d.; Farias Neto, S.R.; Lima, A.G.B. Numerical Simulation of the Separation Process Sand/Water/Heavy Oils in Hydrocyclones. In Proceedings of the Congress of Numerical Methods in Engineering, Barcelona, Spain, 29 June–2 July 2009. [Google Scholar]
- Farias, F.P.M.; Buriti, C.; Lima, W.; Farias Neto, S.R.; Lima, A. The Effect of Droplet Diameter on the Separation of Heavy-Oil from Water Using a Hydrocyclone. Defect and Diffusion Forum; Trans Tech Publications Ltd.: Wollerau, Switzerland, 2010; pp. 131–137, 303–304. [Google Scholar]
- Barbosa, E.S. Geometric and Hydrodynamic Aspects of a Hydrocyclone in the Separation Process of Multiphase Systems: Application to the Petroleum Industry. Ph.D. Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2011. [Google Scholar]
- Souza, J.A.R. Solid Drying via Cyclones: Modeling and Simulation. Ph.D. Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2012. (In Portuguese). [Google Scholar]
- Thomas, J.E. Fundamentals of Petroleum Engineering; Interciência: Rio de Janeiro, Brazil, 2001. (In Portuguese) [Google Scholar]
- Marins, L.P.M. Experimental Characterization of the Flow inside a Gas-Free Hydrocyclone. Master’s Thesis, Graduate Program in Mechanical Engineering, COPPE, Rio de Janeiro, Brazil, 2007. (In Portuguese). [Google Scholar]
- Raposo, G.M. Numerical Simulation of Flow in a Hydrocyclone for High-Oil Content Applications. Master’s Thesis, Pontifical Catholic University of Rio de Janeiro, Rio de Janeiro, Brazil, 2008. (In Portuguese). [Google Scholar]
- Dianyu, E.; Xu, G.; Cui, J.; Ye, Q.; Tan, C.; Zou, R.; Kuang, S. Prediction of instantaneous flow characteristics of hydrocyclone with long short-term memory network based on computational fluid dynamics data. Powder Technol. 2024, 439, 119668. [Google Scholar]
- Ji, L.; Paul, P.; Shanbhag, B.K.; Dixon, I.; Kuang, S.; He, L. Emerging application of hydrocyclone in biotechnology and food processing. Sep. Purif. Technol. 2023, 309, 122992. [Google Scholar] [CrossRef]
- Tan, C.; Hu, H.; Ye, Q.; Dianyu, E.; Cui, J.; Zhou, Z.; Kuang, S.; Zou, R.; Yu, A. Multi-objective optimization of hydrocyclones using meta-heuristic algorithms and preference-informed decision-making. Powder Technol. 2024, 444, 120050. [Google Scholar] [CrossRef]
- Vieira, L.G.M. Optimization of Separation Processes in Filtering Hydrocyclones. Ph.D. Thesis, Federal University of Uberlândia, Uberlândia, Brazil, 2006. (In Portuguese). [Google Scholar]
- Henrique, H.M.; Barrozo, M.A.S.; Damasceno, J.J.R. Study of the Dynamics of a Filtering Settler. In Proceedings of the XV National Meeting on Flow in Porous Media, Uberlândia, Brazil, 21–23 October 1987; pp. 303–310. [Google Scholar]
- Barrozo, M.A.S.; Damasceno, J.J.R.; Lanna, A.E. Performance Study of a Filtering Hydrocyclone. Sci. Eng. J. 1992, 1, 175–186. [Google Scholar]
- Vieira, L.G.M. Analysis of Solid-Liquid Separation in a Filtering Hydrocyclone; Scientific Initiation Report; UFU: Uberlândia, Brazil, 1997. [Google Scholar]
- Vieira, L.G.M. Study of the Performance of Rietema Filtering Hydrocyclones. Master’s Thesis, UFU, Uberlândia, Brazil, 2001; 141p. (In Portuguese). [Google Scholar]
- Barbosa, E.A.; Koboldt, C.A.; Vieira, L.G.M.; Damasceno, J.J.R.; Barrozo, M.A.S. Evaluation of the Behavior of Krebs Filtering Hydrocyclones. In Proceedings of the XXX National Meeting on Flow in Porous Media, São Carlos, Brazil, 2002. [Google Scholar]
- Façanha, J.M.F. Incorporation of a Filtering Cylinder in the Solid-Liquid Separation in Hydrocyclones. Master’s Thesis, Federal University of Uberlândia, Uberlândia, Brazil, 2012. (In Portuguese). [Google Scholar]
- Hamza, J.E.; Al-Kayiem, H.H.; Lemma, T.A. Experimental Investigation of the Separation Performance of Oil/Water Mixture by Compact Conical Axial Hydrocyclone. Therm. Sci. Eng. Prog. 2020, 17, 100358. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, B.; Zhao, H.; He, Y. Oil-Water Separation Performance of Aligned Single-Walled Carbon Nanotubes Membrane: A Reactive Molecular Dynamics Simulation Study. J. Mol. Liq. 2020, 321, 114174. [Google Scholar] [CrossRef]
- Nunes, S.A.; Magalhães, H.L.F.; Farias Neto, S.R.; Lima, A.G.B.; Nascimento, L.P.C.; Farias, F.P.M.; Lima, E.S. Impact of Permeable Membrane on the Hydrocyclone Separation Performance for Oily Water Treatment. Membranes 2020, 10, 350. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Deng, S.; Guam, J.; Chen, M.; Hua, W. Development of a Novel High-Efficiency Dynamic Hydrocyclone for Oil-Water Separation. Chem. Eng. Res. Des. 2018, 130, 266–273. [Google Scholar] [CrossRef]
- Nunes, S.A.; Magalhães, H.L.F.; Gomez, R.S.; Vilela, A.F.; Figueiredo, M.J.; Santos, R.S.; Rolim, F.D.; Souza, R.A.A.; Farias Neto, S.R.; Lima, A.G.B. Oily Water Separation Process Using Hydrocyclone of Porous Membrane Wall: A Numerical Investigation. Membranes 2021, 11, 79. [Google Scholar] [CrossRef] [PubMed]
- Nunes, S.A.; Magalhães, H.L.F.; Gomez, R.S.; Cavalcante, D.C.M.; Oliveira Neto, G.L.; Oliveira, N.G.N.; Farias Neto, S.R.; Pereira, A.S.; Abreu, A.K.F.; Almeida, A.G.F. Impact of the Polarization Layer on the Hydrodynamics and Mechanical Performance of a Filtering Hydrocyclone Applied to Oily Water Separation. Diffus. Found. Mater. Appl. 2022, 30, 33–52. [Google Scholar] [CrossRef]
- Lacerda, A.F. Study of the Effects of Geometric Variables on the Performance of Conventional and Filtering Cyclones. Ph.D. Thesis, Federal University of Uberlândia, Uberlândia, Brazil, 2007. (In Portuguese). [Google Scholar]
- Almeida, C.K.A. Behavior of the Filtering Hydrocyclone in the Face of Modifications in the Underflow Diameter and Vortex Finder Tube. Master’s Thesis, Federal University of Uberlândia, Uberlândia, Brazil, 2008. (In Portuguese). [Google Scholar]
- Wang, B.; Yu, A.B. Numerical Study of Particle-Fluid Flow in Hydrocyclones with Different Body Dimensions, Minerals Engineering. Miner. Eng. 2006, 19, 1022–1033. [Google Scholar] [CrossRef]
- Oliveira, D.C.; Almeida, C.A.K.; Vieira, L.G.M.; Damasceno, J.J.R.; Barrozo, M.A.S. Influence of Geometric Dimensions on the Performance of a Filtering Hydrocyclone: An Experimental and CFD Study. Braz. J. Chem. Eng. 2009, 26, 575–582. [Google Scholar] [CrossRef]
- Cruz, C.C.; Zanini, J.R. Efficiency of a “Rietema” Geometry Hydrocyclone for Water Pre-Filtration. Braz. J. Chem. Eng. 2010, 30, 637–645. [Google Scholar]
- Silva, D.O. Optimization of Solid-Liquid Separation in Hydrocyclones through Geometric Modifications. Master’s Thesis, Federal University of Uberlândia, Uberlândia, Brazil, 2012; 189p. (In Portuguese). [Google Scholar]
- Martins, M.P.B.; Silva, N.K.G.; Barroso, M.A.S. Analysis of the Underflow Orifice Diameter in an Optimal Filtering Hydrocyclone (HFOT 1). In Proceedings of the X Brazilian Congress of Chemical Engineering Scientific Initiation, Vassouras, Brazil, 19–24 December 2013. (In Portuguese). [Google Scholar]
- Salvador, F.F.; Silva, D.O.; Barroso, M.A.S.; Vieira, L.G.M. Influence of Volumetric Concentration on the Feeding of Filtering Hydrocyclones. In Proceedings of the XXV National Meeting on Mineral Processing and Extractive Metallurgy & VIII Meeting of the Southern Hemisphere on Mineral Technology, Goiânia, Brazil, 20–24 October 2013. [Google Scholar]
- Silva, N.K.G.; Silva, D.O.; Vieira, L.G.M.; Barrozo, M.A.S. Effects of Underflow Diameter and Vortex Finder Length on the Performance of a Newly Designed Filtering Hydrocyclone. Powder Technol. 2015, 286, 305–310. [Google Scholar] [CrossRef]
- Gonçalves, M.G. Effect of Solid Concentration and Operational Variables on the Performance of a Concentrator Hydrocyclone. Master’s Thesis, Federal University of Uberlândia, Uberlândia, Brazil, 2016; 109p. (In Portuguese). [Google Scholar]
- Santos, J.S.S.; Farias Neto, S.R.; Lima, A.G.B.; Crivelaro, K.C.O. Transport of Heavy Oils in Catenaries via Core-Flow Technique—Modeling and Simulation. In Proceedings of the VI National Congress of Mechanical Engineering, Campina Grande, Brazil, 18–21 August 2010. (In Portuguese). [Google Scholar]
- Zhang, Z.; Yan, S.; Dong, S.; Dong, K.; Zhang, Y.; Wang, B. Study of the short-circuit flow and circulation flow’s impact on separation performance of cyclone separator with volute-helical inlet. Adv. Powder Technol. 2024, 35, 104281. [Google Scholar] [CrossRef]
- Dianyu, E.; Xu, G.; Fan, H.; Cui, J.; Tan, C.; Zhang, Y.; Zou, R.; Kuang, S.; Yu, A. Numerical investigation of hydrocyclone inlet configurations for improving separation performance. Powder Technol. 2024, 434, 119384. [Google Scholar]
- Dianyu, E.; Fan, H.; Su, Z.; Xu, G.; Zou, R.; Yu, A.; Kuang, S. Numerical study of the multiphase flows and separation performance of hydrocyclone with tapered cross-section inlet. Powder Technol. 2023, 416, 118208. [Google Scholar]
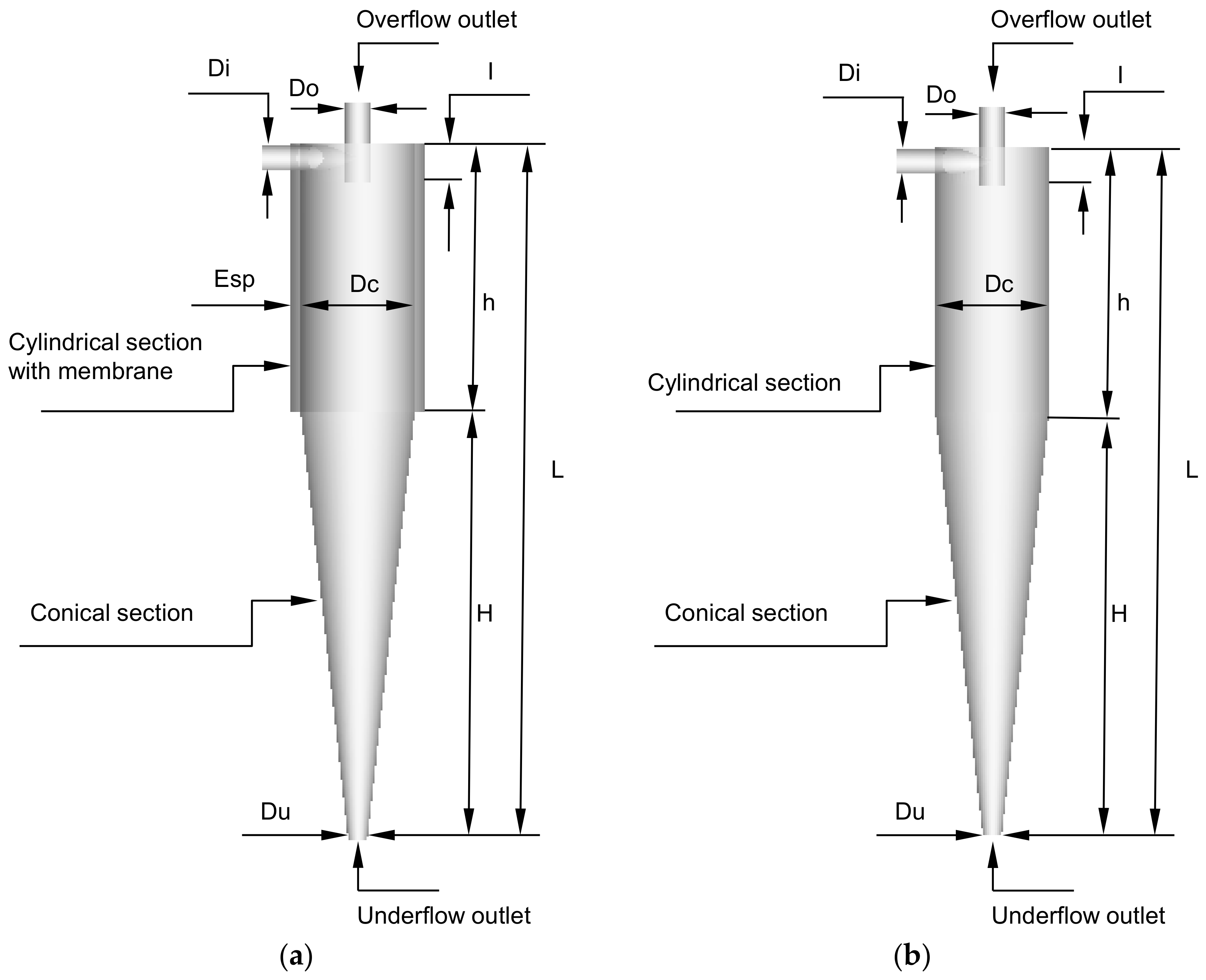
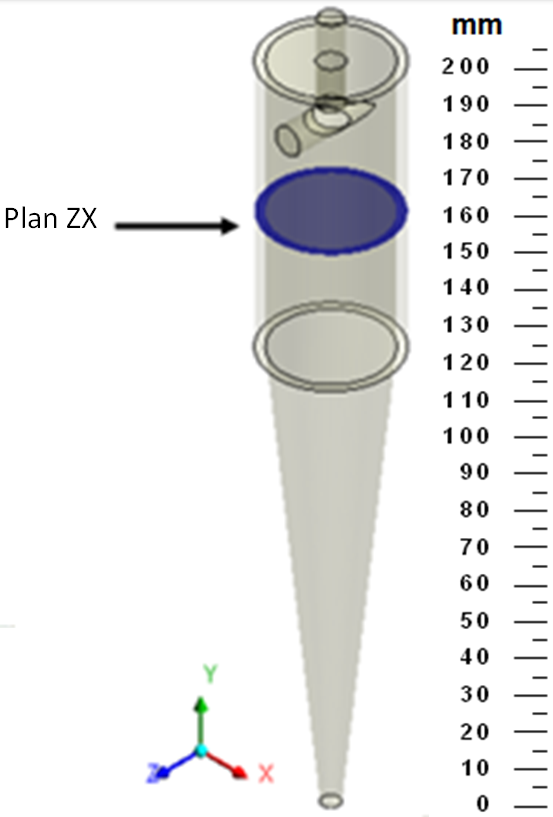
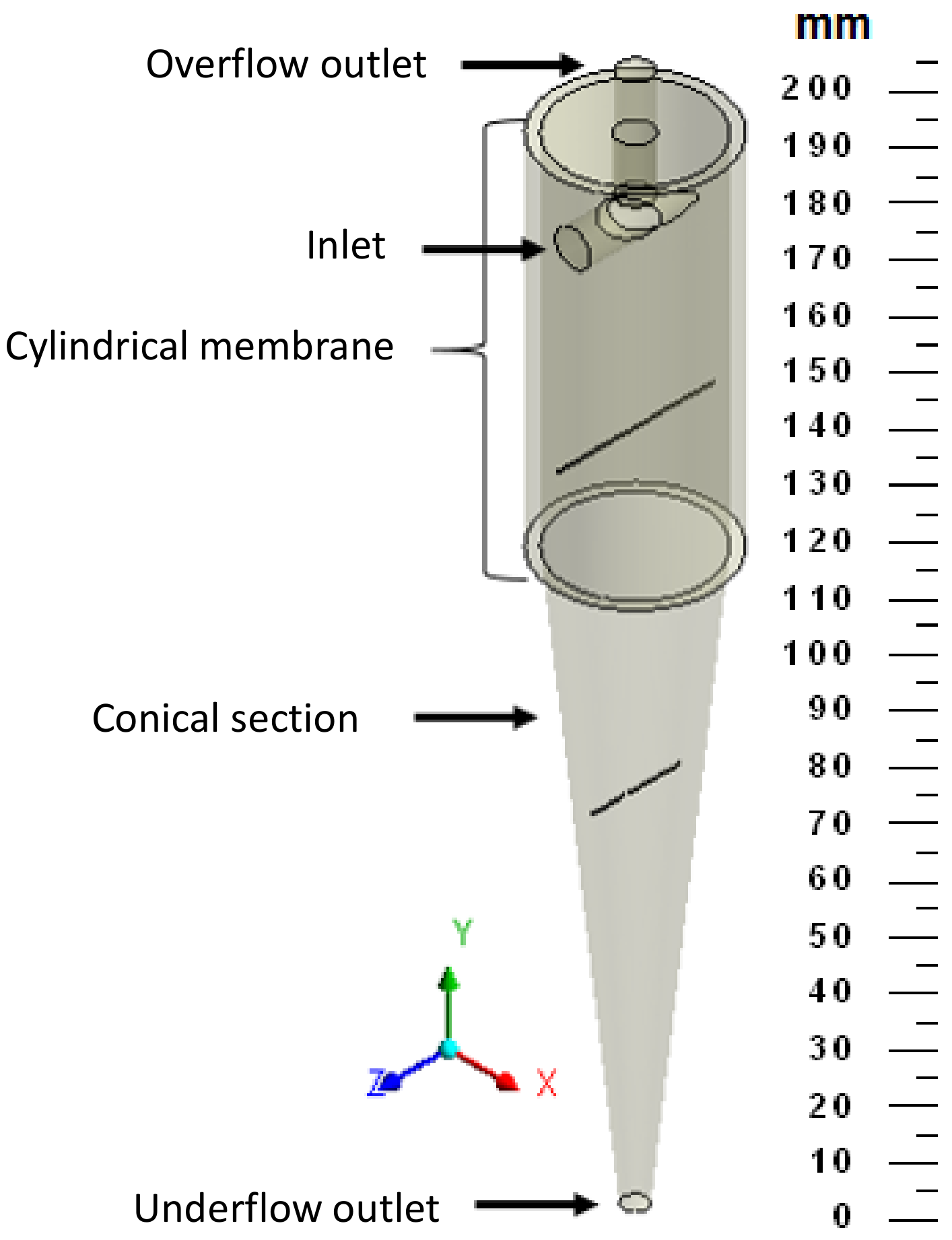



| Dimensions | Hcon | HciF | |
|---|---|---|---|
| Inlet diameter (mm) | Di | 7.8 | 7.8 |
| Underflow diameter (mm) | Du | 5 | 5 |
| Cylinder diameter (mm) | Dc | 30 | 30 |
| Overflow diameter (mm) | Do | 6.6 | 6.6 |
| Vortex finder length (mm) | l | 12 | 12 |
| Cylinder height (mm) | h | 80 | 80 |
| Cone height (mm) | H | 127 | 127 |
| Total Length (mm) | L | 207 | 207 |
| Membrane Thickness (mm) | Esp | - | 2.5 |
| Nodes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | J | K | L |
| 8 | 20 | 2 | 12 | 5 | 10 | 10 | 5 | 20 | 16 | 70 | 80 |
| 10 | 22 | 3 | 12 | 7 | 12 | 12 | 7 | 22 | 18 | 70 | 87 |
| 12 | 24 | 4 | 14 | 9 | 14 | 14 | 9 | 24 | 20 | 72 | 92 |
| Meshes | Number of Elements | Number of Nodes |
|---|---|---|
| 01 | 430,893 | 405,614 |
| 02 | 664,463 | 630,643 |
| 03 | 840,341 | 801,852 |
| Parameter | Material | Source | |
|---|---|---|---|
| Water | Solid Particle | ||
| Density (kg/m3) | 997 | 2860 | Façanha [28] |
| Viscosity (Pa s) | 8.889 × 10−4 | --- | |
| Molar Mass (kg/kmol) | 18.05 | --- | |
| Surface Tension (N/m) | 0.01 | --- | |
| Parameter | Value | Source |
|---|---|---|
| Permeability (m²) | 1.71 × 10−16 | Façanha [28] |
| Porosity (-) | 0.138 |
| Volumetric Flow Rate (cm³/s) | Phase Volumetric Fraction (-) | Fonte | |
|---|---|---|---|
| Continuous | Dispersed | ||
| 295.7 | 0.9 | 0.1 | Façanha [28] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cavalcante, D.C.M.; Magalhães, H.L.F.; Neto, S.R.F.; Gomez, R.S.; Delgado, J.M.P.Q.; Lima, A.G.B.; Vasconcelos, D.B.T.; Silva, M.J.V.; Farias, D.O.; Queiroz, S.F.A.M.; et al. Hydrodynamic Evaluation of a Filtering Hydrocyclone for Solid Particle/Water Separation. Membranes 2024, 14, 171. https://doi.org/10.3390/membranes14080171
Cavalcante DCM, Magalhães HLF, Neto SRF, Gomez RS, Delgado JMPQ, Lima AGB, Vasconcelos DBT, Silva MJV, Farias DO, Queiroz SFAM, et al. Hydrodynamic Evaluation of a Filtering Hydrocyclone for Solid Particle/Water Separation. Membranes. 2024; 14(8):171. https://doi.org/10.3390/membranes14080171
Chicago/Turabian StyleCavalcante, Daniel C. M., Hortência L. F. Magalhães, Severino R. Farias Neto, Ricardo S. Gomez, João M. P. Q. Delgado, Antonio G. B. Lima, Danielle B. T. Vasconcelos, Márcio J. V. Silva, Daniel O. Farias, Suelyn F. A. M. Queiroz, and et al. 2024. "Hydrodynamic Evaluation of a Filtering Hydrocyclone for Solid Particle/Water Separation" Membranes 14, no. 8: 171. https://doi.org/10.3390/membranes14080171
APA StyleCavalcante, D. C. M., Magalhães, H. L. F., Neto, S. R. F., Gomez, R. S., Delgado, J. M. P. Q., Lima, A. G. B., Vasconcelos, D. B. T., Silva, M. J. V., Farias, D. O., Queiroz, S. F. A. M., Santos, A. C. Q., Tito, T. L. H., & Silva, E. F. M. (2024). Hydrodynamic Evaluation of a Filtering Hydrocyclone for Solid Particle/Water Separation. Membranes, 14(8), 171. https://doi.org/10.3390/membranes14080171








