Effects of Varying Spiral-Ring Pitches on CO2 Absorption by Amine Solution in Concentric Circular Membrane Contactors
Abstract
1. Introduction
2. Theory and Analysis
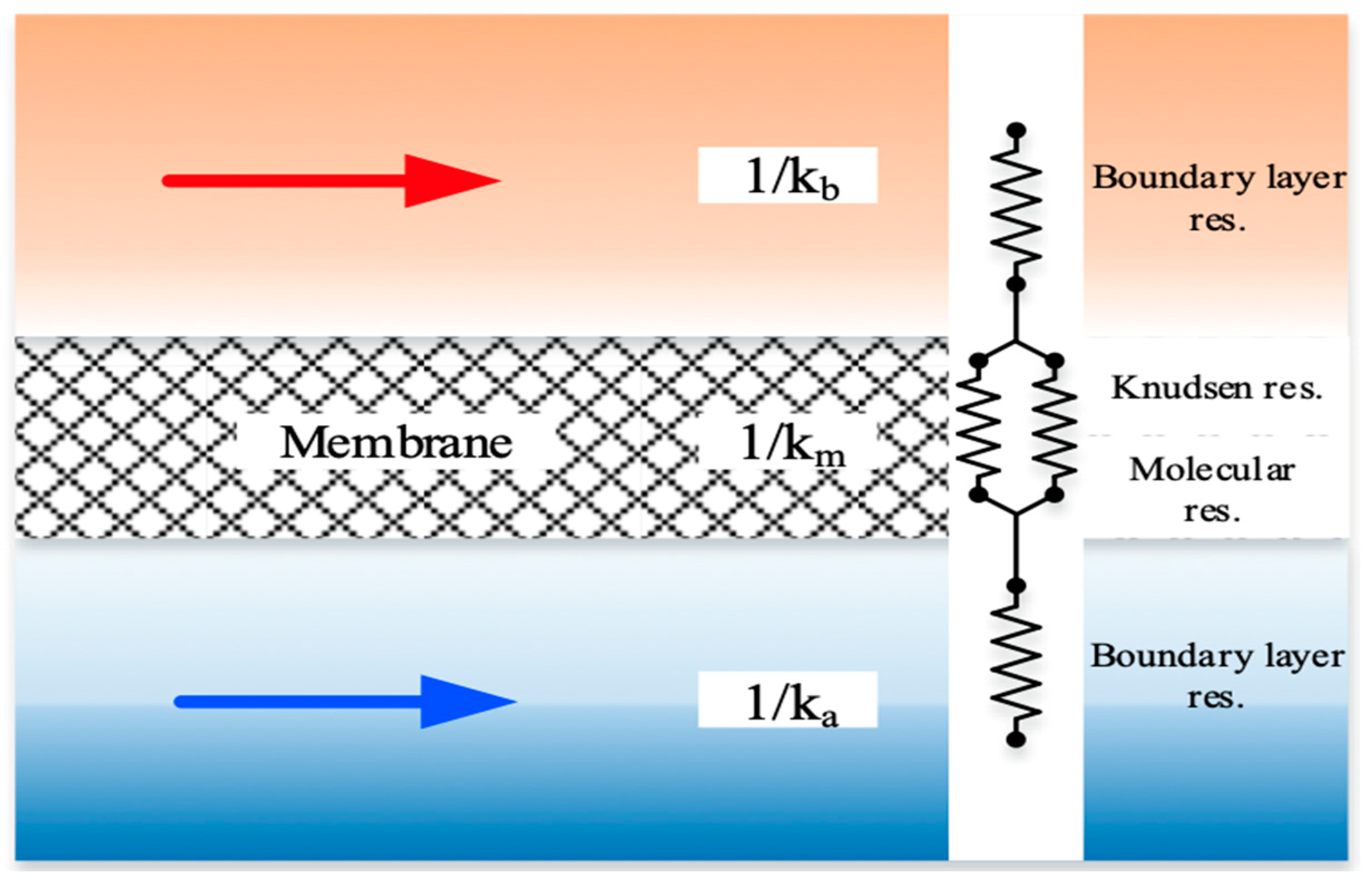
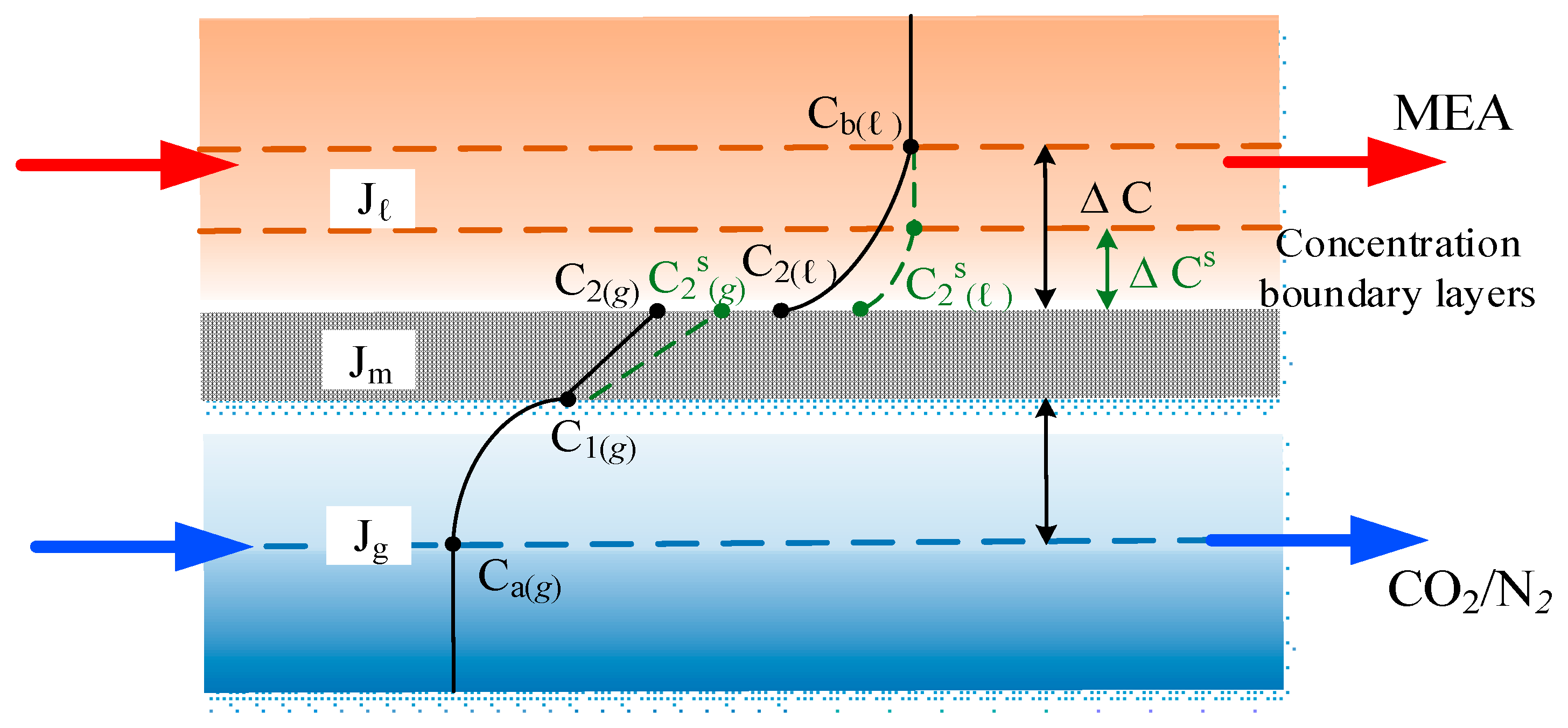
2.1. Mass Transfer
2.2. Concentration Polarization Coefficient
2.3. Design of Spiral-Ring Module
2.4. Model Building by Using Macroscopic Description
2.5. Assessment of Mass Transfer Rate Enhancement
2.6. Power Consumption Increment
3. Membrane Absorption Experiments
4. Results and Discussions
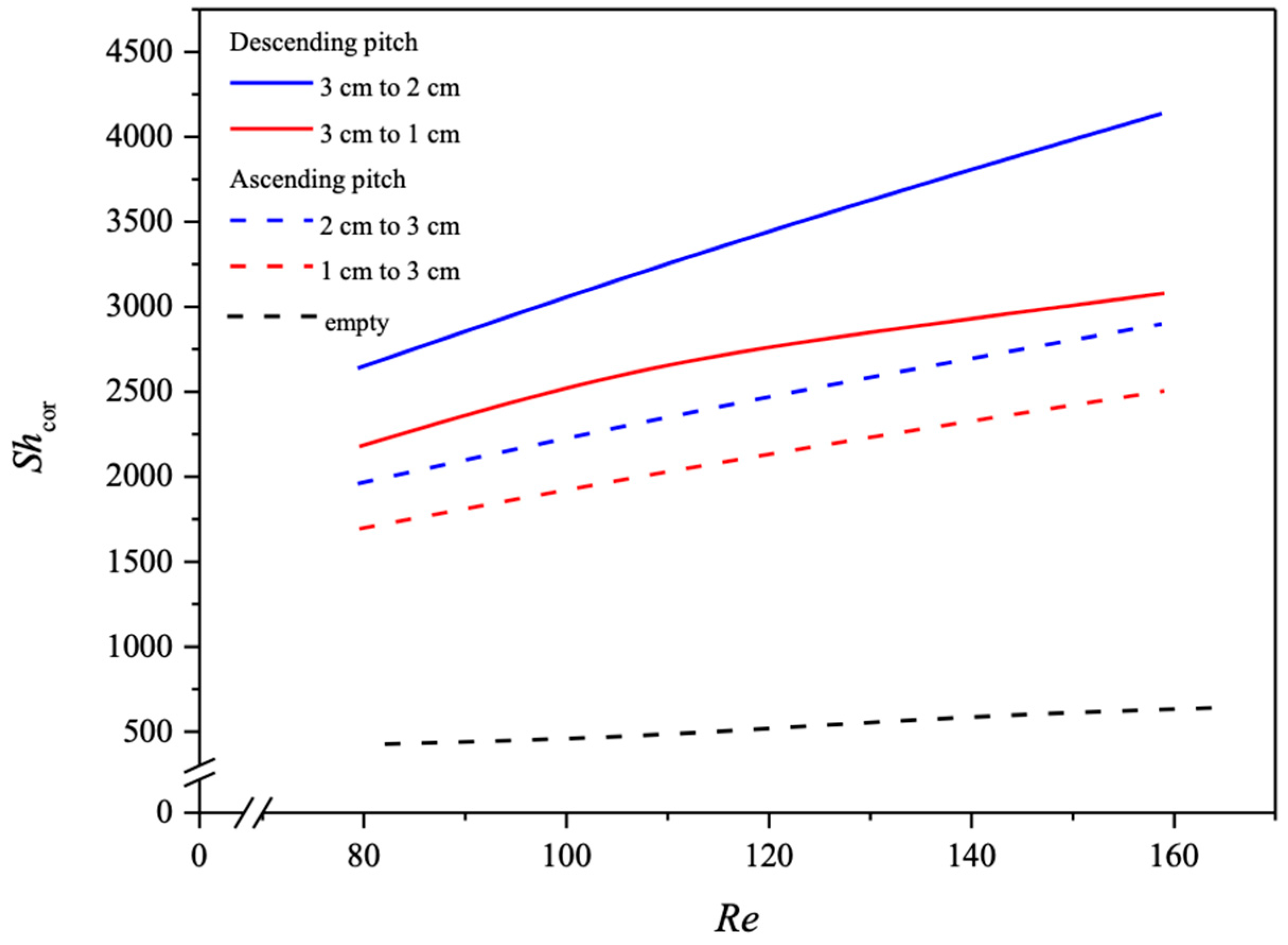
4.1. Correlated Sherwood Numbers
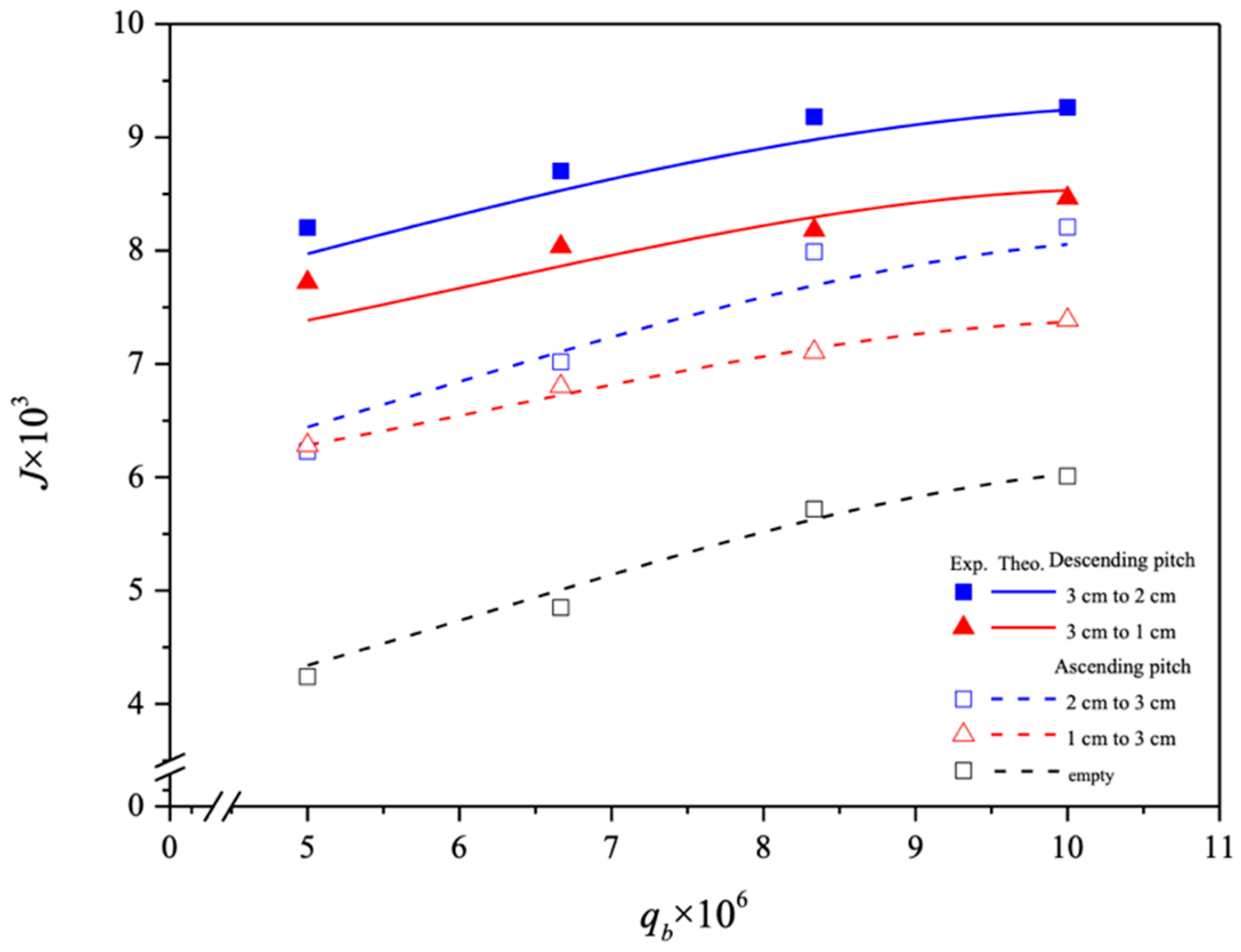
4.2. CO2 Absorption Flux Improvement by Embedding Various Spiral Ring Pitches
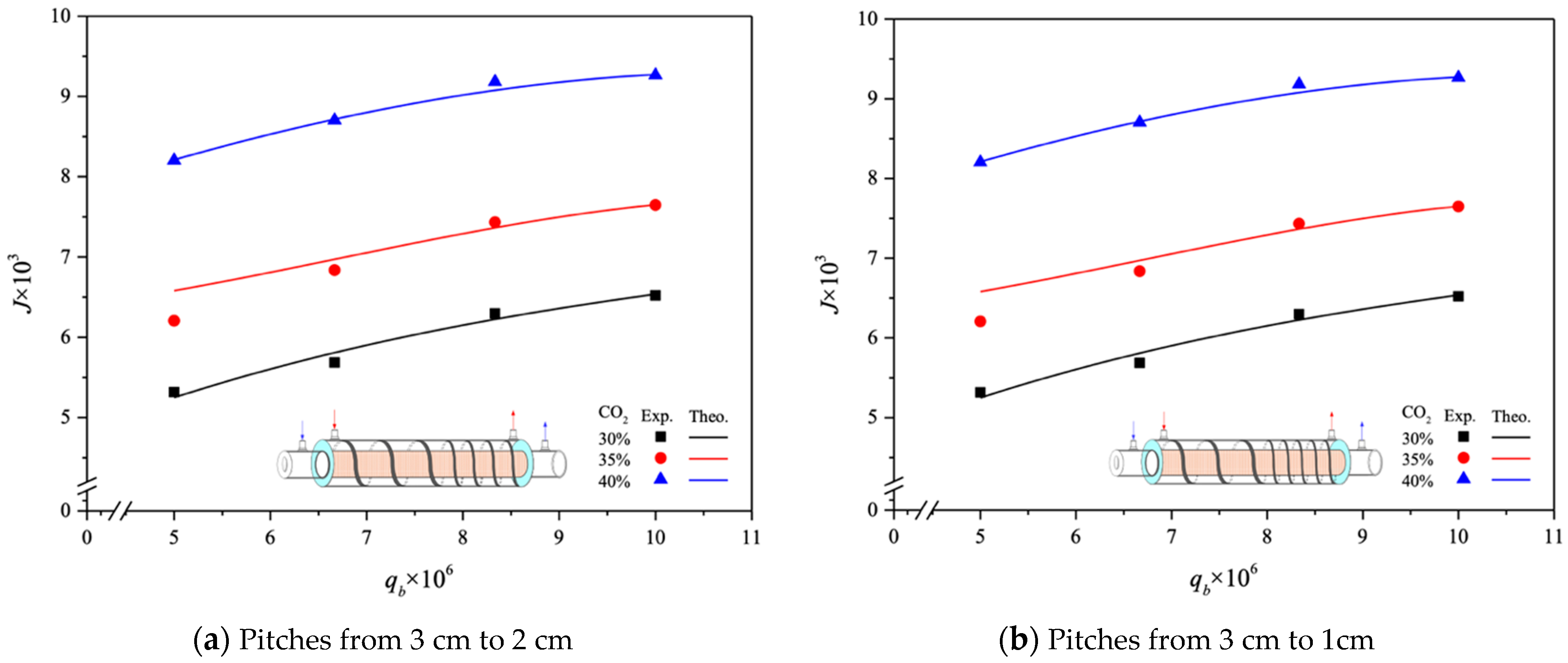
4.3. Further CO2 Absorption Flux Enhancement
4.4. Power Consumption Increment
5. Conclusions
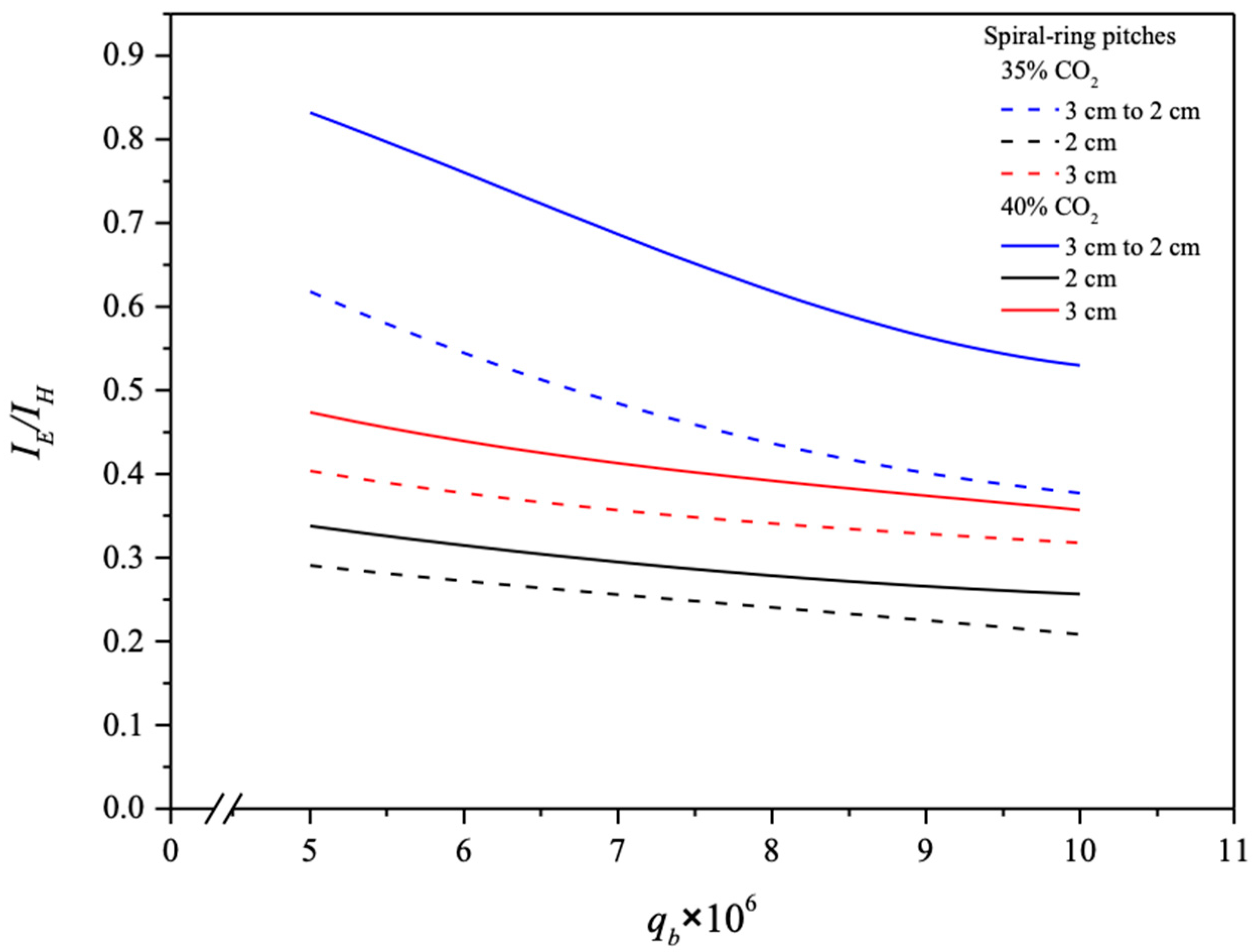
- Embedding spiral ring-filled channels with descending pitches (3 cm to 2 cm) into the MEA flow channel results in a relative increment in absorption flux, achieving a maximum improvement of 83.69% under a 40% inlet CO2 concentration and a 5 cm3/s MEA feed flow rate.
- This study shows a higher absorption flux improvement in modules with constant-spiral-ring-pitch channels compared to those with descending 3 cm to 2 cm spiral ring pitches. However, the ratio of for varying spiral ring pitches follows a reverse order.
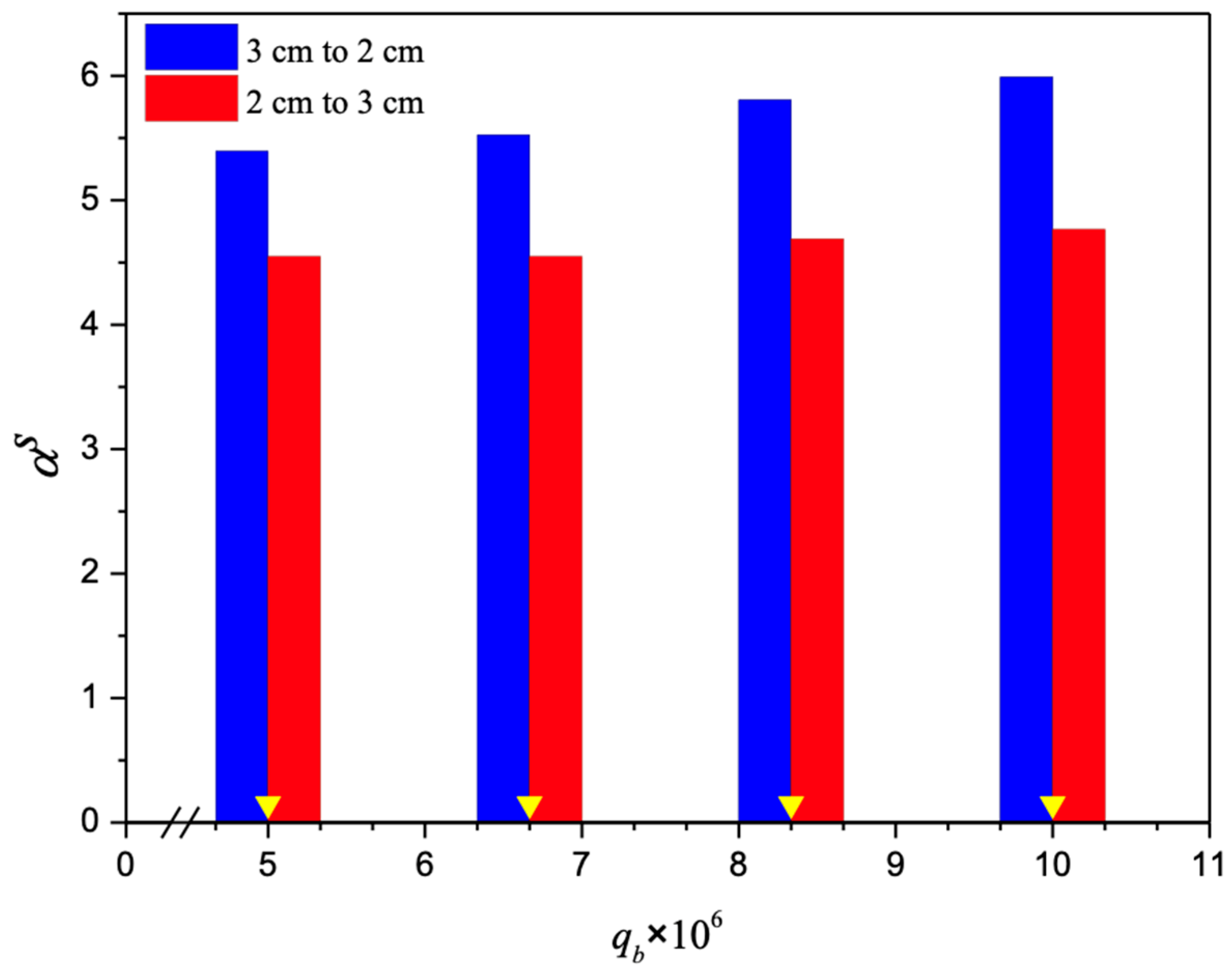
- Absorption flux improvement is more pronounced in descending spiral ring pitch operations compared to ascending ones due to the achievement of a larger concentration gradient across the entire module.
- Among the flow characteristics of varying spiral ring pitches, descending pitches exhibit a strong positive influence on absorption flux, attributed to the concentration gradient effectively induced by properly adjusting these pitches.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Concentration (mol m−3) | |
| Mean value of (mol m−3) | |
| Membrane coefficient based on the Knudsen diffusion model (mol m−2 pa−1 s−1) | |
| Membrane coefficient based on the molecular diffusion model (kg m−2 Pa−1 s−1) | |
| Membrane permeation coefficient (mol m−2 pa−1 s−1) | |
| Diffusion coefficient of CO2 in gas feed stream (m2 s−1) | |
| Diffusion coefficient of CO2 in MEA absorbent feed stream (m2 s−1) | |
| Equivalent hydraulic diameter of channel (m), | |
| Deviation of experimental results from the theoretical predictions | |
| Further absorption flux enhancement | |
| Fanning friction factor | |
| Henry’s law constant (atm L gmol−1) | |
| Dimensionless Henry’s constant | |
| Hydraulic dissipate energy (J kg−1), | |
| Absorption flux improvement | |
| Power consumption relative index | |
| Mass transfer coefficient in the CO2/N2 gas feed stream (m s−1) | |
| Mass transfer coefficient in the MEA absorbent feed stream (m s−1) | |
| Equilibrium constant | |
| Reduced equilibrium constant | |
| Overall mass transfer coefficient of membrane (m s−1) | |
| Friction loss (J kg−1), | |
| Channel length () | |
| Average molecular weight of CO2 and N2 gas mixture ) | |
| Number of experimental measurements | |
| Saturation vapor pressure in the gas feed flow side () | |
| Saturation vapor pressure in the liquid absorbent flow side () | |
| Volumetric flow rate of the gas feed stream () | |
| Volumetric flow rate of the MEA absorbent stream () | |
| Gas constant (8.314 ) | |
| Reynolds number | |
| Inside radius of inner tube () | |
| Outside radius of inner tube () | |
| Inside radius of shell tube () | |
| Membrane pore radius () | |
| Dimensionless Schmidt number | |
| Enhanced dimensionless Sherwood number | |
| Dimensionless Sherwood number for laminar flow | |
| Spiral ring pitch width (m) | |
| Ratio of the various pitches inserted | |
| Absorption flux () | |
| Natural log mean CO2 mole fraction in the membrane | |
| Axial coordinate along the flow direction () | |
| Greek letters | |
| Mass transfer enhancement factor | |
| Thickness of membrane (µm) | |
| Membrane porosity | |
| Average velocity () | |
| Density (), | |
| Concentration polarization coefficients | |
| Subscripts | |
| 1 | Membrane surface in CO2/N2 gas feed side |
| Liquid phase on membrane surface on MEA feed stream | |
| Gas phase on membrane surface on MEA side | |
| a | CO2/N2 gas feed stream |
| b | MEA absorbent feed stream |
| cor | Correlated results |
| spiral | Inserting spiral rings as promoters |
| empty | Empty channel |
| exp | Experimental results |
| Gas feed stream | |
| in | At the inlet |
| MEA absorbent feed stream | |
| out | At the outlet |
| theo | Theoretical predictions |
| Superscripts | |
| as | Ascending spiral ring pitch operations |
| con | Constant spiral ring pitch operations |
| des | Descending spiral ring pitch operations |
References
- Herzog, H.; Eliasson, B.; Kaarstad, O. Capturing greenhouse gases. Sci. Am. 2000, 182, 72–79. [Google Scholar] [CrossRef]
- Nabian, N.; Ghoreyshi, A.A.; Rahimpour, A.; Shakeri, M. Performance evaluation and mass transfer study of CO2 absorption in flat sheet membrane contactor using novel porous polysulfone membrane. Korean J. Chem. Eng. 2015, 32, 2204–2211. [Google Scholar] [CrossRef]
- Li, J.L.; Chen, B.H. Review of CO2 absorption using chemical solvents in hollow fiber membrane contactors. Sep. Purif. Technol. 2005, 41, 109–122. [Google Scholar] [CrossRef]
- Takahashi, N.; Furuta, Y.; Fukunaga, H.; Takatsuka, T.; Mano, H.; Fujioka, Y. Effects of membrane properties on CO2 recovery performance in a gas absorption membrane contactor. Energy Procedia 2011, 4, 693–698. [Google Scholar] [CrossRef]
- Ramakula, P.; Prapasawada, T.; Pancharoena, U.; Pattaveekongkab, W. Separation of radioactive metal ions by hollow fiber-supported liquid membrane and permeability analysis. J. Chin. Inst. Chem. Eng. 2007, 38, 489–494. [Google Scholar] [CrossRef]
- Sea, B.; Park, Y.I. Comparison of porous hollow fibers as a membrane contactor for carbon dioxide absorption. J. Ind. Eng. Chem. 2002, 8, 290–296. [Google Scholar]
- Klaassen, R.; Feron, P.; Jansen, A. Membrane contactor applications. Desalination 2008, 224, 81–87. [Google Scholar] [CrossRef]
- Rezakazemi, M.; Sadrzadeh, M.; Matsuura, T. Thermally stable polymers for advanced high-performance gas separation membranes. Prog. Energy Combust. Sci. 2018, 66, 1–41. [Google Scholar] [CrossRef]
- Lin, Y.F.; Ko, C.C.; Chen, C.H.; Tung, K.L.; Chang, K.S.; Chung, T.W. Sol-gel preparation of polymethylsilsesquioxane aerogel membranes for CO2 absorption fluxes in membrane contactors. Appl. Energy 2014, 129, 25–31. [Google Scholar] [CrossRef]
- Lin, Y.F.; Kuo, J.W. Mesoporous bis(trimethoxysilyl)hexane (BTMSH)/tetraethyl orthosilicate (TEOS)-based hybrid silica aerogel membranes for CO2 capture. Chem. Eng. J. 2016, 300, 29–35. [Google Scholar] [CrossRef]
- Xu, Y.; Lin, Y.; Chew, N.G.P.; Malde, C.; Wang, R. Biocatalytic PVDF composite hollow fiber membranes for CO2 removal in gas-liquid membrane contactor. J. Membr. Sci. 2019, 572, 532–544. [Google Scholar] [CrossRef]
- Wang, W.P.; Lin, H.T.; Ho, C.D. An analytical study of laminar co-current flow gas absorption through a parallel-plate gas-liquid membrane contactor. J. Membr. Sci. 2006, 278, 181–189. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Hu, H.C.; Chai, X.S.; Pan, L.; Xiao, X.M. A novel method for the determination of adsorption partition coefficients of minor gases in a shale sample by headspace gas chromatography. J. Chromatogr. A 2013, 1310, 121–125. [Google Scholar] [CrossRef] [PubMed]
- Bandini, S.; Gostoli, C.; Sarti, G.C. Role of heat and mass transfer in membrane distillation process. Desalination 1991, 81, 91–106. [Google Scholar] [CrossRef]
- Lawson, K.W.; Lloyd, D.R. Membrane distillation II: Direct contact membrane distillation. J. Membr. Sci. 1996, 120, 123–133. [Google Scholar] [CrossRef]
- Rongwong, W.; Boributh, S.; Assabumrungrat, S.; Laosiripojana, N.; Jiraratananon, R. Simultaneous absorption of CO2 and H2S from biogas by capillary membrane contactor. J. Membr. Sci. 2012, 392–393, 38–47. [Google Scholar] [CrossRef]
- Tobiesen, F.A.; Svendsen, H.F. Study of a modified amine-based regeneration unit. Ind. Eng. Chem. Res. 2006, 45, 2489–2496. [Google Scholar] [CrossRef]
- Lepaumier, H.; Picq, D.; Carrette, P.L. Degradation Study of New Solvents for CO2 Capture in Post-Combustion. Energy Procedia 2009, 1, 893–900. [Google Scholar] [CrossRef]
- Tan, L.S.; Shariff, A.M.; Lau, K.K.; Bustam, M.A. Factors Affecting CO2 Absorption Efficiency in Packed Column: A Review. J. Ind. Eng. Chem. 2012, 18, 1874–1883. [Google Scholar] [CrossRef]
- Hamimour, N.; Sandall, O.C. Absorption of carbon dioxide into aqueous methyldiethanolamine. Chem. Eng. Sci. 1984, 39, 1791–1796. [Google Scholar] [CrossRef]
- Bakhshali, N.; Tahery, R.; Banazadeh, H. Modelling and simulation of mass transfer in tubular gas-liquid membrane contactors for turbulent flow conditions and comparison of results with laminar flow conditions. Middle-East J. Sci. Res. 2013, 10, 1419–1430. [Google Scholar]
- Karoor, S.; Sirkar, K.K. Gas absorption studies in microporous hollow fiber membrane modules. Ind. Eng. Chem. Res. 1993, 32, 674–684. [Google Scholar] [CrossRef]
- Nagaraj, N.; Patil, G.; Babu, B.R.; Hebbar, U.H.; Rahavarao, K.S.M.S.; Nene, S. Mass transfer in osmotic membrane distillation. J. Membr. Sci. 2006, 268, 48–56. [Google Scholar] [CrossRef]
- Soldenhoff, K.; Shamieh, M.; Manis, A. Liquid-liquid extraction of cobalt with hollow fiber contactor. J. Membr. Sci. 2005, 252, 183–194. [Google Scholar] [CrossRef]
- Meng, J.; Li, P.; Cao, B. High-flux direct-contact pervaporation membranes for desalination. Appl. Mater. Interfaces 2019, 11, 28461–28468. [Google Scholar] [CrossRef]
- Chang, H.; Hsu, J.A.; Chang, C.L.; Ho, C.D.; Cheng, T.W. Simulation study of transfer characteristics for spacer-filled membrane distillation desalination modules. Appl. Energy 2017, 185, 2045–2057. [Google Scholar] [CrossRef]
- Nasim Afza, K.; Hashemifard, S.A.; Abbasi, M. Modelling of CO2 absorption via hollow fiber membrane contactors: Comparison of pore gas diffusivity models. Chem. Eng. Sci. 2018, 190, 110–121. [Google Scholar] [CrossRef]
- Ho, C.D.; Chen, L.; Chen, L.; Huang, M.C.; Lai, J.Y.; Chen, Y.A. Distillate flux enhancement in the air gap membrane distillation with inserting carbon-fiber spacers. Sep. Sci. Technol. 2017, 52, 2815–2826. [Google Scholar] [CrossRef]
- Shakaib, M.; Hasani, S.M.F.; Mahmood, M. CFD modeling for flow and mass transfer in spacer-obstructed membrane feed channels. J. Membr. Sci. 2009, 326, 270–284. [Google Scholar] [CrossRef]
- Martínez-Díez, L.; Vázquez-González, M.I.; Florido-Díaz, F.J. Study of membrane distillation using channel spacers. J. Membr. Sci. 1998, 144, 45–56. [Google Scholar] [CrossRef]
- Yeh, H.M. Effect of gradually varying baffled-ring distance on ultrafiltration in tubular membranes inserted concentrically with a ring rod. Desalination Water Treat. 2004, 40, 321–325. [Google Scholar] [CrossRef]
- Yeh, H.M. Enrichment of heavy water in rotated wired concentric-tube thermal diffusion columns. Sep. Purif. Technol. 2004, 40, 321–325. [Google Scholar] [CrossRef]
- Ho, C.D.; Chang, H.; Lin, G.H.; Chew, T.L. Enhancing absorption performance of CO2 by amine solution through the spiral wired channel in concentric circular membrane contactors. Membranes 2022, 12, 4. [Google Scholar] [CrossRef] [PubMed]
- Yeh, H.M. Recovery of deuterium from water–isotopes mixture in concentric-tube thermal diffusion columns inserted with wire spiral for improved performance. Int. J. Hydrogen Energy 2004, 29, 521–527. [Google Scholar] [CrossRef]
- Yeh, H.M.; Dong, J.F.; Hsieh, M.J.; Yang, C.C. Prediction of permeate flux for ultrafiltration in wire–rod tubular-membrane modules. J. Membr. Sci. 2002, 209, 19–26. [Google Scholar] [CrossRef]
- Taamneh, Y.; Bataineh, K. Improving the performance of direct contact membrane distillation utilizing spacer-filled channel. Desalination 2017, 408, 25–35. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Dalaq, A.S.; Abu Al-Rub, R.K.; Younes, H.A. Finite element predictions of effective multifunctional properties of interpenetrating phase composites with novel triply periodic solid shell architectured reinforcements. Int. J. Mech. Sci. 2015, 92, 80–89. [Google Scholar] [CrossRef]
- Ding, Z.W.; Ma, R.Y.; Fane, A.G. A new model for mass transfer in direct contact membrane distillation. Desalination 2003, 151, 217–227. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Hwang, S.T. Concentration polarization, separation factor, and Peclet number in membrane processes. J. Membr. Sci. 1997, 132, 73–90. [Google Scholar] [CrossRef]
- Lawson, K.W.; Lloyd, D.R. Membrane distillation. J. Membr. Sci. 1997, 124, 1–25. [Google Scholar] [CrossRef]
- Zheng, Q.; Dong, L.; Chen, J.; Gao, G.; Fei, W. Absorption solubility calculation and process simulation for CO2 capture. J. Chem. Ind. Eng. 2010, 61, 1740–1746. [Google Scholar]
- Iversen, S.B.; Bhatia, V.K.; Dam-Jphasen, K.; Jonson, G. Characterization of microporous membranes for use in membrane contactors. J. Membr. Sci. 1997, 130, 205–217. [Google Scholar] [CrossRef]
- Dimitrov, D.; Schreve, K.; de Beer, N. Advances in three-dimensional printing—State of the art and future perspectives. Rapid Prototyp. J. 2006, 12, 136–147. [Google Scholar] [CrossRef]
- Luelf, T.; Rall, D.; Wypysek, D.; Wiese, M.; Femmer, T.; Bremer, C.; Michaelis, J.U.; Wessling, M. 3D-printed rotating spinnerets create membranes with a twist. J. Membr. Sci. 2018, 555, 7–19. [Google Scholar] [CrossRef]
- Lin, S.H.; Tung, K.L.; Chang, H.W.; Lee, K.R. Influence of Fluorocarbon Fat-Membrane Hydrophobicity on Carbon Dioxide Recovery. Chemosphere 2009, 75, 1410–1416. [Google Scholar] [CrossRef]
- Welty, J.R.; Wicks, C.E.; Wilson, R.E. Fundamentals of Momentum, Heat, and Mass Transfer, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1984. [Google Scholar]
- Moffat, R.J. Describing the uncertainties in experimental results. Exp. Thermal Fluid Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef]
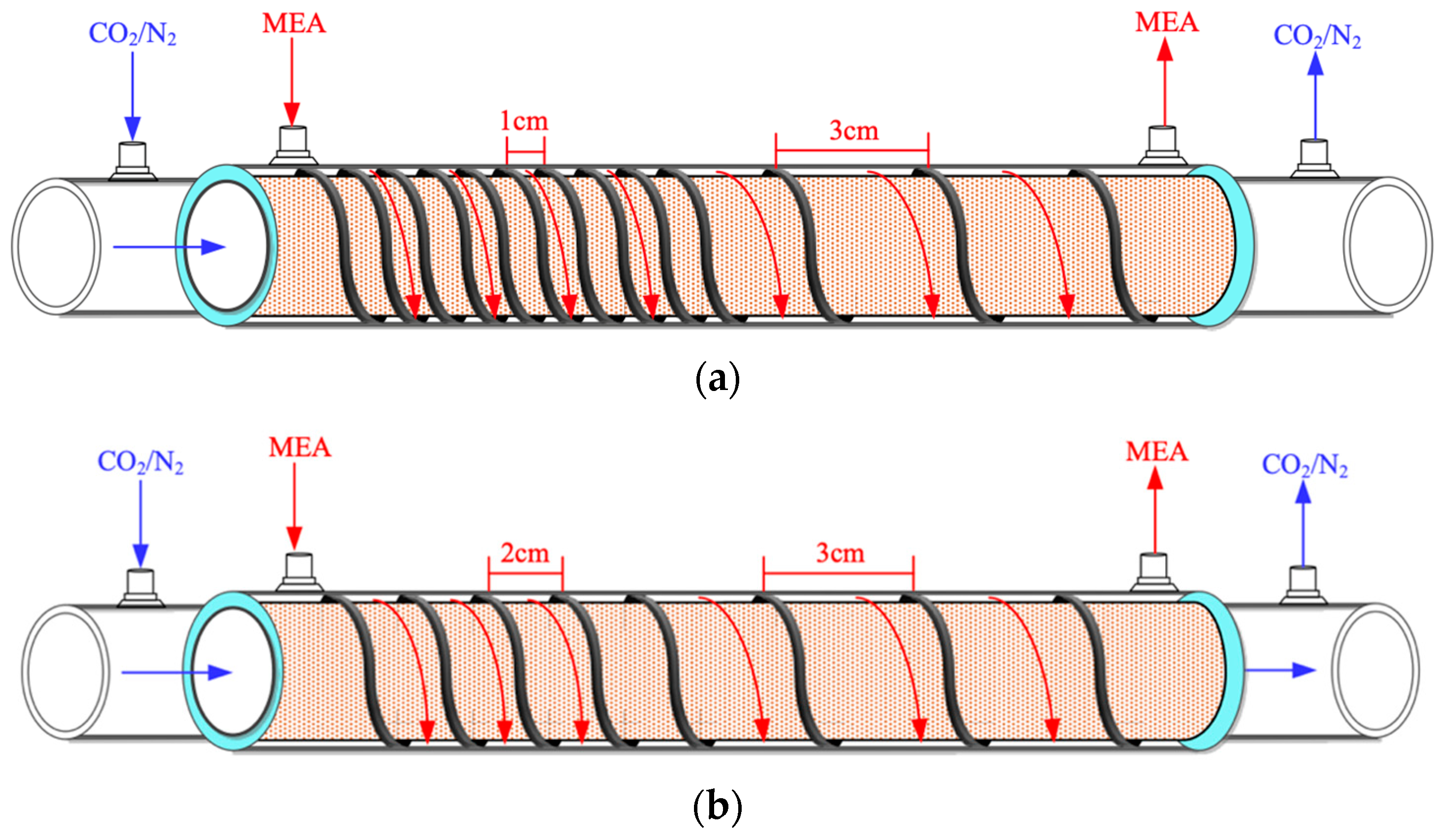
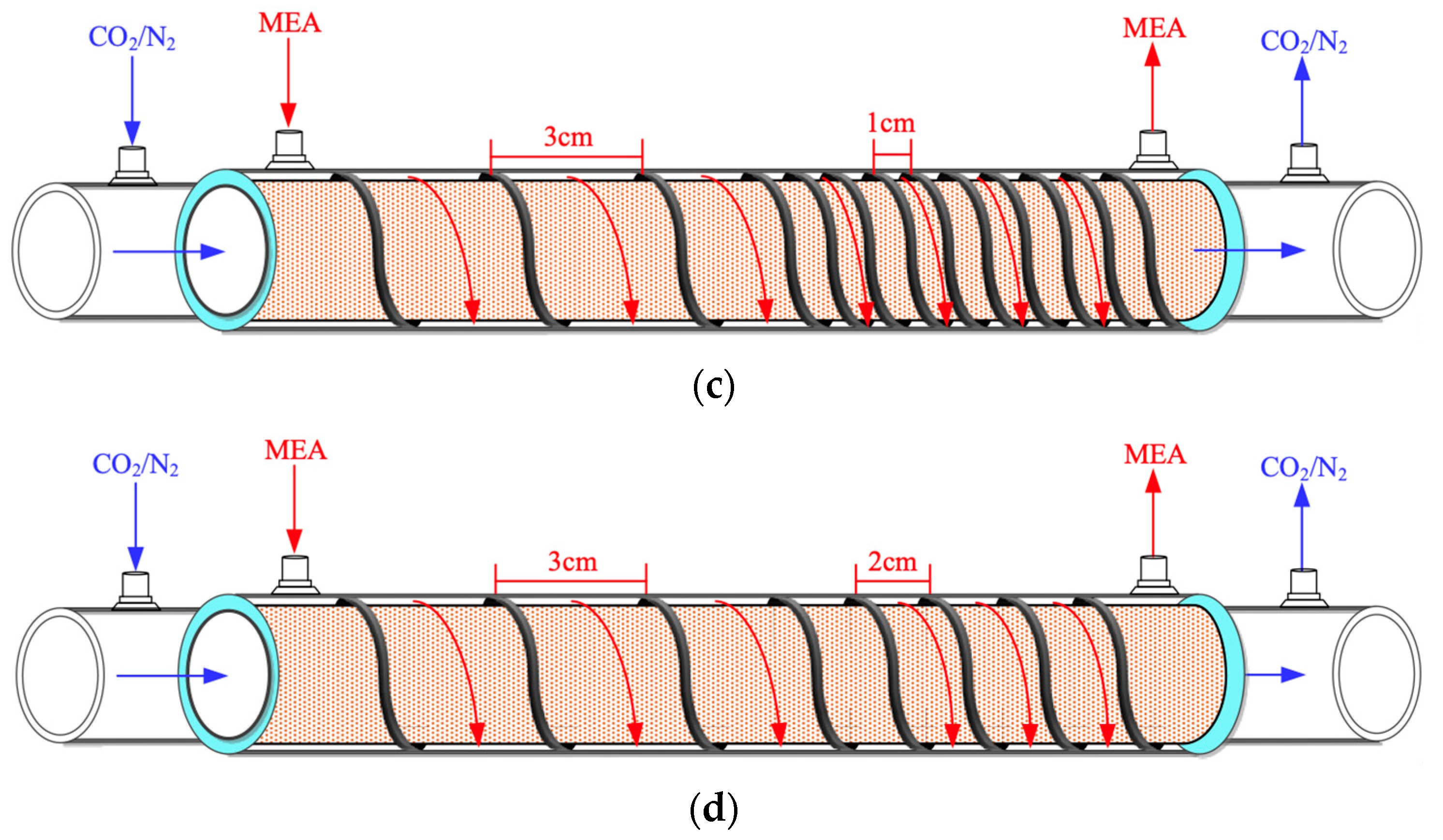

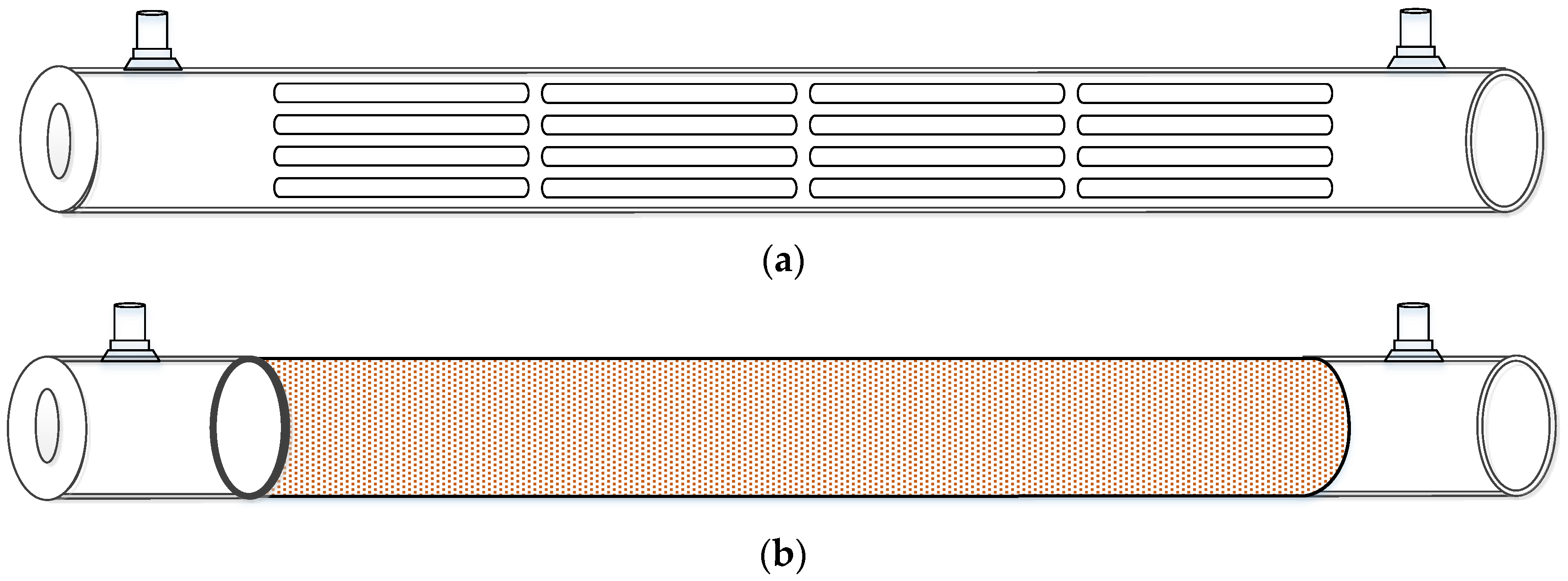
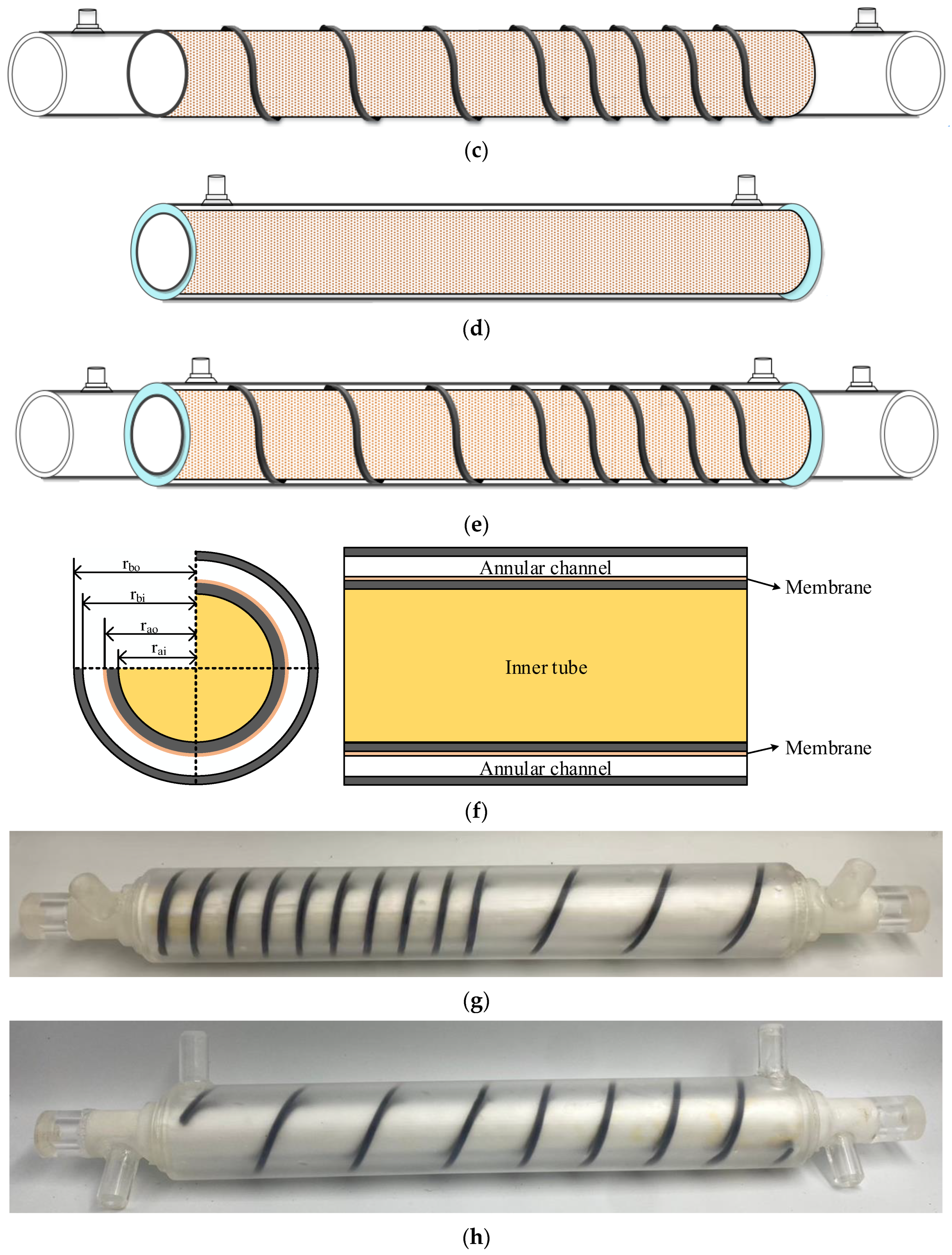
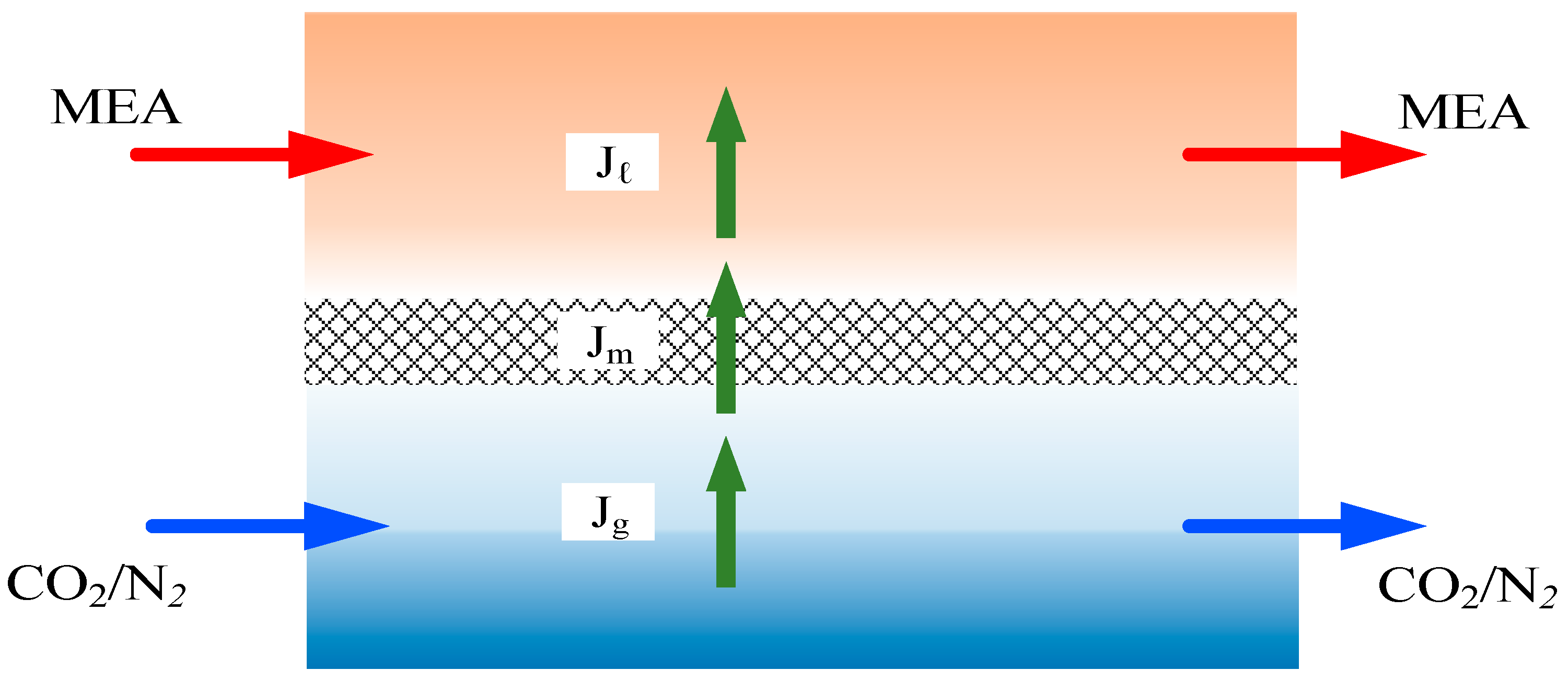
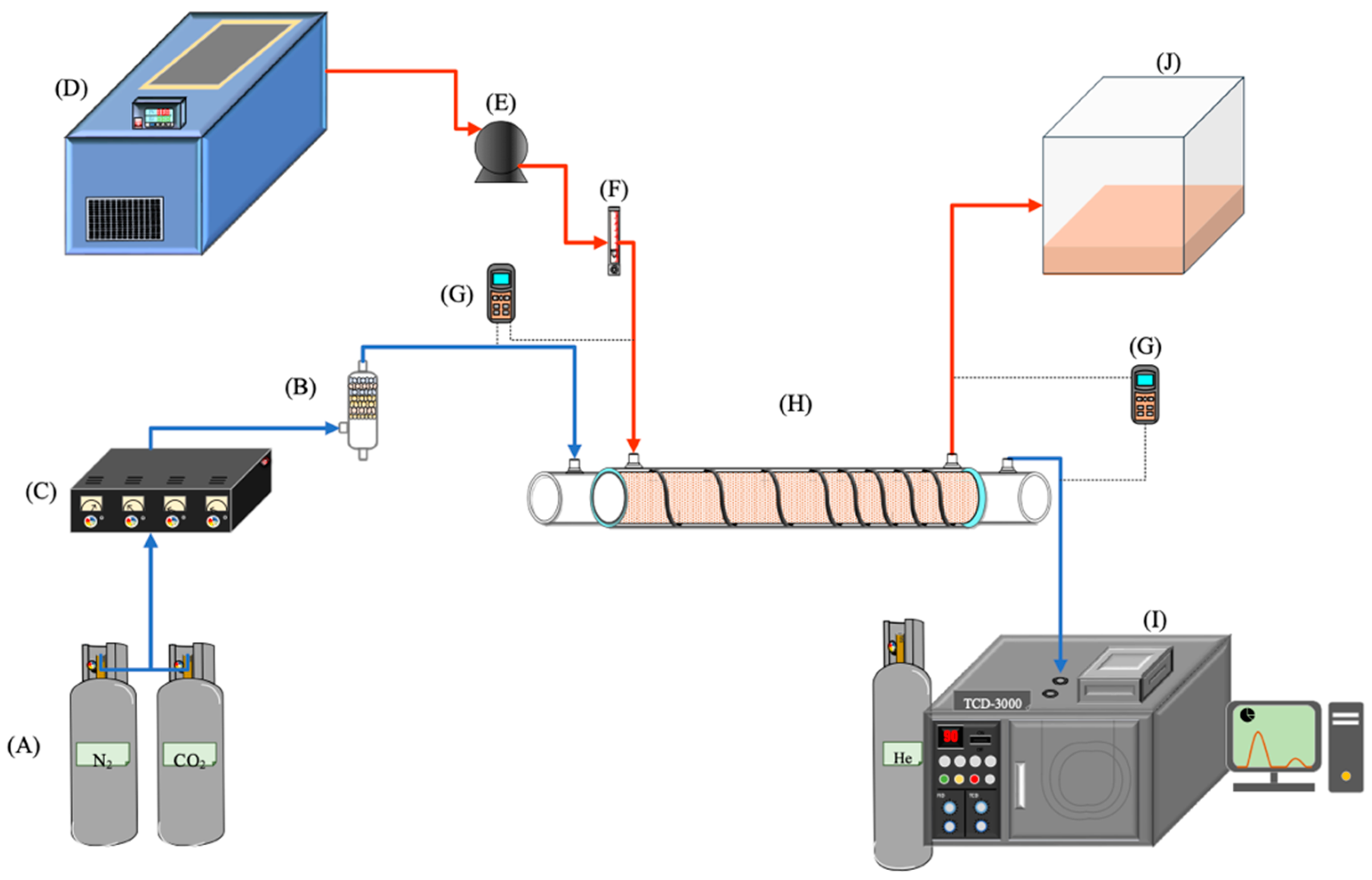




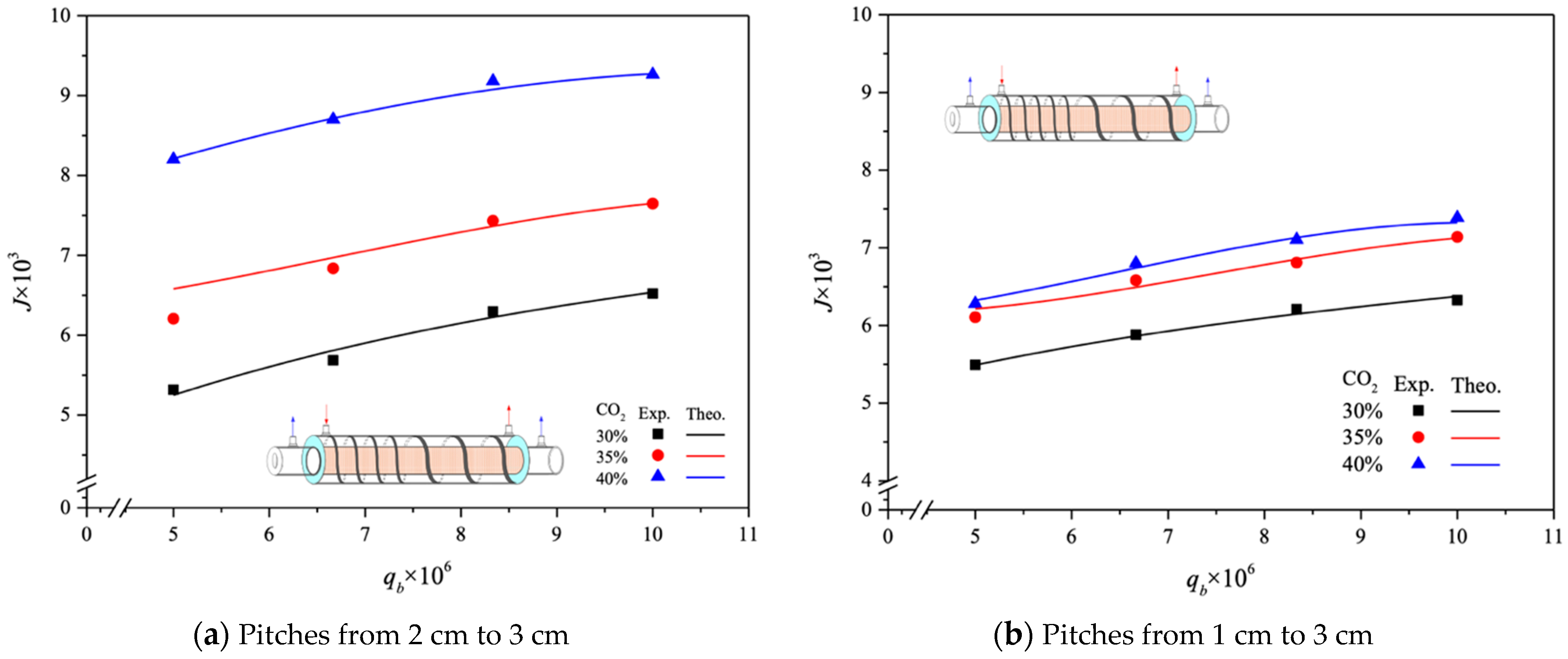

| Ascending Spiral Ring Pitch Operations (mol m−2 s−1) | |||||||
|---|---|---|---|---|---|---|---|
| 2 cm to 3 cm | 1 cm to 3 cm | ||||||
| (%) | m3/s | ||||||
| 30 | 5.0 | 5.15 | 4.93 | 4.46 | 5.49 | 5.66 | 2.95 |
| 6.67 | 5.35 | 5.44 | 1.67 | 5.88 | 5.97 | 1.40 | |
| 8.33 | 5.68 | 5.75 | 1.14 | 6.21 | 6.12 | 1.53 | |
| 10.0 | 6.03 | 6.01 | 0.35 | 6.33 | 6.26 | 1.10 | |
| 35 | 5.0 | 5.65 | 5.74 | 1.51 | 6.11 | 6.11 | 0.02 |
| 6.67 | 6.29 | 6.15 | 2.21 | 6.58 | 6.28 | 4.87 | |
| 8.33 | 6.81 | 6.84 | 0.44 | 6.81 | 6.83 | 0.35 | |
| 10.0 | 7.01 | 7.13 | 1.69 | 7.14 | 7.00 | 1.95 | |
| 40 | 5.0 | 6.23 | 6.44 | 3.31 | 6.28 | 6.28 | 0.04 |
| 6.67 | 7.02 | 7.10 | 1.17 | 6.80 | 6.69 | 1.68 | |
| 8.33 | 7.99 | 7.85 | 1.73 | 7.11 | 7.28 | 2.42 | |
| 10.0 | 8.21 | 8.06 | 1.90 | 7.39 | 7.37 | 0.23 | |
| Descending Spiral Ring Pitch Operations (mol m−2 s−1) | |||||||
|---|---|---|---|---|---|---|---|
| 3 cm to 2 cm | 3 cm to 1 cm | ||||||
| (%) | m3/s | ||||||
| 30 | 5.0 | 5.32 | 5.18 | 2.76 | 5.90 | 6.15 | 4.08 |
| 6.67 | 5.69 | 5.75 | 1.08 | 6.52 | 6.48 | 0.60 | |
| 8.33 | 6.30 | 6.09 | 3.44 | 6.83 | 6.65 | 2.73 | |
| 10.0 | 6.52 | 6.36 | 2.51 | 6.92 | 6.80 | 1.89 | |
| 35 | 5.0 | 6.21 | 6.59 | 5.79 | 6.65 | 6.86 | 3.06 |
| 6.67 | 6.84 | 7.03 | 2.81 | 7.23 | 7.08 | 2.03 | |
| 8.33 | 7.43 | 7.65 | 2.84 | 7.46 | 7.62 | 2.09 | |
| 10.0 | 7.65 | 7.90 | 3.12 | 7.65 | 7.79 | 1.89 | |
| 40 | 5.0 | 8.20 | 7.97 | 2.90 | 7.72 | 7.38 | 4.54 |
| 6.67 | 8.70 | 8.56 | 1.65 | 8.04 | 7.84 | 2.53 | |
| 8.33 | 9.18 | 9.10 | 0.92 | 8.18 | 8.44 | 3.13 | |
| 10.0 | 9.26 | 9.24 | 0.24 | 8.46 | 8.53 | 0.81 | |
| Ascending Spiral Ring Pitch Operations (mol m−2 s−1) | ||||||
|---|---|---|---|---|---|---|
| Empty Channel | 2 cm to 3 cm | 1 cm to 3 cm | ||||
| (%) | (m3 s−1) | (%) | (%) | |||
| 30 | 5.0 | 3.82 | 4.93 | 28.88 | 5.66 | 48.05 |
| 6.67 | 4.37 | 5.44 | 24.42 | 5.97 | 36.38 | |
| 8.33 | 4.81 | 5.75 | 19.57 | 6.12 | 27.20 | |
| 10.0 | 5.06 | 6.01 | 18.76 | 6.26 | 23.71 | |
| 35 | 5.0 | 4.03 | 5.74 | 42.60 | 6.11 | 51.65 |
| 6.67 | 4.60 | 6.15 | 33.88 | 6.28 | 27.97 | |
| 8.33 | 5.34 | 6.84 | 28.18 | 6.83 | 25.59 | |
| 10.0 | 5.58 | 7.13 | 27.86 | 7.00 | 25.59 | |
| 40 | 5.0 | 4.34 | 6.44 | 48.46 | 6.28 | 44.79 |
| 6.67 | 4.97 | 7.10 | 42.90 | 6.69 | 34.58 | |
| 8.33 | 5.80 | 7.85 | 35.39 | 7.28 | 25.55 | |
| 10.0 | 6.03 | 8.06 | 33.63 | 7.37 | 22.27 | |
| Descending Spiral Ring Pitch Operations (mol m−2 s−1) | ||||||
|---|---|---|---|---|---|---|
| Empty Channel | 3 cm to 2 cm | 3 cm to 1 cm | ||||
| (%) | (m3 s−1) | (%) | (%) | |||
| 30 | 5.0 | 3.82 | 5.18 | 35.37 | 6.15 | 60.85 |
| 6.67 | 4.37 | 5.75 | 31.42 | 6.48 | 48.08 | |
| 8.33 | 4.81 | 6.09 | 26.64 | 6.65 | 38.22 | |
| 10.0 | 5.06 | 6.36 | 25.77 | 6.80 | 34.32 | |
| 35 | 5.0 | 4.03 | 6.59 | 63.64 | 6.86 | 70.51 |
| 6.67 | 4.60 | 7.03 | 53.07 | 7.08 | 54.09 | |
| 8.33 | 5.34 | 7.65 | 43.28 | 7.62 | 42.67 | |
| 10.0 | 5.58 | 7.90 | 41.59 | 7.79 | 39.76 | |
| 40 | 5.0 | 4.34 | 7.97 | 83.69 | 7.38 | 70.16 |
| 6.67 | 4.97 | 8.56 | 72.26 | 7.84 | 57.69 | |
| 8.33 | 5.80 | 9.10 | 56.86 | 8.44 | 45.59 | |
| 10.0 | 6.03 | 9.24 | 53.33 | 8.53 | 41.55 | |
| Descending Spiral Ring Pitches | ||||||
|---|---|---|---|---|---|---|
| Constant 3 cm Pitch [33] | 3 cm to 2 cm | 3 cm to 1 cm | ||||
| (%) | m3/s | (%) | (%) | (%) | (%) | (%) |
| 30 | 5.0 | 24.77 | 8.49 | 35.37 | 28.92 | 60.85 |
| 6.67 | 21.17 | 8.46 | 31.42 | 22.21 | 48.08 | |
| 8.33 | 17.93 | 7.38 | 26.64 | 17.21 | 38.22 | |
| 10.0 | 16.03 | 8.40 | 25.77 | 15.77 | 34.32 | |
| 35 | 5.0 | 26.92 | 28.93 | 63.64 | 30.23 | 65.30 |
| 6.67 | 25.98 | 21.50 | 53.07 | 22.32 | 54.09 | |
| 8.33 | 23.41 | 16.10 | 43.28 | 15.61 | 42.67 | |
| 10.0 | 21.41 | 16.62 | 41.59 | 15.11 | 39.76 | |
| 40 | 5.0 | 30.41 | 40.85 | 83.69 | 36.40 | 77.89 |
| 6.67 | 27.36 | 35.25 | 72.26 | 23.81 | 57.69 | |
| 8.33 | 25.17 | 25.32 | 56.86 | 16.32 | 45.59 | |
| 10.0 | 24.25 | 23.40 | 53.33 | 13.92 | 41.55 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ho, C.-D.; Ke, J.-W.; Lim, J.-W. Effects of Varying Spiral-Ring Pitches on CO2 Absorption by Amine Solution in Concentric Circular Membrane Contactors. Membranes 2024, 14, 147. https://doi.org/10.3390/membranes14070147
Ho C-D, Ke J-W, Lim J-W. Effects of Varying Spiral-Ring Pitches on CO2 Absorption by Amine Solution in Concentric Circular Membrane Contactors. Membranes. 2024; 14(7):147. https://doi.org/10.3390/membranes14070147
Chicago/Turabian StyleHo, Chii-Dong, Jui-Wei Ke, and Jun-Wei Lim. 2024. "Effects of Varying Spiral-Ring Pitches on CO2 Absorption by Amine Solution in Concentric Circular Membrane Contactors" Membranes 14, no. 7: 147. https://doi.org/10.3390/membranes14070147
APA StyleHo, C.-D., Ke, J.-W., & Lim, J.-W. (2024). Effects of Varying Spiral-Ring Pitches on CO2 Absorption by Amine Solution in Concentric Circular Membrane Contactors. Membranes, 14(7), 147. https://doi.org/10.3390/membranes14070147








