Pure Hydrogen and Methane Permeation in Carbon-Based Nanoporous Membranes: Adsorption Isotherms and Permeation Experiments
Abstract
1. Introduction
Motivation and Literature Review
2. Experimental
2.1. Membrane Preparation Procedure
2.2. Adsorption Measurements
2.2.1. Casting Material Characterization Measurements
2.2.2. Recording Adsorption Isotherms
2.2.3. Assumptions and Experimental Errors
2.3. Permeation Experiments
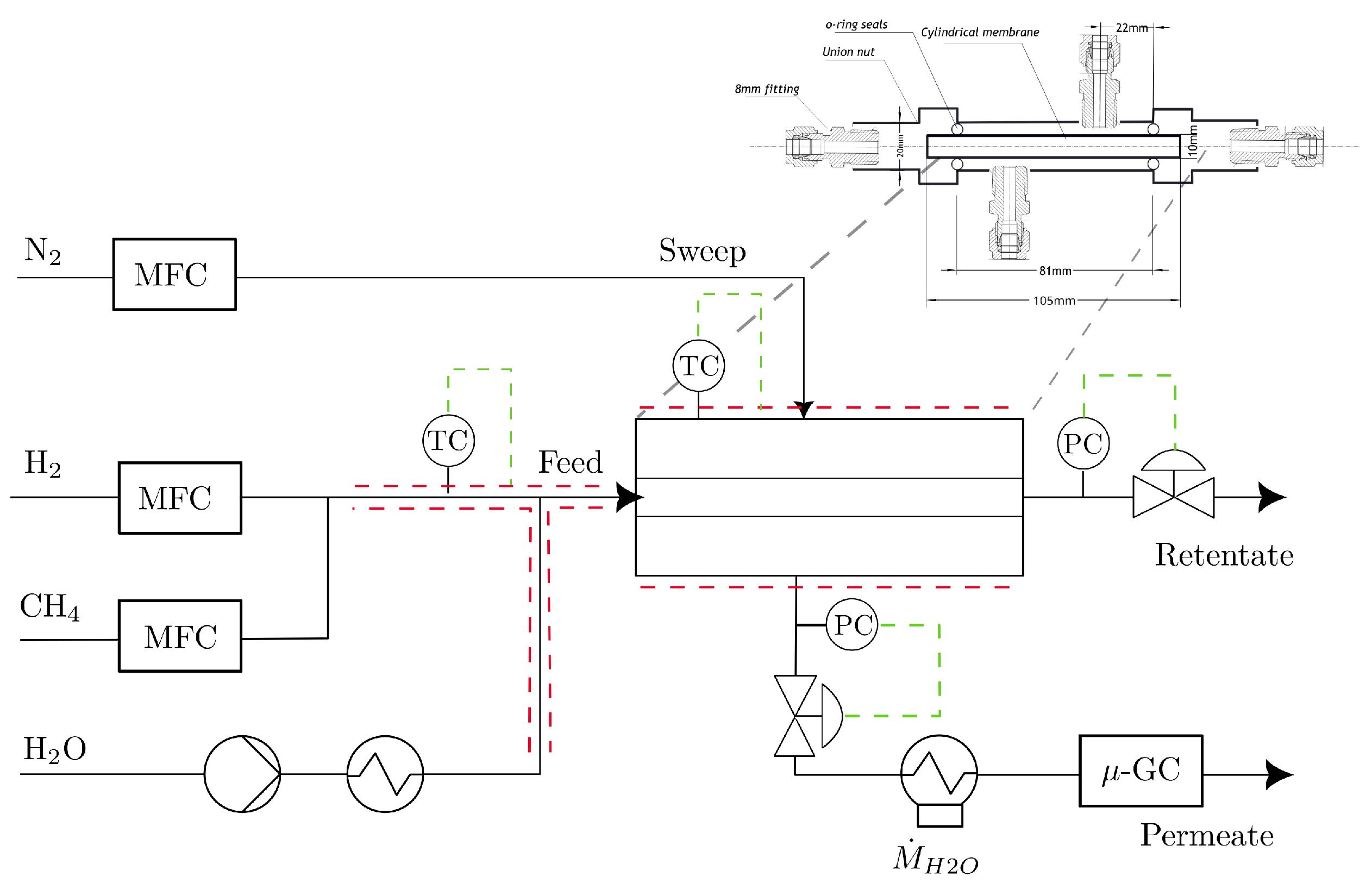
2.3.1. Experimental Setup and Method
2.3.2. Limitations, Assumptions, and Experimental Error
2.4. Diffusion Coefficient Calculation
2.4.1. Adsorption Isotherm Temperature Extrapolation
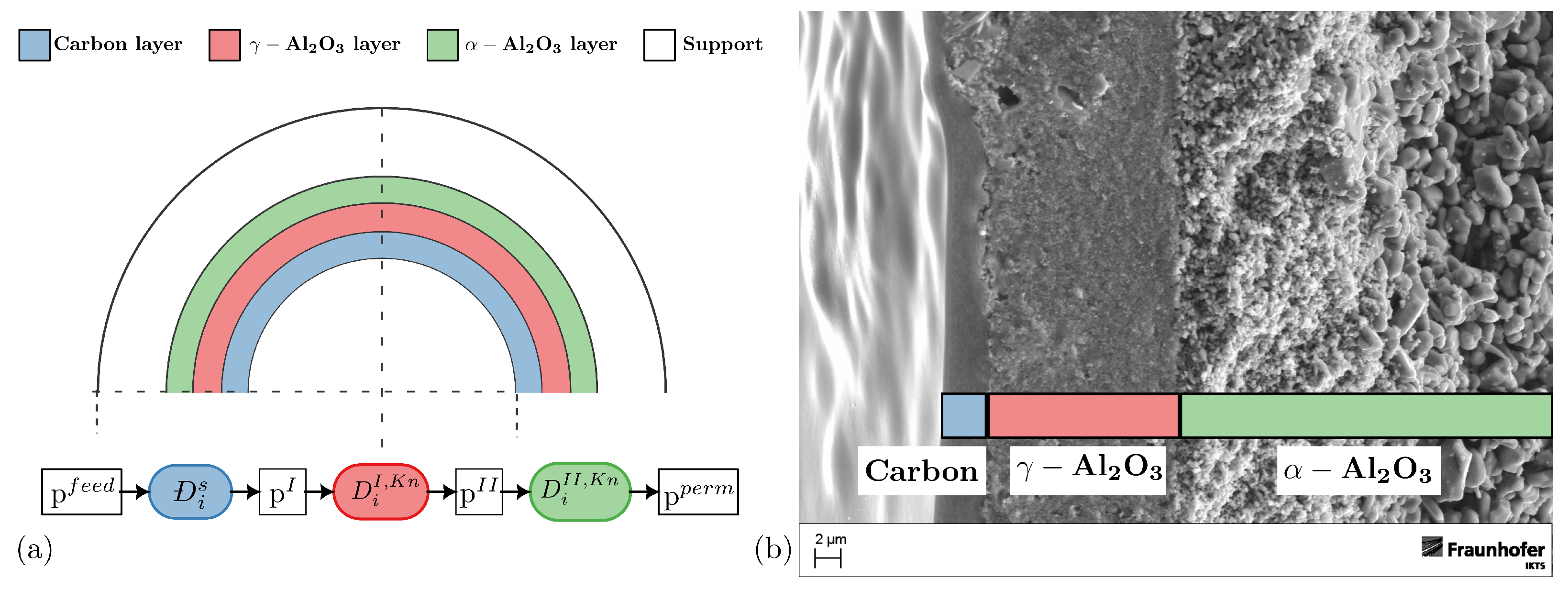
2.4.2. Description of the Different Layers
- Carbon layer:
- γ-Al2O3 layer:
- α-Al2O3 layer:
- And with:
- one can calculate:
3. Results
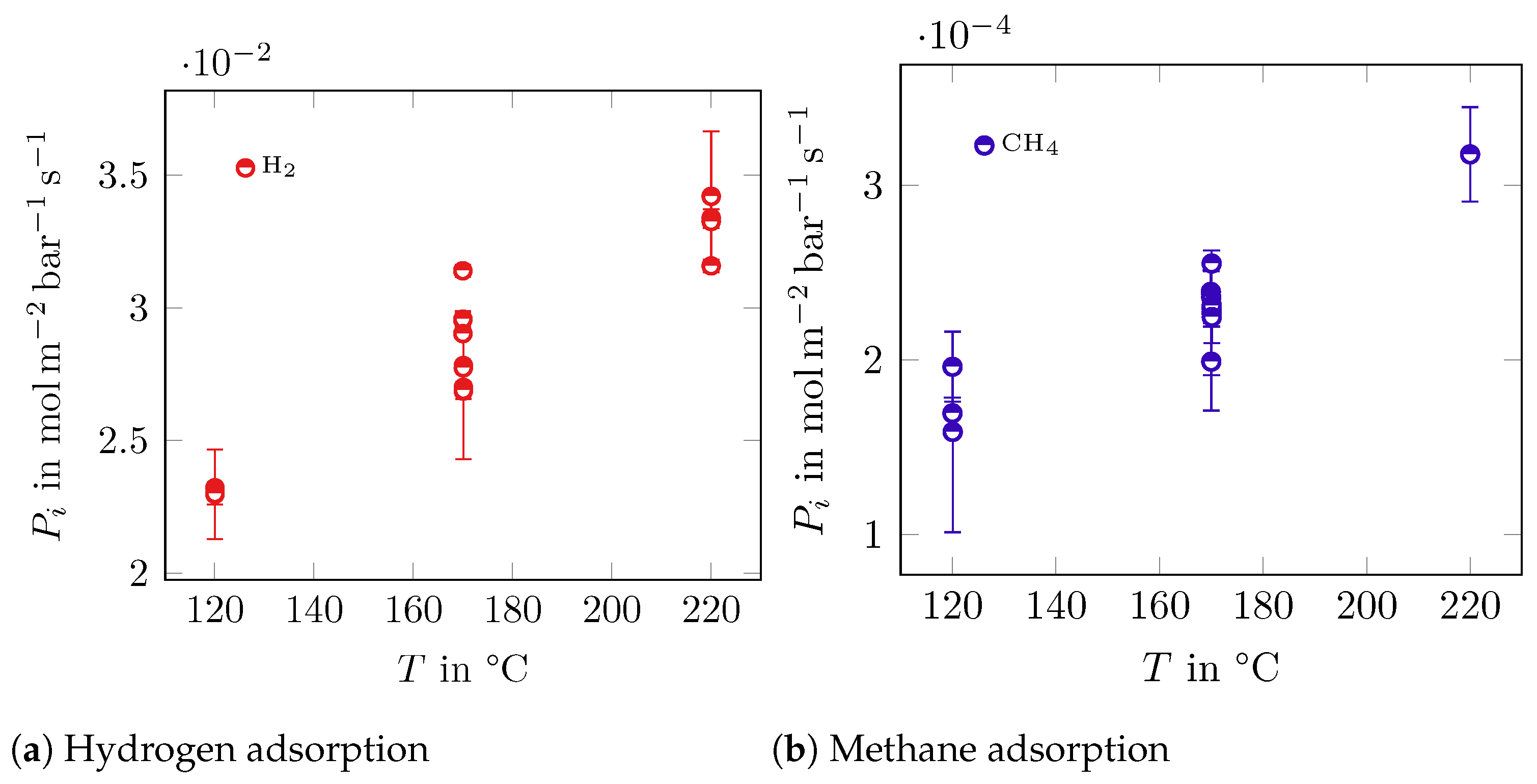
3.1. Adsorption Measurements
3.2. Permeation Experiments
3.3. Calculation of MS Diffusion Coefficients of Single Components
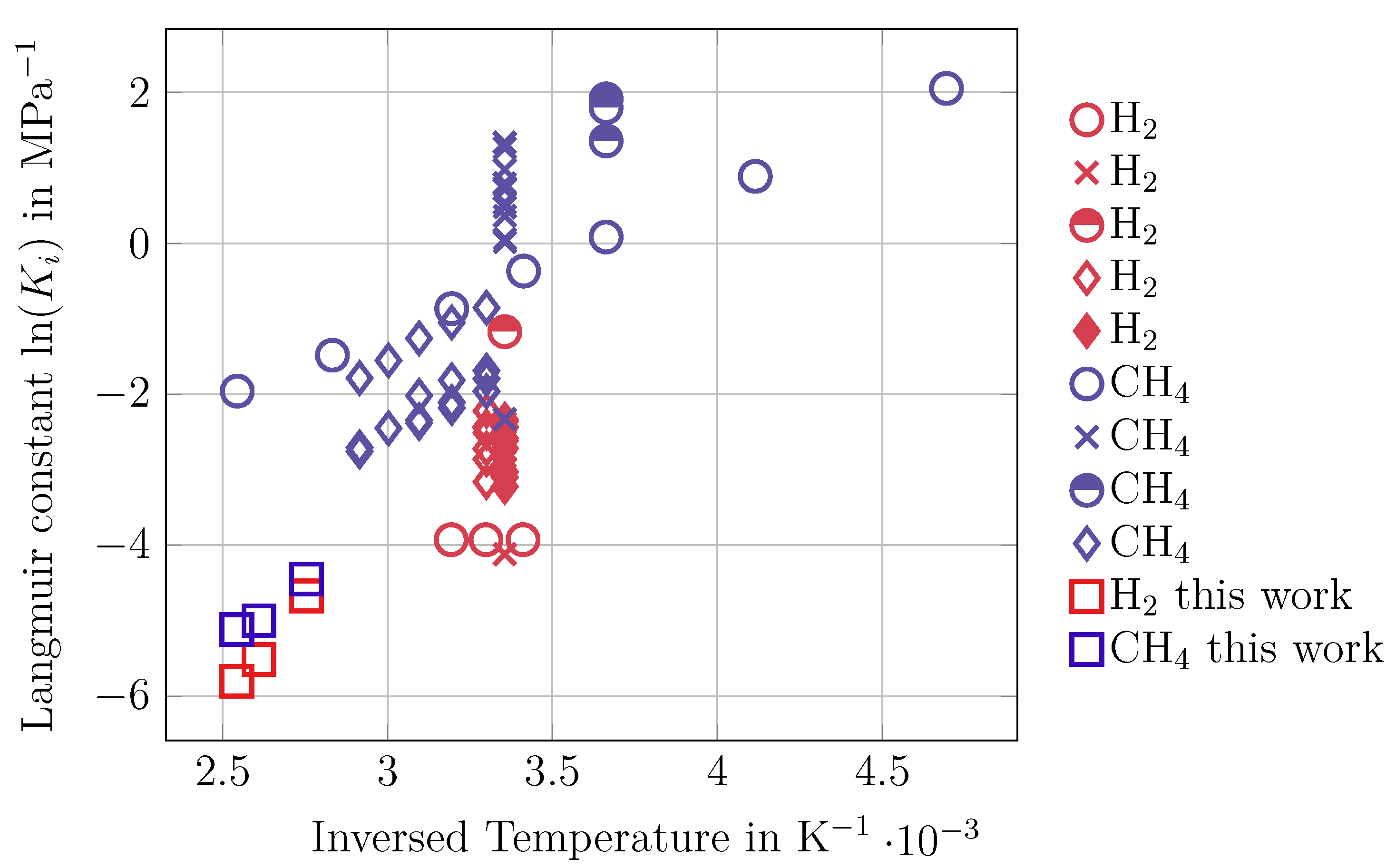
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PID | Piping and instrumentation diagram |
| MS | Maxwell–Stefan |
References
- Yang, R.T. CHAPTER 4—Rate Processes in Adsorbers. In Gas Separation by Adsorption Processes; Yang, R.T., Ed.; Butterworth-Heinemann: Oxford, UK, 1987; pp. 101–139. [Google Scholar] [CrossRef]
- Gugliuzza, A.; Basile, A. Membranes for Clean and Renewable Power Applications; Woodhead Publishing: Sawston, YN, USA; Cambridge, UK, 2014; p. 410. [Google Scholar]
- Melin, T.; Rautenbach, R. Membranverfahren: Grundlagen Der Modul- Und Anlagenauslegung, 3rd ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2007. [Google Scholar]
- Rohde, M.P. In-Situ H2O Removal via Hydorphilic Membranes during Fischer-Tropsch and Other Fuel-Related Synthesis Reactions. Ph.D. Thesis, Karlsruher Institut für Technologie KIT, Karlsruhe, Germany, 2010. [Google Scholar]
- Kohl, A.; Nielsen, R. Gas Purification, 5th ed.; Gulf Publishing Company: Houston, TX, USA, 1997. [Google Scholar]
- Catarina Faria, A.; Miguel, C.V.; Rodrigues, A.E.; Madeira, L.M. Modeling and Simulation of a Steam-Selective Membrane Reactor for Enhanced CO2 Methanation. Ind. Eng. Chem. Res. 2020, 59, 16170–16184. [Google Scholar] [CrossRef]
- Ohya, H.; Fun, J.; Kawamura, H.; Itoh, K.; Ohashi, H.; Aihara, M.; Tanisho, S.; Negishi, Y. Methanation of Carbon Dioxide by Using Membrane Reactor Integrated with Water Vapor Permselective Membrane and Its Analysis. J. Membr. Sci. 1997, 131, 237–247. [Google Scholar] [CrossRef]
- Kaltschmitt, M. Energy from Organic Materials (Biomass): A Volume in the Encyclopedia of Sustainability Science and Technology, 2nd ed.; Encyclopedia of Sustainability Science and Technology Series; Springer: New York, NY, USA, 2019. [Google Scholar]
- Weyd, M.; Richter, H.; Puhlfürß, P.; Voigt, I.; Hamel, C.; Seidel-Morgenstern, A. Transport of Binary Water–Ethanol Mixtures through a Multilayer Hydrophobic Zeolite Membrane. J. Membr. Sci. 2008, 307, 239–248. [Google Scholar] [CrossRef]
- Simon, A.; Seyring, M.; Kämnitz, S.; Richter, H.; Voigt, I.; Rettenmayr, M.; Ritter, U. Carbon Nanotubes and Carbon Nanofibers Fabricated on Tubular Porous Al2O3 Substrates. Carbon 2015, 90, 25–33. [Google Scholar] [CrossRef]
- Rönsch, S.; Schneider, J.; Matthischke, S.; Schlüter, M.; Götz, M.; Lefebvre, J.; Prabhakaran, P.; Bajohr, S. Review on Methanation—From Fundamentals to Current Projects. Fuel 2016, 166, 276–296. [Google Scholar] [CrossRef]
- Tian, C.; Huang, A. Synthesis of a Cu/Zn-BTC@LTA Derivatived Cu–ZnO@LTA Membrane Reactor for CO2 Hydrogenation. J. Membr. Sci. 2022, 662, 121010. [Google Scholar] [CrossRef]
- Rieck, F.; Mundstock, A.; Richter, H.; Huang, A.; Kißling, P.; Hindricks, K.D.J.; Behrens, P.; Caro, J. Controlled Methylamine Synthesis in a Membrane Reactor Featuring a Highly Steam Selective K+-LTA Membrane. Microporous Mesoporous Mater. 2022, 337, 111920. [Google Scholar] [CrossRef]
- Krishna, R. Multicomponent Surface Diffusion of Adsorbed Species: A Description Based on the Generalized Maxwell-Stefan Equations. Chem. Eng. Sci. 1990, 45, 1779–1791. [Google Scholar] [CrossRef]
- Monsalve Bravo, G.M. Engineering Models of Permeation in Mixed-Matrix Membranes. Ph.D. Thesis, University of Queensland, Brisbane, Australia,, 2016. [Google Scholar]
- Cardoso, S.P.; Azenha, I.S.; Portugal, I.; Lin, Z.; Rodrigues, A.E.; Silva, C.M. Single and Binary Surface Diffusion Permeation through Zeolite Membranes Using New Maxwell-Stefan Factors for Dubinin-type Isotherms and Occupancy-Dependent Kinetics. Sep. Purif. Technol. 2017, 182, 207–218. [Google Scholar] [CrossRef]
- Cavenati, S.; Grande, C.A.; Rodrigues, A.E.; Kiener, C.; Müller, U. Metal Organic Framework Adsorbent for Biogas Upgrading. Ind. Eng. Chem. Res. 2008, 47, 6333–6335. [Google Scholar] [CrossRef]
- Choi, B.U.; Choi, D.K.; Lee, Y.W.; Lee, B.K.; Kim, S.H. Adsorption Equilibria of Methane, Ethane, Ethylene, Nitrogen, and Hydrogen onto Activated Carbon. J. Chem. Eng. Data 2003, 48, 603–607. [Google Scholar] [CrossRef]
- Hao, S.; Chu, W.; Jiang, Q.; Yu, X. Methane Adsorption Characteristics on Coal Surface above Critical Temperature through Dubinin–Astakhov Model and Langmuir Model. Colloids Surf. A Physicochem. Eng. Asp. 2014, 444, 104–113. [Google Scholar] [CrossRef]
- Ito, M.; Nishihara, H.; Yamamoto, K.; Itoi, H.; Tanaka, H.; Maki, A.; Miyahara, M.T.; Yang, S.J.; Park, C.R.; Kyotani, T. Reversible Pore Size Control of Elastic Microporous Material by Mechanical Force. Chem.-Eur. J. 2013, 19, 13009–13016. [Google Scholar] [CrossRef]
- Men’shchikov, I.E.; Shkolin, A.V.; Fomkin, A.A.; Khozina, E.V. Thermodynamics of Methane Adsorption on Carbon Adsorbent Prepared from Mineral Coal. Adsorption 2021, 27, 1095–1107. [Google Scholar] [CrossRef]
- Marco-Lozar, J.P.; Kunowsky, M.; Suárez-García, F.; D. Carruthers, J.; Linares-Solano, A. Activated Carbon Monoliths for Gas Storage at Room Temperature. Energy Environ. Sci. 2012, 5, 9833–9842. [Google Scholar] [CrossRef]
- Rother, J.; Fieback, T. Multicomponent Adsorption Measurements on Activated Carbon, Zeolite Molecular Sieve and Metal–Organic Framework. Adsorption 2013, 19, 1065–1074. [Google Scholar] [CrossRef]
- Takagi, H.; Hatori, H.; Soneda, Y.; Yoshizawa, N.; Yamada, Y. Adsorptive Hydrogen Storage in Carbon and Porous Materials. Mater. Sci. Eng. B 2004, 108, 143–147. [Google Scholar] [CrossRef]
- Voskuilen, T.G.; Pourpoint, T.L.; Dailly, A.M. Hydrogen Adsorption on Microporous Materials at Ambient Temperatures and Pressures up to 50 MPa. Adsorption 2012, 18, 239–249. [Google Scholar] [CrossRef]
- NIST/ARPA-E Database of Novel and Emerging Adsorbent Materials. Available online: https://adsorption.nist.gov/isodb/index.php#home (accessed on 15th October 2023).
- Kämnitz, S.; Simon, A.; Richter, H.; Weyd, M.; Lubenau, U.; Geisler, T.; Voigt, I. Hydrogen Conditioning Using Nanoporous Inorganic Membranes. Chem. Ing. Tech. 2022, 94, 49–55. [Google Scholar] [CrossRef]
- Burket, C.L. Genesis and Evolution of Porosity and Microstructure in Nanoporous Carbon Derived from Polyfurfuryl Alcohol. Ph.D. Thesis, The Pennsylvania State University, Pennsylvania, PA, USA, 2007. [Google Scholar]
- Gao, X.; Bonilla, M.R.; da Costa, J.C.D.; Bhatia, S.K. The Transport of Gases in Macroporous α-Alumina Supports. J. Membr. Sci. 2012, 409–410, 24–33. [Google Scholar] [CrossRef]
- Gao, X.; Bonilla, M.R.; da Costa, J.C.D.; Bhatia, S.K. The Transport of Gases in a Mesoporous γ-Alumina Supported Membrane. J. Membr. Sci. 2013, 428, 357–370. [Google Scholar] [CrossRef]
- Gregg, S.; Sing, K. Adsorption, Surface Area and Porosity; Wiley Online Library: Hoboken, NJ, USA, 1982. [Google Scholar]
- Rouquerol, J.; Rouquerol, F.; Llewellyn, P.; Maurin, G.; Sing, K. Adsorption by Powders and Porous Solids: Principles, Methodology and Applications; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Del Moral, P.; Doucet, A.; Jasra, A. Sequential Monte Carlo Samplers. J. R. Stat. Soc. Ser. B Stat. Methodol. 2006, 68, 411–436. [Google Scholar] [CrossRef]
- Geris, L.; Gomez-Cabrero, D. Uncertainty in Biology: A Computational Modeling Approach; Springer: Berlin, Germany, 2016. [Google Scholar]
- Clarkson, W. HOWTO Estimate Parameter-Errors by Monte-Carlo. 2014. Available online: http://www-personal.umd.umich.edu/~wiclarks/AstroLab/HOWTOs/NotebookStuff/MonteCarloHOWTO.html (accessed on 2 October 2023).
- Andersson, J.A.E.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi: A Software Framework for Nonlinear Optimization and Optimal Control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
- Do, D.D. Adsorption Analysis: Equilibria and Kinetics; Chemical Engineering, Imperial College Press: London, UK, 1998; Volume 2. [Google Scholar]
- Krishna, R.; van Baten, J.M. Onsager Coefficients for Binary Mixture Diffusion in Nanopores. Chem. Eng. Sci. 2008, 63, 3120–3140. [Google Scholar] [CrossRef]
- Nagy, E. Basic Equations of Mass Transport Through a Membrane Layer; Elsevier Science: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Fu, S.; Sanders, E.S.; Kulkarni, S.S.; Wenz, G.B.; Koros, W.J. Temperature Dependence of Gas Transport and Sorption in Carbon Molecular Sieve Membranes Derived from Four 6FDA Based Polyimides: Entropic Selectivity Evaluation. Carbon 2015, 95, 995–1006. [Google Scholar] [CrossRef]
- Gilliland, E.R.; Baddour, R.F.; Perkinson, G.P.; Sladek, K.J. Diffusion on Surfaces. I. Effect of Concentration on the Diffusivity of Physically Adsorbed Gases. Ind. Eng. Chem. Fundamen. 1974, 13, 95–100. [Google Scholar] [CrossRef]
- Builes, S.; Sandler, S.I.; Xiong, R. Isosteric Heats of Gas and Liquid Adsorption. Langmuir 2013, 29, 10416–10422. [Google Scholar] [CrossRef] [PubMed]
- Tun, H.; Chen, C.C. Isosteric Heat of Adsorption from Thermodynamic Langmuir Isotherm. Adsorption 2021, 27, 979–989. [Google Scholar] [CrossRef]
- Richter, H.; Voss, H.; Kaltenborn, N.; Kämnitz, S.; Wollbrink, A.; Feldhoff, A.; Caro, J.; Roitsch, S.; Voigt, I. High-Flux Carbon Molecular Sieve Membranes for Gas Separation. Angew. Chem. Int. Ed. 2017, 56, 7760–7763. [Google Scholar] [CrossRef]

| Smic m2g−1 | Vmic cm3g−1 | dp nm | VT cm3g−1 | (Estimation Method) |
|---|---|---|---|---|
| 373 | 0.134 | 0.63 | - | CO2 at 273 K (Monte Carlo) |
| 385 | 0.127 | 0.57 | - | CO2 at 273 K (NLDFT) |
| 415 | 0.156 | 1.03 | - | CO2 at 273 K (DR) |
| 6 | <0.001 | - | <0.01 | N2 at 77 K (BET & DR) |
| Layer | dp m | δ μm | Material | ε % | Kn of H2 at 120 °C | Mass Transport Mechanism |
|---|---|---|---|---|---|---|
| Support | 3.00 × 10−6 | 1500 | α-Al2O3 | 32–35 | 4.87 × 10−3 | None |
| Coarse UF | 7.00 × 10−8 | 150 | α-Al2O3 | 45 | 2.09 × 10−3 | Knudsen |
| Fine UF | 5.00 × 10−9 | 10 | γ-Al2O3 | 55 | 2.92 | Knudsen |
| Porous carbon | 4.00 × 10−10 | 2 | Carbon | 45 | 3.48 × 101 | MS surface diffusion |
| Experiment | Temperature K | Pressure bar | Material | Result |
|---|---|---|---|---|
| H2 adsorption | 363/383/393 | 5–45 | casting material | adsorption isotherm |
| CH4 adsorption | 363/383/393 | 5–45 | casting material | adsorption isotherm |
| CO2 adsorption | 273 | 1 | casting material | characterization |
| N2 adsorption | 77 | 1 | casting material | characterization |
| H2 permeation | 393/443/493 | 2–5 | cylindrical membrane | permeation data |
| CH4 permeation | 393/443/493 | 5–15 | cylindrical membrane | permeation data |
| Component | T °C | mmol g−1 | bar−1 | R2 | R2 | bar−1 | mmol g−1 | R2 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| H2 | 90 | 0.093 | 0.512 | 0.980 | 0.132 | 0.302 | 0.993 | 1.000 | 0.262 | 1.377 | 0.991 |
| H2 | 110 | 0.040 | 0.513 | 0.915 | 0.069 | 0.409 | 0.920 | 0.126 | 0.269 | 2.000 | 0.919 |
| H2 | 120 | 0.030 | 0.407 | 0.147 | 0.007 | 1.000 | 0.138 | 0.030 | 1.000 | 0.407 | 0.147 |
| CH4 | 90 | 0.117 | 1.486 | 0.984 | 0.413 | 0.296 | 0.985 | 0.117 | 1.000 | 1.486 | 0.984 |
| CH4 | 110 | 0.067 | 1.442 | 0.993 | 0.253 | 0.386 | 0.997 | 0.096 | 0.605 | 1.923 | 0.996 |
| CH4 | 120 | 0.060 | 1.399 | 0.993 | 0.253 | 0.366 | 0.998 | 0.108 | 0.531 | 2.000 | 0.998 |
| Component | 120 °C m2s−1 | 170 °C m2s−1 | 220 °C m2s−1 |
|---|---|---|---|
| H2 | 9.81 × ± 2.55 × | 1.84 × ± 3.34 × | 2.01 × ± 4.92 × |
| CH4 | 3.73 × ± 6.28 × | 5.17 × ± 3.54 × | 6.39 × ± 6.07 × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurth, M.; Javed, M.; Schliermann, T.; Brösigke, G.; Kämnitz, S.; Bhatia, S.K.; Repke, J.-U. Pure Hydrogen and Methane Permeation in Carbon-Based Nanoporous Membranes: Adsorption Isotherms and Permeation Experiments. Membranes 2024, 14, 123. https://doi.org/10.3390/membranes14060123
Kurth M, Javed M, Schliermann T, Brösigke G, Kämnitz S, Bhatia SK, Repke J-U. Pure Hydrogen and Methane Permeation in Carbon-Based Nanoporous Membranes: Adsorption Isotherms and Permeation Experiments. Membranes. 2024; 14(6):123. https://doi.org/10.3390/membranes14060123
Chicago/Turabian StyleKurth, Matthis, Mudassar Javed, Thomas Schliermann, Georg Brösigke, Susanne Kämnitz, Suresh K. Bhatia, and Jens-Uwe Repke. 2024. "Pure Hydrogen and Methane Permeation in Carbon-Based Nanoporous Membranes: Adsorption Isotherms and Permeation Experiments" Membranes 14, no. 6: 123. https://doi.org/10.3390/membranes14060123
APA StyleKurth, M., Javed, M., Schliermann, T., Brösigke, G., Kämnitz, S., Bhatia, S. K., & Repke, J.-U. (2024). Pure Hydrogen and Methane Permeation in Carbon-Based Nanoporous Membranes: Adsorption Isotherms and Permeation Experiments. Membranes, 14(6), 123. https://doi.org/10.3390/membranes14060123









