Experimental and Numerical Simulation Study of Oxygen Transport in Proton Exchange Membrane Fuel Cells at Intermediate Temperatures (80 °C–120 °C)
Abstract
1. Introduction
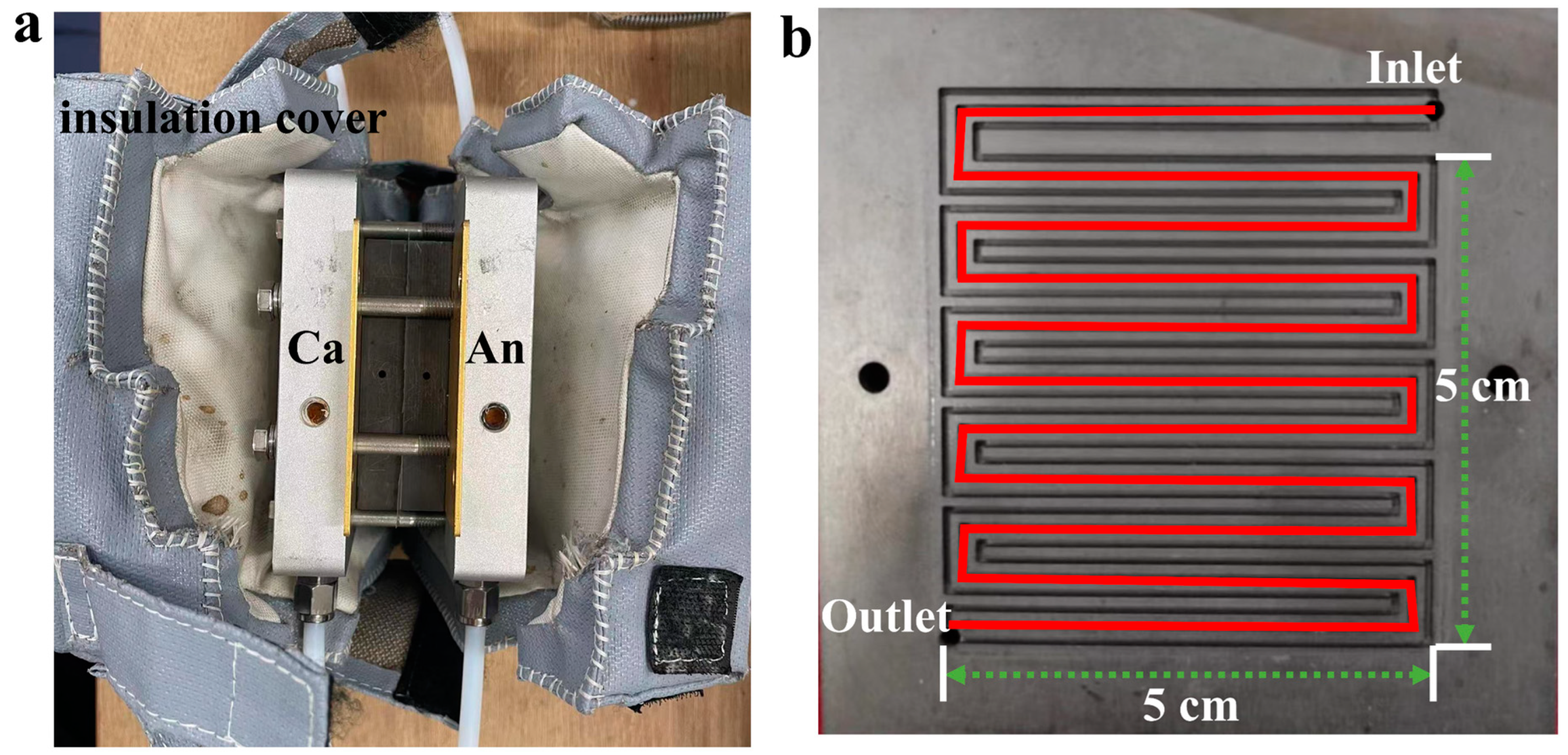
2. Materials and Methods
3. Theoretical Deduction
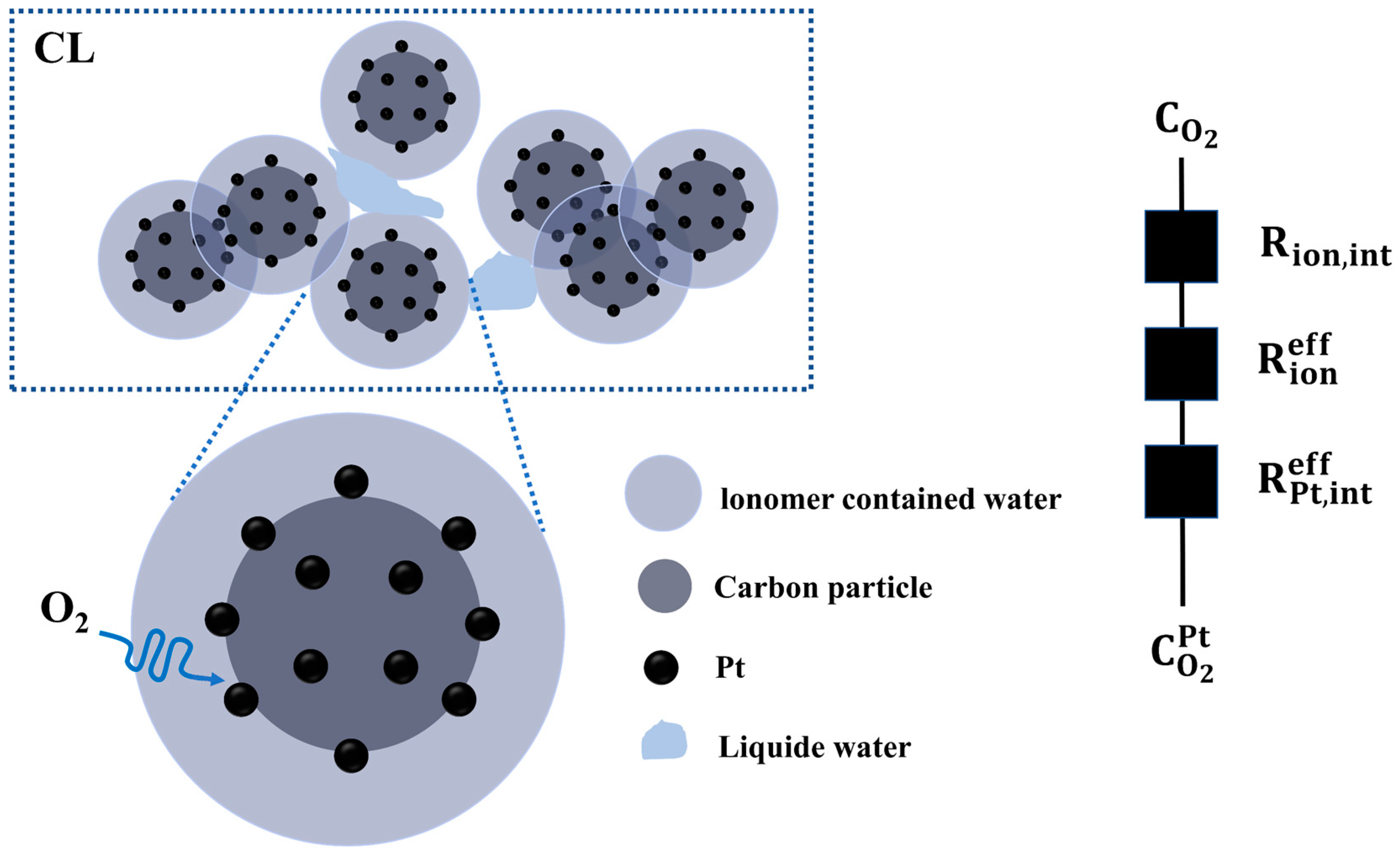
3.1. Cathodic Oxygen Transport Process
3.2. Oxygen Transport Modeling
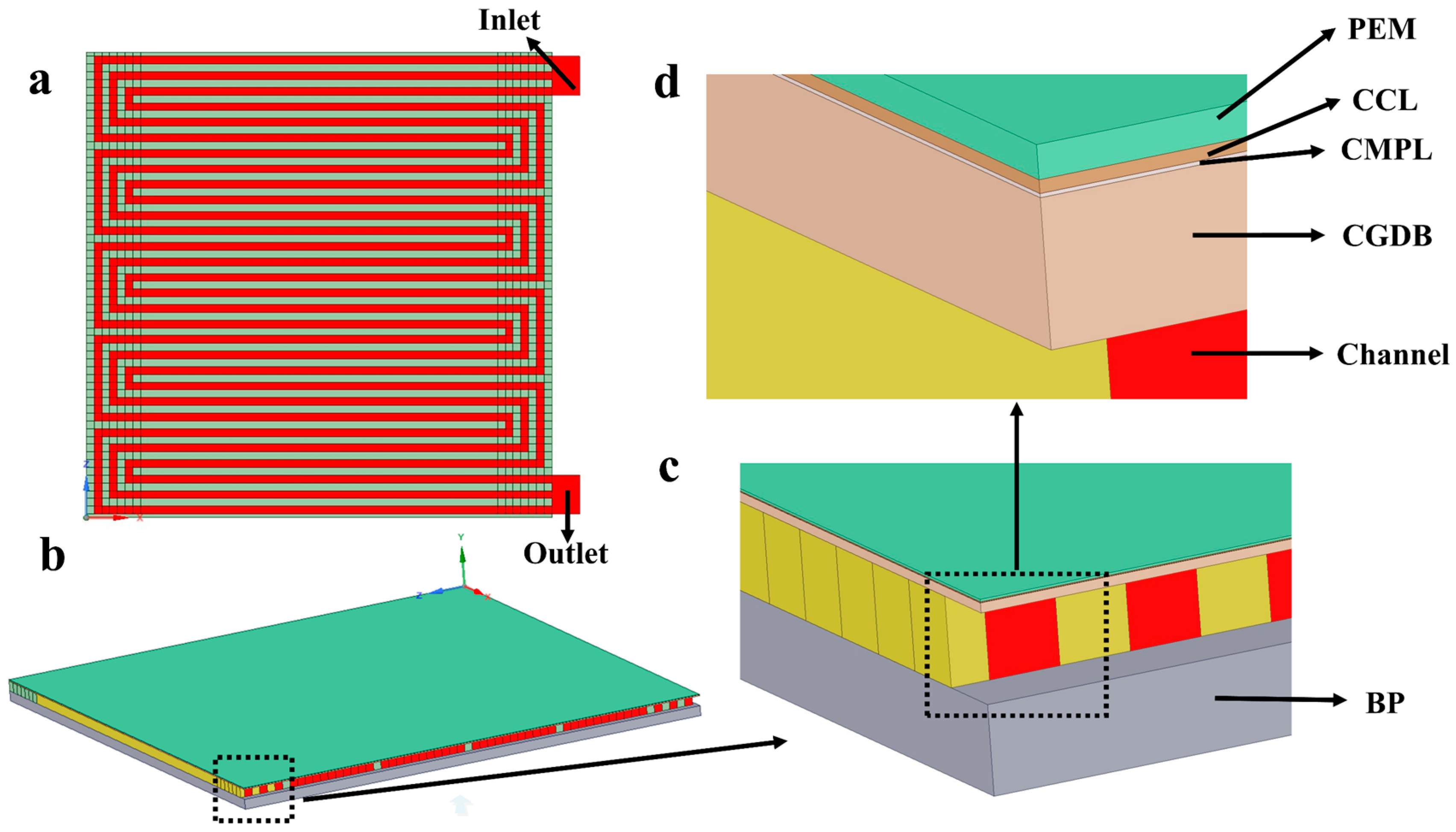
3.2.1. Geometric Model
3.2.2. Mathematical Model
3.2.3. Model Assumptions
- (1)
- The fuel cell operating environment is steady state;
- (2)
- All gases involved in this study are considered ideal gases;
- (3)
- Both GDL and CL are porous media with uniform porosity;
- (4)
- There is no hydrogen permeation in PEM, and only the conduction of protons and hydronium ions in the membrane is considered.
4. Discussion
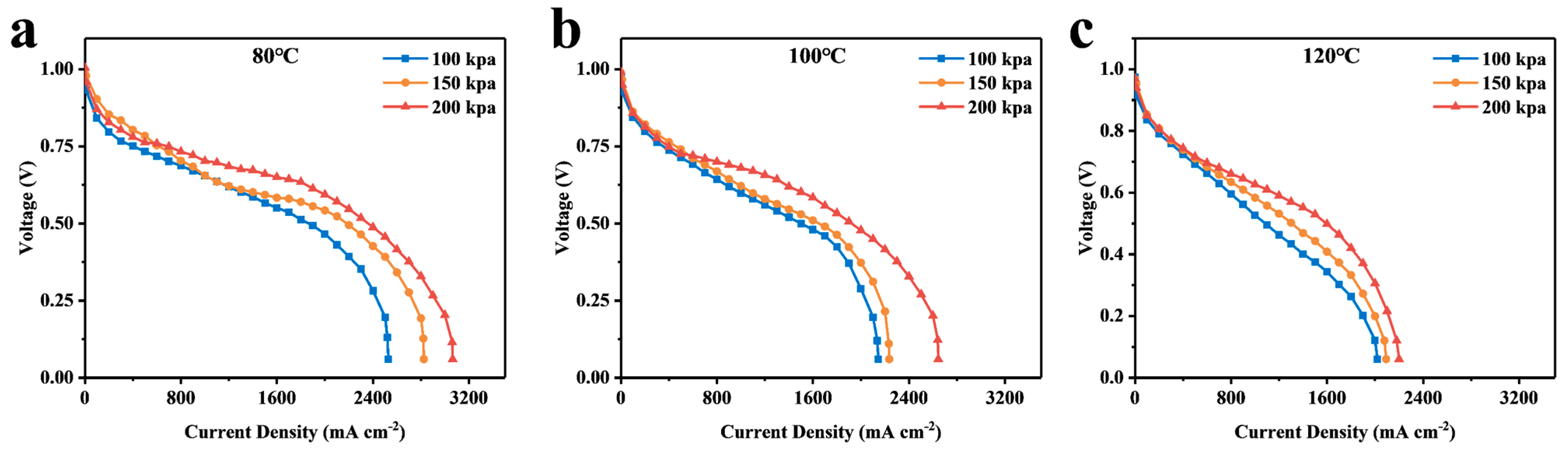
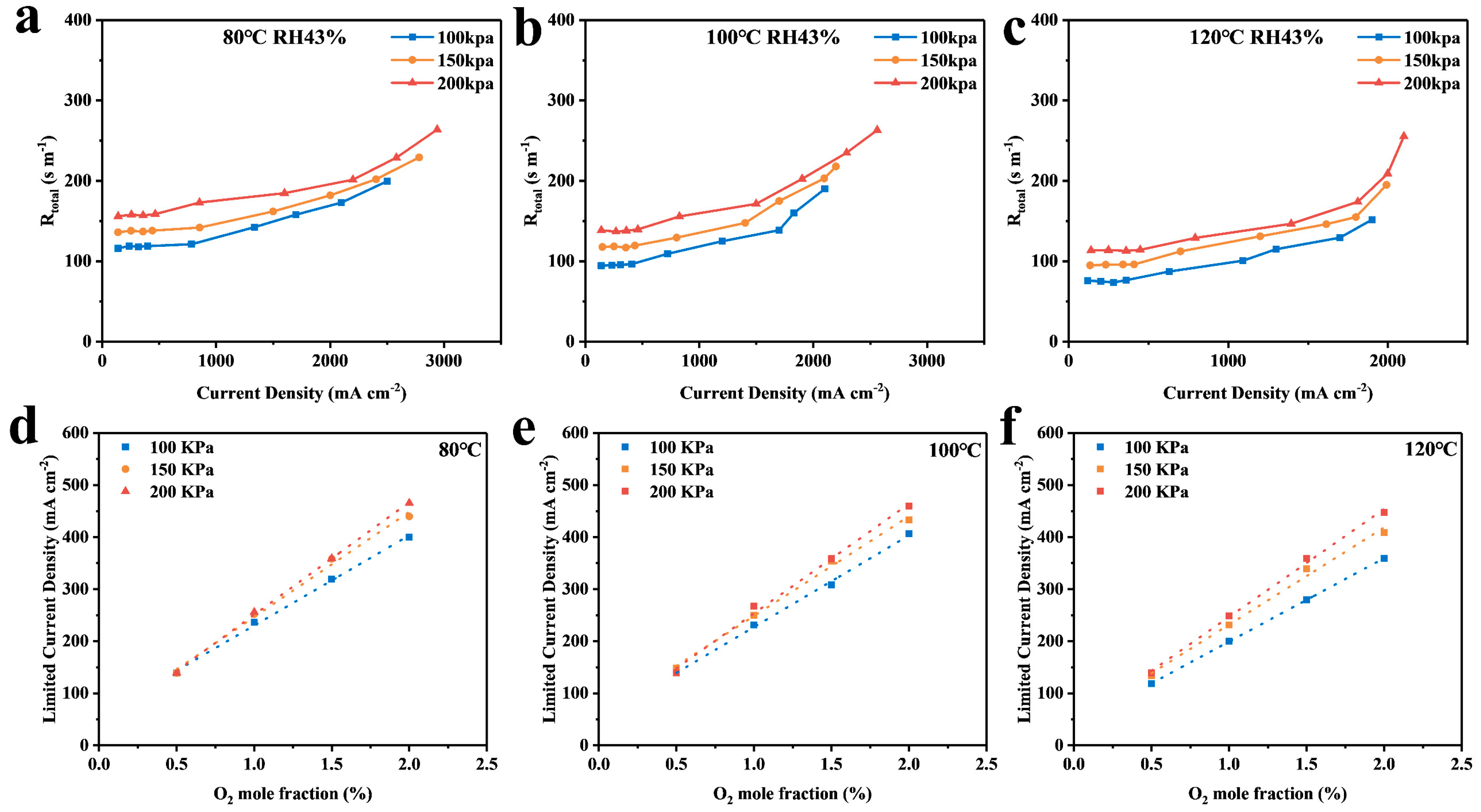
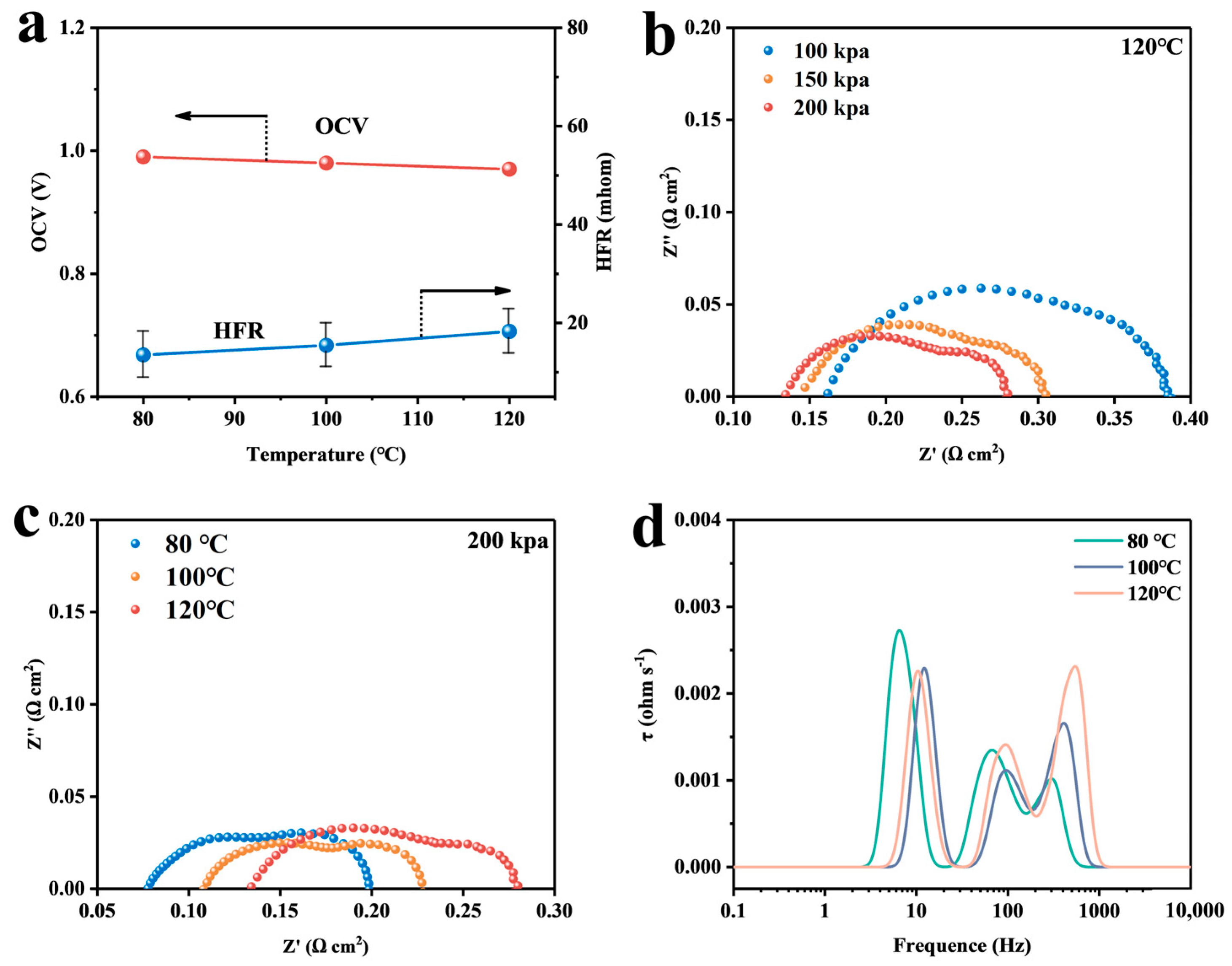
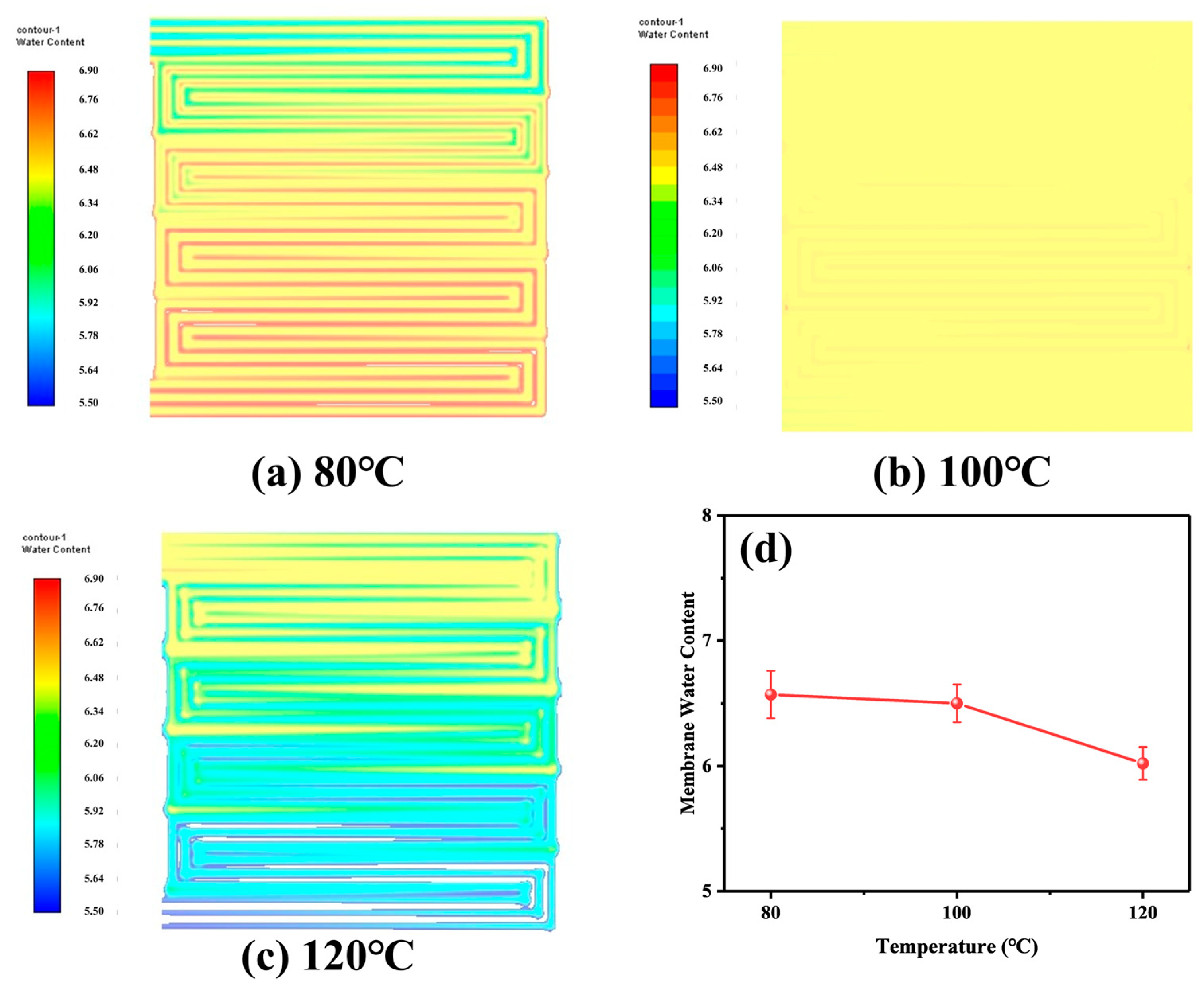
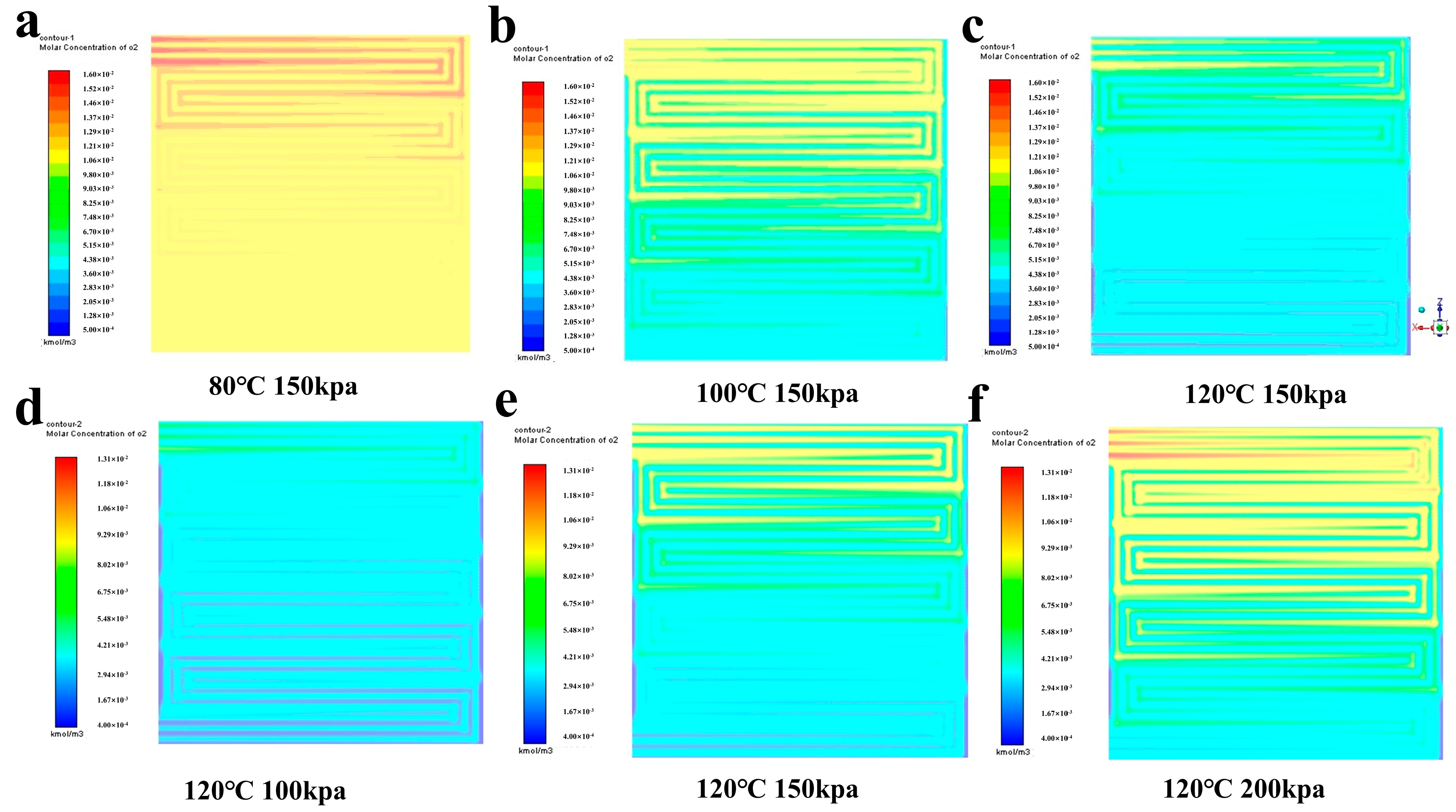
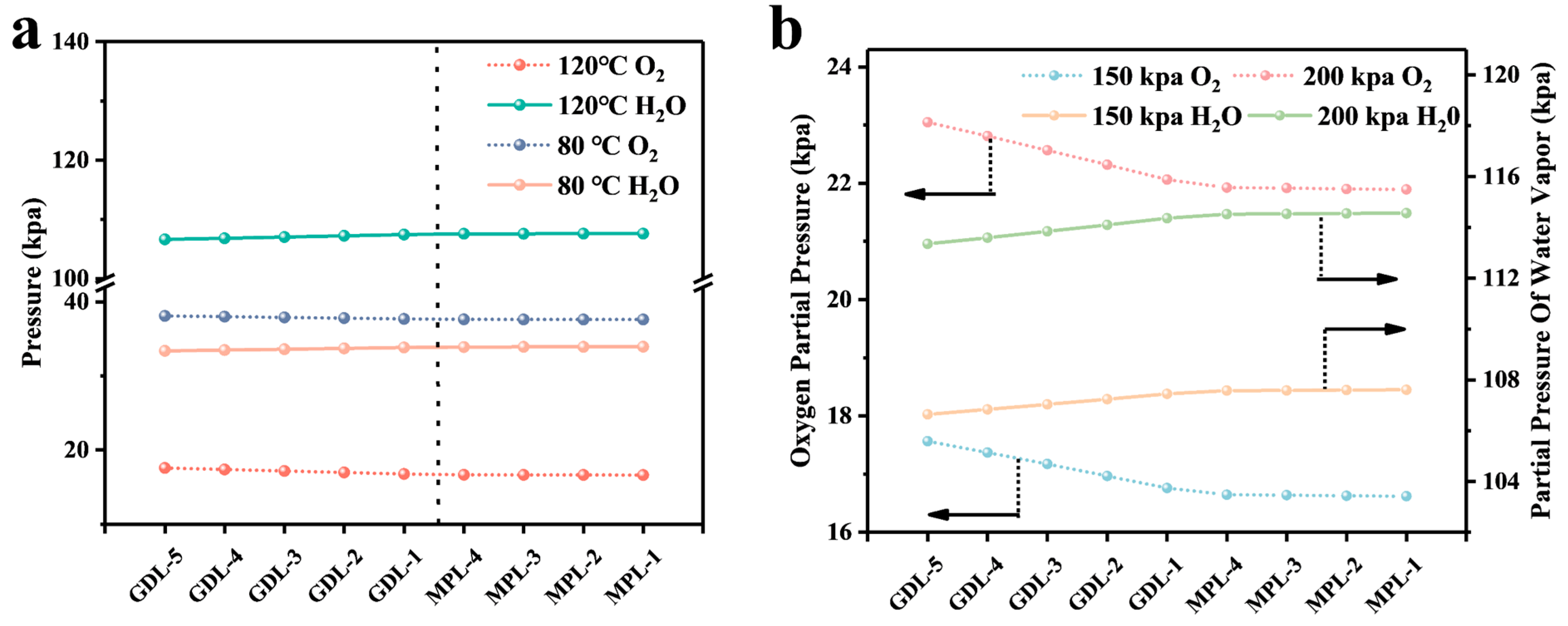
4.1. Calculation and Analysis of the Resistance of Each Part
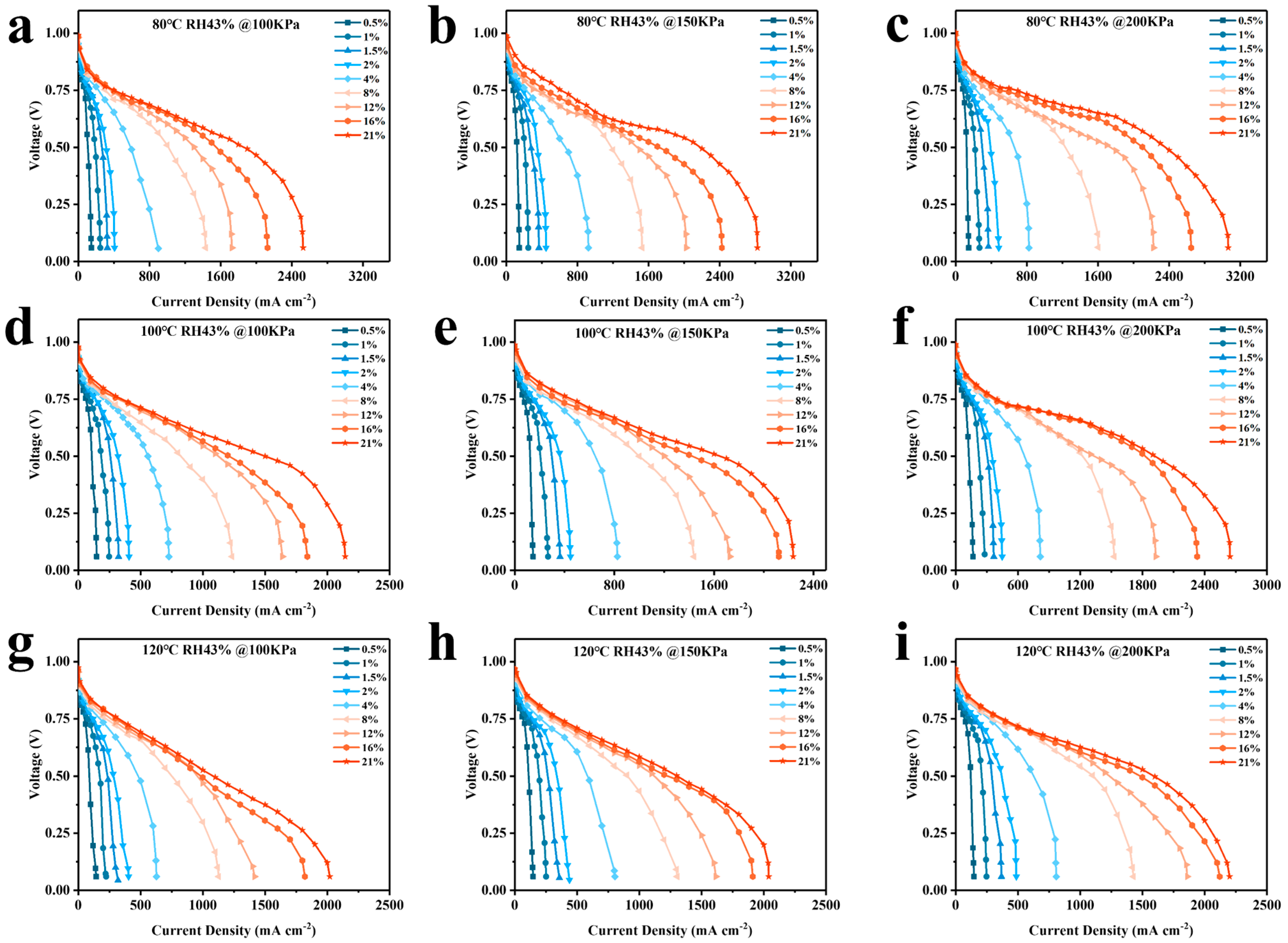
4.2. Analysis of Simulation Results
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| List of Symbols | |||
| The effective surface area of ionomer film per unit area of MEA | m2 | ||
| Effective platinum surface area | m2 | ||
| Water activity | |||
| Electrochemical active area of platinum | cm2 g−1 | ||
| molar heat capacity at constant pressure | J K−1 mol−1 | ||
| The diffusion rate of oxygen in polymer membranes | m2 s−1 | 8.45 × 10−10 | |
| Thermodynamic reversible potential | V | ||
| Equivalent weight of the membrane | g mol−1 | 1000 | |
| F | Faraday’s constant | C mol−1 | 96,485 |
| Enthalpy of phase transition formation | J mol−1 | 44.9 | |
| Current density | mA cm2 | ||
| k1 | Interface resistance constant on the surface of ionomer films | 8.5 | |
| k2 | Interface resistance constant on platinum surface | 16 | |
| Molecular weight | g mol−1 | ||
| Platinum loading in the cathode catalytic layer | mg cm−2 | 0.4 | |
| The molar flux of oxygen | mol s−1 m2 | ||
| The number of platinum particles in Pt/C | |||
| Electro-osmotic drag coefficient | |||
| Total gas pressure | kPa | ||
| Water vapor pressure | kPa | ||
| R | Universal gas constant | J mol−1 K−1 | 8.314 |
| Local mass transfer resistance per unit surface area of pt | 10−3 s m−1 | ||
| Quality source term | kg m−3 s−1 | ||
| Liquid water saturation | |||
| T | Absolute temperature | K | 0 |
| Time | s | ||
| Pt mass fraction in Pt/C mixture | 0.6 | ||
| The ratio of carbon surface normalized by Pt surface | 1 | ||
| The volume fraction of bare carbon | 0 | ||
| Anode/Cathode charge transfer coefficient | 0.5/0.8 | ||
| Equivalent thickness of ionomer film | 10−8 m | ||
| Volume fraction | |||
| Cathodic overpotential | V | ||
| contact angle | ° | 105 | |
| Pt oxide-coverage | |||
| Water content | |||
| Velocity of flow | L min−1 | ||
| Gas flow rate | L min−1 | ||
| Density | kg m−3 | ||
| Surface tension of liquid water | N m−1 | 0.0644 | |
| Potential | V | ||
| Volume fraction of ionomers | 0.25 | ||
| Anode | |||
| Activation | |||
| Catalyst layer | |||
| Cathode | |||
| Effective | |||
| Equilibrium | |||
| Gas diffusion layer | |||
| Gas phase | |||
| Inlet | |||
| Ionic | |||
| Liquid phase | |||
| Solid phase | |||
| Water | |||
References
- Kakinuma, K.; Taniguchi, H.; Asakawa, T.; Miyao, T.; Uchida, M.; Aoki, Y.; Akiyama, T.; Masuda, A.; Sato, N.; Iiyama, A. The Possibility of Intermediate–Temperature (120 °C)–Operated Polymer Electrolyte Fuel Cells using Perfluorosulfonic Acid Polymer Membranes. J. Electrochem. Soc. 2022, 169, 044522. [Google Scholar] [CrossRef]
- Aricò, A.S.; Di Blasi, A.; Brunaccini, G.; Sergi, F.; Antonucci, V.; Asher, P.; Buche, S.; Fongalland, D.; Hards, G.A.; Sharman, J.; et al. High Temperature Operation of a Solid Polymer Electrolyte Fuel Cell Stack Based on a New Ionomer Membrane. ECS Trans. 2009, 25, 1999. [Google Scholar] [CrossRef]
- Dupuis, A.-C. Proton exchange membranes for fuel cells operated at medium temperatures: Materials and experimental techniques. Prog. Mater. Sci. 2011, 56, 289–327. [Google Scholar] [CrossRef]
- Nishimura, A.; Kono, N.; Toyoda, K.; Mishima, D.; Kolhe, M. Impact of Separator Thickness on Temperature Distribution in Single Cell of Polymer Electrolyte Fuel Cell Operated at Higher Temperature of 90 °C and 100 °C. Energies 2022, 15, 4203. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, Z.; Zhang, J.; Tang, Y.; Song, C.; Navessin, T.; Shi, Z.; Song, D.; Wang, H.; Wilkinson, D.P.; et al. High temperature PEM fuel cells. J. Power Sources 2006, 160, 872–891. [Google Scholar] [CrossRef]
- Jiao, K.; Xuan, J.; Du, Q.; Bao, Z.; Xie, B.; Wang, B.; Zhao, Y.; Fan, L.; Wang, H.; Hou, Z.; et al. Designing the next generation of proton-exchange membrane fuel cells. Nature 2021, 595, 361–369. [Google Scholar] [CrossRef] [PubMed]
- Yin, K.M.; Chang, C.P. Effects of Humidification on the Membrane Electrode Assembly of Proton Exchange Membrane Fuel Cells at Relatively High Cell Temperatures. Fuel Cells 2011, 11, 888–896. [Google Scholar] [CrossRef]
- Baker, D.R.; Caulk, D.A.; Neyerlin, K.C.; Murphy, M.W. Measurement of Oxygen Transport Resistance in PEM Fuel Cells by Limiting Current Methods. J. Electrochem. Soc. 2009, 156, B991. [Google Scholar] [CrossRef]
- Mashio, T.; Ohma, A.; Yamamoto, S.; Shinohara, K. Analysis of Reactant Gas Transport in a Catalyst Layer. ECS Trans. 2007, 11, 529. [Google Scholar] [CrossRef]
- Nonoyama, N.; Okazaki, S.; Weber, A.Z.; Ikogi, Y.; Yoshida, T. Analysis of Oxygen-Transport Diffusion Resistance in Proton-Exchange-Membrane Fuel Cells. J. Electrochem. Soc. 2011, 158, B416. [Google Scholar] [CrossRef]
- Oh, H.; Lee, Y.i.; Lee, G.; Min, K.; Yi, J.S. Experimental dissection of oxygen transport resistance in the components of a polymer electrolyte membrane fuel cell. J. Power Sources 2017, 345, 67–77. [Google Scholar] [CrossRef]
- Xu, H.; Kunz, H.R.; Fenton, J.M. Analysis of proton exchange membrane fuel cell polarization losses at elevated temperature 120°C and reduced relative humidity. Electrochim. Acta 2007, 52, 3525–3533. [Google Scholar] [CrossRef]
- Akitomo, F.; Sasabe, T.; Yoshida, T.; Naito, H.; Kawamura, K.; Hirai, S. Investigation of effects of high temperature and pressure on a polymer electrolyte fuel cell with polarization analysis and X-ray imaging of liquid water. J. Power Sources 2019, 431, 205–209. [Google Scholar] [CrossRef]
- Fernihough, O.; Ismail, M.S.; El-kharouf, A. Intermediate Temperature PEFC’s with Nafion® 211 Membrane Electrolytes: An Experimental and Numerical Study. Membranes 2022, 12, 430. [Google Scholar] [CrossRef]
- He, H.; Peng, H.; Li, G. Study on water and oxygen transfer characteristics of HT-PEM fuel cells. Heliyon 2023, 9, e19832. [Google Scholar] [CrossRef]
- Xia, L.; Xu, Q.; He, Q.; Ni, M.; Seng, M. Numerical study of high temperature proton exchange membrane fuel cell (HT-PEMFC) with a focus on rib design. Int. J. Hydrogen Energy 2021, 46, 21098–21111. [Google Scholar] [CrossRef]
- Park, J.-S.; Shin, M.-S.; Kim, C.-S. Proton exchange membranes for fuel cell operation at low relative humidity and intermediate temperature: An updated review. Curr. Opin. Electrochem. 2017, 5, 43–55. [Google Scholar] [CrossRef]
- Butori, M.; Eriksson, B.; Nikolić, N.; Lagergren, C.; Lindbergh, G.; Lindström, R.W. The effect of oxygen partial pressure and humidification in proton exchange membrane fuel cells at intermediate temperature (80–120 °C). J. Power Sources 2023, 563, 232803. [Google Scholar] [CrossRef]
- Wang, Q.; Tang, F.; Li, X.; Zheng, J.P.; Hao, L.; Cui, G.; Ming, P. Revealing the dynamic temperature of the cathode catalyst layer inside proton exchange membrane fuel cell by experimental measurements and numerical analysis. Chem. Eng. J. 2023, 463, 142286. [Google Scholar] [CrossRef]
- He, P.; Mu, Y.-T.; Park, J.W.; Tao, W.-Q. Modeling of the effects of cathode catalyst layer design parameters on performance of polymer electrolyte membrane fuel cell. Appl. Energy 2020, 277, 115555. [Google Scholar] [CrossRef]
- Jiang, P.; Zhan, Z.; Zhang, D.; Wang, C.; Zhang, H.; Pan, M. Two-Dimensional Simulation of the Freezing Characteristics in PEMFCs during Cold Start Considering Ice Crystallization Kinetics. Polymers 2022, 14, 3203. [Google Scholar] [CrossRef] [PubMed]
- Vetter, R.; Schumacher, J.O. Free open reference implementation of a two-phase PEM fuel cell model. Comput. Phys. Commun. 2019, 234, 223–234. [Google Scholar] [CrossRef]
- Fan, L.; Zhang, G.; Jiao, K. Characteristics of PEMFC operating at high current density with low external humidification. Energy Convers. Manag. 2017, 150, 763–774. [Google Scholar] [CrossRef]
- Buck, A.L. New Equations for Computing Vapor Pressure and Enhancement Factor. J. Appl. Meteorol. Climatol. 1981, 20, 1527–1532. [Google Scholar] [CrossRef]
- Mu, Y.-T.; He, P.; Ding, J.; Tao, W.-Q. Modeling of the operation conditions on the gas purging performance of polymer electrolyte membrane fuel cells. Int. J. Hydrogen Energy 2017, 42, 11788–11802. [Google Scholar] [CrossRef]
- Baghban Yousefkhani, M.; Ghadamian, H.; Daneshvar, K.; Alizadeh, N.; Rincon Troconis, B.C. Investigation of the Fuel Utilization Factor in PEM Fuel Cell Considering the Effect of Relative Humidity at the Cathode. Energies 2020, 13, 6117. [Google Scholar] [CrossRef]
- Kiyoi, A.; Kawabata, N.; Nakamura, K.; Fujiwara, Y. Influence of oxygen on trap-limited diffusion of hydrogen in proton-irradiated n-type silicon for power devices. J. Appl. Phys. 2021, 129, 025701. [Google Scholar] [CrossRef]
- O’hayre, R.; Cha, S.-W.; Colella, W.; Prinz, F.B. Fuel Cell Fundamentals; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Wan, Z.; Liu, S.; Zhong, Q.; Jin, A.; Pan, M. Mechanism of improving oxygen transport resistance of polytetrafluoroethylene in catalyst layer for polymer electrolyte fuel cells. Int. J. Hydrogen Energy 2018, 43, 7456–7464. [Google Scholar] [CrossRef]
- Liang, J.; Li, Y.; Wang, R.; Jiang, J. Cross-dimensional model of the oxygen transport behavior in low-Pt proton exchange membrane fuel cells. Chem. Eng. J. 2020, 400, 125796. [Google Scholar] [CrossRef]
- Wilberforce, T.; Ijaodola, O.; Khatib, F.N.; Ogungbemi, E.O.; El Hassan, Z.; Thompson, J.; Olabi, A.G. Effect of humidification of reactive gases on the performance of a proton exchange membrane fuel cell. Sci. Total Environ. 2019, 688, 1016–1035. [Google Scholar] [CrossRef]
- Yano, H.; Inukai, J.; Uchida, H.; Watanabe, M.; Babu, P.K.; Kobayashi, T.; Chung, J.H.; Oldfield, E.; Wieckowski, A. Particle-size effect of nanoscale platinum catalysts in oxygen reduction reaction: An electrochemical and 195Pt EC-NMR study. Phys. Chem. Chem. Phys. 2006, 8, 4932–4939. [Google Scholar] [CrossRef]
- Wakabayashi, N.; Takeichi, M.; Itagaki, M.; Uchida, H.; Watanabe, M. Temperature-dependence of oxygen reduction activity at a platinum electrode in an acidic electrolyte solution investigated with a channel flow double electrode. J. Electroanal. Chem. 2005, 574, 339–346. [Google Scholar] [CrossRef]
- Ito, H.; Maeda, T.; Nakano, A.; Takenaka, H. Properties of Nafion membranes under PEM water electrolysis conditions. Int. J. Hydrogen Energy 2011, 36, 10527–10540. [Google Scholar] [CrossRef]
- Kongkanand, A.; Mathias, M.F. The Priority and Challenge of High-Power Performance of Low-Platinum Proton-Exchange Membrane Fuel Cells. J. Phys. Chem. Lett. 2016, 7, 1127–1137. [Google Scholar] [CrossRef]
- Yousfi-Steiner, N.; Moçotéguy, P.; Candusso, D.; Hissel, D. A review on polymer electrolyte membrane fuel cell catalyst degradation and starvation issues: Causes, consequences and diagnostic for mitigation. J. Power Sources 2009, 194, 130–145. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, J.; Song, C.; Liu, H.; Zhang, J.; Wang, H.; Mackinnon, S.; Peckham, T.; Li, J.; McDermid, S.; et al. Temperature Dependent Performance and In Situ AC Impedance of High-Temperature PEM Fuel Cells Using the Nafion-112 Membrane. J. Electrochem. Soc. 2006, 153, A2036. [Google Scholar] [CrossRef]
- Wan, T.H.; Saccoccio, M.; Chen, C.; Ciucci, F. Influence of the Discretization Methods on the Distribution of Relaxation Times Deconvolution: Implementing Radial Basis Functions with DRTtools. Electrochim. Acta 2015, 184, 483–499. [Google Scholar] [CrossRef]
- Ciucci, F.; Chen, C. Analysis of Electrochemical Impedance Spectroscopy Data Using the Distribution of Relaxation Times: A Bayesian and Hierarchical Bayesian Approach. Electrochim. Acta 2015, 167, 439–454. [Google Scholar] [CrossRef]
- Effat, M.B.; Ciucci, F. Bayesian and Hierarchical Bayesian Based Regularization for Deconvolving the Distribution of Relaxation Times from Electrochemical Impedance Spectroscopy Data. Electrochim. Acta 2017, 247, 1117–1129. [Google Scholar] [CrossRef]
- Tagayi, R.K.; Ezahedi, S.E.; Kim, J.; Kim, J. Employment of relaxation times distribution with improved elastic net regularization for advanced impedance data analysis of a lithium-ion battery. J. Energy Storage 2023, 70, 107970. [Google Scholar] [CrossRef]
- Hao, L.; Moriyama, K.; Gu, W.; Wang, C.-Y. Modeling and Experimental Validation of Pt Loading and Electrode Composition Effects in PEM Fuel Cells. J. Electrochem. Soc. 2015, 162, F854. [Google Scholar] [CrossRef]
- Yoon, W.; Weber, A.Z. Modeling Low-Platinum-Loading Effects in Fuel-Cell Catalyst Layers. J. Electrochem. Soc. 2011, 158, B1007. [Google Scholar] [CrossRef]
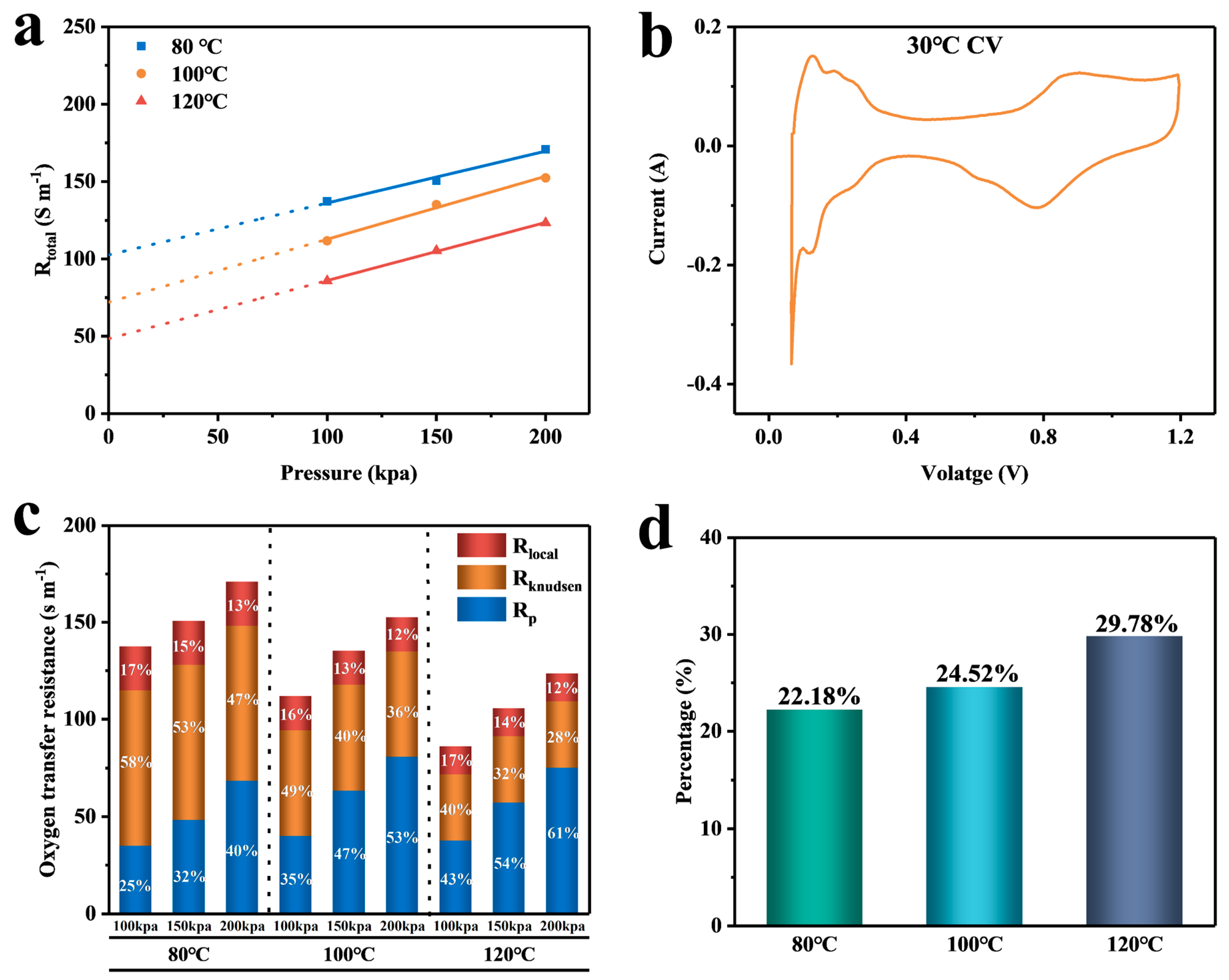
| Temperature | Pressure | (s m−1) | (s m−1) | (s m−1) |
|---|---|---|---|---|
| 80 °C | 100 kpa | 137.3 | 102.63 | 22.76 |
| 150 kpa | 150.56 | 102.63 | 22.76 | |
| 200 kpa | 170.8 | 102.63 | 22.76 | |
| 100 °C | 100 kpa | 111.68 | 72.03 | 17.66 |
| 150 kpa | 135.11 | 72.03 | 17.66 | |
| 200 kpa | 152.36 | 72.03 | 17.66 | |
| 120 °C | 100 kpa | 85.75 | 48.46 | 14.43 |
| 150 kpa | 105.33 | 48.46 | 14.43 | |
| 200 kpa | 123.3 | 48.46 | 14.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Zhang, Y.; Xiao, Z.; Tan, J.; Zhang, H.; Yu, J. Experimental and Numerical Simulation Study of Oxygen Transport in Proton Exchange Membrane Fuel Cells at Intermediate Temperatures (80 °C–120 °C). Membranes 2024, 14, 72. https://doi.org/10.3390/membranes14040072
Zhang J, Zhang Y, Xiao Z, Tan J, Zhang H, Yu J. Experimental and Numerical Simulation Study of Oxygen Transport in Proton Exchange Membrane Fuel Cells at Intermediate Temperatures (80 °C–120 °C). Membranes. 2024; 14(4):72. https://doi.org/10.3390/membranes14040072
Chicago/Turabian StyleZhang, Jian, Yunfei Zhang, Zhengrui Xiao, Jinting Tan, Haining Zhang, and Jun Yu. 2024. "Experimental and Numerical Simulation Study of Oxygen Transport in Proton Exchange Membrane Fuel Cells at Intermediate Temperatures (80 °C–120 °C)" Membranes 14, no. 4: 72. https://doi.org/10.3390/membranes14040072
APA StyleZhang, J., Zhang, Y., Xiao, Z., Tan, J., Zhang, H., & Yu, J. (2024). Experimental and Numerical Simulation Study of Oxygen Transport in Proton Exchange Membrane Fuel Cells at Intermediate Temperatures (80 °C–120 °C). Membranes, 14(4), 72. https://doi.org/10.3390/membranes14040072






