Bis(triethoxysilyl)ethane (BTESE)–Organosilica Membranes for H2O/DMF Separation in Reverse Osmosis (RO): Evaluation and Correlation of Subnanopores via Nanopermporometry (NPP), Modified Gas Translation (mGT) and RO Performance
Abstract
1. Introduction
2. Materials and Methods
2.1. Preparation of BTESE-Derived Sols and Membranes
2.2. Membrane Pore Size Distribution
2.3. Gas Permeation (GP) and Reverse Osmosis (RO) Performance
3. Results and Discussions
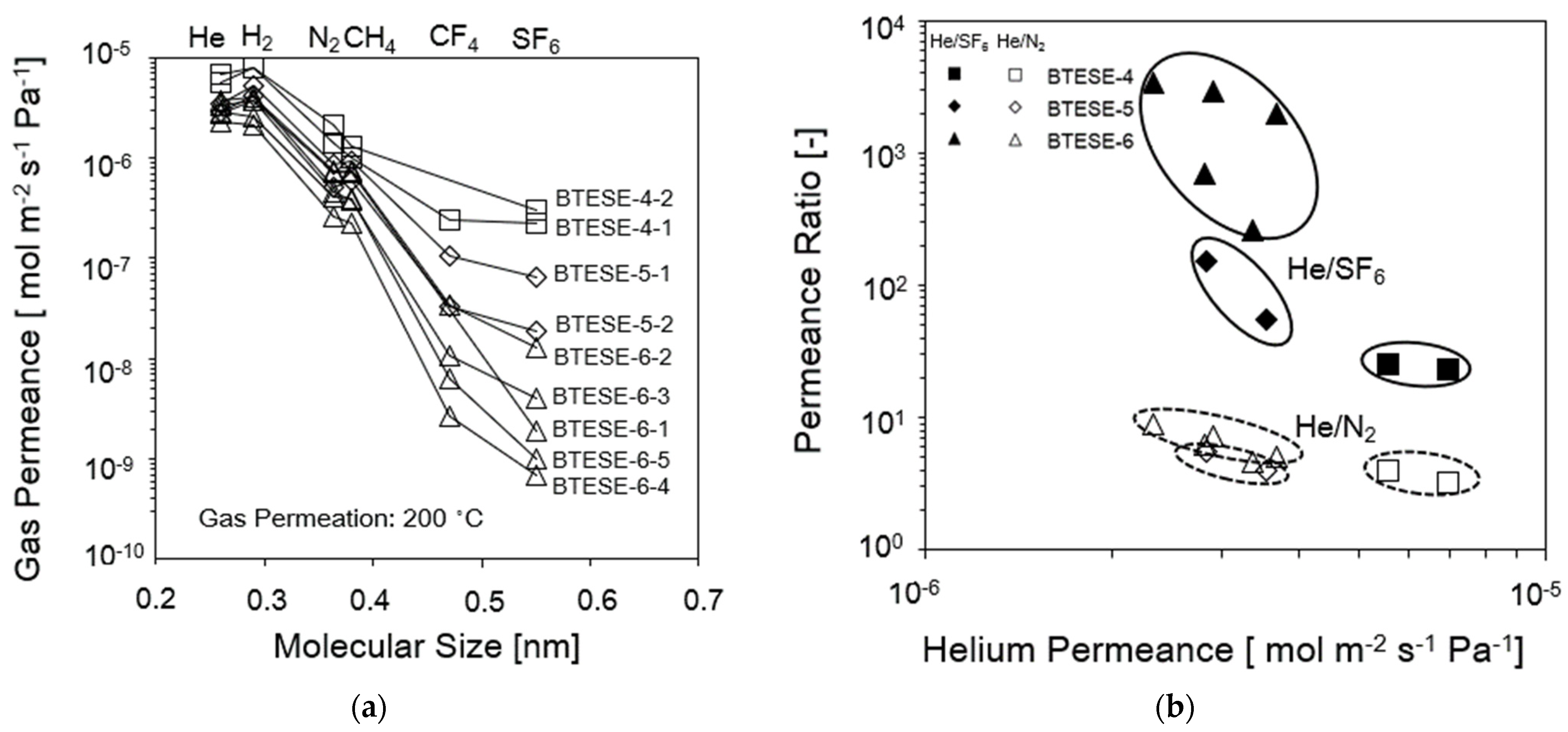
3.1. Gas Permeation (GP) Performance of BTESE Organosilica Membranes
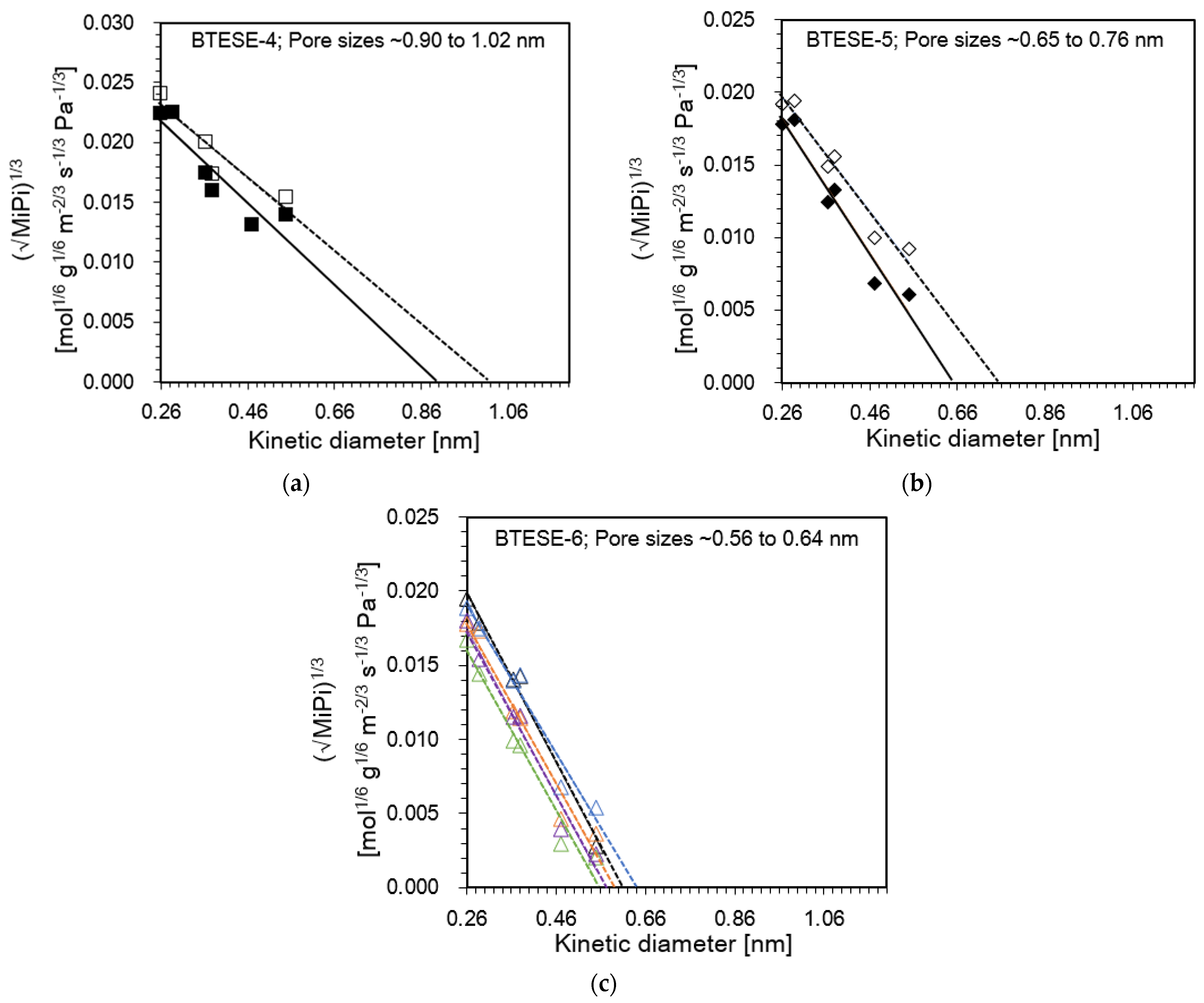
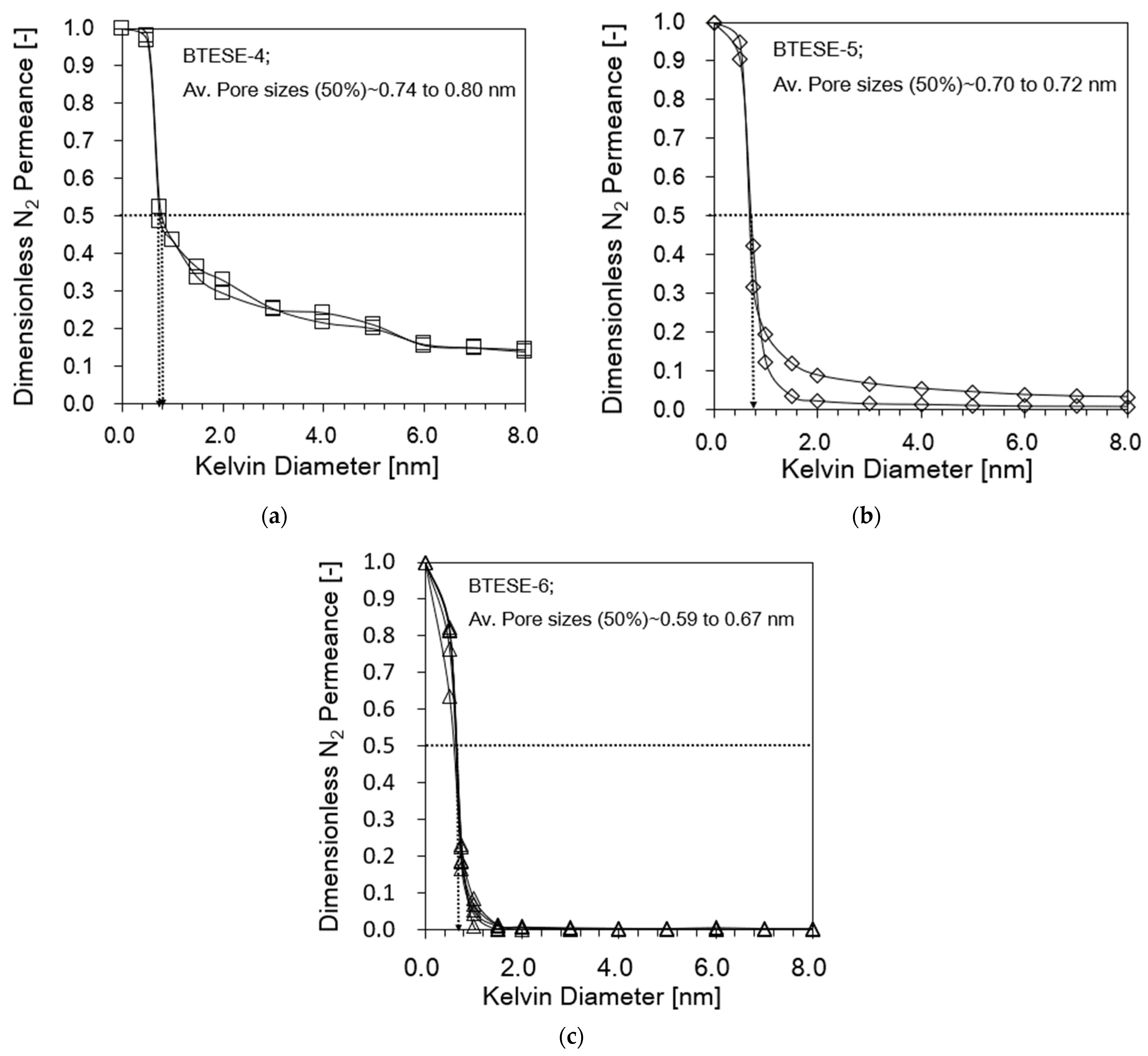
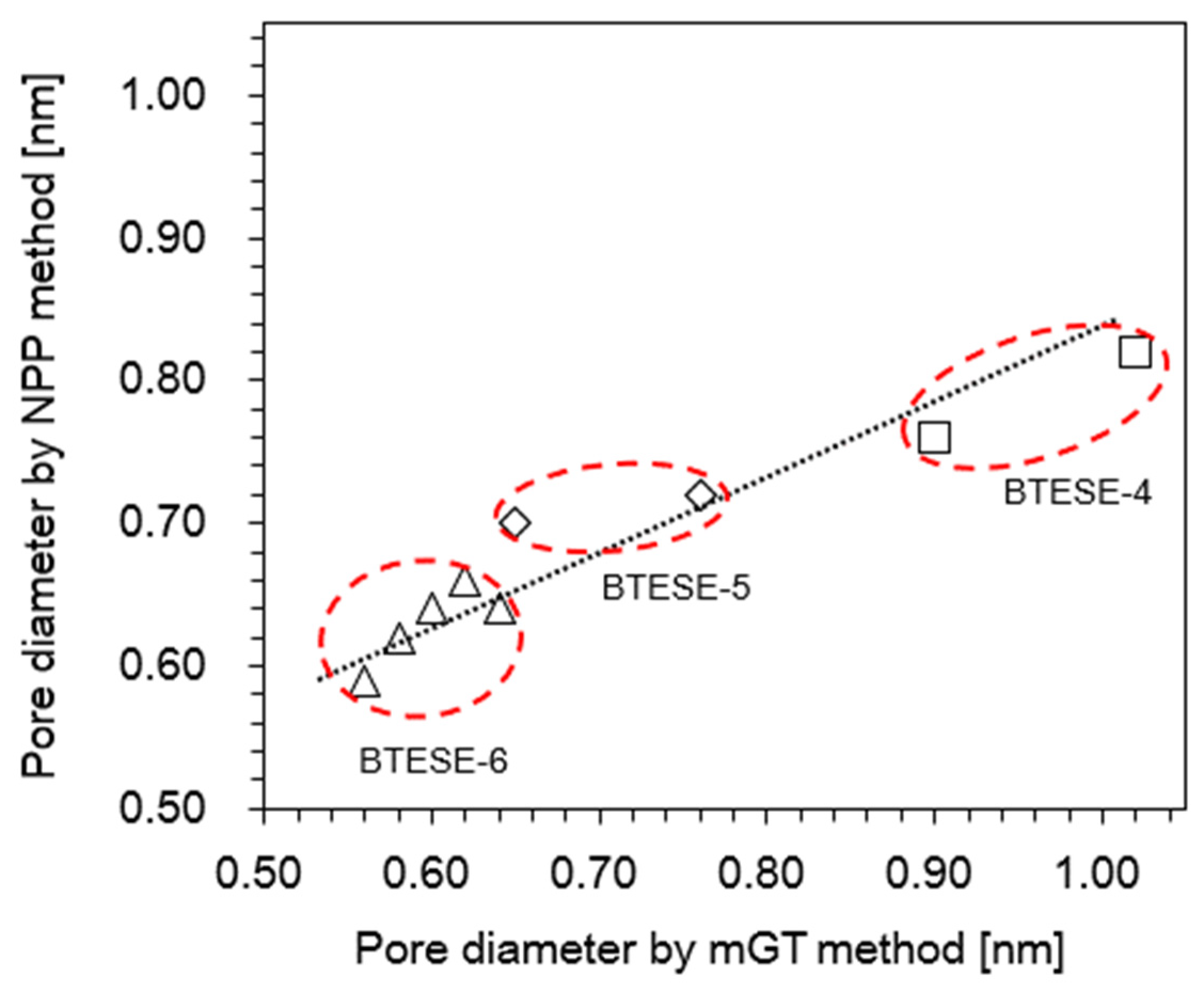
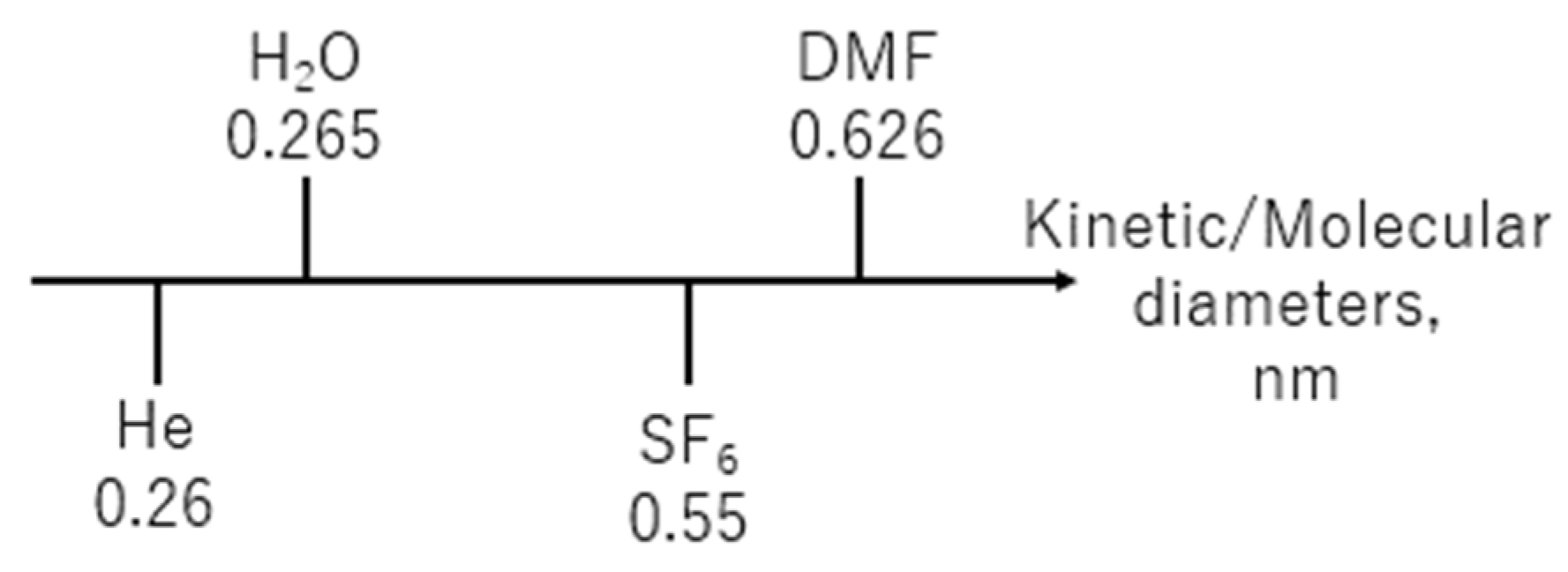
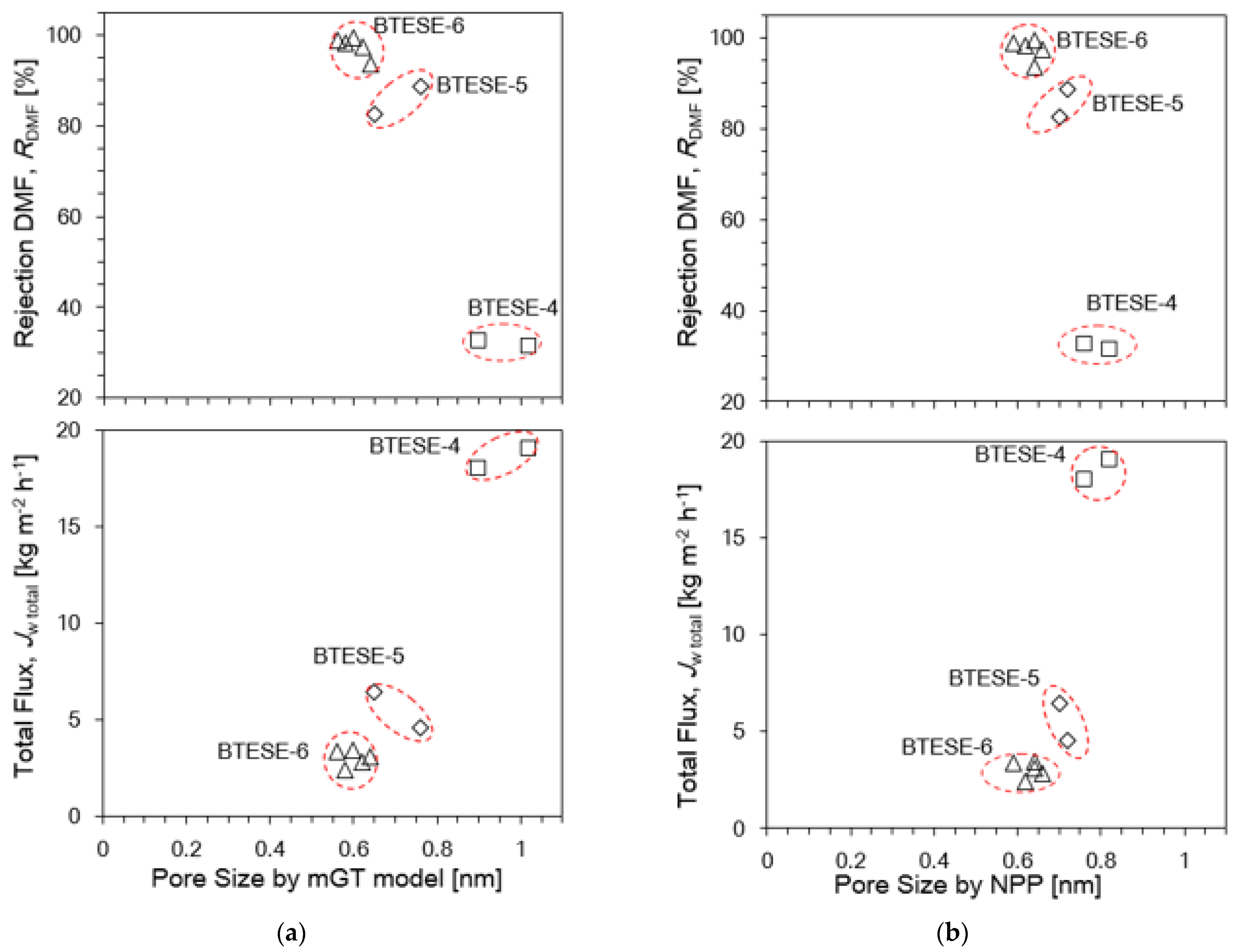
3.2. Evaluation of Pore Size BTESE Membranes
3.3. Reverse Osmosis (RO) Performance of BTESE Organosilica Membranes
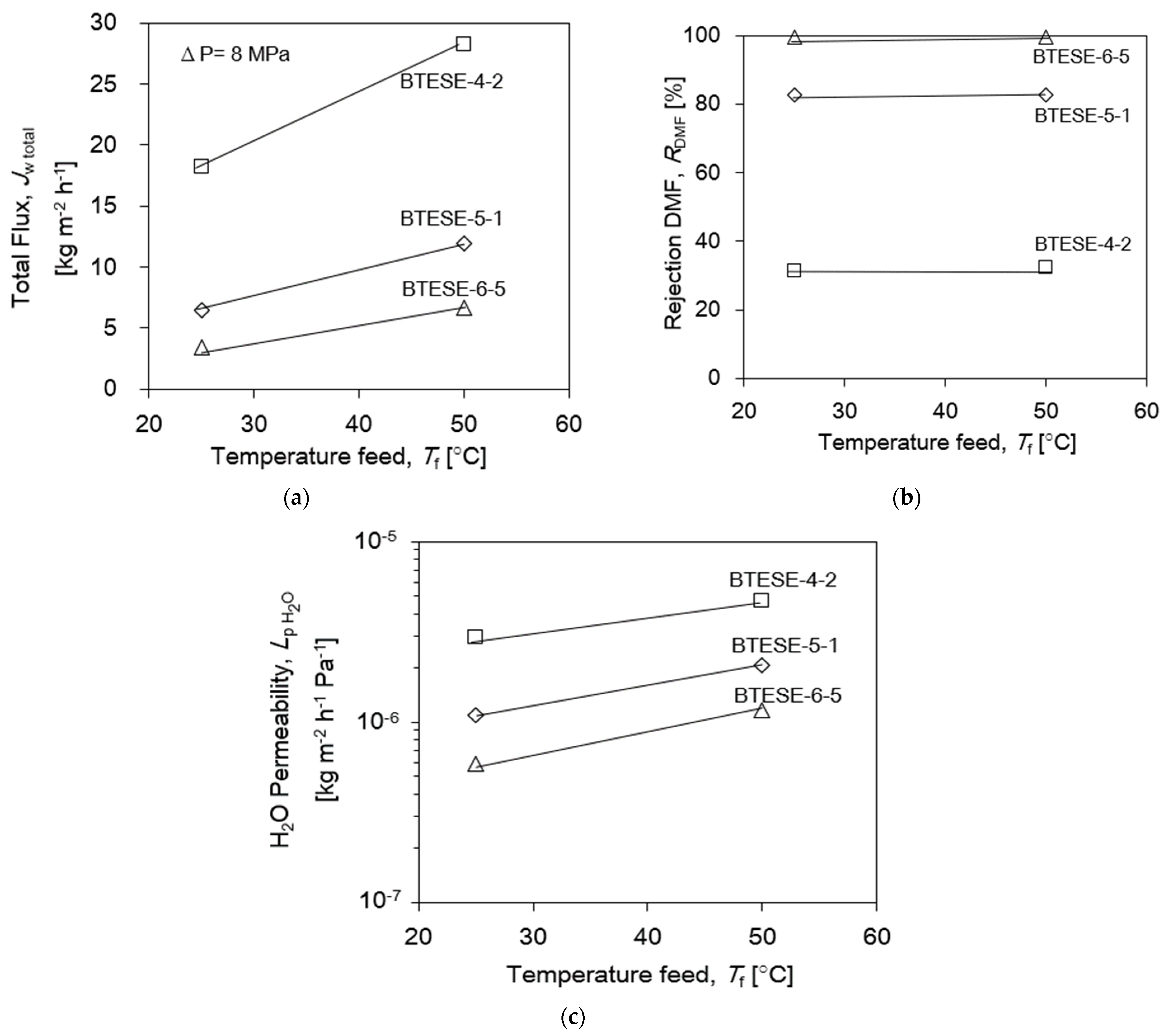
3.3.1. Mechanical and Hydrothermal Dependency on the BTESE Membrane for DMF Separation
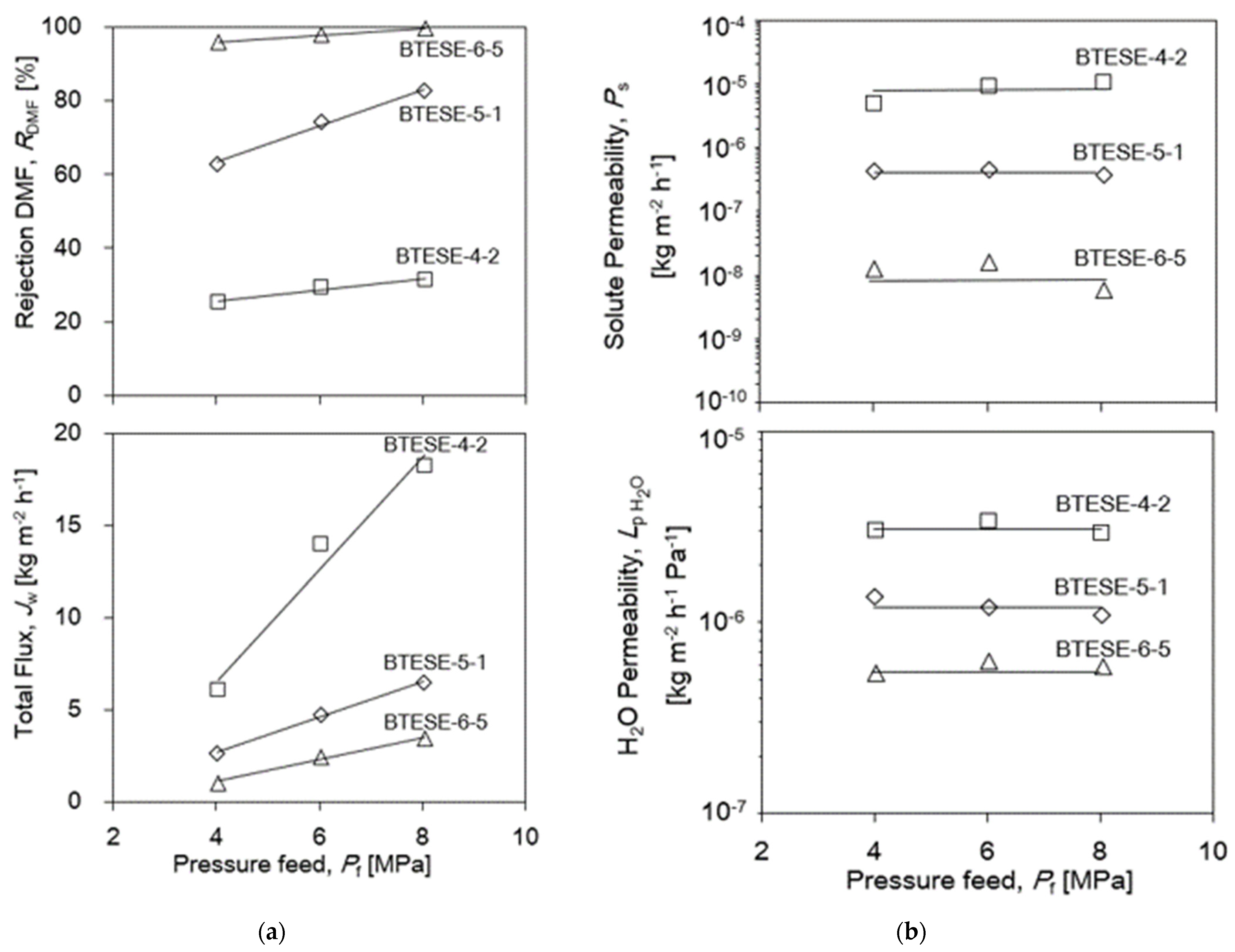
3.3.2. Pressure Dependency of the BTESE Membrane for DMF Separation
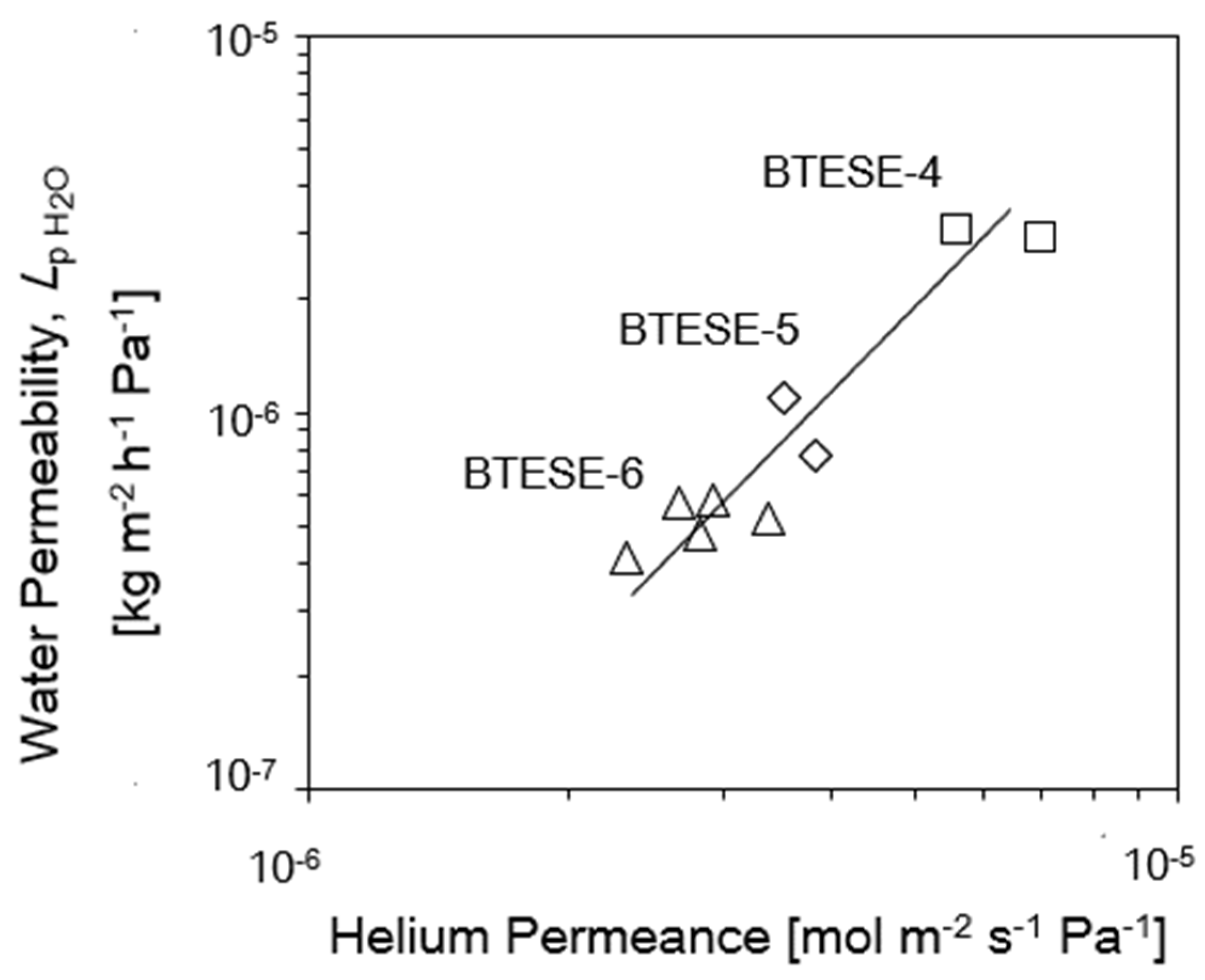
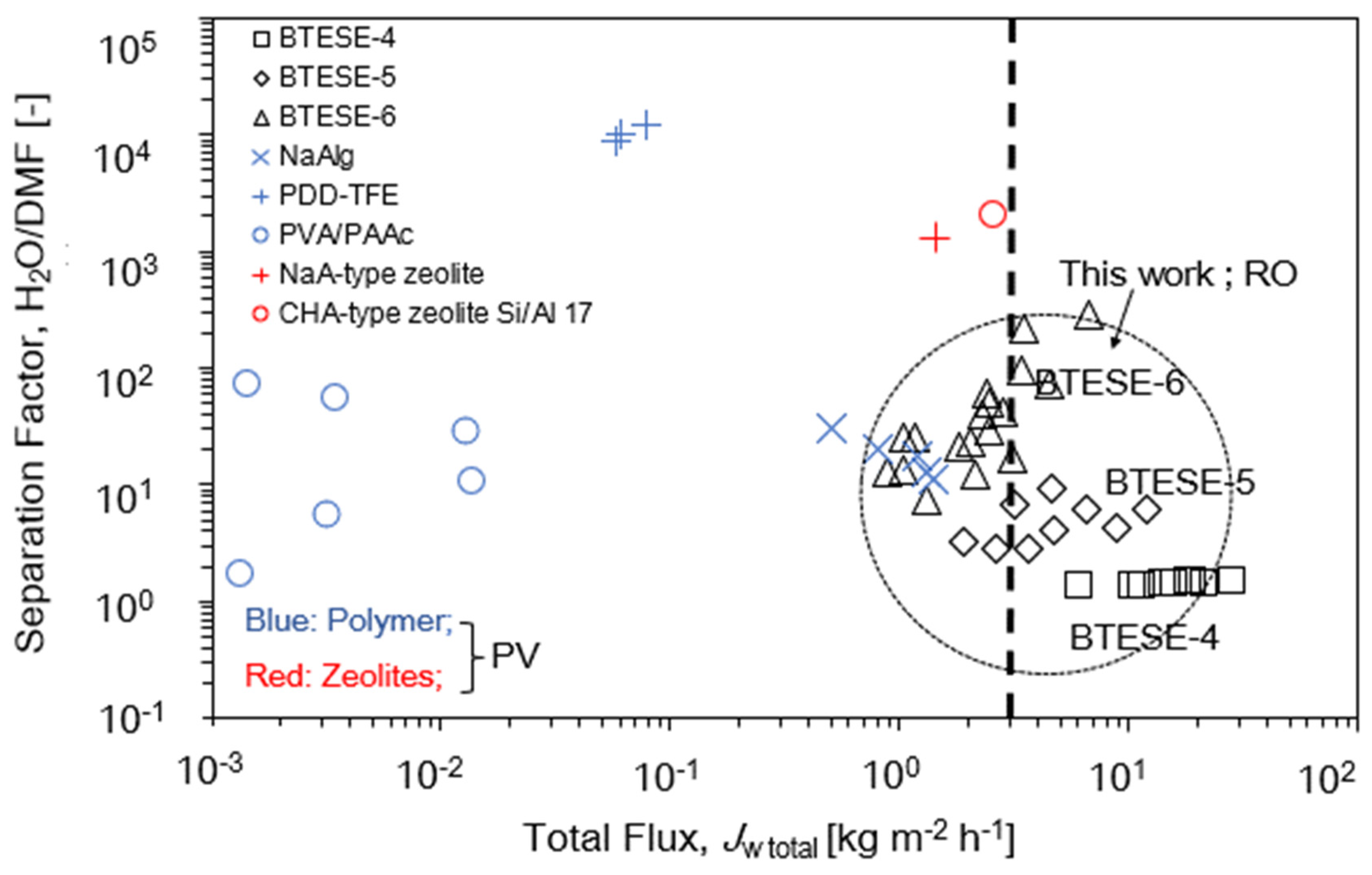
3.4. Relationship of Reverse Osmosis (RO) Performance with the Gas Permeation (GP) and Pore Size
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chau, J.; Basak, P.; Sirkar, K.K. Reverse osmosis separation of particular organic solvent mixtures by a perfluorodioxole copolymer membrane. J. Membr. Sci. 2018, 563, 541–551. [Google Scholar] [CrossRef]
- Solak, E.K.; Sanli, O. Separation Characteristics of Dimethylformamide/Water Mixtures through Alginate Membranes by Pervaporation, Vapor Permeation and Vapor Permeation with Temperature Difference Methods. Sep. Sci. Tech. 2006, 41, 627–646. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, S.; Wu, Y.; Shi, S.; Xiao, G. Recent Advances of Pervaporation Separation in DMF/H2O Solutions: A Review. Membranes 2021, 11, 455–479. [Google Scholar] [CrossRef] [PubMed]
- Shao, H.; Zhou, Y.; Zhong, J.; Wu, Q.; Zhang, Q.; Yang, B. Preparation of Me-silicalite-1 Zeolite Membrane for Pervaporation Separation of DMF/H2O Mixtures. J. Chem. Eng. Chin. Univ. 2014, 28, 965–970. [Google Scholar]
- Li, L.; Dong, J.; Nenoff, T.M.; Lee, R. Desalination by reverse osmosis using MFI zeolite membranes. J. Membr. Sci. 2004, 243, 401–404. [Google Scholar] [CrossRef]
- Li, L.; Liu, N.; McPherson, B.; Lee, R. Enhanced Water Permeation of Reverse Osmosis through MFI-Type Zeolite Membranes with High Aluminium Contents. Ind. Eng. Chem. Res. 2007, 46, 1584–1589. [Google Scholar] [CrossRef]
- Zhu, B.; Hong, Z.; Milne, N.; Doherty, C.M.; Zou, L.; Lin, Y.S.; Hill, A.J.; Gu, X.; Duke, M. Desalination of seawater ion complexes by MFI-type zeolites membrane: Temperature and long-term stability. J. Membr. Sci. 2014, 453, 126–135. [Google Scholar] [CrossRef]
- Kazemimoghadam, M.; Mohammadi, T. Synthesis of MFI zeolite membranes for water desalination. Desalination 2007, 206, 547–553. [Google Scholar] [CrossRef]
- Yamamoto, K.; Amaike, Y.; Tani, M.; Saito, I.; Kozuma, T.; Kaneko, Y.; Gunji, T. Bridged organosilica membranes incorporating carboxyl-functionalized cage silsesquioxanes for water desalination. J. Sol-Gel Sci. Technol. 2022, 101, 315–322. [Google Scholar] [CrossRef]
- Yamamoto, K.; Saito, I.; Amaike, Y.; Nakaya, T.; Ohshita, J.; Gunji, T. Preparation and water desalination properties of bridged polysilsesquioxane membranes with divinylbenzene and divinylpyridine units. Polym J. 2020, 52, 1367–1374. [Google Scholar] [CrossRef]
- Ibrahim, S.M.; Nagasawa, H.; Kanezashi, M.; Tsuru, T. Robust organosilica membranes for high temperature reverse osmosis (RO) application: Membrane preparation, separation characteristics of solutes and membranes regeneration. J. Membr. Sci. 2015, 493, 515–523. [Google Scholar] [CrossRef]
- Ikeda, A.; Matsuyama, E.; Komatsuzaki, M.; Sasaki, M.; Nomura, M. Development of Inorganic Silica Reverse Osmosis Membranes by Using a Counter-Diffusion Chemical Vapor Deposition Method. J. Chem. Eng. Japan 2014, 47, 574–578. [Google Scholar] [CrossRef]
- Ibrahim, S.M.; Nagasawa, H.; Kanezashi, M.; Tsuru, T. Chemical-free cleaning of fouled reverse osmosis (RO) membranes derived from bis(triethoxysilyl)ethane (BTESE). J. Membr. Sci. 2020, 601, 117919–117927. [Google Scholar] [CrossRef]
- Richard, W.B. Membrane Technology and Application, 2nd ed.; John Wiley and Son, Ltd.: Hoboken, NJ, USA, 2004; pp. 1–14. [Google Scholar]
- Brinker, C.J. Hydrolysis and condensation of silicates: Effects on structure. J. Non-Crystal. Solids 1988, 100, 31–50. [Google Scholar] [CrossRef]
- Azolin, D.R.; Moro, C.C.; Costa, T.M.H.; Benvenutti, E.V. Effects of organic content and H2O/TEOS molar ratio on the porosity and pore size distribution of hybrid naphthaleneaminepropylsilica xerogel. J. Non-Crystal. Solids 2004, 337, 201–206. [Google Scholar] [CrossRef]
- De Vos, R.M.; Maier, W.F.; Verweij, H. Hydrophocic silica membranes for gas separation. J. Membr. Sci. 1999, 158, 12. [Google Scholar] [CrossRef]
- Shilova, O.A. Synthesis and structure features of composite silicate and hybrid TEOS derived thin films doped by inorganic and organic additives. J. Sol-Gel Sci Technol. 2013, 68, 387–410. [Google Scholar] [CrossRef]
- Nair, B.N.; Okubo, T.; Nakao, S. Structure and separation properties of silica membranes. Membranes 2000, 25, 73–85. [Google Scholar] [CrossRef]
- Niimi, T.; Nagasawa, H.; Kanezashi, M.; Yoshioka, T.; Ito, K.; Tsuru, T. Preparation of BTESE-derived organosilica membranes for catalytic membranes reactors of methylcyclohexand dehydrogenation. J. Membr. Sci. 2014, 455, 375–383. [Google Scholar] [CrossRef]
- Song, H.; Wei, Y.; Wang, C.; Zhao, S.; Qi, H. Tuning sol size to optimize organosilica membrane for gas separation. Chin. J. Chem. Eng. 2018, 26, 53–59. [Google Scholar] [CrossRef]
- Topuz, B.; Ciftcioglu, M. Sol-gel derived mesoporous and microporous alumina membranes. J. Sol-Gel Sci. Technol. 2010, 56, 287–299. [Google Scholar] [CrossRef][Green Version]
- Hoang, G.C. Pore-Size Control of Silica Gels in Acidic Water Conditions Using Sol-Gel Processing. J. Korean Phys. Soc. 1997, 31, 227–230. [Google Scholar][Green Version]
- Castricum, H.L.; Paradis, G.G.; Mittelmeijer-Hazeleger, M.C.; Kreiter, R.; Vente, J.F.; ten Elshof, J.E. Tailoring the Separation Behaviour of Hybrid Organosilica Membranes by Adjusting the Structure of the Organic Bridging Group. Adv. Funct. Mater. 2011, 21, 2319–2329. [Google Scholar] [CrossRef]
- Castricum, H.L.; Sah, A.; Kreiter, R.; Blank, D.H.A.; Vente, J.F.; ten Elshof, J.E. Hydrothermally stable molecular separation membranes from organically linked silica. J. Mater. Chem. 2008, 18, 2150–2158. [Google Scholar] [CrossRef]
- Castricum, H.L.; Qureshi, H.F.; Nijmeijer, A.; Winnubst, L. Hybrid silica membranes with enhanced hydrogen and CO2 separation properties. J. Membr. Sci. 2015, 488, 121–128. [Google Scholar] [CrossRef]
- Dral, A.P.; ten Elshof, J.E. Organic groups influencing microporosity in organosilicas. Microporous Mesoporous Mater. 2018, 267, 267–273. [Google Scholar] [CrossRef]
- Yamamoto, K.; Saito, I.; Amaike, Y.; Nakaya, T.; Ohshita, J.; Gunji, T. Gel structure and water desalination properties of divinylpyrazinebridged polysilsesquioxanes. J. Sol-Gel Sci. Technol. 2023. [Google Scholar] [CrossRef]
- Lee, H.L.; Kanezashi, M.; Shimomura, Y.; Yoshioka, T.; Tsuru, T. Evaluation and fabrication of pore size tune silica membranes with tetraethoxydimetyl disiloxane for gas separation. AIChE J. 2011, 57, 2755–2765. [Google Scholar] [CrossRef]
- Dong, G.; Nagasawa, H.; Yu, L.; Guo, M.; Kanezashi, M.; Yoshioka, T.; Tsuru, T. Energy-efficient separation of organic liquids using organosilica membranes via a reverse osmosis route. J. Membr. Sci. 2020, 597, 117758. [Google Scholar] [CrossRef]
- Tang, J.; Sirkar, K.K. Perfluoropolymer membrane behaves like a zeolite membrane in dehydration of aprotic solvents. J. Membr. Sci. 2012, 421–422, 211–216. [Google Scholar] [CrossRef]
- Hasegawa, Y.; Matsuura, W.; Abe, C.; Ikeda, A. Influence of Organic Solvent on Dehydration Behaviors of NaA-Type Zeolite Membrane. Membranes 2021, 11, 347. [Google Scholar] [CrossRef] [PubMed]
- Hasegawa, Y.; Abe, C.; Ikeda, A. Pervaporative Dehydration of Organic Solvents Using High-Silica CHA-Type Zeolite Membrane. Membranes 2021, 11, 229. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Ruan, F.; Xu, S.; Wu, W.; Shi, S.; Xiao, G. Pervaporation separation of N,N-dimethylformamide/water using poly(vinyl alcohol) based mixed matrix membranes. Process Saf. Environ. 2022, 159, 779–794. [Google Scholar] [CrossRef]
- Sawamura, K.; Okamoto, S.; Todokoro, Y. Development of Mass Production Technology of Highly Permeable Nano-Porous Supports for Silica-Based Separation Membranes. Membranes 2019, 9, 103–117. [Google Scholar] [CrossRef] [PubMed]
- Xiao, J.; Wei, J. Diffusion mechanism of hydrocarbons in zeolites-I. Theory. Chem. Eng. Sci. 1992, 47, 1123–1142. [Google Scholar] [CrossRef]
- Shelekhin, A.B.; Dixon, A.G.; Ma, Y.H. Theory of gas diffusion and permeation in inorganic molecular-sieve membranes. AIChE J. 1995, 41, 58–67. [Google Scholar] [CrossRef]
- Moriyama, N.; Nagasawa, H.; Kanezashi, M.; Tsuru, T. Selective water vapor permeation from steam/non-condensable gas mixtures via organosilica membranes at moderate-to-high temperatures. J. Membr. Sci. 2019, 589, 117–254. [Google Scholar] [CrossRef]
- Cuperus, F.P.; Bargeman, D.; Smolders, C.A. Characterization of anisotropic UF-membranes: Top layer thickness and pore structure. J. Membr. Sci. 1991, 61, 73. [Google Scholar] [CrossRef]
- Cuperus, F.P.; Bargeman, D.; Smolders, C.A. Permporometry. The determination of the size distribution of active pores in UF membranes. J. Membr. Sci. 1992, 71, 57. [Google Scholar] [CrossRef]
- Huang, P.; Nanping, X.; Shi, J.; Lin, Y.S. Characterization of asymmetric ceramic membranes by modified permporometry. J. Membr. Sci. 1996, 116, 301. [Google Scholar] [CrossRef]
- Wijmans, J.G.; Baker, R.W. The solution-diffusion model: A review. J. Membr. Sci. 1995, 107, 1–21. [Google Scholar] [CrossRef]
- Xu, R.; Jiang, W.; Qi, L.; Zhang, Q.; Zhong, J. Fabrication of PEG crosslinked organosilica hybrid membranes for reverse osmosis desalination. J. Inorganic Mater. 2018, 33, 1154–1160. [Google Scholar]
- Xu, R.; Cheng, X.; Deng, S.; Qi, L.; Ren, X.; Zhang, Q.; Zhong, J. Carboxyl functionalization and reverse osmosis performance of ethylene bridged organosilica membranes. CIESC J. 2019, 70, 2744–2766. [Google Scholar]
- Dong, G.; Nagasawa, H.; Kanezashi, M.; Tsuru, T. Experimental study and modelling of organic solvent reverse osmosis separations through organosilica membranes. AIChE J 2020, 1–13. [Google Scholar] [CrossRef]
- Xu, R.; Ibrahim, S.M.; Kanezashi, M.; Yoshioka, T.; Ito, K.; Oshita, J.; Tsuru, T. New insight into microstructure-separation properties of organosilica membranes with ethane, ethylene, and acetylene bridges. Appl. Mater. Interfaces 2014, 6, 9357–9364. [Google Scholar] [CrossRef] [PubMed]
- Kreiter, R.; Rietkerk, M.D.A.; Castricum, H.L.; van Veen, H.M.; ten Elshof, J.E.; Vente, J.F. Evaluation of hybrid silica sols for stable microporous membranes using high-throughput screening. J. Sol Gel Sci. Technol. 2010, 57, 245–252. [Google Scholar] [CrossRef]
- Castricum, H.L.; Kreiter, R.; van Veen, H.M.; Blank, D.H.A.; Vente, J.F.; ten Elshof, J.E. High-performance hybrid pervaporation membranes with superior hydrothermal and acid stability. J. Membr. Sci. 2008, 324, 111–118. [Google Scholar] [CrossRef]
- Paradis, G.G.; Shanahan, D.P.; Kreiter, R.; van Veen, H.M.; Castricum, H.L.; Nijmeijer, A.; Vente, J.F. From hydrophilic to hydrophobic HybSi membranes: A change of affinity and applicability. J. Membr. Sci. 2013, 428, 157–162. [Google Scholar] [CrossRef]
- Wu, H.; Liu, X.; Yang, X.; Hu, C.; Zhou, Z. Pervaporation performance of BTESE/TEOS -derived organosilica membrane and its stability in isopropanol aqueous solutions. Korean J. Chem. Eng. 2023, 40, 195–204. [Google Scholar] [CrossRef]
- Xu, R.; Liu, Q.; Ren, X.; Lin, P.; Zhong, J. Tuning the Pore Structures of Organosilica Membranes for Enhanced Desalination Performance via the Control of Calcination Temperatures. Membranes 2020, 10, 392. [Google Scholar] [CrossRef]
- Raza, W.; Jianhua, Y.; Wang, J.; Saulat, H.; He, G.; Lu, J.; Zhang, Y. HCl modification and pervaporation performance of BTESE membrane for the dehydration of acetic acid/ water mixture. Sep. Purif. Tech. 2020, 235, 116102. [Google Scholar] [CrossRef]
- Raza, W.; Jianhua, Y.; Wang, J.; Saulat, H.; Wang, L.; Lu, J.; Zhang, Y. A selective organosilica membrane for ethyl acetate dehydration by pervaporation. J. Appl. Polym. Sci. 2021, 138, 50942. [Google Scholar] [CrossRef]
- Rocca, T.L.; Carretier, E.; Dhaler, D.; Louradour, E.; Truong, T.; Moulin, P. Purification of Pharmaceutical Solvents by Pervaporation through Hybrid Silica Membranes. Membranes 2019, 9, 76. [Google Scholar] [CrossRef] [PubMed]




| Membrane Lists | Coating Times of Top Layers | BTESE Sols for Top Layers |
|---|---|---|
| BTESE-4-1 | 4 | 1 wt.% BTESE sol after aged for 8 days at 50 °C |
| BTESE-4-2 | ||
| BTESE-5-1 | 5 | |
| BTESE-5-2 | ||
| BTESE-6-1 | 6 | |
| BTESE-6-2 | ||
| BTESE-6-3 | ||
| BTESE-6-4 | ||
| BTESE-6-5 |
| Membrane Numbers | He Permeance (10−6 mol m−2 s−1 Pa−1) | Permeance Ratio (-) | |
|---|---|---|---|
| He/N2 | He/SF6 | ||
| BTESE-4-1 | 5.6 | 4.0 | 25 |
| BTESE-4-2 | 7.0 | 3.3 | 23 |
| BTESE-5-1 | 3.5 | 4.0 | 54 |
| BTESE-5-2 | 2.8 | 5.5 | 153 |
| BTESE-6-1 | 3.7 | 5.0 | 1968 |
| BTESE-6-2 | 3.4 | 4.6 | 260 |
| BTESE-6-3 | 2.8 | 6.3 | 691 |
| BTESE-6-4 | 2.3 | 9.0 | 3406 |
| BTESE-6-5 | 2.9 | 7.1 | 2940 |
| Membrane Code | Separation Method | Feed/ Permeate Pressure | Temperature (°C) | Types of Chemicals Separation | Total Flux, Jw,total (kg m−2 h−1) | Solutes Rejection, (%) | Separation Factor, (-) | Ref. |
|---|---|---|---|---|---|---|---|---|
| BTESE-4 | RO | 4–8 MPa * | 25–50 | 6wt.% DMF/ 94 wt.% H2O | 6–28 | 25–32 | 1–2 | [This work] |
| BTESE-5 | RO | 4–8 MPa * | 25–50 | 6wt.% DMF/ 94 wt.% H2O | 3–12 | 63–89 | 3–9 | [This work] |
| BTESE-6 | RO | 4–8 MPa * | 25–50 | 6wt.% DMF/ 94 wt.% H2O | 1–7 | 86–99 | 25–285 | [This work] |
| BTESE WR 3 | RO | 1 MPa * | 25–80 | 2wt.% NaCl/ 98 wt.% H2O | 0.5–2.8 | 94–97 | 1700–3401 | [11] |
| BTESE WR 3 | RO | 1 MPa * | 25–80 | 0.5wt.% EtOH/ 99.5 wt.% H2O | 1–3.2 | 49 25 | 197 133 | [11] |
| BTESE WR 3 | RO | 1 MPa * | 25–80 | 0.5wt.% IPA/ 99.5 wt.% H2O | 0.7–3.3 | 79 55 | 478 223 | [11] |
| BTESE WR 240 | RO | 1 MPa * | 25–80 | 2wt.% NaCl/ 98 wt.% H2O | 0.1–0.3 | 94 98 | 1700 5100 | [11] |
| BTESE WR 240 | RO | 1 MPa * | 25–80 | 0.5wt.% EtOH/99.5 wt.% H2O | 0.07–0.4 | 90 70 | 1000 335 | [11] |
| BTESE WR 240 | RO | 1 MPa * | 25–80 | 0.5 wt.% IPA/ 99.5 wt.% H2O | 0.06–0.4 | 96 92 | 2500 1200 | [11] |
| BTESE/ PEG10 | RO | 1.2 MPa * | 25 | 2 wt.% NaCl/ 98 wt.% H2O | 0.72 | 97 | 34 | [43] |
| BTESE/ PEG10 | RO | 1.2 MPa * | 25 | 10 wt.% NaCl/ 90 wt.% H2O | 0.43 | 95 | 22 | [43] |
| BTESEthy | RO | 1.15 MPa | 25 | 2 wt.% NaCl/ 98 wt.% H2O | 0.74 | 97 | [44] | |
| BTESEthy-MSA | RO | 1.15 MPa | 25 | 2 wt.% NaCl/ 98 wt.% H2O | 1.23 | 98 | [44] | |
| BTESA | RO | 2–8 MPa * | 50 | 5 wt.% TOL/ 95 wt.% MeOH | 0.25–2 | 94–98 | 1700–500 | [30] |
| BTESA | RO | 8–14 MPa * | 50 | 55 wt.% TOL/ 45 wt.% MeOH | 0.1–0.9 | 76–93 | 900–3000 | [30] |
| BTESA | RO | 6–12 MPa * | 50 | 95 wt.% MA/ 5 wt.% MeOH | 8.5–19 | 75–85 | 7900–13,000 | [45] |
| BTESA | RO | 6–12 MPa * | 50 | 95 wt.% DMC/ 5 wt.% MeOH | 7.5–17.5 | 85–89 | 13,000–18,000 | [45] |
| BTESA | RO | 6–12 MPa * | 50 | 95 wt.% MTBE/ 5 wt.% MeOH | 7–15.5 | 94–96 | 33,000–49,000 | [45] |
| BTESE | PV | <1 kPa ** | 70 | 95 wt.% EtOH/ 5 wt.% H2O | 0.73 | - | 156 | [47] |
| BTESE | PV | <1 kPa ** | 55 | 95 wt.% MeOH/ 5 wt.% H2O | 0.27 | - | 4 | [47] |
| BTESE | PV | <1 kPa ** | 85 | 95 wt.% IPA/ 5 wt.% H2O | 1.76 | - | 3700 | [47] |
| BTESE | PV | <1 kPa ** | 95 | 95 wt.% BuOH/ 5 wt.% H2O | 2.33 | - | 4700 | [47] |
| BTESE | PV | <1 kPa ** | 95 | 95 wt.% BuOH/ 5 wt.% H2O | 3.3 | - | 2600 | [48] |
| BTESE/ RTES | PV | <1 kPa ** | 90 | 2 wt.% BuOH/ 90 wt.% H2O | 1.2–1.5 | - | 15 | [49] |
| BTESE/ RTES | PV | <1 kPa ** | 60 | 2 wt.% BuOH/ 90 wt.% H2O | 0.5–0.6 | - | 15 | [49] |
| BTESE/ TEOS | PV | <1 kPa ** | 75 | 60 wt.% IPA/ 40 wt.% H2O | 14 | - | 300 | [50] |
| BTESE/ TEOS | PV | <1kPa | 75 | 90 wt.% IPA/ 10 wt.% H2O | 9 | - | 900 | [50] |
| BTESE-600 | PV | <1 kPa ** | 70 | 2 wt.% NaCl/ 98 wt.% H2O | 13 | - | 10,000 | [51] |
| BTESE | PV | <1 kPa ** | 80 | 90 wt.% AA/ 10 wt.% H2O | 2.47 | - | 350 | [52] |
| BTESE | PV | <1 kPa ** | 80 | 90 wt.% AA/ 10 wt.% H2O | 2.07 | - | 780 | [52] |
| BTESE-M3 | PV | <1 kPa ** | 60 | 98 wt.% AA/ 2 wt.% H2O | 0.84 | - | >10,000 | [53] |
| BTESE-M3 | PV | <1 kPa ** | 60 | 95 wt.% AA/ 5 wt.% H2O | 1.20 | - | >10,000 | [53] |
| BTESE hybrid silica | PV | <1 kPa ** | 45 | 90 wt.% Ace/ 10 wt.% H2O | 1.37 | - | 52 | [54] |
| Membrane Types | Membrane Code | Separation Method | Feed/ Permeate Pressure | Temperature (°C) | H2O in Feed (wt.%) | Total Flux, Jw,total (kg m−2 h−1) | DMF Rejection, (%) | Separation Factor, H2O/DMF (-) | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| Inorganic | BTESE-4 | RO | 4–8 MPa * | 25–50 | 94 | 6–28 | 25–32 | 1–2 | [This work] |
| Inorganic | BTESE-5 | RO | 4–8 MPa * | 25–50 | 94 | 3–12 | 63–89 | 3–9 | [This work] |
| Inorganic | BTESE-6 | RO | 4–8 MPa * | 25–50 | 94 | 1–7 | 86–99 | 25–285 | [This work] |
| Polymer | NaAlg | PV | <1 kPa ** | 40 | 80 | 1.2 | - | 18 | [2] |
| Polymer | NaAlg | PV | <1 kPa ** | 40 | 60 | 0.8 | - | 20 | [2] |
| Polymer | NaAlg | PV | <1 kPa ** | 40 | 20 | 0.5 | - | 30 | [2] |
| Polymer | NaAlg | PV | <1 kPa ** | 45 | 80 | 1.3 | - | 13 | [2] |
| Polymer | NaAlg | PV | <1 kPa ** | 50 | 80 | 1.4 | - | 11 | [2] |
| Polymer | PDD-TFE | PV | <1 kPa ** | 30 | 10 | 0.058 | - | 9000 | [31] |
| Polymer | PDD-TFE | PV | <1 kPa ** | 50 | 10 | 0.078 | - | 12,200 | [31] |
| Polymer | PDD-TFE | PV | <1 kPa ** | 60 | 10 | 0.060 | - | 10,500 | [31] |
| Inorganic | NaA | PV | <1 kPa ** | 75 | 10 | 1.45 | - | 1290 | [3,32] |
| Inorganic | CHA | PV | <1 kPa ** | 75 | 10 | 2.6 | - | 2000 | [3,33] |
| Polymer | PVA/ PAAc | PV | <1 kPa ** | 25 | 17 | 0.0006 | - | 3.6 | [34] |
| Polymer | PVA/ PAAc | PV | <1 kPa ** | 50 | 17 | 0.00133 | - | 1.7 | [34] |
| Polymer | PVA/PAAc-NaA 20% | PV | <1 kPa ** | 25 | 17 | 0.00142 | - | 73 | [34] |
| Polymer | PVA/PAAc-NaA 20% | PV | <1 kPa ** | 50 | 17 | 0.00346 | - | 54.6 | [34] |
| Polymer | PVA/PAAc-SBA15% | PV | <1 kPa ** | 50 | 17 | 0.00320 | - | 5.4 | [34] |
| Polymer | PVA/PAAc-SiO220% | PV | <1 kPa ** | 50 | 35 | 0.01368 | - | 10.9 | [34] |
| Polymer | PVA/PAAc-SiO2-NH220% | PV | <1 kPa ** | 50 | 5 | 0.01294 | - | 28 | [34] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohd Ibrahim, S.; Sawamura, K.-i.; Mishina, K.; Yu, X.; Salak, F.; Miyata, S.; Moriyama, N.; Nagasawa, H.; Kanezashi, M.; Tsuru, T. Bis(triethoxysilyl)ethane (BTESE)–Organosilica Membranes for H2O/DMF Separation in Reverse Osmosis (RO): Evaluation and Correlation of Subnanopores via Nanopermporometry (NPP), Modified Gas Translation (mGT) and RO Performance. Membranes 2024, 14, 8. https://doi.org/10.3390/membranes14010008
Mohd Ibrahim S, Sawamura K-i, Mishina K, Yu X, Salak F, Miyata S, Moriyama N, Nagasawa H, Kanezashi M, Tsuru T. Bis(triethoxysilyl)ethane (BTESE)–Organosilica Membranes for H2O/DMF Separation in Reverse Osmosis (RO): Evaluation and Correlation of Subnanopores via Nanopermporometry (NPP), Modified Gas Translation (mGT) and RO Performance. Membranes. 2024; 14(1):8. https://doi.org/10.3390/membranes14010008
Chicago/Turabian StyleMohd Ibrahim, Suhaina, Ken-ichi Sawamura, Kengo Mishina, Xin Yu, Feridoun Salak, Shigeru Miyata, Norihiro Moriyama, Hiroki Nagasawa, Masakoto Kanezashi, and Toshinori Tsuru. 2024. "Bis(triethoxysilyl)ethane (BTESE)–Organosilica Membranes for H2O/DMF Separation in Reverse Osmosis (RO): Evaluation and Correlation of Subnanopores via Nanopermporometry (NPP), Modified Gas Translation (mGT) and RO Performance" Membranes 14, no. 1: 8. https://doi.org/10.3390/membranes14010008
APA StyleMohd Ibrahim, S., Sawamura, K.-i., Mishina, K., Yu, X., Salak, F., Miyata, S., Moriyama, N., Nagasawa, H., Kanezashi, M., & Tsuru, T. (2024). Bis(triethoxysilyl)ethane (BTESE)–Organosilica Membranes for H2O/DMF Separation in Reverse Osmosis (RO): Evaluation and Correlation of Subnanopores via Nanopermporometry (NPP), Modified Gas Translation (mGT) and RO Performance. Membranes, 14(1), 8. https://doi.org/10.3390/membranes14010008






