Evaluating the Efficiency of Magnetic Treatment for Feed Water in Reverse Osmosis Processes
Abstract
1. Introduction
2. Materials and Methods
2.1. Testing Methodology
2.2. Materials
2.3. Apparatuses and Procedures
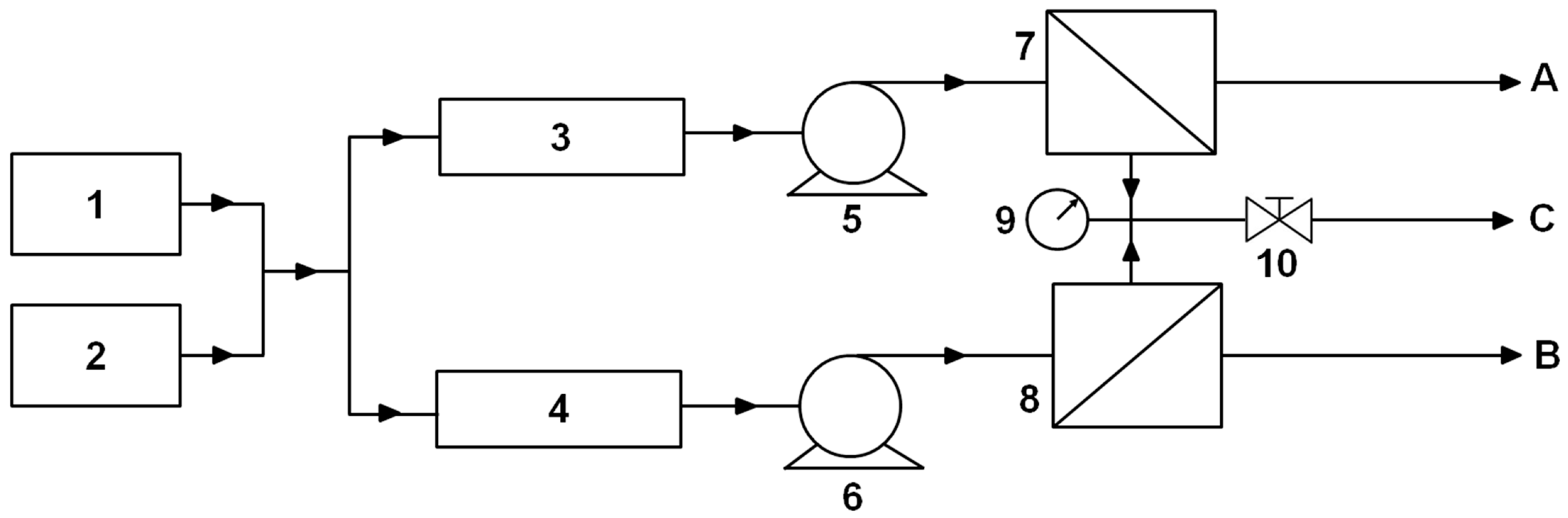
2.3.1. Stirred Reactor
2.3.2. Flow Setup
2.3.3. Characterization Techniques
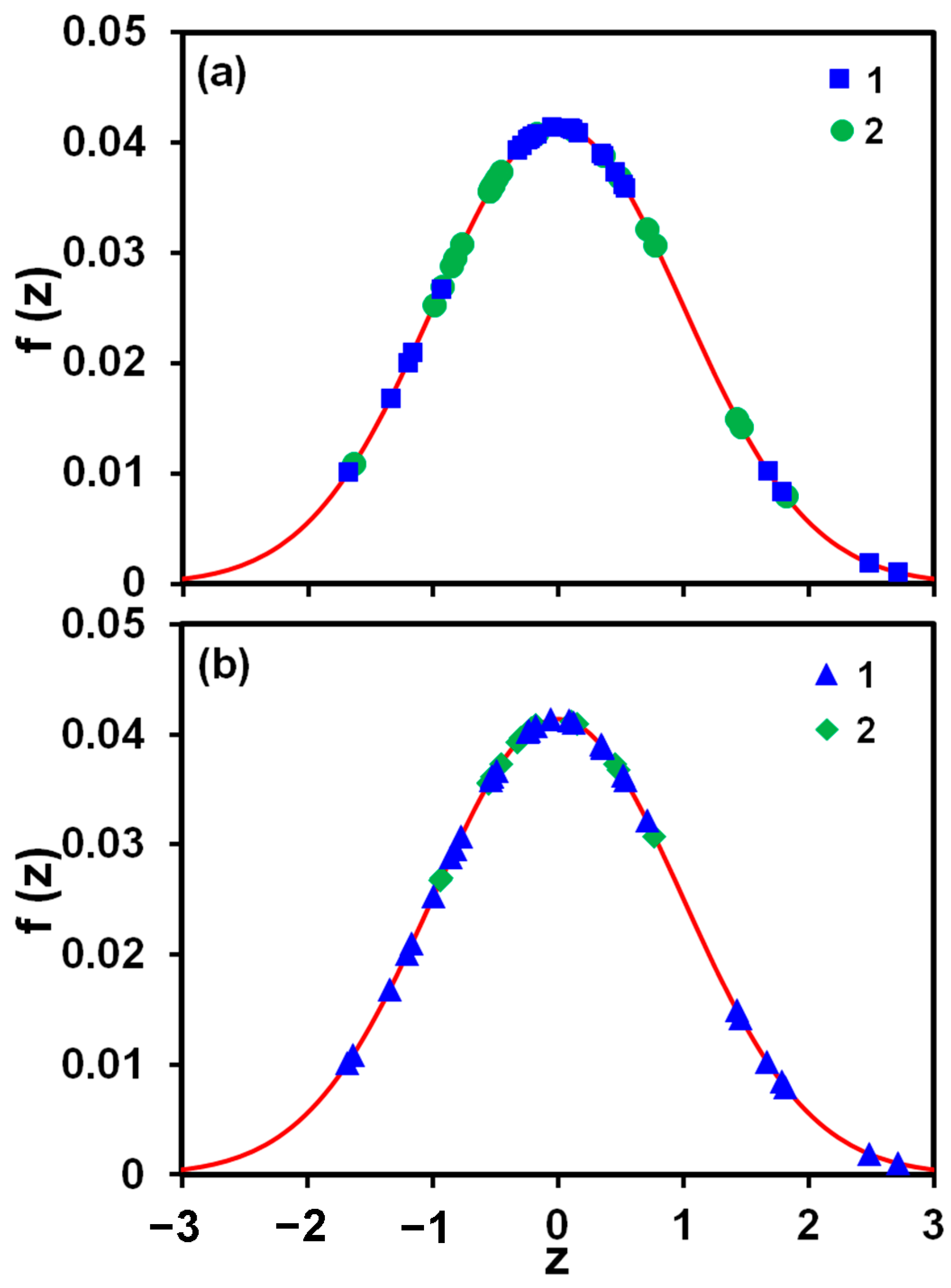
2.3.4. Statistical Analysis of Data
3. Results and Discussion
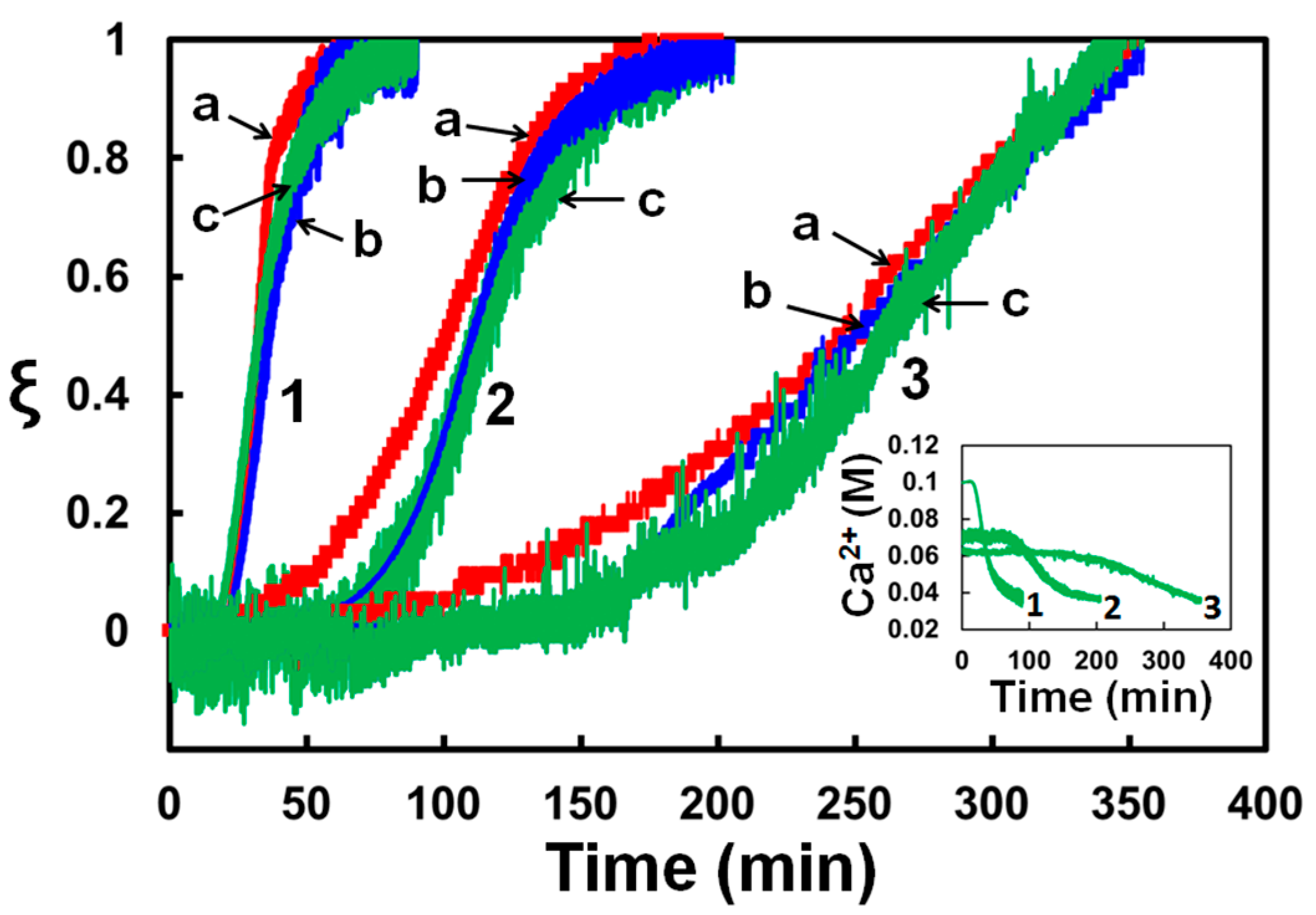
3.1. Precipitation Kinetics
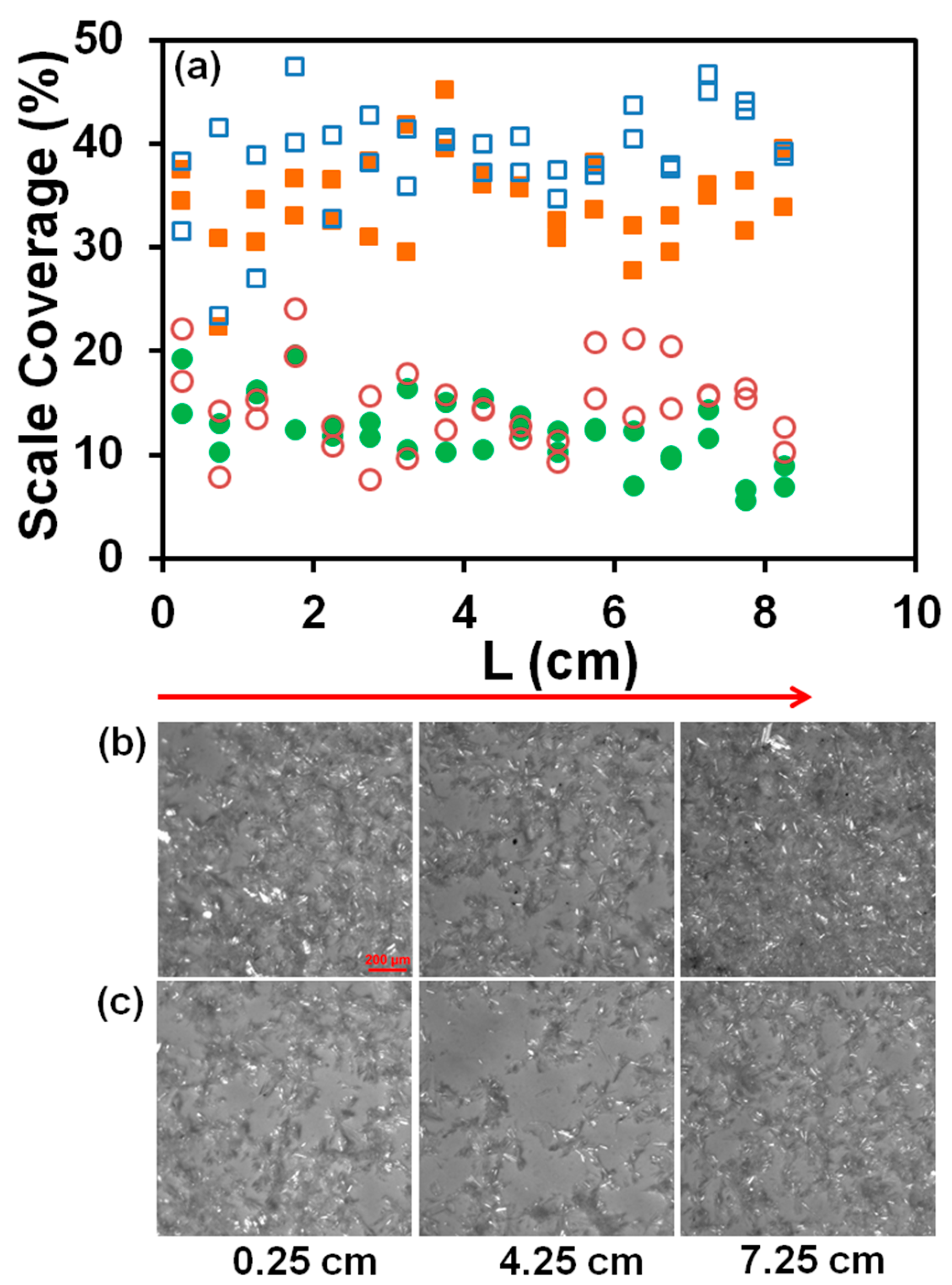
3.2. Scale Formation in RO Unit
3.3. Morphology of Scale Deposits
4. Conclusions
5. Patents
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shannon, M.A.; Bohn, P.W.; Elimelech, M.; Georgiadis, J.G.; Marinas, B.J.; Mayes, A.M. Science and technology for water purification in the coming decades. Nature 2008, 452, 301–310. [Google Scholar] [CrossRef] [PubMed]
- Elimelech, M.; Phillip, W.A. The future of seawater desalination: Energy, technology, and the environment. Science 2011, 333, 712–717. [Google Scholar] [CrossRef] [PubMed]
- Malaeb, L.; Ayoub, G.M. Reverse osmosis technology for water treatment: State of the art review. Desalination 2011, 267, 1–8. [Google Scholar] [CrossRef]
- Shenvi, S.S.; Isloora, A.M.; Ismail, A.F. A review on RO membrane technology: Developments and challenges. Desalination 2015, 368, 10–26. [Google Scholar] [CrossRef]
- Najid, N.; Hakizimana, J.N.; Kouzbour, S.; Gourich, B.; Ruiz-García, A.; Vial, C.; Stiriba, Y.; Semiat, R. Fouling control and modeling in reverse osmosis for seawater desalination: A review. Comput. Chem. Eng. 2022, 162, 107794. [Google Scholar] [CrossRef]
- Ruiz-García, A.; Nuez, I. Long-term performance decline in a brackish water reverse osmosis desalination plant. Predictive model for the water permeability coefficient. Desalination 2016, 397, 101–107. [Google Scholar] [CrossRef]
- Ruiz-García, A.; Feo-García, J. Antiscalant cost and maximum water recovery in reverse osmosis for different inorganic composition of groundwater. Desalin. Water Treat. 2017, 73, 46–53. [Google Scholar] [CrossRef]
- Avlonitis, S.; Kouroumbas, K.; Vlachakis, N. Energy consumption and membrane replacement cost for seawater RO desalination plants. Desalination 2003, 157, 151–158. [Google Scholar] [CrossRef]
- Sweity, A.; Zere, T.R.; David, I.; Bason, S.; Oren, Y.; Ronen, Z.; Herzberg, M. Side effects of antiscalants on biofouling of reverse osmosis membranes in brackish water desalination. J. Membr. Sci. 2015, 481, 172–187. [Google Scholar] [CrossRef]
- Mickley, M. Treatment of Concentrate. Advanced Water Treatment Program; Report No. 155; U.S. Department of the Interior; Bureau of Reclamation; Technical Service Center; Water and Environmental Services Division; Water Treatment Engineering Research Team: Denver, CO, USA, 2009. Available online: https://www.usbr.gov/research/dwpr/reportpdfs/report155.pdf (accessed on 1 May 2023).
- Baker, J.S.; Judd, S.J. Magnetic amelioration of scale formation (review). Water Res. 1996, 30, 247–260. [Google Scholar] [CrossRef]
- Busch, K.W.; Busch, M.A. Laboratory studies on magnetic water treatment and their relationship to a possible mechanism for scale reduction. Desalination 1997, 109, 131–148. [Google Scholar] [CrossRef]
- Baker, J.S.; Judd, S.J.; Parsons, S.A. Antiscale magnetic pretreatment of reverse osmosis feedwater. Desalination 1997, 110, 151–165. [Google Scholar] [CrossRef]
- Ambashtaa, R.D.; Sillanpää, M. Water purification using magnetic assistance: A review. J. Hazard. Mater. 2010, 180, 38–49. [Google Scholar] [CrossRef]
- Xu, P.; Cath, T.Y.; Robertson, A.P.; Reinhard, M.; Leckie, J.O.; Drewes, J.E. Critical review of desalination concentrate management, treatment and beneficial use. Environ. Eng. Sci. 2013, 30, 502–514. [Google Scholar] [CrossRef]
- Gilart, F.; Deas, D.; Ferrer, D.; López, P.; Ribeaux, G.; Castillo, J. High flow capacity devices for anti-scale magnetic treatment of water. Chem. Eng. Process. Process Intensif. 2013, 70, 211–216. [Google Scholar] [CrossRef]
- Zaidi, N.S.; Sohaili, J.; Muda, K.; Sillanpää, M. Magnetic field application and its potential in water and wastewater treatment systems. Sep. Purif. Rev. 2014, 43, 206–240. [Google Scholar] [CrossRef]
- Zhang, W.; Luo, J.; Ding, L.; Jaffrin, M.Y. A review on flux decline control strategies in pressure-driven membrane processes. Ind. Eng. Chem. Res. 2015, 54, 2843–2861. [Google Scholar] [CrossRef]
- Alabi, A.; Chiesa, M.; Garlisi, C.; Palmisano, G. Advances in anti-scale magnetic water treatment. Environ. Sci. Water Res. Technol. 2015, 1, 408–425. [Google Scholar] [CrossRef]
- Rouina, M.; Kariminia, H.R.; Mousavi, S.A.; Shahryari, E. Effect of electromagnetic field on membrane fouling in reverse osmosis process. Desalination 2016, 395, 41–45. [Google Scholar] [CrossRef]
- Piyadasa, C.; Ridgway, H.F.; Yeager, T.R.; Stewart, M.B.; Pelekani, C.; Gray, S.R.; Orbell, J.D. The application of electromagnetic fields to the control of the scaling and biofouling of reverse osmosis membranes—A review. Desalination 2017, 418, 19–34. [Google Scholar] [CrossRef]
- Lin, L.; Jiang, W.; Xu, X.; Xu, P. A critical review of the application of electromagnetic fields for scaling control in water systems: Mechanisms, characterization, and operation. NPJ Clean Water 2020, 3, 25. [Google Scholar] [CrossRef]
- Martínez Moya, S.; Boluda Botella, N. Review of techniques to reduce and prevent carbonate scale. Prospecting in water treatment by magnetism and electromagnetism. Water 2021, 13, 2365. [Google Scholar] [CrossRef]
- Coey, J.M.D.; Cass, S. Magnetic water treatment. J. Magn. Magn. Mater. 2000, 209, 71–74. [Google Scholar] [CrossRef]
- Szcze, A.; Chibowski, E.; Hołysz, L.; Rafalski, P. Effects of static magnetic field on electrolyte solutions under kinetic condition. J. Phys. Chem. A 2011, 115, 5449–5452. [Google Scholar] [CrossRef] [PubMed]
- Corbett, B.E.; Moody, C.D.; Morris, M.D. Evaluation of Reverse Osmosis Scaling Prevention Devices at High Recovery; Advanced Water Treatment Program, Report No. 91; U.S. Department of the Interior; Bureau of Reclamation; Technical Service Center; Environmental Resources Services Division; Water Treatment Engineering and Research Group: Denver, CO, USA, 2003. Available online: https://www.usbr.gov/research/dwpr/reportpdfs/report091.pdf (accessed on 1 May 2023).
- Khusid, B.; Guerra, K.L.; Leitz, F.; Shen, Y.; Elele, E.; Lei, Q. Method and Device for Testing the Effectiveness of Magnetic Treatment of Feed Water for Reducing Mineral Scaling in Reverse Osmosis Processes. U.S. Patent 10,648,957 B2, 12 May 2020. Available online: https://patents.google.com/patent/US10648957B2/en?oq=US10648957B2%2c+ (accessed on 1 May 2023).
- Mulder, M. Basic Principles of Membrane Technology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1996. [Google Scholar] [CrossRef]
- Mullin, J.W. Crystallization, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar] [CrossRef]
- Marshall, W.L.; Slusher, R. Thermodynamics of calcium sulfate dihydrate in aqueous sodium chloride solutions, 0–110°. J. Phys. Chem. 1966, 70, 4015–4027. [Google Scholar] [CrossRef]
- Raju, K.U.G.; Atkinson, G. The thermodynamics of “scale” mineral solubilities. 3. Calcium sulfate in aqueous NaCl. J. Chem. Eng. Data 1990, 35, 361–367. [Google Scholar] [CrossRef]
- Sheikholeslami, R.; Ong, H.W.K. Kinetics and thermodynamics of calcium carbonate and calcium sulfate at salinities up to 1.5 M. Desalination 2003, 157, 217–234. [Google Scholar] [CrossRef]
- Vashisth, S.; Kumar, V.; Nigam, K.D.P. A review on the potential applications of curved geometries in process industry. Ind. Eng. Chem. Res. 2008, 47, 3291–3337. [Google Scholar] [CrossRef]
- Gupta, B.C.; Guttman, I.; Jayalath, K.P. Statistics and Probability with Applications for Engineers and Scientists Using MINITAB, R and JMP, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2020; Available online: https://www.wiley.com/en-us/Statistics+and+Probability+with+Applications+for+Engineers+and+Scientists+Using+MINITAB%2C+R+and+JMP%2C+2nd+Edition-p-9781119516620 (accessed on 1 May 2023).
- Sohnel, O.; Mullin, J.W. Interpretation of crystallization induction periods. J. Colloid Interface Sci. 1988, 123, 43–50. [Google Scholar] [CrossRef]
- Wu, W.; Nancollas, G.H. Determination of interfacial tension from crystallization and dissolution data: A comparison with other methods. Adv. Colloid Interface Sci. 1999, 79, 229–279. [Google Scholar] [CrossRef]
- He, S.; Oddo, J.E.; Tomson, M.B. The seeded growth of calcium sulfate dehydrate crystals in NaCl solutions up to 6 m and 90 °C. J. Colloid Interface Sci. 1994, 163, 372–378. [Google Scholar] [CrossRef]
- Lancia, A.; Musmarra, D.; Prisciandaro, M. Measuring induction period for calcium sulfate dihydrate precipitation. AIChE J. 1999, 45, 390–397. [Google Scholar] [CrossRef]
- Prisciandaro, M.; Lancia, A.; Musmarra, D. Gypsum nucleation into sodium chloride solutions. AIChE J. 2001, 47, 929–934. [Google Scholar] [CrossRef]
- Prisciandaro, M.; Lancia, A.; Musmarra, D. The retarding effect of citric acid on calcium sulfate nucleation kinetics. Ind. Eng. Chem. Res. 2003, 42, 6647–6652. [Google Scholar] [CrossRef]
- Klepetsanis, P.G.; Dalas, E.; Koutsoukos, P.G. Role of temperature in the spontaneous precipitation of calcium sulfate dihydrate. Langmuir 1999, 15, 1534–1540. [Google Scholar] [CrossRef]
- Hasson, D.; Drak, A.; Semiat, R. Induction times induced in an RO system by antiscalants delaying CaSO4 precipitation. Desalination 2003, 157, 193–207. [Google Scholar] [CrossRef]
- Alimi, F.; Elfil, H.; Gadri, A. Kinetics of the precipitation of calcium sulfate dehydrate in a desalination unit. Desalination 2003, 158, 9–16. [Google Scholar] [CrossRef]
- Hina, A.; Nancollas, G.H.; Grynpas, M. Surface induced constant composition crystal growth kinetics studies. The brushite-gypsum system. J. Cryst. Growth 2001, 223, 213–224. [Google Scholar] [CrossRef]
- Mahmoud, M.H.H.; Rashad, M.M.; Ibrahim, I.A.; Abdel-Aal, E.A. Crystal modification of calcium sulfate dihydrate in the presence of some surface-active agents. J. Colloid Interface Sci. 2004, 270, 99–105. [Google Scholar] [CrossRef]
- Inoue, M.; Hirasawa, I. The relationship between crystal morphology and XRD peak intensity on CaSO4·2H2O. J. Cryst. Growth 2013, 380, 169–175. [Google Scholar] [CrossRef]
- Fatu, D. Kinetics of gypsum dehydration. J. Therm. Anal. Calorim. 2001, 65, 213–220. [Google Scholar] [CrossRef]
- Lopez-Beceiro, J.; Gracia-Fernandez, C.; Tarrio-Saavedra, J.; Gomez-Barreiro, S.; Artiaga, R. Study of gypsum by PDSC. J. Therm. Anal. Calorim. 2012, 109, 1177–1183. [Google Scholar] [CrossRef]
- Shih, W.-Y.; Rahardianto, A.; Lee, R.-W.; Cohen, Y. Morphometric characterization of calcium sulfate dihydrate (gypsum) scale on reverse osmosis membranes. J. Memb. Sci. 2005, 252, 253–263. [Google Scholar] [CrossRef]
- Rahardianto, A.; Shih, W.-Y.; Lee, R.-W.; Cohen, Y. Diagnostic characterization of gypsum scale formation and control in RO membrane desalination of brackish water. J. Memb. Sci. 2006, 279, 655–668. [Google Scholar] [CrossRef]
- Uchymiak, M.; Lyster, E.; Glater, J.; Cohen, Y. Kinetics of gypsum crystal growth on a reverse osmosis membrane. J. Membr. Sci. 2008, 314, 163–172. [Google Scholar] [CrossRef]
- Lee, S.; Lee, C.-H. Effect of operating conditions on CaSO4 scale formation mechanism in nanofiltration for water softening. Water Res. 2000, 34, 3854–3866. [Google Scholar] [CrossRef]
- Gilron, J.; Hasson, D. Calcium sulfate fouling of reverse osmosis membranes—Flux decline mechanism. Chem. Eng. Sci. 1987, 42, 2351–2360. [Google Scholar] [CrossRef]
- Weinschenk, E.B. Petrographic Methods; McGraw-Hill: New York, NY, USA, 1912; Available online: https://www.abebooks.com/servlet/BookDetailsPL?bi=31117654874&cm_sp=SEARCHREC-_-WIDGET-F-_-BDP-R&searchurl=an%3Dweinschenk%26bi%3Dh%26sortby%3D100%26tn%3Dpetrographic%2Bmethods (accessed on 1 May 2023).
- Shahidzadeh, N.; Schut, M.F.L.; Desarnaud, J.; Prat, M.; Bonn, D. Salt stains from evaporating droplets. Sci. Rep. 2015, 5, 10335. [Google Scholar] [CrossRef]
- Titiz-Sargut, S.; Sayan, P.; Avci, B. Influence of citric acid on calcium sulfate dihydrate crystallization in aqueous media. Cryst. Res. Technol. 2007, 42, 119–126. [Google Scholar] [CrossRef]
- Saha, A.; Lee, J.; Pancera, S.M.; Bräeu, M.F.; Kempter, A.; Tripathi, A.; Bose, A. New insights into the transformation of calcium sulfate hemihydrate to gypsum using time-resolved cryogenic transmission electron microscopy. Langmuir 2012, 28, 11182–11187. [Google Scholar] [CrossRef]
- Singh, N.B.; Middendorf, B. Calcium sulphate hemihydrate hydration leading to gypsum crystallization. Prog. Cryst. Growth Charact. Mater 2007, 53, 57–77. [Google Scholar] [CrossRef]
- Wang, Y.-W.; Christenson, H.K.; Meldrum, F.C. Confinement leads to control over calcium sulfate polymorph. Adv. Funct. Mater. 2013, 23, 5615–5623. [Google Scholar] [CrossRef]
- Wang, Y.W.; Kim, Y.Y.; Christenson, H.K.; Meldrum, F.C. A new precipitation pathway for calcium sulfate dehydrate (gypsum) via amorphous and hemihydrate intermediates. Chem. Commun. 2012, 48, 504–506. [Google Scholar] [CrossRef] [PubMed]
- Sandhya, S.; Sureshbabu, S.; Varma, H.K.; Komath, M. Nucleation kinetics of the formation of low dimensional calcium sulfate dihydrate crystals in isopropyl alcohol medium. Cryst. Res. Technol. 2012, 47, 780–792. [Google Scholar] [CrossRef]
- Van Driessche, A.E.S.; Benning, L.G.; Rodriguez-Blanco, J.D.; Ossorio, M.; Bots, P.; García-Ruiz, J.M. The role and implications of bassanite as a stable precursor phase to gypsum precipitation. Science 2012, 336, 69–72. [Google Scholar] [CrossRef]
- Ossorio, M.; Van Driessche, A.E.S.; Pérez, P.; García-Ruiz, J.M. The gypsum–anhydrite paradox revisited. Chem. Geol. 2014, 386, 16–21. [Google Scholar] [CrossRef]


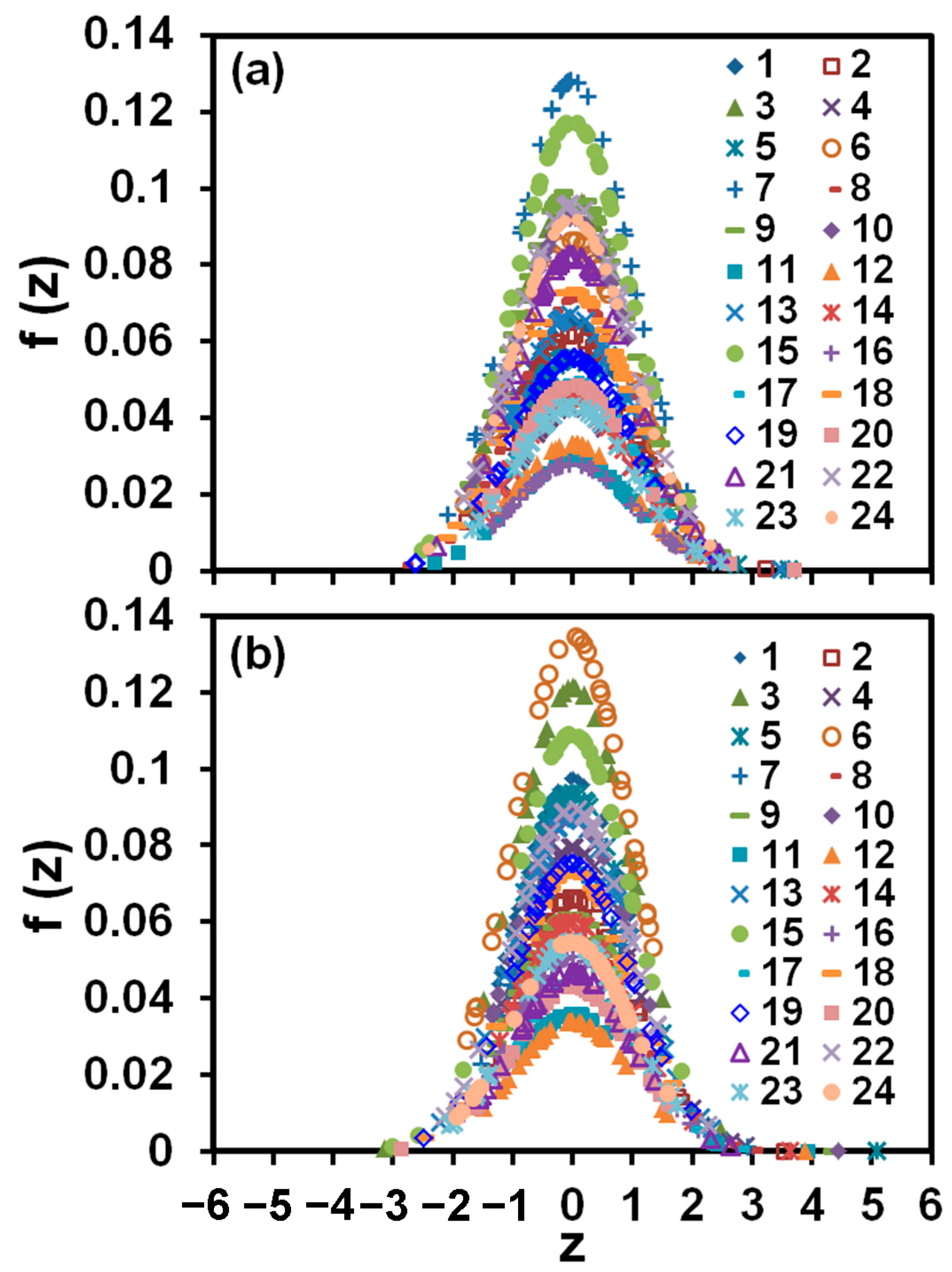
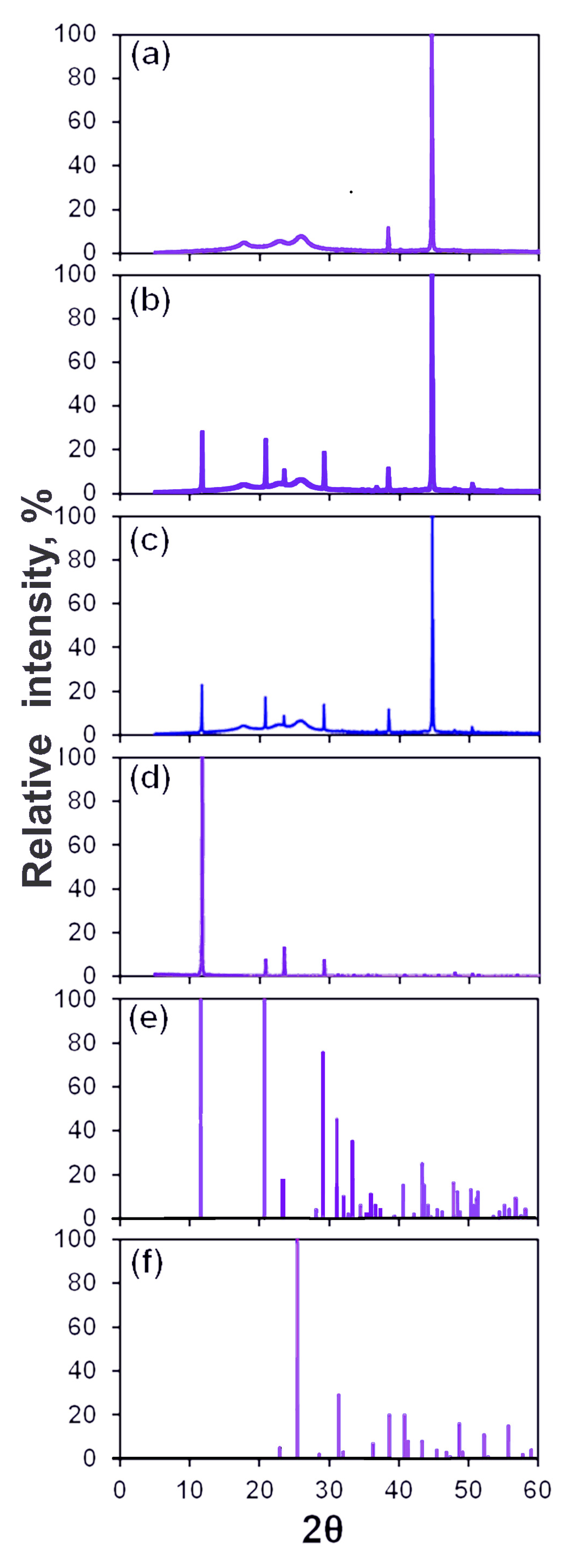
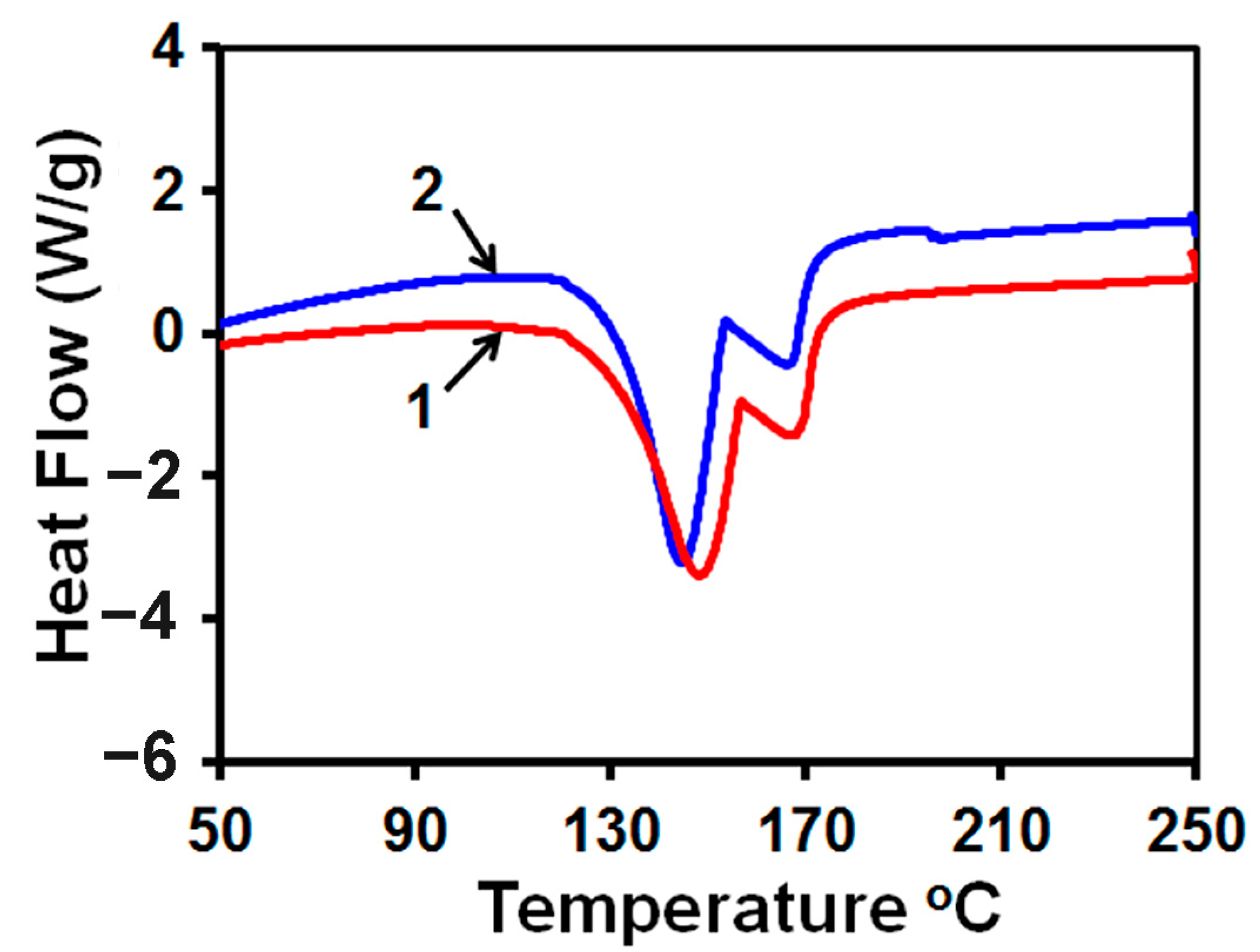

| Q (mL/min) | (cm/s) | (cm/s) | (min) | (min) | (min) | (s) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 2.1 | 0.16 | 67 | 3.6 | 14.0 | 10.1 | 4.8 | 24.1 | 29.0 | 57.7 |
| 15 | 3.2 | 0.24 | 100 | 5.5 | 21.0 | 15.1 | 3.2 | 16.1 | 19.3 | 38.5 |
| 20 | 4.2 | 0.32 | 134 | 7.3 | 28.0 | 20.1 | 2.4 | 12.1 | 14.5 | 28.9 |
| 25 | 5.3 | 0.40 | 167 | 9.1 | 35.0 | 25.2 | 1.9 | 9.7 | 11.6 | 23.1 |
| All tested membranes | , g/min2 | , g/min2 | , g/min | , g/min | |
| 48 | 0.0221 | 0.0005 | 1.115 | 0.147 | |
| Effects of magnetic treatment | |||||
| Groups | , g/min2 | , g/min2 | , g/min | , g/min | |
| exposed to magnetic field | 24 | 0.0272 | 0.0005 | 1.123 | 0.159 |
| not exposed to magnetic field | 24 | 0.0212 | 0.0002 | 1.107 | 0.142 |
| F-test | |||||
| 1.56 | 4.05 | 0.22 | |||
| 0.02 | 4.05 | 0.89 | |||
| Effects of additional 3048 cm (100 ft) | |||||
| Groups | , g/min2 | , g/min2 | , g/min | , g/min | |
| , without 100 ft coiled tubing | 16 | 0.0156 | 0.0003 | 1.047 | 0.184 |
| , with 100 ft coiled tubing | 32 | 0.0253 | 0.0005 | 1.149 | 0.130 |
| F-test | F | p | |||
| 2.22 | 4.05 | 0.14 | |||
| 0.74 | 4.05 | 0.39 | |||
| Effects of feed flow rates | |||||
| Groups | , g/min2 | , g/min2 | , g/min | , g/min | |
| , Q = 10 mL/min | 14 | 0.0416 | 0.0003 | 1.228 | 0.149 |
| , Q = 15 mL/min | 8 | 0.0250 | 0.0003 | 1.287 | 0.165 |
| Q = 20 mL/min | 10 | 0.0154 | 0.0003 | 0.962 | 0.156 |
| Q = 25 mL/min | 6 | 0.0163 | 4 × 10−6 | 0.873 | 0.064 |
| F-test | F | p | |||
| 5.83 | 2.88 | 0.003 | |||
| 2.35 | 2.88 | 0.089 | |||
| All tested membranes | N | , % | , % |
| 48 | 23.45 | 9.63 | |
| Groups | , % | , % | |
| Effects of magnetic treatment of solution | |||
| , exposed to magnetic field | 24 | 24.81 | 8.34 |
| , not exposed to magnetic field | 24 | 22.09 | 10.78 |
| F-test | |||
| 0.95 | 4.05 | 0.33 | |
| Effects of additional 3048 cm (100 ft) coiled tubing | |||
| , without 100 ft coiled tubing | 16 | 21.54 | 4.71 |
| , with 100 ft coiled tubing | 32 | 24.40 | 11.28 |
| F-test | |||
| 0.94 | 4.05 | 0.34 | |
| Effects of feed flow rates | |||
| , Q = 10 mL/min | 14 | 30.83 | 113.44 |
| , Q = 15 mL/min | 8 | 20.50 | 32.94 |
| Q = 20 mL/min | 10 | 21.12 | 108.29 |
| , Q = 25 mL/min | 6 | 21.40 | 16.11 |
| F-test | |||
| 3.53 | 2.88 | 0.025 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, Q.; Elele, E.; Shen, Y.; Tang, J.; Guerra, K.L.; Leitz, F.; Khusid, B. Evaluating the Efficiency of Magnetic Treatment for Feed Water in Reverse Osmosis Processes. Membranes 2023, 13, 641. https://doi.org/10.3390/membranes13070641
Lei Q, Elele E, Shen Y, Tang J, Guerra KL, Leitz F, Khusid B. Evaluating the Efficiency of Magnetic Treatment for Feed Water in Reverse Osmosis Processes. Membranes. 2023; 13(7):641. https://doi.org/10.3390/membranes13070641
Chicago/Turabian StyleLei, Qian, Ezinwa Elele, Yueyang Shen, John Tang, Katherine L. Guerra, Frank Leitz, and Boris Khusid. 2023. "Evaluating the Efficiency of Magnetic Treatment for Feed Water in Reverse Osmosis Processes" Membranes 13, no. 7: 641. https://doi.org/10.3390/membranes13070641
APA StyleLei, Q., Elele, E., Shen, Y., Tang, J., Guerra, K. L., Leitz, F., & Khusid, B. (2023). Evaluating the Efficiency of Magnetic Treatment for Feed Water in Reverse Osmosis Processes. Membranes, 13(7), 641. https://doi.org/10.3390/membranes13070641






