Multifractal Analysis of the Influence of Indole-3-Acetic Acid on Fast-Activating Vacuolar (FV) Channels of Beta vulgaris L. Taproot Cells
Abstract
1. Introduction
2. Materials and Methods
2.1. Plant Material
2.2. Electrophysiological Experiments
2.3. Protocol of Auxin Treatment
3. Mathematical Background
- 1.
- Let (xi) denote i = 1, …, N equidistant measurements.
- 2.
- Then, calculate the integrated signal profile:where
- 3.
- If n denotes a segment’s length (which will also be referred to as the scale), then the analysed time series can be divided into Mn = [N/n] disjoint segments of length n (n < N). By starting the division independently from the beginning and the end, the 2Mn segments are obtained.
- 4.
- At each segment ν, a local trend should be calculated, i.e., fitted l–th order polynomial and the trend subtracted from the signal. For a given segment ν (ν = 1, …, Mn), the variance of the residual series is equal to
- 5.
- Finally, the fluctuation function F2(ν, n) is averaged over ν’s, and the fluctuation function is calculated for all possible segment lengths, n:
4. Results
4.1. Control System
4.2. Influence of IAA on Multifractal Characteristics
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, Y.T.; Yang, L.H.; Ferjani, A.; Lin, W.H. Multiple functions of the vacuole in plant growth and fruit quality. Mol. Hortic. 2021, 1, 4. [Google Scholar] [CrossRef]
- Martinoia, E. Vacuolar Transporters–Companions on a Longtime Journey. Plant Physiol. 2017, 176, 1384–1407. [Google Scholar] [CrossRef] [PubMed]
- Tan, X.; Li, K.; Wang, Z.; Zhu, K.; Tan, X.; Cao, J. A Review of Plant Vacuoles: Formation, Located Proteins, and Functions. Plants 2019, 8, 327. [Google Scholar] [PubMed]
- Ragel, P.; Raddatz, N.; Leidi, E.O.; Quintero, F.J.; Pardo, J.M. Regulation of K+ Nutrition in Plants. Front. Plant Sci. 2019, 10, 281. [Google Scholar] [CrossRef] [PubMed]
- Hedrich, R. Ion Channels in Plants. Physiol. Rev. 2012, 92, 1777–1811. [Google Scholar] [CrossRef]
- Hedrich, R.; Neher, E. Cytoplasmic calcium regulates voltage–dependent ion channels in plant vacuoles. Nature 1987, 329, 833–836. [Google Scholar]
- Ward, J.M.; Schroeder, J.I. Calcium–Activated K+ Channels and Calcium–Induced Calcium Release by Slow Vacuolar Ion Channels in Guard Cell Vacuoles Implicated in the Control of Stomatal Closure. Plant Cell 1994, 6, 669–683. [Google Scholar] [CrossRef]
- Pottosin, I.; Dobrovinskaya, O.; Muñiz, J. Conduction of Monovalent and Divalent Cations in the Slow Vacuolar Channel. J. Membr. Biol. 2001, 181, 55–65. [Google Scholar] [CrossRef]
- Allen, G.J.; Sanders, D. Control of ionic currents in guard cell vacuoles by cytosolic and luminal calcium. Plant J. 1996, 10, 1055–1069. [Google Scholar] [CrossRef]
- Tikhonova, L.I.; Pottosin, I.I.; Dietz, K.J.; Schönknecht, G. Fast–activating cation channel in barley mesophyll vacuoles. Inhibition by calcium. Plant J. 1997, 11, 1059–1070. [Google Scholar] [CrossRef]
- Brüggemann, L.I.; Pottosin, I.I.; Schönknecht, G. Selectivity of the fast activating vacuolar cation channel. J. Exp. Bot. 1999, 50, 873–876. [Google Scholar] [CrossRef]
- Brüggemann, L.I.; Pottosin, I.I.; Schönknecht, G. Cytoplasmic magnesium regulates the fast activating vacuolar cation channel. J. Exp. Bot. 1999, 50, 1547–1552. [Google Scholar] [CrossRef]
- Burdach, Z.; Siemieniuk, A.; Karcz, W. Effect of Auxin (IAA) on the Fast Vacuolar (FV) Channels in Red Beet (Beta vulgaris L.) Taproot Vacuoles. Int. J. Mol. Sci. 2020, 21, 4876. [Google Scholar] [CrossRef] [PubMed]
- Silva, M.P.; Rodrigues, C.G.; Varanda, W.A.; Nogueira, R.A. Memory in Ion Channel Kinetics. Acta Biotheor. 2021, 69, 697–722. [Google Scholar] [CrossRef] [PubMed]
- Wawrzkiewicz–Jałowiecka, A.; Trybek, P.; Borys, P.; Dworakowska, B.; Machura, Ł.; Bednarczyk, P. Differences in Gating Dynamics of BK Channels in Cellular and Mitochondrial Membranes from Human Glioblastoma Cells Unraveled by Short– and Long–Range Correlations Analysis. Cells 2020, 9, 2305. [Google Scholar] [CrossRef]
- Miśkiewicz, J.; Trela, Z.; Burdach, Z.; Karcz, W.; Balińska–Miśkiewicz, W. Long range correlations of the ion current in SV channels. Met3PbCl influence study. PLoS ONE 2020, 15, e0229433. [Google Scholar] [CrossRef]
- Siwy, Z.; Mercik, S.; Weron, K.; Ausloos, M. Application of dwell–time series in studies of long–range correlation in single channel ion transport: Analysis of ion current through a big conductance locust potassium channel. Physica A 2001, 297, 79–96. [Google Scholar] [CrossRef]
- Bershadskii, A.; Dremencov, E.; Fukayama, D.; Yadid, G. Multifractal statistics and underlying kinetics of neuron spiking time–series. Phys. Lett. A 2001, 289, 337–342. [Google Scholar] [CrossRef]
- Kazachenko, V.N.; Astashev, M.E.; Grinevich, A.A. Multifractal analysis of K+ channel activity. Biochem. Moscow Suppl. Ser. A 2007, 1, 169–175. [Google Scholar]
- Wawrzkiewicz–Jałowiecka, A.; Trybek, P.; Dworakowska, B.; Machura, Ł. Multifractal Properties of BK Channel Currents in Human Glioblastoma Cells. J. Phys. Chem. B 2020, 124, 2382–2391. [Google Scholar] [CrossRef] [PubMed]
- Coyaud, L.; Kurkdjian, A.; Kado, R.; Hedrich, R. Ion channels and ATP–driven pumps involved in ion transport across the tonoplast of sugarbeet vacuoles. Biochim. Biophys. Acta Biomembr. 1987, 902, 263–268. [Google Scholar] [CrossRef]
- Hamill, O.P.; Marty, A.; Neher, E.; Sakmann, B.; Sigworth, F.J. Improved patch–clamp techniques for high–resolution current recording from cells and cell–free membrane patches. Pflugers Arch. 1981, 391, 85–100. [Google Scholar] [CrossRef] [PubMed]
- Bertl, A.; Blumwald, E.; Coronado, R.; Eisenberg, R.; Findlay, G.; Gradmann, D.; Hille, B.; Kohler, K.; Kolb, H.A.; MacRobbie, E.; et al. Electrical Measurements on Endomembranes. Science 1992, 258, 873–874. [Google Scholar] [CrossRef] [PubMed]
- Voss, R.F. Evolution of long–range fractal correlations and 1/f noise in DNA base sequences. Phys. Rev. Lett. 1992, 68, 3805–3808. [Google Scholar] [CrossRef]
- Buldyrev, S.V.; Goldberger, A.L.; Havlin, S.; Peng, C.K.; Simons, M.; Sciortino, F.; Stanley, H.E. Long–range fractal correlations in DNA. Phys. Rev. Lett. 1993, 71, 1776. [Google Scholar] [CrossRef] [PubMed]
- Namazi, H.; Kiminezhadmalaie, M. Diagnosis of Lung Cancer by Fractal Analysis of Damaged DNA. Comput. Math. Methods Med. 2015, 2015, 242695. [Google Scholar] [CrossRef]
- Bernaola–Galván, P.; Román–Roldán, R.; Oliver, J.L. Compositional segmentation and long–range fractal correlations in DNA sequences. Phys. Rev. E 1996, 53, 5181–5189. [Google Scholar] [CrossRef]
- Gronwald, T.; Hoos, O. Correlation properties of heart rate variability during endurance exercise: A systematic review. Ann. Noninvasive Electrocardiol. 2020, 25, e12697. [Google Scholar] [CrossRef] [PubMed]
- Echeverría, J.C.; Woolfson, M.S.; Crowe, J.A.; Hayes–Gill, B.R.; Croaker, G.D.H.; Vyas, H. Interpretation of heart rate variability via detrended fluctuation analysis and αβ filter. Chaos: J. Nonlinear Sci. 2003, 13, 467–475. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, E.; Echeverria, J.C.; Alvarez–Ramirez, J. Detrended fluctuation analysis of heart intrabeat dynamics. Physica A 2007, 384, 429–438. [Google Scholar] [CrossRef]
- Vandewalle, N.; Ausloos, M. Coherent and random sequences in financial fluctuations. Physica A 1997, 246, 454–459. [Google Scholar] [CrossRef]
- Ivanov, P.C.; Yuen, A.; Podobnik, B.; Lee, Y. Common scaling patterns in intertrade times of US stocks. Phys. Rev. E 2004, 69, 056107. [Google Scholar]
- Mandelbrot, B.B.; Fisher, A.J.; Calvet, L.E. A Multifractal Model of Asset Returns; Cowless Foundation Discussion Paper, No. 1164; Yale University, Cowles Foundation for Research in Economics: New Haven, CT, USA, 1997. [Google Scholar]
- Ausloos, M.; Ivanova, K. Introducing false EUR and false EUR exchange rates. Physica A 2000, 286, 353–366. [Google Scholar] [CrossRef]
- Ausloos, M.; Ivanova, K. Power–law correlations in the southern–oscillation–index fluctuations characterizing El Niño. Phys. Rev. E 2001, 63, 047201. [Google Scholar] [CrossRef] [PubMed]
- Havlin, S.; Buldyrev, S.; Bunde, A.; Goldberger, A.; Ivanov, P.C.; Peng, C.K.; Stanley, H.E. Scaling in nature: From DNA through heartbeats to weather. Physica A 1999, 273, 46–69. [Google Scholar] [CrossRef] [PubMed]
- Olsen, L. A Multifractal Formalism. Adv. Math. 1995, 116, 82–196. [Google Scholar] [CrossRef]
- Evertsz, C.J.; Mandelbrot, B.B. Multifractal measures. Chaos Solit. Fractals 1992, 1992, 921–953. [Google Scholar]
- Muzy, J.; Bacry, E.; Arneodo, A. The multifractal formalism revisited with wavelets. Int. J. Bifurcat. Chaos 1994, 04, 245–302. [Google Scholar] [CrossRef]
- Pavlov, A.N.; Anishchenko, V.S. Multifractal analysis of complex signals. Phys. Usp. 2007, 50, 819. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Koscielny–Bunde, E.; Rego, H.H.A.; Havlin, S.; Bunde, A. Detecting long–range correlations with detrended fluctuation analysis. Physica A 2001, 295, 441–454. [Google Scholar]
- Oświęcimka, P.; Kwapień, J.; Drożdż, S. Wavelet versus detrended fluctuation analysis of multifractal structures. Phys. Rev. E 2006, 74, 016103. [Google Scholar] [CrossRef] [PubMed]
- Matia, K.; Ashkenazy, Y.; Stanley, H.E. Multifractal properties of price fluctuations of stocks and commodities. Europhys. Lett. 2003, 61, 422–428. [Google Scholar] [CrossRef]
- Ihlen, E.A.F. Introduction to Multifractal Detrended Fluctuation Analysis in Matlab. Front. Physiol. 2012, 3, 141. [Google Scholar] [CrossRef]
- Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.; Shraiman, B.I. Fractal measures and their singularities: The characterization of strange sets. Phys. Rev. A 1986, 33, 1141–1151. [Google Scholar] [CrossRef] [PubMed]
- Rydin Gorjão, L.; Hassan, G.; Kurths, J.; Witthaut, D. MFDFA: Efficient multifractal detrended fluctuation analysis in python. Comput. Phys. Commun. 2022, 273, 108254. [Google Scholar] [CrossRef]
- Laib, M.; Telesca, L.; Kanevski, M. MFDFA R package: Multifractal analysis for time series. Geophysic. Res. Abstr. 2019, 21, 1. [Google Scholar]
- Neher, E.; Sakmann, B. Single–channel currents recorded from membrane of denervated frog muscle fibres. Nature 1976, 260, 799–802. [Google Scholar] [CrossRef] [PubMed]
- Hamill, O.P. Patch–clamp technique; John Wileys & Sons: Hoboken, NJ, USA, 2014; pp. 1–14. [Google Scholar]
- Wu, D.; Saleem, M.; He, T.; He, G. The mechanism of metal homeostasis in plants: A new view on the synergistic regulation pathway of membrane proteins, lipids and metal ions. Membranes 2021, 11, 984. [Google Scholar] [CrossRef] [PubMed]
- Saponaro, A.; Lolicato, M. The key role of lipids in the regulation of ion channels. Front. Physiol. 2022, 13, 1838. [Google Scholar] [CrossRef]
- Hurst, H.E. Long–term storage capacity of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Wawrzkiewicz, A.; Pawelek, K.; Borys, P.; Dworakowska, B.; Grzywna, Z.J. On the simple random–walk models of ion–channel gate dynamics reflecting long–term memory. Eur. Biophys. J. 2012, 41, 505–526. [Google Scholar] [CrossRef] [PubMed]
- Oświęcimka, P.; Minati, L. 5 Multifractal characteristics of singular signals. In Outliers in Control Engineering: Fractional Calculus Perspective; De Gruyter: Berlin, Germany, 2022; Volume 10, p. 99. [Google Scholar]
- Liebovitch, L.S.; Fischbarg, J.; Koniarek, J.P.; Todorova, I.; Wang, M. Fractal model of ion–channel kinetics. Biochim. Biophys. Acta Biomembr. 1987, 896, 173–180. [Google Scholar] [CrossRef]
- Linaro, D.; Giugliano, M. Markov models of ion channels. In Encyclopedia of Computational Neuroscience; Springer: New York, NY, USA, 2022; pp. 1961–1972. [Google Scholar]
- Liebovitch, L.S.; Fischbarg, J.; Koniarek, J.P. Ion channel kinetics: A model based on fractal scaling rather than multistate Markov processes. Math. Biosci. 1987, 84, 37–68. [Google Scholar] [CrossRef]
- Whittaker, D.G.; Wang, J.; Shuttleworth, J.G.; Venkateshappa, R.; Kemp, J.M.; Claydon, T.W.; Mirams, G.R. Ion channel model reduction using manifold boundaries. J. Royal Soc. Interface 2022, 19, 20220193. [Google Scholar] [CrossRef]
- Philippar, K.; Fuchs, I.; Lüthen, H.; Hoth, S.; Bauer, C.S.; Haga, K.; Thiel, G.; Ljung, K.; Sandberg, G.; Bottger, M.; et al. Auxin–induced K+ channel expression represents an essential step in coleoptile growth and gravitropism. Proc. Nat. Acad. Sci. USA 1999, 96, 12186–12191. [Google Scholar] [CrossRef] [PubMed]
- Becker, D.; Hedrich, R. Channelling auxin action: Modulation of ion transport by indole–3–acetic acid. Plant Mol. Biol. 2002, 49, 349–356. [Google Scholar] [CrossRef] [PubMed]
- Burdach, Z.; Siemieniuk, A.; Trela, Z.; Kurtyka, R.; Karcz, W. Role of auxin (IAA) in the regulation of slow vacuolar (SV) channels and the volume of red beet taproot vacuoles. BMC Plant Biol. 2018, 18, 102. [Google Scholar] [CrossRef]
- Singh, A.; Kukreti, R.; Saso, L.; Kukreti, S. Oxidative stress: A key modulator in neurodegenerative diseases. Molecules 2019, 24, 1583. [Google Scholar] [CrossRef]
- Hąc–Wydro, K.; Sroka, A.; Jabłońska, K. The impact of auxins used in assisted phytoextraction of metals from the contaminated environment on the alterations caused by lead (II) ions in the organization of model lipid membranes. Colloids Surf. B 2016, 143, 124–130. [Google Scholar] [CrossRef] [PubMed]

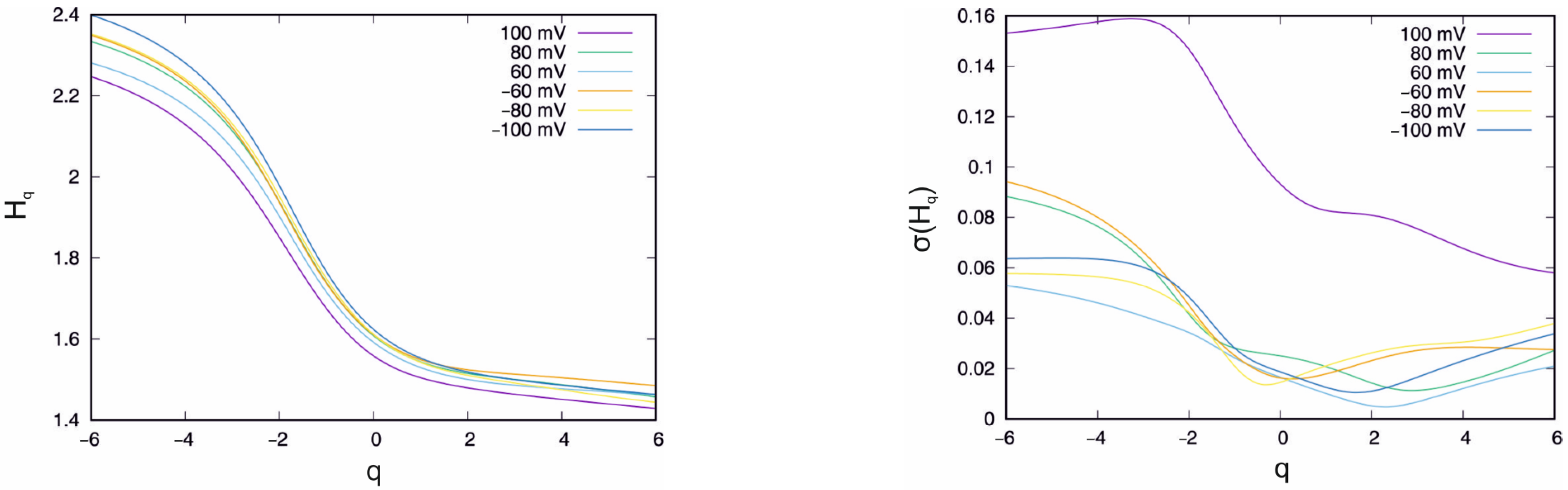


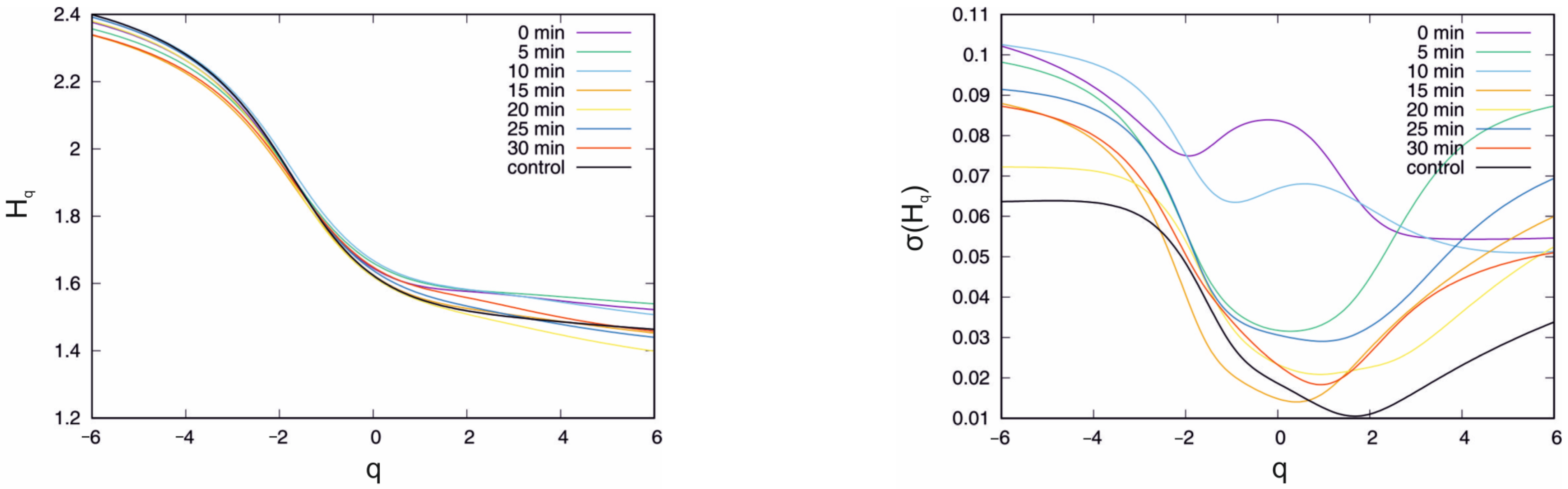
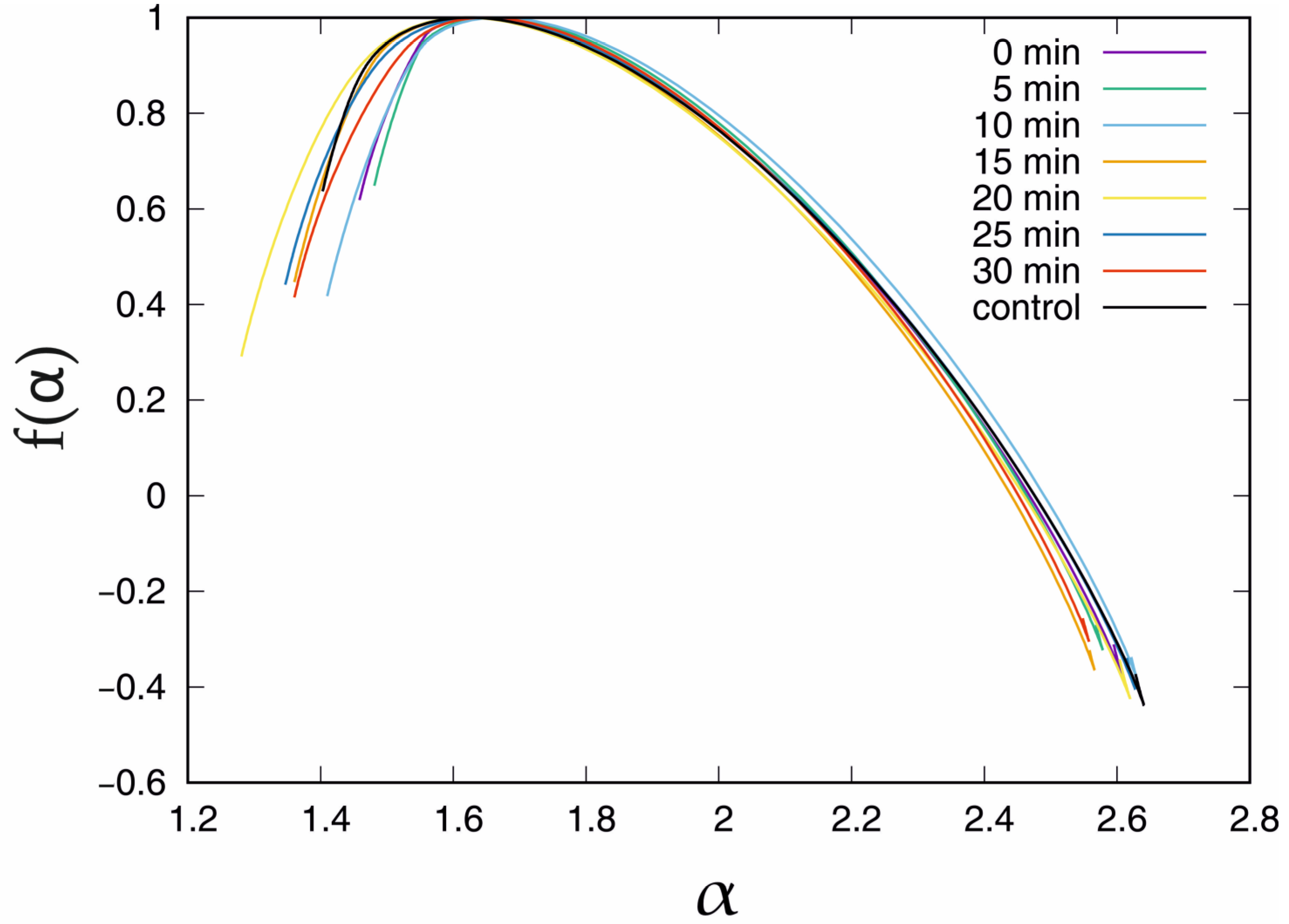
| U(mV) | <max (Hq) − min(Hq)> | σ(max(Hq) − min(Hq)) |
|---|---|---|
| 100 | 1.135 | 0.168 |
| 80 | 1.194 | 0.125 |
| 60 | 1.081 | 0.075 |
| −60 | 1.159 | 0.134 |
| −80 | 1.218 | 0.085 |
| −100 | 1.239 | 0.067 |
| Incubation | α | f(α) |
|---|---|---|
| control | 1.403 | 0.637 |
| 0 min | 1.459 | 0.619 |
| 5 min | 1.481 | 0.649 |
| 10 min | 1.410 | 0.418 |
| 15 min | 1.360 | 0.447 |
| 20 min | 1.281 | 0.291 |
| 25 min | 1.347 | 0.441 |
| 30 min | 1.360 | 0.415 |
| Incubation | <max (Hq) − min(Hq)> | σ(max(Hq) − min(Hq)) |
|---|---|---|
| control | 1.239 | 0.067 |
| 0 min | 1.152 | 0.142 |
| 5 min | 1.104 | 0.117 |
| 10 min | 1.226 | 0.145 |
| 15 min | 1.209 | 0.132 |
| 20 min | 1.342 | 0.156 |
| 25 min | 1.285 | 0.164 |
| 30 min | 1.200 | 0.119 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miśkiewicz, J.; Burdach, Z.; Trela, Z.; Siemieniuk, A.; Karcz, W. Multifractal Analysis of the Influence of Indole-3-Acetic Acid on Fast-Activating Vacuolar (FV) Channels of Beta vulgaris L. Taproot Cells. Membranes 2023, 13, 406. https://doi.org/10.3390/membranes13040406
Miśkiewicz J, Burdach Z, Trela Z, Siemieniuk A, Karcz W. Multifractal Analysis of the Influence of Indole-3-Acetic Acid on Fast-Activating Vacuolar (FV) Channels of Beta vulgaris L. Taproot Cells. Membranes. 2023; 13(4):406. https://doi.org/10.3390/membranes13040406
Chicago/Turabian StyleMiśkiewicz, Janusz, Zbigniew Burdach, Zenon Trela, Agnieszka Siemieniuk, and Waldemar Karcz. 2023. "Multifractal Analysis of the Influence of Indole-3-Acetic Acid on Fast-Activating Vacuolar (FV) Channels of Beta vulgaris L. Taproot Cells" Membranes 13, no. 4: 406. https://doi.org/10.3390/membranes13040406
APA StyleMiśkiewicz, J., Burdach, Z., Trela, Z., Siemieniuk, A., & Karcz, W. (2023). Multifractal Analysis of the Influence of Indole-3-Acetic Acid on Fast-Activating Vacuolar (FV) Channels of Beta vulgaris L. Taproot Cells. Membranes, 13(4), 406. https://doi.org/10.3390/membranes13040406







