Determining the Bending Rigidity of Free-Standing Planar Phospholipid Bilayers
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Lipid Bilayer Preparation
2.3. Asymmetric Ion Composition Experiments
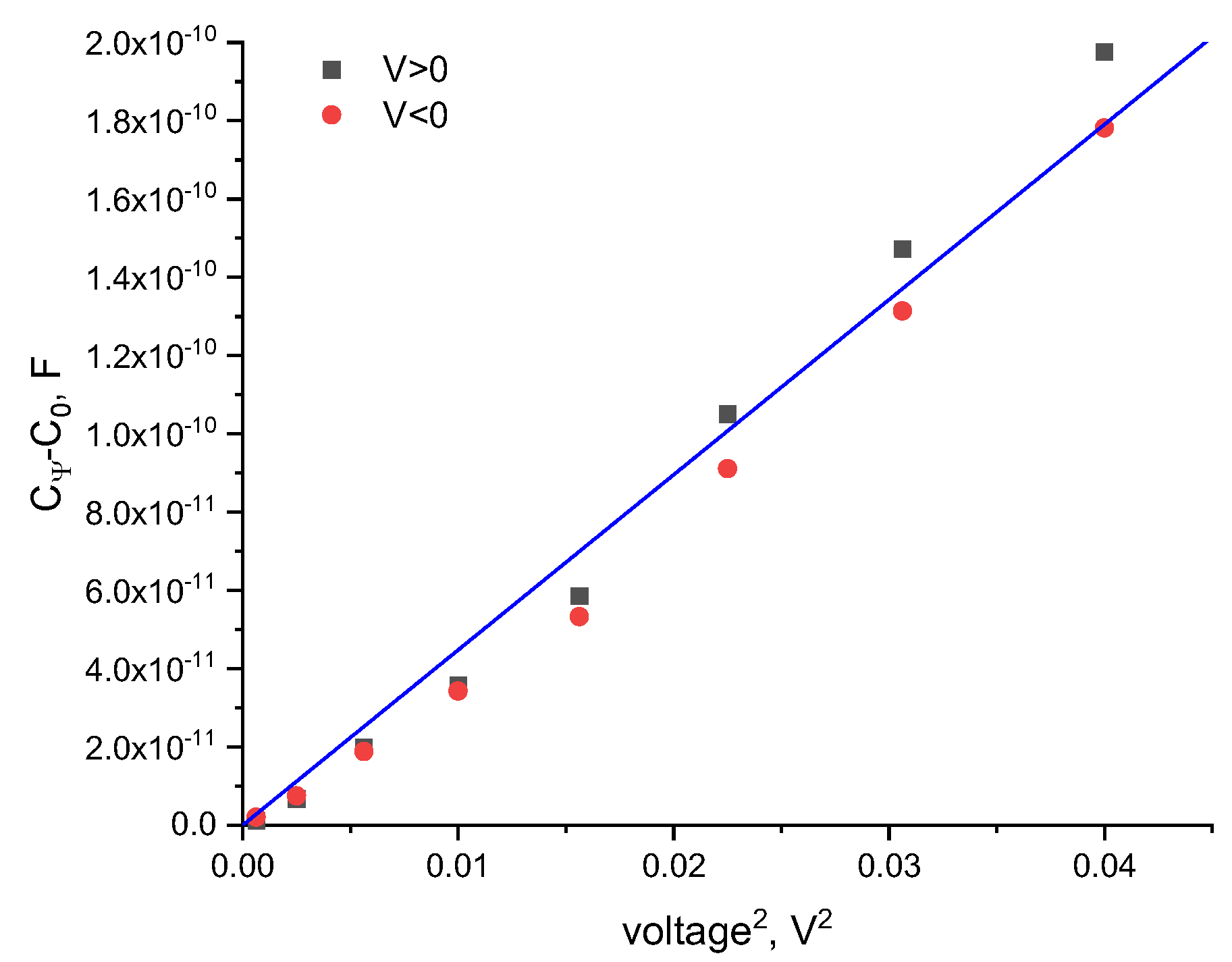
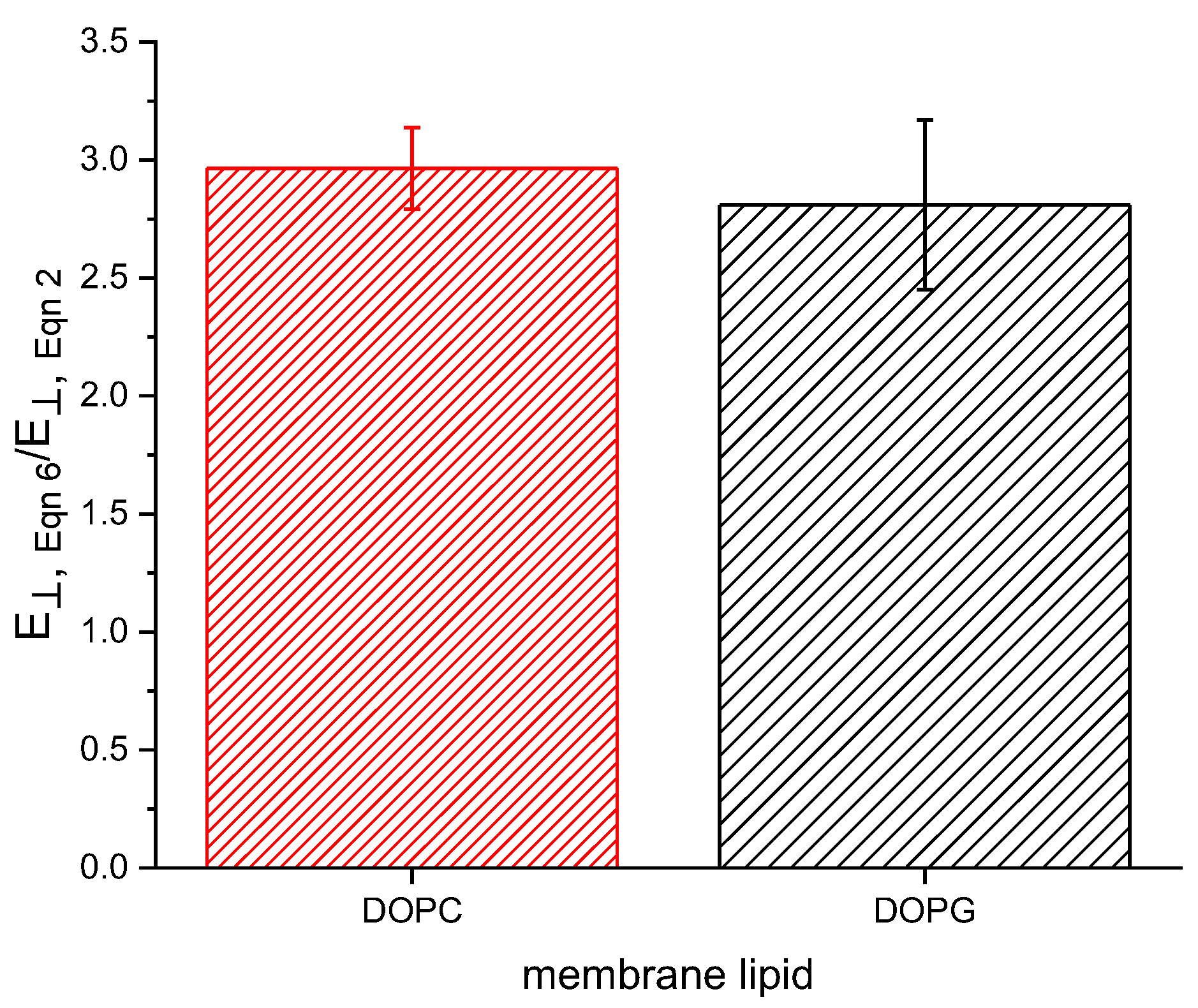
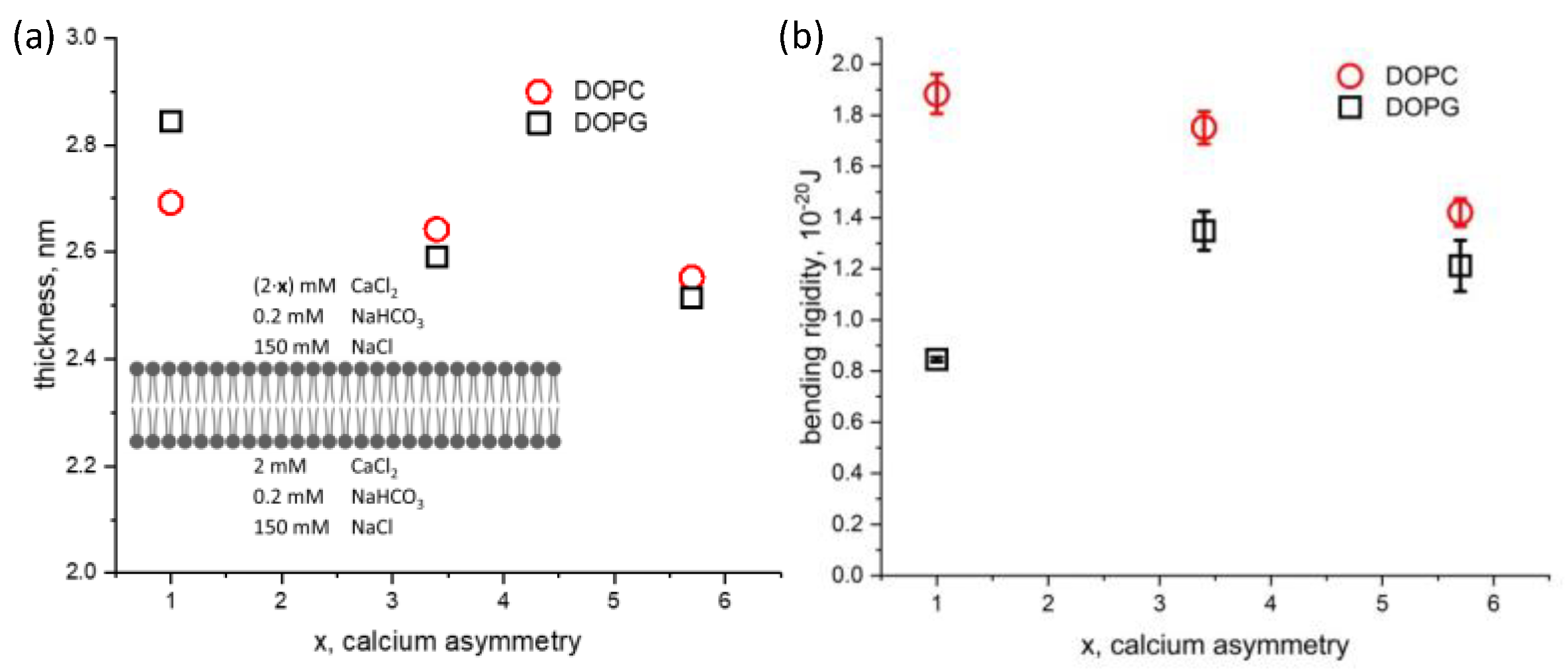
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harayama, T.; Riezman, H. Understanding the diversity of membrane lipid composition. Nat. Rev. Mol. Cell Biol. 2018, 19, 281–296. [Google Scholar] [CrossRef] [PubMed]
- Brannigan, G.; Brown, F.L.H. Composition dependence of bilayer elasticity. J. Chem. Phys. 2005, 122, 074905. [Google Scholar] [CrossRef] [PubMed]
- Cavalcanti, L.P.; Tho, I.; Konovalov, O.; Fossheim, S.; Brandl, M. Compressibility study of quaternary phospholipid blend monolayers. Colloids Surf. B Biointerfaces 2011, 85, 153–160. [Google Scholar] [CrossRef] [PubMed]
- Saavedra, V.O.; Fernandes, T.F.D.; Milhiet, P.E.; Costa, L. Compression, Rupture, and Puncture of Model Membranes at the Molecular Scale. Langmuir 2020, 36, 5709–5716. [Google Scholar] [CrossRef]
- Dowhan, W.; Bogdanov, M. Lipid-protein interactions as determinants of membrane protein structure and function. Biochem. Soc. Trans. 2011, 39, 767–774. [Google Scholar] [CrossRef] [PubMed]
- Ramalho, M.J.; Andrade, S.; Coelho, M.A.N.; Loureiro, J.A.; Pereira, M.C. Molecular interactions between Vitamin B12 and membrane models: A biophysical study for new insights into the bioavailability of Vitamin. Colloids Surf. B Biointerfaces 2020, 194, 111187. [Google Scholar] [CrossRef] [PubMed]
- Alves, A.C.; Ribeiro, D.; Horta, M.; Lima, J.L.F.C.; Nunes, C.; Reis, S. A biophysical approach to daunorubicin interaction with model membranes: Relevance for the drug’s biological activity. J. R. Soc. Interface 2017, 14, 527–532. [Google Scholar] [CrossRef] [PubMed]
- Phillips, R.; Ursell, T.; Wiggins, P.; Sens, P. Emerging roles for lipids in shaping membrane-protein function. Nature 2009, 459, 379–385. [Google Scholar] [CrossRef]
- Dimova, R. Recent developments in the field of bending rigidity measurements on membranes. Adv. Colloid Interface Sci. 2014, 208, 225–234. [Google Scholar] [CrossRef]
- Evans, E.; Needham, D. Physical Properties of Surfactant Bilayer Membranes: Thermal Transitions, Elasticity, Rigidity, Cohesion, and Colloidal Interactions. J. Phys. Chem. 1987, 91, 4219–4228. [Google Scholar] [CrossRef]
- Drabik, D.; Przybyło, M.; Chodaczek, G.; Iglič, A.; Langner, M. The modified fluorescence based vesicle fluctuation spectroscopy technique for determination of lipid bilayer bending properties. Biochim. Biophys. Acta Biomembr. 2016, 1858, 244–252. [Google Scholar] [CrossRef] [PubMed]
- De Mel, J.U.; Gupta, S.; Perera, R.M.; Ngo, L.; Zolnierczuk, P.; Bleuel, M.; Pingali, S.V.; Schneider, G.J. Influence of External NaCl Salt on Membrane Rigidity of Neutral DOPC Vesicles. Langmuir 2020, 36, 9356–9367. [Google Scholar] [CrossRef] [PubMed]
- Scanavachi, G.; Coutinho, A.; Fedorov, A.A.; Prieto, M.; Melo, A.M.; Itri, R. Lipid Hydroperoxide Compromises the Membrane Structure Organization and Softens Bending Rigidity. Langmuir 2021, 37, 9952–9963. [Google Scholar] [CrossRef] [PubMed]
- Salditt, T. Thermal fluctuations and stability of solid-supported lipid membranes. J. Phys. Condens. Matter 2005, 17, R287. [Google Scholar] [CrossRef]
- Schneck, E.; Demé, B.; Gege, C.; Tanaka, M. Membrane Adhesion via Homophilic Saccharide-Saccharide Interactions Investigated by Neutron Scattering. Biophys. J. 2011, 100, 2151–2159. [Google Scholar] [CrossRef]
- Schäfer, A.; Salditt, T.; Rheinstädter, M.C. Atomic force microscopy study of thick lamellar stacks of phospholipid bilayers. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2008, 77, 021905. [Google Scholar] [CrossRef]
- Drabik, D.; Gavutis, M.; Valiokas, R.N.; Ulčinas, A.R. Determination of the Mechanical Properties of Model Lipid Bilayers Using Atomic Force Microscopy Indentation. Langmuir 2020, 36, 13251–13262. [Google Scholar] [CrossRef]
- Calò, A.; Reguera, D.; Oncins, G.; Persuy, M.A.; Sanz, G.; Lobasso, S.; Corcelli, A.; Pajot-Augy, E.; Gomila, G. Force measurements on natural membrane nanovesicles reveal a composition-independent, high Young’s modulus. Nanoscale 2014, 6, 2275–2285. [Google Scholar] [CrossRef]
- Doktorova, M.; Harries, D.; Khelashvili, G. Determination of bending rigidity and tilt modulus of lipid membranes from real-space fluctuation analysis of molecular dynamics simulations. Phys. Chem. Chem. Phys. 2017, 19, 16806–16818. [Google Scholar] [CrossRef]
- Smirnova, Y.G.; Müller, M. Calculation of membrane bending rigidity using field-theoretic umbrella sampling. J. Chem. Phys. 2015, 143, 243155. [Google Scholar] [CrossRef]
- Beltramo, P.J.; Van Hooghten, R.; Vermant, J. Millimeter-area, free standing, phospholipid bilayers. Soft Matter 2016, 12, 4324–4331. [Google Scholar] [CrossRef] [PubMed]
- Beltramo, P.J.; Scheidegger, L.; Vermant, J. Toward Realistic Large-Area Cell Membrane Mimics: Excluding Oil, Controlling Composition, and Including Ion Channels. Langmuir 2018, 34, 5880–5888. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Zabala-Ferrera, O.; Beltramo, P.J. Fabrication and electromechanical characterization of freestanding asymmetric membranes. Biophys. J. 2021, 120, 1755–1764. [Google Scholar] [CrossRef]
- Alvarez, O.; Latorre, R. Voltage-dependent capacitance in lipid bilayers made from monolayers. Biophys. J. 1978, 21, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Hianik, T.; Dlugopolsky, J.; Gyepessova, M. Electrostriction of lipid bilayers on a solid support. Influence of hydrocarbon solvent and d.c. voltage. Bioelectrochem. Bioenerg. 1993, 31, 99–111. [Google Scholar] [CrossRef]
- Hianik, T.; Passechnik, V.; Sargent, D.; Ivanov, S. Electrostriction and membrane potential of lipid bilayers on a metal support. A Physicochem. Eng. Asp. 1996, 106, 118. [Google Scholar] [CrossRef]
- Allen Rodowicz, K.; Francisco, H.; Layton, B. Determination of the mechanical properties of DOPC:DOPS liposomes using an image procession algorithm and micropipette-aspiration techniques. Chem. Phys. Lipids 2010, 163, 787–793. [Google Scholar] [CrossRef]
- Zoni, V.; Campomanes, P.; Vanni, S. Investigating the structural properties of hydrophobic solvent-rich lipid bilayers. Soft Matter 2021, 17, 5329–5335. [Google Scholar] [CrossRef]
- Tarun, O.B.; Eremchev, M.Y.; Roke, S. Interaction of Oil and Lipids in Freestanding Lipid Bilayer Membranes Studied with Label-Free High-Throughput Wide-Field Second-Harmonic Microscopy. Langmuir 2018, 34, 11305–11310. [Google Scholar] [CrossRef]
- Scheidegger, L.; Stricker, L.; Beltramo, P.J.; Vermant, J. Domain Size Regulation in Phospholipid Model Membranes Using Oil Molecules and Hybrid Lipids. J. Phys. Chem. B 2022, 126, 5842–5854. [Google Scholar] [CrossRef]
- White, R.H. Comments on “Electrical Breakdown of Bimolecular Lipid Membranes as an Electromechanical Instability”. Biophys. J. 1974, 14, 155–158. [Google Scholar] [CrossRef] [PubMed]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity; Pergamon Press: Oxford, UK, 1959. [Google Scholar]
- Claessens, M.M.A.E.; Van Oort, B.F.; Leermakers, F.A.M.; Hoekstra, F.A.; Stuart, M.A.C. Bending rigidity of mixed phospholipid bilayers and the equilibrium radius of corresponding vesicles. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2007, 76, 011903. [Google Scholar] [CrossRef] [PubMed]
- Picas, L.; Rico, F.; Scheuring, S. Direct measurement of the mechanical properties of lipid phases in supported bilayers. Biophys. J. 2012, 102, L01–L03. [Google Scholar] [CrossRef]
- Faucon, J.F.; Mitov, M.D.; Méléard, P.; Bivas, I.; Bothorel, P. Bending elasticity and thermal fluctuations of lipid membranes. Theoretical and experimental requirements. J. Phys. 1989, 50, 2389–2414. [Google Scholar] [CrossRef]
- Elani, Y.; Purushothaman, S.; Booth, P.J.; Seddon, J.M.; Brooks, N.J.; Law, R.V.; Ces, O. Measurements of the effect of membrane asymmetry on the mechanical properties of lipid bilayers. Chem. Commun. 2015, 51, 6976–6979. [Google Scholar] [CrossRef]
- Niggemann, G.; Kummrow, M.; Helfrich, W. The Bending Rigidity of Phosphatidylcholine Bilayers: Dependences on Experimental Method, Sample Cell Sealing and Temperature. J. Phys. II 1995, 5, 413–425. [Google Scholar] [CrossRef]
- Mitkova, D.; Vitkova, V. The aqueous surroundings alter the bending rigidity of lipid membranes. Russ. J. Electrochem. 2016, 52, 1172–1178. [Google Scholar] [CrossRef]
- Liu, C.; Li, L.; Qiu, F.; Yang, Y. Effects of salt concentration and structure of lipid molecules on the bending rigidity of multi-component charged membranes. Acta Chim. Sin. 2010, 68, 1325–1330. [Google Scholar]
- Claessens, M.M.A.E.; Van Oort, B.F.; Leermakers, F.A.M.; Hoekstra, F.A.; Stuart, M.A.C. Charged Lipid Vesicles: Effects of Salts on Bending Rigidity, Stability, and Size. Biophys. J. 2004, 87, 3882–3893. [Google Scholar] [CrossRef] [PubMed]
- Kučerka, N.; Tristram-Nagle, S.; Nagle, J.F. Structure of fully hydrated fluid phase lipid bilayers with monounsaturated chains. J. Membr. Biol. 2006, 208, 193–202. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Marquardt, D.; Heberle, F.A.; Kučerka, N.; Katsaras, J. Revisiting the bilayer structures of fluid phase phosphatidylglycerol lipids: Accounting for exchangeable hydrogens. Biochim. Biophys. Acta Biomembr. 2014, 1838, 2966–2969. [Google Scholar] [CrossRef] [PubMed]
- Bolik, S.; Albrieux, C.; Schneck, E.; Demé, B.; Jouhet, J. Sulfoquinovosyldiacylglycerol and phosphatidylglycerol bilayers share biophysical properties and are good mutual substitutes in photosynthetic membranes. Biochim. Biophys. Acta Biomembr. 2022, 1864, 184037. [Google Scholar] [CrossRef] [PubMed]
- Graber, Z.T.; Shi, Z.; Baumgart, T. Cations induce shape remodeling of negatively charged phospholipid membranes. Phys. Chem. Chem. Phys 2017, 19, 15285. [Google Scholar] [CrossRef] [PubMed]
- Karimi, M.; Steinkühler, J.; Roy, D.; Dasgupta, R.; Lipowsky, R.; Dimova, R. Asymmetric Ionic Conditions Generate Large Membrane Curvatures. Nano Lett. 2018, 18, 7816–7821. [Google Scholar] [CrossRef]
- Filippov, A.; Orädd, G.; Lindblom, G. Effect of NaCl and CaCl2 on the lateral diffusion of zwitterionic and anionic lipids in bilayers. Chem. Phys. Lipids 2009, 159, 81–87. [Google Scholar] [CrossRef]
- Hossein, A.; Deserno, M. Spontaneous Curvature, Differential Stress, and Bending Modulus of Asymmetric Lipid Membranes. Biophys. J. 2020, 118, 624–642. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zabala-Ferrera, O.; Liu, P.; Beltramo, P.J. Determining the Bending Rigidity of Free-Standing Planar Phospholipid Bilayers. Membranes 2023, 13, 129. https://doi.org/10.3390/membranes13020129
Zabala-Ferrera O, Liu P, Beltramo PJ. Determining the Bending Rigidity of Free-Standing Planar Phospholipid Bilayers. Membranes. 2023; 13(2):129. https://doi.org/10.3390/membranes13020129
Chicago/Turabian StyleZabala-Ferrera, Oscar, Paige Liu, and Peter J. Beltramo. 2023. "Determining the Bending Rigidity of Free-Standing Planar Phospholipid Bilayers" Membranes 13, no. 2: 129. https://doi.org/10.3390/membranes13020129
APA StyleZabala-Ferrera, O., Liu, P., & Beltramo, P. J. (2023). Determining the Bending Rigidity of Free-Standing Planar Phospholipid Bilayers. Membranes, 13(2), 129. https://doi.org/10.3390/membranes13020129




