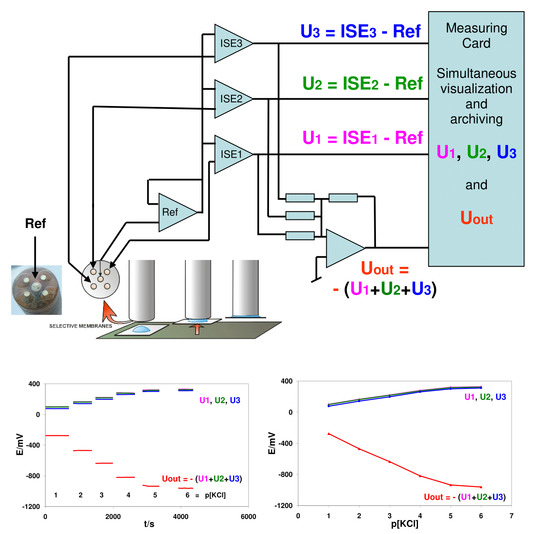
Electrically Enhanced Sensitivity (EES) of Ion-Selective Membrane Electrodes and Membrane-Based Ion Sensors
Abstract
1. Introduction
2. Materials and Methods
2.1. Apparatus
2.2. Chemicals
2.2.1. ISE Membranes
2.2.2. Other Reagents
2.3. Electrodes
2.3.1. Flow-Through Electrodes
2.3.2. Multielectrode Platforms
2.3.3. Procedures
3. Results and Discussion
3.1. Slope Amplification by Summing Signals in Flow through Blocks or Multielectrode Platforms with n-Sensors for the Same Ion
3.1.1. Amplification of the Slope with Highly Resistive Sodium Glass Membrane Electrodes Set in a Flow-Through Block
| pNa | E/mV ± SD | |||
|---|---|---|---|---|
| Na1 Glass | Na2 Glass | Na3 Glass | −(Na1 + Na2 + Na3) Glass | |
| 1.12 | −1.25 ± 0.03 | 91.52 ± 0.03 | 91.84 ± 0.05 | −182.16 ± 0.02 |
| 2.05 | −59.41 ± 0.04 | 33.68 ± 0.02 | 33.86 ± 0.03 | −8.12 ± 0.04 |
| 3.02 | −113.34 ± 0.06 | −20.21 ± 0.06 | −20.32 ± 0.05 | 153.78 ± 0.09 |
| 4.01 | −159.04 ± 0.15 | −64.99 ± 0.19 | −66.39 ± 0.16 | 290.41 ± 0.24 |
| Slope mV/pNa pNa 1–3 | −59.18 | −59.00 | −59.22 | 177.38 |
| R pNa 1–3 | −0.99937 | −0.99942 | −0.99945 | 0.99941 |
| Mean S/N pNa 1–3 | 1480 | 1967 | 1448 | 5092 |
| Potential changes between pNa 3–4 | −45.70 | −44.7 | −46.07 | 136.63 |
3.1.2. Amplification of the Slope in the Case of Non-Linear Calibration: The Interference of Sodium Ions on Flow-Through Lithium ISEs
| LiCl (mmol/L) | E/mV ± SD | ||||
|---|---|---|---|---|---|
| Li1 | Li2 | Li3 | −(Li1 + Li2 + Li3) | REF Metrohm vs. KONE REF Difference | |
| 0.0 | 1.12 ± 0.02 | 0.91 ± 0.02 | 0.33 ± 0.02 | −4.20 ± 0.04 | 5.58 ± 0.02 |
| 0.5 | 4.36 ± 0.03 | 4.11 ± 0.02 | 3.58 ± 0.03 | −13.91 ± 0.06 | 5.45 ± 0.02 |
| 1.0 | 7.31 ± 0.02 | 7.05 ± 0.02 | 6.48 ± 0.04 | −22.72 ± 0.07 | 5.41 ± 0.02 |
| 1.5 | 10.30 ± 0.03 | 10.06 ± 0.04 | 9.43 ± 0.05 | −31.64 ± 0.09 | 5.37 ± 0.02 |
| 2.0 | 12.80 ± 0.07 | 12.48 ± 0.06 | 11.87 ± 0.06 | −39.04 ± 0.09 | 5.28 ± 0.04 |
| 3.0 | 16.77 ± 0.02 | 16.42 ± 0.02 | 15.89 ± 0.03 | −50.99 ± 0.05 | 5.23 ± 0.02 |
| 3.5 | 18.70 ± 0.03 | 18.35 ± 0.02 | 17.78 ± 0.03 | −56.68 ± 0.09 | 5.58 ± 0.02 |
| 4.0 | 20.66 ± 0.02 | 20.30 ± 0.02 | 19.71 ± 0.02 | −62.54 ± 0.06 | 5.19 ± 0.02 |
| Slope mV/Δlog [Li + 3.5] | 58.99 | 58.52 | 58.50 | −176.09 | |
| R | 0.9944 | 0.9943 | 0.9945 | −0.9944 | |
| Mean S/N | 2316 | 2499 | 1913 | 2772 | |
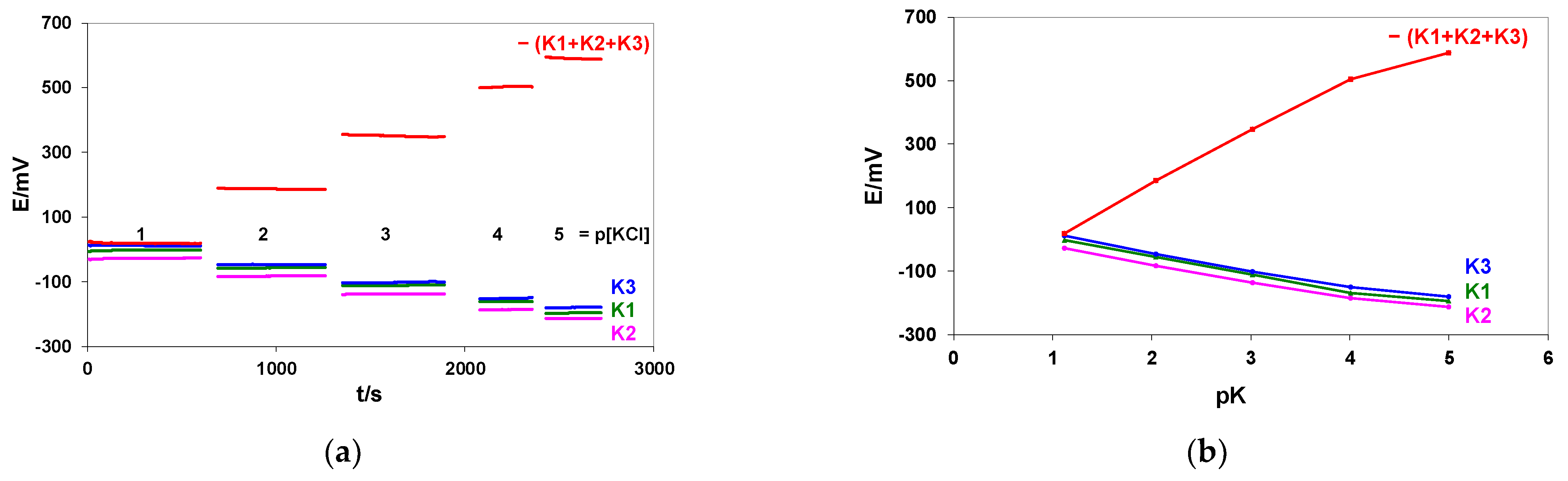
3.1.3. Discriminating Malfunctioning Ion Sensors in Systems of the Flat Multielectrode ISs and Solid Contact Reference Electrode
| pK | E/mV ±SD | ||||
|---|---|---|---|---|---|
| K1 | K2 | K3 | −(K1 + K2 + K3) | REF Metrohm vs. SC-REF | |
| 1.12 | −2.43 ± 0.04 | −27.19 ± 0.09 | 10.35 ± 0.09 | 17.84 ± 0.15 | 3.74 ± 0.08 |
| 2.05 | −56.56 ± 0.08 | −82.45 ± 0.07 | −47.08 ± 0.08 | 184.39 ± 0.15 | 3.72 ± 0.09 |
| 3.02 | −110.94 ± 0.10 | −137.56 ± 0.10 | −101.03 ± 0.51 | 347.81 ± 0.51 | 3.67 ± 0.08 |
| 4.01 | −168.48 ± 0.30 | −186.57 ± 0.07 | −150.58 ± 0.65 | 503.80 ± 0.63 | 3.34 ± 0.07 |
| 5.00 | −195.80 ± 0.14 | −214.04 ± 0.08 | −180.02 ± 0.06 | 587.80 ± 0.21 | 3.02 ± 0.06 |
| Slope mV/pK pK 1–4 | −57.45 | −55.41 | −55.76 | 168.49 | |
| R pK 1–4 | −0.99997 | −0.99910 | −0.99884 | 0.99955 | |
| Mean S/N pK 1–4 | 730 | 688 | 378 | 711 | |
| Potential changes between pK 4–5 | −27.32 | −27.47 | −29.44 | 84.00 | |
3.2. Extended Benefits: Summing Signals of the Same Electrode Connected Simultaneously to Different Ion-Meter Channels
| pNa | E/mV ± SD | |||
|---|---|---|---|---|
| Na-ISE Channel 1 | Na-ISE Channel 2 | Na-ISE Channel 3 | Sum of Channel Signals −(1 + 2 +3) | |
| 1.12 | 9.78 ± 0.05 | 9.75 ± 0.05 | 9.73 ± 0.07 | −30.49 ± 0.06 |
| 2.05 | −48.02 ± 0.09 | −48.18 ± 0.08 | −48.13 ± 0.09 | 142.76 ± 0.12 |
| 3.02 | −103.74 ± 0.05 | −103.90 ± 0.08 | −103.80 ± 0.07 | 309.76 ± 0.16 |
| 4.01 | −162.56 ± 0.20 | −162.80 ± 0.21 | −162.63 ± 0.21 | 486.03 ± 0.36 |
| 5.00 | −205.51 ± 0.06 | −205.83 ± 0.06 | −205.63 ± 0.08 | 615.09 ± 0.18 |
| 6.00 | −218.59 ± 0.20 | −218.92 ± 0.21 | −218.68 ± 0.21 | 654.26 ± 0.65 |
| Slope mV/pNa pNa 1–4 | −59.54 | −59.60 | −59.54 | 178.44 |
| R pNa 1–4 | −0.99987 | −0.99986 | −0.99986 | 0.99987 |
| Mean S/N pNa 1–4 | 835 | 741 | 661 | 1518 |
| Potential changes between pNa 4–5 | −42.95 | −43.03 | −43.00 | 129.06 |
| Potential changes between pNa 5–6 | −13.08 | −13.09 | −13.05 | 39.17 |
3.3. Comparison of the EES with CCS and SCP Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Summing Amplifier

Appendix A.2. Application of Different Gains for Cl-Ion Sensors
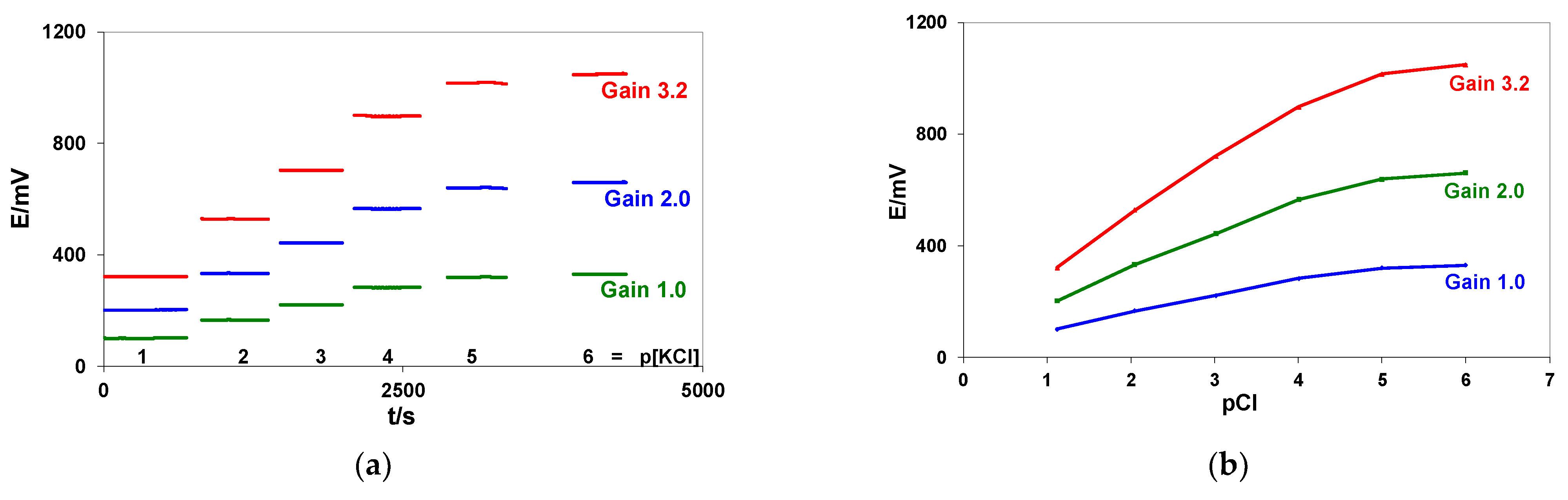
| pCl | E/mV ± SD | ||
|---|---|---|---|
| Cl4 Gain 1.0 | Cl4 Gain 2.0 | Cl4 Gain 3.2 | |
| 1.12 | 100.31 ± 0.08 | 201.89 ± 0.08 | 321.20 ± 0.08 |
| 2.05 | 165.27 ± 0.05 | 331.84 ± 0.09 | 527.45 ± 0.15 |
| 3.02 | 220.33 ± 0.03 | 441.96 ± 0.08 | 720.27 ± 0.09 |
| 4.01 | 281.95 ± 0.13 | 565.28 ± 0.25 | 897.98 ± 0.39 |
| 5.00 | 318.94 ± 0.49 | 639.10 ± 1.01 | 1015.20 ± 1.62 |
| 6.00 | 329.46 ± 0.15 | 660.32 ± 0.25 | 1048.93 ± 0.41 |
| Slope mV/pCl pCl 1–4 | 62.35 | 124.73 | 199.80 |
| R pCl 1–4 | 0.99917 | 0.99917 | 0.99882 |
| Mean S/N pCl 1–4 | 1146 | 1250 | 1640 |
| Potential changes between pCl 4–5 | 36.99 | 73.82 | 117.22 |
| Potential changes between pCl 5–6 | 10.52 | 21.22 | 33.73 |
References
- Bobacka, J.; Ivaska, A.; Lewenstam, A. Potentiometric Ion Sensors. Chem. Rev. 2008, 108, 329–351. [Google Scholar] [CrossRef]
- Lewenstam, A.; Dołowy, K. Advances in Artificial and Biological Membranes: Mechanisms of Ionic Sensitivity, Ion-Sensor Designs, and Applications for Ion Measurement. Membranes 2020, 9, 427. [Google Scholar] [CrossRef]
- Huang, M.-R.; Li, X.-G. Highly sensing and transducing materials for potentiometric ion sensors with versatile applicability. Prog. Mater. Sci. 2022, 125, 100885. [Google Scholar] [CrossRef]
- Szyszkiewicz, K.; Jasielec, J.J.; Danielewski, M.; Lewenstam, A.; Filipek, R. Modeling of Electrodiffusion Processes from Nano to Macro Scale. J. Electrochem. Soc. 2017, 164, E3559–E3568. [Google Scholar] [CrossRef]
- Lindner, E.; Pendley, B.D. A tutorial on the application of ion-selective electrode potentiometry: An analytical method with unique qualities, unexplored opportunities and potential pitfalls. Anal. Chim. Acta 2013, 762, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Lewenstam, A. Routines and Challenges in Clinical Application of Electrochemical Ion-Sensors. Electroanalysis 2014, 26, 1171–1181. [Google Scholar] [CrossRef]
- Shao, Y.; Ying, Y.; Ping, J. Recent advances in solid-contact ion-selective electrodes: Functional materials, transduction mechanisms and development trends. Chem. Soc. Rev. 2020, 49, 4405–4465. [Google Scholar] [CrossRef]
- Cheong, Y.H.; Ge, L.; Lisak, G. Highly reproducible solid contact ion selective electrodes: Emerging opportunities for potentiometry—A review. Anal. Chim. Acta 2021, 1162, 338304. [Google Scholar] [CrossRef] [PubMed]
- Rousseau, C.R.; Bühlmann, P. Calibration-free potentiometric sensing with solid-contact ion-selective electrodes. TrAC Trends Anal. Chem. 2021, 140, 116277. [Google Scholar] [CrossRef]
- Paczosa-Bator, B. Ion-selective electrodes with superhydrophobic polymer/carbon nanocomposites as solid contact. Carbon 2015, 95, 879–887. [Google Scholar] [CrossRef]
- Ocaña, C.; Muñoz-Correas, M.; Abramova, N.; Bratov, A. Comparison of Different Commercial Conducting Materials as Ion-to-Electron Transducer Layers in Low-Cost Selective Solid-Contact Electrodes. Sensors 2020, 20, 1348. [Google Scholar] [CrossRef]
- Jiang, C.; Yao, Y.; Cai, Y.; Ping, J. All-solid-state potentiometric sensor using single-walled carbon nanohorns as transducer. Sens. Actuators B Chem. 2019, 283, 284–289. [Google Scholar] [CrossRef]
- Ding, J.; Qin, W. Recent advances in potentiometric biosensors. TrAC Trends Anal. Chem. 2020, 124, 115803. [Google Scholar] [CrossRef]
- Lyu, Y.; Gan, S.; Bao, Y.; Zhong, L.; Xu, J.; Wang, W.; Liu, Z.; Ma, Y.; Yang, G.; Niu, L. Solid-Contact Ion-Selective Electrodes: Response Mechanisms, Transducer Materials and Wearable Sensors. Membranes 2020, 10, 128. [Google Scholar] [CrossRef]
- Maksymiuk, K.; Stelmach, E.; Michalska, A. Unintended Changes of Ion-Selective Membranes Composition—Origin and Effect on Analytical Performance. Membranes 2020, 10, 266. [Google Scholar] [CrossRef] [PubMed]
- Dybko, A. Errors in Chemical Sensor Measurements. Sensors 2001, 1, 29–37. [Google Scholar] [CrossRef]
- Stepak, R. Application of cells connected in series as a means to enhance the sensitivity of potentiometric analysis. Z. Anal. Chem. 1983, 315, 629–630. [Google Scholar] [CrossRef]
- Zdrachek, E.; Bakker, E. Potentiometric Sensor Array with Multi-Nernstian Slope. Anal. Chem. 2020, 92, 2926–2930. [Google Scholar] [CrossRef] [PubMed]
- Parczewski, A.; Stepak, R. Random error in the CCS (cells connected in series) potentiometric method. Z. Anal. Chem. 1983, 316, 29–31. [Google Scholar] [CrossRef]
- Stepak, R. Comparison of the potentiometric determination of copper with the CCS and SC methods. Z. Anal. Chem. 1987, 328, 268. [Google Scholar] [CrossRef]
- Blaz, T.; Bas, B.; Kupis, J.; Migdalski, J.; Lewenstam, A. Multielectrode potentiometry in a one-drop sample. Electrochem. Commun. 2013, 34, 181–184. [Google Scholar] [CrossRef]
- Bartoszewicz, B.; Dabrowska, S.; Lewenstam, A.; Migdalski, J. Calibration free solid contact electrodes with two PVC based membranes. Sens. Actuators B Chem. 2018, 274, 268–273. [Google Scholar] [CrossRef]
- Parrilla, M.; Cuartero, M.; Crespo, G.A. Wearable potentiometric ion sensors. Trends Anal. Chem. 2019, 110, 303–320. [Google Scholar] [CrossRef]
- Wang, S.; Liu, M.; Shi, Y.; Yang, X.; Li, L.; Lu, O.; Zheng, H.; Feng, S.; Bai, Y.; Zhang, T. Vertically aligned conductive metal-organic framework nanowires array composite fiber as efficient solid-contact for wearable potentiometric sweat sensing. Sens. Actuators B Chem. 2022, 369, 132290. [Google Scholar] [CrossRef]
- Dunn, J.; Kidzinski, L.; Runge, R.; Witt, D.; Hicks, J.L.; Schüssler-Fiorenza Rose, S.M.; Li, X.; Bahami, A.; Delp, S.L.; Hastie, T.; et al. Wearable sensors enable personalized predictions of clinical laboratory measurements. Nat. Med. 2021, 27, 1105–1112. [Google Scholar] [CrossRef] [PubMed]
- Lim, H.-R.; Lee, S.M.; Park, S.; Choi, C.; Kim, H.; Kim, J.; Mahmood, M.; Lee, Y.; Kim, J.-H.; Yeo, W.-H. Smart bioelectronic pacifier for real-time continuous monitoring of salivary electrolytes. Biosens. Bioelectron. 2022, 210, 114. [Google Scholar] [CrossRef] [PubMed]
- Tan, Z.-B.; Wang, L.-Y.; Wang, H. Signal averaging for noise reduction in anesthesia monitoring and control with communication channels. J. Biomed. Sci. Eng. 2009, 2, 564–573. [Google Scholar] [CrossRef][Green Version]
- Hassan, U.; Anwar, M.S. Reducing noise by repetition: Introduction to signal averaging. Eur. J. Phys. 2010, 31, 453–465. [Google Scholar] [CrossRef]

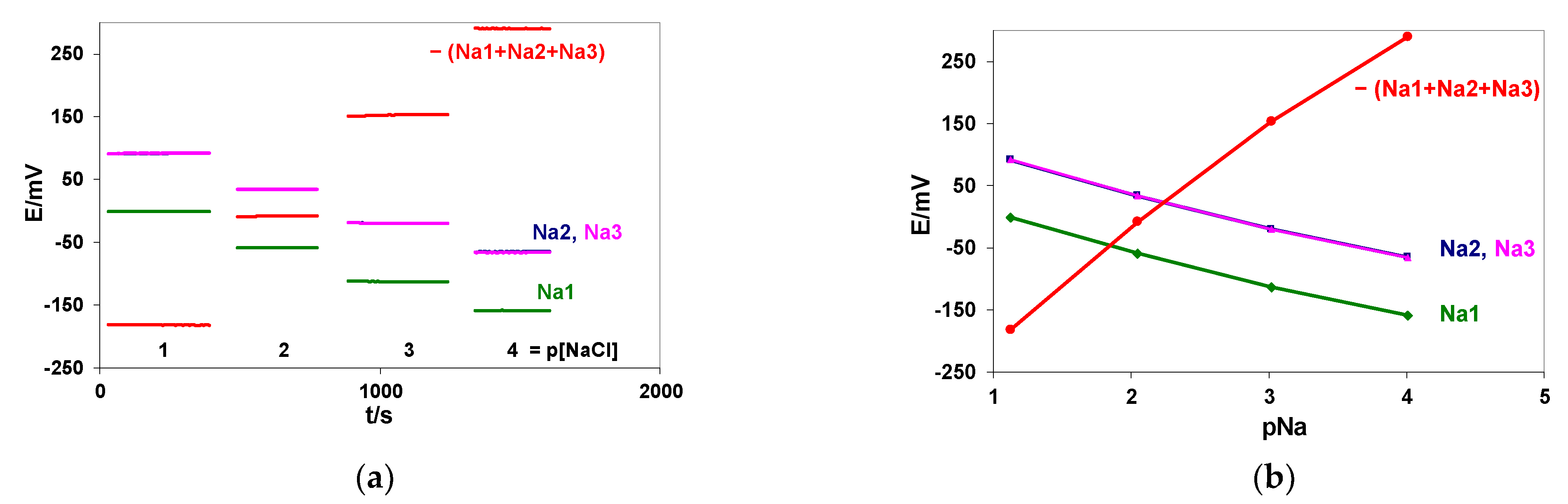


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Migdalski, J.; Lewenstam, A. Electrically Enhanced Sensitivity (EES) of Ion-Selective Membrane Electrodes and Membrane-Based Ion Sensors. Membranes 2022, 12, 763. https://doi.org/10.3390/membranes12080763
Migdalski J, Lewenstam A. Electrically Enhanced Sensitivity (EES) of Ion-Selective Membrane Electrodes and Membrane-Based Ion Sensors. Membranes. 2022; 12(8):763. https://doi.org/10.3390/membranes12080763
Chicago/Turabian StyleMigdalski, Jan, and Andrzej Lewenstam. 2022. "Electrically Enhanced Sensitivity (EES) of Ion-Selective Membrane Electrodes and Membrane-Based Ion Sensors" Membranes 12, no. 8: 763. https://doi.org/10.3390/membranes12080763
APA StyleMigdalski, J., & Lewenstam, A. (2022). Electrically Enhanced Sensitivity (EES) of Ion-Selective Membrane Electrodes and Membrane-Based Ion Sensors. Membranes, 12(8), 763. https://doi.org/10.3390/membranes12080763