Calculation of Lipophilicity of Organophosphate Pesticides Using Density Functional Theory
Abstract
:1. Introduction
2. Computational Details
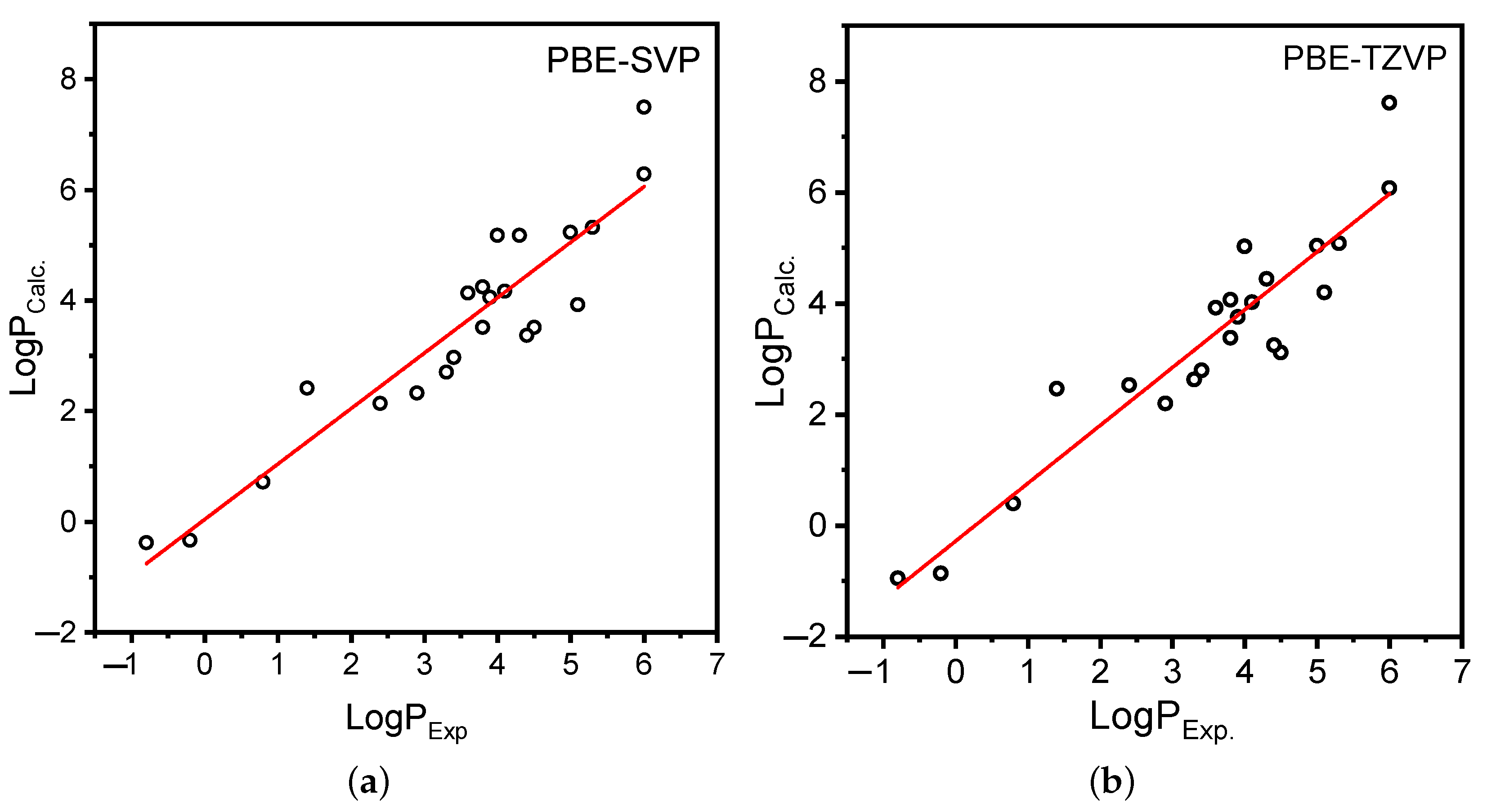
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Z. Modeling pesticide residues in nectar and pollen in support of pesticide exposure assessment for honeybees: A generic modeling approach. Ecotoxicol. Environ. Saf. 2022, 236, 113507. [Google Scholar] [CrossRef] [PubMed]
- Swale, D.R. Perspectives on new strategies for the identification and development of insecticide targets. Pestic. Biochem. Physiol. 2019, 161, 23–32. [Google Scholar] [CrossRef] [PubMed]
- Kaushal, J.; Khatri, M.; Arya, S.K. A treatise on Organophosphate pesticide pollution: Current strategies and advancements in their environmental degradation and elimination. Ecotoxicol. Environ. Saf. 2021, 207, 111483. [Google Scholar] [CrossRef] [PubMed]
- Golubev, V.N. Mechanisms of interaction of pesticides with the lipid bilayer in cell membranes. Russ. Chem. Rev. 1993, 62, 683–691. [Google Scholar] [CrossRef]
- Karami-Mohajeri, S.; Abdollahi, M. Toxic influence of organophosphate, carbamate, and organochlorine pesticides on cellular metabolism of lipids, proteins, and carbohydrates: A systematic review. Hum. Exp. Toxicol. 2011, 30, 1119–1140. [Google Scholar] [CrossRef]
- Eddleston, M. Novel Clinical Toxicology and Pharmacology of Organophosphorus Insecticide Self-Poisoning. Annu. Rev. Pharmacol. Toxicol. 2019, 59, 341–360. [Google Scholar] [CrossRef] [Green Version]
- Costa, L.G.; Giordano, G.; Guizzetti, M.; Vitalone, A. Neurotoxicity of pesticides: A brief review. Front. Biosci. 2008, 13, 1240–1249. [Google Scholar] [CrossRef] [Green Version]
- Mukherjee, S.; Gupta, R.D. Organophosphorus Nerve Agents: Types, Toxicity, and Treatments. J. Toxicol. 2020, 2020, 3007984. [Google Scholar] [CrossRef]
- Gilbert, E.P.K.; Edwin, L. A Review on Prediction Models for Pesticide Use, Transmission, and Its Impacts. Rev. Environ. Contam. Toxicol. 2021, 257, 37–68. [Google Scholar] [CrossRef]
- Madariaga-Mazón, A.; Osnaya-Hernández, A.; Chávez-Gómez, A.; García-Ramos, J.C.; Cortés-Guzmán, F.; Castillo-Pazos, D.J.; Martínez-Mayorga, K. Distribution of toxicity values across different species and modes of action of pesticides from PESTIMEP and PPDB databases. Toxicol. Res. 2019, 8, 146–156. [Google Scholar] [CrossRef] [Green Version]
- Hamadache, M.; Benkortbi, O.; Hanini, S.; Amrane, A.; Khaouane, L.; Si Moussa, C. A Quantitative Structure Activity Relationship for acute oral toxicity of pesticides on rats: Validation, domain of application and prediction. J. Hazard. Mater. 2016, 303, 28–40. [Google Scholar] [CrossRef] [PubMed]
- Winiwarter, S.; Ridderström, M.; Ungell, A.L.; Andersson, T.; Zamora, I. 5.22—Use of Molecular Descriptors for Absorption, Distribution, Metabolism, and Excretion Predictions. In Comprehensive Medicinal Chemistry II; Taylor, J.B., Triggle, D.J., Eds.; Elsevier: Oxford, UK, 2007; pp. 531–554. [Google Scholar] [CrossRef]
- Turek, M.; Pawłowska, B.; Różycka-Sokołowska, E.; Biczak, R.; Skalik, J.; Owsianik, K.; Marciniak, B.; Bałczewski, P. Ecotoxicity of ammonium chlorophenoxyacetate derivatives towards aquatic organisms: Unexpected enhanced toxicity upon oxygen by sulfur replacement. J. Hazard. Mater. 2020, 382, 121086. [Google Scholar] [CrossRef] [PubMed]
- Chmiel, T.; Mieszkowska, A.; Kempińska-Kupczyk, D.; Kot-Wasik, A.; Namieśnik, J.; Mazerska, Z. The impact of lipophilicity on environmental processes, drug delivery and bioavailability of food components. Microchem. J. 2019, 146, 393–406. [Google Scholar] [CrossRef]
- Duarte, I.A.; Fick, J.; Cabral, H.N.; Fonseca, V.F. Bioconcentration of neuroactive pharmaceuticals in fish: Relation to lipophilicity, experimental design and toxicity in the aquatic environment. Sci. Total Environ. 2022, 812, 152543. [Google Scholar] [CrossRef]
- Bora, A.; Crisan, L.; Borota, A.; Funar-Timofei, S.; Ilia, G. Ecotoxicological QSAR Modeling of Organophosphorus and Neonicotinoid Pesticides. In Methods in Pharmacology and Toxicology; Springer: New York, NY, USA, 2020; pp. 513–544. [Google Scholar] [CrossRef]
- Leo, A.; Hansch, C.; Elkins, D. Partition Coefficients and Their Uses. Chem. Rev. 1971, 71, 525–616. [Google Scholar] [CrossRef]
- Dinten, O.; Spichiger, U.E.; Chaniotakis, N.; Gehrig, P.; Rusterholz, B.; Morf, W.E.; Simon, W. Lifetime of Neutral-Carrier-Based Liquid Membranes in Aqueous Samples and Blood and the Lipophilicity of Membrane Components. Anal. Chem. 1991, 63, 596–603. [Google Scholar] [CrossRef]
- Mikhelson, K.N. Ion-Selective Electrodes (The Lecture Notes in Chemistry, V. 81); Springer: London, UK, 2013; p. 162. [Google Scholar] [CrossRef]
- Anarakdim, K.; Gutiérrez, G.; Cambiella, Á.; Senhadji-Kebiche, O.; Matos, M. The Effect of Emulsifiers on the Emulsion Stability and Extraction Efficiency of Cr(VI) Using Emulsion Liquid Membranes (ELMs) Formulated with a Green Solvent. Membranes 2020, 10, 76. [Google Scholar] [CrossRef] [Green Version]
- Vlahovic, F.; Ivanovic, S.; Zlatar, M.; Gruden, M. Density functional theory calculation of lipophilicity for organophosphate type pesticides. J. Serbian Chem. Soc. 2017, 82, 1369–1378. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Tirado-Rives, J.; Jorgensen, W.L. Performance of B3LYP Density Functional Methods for a Large Set of Organic Molecules. J. Chem. Theory Comput. 2008, 4, 297–306. [Google Scholar] [CrossRef]
- Hellweg, A.; Rappoport, D. Development of new auxiliary basis functions of the Karlsruhe segmented contracted basis sets including diffuse basis functions (def2-SVPD, def2-TZVPPD, and def2-QVPPD) for RI-MP2 and RI-CC calculations. Phys. Chem. Chem. Phys. 2015, 17, 1010–1017. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Brandenburg, J.G.; Bannwarth, C.; Hansen, A. Consistent structures and interactions by density functional theory with small atomic orbital basis sets. J. Chem. Phys. 2015, 143, 054107. [Google Scholar] [CrossRef] [PubMed]
- Brandenburg, J.G.; Bannwarth, C.; Hansen, A.; Grimme, S. B97-3c: A revised low-cost variant of the B97-D density functional method. J. Chem. Phys. 2018, 148, 064104. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system, version 4.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA quantum chemistry program package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system—Version 5.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2022, e1606. [Google Scholar] [CrossRef]
- Wolfram Research, Inc. Mathematica, Version 13.0.1.0; Wolfram Research, Inc.: Champaign, IL, USA, 2021. [Google Scholar]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [Green Version]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Martin, Y.C. Exploring QSAR Fundamentals and Applications in Chemistry and Biology, Volume 1. Hydrophobic, Electronic and Steric Constants, Volume 2. J. Med. Chem. 1996, 39, 1189–1190, Erratum in J. Med. Chem. 1996, 39, 1189–1190. [Google Scholar] [CrossRef]
- Sangster, J. Octanol-Water Partition Coefficients of Simple Organic Compounds. J. Phys. Chem. Ref. Data 1989, 18, 1111–1229. [Google Scholar] [CrossRef]
- Garten, C.T.; Trabalka, J.R. Evaluation of models for predicting terrestrial food chain behavior of xenobiotics. Environ. Sci. Technol. 1983, 17, 590–595. [Google Scholar] [CrossRef] [PubMed]
- Bowman, B.; Sans, W. Determination of octanol-water partitioning coefficients (KOW) of 61 organophosphorus and carbamate insecticides and their relationship to respective water solubility (S) values. J. Environ. Sci. Health Part B 1983, 18, 667–683. [Google Scholar] [CrossRef]

| No. | Organophosphate | B3LYP-SVP | PBE-SVP | PBE-TZVP | B3LYP-TZVP | PBEh-3c | B97-3c | PBE0-SVP | PBE0-TZVP | LogP | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Acephate | −0.73 | −0.38 | −0.95 | −0.97 | −1.10 | −1.10 | −0.80 | −1.24 | −0.80 | [21,35] |
| 2 | Aspon | 7.44 | 7.49 | 7.60 | 7.24 | 7.19 | 7.47 | 7.27 | 7.30 | 6.00 | [21,35] |
| 3 | Carbophenothion | 5.23 | 5.32 | 5.08 | 4.90 | 4.89 | 4.88 | 5.05 | 4.90 | 5.30 | [21,35] |
| 4 | Chlorpyrifos | 5.45 | 5.23 | 5.04 | 4.61 | 4.82 | 4.88 | 5.28 | 4.84 | 5.00 | [21,36] |
| 5 | Coumaphos | 3.30 | 3.52 | 3.12 | 2.88 | 3.11 | 2.86 | 3.25 | 3.06 | 4.50 | [21,37] |
| 6 | Crufomate | 2.31 | 2.97 | 2.79 | 2.58 | 2.42 | 2.56 | 2.70 | 2.60 | 3.40 | [21,35] |
| 7 | Diazinon | 4.19 | 4.25 | 4.06 | 3.97 | 3.92 | 3.90 | 4.08 | 4.02 | 3.80 | [21,35] |
| 8 | Dichlorvos | 2.16 | 2.41 | 2.47 | 2.26 | 2.07 | 2.30 | 2.16 | 2.33 | 1.40 | [21,35] |
| 9 | Dimethoate | 0.38 | 0.71 | 0.39 | 0.13 | 0.10 | 0.13 | 0.20 | 0.12 | 0.80 | [21,35] |
| 10 | Dioxathion | 5.60 | 5.18 | 4.44 | 5.45 | 5.32 | 5.47 | 5.45 | 5.57 | 4.30 | [21,35] |
| 11 | Disulfoton | 4.97 | 5.17 | 5.02 | 4.80 | 4.78 | 4.85 | 4.88 | 4.97 | 4.00 | [21,35] |
| 12 | Ethion | 3.54 | 3.92 | 4.19 | 4.11 | 3.50 | 4.06 | 3.21 | 4.15 | 5.10 | [21,35] |
| 13 | Fenitrothion | 2.52 | 2.70 | 2.63 | 2.42 | 2.50 | 2.51 | 2.51 | 2.58 | 3.30 | [21,35] |
| 14 | Fenthion | 4.16 | 4.17 | 4.02 | 4.13 | 3.95 | 3.90 | 4.07 | 4.12 | 4.10 | [21,38] |
| 15 | Fonofos | 3.98 | 4.06 | 3.75 | 3.67 | 3.63 | 3.58 | 3.85 | 3.65 | 3.90 | [21,35] |
| 16 | Malathion | 1.89 | 2.14 | 2.53 | 2.22 | 1.83 | 2.35 | 2.23 | 2.12 | 2.40 | [21,35] |
| 17 | Methyl Parathion | 2.16 | 2.32 | 2.19 | 2.14 | 2.15 | 2.10 | 2.17 | 2.32 | 2.90 | [21,35] |
| 18 | Monocrotophos | −0.86 | −0.34 | −0.86 | −1.32 | −1.36 | −1.16 | −0.92 | −1.22 | −0.20 | [21,35] |
| 19 | Parathion | 3.20 | 3.52 | 3.38 | 3.18 | 3.38 | 3.13 | 3.26 | 3.35 | 3.80 | [21,35] |
| 20 | Phorate | 4.49 | 4.13 | 3.92 | 4.16 | 3.97 | 4.03 | 4.35 | 4.29 | 3.60 | [21,35] |
| 21 | Phosalone | 3.12 | 3.37 | 3.25 | 3.02 | 2.95 | 2.92 | 3.05 | 3.03 | 4.40 | [21,35] |
| 22 | Temephos | 5.94 | 6.28 | 6.07 | 5.88 | 5.76 | 5.74 | 5.91 | 5.91 | 6.00 | [21,35] |
| MFA | ME | MAD | MSE | MPE | MAPE | r | SLRL | PCC |
|---|---|---|---|---|---|---|---|---|
| B3LYP-SVP | −0.12 | 0.70 | 0.71 | 11 | 35.3 | 0.9148 | 1.054 | 0.8368 |
| PBE-SVP | 0.05 | 0.56 | 0.49 | 2.59 | 20.88 | 0.9315 | 1.002 | 0.8677 |
| PBE-TZVP | −0.13 | 0.55 | 0.51 | 13.45 | 32.47 | 0.9356 | 1.042 | 0.8754 |
| B3LYP-TZVP | −0.25 | 0.69 | 0.66 | 19.76 | 46.57 | 0.9257 | 1.058 | 0.8568 |
| PBEh-3c | −0.33 | 0.71 | 0.69 | 19.02 | 48.36 | 0.9286 | 1.064 | 0.8623 |
| B97-3c | −0.26 | 0.70 | 0.70 | 16.78 | 43.84 | 0.9213 | 1.057 | 0.8487 |
| PBE0-SVP | −0.17 | 0.66 | 0.68 | 11.19 | 35.84 | 0.9164 | 1.033 | 0.8397 |
| PBE0-TZVP | −0.19 | 0.68 | 0.65 | 20.79 | 45.69 | 0.9288 | 1.082 | 0.8627 |
| PBE/6-31 [21] | 0.48 | 0.6 | 0.58 | −5.66 | 33.83 | 0.9483 | 0.999 | 0.8993 |
| M062X/6-31 [21] | 0.08 | 0.45 | 0.27 | 14.48 | 28.12 | 0.962 | 1.022 | 0.9255 |
| M06L/6-31 [21] | 0.21 | 0.44 | 0.28 | −6.61 | 24.59 | 0.9631 | 0.971 | 0.9276 |
| No | Organophosphate | LogP | LogP | Ref. | ||
|---|---|---|---|---|---|---|
| 1 | Acephate | −60.27 | −58.11 | −0.38 | −0.80 | [21,35] |
| 2 | Aspon | −18.39 | −61.15 | 7.49 | 6.00 | [21,35] |
| 3 | Carbophenothion | −36.73 | −67.08 | 5.32 | 5.30 | [21,35] |
| 4 | Chlorpyrifos | −13.10 | −42.92 | 5.23 | 5.00 | [21,36] |
| 5 | Coumaphos | −49.89 | −69.94 | 3.52 | 4.50 | [21,37] |
| 6 | Crufomate | −44.09 | −61.05 | 2.97 | 3.40 | [21,35] |
| 7 | Diazinon | −25.48 | −49.70 | 4.25 | 3.80 | [21,35] |
| 8 | Dichlorvos | −16.70 | −30.45 | 2.41 | 1.40 | [21,35] |
| 9 | Dimethoate | −60.84 | −64.91 | 0.71 | 0.80 | [21,35] |
| 10 | Dioxathion | −47.37 | −76.90 | 5.18 | 4.30 | [21,35] |
| 11 | Disulfoton | −26.74 | −56.24 | 5.17 | 4.00 | [21,35] |
| 12 | Ethion | −45.09 | −67.44 | 3.92 | 5.10 | [21,35] |
| 13 | Fenitrothion | −25.87 | −41.28 | 2.70 | 3.30 | [21,35] |
| 14 | Fenthion | −23.46 | −47.25 | 4.17 | 4.10 | [21,38] |
| 15 | Fonofos | −37.40 | −60.55 | 4.06 | 3.90 | [21,35] |
| 16 | Malathion | −43.06 | −55.25 | 2.14 | 2.40 | [21,35] |
| 17 | Methyl Parathion | −25.70 | −38.94 | 2.32 | 2.90 | [21,35] |
| 18 | Monocrotophos | −62.72 | −60.78 | −0.34 | −0.20 | [21,35] |
| 19 | Parathion | −25.55 | −45.61 | 3.52 | 3.80 | [21,35] |
| 20 | Phorate | −26.15 | −49.70 | 4.13 | 3.60 | [21,35] |
| 21 | Phosalone | −48.89 | −68.13 | 3.37 | 4.40 | [21,35] |
| 22 | Temephos | −34.90 | −70.76 | 6.28 | 6.00 | [21,35] |
| Average Computing Resources | B3LYP-SVP | PBE-SVP | PBE-TZVP | B3LYP-TZVP | PBEh-3c | B97-3c | PBE0-SVP | PBE0-TZVP | PBE /6-31 | M062X /6-31 | M06L /6-31 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Days per Core CPU | 51 | 13.5 | 23 | 126 | 39.5 | 21.2 | 37 | 133 | - | - | - |
| Memory per Core CPU, Mb | <8000 | <20,000 | <20,000 | <8000 | <4000 | <4000 | <8000 | <8000 | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magomedov, K.E.; Zeynalov, R.Z.; Suleymanov, S.I.; Tataeva, S.D.; Magomedova, V.S. Calculation of Lipophilicity of Organophosphate Pesticides Using Density Functional Theory. Membranes 2022, 12, 632. https://doi.org/10.3390/membranes12060632
Magomedov KE, Zeynalov RZ, Suleymanov SI, Tataeva SD, Magomedova VS. Calculation of Lipophilicity of Organophosphate Pesticides Using Density Functional Theory. Membranes. 2022; 12(6):632. https://doi.org/10.3390/membranes12060632
Chicago/Turabian StyleMagomedov, Kurban E., Ruslan Z. Zeynalov, Sagim I. Suleymanov, Sarizhat D. Tataeva, and Viktoriya S. Magomedova. 2022. "Calculation of Lipophilicity of Organophosphate Pesticides Using Density Functional Theory" Membranes 12, no. 6: 632. https://doi.org/10.3390/membranes12060632
APA StyleMagomedov, K. E., Zeynalov, R. Z., Suleymanov, S. I., Tataeva, S. D., & Magomedova, V. S. (2022). Calculation of Lipophilicity of Organophosphate Pesticides Using Density Functional Theory. Membranes, 12(6), 632. https://doi.org/10.3390/membranes12060632







